A π-Type Memristor Synapse and Neuron With Structural Plasticity

A synaptic structure with memristor state initialization function and a neuronal circuit with structural variability are presented in this article. In contrast to the popular use of voltage as a medium for containing information and realizing the computational function of a neuron in the form of voltage–current–voltage, the proposed neuron circuit adopts current as a carrier of information; also the computation will be realized in the form of current–voltage instead. Since the sum of currents can be achieved by direct connection, this will greatly reduce the hardware area of the artificial neuron. In addition, by adjusting the switches, the initialization of the memristor can be implemented, and the process of structural changes of neurons in biology can also be mimicked. Comparing with several popular synaptic circuits, it is proven that the π-type synapse has more structural advantages. Simulations show that the π-type synaptic structure can obtain the specified weight value faster and complete the initial state setting of the memristors in 1.502 ms. Even in the worst case, where the weight needs to be changed from −1 to 1, it can be completed in only 1.272 ms. Under the condition of achieving the same function, the area of the proposed neuron with 100 synapses will be reduced by at least 97.42%. Moreover, there is better performance in terms of linearity.

Introduction

Synapses are abundant in the human brain which consists of approximately ${10}^{11}$ neurons with ${10}^{15}$ synapses [1], and they play a fundamental role in the human brain’s rapid processing. Each neuron contains thousands to tens of thousands of synapses to receive signals from higher-level neurons, and these signals are transmitted in complex networks comprising neurons that guide humans to perform a series of complex actions and other advanced behaviors. As a starting point, the biological structure of the human brain has been used to develop research on artificial neural networks [2], and due to the indispensability of synapses, the design of synaptic analog circuits to realize the function of artificial neural networks has always been a hot topic of research.

When information is transmitted in a neuron, the postsynaptic membrane will produce different degrees of physiological response depending on the number of neurotransmitters, which is always abstracted as the degree of involvement of each synapse in a practical circuit design, that is, the weight that each synapse occupies in the neuron and the storage of such non-volatile weights is often hosted by resistors, capacitors, or CMOS transistors. However, in the previous implemented circuits, the storage of weights in resistors cannot change with the network due to the fixed resistance value, and those stored by capacitors are subject to charge leakage as well. To represent a synapse through conventional CMOS circuits, approximately 10 transistors will be required, [3] which will be limited by the hardware size in the post-Moore era, making it difficult to carry out the demand for smaller size.

Since the concept of the memristor was proposed [4], it has attracted much attention in bio-synaptic implementation circuits due to its unique hysteresis curve characteristics, non-volatility of its resistive state and smaller size, and the good compatibility with conventional CMOS processes. Take the voltage-controlled memristor in [5] as an example; it is the first device with the function of the memristor whose resistance value will change accordingly by adjusting the voltage applied to both ends of the memristor, showing its potential as a malleable small-sized synapse. More memristor models have been proposed later, and they can be divided into flux-controlled [6, 7] and charge-controlled [8–10] memristors according to the factors which determine the memristance. Recently, some new models have been proposed, such as the discrete memristor [11]. Because of its unique nonlinearity, it has been widely used in chaotic circuits [12, 13]. Using the hysteresis characteristics of the memristor, it can also be used to connect [14] and construct neurons [15–20]. As the production process of memristors becomes more and more mature, they are now widely used in the fields of intelligent bionics, human–computer interaction, and neural network computing, etc. [21–25].

The application of memristors in artificial neurons has become very general. Several common circuits [26] that used memristors to achieve synaptic function either did not achieve the full range of weights, such as positive, negative, and 0 for they used memristance as weight [15, 20, 27], or the change of weight was in a nonlinear form [15, 20, 28] or the weight symbol needed to be set additionally [20]; even the most commonly used memristor bridge circuit, called 4M structure [23, 29], did not take it into account that it is not enough to simply indicate the initial state of the memristor since memristors are generally manufactured in a high-resistance state from the factory. The 4M circuit structure did not involve the problem of setting the initial state value of the memristor. In addition, none of the abovementioned existing structures have been designed for this phenomenon, which is, in the developing process of the actual living organism; synapses will have fresh growth and fading, and that will result in the change of the neuronal structure. Although the 2M structure and with dual input modes [18, 30] in recent years are improved compared with those mentioned above, they still do not have any advantage in the area due to the existence of resistances.

Changes in the structure of a single neuron and in the connection of multiple neurons can reflect the flexibility of the design, and there are many ways to realize the plasticity. The coupling channel between different neurons structured by Josephson junction is proven to be able to detect the synchronization between two neural circuits and speed up the calculation [31, 32]. Several combinations of capacitance, inductance, and resistance can constitute hybrid synapses [33–36]and effectively bridge the neural circuit, which regulates the synchronization of different neurons. Memristors can also be used as part of the coupling channel [14]. By selecting the composition of the coupling channel and adjusting the parameters, the neural circuit can be induced to transition from synchronization to non-synchronization. This process can also be seen as the plasticity of the circuit structure.

In this article, a new basic unit π-type structure of the synapse, and in addition to this, the artificial neuron unit composed of this synapse has been proposed. First of all, this structure can realize the basic functions of synapses, implying it can represent the full range of weights, namely, positive, negative, and zero. Second, the initial resistance states of the memristors can be adjusted by controlling the switches of the π-type basic unit; third, the structural plasticity of the neurons and the degradation and regeneration process of synapses that happen in actual neurons by controlling the working state of each basic unit are also simulated; at last, considering the large number of synapses on each neuron, when the π-structure synapses are used to build a complete neuron, the information contained in each synapse is aggregated in the form of current and then passed through the same conversion circuit that takes current into voltage, which has greatly reduced the area required to simulate neurons.

In the following article, Memristor Models introduced the basic principles of the memristor and ${\mathrm{TiO}}_2$ model that is the most commonly used. In π-Type Memristor Synapse and Neuron, the proposed $\pi$-structure synaptic basic unit and the neuron comprising it were elucidated. The superiority of the $\pi$-type synapse is demonstrated by comparing several synaptic circuits, and it has also been explained how to regulate the initial state of the memristors. Analysis and simulation results are written in Weight Setting of π-Structure and Simulations and Analysis, respectively. Conclusion summarized the full text.

Memristor Models

The memristor is proposed by Leon Chua as the fourth type of electronic devices and is defined as a certain connection between flux and charge [4]:

$M\left(q\right)=\frac{d\phi \left(t\right)}{dq\left(t\right)}=\frac{{\displaystyle {\int }_{-\infty }^{t}v\left(t\right)dt}}{{\displaystyle {\int }_{-\infty }^t\mathit{i}\left(t\right)dt}}=\frac{v\left(t\right)}{i\left(t\right)}.(1)$

HP Labs [5] reported that the metal–oxide–metal structure can be used as a mathematical model of the memristor and made electronic components with memristor characteristics successfully by using two layers of the $Ti{O}_2$ film. The so-called sandwich structure is illustrated in Figure 1. $Ti{O}_2$ and $Ti{O}_{2-x}$ correspond to the undoped area and the doped area, respectively, and owing to the lack of oxygen ions, the conductivity of $Ti{O}_{2-x}$ is much stronger than that of $Ti{O}_2$. When external excitation is applied to the Pt electrodes, the oxygen ions in $Ti{O}_{2-x}$ will drift under the influence of the electric field, which will modify the position of the boundary between $Ti{O}_2$ and $Ti{O}_{2-x}$, and will affect the resistance value as a result. When the oxides are completely covered by $Ti{O}_{2-x}$, the corresponding resistance is the minimum value $R_{on}$, and conversely, if the oxides are completely covered by $Ti{O}_2$, it corresponds to the high-resistance state $R_{off}$. Figure 1 shows the actual symbol of the memristor in circuit.

FIGURE 1

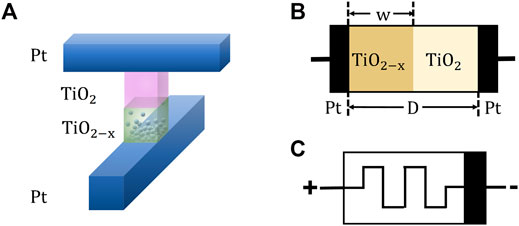
FIGURE 1. (A) Schematic diagram of the implementation of the HP model in physics. (B) Sandwich structure comprising $Ti{O}_{2-x}$ and ${\text{TiO}}_2$ layers and Pt. (C) Symbol of the memristor in circuit.

The resistance of the memristor can be expressed as follows:

$M\left(q\right)=R_{on}\frac{w\left(t\right)}{D}+R_{off}\left(1-\frac{w\left(t\right)}{D}\right).(2)$

And the v–i characteristics can be expressed as follows:

$v\left(t\right)=\left[R_{on}\frac{w\left(t\right)}{D}+R_{off}\left(1-\frac{w\left(t\right)}{D}\right)\right]i\left(t\right),(3)$

where $w\left(t\right)$ is the width of the doped area and $D$ is the thickness of the two layers of the $Ti{O}_2$ memristor. In this $Ti{O}_2$ model, the thickness of the doped region is affected by current $i$; so the relationship between the width $w$ and the current $\text{i}$ is given by

$\frac{dw\left(t\right)}{dt}={\mu }_v\frac{R_{on}}{D}i\left(t\right),(4)$

$w\left(t\right)={\mu }_v\frac{R_{on}}{D}q\left(t\right)+w_0,(5)$

where $w_0$ is the initial state of the memristor, $q\left(t\right)$ is the charge injected into the memristor during time $t,$ and ${\mu }_v$ is the dopant mobility. It should be noted that the amount of charge must be limited since the value of $w$ should be controlled within the range of [0, D], and the total charge required to switch from a low-resistance state to a high-resistance state is $Q=D^2/{\mu }_v{R}_{on}$.

The difference from the abovementioned fact is that it is believed that the boundary between the doped and undoped parts moves at a uniform speed in the linear drift model, but in fact, when $w$ approaches 0 and D, ions always tend to exhibit nonlinear migration, so the boundary between the two parts will move in a non-linear manner. Joglekar [37] proposed a window function to interpret this nonlinear drift phenomenon:

$F\left(x\right)=1-{\left(2x-1\right)}^{2p}.(6)$

The relationship between the width of the doped region $w$ and the current $i$ needs to be expressed as follows:

$\frac{dw\left(t\right)}{dt}={\mu }_v\frac{R_{on}}{D}i\left(t\right)F\left(x\right),(7)$

where $x$ is the location of the interface between $Ti{O}_2$ and $Ti{O}_{2-x}$, which can be expressed as $x=w/D$, and $P$ is restricted to a positive integer.

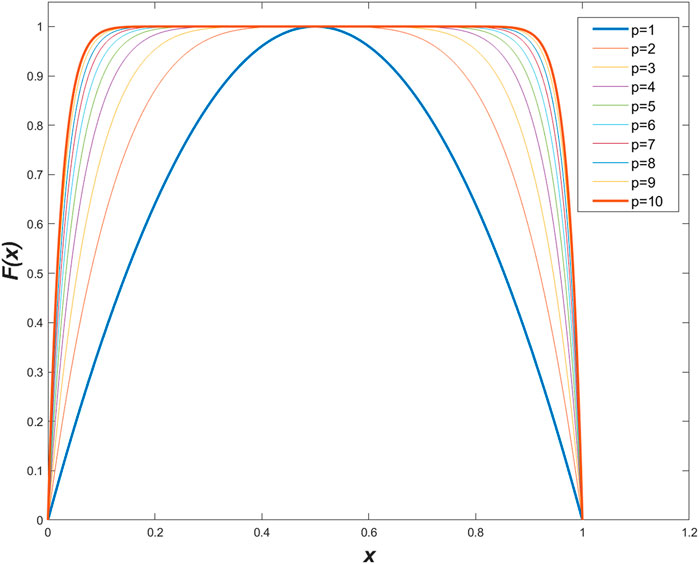
The curve of $F\left(x\right)$ can be represented as shown in Figure 2. The value of $F\left(x\right)$ also approaches 0 when $x$ approaches the boundary value on both sides, which means the movement of the interface between the doped and the undoped region will be restricted near the two ends of the memristor. The memristor model with window function is more consistent with the actual situation and increases authenticity.

FIGURE 2

FIGURE 2. Variation curve of window function $F\left(x\right)$ with $x$ for different values of $p$.

The influence of the direction of the connected memristor on its resistance when the memristor is input voltages in different directions is discussed as follows. The difference in the concentration of drifting oxygen ions at both ends of the memristor determines that the input of positive and negative excitations to the memristor will have different results.

It is stipulated that the doped end is the positive side of the memristor, and the non-doped end is the negative side, and it can be divided into the following four cases as shown in Table 1:

TABLE 1

TABLE 1. Influence of input direction and voltage polarity on memristance.

Case 1. When a positive voltage is connected to the positive terminal of the memristor, the interface between the doped region and undoped of memristor will float along the direction of the voltage decrease, which will cause the width of the doped region to increase and the memristance to decrease. The memristor at this time is connected in the forward direction.

Case 2. When a negative voltage is connected to the positive electrode of the memristor, the voltage tends to cause the interface to float toward the positive electrode of the memristor, and the width will decrease, which will cause the memristance value to increase.

In the same way, from case 3 and case 4, it can be known that when the voltage is input from the negative terminal of the memristor, the positive and negative voltages will increase and decrease the resistance of the memristor, respectively.

The memristance curves of the four cases are shown in Figure 3. It should be noted that the minimum value of the resistance of the memristor needs to be controlled and the maximum value needs to be $R_{off}$. If the initial value of the memristor is $R_{on}$, the memristive value under the conditions of Figures 3A–C will no longer reduce, and the resistance value will remain at $R_{on}$. Similarly, if the initial value is $R_{off}$, the memristance will not increase any more under the conditions shown in Figures 3B–D, and the resistance value will remain at $R_{off}$.

FIGURE 3

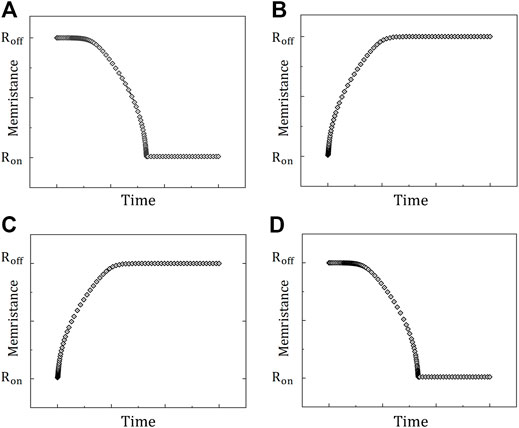
FIGURE 3. Influence of the memristor access direction and excitation direction to memristance. (A) Memristor is positively connected and positive excitation is applied (B) Memristor is positively connected and negative excitation is applied. When the memristor is connected in reverse, (C) applying a forward excitation to the memristor will increase the resistance, and (D) a reverse excitation will reduce the resistance.

π-Type Memristor Synapse and Neuron

$\pi$-Type Memristor Synapse

The proposed basic unit of the synaptic circuit based on the memristor is shown in Figure 4. It consists of five flux-controlled memristors and three switches, in which $M_1, M_2, M_3$ play the role of a voltage divider, and the two node voltages generate different currents through $M_4$ and $M_5$ with different resistance values, from where the proportional relationship between the input voltage and the difference between two currents can be obtained. Through $M_{01}$ and $M_{02}$, the currents will be expressed in the form of voltage according to Ohm’s law. The π-structure comprising five memristors can play the role of synapses and express the weight of positive, negative, and zero.

FIGURE 4

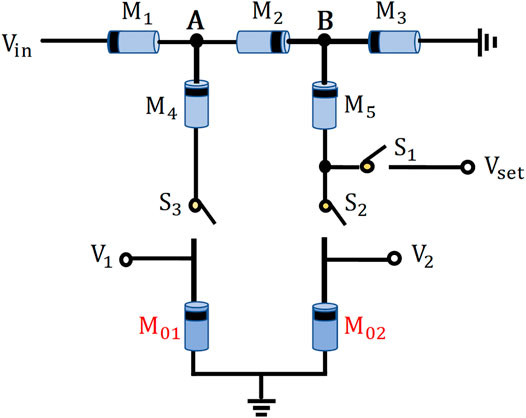
FIGURE 4. Proposed $\pi$-structure memristor synapse. It is divided into a basic repeatable unit and two additional memristors, where the repeatable unit forms two currents of different sizes by dividing the voltage and passing through memristors of different values, and the two additional memristors convert the current signal into voltage.

Initialization State Setting

Part of the existing synaptic circuits based on memristors [19, 20]only specified the initial status of memristors and did not explain how to complete the initial resistance setting in their actual circuits, without considering that memristors are often in a high-impedance state when they are manufactured. The method to set the initial states in our synaptic circuit based on the memristor is proposed, as shown in Figure 5.

FIGURE 5

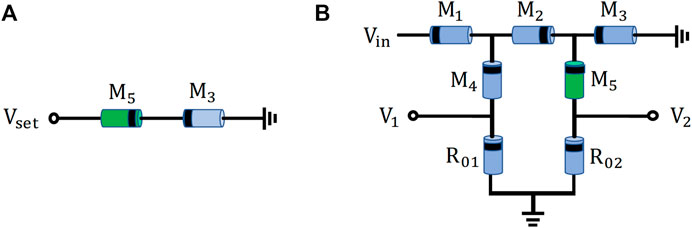
FIGURE 5. Method of initializing the memristors. (A) Positive excitation initialization signal is input and passes only through $M_5$ and $M_3$ due to $S_2$ and $S_3$ break. Since $M_5$ is positively connected, the resistance is reduced until it becomes state 1. (B) After the initialization is complete, $M_5$ will be normally accessed into the circuit for work.

$V_{set}$ is an initialization pulse signal for adjusting the state of $M_5$. $S_1$ is responsible for controlling whether to initialize the $M_5$ and $S_2$ and $S_3$ are responsible for explaining whether this synaptic unit functions in the neuron. We stipulate that $V_{set}$ is a positive voltage greater than the threshold voltage of the memristor. $S_1$ is active at the high level, while $S_2$ and $S_3$ are active at the low level. Figure 5 shows that when we initialize the memristive value, $S_1$ is closed, while $S_{\mathrm{2,3}}$ are disconnected, and $M_5$ is connected in the forward direction, so the boundary between $Ti{O}_2$ and $Ti{O}_{2-x}$ will move in the direction of the voltage drop, which will result in the resistance of $M_5$ being dropped until it reaches $R_{on}$ and not changing any more. Because $M_3$ is in the opposite connection, its resistance value will always remain at $R_{off}$ according to Figure 3, and the disconnection of $S_2$ and $S_3$ can ensure that the process of initializing $M_5$ will not affect the states of memristors that constitute other synapses in the neuron. The initialization will be completed when $S_1$ is disconnected and $S_{\mathrm{2,3}}$ are closed.

During the growth of neurons, new synapses often appear, and a part of them is also pruned, and this variability is called structural plasticity, whereas in the previously proposed analog synaptic circuits, only the weights occupied by the synapses can be changed, but not the structure because of their fixity. The $\pi$-type basic unit can compensate for this regret by simultaneously closing $S_2$ and $S_3$ so that the unit can enter the operating state, and on the contrary, the basic unit is pruned when $S_2$ and $S_3$ are simultaneously disconnected.

Weight Setting

The states of the memristors after the initial setup are set as $M_1=M_2=M_3=M_4=R_{off}$, $M_5=R_{on}$. At this time, $S_1$ is disconnected, and $S_2$ and ${\text{S}}_3$ are always closed. The circuit is shown in Figure 5B. When there is a strong pulse signal input $V_{in}\left(t\right)$, the resistance values will be changed according to their own polarity, which will result in the change in current.

The resistances between the node A and ground and between node B and ground can be expressed as follows:

$M_4^{\text{'}}=M_4+M_{01},(10)$

$M_5^{\text{'}}=M_5+M_{02},(11)$

$M_A=\left(M_2+M_3\parallel M_5^{\prime }\right)\parallel M_4^{\prime },(12)$

$M_B=M_3\parallel M_5^{\prime }.(13)$

The total resistance of one synapse can be expressed as follows:

$M_{total}=M_1+\left(M_2+M_3\parallel M_5^{\text{'}}\right)\parallel M_4^{\text{'}}.(14)$

Suppose there is an input voltage $v_{in}$ at time $t$, according to the voltage divider formula, the two node voltages $v_A$ and $v_B$ can be written as follows:

$v_A=\frac{M_A}{M_A+M_1}{v}_{in},(15)$

$v_B=\frac{M_B}{M_2+M_B}{v}_A.(16)$

The currents passing through the branches where $M_4^{\text{'}}$ and $M_5^{\text{'}}$ are located are follows:

$i_4=\frac{v_A}{M_4^{\text{'}}}=\frac{M_A}{\left(M_A+M_1\right)M_4^{\text{'}}}{v}_{in},(17)$

$i_5=\frac{v_B}{M_5^{\text{'}}}=\frac{M_B}{M_2+M_B}\ast \frac{M_A}{M_A+M_1}\ast \frac{1}{M_5^{\text{'}}}{v}_{in},(18)$

$i_5-i_4=\left(\frac{M_A{M}_B}{(M_2+M_B)(M_A+M_1)M_5^{\text{'}}}-\frac{M_A}{(M_A+M_1)M_4^{\text{'}}}\right)v_{in}.(19)$

Using two transistors can convert the current signal into voltage, and the output voltage $v_{out}$ is equal to the difference between ${\text{v}}_1$ and ${\text{v}}_2$:

$v_{out}=v_2-v_1=M_{02}{i}_5-M_{01}{i}_4$

$=\left(\frac{M_A{M}_B{M}_{02}}{\left(M_2+M_B\right)\left(M_A+M_1\right)M_5^{\text{'}}}-\frac{M_A{M}_{01}}{\left(M_A+M_1\right)M_4^{\text{'}}}\right)v_{in}.(20)$

This formula can be interpreted as the relationship between a synaptic input ${\text{v}}_{\text{in}}$ and a synaptic weight $\text{W}$, and it can be rewritten as follows:

$v_{out}=W\times v_{in},(21)$

$W=\frac{M_A{M}_B{M}_{02}}{\left(M_2+M_B\right)\left(M_A+M_1\right)M_5^{\text{'}}}-\frac{M_A{M}_{01}}{\left(M_A+M_1\right)M_4^{\text{'}}}.(22)$

The abovementioned equations can be considered a weighting operation of every $\pi$-structure synapse in a neuron. The current flowing on both branches in [29] is the same, for that the total resistance of each branch is fixed as $R_{in}+R_{off}$, which determines that there is no way for the 4M structure [23, 29] but can only obtain the weights of the synapses by detecting the potential at the middle point of the two memristors and evaluating the difference between them. However, the voltages cannot add up in a straightforward way like the currents; so each synaptic basic unit of the 4M structure has to include two CMOS tubes to convert the voltage signal into a current signal, which to a large extent will take up a considerable part of the area. Also, the differential structure can help reduce the influence of noise and improve robustness.

The current memristor-based synapses can be classified according to the number of memristors into 1M [15, 16], 2M [17, 18], 4M [19], and 5M [20]. Table 2 lists the following points: The components of the synapse, the range of weights that can be expressed, whether it is necessary to set the weight symbols in advance, the performance of linearity, and whether it has the initialization function of the memristor. It intuitively demonstrated the superiority of the $\pi$-type synapse.

TABLE 2

TABLE 2. Comparison of the characteristics of several common memristor synapses.

Artificial Neuron Structure Based on the Proposed Synapse

In the actual biological nervous system, the network-like information interactions will be completed in the form of which neurons collect and process different information collected by each synapse, and then they transmit the processed signals to the neurons of the next layer. A neuron structure based on this synaptic structure is further designed, which can realize the transmission of information in the form of electric current in the neuron so that it will eliminate the traditional cumbersome steps when building a large neural network and save a lot of area. The complete circuit of the multi-input memristor neuron comprising the $\pi$-type synapse circuit is shown in Figure 6.

FIGURE 6

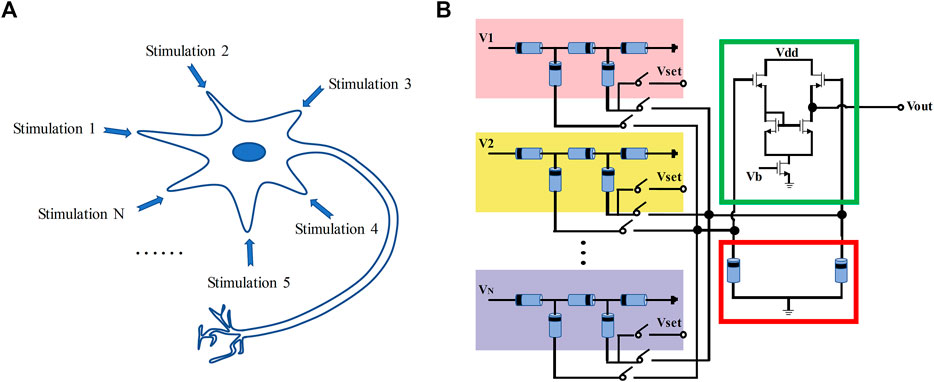
FIGURE 6. Comparison of neuronal biological schematics with the proposed neuron structure. (A) Neuronal biological schematics. (B) Structural diagram of a neuronal circuit composed of the $\pi$-type synaptic structure.

$V_1$ to $V_N$ are the input signals received by the synapses, and $V_{out}$ is the output signal transmitted from the neuron to the next neuron. Each current passing through $M_{4N}$ is brought together by direct connection, and all signals through $M_{5N}$ are similarly aggregated in the same way. These two signals are converted into voltage signals by two additional memristors in the red frame, and the subtraction function is implemented with two pmos and three nmos in the green frame. That is, both additional memristors and the subtractive circuit are shared by all the basic units in operation; so whenever a neuron needs to access an additional synapse, only five more memristors need to be added, which means it is an advantage that makes the proposed structure more power-efficient and smaller in area when more messages need to be received. Different from [31–36], the structural plasticity of neurons is realized by controlling the state of the switches with the clock signal and the degree of connection between different neurons through the memristors. It is more reliable and easier to operate by controlling the physical connection of the circuit.

Weight Setting of π-Structure

As the input signal for setting weight of the $\text{π}$-structure is a positive pulse with a sufficiently wide pulse width, the memristance of ${\text{M}}_2$ decreases and ${\text{M}}_5$ increases, which will change the currents of the branch where ${\text{M}}_4$ and ${\text{M}}_5$ are located. It can lead to the result that the branch current difference will have three cases as follows: positive, negative, and 0. According to (22), when a positive weight is needed, the condition that needs to be met should be as follows:

$\frac{M_A{M}_B{M}_{02}}{\left(M_2+M_B\right)\left(M_A+M_1\right)M_5^{\text{'}}}-\frac{M_A{M}_{01}}{\left(M_A+M_1\right)M_4^{\text{'}}}>0$

$\frac{M_A{M}_B{M}_{02}}{\left(M_2+M_B\right)\left(M_A+M_1\right)M_5^{\text{'}}}>\frac{M_A{M}_{01}}{\left(M_A+M_1\right)M_4^{\text{'}}}$

$\frac{M_B{M}_{02}}{\left(M_2+M_B\right)M_5^{\text{'}}}>\frac{M_{01}}{M_4^{\text{'}}}.(23)$

Similarly, when negative and zero weights are required, the conditions should be satisfied as follows:

Negative weight:

$\frac{M_B{M}_{02}}{\left(M_2+M_B\right)M_5^{\text{'}}}<\frac{M_{01}}{M_4^{\text{'}}}.(24)$

Zero weight:

$\frac{M_B{M}_{02}}{\left(M_2+M_B\right)M_5^{\text{'}}}=\frac{M_{01}}{M_4^{\text{'}}}.(25)$

It is essential to be note here that the pulse width of the setting signal must be wide enough to bring about a change in the memristor value, as opposed to the need to keep the pulse width of the input signal within a small range when calculating with the given weights, which can avoid the change of the memristors.

Simulations and Analysis

Simulations were all performed in the MATLAB R2020a environment and based on the $Ti{O}_2$ model for the memristor. A series of physical models have been created in Simulink with Simscape, including the Simscape model of the memristor, and the proposed neuron is described through the physical connection between the models. $R_{on}$ was set as $100\text{Ω}$, and there are several different chosen values for $R_{off}$: $M_1=M_3=M_5=10K\Omega$, ${\text{M}}_2=13\text{KΩ},$ ${\text{M}}_4=16\text{KΩ}.$ The remaining parameters are set as follows: $D=10nm$, ${\mu }_v={10}^{-14}{m}^2{V}^{-1}{S}^{-1}$, and $p=7$.Validation for the initialization function and weight setting is included in the following simulations, and the feasibility of forming a neuron from this synaptic structure was determined. The degree of memristor nonlinearity in relation to the initialization and weight setting was also analyzed. The amplitude of input signals with variable width for both the initialization process and the weight setting process was fixed at 1V. Since the hysteresis loop of the memristor will shrink into a single-valued function when the external excitation frequency becomes larger [38], in order to maintain the state of the memristor during the calculation, the frequency of the input pulse needs to be adjusted higher.

Initial State Setting of the Memristor

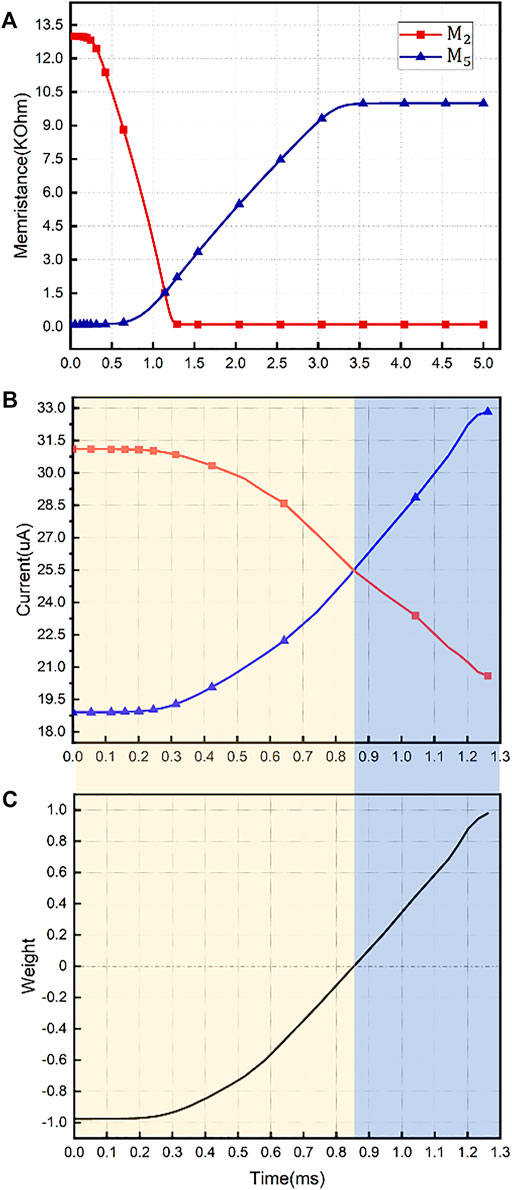
Considering that the freshly shipped memristors generally present a high-resistance state, we simulated the setting of the memristor state to the desired initial state by controlling the switch statement. Figure 5A demonstrates that $M_3$ forms a separate complete circuit with $M_5$ when switch $S_1$ is closed and $S_{\mathrm{2,3}}$ are disconnected.

According to Figure 7, in that $M_5$ is forward connected to the circuit, so its resistance will keep decreasing to $R_{on}$ under the influence of the initialization voltage $V_{set}$ in a long enough time; meanwhile the resistance of $M_3$ will remain constant at the same time due to its reverse connection. As soon as the switch $S_1$ is disconnected and $S_{\mathrm{2,3}}$ is closed, the $\pi$-type synaptic basic unit will be accessed to the neuron normally. That $S_{\mathrm{1,2,3}}$ are all disconnected represents that the synapse has entered a fading state; however, when $S_2$ and $S_3$ are re-closed, it indicates the growth of a new synapse. The process in the synapse will have no impact on the state of other synapse blockers in the neuron.

FIGURE 7

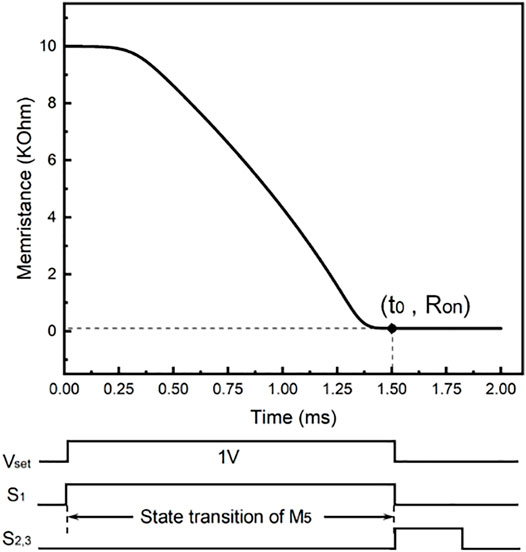
FIGURE 7. Curve of memristance of $M_5$ with $V_{set}$ in variable width. When $S_1$ is on and $S_{\mathrm{2,3}}$ off, the memristance of $M_5$ starts to reduce until $R_{off}$ or $S_1$ is turned off in advance.

Weight Setting

A pulse signal with an amplitude of 1V and a width that varies with the time required to traverse the full range of weights was used for setting the weight. Weight setting should be performed after all available synapses have been initialized. After that, when $M_5$ resistance is $R_{on}$ and the other four memristors in the basic unit are in a high-resistance state $R_{off}$, it leads to the small value of $M_5$ and $M_3$ parallel resistance which means a small proportion in the voltage dividing process. It makes a huge difference in the voltage at the two points A and B; so the current flowing through $M_4$ will be higher than the current flowing through $M_5$. With the input pulse signal as shown in Figure 8, the resistance of $M_2$ decreases and the resistance of $M_5$ increases, the node voltage of A and B will narrow the gap, and in the process of narrowing, the difference between $i_5$ and $i_4$ will have a maximum value. As $M_2$ decreases to $R_{on}$ and $M_5$ rises to $R_{off}$, the two node voltage values will be closer, and the difference of $i_4$ and $i_5$ will no longer change since the resistance value of $M_{\mathrm{2,5}}$ will not change anymore. Only the minimum to maximum value of the $i_{\mathrm{4,5}}$ difference interval was adopted here. The simulation containing only one synapse is illustrated with resistance of $20K\Omega$ for $R_{01}$ and $R_{02}$, and the weights from -1 to 1 can be traversed after 1.272 ms. The commonly used weights are concentrated between the central region around 0, and the obtained weight curve exhibits a superior linearity so that the value of the desired weight can be established by controlling the width of the input pulse.

FIGURE 8

FIGURE 8. (A) Memristance curve of $M_2$ and $M_5$ (B) Current $i_4$, $i_5$, and the weight (C).

Analysis

Considering the boundary effect of the actual memristive device, the nonlinear $Ti{O}_2$ model is used to perform all the simulations in the article. Figure 9A shows the curve of resistance of $M_5$ over time according to the $p$ value of the window function. Under the same $V_{set}$ action, the larger the $p$ value, the shorter the initialization time required to reduce $M_5\left(0\right)$ from $10K\Omega$ to $100\Omega$, and the higher the order of the window function, the greater the resistance state change curve can show good linearity. The influence of $p$ on the weight setting was also simulated in the same synaptic structure. During the process of setting weight, due to the decrease of the window function, the time required for the resistance of $M_2$ to decrease becomes longer, and the time for the increase of the resistance of $M_5$ also increases, as shown in Figures 9B–C, and the resistance changes are nonlinear. The slower state transition process of $M_2$ and $M_5$ will cause the weight change to be relatively lagging; so the time required to go through the weight from −1 to 1 increases. However, despite the time for setting increases, the weight change curve still shows superior linearity within the commonly used weight range, which proves that the $\text{π}$- type synapse structure is suitable for any $\text{p}$ value. $p=7$ takes the principle of avoiding redundant calculations into account, the reaction speed is raised, and the time for initialization and weight preset is reduced.

FIGURE 9

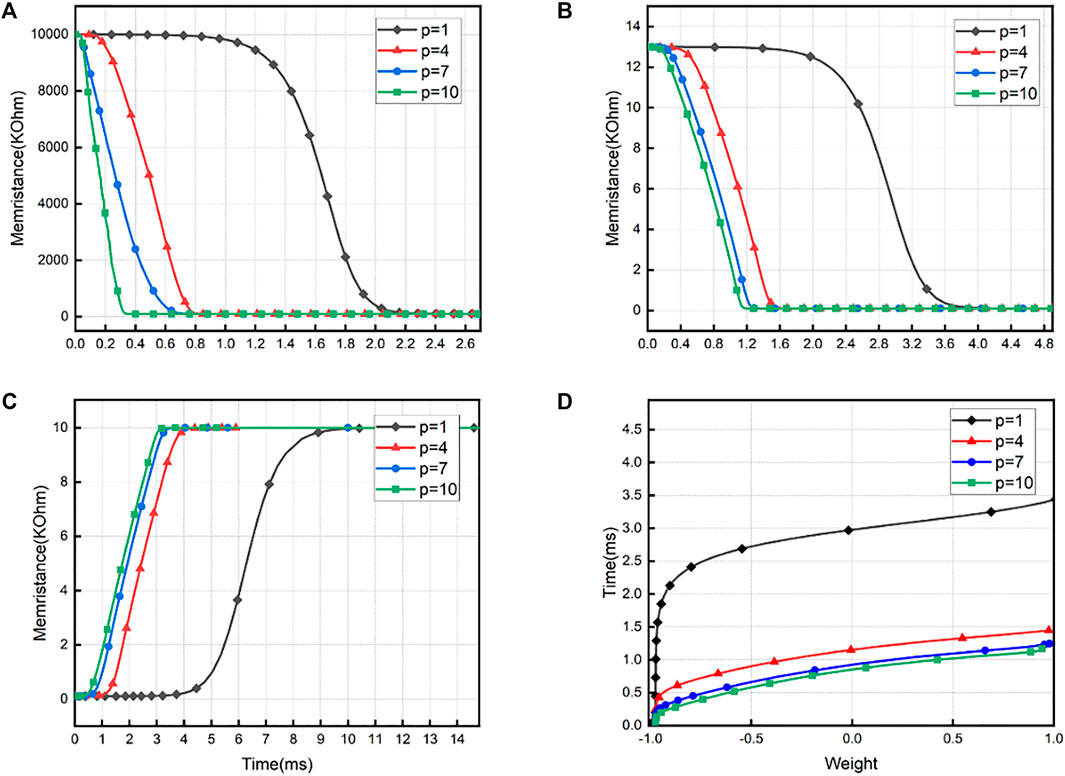
FIGURE 9. Influence of $\text{p }$ on linearity. (A) Time needed for $M_5$ initialization increased as $p$ declined. (B) $M_2$ and (C) $M_5$ shows that the lower $p$ value is, the slower the speed of memristor state transition. (D) Although the time of set weight increases, it still maintains good linearity.

In the case of achieving the same function, a neuron comprising 100 synapses is represented by the most commonly used memristor bridge circuit, which requires 401 memristors and 304 transistors, while that in the proposed neuron structure with the $\pi$-type synapse only needs 502 memristors and five transistors. Assuming that the memristors here are of the 10-nm level, even if the number of memristors increases, the area of the neuron circuit is still reduced by 97.42% due to the smaller individual area of the memristor than the transistor. The energy consumption expression of a neuron with n $\pi$-type synapses can be approximately expressed as (5.61 + 0.1178n) $\mu W$; however, M4 neuron under the same conditions requires (2.5 + 2.7094n) $\mu W$. So, as the number of synapses n increases, the energy consumption will decrease more obviously. However, some recent structures, such as the 2M2R [18, 30], due to the large area occupied by the resistance, do not have advantages in terms of power consumption and area.

Conclusion

A π-type artificial synaptic structure that utilizes the nonvolatile nature of amnestic resistors was suggested by this article, and further an artificial neuron structure with structural variability is also proposed based on this synaptic structure. Our artificial synaptic basic unit consists of five amnestic resistors, and by applying a variable-width pulse input signal with a forward amplitude of 1V, the information will be located in the form of current, and the weight setting is implemented. Simulations using the nonlinear model of $Ti{O}_2$ showed that the $\pi$-type synapse has good linearity over the full range of weight. The information contained in each synapse is summed in the form of currents which are transformed into voltages through a common resistor and computed, which makes it have more significant advantages in terms of size and power consumption. The $\pi$-type synaptic structure also enables the setting of the initial state of the memristor in circuit, compensating for the neglect of previous artificial synapses. This neuron structure can also achieve synaptic fading and renewal in biological neurons, providing a new way of thinking for a more visual implementation of neuronal cell hardware.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

BS, ZW, and YZ designed the research. JC and JC guided the research. All authors contributed to the interpretation of the results, discussions, and editing of the manuscript. Furthermore, all authors have read and agreed to the published version of the manuscript.

Funding

This study was supported by the Natural Science Basic Research Plan in Shaanxi Province of China (2021ZDLGY02-01) and the National 111 Center.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zidan MA, Chen A, Indiveri G, Lu WD. Memristive Computing Devices and Applications. J Electroceram (2017) 39(1):4–20. doi:10.1007/s10832-017-0103-0

CrossRef Full Text | Google Scholar

2. Guo T, Sun B, Ranjan S, Jiao Y, Wei L, Zhou YN, et al. From Memristive Materials to Neural Networks. ACS Appl Mater Inter (2020) 12(49):54243–65. doi:10.1021/acsami.0c10796

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Yang R, Huang HM, Guo X. Memristive Synapses and Neurons for Bioinspired Computing. Adv Electron Mater (2019) 5:1900287. doi:10.1002/aelm.201900287

CrossRef Full Text | Google Scholar

4. Chua L. Memristor-The Missing Circuit Element. IEEE Trans Circuit Theor (1971) 18(5):507–19. doi:10.1109/TCT.1971.1083337

CrossRef Full Text | Google Scholar

5. Strukov DB, Snider GS, Stewart DR, Williams RS. The Missing Memristor Found. Nature (2008) 453(7191):80–3. doi:10.1038/nature06932

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Si G, Diao L, Zhu J. Fractional-order Charge-Controlled Memristor: Theoretical Analysis and Simulation. Nonlinear Dyn (2017) 87(4):2625–34. doi:10.1007/s11071-016-3215-1

CrossRef Full Text | Google Scholar

7. Wang L, Drakakis E, Duan S, He P, Liao X. Memristor Model and its Application for Chaos Generation. Int J Bifurcation Chaos (2012) 22(8):1250205. doi:10.1142/S0218127412502057

CrossRef Full Text | Google Scholar

8. Batas D, Fiedler H. A Memristor SPICE Implementation and a New Approach for Magnetic Flux-Controlled Memristor Modeling. IEEE Trans Nanotechnology (2011) 10(2):250–5. doi:10.1109/TNANO.2009.2038051

CrossRef Full Text | Google Scholar

9. Xie X, Zou L, Wen S, Zeng Z, Huang T. A Flux-Controlled Logarithmic Memristor Model and Emulator. Circuits Syst Signal Process (2019) 38:1452–65. doi:10.1007/s00034-018-0926-1

CrossRef Full Text | Google Scholar

10. Bao H, Hu A, Liu W, Bao B. Hidden Bursting Firings and Bifurcation Mechanisms in Memristive Neuron Model with Threshold Electromagnetic Induction. IEEE Trans Neural Netw Learn Syst. (2020) 31(2):502–11. doi:10.1109/TNNLS.2019.2905137

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Bao H, Hua Z, Li H, Chen M, Bao B. Discrete Memristor Hyperchaotic Maps. IEEE Trans Circuits Syst (2021) 68(11):4534–44. doi:10.1109/TCSI.2021.3082895

CrossRef Full Text | Google Scholar

12. Wang C, Xia H, Zhou L. A Memristive Hyperchaotic Multiscroll Jerk System with Controllable Scroll Numbers. Int J Bifurcation Chaos (2017) 27(6):1750091–1219. doi:10.1142/S0218127417500912

CrossRef Full Text | Google Scholar

13. Bao H, Wang N, Bao B, Chen M, Jin P, Wang G. Initial Condition-dependent Dynamics and Transient Period in Memristor-Based Hypogenetic Jerk System with Four Line Equilibria. Commun Nonlinear Sci Numer Simulation (2018) 57:264–75. doi:10.1016/j.cnsns.2017.10.001

CrossRef Full Text | Google Scholar

14. Xu Y, Jia Y, Ma J, Alsaedi A, Ahmad B. Synchronization between Neurons Coupled by Memristor. Chaos, Solitons & Fractals (2017) 104:435–42. doi:10.1016/j.chaos.2017.09.002

CrossRef Full Text | Google Scholar

15. Jo SH, Chang T, Ebong I, Bhadviya BB, Mazumder P, Lu W. Nanoscale Memristor Device as Synapse in Neuromorphic Systems. Nano Lett (2010) 1410(4):1297–301. doi:10.1021/nl904092h

CrossRef Full Text | Google Scholar

16. Wen S, Xie X, Yan Z, Huang T, Zeng Z. General Memristor with Applications in Multilayer Neural Networks. Neural Networks (2018) 103:142–9. doi:10.1016/j.neunet.2018.03.015

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Vo M-H. Multilayer Neural Network with Synapse Based on Two Successive Memristors. Toeej (2018) 12:132–47. doi:10.2174/1874129001812010132

CrossRef Full Text | Google Scholar

18. Hong Q, Zhao L, Wang X. Novel Circuit Designs of Memristor Synapse and Neuron. Neurocomputing (2019) 330:11–6. doi:10.1016/j.neucom.2018.11.043

CrossRef Full Text | Google Scholar

19. Kim H, Sah MP, Yang C, Roska T, Chua LO. Memristor Bridge Synapses. Proc IEEE (2012) 100(6):2061–70. doi:10.1109/JPROC.2011.2166749

CrossRef Full Text | Google Scholar

20. Kim H, Sah MP, Yang C, Roska T, Chua LO. Neural Synaptic Weighting with a Pulse-Based Memristor Circuit. IEEE Trans Circuits Syst (2012) 59(1):148–58. doi:10.1109/TCSI.2011.2161360

CrossRef Full Text | Google Scholar

21. Wen S, Xie X, Yan Z, Huang T, Zeng Z. General Memristor with Applications in Multilayer Neural Networks. Neural Networks (2018) 103:142–9. doi:10.1016/j.neunet.2018.03.015

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Zhang Y, Wang X, Friedman EG. Memristor-Based Circuit Design for Multilayer Neural Networks. IEEE Trans Circuits Syst (2018) 65(2):677–86. doi:10.1109/tcsi.2017.2729787

CrossRef Full Text | Google Scholar

23. Adhikari SP, Kim H, Budhathoki RK, Yang C, Chua LO. A Circuit-Based Learning Architecture for Multilayer Neural Networks with Memristor Bridge Synapses. IEEE Trans Circuits Syst (2015) 62(1):215–23. doi:10.1002/adfm.20200677310.1109/tcsi.2014.2359717

CrossRef Full Text | Google Scholar

24. Sun K, Chen J, Yan X. The Future of Memristors: Materials Engineering and Neural Networks. Adv Funct Mater (2021) 31(8):2006773. doi:10.1002/adfm.202006773

CrossRef Full Text | Google Scholar

25. Di Marco M, Forti M, Pancioni L. Memristor Standard Cellular Neural Networks Computing in the Flux-Charge Domain. Neural Networks (2017) 93:152–64. doi:10.1016/j.neunet.2017.05.009

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Krestinskaya O, James AP, Chua LO. Neuromemristive Circuits for Edge Computing: A Review. IEEE Trans Neural Netw Learn Syst. (2020) 31(1):4–23. doi:10.1109/TNNLS.2019.2899262

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Yang L, Zeng Z, Shi X. A Memristor-Based Neural Network Circuit with Synchronous Weight Adjustment. Neurocomputing (2019) 363:114–24. doi:10.1016/j.neucom.2019.06.048

CrossRef Full Text | Google Scholar

28. Luo L, Hu X, Duan S, Dong Z, Wang L. Multiple Memristor Series-Parallel Connections with Use in Synaptic Circuit Design. IET Circuits, Devices Syst (2017) 11(2):123–34. doi:10.1049/iet-cds.2015.0357

CrossRef Full Text | Google Scholar

29. Adhikari SP, Changju Yang C, Hyongsuk Kim H, Chua LO. Memristor Bridge Synapse-Based Neural Network and its Learning. IEEE Trans Neural Netw Learn Syst. (2012) 23(9):1426–35. doi:10.1109/TNNLS.2012.2204770

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Wang L, Wang X, Duan S, Li H. A Spintronic Memristor Bridge Synapse Circuit and the Application in Memrisitive Cellular Automata. Neurocomputing (2015) 167:346–51. doi:10.1016/j.neucom.2015.04.061

CrossRef Full Text | Google Scholar

31. Crotty P, Schult D, Segall K. Josephson junction Simulation of Neurons. Phys Rev E (2010) 82:011914. doi:10.1103/PhysRevE.82.011914

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Zhang Y, Wang C, Tang J, Ma J, Ren G. Phase Coupling Synchronization of FHN Neurons Connected by a Josephson junction. Sci China Technol Sci (2020) 63:2328–38. doi:10.1007/s11431-019-1547-5

CrossRef Full Text | Google Scholar

33. Wang C, Tang J, Ma J. Minireview on Signal Exchange between Nonlinear Circuits and Neurons via Field Coupling. Eur Phys J Spec Top (2019) 228:1907–24. doi:10.1140/epjst/e2019-800193-8

CrossRef Full Text | Google Scholar

34. Ma J, Yang Z-q., Yang L-j., Tang J. A Physical View of Computational Neurodynamics. J Zhejiang Univ Sci A (2019) 20:639–59. doi:10.1631/jzus.A1900273

CrossRef Full Text | Google Scholar

35. Xu Y-m., Yao Z, Hobiny A, Ma J. Differential Coupling Contributes to Synchronization via a Capacitor Connection between Chaotic Circuits. Front Inf Technol Electron Eng (2019) 20(4):571–83. doi:10.1631/FITEE.1800499

CrossRef Full Text | Google Scholar

36. Liu Z, Wang C, Zhang G, Zhang Y. Synchronization between Neural Circuits Connected by Hybrid Synapse. Int J Mod Phys B (2019) 33(16):1950170. doi:10.1142/S0217979219501704

CrossRef Full Text | Google Scholar

37. Joglekar YN, Wolf SJ. The Elusive Memristor: Properties of Basic Electrical Circuits. Eur J Phys (2009) 30(4):661–75. doi:10.1088/0143-0807/30/4/001

CrossRef Full Text | Google Scholar

38. Adhikari SP, Sah MP, Kim H, Chua LO. Three Fingerprints of Memristor. IEEE Trans Circuits Syst (2013) 60(11):3008–21. doi:10.1109/TCSI.2013.2256171

CrossRef Full Text | Google Scholar