- 1School of Mathematical Science, Jiangsu University, Zhenjiang, China
- 2School of Information and Control Engineering, Xi’an University of Architecture and Technology, Xi’an, China
- 3School of Communication Engineering, Hangzhou Dianzi University, Hangzhou, China
In real-world scenarios, networks do not exist in isolation but coupled together in different ways, including dependent, multi-support, and inter-connected patterns. And, when a coupled network suffers from structural instability or dynamic perturbations, the system with different coupling patterns shows rich phase transition behaviors. In this review, we present coupled network models with different coupling patterns developed from real scenarios in recent years for studying the system robustness. For the coupled networks with different coupling patterns, based on the network percolation theory, this paper mainly describes the influence of coupling patterns on network robustness. Moreover, for different coupling patterns, we here show readers the research background, research context, and the latest research results and applications. Furthermore, different approaches to improve system robustness with various coupling patterns and future possible research directions for coupled networks are explained and considered.
1 Introduction
With the significant improvement of the ability of high-performance computer clusters, the in-depth study of cloud storage and computing, internet of things application, and pervasive mobile internet, the amount of data about people’s livelihood is increasing and available [1, 2]. These huge amounts of data show network features of extensive distribution, multi-source heterogeneous, such as social network, communication network, power network, energy network, financial network, transportation network, trade network, ecological network and climate network, etc. [3–10]. And, there exists the complex coupling relationship among these real networks, such as spatial relevance, economic connection, strategic linkage, and coexistence relationship [11, 12]. This makes various network systems form a co-generation unit, coupled network [13–16]. Multi-layer network as an important coupled network describes the relevance of real systems from the perspective of coupling between networks [17]. In a multilayered system, each layer represents a separate network system. These coupling links between different networks (layers) may have different functions to each layer and can change the basic characteristics of the individual network and the robustness of the entire coupling system. Coupled patterns with dependent and interconnected features in the real scenarios can be described as interconnected networks, networks of networks, interdependent networks, and so on.
Interdependent networks mean that failure of dependent nodes between coupled networks will cause cascading failures between the networks. Buldyrev et al. [18] initially developed a theoretical framework to understand the robustness of two interdependent networks. Based on this, Gao et al. [19] extended two dependent networks to basic coupling dependent networks, Network of Networks (NON), to study the system structural robustness. The coupling structure between networks not only includes basic coupling modes like tree, star, and chain but also has more complex generalized topological structure [20–23]. They found that interdependent networks are more vulnerable than isolated networks. With the decreases in dependent coupling strength between networks, the percolation transition changes from the first order to the second order at the critical coupling strength [24]. And, for star-like partially dependent networks, number of dependent networks has an influence on the robustness of networks, but robustness of a loop-like system is independent of the number of coupled networks [25, 26]. Each node within the network is not only connected to its own network nodes but also has coupled relationship with nodes in other networks, and this allows seemingly harmless interference to spread like ripples through the coupled network, and ultimately lead to catastrophic consequences [17, 27].
In addition to interdependence between networks, there often exists interconnected coupling relationship in the real system. Bagrow et al. showed that interconnected networks exhibit surprising percolation properties like the decoupling of interconnected network due to random failures before the network collapses [28]. And interconnected nodes play a key role in the interconnected networks, and failures of these nodes will have a significant impact on network integrity such as Alzheimer’s disease has a destructive effect on the connections between systems [29, 30]. In the case of epidemics with a high transmission rate, vaccination of interconnected nodes is more effective in controlling the spread of diseases than vaccination of high-degree nodes [31]. Otherwise, the density of interconnected links also has a significant impact on the system robustness. For example, the level of mobility between cities has been shown to affect the epidemiological transition at the meta-population level [32].
The research on dynamic networks has also attracted more and more attention. For better understanding dynamical characteristic of real networks such as web of sexual contacts, the nervous system, power grid, and metabolism system, Holme et al. proposed the concept of temporal network and defined that the links only exist intermittently to describe the dynamic changes of network structure over time [33]. Considerable research has found that this intermittency has a profound impact on dynamic resilience [34]. Recently, Gao et al. proposed an analytical framework to identify the natural control and state parameters of a multi-dimensional complex system, thereby helping to derive effective one-dimensional dynamical expression and accurately predict system resilience behaviors [35]. Furthermore, Duan et al. found that dynamical coupled network can accelerate the cascading process [36].
This makes us ask the following questions: Is the network system with different coupling patterns safe and stable? How do we prevent system failure? System structural robustness and dynamical resilience play a crucial role in reducing risk and mitigating damage [37–39]. The network structural robustness relies on their network connectivity and can be defined that the ability to retain their connectivity when a portion of their nodes or edges are removed. And, system dynamical resilience characterizes the ability of a system to adjust its activity to maintain its basic functionality in the face of internal disturbances or external environmental changes. In this review, we will focus on recent studies in robustness of coupled network with different coupling patterns to learn more about the subject for more readers.
2 One-to-One Dependency Coupled Pattern
Based on dependency relationship between a power network and an Internet network were implicated in an electrical blackout that occurred in Italy, Buldyrev et al. proposed a fully interdependent network model, in which the coupling pattern means one-to-one interdependence of nodes within two networks [18]. When a node in the network is under attack or disabled, the dependent node within the other network will also fail, and cascading failure occurs in the network system. They studied the percolation behaviors in this system under random attack, which triggered a surge of coupled network robustness. Their findings highlighted that the giant component of the system shows a first-order abrupt transition phenomenon with the increase of attack strength that is different from continuous second-order phenomenon of single network. And the results also implied that the broader degree distribution makes the system more vulnerable by using the percolation theory. Since not all nodes in the network are dependent on each other in the real scenario, Parshani et al. presented a partial dependent network model, that is, only partial nodes are interdependent between two networks, as shown in Figure 1A [24]. Based on the same failure mechanism with a fully dependent network model, they found the phase transition behavior of network changes from a first-order phase transition to a second-order phase transition with the decrease of coupling strength q between two networks.
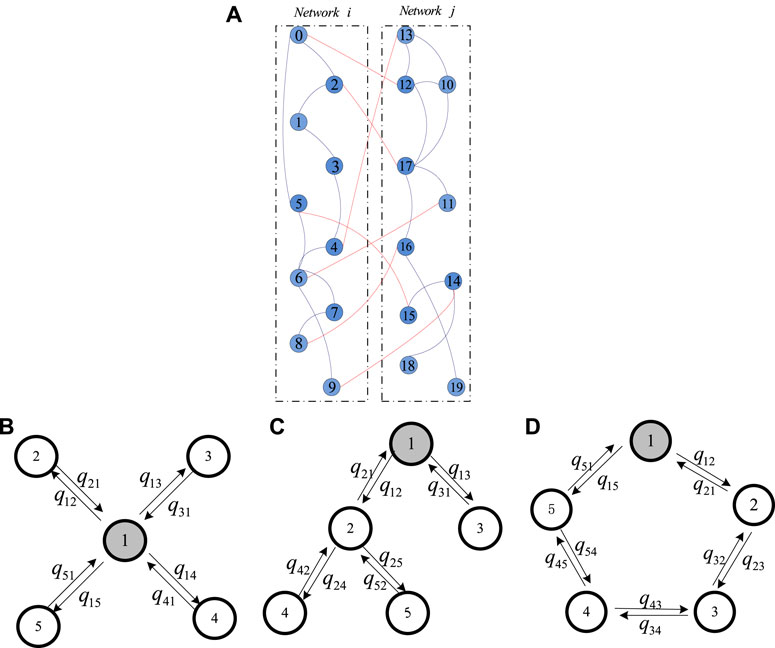
FIGURE 1. (A) Schematic illustration of partial one-to-one dependency relationship, where only faction
Some important infrastructures in the real network have high connection strength and are often considered as attack targets in the network system. Huang and Dong et al. studied the robustness of fully and partial interdependent networks under targeted attacks based on nodes degree [40, 41]. The results show that it is difficult to maintain the robustness of interdependent network by protecting high degree nodes. Xia et al. studied the robustness based on the dependencies in real power and communication networks and revealed the maximum expected payoff for an attacker is affected by the coupling pattern [42, 43].
In fact, more than two networks dependent on each other depend on each other to form a real system. This makes multiple interdependent network systems attract more attention. Furthermore, Gao et al. generalized two dependent networks to n networks (NON) with one-to-one dependency coupling pattern, including some coupled structures like tree, star, and loop which are shown in Figure 1B–D [25]. By developing mathematical frameworks, they numerically and analytically studied the robustness of the system. And, Duan et al. studied the robustness of dependent network by considering dynamical behaviors of nodes within networks triggered by marginal perturbations [36]. They proposed a more generalized framework based on the dynamics of dependent networks and studied the phase transition conditions of dependent networks under various failure mechanisms. They found the analytical expressions for the critical conditions of the first and second phase transitions, and the first phase transition occurred in the weakly dependent network. About directed dependency links, Liu et al. developed a framework to study the system robustness by comparing undirected dependency links. They also found that effect of in-degree and out-degree correlations within the system [44, 45]. Further studies on the impact of different attacks on the one-to-one dependent networks, such as localized attacks [46, 47], overload failures [48], and k-core failure mechanisms [49], have also yielded meaningful results. And different topologies within the network such as group [50], similarity [51, 52], correlation [53], and clustering [54–56] have significant implications for real systems.
For this coupling pattern, one-to-one dependency links is the primary factor leading to network cascading failure. These results generally revealed when connection density within networks is strengthened, and the proportion of dependent nodes within the network is reduced, it can resist attacks to a large extent and reduce the scale of cascading failure. Moreover, unlike the phase transition behavior of a single network, the phase transition behavior exhibited in the system is the first-order jump behavior. This mutation-like behavior further expands the vulnerability of network system and makes it less easy to protect. And these results also gave us on how to design more robust and resilient real networked systems.
3 Coupled Pattern With Multiple-Support Relationship
The studies of the above dependent networks are restricted by the condition that a functional node in a network depends on one and only one node in the other networks. However, in the real networks, the dependent relationship is often multiple support, as shown in Figure 2 from Ref. [57]. For example, multiple directed-support links exist between power stations and communication base stations in power and communication networks. Shao and Dong et al. proposed a coupled network model with multiple support-dependency relationships [58, 59]. And for this case, functional nodes have at least one functional support link from other networks and belong to the giant component during the cascading failure process. Then they also provided the analytical expressions on remaining size of the giant component and critical threshold, where the size of the giant component approaches zero. And for the different coupling structures, star, tree, and loop, Dong et al. developed a framework and extended the case of two networks to n networks with multiple support-dependence relationship [23]. And the findings implied that as connectivity density within network increases, the first-order transition region becomes smaller and the second-order transition region becomes larger. Recently, Zhou et al. proposed a two-layer coupled network model with multiple support-relationship and assumed that functional nodes belonging to giant component within own network have only dependent m support-link that can be survived during a cascading failure process [60]. They also studied the influence on intra-layer and inter-layer degree correlation on network robustness behaviors. The results suggest that such correlations have a significant effect on continuous phase transitions and a small effect on discontinuous phase transitions. Very recently, Dong et al. developed a theoretical framework to study the structural robustness of the coupled network with multiple effective dependency links [57]. It is defined that a functional node requires at least M support-links from the other network to function. In the model, the authors presented exact analytical expressions for the process of cascading failures, the fraction of functional nodes in the stable state, and provided a calculation method of the critical threshold. The results indicated that the system will undergo an abrupt phase transition behavior after initial failure.
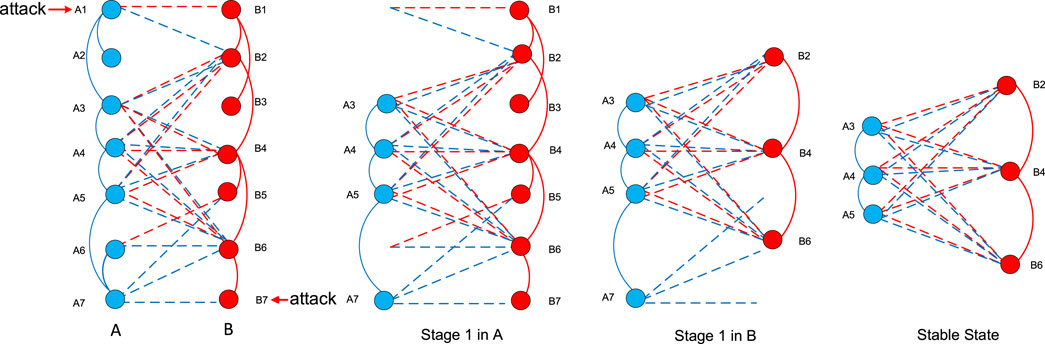
FIGURE 2. Schematic illustration of cascading failure of two networks with multiple support relationship [57]. The curve links denote intra connectivity links within networks A and B, and red (blue) dash links are multiple support links from network A (B) to B (A). Here we assume that the functional nodes not only belong to the giant component within own network but also have at least M support links from other network. After suffering initial attacks, the system undergoes different stages of cascading failures and reaches a steady stable state. During the cascading failure, the functional nodes belonging to the giant component only have M support links is the case of the Ref. [60], and M = 1 is the similar to the Ref. [58].
Different from the one-to-one dependent network model, the multiple dependent network model describes more realistic dependency relationship in the real system. It can be observed in the real systems, such as communication and grid systems multiple-support each other [18]; social networks (e.g., Twitter) are multiple coupled because they share the same participants [61], and multi-modal transport networks are composed of different traffic systems (e.g., buses, subways) sharing the same location [62]. Similar to one-to-one interdependent network, above studies found that the system occurs a first order phase transition by defining failure mechanisms. And, the system needs more internal connection density to avoid collapse when it requires more effective support-links. These studies revealed the robustness of multiple effective dependent networks, which can help to better understand the cascading failure propagation mechanism of the real system.
4 Interconnected Network
From the above analysis, one can observe that the occurrence of cascading failures largely relies on dependency relationship between networks, such as blackouts in power grids, financial crisis, etc. Since the existence of dependency attributes, small perturbations in one network are amplified throughout the dependent network system. However, the natural networks (systems) are often coupled together in the way of interconnected networks like brain and cellular networks are comparatively stable and do not crash [63]. In this kind of coupled network, the interaction between one network and another leads to the necessary expansion of the complex network paradigm, including different types of networks and different types of interactions between them. Unlike the dependency links, the links within and between interacting networks have the same attributes that underpin inter-network connectivity and maintain nodes functionality of the network system [64].
Leicht et al. developed an analytical framework from generating functions and studied the robustness of interconnected networks assuming the similar connectivity links exist within and between networks [13].
They found that when considering the interaction with other networks, the threshold to measure network connectivity becomes very small and the system becomes more robust. Furthermore, Dong et al. proposed a partial interacting network model, that means only part of nodes are interconnected with other nodes in the network and all sub-networks coupled together in this way, as shown in Figure 3A from [65]. They found that increasing the interlinks and interconnected nodes can significantly increase the robustness of the system. Additionally, the continuous phase transition that occurs in a single network disappears, the divergence of the continuous phase transition response function is eliminated, and the system becomes more stable. And, for this kind of network model, the results imply that both analytically and numerically that influence of interlinks on the percolation phase transition is similar to an external field in a ferromagnetic-paramagnetic spin system. By defining the critical exponents δ and γ, these scaling indexes govern the external field and these exponents are consistent with Widom’s identity [65, 66]. Moreover, in the real-world scenarios, tons of sub-networks interconnect with others to form a more generalized network, modular interacting network system, and any pair of sub-networks is randomly selected and coupled each other, as shown in Figure 3B from [26]. Furthermore, the results implied that there exists an optimal coupling structure, where the system shows the most resilient behavior to withstand failures.
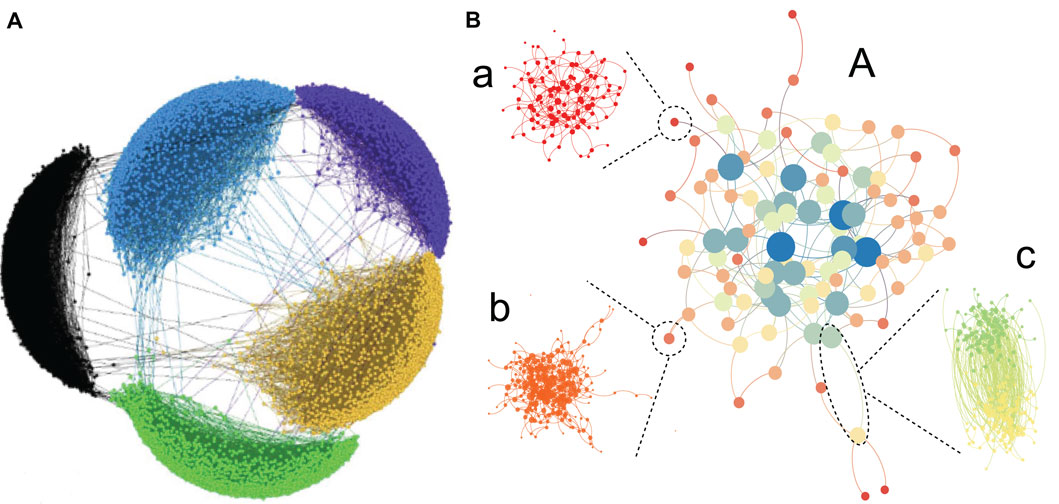
FIGURE 3. Schematic illustration of interacting network with different topological structures. (A) Every sub-network is coupled to all other sub-networks from inter-connected coupling pattern in the Ref. [50]. And, different colors denote different topological structures of sub-networks. (B) Each sub-network has connections to other specific sub-networks not all other sub-networks from [26]. Network A follows a power-law degree distribution. Sub-networks a and b within network A follow Poisson sub-degree distribution. The links in network A follow the Poisson inter-degree distribution, as shown in sub-networks c.
For this case of coupling pattern, network failure behavior was studied by considering functional nodes in the network belong to the giant component of whole coupled networks. As a realistic network model, the interacting network model shows potential applications to epidemic and information spreading, link prediction, and recommendation algorithms. In addition, this interconnected network can also be applied to many different real systems. For example, in the climate network, each isobaric layer of the atmosphere is represented as a complex network, and different isobaric networks are connected [67], the European air transport multi-path network, in which each airline is a sub-network, and public airports can be modeled as coupling nodes [68], the epidemic spreads on interconnected social networks [69]. Due to the same attributes within and between this kind of coupled network, its phase transition behavior often occurs in a second-order phase transition. When the proportion of functional nodes belonging to the largest connected group in the network approaches zero, the critical threshold of the network can be determined. Basically, the research results of this coupled network show that increasing the connection density of network can significantly improve the system robustness.
5 Discussion
In addition to the above coupling patterns, there is a mixed coupling, and dependency links together with inter-connected links between networks. In the model, researchers investigated the case of both interdependent and interconnected links coexistence, where two types of coupled links are randomly connected between two networks. And, they found an interesting phase transition phenomenon, hybrid transition, where the size of giant component both shows abrupt and continuous transition as attacking strength increases [70]. This mixed coupling pattern has not only inter-network interdependence but also includes inter-network connectivity to describe the coupling pattern of real-world scenario [71]. With the development and popularization of the Internet of Things, all things will be interconnected in the near future, where there exists the physical structure of interdependence, and at the same time there exists the interconnected property.
6 Conclusion
Network robustness is becoming increasingly important as we enter age of smart technologies, such as data analysis, SMART Grid, and the Internet of Things (IOT), etc. Complex networks can realistically reflect the coupled relationship in the real scenarios and also permeate different disciplines at the same time, gradually sublimates into an important research field, network science. The research of coupled networks with various patterns is driven by the development of current science and technology; at the same time, it can simulate and guide the system, where we live, from a multi-high-dimensional perspective. In this review, we briefly introduced the advances in robustness of coupled network with various patterns. The phase transition behaviors between networks, how to mitigate failure, and possible future filed of coupled network are explained and considered. In addition, coupled networks have found important application and help us to deal with crises and hidden dangers in the real systems.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This research is supported by grants from National Natural Science Foundation of China (Grant Nos. 61 973 143, 71 974 080, and 71 690 242), the National Natural Science Foundation of China (Grant No. 11 731 014), the National Key Research and Development Program of China (Grant No. 2020YFA0608601) and Young backbone teachers of Jiangsu Province.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Barabási A-L. Scale-free Networks: a Decade and beyond. Science (2009) 325(5939):412–3. doi:10.1126/science.1173299
2. Shekhtman LM, Danziger MM, Havlin S. Recent Advances on Failure and Recovery in Networks of Networks. Chaos Solitons Fractals (2016) 90:28–36. doi:10.1016/j.chaos.2016.02.002
3. Barabási A-L, Albert R. Emergence of Scaling in Random Networks. Science (1999) 286(5439):509–12.
4. Caldarelli G. Scale-free Networks: Complex Webs in Nature and Technology. Oxford, United Kingdom: Oxford University Press (2007).
5. Girvan M, Newman MEJ. Community Structure in Social and Biological Networks. Proc Natl Acad Sci (2002) 99(12):7821–6. doi:10.1073/pnas.122653799
6. Dong G, Qing T, Du R, Wang C, Li R, Wang M, et al. .Complex Network Approach for the Structural Optimization of Global Crude Oil Trade System. J Clean Prod (2020) 251:119366. doi:10.1016/j.jclepro.2019.119366
7. Pastor-Satorras R, Vázquez A, Vespignani A. Dynamical and Correlation Properties of the Internet. Phys Rev Lett (2001) 87(25):258701. doi:10.1103/physrevlett.87.258701
8. Dong G, Qing T, Tian L, Du R, Li J. Optimization of Crude Oil Trade Structure: A Complex Network Analysis. Complexity (2021) 2021:1–11. doi:10.1155/2021/3480546
9. Zhang X, Shao S, Stanley HE, Havlin S. Dynamic Motifs in Socio-Economic Networks. EPL (2014) 108(5):58001. doi:10.1209/0295-5075/108/58001
10. Kossinets G, Watts DJ. Empirical Analysis of an Evolving Social Network. Science (2006) 311(5757):88–90. doi:10.1126/science.1116869
11. Boccaletti S, Bianconi G, Criado R, Del Genio CI, Gómez-Gardeñes J, Romance M, et al. .The Structure and Dynamics of Multilayer Networks. Phys Rep (2014) 544(1):1–122. doi:10.1016/j.physrep.2014.07.001
12. Vespignani A. The Fragility of Interdependency. Nature (2010) 464(7291):984–5. doi:10.1038/464984a
13. Leicht E, D’Souza RM. Percolation on Interacting Networks. arXiv (2009). arXiv preprint (arXiv:0907.0894).
14. De Domenico M, Solé-Ribalta A, Cozzo E, Kivelä M, Moreno Y, Porter MA, et al. .Mathematical Formulation of Multilayer Networks. Phys Rev X (2013) 3(4):041022. doi:10.1103/physrevx.3.041022
15. Danziger MM, Bashan A, Berezin Y, Shekhtman LM, Havlin S. An Introduction to Interdependent Networks. In: International Conference on Nonlinear Dynamics of Electronic Systems, July 4–6, 2014 Albena, Bulgaria: Springer (2014). p. 189–202. doi:10.1007/978-3-319-08672-9_24
16. Radicchi F. Percolation in Real Interdependent Networks. Nat Phys (2015) 11(7):597–602. doi:10.1038/nphys3374
17. Kivelä M, Arenas A, Barthelemy M, Gleeson JP, Moreno Y, Porter MA. Multilayer Networks. J Complex Netw (2014) 2(3):203–71. doi:10.1093/comnet/cnu016
18. Buldyrev SV, Parshani R, Paul G, Stanley HE, Havlin S. Catastrophic cascade of Failures in Interdependent Networks. Nature (2010) 464(7291):1025–8. doi:10.1038/nature08932
19. Gao J, Buldyrev SV, Stanley HE, Havlin S. Networks Formed from Interdependent Networks. Nat Phys (2012) 8(1):40–8. doi:10.1038/nphys2180
20. Gao J, Buldyrev SV, Stanley HE, Xu X, Havlin S. Percolation of a General Network of Networks. Phys Rev E Stat Nonlin Soft Matter Phys (2013) 88(6):062816. doi:10.1103/PhysRevE.88.062816
21. Bianconi G, Dorogovtsev SN. Multiple Percolation Transitions in a Configuration Model of a Network of Networks. Phys Rev E Stat Nonlin Soft Matter Phys (2014) 89(6):062814. doi:10.1103/PhysRevE.89.062814
22. Dong G, Du R, Tian L, Liu R. Robustness of Network of Networks with Interdependent and Interconnected Links. Physica A Stat Mech its Appl (2015) 424:11–8. doi:10.1016/j.physa.2014.12.019
23. Dong G, Gao J, Du R, Tian L, Stanley HE, Havlin S. Robustness of Network of Networks under Targeted Attack. Phys Rev E Stat Nonlin Soft Matter Phys (2013) 87(5):052804. doi:10.1103/PhysRevE.87.052804
24. Parshani R, Buldyrev SV, Havlin S. Interdependent Networks: Reducing the Coupling Strength Leads to a Change from a First to Second Order Percolation Transition. Phys Rev Lett (2010) 105(4):048701. doi:10.1103/PhysRevLett.105.048701
25. Gao J, Buldyrev SV, Havlin S, Stanley HE. Robustness of a Network of Networks. Phys Rev Lett (2011) 107(19):195701. doi:10.1103/physrevlett.107.195701
26. Dong G, Wang F, Shekhtman LM, Danziger MM, Fan J, Du R, et al. .Optimal Resilience of Modular Interacting Networks. Proc Natl Acad Sci (2021) 118(22):e1922831118. doi:10.1073/pnas.1922831118
27. Stanley HE. Introduction to Phase Transitions and Critical Phenomena, International Series of Monographs on Physics. Oxford, United Kingdom: Oxford University Press (1971).
28. Bagrow JP, Lehmann S, Ahn Y-Y. Robustness and Modular Structure in Networks. Net Sci (2015) 3(4):509–25. doi:10.1017/nws.2015.21
29. Han J-DJ, Bertin N, Hao T, Goldberg DS, Berriz GF, Zhang LV, et al. .Evidence for Dynamically Organized Modularity in the Yeast Protein-Protein Interaction Network. Nature (2004) 430(6995):88–93. doi:10.1038/nature02555
30. van Straaten ECW, Stam CJ. Structure Out of Chaos: Functional Brain Network Analysis with Eeg, Meg, and Functional Mri. Eur Neuropsychopharmacol (2013) 23(1):7–18. doi:10.1016/j.euroneuro.2012.10.010
31. Stam CJ. Modern Network Science of Neurological Disorders. Nat Rev Neurosci (2014) 15(10):683–95. doi:10.1038/nrn3801
32. Colizza V, Vespignani A. Invasion Threshold in Heterogeneous Metapopulation Networks. Phys Rev Lett (2007) 99(14):148701. doi:10.1103/physrevlett.99.148701
33. Holme P, Saramäki J. Temporal Networks. Phys Rep (2012) 519(3):97–125. doi:10.1016/j.physrep.2012.03.001
34. Almaas E, Kovács B, Vicsek T, Oltvai ZN, Barabási A-L. Global Organization of Metabolic Fluxes in the Bacterium escherichia Coli. Nature (2004) 427(6977):839–43. doi:10.1038/nature02289
35. Gao J, Barzel B, Barabási A-L. Universal Resilience Patterns in Complex Networks. Nature (2016) 530(7590):307–12. doi:10.1038/nature16948
36. Duan D, Lv C, Si S, Wang Z, Li D, Gao J, et al. .Universal Behavior of Cascading Failures in Interdependent Networks. Proc Natl Acad Sci USA (2019) 116(45):22452–7. doi:10.1073/pnas.1904421116
37. Li M, Liu R-R, Lu L, Hu M-B, Xu S, Zhang Y-C. Percolation on Complex Networks: Theory and Application. Physics Reports (2021), Vol. 907, 1–68.
38. Liu Y, Sanhedrai H, Dong G, Shekhtman LM, Wang F, Buldyrev SV, et al. .Efficient Network Immunization under Limited Knowledge. Natl Sci Rev (2021) 8(1):nwaa229. doi:10.1093/nsr/nwaa229
39. Liu X, Li D, Ma M, Szymanski BK, Stanley HE, Gao J. Network Resilience. arXiv (2020). arXiv preprint (arXiv:2007.14464).
40. Huang X, Gao J, Buldyrev SV, Havlin S, Stanley HE. Robustness of Interdependent Networks under Targeted Attack. Phys Rev E Stat Nonlin Soft Matter Phys (2011) 83(6):065101. doi:10.1103/PhysRevE.83.065101
41. Dong G, Gao J, Tian L, Du R, He Y. Percolation of Partially Interdependent Networks under Targeted Attack. Phys Rev E Stat Nonlin Soft Matter Phys (2012) 85(1):016112. doi:10.1103/PhysRevE.85.016112
42. Jiang J, Xia Y, Xu S, Shen H-L, Wu J. An Asymmetric Interdependent Networks Model for Cyber-Physical Systems. Chaos (2020) 30(5):053135. doi:10.1063/1.5139254
43. Xu S, Xia Y, Shen H-L. Analysis of Malware-Induced Cyber Attacks in Cyber-Physical Power Systems. IEEE Trans Circuits Syst (2020) 67(12):3482–6. doi:10.1109/tcsii.2020.2999875
44. Liu X, Stanley HE, Gao J. Breakdown of Interdependent Directed Networks. Proc Natl Acad Sci USA (2016) 113(5):1138–43. doi:10.1073/pnas.1523412113
45. Liu X, Pan L, Stanley HE, Gao J. Multiple Phase Transitions in Networks of Directed Networks. Phys Rev E (2019) 99(1):012312. doi:10.1103/PhysRevE.99.012312
46. Berezin Y, Bashan A, Danziger MM, Li D, Havlin S. Localized Attacks on Spatially Embedded Networks with Dependencies. Sci Rep (2015) 5(1):8934–5. doi:10.1038/srep08934
47. Yuan X, Shao S, Stanley HE, Havlin S. How Breadth of Degree Distribution Influences Network Robustness: Comparing Localized and Random Attacks. Phys Rev E Stat Nonlin Soft Matter Phys (2015) 92(3):032122. doi:10.1103/PhysRevE.92.032122
48. Wang F, Tian L, Du R, Dong G. The Robustness of Interdependent Weighted Networks. Physica A: Stat Mech its Appl (2018) 508:675–80. doi:10.1016/j.physa.2018.05.110
49. Yuan X, Dai Y, Stanley HE, Havlin S. K-Core Percolation on Complex Networks: Comparing Random, Localized, and Targeted Attacks. Phys Rev E (2016) 93(6):062302. doi:10.1103/PhysRevE.93.062302
50. Shekhtman LM, Shai S, Havlin S. Resilience of Networks Formed of Interdependent Modular Networks. New J Phys (2015) 17(12):123007. doi:10.1088/1367-2630/17/12/123007
51. Parshani R, Rozenblat C, Ietri D, Ducruet C, Havlin S. Inter-similarity between Coupled Networks. EPL (2011) 92(6):68002. doi:10.1209/0295-5075/92/68002
52. Hu Y, Zhou D, Zhang R, Han Z, Rozenblat C, Havlin S. Percolation of Interdependent Networks with Intersimilarity. Phys Rev E Stat Nonlin Soft Matter Phys (2013) 88(5):052805. doi:10.1103/PhysRevE.88.052805
53. Valdez LD, Macri PA, Stanley HE, Braunstein LA. Triple point in Correlated Interdependent Networks. Phys Rev E Stat Nonlin Soft Matter Phys (2013) 88(5):050803. doi:10.1103/PhysRevE.88.050803
54. Dong G, Xiao H, Wang F, Du R, Shao S, Tian L, et al. .Localized Attack on Networks with Clustering. New J Phys (2019) 21(1):013014. doi:10.1088/1367-2630/aaf773
55. Fan W, Gaogao D, Ruijin D, Lixin T. Robustness of Multiple Interdependent Networks under Shell Attack. In: 2017 36th Chinese Control Conference (CCC), Dalian, China, July 26–28, 2017. IEEE (2017). p. 1447–50. doi:10.23919/chicc.2017.8027554
56. Dong G, Du R, Hao H, Tian L. Modified Localized Attack on Complex Network. EPL (2016) 113(2):28002. doi:10.1209/0295-5075/113/28002
57. Dong G, Yao Q, Wang F, Du R, Vilela ALM, Eugene Stanley H. Percolation on Coupled Networks with Multiple Effective Dependency Links. Chaos (2021) 31(3):033152. doi:10.1063/5.0046564
58. Shao J, Buldyrev SV, Havlin S, Stanley HE. Cascade of Failures in Coupled Network Systems with Multiple Support-Dependence Relations. Phys Rev E Stat Nonlin Soft Matter Phys (2011) 83(3):036116. doi:10.1103/PhysRevE.83.036116
59. Dong G, Tian L, Du R, Fu M, Stanley HE. Analysis of Percolation Behaviors of Clustered Networks with Partial Support-Dependence Relations. Physica A: Stat Mech its Appl (2014) 394:370–8. doi:10.1016/j.physa.2013.09.055
60. Zhang H, Zhou J, Zou Y, Tang M, Xiao G, Stanley HE. Asymmetric Interdependent Networks with Multiple-Dependence Relation. Phys Rev E (2020) 101(2):022314. doi:10.1103/PhysRevE.101.022314
61. Szell M, Lambiotte R, Thurner S. Multirelational Organization of Large-Scale Social Networks in an Online World. Proc Natl Acad Sci (2010) 107(31):13636–41. doi:10.1073/pnas.1004008107
62. De Domenico M, Sole-Ribalta A, Gomez S, Arenas A. Navigability of Interconnected Networks under Random Failures. Proc Natl Acad Sci (2014) 111(23):8351–6. doi:10.1073/pnas.1318469111
63. Reis SDS, Hu Y, Babino A, Andrade Jr JS, Canals S, Sigman M, et al. .Avoiding Catastrophic Failure in Correlated Networks of Networks. Nat Phys (2014) 10(10):762–7. doi:10.1038/nphys3081
64. Goswami B, Shekatkar SM, Rheinwalt A, Ambika G, Kurths J. A Random Interacting Network Model for Complex Networks. Sci Rep (2015) 5(1):18183–10. doi:10.1038/srep18183
65. Dong G, Fan J, Shekhtman LM, Shai S, Du R, Tian L, et al. .Resilience of Networks with Community Structure Behaves as if under an External Field. Proc Natl Acad Sci USA (2018) 115(27):6911–5. doi:10.1073/pnas.1801588115
66. Fan J, Dong G, Shekhtman LM, Zhou D, Meng J, Chen X, et al. .Structural Resilience of Spatial Networks with Inter-links Behaving as an External Field. New J Phys (2018) 20(9):093003. doi:10.1088/1367-2630/aadceb
67. Donges JF, Schultz HCH, Marwan N, Zou Y, Kurths J. Investigating the Topology of Interacting Networks. Eur Phys J B (2011) 84(4):635–51. doi:10.1140/epjb/e2011-10795-8
68. Cardillo A, Gómez-Gardeñes J, Zanin M, Romance M, Papo D, Del Pozo F, et al. .Emergence of Network Features from Multiplexity. Sci Rep (2013) 3(1):1344–6. doi:10.1038/srep01344
69. Dickison M, Havlin S, Stanley HE. Epidemics on Interconnected Networks. Phys Rev E Stat Nonlin Soft Matter Phys (2012) 85(6):066109. doi:10.1103/PhysRevE.85.066109
70. Hu Y, Ksherim B, Cohen R, Havlin S. Percolation in Interdependent and Interconnected Networks: Abrupt Change from Second- to First-Order Transitions. Phys Rev E Stat Nonlin Soft Matter Phys (2011) 84(6):066116. doi:10.1103/PhysRevE.84.066116
Keywords: complex network, robustness, resilience, coupled network, coupling pattern
Citation: Dong G, Duan D and Xia Y (2021) A Briefing Survey on Advances of Coupled Networks With Various Patterns. Front. Phys. 9:795279. doi: 10.3389/fphy.2021.795279
Received: 14 October 2021; Accepted: 19 November 2021;
Published: 24 December 2021.
Edited by:
Huijia Li, Central University of Finance and Economics, ChinaCopyright © 2021 Dong, Duan and Xia. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gaogao Dong, Z2Fnbzk5OUAxMjYuY29t; Dongli Duan, bWluZWR1YW5AMTYzLmNvbQ==; Yongxiang Xia, eGlheXhAaGR1LmVkdS5jbg==
 Gaogao Dong
Gaogao Dong Dongli Duan
Dongli Duan Yongxiang Xia
Yongxiang Xia