Clarifying Nonstatic-Quantum-Wave Behavior Through Extending Its Analysis to the p-Quadrature Space: Interrelation Between the q- and p-Space Wave-Nonstaticities

If electromagnetic parameters of a medium vary in time, quantum light waves traveling in it become nonstatic. A recent report shows that such nonstatic waves can also appear even when the environment is static where the parameters of the medium do not vary. In this work, the properties of nonstatic waves in a static environment are investigated from their p-space analysis, focusing on the interrelation between the q- and p-space nonstatic waves. The probability densities in p-space (as well as in q-space) for both the nostatic Fock and Gaussian states evolve in a periodic manner, i.e., they constitute belly and node in turn successively as time goes by. If we neglect the displacement of waves, the q- and p-space wave phases are opposite each other. Since the intensity of the wave in each space is relatively large whenever the wave forms a belly, such a phase difference indicates that periodical intensity exchange between the q- and p-component waves takes place through their nonstatic evolutions. This is the novel reciprocal optical phenomenon arisen on account of the wave nonstaticity.

Introduction

If the characteristics of a medium vary in time by external perturbations, quantum light waves propagating through it may exhibit nonstatic properties [1–8]. Then, the shapes of the waves would be modified through the change of parameters. The dissipation and amplification of the wave amplitudes are also classified as the phenomena of wave nonstaticity. The light waves in such cases are usually described by time-dependent Hamiltonians, where their mathematical treatment is somewhat complicated.

Owing to the temporal and/or spatial variations of electromagnetic parameters in media, nonstatic quantum waves exhibit many novel physical properties that are absent in common light waves. As a noticeable consequence of wave nonstaticity, highly rapid periodic or arbitrary modulations of the wave phases and amplitudes are possible under appropriate conditions [8–13]. Such ultrafast modulations at a weak photon level can be applied to a time-resolved optical heterodyne detection in nano quantum dots [8, 11]. On one hand, temporal modulation of a driving electromagnetic field can be used in enhancing the entanglement between a microwave mode and a mechanical resonator [12, 13]. Another main consequence achieved through wave nonstaticity is a frequency shift [7, 14] in subwavelength optics. Frequency shifts are potential tools for producing millimeter-waves and terahertz signals whose generations can hardly be realized by other technological means.

In a previous work [15], we showed a notable feature in optics, which is that nonstatic waves can also appear even in a static environment, i.e., without changes of the parameter values in media. The properties of such nonstatic waves have been studied in a rigorous way from the fundamental quantum-mechanical point of view in that work. Through this, we confirmed that the width of the waves varies periodically in time as a consequence of their nonstaticity. The related quantitative measure of nonstaticity, resulting from the modification of the waveform, was defined. Further, the mechanism of wave expansion and collapse was elucidated in Ref. [16].

However, the above mentioned research was in principle confined in q-quadrature space only. In this work, we will investigate such nonstatic waves especially on their p-quadrature space characteristics. The behavior of nonstatic waves described in p-space will be compared to that in q-space; through this, we clarify how they are mutually connected, as well as demonstrate the differences and similarities between them. A rigorous analysis of the relation between the two conjugate space evolutions of the nonstatic waves is necessary in understanding the peculiar wave behavior caused by its nonstaticity as a whole. Our analyses will be carried out separately for the Fock state waves and the Gaussian ones.

Results and Discussion

Nonstatic Waves in the Fock States

We investigate the properties of nonstatic waves in the Fock states in a static environment through the p-space analysis in this section. As a preliminary step for understanding the theory of wave nonstaticity along this line, the readers may need to know its previous research consequence in q-quadrature space, reported in Ref. [15]. For the convenience of readers, the research of Ref. [15] including its outcome is briefly introduced in Supplementary Material.

Let us consider a medium where the electric permittivity ϵ and the magnetic permeability μ do not vary in time, whereas the electric conductivity σ is zero. The vector potential relevant to the light-wave propagation in that medium can be written as A(r, t) = u(r)q(t), where r is a position in three dimensions. Whereas u(r) follows position boundary conditions, the time function q(t) exhibits an oscillatory behavior. In order to describe the light waves from quantum mechanical point of view, we need to change q(t) into an operator $\widehat{q}$. Then, the waves that propagate through the static medium is described by a simple Hamiltonian of the form $\widehat{H}={\widehat{p}}^2/(2ϵ)+ϵ{\omega }^2{\widehat{q}}^2/2$, where $\widehat{p}$ is the conjugate variable of $\widehat{q}$, which is defined as $\widehat{p}=-i\hslash \partial /\partial q$. According to a previous report [15], quantum waves that have nonstatic properties in q-space can appear even in this static situation as mentioned in the introductory part.

The nonstatic waves propagating in the static environment can be represented in terms of a time function of the form

$W\left(t\right)=W_{\mathrm{R}}\left(t\right)+i{W}_{\mathrm{I}}\left(t\right),(1)$

where W_R(t) and W_I(t) are its real and imaginary parts, respectively (i.e., both W_R(t) and W_I(t) are real). The formulae of the real and imaginary parts are given by [15].

$W_{\mathrm{R}}\left(t\right)=\frac{ϵ\omega }{\hslash f\left(t\right)},W_{\mathrm{I}}\left(t\right)=-\frac{ϵ\dot{f}\left(t\right)}{2\hslash f\left(t\right)},(2)$

where

$\begin{array}{ccc}\hfill & \hfill & f\left(t\right)=A{\sin }^2\tilde{\phi }\left(t\right)+B{\cos }^2\tilde{\phi }\left(t\right)+C\sin \left[2\tilde{\phi }\left(t\right)\right],\hfill \end{array}(3)$

$\begin{array}{ccc}\hfill & \hfill & \tilde{\phi }\left(t\right)=\omega \left(t-t_0\right)+\phi ,\hfill \end{array}(4)$

with a constant phase φ and a constant time t₀. In Eq. 3, A, B, and C are real values that obey the conditions AB − C² = 1 and AB ≥ 1. We note that Eq. 3 is a general solution of the nonlinear equation [15]

$\ddot{f}-{\left(\dot{f}\right)}^2/\left(2f\right)+2{\omega }^2\left(f-1/f\right)=0.(5)$

The wave functions in p-space, which exhibit nonstatic properties, may also be represented in terms of the time function given in Eq. 1. An exact evaluation of the wave functions for such waves in the Fock states results in (see Appendix A)

$\langle p|{\psi }_n\left(t\right)\rangle =\langle p|{\varphi }_n\left(t\right)\rangle \exp \left[i{\gamma }_n\left(t\right)\right],(6)$

where

$\begin{array}{ccc}\hfill ⟨p|{\varphi }_n⟩& =\hfill & {\left(-i\right)}^n{\left(\frac{W_{\mathrm{R}}\left(t\right)}{\pi {\hslash }^2}\right)}^{1/4}\sqrt{\frac{{\left[W^{\ast }\left(t\right)\right]}^n}{{\left[W\left(t\right)\right]}^{n+1}}}\frac{1}{\sqrt{2^{n}n!}}\hfill \\ \hfill & \hfill & \times H_n\left(\sqrt{\frac{W_{\mathrm{R}}\left(t\right)}{W_{\mathrm{R}}^2\left(t\right)+W_{\mathrm{I}}^2\left(t\right)}}\frac{p}{\hslash }\right)\exp \left[-\frac{W_p\left(t\right)}{2}{p}^2\right],\hfill \end{array}(7)$

$\begin{array}{ccc}\hfill {\gamma }_n\left(t\right)& =\hfill & -\omega \left(n+1/2\right){\int }_{t_0}^t{f}^{-1}\left(t^{\prime }\right)d{t}^{\prime }+{\gamma }_n\left(t_0\right),\hfill \end{array}(8)$

with

$W_p\left(t\right)=\frac{W_{\mathrm{R}}\left(t\right)-i{W}_{\mathrm{I}}\left(t\right)}{{\hslash }^2\left[W_{\mathrm{R}}^2\left(t\right)+W_{\mathrm{I}}^2\left(t\right)\right]}\equiv W_{p,\mathrm{R}}\left(t\right)+i{W}_{p,\mathrm{I}}\left(t\right).(9)$

Here, H_n are nth order Hermite polynomials, whereas W_p,R(t) and W_p,I(t) are real and imaginary parts of W_p(t), respectively. We can also represent Eq. 9 simply as W_p(t) = 1/[ℏ²W(t)].

Now it is possible to analyze quantum optical phenomena associated with the nonstatic waves on the basis of the wave functions given in Eq. 6, Figure 1 shows the temporal evolution of the probability density which is defined as |⟨p|ψ_n(t)⟩|². We see from Figure 1A that there are bellies and nodes in the p-space wave evolution like the q-space evolution represented in Figure 1B. While the period of such evolutions is π/ω for both |⟨p|ϕ_n⟩|² and |⟨q|ϕ_n⟩|², the corresponding wave phases associated with wave nonstaticity are different from each other. We confirm, from the comparison of Figure 1A and Figure 1B, that such a phase difference between the two probability densities is π, i.e., the phases are opposite each other. Notice that the phase of nonstatic evolution that we use here is the one that emerges due to nonstatic characteristics of the wave: this concept of the phase is essentially different from the generally used quantum phase which is composed of the dynamical and geometric phases as shown, for example, in Ref. [17]. Since the wave intensity is strong at a belly and weak at a node, the π difference between the q- and p-space wave phases implies the exchange of the wave intensity between the two conjugate components of the wave.

FIGURE 1

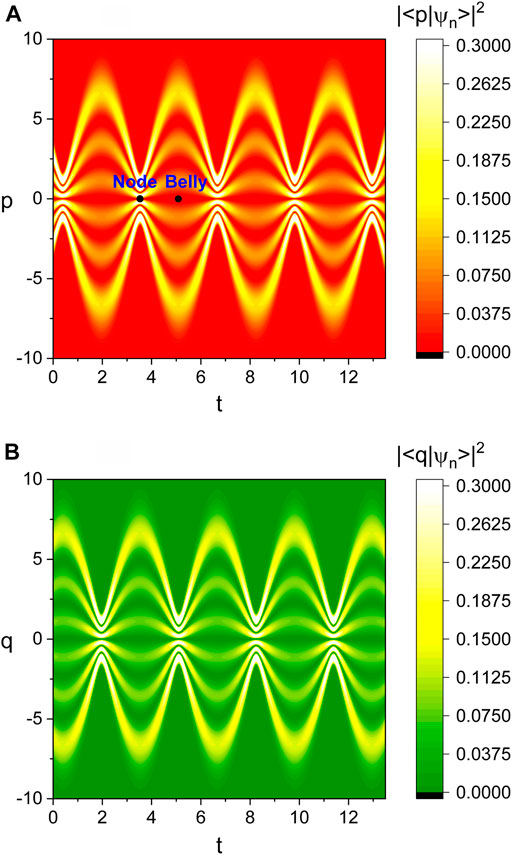
FIGURE 1. (A) is the density plot of the probability density in p-space, |⟨p|ψ_n(t)⟩|², as a function of p and t. For comparison purposes, we have also represented the probability density in q-space, |⟨q|ψ_n(t)⟩|², in (B) as a function of q and t. The values that we used are A = 1, B = 5, C = 2, ω = 1, n = 5, ℏ = 1, ϵ = 1, t₀ = 0, and φ = 0. All values are taken to be dimensionless for convenience; this convention will also be used in all subsequent figures.

As stated in Supplementary Material, it was shown in the previous work [15] that the non-zero value of W_I(t) is responsible for the appearance of the nonstatic properties of the waves in q-space. In addition, the quantitative measure of nonstaticity in q-space was defined in the same reference as the root-mean-square (RMS) value of W_I(t)/W_R(t).

For the case of the wave description in p-space, the associated wave nonstaticity originates from the non-zero value of W_p,I. Hence, the nonstaticity measure in p-space can also be defined as the RMS value of W_p,I/W_p,R. We see from Figure 2 that the evolution of W_p,I/W_p,R exhibits sinusoidal behavior as that of W_I/W_R. However, there is a phase difference π between them. This difference is responsible for the phase difference between the evolutions of |⟨p|ψ_n⟩|² and |⟨q|ψ_n⟩|². From a minor evaluation, we can easily confirm that

$\frac{W_{p,\mathrm{I}}}{W_{p,\mathrm{R}}}=\frac{1}{2}\sqrt{{\left(A+B\right)}^2-4}\cos \left[2\tilde{\phi }\left(t\right)+\delta \right],(10)$

where δ = atan(2C, B − A). Here, θ ≡ atan(x, y) is the two-arguments inverse function of tan θ = y/x, which is defined in the range 0 ≤ θ < 2π. We have depicted the temporal evolution of W_p,I/W_p,R and its components W_p,R and W_p,I in Figure 2. While W_p,I/W_p,R varies sinusoidally, W_p,R and W_p,I vary abruptly at certain instants of time where the p-space probability density constitutes nodes. By taking the RMS value of Eq. 10 for a cycle, we have the measure of nonstaticity in p-space as

$D_{p,\mathrm{F}}=\frac{\sqrt{{\left(A+B\right)}^2-4}}{2\sqrt{2}}.(11)$

FIGURE 2

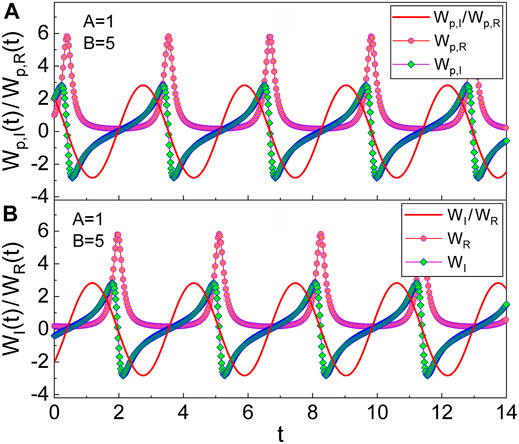
FIGURE 2. (A) is the evolution of W_p,I/W_p,R and its components W_p,R and W_p,I, relevant to p-space, with the choice of A = 1, B = 5, and C = 2. (B) is the evolution of W_I/W_R and its components relevant to q-space (comparison purpose). The values that we have taken are ω = 1, ℏ = 1, ϵ = 1, t₀ = 0, and φ = 0.

This is exactly the same as the measure of nonstaticity in q-space, which was previously evaluated in Ref. [15]. Thus, the definition of the measure of nonstaticity shown above, can be generally used irrespective of the given space. For instance, we confirm that the measure of nonstaticity for the wave given in Figure 2 is 2.0 from a simple calculation using A = 1 and B = 5.

Nonstatic Waves in the Gaussian States

Our theory for the evolution of nonstatic waves can be extended to a more general case which is the Gaussian wave. To see the nonstatic properties of a Gaussian wave that evolves in a static environment, we take an initial waveform as

$⟨q|\psi \left(0\right)⟩=\sqrt[4]{\frac{K_{\mathrm{R}}}{\pi }}{e}^{-\frac{1}{2}K{\left(q-\xi \right)}^2},(12)$

where ξ is a displacement and K = K_R + iK_I. Here, K_R and K_I mean real and imaginary parts, respectively. The existence of K_I is responsible for the nonstatic evolution of the wave in this case [15]. To see the evolution of this Gaussian quantum wave in p-space, it is necessary to evaluate the wave function ⟨p|ψ(t)⟩ at an arbitrary time t from Eq. 12. We have provided the method of evaluating the analytical formula for such a wave function in Appendix B, and the result is given by

$⟨p|\psi \left(t\right)⟩=\frac{N\left(t\right)}{\sqrt{\hslash \mathcal{W}\left(t\right)}}\exp \left(-\frac{{\mathcal{W}}_p\left(t\right)}{2}{\left[p+i\hslash R\left(t\right)\right]}^2\right),(13)$

where

$\begin{array}{ccc}\hfill & \hfill & N\left(t\right)={\left(\frac{W_{\mathrm{R}}\left(0\right)W_{\mathrm{R}}\left(t\right)}{\pi }\right)}^{1/4}{\left(\frac{2K_{\mathrm{R}}^{1/2}}{g\left(t\right)\exp \left[-2i\mathrm{\Theta }\left(t\right)\right]}\right)}^{1/2}\exp \left[-\frac{1}{2}\left(K{\xi }^2+i\mathrm{\Theta }\left(t\right)\right)\right]\hfill \\ \hfill & \hfill & \times \exp \left[\frac{K^2{\xi }^2}{K+W^{\ast }\left(0\right)}\left(\frac{1}{2}-\frac{W_{\mathrm{R}}\left(0\right)}{g\left(t\right)}\right)\right],\hfill \end{array}(14)$

$\begin{array}{ccc}\hfill & \hfill & \mathcal{W}\left(t\right)=W\left(t\right)+\frac{2W_{\mathrm{R}}\left(t\right)\left[K-W\left(0\right)\right]}{g\left(t\right)}\equiv {\mathcal{W}}_{\mathrm{R}}\left(t\right)+i{\mathcal{W}}_{\mathrm{I}}\left(t\right),\hfill \end{array}(15)$

$\begin{array}{ccc}\hfill & \hfill & {\mathcal{W}}_p\left(t\right)=\frac{{\mathcal{W}}_{\mathrm{R}}\left(t\right)-i{\mathcal{W}}_{\mathrm{I}}\left(t\right)}{{\hslash }^2\left[{\mathcal{W}}_{\mathrm{R}}^2\left(t\right)+{\mathcal{W}}_{\mathrm{I}}^2\left(t\right)\right]}\equiv {\mathcal{W}}_{p,\mathrm{R}}\left(t\right)+i{\mathcal{W}}_{p,\mathrm{I}}\left(t\right),\hfill \end{array}(16)$

$\begin{array}{ccc}\hfill & \hfill & R\left(t\right)=\frac{2K\xi \sqrt{W_{\mathrm{R}}\left(0\right)W_{\mathrm{R}}\left(t\right)}}{g\left(t\right)\exp \left[-i\mathrm{\Theta }\left(t\right)\right]},\hfill \end{array}(17)$

with

$\begin{array}{ccc}\hfill \mathrm{\Theta }\left(t\right)& =\hfill & \omega {\int }_0^t{f}^{-1}\left(t^{\prime }\right)d{t}^{\prime },\hfill \end{array}(18)$

$\begin{array}{ccc}\hfill g\left(t\right)& =\hfill & \left[K+W^{\ast }\left(0\right)\right]\exp \left[2i\mathrm{\Theta }\left(t\right)\right]-\left[K-W\left(0\right)\right].\hfill \end{array}(19)$

We have illustrated the probability density that corresponds to Eq. 13 in Figures 3, 4. Figure 3 is the case where the displacement ξ is zero, whereas Figure 4 corresponds to the case of the displaced Gaussian wave. We see from Figure 3 that the width of the probability density varies periodically over time with the period 3.14 (= π/ω), which is the same period as that of the Fock-state wave functions that we have already seen. The comparison of Figure 3A and Figure 3B shows that the phase difference between |⟨p|ψ(t)⟩|² and |⟨q|ψ(t)⟩|² is π, which is also the same as that between the Fock-state probability densities |⟨p|ψ_n(t)⟩|² and |⟨q|ψ_n(t)⟩|².

FIGURE 3

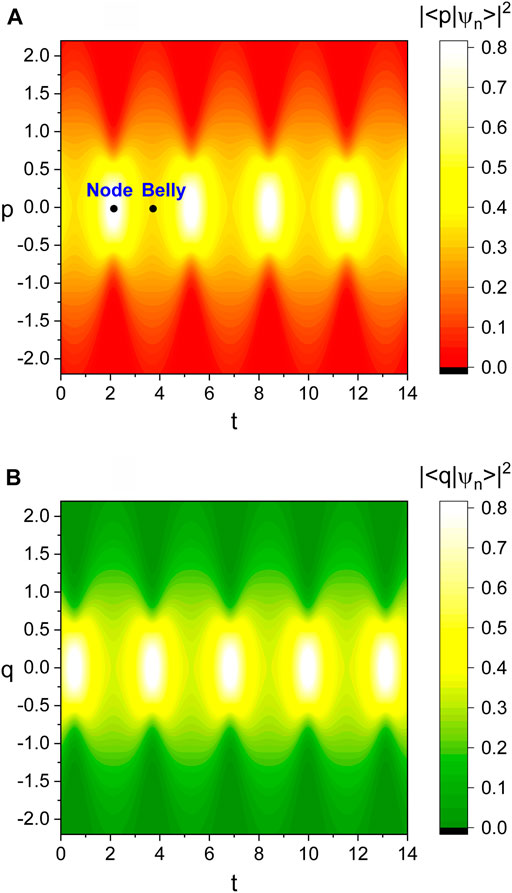
FIGURE 3. (A) is the density plot of the probability density |⟨p|ϕ_n⟩|² given as a function of p and t. (B) is the density plot of |⟨q|ϕ_n⟩|² given as a function of q and t (comparison purpose). The values that we have taken are K_R = 1, K_I = 1, A = 1, B = 5, C = 2, ξ = 0, ω = 1, ℏ = 1, ϵ = 1, t₀ = 0, and φ = 0.

FIGURE 4

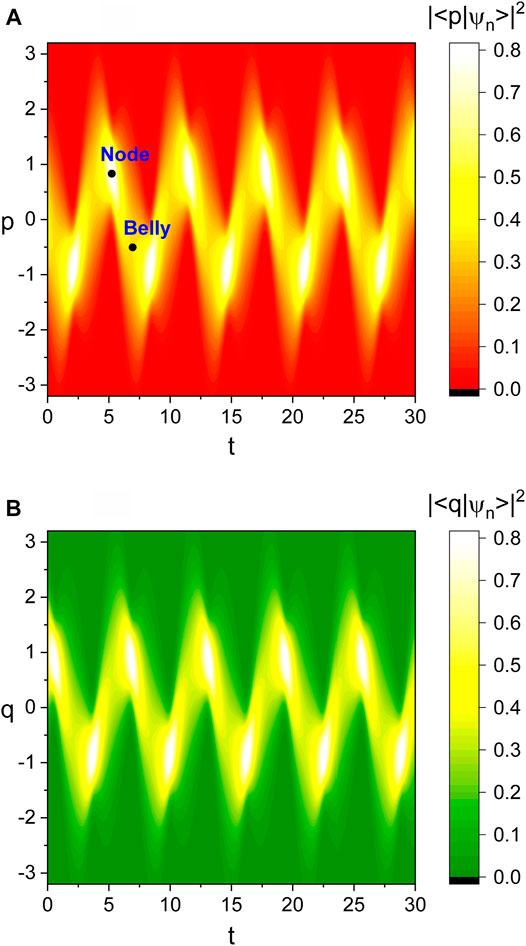
FIGURE 4. This is the same as Figure 3, but with the choice of ξ = 1.

On the other hand, the period of wave evolution (oscillation) in the case of Figure 4 is not 3.14 but 6.28 (= 2π/ω). This means that the wave evolves a one-cycle (2π rad) during T = 6.28. Based on this, we can conclude that the phase difference between Figure 4A and Figure 4B is π/2 which is different from the previous cases. The difference of the period in this case from that in the previous cases is responsible for such an inconsistency in the phase differences (p-space wave phase minus q-space wave phase) between them. However, if we neglect the oscillation of the Gaussian wave in Figure 4, the period of its evolution reduces to π and as a consequence, the phase difference between |⟨p|ψ(t)⟩|² and |⟨q|ψ(t)⟩|² becomes π which is identical to the previous two cases (Figures 1, 3).

The displaced Gaussian wave that can be seen from Figure 4 oscillates back and forth like a classical state. However, the shape of the wave varies in an abnormal manner in time due to its nonstatic properties. The value of the probability density is highly peaked whenever the value of p becomes one of certain two values (one is plus and the other is minus) just after the turning points of the oscillation in p-space. Such peaks are in fact nodes as designated in the figure. Because the Gaussian nonstatic wave also exhibits node and belly in turn regularly, the intensity exchange between the q- and p-space waves occurs.

We can define the measure of nonstaticity for the Gaussian wave in a similar manner as that of the previous section. It is the RMS value of ${\mathcal{W}}_{p,\mathrm{I}}(t)/{\mathcal{W}}_{p,\mathrm{R}}(t)$. The temporal evolution of ${\mathcal{W}}_{p,\mathrm{I}}(t)/{\mathcal{W}}_{p,\mathrm{R}}(t)$ has been represented in Figure 5 with its comparison to the evolution of the counterpart q-space value ${\mathcal{W}}_{\mathrm{I}}(t)/{\mathcal{W}}_{\mathrm{R}}(t)$. The amplitude of both ${\mathcal{W}}_{p,\mathrm{I}}(t)/{\mathcal{W}}_{p,\mathrm{R}}(t)$ and ${\mathcal{W}}_{\mathrm{I}}(t)/{\mathcal{W}}_{\mathrm{R}}(t)$ in Figure 5 is 2.83. From this, the corresponding measure of nonstaticity is 2.0 and this value is the same as that of the wave shown in Figure 2. We can confirm that the patterns of the evolutions of ${\mathcal{W}}_{p,\mathrm{R}}(t)$ and ${\mathcal{W}}_{p,\mathrm{I}}(t)$ given in Figure 5 are the same as those of W_p,R(t) and W_p,I(t) given in Figure 2, respectively, except for the phases in their evolutions. From this, we can conclude that if the measure of nonstaticity is the same as each other, the patterns of their temporal evolutions are also the same. On the other hand, we can confirm by comparing panels of Fig. 3 and Fig. 6 in Ref. [15] each other that, if the measure of nonstaticity is different, the patterns of their evolutions are no longer the same. However, ${\mathcal{W}}_{p,\mathrm{I}}(t)/{\mathcal{W}}_{p,\mathrm{R}}(t)$ and W_p,I(t)/W_p,R(t) always undergo sinusoidal evolution in any case in the static environment.

FIGURE 5

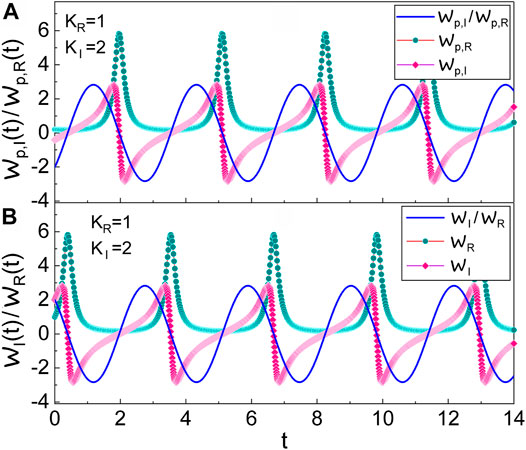
FIGURE 5. (A) is the evolution of ${\mathcal{W}}_{p,\mathrm{I}}/{\mathcal{W}}_{p,\mathrm{R}}$ with the components ${\mathcal{W}}_{p,\mathrm{R}}$ and ${\mathcal{W}}_{p,\mathrm{I}}$, where K_R = 1 and K_I = 2. (B) is the evolution of ${\mathcal{W}}_{\mathrm{I}}/{\mathcal{W}}_{\mathrm{R}}$ and its relevant components (comparison purpose). The values that we have used are A = 1, B = 5, C = 2, ω = 1, ℏ = 1, ϵ = 1, t₀ = 0, and φ = 0.

Conclusion

Through the extension of the research in q-space nonstatic-wave phenomena to its conjugate p-space ones, we pursued better understanding of wave nonstaticity including the interaction of the two component waves. Our analysis was carried out purely on the basis of analytical methods, where we did not use any approximation.

We have shown that bellies and nodes appear in the p-space evolution of the Fock and Gaussian state quantum-waves as a manifestation of their nonstaticity, like in the case of q-space evolution. The evolving pattern of the p-space wave caused by its nonstaticity is in general out of phase by π with the q-space evolution of the wave. This implies that the two wave components are reciprocally linked. Because the wave intensity is large when it constitutes a belly, the wave in each space gives and receives intensity from the conjugate wave-component periodically. If there is an initial displacement in the Gaussian wave, the wave in p-space oscillates back and forth like the q-space wave. This behavior very much resembles classical waves. However, the waveform in such an oscillation was altered due to the appearance of bellies and nodes.

Whenever the wave in q-space (p-space) poses a node, the uncertainty of q (p) reduces below its standard quantum level. From this, we can conclude that the nonstatic wave treated here is a kind of squeezed state. Several methods of generating squeezed states are known until now [18–22]. Likewise, the nonstatic wave may also be generated by using the technique of squeezed-state generation. The nonstatic wave can be used in physical disciplines where the squeezed state plays a major role, such as interferometers in gravitational-wave detection [23–25], quantum information processing [26–28], and high-precision measurements [29, 30].

It may be noticeable that nonstatic waves can arise without temporal changes of the electromagnetic parameters in media. However, we can never say that we know wave nonstaticity well if our related knowledge is limited to only q–space behavior of the light waves. The outcome of this research complements previous q-quadrature analyses in this context [15]. Based on this research, we can outline the entire aspect of wave nonstaticity including the integral connection between the q- and p-space wave behaviors.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JRC wrote the paper and approved it.

Funding

This work was supported by the National Research Foundation of Korea(NRF) grant funded by the Korea government(MSIT) (No.: NRF-2021R1F1A1062849).

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

This work is focused on the behavior of p-quadrature wave functions, but we also provide the graphics of the physical quantities associated with q-quadrature for comparison purposes. The graphics that belong to q-quadrature were depicted using the analytical evaluations given in Ref. [15].

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.789652/full#supplementary-material

References

1. Dodonov VV, Klimov AB, Nikonov DE. Quantum Phenomena in Nonstationary Media. Phys Rev A (1993) 47(5):4422–9. doi:10.1103/physreva.47.4422

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Akhmanov SA, Sukhorukov AP, Chirkin AS. Nonstationary Phenomena and Space-Time Analogy in Nonlinear Optics. Soviet Phys JETP (1969) 28(4):748–57.

Google Scholar

3. Vorgul I. On Maxwell's Equations in Non-Stationary Media. Phil Trans R Soc A (2008) 366(1871):1781–8. doi:10.1098/rsta.2007.2186

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Dodonov AV. Photon Creation from Vacuum and Interactions Engineering in Nonstationary Circuit QED. J Phys Conf Ser (2009) 161(1):012029. doi:10.1088/1742-6596/161/1/012029

CrossRef Full Text | Google Scholar

5. Portí JA, Salinas A, Morente JA, Rodríguez-Sola M, Nerukh AG. Time-Varying Electromagnetic-Media Modelling with TLM Method. Electron Lett (2003) 39(6):505–7. doi:10.1049/el:20030390

CrossRef Full Text | Google Scholar

6. Bakunov MI, Grachev IS. Energetics of Electromagnetic Wave Transformation in a Time-Varying Magnetoplasma Medium. Phys Rev E (2002) 65(3):036405. doi:10.1103/PhysRevE.65.036405

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Shvartsburg AB, Petite G. Instantaneous Optics of Ultrashort Broadband Pulses and Rapidly Varying Media. Prog Opt (2002) 44:143–214. doi:10.1016/S0079-6638(02)80016-6

CrossRef Full Text | Google Scholar

8. Moody G, McDonald C, Feldman A, Harvey T, Mirin RP, Silverman KL. Quadrature Demodulation of a Quantum Dot Optical Response to Faint Light fields. Optica (2016) 3(12):1397–403. doi:10.1364/OPTICA.3.001397

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Bogatov AP, D'yachkov NV, Drakin AE, Gushchik TI. Amplitude and Phase Modulation of Radiation in a Travelling-Wave Amplifier Based on a Laser Diode. Quan Electron. (2013) 43(8):699–705. doi:10.1070/QE2013v043n08ABEH015166

CrossRef Full Text | Google Scholar

10. Waarts RG, Friesem AA, Hefetz Y. Frequency-modulated to Amplitude-Modulated Signal Conversion by a Brillouin-Induced Phase Change in Single-Mode Fibers. Opt Lett (1988) 13(2):152–4. doi:10.1364/OL.13.000152

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Liu B, Li X, Zhang Y, Xin X, Yu J. Probabilistic Shaping for ROF System with Heterodyne Coherent Detection. APL Photon (2017) 2(5):056104. doi:10.1063/1.4981393

CrossRef Full Text | Google Scholar

12. Mari A, Eisert J. Opto- and Electro-Mechanical Entanglement Improved by Modulation. New J Phys (2012) 14:075014. doi:10.1088/1367-2630/14/7/075014

CrossRef Full Text | Google Scholar

13. Averchenko V, Sych D, Schunk G, Vogl U, Marquardt C, Leuchs G. Temporal Shaping of Single Photons Enabled by Entanglement. Phys Rev A (2017) 96(4):043822. doi:10.1103/PhysRevA.96.043822

CrossRef Full Text | Google Scholar

14. Savage RL, Joshi C, Mori WB. Frequency Upconversion of Electromagnetic Radiation upon Transmission into an Ionization Front. Phys Rev Lett (1992) 68(7):946–9. doi:10.1103/PhysRevLett.68.946

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Choi JR. On the Possible Emergence of Nonstatic Quantum Waves in a Static Environment. Nonlinear Dyn (2021) 103(3):2783–92. doi:10.1007/s11071-021-06222-8

CrossRef Full Text | Google Scholar

16. Choi JR. Characteristics of Nonstatic Quantum Light Waves: the Principle for Wave Expansion and Collapse. Photonics (2021) 8(5):158. doi:10.3390/photonics8050158

CrossRef Full Text | Google Scholar

17. Choi JR. Quadrature Squeezing and Geometric-Phase Oscillations in Nano-Optics. Nanomaterials (2020) 10(7):1391. doi:10.3390/nano10071391

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Han Y, Wen X, Liu J, He J, Wang J. Generation of Polarization Squeezed Light with an Optical Parametric Amplifier at 795 nm. Opt Commun (2018) 416:1–4. doi:10.1016/j.optcom.2018.01.038

CrossRef Full Text | Google Scholar

19. Ma L, Guo H, Sun H, Liu K, Su B, Gao J. Generation of Squeezed States of Light in Arbitrary Complex Amplitude Transverse Distribution. Photon Res (2020) 8(9):1422–7. doi:10.1364/PRJ.388956

CrossRef Full Text | Google Scholar

20. Li Y-q., Xiao M. Generation and Applications of Amplitude-Squeezed States of Light from Semiconductor Diode Lasers. Opt Express (1998) 2(3):110–7. doi:10.1364/OE.2.000110

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Raizen MG, Orozco LA, Xiao M, Boyd TL, Kimble HJ. Squeezed-State Generation by the Normal Modes of a Coupled System. Phys Rev Lett (1987) 59(2):198–201. doi:10.1103/PhysRevLett.59.198

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Yurke B. Use of Cavities in Squeezed-State Generation. Phys Rev A (1984) 29(1):408–10. doi:10.1103/PhysRevA.29.408

CrossRef Full Text | Google Scholar

23. Grote H, Danzmann K, Dooley KL, Schnabel R, Slutsky J, Vahlbruch H. First Long-Term Application of Squeezed States of Light in a Gravitational-Wave Observatory. Phys Rev Lett (2013) 110(18):181101. doi:10.1103/PhysRevLett.110.181101

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Aasi J, Abadie J, Abbott BP, Abbott R, Abbott TD, Abernathy MR, et al. The LIGO Scientific Collaboration. Enhanced Sensitivity of the LIGO Gravitational Wave Detector by Using Squeezed States of Light. Nat Photon (2013) 7(8):613–9. doi:10.1038/nphoton.2013.177

CrossRef Full Text | Google Scholar

25. Abadie J, Abbott BP, Abbott R, Abbott TD, Abernathy M, Adams C, et al. The LIGO Scientific Collaboration. A Gravitational Wave Observatory Operating beyond the Quantum Shot-Noise Limit. Nat Phys (2011) 7:962–5. doi:10.1038/nphys2083

CrossRef Full Text | Google Scholar

26. Appel J, Figueroa E, Korystov D, Lobino M, LLvovsky AI. Quantum Memory for Squeezed Light. Phys Rev Lett (2008) 100(9):093602. doi:10.1103/PhysRevLett.100.093602

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Honda K, Akamatsu D, Arikawa M, Yokoi Y, Akiba K, Nagatsuka S, et al. Storage and Retrieval of a Squeezed Vacuum. Phys Rev Lett (2008) 100(9):093601. doi:10.1103/PhysRevLett.100.093601

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Hétet G, Buchler BC, Glöeckl O, Hsu MTL, Akulshin AM, Bachor HA, et al. Delay of Squeezing and Entanglement Using Electromagnetically Induced Transparency in a Vapour Cell. Opt Express (2008) 16(10):7369–81. doi:10.1364/OE.16.007369

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Liu K, Cai C, Li J, Ma L, Sun H, Gao J. Squeezing-enhanced Rotating-Angle Measurement beyond the Quantum Limit. Appl Phys Lett (2018) 113(26):261103. doi:10.1063/1.5066028

CrossRef Full Text | Google Scholar

30. Smithey DT, Beck M, Raymer MG, Faridani A. Measurement of the Wigner Distribution and the Density Matrix of a Light Mode Using Optical Homodyne Tomography: Application to Squeezed States and the Vacuum. Phys Rev Lett (1993) 70(9):1244–7. doi:10.1103/PhysRevLett.70.1244

PubMed Abstract | CrossRef Full Text | Google Scholar

Appendix A Evaluation of the Fock-State Wave Functions in p-space

The wave functions which exhibit nonstatic properties in p-space can be obtained from the Fourier transformation of the wave functions in q-space. The wave functions for the nonstatic waves in q-space, which propagate in a static environment, are given by [15].

$⟨q|{\psi }_n(t)⟩=⟨q|{\varphi }_n(t)⟩\exp [i{\gamma }_n(t)],(\mathrm{A1})$

where $⟨q|{\varphi }_n⟩$ are eigenstates of the form

$⟨q|{\varphi }_n⟩={\left(\frac{W_R(t)}{\pi }\right)}^{1/4}\frac{1}{\sqrt{2^{n}n!}}{H}_n\left(\sqrt{W_R(t)}q\right)\exp \left[-\frac{W(t)}{2}{q}^2\right].(\mathrm{A2})$

Let us carry out the Fourier transformation of these waves, such that

$⟨p|{\psi }_n(t)⟩=\frac{1}{\sqrt{2\pi \hslash }}{\int }_{-\infty }^{\infty }⟨q|{\psi }_n(t)⟩e^{-ipq/\hslash }dq.(\mathrm{A3})$

By evaluating the above equation using Eqs. A1, A2 straightforwardly, we easily have the p-space wave functions, which are given in Eq. 6 with Eqs. 7-9 in the text.

Appendix B The Gaussian Wave in p-space

The Gaussian wave in q-space, that exhibits nonstatic properties, was suggested in Ref. [15]. From that reference, the corresponding wave function is given by

$⟨q|\psi (t)⟩=N(t)\exp \left[-\frac{\mathcal{W}(t)}{2}{q}^2+R(t)q\right],(\mathrm{B1})$

where N(t), $\mathcal{W}(t)$, and R(t) are defined in the text. From the Fourier transformation of this, we have the exact wave function for the Gaussian wave in p-space, which is given in Eq. 13 with Eqs. 14-19.