Synchronizability of Multi-Layer Dual-Center Coupled Star Networks

In the research on complex networks, synchronizability is a significant measurement of network nature. Several research studies center around the synchronizability of single-layer complex networks and few studies on the synchronizability of multi-layer networks. Firstly, this paper calculates the Laplacian spectrum of multi-layer dual-center coupled star networks and multi-layer dual-center coupled star–ring networks according to the master stability function (MSF) and obtains important indicators reflecting the synchronizability of the above two network structures. Secondly, it discusses the relationships among synchronizability and various parameters, and numerical simulations are given to illustrate the effectiveness of the theoretical results. Finally, it is found that the two sorts of networks studied in this paper are of the same synchronizability, and compared with that of a single-center network structure, the synchronizability of two dual-center structures is relatively weaker.

1 Introduction

In recent years, the multi-layer complex networks have been applied in many fields, such as communication networks, coupled financial networks, transportation networks, power networks, and social networks [1, 2]. With the furthering of the study, many good results were obtained in different research branches, such as complex network synchronization [3–14], stochastic dynamics [15–17], multi-layer network modeling and consensus problems [18–22], and robustness of multi-layer networks [23–25]. The star network is a more common network structure in computer science. It has one center node, which connects the rest of the nodes. So, it is convenient to add nodes in an actual network when it is needed. At the same time, it can easily control the security of data and monitor the network. In addition, if a leaf node fails working, the network will not be paralyzed. These good properties of star structures attracted attention of many researchers. Li et al. gave three different inter-layer connection modes for the dual networks and analyzed the synchronizability of multi-layer networks according to the MSF [26]. Xu et al. studied the relationships among the synchronizability of two-layer star networks and parameters in the case of the unbounded and bounded synchronous regions [27]. Zhang et al. studied the synchronizability of multi-layer K-nearest-neighbor networks and analyzed the impacts of some parameters (such as the network size, the number of layers) on network synchronizability [28]. Deng et al. compared the synchronizability of single-center three-layer star–ring networks and discussed the relationships among the parameters in the case of the unbounded and bounded synchronous regions [29]. Inspired by the above literature, the main contributions of this paper are as follows:

1) We defined two kinds of multi-layer dual-center star networks. One is a class of multi-layer dual-center coupled star networks, and the other is a class of multi-layer dual-center coupled star–ring networks.

2) We derived the eigenvalue spectrum of the multi-layer dual-center coupled star networks and star–ring networks according to the MSF and obtained important indicators reflecting the synchronizability of the two network structures.

3) According to the real situation, the networks of coupling strengths are considered, and the specific relationships among synchronizability and some parameters, such as the intra-layer and inter-layer coupling strengths, are analyzed.

4) Under the same initial conditions, we compared the synchronizability of multi-layer single-center and dual-center star networks.

The structure of this paper is as follows: the preliminaries of the multi-layer dual-center networks’ synchronizability are given in Section 2. Section 3 studies the synchronizability index of the multi-layer dual-center star networks. Section 4 explores the synchronizability index of the multi-layer dual-center star–ring networks. The numerical simulations are shown in Section 5. Finally, the conclusions are given in Section 6.

2 Preliminaries

The dynamics of the ith node of the Pth layer in an M-layer network can be written as follows:

${\dot{x}}_i^P=f\left(x_i^P\right)-a_P\sum _{j=1}^N{l}_{ij}^{P}Q\left(x_j^P\right)-d_{PL}\sum _{L=1}^M{d}_i^{PL}\mathrm{\Gamma }\left(x_i^L\right),\left(1\right)$

$i=\mathrm{1,2,3},\dots ,N;P=\mathrm{1,2,3},\dots ,M.$

Here, $x_i^P\in {\mathbb{R}}^{\mathbb{N}}$ represents the state of the ith node of the Pth layer, f (◦) represents the dynamic function, and Q and Γ are the intra-layer and the inter-layer coupling function. a_P and d_PL represent the intra-layer coupling strength and the inter-layer coupling strength.

Let $L^P=(l_{ij}^P)$ be the Laplacian matrix of the Pth layer, where L^P = S^P−W^P. S^P is the degree matrix of the Pth layer. $W^P=(W_{ij}^P)$ is the adjacency matrix of the Pth layer, if the node v_i is connected with the node v_j in the Pth layer, $W_{ij}^P=1$; otherwise, $W_{ij}^P=0$, i, j = 1, 2, …, N. Let L^(P) = a_P (S^P−W^P) be the intra-layer weighted supra-Laplacian matrix of the Pth layer.

The intra-layer weighted supra-Laplacian matrix of the M layers is denoted by Ψ_L, and it can be represented by the supra-Laplacian matrix L^(P),

${\mathrm{\Psi }}_L=\left(\begin{array}{ccccc}\hfill L^{\left(1\right)}\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill L^{\left(2\right)}\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill L^{\left(M-1\right)}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill L^{\left(M\right)}\hfill \end{array}\right)=\underset{P=1}{\overset{M}{\oplus }}{L}^{\left(P\right)}.$

The inter-layer weighted supra-Laplacian matrix of the M layers is Ψ_I = L_I ⊗I_N, where ⊗ is the Kronecker product and I_N is the N × N identity matrix. $L_I=-d(d_i^{PL})\in {\mathbb{R}}^{M\times M}$, if the ith nodes of the Pth layer and the Lth layer are connected, $d_i^{PL}=1$; otherwise, $d_i^{PL}=0$, and there is

$d_i^{PP}=-\sum _{L=1L\ne P}^M{d}_i^{PL},L,P=\mathrm{1,2},\dots ,M.$

Let Ψ be the supra-Laplacian matrix of the M layers, Ψ = Ψ_I + Ψ_L.

λ₂ and λ_max represent the minimum non-zero eigenvalue and the maximum eigenvalue of the supra-Laplacian matrix. According to the MSF, we study the synchronizability of networks under the background of two synchronous regions. (I) When the synchronous region is bounded, we use r = λ_max/λ₂ as an indicator to measure synchronizability: the smaller the r, the stronger the synchronizability of networks. (II) When the synchronous region is unbounded, we use λ₂ as an indicator to measure synchronizability. The larger the λ₂, the stronger the synchronizability of networks [30, 31].

Lemma 1 ([8]). Let A, B be two square matrices and M be an integer. Then,

${\left|\begin{array}{cccc}\hfill A\hfill & \hfill B\hfill & \hfill \dots \hfill & \hfill B\hfill \\ \hfill B\hfill & \hfill A\hfill & \hfill \dots \hfill & \hfill B\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill B\hfill & \hfill B\hfill & \hfill \dots \hfill & \hfill A\hfill \end{array}\right|}_{M\times M}=|A+\left(M-1\right)B|\cdot |A-B{|}^{\left(M-1\right)}.$

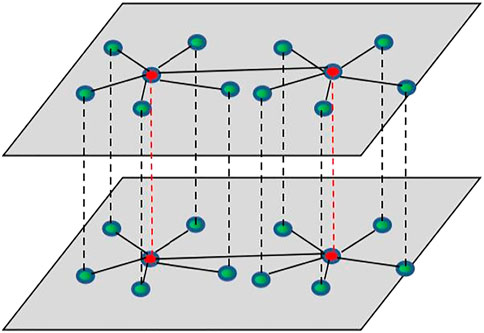
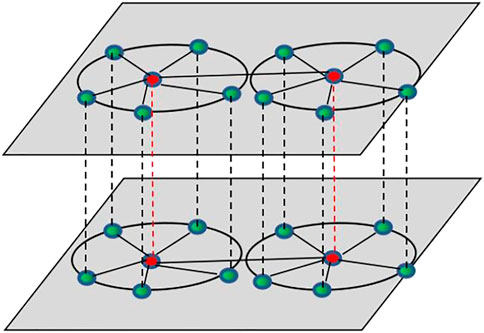
In the following, the M-layer dual-center coupled star networks and star–ring networks will be considered. The two-layer dual-center coupled star network and star–ring network are shown in Figure 1 and Figure 2, respectively. The red nodes represent the center nodes, the blue nodes represent the leaf nodes, the solid lines represent the coupling between the corresponding nodes in the layer, and the dotted lines denote the coupling between the corresponding nodes between the layers.

FIGURE 1

FIGURE 1. A two-layer dual-center coupled star network.

FIGURE 2

FIGURE 2. A two-layer dual-center coupled star–ring network.

3 The Synchronizability Index of Multi-Layer Dual-Center Coupled Star Networks

The M-layer dual-center coupled star networks are considered in this section. It is assumed that the networks of each layer contain two center nodes and 2N−2 leaf nodes. The intra-layer coupling strength is denoted by a, and the inter-layer coupling strength is denoted by d. Then, the supra-Laplacian matrix of the M-layer dual-center coupled star networks is

$\mathrm{\Psi }=\left(\begin{array}{cccccccc}\hfill A_1\hfill & \hfill B_1\hfill & \hfill -d{I}_N\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill -d{I}_N\hfill & \hfill 0\hfill \\ \hfill B_1\hfill & \hfill A_1\hfill & \hfill 0\hfill & \hfill -d{I}_N\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill -d{I}_N\hfill \\ \hfill -d{I}_N\hfill & \hfill 0\hfill & \hfill A_1\hfill & \hfill B_1\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill -d{I}_N\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -d{I}_N\hfill & \hfill B_1\hfill & \hfill A_1\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill -d{I}_N\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill -d{I}_N\hfill & \hfill 0\hfill & \hfill -d{I}_N\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill A_1\hfill & \hfill B_1\hfill \\ \hfill 0\hfill & \hfill -d{I}_N\hfill & \hfill 0\hfill & \hfill -d{I}_N\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill B_1\hfill & \hfill A_1\hfill \end{array}\right),$

$A_1={\left(\begin{array}{ccccc}\hfill Na+(M-1)d\hfill & \hfill -a\hfill & \hfill -a\hfill & \hfill \dots \hfill & \hfill -a\hfill \\ \hfill -a\hfill & \hfill a+(M-1)d\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill -a\hfill & \hfill 0\hfill & \hfill a+(M-1)d\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill -a\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill a+(M-1)d\hfill \end{array}\right)}_{N\times N},$

$B_1={\left(\begin{array}{ccccc}\hfill -a\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \end{array}\right)}_{N\times N}$.

Let $A=\left(\begin{array}{cc}\hfill A_1\hfill & \hfill B_1\hfill \\ \hfill B_1\hfill & \hfill A_1\hfill \end{array}\right)$,

$B=\left(\begin{array}{cc}\hfill -d{I}_N\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -d{I}_N\hfill \end{array}\right).$

By Lemma 1, we have |λI − Ψ| = |λI − A−(M−1)B‖λI − A+ B|^(M−1),

$|\lambda I-A-\left(M-1\right)B|={\left|\begin{array}{cccccccccc}\hfill \mathrm{\Delta }\hfill & \hfill a\hfill & \hfill a\hfill & \hfill \dots \hfill & \hfill a\hfill & \hfill a\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill a\hfill & \hfill \mathrm{\Upsilon }\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill a\hfill & \hfill 0\hfill & \hfill \mathrm{\Upsilon }\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill a\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill \mathrm{\Upsilon }\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill a\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill \mathrm{\Delta }\hfill & \hfill a\hfill & \hfill a\hfill & \hfill \dots \hfill & \hfill a\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill a\hfill & \hfill \mathrm{\Upsilon }\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill a\hfill & \hfill 0\hfill & \hfill \mathrm{\Upsilon }\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill a\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill \mathrm{\Upsilon }\hfill \end{array}\right|}_{\left(2N\right)\times \left(2N\right)},(1)$

where Δ = λ−Na, ϒ = λ−a.

$|\lambda I-A+B|={\left|\begin{array}{cccccccccc}\hfill \mathrm{\Omega }\hfill & \hfill a\hfill & \hfill a\hfill & \hfill \dots \hfill & \hfill a\hfill & \hfill a\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill a\hfill & \hfill ○\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill a\hfill & \hfill 0\hfill & \hfill ○\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill a\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill ○\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill a\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill \mathrm{\Omega }\hfill & \hfill a\hfill & \hfill a\hfill & \hfill \dots \hfill & \hfill a\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill a\hfill & \hfill ○\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill a\hfill & \hfill 0\hfill & \hfill ○\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill a\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill ○\hfill \end{array}\right|}_{\left(2N\right)\times \left(2N\right)},(2)$

where Ω = λ−Na−Md, ○ = λ−a−Md.

The eigenvalues of (2) are

$Md,Na+Md,\underset{2N-4}{\underbrace{a+Md,\dots ,a+Md}},$

$\frac{Na+2Md+2a+a\sqrt{N^2+4N-4}}{2},\frac{Na+2Md+2a-a\sqrt{N^2+4N-4}}{2}.$

When M = 0, one can get the eigenvalues of (1).

Therefore, the eigenvalue spectrum of the supra-Laplacian matrix can be acquired:

$0,Na,\frac{Na+2a+a\sqrt{N^2+4N-4}}{2},\frac{Na+2a-a\sqrt{N^2+4N-4}}{2},\underset{2N-4}{\underbrace{a,\dots ,a}},$

$\underset{M-1}{\underbrace{\frac{Na+2Md+2a+a\sqrt{N^2+4N-4}}{2}}},\underset{M-1}{\underbrace{\frac{Na+2Md+2a-a\sqrt{N^2+4N-4}}{2}}},$

$\underset{M-1}{\underbrace{Md}},\underset{M-1}{\underbrace{Na+Md}},\underset{\left(2N-4\right)\left(M-1\right)}{\underbrace{a+Md,\dots ,a+Md}}.$

The minimum non-zero eigenvalue is

${\lambda }_2=\mathit{min}\left\{Md,\frac{Na+2a-a\sqrt{N^2+4N-4}}{2}\right\}.$

The maximum eigenvalue is

${\lambda }_{\mathit{max}}=\frac{Na+2Md+2a+a\sqrt{N^2+4N-4}}{2}.$

4 The Synchronizability Index of Multi-Layer Dual-Center Coupled Star–Ring Networks

The case of M-layer dual-center star–ring networks is considered in this section. Each layer is supposed to contain two center nodes and 2N−2 leaf nodes, the intra-layer coupling strength is a, and the inter-layer coupling strength is d. Then, the supra-Laplacian matrix of the dual-center coupled star–ring networks of M layers is

$\tilde{\mathrm{\Psi }}=\left(\begin{array}{cccccccc}\hfill A_2\hfill & \hfill B_2\hfill & \hfill -d{I}_N\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill -d{I}_N\hfill & \hfill 0\hfill \\ \hfill B_2\hfill & \hfill A_2\hfill & \hfill 0\hfill & \hfill -d{I}_N\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill -d{I}_N\hfill \\ \hfill -d{I}_N\hfill & \hfill 0\hfill & \hfill A_2\hfill & \hfill B_2\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill -d{I}_N\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -d{I}_N\hfill & \hfill B_2\hfill & \hfill A_2\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill -d{I}_N\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill -d{I}_N\hfill & \hfill 0\hfill & \hfill -d{I}_N\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill A_2\hfill & \hfill B_2\hfill \\ \hfill 0\hfill & \hfill -d{I}_N\hfill & \hfill 0\hfill & \hfill -d{I}_N\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill B_2\hfill & \hfill A_2\hfill \end{array}\right),$

$A_2={\left(\begin{array}{ccccc}\hfill Na+(M-1)d\hfill & \hfill -a\hfill & \hfill -a\hfill & \hfill \dots \hfill & \hfill -a\hfill \\ \hfill -a\hfill & \hfill 3a+(M-1)d\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill 0\hfill & \hfill 3a+(M-1)d\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill -a\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 3a+(M-1)d\hfill \end{array}\right)}_{N\times N},$ $B_2={\left(\begin{array}{ccccc}\hfill -a\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \end{array}\right)}_{N\times N}$.

Similar to the method in Section 3, one can get the eigenvalue spectrum of the star–ring networks as follows.

When N is odd,

$0,Na,\frac{Na+2a+a\sqrt{N^2+4N-4}}{2},\frac{Na+2a-a\sqrt{N^2+4N-4}}{2},$

$\underset{2}{\underbrace{5a}},\underset{4}{\underbrace{a+4a{\sin }^2\left(k\pi /\left(2\left(N-1\right)\right)\right)}},k=\mathrm{2,4,6},\dots ,N-3,$

$\underset{M-1}{\underbrace{\frac{Na+2Md+2a+a\sqrt{N^2+4N-4}}{2}}},\underset{M-1}{\underbrace{\frac{Na+2Md+2a-a\sqrt{N^2+4N-4}}{2}}},$

$\underset{M-1}{\underbrace{Md}},\underset{M-1}{\underbrace{Na+Md}},\underset{2\left(M-1\right)}{\underbrace{Md+5a}},$

$\underset{4\left(M-1\right)}{\underbrace{Md+a+4a{\sin }^2\left(k\pi /\left(2\left(N-1\right)\right)\right)}},k=\mathrm{2,4,6},\dots ,N-3.$

When N is even,

$\frac{Na+2a+a\sqrt{N^2+4N-4}}{2},\frac{Na+2a-a\sqrt{N^2+4N-4}}{2},$

$0,Na,\underset{M-1}{\underbrace{Md}},\underset{M-1}{\underbrace{Na+Md}},\underset{4}{\underbrace{a+4a{\sin }^2\left(k\pi /\left(2\left(N-1\right)\right)\right)}},k=\mathrm{2,4,6},\dots ,N-2,$

$\underset{M-1}{\underbrace{\frac{Na+2Md+2a+a\sqrt{N^2+4N-4}}{2}}},\underset{M-1}{\underbrace{\frac{Na+2Md+2a-a\sqrt{N^2+4N-4}}{2}}},$

$\underset{4\left(M-1\right)}{\underbrace{Md+a+4a{\sin }^2\left(k\pi /\left(2\left(N-1\right)\right)\right)}},k=\mathrm{2,4,6},\dots ,N-2.$

Whenever N is odd or even, the minimum non-zero eigenvalue is

${\lambda }_2=\mathit{min}\left\{Md,\frac{Na+2a-a\sqrt{N^2+4N-4}}{2}\right\}.$

The maximum eigenvalue is

${\lambda }_{\mathit{max}}=\frac{Na+2Md+2a+a\sqrt{N^2+4N-4}}{2}.$

5 Numerical Simulation

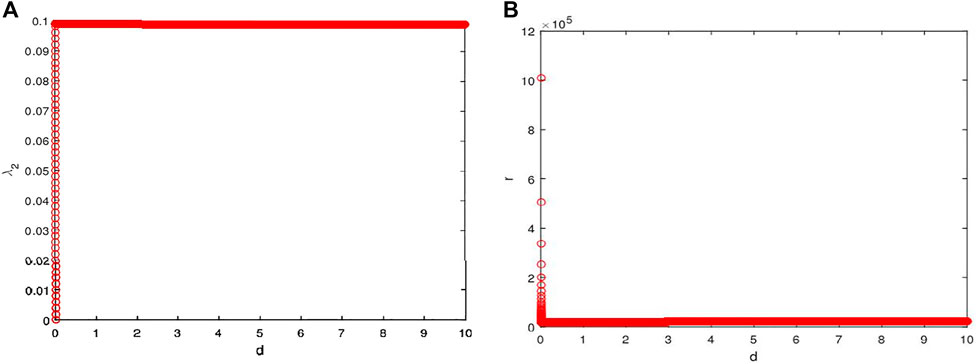
Let N = 200, a = 10, M = 20. As shown in Figure 3A, λ₂ increases with $d(d<d_0=\frac{Na+2a-a\sqrt{N^2+4N-4}}{2M})$ and reaches Md₀ (d > d₀) in the case of the unbounded synchronous region. This means that synchronizability is first strengthened, which then remained unchanged with increasing d. As shown in Figure 3B, r first decreases with d (d < d₀) and then increases slowly d (d > d₀) in the case of the bounded synchronous region. It implies that synchronizability is strengthened firstly, which then slowly gets weakened after reaching the maximum. The synchronizability of networks is maximized at $d_0=\frac{Na+2a-a\sqrt{N^2+4N-4}}{2M}$.

FIGURE 3

FIGURE 3. (A) Variance of λ₂. (B) Variance of r = λ_max/λ₂.

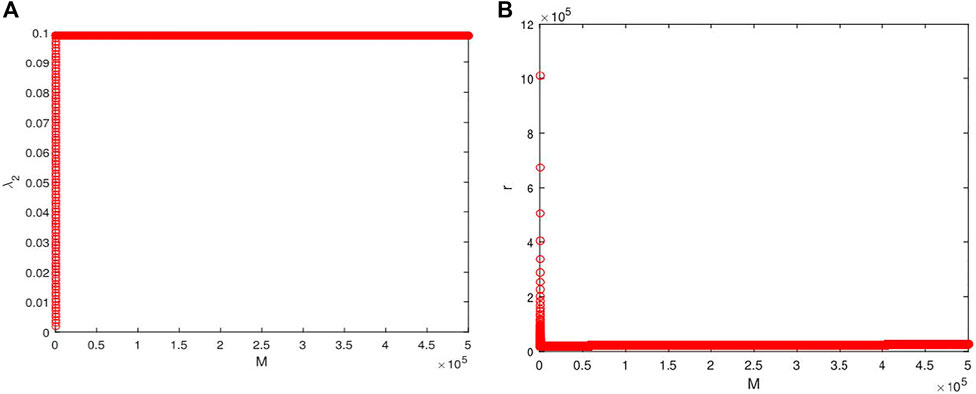
Let N = 200, d = 0.001, M = 20. As shown in Figure 4A, λ₂ increases with $a(a<a_0=\frac{Md(N+2+\sqrt{N^2+4N-4})}{4})$ and reaches Md (a > a₀) in the case of the unbounded synchronous region. This means that synchronizability is first strengthened, which then remained unchanged with increasing a. As shown in Figure 4B, r first decreases with a (a < a₀) and increases monotonically a (a > a₀) in the case of the bounded synchronous region. It implies that synchronizability is strengthened firstly, which then slowly gets weakened after reaching the maximum. The synchronizability of networks is maximized at $a_0=\frac{Md(N+2+\sqrt{N^2+4N-4})}{4}$.

FIGURE 4

FIGURE 4. (A) Variance of λ₂. (B) Variance of r = λ_max/λ₂.

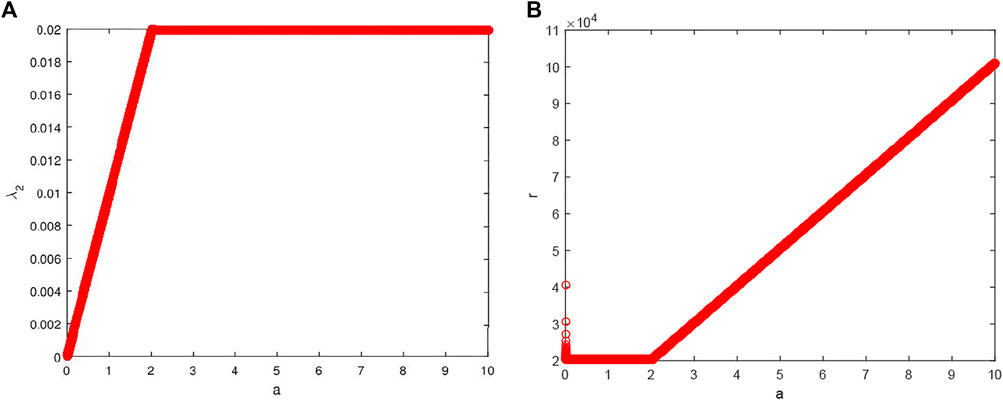
Let N = 200, d = 0.001, a = 10. As shown in Figure 5A, λ₂ increases with $M(M<M_0=\frac{Na+2a-a\sqrt{N^2+4N-4}}{2d})$ and reaches dM₀ (M > M₀) in the case of the unbounded synchronous region. This means that synchronizability is first strengthened, which then remained unchanged with increasing M. As shown in Figure 5B, r first decreases with M (M < M₀) and increases monotonically M (M > M₀) in the case of the bounded synchronous region. It implies that synchronizability is strengthened, which then reaches its maximum at M₀ and finally gets weakened with increasing M. The synchronizability of networks is maximized at $M_0=\frac{Na+2a-a\sqrt{N^2+4N-4}}{2d}$.

FIGURE 5

FIGURE 5. (A) Variance of λ₂. (B) Variance of r = λ_max/λ₂.

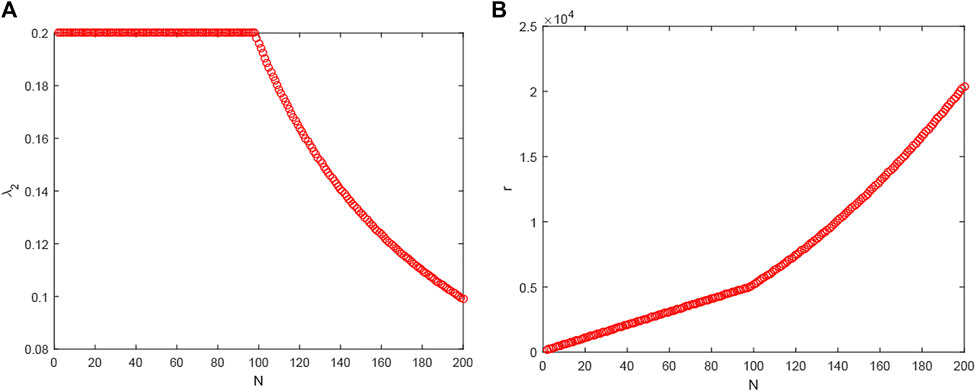
Let M = 20, d = 0.01, a = 10. As shown in Figure 6A, λ₂ remains unchanged with $N(N<N_0=\lfloor \frac{2a}{Md}+\frac{Md}{a}-2\rfloor )$ and decreases with N (N > N₀) in the case of the unbounded synchronous region. This means that the synchronizability of networks first remained unchanged and then weakened with increasing N. As shown in Figure 6B, r increases with increasing N in the case of the bounded synchronous region. This implies that synchronizability is weakened with increasing N.

FIGURE 6

FIGURE 6. (A) Variance of λ₂. (B) Variance of r = λ_max/λ₂.

6 Conclusion

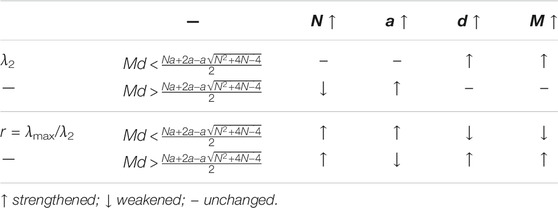
Considering the above cases, we found that the synchronizability of the two sorts of networks is the same. Whether the synchronous region is unbounded or bounded, the synchronizability of both networks is related to the intra-layer and the inter-layer coupling strength and the number of layers and nodes. The specific relation of synchronizability is given in Table 1, and the relationship among parameters is well verified by numerical simulation.

TABLE 1

TABLE 1. Synchronizability of star networks with N, a, d, M.

When N is large enough, we can calculate λ₂ and r of a single-center star network with 2N nodes as follows [27]:

${\lambda }_2=\mathit{min}\left\{Md,a\right\},r=\left(2Na+Md\right)/\mathit{min}\left\{Md,a\right\}.$

Compared with the numbers of 2N nodes in this paper, the synchronizability of multi-layer dual-center coupled star networks is weaker than that of single-center coupled star networks. When N is large enough, we can calculate λ₂ and r of single-center star–ring networks with 2N nodes as follows [29]:

${\lambda }_2=\mathit{min}\left\{Md,a+4a{\sin }^2\left(\pi /\left(2N-1\right)\right)\right\},$

$r=\left(2Na+Md\right)/\mathit{min}\left\{Md,a+4a{\sin }^2\left(\pi /\left(2N-1\right)\right)\right\}.$

Based on the above situations, through the comparison with the synchronizability of multi-layer dual-center coupled star–ring networks in this paper, the following conclusion is obtained: the synchronizability of multi-layer dual-center coupled star–ring networks is weaker than that of multi-layer single-center star–ring networks.

There are still many problems to be solved in multi-layer dual-center star networks, for example, how the synchronizability of multi-layer dual-center coupled star networks and star–ring networks changes when the coupling strengths are different in each layer. When a single center is converted to a dual center, the network synchronizability will be correspondingly weakened. If it is transformed into a multi-center, how will the network synchronizability change? These are worthy of our further study.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.

Author Contributions

DH and JZ; methodology, DH, JZ, and ZY; software, JZ and PP; validation, DH, JZ, and ZY, formal analysis, JZ and DH; writing—original draft preparation, JZ and PP; writing—review and editing, DH, JZ, and ZY; supervision, ZY, HJ, and PP.

Funding

This work was supported by the Natural Science Foundation of Xinjiang (NSFXJ) (No. 2019D01B10), Scientific Research and Education Project of Xinjiang Institute of Engineering (2020xgy332302), National Innovation and Entrepreneurship Training Program for College Students (No. 202110994006) and the project of Key Laboratory of New Energy and Materials Research of Xinjiang Institute of Engineering.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We express our sincere gratitude to the persons who gave us valuable comments.

References

1. Cozzo E, Baños RA, Meloni S, Moreno Y. Contact-based Social Contagion in Multiplex Networks. Phys Rev E Stat Nonlin Soft Matter Phys (2013) 88(5):050801. doi:10.1103/PhysRevE.88.050801

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Huang S, Zhang J, Wang L, Hua XS. Social Friend Recommendation Based on Multiple Network Correlation. IEEE Trans Multimedia (2016) 18(2):87–299. doi:10.1109/tmm.2015.2510333

CrossRef Full Text | Google Scholar

3. Zhang S, Wu X, Lu J-A, Feng H, Lu J. Recovering Structures of Complex Dynamical Networks Based on Generalized Outer Synchronization. IEEE Trans Circuits Syst (2014) 61(11):3216–24. doi:10.1109/tcsi.2014.2334951

CrossRef Full Text | Google Scholar

4. Shen J, Tang LK. Intra-layer Synchronization in Duplex Networks. Chin Phys B (2018) 27(10):100701. doi:10.1088/1674-1056/27/10/100503

CrossRef Full Text | Google Scholar

5. Gambuzza LV, Frasca M, Gómez-Gardeñes J. Intra-layer Synchronization in Multiplex Networks. Epl (2015) 110(2):20010. doi:10.1209/0295-5075/110/20010

CrossRef Full Text | Google Scholar

6. Wei X, Emenheiser J, Wu X, Lu J-a., D'Souza RM. Maximizing Synchronizability of Duplex Networks. Chaos (2018) 28(1):013110. doi:10.1063/1.5008955

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Sevilla-Escoboza R, Sendiña-Nadal I, Leyva I, Gutiérrez R, Buldú JM, Boccaletti S. Inter-layer Synchronization in Multiplex Networks of Identical Layers. Chaos (2016) 26:065304. doi:10.1063/1.4952967

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Deng Y, Jia Z, Deng G, Zhang Q. Eigenvalue Spectrum and Synchronizability of Multiplex Chain Networks. Physica A: Stat Mech its Appl (2020) 537:122631. doi:10.1016/j.physa.2019.122631

CrossRef Full Text | Google Scholar

9. Aguirre J, Sevilla-Escoboza R, Gutiérrez R, Papo D, Buldú JM. Synchronization of Interconnected Networks: the Role of Connector Nodes. Phys Rev Lett (2014) 112(24):248701. doi:10.1103/physrevlett.112.248701

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Li N, Zheng WX. Bipartite Synchronization for Inertia Memristor-Based Neural Networks on Coopetition Networks. Neural networks (2020) 124:39–49. doi:10.1016/j.neunet.2019.11.010

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Li J, Luan Y, Wu X, Lu J-a.. Synchronizability of Double-Layer Dumbbell Networks. Chaos (2021) 31:073101. doi:10.1063/5.0049281

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Wei J, Wu X, Lu J, Wei X. Synchronizability of Duplex Regular Networks. Europhysics Lett (2017) 120(2):20005. doi:10.1109/TCSII.2015.2468924

CrossRef Full Text | Google Scholar

13. Rakshit S, Majhi S, Bera BK, Sinha S, Ghosh D. Time-varying Multiplex Network: Intralayer and Interlayer Synchronization. Phys Rev E (2017) 96(6):062308. doi:10.1103/PhysRevE.96.062308

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Zhu J, Huang D, Jiang H, Bian J, Yu Z. Synchronizability of Multi-Layer Variable Coupling Windmill-type Networks. Mathematics (2021) 9:2721. doi:10.3390/math9212721

CrossRef Full Text | Google Scholar

15. Feng Y, Zheng WX. Adaptive Tracking Control for Nonlinear Heterogeneous Multi-Agent Systems with Unknown Dynamics. J Franklin Inst (2019) 356(5):2780–97. doi:10.1016/j.jfranklin.2018.12.003

CrossRef Full Text | Google Scholar

16. Boccaletti S, Bianconi G, Criado R, del Genio CI, Gómez-Gardeñes J, Romance M, et al. The Structure and Dynamics of Multilayer Networks. Phys Rep (2014) 544(1):1–122. doi:10.1016/j.physrep.2014.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Wang Y, Wu X, Lu J, Lu JA, D’Souza R. Topology Identification in Two-Layer Complex Dynamical Networks. IEEE Trans Netw Sci Eng (2018) 7(1):538–48.

Google Scholar

18. Wei X, Wu X, Chen S, Lu J-a., Chen G. Cooperative Epidemic Spreading on a Two-Layered Interconnected Network. SIAM J Appl Dyn Syst (2018) 17(2):1503–20. doi:10.1137/17m1134202

CrossRef Full Text | Google Scholar

19. Tang L, Wu X, Lü J, Lu JA, D'Souza RM. Master Stability Functions for Complete, Intralayer, and Interlayer Synchronization in Multiplex Networks of Coupled Rössler Oscillators. Phys Rev E (2019) 99(1):012304. doi:10.1103/PhysRevE.99.012304

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Hu C, He H, Jiang H. Fixed/preassigned-time Synchronization of Complex Networks via Improving Fixed-Time Stability. IEEE Trans Cybernetics (2019) 99:1–11.

Google Scholar

21. Mei G, Wu X, Wang Y, Hu M, Lu J-A, Chen G. Compressive-Sensing-Based Structure Identification for Multilayer Networks. IEEE Trans Cybern (2018) 48(2):754–64. doi:10.1109/tcyb.2017.2655511

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Huang D, Zhu J, Yu Z, Jiang H. On Consensus index of Triplex star-like Networks: a Graph Spectra Approach. Symmetry (2021) 13(7):1248. doi:10.3390/sym13071248

CrossRef Full Text | Google Scholar

23. Shang Y. Generalized K-Core Percolation on Correlated and Uncorrelated Multiplex Networks. Phys Rev E (2020) 101(4):042306. doi:10.1103/PhysRevE.101.042306

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Wang D, Huang L. Robust Synchronization of Discontinuous Cohen-Grossberg Neural Networks: Pinning Control Approach. J Franklin Inst (2018) 355(13):5866–92. doi:10.1016/j.jfranklin.2018.05.048

CrossRef Full Text | Google Scholar

25. Shang Y. Resilient Consensus for Robust Multiplex Networks with Asymmetric Confidence Intervals. IEEE Trans Netw Sci Eng (2021) 8(1):65–74. doi:10.1109/tnse.2020.3025621

CrossRef Full Text | Google Scholar

26. Li Y, Wu X, Lu J-a., Lu J. Synchronizability of Duplex Networks. IEEE Trans Circuits Syst (2016) 63(2):206–10. doi:10.1109/tcsii.2015.2468924

CrossRef Full Text | Google Scholar

27. Xu MM, Lu JA, Zhou J. Synchronizability and Eigenvalues of Two-Layer star Networks. Acta Physica Sinica (2016) 65:028902. doi:10.7498/aps.65.028902

CrossRef Full Text | Google Scholar

28. Zhang L, Wu Y. Synchronizability of Multilayer Networks with K-Nearest-Neighbor Topologies. Front Phys (2020) 8:571507. doi:10.3389/fphy.2020.571507

CrossRef Full Text | Google Scholar

29. Deng Y, Jia Z, Yang F. Synchronizability of Multi-Layer star and star-ring Networks. Discrete Dyn Nat Soc (2020) 2020:9143917. doi:10.1155/2020/9143917

CrossRef Full Text | Google Scholar

30. Gómez S, Díaz-Guilera A, Gómez-Gardeñes J, Pérez-Vicente CJ, Moreno Y, Arenas A. Diffusion Dynamics on Multiplex Networks. Phys Rev Lett (2013) 110:028701. doi:10.1103/PhysRevLett.110.028701

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Liang Y, Wang XY. Pinning Chaotic Synchronization in Complex Networks on Maximum Eigenvalue of Low Order Matrix. wlxb (2012) 61:038901. doi:10.7498/aps.61.038901

CrossRef Full Text | Google Scholar