Investigation Into Magnetic Reconnection Formation on Propellant Ignition in Electrical Explosion

In magnetic reconnection, magnetic lines break and reconnect to change their topology to a lower-energy state. This process can liberate stored magnetic field energy and accelerate particles during unsteady explosive events. Here, we report the observations of the magnetic reconnection and kink instability of plasma jet in single wire electrical explosion and their effect on propellant ignition. The results showed that the initial velocity of plasma was ∼2,000 m/s, and when the magnetic reconnection occurred, the velocity increased by ∼400–∼2,400 m/s. The evaluated Alfvén velocity was ∼500 m/s, the Alfvén time was ∼20 µs, and the Lundquist number S = 1.7 × 10⁷. Based on these experimental results and model, the three-dimensional magnetic field topology and its evolution process was evaluated and presented. Furthermore, the magnetic reconnection occurred when its curvature reached a certain value due to the fact that the motion of the current sheet changes the topology of the magnetic field, and then, the plasma jet was accelerated and exhausted. The plasma jet angle was ∼50° in experiment 1, and it was consistent with the calculated results. The resulting magnetic reconnection plays an important role in propellant ignition, which enhances the ignition ability of wire electrical explosion. Furthermore, the results represent a key step towards resolving one of the most important problems of plasma physics and can be used to improve the understanding of wire array explosion and propellant ignition.

Introduction

In the last decades, it has been realized that a class of processes known variously as magnetic merging, magnetic field annihilation, or magnetic reconnection must be the key to change in magnetic topology [1–3]. Magnetic reconnection, which is the breaking and topological rearrangement of magnetic field lines in plasma, occurs everywhere in the universe, in solar flares, in solar corona, the Earth’s magnetosphere, and laboratory plasmas [4–15]. The laboratory plasmas mainly include magnetized plasma (16), laser-driven plasma [17], and two-gun plasma [18]. Furthermore, the most important feature of magnetic reconnection is the acceleration and heating of plasma particles.

Reference [18] suggested that the magnetic reconnection did not start or proceed in a steady manner, but rather, there were unsteady periods of time during which magnetic flux was accumulated and followed by rapid energy dissipation events. In this experiment, two plasma guns generated two hydrogen plasma current channels and embedded in a background magnetic guide field, and then, the flux ropes were merged and reconnected. Furthermore, the conversion of magnetic energy in the magnetic reconnection had also been studied [19, 20]. The results showed that electron heating occurred outside the electron diffusion region and that ion acceleration and heating dominated in a wide region of the exhaust of the reconnection layer. Approximately 50% of the magnetic energy was converted to particle energy, and two-thirds of magnetic energy was transferred to ions and one-third to electrons.

Recently, laser-driven high-energy-density plasmas have been used to study magnetic reconnection in the laboratory [17, 21, 22]. In these experiments, by focusing terawatt class lasers onto solid foils, plasma bubbles were produced and then expanded and generated megagauss-scale toroidal magnetic fields by the expansion of two bubbles placed in close proximity. Subsequently, these drove the reconnection between the self-generated or externally imposed magnetic fields [5]. Furthermore, many of the prominent fdeatures of reconnection had been observed in these experiments, including plasma jets, plasma heating, topological changes of magnetic field, and plasmoid formation. Until now, no research has been performed for magnetic reconnection in wire electrical explosion.

In this paper, we investigate the magnetic reconnection and kink instability of plasma jets in wire electrical explosion and its effect on propellant ignition. In addition, based on the experimental results, the Lundquist number, Alfvén velocity, Lorentz force, the magnetic field of discharge current, and the moving plasma are evaluated. The three-dimensional magnetic field topology and its evolution process is evaluated and presented. Finally, the effect of propellant ignition is verified by experiments.

Details of the Plasma Experiment

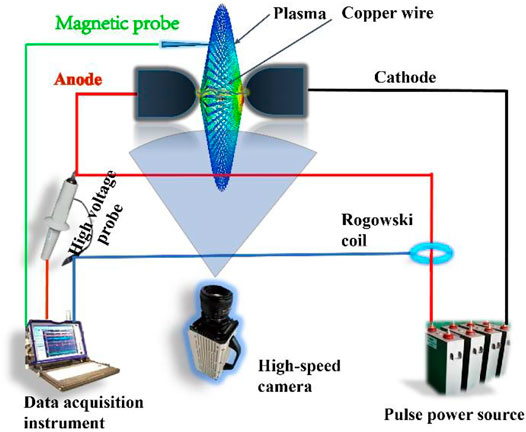
Figure 1 shows a schematic diagram of the experimental setup. A copper wire of 100 μm in diameter and ∼60 mm in length crossed the gap (the distance ∼50 mm) and connected the anode and the cathode. The electrodes were made of steel, were spherical, and had a diameter of 50 mm. The propellant was located ∼50 mm below the copper wire; the detailed compositions are listed in Table 1. A magnetic probe (TIANDUN, TR600) was located above the center of the gap (the distance ∼30 mm). The pulse power source applied in our experiments had a total capacitance of 750 μF and an inductance of 40 μH. The currents were measured by a Pearson 101 type self-integrated Rogowski coil (0.01 V A-1 and 4 MHz) with a 20-dB attenuator. The voltages were measured by a high voltage probe (Tektronix, P6015A, 1,000:1). The surface morphology of the plasma jet was recorded by a high-speed camera, using a 50,000 frames per second (fps) frequency and 20 μs exposure. The charging voltage of the pulse power source was 8 kV in the experiments. A scanning electron microscope (SEM, Keyence VE-9800S) was used to study the surface conditions of the propellant after experiments.

FIGURE 1

FIGURE 1. Schematic diagram of the experiment setup.

TABLE 1

TABLE 1. The propellant component.

According to Ampere’s law, there are two sources for creating magnetic fields in electrical explosions. One source is the discharge current, and the other source is the moving plasma. Due to the instability of plasma, the phenomenon of magnetic reconnection may occur under the interaction of two magnetic fields. In addition, the stability and instability of the plasma were observed in our experiments.

Numerical Methods

Magnetic reconnection plays a crucial role in fast changing the magnetic field topology and converting electric and magnetic energy into the plasma kinetic energy. Here, we presented a simplified numerical method that ignored thermal energy, which was ∼10% [23]. The detailed numerical methods are presented in [4, 19, 23–25].

MHD Equations of Reconnection in Resistive Magneto-hydrodynamics

The paradigm of a magnetic reconnection can only be unambiguously formulated within the framework of the resistive magneto-hydrodynamics [4]. Here, we used the brevity MHD equations where only the Ohmic dissipation was retained. It can be written in the form

${\partial }_t\rho +\nabla \left(\rho \mathrm{v}\right)=0,(1)$

${\partial }_t\mathrm{v}+\left(\mathrm{v}\nabla \right)\mathrm{v}=-\frac{1}{\rho }\nabla p+\frac{1}{\rho }\mathbf{j}\times \mathbf{B},(2)$

where $\rho$ is the plasma density, and v is the plasma velocity.

The plasma motion was caused by the pressure p gradients and Lorentz force $\mathbf{j}\times \mathbf{B}/c$. The relationship between the electric current density j and the magnetic field B is given by the equations,

$\mathbf{j}=\frac{c}{4\pi }\nabla \times \mathbf{B},(3)$

${\partial }_t\mathbf{B}=-\mathrm{c}\nabla \times \mathbf{E},(4)$

$\nabla \cdot \mathbf{B}=0,(5)$

In the ideal MHD limit [26], when the magnetic diffusivity $v_m=c^2/4\pi \sigma$ vanishes, the magnetic field lines cannot reconnect due to the Alfvén’s frozen-in theorem, which states that the magnetic flux through the surface encircled by the contour moving with the plasma is conserved.

Energy Conversion of Reconnection

Conservation law of electric and magnetic energy into the plasma kinetic energy is derived from Maxwell Eq. 23,

$\frac{\partial u}{\partial t}+\nabla \cdot S=-\mathit{E}\cdot \mathit{j},(6)$

where the total electric and magnetic energy $u=\frac{{\epsilon }_0}{2}{\mathit{E}}^2/2+{\mathit{B}}^2/2{\mu }_0$, and Poynting flux $\mathit{S}={\mu }_0^{-1}\mathit{E}\times \mathit{B}$. ${\epsilon }_0$ is the vacuum dielectric constant, and ${\mu }_0$ is the permeability of vacuum.

The $\mathit{E}\cdot \mathit{j}$ is an energy source term for plasmas; the converted energy is distributed as kinetic energy of plasmas.

Based on the method, the magnetic reconnection and its energy conversion are calculated and discussed in the next section.

Results and Discussion

Comparison Between Experiment and Calculation of Magnetic Reconnection

Figure 2 shows the time series images of plasma jet evolution for experiment 1. According to the images recorded by high-speed camera, the velocity of plasma is ∼2,000 m/s in the initial stage. Subsequently, the phenomenon of the plasma re-acceleration is obviously observed in Figures 2B–D. At this time, the kink instability of the plasma occurs. The plasma velocity increases by ∼ 400 m/s and moves towards the top of the cathode. With the further development of the discharge process, the Rayleigh–Taylor instability of plasma gradually formed, as shown in Figures 2E–H. Our observations are similar to that in the literature [16, 27, 28]. It is considered to be the Rayleigh–Taylor instability and kink instability, which is explained by magnetic reconnection. Figure 3 shows the time series images of plasma jet evolution for experiment 2, although the measured voltage and current curves in experiment 2 were similar to that in experiment 1, as shown in Figure 4A. However, the phenomenon of plasma instability was not observed; the possible reason is that the plasma kink instability did not happen, or its intensity was not enough to be observed. Figure 4B shows the magnetic probe signal. The probe signal was enhanced significantly between 1.5 and 2 ms in experiment 1. It shows that the magnetic field has been enhanced, and this occurs at the same time as shown in Figures 2B–D. However, the probe signal remained unchanged in experiment 2, which is consistent with Figure 3.

FIGURE 2

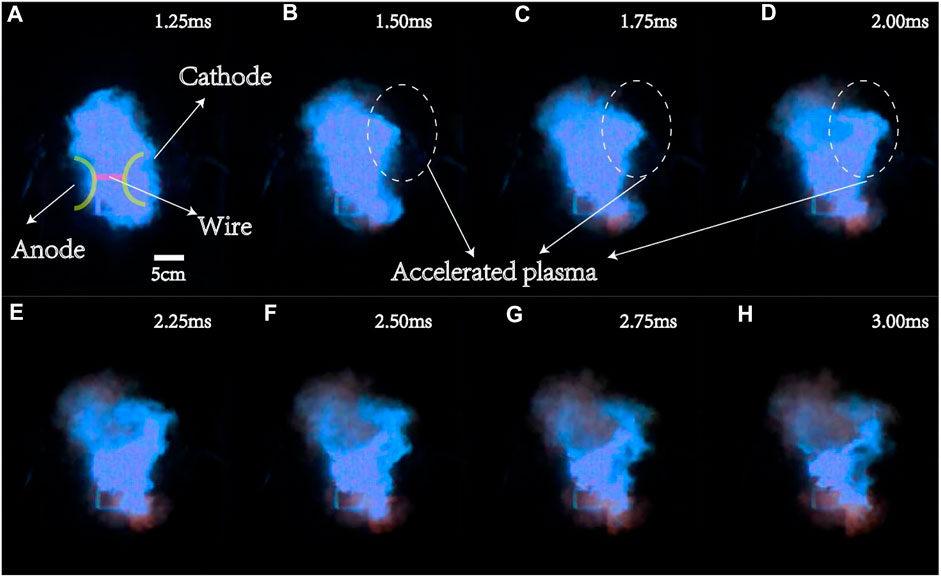
FIGURE 2. Time-series images of plasma jet evolution for experiment 1. The solid lines show the position of the electrodes in the first image; the plasma acceleration is observed in Panels (B–D), and the kink instability of plasma is observed in Panels (E, F).

FIGURE 3

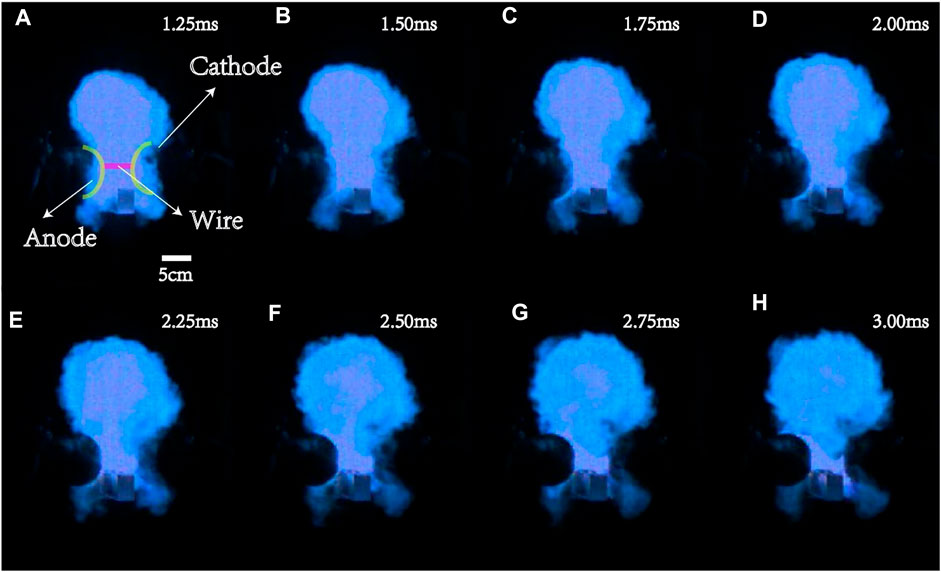
FIGURE 3. Time-series images of plasma jet evolution for experiment 2. The solid lines show the position of the electrodes in the first image, and the plasma instability is not observed.

FIGURE 4

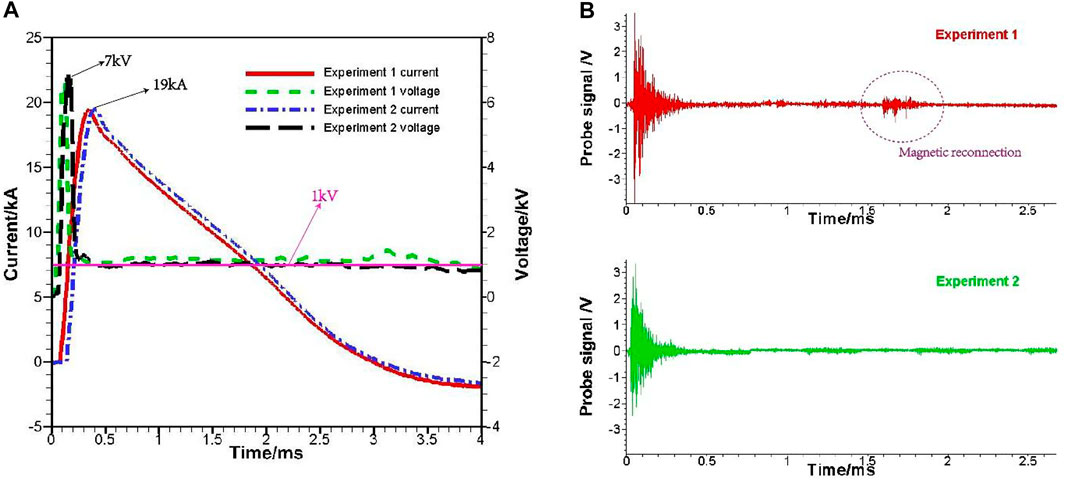
FIGURE 4. Measured discharge waveform and magnetic probe signal in the experiments. (A) The voltage and current curves of the discharge process. (B) The magnetic probe signal of the discharge process.

In magnetic reconnection, an important figure of merit in the characterization of reconnection environments is the Lundquist number (23), $S=L{V}_A/\eta$, where L is the fundamental plasma scale lengths, $V_A$ is the Alfvén velocity, and $\eta$ is the collisional resistivity. In typical solar coronal conditions (23), S ∼10¹²–10¹⁴; in the Earth’s magnetotail, S ∼10¹⁵–10¹⁶; and in a modern tokamak such as JET, S ∼10⁶–10⁸. In our experiment, the peak voltage is 7 kV and the peak current is 19 kA, the measured half-peak discharge current is ∼10 kA, and the variation trend in experiment 1 is consistent with that in experiment 2, as shown in Figure 4A. The plasma density n can be evaluated to be ∼2.5 × 10²³ m⁻³, which is similar to that in electrical explosion experiment [29]. In the discharge process, the whole magnetic fields are composed of the magnetic field formed by the discharge current and the magnetic field formed by the moving plasma to the radial direction. The evaluated magnetic field of the discharge current is ∼2 T $\left(B={\mu }_{0}I/2\pi r\right)$. In addition, according to the radial velocity of the plasma (∼2000 m/s), the evaluated current is ∼8 kA (I = nesv), and then the evaluated magnetic field of the moving plasma is ∼1.6 T. Therefore, it can be considered that the radial plasma jet is moving in the magnetic field (∼2T). Furthermore, the evaluated Alfvén velocity is ∼500 m/s ( $V_A=B/\sqrt{4\pi \rho }$, $\rho$ is the plasma mass density), the Alfvén time is ∼20 µs$\left({\mathrm{\tau }}_A=L/V_A\right)$, and the evaluated Lundquist number S = 1.7 × 10⁷. Furthermore, our observations are carried out in a steady reconnection stage, which lasted ∼1 ms, and significantly longer than its Alfvén time (∼20 µs) [19].

The electric field between electrodes is ∼20,000 V/m, as calculated in Figure 4A. The Lorentz force of the moving plasma in radial is ∼840 N $\left(F=q\left(E+v\times B\right)\right)$, as evaluated by the data in the direction of the center. However, as the distance between plasma and axis increases, the Lorentz force decreases. Furthermore, the Lorentz force changes the direction of plasma movement and the topological structure of the magnetic field. Therefore, the magnetic reconnection can occur under specific conditions. For example, the plasma jet undergoes a kink instability in agreement with the prediction of Kruskal–Shafranov theory [30]: the jet is unstable to kinking when ${\mu }_{0}I/\psi >4\pi /L$, where L is the jet length, I is the current measured at the electrodes, and $\psi$ is the poloidal magnetic flux. We assumed that the magnetic field region is on the order of millimeter, and the plasma jet length is on the order of centimeter. Accordingly, the evaluated ${\mu }_{0}I/\psi$ ≈ 2,000 and $4\pi /L$ ≈ 200. Therefore, it is possible that the kink instability of plasma occurs in the experiment according to the theoretical analysis.

Overall, the magnetic reconnection and kink instability and Rayleigh–Taylor instability of plasma were observed. When the magnetic reconnection occurs, a large part of magnetic field energy transforms into kinetic energy of plasma jet [19], and the plasma jet velocity increases by ∼ 400 m/s.

Topology of Coupled Magnetic Field

Based on the experiment and numerical method, the topological structure of magnetic field was drawn. Figure 5 shows the schematic diagram of the formed magnetic field of electrical explosion. Obviously, the magnetic field was formed by axial current and radial moving plasma in the electrical explosion. Figure 5A shows the magnetic field topology formed by the axial current. According to Ampere’s law, the magnetic field presents a counter-clockwise toroidal structure, and its value can be evaluated by $B={\mu }_{0}I/2\pi r$. As shown in Figure 5B, when an electrical explosion occurs, the plasma moves in all directions. However, to simplify the process, we assume that the plasma is moving outward from the center. Thus, the plasma jet can be regarded as an infinite number of current sheets due to its own motion, each of which forms a toroidal magnetic field. On either side of the plasma jet, the entire magnetic field is superimposed by the magnetic field formed by each current sheet, in opposite directions. Therefore, on the left side of the plasma jet, the direction of the entire magnetic field is counter-clockwise. On the right side of the plasma jet, the direction of the entire magnetic field is clockwise.

FIGURE 5

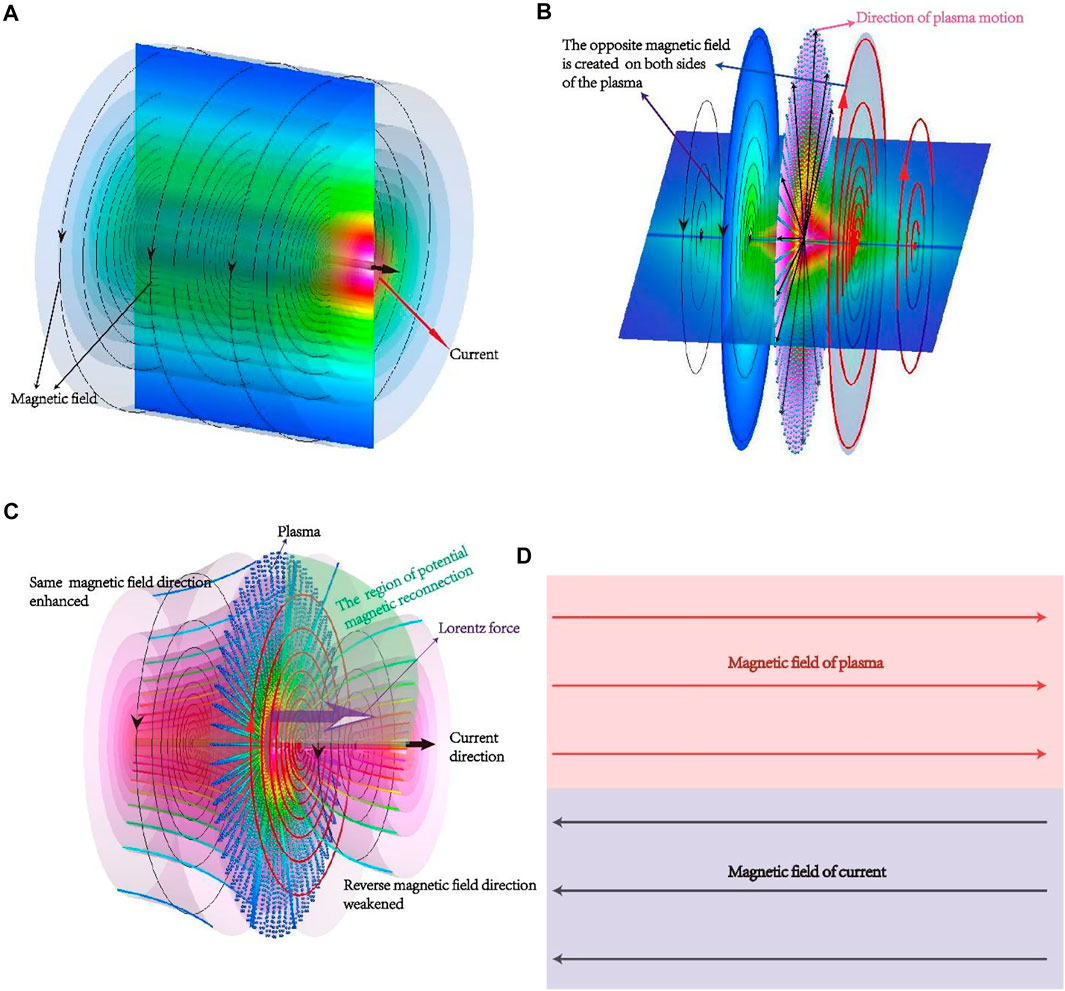
FIGURE 5. Schematic diagram of the formed magnetic field of electrical explosion. (A) The counter-clockwise toroidal magnetic field formed by the axial current. (B) The plasma and the magnetic field it creates in the electrical explosion; the direction of the magnetic field is opposite on both sides of the plasma. (C) Three-dimensional magnetic field topological map obtained by superimposing the image (A, B). (D) The distribution of the magnetic lines of force on the slice plane of the inverted magnetic field region, and this slice plane is parallel to the direction of plasma motion.

Figure 5C shows the three-dimensional magnetic field topological map obtained by superimposing Figures 5A,B. Obviously, on the left side of the plasma jet, the entire magnetic field intensity increased by superimposing the magnetic field in the same direction. On the right side of the plasma jet, the entire magnetic field intensity decreased by superimposing the magnetic field in the reverse direction. In the isosurface, it can be found that the magnetic field on the right side of the central location is small, and this region is fan-shaped on the slice plane. Under the effect of Lorentz force, the plasma moves to the right, resulting in the transformation of the magnetic field topology. The region of potential magnetic reconnection is shown in Figure 5C. In addition, since the magnetic field direction in other regions is the same, magnetic reconnection will not occur.

Figure 5D shows the distribution of the magnetic lines of force on the slice plane of the inverted magnetic field region, and this slice plane is parallel to the direction of plasma motion. The direction of the plasma motion is perpendicular to the axial current direction. Therefore, with the movement of plasma, the three-dimensional magnetic field topology and the distribution of the magnetic lines of force change. When the plasma is disturbed, magnetic reconnection occurs due to the instability of the plasma.

Evolution of Magnetic Reconnection Topology

Figure 6 shows the evolution of calculated magnetic field topology with plasma motion. The angle between the moving plasma and the axis is 75°, 60°, 45°, and 30°, corresponding to Figures 6A–D, respectively. The distribution of the magnetic lines of force in Figures 6E–H corresponds to Figures 6A–D, respectively. As the plasma moves, the topological structure of the magnetic field changes, especially in the region where the plasma moves; the right side region of the plasma changes to the left side region. Because the magnetic fields on both sides of the plasma are in opposite directions, the magnetic field in this region suddenly changes direction, which may be the reason for magnetic reconnection.

FIGURE 6

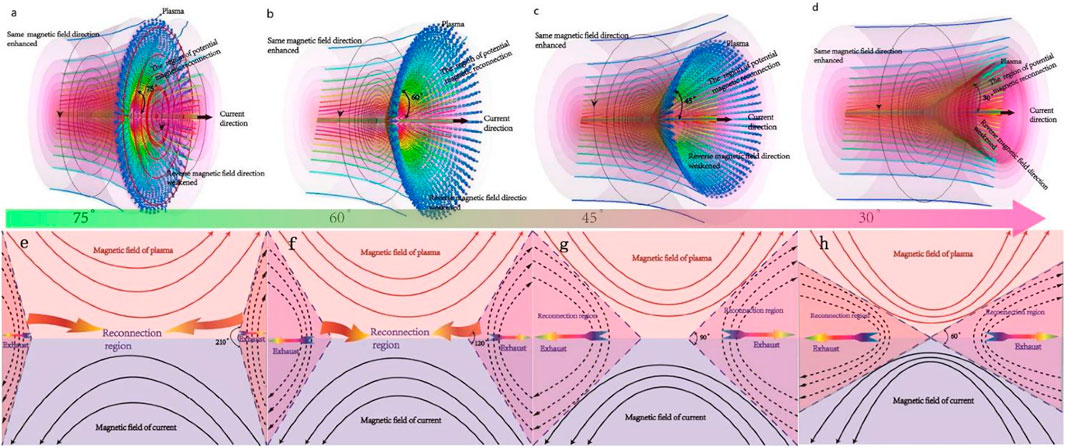
FIGURE 6. The evolution of magnetic field topology with plasma motion. (A–D) Three-dimensional magnetic field topological map, the angle between the moving plasma, and the axis of 75°, 60°, 45°, and 30°, corresponding to Panels (A–D), respectively. (E–H) Distribution of the magnetic lines of force on the slice plane of the inverted magnetic field region, which is parallel to the direction of plasma motion. In addition, Panels (E–H) correspond to Panels (A–D) respectively.

As shown in Figures 6A–D, as the angle between the moving plasma and the axis decreases, the area in the direction of the same magnetic field increases and that in the direction of the opposite magnetic field decreases. In addition, the moving plasma presents a cone shape, and the area of potential magnetic reconnection decreases. Figures 6E–H show the distribution of magnetic lines of force. As the angle between the moving plasma and the axis decreases, the curvature of the magnetic lines of force increases. Due to the elasticity of magnetic lines, the magnetic reconnection occurs when its curvature reaches a certain value, and the plasma jet is accelerated and exhausted. In this experiment, the motion of the current sheet changes the topology of the magnetic field, which leads to magnetic reconnection. Obviously, the plasma jet has two opposite directions of exhaust, as shown in Figures 6E–H. However, according to the distribution of magnetic field topology, the direction that parallels to the plasma jet motion direction is easier to exhaust.

In addition, in experiment 1, the plasma jet angle is ∼50°, as shown in Figure 2. The calculation results are consistent with those in Figures 6B, C. This shows that the proposed theory explains the experimental phenomenon well.

Effect on Propellant Ignition

The surface conditions of the propellant are examined by a SEM after the experiments. Figure 7 shows the surface conditions of the propellant after being ignited. In experiment 1, obviously, more, larger, and deeper circular pits are illustrated in the image, as shown in Figure 7A. The reason is that magnetic reconnection increases the temperature and the velocity of plasma (from ∼2,000 to ∼2,400 m/s, as shown in Figures 2 and 3), causing more particles to form, thus increasing the impact capacity of plasma on the propellant surface. In experiment 2, compared with Figure 7A, the circular pits formed are fewer and shallower in the image, as shown in Figure 7B. Therefore, the resulting magnetic reconnection plays an important role in propellant ignition, which enhances the ignition ability of wire electrical explosion.

FIGURE 7

FIGURE 7. The surface conditions of the propellant after being ignited. (A) Experiment 1. (B) Experiment 2.

The results in this paper are useful for wire array explosion and propellant ignition. For example, in wire array explosion, the exhausted direction of magnetic reconnection can be controlled by designing the location of the wires properly, and the collision energy of plasma can be further improved. In propellant ignition, magnetic reconnection can increase the temperature and velocity of plasma and further improve the ignition ability of wire electric explosion.

Conclusion

In this paper, we investigated the magnetic reconnection and kink instability of plasma jet in single wire electrical explosion and their effect on propellant ignition. The experiment was carried out under the charging voltage of 8 kV. Furthermore, based on the experimental results, the Lundquist number, Alfvén velocity, Lorentz force, the magnetic field of discharge current, and the moving plasma were evaluated. The three-dimensional magnetic field topology and its evolution process was evaluated and presented. Finally, the effect on propellant ignition was verified by experiments.

The initial velocity of plasma was ∼2,000 m/s, and when the magnetic reconnection occurred, the velocity increased by ∼ 400 to ∼2,400 m/s. The probe signal was significantly enhanced at 1.5–2 ms in experiment 1. In addition, the evaluated Alfvén velocity was ∼500 m/s, the Alfvén time was ∼20 µs, and the Lundquist number S = 1.7 × 10⁷. Furthermore, the three-dimensional magnetic field topology and its evolution process was evaluated, presented, and analyzed. Due to the motion of the current sheet changes the topology of the magnetic field, the magnetic reconnection occurs when the curvature of magnetic lines reached a certain value. The direction that parallels to the plasma jet motion direction is easier to exhaust. The plasma jet angle is ∼50° in experiment 1, which is consistent with the calculated results. Magnetic reconnection enhances the ignition ability of wire electrical explosion to the propellant.

The results can be used to improve the understanding of wire array explosion and propellant ignition. Furthermore, we believe that the present results represent a key step towards resolving one of the most important problems of plasma physics: how is the plasma jet acting on the wire array explosion.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

JZ conceived this study. JZ and FX analyzed the data and wrote the paper. WL and TL and SZ revised the manuscript. All authors reviewed the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Drake JF, Swisdak M, Che H, Shay MA. Electron Acceleration from Contracting Magnetic Islands during Reconnection. Nature (2006) 443:553–6. doi:10.1038/nature05116

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Ashour-Abdalla M, El-Alaoui M, Goldstein ML, Zhou M, Schriver D, Richard R, et al. Observations and Simulations of Non-local Acceleration of Electrons in Magnetotail Magnetic Reconnection Events. Nat Phys (2011) 7:360–5. doi:10.1038/nphys1903

CrossRef Full Text | Google Scholar

3. Daughton W, Roytershteyn V, Karimabadi H, Yin L, Albright BJ, Bergen B, et al. Role of Electron Physics in the Development of Turbulent Magnetic Reconnection in Collisionless Plasmas. Nat Phys (2011) 7:539–42. doi:10.1038/nphys1965

CrossRef Full Text | Google Scholar

4. Bulanov SV. Magnetic Reconnection: from MHD to QED. Plasma Phys Control Fusion (2017) 59:014029. doi:10.1088/0741-3335/59/1/014029

CrossRef Full Text | Google Scholar

5. Fiksel G, Almagri AF, Chapman BE, Mirnov VV, Ren Y, Sarff JS, et al. Mass-Dependent Ion Heating during Magnetic Reconnection in a Laboratory Plasma. Phys Rev Lett (2009) 103:145002. doi:10.1103/PhysRevLett.103.145002

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Che H, Drake JF, Swisdak M. A Current Filamentation Mechanism for Breaking Magnetic Field Lines during Reconnection. Nature (2011) 474:184–7. doi:10.1038/nature10091

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Chatterjee G, Schoeffler KM, Kumar Singh P, Adak A, Lad AD, Sengupta S, et al. Magnetic Turbulence in a Table-Top Laser-Plasma Relevant to Astrophysical Scenarios. Nat Commun (2017) 8:15970. doi:10.1038/ncomms15970

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Yi L, Shen B, Pukhov A, Fülöp T. Relativistic Magnetic Reconnection Driven by a Laser Interacting with a Micro-scale Plasma Slab. Nat Commun (2018) 9:1601. doi:10.1038/s41467-018-04065-3

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Wu L, Ma Z, Zhang H. Shock Formation and Structure in Magnetic Reconnection with a Streaming Flow. Sci Rep (2017) 7:1–9. doi:10.1038/s41598-017-08836-8

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Jiang C, Wu ST, Feng X, Hu Q. Data-driven Magnetohydrodynamic Modelling of a Flux-Emerging Active Region Leading to Solar Eruption. Nat Commun (2016) 7:11522. doi:10.1038/ncomms11522

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Yang KE, Longcope DW, Ding MD, Guo Y. Observationally Quantified Reconnection Providing a Viable Mechanism for Active Region Coronal Heating. Nat Commun (2018) 9:692. doi:10.1038/s41467-018-03056-8

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Phan TD, Eastwood JP, Shay MA, Drake JF, Sonnerup BUÖ, Fujimoto M, et al. Electron Magnetic Reconnection without Ion Coupling in Earth's Turbulent Magnetosheath. Nature (2018) 557:202–6. doi:10.1038/s41586-018-0091-5

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Egedal J, Fox W, Katz N, Porkolab M, Reim K, Zhang E. Laboratory Observations of Spontaneous Magnetic Reconnection. Phys Rev Lett (2007) 98:015003. doi:10.1103/PhysRevLett.98.015003

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Srivastava AK, Mishra SK, Jelínek P. The Prominence Driven Forced Reconnection in the Solar Corona and Associated Plasma Dynamics. Astrophysical J (2021) 920(1):18. doi:10.3847/1538-4357/ac1519

CrossRef Full Text | Google Scholar

15. Srivastava AK, Mishra SK, Jelínek P, Samanta T, Tian H, Pant V, et al. On the Observations of Rapid Forced Reconnection in the Solar Corona. Astrophysical J (2019) 887(2):137. doi:10.3847/1538-4357/ab4a0c

CrossRef Full Text | Google Scholar

16. Moser AL, Bellan PM. Magnetic Reconnection from a Multiscale Instability cascade. Nature (2012) 482:379–81. doi:10.1038/nature10827

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Totorica SR, Abel T, Fiuza F. Nonthermal Electron Energization from Magnetic Reconnection in Laser-Driven Plasmas. Phys Rev Lett (2016) 116:095003. doi:10.1103/PhysRevLett.116.095003

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Intrator TP, Sun X, Lapenta G, Dorf L, Furno I. Experimental Onset Threshold and Magnetic Pressure Pile-Up for 3D Reconnection. Nat Phys (2009) 5:521–6. doi:10.1038/nphys1300

CrossRef Full Text | Google Scholar

19. Yamada M, Yoo J, Jara-Almonte J, Ji H, Kulsrud RM, Myers CE. Conversion of Magnetic Energy in the Magnetic Reconnection Layer of a Laboratory Plasma. Nat Commun (2014) 5:4774. doi:10.1038/ncomms5774

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Birn J, Hesse M. Energy Release and Conversion by Reconnection in the Magnetotail. Ann Geophys (2005) 23:3365–73. doi:10.5194/angeo-23-3365-2005

CrossRef Full Text | Google Scholar

21. Rosenberg MJ, Li CK, Fox W, Igumenshchev I, Séguin FH, Town RPJ, et al. A Laboratory Study of Asymmetric Magnetic Reconnection in Strongly Driven Plasmas. Nat Commun (2015) 6:6190. doi:10.1038/ncomms7190

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Egedal J, Daughton W, Le A. Large-scale Electron Acceleration by Parallel Electric fields during Magnetic Reconnection. Nat Phys (2012) 8:321–4. doi:10.1038/nphys2249

CrossRef Full Text | Google Scholar

23. Inoue S, Ono Y, Tanabe H, Horiuchi R, Cheng CZ. Numerical Study of Energy Conversion Mechanism of Magnetic Reconnection in the Presence of High Guide Field. Nucl Fusion (2015) 55:083014. doi:10.1088/0029-5515/55/8/083014

CrossRef Full Text | Google Scholar

24. Mendoza M, Muñoz JD. Three-dimensional Lattice Boltzmann Model for Magnetic Reconnection. Phys Rev E (2008) 77:026713. doi:10.1103/PhysRevE.77.026713

CrossRef Full Text | Google Scholar

25. Loureiro NF, Uzdensky DA. Magnetic Reconnection: from the Sweet-Parker Model to Stochastic Plasmoid Chains. Plasma Phys Control Fusion (2016) 58:014021. doi:10.1088/0741-3335/58/1/014021

CrossRef Full Text | Google Scholar

26. Pucci F, Velli M. Reconnection of Quasi-Singular Current Sheets: the "Ideal" Tearing Mode. Astrophysical J (2013) 780(2):L19. doi:10.1088/2041-8205/780/2/l19

CrossRef Full Text | Google Scholar

27. Botha GJJ, Arber TD, Srivastava AK. Observational Signatures of the Coronal Kink Instability with Thermal Conduction. Astrophysical J (2012) 745(1):53. doi:10.1088/0004-637x/745/1/53

CrossRef Full Text | Google Scholar

28. Srivastava AK, Zaqarashvili TV, Kumar P, Khodachenko ML. Observation of Kink Instability during Small B5.0 Solar Flare on 2007 June 4. Astrophysical J (2010) 715(1):292–9. doi:10.1088/0004-637x/715/1/292

CrossRef Full Text | Google Scholar

29. Wu J, Lu Y, Li X, Zhang D, Qiu A. Investigations on Stratification Structure Parameters Formed from Electrical Exploding Wires in Vacuum. Phys Plasmas (2017) 24:112701. doi:10.1063/1.4999498

CrossRef Full Text | Google Scholar

30. Hsu SC, Bellan PM. Experimental Identification of the Kink Instability as a Poloidal Flux Amplification Mechanism for Coaxial Gun Spheromak Formation. Phys Rev Lett (2003) 90:215002. doi:10.1103/PhysRevLett.90.215002

PubMed Abstract | CrossRef Full Text | Google Scholar