Node Classification in Attributed Multiplex Networks Using Random Walk and Graph Convolutional Networks

Node classification, as a central task in the graph data analysis, has been studied extensively with network embedding technique for single-layer graph network. However, there are some obstacles when extending the single-layer network embedding technique to the attributed multiplex network. The classification of a given node in the attributed multiplex network must consider the network structure in different dimensions, as well as rich node attributes, and correlations among the different dimensions. Moreover, the distance node context information of a given node in each dimension will also affect the classification of the given node. In this study, a novel network embedding approach for the node classification of attributed multiplex networks using random walk and graph convolutional networks (AMRG) is proposed. A random walk network embedding technique was used to extract distant node information and the results are considered as pre-trained node features to be concatenated with the original node features inputted into the graph convolutional networks (GCNs) to learn node representations for each dimension. Besides, the consensus regularization is introduced to capture the similarities among different dimensions, and the learnable neural network parameters of GCNs for different dimensions are also constrained by the regularization mechanism to improve the correlations. As well as an attention mechanism is explored to infer the importance for a given node in different dimensions. Extensive experiments demonstrated that our proposed technique outperforms many competitive baselines on several real-world multiplex network datasets.

1 Introduction

Node classification [1,2] is a basic and central task in the graph data analysis, such as the user division in social networks [3], the paper classification in citation network [4]. Network embedding techniques (or network representation learning or graph embedding) utilize a dense low-dimensional vector to represent nodes [5–7]. This provides an efficient way to solve various graph analytic problems, including node classification [5–7], recommendation [8,9], link prediction [10,11]. Most existing network embedding techniques for node classification are designed for standard single-layer graph networks [1,2,5,12–14], such as DeepWalk [13], node2vec [10], LINE [12], and classical graph neural networks (GNNs) such as graph convolutional networks (GCNs) [5], GAT Veličković and Cucurull [15], and GraphSAGE [14]. However, most real-world complex interacting systems [16] are modeled as multilayer graph networks, including social networks [3], citation-collaboration networks [4], which are formed by several layers describing interactions of various types. For example, two users could be connected to each other across multiple social networks (e.g., Twitter, Facebook, and LinkedIn). Using multilayer graph networks can provide more comprehensive and accurate description about these two users. When the same set of nodes are connected in the way of multiple link types or relationship types, the resulting multilayer graph network is also called multiplex graph network or multiplex network [17,18] ¹ If the nodes in multiplex graph network contain attributes, such network is called attributed multiplex graph network. The attributes can provide useful guidance to perform node classification graph data analysis. For example, if two users in a social network share hobbies or interests, these two users may belong to the same cluster.

Several studies have been conducted on multiplex network representation learning. However, some issues remain that require further consideration. For instance, previous techniques such as PMNE [19], MELL [20], MVE [21] and MNE [11] have learned to integrate node embedding information from different dimensions in multiplex network representations. However, these techniques have mostly overlooked node attributes. Other models that consider node attributes (e.g., mGCN [22], MGCN [23], DMGI [24], and HAN [25]) have either failed to consider interactions among diverse dimensions (mGCN) or focus on multiplex graphs with explicit adjacency links among different dimensions (MGCN [23]). DMGI and HAN consider heterogeneous graphs constructed based on the meta-path between different node, which differs from the multiplex network. MGAT [26] introduces a constrained regularization term in GAT [15] to learn the interactions between different dimensions, that is learnable parameters constraint of GAT. However, MGAT fails to consider the node embedding matrices similarity [27] among different relationships. Furthermore, while GAT can be calculated in parallel with multi-head attention, the memory complexity for parameter storage is higher than that of the GCN model [5]. In addition, MGAT utilizes a two-layer GAT to integrate node information from its neighbors, which only captures information from 2-hop nodes. Including more than two layers in a GNN often results in over-smoothing [7]. However, the node2vec network embedding [10], which is based on random walk technique, can be used to search for 10-hop contextual information [10] and to capture the structural equivalence (i.e. two nodes are far apart each other but have the same structural roles). This suggests that information from a larger receptive domain helps to capture more comprehensive node representations, which can be used to improve the results of node classification.

Recently, the Graph Neural Network (GNN) deep nonlinear network embedding framework represented by GCN [5], which can encode node attributes and network structure simultaneously, has achieved great success on the node classification graph data analysis task for attributed single-layer network. The direct method about node classification of the attributed multiplex network is to extend the GCN [5] to multiplex network. However, some obstacles are existed. First, different dimensions of an given attributed multiplex network share the same node set and node attributes. Hence, different dimensions are typically similarities or may have some characteristics in common [28]. For instance, citation networks represent citations between papers. Similarly, paper similarity networks represent the commonality among papers as articles that cite each other typically share a common research topic. Therefore, the citation and paper similarity dimensional networks exhibit a certain degree of overlap. Second, different dimensions of multiplex networks are related [17]. For example, in social networks, friend relationship dimensional network can determine the topology of a message forwarding dimensional network. Besides, the degree of importance differs in dimensional networks as the significance of a given node may vary in different dimensions. Third, two nodes may share similar structure roles but are far apart each other (i.e. structural equivalence [10]). These two distance nodes may belong to the same cluster. Therefore, the primary challenge for node classification of multiplex network is then designing a model to extract the node information, oriented by the downstream node classification task, capable of generating a comprehensive embedding (consensus) that considers node attributes, their interaction and similarities among different dimensions, the corresponding degree of importance in diverse dimension networks, and the distance node context information.

In this paper, we propose a novel graph embedding framework for the node classification of attributed multiplex graph to solve the above mentioned problems. At first, a random walk network embedding technique was included to address the over-smoothing problem [7] that occurs in GCNs, which is unable to capture distance node context information (more than 2-hop). We use the node2vec random walk network embedding to learn distance node context information for each dimension, and the obtained node embeddings are considered as pre-trained node features, which learn the distance node neighborhood to capture the structural equivalence. Then, pre-trained node features are concatenated with the original node attributes to form new node attributes inputted into the two-layer GCNs [5] to learn each dimensional graph network respectively. At the same time, a regularized consistency constraint was then introduced to node embeddings from different dimension to learn similarities [28] between nodes and their counterparts in others dimension. And the learnable weight parameters of different GCNs for different dimensional graph networks were then constrained using a regularization term [26]. Finally, the attention mechanism is used to adaptively learn the importance weights of a given node in different dimensional, prior to integrating the node embedding results from different dimensions to generate global consensus node representations. This model can be trained end-to-end oriented by the downstream node classification task. In this way, a more comprehensive, informative, and high-quality node representation for the node classification can be achieved using these strategies discussed above. The primary contributions of the proposed technique can be summarized as follows.

• We provide a novel node classification methodology for attributed multiplex networks using random walk network embedding and graph convolutional networks (AMRG), which can fuse the node attributes and capture distant node context information.

• We use regularized constraints to learn cross dimensional similarities and correlations among different dimensions. Then, the integration of node embeddings from different dimensional is performed based on an attention mechanism.

• Extensive experiments were conducted to evaluate the effectiveness and efficiency of this approach, by comparing it with some competitive baselines on real-world attributed multiplex networks.

The remainder of this paper is organized as follows. First, we summarize related work in Section 2 and then introduce our approach in Section 3. Section 4 provides experimental conditions and results. Finally, conclusions are discussed in Section 5.

2 Related Work

This section summarizes related studies on network embedding for single-layer networks (Figure 1A) and multiplex networks (Figure 1B). The acquired node embeddings can be used to perform node classification tasks.

FIGURE 1

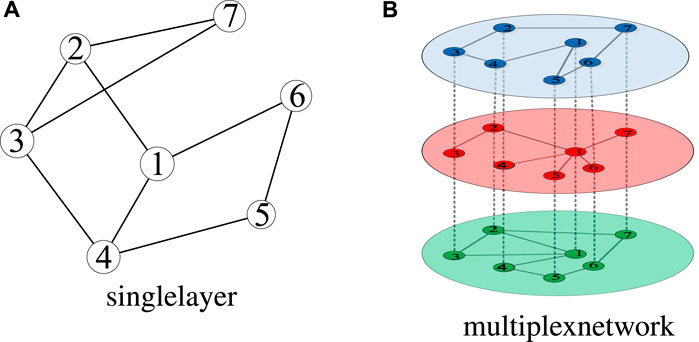
FIGURE 1. Single-layer and multiplex networks with the same set of nodes but different link types. (A) The single-layer network. (B) Different nodes are connected to each other by a continuous line in each relationship. A single node is connected to its counterparts by a dashed line.

2.1 Single-Layer Network Embedding

Network embedding methods [1,5,10,12,13] are used to learn low-dimensional and dense vector representations for nodes in real graph networks, while preserving network structure and facilitating further analysis of graph networks. Various network embedding techniques have been proposed based on deep learning, inspired by word2vec models such as Skip-Gram [29], including DeepWalk [13] and node2vec [10]. DeepWalk [13] first performs a random walk on a network to generate an unbiased random sequence composed of nodes. The neural network (Skip-Gram) is subsequently used to train network node representations by treating nodes as words and node sequences as sentences. Node2vec [10] extends DeepWalk by introducing two parameters (p and q) used to improve the random walk strategy (i.e. BFS and DFS) exploring a more comprehensive graph structure (a biased random walk). Other network embedding models have focused on mining and analysis for specific network structures. For example, LINE [12] is a classic approach that learns node embedding information by preserving both first-order and second-order proximities in the graph. Similarly, SDNE [30] utilizes a semi-supervised deep autoencoder model to capture first-order and second-order proximities. NetMF [31] unifies DeepWalk, LINE, and node2vec into a single matrix factorization framework.

The techniques discussed above focus on mining graph structure, without considering node attribute information. However, nodes in real-world networks often contain rich attribute data, such as abstract text in a publication network and user profiles in social networks (called attributed networks). Considering node attribute information in the learning process has been shown to improve the quality of network representation learning and provide a more comprehensive node embedding strategy to facilitate downstream tasks [5,32–34]. TADW [32] has been used to demonstrate the equivalence between DeepWalk and matrix factorization in attributed network representation learning. It was also the first algorithm used to jointly learn node attributes (textural features) and network structure, which are achieved via matrix factorization. However, TADW only considers second-order and higher-order proximity, leaving out first-order proximity considerations (i.e., homophily properties). HSCA [33] jointly learns homophily data, structural content, and node attributes to develop an effective node representation. MIRand [34] is an unsupervised algorithm for attributed single-layer graph network embedding based on random walk. This approach first establishes a two-layer graph network, one of which depicts structural information from the input graph while the other describes node attributes or content. MIRand performs the random walk according to node informativeness, intelligently traversing between structure and attribute layers.

Inspired by the success of CNNs in computer vision, graph neural networks (GNNs) [35] generalize 2D convolutions from Euclidean images to non-Euclidean graph data, which provides a powerful end-to-end method for learning node representations while addressing graph-related tasks. Graph convolutions are performed by aggregating neighborhood node information, which naturally considers node attributes. Representative work concerning convolution operators applied to graph data is found in Graph Convolutional Network (GCN) [5]. Michael Schlichtkrull et al. first applied a GCN framework to model relational data, focusing on knowledge graph datasets, which is called Relational Graph Convolutional Networks (R-GCNs) [36]. In contrast, GAT [15] models specify different weights for varying neighborhood nodes when performing convolution operations. GAT assumes that different neighboring nodes exhibit different importance levels for the objective node while aggregating neighboring nodes. GraphSAGE [14] is an extension of the GCN framework that uses inductive node embedding. For a complete overview of network embedding techniques, readers are referred to recent studies on the topic [35,37].

2.2 Multiplex Network Embedding

Although these techniques have proven to be effective and efficient in various scenarios, they each attempt to process standard single-layer graphs, which implies the graph only consists of one type of relationship as shown in Figure 1A. However, in practical applications, most networks exhibit multiple relationships between nodes. For example, in social networks, the relationship between two users could be friendship, co-worker, or simply advice [38]. Although these diverse relationships can independently form different networks to be analyzed separately, specific interactions and associations exist among them [17,28].

PMNE [19] uses three methods to learn global embedding information for analyzing multiplex networks, including network aggregation, result aggregation, and layer co-analysis which considers interaction information and thus achieves the best overall performance than network aggregation and result aggregation. Ryuta Matsuno et al. proposed MELL [20] for multiplex networks. It first requires embedding vectors, for the same nodes in diverse relationships, to be close to each other in order to share all layer structures. It then introduces a layer vector that can capture each layer’s connectivity for use in differentiating edge probabilities in each relationship. As such, MELL focuses specifically on link prediction tasks. MVE [21] is a novel collaboration framework for multiplex network embedding, which promotes the collaboration of different views and introduces an attention mechanise to learning the weights of different views. Such can obtain robust node embedding results. However, MVE only consideres the network structure (i.e. attributes of nodes are ignored). MNE [11] uses one high-dimensional common embedding and a lower-dimensional additional embedding for each type of relationship, each of which can be learned jointly based on a unified framework. MANE [39] jointly models both connections in each relationship and network interactions from different relationships in a unified framework. Essentially, MANE focuses on processing heterogeneous graphs with different types of nodes and edges. However, node attributes are not considered by the models discussed above.

HAN [25] uses a novel heterogeneous graph neural network with node-level and semantic-level attentions for attributed multiplex networks, generating node embeddings via aggregating features from meta-path based neighbors. This approach attempts to describe heterogeneous graphs generated from meta-paths considering the semantics between nodes. Similarly, mGCN [22] utilizes GCN to learn node representations for each relationship. In order to jointly learn cross-layer interactions, the authors used a weighted average over relation-specific representations to produce generalized descriptions in which weights were calculated based on projection matrices from different networks. Unlike in mGCN, our proposed approach adds regularized consensus constraints and trainable weight parameters constraints among GCN for different dimensional graph networks on the objective function. In fact, the mGCN only learns node embeddings for each dimension, using a weighted average of the embedding results to generate overall node representations without considering the interactions between different dimensional networks. Masha Ghorbani et al. extended the GCN model to form a multi-layer graph embedding called MGCN [23]. This approach utilizes GCN models to learn node representations within relationships. However, MGCN focuses on multi-layer graphs with explicit adjacency links between nodes with different relationship types. The types of nodes found in these relationship networks can vary widely. For instance, one layer could denote an airport network, while another describes a power grid. MGAT [26], an extension of the GAT model, introduces regularization terms for model parameters on the objective function to optimize multiplex network embedding. The primary difference between our method and MGAT is that we extend the GCN model while requiring less memory than GAT for parameter storage [15]. Furthermore, our technique is advantageous because it uses a random walk network embedding technique to learn 10-hop node information [10] as the pre-trained node feature which concatenated with the original node features, and resulting new node features were input into the GCN model, while MGAT only learns 2-hop data. MGAT also fails to consider the similarities of node embeddings between different dimensional graph network.

The difference between single-layer and multiplex graph network embedding: With the advent of the big data where many different links of interconnected objects, it is difficult to model these interacting objects as single-layer graph networks but can naturally model using multiplex graph networks to describe different links. For example, two users could be connected to each other across multiple social platform (e.g. Twitter, Facebook, and LinkedIn). Therefore, each social relationship can be modeled as a graph network. The traditional graph network analysis methods with single-layer network embedding technique can be utilized to analyze these three graph networks separately, which may result in incorrect analysis results. As the single-layer graph network can only describe some or even biased information between nodes. Another way is to transform these three graph network (e.g. Twitter, Facebook, and LinkedIn) as a weighted or an unweighted single-layer graph network. The weight represents the number of link types (i.e. 0, 1, 2, 3) between connected nodes. Then the single-layer network embedding methods can be used on the transformed single-layer graph network. Although it is easy to perform the graph network analysis in this way, the interactive information among different relationships through the same nodes in different links are ignored. The multiplex graph network can model more comprehensively characterize of the complex systems than single-layer graph network. Besides, most of the multiplex graph network embedding methods capture the interactive information and common information among different relationships, and the differences between different relationships. Therefore, the graph analysis results of the multiplex graph network embedding are more accurate than single-layer network embedding.

3 Proposed Model

3.1 Problem Statement and Framework

Attributed Multiplex Graph Network. Given a single-layer attributed network formally denoted as G = {V, E, X}, the vertices V represent n nodes in the graph. The term E is a set of edges representing the presence of a connection or relationship between two nodes, where $e_{ij}=\left(v_i,v_j\right)\in E$ describes the relationship between node v_i and node v_j. In addition, |V| and |E| denote the size of the vertice and edge sets respectively, and X ∈ R^n×F is a matrix that represents attributes for the n nodes, F represents the dimension of node features, A is an adjacency matrix for the graph G (with a size of $\left|V\right|\times \left|V\right|$), and $A_{ij}\in \left\{\mathrm{0,1}\right\}$ denotes connections for unweighted network graphs. The condition A_ij = 1 represents a link between v_i and v_j, otherwise A_ij = 0. In practical applications, A is typically sparse and high-dimensional, especially for very large-scale networks. Attributed multiplex networks with $\left|M\right|$ different relationship types can be represented as G = {V, E⁽¹⁾, E⁽²⁾, …, E^(M), X}, where G^(r) = {V, E^(r), X} is a graph of the relation type (or dimension) r and $A=\left\{A^{(1)},A^{(2)},\dots ,A^{(M)}\right\}$ is a set of adjacency matrices for the graph G. Multiplex network embedding attempts to learn global consensus node representations for each node v_i ∈ V with a d dimensional dense vector, through better collaboration among different dimensions. This suggests the correlations among diverse relation types should be considered for a comprehensive and informative node representation. Low dimensional and consensus vectors can be represented as z_i ∈ Z ∈ R^n×d for each node v_i ∈ V, where $d\ll \left|V\right|$. These notations are summarized in Table 1.

TABLE 1

TABLE 1. Notations.

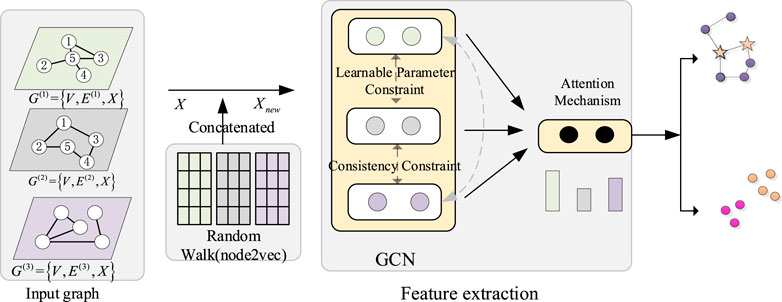
An Overview of the Framework. The overall framework for AMRG is illustrated in Figure 2. It is primarily composed of four components, including 1) a random walk network embedding model used to capture distance neighboring node information as pre-trained node features, 2) dimension specific node embeddings with the GCN model, 3) cross dimension learning, and 4) an attention-based mechanism used to learn node importance in different dimensions for fusing different dimensions adequately.

FIGURE 2

FIGURE 2. The framework for our proposed method of attributed multiplex network embedding.

We use the node2vec random walk network embedding technique to capture distance node feature of each dimensional graph network, and then the averaged node embedding of $\left|M\right|$ node embeddings are concatenated with the original node feature. The resulting is considered as new node features, which are inputted into the GCN model. Then the GCN model can be utilized for the relation-type specific network G^r, to learn a set of node representations H_r. However, unlike the conventional GCN method [5], a weight was added to the self-connections which is down in the same way in [24]. Large weights (w > 1) indicate the node itself plays a more important role in generating its embedding than its neighboring nodes in the process of aggregating neighbor information. Furthermore, learnable weight parameters of $\left|M\right|$ GCNs are constrained using a regularization term [26]. In addition, we introduce a regularized consistency constraint for each network embedding H_r∈M to capture node similarities from their counterparts. These two constraints from different dimensional graph network can be beneficial [17,19,24] for the downstream node classification, as this can capture more comprehensive information of the multiplex network. Finally, a global consensus node embedding was generated by weighted average different dimensional network embeddings based on the attention mechanism. This obtained embedding is a comprehensive, higher-quality, informative node representation, which can be used for classification and visualization tasks.

3.2 Capturing Distance Neighboring Node Information

The advantage of GCN is that it not only considers the network structure, but also fuses the node attributes. GCN is typically using two convolution layers [5], which means that it can only captures 2-hop node neighboring information. However, more than two convolution layers will result in the over-smoothing problem. Node information from a larger receptive domain (10-hop) with node2vec random walk network embedding technique [10] can help to capture richer node features. However, node2vec leaves out of consideration the node attributes. We thus combine the node2vec random walk network embedding technique and GCN to learn the node embeddings of multiplex graph network. The resulting node embeddings can not only fuse node’s attributes, but also make up for GCN’s inability to learn distance node information to capture the structural equivalence.

Given the rth dimensional network, we can utilize the node2vec random walk technique to learn 10-hop neighboring node information. The resulting network embedding can be represented as $X_{rw}^r\in R^{n\times d_{rw}}$ (d_rw ≪ n). For $\left|M\right|$ different dimensional networks of multiplex graph network, we can use the same method to acquire $X_{rw}^1,X_{rw}^2,\dots ,X_{rw}^r,\dots ,X_{rw}^M$. Then, we average $\left|M\right|$ node embeddings as:

$X_{rw}=\frac{1}{|M|}\cdot \left(X_{rw}^1+X_{rw}^2+\cdots +X_{rw}^r+\cdots +X_{rw}^M\right)(1)$

The X_rw is considered as the pre-trained node feature which contains the distance neighboring node information. Then the X_rw is concatenated with the original node attributes X (i.e., $X_{new}=X+X_{rw},X_{new}\in R^{n\times (F+d_{rw})}$). X_new, considered as the new node feature, is inputted into the GCN model.

3.3 Dimension Specific Node Embedding With GCN

Graph convolutional neural networks provide a powerful solution for generating node representations for a given graph [5], which naturally incorporate node attributes. In this section, we utilize multi-layer GCN to learn the dimension specific node embedding. For a given input graph (A, X), the layer-wise propagation rule can be expressed as [5]:

$H^{\left(l+1\right)}=\sigma \left({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^{\left(l\right)}{W}^{\left(l\right)}\right)(2)$

where $\tilde{A}=A+I_n$ is an adjacency matrix with added self-connections, I_n is the identity matrix,X ∈ R^n×F is a feature matrix for the input graph, ${\tilde{D}}_{ii}={\sum }_j{\tilde{A}}_{ij}$ is the degree matrix for $\tilde{A}$, W^(l) is the trainable weight parameters matrix for the lth layer in the GCN, σ(⋅) denotes an activation function (i.e., $\mathrm{Re}LU\left(•\right)=\max \left(0,•\right)$), and H^(l) ∈ R^n×D is the activation matrix for the lth layer, initialized as H⁽⁰⁾ = X. In this way, the resulting node embeddings that capture node attributes X and the graph structure A simultaneously [5].

For a dimension specific network G^r, the representation learning model can be denoted as:

$H_r^{\left(l+1\right)}=\sigma \left({\tilde{D}}_r^{-\frac{1}{2}}{\tilde{A}}_r{\tilde{D}}_r^{-\frac{1}{2}}{H}_r^{\left(l\right)}{W}_r^{\left(l\right)}\right)(3)$

where A^r ∈ R^|V|×|V| is an adjacency matrix for the graph G^r and D^r is the corresponding diagonal degree matrix. Unlike in conventional GCN, we modify ${\tilde{A}}_r$ and define it as ${\tilde{A}}_r=A_r+w{I}_n$ Park and Kim [24]. In this expression,w ∈ R is the weight of self-connections used to measure the relative importance between objective nodes and its neighboring nodes in generating objective node embeddings. A value of w > 1 implies the objective node itself is more important than its neighboring nodes, with increasing values of w representing higher importance. The term ${\tilde{D}}_{ii}^r={\sum }_j{\tilde{A}}_{ij}^r$ represents the degree matrix for ${\tilde{A}}_r$. In this paper, a two-layer GCN was used to learn dimension specific node embeddings, and the node feature of the input graph is X_new, i.e.H⁽⁰⁾ = X_new. The last layer output embedding matrix was denoted H_r, which describes a dimension specific node embedding for the graph G^r. The resulting node embeddings H_r that capture node original attributes X, distance node neighboring information X_rw and the graph structure A simultaneously [5].

3.4 Cross Dimension Modeling

For a given dimension r ∈ M, we can obtain the node representation H_r∈M ∈ R^n×d, which provides distance information for G^r. Each H_r∈M is acquired independently by training a two-layer GCN model, as described by Eq. 3. However, these embedding matrices fail to take advantage of interactions and similarities between diverse dimensions. This inspired us to devise a way of jointly learning embedding information from diverse dimensional networks to develop a more comprehensive node representation. This task was accomplished by adding two regularization constraint mechanisms to the objective function representing the consistency constraint among the $\left|M\right|$ network embedding matrices H_r∈M, and the trainable weight parameter constraint among $\left|M\right|$ GCNs. These two constraints are discussed below.

Regularized consistency constraints: We first applied the normalization to each node embedding matrix to obtain the normalized matrices (i.e. transforming the H_r to H_r−nor). The normalized matrices were then exploited to collect similarity information between each pair of counterpart nodes by $H_{r-nor}\cdot H_{r-nor}^T$, and the resulting is the similarity of n nodes. The regularized consistency constraint can be defined as follows:

$L_{CC}=\Vert H_{r-nor}\cdot H_{r-nor}^T-H_{r^{\prime }-nor}\cdot H_{r^{\prime }-nor}^T{\Vert }_2^2,r\in M,r^{\prime }\in M,r\ne r^{\prime }(4)$

where ⋅^T represents the transpose. This constraint can adaptively capture node similarity information among diverse dimensional graph networks when training the proposed model oriented by the node classification task.

Regularized trainable weight parameter constraints among $\left|M\right|$ GCNs: As in Xie et al. [26], we utilize regularized constraints for trainable weight parameters among $\left|M\right|$ GCNs models. This constraint can be defined as follows:

$L_{WP}=\sum _{r=1}^M\sum _{r^{\prime }=1,r^{\prime }\ne r}^M{‖W_r-W_{r^{\prime }}‖}_2^2(5)$

where W_r and W_r’ are trainable GCN weight matrices for the relation type r and r′.

3.5 Attention Mechanisms for Fusing Different Dimensions

Now attention mechanisms were used to learn corresponding importance weights from different dimensional graph network during each step of model iteration. When optimization of the proposed model ceases, the learned weights represent the importance of diverse dimensional graph networks. The learned dimensional attention matrices for the n nodes were used to embed H_r∈M into the final global consensus node representation as follows:

$Z_{global}={\sum }_{r=1}^M{\alpha }_r{H}_r,{\alpha }_r\in R^{n\times n},H_r\in R^{n\times d}(6)$

where α_r is the learned importance of n nodes for the r dimension network.

Now, the node v_i can be used as an example to illustrate how importance values can be acquired for the node v_i and how attention matrices α_r were acquired for the relation type r. For each r ∈ M, the embedding of node v_i in H_r is given by the row vector $h_r^i\in R^{1\times d}$. We first transform $h_r^i$ via a nonlinear transformation (i.e. the f(x) function in Eq. 7) and then apply a shared attention vector p ∈ R^h′^×1, designed to determine the weight ${\epsilon }_r^i$:

${\epsilon }_r^i=p^T\cdot f\left(W\cdot {\left(h_r^i\right)}^T+b\right)(7)$

Here, W ∈ R^h′^×d is a weight matrix, b ∈ R^h′^×1 is a bias vector, and $f(x)=\frac{\exp (x)-\exp (-x)}{\exp (x)+\exp (-x)}$ is the tanh function (an activation function). The Softmax function can then be used to normalize different attention values in diverse dimensional graph networks. The final weight for node v_i can be calculated as:

$a_r^i=\frac{\exp \left({\epsilon }_r^i\right)}{{\sum }_{r=1}^M\exp \left({\epsilon }_r^i\right)}(8)$

Larger values of $a_r^i$ imply that corresponding embeddings are more important. For n nodes in the r dimension network, we can first obtain a learned weight column vector $a_r=[a_r^i],a_r\in R^{n\times 1}$ and then transform the column vector a_r into a α_r = diag (a_r), α_r ∈ R^n×n diagonal matrix.

3.6 Optimization Objective

Node Classification: The output embedding matrix in Eq. 6 was used for node classification tasks in combination with a linear transformation and a Softmax function. Prediction results were then calculated as follows:

$\widehat{Y}=softmax\left(W_{nc}\cdot Z_{global}+b_{nc}\right)(9)$

where W_nc ∈ R^n×n is a weight matrix, b_nc ∈ R^n×C is a bias vector,$\widehat{Y}=\left[{\widehat{y}}_{ic}\right]\in R^{n\times C}$ is the predicted result for n nodes, and ${\widehat{y}}_{ic}$ represents the predicted probability of node v_i belonging to class c. The $softmax\left(x\right)=\frac{\exp (x)}{{\sum }_{c=1}^C\exp (x_c)}$ function is a normalizer across all classes. The cross-entropy loss was then minimized over all training nodes using a loss function defined as follows:

$L_{nc}=\sum _{v_i\in S}{\sum }_{i=1}^C\left[-y_i\ln {\widehat{y}}_i\right](10)$

where S represents the training set, y_i is the real label for node v_i, and ${\widehat{y}}_i$ is the predicted label.

Overall Objective Function: The consistency constraint in Eq. 4 was jointly optimized, along with the trainable weight parameter constraints in Eq. 5 and the node classification function in Eq. 10. An overall objective function was given by:

$\underset{\theta }{\min }L=\underset{\theta }{\min }\left(L_{nc}+\alpha L_{CC}+\beta L_{WP}\right)(11)$

Here, α and β are hyper-parameters used to control the importance of consistency constraints and trainable weight parameter constraint terms. Labeled data were then used to guide the learnable parameters $\theta =\left\{W_r,{\alpha }_r,W,b,W_{nc},b_{nc}\right\},r=\mathrm{1,2},\dots ,M$, which were automatically learned and updated via gradient descent and back-propagation algorithms. Convergence of the overall objective function L could then be used to obtain a global node representation Z_global. This process is summarized in Algorithm 1.

Algorithm 1 The proposed technique.

For a given multiplex graph network $G=\left\{V,E^{(1)},E^{(2)},\dots ,E^{(M)},X\right\}$ with M relationships, we first use the node2vec random walk technique to capture the 10-hop neighnoring node information, and then Eq. 1 is utilized to obtain the pre-trained node feature X_rw concatenating with the original node attributes X to get X_new. The proposed multiplex graph convolutional network is used to encode all nodes of the multiplex graph network into vectors. We first set the hyper-parameters including the embedding dimension d, parameters α, β, w. When training the proposed model oriented with the node classification task, the learnable parameters are first random initialized, and optimized with the back-propagation algorithm. While the loss function in Eq. 11 has not converged, the proposed model will computer each dimension (relationship) node embedding with Eq. 3, cross dimension interactions with Eq 4 and Eq. 5 and attention coefficient using Eq. 7 and Eq. 8. The global node embedding Z_global for all nodes from the multiplex relationships is generated according to the obtained attention coefficient.

3.7 Time Complexity

Our proposed technique is primarily composed of four components: 1) the pre-training of node features using a random walk network embedding method, 2) dimension specific node embedding using a GCN model, 3) cross dimension modeling terms, and 4) an attention-based mechanism used to generate global node representations by integrating embeddings of different dimensions. The time complexity of random walk can be expressed as O (|V|). Dimension specific embeddings O (L|E|d′ + L|V|(F + d_rw)d′) could then be learned using a GCN model, where F + d_rw is the dimension of input node features and d′ is the output dimension of one convolution layer. The term L represents the number of GCN layers (2 in this study). The time complexity required for learning global node representations is given by O (|V|d′|M|), where |M| is the number of relation types. Updating attention weights for diverse dimensions in the process of model training, the time complexity can be expressed as O (|S|d′|M|), where |S| is the number of training data. In practice, this quantity of training data is typically small, such that |S| ≪ |E|. In most practical networks, |V| ≪ |E|. As such, the total time complexity of node classification tasks can be simplified as O (|V|(F + d_rw)d′ + |E|d′).

4 Experiments

4.1 Experimental Setup

We construct our experiment on the popular Pytorch framework (https://pytorch.org). All the experiments are performed on a computer with 2.6 GHz 4-core Intel Core i9 processor and the GPU is RTX2080.

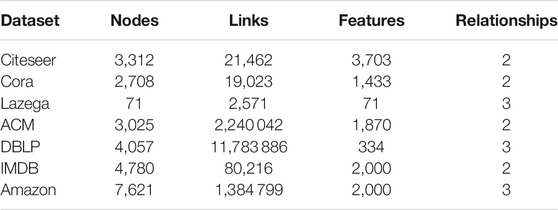
Datasets: The proposed method was evaluated on several real-world datasets, as described in Table 2. Lazega is a dense network, while the other datasets are sparse networks.

• Citeseer [5]:Citeseer is a citation network consisting of 3,312 research papers, where nodes are publications divided into six different research areas [5]. Node features are bag-of-words representations for individual papers. We can construct the multiplex graph network including two dimensional: a citation dimensional network (where edges represent citation links between papers) and a paper similarity dimensional network. It is a k-nearest neighbor (kNN) graph constructed by calculating the cosine similarity based on the node features and edges representing the top 10 similar papers (i.e., k is 10).

• Cora [5]: Cora is a citation network containing 2,708 machine learning papers divided into seven classes [5]. Node features are bag-of-words representations of individual papers. We can utilize the same approach as for the Citeseer dataset to construct a multiplex network with two dimensions (i.e., citation and node similarity dimensions).

• Lazega [38]: Lazega is a multiplex social network with three relationship types (i.e., strong coworker, advice, and friendship networks) among 71 attorneys (partners and associates) at a law firm. The law school was selected for node label classification.

• ACM [24,28]: It is a multiplex network about the paper-paper relationships consisting of two views which are the two papers are written by same author and two papers contain same subjects respectively. The features of nodes are the elements of a bag-of-words represented of keywords. The nodes are divided into three classes.

• DBLP [24,28]: The dataset is made up of three views about the authors-authors re-pationships, which is another multiplex network from the DBLP. The three views are the two authors have worked together on papers, two authors have published papers with the same terms, and two papers have published papers with the same terms. The classes of the nodes represent the DM(KDD,WSDM, ICDM), AI(ICML, AAAI,IJCAI), CV(CVPR),NLP (ACL,NAACL, EMNLP), which are the authors’ research areas.

• IMDB [24,28]: This is a movie network from the IMDB dataset. In this paper, the IMDB dataset is made up of two relationships (i.e. movies are acted by the same actor and movies are directed by the same director). The features of nodes are the bag-of-words represented of plots. The nodes are divided according to the movies’ genre.

• Amazon [24,28]: This dataset is a multiplex network including three views (i.e. also-viewed, also-bought, and bought-together) between items. The items are divided into four different categories (i.e. Beauty, Automotive, Patio Lawn and Garden). The features of the items are the description of items.

TABLE 2

TABLE 2. Dataset statistics.

Baseline: AMRG was compared with the following competitive baselines.

• DeepWalk [13]: DeepWalk is designed for standard single-layer network embedding without considering node attributes [13]. This approach first utilizes random walk in the networks and then applies a skip-gram algorithm to learn node representations.

• node2vec [10]: On the top of the DeepWalk, node2vec adds two parameters to control the random walk process, forming a biased random walk [10].

• NetMF [31]: It is a general framework that unifies DeepWalk, LINE, node2vec, and PTE by converting a negative sampling into a matrix factorization method for learning network representations.

• MGAT [26]: MGAT is a multiplex network embedding with the Graph Attention Networks (GAT) model.

MGAT was implemented using Pytorch, though the source code is not provided here. The source code published by the authors was utilized for all other baselines.

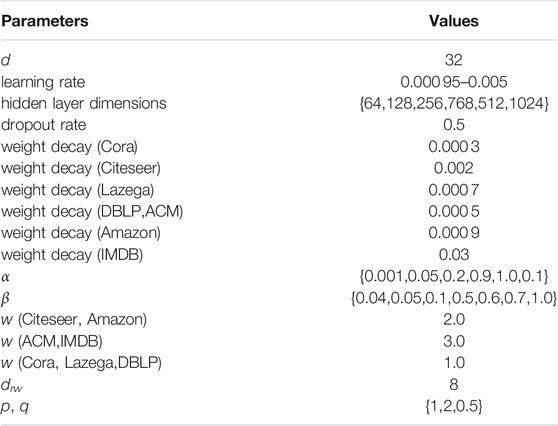
Parameter Settings: The output node embedding dimension for all datasets was set to 32 to provide a fair comparison. We carefully turn parameters of our proposed model to get optimal performance. For our method, a two-layer GCN was trained with hidden layer dimensions of 64, 128, 256,768, 512, 1024 and output dimensions of 32. The objective function in Eq. 11 was minimized for the training set using a learning rate of 0.000 95–0.005 and the Adam optimizer. A dropout rate of 0.5 was used in addition to weight decay values of 0.000 three for Cora, 0.002 for Citeseer, 0.000 seven for Lazega, 0.000 five for DBLP and ACM, 0.000 nine for Amazon and 0.03 for IMDB. Consistency constraint coefficients and trainable weight parameters (α and β) were searched in the intervals $\left\{0.001,0.05,0.2,0.9,1.0,0.1\right\}$ and $\left\{0.04,0.05,0.1,0.5,0.6,0.7,1.0\right\}$, respectively. The self-connection weight was set to 2.0 for Citeseer and Amazon datasets, 3.0 for ACM and IMDB datasets and to 1.0 for Cora, Lazega and DBLP datasets. The Lazega dataset contains node relationship types but not node features. As such, a unit diagonal matrix was used as the feature matrix. The node2vec random walk node embedding dimension (d_rw) for learning distance node information was set to 8. These values of parameters are summarized in Table 3.

TABLE 3

TABLE 3. The values of parameters.

For baselines, DeepWalk is a special case of node2vec with p = q = 1. In the conventional node2vec algorithm, hyperparameters were set to p = 2 and q = 0.5, with a window size of 10 and five for negative samples. Other baseline hyperparameters were set as in the original papers.

4.2 Node Classification

Accuracy (ACC) was used to evaluate node classification performance for the all datasets. We randomly selected 10% of the nodes to establish a training set, 10% to form the validation set, and the remaining 80% formed the test set. A total of 120 epochs were used for each of the three datasets. The proposed approach was compared with its variants and state-of-the-art baselines to monitor node classification performance for the following scenarios.

• AMRG/rw: A random walk strategy was not used to learn distance neighboring node information.

• AMRG/att: Our proposed method without the attention mechanism.

• AMRG/cc: Our proposed method without the regularized consistency constraint.

• AMRG/wp: Our proposed method without the regularized trainable weight parameters constraints among |M| GCNs.

The baselines of Node2vec and NetMF were designed for standard single-layer networks. As such, we first acquired node embeddings for each dimension separately and averaged the resulting embeddings together to produce the overall node embeddings. This process was repeated 5 times to produce averaged results for baselines. For our proposed method, as the node2vec random walk technique to capture the 10-hop distance node information and the GCN model will produce a slightly different outcome each time, so the performance of the node classification for our proposed model will be evaluated 5 times, and average 5 times results.

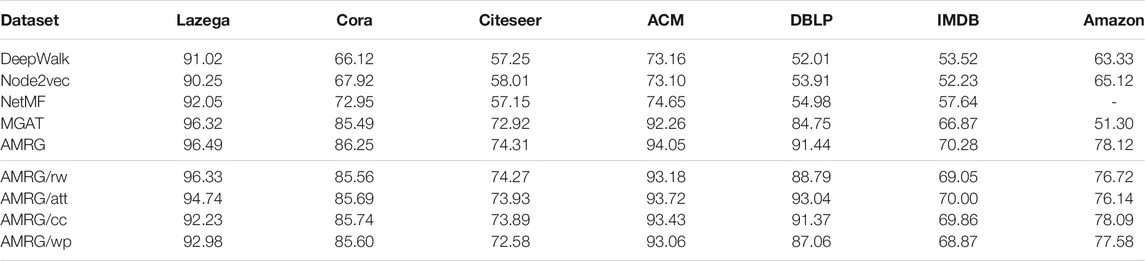
Node classification accuracy (ACC) values are reported in Table 4, where the bolded number denotes the best result. The following are evident from the table:

• Compared with all other baselines, our proposed method consistently achieved the best performance for all datasets. These results demonstrate the effectiveness of our model for attributed multiplex network embedding, oriented by node classification tasks. From Table 4, we observe the random walk technique improved the accuracy of node classification by learning 10-hop node information. This suggests that node information from larger receptive fields is important.

• AMRG/att generates node embeddings using a two-layer GCN for each dimensional network and simply averages the embeddings without considering the attention mechanism. Table 4 suggests that attention-based weighting in each dimension can boost overall performance. This result is consistent with our assumption that node importance differs in each dimension. However, DBLP can obtain better performance on AMRG/att, it implies that three dimensional graph networks are almost equal degree of importance.

• The coefficients (α and β) for AMRG/cc and AMRG/wp were set to zero respectively in Eq. 11. The results suggest these two methods are inferior to AMRG. This indicates that consistency and weight parameters constraints are important for improving the overall performance, demonstrating the need to capture similarities and interactions among diverse dimensions.

• In addition, our technique improved on the classification performance of MGAT (the best performing baseline method except for Amazon dataset, the MGAT is not suitable for Amazon) by as much as 6.69% for the DBLP dataset. This performance was only slightly better than MGAT for the Lazega data. This is likely because Lazega is a small, dense multiplex network with only 71 nodes. As such, node information spreads quickly in graphs through the two-layer GCN. The accuracy of node classification for the Cora all dataset was worse than that of other variants without pre-trained node features, which again indicates the importance of node information from larger receptive fields. However, as NetMF method uses the matrix factorization, the model does not convergence for Amazon, which explains the shortcomings of the NetMF.

• The difference between our method and MGAT is that we used consistency constraints to embed each dimension network with pre-trained 10-hop node information. Table 4 indicates the overall performance of our method is superior to MGAT, which suggests that consistency constraints and pre-trained methods with random walk are important mechanisms for learning high-quality node embeddings for multiplex network. Furthermore, compared with MGAT, our approach achieved superior node embeddings through two-layer general and simple GCNs with fewer model parameters than MGAT, which is based on the GAT model with multiple attention heads that lead to rapid growth in the number of parameters Veličković and Cucurull [15].

TABLE 4

TABLE 4. Node classification Accuracy (%) (bold: Best).

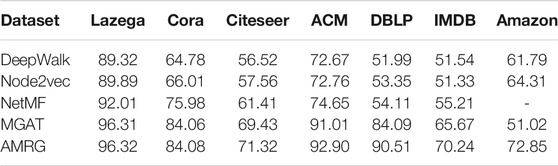
Similarly, node classification F1-score values also are presented in Table 5, where the bolded number denotes the best result. These results demonstrate that our method is stable and competitive.

TABLE 5

TABLE 5. Node classification F1-score (%) (bold: Best).

4.3 Analysis of Attention Mechanisms

Now we use the Lazega,a dense network, and three sparse networks (Cora, IMDB, and DBLP) as examples to were used to analyze changing trends in attention values for node classification tasks. The results are shown in Figure 3, where the x-axis denotes different numbers of epochs during the model training process and the y-axis is the corresponding attention value. As seen in Figure 3A, the attention values for advice, friendship, and strong coworker dimensional networks are nearly the same for the Lazega dataset in epoch 0. However, this attention value varies with increasing training epochs. The attention value for the advice dimensional network increases in epoch 20 (compared to epoch 0), while the attention value for the strong coworkers dimensional network decreases. Similarly, the attention values for the advice and strong coworker dimensional networks gradually decrease until the model converges. However, the attention value continues increasing for the friendship dimensional network during the training process. This illustrates that our approach can adaptively learn the importance weights of diverse relation type network embeddings during individual steps. For example, information provided by the friendship dimension network was more important than that of the advice and strong coworker dimension for the Lazega dataset. Similar trends were observed for the Cora, IMDB and DBLP datasets. The citation dimension network also proved to be more important than the paper similarity dimension network in the overall system, as shown in Figure 3B.

FIGURE 3

FIGURE 3. (A) Lazega. (B) Cora. (C) IMDB. (D) DBLP.

For the IMDB dataset, when the epoch is 18, the accuracy of node classification is the best (i.e. 70.28). At this moment, the attention value for co-actor network and co-director network is almost equal. From Table 4, we can see that when the attention value for co-actor network and co-director network is equal (i.e.AMRG/att, attention values are 0.5 and 0.5 respectively), the accuracy is 70.00, which is in close proximity to 70.28. This demonstrate that the attention mechanism is important. For DBLP, when the epoch is 103, the accuracy of node classification is the best.

4.4 Analysis of Variants

In this section, we analyze the effectiveness and sensitivity of pre-trained node vector dimensions, two regularization constraints, and the weight of self-connections. Specifically, we evaluate the performance (i.e., accuracy and macro-F1) of our method for node classification tasks with respect to α,β,w and d_rw. Since these datasets produced similar results, we use the Citeseer, ACM and Cora datasets as examples respectively.

Analysis for α: In this test, the value of β was set to zero, which eliminates L_WP in Eq. 11. The parameter α was varied from 0.1 to 1.0, as shown in Figure 4A. The accuracy and macro-F1 score for these node classification tasks remained relatively stable with increasing α for Citeseer. And when the α is 0.3, the accuracy and macro-F1 score is the best for ACM in Figure 4D.

FIGURE 4

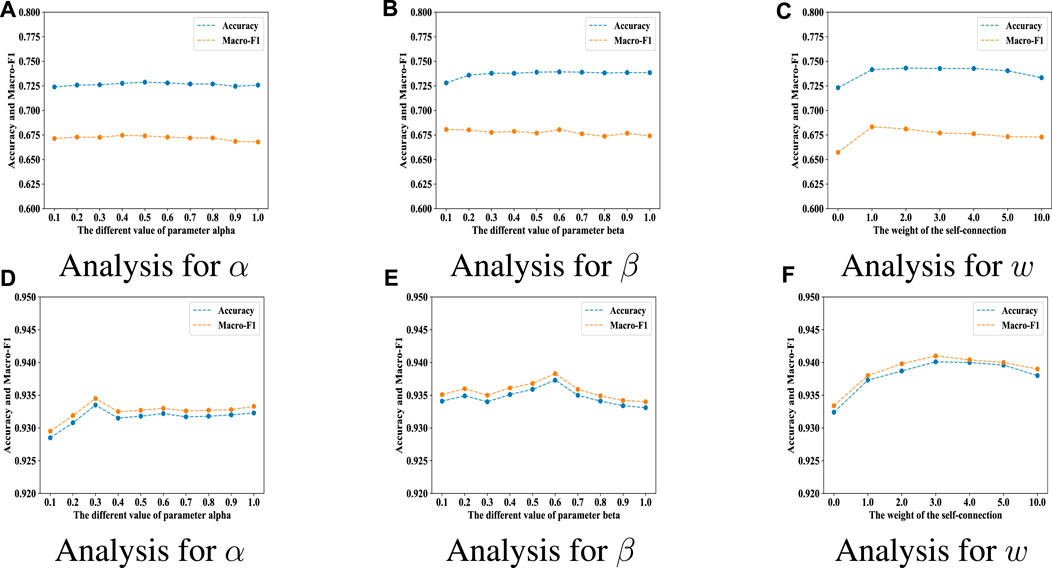
FIGURE 4. The performance of our method for parameters α, β, w on the Citeseer (A–C) and ACM (D–F) datasets for node classification task.

Analysis for β: Here, the value of α was set to zero, which eliminates the consistency constraint L_CC in Eq. 11. Figure 4B demonstrates how different values of the coefficient β affected node classification performance. The value of β was increased from 0.1 to 1.0, as the accuracy slowly increased and decreased (the maximum was in 0.7), and the macro-F1 score remained nearly constant. Similarity trends can be found in Figure 4E and the maximum was β in 0.6.

Analysis for w: The impact of the weight on these self-connections was observed by varying w from 0.0 to 10.0, as shown in Figure 4C for Citeseer. A value of w = 0.0 implies the node itself only considers neighboring nodes in generating embeddings, producing low accuracy and macro-F1 scores. Larger values (w > 1) indicate the node itself is more important than its neighboring nodes. The accuracy first increases and then remains relatively stable, before dropping quickly for w = 10.0. The maximum accuracy and macro-F1 scores occurred for w = 2 and w = 1, respectively, with macro-F1 decreasing slowly as w increased. For ACM in Figure 4F, the best accuracy and macro-F1 occurred for w = 3.

Analysis of random walk dimension d_rw: Figure 5 suggests the accuracy of node classification was maximized for d_rw in 8, decreasing for higher dimensions. This demonstrates that pre-trained node features, which contains distance node neighboring information, can improve model performance. When the embedding dimension d_rw is small, the obtained pre-trained node features are not enough to describe the distance neighborhood information. On the contrary, if the value of embedding dimension d_rw is large, it will introduce some noise on the obtained pre-trained node features.

FIGURE 5

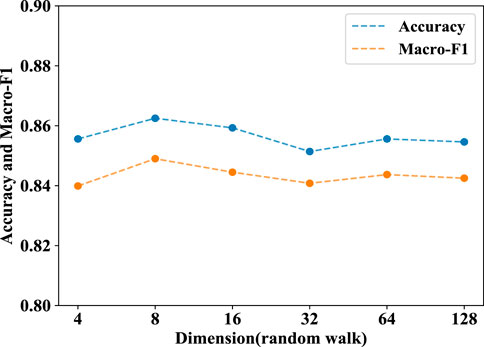
FIGURE 5. The performance of our method for parameters d_rw on the Cora dataset for node classification task.

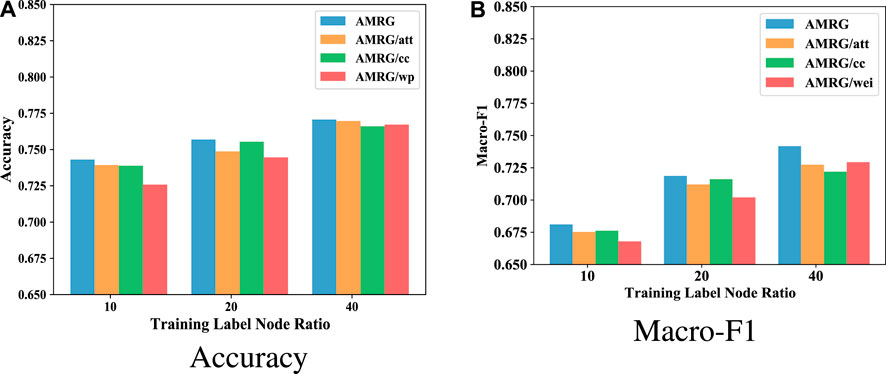
Analysis of different training nodes: We tested the performance of our method and its variants using training node fractions of 10, 20, and 40% for the attributed multiplex Citeeer network, as shown in Figure 6. The proposed method consistently outperformed its variants, indicating the importance and effectiveness of attention mechanisms, consistency constraints, and trainable weight parameter constraints of |M| GCN for each dimensional graph network for boosting overall performance. The influence of attention mechanisms and these two constraints on node classification performance varied with different training label node ratios.

FIGURE 6

FIGURE 6. (A) Accuracy. (B) B Macro-F1.

4.5 Analysis of Key Factor

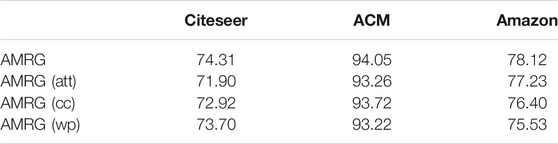
In the previous section, we analyse the effect of the different single variant on the performance of the proposed model. At present, we take the Citeseer, ACM and Amazon as examples to evaluate the key factor of regularized consistency constraints, weight constraints and attention mechanism. That is to say, which one of three factors is the most significant to improve the AMRG. The evaluation indicator is the node classification accuracy.

• AMRG(wp): The AMRG only with the weight constraints.

• AMRG(cc): The AMRG only with the regularized consistency constraints.

• AMRG(att): The AMRG only with the attention mechanism.

Table 6 shows that these three strategies (i.e. regularized consistency constraints, weight constraints and attention mechanism) have different importance on the three datasets. For Citeseer, it shows that the weight constraints is the key factor, as the performance of AMRG (wp) is better than AMRG (att) and AMRG (cc). From the results of ACM and Amazon, we can see that the regularized consistency constraints is the key factor for ACM and the attention mechanism is the key factor for Amazon. As the performance of AMRG (cc) is better and AMRG (att) is better than the other variants.

TABLE 6

TABLE 6. Node classification accuracy (%) (Bold: Best; underline: Runner-up).

4.6 Visualization

Task visualization will be performed to provide a more intuitive comparison and to further show the effectiveness of our proposed method. As the results on different datasets will exhibit similar trends, we take the Citeseer dataset as an example to evaluate our method. Output embeddings in the last layer, prior to the Softmax operation, were utilized for node classification tasks and to plot the resulting node embeddings using t-SNE Maaten and van der Hinton [40]. Results for the Citeseer dataset are shown in Figure 7 and are colored using real labels.

FIGURE 7

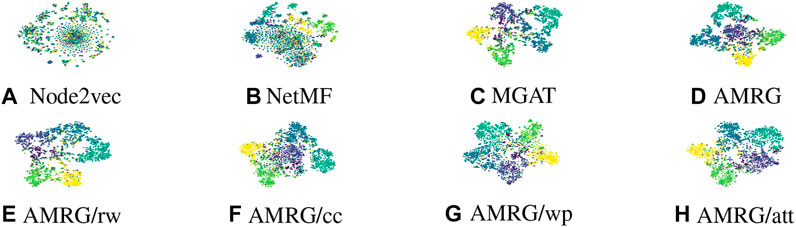
FIGURE 7. (A) Node2vec. (B) NetMF. (C) MGAT. (D) AMRG. (E) AMRG/rw. (F) AMRG/cc. (G) AMRG/wp (H) AMRG/att.

It is evident from the figure that the results of the node2vec and NetMF baselines are not satisfactory because nodes with different classes are mixed together. In contrast, MGAT and our method consider node features, producing better results than node2vec and NetMF. This further demonstrates the importance of node features for mining hidden graph information. The three variants are inferior to our method, which is consistent with the results of Table 4. Our approach has the clearest distinct boundaries among the diverse classes and the same classes are grouped together. This demonstrates the importance of pre-trained mechanisms with random walk network embedding, consistency constraints, trainable weight parameter constraints among $\left|M\right|$ GCN, and attention mechanisms.

5 Conclusion

In this paper, a new approach for node classification in attributed multiplex networks was developed using random walk network embedding and GCN. Random walk network embedding was first used to capture 10-hop node information as pre-trained node features. Then they were concatenated with the original node attributes, the resulting as the new node features inputted into the GCN model. A two-layer GCN was then utilized to learn each dimensional network. In order to achieve more comprehensive, informative, higher-quality and global consensus node representations, we introduced regularized consistency constraints to capture the similarities among different dimensional network embeddings. Besides, trainable weight parameter constraints were used to learn the interactive information from diverse dimensions. Furthermore, an attention mechanism was utilized to learn weights for diverse dimensional networks, and then to fuse them based on the weights. Extensive experiments were conducted using real-world networks applied to node classification, visualization, analysis of attention mechanisms, and parameter sensitivity. The results demonstrated that these strategies of our approach can boost overall performance of node classification for multiplex graph networks, which outperformed many competitive baselines. In the future, we plan to extend this framework to larger, more complex, and time-varying graphs. Another promising direction involves learning node representations combining edge features.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

Conceptualization, BH, YW, and LK; Data curation, BH, QW, and YY; Funding acquisition, YW and LK; Methodology, BH, YW, LK, and QW; Validation, Visualization, BH and YW; Supervision, YW and LK; Writing—Original draft preparation, BH and YW; Writing—Reviewing and Editing, BH, YW, LK, QW, and YY; All authors have read and agreed to the published version of the manuscript.

Funding

This paper is support by the National Natural Science Foundation of China (NSFC) under grant number 61 873 274 and Postgraduate Scientific Research Innovation Project of Hunan Province under grant number CX20200075.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹In this paper, we use the terminology graph network, network, graph interchangeably.

References

1. Wang Z, Wang J, Guo Y, Gong Z. Zero-shot Node Classification with Decomposed Graph Prototype Network. In: KDD ’21: Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. New York, NY, USA: Association for Computing Machinery (2021). p. 1769–79. doi:10.1145/3447548.3467230

CrossRef Full Text | Google Scholar

2. Zhu Y, Xu Y, Yu F, Liu Q, Wu S, Wang L. Graph Contrastive Learning with Adaptive Augmentation. In: WWW ’21: Proceedings of the Web Conference 2021. New York, NY, USA: Association for Computing Machinery (2021). p. 2069–80. doi:10.1145/3442381.3449802

CrossRef Full Text | Google Scholar

3. Tajeuna EG, Bouguessa M, Wang S. Modeling and Predicting Community Structure Changes in Time-Evolving Social Networks. IEEE Trans Knowl Data Eng (2019) 31:1166–80. doi:10.1109/TKDE.2018.2851586

CrossRef Full Text | Google Scholar

4. Sun Y, Yu Y, Han J. Ranking-based Clustering of Heterogeneous Information Networks with star Network Schema. In: KDD ’09: Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, NY, USA: Association for Computing Machinery (2009). p. 797–806. doi:10.1145/1557019.1557107

CrossRef Full Text | Google Scholar

5. Kipf TN, Welling M. Semi-supervised Classification with Graph Convolutional Networks. In: International Conference on Learning Representations (ICLR) (2017).

Google Scholar

6. Li ZWX-M, Han Q. Deeper Insights into Graph Convolutional Networks for Semi-supervised Learning. Menlo Park, California, USA: AAAI (2018).

Google Scholar

7. Li G, Muller M, Thabet A, Ghanem B. Deepgcns: Can Gcns Go as Deep as Cnns?. In: 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, South Korea, October 27–November 3, 2019 (2019). p. 9266–75. doi:10.1109/ICCV.2019.00936

CrossRef Full Text | Google Scholar

8. Wang M, Lin Y, Lin G, Yang K, Wu X-m. M2grl: A Multi-Task Multi-View Graph Representation Learning Framework for Web-Scale Recommender Systems. In: KDD ’20: Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, NY, USA: Association for Computing Machinery (2020). p. 2349–58. doi:10.1145/3394486.3403284

CrossRef Full Text | Google Scholar

9. Ying R, He R, Chen K, Eksombatchai P, Hamilton WL, Leskovec J. Graph Convolutional Neural Networks for Web-Scale Recommender Systems. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, London, August 19 - 23, 2018. New York, NY, USA: Association for Computing Machinery (2018). 974–83. doi:10.1145/3219819.3219890

CrossRef Full Text | Google Scholar

10. Grover A, Leskovec J.. node2vec: Scalable Feature Learning for Networks. KDD (2016) 2016:855–64. doi:10.1145/2939672.2939754

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Zhang H, Qiu L, Yi L, Song Y. Scalable Multiplex Network Embedding. In: IJCAI'18: Proceedings of the 27th International Joint Conference on Artificial Intelligence, Stockholm, Sweden, July 13-19, 2018. AAAI Press (2018). p. 3082–8. doi:10.24963/ijcai.2018/428

CrossRef Full Text | Google Scholar

12. Tang J, Qu M, Wang M, Zhang M, Yan J, Mei Q. Line. In: Proceedings of the 24th International Conference on World Wide Web (WWW’15), Montréal, Québec, Canada, April 11 - 15, 2016 (2015). p. 1067–77. doi:10.1145/2736277.2741093

CrossRef Full Text | Google Scholar

13. Perozzi B, Al-Rfou R, Skiena S. DeepWalk. In: Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, August 24 - 27, 2014. New York, NY: Association for Computing Machinery (2014). p. 701–10. doi:10.1145/2623330.2623732

CrossRef Full Text | Google Scholar

14. Hamilton WL, Ying R, Leskovec J. Inductive Representation Learning on Large Graphs. Granada, Spain: NIPS (2017).

Google Scholar

15. Veličković GCARALPBY, Cucurull P. Graph Attention Networks. Vienna: ICLR (2018).

Google Scholar

16. Li C, Wang L, Sun S, Xia C. Identification of Influential Spreaders Based on Classified Neighbors in Real-World Complex Networks. Appl Maths Comput (2018) 320:512–23. doi:10.1016/j.amc.2017.10.001

CrossRef Full Text | Google Scholar

17. Nicosia V, Latora V. Measuring and Modeling Correlations in Multiplex Networks. Phys Rev E (2015) 92:032805. doi:10.1103/PhysRevE.92.032805

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Wang Z, Guo Q, Sun S, Xia C. The Impact of Awareness Diffusion on Sir-like Epidemics in Multiplex Networks. Appl Maths Comput (2019) 349:134–47. doi:10.1016/j.amc.2018.12.045

CrossRef Full Text | Google Scholar

19. Liu W, Chen P-Y, Yeung S, Suzumura T, Chen L. Principled Multilayer Network Embedding. Principled multilayer Netw embedding (2017) 2017:134–41. doi:10.1109/ICDMW.2017.23

CrossRef Full Text | Google Scholar

20. Murata R, Matsuno T. Mell: Effective Embedding Method for Multiplex Networks. In: WWW '18: Companion Proceedings of the The Web Conference 2018, Lyon, France, April 23–27, 2018. New York, NY: Association for Computing Machinery (2018). p. 1261–8. doi:10.1145/3184558.3191565

CrossRef Full Text | Google Scholar

21. Qu M, Tang J, Shang J, Ren X, Zhang M, Han J. An Attention-Based Collaboration Framework for Multi-View Network Representation Learning. In: Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, Singapore, November 6–10, 2017. New York, NY: Association for Computing Machinery (2017). p. 1767–76. doi:10.1145/3132847.3133021

CrossRef Full Text | Google Scholar

22. Ma SACYDTJ, Wang Y. Multi-dimensional Graph Convolutional Networks (2018).

Google Scholar

23. Ghorbani M, Baghshah MS, Rabiee HR. MGCN: Semi-supervised Classification in Multi-Layer Graphs with Graph Convolutional Networks. In: ASONAM '19: International Conference on Advances in Social Networks Analysis and Mining (2019). p. 208–11. doi:10.1145/3341161.3342942

CrossRef Full Text | Google Scholar

24. Park DHJYH, Kim C. Unsupervised Attributed Multiplex Network Embedding. Menlo Park, California, USA: AAAI (2020).

Google Scholar

25. Wang X, Ji H, Shi C, Wang B, Ye Y, Cui P, et al. Heterogeneous Graph Attention Network. In: The World Wide Web Conference (WWW ’19). New York, NY: Association for Computing Machinery (2019). 2022–2032.

CrossRef Full Text | Google Scholar

26. Xie Y, Gong Y, Tang MZ, Han C. Mgat: Multi-View Graph Attention Networks. Neural Networks (2020) 132:180–9. doi:10.1016/j.neunet.2020.08.021

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Gong M, Liu W, Xie Y, Tang Z, Xu M. Heuristic 3d Interactive Walk for Multilayer Network Embedding. IEEE Trans Knowl Data Eng (2020) 2020:1. doi:10.1109/TKDE.2020.3021393

CrossRef Full Text | Google Scholar

28. Fan S, Wang X, Shi C, Lu E, Lin K, Wang B.. One2multi Graph Autoencoder for Multi-View Graph Clustering. In: Proceedings of The Web Conference 2020 (WWW ’20), Taipei, Taiwan, April 20–24, 2020. New York, NY: Association for Computing Machinery (2020). 3070–76. doi:10.1145/3366423.3380079

CrossRef Full Text | Google Scholar

29. Mikolov ICKCGJ, Sutskever T. Distributed Representations of Words and Phrases and Their Compositionality. Granada, Spain: NIPS (2013). p. 3111–9.

Google Scholar

30. Wang D, Cui P, Zhu W. Structural Deep Network Embedding. In: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 2016, San Francisco, CA, August 13–17, 2016. New York, NY: Association for Computing Machinery (2016). p. 1225–34. doi:10.1145/2939672.2939753

CrossRef Full Text | Google Scholar

31. Qiu J, Dong Y, Ma H, Li J, Wang K, Tang J. Network Embedding as Matrix Factorization: Unifying Deepwalk, Line, Pte, and Node2vec. In: WSDM '18: Proceedings of the Eleventh ACM International Conference on Web Search and Data Mining, Marina Del Rey, CA, February 5–9, 2018. New York, NY: Association for Computing Machinery (2018). p. 459–67. doi:10.1145/3159652.3159706

CrossRef Full Text | Google Scholar

32. Yang C, Liu Z, Zhao D, Sun M, Chang EY. Network Representation Learning with Rich Text Information. In Proceedings of the 24th International Conference on Artificial Intelligence (IJCAI'15). Buenos Aires Argentina (2015). July 25 - 31, 2015. AAAI Press, 2111–2117.

Google Scholar

33. Zhang D, Yin J, Zhu X, Zhang C. Homophily, Structure, and Content Augmented Network Representation Learning. In: 2016 IEEE 16th International Conference on Data Mining (ICDM), Barcelona, Spain, December 12–15, 2016. IEEE (2016). p. 609–18. doi:10.1109/ICDM.2016.0072

CrossRef Full Text | Google Scholar

34. Bandyopadhyay AKHMM, Biswas S. A Multilayered Informative Random Walk for Attributed Social Network Embedding. Santiago de Compostela: ECAI (2020).

Google Scholar

35. Zhou GZZYCLZWLLCSM, Cui J. Graph Neural Networks: A Review of Methods and Applications. arXiv:1812.08434 [Cs, Stat] 2019 (2019).

Google Scholar

36. Schlichtkrull M, Kipf TN, Bloem P, van den Berg R, Titov I, Welling M. Modeling Relational Data with Graph Convolutional Networks. In: European Semantic Web Conference. Heraklion, Greece: Springer, Cham (2018). p. 593–607. doi:10.1007/978-3-319-93417-4_38

CrossRef Full Text | Google Scholar

37. Goyal P, Ferrara E. Graph Embedding Techniques, Applications, and Performance: A Survey. Knowledge-Based Syst (2018) 151:78–94. doi:10.1016/j.knosys.2018.03.022

CrossRef Full Text | Google Scholar

38. Grossetti M, Lazega E. The Collegial Phenomenon. The Social Mechanisms of Cooperation Among Peers in a Corporate Law Partnership. Revue Française de Sociologie (2003) 44:186. doi:10.2307/3323128

CrossRef Full Text | Google Scholar

39. Li J, Chen C, Tong H, Liu H. Multi-layered Network Embedding. In: Proceedings of the 2018 SIAM International Conference on Data Mining (SDM). San Diego: Society for Industrial and Applied Mathematics (2018) p. 684–92. doi:10.1137/1.9781611975321.77

CrossRef Full Text | Google Scholar

40. Maaten G, van der Hinton LJP. Visualizing High-Dimensional Data Using T-Sne. J Machine Learn Res (2008) 9:2579–605.

Google Scholar