Analysis of Stock Price Data: Determinition of The Optimal Sliding-Window Length

Introduction

Along with the big data era, time series widely exists in practice and is a popular data representation means, e.g., the stock price, the carbon price, white Gaussian noise, surface concentration ozone and etc. Specifically, time series is a sequence of data points represented in time order, while the time intervals between any consecutive points are always the same [1]. Due to the nonlinear and discrete properties, a bunch of analyzing approaches have been proposed [2]. Afterwards, complex network theory is developing rapidly [3] and applied to the analysis of time series data [1–9]. Hence, a technique, i.e., time series data visualization, and some improved versions, are developed by constructing complex networks from the initial data. Hence, sufficient analysis of the time series data can be performed accordingly.

Among those approaches, a technique, named Visibility Graph (VG), is widely adopted, and attracts the intensive interests [10]. This is initially proposed by Lacasa and his coworkers when investigating the time series data of robot movement [10]. Through VG, a corresponding complex network can be constructed, while the inherent properties and implied information of the original data can be preserved properly, such as Hurst coefficient, fractal properties [8, 11]. It is proved to be an efficient tool for the analysis of times series data [12–14]. Hence, the VG-based complex network and corresponding derivative theories are becoming a hot topic and various scholars have devoted their endless efforts into applying such theories into the various studies.

Initially, VG-based analysis mainly focuses on one-dimensional time series data. Recently, scholars start to investigate multiple time series data jointly to reveal inclined information. For instance, the authors in [10, 15] proposed a Multiplex Visibility Graphs (MVG) approach and conducted analysis of the surface concentration ozone, while complex networks are constructed for two time series data sets, i.e., the surface concentration ozone and the concentration of NO2 which are closely related with each other. Similarly, with the development of VG, a bunch of improved approaches have been proposed, such as sliding window-based Visibility Graph (SVG) [16], Multiplex Visibility Graph (MVG) [10, 15], Horizontal Visibility Graph (HVG) [17], and Limited Penetrating Visibility Graph (LPVG) [14, 18]. With the application of these approaches, it becomes easier for us to extract implied information from time series data.

Stock price time-series data is also one of the common time-series data. The analysis of stock price data, especially stock price trend prediction based on the analysis result, attracts the interests of various scholars [19, 20]. The authors in [20, 21] performed stock price forecasts and trend research study of stock price time-series data through machine learning approaches. While, we analyzed the stock price time-series data by complex network theory in which the corresponding complex network is constructed for stock time-series data, and relevant information can be studied accordingly. Here, we mainly adopt the SVG model to visualize the time series data of stock price. As revealed in [16], the appropriate window length for the analysis of different time series data sets varies. Hence, analyses of different stock price data are performed to determine the appropriate window length of SVG. Furthermore, corresponding multi-layer networks are constructed through MVG, then the correlations between time series data of multiple stock prices are thoroughly studied.

Model Description

Firstly, the VG and corresponding spin-off technologies are introduced. For VG, it is typically an undirected graph with the corresponding weight of each link equals to 1. For an original time series sequence, each data point is assigned an index indicating the time flag, i.e., $X_i$, while the data value for $X_i$ equals to $Y_i$. Hence, each data point can be indicated by ($X_i$, $Y_i$) for simplicity. Aiming to construct the network through VG, we are supposed to determine whether a link exists between two data points from the original time series data while the corresponding criterion is provided as [10]:

1) If two data points A ($X_a$, $Y_a$) and B ($X_b$, $Y_b$) are consecutive, i.e., no data points exist between these two points, there definitely exists a link connecting A and B.

2) If two data points are not consecutive, i.e., a point C ($X_c$, $Y_c$) exists where ($X_a$ < $X_c$ < $X_b$), and the relationship described by Eq. 1 is satisfied, then we can obtain a link connecting A and B.

$Y_c<Y_a+(Y_b-Y_a)\frac{(X_c-X_a)}{(X_b-X_a)}(1)$

For any data point combination, the above criterion is applied to discriminate the existence of links, and the corresponding VG network can be derived accordingly which can be further indicated by an adjacent matrix. If a link exists between two data points, then the corresponding value in the adjacent matrix equals to 1; otherwise, it is 0. An illustrative example is shown in Figure 1A indicating the network construction process of a time series data set consisting of 10 points.

FIGURE 1

FIGURE 1. (A) An example of the network construction process through VG. (B–D) A network construction process through SVG. Here, the lines connecting the top of data columns indicate the existed links.

Sliding-window is widely applied in various areas and related algorithms are proved to be of high computational efficiency and able to reduce the required storage [22]. Hence, an improved method is developed as in [16] by introducing the sliding-window idea into the network constructing process of VG to improve construction efficiency. Because of sliding-window, the afore-mentioned criterion is only necessary to be applied between a data point and a certain point within the sliding-window. Thus, the necessary times of applying the above discriminate criteria will be reduced tremendously. As in [16], we suppose the time series data is composed of $N$ data points while the selected sliding-window length equals to $W$. Then, the network construction procedure through SVG is provided as:

1) Step 1: For the first $W$ data points, the discriminate criteria of the original VG algorithm are applied to determine the existence of links;

2) Step 2: The window moved forward by the distance of a data point, and a new data point enters the window. Thus, the sliding-window covers the new data point and the previously existed $W$-1 data points. Hence, the discriminate criteria of the original VG will be applied.

3) Step 3: Repeat Step 2 until we reach the end of the time series data.

Examples are provided in Figure 1 which illustrates the construction process through VG and SVG with a window length of 4. For Figures 1B–D, the data points indicated by red columns are within the sliding-window, whereas those represented by blue columns are outside the sliding-window.

Accordingly, the computational complexity of SVG is largely determined by the required times of applying the discriminate criteria (fundamentally affected by the sliding-window length). For a time series consisting of $N$ data points and a provided window length $W$, the required times of applying the discrimination criteria to construct the complex network, i.e., S, is calculated as

$S=\frac{W\times (W-1)}{2}+(N-W)\times (W-1)(2)$

where $W$*($W$-1)/2 indicates the times of applying the discrimination criteria to the first $W$ data points, while ($N$-$W$) refers to the total number of times when moving forward, and the discrimination criteria is anticipated to be applied for $W$-1 for each movement. When $W$ is infinitely close to 1, the computational time complexity will be O ($n$). In practice, it is unlikely for $W$ to be close to 1, then the practical complexity will fall into the range of O (n)and O ($n^2$). Generally, the average time complexity is around O (nlogn) [23].

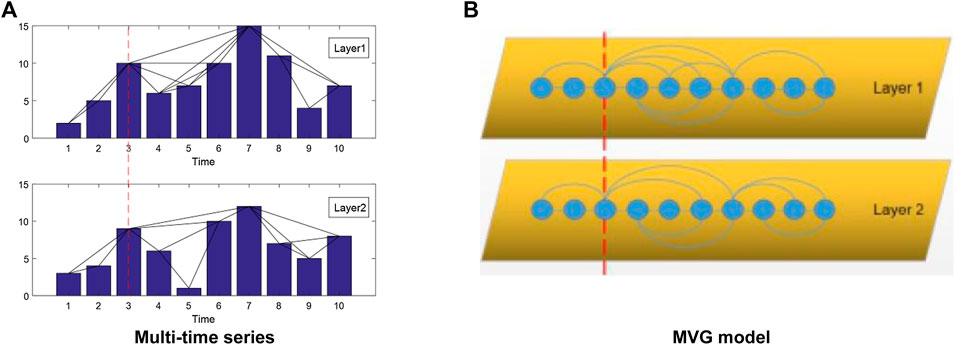
In this manuscript, we also study time series data sets of multiple stocks, thus the MVG is also introduced [15]. For MVG, there exists one time axis in common reflecting the varying of different types of data at the same time. Such types of data have inclined relationships which can be analyzed through calculating corresponding network parameters of the MVG. An example of MVG is provided as in Figure 2. As illustrated by Figure 3B, the 3rd data points on different layers seem to possess similar properties.

FIGURE 2

FIGURE 2. An illustration of the MVG.

FIGURE 3

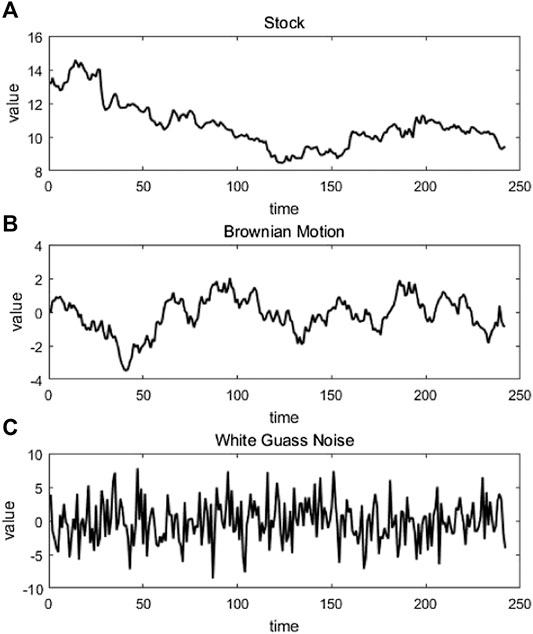
FIGURE 3. Three types of representative time series data. (A) stock, (B) Brownian motion, and (C) Guass noize.

As in [24], similar analysis can be performed to explore the implicit information of MVG. Here, two parameters are adopted aiming to investigate the interlayer information, i.e., Average Edge Overlap (AEO) and Interlayer Mutual Information (IMI) [25]. AEO is the average of the existence probabilities of a common link in all layers of the MVG which reflects the similarity of links on different layers (being denoted as ω). Corresponding value is calculated as

$\omega =\frac{{\displaystyle {\sum }_{\text{i}}{\displaystyle {\sum }_{j>i}{{\displaystyle {\sum }_{\alpha }aij}}^{\left[\alpha \right]}}}}{M{\displaystyle {\sum }_{\text{i}}{\displaystyle {\sum }_{j>i}(1-\delta (0,{{\displaystyle {\sum }_{\alpha }aij}}^{\left[\alpha \right]}))}}}(3)$

where the numerator indicates the total number of the appearance of the link between any two data points $i$ and $j$ in the layers of MVG. While $M$ represents the total number of layers for the MVG. If $\delta$ equals to 1, this indicates the link between the two data points does not exist in any of the layers. According to (Eq. 3), the maximum value of $\omega$ equals to 1, this indicates all layers of the MVG are identical. Correspondingly, the minimum value of ω equals to 1/M which corresponds to the scenario that every link only exists in one layer.

Another metrics, i.e., Interlayer Mutual Information (IMI), is introduced to reflect the relationship between the degree distributions of different layers [25]. Here $I$($\alpha$,$\beta$) indicates the IMI for two layers α and β which is provided as

$I(\alpha ,\beta )={\displaystyle \sum _{k\left[\alpha \right]}{\displaystyle \sum _{k\left[\beta \right]}P(k\left[\alpha \right],k\left[\beta \right])}}\log \frac{P(k\left[\alpha \right],k\left[\beta \right])}{P\left(k\left[\alpha \right]\right)P\left(k\left[\beta \right]\right)}(4)$

where $P$($k$[$\alpha$], $k$[$\beta$]) denotes the occurring probability of the case that a point on layer $\alpha$ possesses a degree of $k$[$\alpha$] while the corresponding data point on layer $\beta$ is of a degree of $k$[$\beta$]. P ($k$[$\alpha$]) represents the probability of a data point on layer $\alpha$ possessing a degree of $k$[$\alpha$], while $P$(k [$\beta$]) indicates the probability of a data point on layer $\beta$ possessing a degree of $k$[β]. A higher $I$($\alpha$,$\beta$) indicates that the degree distributions of the two layers seem to be even more similar.

Analysis of Stock Prices

In this section, we focus on analyzing the time series data of stock price through the afore-mentioned approaches. Three representative types of data are selected for illustrations. Figure 3A illustrates the time series data for the stock opening price of Ping An Bank Co., Ltd. consisting of a total number of 242 data points. For comparison, Figure 3B and Figure 3C indicate the data by adding Brownian Motion with Hurst coefficient of 0.5 and one-dimensional White Gaussian noise of 10 dB, respectively. For ease of reference, the data series are assumed to be of the same lengths. Among the three data sets, the transition of the data indicated by Figure 3A seems to be the smoothest; while the varying trend of the data indicated by Figure 3C is the most violent.

As afore-mentioned, networks obtained through SVG for different sliding-window lengths are likely to be of different properties. First, we investigated the relationship between the maximum degree of the obtained network and the sliding-window length with corresponding results being presented in Figures 4A–C, respectively. As illustrated, the maximum degree varies if a different sliding-window length is adopted. Whereas, once the sliding window length arrives at a certain threshold, the maximum degree maintains. However, for different types of data, the maximum degree varies. For the stock opening price of Ping An Bank Co., Ltd., the maximum degree is approximately 60, while the maximum degrees for data incorporating Brownian Motion and White Gaussian noise are 40 and 20, respectively. Furthermore, the corresponding velocity of convergence also varies. For the stock opening price of Ping An Bank Co., the maximum degree converges until $W$ increases to approximately 70% of the total number of data points ($W$ is supposed to be larger than 164 which is approximately 68% of the total data points). For data incorporating Brownian Motion, the maximum degree converges when $W$ approximately equals to 35% of the total number. While for the data with White Gaussian noise, the corresponding value converges when $W$ is around 20% of the total number.

FIGURE 4

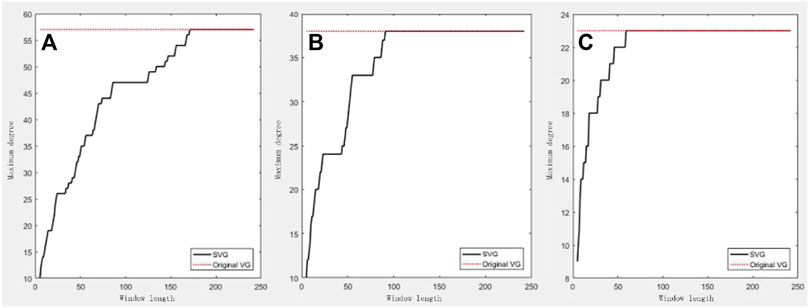
FIGURE 4. Illustrations of the relationships between the maximum degrees of the obtained complex networks through SVG and $W$ for different types of time series data (A) Original data; (B) Brownian Motion incorporated (C) Gaussian white noise considered.

The discrepancy of the maximum degree or the velocity of convergence can reflect the characteristics of different types of data. Compared with the other types of data, the transition of the stock opening price of Ping An Bank Co., Ltd. seems to be the smoothest; thus, it is likely for more data points to meet the discriminate criteria. Hence, the derived network is likely to possess a large maximum degree. In other words, it is highly likely for data points that are far from each other to be connected if the transition is smooth. Whereas, for the data with Gaussian white noise, the discriminate criteria condition is less likely to be met due to the sudden variance of the original data series. Thus, the maximum degree is relatively small. Reversely, if the maximum degree of an obtained network is relatively small, we can predict that the transition of the original data is sharp.

Previously, we mainly investigated the maximum degree of the obtained network, whereas, the optimum window length is also of great significance. Afterwards, we also investigated the relationship between the average degree of the obtained network and $W$ to provide information regarding the determination of the optimum $W$ with the corresponding results being provided in Figure 5.

FIGURE 5

FIGURE 5. Relationships between the average degree of the obtained complex network through SVG and the sliding-window length for different types (A) Original data; (B) Brownian Motion incorporated (C) Gaussian white noise considered.

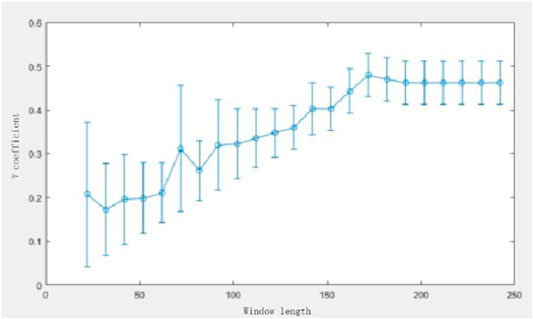
The criteria of optimum $W$ are provided as: for a given $W$, if the primary parameters of the obtained network, such as maximum degree, is approximately the same as the corresponding value obtained through original VG, and the percentage of varying velocity is smaller than 5% with the increase of $W$, we can regard it as the optimum value. Accordingly, we find that the optimum $W$ for the original stock price data is also approximately 168 (about 69% of the total data points). Similarly, analyses can also be conducted on the other types of data to find the optimum $W$. Corresponding results are provided in Table 1 which illustrate the computational efficiency of SVG and original VG.

TABLE 1

TABLE 1. Comparison of network construction through SVG for different types of time series data.

Moreover, the degree distribution of the obtained network is provided as in Figure 6. We see that the derived network for the stock opening price data follows power-law distribution while the relationship between γ and $W$ is given in Figure 7. As indicated, a sliding-window length of 168 (approximate 69% of the total number of data points) seems to be the appropriate value for the construction of the complex network from the stock opening price when considering parameter γ.

FIGURE 6

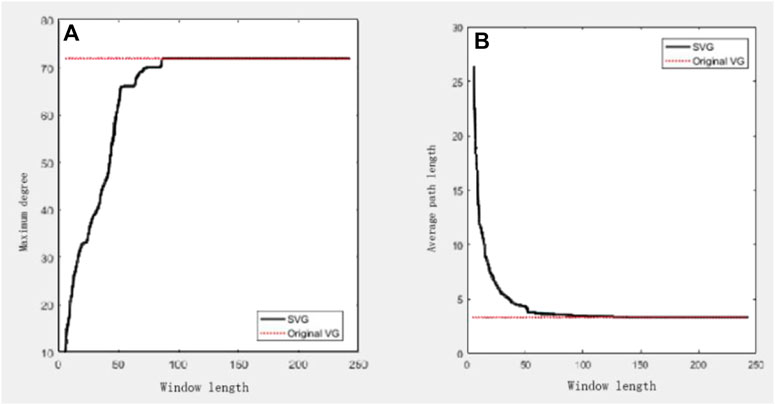
FIGURE 6. Illustration of the relationships between different parameters and window length for the stock opening price data of Shenzhen Cau Technology Co., Ltd. in 2018 (A) maximum degree; (B) maximum average length.

FIGURE 7

FIGURE 7. Illustration of the coefficient γ vs. $W$.

In order to derive a general conclusion, we also take the stock opening price data for 500 stocks from the A-share market. After sufficient analyses, we find that for the one-year-long data, a window length of 75% of the total data points is sufficient for the construction of the network. Here, sufficient length means it is safe and incurs no information loss, but it does not necessarily to be the optimum window length. After further analysis, we find that the optimum window length might be smaller than 60% of the total points for the data of some stocks. Another stock of Shenzhen Cau Technology Co., Ltd. is taken for an illustration. This company mainly focus on computer software and bio-pharmacy technology which is likely to be affected by market fluctuations. Hence, the stock price data is likely to fluctuate rapidly [17]. The optimum $W$ for constructing a network through SVG is only 100 for Shenzhen Cau Technology Co., Ltd. as illustrated in Figure 6. This validates the previous conclusion that when the data fluctuate rapidly, the maximum degree of the network obtained through SVG is likely to be smaller. Whereas for stock prices of bank and real estate companies, the optimum window length is around 160. This verifies the conclusion that the optimum window length is largely affected by the characteristic of the original data.

Furthermore, we also performed an analysis of the stock opening price data for Ping An Bank Co. from 2018 to 2019. The relationships between incorporated parameters and window length are provided in Figure 8. As presented, for a two-year-long data, the optimum window length is approximately 378 (which is about 77.8% of the total data points) according to the above criteria of discriminating the optimum $W$. We can find that for data of different lengths, the percentage obtained by dividing the obtained window length with the total data points varies slightly. Furthermore, to construct the network through SVG for different data lengths, the obtained optimum window lengths are provided in Table 2.

FIGURE 8

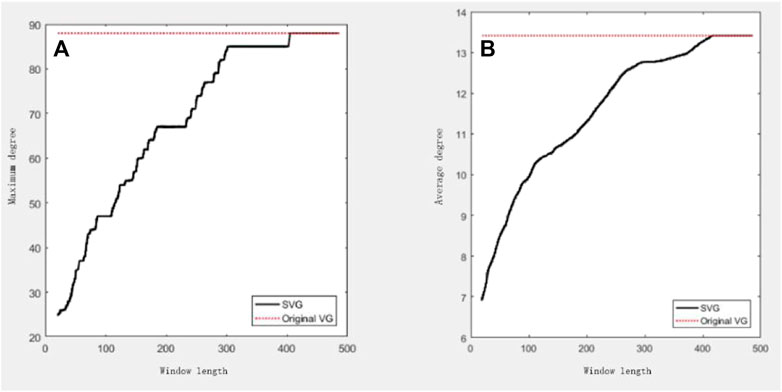
FIGURE 8. Illustration of the relationship between incorporated parameter and $W$ through SVG. Here, a two-year stock opening price data for Ping An Bank Co. is considered. (A) maximum degree; (B) average degree.

TABLE 2

TABLE 2. Optimum window length for constructing network through SVG for stock opening price of Ping An Bank Co. with different total data points.

As aforementioned, it is necessary to analyze multiple time series data to mine implicit information. Hence, experiments are conducted into the investigation of different stock price data by applying MVG. First, a two-layered network is constructed from the opening stock price and the highest stock price of Ping An Bank Co. Figure 9A illustrates the corresponding original time series data, while the obtained adjacent matrices are provided in Figures 9B,C. As presented in Figure 9A, the opening stock price and the highest stock price of Ping An Bank Co. are of a similar trend; this can also be observed by similar adjacent matrices of the networks for different data series.

FIGURE 9

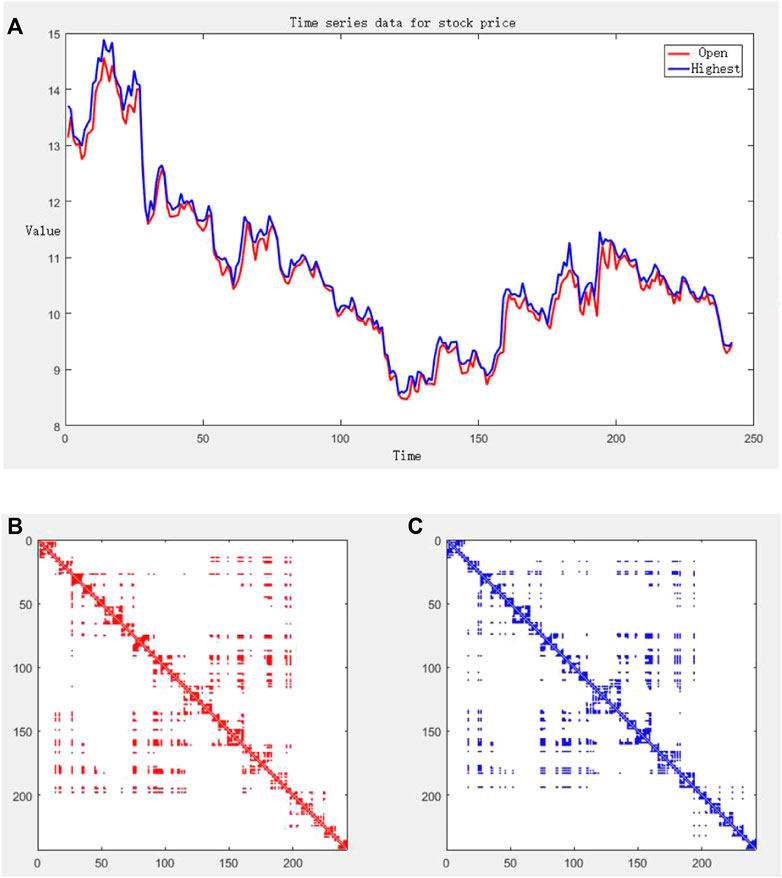
FIGURE 9. (A) The opening stock price and highest stock price of Ping An Bank Co.; (B) Adjacent matrices of the networks obtained through MVG for opening price; (C) Adjacent matrices of the networks obtained through MVG for highest price.

Regarding the obtained two-layered networks, the aforementioned parameters can be calculated, being listed as $\omega$ = 0.7285 and $I$($\alpha$,$\beta$) = 1.3096. These parameters can be used to predict the correlations of the provided data series. ω can be used to indicate the link distributions of different layers; thus, the obtained networks are similar. Later, we performed an analysis of different time series data combinations and the corresponding parameters are calculated, provided in Table 3. As illustrated, the correlations of different data combination for the same stock price varies. But even the scenario with the least correlation, the corresponding value is much higher than the correlation between No2 and surface concentration ozone.

TABLE 3

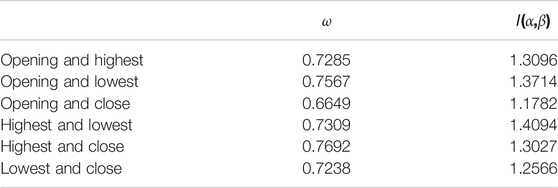
TABLE 3. Parameter obtained for the two layered networks for different combinations of time series data for Ping An Bank Co.

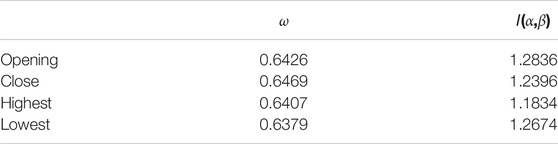
Moreover, we concern about the relationship between the stock prices of different stocks. Thus, we build an MVG network for the price data of different stocks. For example, we build a two-layer complex network based on the time-series of the opening prices of Ping An Bank and Vanke Co. Ltd. Class A. Similarly, Figure 10A below shows the opening stock price time-series data of two stocks in 2018, and Figures 10B,C shows the non-zero elements’ distribution of the complex network adjacency matrix generated by the opening price data of two stocks. After calculating the interlayer parameters of MVG, we can obtain ω = 0.6426 and I(α,β) = 1.2836 for the two-layer network. Such values almost reach the value of the two-layer network of surface ozone concentration and nitrogen dioxide concentration mentioned earlier. This means that the two stocks of Ping An Bank Co. and Vanke Co. Ltd. Class A have a relatively close relationship in the trend of stock data. More results are provided in Table 4. Obviously, the opening data is consistent with the above conclusion, while conclusions hold true for all the other price data. The close relationship between Ping An Bank Co. and Vanke Co. Ltd. A on the trend of stock data can be explained from the perspective of economics as the relationship between finance and real estate. The investment cost and investment income of the real estate industry are closely related to the financial environment, while the market in turn affects the economy and finance [15, 17]. Therefore, this mutual influence relationship in economics can be seen on the interlayer parameters of the two-layer MVG of stock prices.

FIGURE 10

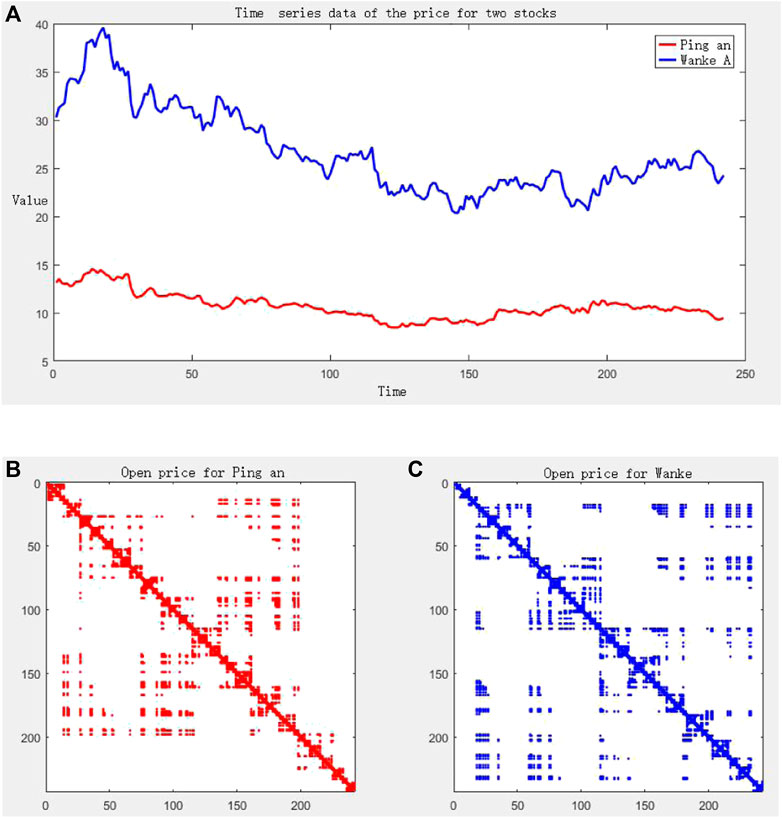
FIGURE 10. (A) Two stocks’ opening price time-series data; (B,C) denote the adjacent matrices of two-layer MVG network built with provided time-series data for Ping An Bank Co. and Vanke Co. Ltd., respectively.

TABLE 4

TABLE 4. Parameters obtained for the price data for Ping An Bank Co. and Vanke Co. Ltd. Class A.

In contrast, there exists no such strong correlation between Ping An Bank Co. and the biopharmaceutical stock Shenzhen CAU Technology Co. Ltd. Table 5 below shows the interlayer parameters of the two-layer MVG networks obtained for the opening prices of some other stocks and Ping An Bank Co.

TABLE 5

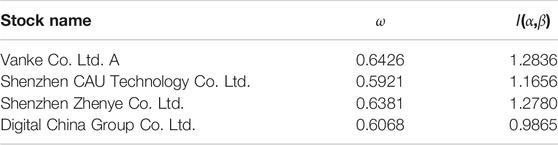
TABLE 5. Parameters obtained for the two layered networks for different combinations of Ping An Bank Co. and four different stocks.

In Table 5, both Vanke Co. Ltd. A and Shenzhen Zhenye Co. Ltd. A are real estate stocks. According to the previous analysis, after building a two-layered MVG network for other stock data and Ping An Bank Co., the inter-layer parameters tend to indicate the tightness of the relationship between the two stocks. In contrast, Shenzhen CAU Technology Co. Ltd. is a biopharmaceutical stock, while Digital China Group Co. Ltd. is an Internet stock. They are not closely related to Ping An Bank Co. from the perspective of stock, and therefore we can see a relatively low correlation. After analyzing other stocks, we found similar conclusions. For example, after constructing a two-layer network with the opening price data of Changan Automobile stock and Daye Special Steel stock, the average edge overlap ω obtained equals 0.6489. This value almost even exceeds the ω value of the two-layer network constructed with Ping An Bank Co. and Vanke Co. Ltd. A. Daye Special Steel Co. Ltd. belongs to steel and metal shares, while Chongqing Changan Automobile Co. Ltd. belongs to industrial machinery shares. The industrial production of the latter depends on the raw materials provided by the former type of enterprises. It is the correlation between the two in the background of the stock industry that causes the inter-layer parameters of the two-layer network constructed by the two stock price data also show a relatively close correlation.

Complex Analysis

When I = 0, the inner loop executes n times; when I = 1, the inner loop executes n−1 times, and when I = n−1, the total execution times can be calculated as follows:

$\begin{array}{l}n+\left(n-1\right)+\left(n-3\right)+\dots \dots +I\\ =\left(n-1\right)+\left[\left(n-1\right)+2\right]+\left[\left(n-2\right)+3\right]+\left[\left(n-3\right)+4\right]+\dots \dots \\ =\left(n-1\right)+\left(n-1\right)+\left(n+1\right)+\left(n+1\right)+\dots \dots \\ =\left(n+1\right)n/2\\ =\left(n+1\right)/2\\ =n^2/2+n/2\end{array}$

According to the second rule of derivation of large order o previously mentioned: only the highest order is reserved, so n2/2 is reserved. According to the third article, if the constant of this item is removed, then 1/2 of the time complexity of this code will be removed. Finally, the timev complexity of this code is O (n2).

Conclusion

Tvhrough VG and related techniques (SVG and MVG) for analyzing time-series data, we conducted intensive experiments on various stocks, and we also combine the knowledge of securities and social economics to obtain more meaningful research results. In this paper, we try to find out the size of the window length $W$ that should be selected when constructing the network through SVG for stock price time-series with the length of $N$. According to the above analysis, for one-year-long stock price time-series data, the length of the security window that does not lose the original data information in most cases due to the establishment of the SVG network is approximately $W$/$N$ = 70%. At this time, compared with the traditional VG model, the reduction in the amount of calculation when constructing the network is about 10%. Although such a window length may compromise the effect of using the SVG algorithm, such a window length is safe and sufficient. Such a long window length is not always necessary, in other words, it is not optimal. The actual optimal window length for some stocks can even be W/N < 50%. And this optimal window length has been proved in this paper to be related to the type and nature of stocks. Different types of stock data may have different optimal window length values, which requires further research. Besides, it is found that for stock price time series data of different lengths, the optimal value when applying the SVG model and the value of the security window length ratio W/N is different, which calls for further research. We believe that the SVG algorithm will play a more significant advantage in building a complex network for stock price data with further research conducted.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: http://www.10jqka.com.cn/.

Author Contributions

XL: Visualization, Software, Computation, Drawing Writing, XY: Investigation, CL: Writing-Reviewing and Editing, HM: Visualization, Software, CL: Conceptualization, Methodology, Validation.

Conflict of Interest

XY was employed by Ansteel Company Limited Cold-Rolling Silicon Steel Mill.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zou Y, Donner RV, Marwan N. Complex Network Approaches to Nonlinear Time Series Analysis[J]. Phys Rep (2018) 787:1–97. doi:10.1016/j.physrep.2018.10.005

CrossRef Full Text | Google Scholar

2. Pavón-Domínguez P, Jiménez-Hornero FJ, Gutiérrez de Ravé E. Joint Multifractal Analysis of the Influence of Temperature and Nitrogen Dioxide on Tropospheric Ozone. Stoch Environ Res Risk Assess (2015) 29(7):1881–9. doi:10.1007/s00477-014-0973-5

CrossRef Full Text | Google Scholar

3. Albert R, Barabási A-L. Statistical Mechanics of Complex Networks. Rev Mod Phys (2002) 74(1):47–97. doi:10.1103/revmodphys.74.47

CrossRef Full Text | Google Scholar

4. Zhou C, Ding L, Skibniewski MJ, Luo H, Jiang S. Characterizing Time Series of Near-Miss Accidents in Metro Construction via Complex Network Theory. Saf Sci (2017) 98:145–58. doi:10.1016/j.ssci.2017.06.012

CrossRef Full Text | Google Scholar

5. Fan X, Li X, Yin J, Tian L, Liang J. Similarity and Heterogeneity of price Dynamics across China's Regional Carbon Markets: A Visibility Graph Network Approach. Appl Energ (2019) 235:739–46. doi:10.1016/j.apenergy.2018.11.007

CrossRef Full Text | Google Scholar

6. Hu J, Xia C, Li H, Zhu P, Xiong W. Properties and Structural Analyses of USA's Regional Electricity Market: A Visibility Graph Network Approach. Appl Maths Comput (2020) 385:125434. doi:10.1016/j.amc.2020.125434

CrossRef Full Text | Google Scholar

7. Gao Z, Li S, Dang W. Wavelet Multiresolution Complex Network for Analyzing Multivariate Nonlinear Time Series[J]. Int J Bifurcation Chaos (2017) 27(8):1750123. doi:10.1142/s0218127417501231

CrossRef Full Text | Google Scholar

8. Carmona-Cabezas R, Ariza-Villaverde AB, Gutiérrez de Ravé E, Jiménez-Hornero FJ. Visibility Graphs of Ground-Level Ozone Time Series: A Multifractal Analysis. Sci Total Environ (2019) 661:138–47. doi:10.1016/j.scitotenv.2019.01.147

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Dai P-F, Xiong X, Zhou W-X. Visibility Graph Analysis of Economy Policy Uncertainty Indices. Physica A: Stat Mech its Appl (2019) 531:121748. doi:10.1016/j.physa.2019.121748

CrossRef Full Text | Google Scholar

10. Lacasa L, Luque B, Ballesteros F, Luque J, Nuño JC. From Time Series to Complex Networks: The Visibility Graph. Pnas (2008) 105(13):4972–5. doi:10.1073/pnas.0709247105

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Lacasa L, Luque B, Luque J, Nuño JC. The Visibility Graph: A New Method for Estimating the Hurst Exponent of Fractional Brownian Motion. Europhys Lett (2009) 86(3):30001. doi:10.1209/0295-5075/86/30001

CrossRef Full Text | Google Scholar

12. Liu K, Weng T, Gu C, Yang H. Visibility Graph Analysis of Bitcoin price Series. Physica A: Stat Mech its Appl (2020) 538:122952. doi:10.1016/j.physa.2019.122952

CrossRef Full Text | Google Scholar

13. Lacasa L, Nuñez A, Roldán É, Parrondo JMR, Luque B. Time Series Irreversibility: a Visibility Graph Approach. Eur Phys J B (2012) 85(6):217. doi:10.1140/epjb/e2012-20809-8

CrossRef Full Text | Google Scholar

14. Gao Z-K, Cai Q, Yang Y-X, Dang W-D, Zhang S-S. Multiscale Limited Penetrable Horizontal Visibility Graph for Analyzing Nonlinear Time Series. Sci Rep (2016) 6:35622. doi:10.1038/srep35622

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Carmona-Cabezas R, Gómez-Gómez J, Ariza-Villaverde AB, Gutiérrez de Ravé E, Jiménez-Hornero FJ. Multiplex Visibility Graphs as a Complementary Tool for Describing the Relation between Ground Level O3 and No2. Atmos Pollut Res (2020) 11(1):205–12. doi:10.1016/j.apr.2019.10.011

CrossRef Full Text | Google Scholar

16. Carmona-Cabezas R, Gómez-Gómez J, Gutiérrez de Ravé E, Jiménez-Hornero FJ. A Sliding Window-Based Algorithm for Faster Transformation of Time Series into Complex Networks. Chaos (2019) 29(10):103121. doi:10.1063/1.5112782

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Luque B, Lacasa L, Ballesteros F, Luque J. Horizontal Visibility Graphs: Exact Results for Random Time Series. Phys Rev E Stat Nonlin Soft Matter Phys (2009) 80:046103. doi:10.1103/PhysRevE.80.046103

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Ren W, Jin N. Sequential Limited Penetrable Visibility-Graph Motifs. Nonlinear Dyn (2020) 99(3):2399–408. doi:10.1007/s11071-019-05439-y

CrossRef Full Text | Google Scholar

19. Davis EP, Zhu H. Bank Lending and Commercial Property Cycles: Some Cross-Country Evidence. J Int Money Finance (2011) 30(1):1–21. doi:10.1016/j.jimonfin.2010.06.005

CrossRef Full Text | Google Scholar

20. Du K, Fu Y, Qin Z. Regime Shift, Speculation, and Stock Price[J]. Res Int Business Finance (2010) 52:101181.

Google Scholar

21. Rapach DE, Strauss JK, Zhou G. International Stock Return Predictability: What Is the Role of the United States?. J Finance (2013) 68(4):1633–62. doi:10.1111/jofi.12041

CrossRef Full Text | Google Scholar

22. Tanbeer SK, Ahmed CF, Jeong B-S, Lee Y-K. Sliding Window-Based Frequent Pattern Mining over Data Streams. Inf Sci (2009) 179(22):3843–65. doi:10.1016/j.ins.2009.07.012

CrossRef Full Text | Google Scholar

23. Lan X, Mo H, Chen S, Liu Q, Deng Y. Fast Transformation from Time Series to Visibility Graphs. Chaos (2015) 25:083105. doi:10.1063/1.4927835

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Lacasa L, Nicosia V, Latora V. Network Structure of Multivariate Time Series. Sci Rep (2015) 5:15508. doi:10.1038/srep15508

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Dimitri GM, Agrawal S, Young A, Donnelly J, Liu X, Smielewski P, et al. A Multiplex Network Approach for the Analysis of Intracranial Pressure and Heart Rate Data in Traumatic Brain Injured Patients. Appl Netw Sci (2017) 2(1):29. doi:10.1007/s41109-017-0050-3

PubMed Abstract | CrossRef Full Text | Google Scholar