Effect of Sterile Neutrino on Low-Energy Processes in Minimal Extended Seesaw With Δ(96) Symmetry and TM1 Mixing

We study the effect of sterile neutrino on some low-scale processes in the framework of the minimal extended seesaw (MES). MES is the extension of the seesaw mechanism with the addition of sterile neutrino of intermediate mass. The MES model in this work is based on Δ(96) × C₂ × C₃ flavor symmetry. The structures of mass matrices in the framework lead to TM₁ mixing with μ–τ symmetry. The model predicts the maximal value of the Dirac CP phase. We carry out our analysis to study the new physics contributions from the sterile neutrino to different charged lepton flavor violation (cLFV) processes involving muon and tau leptons as well as neutrinoless double beta decay (0νββ). The model predicts normal ordering (NO) of neutrino masses, and we perform the numerical analysis considering normal ordering (NO) only. We find that a heavy sterile neutrino can lead to cLFV processes that are within the reach of current and planned experiments. The sterile neutrino present in our model is consistent with the current limits on the effective neutrino mass set by 0νββ experiments.

I Introduction

The observed neutrino oscillation phenomenon, the origin of the idea behind the massive nature of neutrinos, has been one of the most appealing evidence to expect physics beyond the standard model (BSM). Neutrino oscillation probabilities are dependent on the three mixing angles, the neutrino mass-squared differences ($\mathrm{\Delta }{m}_{21}^2$, $\mathrm{\Delta }{m}_{31}^2$), and the Dirac CP phase (δ_CP). Though there are precise measurements of the mixing angles and mass-squared differences, yet there are no conclusive remarks on δ_CP or the mass ordering of the neutrinos. NOνA [1] and T2K [2] experiments have recently provided hint toward the CP violation in the Dirac neutrino matrix. Again, another important unsolved issue is the mass ordering of the neutrinos whether it is normal (m₁ < m₂ < m₃) or inverted (m₃ < m₁ < m₂). There are some other open questions in particle physics as well as cosmology such as CP violation in the lepton sector, baryon asymmetry of the universe, and particle nature of dark matter. Motivated by these shortcomings, different beyond standard model (BSM) theories [3] are pursued in different experiments.

Many searches for new physics beyond the standard model are going on in different experiments. Charged lepton flavor violation (cLFV) processes can provide a way to search for new physics beyond the standard model. cLFV processes are heavily suppressed in the standard model. However, the well-established neutrino oscillation phenomenon gives a signal toward the flavor violation in the charged lepton sector also. There are present and planned experiments to search for lepton flavor violating radiative decay (l_i → l_jγ) [4] and also three body decays (l_i → l_jl_kl_k) [5]. The present and future experimental constraints on cLFV processes can be found in Tables 1, 2. In this work, we study the transition among the three charged leptons. However, the transitions of muon such as μ − e, N, μ → eee, μ → eγ [6, 7] and recently proposed μ⁻e⁻ → e⁻e⁻ [8] are extensively analyzed as the parent particle is substantially available in the cosmic radiation as well as in dedicated accelerators [9]. Many other challenging cLFV processes are those which involve the third family of leptons (taus) as it opens many flavor violating channels. Among these, τ → eγ, τ → μγ, τ → 3e, and τ → 3μ are significant. The processes involving taus also open up many channels involving hadrons in the final state such as τ → lπ⁰, τ → lπ⁺π⁻ [9, 10].

TABLE 1

TABLE 1. Current experimental bounds and future sensitivities of different cLFV processes [10–13].

TABLE 2

TABLE 2. Experimental bounds for the process CR (μ − e, N) [13].

There are various theoretical models which are the extension of the SM that can account for cLFV processes [14–17]. These models usually introduce new particle fields to act as a source of flavor violation. The models with heavy sterile neutrinos can provide prominent contributions to cLFV processes. There are many theoretical motivations as well as experimental background for the existence of sterile neutrinos. The anomalies of the LSND [18] and MiniBooNE [19] results provide a hint toward the presence of one or two sterile neutrino states. Again from the theoretical point of view, the addition of sterile fermions into the standard model can explain the neutrino mass and also mixing [20, 21]. Moreover, sterile neutrinos can account for many cosmological observations such as dark matter [22–26] and baryon asymmetry of the universe (BAU) [27, 28]. Furthermore, their mixing with the active neutrinos can contribute to certain non-oscillation processes such as neutrinoless double decay (0νββ) amplitude or to beta decay spectra in the KATRIN experiment [29, 30]. To study the effect of sterile neutrino on low-scale processes, we have chosen the minimal extended seesaw (MES) framework augmented with Δ(96) flavor symmetry. In the MES framework, three right-handed neutrinos and one additional gauge singlet field S are added to the SM particle content [31, 32]. The extra sterile state may have a significant contribution to cLFV processes and 0νββ depending on its mass and mixing with the active neutrinos in the model. In the present work, C₂ and C₃ discrete groups are introduced along with Δ(96) to avoid the unwanted couplings among the particles. The mass matrices constructed in the MES model embedded with Δ(96) flavor symmetry lead to a particular mixing pattern widely known as TM₁ mixing [33]. TM₁ mixing is one of the most significant mixing patterns which comply with the experimental predictions on mixing angles and Dirac CP phase. In the present work, after constructing the mass matrices leading to TM₁ mixing, the model parameters have been evaluated using three neutrino oscillation parameters, and then mass and mixing of the particles are calculated as a function of these model parameters. Furthermore, we have evaluated different observables characterizing the different cLFV processes and neutrinoless double beta decay (0νββ).

This paper is organized as follows. In Section II, we describe TM₁ mixing and the model with Δ(96) flavor symmetry. The particles are assigned with different charges under the symmetry group, and the mass matrices involved in the model are constructed. Section III gives the brief discussion of different cLFV processes and contribution of sterile neutrinos to such processes. In Section IV, we briefly discuss the neutrinoless double beta decay process in the presence of heavy sterile neutrinos. The results of the numerical analysis are discussed in detail in Section V. Finally, we conclude in Section VI.

II Minimal Extended Seesaw With Δ(96) Flavor Symmetry and TM₁ Mixing

A The Minimal Extended Seesaw Framework

The minimal extended seesaw (MES) is the extension of the canonical type I seesaw by the addition of extra gauge singlet field, ν_s, to accommodate sterile neutrinos. This field has a coupling with the heavy right-handed neutrino fields that are present in the type I seesaw [34, 35]. Thus, the Lagrangian in this MES model can be obtained as [36]

$-\mathcal{L}=\overline{{\nu }_L}{M}_{D}N+\frac{1}{2}{N}^c{M}_{R}N+\bar{S}{M}_{S}N+h.c.(1)$

Subsequently, the mass matrix arising from the Lagrangian in Eq. 1 in the basis (ν_L, N^c, S^c) can be written as

$M_{\nu }^{7\times 7}=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill M_D\hfill & \hfill 0\hfill \\ \hfill {M_D}^T\hfill & \hfill M_R\hfill & \hfill M_S^T\hfill \\ \hfill 0\hfill & \hfill M_S\hfill & \hfill 0\hfill \end{array}\right).(2)$

Since the right-handed neutrinos are much heavier than the electroweak scale as in the case of the type I seesaw, they should be decoupled at low scales. Effectively, the full 7 × 7 matrix can be block diagonalized into a 4 × 4 neutrino mass matrix as follows [36]:

$M_{\nu }^{4\times 4}=-\left(\begin{array}{cc}\hfill M_D{M_R}^{-1}{M_D}^T\hfill & \hfill M_D{M_R}^{-1}{M_S}^T\hfill \\ \hfill M_S{({M_R}^{-1})}^T{M_D}^T\hfill & \hfill M_S{M_R}^{-1}{M_S}^T\hfill \end{array}\right).(3)$

Assuming M_S > M_D, the active neutrino mass matrix of Eq. 3 takes the form

$M_{\nu }\simeq M_D{M}_R^{-1}{M}_S^T{(M_S{M}_R^{-1}{M}_S^T)}^{-1}{M}_S{M}_R^{-1}{M}_D^T-M_D{M}_R^{-1}{M}_D^T.(4)$

The sterile neutrino mass can be obtained as

$m_4\simeq M_S{M}_R^{-1}{M}_S^T.(5)$

The charged lepton mass matrix, in general, can be diagonalized using unitary matrices U_L and U_R as follows:

$U_L{M}_l{U}_R^{†}=\text{diag}(m_e,m_{\mu },m_{\tau }).(6)$

Again, we obtain the light neutrino masses using the unitary matrix U_ν as

$U_{\nu }^{†}{M}_{\nu }^{3\times 3}{U}_{\nu }=\text{diag}(m_1,m_2,m_3).(7)$

The 4 × 4 neutrino mixing matrix in the MES model using U_L and U_ν can be obtained as [36]

$V=\left(\begin{array}{cc}\hfill U_L\left(1-\frac{1}{2}R{R}^{†}\right)U_{\nu }\hfill & \hfill U_{L}R\hfill \\ \hfill -R^{†}{U}_{\nu }\hfill & \hfill 1-\frac{1}{2}{R}^{†}R\hfill \end{array}\right).(8)$

The matrix U_LR that governs the active–sterile mixing in which R can be expressed as

$R=M_D{M}_R^{-1}{M}_S^T{(M_S{M}_R^{-1}{M}_S^T)}^{-1}(9)$

is given as

$U_{L}R=\text{diag}{(U_{e4},U_{\mu 4},U_{\tau 4})}^T.(10)$

Finally, the 3 × 3 lepton mixing matrix (PMNS matrix) can be written as [36]

$U_{PMNS}=U_L\left(1-\frac{1}{2}R{R}^{†}\right)U_{\nu },(11)$

$U_{PMNS}\simeq U_L{U}_{\nu }.(12)$

Thus, the PMNS matrix can be obtained by multiplying the diagonalizing matrix of the charged lepton mixing matrix and that of the effective seesaw matrix. U_L is an identity matrix in the framework where the charged lepton mass matrix is diagonal.

B TM₁ Mixing

Trimaximal (TM₁) mixing is a mixing ansatz that preserves the first column of tri–bimaximal mixing U_TBM and mixes its second and third columns. It is a perturbation to TBM mixing, and we can write the mixing matrix as [37, 38]

$U_{T{M}_1}=U_{\text{TBM}}\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \cos \theta \hfill & \hfill \sin \theta e^{-i\zeta }\hfill \\ \hfill 0\hfill & \hfill -\sin \theta e^{i\zeta }\hfill & \hfill \cos \theta \hfill \end{array}\right),(13)$

$U_{T{M}_1}=\left(\begin{array}{ccc}\hfill \frac{\sqrt{2}}{\sqrt{3}}\hfill & \hfill \frac{\cos \theta }{\sqrt{3}}\hfill & \hfill \frac{\sin \theta }{\sqrt{3}}{e}^{-i\zeta }\hfill \\ \hfill \frac{-1}{\sqrt{6}}\hfill & \hfill \frac{\cos \theta }{\sqrt{3}}-\frac{\sin \theta }{\sqrt{2}}{e}^{i\zeta }\hfill & \hfill \frac{\sin \theta }{\sqrt{3}}{e}^{-i\zeta }+\frac{\cos \theta }{\sqrt{2}}\hfill \\ \hfill \frac{-1}{\sqrt{6}}\hfill & \hfill \frac{\cos \theta }{\sqrt{3}}+\frac{\sin \theta }{\sqrt{2}}{e}^{i\zeta }\hfill & \hfill \frac{\sin \theta }{\sqrt{3}}{e}^{-i\zeta }-\frac{\cos \theta }{\sqrt{2}}\hfill \end{array}\right).(14)$

Comparing the above mixing matrix in Eq. 14 with the standard PMNS mixing matrix, one can obtain the three mixing angles in terms of θ as follows [39]:

${\sin }^2{\theta }_{13}=\frac{{\sin }^2\theta }{3},(15)$

${\sin }^2{\theta }_{23}=\frac{1}{2}\left(1+\frac{\sqrt{6}\sin 2\theta \cos \zeta }{3-{\sin }^2\theta }\right),(16)$

${\sin }^2{\theta }_{12}=1-\frac{2}{3-{\sin }^2\theta },(17)$

$J_{\text{CP}}=\frac{\sin 2\theta \sin \zeta }{6\sqrt{6}}.(18)$

Jarlskog’s rephasing invariant J_CP can be written in terms of the elements of the mixing matrix as

$\begin{array}{l}\hfill J_{\text{CP}}=\text{Im}(U_{\mu 3}{U}_{e3}^{*}{U}_{e2}{U}_{\mu 2}^{*})\\ =\frac{1}{8}\sin \delta \sin 2{\theta }_{12}\sin 2{\theta }_{23}\sin 2{\theta }_{13}\text{cos}{\theta }_{13}.\hfill \end{array}(19)$

One can write the expression for the CP phase in the TM₁ scenario as

${\sin }^2\delta =\frac{8{\sin }^2{\theta }_{13}(1-3{\sin }^2{\theta }_{13})-{\text{cos}}^4{\theta }_{13}{\text{cos}}^{2}2{\theta }_{23}}{8{\sin }^2{\theta }_{13}{\sin }^{2}2{\theta }_{23}(1-3{\sin }^2{\theta }_{13})}.(20)$

For a given θ₁₃(θ), TM₁ mixing with μ–τ reflection symmetry leads to maximal CP violation. Again, it can be seen that if $\zeta =\pm \frac{\pi }{2}$, ${\theta }_{23}=\frac{\pi }{4}$, which leads to μ–τ reflection symmetry.

C The Lagrangian

In this work, we have used Δ(96) flavor symmetry [40–43] giving rise to unique textures of the mass matrices involved in the MES model. For a brief discussion about properties of Δ(96) and its character table and tensor product rules, refer to Appendix A. Δ(96) symmetry is further augmented by C₂ and C₃ discrete flavor symmetries to get rid of some unwanted interactions. The particle assignments in the model are shown in Table 3.

TABLE 3

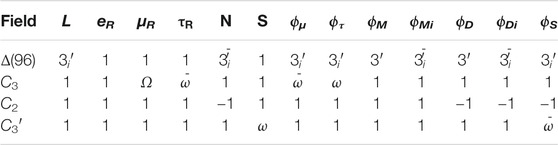
TABLE 3. Fields and their respective transformations under the symmetry group of the model. Here, ω = e^i2π/3 and $\bar{\omega }=e^{-i2\pi /3}$ are the complex roots of unity.

In our MES model, the lepton doublets of the SM and the SM gauge singlets transform as triplets 3_i and $\overline{3_i}$ of Δ(96), respectively. The sterile neutrino and the three right-handed charged leptons transform as singlets under this symmetry group. We introduce flavons ϕ_μ, ϕ_τ, ϕ_S transforming as triplets 3_i′, while ϕ_M, ϕ_D are triplet 3′ and ϕ_Mi, ϕ_Di are $\overline{3_i^{\prime }}$ under Δ(96). These fields are also assigned various charges under the Abelian groups C₂, C₃, and C₃′ which can be found in Table 3. C₃, C₂, and C₃′ are associated with charged leptons, Dirac neutrino sectors, and sterile neutrino sectors, respectively. These symmetries ensure that various flavons couple to their respective scalars only. For example, C₃ symmetry ensures that τ_R couples to ϕ_τ and μ_R couples to ϕ_μ. C₃′ prevents the term $\overline{S^C}S$ which ensures that the (3, 3) element of $M_{\nu }^{7\times 7}$ in Eq. 2 is zero. Besides the flavor symmetries, we assume that the model is CP conserving above the flavor symmetry breaking scale. Therefore, all the coupling constants appearing in the model Lagrangian will be real above this scale.

The Yukawa Lagrangian for the charged leptons and also for the neutrinos can be expressed as

$-\mathcal{L}={\mathcal{L}}_{{\mathcal{M}}_{\mathcal{L}}}+{\mathcal{L}}_{{\mathcal{M}}_{\mathcal{D}}}+{\mathcal{L}}_{\mathcal{M}}+{\mathcal{L}}_{{\mathcal{M}}_{\mathcal{S}}}+h.c.(21)$

We assume that the above Lagrangian is CP conserving. As a result, all parameters appearing in the Lagrangian become real. However, CP along with most of the discrete symmetries in the model is broken at a low-energy scale by the VEVs of the flavons.

In Eq. 21, ${\mathcal{L}}_{{\mathcal{M}}_{\mathcal{D}}}$ represents the Dirac neutrino Lagrangian given as

${\mathcal{L}}_{{\mathcal{M}}_{\mathcal{D}}}=\frac{y_D}{\mathrm{\Lambda }}{(\bar{L}N)}_{3^{\prime }}\tilde{H}{\varphi }_D+\frac{y_{Di}}{\mathrm{\Lambda }}{(\bar{L}N)}_{3_i^{\prime }}\tilde{H}{\varphi }_{Di}.(22)$

The neutrino Majorana mass term ${\mathcal{L}}_{\mathcal{M}}$ can be expressed as

${\mathcal{L}}_{\mathcal{M}}=y_M{(\overline{N^c}N)}_{3^{\prime }}{\varphi }_M+y_{Mi}{(\overline{N^c}N)}_{3_i^{\prime }}{\varphi }_{Mi}.(23)$

The interactions between the sterile and the right-handed neutrinos are involved in ${\mathcal{L}}_{{\mathcal{M}}_{\mathcal{S}}}$ given as

${\mathcal{L}}_{{\mathcal{M}}_{\mathcal{S}}}=y_S\overline{S^c}N{\varphi }_S.(24)$

${\mathcal{L}}_{{\mathcal{M}}_{\mathcal{L}}}$ is the Lagrangian for the charged leptons which can be written as

${\mathcal{L}}_{{\mathcal{M}}_{\mathcal{L}}}=\frac{y_{\mu }}{\mathrm{\Lambda }}\bar{L}H{\varphi }_{\mu }{\mu }_R+\frac{y_{\tau }}{\mathrm{\Lambda }}\bar{L}H{\varphi }_{\tau }{\tau }_R+\frac{y_e}{{\mathrm{\Lambda }}^2}\bar{L}H{(\overline{{\varphi }_{\tau }}\overline{{\varphi }_{\mu }})}_{3_i}{e}_R.(25)$

After spontaneous symmetry breaking (SSB), the scalar fields acquire VEVs which are assigned as

$⟨{\varphi }_{\mu }⟩=v_{\mu }{(1,\bar{\omega },\omega )}^T,⟨{\varphi }_{\tau }⟩=v_{\tau }{(1,\omega ,\bar{\omega })}^T,⟨{\varphi }_S⟩=(0,v_S,-v_S),$

$⟨{\varphi }_M⟩=v_M{(\mathrm{1,1,1})}^T,⟨{\varphi }_{Mi}⟩=v_{Mi}{(\mathrm{1,0},-1)}^T,⟨{\varphi }_D⟩=v_D{(\mathrm{0,1,0})}^T,⟨{\varphi }_{Di}⟩=v_{Di}{(\mathrm{1,0},-1)}^T.(26)$

The above VEVs remain invariant under the following group actions:

$\omega Q\langle {\varphi }_{\mu }\rangle =\langle {\varphi }_{\mu }\rangle ,QP{Q}^2{\langle {\varphi }_{\mu }\rangle }^{\star }=\langle {\varphi }_{\mu }\rangle ,(27)$

$\bar{\omega }Q\langle {\varphi }_{\tau }\rangle =\langle {\varphi }_{\tau }\rangle ,QP{Q}^2{\langle {\varphi }_{\tau }\rangle }^{\star }=\langle {\varphi }_{\tau }\rangle ,(28)$

$-QP{Q}^2\langle {\varphi }_S\rangle =\langle {\varphi }_S\rangle ,{\langle {\varphi }_S\rangle }^{\star }=\langle {\varphi }_S\rangle ,(29)$

$Q\langle {\varphi }_M\rangle =\langle {\varphi }_M\rangle ,{\langle {\varphi }_M\rangle }^{\star }=\langle {\varphi }_M\rangle ,(30)$

$-P\langle {\varphi }_{Mi}\rangle =\langle {\varphi }_{Mi}\rangle ,{\langle {\varphi }_{Mi}\rangle }^{\star }=\langle {\varphi }_{Mi}\rangle ,(31)$

$C^2\langle {\varphi }_D\rangle =\langle {\varphi }_D\rangle ,{\langle {\varphi }_D\rangle }^{\star }=\langle {\varphi }_D\rangle ,(32)$

$-P\langle {\varphi }_{Di}\rangle =\langle {\varphi }_{Di}\rangle ,{\langle {\varphi }_{Di}\rangle }^{\star }=\langle {\varphi }_{Di}\rangle .(33)$

Here, p, Q, and C are generators of Δ(96) provided in Appendix A. These group actions generate the residual symmetries of the corresponding VEVs. Also, they uniquely define the VEVs up to their norms. It can be shown that every potential constructed using an irreducible multiplet will have such unique alignments as stationary points (assuming a condition of non-vanishing norm) [44–46]. In Eqs. 27, 28, ω and $\bar{\omega }$ appear as a consequence of C₃ symmetry associated with the charged lepton sector. The resulting VEVs ⟨ϕ_μ⟩ and ⟨ϕ_τ⟩ are complex which spontaneously break the CP symmetry of the high–energy scale Lagrangian. Since ϕ_μ and ϕ_τ couple to μ_R and τ_R, we obtain a complex charged lepton mass matrix, which becomes the sole source of CP violation in our model.

D The Mass Matrices Involved in the Model

The textures of the mass matrices involved in the MES model can be obtained using flavon alignments defined with residual symmetries under our flavor group. With these flavon alignments mentioned above, we obtain the charged lepton and the neutrino mass matrices. In the charged lepton sector, $\bar{L}$ couples to l_R (l = e, μ, τ) through the flavons ϕ_μ and ϕ_τ. Using the VEVs of the flavons and the Higgs in the Lagrangian given by Eq. 25, the charged lepton mass matrix can be written as

$M_C=\frac{i\sqrt{3}v{v}_{\mu }{v}_{\tau }}{{\mathrm{\Lambda }}^2}\left(\begin{array}{ccc}\hfill y_e\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill y_e\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill y_e\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)+\frac{v}{\mathrm{\Lambda }}\left(\begin{array}{ccc}\hfill 0\hfill & \hfill y_{\mu }{v}_{\mu }\hfill & \hfill y_{\tau }{v}_{\tau }\hfill \\ \hfill 0\hfill & \hfill {\omega }^{̄}{y}_{\mu }{v}_{\mu }\hfill & \hfill \omega y_{\tau }{v}_{\tau }\hfill \\ \hfill 0\hfill & \hfill \omega y_{\mu }{v}_{\mu }\hfill & \hfill {\omega }^{̄}{y}_{\tau }{v}_{\tau }\hfill \end{array}\right).(34)$

The charged lepton mass matrix M_C is diagonalized using the unitary matrix U_L given as

$U_L=\frac{1}{\sqrt{3}}\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill \omega \hfill & \hfill {\omega }^{̄}\hfill \\ \hfill 1\hfill & \hfill {\omega }^{̄}\hfill & \hfill \omega \hfill \end{array}\right).(35)$

U_L is referred to as the 3 × 3 trimaximal matrix (TM) or the magic matrix:

$U_L{M}_C\text{diag}(-i,\mathrm{1,1})=\text{diag}(m_e,m_{\mu },m_{\tau }),(36)$

and we obtain the masses of the charged leptons as

$m_e=3y_{e}v\frac{v_{\mu }{v}_{\tau }}{{\mathrm{\Lambda }}^2},m_{\mu }=\sqrt{3}{y}_{\mu }v\frac{v_{\mu }}{\mathrm{\Lambda }},m_{\tau }=\sqrt{3}{y}_{\tau }v\frac{v_{\tau }}{\mathrm{\Lambda }}.(37)$

It is seen from Eq. 37 that the mass scale of the electron is suppressed by an additional factor $\frac{\mathcal{O}(v_{\alpha })}{\mathrm{\Lambda }}$ (where $\mathcal{O}(v_{\alpha })$ represents the order of magnitude of the flavon VEVs) compared to tau or muon mass similar to the Froggatt–Nielsen mechanism of obtaining the mass hierarchy.

Again, from Eq. 22, we obtain the Dirac neutrino mass matrix as

$M_D=\frac{v}{\mathrm{\Lambda }}\left(\begin{array}{ccc}\hfill 0\hfill & \hfill -y_{Di}{v}_{Di}\hfill & \hfill 0\hfill \\ \hfill -y_{Di}{v}_{Di}\hfill & \hfill y_D{v}_D\hfill & \hfill y_{Di}{v}_{Di}\hfill \\ \hfill 0\hfill & \hfill y_{Di}{v}_{Di}\hfill & \hfill 0\hfill \end{array}\right).(38)$

Denoting $\frac{y_D{v}_{D}v}{\mathrm{\Lambda }}=m_D$ and $\frac{y_{Di}{v}_{Di}}{y_D{v}_D}=r_1$, we rewrite the Dirac mass matrix in Eq. 38 as

$M_D=m_D\left(\begin{array}{ccc}\hfill 0\hfill & \hfill -r_1\hfill & \hfill 0\hfill \\ \hfill -r_1\hfill & \hfill 1\hfill & \hfill r_1\hfill \\ \hfill 0\hfill & \hfill r_1\hfill & \hfill 0\hfill \end{array}\right).(39)$

m_D has the dimension of mass similar to the order of the SM fermion masses and r₁ is dimensionless. The Majorana mass matrix for the heavy right-handed neutrinos can be obtained using the VEVs of ϕ_M and ϕ_Mi in Eq. 23 as

$M_R=\left(\begin{array}{ccc}\hfill y_M{v}_M\hfill & \hfill -y_{Mi}{v}_{Mi}\hfill & \hfill 0\hfill \\ \hfill -y_{Mi}{v}_{Mi}\hfill & \hfill y_M{v}_M\hfill & \hfill y_{Mi}{v}_{Mi}\hfill \\ \hfill 0\hfill & \hfill y_{Mi}{v}_{Mi}\hfill & \hfill y_M{v}_M\hfill \end{array}\right).(40)$

Here also, we denote y_Mv_M = m_R and $\frac{y_{Mi}{v}_{Mi}}{y_M{v}_M}=r_2$ and rewrite the above matrix as

$M_R=m_R\left(\begin{array}{ccc}\hfill 1\hfill & \hfill -r_2\hfill & \hfill 0\hfill \\ \hfill -r_2\hfill & \hfill 1\hfill & \hfill r_2\hfill \\ \hfill 0\hfill & \hfill r_2\hfill & \hfill 1\hfill \end{array}\right).(41)$

m_R has the dimension of mass at the scale of flavon VEV and r₂ is dimensionless.

Finally, we obtain the mass matrix representing the coupling between right-handed neutrinos and sterile neutrinos as

$M_S=y_S{v}_S\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 1\hfill & \hfill -1\hfill \end{array}\right),(42)$

or we can rewrite it as

$M_S=m_S\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 1\hfill & \hfill -1\hfill \end{array}\right),(43)$

where m_S = y_Sv_S has the dimension of mass.

The light neutrino mass matrix in the framework of the MES arising from the mass matrices in Eqs. 39, 41, 43 can be written using Eq. 3 as

$M_{\nu }=\left(\begin{array}{ccc}\hfill K_1\hfill & \hfill -K_2\hfill & \hfill -K_1\hfill \\ \hfill -K_2\hfill & \hfill K_3\hfill & \hfill K_2\hfill \\ \hfill -K_1\hfill & \hfill K_2\hfill & \hfill K_1\hfill \end{array}\right),(44)$

where

$K_1=-\frac{m_D^2{r}_1^2}{m_R(2+r_2-r_2^2)},(45)$

$K_2=\frac{m_D^2{r}_1(-1+r_1(-1+r_2))}{m_R(2+r_2-r_2^2)},(46)$

$K_3=-\frac{m_D^2(1+3r_1^2-2r_1(-1+r_2))}{m_R(2+r_2-r_2^2)}.(47)$

The effective seesaw mass matrix in Eq. 44 can be diagonalized in two steps using the unitary matrices U_BM and U_θ as

$U_{\theta }^T{U}_{BM}^T{M}_{\nu }{U}_{BM}{U}_{\theta }=\text{diag}(m_1,m_2,m_3),(48)$

or one may write

$M_{\nu }=U_{BM}{U}_{\theta }\text{diag}(m_1,m_2,m_3)U_{\theta }^T{U}_{BM}^T.(49)$

In MES models, the mass of the lightest neutrino vanishes in the lowest order. The suppression of higher order terms will be at least of the order of $\frac{\mathcal{O}(v_{\alpha })}{\mathrm{\Lambda }}$. It has been mentioned above that this factor is responsible for the suppression of the electron mass in relation to the muon and tau. This implies that $\frac{\mathcal{O}(v_{\alpha })}{\mathrm{\Lambda }}$ should be $\mathcal{O}(10^{-2})$. Therefore, the mass of the lightest neutrino obtained from higher order corrections will be in the sub-millieV range.

The matrix U_θ and the bimaximal matrix U_BM in Eq. 48 are given by

$U_{\theta }=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \cos \theta \hfill & \hfill \sin \theta \hfill \\ \hfill 0\hfill & \hfill -\sin \theta \hfill & \hfill \cos \theta \hfill \end{array}\right),U_{BM}=\left(\begin{array}{ccc}\hfill \frac{1}{\sqrt{2}}\hfill & \hfill 0\hfill & \hfill -\frac{1}{\sqrt{2}}\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill \frac{1}{\sqrt{2}}\hfill & \hfill 0\hfill & \hfill \frac{1}{\sqrt{2}}\hfill \end{array}\right),(50)$

where θ can be expressed in terms of the model parameters as

$\tan 2\theta =\frac{2\sqrt{2}{K}_2}{2K_1-K_3}.(51)$

Comparing Eq. 48 with Eq. 7, we can write the neutrino diagonalizing matrix U_ν as

$U_{\nu }=U_{BM}{U}_{\theta }.(52)$

Therefore, using Eq. 12, the PMNS matrix in this model can be expressed as

$U_{PMNS}\simeq U_L{U}_{BM}{U}_{\theta }.(53)$

Here, U_LU_BM is the tri–bimaximal (TBM) mixing matrix with phases:

$U_L{U}_{BM}=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \omega \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\omega }^{̄}\hfill \end{array}\right)\left(\begin{array}{ccc}\hfill \frac{\sqrt{2}}{\sqrt{3}}\hfill & \hfill \frac{1}{\sqrt{3}}\hfill & \hfill 0\hfill \\ \hfill \frac{-1}{\sqrt{6}}\hfill & \hfill \frac{1}{\sqrt{3}}\hfill & \hfill \frac{1}{\sqrt{2}}\hfill \\ \hfill \frac{-1}{\sqrt{6}}\hfill & \hfill \frac{1}{\sqrt{3}}\hfill & \hfill \frac{-1}{\sqrt{2}}\hfill \end{array}\right)\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill i\hfill \end{array}\right).(54)$

The multiplication of U_LU_BM with U_θ mixes its second and third columns resulting in the TM₁ mixing matrix $U_{T{M}_1}$. Since our effective seesaw matrix M_ν is real, we obtain a real diagonalizing matrix U_BMU_θ. Therefore, the neutrino sector does not contribute toward the phases e^±iζ in TM₁ mixing of Eq. 14. Rather, these phases are a direct manifestation of i appearing in Eq. 54, and we obtain $\zeta =\pm \frac{\pi }{2}$. The resulting TM₁ matrix possesses μ–τ reflection symmetry as can be seen by assigning $\zeta =\pm \frac{\pi }{2}$ in Eq. 14. This symmetry is not apparent in the light neutrino mass matrix M_ν given in Eq. 44. However, it becomes apparent if we express M_ν in the basis where the charged lepton mass matrix, M_C in Eq. 34, is diagonal, μ–τ reflection can be explicitly observed in the mass matrix $U_L^{\star }{M}_{\nu }{U}_L^{†}$.

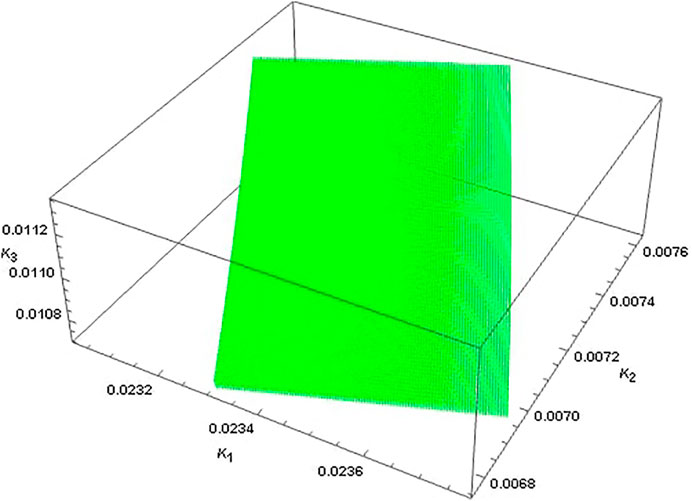
Our construction of M_ν given in Eq. 44 leading to TM₁ mixing implies that m₁ = 0, which rules out inverted hierarchy. Using this in Eq. 49 and comparing with Eq. 44, we can find the expressions for model parameters K₁, K₂, and K₃ in terms of the parameters θ, m₂, and m₃ as

$K_1=\frac{1}{2}(m_3{\text{cos}}^2\theta +m_2{\sin }^2\theta ),(55)$

$K_2=\frac{1}{\sqrt{2}}(m_3-m_2)\text{cos}\theta \sin \theta ,(56)$

$K_3=m_2{\text{cos}}^2\theta +m_3{\sin }^2\theta .(57)$

E- Sterile Neutrino Mass and Mixing in the Model

Apart from the active neutrinos, the mass and mixing of the sterile neutrino present in the model play a crucial role in cLFV processes which will be discussed in the next section. As mentioned above, the sterile neutrino mass can be obtained using Eq. 5, and we can write the mass term for sterile neutrinos as

$m_4=\frac{m_S^2(-2-2r_2+2r_2^2)}{m_R(-1+2r_2^2)}.(58)$

The active–sterile mixing using Eqs. 9, 10 can be obtained as

$U_{e4}=\frac{m_D(-1+r_1-r_2+2r_1{r}_2)}{\sqrt{3}{m}_S(-2-2r_2+2r_2^2)},(59)$

$U_{\mu 4}=\frac{m_D((1-i\sqrt{3})(1+r_2)+r_1(2+2i\sqrt{3}+r_2+3i\sqrt{3}{r}_2))}{2\sqrt{3}{m}_S(-2-2r_2+2r_2^2)},(60)$

$U_{\tau 4}=\frac{m_D((1+i\sqrt{3})(1+r_2)+r_1(2-2i\sqrt{3}+r_2-3i\sqrt{3}{r}_1))}{2\sqrt{3}{m}_S(-2-2r_2+2r_2^2)}.(61)$

In Eqs. 58–61, m_D, m_R, r₁, and r₂ are the model parameters.

III Charged Lepton Flavor Violation Processes

A Processes Involving Muonic Atoms

Many experiments such as MECO, SINDRUM II [46], and COMET [47] involved in searching for μ − e conversion with different targets. The observable characterizing this process is defined as

$CR(\mu -e,N)=\frac{\mathrm{\Gamma }({\mu }^{-}+N\to e^{-}+N)}{\mathrm{\Gamma }({\mu }^{-}+N\to \text{all\hspace{0.17em}capture})}.(62)$

These experiments are running with different targets such as titanium (Ti), lead (Pb), gold (Au), and aluminum (Al) and give bounds for different targets. There are also some planned future experiments like the second phase of the COMET experiment, Mu2e [48], to improve the sensitivity of this cLFV process.

There are several theoretical models to account for such rare LFV processes. As explained in [49], in the extension of the standard model with one heavy sterile neutrino, such processes originate from one-loop diagrams involving active and sterile neutrinos with non-zero mixing angles. In the MES model, the conversion ratio can be written as [49]

$CR(\mu -e,N)=\frac{2G_F^2{\alpha }_{\omega }^2{m}_{\mu }^5}{{(4\pi )}^2{\mathrm{\Gamma }}_{cap}(Z)}{\left|4V^{(p)}(2\widetilde{F_u^{\mu e}}+\widetilde{F_d^{\mu e}})+4V^{(n)}(\widetilde{F_u^{\mu e}}+2\widetilde{F_d^{\mu e}})+D{G}_{\gamma }^{\mu e}\frac{s_{\omega }^2}{2\sqrt{4\pi \alpha }}\right|}^2.(63)$

Here, G_F, s_ω, Γ_cap(Z) are the Fermi constant, sine of the weak mixing angle, and capture rate of the nucleus, respectively. Here, $\alpha =\frac{e^2}{4\pi }$ and ${\tilde{F}}_q^{\mu e}$ are form factors given as

${\tilde{F}}_q^{\mu e}=Q_q{s}_{\omega }^2{F}_{\gamma }^{\mu e}+F_Z^{\mu e}\left(\frac{I_q^3}{2}-Q_q{s}_{\omega }^2\right)+\frac{1}{4}{F}_{Box}^{\mu eqq}.(64)$

Here, Q_q represents the quark electric charge which is $\frac{2}{3}$ and $-\frac{1}{3}$ for up and down quarks, respectively. The weak isospin $I_q^3$ is $\frac{1}{2}$ and $-\frac{1}{2}$ for up and down quarks, respectively. The numerical values of V^(p), V⁽ⁿ⁾, and D can be found in [49]. In the small limit of masses ($x_i=\frac{m_{\nu i}^2}{m_W^2}\ll 1$), the form factors can be written as [49]

$F_{\gamma }^{\mu e}\to \sum _{j=1}^{3+n_S}{U}_{ej}{U}_{\mu j}^{*}[-x_j],(65)$

$G_{\gamma }^{\mu e}\to \sum _{j=1}^{3+n_S}{U}_{ej}{U}_{\mu j}^{*}\left[\frac{x_j}{4}\right],(66)$

$F_Z^{\mu e}\to \sum _{j=1}^{3+n_S}{U}_{ej}{U}_{\mu j}^{*}\left[x_j\left(-\frac{5}{2}-ln{x}_j\right)\right],(67)$

$F_{Box}^{\mu eee}\to \sum _{j=1}^{3+n_S}{U}_{ej}{U}_{\mu j}^{*}[2x_j(1+ln{x}_j)].(68)$

However, for the heavier neutrinos which do not satisfy the small mass limit, we use the expressions of form factors given in [49]:

$F_{\gamma }^{\mu e}=\sum U_{ej}{U}_{\mu j}^{*}{F}_{\gamma }(x_j),(69)$

$G_{\gamma }^{\mu e}=\sum U_{ej}{U}_{\mu j}^{*}{G}_{\gamma }(x_j),(70)$

$F_Z^{\mu e}=\sum U_{ej}{U}_{\mu k}^{*}({\delta }_{ij}{F}_Z(x_j)+C_{jk}{G}_Z(x_j,x_k)+C_{jk}^{*}{H}_Z(x_j,x_k)),(71)$

$F_{Box}^{\mu eee}=\sum U_{ej}{U}_{\mu k}^{*}(U_{ej}{U}_{ek}^{*}{G}_{Box}(x_j,x_k)-2U_{ej}^{*}{U}_{ek}{F}_{XBox}(x_j,x_k)).(72)$

There may be flavor violating non-radiative decay of μ⁻ into three electrons (μ → eee) [50]. The Mu3e experiment running at PSI is aimed at finding the signatures of this type of decay [51]. The branching ratio of this decay process can be written as

$\begin{array}{l}\hfill BR(\mu \to eee)=\frac{{\alpha }_{\omega }^4}{24576{\pi }^3}\frac{m_{\mu }^4}{m_W^4}\frac{m_{\mu }}{{\mathrm{\Gamma }}_{\mu }}2{\left|\frac{1}{2}{F}_{Box}^{\mu eee}+F_Z^{\mu e}-2s_{\omega }^2(F_Z^{\mu e}-F_{\gamma }^{\mu e})\right|}^2+4s_{\omega }^4|F_Z^{\mu e}-F_{\gamma }^{\mu e}{|}^2\\ +16s_{\omega }^2\mathrm{R}\mathrm{e}\left[\left(F_Z^{\mu e}+\frac{1}{2}{F}_{Box}^{\mu eee}\right)G_{\gamma }^{\mu e*}\right]-48s_{\omega }^4\mathrm{R}\mathrm{e}[(F_Z^{\mu e}-F_{\gamma }^{\mu e})G_{\gamma }^{\mu e*}]\hfill \\ +32s_{\omega }^4|G_{\gamma }^{\mu e}{|}^2\left[ln\frac{m_{\mu }^2}{m_e^2}-\frac{11}{4}\right].\hfill \end{array}(73)$

Here, the form factors can be obtained from Eqs. 65–68.

The MEG experiment [52] is aimed at investigating the LFV process μ → eγ, and there are many planned projects in the search for this kind of decay. In the framework of the minimal extended seesaw, the heavy neutrinos can cause μ → eγ decay. The branching ratio of the process can be given as

$BR(\mu \to e\gamma )=\frac{{\alpha }_{\omega }^3{s}_{\omega }^2}{256{\pi }^2}\frac{m_{\mu }^4}{M_W^4}\frac{m_{\mu }}{{\mathrm{\Gamma }}_{\mu }}|G_{\gamma }^{\mu e}{|}^2.(74)$

Here, the total decay width of the muon (Γ_μ) is obtained as

${\mathrm{\Gamma }}_{\mu }=\frac{G_F^2{m}_{\mu }^5}{192{\pi }^3}\left(1-8\frac{m_e^2}{m_{\mu }^2}\right)\left[1+\frac{{\alpha }_{em}}{2\pi }\left(\frac{25}{4}-{\pi }^2\right)\right].(75)$

Another possible cLFV process is the decay of a bound μ⁻ in a muonic atom into a pair of electrons (μ⁻e⁻ → e⁻e⁻) proposed in [53]. This particular decay process offers several advantages over three body decay processes from the experimental point of view. There are different classes of extension of the SM which can show a contribution to such processes. In this model with one extra sterile state, the effective Lagrangian describing this process contains long-range interactions and local interaction terms. The branching ratio of such processes in muonic atoms, with an atomic number Z, can be expressed as

$\begin{array}{l}\hfill BR({\mu }^{-}{e}^{-}\to e^{-}{e}^{-},N)=24\pi f_{Coul}(Z){\alpha }_{\omega }\frac{m_e^3}{m_{\mu }^3}\frac{{\tilde{\tau }}_{\mu }}{{\tau }_{\mu }}\left(16{\left|\frac{1}{2}{\left(\frac{g_{\omega }}{4\pi }\right)}^2\left(\frac{1}{2}{F}_{Box}^{\mu eee}+F_Z^{\mu e}-2s_{\omega }^2(F_Z^{\mu e}-F_{\gamma }^{\mu e})\right)\right|}^2\right.\\ +4{\left|\frac{1}{2}{\left(\frac{g_{\omega }}{4\pi }\right)}^{2}2s_{\omega }^2(F_Z^{\mu e}-F_{\gamma }^{\mu e})\right|}^2.\hfill \end{array}(76)$

Here, τ_μ represents the lifetime of free muons and the lifetime ${{\tau }^{̃}}_{\mu }$ depends on specific elements. In our analysis, we have considered Al and Au whose values of ${\tilde{\tau }}_{\mu }$ are 8.64 × 10^–7 and 7.26 × 10^–8, respectively. f_Coul(Z) ≈ (Z − 1)³ represents the enhancement of muonic atom decay due to Coulomb interactions. This decay process would possibly be probed in the COMET collaboration. As suggested in many literature studies, we have used the future sensitivity of CR (μ − e, N) to constrain such a decay process.

B Processes Involving Tau Leptons

There are many flavor violating channels open for tau lepton decays. The search for such decays involving taus is also challenging. Theoretical models which predict cLFV in the muon indicate a violation in the tau sector also. However, the amplitude of the process involving the tau channel is enhanced by many orders of magnitude in comparison with muon decays. Experiments such as BaBar [53] and Belle [54] provide limits to cLFV decays involving tau leptons. In this work, we have investigated three processes involving tau leptons τ → eγ, τ → μγ, and τ → eee. The branching ratios of these mentioned processes can be written as [54]

$BR(\tau \to e\gamma )=\frac{{\alpha }_{\omega }^3{s}_{\omega }^2}{256{\pi }^2}\frac{m_{\tau }^4}{m_W^4}\frac{m_{\tau }}{{\mathrm{\Gamma }}_{\tau }}|G_{\gamma }^{\tau e}{|}^2,(77)$

$BR(\tau \to \mu \gamma )=\frac{{\alpha }_{\omega }^3{s}_{\omega }^2}{256{\pi }^2}\frac{m_{\tau }^4}{m_W^4}\frac{m_{\tau }}{{\mathrm{\Gamma }}_{\tau }}|G_{\gamma }^{\tau \mu }{|}^2.(78)$

Here, Γ_τ represents the total width of tau leptons with an experimental value Γ_τ = 2.1581 × 10^–12 GeV [55].

$\begin{array}{l}\hfill BR(\tau \to eee)=\frac{{\alpha }_{\omega }^4}{24576{\pi }^3}\frac{m_{\tau }^4}{m_W^4}\frac{m_{\tau }}{{\mathrm{\Gamma }}_{\tau }}2{\left|\frac{1}{2}{F}_{Box}^{\tau eee}+F_Z^{\tau e}-2s_{\omega }^2(F_Z^{\tau e}-F_{\gamma }^{\tau e})\right|}^2+4s_{\omega }^4|F_Z^{\tau e}-F_{\gamma }^{\tau e}{|}^2+16s_{\omega }^2\mathrm{R}\mathrm{e}\left[\left(F_Z^{\tau e}+\frac{1}{2}{F}_{Box}^{\tau eee}\right)G_{\gamma }^{\tau e*}\right]-48s_{\omega }^4\mathrm{R}\mathrm{e}[(F_Z^{\tau e}-F_{\gamma }^{\tau e})G_{\gamma }^{\tau e*}]+32s_{\omega }^4|G_{\gamma }^{\tau e}{|}^2\left[ln\frac{m_{\tau }^2}{m_e^2}-\frac{11}{4}\right],\end{array}(79)$

where the composite form factors $F_{\gamma }^{\tau e},G_{\gamma }^{\tau e},F_Z^{\tau e}$ and $F_{Box}^{\tau eee}$ for the light neutrinos assume the following form:

$F_{\gamma }^{\tau e}\to \sum U_{ej}{U}_{\tau j}^{*}[-x_j],(80)$

$G_{\gamma }^{\tau e}\to \sum U_{ej}{U}_{\tau j}^{*}\left[\frac{x_j}{4}\right],(81)$

$F_Z^{\tau e}\to \sum U_{ej}{U}_{\tau j}^{*}\left[x_j\left(-\frac{5}{2}-ln{x}_j\right)\right],(82)$

$F_{Box}^{\tau eee}\to \sum U_{ej}{U}_{\tau j}^{*}[2x_j(1+ln{x}_j)].(83)$

For the heavier neutrinos, we can use the expressions

$F_{\gamma }^{\tau e}=\sum U_{ej}{U}_{\tau j}^{*}{F}_{\gamma }(x_j),(84)$

$G_{\gamma }^{\tau e}=\sum U_{ej}{U}_{\tau j}^{*}{G}_{\gamma }(x_j),(85)$

$F_Z^{\tau e}=\sum U_{ej}{U}_{\tau k}^{*}({\delta }_{ij}{F}_Z(x_j)+C_{jk}{G}_Z(x_j,x_k)+C_{jk}^{*}{H}_Z(x_j,x_k)),(86)$

$F_{Box}^{\tau eee}=\sum U_{ej}{U}_{\tau k}^{*}(U_{ej}{U}_{ek}^{*}{G}_{Box}(x_j,x_k)-2U_{ej}^{*}{U}_{ek}{F}_{XBox}(x_j,x_k)).(87)$

The different loop functions involved in the above expressions can be seen in [55].

IV Neutrinoless Double Beta Decay (0νββ)

The presence of sterile neutrinos in addition to the standard model particles may lead to new contributions to lepton number violating interactions like neutrinoless double beta decay (0νββ) [55–57]. We have studied the contributions of the sterile state to the effective electron neutrino Majorana mass m_ββ [57, 58]. The most stringent bounds on the effective mass are provided by the KamLAND-ZEN experiment [59]:

$m_{\beta \beta }<0.061-0.165eV.(88)$

The amplitude of these processes depends upon the neutrino mixing matrix elements and the neutrino masses. The decay width of the process is proportional to the effective electron neutrino Majorana mass m_ββ which in the case of standard contribution, i.e., in the absence of any sterile neutrino, is given as

$m_{\beta \beta }=\left|\sum _{i=1}^3{U_{ei}}^2{m}_i\right|.(89)$

The above equation is modified with the addition of sterile fermions and is given by [50, 60]

$m_{\beta \beta }=\left|\sum _{i=1}^3{U_{ei}}^2{m}_i\right|+U_{e4}^2\frac{m_4}{k^2-m_4^2}|<k>{|}^2,(90)$

where m₄ and U_e4 are the mass of the sterile neutrino and its couplings to the electron neutrino, respectively. | < k > |≃ 190 MeV represents the neutrino virtuality momentum.

V Results of Numerical Analysis and Discussions

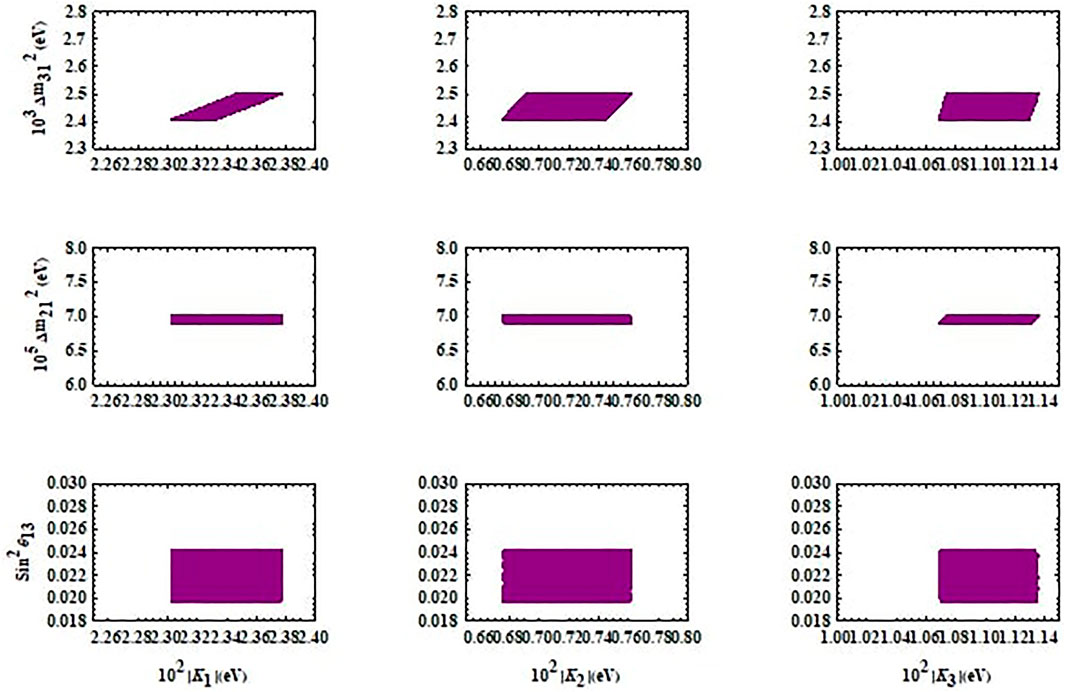
It is evident from the above discussion that the neutrino mass matrix in Eq. 44 contains three model parameters K₁, K₂, K₃. We can express the experimentally measured six oscillation parameters $\mathrm{\Delta }{m}_{21}^2$, $\mathrm{\Delta }{m}_{31}^2$,  sin²θ₁₂,  sin²θ₂₃,  sin²θ₁₃, δ_CP in terms of these model parameters. Hence, the three model parameters can be evaluated by comparing with the three oscillation parameters in the 3σ range as given in Table 4 and then constraining the other parameters. These parameters K₁, K₂, K₃ in turn are related to m_D, m_R, r₁, and r₂ as given in Eqs. 45–47 which are functions of Yukawa couplings and VEVs of the scalars. In our model, we have evaluated the model parameters comparing with the experimental range of $\mathrm{\Delta }{m}_{21}^2$, $\mathrm{\Delta }{m}_{31}^2$,  sin²θ₁₃. Since the lightest neutrino mass is zero in the MES model, $\mathrm{\Delta }{m}_{21}^2$ and $\mathrm{\Delta }{m}_{31}^2$ will correspond to the other two masses. Our construction of the MES model with TM₁ mixing rules out the inverted ordering (IO) of the neutrino masses. The inverted ordering is disfavored with Δχ² = 7.3 including atmospheric data from Super-Kamiokande [60–62]. Hence, our results are in good agreement with the latest global data. Figure 1 represents the correaltion plots for the model parameters in our model. Figure 2 shows the variation of different neutrino oscillation parameters as a function of the model parameters.

TABLE 4

TABLE 4. Latest global fit neutrino oscillation data [60, 61].

FIGURE 1

FIGURE 1. Correlation plots for the model parameters (in eV).

FIGURE 2

FIGURE 2. The allowed region of $\mathrm{\Delta }{m}_{31}^2,\mathrm{\Delta }{m}_{21}^2$ and mixing angle   sin²θ₁₃ as a function of model parameters.

The model leads to the TM₁ parameter $\zeta =\pm \frac{\pi }{2}$ resulting in μ–τ reflection symmetry, ${\theta }_{23}=\frac{\pi }{4}$, and ${\delta }_{CP}=\pm \frac{\pi }{2}$. The values ${\theta }_{23}=\frac{\pi }{4}$ and ${\delta }_{CP}=-\frac{\pi }{2}$ are consistent with the current global fit. Again using Eqs. 15, 17 and the values of   sin²θ₁₃ given in Table 4, we obtain the range of   sin²θ₁₂ as 0.3167–0.3195. This is also consistent with the global fit. We have also calculated the sum of the three light neutrino masses from the model parameters. It predicts ∑m_i within the range 0.057–0.059, which is below the cosmological upper bounds. Thus, it is clear that the predictions of the model comply with the latest neutrino and cosmology data.

Apart from studying active neutrino phenomenology, we have calculated different observables related to the different cLFV processes with the numerically evaluated model parameters. All the masses and mixing in the model are dependent on the model parameters which are highly constrained by the neutrino oscillation data. The masses and mixing of the active and sterile neutrinos in turn are related to the observables of different cLFV processes and also the 0νββ process as mentioned above. Hence, the same set of model parameters that are supposed to produce correct neutrino phenomenology can also be used to estimate the observables of different low-energy processes. Thus, this model is constrained by these processes also. The predictions of our model on the sum of the neutrino masses and the 0νββ can be found in Table 5. The motivation is to see if the neutrino mass matrix that can explain the neutrino phenomenology can also provide sufficient parameter space for other low-energy observables 0νββ, cLFV, etc. We also correlate the sterile neutrino mass with 0νββ and cLFV processes to see the impact of the sterile neutrino.

TABLE 5

TABLE 5. Predictions of the model on different parameters. The value of m_ββ is taken from the KamLAND-ZEN experiment [62] and ∑m_i from latest Planck data [63].

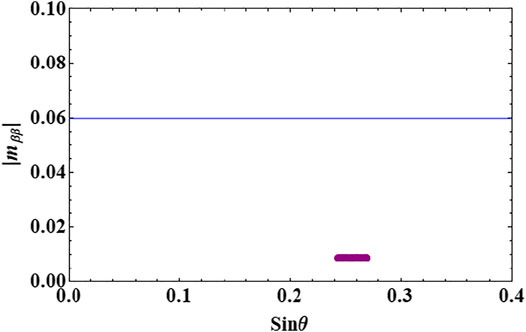
The effective mass (m_ββ) characterizing the 0νββ process along with the presence of heavy sterile neutrinos is calculated using Eq. 90. Figure 3 shows the effective mass against the sterile neutrino mass and mixing. For new physics contributions coming from extra sterile neutrinos, the effective mass is consistent with the upper bound (|m_ββ| ≤ 0.06 eV) followed by the data of the KamLAND-ZEN [59] experiment. It has been observed that the presence of very heavy sterile neutrinos in the model has no significant effect on the 0νββ process since m_ββ is proportional to $\frac{1}{m_4}$. Figure 4 shows variation of effective mass as a function of the parameter θ characterizing TM₁ mixing. This plot shows how the model with TM₁ mixing constrains the effective neutrino mass m_ββ.

FIGURE 3

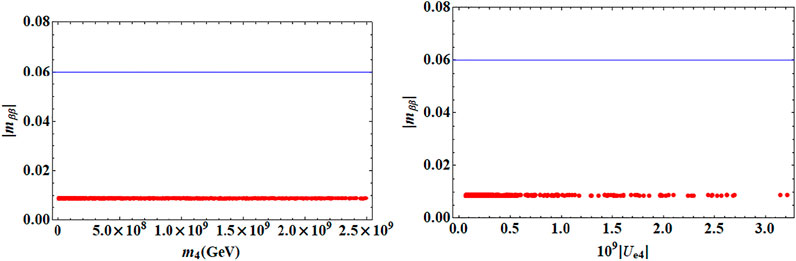
FIGURE 3. Prediction of the effective neutrino mass as a function of the sterile neutrino mass and mixing.

FIGURE 4

FIGURE 4. Prediction of the effective neutrino mass as a function of the TM₁ mixing parameter sinθ.

We have performed the analysis of μ − e conversion with two different targets—aluminum (Al) and gold (Au). Figure 5 shows the calculated conversion ratios with these two targets as a function of the mass of the sterile neutrinos. In both cases, the results are within the reach of current and future experiments. It has been observed that sterile neutrinos with mass 10⁸ GeV can lead to such a process within the experimental bound.

FIGURE 5

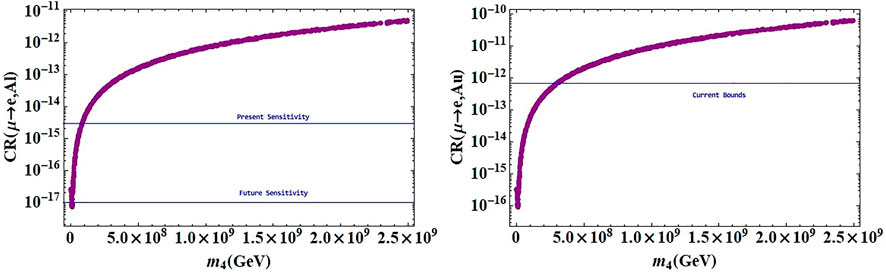
FIGURE 5. CR (μ − e, N) as a function of the sterile neutrino mass with two different targets. The blue horizontal line represents the experimental bounds on this process.

We have seen the sterile neutrino contribution to the process μ⁻e⁻ → e⁻e⁻ in the model. Figure 6 shows the variation of branching ratios with the mass of the sterile neutrinos. It has been observed that, for targets with Al, the experimental limits are reached for a lower value of the mass of the sterile neutrinos (around 10⁸ GeV) than in the case with Au (around 2.5 × 10⁹ GeV). This shows that the cLFV process induced by an additional sterile neutrino could certainly be probed in near future experiments with aluminum targets. The stringent bound on the sterile neutrino mass to cause such a process is around 3 × 10⁸ GeV.

FIGURE 6

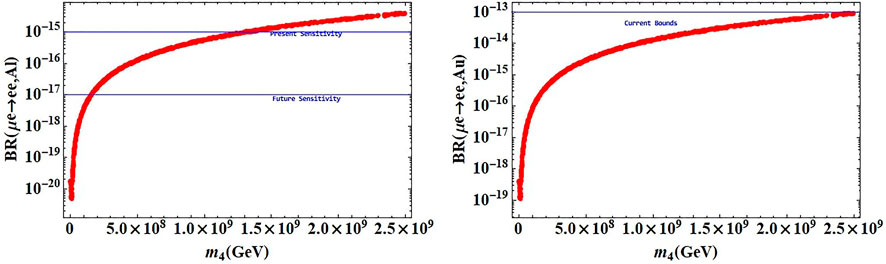
FIGURE 6. BR (μ⁻e⁻ → e⁻e⁻, N) as a function of the sterile neutrino mass with two different targets. The blue horizontal line represents the experimental bounds on this process.

Figure 7 indicates the impacts of sterile neutrino in the μ → eee process. It is evident from the figure that the branching ratios have a stronger experimental potential, with contributions well within the current (future) experimental reach for sterile masses above 2 × 10⁹ (10⁸) GeV.

FIGURE 7

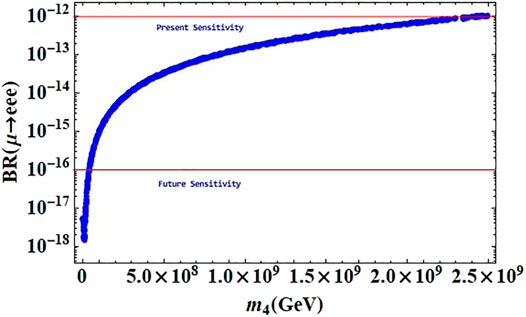
FIGURE 7. BR (μ − eee) as a function of the sterile neutrino mass. The red horizontal line represents the experimental bounds on this process.

The branching ratios of another appealing process μ → eγ in the presence of the heavy sterile neutrino as a function of its mass are shown in Figure 8. It is seen that the results are well within the current (future) experimental reach for sterile masses above 2 × 10⁹ (10⁹) GeV.

FIGURE 8

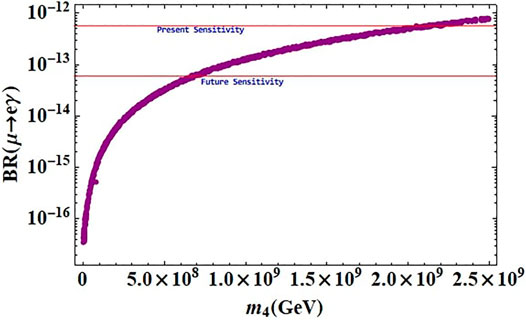
FIGURE 8. BR (μ − eγ) as a function of the sterile neutrino mass. The red horizontal line represents the experimental bounds on this process.

Similarly, we have carried out our analysis for processes involving tau atoms and calculated the observables using Eqs. 77–79. The results are shown in Figures 9–11. It is observed that the sterile neutrino can have sizable contributions to such processes only when it has mass above 10⁹ GeV which is quite higher than that in the case of processes involving muonic atoms. For the process τ → eγ, the current experimental bound on the branching ratio is achieved for m_s > 2 × 10¹² GeV, and however, a lower mass of sterile neutrino (around 10¹²) can contribute to such processes in future experiments as shown in Figure 9. Figure 10 indicates that the contributions of sterile neutrino to the process τ → μγ are well within the current experimental limit for m_s > 2 × 10¹² GeV and the sensitivity of future experiments is reached for a lower mass of sterile neutrino (around 5 × 10¹¹). For the process τ → eee, the current and future experimental bounds on the branching ratio are achieved for m_s > 10¹² GeV and around 3 × 10¹¹, respectively, which can be seen in Figure 9. In Table 6, we have summarized the constraints on the sterile neutrino mass coming from different cLFV processes.

FIGURE 9

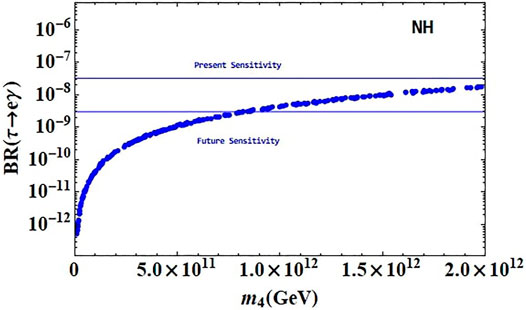
FIGURE 9. BR (τ − eγ) as a function of the sterile neutrino mass. The blue horizontal line represents the experimental bounds on this process.

FIGURE 10

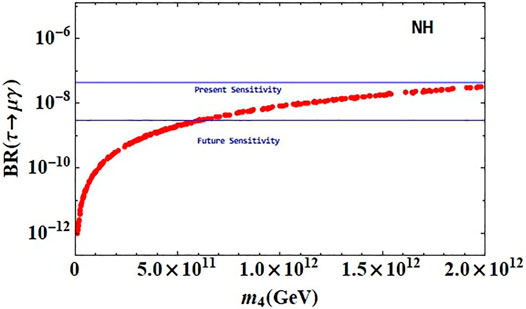
FIGURE 10. BR (τ − μγ) as a function of the sterile neutrino mass. The blue horizontal line represents the experimental bounds on this process.

FIGURE 11

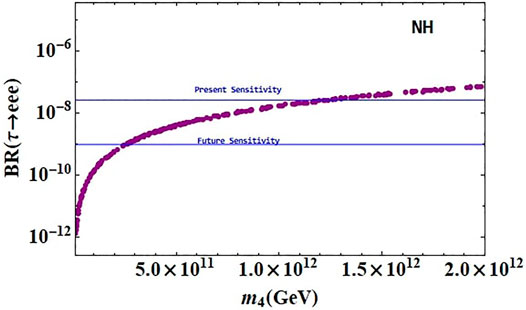
FIGURE 11. BR (τ − eee) as a function of the sterile neutrino mass. The blue horizontal line represents the experimental bounds on this process.

TABLE 6

TABLE 6. Constraints on the sterile neutrino mass from different cLFV processes.

VI Conclusion

In this work, we have studied the effect of sterile neutrino on the low-energy processes focusing on charged lepton flavor violation and neutrinoless double beta decay. The framework of our study is an MES model which is obtained by the addition of a triplet of right-handed neutrinos and a sterile neutrino singlet field to the standard model. The gauge group of the standard model is extended by the flavor symmetry group Δ(96) along with two C₂ groups and one C₃ group. The model is constructed in such a way that it gives rise to a special mixing pattern known as TM₁ mixing. Implementation of TM₁ mixing in the MES framework with an extra sterile neutrino has been not done before. The model leads to TM₁ mixing with μ–τ reflection symmetry which predicts the maximal atmospheric mixing angle and maximal breaking of the CP symmetry. These two important constraints of the model comply with the experimental data. Moreover, our construction of the model rules out the inverted ordering of the neutrino masses. The model is represented by three model parameters that have been evaluated by comparing the light neutrino oscillation parameters in the 3σ range. We have obtained the sterile neutrino mass and mixing from the model parameters. We then fed the model parameters in calculating different observables characterizing different low-energy processes. The textures of the mass matrices in our model predict the effective mass m_ββ that is consistent with the experimental data. We have investigated different cLFV processes involving muon and tau leptons. It has been observed that a wide range of parameter space can be probed in near future experiments. There are no theoretical upper bounds on the mass of the sterile neutrino. However, in this model, the different cLFV processes highly constrain the mass of the sterile neutrino. In this work, we have summarized the limits on the mass of the sterile neutrino to contribute such processes. Another important conclusion that can be drawn from the present work is that the sterile neutrino mass range allowed by different cLFV processes can give rise to an effective neutrino mass within the experimental limits. Thus, the two low-energy observables can also be correlated in the proposed model.

In conclusion, the MES model with Δ(96) discrete flavor symmetry can address neutrino phenomenology in the presence of heavy sterile neutrinos with the prediction of experimentally observed neutrino parameters. We have shown that the model has interesting implications in rare decay experiments such as lepton flavor violation and also neutrinoless double beta decay. The estimation of the model on baryon asymmetry of the universe (BAU) can also be studied in the future.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

NG, RK, and MD conceptualized the idea. NG and RK performed the methodology, ran the software, involved in formal analysis, and visualized the results. NG wrote the original draft. RK and MD reviewed and edited the manuscript. MD involved in supervision, funding acquisition, and project administration.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

NG would like to acknowledge the Department of Science and Technology (DST), India (grant DST/INSPIRE Fellowship/2016/IF160994), for the financial assistantship. MKD acknowledges the Department of Science and Technology, Government of India, for the support under project no. EMR/2017/001436.

References

1. Acero MA, Adamson P, Aliaga L, Alion T, Allakhverdian V, Anfimov N, et al. New Constraints on Oscillation Parameters from ν_e Appearance and ν_μ Disappearance in the NOvA experiment. Phys Rev D (2018) 98:032012. doi:10.1103/PhysRevD.98.032012

Google Scholar

2. Abe K. Measurements of Neutrino Oscillation in Appearance and Disappearance Channels by the T2K experiment with 6.6 × 10²⁰ Protons on Target. Phys Rev D (2015) 91(7):072010. doi:10.1103/PhysRevD.91.072010

CrossRef Full Text | Google Scholar

3. Mohapatra RN, Senjanović G. Neutrino Masses and Mixings in Gauge Models with Spontaneous Parity Violation. Phys Rev D (1981) 23:165–80. doi:10.1103/physrevd.23.165

CrossRef Full Text | Google Scholar

4. Bernstein RH, Cooper PS. Charged Lepton Flavor Violation: An Experimenter’s Guide. Phys Rept (2013) 532(27–64). doi:10.1016/j.physrep.2013.07.002

CrossRef Full Text | Google Scholar

5. Mihara S, Miller JP, Paradisi P, Piredda G. Charged Lepton Flavor-Violation Experiments. Annu Rev Nucl Part Sci (2013) 63:531–52. doi:10.1146/annurev-nucl-102912-144530

CrossRef Full Text | Google Scholar

6. Lindner M, Platscher M, Queiroz FS. A Call for New Physics : The Muon Anomalous Magnetic Moment and Lepton Flavor Violation. Phys Rept (2018) 731:1–82. doi:10.1016/j.physrep.2017.12.001

CrossRef Full Text | Google Scholar

7. Bertl W, au fnm, Engfer R, Hermes EA, Kurz G, Kozlowski T, et al. A Search for μ-e Conversion in Muonic Gold. Eur Phys J C (2006) 47:337–46. doi:10.1140/epjc/s2006-02582-x

CrossRef Full Text | Google Scholar

8. Koike M, Kuno Y, Sato J, Yamanaka M. New Process for Charged Lepton Flavor Violation Searches:μ−e−→e−e−in a Muonic Atom. Phys Rev Lett (2010) 105:121601. doi:10.1103/physrevlett.105.121601

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Calibbi L, Signorelli G. Charged Lepton Flavour Violation: An Experimental and Theoretical Introduction. Riv Nuovo Cim (2018) 41(2):71–174. doi:10.1393/ncr/i2018-10144-0

CrossRef Full Text | Google Scholar

10. Hayasaka K, Inami K, Miyazaki Y. Search for Lepton Flavor Violating Tau Decays into Three Leptons with 719 Million Produced Tau+Tau- Pairs. Phys Lett B (2010) 687:139–43. doi:10.1016/j.physletb.2010.03.037

CrossRef Full Text | Google Scholar

11. Baldini A. Search for the lepton flavour violating decay μ⁺ → e⁺γ with the full dataset of the MEG experiment. Eur Phys J C (2016) 76(8):434. doi:10.1140/epjc/s10052-016-4271-x

Google Scholar

12. Aubert B, Karyotakis Y, Lees JP, Poireau V, Prencipe E, Prudent X, et al. Searches for Lepton Flavor Violation in the Decays τ^± → e^±γ and τ^± → μ^±γ. Phys Rev Lett (2010) 104:021802. doi:10.1103/PhysRevLett.104.021802

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Bellgardt U, Otter G, REichler , Felawka L, Niebuhr C, Walter HK, et al. Search for the Decay mu+ — > e+ e+ e-. Nucl Phys B (1988) 299(1–6). doi:10.1016/0550-3213(88)90462-2

CrossRef Full Text | Google Scholar

14. Deppisch F, Valle J. Enhanced Lepton Flavor Violation in the Supersymmetric Inverse Seesaw Model. Phys Rev D (2005) 72:036001. doi:10.1103/physrevd.72.036001

CrossRef Full Text | Google Scholar

15. Ilakovac A, Pilaftsis A. Flavour-violating Charged Lepton Decays in Seesaw-type Models. Nucl Phys B (1995) 437:491–519. doi:10.1016/0550-3213(94)00567-x

CrossRef Full Text | Google Scholar

16. Abada A, De Romeri V, Orloff J, Teixeira AM. In-flight cLFV conversion: $${e-\mu }$$ e - μ , $${e-\tau }$$ e - τ and $${\mu -\tau }$$ μ - τ in minimal extensions of the standard model with sterile fermions. Eur Phys J C (2017) 77(5):304. doi:10.1140/epjc/s10052-017-4864-z

CrossRef Full Text | Google Scholar

17. Hernández-Tomé G, Illana J, Masip M, López Castro G, Roig P. Effects of Heavy Majorana Neutrinos on Lepton Flavor Violating Processes. Phys Rev D (2020) 101(7), 075020. doi:10.1103/PhysRevD.101.075020

CrossRef Full Text | Google Scholar

18. Athanassopoulos C, Auerbach LB, Burman RL, Caldwell DO, Church ED, Cohen I, et al. Evidence for nu(mu) — > nu(e) neutrino oscillations from LSND. Phys Rev Lett (1998) 81:1774–7.

Google Scholar

19. Aguilar-Arevalo AA, Brown BC, Bugel L, Cheng G, Conrad JM, Cooper RL, et al. Significant Excess of ElectronLike Events in the MiniBooNE Short-Baseline Neutrino Experiment. Phys Rev Lett (2018) 121(22):221801. doi:10.1103/physrevlett.121.221801

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Naumov DV. The Sterile Neutrino: A Short Introduction. EPJ Web Conf (2019) 207:04004. doi:10.1051/epjconf/201920704004

CrossRef Full Text | Google Scholar

21. Dev PSB, Pilaftsis A. Light and Superlight Sterile Neutrinos in the Minimal Radiative Inverse Seesaw Model. Phys Rev D (2013) 87(5), 053007. doi:10.1103/physrevd.87.053007

CrossRef Full Text | Google Scholar

22. Gautam N, Das MK. Phenomenology of keV Scale Sterile Neutrino Dark Matter with S₄ Flavor Symmetry. JHEP (2020) 2020. doi:10.1007/jhep01(2020)098

CrossRef Full Text | Google Scholar

23. Adhikari R, Agostini M, Anh Ky N, Araki T, Archidiacono M, Bahr M, et al. A White Paper on keV Sterile Neutrino Dark Matter. JCAP (2017) 2017:025. doi:10.1088/1475-7516/2017/01/025

CrossRef Full Text | Google Scholar

24. Dolgov A, Hansen S. Massive Sterile Neutrinos as Warm Dark Matter. Astropart Phys (2002) 16:339–44. doi:10.1016/s0927-6505(01)00115-3

CrossRef Full Text | Google Scholar

25. Hamann J, Hannestad S, Raffelt GG, Wong YY. Sterile Neutrinos with eV Masses in Cosmology: How Disfavoured Exactly? JCAP (2011) 2011:034. doi:10.1088/1475-7516/2011/09/034

CrossRef Full Text | Google Scholar

26. Dodelson S, Widrow LM. Sterile Neutrinos as Dark Matter. Phys Rev Lett (1994) 72(17–20):17–20. doi:10.1103/PhysRevLett.72.17

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Lucente M. Implication of Sterile Fermions in Particle Physics and Cosmology. Ph.D. thesis. Orsay (2015).

28. Gautam N, Das MK. Neutrino Mass, Leptogenesis and Sterile Neutrino Dark Matter in Inverse Seesaw Framework. arXiv: 2001.00452 (2020).

29. Abada A, Hernández-Cabezudo A, Marcano X. Beta and Neutrinoless Double Beta Decays with KeV Sterile Fermions. JHEP (2019) 2019. doi:10.1007/jhep01(2019)041

CrossRef Full Text | Google Scholar

30. Abazajian KN. Sterile Neutrinos in Cosmology. Phys Rept (2017) 711:1–28. doi:10.1016/j.physrep.2017.10.003

CrossRef Full Text | Google Scholar

31. Zhang H. Light Sterile Neutrino in the Minimal Extended Seesaw. Phys Lett B (2012) 714:262. doi:10.1016/j.physletb.2012.06.074

CrossRef Full Text | Google Scholar

32. Barry J, Rodejohann W, Zhang H. Light Sterile Neutrinos: Models and Phenomenology. JHEP (2011) 2011. doi:10.1007/jhep07(2011)091

CrossRef Full Text | Google Scholar

33. Luhn C. Trimaximal TM1 Neutrino Mixing in with Spontaneous CP Violation. Nucl Phys B (2013) 875:80–100. doi:10.1016/j.nuclphysb.2013.07.003

CrossRef Full Text | Google Scholar

34. Nath N, Ghosh M, Goswami S, Gupta S. Phenomenological Study of Extended Seesaw Model for Light Sterile Neutrino. JHEP (2017) 2017. doi:10.1007/jhep03(2017)075

CrossRef Full Text | Google Scholar

35. Das P, Mukherjee A, Das MK. Active and Sterile Neutrino Phenomenology with A4 Based Minimal Extended Seesaw. Nucl Phys B (2019) 941:755–79. doi:10.1016/j.nuclphysb.2019.02.024

CrossRef Full Text | Google Scholar

36. Krishnan R, Mukherjee A, Goswami S. Realization of the Minimal Extended Seesaw Mechanism and the TM₂ Type Neutrino Mixing. JHEP (2020) 2020. doi:10.1007/jhep09(2020)050

CrossRef Full Text | Google Scholar

37. King SF, Zhou Y-L. Trimaximal TM₁ Mixing with Two Modular S₄ Groups. Phys Rev D (2020) 101(1):015001. doi:10.1103/physrevd.101.015001

CrossRef Full Text | Google Scholar

38. Chakraborty M, Krishnan R, Ghosal A. Predictive S₄ Flavon Model with TM₁ Mixing and Baryogenesis through Leptogenesis. JHEP (2020) 09.

Google Scholar

39. Krishnan R. TM₁ Neutrino Mixing with $\sin {\theta }_{13}=\frac{1}{\sqrt{3}}\sin \frac{\pi }{12}$ (2019). arXiv:1912.02451.

Google Scholar

40. Ding G-J. TFH Mixing Patterns, Large θ₁₃ and Δ(96) Flavor Symmetry. Nucl Phys B (2012) 862:1–42. doi:10.1016/j.nuclphysb.2012.04.002

CrossRef Full Text | Google Scholar

41. King SF, Luhn , C, Stuart AJ. A Grand Delta(96) X SU(5) Flavour Model. Nucl Phys B (2013) 867:203–35.

CrossRef Full Text | Google Scholar

42. King SF, Neder T, Stuart AJ. Lepton Mixing Predictions from Δ(6n²) Family Symmetry. Phys Lett B (2013) 726:312–5. doi:10.1016/j.physletb.2013.08.052

CrossRef Full Text | Google Scholar

43. Fonseca RM, Grimus W. Classification of Lepton Mixing Matrices from Finite Residual Symmetries. JHEP (2014) 2014. doi:10.1007/jhep09(2014)033

CrossRef Full Text | Google Scholar

44. Michel L, Zhilinskii B. Symmetry, Invariants, Topology. Basic Tools. Phys Rep (2001) 341:7–9. doi:10.1016/s0370-1573(00)00087-9

CrossRef Full Text | Google Scholar

45. Michel M. La genèse du recrutement de 1918 en Afrique noire française. Revue française d'histoire d'outre-mer (1971) 58:433–50. doi:10.3406/outre.1971.1561

CrossRef Full Text | Google Scholar

46. Krishnan R. Symmetries of Stationary Points of the Potential and the Framework of the Auxiliary Group. Physical Review D (2021) 103. doi:10.1103/physrevd.103.l051701

47. Cui Y. Conceptual Design Report for Experimental Search for Lepton Flavor Violating Mu- - E- Conversion at Sensitivity of 10**(-16) with a Slow-Extracted Bunched Proton Beam (COMET) (2009):208.

48. Carey RM, Lynch KR, Miller JP, Roberts BL, Marciano WJ, Semertzidis YK, et al. Proposal to search for μ⁻N → e⁻N with a single event sensitivity below 10⁻¹⁶ (2008).

49. Abada A, De Romeri V, Teixeira A. Impact of Sterile Neutrinos on Nuclear-Assisted cLFV Processes. JHEP (2016) 2016. doi:10.1007/jhep02(2016)083

CrossRef Full Text | Google Scholar

50. Kitano R, Koike M, Okada Y. Detailed Calculation of Lepton Flavor Violating Muon Electron Conversion Rate for Various Nuclei. Phys Rev D (2002) 66:096002. doi:10.1103/physrevd.66.096002

CrossRef Full Text | Google Scholar

51. Willmann L, Schmidt PV, Wirtz HP, Abela R, Baranov V, Bagaturia J, et al. New Bounds from Searching for Muonium to Anti-muonium Conversion. Phys Rev Lett (1999) 82(49–52). doi:10.1103/physrevlett.82.49

CrossRef Full Text | Google Scholar

52. Adam J, Bai X, Baldini AM, Baracchini E, Bemporad C, Boca G, et al. New constraint on the existence of the μ⁺ → e⁺γ decay. Phys Rev Lett (2013) 110:201801. doi:10.1103/PhysRevLett.110.201801

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Miyazaki Y, Aihara H, Arinstein K, Aulchenko V, Bakich AM, Balagura V, et al. Search for Lepton-Flavor-Violating Tau Decays into a Lepton and a Vector Meson. Phys Lett B (2011) 699:251–7. doi:10.1016/j.physletb.2011.04.011

CrossRef Full Text | Google Scholar

54. Benes P, Faessler A, Simkovic F, Kovalenko S. Sterile Neutrinos in Neutrinoless Double Beta Decay. Phys Rev D (2005) 71:077901.

Google Scholar

55. Awasthi RL, Parida M, Patra S. Neutrinoless Double Beta Decay and Pseudo-dirac Neutrino Mass Predictions through Inverse Seesaw Mechanism (2013).

56. Borgohain H, Das MK. Phenomenology of Two Texture Zero Neutrino Mass in Left-Right Symmetric Model with Z₈ × Z₂. JHEP (2019). doi:10.1007/jhep02(2019)129

CrossRef Full Text | Google Scholar

57. Blennow M, Fernandez-Martinez E, Lopez-Pavon J, Menendez J. Neutrinoless Double Beta Decay in Seesaw Models. JHEP (2010) 2010. doi:10.1007/jhep07(2010)096

CrossRef Full Text | Google Scholar

58. Gando A, Gando Y, Hachiya T, Hayashi A, Hayashida S, Ikeda H, et al. Search for Majorana Neutrinos Near the Inverted Mass Hierarchy Region with KamLAND-Zen. Phys Rev Lett (2016) 117(8):082503-1–082503-6. doi:10.1103/PhysRevLett.117.082503

PubMed Abstract | CrossRef Full Text | Google Scholar

59. de Salas PF, Forero DV, Gariazzo S, Martínez-Miravé P, Mena O, Ternes CA, et al. 2020 Global Reassessment of the Neutrino Oscillation Picture. J High Energ Phys (2020) 2021. doi:10.1007/jhep02(2021)071

CrossRef Full Text | Google Scholar

60. Capozzi F, Di Valentino E, Lisi E, Marrone A, Melchiorri A, Palazzo A, et al. Addendum to “Global Constraints on Absolute Neutrino Masses and Their Ordering”. Phys Rev D (2020) 101. doi:10.1103/physrevd.101.116013

CrossRef Full Text | Google Scholar

61. Esteban I, Gonzalez-Garcia M, Maltoni M, Schwetz T, Zhou A. The Fate of Hints: Updated Global Analysis of Three-Flavor Neutrino Oscillations. J High Energ Phys (2020)(9) 2020. doi:10.1007/jhep09(2020)178

CrossRef Full Text | Google Scholar

62. Aghanim N. Planck 2018 Results. VI. Cosmological Parameters. A&A (2018) 641:67. doi:10.1051/00046361/201833910

63. King SF, Neder T. Lepton Mixing Predictions Including Majorana Phases from Δ(6n²) Flavour Symmetry and Generalised CP. Phys Lett B (2014) 736:308–16. doi:10.1016/j.physletb.2014.07.043

CrossRef Full Text | Google Scholar

Appendix AProperties of δ(96) Group

Δ(96) is one of the members of Δ6n² with n = 4. The triplets $3_i,\overline{3_i^{\prime }},3_i^{\prime }$ and $\overline{3_i^{\prime }}$ are faithful representations of Δ(96). To generate 3 _i ′, we may conveniently use the matrices given by

$P=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),Q=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),C=\left(\begin{array}{ccc}\hfill i\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -i\hfill \end{array}\right).(\mathrm{A1})$

There are 11 irreducible representations of Δ(96), two singlets 1 and 1′, one doublet 2, six triplets 3, $3^{\prime },3_i,3_i^{\prime },\overline{3_i^{\prime }}$ , $\overline{3_i^{\prime }}$ and 6. We note that the first five representations correspond to those of S ₄ which is a subgroup of Δ(96). The character table for Δ(96) is given in Appendix Table A7.

TABLE A7

TABLE A7. Character table of the Δ(96) group.

Here, the tensor products of 1, 1′, 2, 3, 3′ follow the product rules of S ₄:

$3\times 1=\mathrm{3,3}\times 1^{\prime }=3^{\prime },3^{\prime }\times 1^{\prime }=\mathrm{3,2}\times 1^{\prime }=2.(\mathrm{A2})$

$\begin{array}{l}\hfill 2\otimes 3=3\oplus 3^{\prime },\end{array}(\mathrm{A3})$

$\begin{array}{l}\hfill 3\otimes 3=1\oplus 2\oplus 3^{\prime }\oplus 3,\end{array}(\mathrm{A4})$

$\begin{array}{l}\hfill 3^{\prime }\otimes 3^{\prime }=1\oplus 2\oplus 3^{\prime }\oplus 3,\end{array}(\mathrm{A5})$

$\begin{array}{l}\hfill 3_i^{\prime }\otimes 3_i^{\prime }=3^{\prime }\oplus \overline{3_i^{\prime }}\oplus \overline{3_i^{\prime }},\end{array}(\mathrm{A6})$

$\begin{array}{l}\hfill \overline{3_i^{\prime }}\otimes 3_i^{\prime }=1\oplus 2\oplus 6.\end{array}(\mathrm{A7})$

For the Clebsch–Gordan coefficients all the above expansion, refer to [62, 63]. The tensor products involving 3 _i and $\overline{3_i^{\prime }}$ are given by

${\left(\begin{array}{c}\hfill a_1\hfill \\ \hfill a_2\hfill \\ \hfill a_3\hfill \end{array}\right)}_{{3_i}^{\prime }}\otimes {\left(\begin{array}{c}\hfill b_1\hfill \\ \hfill b_2\hfill \\ \hfill b_3\hfill \end{array}\right)}_{{3_i}^{\prime }}={\left(\begin{array}{c}\hfill a_1{b}_1\hfill \\ \hfill a_2{b}_2\hfill \\ \hfill a_3{b}_3\hfill \end{array}\right)}_{3^{\prime }}\oplus {\left(\begin{array}{c}\hfill a_2{b}_3+a_3{b}_2\hfill \\ \hfill a_2{b}_3+a_3{b}_2\hfill \\ \hfill a_1{b}_2+a_2{b}_1\hfill \end{array}\right)}_{\overline{3_i^{\prime }}}\oplus {\left(\begin{array}{c}\hfill a_2{b}_3-a_3{b}_2\hfill \\ \hfill a_2{b}_3-a_3{b}_2\hfill \\ \hfill a_1{b}_2-a_2{b}_1\hfill \end{array}\right)}_{\overline{3_i^{\prime }}},(\mathrm{A8})$

${\left(\begin{array}{c}\hfill a_1\hfill \\ \hfill a_2\hfill \\ \hfill a_3\hfill \end{array}\right)}_{{3_i}^{\prime }}\otimes {\left(\begin{array}{c}\hfill b_1\hfill \\ \hfill b_2\hfill \\ \hfill b_3\hfill \end{array}\right)}_{\overline{3_i^{\prime }}}={(a_1{b}_1+a_2{b}_2+a_3{b}_3)}_1\oplus {\left(\begin{array}{c}\hfill 1/\sqrt{2}(a_2{b}_2-a_3{b}_3)\hfill \\ \hfill 1/\sqrt{6}(-2a_1{b}_1+a_2{b}_2+a_3{b}_3)\hfill \end{array}\right)}_2\oplus {\left(\begin{array}{c}\hfill a_2{b}_3\hfill \\ \hfill a_3{b}_1\hfill \\ \hfill a_1{b}_2\hfill \\ \hfill a_3{b}_2\hfill \\ \hfill a_1{b}_3\hfill \\ \hfill a_2{b}_1\hfill \end{array}\right)}_6.(\mathrm{A9})$