Association, Correlation, and Causation Among Transport Variables of PM2.5

The issue of $P{M}_{2.5}$ pollution has received significant attention in the literature as it has social, economic, and political implications. Big data sets have been collected by pollution monitoring stations (i.e., nodes) throughout the world, and this has made it possible to quantitatively characterize the dependence of $P{M}_{2.5}$ pollution in different regions. Here we divide the dependency relationship into three types: association, correlation, and causation. This study conducted such relationships using three approaches: the random matrix theory (RMT), cross-correlation, and convergent cross-mapping (CCM). The aim of this study is to determine the above three relationships between pollution data from different nodes. A random matrix analysis revealed that pollutant time series are not completely random, but are associated. Further analysis showed that $P{M}_{2.5}$ sequences had clear short-range correlations, yet the long-range correlations were blurred. Moreover, at the collect level, there were no clear causalities among pollutant concentrations from different geographical regions, regardless of distance and direction. These results indicate that the dependence of $P{M}_{2.5}$ pollution between different sites is complex. Nonetheless, this comprehensive analysis based on big data provided insights into critical issues of general interest, including pollution-induced climate change, and pollution abatement.

1 Introduction

Air quality is a significant environmental concern around the world. Air pollution and aerosols have significant impacts on human health, climates, meteorological phenomena, and the environment, and many studies have focused on these effects [1–4]. $P{M}_{2.5}$, as an airborne particulate, is the deadliest form of air pollution due to its ability to penetrate deep into the lungs and bloodstream, unfiltered [4]. This allows it to cause permanent DNA mutations, heart attacks, and premature deaths, and lead to the deaths of three to seven million people every year [5, 6]. Moreover, the local nature of air pollution means that the particle can significantly impact temperature, precipitation, and extreme events at a regional level, e.g., aerosols affect regional climates and ocean-atmosphere feedback [2, 7]. Thus, as Booth et al. have demonstrated, anthropogenic aerosol emissions influence historical climate events, such as peaks in hurricane activity and Sahel droughts [8]. Thus, scientists have developed new ways to understand the different factors that contribute to poor air quality, and this research has been used to develop observational systems using models and data and to assist decision makers with air quality assessments.

To investigate these influences, Rohde et al. developed a technique for mapping air pollution concentrations and sources using data from monitoring stations; after studying $P{M}_{2.5}$ pollution in China for about four months, a short-distance effect was found [9]. Dai et al. analyzed six pollutants in 350 Chinese cities and found both long-term correlations and a relationship between spatial correlations and provincial administrative divisions [10]. Additionally, teleconnections were found to indicate relationships between climate anomalies at significant distances (i.e., thousands of km) [11, 12]. Moreover, Yu et al. conducted mineral analyses to demonstrate that the long-range transport of soil particles contributed significantly to high concentrations of $P{M}_{2.5}$ during “dust days” [13]. Kaneyasu et al. focused on the impacts of long-range $P{M}_{2.5}$ transports in Kyushu area and noticed that the $P{M}_{2.5}$ concentration is primarily dominated by the inflow of long-range transported aerosols [14]. Perrone et al. demonstrated that Mediterranean sites may be affected by long-range transported pollution, and its pollution depends on the airflow [15]. Zhang $etal.$ found that the strongest correlation between winter and the $P{M}_{2.5}$ concentration in the North China Plain, which is mainly caused by the transport of $P{M}_{2.5}$ [16]. Recently, numerous researchers have used network methods to study climate and environmental issues, where nodes in the network represent geographic coordinate sites, and cross-correlation and mutual information about the time series of two nodes are used to represent connected edges. And they found that climate networks had very strong links that were caused by a proximity (i.e., distance) effect. Namely, pairs of sites close to each other (less than 2,000 km apart) were often strongly and positively correlated [17–26].

Technically speaking, the association is different from the correlation. Association means that one variable provides information about another, but correlation means that two variables show an increasing or decreasing trend. Correlation means an association, but not causation. On the contrary, causality means an association, not correlation [27]. Despite this research, little attention was given to PM_2.5 in regards to different temporalspatial scales and causal-effect among different sites. It was generally accepted that climate change causality detection and human crizes had important roles in future research on climate and environmental policies [28–30].

In order to explore the association, correlation and causality between $P{M}_{2.5}$ time series in different regions with the changes in the direction and distance of the monitoring sites, we use the RMT method to detect the association, the cross-correlation method to measure the correlation, and finally the CCM to understand the causality. The latter was recently developed as a non-linear dynamics based method for ascertaining and quantifying causal relationships between time series [30, 31]. The results of the study are as follows. First, the RMT analysis revealed that the time series of PM_2.5 at different sites is not completely random, and there is a certain association. Secondly, a conventional correlation analysis indicated that there is a clear short-distance correlation between the time series from different sites, but there is no concise and clear correlation in the long-distance range. Finally, the analysis results of the causality detection algorithm CCM demonstrated that at the collect level, the causality between the $P{M}_{2.5}$ time series of different nodes is not obvious, and there is no distinct relationship with the distance and direction between the sites.

2 Data Collection

Empirical big data sets were analyzed for this study. They were obtained from global, Chinese, and American monitoring stations. Time resolutions were given in hours, which allowed the researchers to capture time evolutions in relation to $P{M}_{2.5}$. Moreover, in order to meet calculation requirements for correlation and causality algorithms, the data was cleaned: empty data segments were removed, it was ensured that the length of each original time series was more than 8,760 h (about 1 y: $24\ast 365$), and all the time series were adjusted to have common starting and ending points. As a result, the length, $L_h$, of each time series (after the cleaning) was less than 8,760 h. The basic statistical properties of the filtered data sets can be seen in Table 1, where N is the number of nodes (i.e., cities, counties, or regions) and $L_h$ is the length of each time series in an hourly resolution. Detailed descriptions of the different public data sets are given below.

TABLE 1

TABLE 1. The basic properties of the three data and parameters of the RMT analyses.

2.1 Global Stations

The global data was collected from [32]. It comprised names, longitudes and latitudes, recorded times (years, months, and hours), and $P{M}_{2.5}$ values. The data was obtained from December 2016 to December 2017 through a monitoring network that operated in 632 regions (or cities) across the world.

2.2 Chinese Stations

The Chinese data was collected from [33]. It comprised names, longitudes and latitudes, recorded times (years, months, and hours), and $P{M}_{2.5}$ time series. The data was obtained from January 2015 to June 2017 through a monitoring network that operated in 365 cities across China.

2.3 United States Stations

The American data was collected from [34]. It comprised names, longitudes and latitudes, and $P{M}_{2.5}$ time stamps. The $P{M}_{2.5}$ data was divided into two categories, firm and non-firm, and the non-firm data was used for the analyses. The data was obtained from January 2016 to December 2016 through a monitoring network that operated in 137 regions (or counties) across the United States (USA).

3 Methods

This chapter discusses the two correlation calculation methods, i.e., cross correlation and the RMT, which were used in this study to determine correlations between nodes. Moreover, this chapter discusses the causality detection algorithm, CCM, which was used to measure causalities between the nodes. Finally, the azimuth (α) polar coordinate system and distance (d) are discussed.

3.1 Cross Correlation

Previous studies used cross-correlation analyses to measure correlations between node distances [17–21]. For this study, a cross-correlation method [18–20] was used to calculate the $W_{max}$ and hour resolution ($L_h$ of each time series; (see Table 1). Given ${\tilde{\text{T}}}^d\left(h\right)$, where d was a day and h was an hour (from zero to 23), each filtered record was defined as $T^d\left(h\right)={\tilde{T}}^d\left(h\right)-\left(1/L_d\right){\displaystyle \sum }_d{\tilde{T}}^d\left(h\right)$, where $L_d$ was the total number of days, as shown in Table 1. For each pair of nodes, i.e., i and j, a cross-correlation in time series was calculated as follows.

$C_{ij}^d\left(\tau \right)=\frac{\langle T_i^d\left(h\right)T_j^d\left(h-\tau \right)\rangle -\langle T_i^d\left(h\right)\rangle \langle T_j^d\left(h-\tau \right)\rangle }{{\sigma }_{T_i^d\left(h\right)}{\sigma }_{T_i^d\left(h-\tau \right)}}(1)$

where ${\sigma }_{T_i^d\left(h\right)}$ was the standard deviation of $T_i^d\left(h\right)$, τ was the time lag with a max value of 30 days and $C_{ij}^d\left(\tau \right)=C_{ji}^d\left(-\tau \right)$. Maximum time lag was defined as ${\tau }_{\max }$, with which $C_{ij}^d\left({\tau }_{\max }\right)$ is maximum. Then, positive link weights $\left(W_{\max }\right)$ were defined as follows.

$W_{\max }^{ij}=\frac{C_{ij}^d\left({\tau }_{\max }\right)-mean\left[C_{ij}^d\left(\tau \right)\right]}{std\left[C_{ij}^d\left(\tau \right)\right]},(2)$

where the average was a mean and standard deviation was denoted by “std.”

3.2 Random Matrix Theory

A challenge could arise when interpreting correlations involving the $P{M}_{2.5}$ time series in that the exact natures of interactions were unknown. However, the RMT was a significant theory in data analysis often used to extract underlying information in a time series. Therefore, with minimum assumptions about random Hamiltonian statistics and a real symmetric matrix with independent random elements, the RMT was implemented to address significant amounts of spectroscopic data in regards to the energy levels of complex quantum systems [35, 36]. The simplest way to determine correlations between the different time series was to use the equal time cross correlation matrix C, which had elements of one in that $\tau =0$ [37, 38].

After this was completed, the statistical properties of matrix C were determined by employing the RMT’s processes. Following this RMT procedure, C was first diagonalized and the eigenvalue λ was obtained. Next, $p\left(\lambda \right)$ was defined as an eigenvalue density as follows.

$p\left(\lambda \right)=\frac{1}{N}\frac{dn\left(\lambda \right)}{d\lambda }(3)$

where N is the number of nodes (as shown in Table 1), and $n\left(\lambda \right)$ was the number of eigenvalues for C that were less than λ. Following previous studies, it was determined that $Q\equiv L_d/N$ and $L_d$ indicated the length of a time series in a day resolution. Then, $p\left(\lambda \right)$ was computed as follows.

$p\left(\lambda \right)=\frac{Q}{2\pi {\sigma }^2}\frac{\sqrt{\left({\lambda }_{\max }-\lambda \right)\left(\lambda -{\lambda }_{\min }\right)}}{\lambda }(4)$

where ${\lambda }_{\min }\le \lambda \le {\lambda }_{\max }$ and ${\sigma }^2$ were equal to 1 with this normalization. Additionally, ${\lambda }_{\max }$ and ${\lambda }_{\min }$ were calculated as follows.

${\lambda }_{\min }^{\max }={\sigma }^2\left(1+1/Q\pm 2\sqrt{1/Q}\right).(5)$

It should be noted that although the RMT was a powerful method for identifying clues to the underlying interactions of the systems, its parameter choices differed slightly from the datasets. The basic parameters of the RMT used in this study are listed in Table 1, where ${\lambda }_{\max }$ and ${\lambda }_{\min }$ are the maximum and minimum eigenvalues from Eq. 4 and ${\lambda }_{\max }^{real}$ is the maximum eigenvalue from the real data.

3.3 Convergent Cross-Mapping

Causality has been investigated in many studies, such as social, economic, climatology, and gene perturbation experiments [39–41]. Indeed, identifying causality in complex systems can be difficult but exciting in nature, and determining causal relationships is pertinent to many disciplines with broad applications. Traditionally, Granger causality analyses can be used as paradigmatic frameworks to determine such relations [39, 42]. However, Granger causality is linear and multivariate in nature and involves statistical regression, so various methods derived from such causality are required for extensive data [31]. Entropy based methods result in similar difficulties [43], but CCM [31] is based on non-linear time series analyses [44] and was developed to overcome these challenges. That is, CCM is powerful for detecting and quantifying causations between pairs of dynamic variables based on time series [31].

For this study, a phase space was developed for each variable based on a delay-coordinate embedding method [44]. For example, for time series $x\left(t\right),$ the reconstructed vector $X\left(t\right)=\left\{x\left(t\right),x\left(t\tau \right),\dots ,x\left[t\left(E_x-1\right)\tau \right]\right\}$ was used, where τ was a delay time and $E_x$ was an embedding dimension. The same could be done for time series $y\left(t\right)$ of variable y to yield a reconstructed vector in dimensional space $E_y$. The basic principle was to compare the predictions in each subspace. Consider the pair of vectors $\left[X\left(t\right),Y\left(t\right)\right]$ at time t, one vector from each subspace. In subspace Y, one could find a set of neighboring vectors for $Y\left(t\right)$ and identify the corresponding set in subspace X based on which one could be used to predict the value of $X\left(t\right)$. The difference between $X\left(t\right)$ and its predicted value characterized the accuracy of the prediction. Similarly, based on neighboring vectors in subspace X, a prediction in subspace Y could be made. Comparing prediction accuracies regarding the two subspaces could determine the causal relationship between X and Y.

The principle underlying this method was asymmetry in regards to directional predictability. Suppose one wished to detect a causal interaction between two subsystems with the state variables $X\left(t\right)$ and $Y\left(t\right)$, respectively. Using $X\left(t\right)$, the value of $Y\left(t\right)$ could be predicted, such as $\widehat{Y}\left(t\right)$, and correlation ${\rho }_{YX}\left(t\right)$ could be predicted between $Y\left(t\right)$ and $\widehat{Y}\left(t\right)$. Similarly, using $Y\left(t\right)$, a prediction could be obtained for $\mathbf{X}\left(t\right)$, such as $\widehat{\mathbf{X}}\left(t\right)$, and the correlation ${\rho }_{XY}\left(t\right)$ between $X\left(t\right)$ and $\widehat{X}\left(t\right)$ could be calculated. If no causal relationship existed between $\mathbf{X}\left(t\right)$ and $\mathbf{Y}\left(t\right)$, the predictions in both directions were even, so statistically, the correlations ${\rho }_{YX}\left(t\right)$ and ${\rho }_{XY}\left(t\right)$ could not be distinguished from each other. That is, $\Delta \equiv {\rho }_{XY}\left(t\right)-{\rho }_{YX}\left(t\right)=0$. However, if $X\left(t\right)$ was more a cause of $Y\left(t\right)$ than the opposite, the prediction $X\left(t\right)$, obtained from $\mathbf{Y}\left(t\right)$, was better than that of $Y\left(t\right)$ [from $X\left(t\right)$]. This was because information about $X\left(t\right)$ was contained in $Y\left(t\right)$. Thus, it was determined that ${\rho }_{XY}\left(t\right)$ was greater than ${\rho }_{YX}\left(t\right)$, or $\Delta$ was greater than 0. Moreover, statistically positive $\Delta$ values could be considered heuristic criteria for determining that the direction of the causal interaction was from $X\left(t\right)$ to $Y\left(t\right)$. Likewise, if $\Delta$ was less than 0, it indicated that $Y\left(t\right)$ was more a cause of $\mathbf{X}\left(t\right)$ than the opposite [31].

3.4 Polar Coordinate System

Generally, the polar system is a two-dimensional coordinate method in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point (analogous to the origin of a Cartesian coordinate system) was called a pole, and a ray from the pole in the reference direction was the polar axis. The distance from the pole was called a radial coordinate, radial distance, or simply radius, and the angle was called an angular coordinate, polar angle, or azimuth.

3.5 Distance

Orthodromic distance, the shortest distance between two points on the surface of a sphere, was measured along each surface. In particular, for any two i and j points specified by ${\varphi }_i$, ${\eta }_i$ and ${\varphi }_j$, ${\eta }_j$, where ϕ was a geographical latitude and η was a geographical longitude, $\text{Δ}\varphi$ and $\text{Δ}\eta$ were absolute differences. The spherical law of cosines was then used for the central angle $\Delta \sigma$ between i and j as follows.

$\Delta \sigma =\arccos \left[\sin {\varphi }_i\cdot \sin {\varphi }_j+\cos {\varphi }_i\cdot \cos {\varphi }_j\cdot \cos \left(\Delta \eta \right)\right].(6)$

The distance was obtained using $d=r\Delta \sigma$, where r was the radius of the sphere.

3.6 Azimuth

Azimuth, denoted as α, was defined as a horizontal angle measured clockwise from a north base line or meridian. For example, for reference point i with the latitude ${\varphi }_i$ and the longitude ${\eta }_i$, the azimuth of point j (${\varphi }_j$, ${\eta }_j$) was determined using the following equation [45].

${\alpha }_{ij}=\arctan \left(\frac{\sin \left({\eta }_j-{\eta }_i\right)}{\cos {\varphi }_i\tan {\varphi }_j-\sin {\varphi }_i\cos \left({\eta }_j-{\eta }_i\right)}\right).(7)$

As Eq. 7 returned a value in the range ($-{180}^{\circ }$,${180}^{\circ }$), the result was normalized to a compass bearing in the range ($0^{\circ }$, ${360}^{\circ }$). The transformed formula was as follows:

${\widehat{\alpha }}_{ij}=\left({\alpha }_{ij}+360\right)\%360,(8)$

where $\%$ is (floating point) modulo. Then, moving clockwise in a circle, the east, south, and west directions had azimuths ${90}^{\circ }$, ${180}^{\circ }$, and ${270}^{\circ }$, respectively.

4 Results

This section introduces the analysis results of the RMT algorithm, cross-correlation algorithm, and CCM algorithm. First, we statistically analyze the distribution of the direction and distance of the monitoring stations. Secondly, the RMT algorithm is used to calculate the association between the monitoring stations. Then, the correlation between the stations is analyzed using the cross-correlation algorithm. Finally, it shows the changes of CCM causality between different sites in different directions and distances.

4.1 Empirical Statistical Characteristics

4.1.1 Distribution of Azimuth α

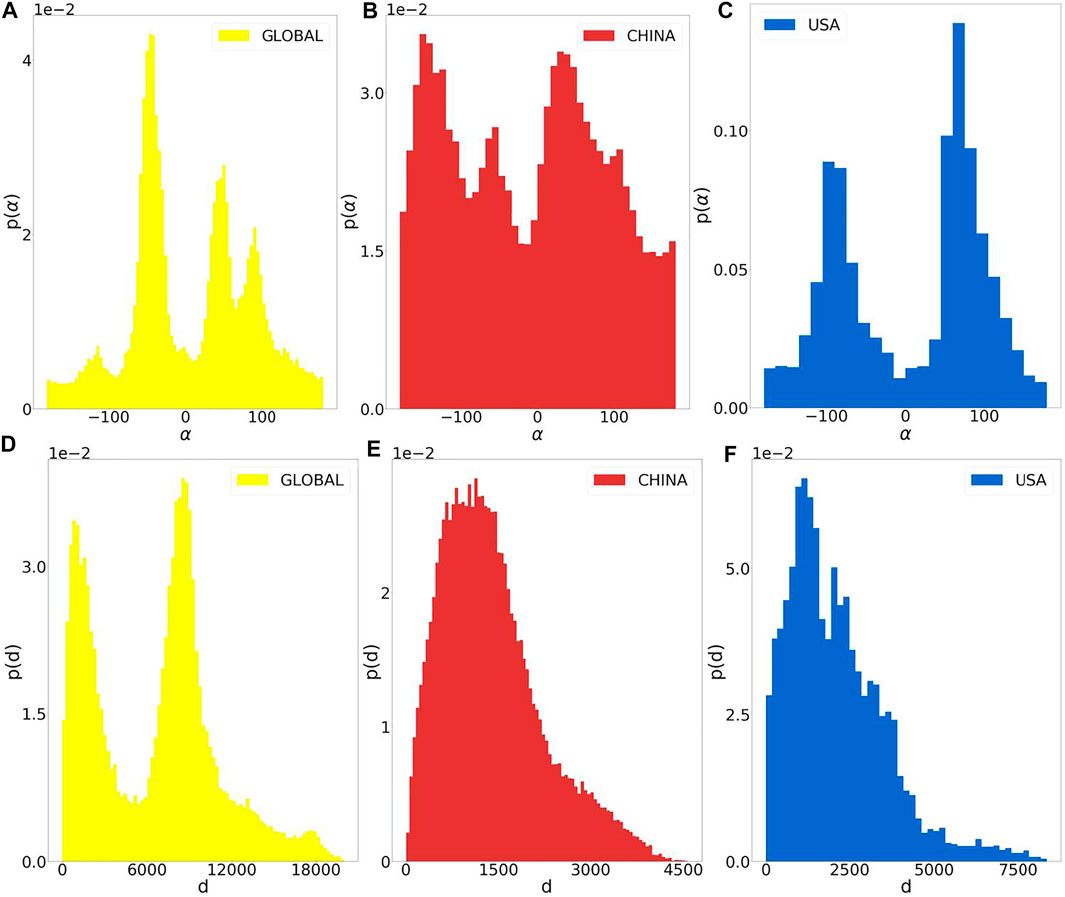
As aforementioned, one of the main aims of this work was to study correlations and causalities between $P{M}_{2.5}$ monitoring station data sequences in different directions. Therefore, the distribution of $P{M}_{2.5}$ monitoring site directions was significant. This section discusses the distribution of the azimuth α. As can be seen in Figures 1A–C, the azimuth α distribution for the three different data sets (Global, China and the United States) had peaked at different values of α. Figure 1A reports the four main peaks for α in the global data, which was the largest dataset at around ${45}^{\circ }$. Most neighbors were located in the northwest section of the region. Similarly, many neighbors were located in the east ($\approx {90}^{\circ }$), northeast ($\approx {60}^{\circ }$), and southwest ($\approx -{110}^{\circ }$) sections.

FIGURE 1

FIGURE 1. The distribution of azimuth α and distance d. (A) shows the distribution of Azimuth a for the global dataset, (B) shows the distribution of the Chinese data set, and (C) shows the distribution of the American data set. (D) presents the distribution of distance d for the global station; (E) presents the distribution for the Chinese station, and (F) presents the distribution for the American station.

Additionally, Figure 1B shows that cities neighboring each other in China were generally distributed in the northeast and southwest directions of the city. Further, Figure 1C demonstrates that the neighboring cities in the $USA$ United States were generally located to the east and west. These results were in agreement with the distributions of urban belts globally, in China, and in the United States. It should, however, be noted that most of the $P{M}_{2.5}$ detection sites were located in urban, i.e., densely populated areas; $P{M}_{2.5}$ monitoring in non-urban or sparsely populated areas was needed. Nonetheless, this study’s examination of α distribution diversity provided an understanding of the influence of α on the associations, correlations and causalities of $P{M}_{2.5}$ sequences. These results help to understand the distribution of the direction as a whole and avoid the deviation of the conclusion caused by the statistical differences of the direction in the subsequent data analysis.

4.1.2 Distribution of Distance d

To study trends regarding correlations and causalities between $P{M}_{2.5}$ sites and the distances between the monitored locations, the distance distributions of the sites were needed. Figures 1D,E illustrate these distributions with distance d for the three different data sets; it was found that there were peaks for different values of d. The distance distribution for the global data set had two peaks, while the distance distributions for the Chinese and American data sets had only one peak each. The two peaks noted in the global site distribution (Figure 1D) suggested that the monitoring sites were distributed throughout two relatively concentrated places. In contrast, the single-peak distributions of China and the United States (Figures 1E,F) showed that the monitoring sites were relatively concentrated and closely connected. Nevertheless, these distributions were not perfectly bimodal or normal. One reason for this is that the distributions of the monitoring sites conformed to non-uniform population distributions. These results help to understand the distance distribution of the monitoring stations, and at the same time avoid the deviation of the conclusion caused by the difference in distance distribution in the subsequent data analysis.

4.2 Random Matrix Theory

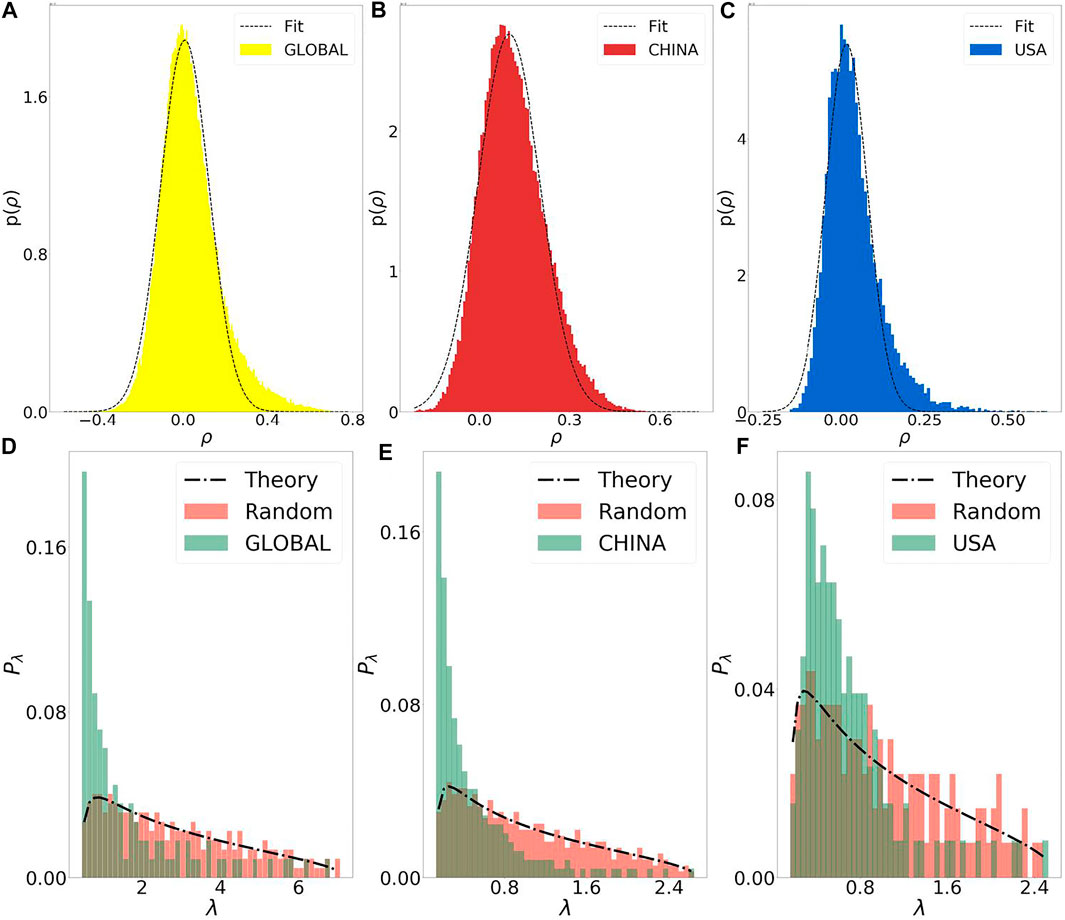
The RMT was helpful for comparing the properties of a null hypothesis purely random matrix (a strictly independent and identically distributed random time series) to those of the empirical correlation matrix C. Deviations from the purely random matrix could suggest the presence of underlying interactions [37, 38]. The RMT method was thus used to study the statistical properties of C in regards to the cross correlations of $P{M}_{2.5}$ changes. Initially, the elements of C were from Eq. 1 when $\tau =0$; then, they degenerated into Pearson’s correlation coefficient ρ from a two-time series. Figures 2A–C demonstrates the distribution of ρ for the global, China and United States data sets, respectively. The means, $\overline{\rho }$s, and standard deviations, σs, of the three distributions were as follows: $\overline{\rho }\approx 0.04$ and $\sigma =0.14$ for global sites; $\overline{\rho }\approx 0.11$ and $\sigma =0.11$ for the Chinese sites; and $\overline{\rho }\approx 0.04$ and $\sigma =0.08$ for the American sites. Thus, a clear deviation could be seen between the distribution of ρ and the curve fit by the normal distribution. These results indicated that the $P{M}_{2.5}$ time series associations for the data were not completely random [37, 38]. Future research should investigate the causes of these non-random associations, such as whether they were affected by climatic conditions. These non-normal distributions suggested the existence of non-trivial relationships between detection sites.

FIGURE 2

FIGURE 2. The statistical properties of the cross correlation matrix C for the $P{M}_{2.5}$ time series. (A) presents the distributions of ρ ($\tau =0$) for the global data, (B) presents the distributions for the Chinese data, and (C) presents the distributions for the American data, respectively. In (D–F), the green and red bars represent the probability distributions of the eigenvalues from the real data and the random series, respectively. The black dashed-dotted line is the theoretical result of Eq. 4.

As aforementioned, C was diagonalized to obtain λ eigenvalues. Finally, the distributions of the eigenvalues from the empirical time series were considered in regards to the finite strictly independent and identically distributed random time series. Figures 2D–F represent the distributions of the eigenvalues of real (green bar) and random (red bar) time series globally (d), for China (e), and for the United States (f) with the length $L_d$ (see Table 1). As can be seen, there were dramatic differences between the random series and the real $P{M}_{2.5}$ time series. The results are qualitatively similar to those of earlier studies about the global crude oil market and the global stock market, in which they observed that the largest eigenvalue reflects the collective effect of the global market, the second to fifth largest eigenvalues can distinguish six clusters, and the smaller eigenvalues portray the time series pair with the largest correlation coefficient [46, 47].

Moreover, the RMT predictions indicated that the distributions of the eigenvalues should follow the black dash line, which shows a distinct deviation from the real $P{M}_{2.5}$ time series but it is in good agreement with mimic random series. This result indicates that there are deviations in the eigenvalue distributions of the correlation matrix from the empirical data from purely random time series, implying that $P{M}_{2.5}$ time series are not purely random but with a finite amount of association. These findings were consistent with results obtained by examining the distribution of ρ, as shown in Figures 2A–C. However, this work represented only a preliminary attempt to identify the associations of real $P{M}_{2.5}$ time series. The actual relationship may be more complex, and the underlying mechanism of the associations was not within the scope of the RMT. This indicates that there is a non-random association between $P{M}_{2.5}$ sites, suggesting that there is some association between our $P{M}_{2.5}$ sequences, for example, the correlation changes with distance [17–21]. Furthermore, future research should focus on the time-lag cross-correlations RMT, because this method focuses on the magnitudes of the sequence, so that the method can quantitatively mine the long-range collective movements hidden behind the short-range correlation features [48].

4.3 Cross-Correlation Analysis

4.3.1 Illustration of Cross-Correlation

To characterize the transport dynamics of $P{M}_{2.5}$, this study aimed to determine the various hidden relationships between the distinct time-series measurement nodes. A straightforward method was used: cross-correlation. It had been used in research on pollution transports to detect Rossby Waves, teleconnection paths, and El Ni$\tilde{n}$o impacts [18–20]. Relationships depended on distance, and with the growth of distance, relationship values followed some specific features (e.g., monotonic decreases or increases to relation values, distances that showed concentration values, and more). To understand the relationships between distances (radial) and angles (azimuth αs) from a site (i.e., a pole or reference point), the polar coordinate system was employed (see Methods). For example, given the $P{M}_{2.5}$ time series recorded from a large number of monitoring stations (nodes) in a given geographical region, a distance and azimuthal angle could be calculated for each nodal pair. The value of the correlation could then be represented in terms of color in the polar coordinates for distance and angle.

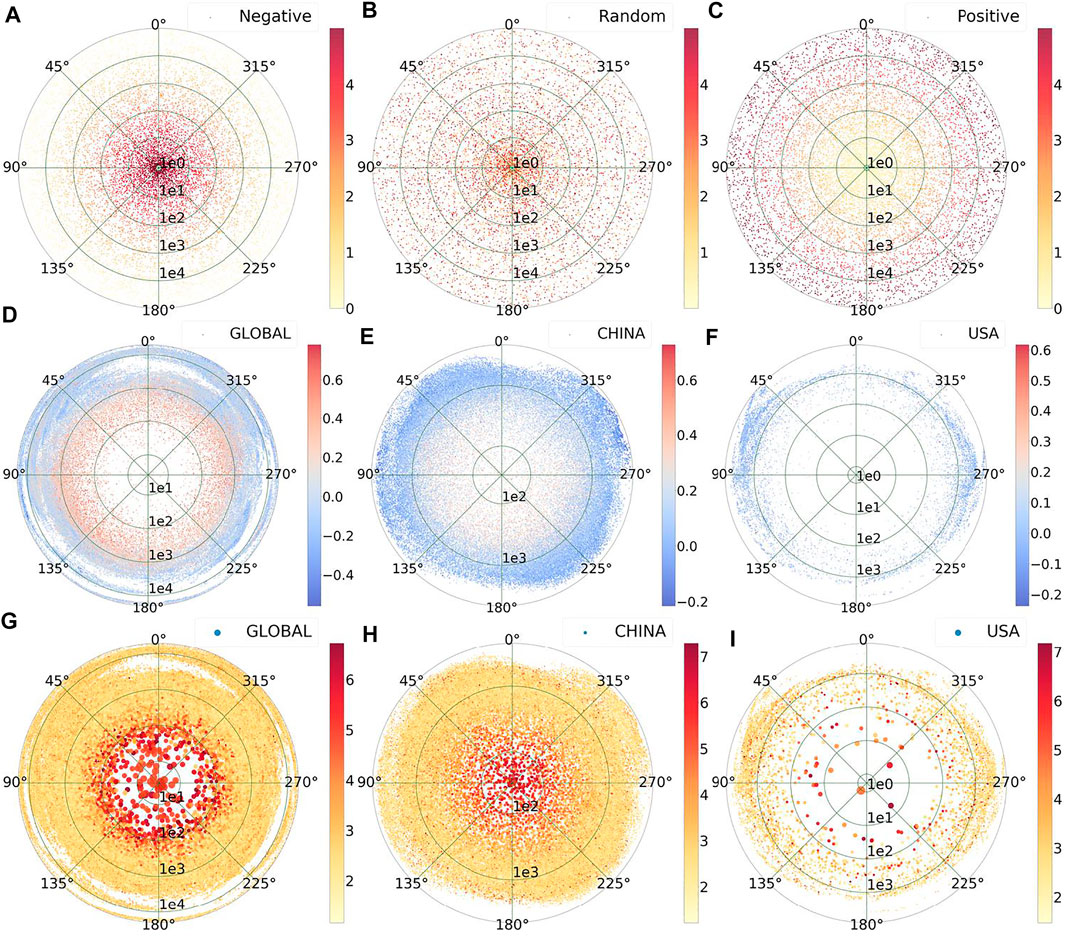
Initially, it was demonstrated that cross-correlation was associated with distance, as shown in panels $\left(a\right)$, $\left(b\right)$ and $\left(c\right)$ of Figure 3. Further, Figure 3A was a representative case in which correlation decreased with distance, regardless of direction. Finally, Figure 3B showed correlations that were random in regards to both distance and direction, and could have been a result of a completely random time series. In contrast, Figure 3C revealed that as the distance increased, the correlations between the stations became increasingly stronger but did not suggest differences in regards to direction. These figures thus indicated the different types of relationships between distance and cross-correlation.

FIGURE 3

FIGURE 3. The correlations and polar coordinates for $P{M}_{2.5}$ cross correlations globally, in China, and in the USA. (A) shows that cross correlations decreased with distance, regardless of direction; correlation strength is represented by the color of the bar. (B) shows the cross correlation distributions for the random time series; a random relationship was present between cross correlation and distance. (C) shows that cross-correlations increased with distance, regardless of direction; correlation strength is represented by the color of the bar. (D–F) show Pearson’s correlation coefficient ρ for all possible nodal pairs worldwide, in China, and the United States, respectively; distance is plotted on a logarithmic scale. Finally, (G–I) show the cross correlation $W_{max}$ for all possible nodal pairs worldwide, in China, and in the United States, respectively. Angles indicate directions between pairs of nodes, and radii indicate distances between pairs of nodes on a logarithmic scale. Dot colors show relationship values.

4.3.2 Pearson’s Correlation Coefficient ρ in Polar Coordinates

As aforementioned, one aim of this study was to detect variations in correlations between different sites with distance d and direction $\widehat{\alpha }$ (see Methods). Pearson’s correlation coefficient was a classic method of measuring a correlation between two sequences. Using the method, a distribution was thus obtained for Pearson’s correlation coefficients (ρ) for the three different data sets in the polar coordinate system $\left(d,\widehat{\alpha }\right)$. According to Figure 3D, the global data had a clear anti-correlation between Pearson’s correlation coefficient ρ and distance d; that is, the shorter the distance, the stronger the correlation. However, Pearson’s correlation coefficient ρ did not have significant differences in regards to the different directions, $\widehat{\alpha }$. Similar results were observed for both China and the United States, as shown in Figures 3E,F. However, the anti-correlation characteristics of ρ and d for the United States and China data were not as apparent as those in the global data, which may have been due to a relatively small number of observation stations in the United States and China. In the future, more sites and further detailed data are needed to study the relationships between ρ, $\widehat{\alpha }$, and d. This result, on a larger scale and more source data, validates the inverse correlation between $P{M}_{2.5}$ sequences and distances found in previous studies [9].

4.3.3 Cross-Correlation of $W_{max}$ in Polar Coordinates

In recent climate network models articulated to study the spatiotemporal behavior of the climate system, nodes denote geographical coordinate sites and a link between a pair of nodes is defined by the cross-correlation and mutual information between the time series from the two nodes [17–20]. Following this approach, one related type of cross-correlation, denoted as $W_{max}$ (see Methods) was calculated: so-called positive link weights between $P{M}_{2.5}$ recordings and pairs of nodes for the $L_h$ time series. Detailed information on the ($L_h$) data is shown in Table 1 and the Methods section.

As aforementioned, one goal of this study was to determine whether there were long-range correlations between the $P{M}_{2.5}$ recordings from the different sites. To accomplish this goal, a polar representation of cross-correlation was used. Specifically, for any nodal pair, the distance d and the azimuthal angle $\widehat{\alpha }$ could be defined (e.g., the zero angle $0^{\circ }$ meant that one node was exactly north of another node, and ${90}^{\circ }$ indicated that one node was east of another node). The correlation between the nodal pair was then color coded and represented in the polar coordinates $\left(d,\widehat{\alpha }\right)$.

In Figure 3G and in regards to worldwide $P{M}_{2.5}$s, $W_{max}$ correlation values were represented by color-coded dots in the polar coordinates. Larger values were noted for the positive link weight $W_{\max }$ at short distances (fewer than hundreds of km). Small $W_{\max }$ values were distributed approximately uniformly at larger distances and in other directions. This phenomenon was in agreement with climate network results and was called the proximity (distance) effect [18–20]. Namely, pairs of sites close to each other (fewer than 2,000 km apart) were often strongly positively correlated [18, 21].

However, there were no long-range correlations for the $P{M}_{2.5}$ time series. Similar results were obtained for the China and American $P{M}_{2.5}$s, as shown in Figures 3H,I, respectively. While this was not ideal, a few points had the large positive link weight $W_{\max }$ distributed across a long-distance range. The reasons for these outliers were not the focus of this paper, but future research should investigate these anomalies with more detailed data. The phenomenon implied that $P{M}_{2.5}$ could not transmit at long ranges. Nonetheless, these results did not seem to depend on the length of the time series, insofar as it was reasonable, as shown in Figures 3G–I for the respective data sets. Moreover, the results indicated only short-range correlations and a lack of long-range correlations, which suggested that $P{M}_{2.5}$ could transport across only short distances (fewer than hundreds of km) [9]. This result was in sharp contrast, for example, to climate phenomena in teleconnections [11, 12] and temperature [18–20]. These results indicate that the $P{M}_{2.5}$ sequence and the temperature etc. meteorological sequences are different, and there is no teleconnections. Furthermore, our results only display the lack of long-range correlation between different sequences in the spatial distance range, but a large number of previous studies including detrended fluctions analysis (DFA), Detrended Cross-Correlation Analysis (DCCA) and multifractal detrended fluctuation analysis (MFDFA) have observed that there is a long-range correlation in the time dimension [49–51]. Therefore, future research should pay attention to the correlation of $P{M}_{2.5}$ sequence at the time dimension, so as to be able to deeply understand the trend of $P{M}_{2.5}$. Moreover, future research should focus more on the deeper causes of different transmission phenomena, for example, the difference in transmission media [52–55].

4.4 Causality Analysis

4.4.1 The Distribution of Causation $\mathit{\Delta }$

Although previous research expressed non-trivial correlations between monitoring stations in regards to distance, the detection of causality between stations had always been a problem of great theoretical significance and practical value [39–42]. In general, causation and correlation are not equivalent to each other: two time series can be highly correlated but without any causal relation [27]. However, this study applied CCM to the $P{M}_{2.5}$ data to determine the existence of causal relationships between the time series and the different geographical locations [31]. This method is suitable for nonlinear systems in the presence of noise [31, 56].

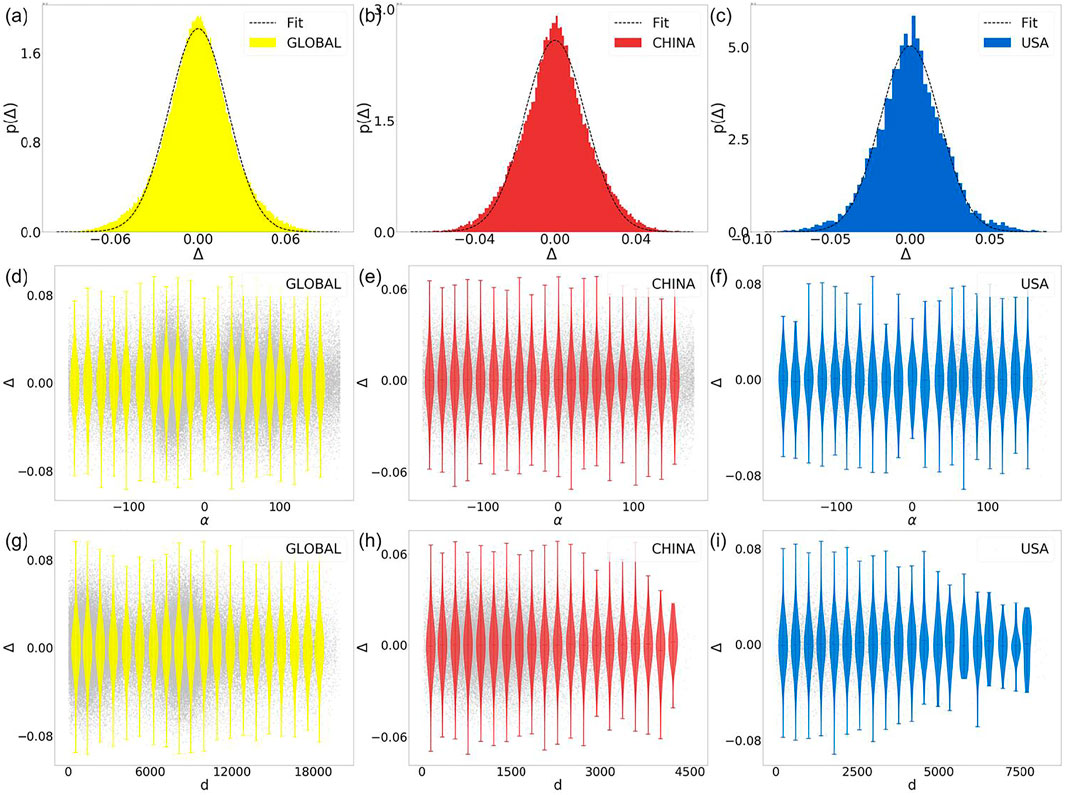
In particular, for a nodal pair, non-zero $\Delta$ value could indicate a causal relationship between the $P{M}_{2.5}$ time series. First, the relative strength of causation $\Delta$ was computed (see Methods) for the three datasets; their representative distributions can be seen in Figures 4A–C. These distributions showed that the causation $\Delta$ distribution fit the data well in regards to normal distributions of the global, Chinese, and American data, respectively. It was found that the means, $\overline{\Delta }$s, and standard deviations, $\overline{\sigma }$s, of the three distributions were as follows. $\overline{\Delta }\approx 0.00$ and $\sigma =0.02$ for the global data; $\overline{\Delta }\approx 0.00$ and $\sigma =0.02$ for the Chinese data; and $\overline{\Delta }\approx 0.00$ and $\sigma =0.02$ for the American data. These perfect normal distributions suggested that there may be no significant causality between the $P{M}_{2.5}$ sequences at the collective level. Although no clear causality was observed at the collective level, this is a useful exploration of the causal-effect in the $P{M}_{2.5}$ sequence data. Causality detection would have important roles in future research on climate and environmental policies [28–30].

FIGURE 4

FIGURE 4. The causality analysis of the $P{M}_{2.5}$ time series. (A–C) show the $\Delta$ distributions for the global, Chinese, and American stations, respectively. The bar graph shows the distribution characteristics of the real data, and the black dotted line shows the normal fit of the curve. (D–F) show azimuth α in comparison to $\Delta$ regarding the global, China, and American data, respectively. Finally, (G–I) compare distance d to $\text{Δ}$ regarding the global, Chinese, and American data, respectively. The violin plots present the overall distribution characteristics of each data group. The upper and lower ends are the top and the bottom of each violin’s distribution, and the middle lines are the means of each violin’s distribution. The gray dots are a scatterplot of the original data.

4.4.2 Causation $\mathit{\Delta }$ in Comparison to Azimuth α

In order to deeply understand the relationship between causation $\Delta$ and direction α between $P{M}_{2.5}$ monitoring sites, we examined the trend of causality with the directions of the sites. It is apparent that in all three data, causality is basically symmetrically distributed in different directions. In particular, Figure 4D shows that the mean value of $\Delta$ followed the straight line $\Delta =0$. This result indicated that at the collective level, the causalities and directions between the different $P{M}_{2.5}$ stations were irrelevant. The dense distribution in some directions, e.g. $\alpha \approx 45$ in Figure 4D was consistent with the distribution characteristics in Figure 1A. Additionally, Figure 4E,F indicated similar relationships concerning China and the United States. It was thus concluded that there is no apparent causal-effect trend among the different sites in the different directions. It is apparent that one cannot simply judge the causality of $P{M}_{2.5}$ observation sites based on their direction.

4.4.3 Causation $\mathit{\Delta }$ in Comparison to Distance d

As aforementioned, a non-trivial correlation was present between the monitoring sites as distance d changed. This study thus investigated causality trends between the monitoring sites and distance d. Figure 4G revealed that as distance d changed, causation $\Delta$ was almost evenly distributed on both sides of the central $\Delta =0$ axis. This result clearly indicated that at the collective level, there were no relations between causality and distance d. A similar result was observed in both cases from China (Figure 4H) and the United States (Figure 4I). Although no consistent causality was observed at the collect level, a relative causality seemed likely at the individual level. Future research should therefore investigate this at the individual level, particularly the impact of $P{M}_{2.5}$ sequence length. This result indicates that there is no definite conclusion about the causality and distance between $P{M}_{2.5}$ monitoring stations, and they should be studied separately according to the different situations of $P{M}_{2.5}$ stations.

5 Conclusion

With the development of data collection technology, more and more studies focus on $P{M}_{2.5}$ sequence, some studies focus on the impact of $P{M}_{2.5}$ sequence on climate and meteorology in some places and periods, and others focus on the correlation of $P{M}_{2.5}$ sequence and distance. However, these studies rarely focus on the various relationships of $P{M}_{2.5}$ in a large-scale spatiotemporal range, not to mention the causal-effect between $P{M}_{2.5}$ sequences. We have conducted a study of the relations of $P{M}_{2.5}$ time series based purely on massive data. Our statistical and nonlinear analysis of worldwide $P{M}_{2.5}$ time series over the period of one year leads to a number of findings. Firstly, a random matrix based analysis indicates that the spatiotemporal $P{M}_{2.5}$ data are not purely random, but with associations. Secondly, correlation among the $P{M}_{2.5}$ time series exists over a short distance, which is consistent with the first finding. However, there is lack of consistent Long-range cross correlation, suggesting that transport of $P{M}_{2.5}$ over long distance is complex and changeable. Thirdly, since correlation does not imply causation in general, a causality analysis is necessary to assess the likelihood of Long-range transport, which we carry out by employing the nonlinear dynamics based CCM method. The analysis reveals an unequivocal absence of consistent indication of transport of $P{M}_{2.5}$ over long distance (e.g., over 1,000 km). The simultaneous absence of consistent long-range correlation and statistical causation leads to the conclusion that transport of $P{M}_{2.5}$ over long distance is sophisticated and varied.

It should be noted that these analyses were only statistical. However, for numerous pairs across a significant distance, a lack of consistent and definitive casual relations was found (as shown in Figures 4D–I. That is, over the given distance, the direction of causal interaction appeared completely random, and this implied a lack of causation in general. These findings extended prior work about $P{M}_{2.5}$ series to a large spatial-temporal scale with causality analysis [30]. Moreover, an absence of consistent long-range transport was found for three different data sets, both with cross-correlation analyses and causality detection methods. This finding is promising, however, it should be explored using other association and causal analyses as well as different data sets.

Generally, $P{M}_{2.5}$ pollution affects only a short distance (no more than several hundred km); policies should be changed to address this. However, while this study was an empirical analysis of direct $P{M}_{2.5}$ time series collected from various monitoring stations, it was only a preliminary attempt to identify the associations, correlations and causal effects of real $P{M}_{2.5}$ time series. Actual relationships may be more complex, and the underlying mechanisms that cause these relationships were not within the scope of this study. Our results demonstrate that the random matrix theory can also play an important role in $P{M}_{2.5}$ sequences. Future research should pay more attention to the specific meaning of eigenvalues and their corresponding eigenvectors [46, 47]. Meanwhile, the research on magnitude based on the time-lag cross-correlations RMT is also a very promising direction [48]. In addition, future research should focus on the correlation of $P{M}_{2.5}$ in the time dimension [49–51]. Moreover, this analysis did not investigate other pollutants, such as $C{O}_X$, $N{O}_X$, and $S{O}_X$, etc [10], nor did it consider meteorological variables, such as temperature, relative humidity, precipitation, cloud cover, wind speed, and wind direction [57]. Additionally, it did not conduct mineralogical composition analyses [52–55], Total Ozone Mapping Spectrometers [54], or climate models and biogeochemical interactions [8]. Further research should investigate these topics and examine the role of $P{M}_{2.5}$ in the spread of disease, especially concerning the recent impact the coronavirus (COVID-19) has had on the world [58]. Nonetheless, this research is significant as a basis for these future researches.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: http://berkeleyearth.org/data/, https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/24826, https://www.epa.gov/outdoor-air-quality-data.

Author Contributions

Devised the research project: Z-DZ, NZ, and NY; Performed numerical simulations: Z-DZ; Analyzed the results: Z-DZ, NY, and NZ; Wrote the paper: Z-DZ.

Funding

This work is partially supported by the Scientific Research Foundation of Shantou University (Grant No. NTF19015), the 2020 Li Ka Shing Foundation Cross-Disciplinary Research (Grant No. 2020LKSFG09D), the Guangdong Basic and Applied Basic Research Foundation (Grant No. 2021A1515012294), the National Key Research and Development Program of China (Grant No. 2016YFA0602503) and National Natural Science Foundation of China (No.62066048). The funders had no role in study design, data collection and analysis, decision to publish or preparation of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Buseck PR, Posfai M. Airborne Minerals and Related Aerosol Particles: Effects on Climate and the Environment. Proc Natl Acad Sci (1999) 96(7):3372–9. doi:10.1073/pnas.96.7.3372

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Samset BH. How Cleaner Air Changes the Climate. Science (2018) 360(6385):148–50. doi:10.1126/science.aat1723

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Matthews HD, Zickfeld K. Climate Response to Zeroed Emissions of Greenhouse Gases and Aerosols. Nat Clim Change (2012) 2:338–41. doi:10.1038/nclimate1424

CrossRef Full Text | Google Scholar

4.World Health Organization. WHO Methods and Data Sources for Global Causes of Death 20002012 (2014). Technical Paper. Global Health Estimates WHO/HIS/HSI/GHE/2014.7.

Google Scholar

5. Hoek G, Krishnan RM, Beelen R, Peters A, Ostro B, Brunekreef B, et al. Long-term Air Pollution Exposure and Cardio- Respiratory Mortality: a Review. Environ Health (2013) 12(1):43. doi:10.1186/1476-069x-12-43

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Heft-Neal S, Burney J, Bendavid E, Burke M. Robust Relationship between Air Quality and Infant Mortality in Africa. Nature (2018) 559:254. doi:10.1038/s41586-018-0263-3

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Evan AT, Vimont DJ, Heidinger AK, Kossin JP, Bennartz R. The Role of Aerosols in the Evolution of Tropical north atlantic Ocean Temperature Anomalies. Science (2009) 324(5928):778–81. doi:10.1126/science.1167404

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Booth BBB, Dunstone NJ, Halloran PR, Andrews T, Bellouin N. Aerosols Implicated as a Prime Driver of Twentieth-century north atlantic Climate Variability. Nature (2012) 484:228–32. doi:10.1038/nature10946

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Rohde RA, Muller RA. Air Pollution in china: Mapping of Concentrations and Sources. PLoS One (2015) 10(8):e0135749. doi:10.1371/journal.pone.0135749

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Dai YH, Zhou WX. Temporal and Spatial Correlation Patterns of Air Pollutants in Chinese Cities. PloS One (2017) 12(8):e0182724. doi:10.1371/journal.pone.0182724

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Bjerknes J. Atmospheric Teleconnections from the Equatorial Pacific1. Mon Wea Rev (1969) 97(3):163–72. doi:10.1175/1520-0493(1969)097<0163:atftep>2.3.co;2

CrossRef Full Text | Google Scholar

12. Wallace JM, Gutzler DS. Teleconnections in the Geopotential Height Field during the Northern Hemisphere winter. Mon Wea Rev (1981) 109(4):784–812. doi:10.1175/1520-0493(1981)109<0784:titghf>2.0.co;2

CrossRef Full Text | Google Scholar

13. Yu Y, Schleicher N, Norra S, Fricker M, Dietze V, Kaminski U, et al. Dynamics and Origin of PM2.5during a Three-Year Sampling Period in Beijing, China. J Environ Monit (2011) 13(2):334–46. doi:10.1039/c0em00467g

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Perrone MR, Becagli S, Garcia Orza JA, Vecchi R, Dinoi A, Udisti R, et al. The Impact of Long-Range-Transport on Pm1 and pm2.5 at a central Mediterranean Site. Atmos Environ (2013) 71:176–86. doi:10.1016/j.atmosenv.2013.02.006

CrossRef Full Text | Google Scholar

15. Kaneyasu N, Yamamoto S, Sato K, Takami A, Hayashi M, Hara K, et al. Impact of Long-Range Transport of Aerosols on the pm2.5 Composition at a Major Metropolitan Area in the Northern Kyushu Area of japan. Atmos Environ (2014) 97:416–25. doi:10.1016/j.atmosenv.2014.01.029

CrossRef Full Text | Google Scholar

16. Zhang Y, Chen D, Fan J, Havlin S, Chen X. Correlation and Scaling Behaviors of fine Particulate Matter (PM 2.5) Concentration in China. Epl (2018) 122(5):58003. doi:10.1209/0295-5075/122/58003

CrossRef Full Text | Google Scholar

17. Donges JF, Zou Y, Marwan N, Kurths J. The Backbone of the Climate Network. Europhys Lett (2009) 87(4):48007. doi:10.1209/0295-5075/87/48007

CrossRef Full Text | Google Scholar

18. Wang Y, Gozolchiani A, Ashkenazy Y, Berezin Y, Guez O, Havlin S. Dominant Imprint of Rossby Waves in the Climate Network. Phys Rev Lett (2013) 111(13):138501. doi:10.1103/physrevlett.111.138501

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Zhou D, Gozolchiani A, Ashkenazy Y, Havlin S. Teleconnection Paths via Climate Network Direct Link Detection. Phys Rev Lett (2015) 115(26):268501. doi:10.1103/physrevlett.115.268501

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Fan J, Meng J, Ashkenazy Y, Havlin S, Schellnhuber HJ. Network Analysis Reveals Strongly Localized Impacts of El Niño. Proc Natl Acad Sci USA (2017) 114(29):7543–8. doi:10.1073/pnas.1701214114

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Berezin Y, Gozolchiani A, Guez O, Havlin S. Stability of Climate Networks with Time. Sci Rep (2012) 2(1):666. doi:10.1038/srep00666

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Fan J, Meng J, Ashkenazy Y, Havlin S, Schellnhuber HJ. Climate Network Percolation Reveals the Expansion and Weakening of the Tropical Component under Global Warming. Pro Nat Acad Sci USA (2018) 115(52):12128–34. doi:10.1073/pnas.1811068115

CrossRef Full Text | Google Scholar

23. Zhang Y, Fan J, Chen X, Ashkenazy Y, Havlin S. Significant Impact of Rossby Waves on Air Pollution Detected by Network Analysis. Geophys Res Lett (2019) 46(21):12476–85. doi:10.1029/2019gl084649

CrossRef Full Text | Google Scholar

24. Ying N, Zhou D, Chen Q, Ye Q, Han Z. Long-term Link Detection in the Co2 Concentration Climate Network. J Clean Prod (2019) 208:1403–8. doi:10.1016/j.jclepro.2018.10.093

CrossRef Full Text | Google Scholar

25. Ying N, Zhou D, Han Z, Chen Q, Ye Q, Xue Z. Rossby Waves Detection in the Co2 and Temperature Multilayer Climate Network. Geophys Res Lett (2020) 47(2):2019. doi:10.1029/2019gl086507

CrossRef Full Text | Google Scholar

26. Ying N, Zhou D, Han Z, Chen Q, Ye Q, Xue Z, et al. Climate Networks Suggest Rossby-Waves-Related CO2 Concentrations to Surface Air Temperature. Epl (2020) 132(1):19001. doi:10.1209/0295-5075/132/19001

CrossRef Full Text | Google Scholar

27. Altman N, Krzywinski M. Association, Correlation and Causation. Nat Methods (2015) 12(10):899–900. doi:10.1038/nmeth.3587

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Zhang DD, Lee HF, Wang C, Li B, Pei Q, Zhang J, et al. The Causality Analysis of Climate Change and Large-Scale Human Crisis. Proc Natl Acad Sci (2011) 108(42):17296–301. doi:10.1073/pnas.1104268108

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Driscoll CT, Buonocore JJ, Levy JI, Lambert KF, Burtraw D, Reid SB, et al. Us Power Plant Carbon Standards and Clean Air and Health Co-benefits. Nat Clim Change (2015) 5:535–40. doi:10.1038/nclimate2598

CrossRef Full Text | Google Scholar

30. Huang Y, Franzke CLE, Yuan N, Fu Z. Systematic Identification of Causal Relations in High-Dimensional Chaotic Systems: Application to Stratosphere-Troposphere Coupling. Clim Dynam (2020) 55(9):2469–81. doi:10.1007/s00382-020-05394-0

CrossRef Full Text | Google Scholar

31. Sugihara G, May R, Ye H, Hsieh C-h., Deyle E, Fogarty M, et al. Detecting Causality in Complex Ecosystems. Science (2012) 338(6106):496–500. doi:10.1126/science.1227079

PubMed Abstract | CrossRef Full Text | Google Scholar

32.Global. Available at: http://berkeleyearth.org/data/ (Accessed Feb 18, 2018).

33.China. Available at: https://dataverse.harvard.edu/dataset.xhtml?persistentId=10.7910/DVN/24826 (Accessed Jan 8, 2018).

34.U.S.A. Available at: https://www.epa.gov/outdoor-air-quality-data (Accessed Jan 28, 2018).

35. Wigner EP. On a Class of Analytic Functions from the Quantum Theory of Collisions. Ann Math (1951) 53(1):36–67. doi:10.2307/1969342

CrossRef Full Text | Google Scholar

36. Brody TA, Flores J, French JB, Mello PA, Pandey A, Wong SSM. Random-matrix Physics: Spectrum and Strength Fluctuations. Rev Mod Phys (1981) 53(3):385–479. doi:10.1103/revmodphys.53.385

CrossRef Full Text | Google Scholar

37. Laloux L, Cizeau P, Bouchaud J-P, Potters M. Noise Dressing of Financial Correlation Matrices. Phys Rev Lett (1999) 83(7):1467–70. doi:10.1103/physrevlett.83.1467

CrossRef Full Text | Google Scholar

38. Plerou V, Gopikrishnan P, Rosenow B, Nunes Amaral LA, Stanley HE. Universal and Nonuniversal Properties of Cross Correlations in Financial Time Series. Phys Rev Lett (1999) 83(7):1471–4. doi:10.1103/physrevlett.83.1471

CrossRef Full Text | Google Scholar

39. Granger CWJ. Investigating Causal Relations by Econometric Models and Cross-Spectral Methods. Econometrica (1969) 37:424–38. doi:10.2307/1912791

CrossRef Full Text | Google Scholar

40. Pearl J, Glymour M, Jewell NP. Causal Inference in Statistics: A Primer. Hoboken, New Jersey: John Wiley & Sons (2016).

41. Meinshausen N, Hauser A, Mooij JM, Peters J, Versteeg P, Bühlmann P. Methods for Causal Inference from Gene Perturbation Experiments and Validation. Proc Natl Acad Sci USA (2016) 113(27):7361–8. doi:10.1073/pnas.1510493113

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Wiener N. The Theory of Prediction. In: Beckenbach, E. (Ed.), Modern Mathematics for Engineers (1956)New YorkMcGraw-Hill.

Google Scholar

43. Schreiber T. Measuring Information Transfer. Phys Rev Lett (2000) 85(2):461–4. doi:10.1103/physrevlett.85.461

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Takens F. Detecting Strange Attractors in Turbulence. New York, NY: Springer (1981). p. 366–81. doi:10.1007/bfb0091924

CrossRef Full Text

45. Snyder JP. Map Projections: A Working Manual. Geological Survey (US) (1987). Available at: https://pubs.usgs.gov/pp/1395/report.pdf.USGS series, Professional Paper 1395 (Accessed June 25, 2021).

Google Scholar

46. Dai Y-H, Xie W-J, Jiang Z-Q, Jiang GJ, Zhou W-X. Correlation Structure and Principal Components in the Global Crude Oil Market. Empir Econ (2016) 51(4):1501–19. doi:10.1007/s00181-015-1057-1

CrossRef Full Text | Google Scholar

47. Song D-M, Tumminello M, Zhou W-X, Mantegna RN. Evolution of Worldwide Stock Markets, Correlation Structure, and Correlation-Based Graphs. Phys Rev E (2011) 84(2):026108. doi:10.1103/physreve.84.026108

CrossRef Full Text | Google Scholar

48. Podobnik B, Wang D, Horvatic D, Grosse I, Stanley HE. Time-lag Cross-Correlations in Collective Phenomena. Epl (2010) 90(6):68001. doi:10.1209/0295-5075/90/68001

CrossRef Full Text | Google Scholar

49. Peng C-K, Buldyrev SV, Havlin S, Simons M, Stanley HE, Goldberger AL. Mosaic Organization of Dna Nucleotides. Phys Rev E (1994) 49(2):1685–9. doi:10.1103/physreve.49.1685

CrossRef Full Text | Google Scholar

50. Podobnik B, Stanley HE. Detrended Cross-Correlation Analysis: A New Method for Analyzing Two Nonstationary Time Series. Phys Rev Lett (2008) 100:084102. doi:10.1103/PhysRevLett.100.084102

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Qin Y-H, Zhao Z-D, Cai S-M, Gao L, Stanley HE. Dual-induced Multifractality in Online Viewing Activity. Chaos (2018) 28(1):013114. doi:10.1063/1.5003100

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Duce RA, Unni CK, Ray BJ, Prospero JM, Merrill JT. Long-range Atmospheric Transport of Soil Dust from Asia to the Tropical north pacific: Temporal Variability. Science (1980) 209(4464):1522–4. doi:10.1126/science.209.4464.1522

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Prospero JM, Glaccum RA, Nees RT. Atmospheric Transport of Soil Dust from Africa to South america. Nature (1981) 289:570–2. doi:10.1038/289570a0

CrossRef Full Text | Google Scholar

54. Prospero JM. Long-range Transport of mineral Dust in the Global Atmosphere: Impact of African Dust on the Environment of the southeastern united states. Proc Natl Acad Sci (1999) 96(7):3396–403. doi:10.1073/pnas.96.7.3396

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Prospero JM, Lamb PJ. African Droughts and Dust Transport to the Caribbean: Climate Change Implications. Science (2003) 302(5647):1024–7. doi:10.1126/science.1089915

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Ye H, Sugihara G. Information Leverage in Interconnected Ecosystems: Overcoming the Curse of Dimensionality. Science (2016) 353(6302):922–5. doi:10.1126/science.aag0863

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Tai APK, Mickley LJ, Jacob DJ. Correlations between fine Particulate Matter (PM2.5) and Meteorological Variables in the United States: Implications for the Sensitivity of PM2.5 to Climate Change. Atmos Environ (2010) 44(32):3976–84. doi:10.1016/j.atmosenv.2010.06.060

CrossRef Full Text | Google Scholar

58. Zhang R, Li Y, Zhang AL, Wang Y, Molina MJ. Identifying Airborne Transmission as the Dominant Route for the Spread of Covid-19. Proc Natl Acad Sci USA (2020) 117(26):14857–63. doi:10.1073/pnas.2009637117

PubMed Abstract | CrossRef Full Text | Google Scholar