
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 03 January 2022
Sec. Interdisciplinary Physics
Volume 9 - 2021 | https://doi.org/10.3389/fphy.2021.665828
This article is part of the Research TopicImpacts of Global Warming on Ecology and Meteorology and the Related Physical Mechanisms, Evaluation and PredictionView all 18 articles
How to improve the subseasonal forecast skills of dynamic models has always been an important issue in atmospheric science and service. This study proposes a new dynamical-statistical forecast method and a stable components dynamic statistical forecast (STsDSF) for subseasonal outgoing long-wave radiation (OLR) over the tropical Pacific region in January-February from 2004 to 2008. Compared with 11 advanced multi-model ensemble (MME) daily forecasts, the STsDSF model was able to capture the change characteristics of OLR better when the lead time was beyond 30 days in 2005 and 2006. The average pattern correlation coefficients (PCC) of STsDSF are 0.24 and 0.16 in 2005 and 2006, while MME is 0.10 and 0.05, respectively. In addition, the average value of PCC of the STsDSF model in five years is higher than MME in 7–11 pentads. Although both the STsDSF model and MME show a similar temporal correlation coefficient (TCC) pattern over the tropical Pacific region, the STsDSF model error grows more slowly than the MME error during 8–12 pentads in January 2005. This phenomenon demonstrates that STsDSF can reduce dynamical model error in some situations. According to the comparison of subseasonal forecasts between STsDSF and MME in five years, STsDSF model skill depends strictly on the predictability of the dynamical model. The STsDSF model shows some advantages when the dynamical model could not forecast well above a certain level. In this study, the STsDSF model can be used as an effective reference for subseasonal forecast and could feasibly be used in real-time forecast business in the future.
The atmosphere is a complex nonlinear giant system with external forcings and internal dissipations. Under the impact of external forcing factors, such as the sun, ocean, land, and human activities, a series of physical and chemical changes and interactions occur in the atmosphere, which brings great difficulties to weather and climate prediction [1–3]. A small error can be dramatically amplified over time, which allows for a predictable limit on the weather forecast. Moreover, some studies suggest that the chaotic effects could prove the predictable limits of weather systems in theoretical ways [4, 5]. It is now accepted that the upper limit on the predictability of actual weather systems is approximately 2 weeks [6, 7]. However, studies have shown that the predictability of some large-scale components is significantly higher than that of small-scale components, which could be more than 2 weeks [8, 9]. At the same time, some low frequency weather systems with a duration of more than 2 weeks were found in the observations.
Based on the theory of predictability, the prediction error of dynamic models mainly results from the following aspects: the initial error of observation data, the error caused by the set scheme in the dynamic model simulation, and the systematic error of the model in the single variable simulation [10]. The initial error of the observation data is mainly caused by the inaccuracy of the observation value and the uneven distribution of observation stations. The error of set scheme in dynamic mode simulations is mainly caused by the numerical set in order to deduct the random error. The systematic error of the single variable simulation is mainly caused by the performance of the model itself, such as the model resolution, parameterization scheme for the physical processes, and the calculations of the discrete numerical difference scheme [11–13]. The reasons described above limit the forecast accuracy of dynamic models and are the main obstacles to the further improvement of the subseasonal forecast.
Given the shortcomings of error growth theory based on the linear framework, Chen et al. and Ding et al. developed a new theory of nonlinear error growth to measure the predictability of atmosphere and the nonlinear local Lyapunov exponent (NLLE), revealing the temporal and spatial distribution of the predictable duration in different weather and climate variables [14, 15]. Theoretical studies show that climate variables are composed of climate signals and noises, and climate signal is mainly affected by the external boundary conditions of the climate system [16, 17]. For example, the heat capacity of subsurface water during an El Niño event can significantly enhance the East Pacific tropical cyclone [18]. When the proportion of climate signals in variables is large enough to overcome the destructive effects of noises, climate anomalies may show a certain degree of predictability [19]. Observational studies show that there are some slow changing processes in atmospheric evolution above the level of weather noises, these slow changing processes are associated with large-scale atmospheric motions and a timescale of several weeks, which is much longer than that estimated by nonlinear hydrodynamics [20–22]. There are still some predictable meteorological characteristics in the subseasonal time scale, and the atmospheric stable component can be robustly predicted [23, 24].
Although the development of extended period forecast skills is remarkable, its technical difficulty can not be covered up. On the one hand, it is difficult to use commonly used methods to predict the intensity and duration of the weather process objectively. On the other hand, the ability of the daily weather forecast depends on the increase of initial error by chaotic motion in the atmosphere [25, 26]. According to the chaotic characteristics of the atmospheric system, Chou et al. expounded the extraction method of the predictable components in the 10–30 days extended period, and further suggest that different strategies and methods should be adopted for predictable components and random components [27]. However, if each time step needs to be checked in the actual forecast process, the computation expenses will be very large. Ren et al. proposed a similar evolution method, assuming that similar initial conditions have similar prediction errors in the allowable time range [28]. By synthesizing and analyzing the prediction errors of historical similar initial conditions, the current prediction errors are estimated. The calculations are greatly simplified and more easily incorporated into numerical prediction models. Zheng et al. discussed the properties of predictable components in the extension period and their application in numerical models [29].
Based on predictable components theory, the model subseasonal forecasts can be divided into two parts: the predictable component and the random component. The numerical model error can also be reduced in the process of integration by using historical observation data. Therefore, it is obvious that the method exists on model dependence. For different numerical models, the model performance is different, and the definition and extraction of predictable components are different too. Focusing on the prediction of weather or climate at different time and spatial scales, the stable components should be especially investigated. To improve subseasonal process diagnosis and prediction skills, it is important to grasp the main characteristics of the subseasonal stable component [30, 31]. Under the same initial and exogenous forcing characteristics, the atmospheric system with a large-space time scale is more predictable. Therefore, it is necessary to distinguish the stable components from atmospheric circulation on a subseasonal scale and analyze the properties and improve subseasonal prediction skills by using stable components [32, 33]. Moreover, because the extraction method of stable components is based on historical observation data instead of model data, it can overcome the shortcoming of model dependence.
Subseasonal precipitation prediction is one of the most important aspects of weather forecasting [34, 35]. The tropical area accounts for about half of the total global area, of which the ocean accounts for about 3/4. The solar radiation energy received in the tropical area is much more than that be reflected into space, which makes the tropical ocean a vital energy source for global atmospheric circulation movement [36, 37]. In addition, the tropical ocean is one of the most important water vapor sources for the global atmosphere [38, 39]. Due to the abundant water vapor contents in tropical marine areas, precipitation generation is closely related to atmospheric vertical convection intensity. The intensity of precipitation can be characterized by OLR in the tropics. If the subseasonal variability of OLR can be forecasted well, the tropical precipitation forecast skills will be robust [40, 41]. Therefore, this study mainly uses a dynamic statistical forecast model (STsDSF) to improve the subseasonal forecast skills of 11 advanced multi-model ensembles for OLR over the tropical Pacific region (140°E-100°W, 30°S-30°N) and discusses the predictability of STsDSF in January and February from 2004 to 2008. It proposes a new application of the dynamic-statistical method in subseasonal forecast.
The daily OLR data was published by the National Oceanic and Atmospheric Administration (NOAA) over the period from 1979 to 2008 with a horizontal resolution of 2.5° × 2.5° [42]. The external boundary conditional forcing of sea surface temperature (SST) is represented by Oceanic Niño Index (Niño 3.4), which is also published by NOAA.
The hindcast data of the dynamical model is from Intraseasonal Variability Hindcast Experiment (ISVHE), which is jointly supported by the Asian Pacific Climate Center (APCC), NOAA, Climate Variability and Predictability (CLIVAR) Asian-Australian Monsoon Panel, and some other organizations [43]. The model products of ISVHE have been studied at the predictability of intraseasonal variability as a whole [44, 45]. In total, ten one-tier hindcasts and one two-tier hindcast from ISVHE were used in this study, including the Australian Bureau of Meteorology (AOBM) coupled model, the coupled model of Euro-Mediterranean Center on Climate Change (CMCC), the European Centre for Medium-Range Weather Forecasts (ECMWF) model, the Geophysical Fluid Dynamics Laboratory (GFDL) model, the Japan Meteorological Agency (JMA) coupled model, the Japan Agency for Marine-Earth Science and Technology (JAMSTEC) model, the NCEP/Climate Prediction Center (CPC) coupled model, the Pusan National University (PNU) model, the Seoul National University (SNU) coupled model, University of Hawaii (UH)/International Pacific Research Center (IPRC) model, and the European Centre (EC) model [46–51]. The details of the model data and operation scheme are briefly shown in Table 1. Because the skill of MME is better than that of any single model in seasonal forecasting [52, 53], the improvement of STsDSF is mainly based on the MME forecast. In this study, five daily OLR forecast cases were selected. The start time of each was January 1 every year from 2004 to 2008.
STsDSF is a hybrid dynamical-statistical method for subseasonal prediction, which consists of four steps 1) distinguish the stable components from climatic state vector by training daily contribution rate of variance and persist time 2) divide the dynamical model output into predictable components and random components by projection 3) forecast predictable components in dynamical simulation and forecast random components in statistical estimation 4) make ensemble predictands for dynamical simulation and statistical estimation. Figure 1 is the schematic diagram of the STsDSF model, and the details of the STsDSF model have been introduced in [32, 33]. In this study, the Niño 3.4 index is considered as a similarity criterion that represents the external boundary conditions of tropical SST, and three similar years chosen for statistical estimation in the STsDSF model from 1979 to 2003.
In this study, the subseasonal forecast skill of OLR is measured by PCC and TCC. The PCC formula is expressed as follows:
where Xf, Xv, and Xc are the predicted value, observed value, and climate mean, respectively; Mf,c and Mv,c represent the deviation means of Xf and Xv from Xc, respectively; n represents the number of grids in the chosen area, and cosφi is the latitude of grid i.
The TCC formula is expressed as follows:
where Xf and Xv are the predicted value and observed value;
For subseasonal forecast products, the development trend is more reliable than daily outputs [54, 55]. In this study, five-day mean PCCs for both MME and STsDSF are calculated as 12 pentads. The comparison between MME PCC and STsDSF PCC shows that the trend of STsDSF is similar to MME. However, the variance of MME PCC is greater than STsDSF PCC. For example, MME PCC ranges from 0.80 to -0.18, while STsDSF PCC ranges from 0.36 to -0.15 in 2004 (Figure 2A). The reason for this is that MME is effective at simulating OLR at the start time, but the accuracy drops quickly over time. According to five OLR subseasonal forecasting cases from 2004 to 2008 (Figure 2), the PCC of STsDSF was higher than that of MME when the lead time was beyond 6 pentads.
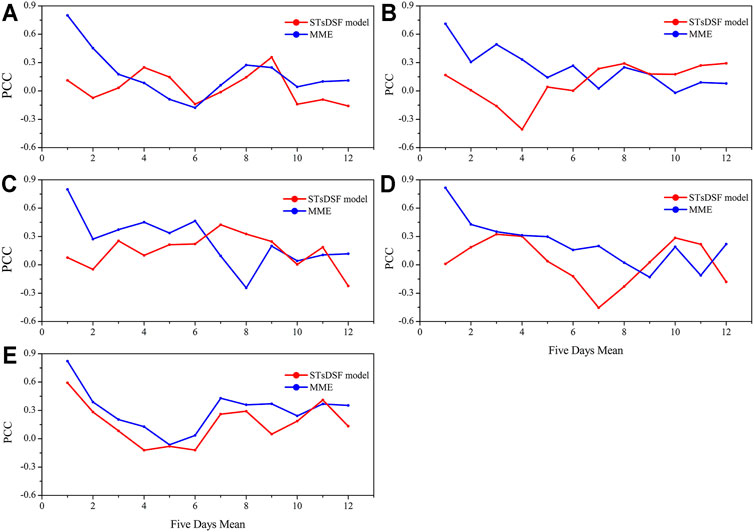
FIGURE 2. PCC of STsDSF model and MME for OLR subseasonal forecasting over the tropical Pacific region during 2004–2008: (A) 2004; (B) 2005; (C) 2006; (D) 2007; (E) 2008. Red line is STsDSF model and blue line is MME.
During 7–12 pentads, the average value PCC of STsDSF is 0.24 and 0.16 in 2005 and 2006, verses 0.10 and 0.05 from MME, respectively. For instance, the PCC of STsDSF is higher than that of MME during 7–12 pentads in 2005 and 7–11 pentads in 2006 (Figures 2B,C). In 2007, the PCC of STsDSF is higher than that of MME in 9–11 pentads (Figure 2D), while the forecasting skill of STsDSF is worse than MME in 2008 (Figure 2E). The possible reason may be attributed to the PCC of the MME forecast being very accurate compared to other cases, which means MME PCC drop slowly over time, and there is no capacity for improvement by STsDSF in 2008. The OLR forecast skill of STsDSF depends on the performance of the model simulation. If the model can reasonably capture the climatic patterns on a subseasonal scale, the forecast skill of STsDSF will be reduced.
Different from 1–6, the STsDSF model shows some advantages in 7–12 pentads. The five-year mean PCC of the STsDSF model is compared with MME for OLR in 7–12 pentads in Figure 3. The PCC of the STsDSF model ranges from -0.03 to 0.20, and the PCC of MME ranges from 0.10 to 0.18. Besides 12 pentads, the STsDSF model is more skillful than MME in 7–11 pentads. Therefore, the numerical simulation for the five consecutive year average also agrees with the conclusion above. Only when the skill of MME reduces to a certain level, the improvement of MME by STsDSF can show some advantages.
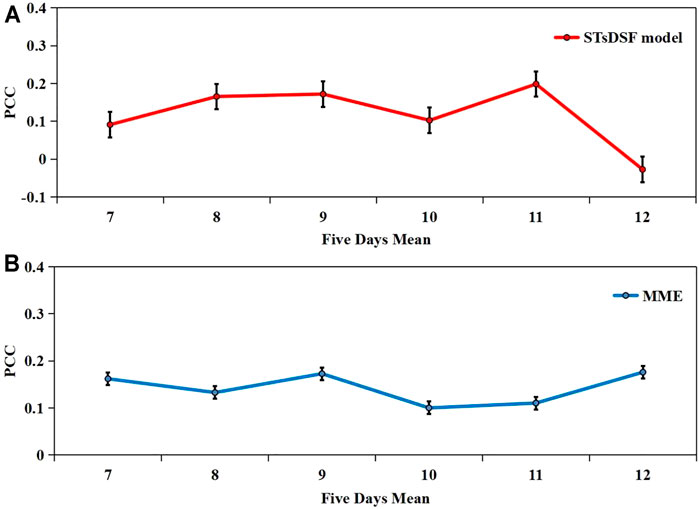
FIGURE 3. Five-year mean PCC of (A) STsDSF model and (B) MME for OLR subseasonal forecasting over the tropical Pacific region in 7–12 pentads. The standard deviation is marked as a vertical black line.
The standard deviation of STsDSF PCC is less than that of MME PCC (Figure 3), which indicates that the STsDSF model is more stable. The reason is that the principle of the STsDSF model is to distinguish model predictable information based on climate state and to replace random information with climate analogue. For the subseasonal OLR forecast over tropical Pacific region after 30 days, statistical methods still have the potential to surpass the dynamic model. To further investigate the STsDSF model performance in subseasonal time scale pentad by pentad, in the next section of the article, a case study from 2005 is presented to analyze the characteristics of OLR forecast error over the Pacific region.
In this section, a forecast case covering January-February 2005 is selected as an example for specific analysis. TCC is a common way to investigate the predictability distribution. The TCC of the STsDSF model and MME is shown in Figure 4. The red area indicates that the forecasting skill is high, and the blue area indicates that the forecasting skill is low. As shown in Figure 4B, MME forecasts well in most tropical regions, with TCC exceeding 0.993. Only in two meridional zonal regions (180° and 120°W), the TCC is lower than 0.989 and the distribution patterns of the two regions are very similar. The corresponding TCC of the STsDSF model in Figure 4A shows that the overall distribution pattern is the same as that of MME, and the values are close. However, the TCC of the STsDSF model is more complete and more continuous in the blue areas, and the TCC of MME is more dispersed. Comparing Figure 4A with Figure 4B, the overall forecast skill pattern has no great change in the subseasonal period, and the distribution characteristics of MME are retained in the STsDSF model.
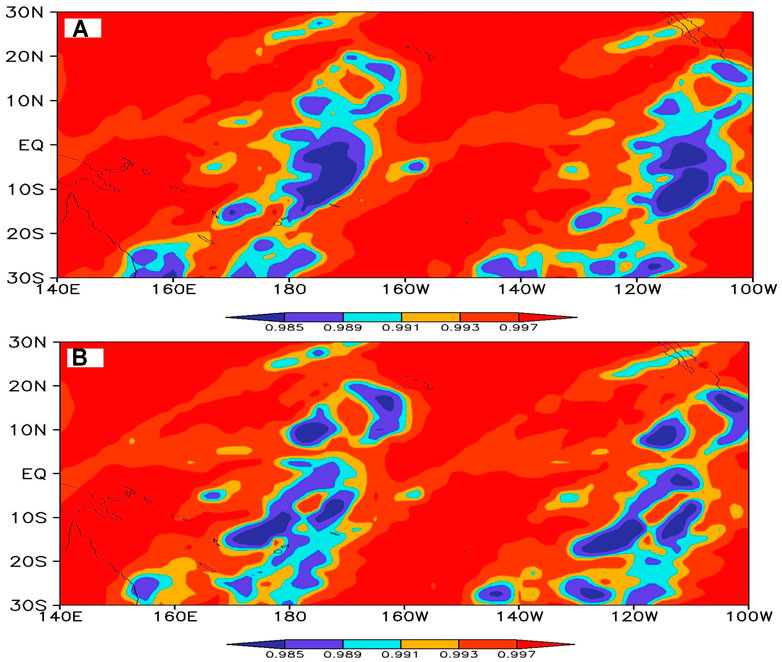
FIGURE 4. TCC of (A) STsDSF model and (B) MME for OLR subseasonal forecasting over tropical Pacific region.
The variation of MME forecast error for OLR in January-February 2005 is exhibited pentad by pentad (Figure 5). MME can capture the movement of OLR very well in pentad 1 (Figure 5A). During pentad two to five, the forecast error increases to 60 W/m2, and the discrete anomaly is mainly distributed in the southwest and northeast of the tropical Pacific (Figures 5A–E). During pentads 8–12, the forecast error increases to 80 W/m2, and the error region are complete and continuous. Overall, MME forecast error is mainly negative anomalous, and the skill is poor over southwest and northeast of the tropical Pacific. MME can capture the patterns of OLR over the tropical Pacific in the beginning, and the error grows gradually over time, which is consistent with the PCC changes in the above analysis (Figure 2).

FIGURE 5. The error distribution of MME for OLR subseasonal forecasts over the tropical Pacific region in 1(A)–12(L) pentad. (Unit: W/m2).
Different from the error distribution of MME for OLR subseasonal forecasts, the forecast error of the STsDSF model shows larger negative anomalies in 1–4 pentads (Figures 6A–D). The error is smaller in equatorial and larger in the higher latitudes over the Pacific. In addition, the pattern and intensity of STsDSF model error change little during 5–12 pentads (Figure 6E–l). Based on the diagnosis of OLR subseasonal forecast skill of STsDSF model and MME in January-February 2005, although STsDSF model error is larger than MME at the beginning, it grows slowly and shows some advantages in 8–12 pentad (Figure 6H–l).

FIGURE 6. The error distribution of STsDSF model for OLR subseasonal forecasts over tropical Pacific region in 1(A)–12(L) pentad. (Unit: W/m2).
The predictability of atmospheric stable component mainly comes from three aspects: outer boundary condition forcing, a continuous component of low frequency wave, and atmospheric periodic component. Furthermore, these atmospheric components are statistically regular [56, 57]. In this study, a new method called the STsDSF model is proposed, to improve the subseasonal dynamic model for OLR over the tropical Pacific region in January-February from 2004 to 2008. We compare subseasonal forecast skills of the STsDSF model and MME of 11 advanced models and analyze the growth characteristics of subseasonal forecast error.
The conclusions of this study reveal that the performance of the STsDSF model is largely determined by the forecasting skill of the dynamical model. The STsDSF model only provides additional improvement information when the dynamical model output incredible data. According to five OLR subseasonal forecasting cases from 2004 to 2008, the PCC of STsDSF will be higher than that of MME when the lead time is beyond 6 pentads. These results demonstrate that the STsDSF model can be used as an important reference for subseasonal forecasting after 30 days. The numerically simulated results for five consecutive years on average have a good agreement with the above discussion.
Moreover, the overall OLR TCC pattern of the STsDSF model is similar to that of MME, and the TCC values are close over the tropical Pacific. The change characteristics of MME are retained in the STsDSF model in time scale, as well as in the space scale. In addition, by comparing the subseasonal forecast error pentad by pentad, the error of the STsDSF model grows more slowly than that of the MME model in 12 pentads.
The STsDSF model only uses the initial condition and historical observation data to improve the subseasonal dynamical model and could feasibly be incorporated into existing business real-time forecast products. However, further studies are still needed. For example, we focus on the subseasonal forecast over tropical Pacific OLR in January-February 2004–2008. Further investigations of the STsDSF model, considering different meteorological elements, periods, and regions, needs more modeling studies. In this study, the similarity criterion of selecting historical data is Niño 3.4, considered as an important external boundary forcing signal. However, Niño 3.4 is a Pacific index and can not stand for all SST forcings [58, 59]. Therefore, a more comprehensive index considering different weights for different ocean forcings could be developed. In addition, when we analyze the subseasonal forecast skill of the STsDSF model, considering El Niño-Southern Oscillation (ENSO) cycle in interannual timescale, the relationship between subseasonal forecast skill and ENSO cycle is intriguing, a new story which could be further discussed in the future.
The hindcast skill of ISVHE performs better than the business model, so it needs to be further verified whether the improvement effect of the STsDSF model is different for the dynamical model forecasts with different forecasting skills. Moreover, due to the limitation of the time span of dynamical model data, we only select cases of five consecutive years for comparative analysis. Therefore, more simulation experiments are needed in further studies.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
KW and G-LF designed the research. KW performed analysis. Both KW, G-FF and G-LF contributed to the writing of the paper.
This work was supported by the National Key R&D Program of China (2017YFC1502303), the Basic Public Welfare Project of Zhejiang Province (LGF22D050001), the Natural Science Foundation of China (41605049, 42005027), the Key R&D Program of Zhejiang Province (2021C02036), the Natural Science Foundation of Zhejiang Province (LQ20D050003), the Fund for Meteorological Science and Technology of Zhejiang Province, China (2021ZD08, 2019ZD07), and the Hangzhou Agricultural and Social Development Scientific Research Project (20201203B155).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The ISVHE model data was sorted out by Dr. Song-Sun Lee in International Pacific Research Center (IPRC).
1. Charney JG, Fleagle RG, Lally VE, Riehl H, Wark DQ. The Feasibility of a Global Observation and Analysis experiment. Bull Amer Meteorol Soc. (1966) 47:200. doi:10.1175/1520-0477-47.3.200
2. Simmons AJ, Hollingsworth A. Some Aspects of the Improvement in Skill of Numerical Weather Prediction. Q J R Meteorol Soc (2002) 128:647–77. doi:10.1256/003590002321042135
3. Kalnay E, Lord SJ, Mcpherson RD. Maturity of Operational Numerical Weather Prediction: Medium Range. Bull Amer Meteorol Soc. (1998) 79:2753–69. doi:10.1175/1520-0477(1998)079<2753:moonwp>2.0.co;2
4. Lorenz EN. A Study of the Predictability of a 28-variable Atmospheric Model. Tellus (1965) 17:321–33. doi:10.3402/tellusa.v17i3.9076
5. Lorenz EN. Atmospheric Predictability as Revealed by Naturally Occurring Analogues. J Atmos Sci (1969) 26:636–46. doi:10.1175/1520-0469(1969)26<636:aparbn>2.0.co;2
6. Dalcher A, Kalnay E. Error Growth and Predictability in Operational ECMWF Forecasts. Tellus (1987) 39A:474–91. doi:10.1111/j.1600-0870.1987.tb00322.x
7. Li J, Ding R. Temporal-Spatial Distribution of Atmospheric Predictability Limit by Local Dynamical Analogs. Mon Wea Rev (2011) 139:3265–83. doi:10.1175/mwr-d-10-05020.1
8. Shukla J. Dynamical Predictability of Monthly Means. J Atmos Sci (1981) 38:2547–72. doi:10.1175/1520-0469(1981)038<2547:dpomm>2.0.co;2
9. Shukla J. Predictability in the Midst of Chaos: A Scientific Basis for Climate Forecasting. Science (1998) 282:728–31. doi:10.1126/science.282.5389.728
10. Kumar A, Jha B, Zhang Q, Bounoua L. A New Methodology for Estimating the Unpredictable Component of Seasonal Atmospheric Variability. J Clim (2007) 20(15):3888–901. doi:10.1175/jcli4216.1
11. Huang JP, Yi YH, Wang SW, Chou JF. An Analogue-Dynamical Long-Range Numerical Weather Prediction System Incorporating Historical Evolution. Quart J Roy Meteorol Soc. (1993) 119(511):547. doi:10.1002/qj.49711951111
12. Wang B, Lee J-Y, Kang I-S, Shukla J, Park C-K, Kumar A, et al. Advance and Prospectus of Seasonal Prediction: Assessment of the APCC/CliPAS 14-model Ensemble Retrospective Seasonal Prediction (1980-2004). Clim Dyn (2009) 33(1):93–117. doi:10.1007/s00382-008-0460-0
13. Xue H-L, Shen X-S, Chou J-F. A Forecast Error Correction Method in Numerical Weather Prediction by Using Recent Multiple-Time Evolution Data. Adv Atmos Sci (2013) 30(5):1249–59. doi:10.1007/s00376-013-2274-1
14. Chen B, Li J, Ding R. Nonlinear Local Lyapunov Exponent and Atmospheric Predictability Research. Sci China Ser D (2006) 49(10):1111–20. doi:10.1007/s11430-006-1111-0
15. Ding R, Li J. Nonlinear Finite-Time Lyapunov Exponent and Predictability. Phys Lett A (2007) 364(5):396–400. doi:10.1016/j.physleta.2006.11.094
16. Horel JD, Wallace JM. Planetary-Scale Atmospheric Phenomena Associated with the Southern Oscillation. Mon Wea Rev (1981) 109(4):813–29. doi:10.1175/1520-0493(1981)109<0813:psapaw>2.0.co;2
17. Hoskins BJ, Karoly DJ. The Steady Linear Response of a Spherical Atmosphere to thermal and Orographic Forcing. J Atmos Sci (1981) 38(6):1179–96. doi:10.1175/1520-0469(1981)038<1179:tslroa>2.0.co;2
18. Jin F-F, Boucharel J, Lin I-I. Eastern Pacific Tropical Cyclones Intensified by El Niño Delivery of Subsurface Ocean Heat. Nature (2014) 516(7529):82–5. doi:10.1038/nature13958
19. Chen WY, Van den Dool HM. Atmospheric Predictability of Seasonal, Annual, and Decadal Climate Means and the Role of the ENSO Cycle: A Model Study. J Clim (1996) 10(6):1236. doi:10.1175/1520-0442(1997)010<1236:aposaa>2.0.co;2
20. Li C, Pan J. Atmospheric Circulation Characteristics Associated with the Onset of Asian Summer Monsoon. Adv Atmos Sci (2006) 23(6):925–39. doi:10.1007/s00376-006-0925-1
21. Li T. Recent advance in Understanding the Dynamics of the Madden-Julian Oscillation. Acta Meteorol Sin (2014) 28(1):1–33. doi:10.1007/s13351-014-3087-6
22. Wang K, Ma H, Li J, Gu BH, Wu H. Assessment of the POEM2 Model for Simulating Tropical Intraseasonal Oscillation. J Trop Meteorol (2018) 24(3):323. doi:10.16555/j.1006-8775.2018.03.006
23. Blackmon ML, Geisler JE, Pitcher EJ. A General Circulation Model Study of January Climate Anomaly Patterns Associated with Interannual Variation of Equatorial Pacific Sea Surface Temperatures. J Atmos Sci (1983) 40(6):1410–25. doi:10.1175/1520-0469(1983)040<1410:agcmso>2.0.co;2
24. DelSole T, Tippett MK. Predictable Components and Singular Vectors. J Atmos Sci (2008) 65(5):1666–78. doi:10.1175/2007jas2401.1
25. Weber NJ, Mass CF. Subseasonal Weather Prediction in a Global Convection-Permitting Model. Bull Amer Meteorol Soc. (2019) 100(6):1079–89. doi:10.1175/bams-d-18-0210.1
26. Zhou T, Zou L. Understanding the Predictability of East Asian Summer Monsoon from the Reproduction of Land-Sea Thermal Contrast Change in AMIP-type Simulation. J Clim (2010) 23(22):6009–26. doi:10.1175/2010jcli3546.1
27. Chou JF, Zheng ZH, Sun SP. The Think about 10∼30 D Extendedrange Numerical Weather Prediction Strategy-Facing the Atmosphere Chaos. Scientia Meteorologica Sinica (Qixiang Kexue) (2010) 30(5):569. (in Chinese).
28. Ren H, Chou J, Huang J, Zhang P. Theoretical Basis and Application of an Analogue-Dynamical Model in the Lorenz System. Adv Atmos Sci (2009) 26(1):67–77. doi:10.1007/s00376-009-0067-3
29. Zheng Z, Huang J, Feng G, Chou J. Forecast Scheme and Strategy for Extended-Range Predictable Components. Sci China Earth Sci (2012) 56:878–89. doi:10.1007/s11430-012-4513-1
30. Ren F, Ding C, Zhang D-L, Chen D, Ren H-l., Qiu W. A Dynamical-Statistical-Analog Ensemble Forecast Model: Theory and an Application to Heavy Rainfall Forecasts of Landfalling Tropical Cyclones. Mon Wea Rev (2020) 148:1503–17. doi:10.1175/mwr-d-19-0174.1
31. Wang K, Feng G-L, Zeng Y-X, Wang X-J. Analysis of Stable Components in the Extended-Range Forecast for the Coming 10-30 Days in winter 2010 and 2011. Chin Phys. B (2013) 22:129202. doi:10.1088/1674-1056/22/12/129202
32. Feng G, Sun S, Zhao J, Zheng Z. Analysis of Stable Components for Extended-Range (10-30 Days) Weather Forecast: A Case Study of Continuous Overcast-Rainy Process in Early 2009 over the Mid-lower Reaches of the Yangtze River. Sci China Earth Sci (2013) 56:1576–87. doi:10.1007/s11430-012-4527-8
33. Wang K, Feng GL, Zeng YX, Li ZQ. Extraction of 10-30-day Stable Components from a Boreal Atmosphere during ENSO Phases. Discrete Dyn Nat Soc (2015) 2015 919286. doi:10.1155/2015/919286
34. Vitart F, Ardilouze C, Bonet A, Brookshaw A, Chen M, Codorean C, et al. The Subseasonal to Seasonal (S2S) Prediction Project Database. Bull Amer Meteorol Soc. (2017) 98(1):163–73. doi:10.1175/bams-d-16-0017.1
35. Zhu ZW, Li T. Extended-range Forecasting of Chinese Summer Surface Air Temperature and Heat Waves. Clim Dyn (2017) 50:1. doi:10.1007/s00382-017-3733-7
36. Zheng Z, Hu Z-Z, L’Heureux M. Predictable Components of ENSO Evolution in Real-Time Multi-Model Predictions. Sci Rep (2016) 6:35909. doi:10.1038/srep35909
37. Wang K, Zhang H, Fan G-F, Li Z-Q, Yu Z-Y, Liu P-P. Simulated Variation Characteristics of Oceanic CO2 Uptake, Surface Temperature, and Acidification in Zhejiang Province, China. Front Phys (2021) 9:718968. doi:10.3389/fphy.2021.718968
38. Wu Y-P, Shen Y-P, Larry Li B. Possible Physical Mechanism of Water Vapor Transport over Tarim River Basin. Ecol Complexity (2012) 9:63–70. doi:10.1016/j.ecocom.2011.12.002
39. Han ZX, Su T, Zhang Q, Wen Q, Feng GL. Thermodynamic and Dynamic Effects of Increased Moisture Sources over the Tropical Indian Ocean in Recent Decades. Clim Dyn (2019) 53(9):7081. doi:10.1007/s00382-019-04977-w
40. Weaver SJ, Wang W, Chen M, Kumar A. Representation of MJO Variability in the NCEP Climate Forecast System. J Clim (2011) 24:4676–94. doi:10.1175/2011jcli4188.1
41. Liu F, Wang B. A Frictional Skeleton Model for the Madden-Julian Oscillation*. J Atmos Sci (2012) 69:2749–58. doi:10.1175/jas-d-12-020.1
42. Chelliah M, Arkin P. Large-Scale Interannual Variability of Monthly Outgoing Longwave Radiation Anomalies over the Global Tropics. J. Clim. (1992) 5(4):371–89. doi:10.1175/1520-0442(1992)005<0371:LSIVOM>2.0.CO;2
43. Neena JM, Lee JY, Waliser D, Wang B, Jiang X. Predictability of the Madden-Julian Oscillation in the Intraseasonal Variability Hindcast Experiment (ISVHE)*. J Clim (2014) 27(12):4531–43. doi:10.1175/jcli-d-13-00624.1
44. Neena JM, Jiang X, Waliser D, Lee J-Y, Wang B. Eastern Pacific Intraseasonal Variability: a Predictability Perspective. J Clim (2014) 27(23):8869–83. doi:10.1175/jcli-d-14-00336.1
45. Lee SS, Wang B. Regional Boreal Summer Intraseasonal Oscillation over Indian Ocean and Western Pacific: Comparison and Predictability Study. Clim Dyn (2016) 46(7-8):2213. doi:10.1007/s00382-015-2698-7
46. Cottrill A, Hendon HH, Lim E-P, Langford S, Shelton K, Charles A, et al. Seasonal Forecasting in the Pacific Using the Coupled Model POAMA-2. Wea Forecast (2013) 28:668–80. doi:10.1175/waf-d-12-00072.1
47. Scoccimarro E, Gualdi S, Bellucci A, Sanna A, Giuseppe Fogli P, Manzini E, et al. Effects of Tropical Cyclones on Ocean Heat Transport in a High-Resolution Coupled General Circulation Model. J Clim (2011) 24:4368–84. doi:10.1175/2011jcli4104.1
48. Alves O, Balmaseda MA, Anderson D, Stockdale T. Sensitivity of Dynamical Seasonal Forecasts to Ocean Initial Conditions. Q J R Meteorol Soc (2004) 130:647–67. doi:10.1256/qj.03.25
49. Theja PK, Sreejith OP, Pai DS. Monsoon Teleconnections over Indian and Pacific Oceans in Japan Meteorological Agency Model Simulation. Int J Climatol (2015) 35:4728–37. doi:10.1002/joc.4319
50. Saha S, Nadiga S, Thiaw C, Wang J, Wang W, Zhang Q, et al. The NCEP Climate Forecast System. J Clim (2006) 19:3483–517. doi:10.1175/jcli3812.1
51. Kug J-S, Kang I-S, Choi D-H. Seasonal Climate Predictability with Tier-One and Tier-Two Prediction Systems. Clim Dyn (2008) 31:403–16. doi:10.1007/s00382-007-0264-7
52. Thomson MC, Doblas-Reyes FJ, Mason SJ, Hagedorn R, Connor SJ, Phindela T, et al. Malaria Early Warnings Based on Seasonal Climate Forecasts from Multi-Model Ensembles. Nature (2006) 439:576–9. doi:10.1038/nature04503
53. Feng G-L, Yang J, Zhi R, Zhao J-H, Gong Z-Q, Zheng Z-H, et al. Improved Prediction Model for Flood-Season Rainfall Based on a Nonlinear Dynamics-Statistic Combined Method. Chaos, Solitons & Fractals (2020) 140:110160. doi:10.1016/j.chaos.2020.110160
54. Vitart F, Robertson AW. The Sub-seasonal to Seasonal Prediction Project (S2S) and the Prediction of Extreme Events. Npj Clim Atmos. Sci. (2018) 1:1. doi:10.1038/s41612-018-0013-0
55. Zhang T, Yang S, Jiang X, Dong S. Sub-Seasonal Prediction of the Maritime Continent Rainfall of Wet-Dry Transitional Seasons in the NCEP Climate Forecast Version 2. Atmosphere (2016) 7:28. doi:10.3390/atmos7020028
56. Lo F, Hendon HH. Empirical Extended-Range Prediction of the Madden-Julian Oscillation. Mon Wea Rev (2000) 128(7):2528–43. doi:10.1175/1520-0493(2000)128<2528:eerpot>2.0.co;2
57. Jones C, Waliser DE, Lau KM, Stern W. The Madden-Julian Oscillation and its Impact on Northern Hemisphere Weather Predictability. Mon Wea Rev (2004) 132(6):1462–71. doi:10.1175/1520-0493(2004)132<1462:tmoaii>2.0.co;2
58. Walter K, Graf H-F. Life Cycles of North Atlantic Teleconnections under strong and Weak Polar Vortex Conditions. Q J R Meteorol Soc (2006) 132(615):467–83. doi:10.1256/qj.05.25
Keywords: subseasonal forecast, dynamic-statistical method, STsDSF model, stable components, multi-model ensemble
Citation: Wang K, Fan G-F and Feng G-L (2022) A Dynamic Statistical Subseasonal Forecast Model for OLR Over Tropical Pacific Region. Front. Phys. 9:665828. doi: 10.3389/fphy.2021.665828
Received: 09 February 2021; Accepted: 25 November 2021;
Published: 03 January 2022.
Edited by:
Bai-Lian Li, University of California, Riverside, United StatesReviewed by:
Boris Podobnik, University of Zagreb, CroatiaCopyright © 2022 Wang, Fan and Feng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guo-Lin Feng, ZmVuZ2dsQGNtYS5nb3YuY24=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.