Quark Structure of the X (4500), X (4700) and (4P,5P) States

We study some of the main properties (masses and open-flavor strong decay widths) of $4P$ and $5P$ charmonia. While there are two candidates for the ${\chi }_{\text{c}0}\left(4P,5P\right)$ states, the $X\left(4500\right)$ and $X\left(4700\right)$, the properties of the other members of the ${\chi }_{\text{c}}\left(4P,5P\right)$ multiplets are still completely unknown. With this in mind, we start to explore the charmonium interpretation for these mesons. Our second goal is to investigate if the apparent mismatch between the Quark Model (QM) predictions for ${\chi }_{\text{c}0}\left(4P,5P\right)$ states and the properties of the $X\left(4500\right)$ and $X\left(4700\right)$ mesons can be overcome by introducing threshold corrections in the QM formalism. According to our coupled-channel model results for the threshold mass shifts, the ${\chi }_{\text{c}0}\left(5P\right)\to X\left(4700\right)$ assignment is unacceptable, while the ${\chi }_{\text{c}0}\left(4P\right)\to X\left(4500\right)$ or $X\left(4700\right)$ assignments cannot be completely ruled out.

1 Introduction

In the past few years, our knowledge of the heavy-light and fully heavy baryon and meson spectra has considerably improved [1]. A large fraction of the newly discovered hadrons perfectly fits into a standard quark-antiquark or three valence quark description. Some examples include the recently discovered ${\text{Ω}}_{\text{c}}$s [2, 3], the ${\text{Ξ}}_{\text{b}}{\left(6227\right)}^{-}$ [4] and ${\text{Σ}}_{\text{b}}{\left(6097\right)}^{\pm }$ [5] baryon states, and the ${\chi }_{\text{b}\mathrm{1,2}}\left(3P\right)$ heavy quarkonium resonances [6–8]. There are, however, strong indications of the existence of exotic hadron configurations, which cannot be interpreted in terms of conventional quark-antiquark or three-quark degrees of freedom. They include tetraquark and pentaquark candidates [1, 9–13], and suspected hybrid and glue-ball states [1, 9–11, 13].

An important fraction of the suspected exotic mesons, the so-called $XYZ$ states, may require the introduction of complicated multiquark structures. The most famous example is the $X\left(3872\right)$ [now ${\chi }_{\text{c}1}\left(3872\right)$] [14–16], but one could also mention the $X\left(4274\right)$ [also known as ${\chi }_{\text{c}1}\left(4274\right)$] [17, 18]. Some of these exotics, the $Z_{\text{b}}$ and $Z_{\text{c}}$ resonances, like the $Z_c\left(3900\right)$ [19, 20], $Z_b\left(10610\right)$ and $Z_b\left(10650\right)$ [21], are characterized by very peculiar quark structures. $Z_{\text{Q}}$ exotics are charged particles and, because of their energy and decay properties, they must contain a heavy $Q\overline{Q}$ pair (with $Q=c$ or b) too; thus, their adequate description requires the introduction of $Q\overline{Q}q\overline{q}$ four-quark configurations, where q are light (u or d) quarks. If $Z_{\text{b}}$ and $Z_{\text{c}}$ states exist, one may also expect the emergence of hidden-charm/bottom tetraquarks with non-null strangeness content, the so-called $Z_{\text{cs}}$ and $Z_{\text{bs}}$ mesons; for example, see Refs. 22 and 23. Recent indications of the possible existence of $Z_{\text{cs}}$ states have been given by BESIII Collaboration [24].

In this paper, we study the main properties (masses, open-flavor and radiative decay widths) of the $4P$ and $5P$ charmonium multiplets. While there are two candidates for the ${\chi }_{\text{c}0}\left(4P,5P\right)$ states, the $X\left(4500\right)$ and $X\left(4700\right)$ resonances [also known as ${\chi }_{\text{c}0}\left(4500\right)$ and ${\chi }_{\text{c}0}\left(4700\right)$] [1, 18, 25], the properties of the other members of the ${\chi }_{\text{c}}\left(4P,5P\right)$ multiplets are still completely unknown. With this in mind, we start to explore the quark-antiquark interpretation for these mesons by computing their open-flavor strong decay widths. Our predictions may help the experimentalists in their search for the still unobserved ${\chi }_{\text{c}}\left(4P,5P\right)$ resonances. The calculation of the ${\chi }_{\text{c}0}\left(4P,5P\right)$ radiative and hidden-flavor decay widths will be the subject of a subsequent paper.

We also provide Coupled-Channel Model (CCM) [26, 27] predictions for the physical masses¹ of $4P$ and $5P$ charmonia, which may serve as a test for the ${\chi }_{\text{c}0}\left(4P,5P\right)\to X\left(4500\right)$ or $X\left(4700\right)$ controversial assignments. According to our CCM results, the introduction of threshold effects can hardly reconcile the Relativized Quark Model (RQM) predictions for the ${\chi }_{\text{c}0}\left(4P,5P\right)$ meson masses [28] with the properties of the experimentally observed $X\left(4500\right)$ and $X\left(4700\right)$ states [1, 18, 25]. Therefore, the two previous resonances are unlikely to be associated with ${\chi }_{\text{c}0}\left(4P,5P\right)$ charmonia, with the possible exception of ${\chi }_{\text{c}0}\left(4P\right)\to X\left(4500\right)$ or $X\left(4700\right)$.

There are several alternative interpretations for the ${\chi }_{\text{c}0}\left(4500\right)$ and ${\chi }_{\text{c}0}\left(4700\right)$ states [29–35]. A possible explanation of the ${\chi }_{\text{c}0}\left(4500\right)$ and ${\chi }_{\text{c}0}\left(4700\right)$ unusual properties without resorting to exotic interpretations may be to hypothesize a progressive departure of the $c\overline{c}$ linear confining potential from the $\propto r$ behavior as one goes up in energy. This departure could be either due to limitations of the relativized QM fit [28], which little by little make their appearance at higher meson energies, or to the need of renormalizing the $c\overline{c}$ color string tension at higher energies to take relativistic effects (like $q\overline{q}$ light quark pair creation) explicitly into account. For example, see Ref. 36.

The $X\left(4500\right)$ and $X\left(4700\right)$ were interpreted as compact tetraquarks in Refs. 29–31 and 33. In particular, in Ref. 30 the authors made use of a relativized diquark model to calculate the spectrum of hidden-charm tetraquarks. According to their findings, the $X\left(4500\right)$ and $X\left(4700\right)$ can be described as $0^{++}$ radial excitations of S-wave axial-vector diquark-antidiquark and scalar diquark-antidiquark bound states, respectively. A similar interpretation was provided in Ref. 29. Stancu calculated the $s\overline{s}c\overline{c}$ tetraquark spectrum within a quark model with chromomagnetic interaction [37]. She interpreted the $X\left(4140\right)$ as the strange partner of the $X\left(3872\right)$, but she could not accommodate the other $s\overline{s}c\overline{c}$ states, the $X\left(4274\right)$, $X\left(4500\right)$ and $X\left(4700\right)$.² By using QCD sum rules, the $X\left(4500\right)$ and $X\left(4700\right)$ were interpreted as D-wave $c\overline{c}s\overline{s}$ tetraquark states with opposite color structures [33]. Maiani et al. could accommodate the $X\left(4140\right)$, $X\left(4274\right)$, $X\left(4500\right)$ and $X\left(4700\right)$ in two tetraquark multiplets. They also suggested that the $X\left(4500\right)$ and $X\left(4700\right)$ are $2S$$cs\overline{c}\overline{s}$ tetraquark states [31].

In Ref. 32, the authors investigated possible assignments for the four $J/\psi \varphi$ structures reported by LHCb [38] in a coupled channel scheme by using a nonrelativistic constituent quark model [39, 40].³ In particular, they showed that the $X\left(4274\right)$, $X\left(4500\right)$ and $X\left(4700\right)$ mesons can be described as conventional $3^3{P}_1$, $4^3{P}_0$, and $5^3{P}_0$ charmonium states, respectively. In Ref. 35, the author studied the nature of the $X\left(4140\right)$, $X\left(4274\right)$, $X\left(4500\right)$, and $X\left(4700\right)$ states in the process $B^{+}\to J/\psi \varphi K^{+}$ by means of the rescattering mechanism. According to his results, the properties of the $X\left(4700\right)$ and $X\left(4140\right)$ can be explained by the rescattering effects, while those of the $X\left(4274\right)$ and $X\left(4500\right)$ cannot if the quantum numbers of the $X\left(4274\right)$ and $X\left(4500\right)$ are $1^{++}$ and $0^{++}$, respectively. This indicates that, unlike the $X\left(4700\right)$ and $X\left(4140\right)$, the $X\left(4274\right)$, and $X\left(4500\right)$ could be genuine resonances.

In the study of heavy quarkonium hybrids based on the strong coupling regime of potential nonrelativistic QCD of Ref. 34, the authors found that most of the isospin zero $XYZ$ states fit well either as the hybrid or standard quarkonium candidates. According to their results, the $X\left(4500\right)$ is compatible with a $0^{++}$ hybrid state, even though its mixing with the spin-1 charmonium is little and it is difficult to understand its observation in the $J/\psi \varphi$ channel; the $X\left(4700\right)$ is compatible with the charmonium ${\chi }_{\text{c}0}\left(4P\right)$.

Finally, it is worth to remind that both the $X\left(4500\right)$ and $X\left(4700\right)$ are omitted from the PDG summary table [1]. This means that their existence still needs to be proved. Future experimental searches may thus confirm their presence at similar or slightly different energies or even rule out their existence.

2 Open-Flavor Strong Decays of $4P$ and $5P$ Charmonium States

Our analysis starts with the calculation of the open-charm strong decays of the ${\chi }_{\text{c}}(4P,5P)$ states within the ³$P_0$ pair-creation model [45–48]. Open-charm are usually the dominant decay modes of hadron higher radial excitations; the contributions of hidden-charm and radiative decay modes to the total width of a higher-lying charmonium state are indeed expected to be in the order of a few percent or even less. This is why the calculated open-flavor total decay widths of higher charmonia are precious informations, which can be directly used for a comparison with the experimental total widths of those states within a reasonable grade of accuracy.

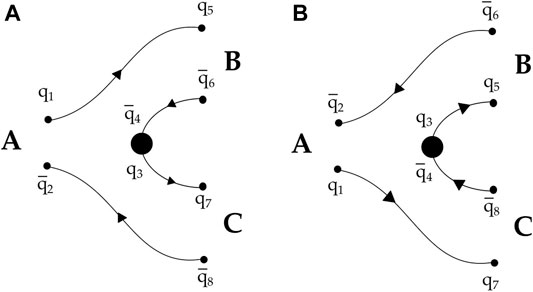
In the ³$P_0$ pair-creation model, the open-flavor strong decay $A\to BC$ takes place in the rest frame of the parent hadron A and proceeds via the creation of an additional $q\overline{q}$ pair (with $q=u,d$ or s) characterized by $J^{PC}=0^{++}$ quantum numbers [45–48] (see Figure 1).

FIGURE 1

FIGURE 1. Diagrams contributing to the $A\to BC$ open-flavor decay process. $q_{\text{i}}$, with i = 1, … , 4, and ${\overline{q}}_{\text{j}}$, with j = 5, … , 8, are the quarks and antiquarks in the parent and daughter states, respectively. Picture from Ref. 54. APS copyright.

The width is calculated as [45–47, 49, 50].

${\text{Γ}}_{A\to BC}={\text{Φ}}_{A\to BC}\left(k_0\right){\displaystyle \sum _{\ell }{\left|\langle BC{k}_0\ell J\left|T^{†}\right|A\rangle \right|}^2},(1)$

where $\ell$ is the relative angular momentum between the hadrons B and C, $\mathbf{J}={\mathbf{J}}_B+{\mathbf{J}}_C+\ell$ is their total angular momentum, and

${\text{Φ}}_{A\to BC}\left(k_0\right)=2\pi k_0\frac{E_B\left(k_0\right)E_C\left(k_0\right)}{M_A}(2)$

is the phase-space factor for the decay. Here, $k_0$ is the relative momentum between B and C, $M_A$ and $E_{B,C}\left(k_0\right)$ are the energies of the parent and daughter hadrons, respectively. We assume harmonic oscillator wave functions for the parent and daughter hadrons, A, B, and C, depending on a single oscillator parameter ${\alpha }_{\text{ho}}$. The values of the oscillator parameter, ${\alpha }_{\text{ho}}$, and of the other pair-creation model parameters, ${\alpha }_{\text{d}}$ and ${\gamma }_0$, were fitted to the open-charm strong decays of higher charmonia [51] and also used later in the study of charmed and charmed-strange meson open-flavor strong decays [52] and of the quasi two-body decay of the $X\left(3872\right)$ into $D^0{\left({\overline{D}}^0{\overline{\pi }}^0\right)}_{{\overline{D}}^{\text{*}0}}$ [53]; see Table 1.

TABLE 1

TABLE 1. ³P₀ pair-creation model parameters for the charmonium sector, extracted from Refs. 51, Table II and 52, Table II.

Some changes are introduced in the original form of the ³$P_0$ pair-creation model operator, $T^{†}$. They include: 1) the substitution of the pair-creation strength, ${\gamma }_0$, with an effective one [54], ${\gamma }_0^{\text{eff}}$, to suppress heavy quark pair-creation [54–56]; 2) the introduction of a Gaussian quark form-factor, because the $q\overline{q}$ pair of created quarks has an effective size [36, 54, 56, 57]. More details on the ³$P_0$ pair-creation model can be found in Supplementary Appendix.

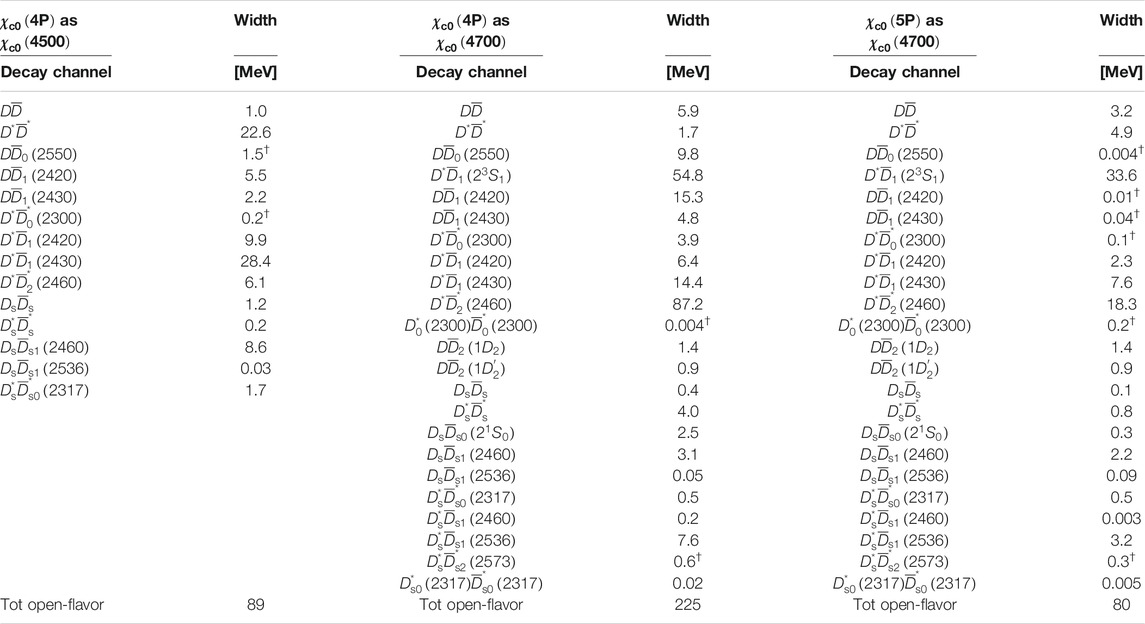
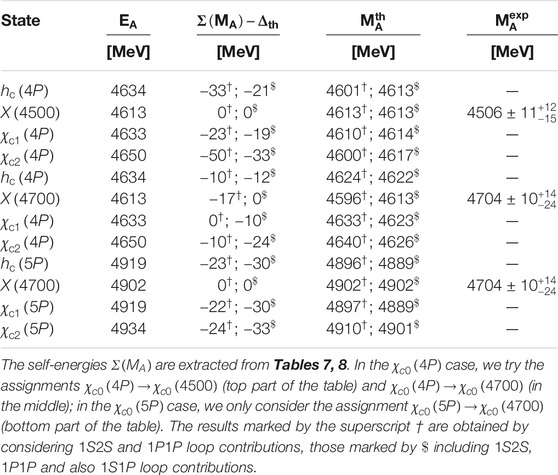
When available, we extract the masses of the parent and daughter mesons from the PDG [1]; otherwise, we calculate them by using the relativized QM with the original values of its parameters; see Ref. 28, Table II. The masses of the ${\chi }_{\text{c}0}\left(4500\right)$ and ${\chi }_{\text{c}0}\left(4700\right)$ resonances [1, 18, 25], $4506\pm {11}_{-15}^{+12}$ MeV and $4704\pm {10}_{-24}^{+14}$ MeV, seem to be incompatible with the relativized QM predictions for the ${\chi }_{\text{c}0}\left(4P,5P\right)$ states; see Table 2. A coupled-channel model calculation, with the goal of reconciling relativized QM predictions and the experimental data, is carried out in Section 3.

TABLE 2

TABLE 2. Bare masses of ${\chi }_{\text{c}}\left(4P,5P\right)$ charmonia, computed in a variational program by using the original relativized QM parameters [28, Table II].

Given the previous apparent incompatibility, in the ${\chi }_{\text{c}0}\left(4P,5P\right)$ cases we provide results by using: 1) the relativized QM values of the masses from Table 2; 2) the tentative assignments ${\chi }_{\text{c}0}\left(4500\right)\to {\chi }_{\text{c}0}\left(4P\right)$ and ${\chi }_{\text{c}0}\left(4700\right)\to {\chi }_{\text{c}0}\left(4P\right)$ or ${\chi }_{\text{c}0}\left(5P\right)$, with the experimental values of the ${\chi }_{\text{c}0}\left(4500\right)$ and ${\chi }_{\text{c}0}\left(4700\right)$ masses as inputs in the calculation.

The mixing angles between $1^1{P}_1$ and $1^3{P}_1$, $2^1{P}_1$ and $2^3{P}_1$ and also $2^1{D}_2$ and $2^3{D}_2$ charmed and charmed-strange states are taken from Ref. 52, Tables III, IV. In the case of $1P$ charmed-strange mesons, the mass difference between $|1P_1\rangle$ and $|1P_1^{\prime }\rangle$ states (75 MeV) is much larger than that in the charmed sector (6 MeV). Thus, for $1P$ charmed-strange mesons we make use of the approximation: $|1P_1\rangle \simeq |1^1{P}_1\rangle$ and $|1P_1^{\prime }\rangle \simeq |1^3{P}_1\rangle$.

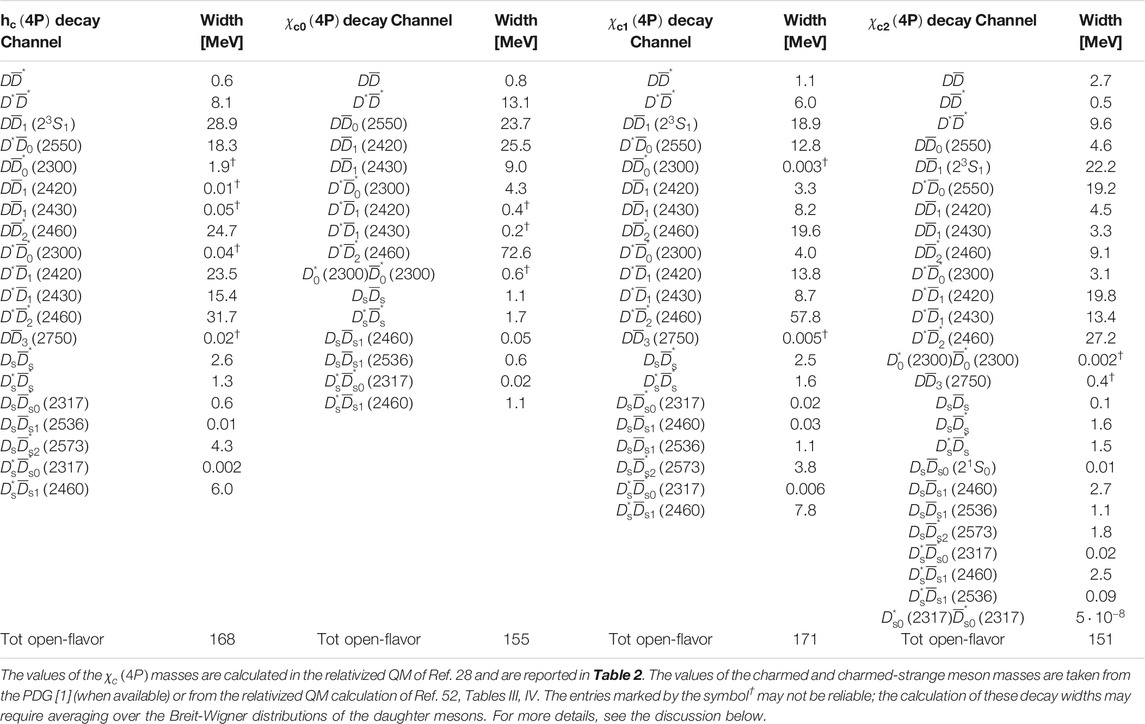
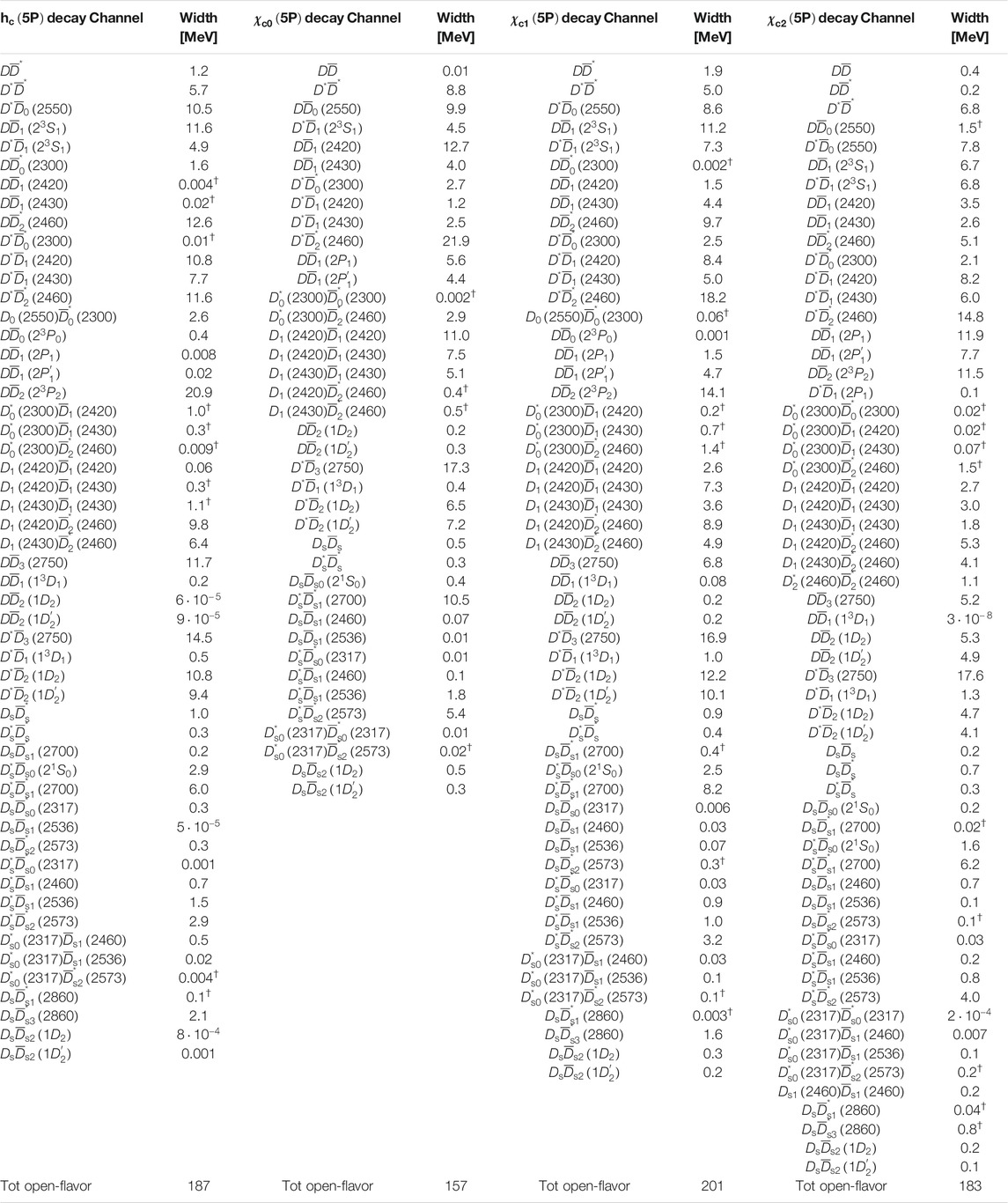
Our theoretical results, obtained by using the pair-creation model parameters of Table 1, are given in Tables 3–5. It is worth to note that: 1) the calculated total open-charm strong decay widths of ${\chi }_{\text{c}}\left(4P\right)$ s and ${\chi }_{\text{c}}\left(5P\right)$ s of Tables 3,4 are quite large; they are in the order of $150-200$ MeV. If we make the hypothesis of considering the open-charm as the largely dominant decay modes of higher charmonia, a comparison with the existing and forthcoming experimental data can be easily done. If our pair-creation model results are confirmed by the future experiment data, the ${\chi }_{\text{c}}\left(4P,5P\right)$ states will be reasonably interpreted as charmonium (or charmonium-like) states dominated by the $c\overline{c}$ component; 2) the results of Table 5, obtained by making the tentative assignments ${\chi }_{\text{c}0}\left(4500\right)\to {\chi }_{\text{c}0}\left(4P\right)$ and ${\chi }_{\text{c}0}\left(4700\right)\to {\chi }_{\text{c}0}\left(4P\right)$ or ${\chi }_{\text{c}0}\left(5P\right)$, seem to span a wider interval. In particular, one can notice that the assignments ${\chi }_{\text{c}0}\left(4700\right)\to {\chi }_{\text{c}0}\left(4P\right)$ and ${\chi }_{\text{c}0}\left(4700\right)\to {\chi }_{\text{c}0}\left(5P\right)$ produce results for the total open-flavor widths of 225 and 80 MeV, respectively. A comparison with the total experimental width of the ${\chi }_{\text{c}0}\left(4700\right)$ [1], $120\pm {31}_{-33}^{+42}$ MeV, seems to favor the ${\chi }_{\text{c}0}\left(5P\right)$ assignment, even though the experimental error is so large that it is difficult to draw a definitive conclusion. Our result for the total open-flavor width of the ${\chi }_{\text{c}0}\left(4500\right)$ as ${\chi }_{\text{c}0}\left(4P\right)$, 89 MeV, is in good accordance with the experimental total decay width of the ${\chi }_{\text{c}0}\left(4500\right)$, $92\pm {21}_{-20}^{+21}$ MeV. In light of this, our ³$P_0$ model results would suggest the assignments ${\chi }_{\text{c}0}\left(4500\right)\to {\chi }_{\text{c}0}\left(4P\right)$ and ${\chi }_{\text{c}0}\left(4700\right)\to {\chi }_{\text{c}0}\left(5P\right)$, even though ${\chi }_{\text{c}0}\left(4700\right)\to {\chi }_{\text{c}0}\left(4P\right)$ cannot be ruled out completely; 3) there are decay channels whose widths change notably by switching from a specific assignment to another; see e.g., the $D^{\text{*}}{\overline{D}}^{\text{*}}$ and $D^{\text{*}}{\overline{D}}_2^{\text{*}}\left(2460\right)$ decay mode results from Table 5. Therefore, a detailed study of the $D^{\text{*}}{\overline{D}}^{\text{*}}$, $D^{\text{*}}{\overline{D}}_2^{\text{*}}\left(2460\right)$, $D^{\text{*}}{\overline{D}}_1\left(2^3{S}_1\right)$ … decay channels may help considerably in the assignment procedure.

TABLE 3

TABLE 3. Open-charm strong decays of ${\chi }_{\text{c}}\left(4P\right)$ states in the ³$P_0$ pair-creation model.

TABLE 4

TABLE 4. As Table 3, but for ${\chi }_{\text{c}}\left(5P\right)$ states.

TABLE 5

TABLE 5. As Table 3, but for the decays of ${\chi }_{\text{c}0}\left(4P\right)$ as ${\chi }_{\text{c}0}\left(4500\right)$ or ${\chi }_{\text{c}0}\left(4700\right)$ and ${\chi }_{\text{c}0}\left(5P\right)$ as ${\chi }_{\text{c}0}\left(4700\right)$. Here, we use the experimental values of the ${\chi }_{\text{c}0}\left(4500\right)$ and ${\chi }_{\text{c}0}\left(4700\right)$ meson masses [1].

Finally, it is interesting to discuss, in the context of a ³$P_0$ model calculation, the possible importance of: 1) averaging the open-flavor widths of charmonia over the Breit-Wigner distributions of the daughter mesons. One can observe that, in the present study, the decay widths into charmed meson pairs do not take the widths of the final states into account. However, these are sizable, $\mathrm{}\left(100\text{ MeV}\right)$, for several of the decays discussed here, and may thus affect some of the results; see e.g., the $D_0^{\text{*}}\left(2300\right)$, whose width is $274\pm 40$ MeV, and the $D_0\left(2550\right)$, whose width is $135\pm 17$ MeV [1]. There are even cases of charmed-strange mesons whose width is large, like the $D_{s1}^{\text{*}}\left(2860\right)$. However, the contribution of the charmed-strange meson decay channels to the total widths of charmonia is expected to be smaller because of the effective pair-creation strength suppression mechanism of Supplementary Eq. S9. In light of this, we conclude that some of our results for the open-flavor strong decay widths of ${\chi }_{\text{c}}\left(4P,5P\right)$ states may not be reliable. In particular, this might the case of channels like $h_{\text{c}}\left(4P\right)\to D{\overline{D}}_1\left(2420\right)$ or $D{\overline{D}}_1\left(2430\right)$, whose calculated widths are small but they could be larger once the effects of averaging over the widths of the final states are taken into account. In conclusion, we believe that it would be interesting to see how our results for the open-flavor strong decay widths of charmonia will change after this averaging procedure is performed. This will be the subject of a subsequent paper [58]; 2) including the quark form factor (QFF) in the ³$P_0$ model transition operator; see Supplementary Appendix. The QFF was not considered in the original formulation of the ³$P_0$ model [45–47], but it was introduced in a second stage with the phenomenological purpose to take the effective size of the $q\overline{q}$ pair of created quarks into account [36, 54, 56, 57]. Its possible importance in our results can be somehow quantified by calculating the widths of some specific decay channels, like $\psi \left(3770\right)\to D\overline{D}$, by means of the standard ³$P_0$ model transition operator and the modified one, which includes the quark form factor. In the former case, we get $\text{Γ}[\psi \left(3770\right)\to D\overline{D}]=27$ MeV; in the latter, we obtain $\text{Γ}[\psi \left(3770\right)\to D\overline{D}]=80$ MeV. The second result for the width, i.e., 80 MeV, is outsize. It is clear that realistic results for the open-flavor strong decay widths of charmonia can be obtained in both cases; however, if the QFF is not taken into account, the values of the model parameters of Table 1 need to be re-fitted to the data; 3) extracting a different value of the harmonic oscillator (h.o.) parameter for each state involved in the decays rather than using a single value for them all, as it is done here. The former approach was used e.g. in Refs. 59–61. Consider, in particular, the prescriptions of Ref. 60. There, the h. o. parameters of charmonia were fitted to their squared radii from potential model calculations [62]. In the case of the $J/\psi$, $\psi \left(2S\right)$ and $\psi \left(3770\right)$, the authors got ${\alpha }_{\text{ho}}=0.52,0.39$ and 0.37 GeV, respectively. Furthermore, the value of ${\alpha }_{\text{ho}}$ for D mesons (and that of ${\gamma }_0$) were fitted to the open-charm decays of the $\psi \left(3770\right)$ and $\psi \left(4040\right)$. The main advantage of the previous approach with respect to that used in the present paper resides in the possibility of obtaining results for the decays based on more realistic wave functions for the parent mesons. On the contrary, the prescriptions used here have the advantage of a greater flexibility and of a smaller number of free parameters; 4) finally, we have to comment that a realistic value of ${\gamma }_0$ can be found in the range $0.3-0.5$, approximately. See e.g., Ref. 60, where ${\gamma }_0=0.35$ was fitted to the open-charm decays of the $\psi \left(3770\right)$ and $\psi \left(4040\right)$, and Ref. 63, where a value of ${\gamma }_0=0.4$ made it possible to obtain a good reproduction of the open-charm decay widths of charmonia up to $2F$ and $1G$ resonances. The value used here and in Refs. 51–53, ${\gamma }_0=0.510$ (see Table 1), was fitted to the strong decay widths of $3S$, $2P$, $1D$, and $2D$ charmonia. This value is different from those used in other studies [60, 63] because of the presence here of the QFF and of different choices of ${\alpha }_{\text{ho}}$. Evidently, all the model parameter values are tightly connected to one another: changing the value of one of them will automatically require a redefinition of the values of all the other model parameters or, at least, of a part of them.

3 Threshold Mass-Shifts of ${\chi }_{\text{c}}\left(4P,5P\right)$ States in a Coupled Channel Model

Here, we make use of the UQM-based CCM of Refs. 26 and 27 to explore the possible assignments ${\chi }_{\text{c}0}\left(4P\right)\to {\chi }_{\text{c}0}\left(4500\right)$ or ${\chi }_{\text{c}0}\left(4700\right)$ and ${\chi }_{\text{c}0}\left(5P\right)\to {\chi }_{\text{c}0}\left(4700\right)$. To do that, we calculate the threshold corrections to the bare masses of the ${\chi }_{\text{c}0}\left(4500\right)$ and ${\chi }_{\text{c}0}\left(4700\right)$ resonances to see if the introduction of loop effects can help to reconcile the relativized QM [28] results for ${\chi }_{\text{c}0}\left(4P,5P\right)$ states, see Table 2 herein, with the experimental data [1, 18, 25].

In the UQM [36, 54, 57, 64–70], the wave function of a hadron,

$\begin{array}{c}|{\psi }_A\rangle =\mathcal{N}\left[|A\rangle +{\displaystyle \sum _{BC}{\displaystyle \int {\mathit{k}}^{\mathit{2}}\mathit{dk}|\mathit{BCk}\mathit{lJ}\rangle }}\frac{\langle BCk\ell J\left|T^{†}\right|A\rangle }{M_A-E_B-E_C}\right],\end{array}(3)$

is the superposition of a valence core, $|A\rangle =|Q\overline{Q}\rangle$, plus higher Fock components, $|BC\rangle =\mathrm{ }|Q\overline{q};q\overline{Q}\rangle$, due to the creation of light $q\overline{q}$ pairs. The sum is extended over a complete set of meson-meson intermediate states $|BC\rangle$ and the amplitudes, $\langle BCk\ell J\left|T^{†}\right|A\rangle$, are computed within the ³$P_0$ pair-creation model of Section 2.

The physical masses of hadrons are calculated as

$M_A^{\text{UQM}}=E_A+\text{Σ}\left(M_A\right).(4)$

Here, $E_A$ is the bare mass of the hadron A, and

$\text{Σ}\left(M_A\right)={\displaystyle \sum _{BC}{\displaystyle {\int }_0^{\infty }{k}^{2}dk}}\frac{{\left|\langle BCk\ell J\left|T^{†}\right|A\rangle \right|}^2}{M_A-E_B\left(k\right)-E_C\left(k\right)}(5)$

is a self-energy correction. The bare masses $E_A$ are usually computed in a potential model, whose parameters are fixed by fitting Eq. 4 to the reproduction of the experimental data; see e.g., Refs. 51 and 71.

The idea at the basis of the coupled-channel approach of Refs. 26 and 27 is slightly different. There, one can study a single multiplet at a time, like ${\chi }_{\text{c}}\left(2P\right)$ or ${\chi }_{\text{b}}\left(3P\right)$, without the need of considering an entire meson sector to re-fit the potential model parameters to the reproduction of the physical masses of Eq. 4. This is because the bare masses $E_A$ are directly extracted from the relativized QM predictions of Refs. 28 and 63; see Table 2. In our coupled-channel model approach, the physical masses of the meson multiplet members are given by Refs. 26 and 27.

$M_A^{\text{CCM}}=E_A+\text{Σ}\left(M_A\right)+{\text{Δ}}_{\text{th}},(6)$

where $E_A$ and $\text{Σ}\left(M_A\right)$ have the same meaning as in Eq. 4 and ${\text{Δ}}_{\text{th}}$ is a parameter. For each multiplet we consider, this is the only free parameter of our calculation. It is defined as the smallest self-energy correction (in terms of absolute value) among those of the multiplet members; see Ref. 26, Section 2, and 27, Section IIIC. The introduction of ${\text{Δ}}_{\text{th}}$ in Eq. 6 represents our “renormalization” or “subtraction” prescription for the threshold mass-shifts in the UQM. The UQM model parameters, which we need in the calculation of the $\langle BCk\ell J\left|T^{†}\right|A\rangle$ vertices and the self-energies of Eq. 5, are reported in Table 1. See also Supplementary Appendix.

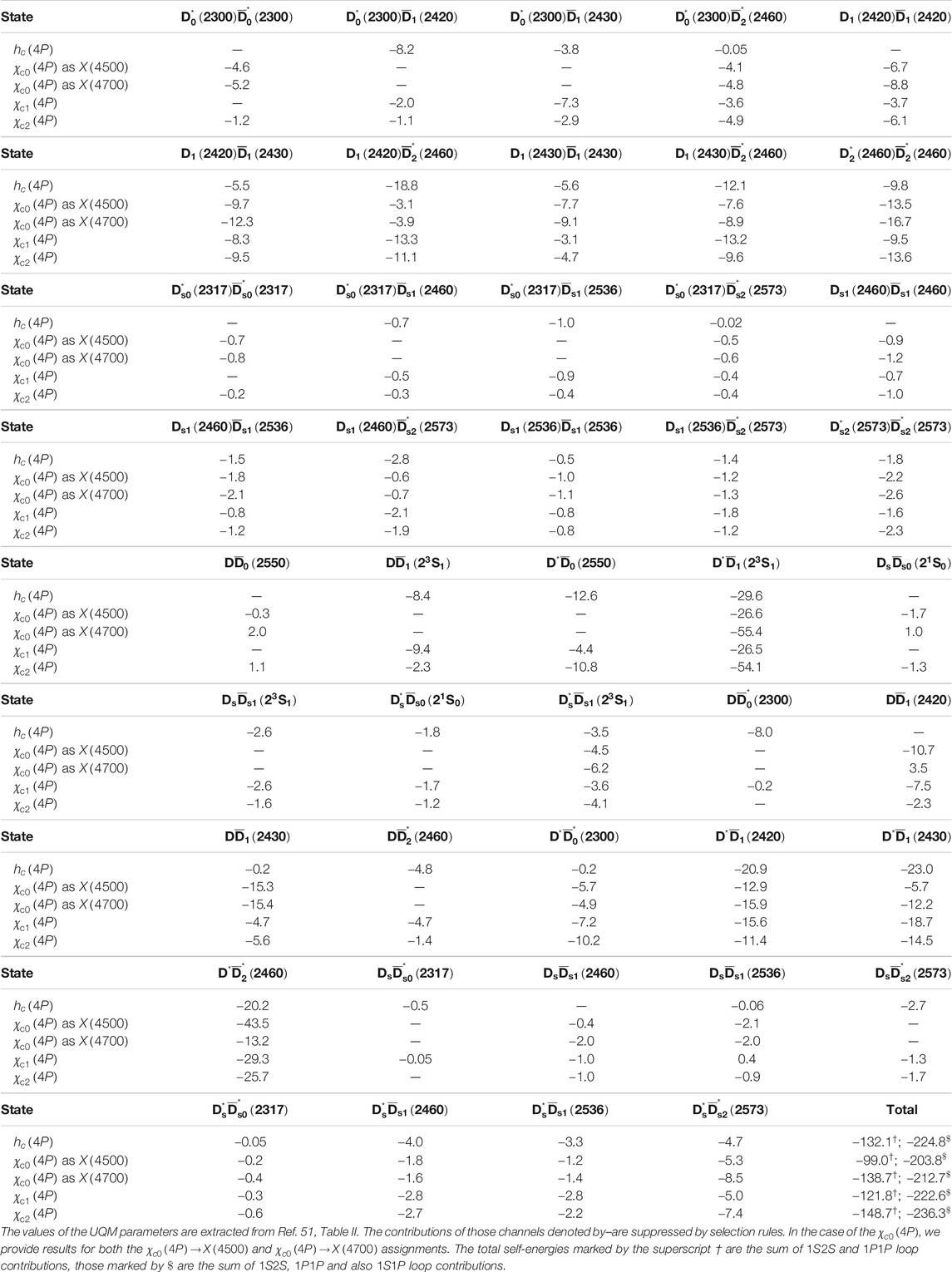
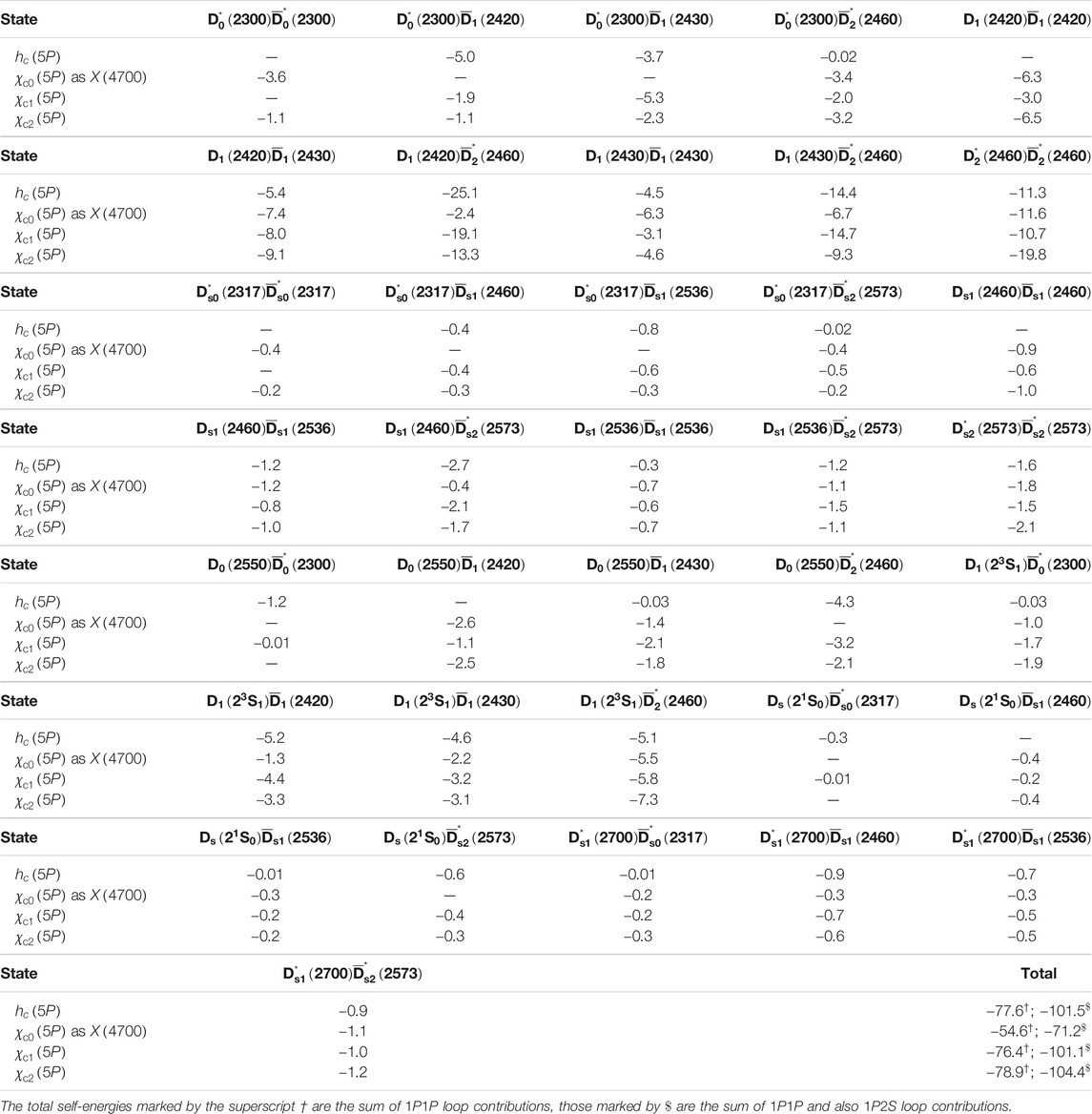
By making use of the above coupled-channel approach, we calculate the relative threshold mass shifts between the ${\chi }_{\text{c}}\left(4P,5P\right)$ multiplet members due to a complete set of $\left(nL,n^{\prime }{L}^{\prime }\right)$ meson-meson loops; see Refs. 26, Section 2 and 27, Section IIIC. In particular, in the ${\chi }_{\text{c}}\left(5P\right)$ case it is easy to identify the relevant set of intermediate states: one has to consider both $1P1P$ meson-meson loops, whose energies range from 4600 MeV [$D_0^{\text{*}}\left(2300\right){\overline{D}}_0^{\text{*}}\left(2300\right)$] to 5138 MeV [$D_{\text{s}2}^{\text{*}}\left(2573\right){\overline{D}}_{\text{s}2}^{\text{*}}\left(2573\right)$], and $1P2S$ loops, whose intermediate state energies span the interval 4864 MeV [$D_0^{\text{*}}\left(2300\right){\overline{D}}_0\left(2550\right)$]–5277 MeV [$D_{\text{s}2}^{\text{*}}\left(2573\right){\overline{D}}_{\text{s}1}^{\text{*}}\left(2700\right)$]. In the case of ${\chi }_{\text{c}}\left(4P\right)$ s, we need to include both $1S2S$ and $1P1P$ loops: this is because the masses of $4P$ charmonia overlap with both $1S2S$ and $1P1P$ intermediate-state energies. We also give results obtained by considering $1S2S$, $1P1P$, and $1S1P$ sets of intermediate states, because the $1S1P$ loops may have an important impact on the properties of the $X\left(4500\right)$ as ${\chi }_{\text{c}0}\left(4P\right)$. Furthermore, we neglect charmonium loops, like ${\eta }_{\text{c}}{\eta }_{\text{c}}\left(2S\right)$, whose contributions are expected to be very small because of the suppression mechanism of Supplementary Eq. S9, and Ref. 47, Eq. 12; see also Ref. 27.

The values of the physical masses, $M_A$, of the ${\chi }_{\text{c}}\left(4P,5P\right)$ states should be extracted from the experimental data [1]. However, except for the existing ${\chi }_{\text{c}0}\left(4P,5P\right)$ candidates, $X\left(4500\right)$ and $X\left(4700\right)$, nothing is known about the remaining and still unobserved ${\chi }_{\text{c}}\left(4P,5P\right)$ states, namely the $h_{\text{c}}\left(4P,5P\right)$, ${\chi }_{\text{c}1}\left(4P,5P\right)$, and ${\chi }_{\text{c}2}\left(4P,5P\right)$ resonances. Therefore, for the physical masses of the previous unobserved states we use the same values as the bare ones; see Table 2. In the case of ${\chi }_{\text{c}0}\left(4P,5P\right)$ states, we make the tentative assignments: ${\chi }_{\text{c}0}\left(4500\right)\to {\chi }_{\text{c}0}\left(4P\right)$ and ${\chi }_{\text{c}0}\left(4700\right)\to {\chi }_{\text{c}0}\left(4P\right)$ or ${\chi }_{\text{c}0}\left(5P\right)$. We thus provide three sets of results for the relative or renormalized threshold corrections, one for each of the previous ${\chi }_{\text{c}0}\left(4P,5P\right)$ assignments. For simplicity, in the present self-energy calculations we do not consider mixing effects between $|1^1{P}_1\rangle$ and $|1^3{P}_1\rangle$ charmed and charmed-strange mesons. Thus, the $\langle BCk\ell J\left|T^{†}\right|A\rangle$ vertices of Eq. 5 are computed under the approximation: $|1P_1\rangle \simeq |1^1{P}_1\rangle$ and $|1P_1^{\prime }\rangle \simeq |1^3{P}_1\rangle$.

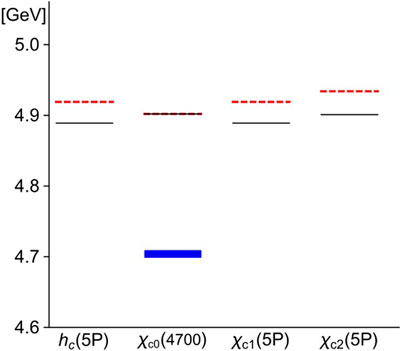
Finally, the self-energy and “renormalized” threshold corrections, calculated according to Eqs. 5 and 6, are reported in Tables 6–8. It is worth noting that: 1) the threshold corrections cannot provide an explanation of the discrepancy between the relativized QM value of the ${\chi }_{\text{c}0}\left(4P\right)$ mass, 4613 MeV, and the experimental mass of either the ${\chi }_{\text{c}0}\left(4500\right)$ or ${\chi }_{\text{c}0}\left(4700\right)$ suspected exotics. One may attempt to use a different renormalization prescription. For example, in the case of the ${\chi }_{\text{c}0}\left(4P\right)\to {\chi }_{\text{c}0}\left(4700\right)$ assignment, one may define the quantity ${\widetilde{\text{Δ}}}_{\text{th}}=\text{Σ}\left[{\chi }_{\text{c}2}\left(4P\right)\right]$ rather than ${\text{Δ}}_{\text{th}}=\text{Σ}\left[{\chi }_{\text{c}0}\left(4P\right)\right]$ and then plug ${\widetilde{\text{Δ}}}_{\text{th}}$ into Eq. 6. As a result, the calculated physical mass of the $X\left(4700\right)$ would be shifted 24 MeV upwards (to 4637 MeV) and would thus be closer to the experimental value, $4704\pm {10}_{-24}^{+14}$ MeV [1]. However, the difference between the calculated and experimental masses, 67 MeV, would still be larger than the typical error of a QM calculation, $\mathrm{}\left(30-50\right)$ MeV; 2) something similar happens in the ${\chi }_{\text{c}0}\left(5P\right)$ case. Here, the tentative assignment ${\chi }_{\text{c}0}\left(5P\right)\to {\chi }_{\text{c}0}\left(4700\right)$ does not work because of the large discrepancy between the calculated and experimental masses of the ${\chi }_{\text{c}0}\left(5P\right)$ as ${\chi }_{\text{c}0}\left(4700\right)$, namely 4902 and 4704 MeV, respectively; see Figure 2; 3) the renormalized threshold corrections of Table 6 are of the order of $20-30$ MeV. The difference between the relativized QM predictions for ${\chi }_{\text{c}0}\left(4P,5P\right)$ and the experimental masses of the ${\chi }_{\text{c}0}\left(\mathrm{4500,4700}\right)$ ranges from $\mathrm{}\left(100\right)$ MeV in the ${\chi }_{\text{c}0}\left(4P\right)$ case to $\mathrm{}\left(200\right)$ MeV for the ${\chi }_{\text{c}0}\left(5P\right)$. Because of the wide difference between the data and the QM predictions, the previous threshold corrections do not seem large enough to provide a realistic solution to the mismatch. We thus state that the assignment ${\chi }_{\text{c}0}\left(5P\right)\to {\chi }_{\text{c}0}\left(4700\right)$ is unacceptable; the tentative assignments ${\chi }_{\text{c}0}\left(4P\right)\to {\chi }_{\text{c}0}\left(4500\right)$ or ${\chi }_{\text{c}0}\left(4700\right)$ are quite difficult to justify, but cannot be completely excluded.

TABLE 6

TABLE 6. Coupled-channel model results for the relative threshold corrections of ${\chi }_{\text{c}}\left(4P\right)$ and ${\chi }_{\text{c}}\left(5P\right)$ states, calculated via Eq. 6.

TABLE 7

TABLE 7. Self-energy corrections, $\text{Σ}\left(M_A\right)$ (in MeV), to the bare masses of ${\chi }_{\text{c}}\left(4P\right)$ states, calculated via Eq. 5.

TABLE 8

TABLE 8. As Table 7, but for ${\chi }_{\text{c}}\left(5P\right)$ charmonia.

FIGURE 2

FIGURE 2. Masses of the ${\chi }_{\text{c}}\left(5P\right)$ multiplet members with threshold corrections; see Table 6. Here, we consider the assignment ${\chi }_{\text{c}0}\left(5P\right)\to {\chi }_{\text{c}0}\left(4700\right)$. The blue box stands for the available experimental data [1], the dashed and continuous lines for the calculated bare and physical masses, respectively. The wide energy gap between the experimental and calculated mass of the ${\chi }_{\text{c}0}\left(5P\right)$ state as ${\chi }_{\text{c}0}\left(4700\right)$ is a strong indication of the unlikelihood of this assignment.

4 Conclusion

We studied the main properties (masses and open-flavor strong decays) of the $4P$ and $5P$ charmonium multiplets. While there are two candidates for the ${\chi }_{\text{c}0}\left(4P,5P\right)$ states, the $X\left(4500\right)$ and $X\left(4700\right)$ resonances [1, 18, 25], the properties of the other members of the ${\chi }_{\text{c}}\left(4P,5P\right)$ multiplets are still completely unknown.

With this in mind, we first explored the pure charmonium interpretation for these mesons by means of Quark Model (QM) calculations of their open-flavor and radiative decay widths. Our QM results, although not conclusive, would suggest the assignments ${\chi }_{\text{c}0}\left(4500\right)\to {\chi }_{\text{c}0}\left(4P\right)$ and ${\chi }_{\text{c}0}\left(4700\right)\to {\chi }_{\text{c}0}\left(5P\right)$, even if ${\chi }_{\text{c}0}\left(4700\right)\to {\chi }_{\text{c}0}\left(4P\right)$ cannot be ruled out completely.

We also discussed the ${\chi }_{\text{c}0}\left(4500\right)$ and ${\chi }_{\text{c}0}\left(4700\right)$ “mass problem”, i.e., the incompatibility between the QM predictions for their masses [28] and the experimental data [1, 18, 25], by making use of a Coupled-Channel Model (CCM) based on the UQM formalism [26, 27]. According to our results for the ${\chi }_{\text{c}0}\left(4500\right)$ and ${\chi }_{\text{c}0}\left(4700\right)$ masses with threshold/loop corrections, it seems difficult to reconcile the QM predictions with the experimental data, with the possible exception of ${\chi }_{\text{c}0}\left(4P\right)\to {\chi }_{\text{c}0}\left(4500\right)$ or ${\chi }_{\text{c}0}\left(4700\right)$.

We thus conclude that the ${\chi }_{\text{c}0}\left(4500\right)$ and ${\chi }_{\text{c}0}\left(4700\right)$ states, which are at the moment excluded from the PDG summary table [1], are more likely to be described as multiquark states rather than charmonium or charmonium-like ones.

Data Availability Statement

All the raw data supporting the conclusions of this article are already published in the present article.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The authors acknowledge financial support from the Academy of Finland, Project no. 320062, and INFN, Italy.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer AP declared a past co-authorship with the authors to the handling editor.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.642028/full#supplementary-material.

Footnotes

¹The physical masses of heavy quarkonia are the sum of a bare energy term and a self-energy/threshold correction.

²The $X\left(4500\right)$ and $X\left(4700\right)$ were observed at LHCb in 2016 [18], and the $X\left(4274\right)$ was first observed in 2011 by CDF with a small significance of $3.1\sigma$ [17], while Stancu’s analysis dates back to 2010.

³Four $J/\psi \varphi$ structures were reported by LHCb only on the basis of a 6D amplitude analysis [38]. A narrow $X\left(4140\right)$ was reported by CDF [41] and then confirmed by D0 [42]. BaBar did not see anything statistically significant [43]. CMS confirmed a slightly broader X(4140) and a less significant second peak [44]. The LHCb amplitude analysis supersedes all this, and finds a much broader X(4140) [18].

References

1. Zyla PA, Barnett RM, Beringer J, Dahl O, Dwyer DA, Groom DE, et al. Particle data group. Review of Particle Physics. PTEP (2020) no. 8:083C01. doi:10.1093/ptep/ptaa104

CrossRef Full Text | Google Scholar

2. Aaij R, Adeva B, Adinolfi M, Ajaltouni Z, Akar S, Albrecht J, et al. [LHCb collaboration]. First Observation of Excited Ω_b^- States. Phys Rev Lett (2017) 118:182001. doi:10.1103/physrevlett.118.109901

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Yelton Y, Adachi I, Aihara H, Said SA, Asner DM, Aulchenko V, et al. Belle collaboration. Observation of excited Ω_c charmed baryons in e⁺ e^- collisions. Phys Rev D (2018) 97:051102. doi:10.1103/PhysRevD.97.051102

CrossRef Full Text | Google Scholar

4. Aaij R, Adeva B, Adinolfi M, Aidala CA, Ajaltouni Z, Akar S, et al. [LHCb collaboration]. Observation of a new Ξ_b⁻ resonance. Phys Rev Lett (2018) 121:072002. doi:10.1103/PhysRevLett.121.072002

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Aaij R, Beteta CA, Adeva B, Adinolfi M, Aidala CA, Ajaltouni Z, et al. [LHCb collaboration]. Observation of Two Resonances in the ${\Lambda }_b^0{\pi }^{\pm }$ Systems and Precise Measurement of ${\mathrm{\sum }}_b^{\pm }$ and ${\mathrm{\sum }}_b^{\ast \pm }$ Properties. Phys Rev Lett (2019) 122:012001. doi:10.1103/PhysRevLett.122.012001

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Aad G, Abbott B, Abdallah J, Abdelalim AA, Abdesselam A, Abdinov O, et al. [ATLAS collaboration].Observation of a New χb State in Radiative Transitions to $r\left(\mathrm{1}\mathit{S}\right)$ and $r\left(\mathrm{2}\mathit{S}\right)$ at ATLAS. Phys Rev Lett (2012) 108:152001. doi:10.1103/PhysRevLett.108.152001

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Abazov VM, Abbott B, Acharya BS, Adams M, Adams T, Alexeev GD, et al. [D0 collaboration]. Observation of a narrow mass state decaying into $\text{r}\left(1\mathit{S}\right)+\gamma$ in $\mathrm{p}\overline{\mathrm{p}}$ collisions at $\sqrt{s}=1.96\mathrm{TeV}$. Phys Rev D (2012) 86:031103. doi:10.1103/PhysRevD.86.031103

CrossRef Full Text | Google Scholar

8. Sirunyan AM, Tumasyan A, Adam W, Ambrogi F, Asilar E, Bergauer T, et al. [Cms Collaboration]. Observation of the χb1(3P) and χb2(3P) and measurement of their masses. Phys Rev Lett (2018) 121:092002. doi:10.1103/PhysRevLett.121.092002

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Esposito A, Pilloni A, Polosa AD. Multiquark Resonances. Phys Rep (2016) 668:1. doi:10.1016/j.physrep.2016.11.002 Available from: arXiv:1611.07920.

CrossRef Full Text | Google Scholar

10. Ali A, Lange JS, Stone S. Exotics: heavy pentaquarks and tetraquarks. Prog Part Nucl Phys (2017) 97:123. doi:10.1016/j.ppnp.2017.08.003

CrossRef Full Text | Google Scholar

11. Olsen SL, Skwarnicki T, Zieminska D. Nonstandard heavy mesons and baryons: experimental evidence. Rev Mod Phys (2018) 90:015003. doi:10.1103/revmodphys.90.015003

CrossRef Full Text | Google Scholar

12. Guo FK, Hanhart C, Meißner UG, Wang Q, Zhao Q, Zou BS. Hadronic molecules. Rev Mod Phys (2018) 90:015004. doi:10.1103/revmodphys.90.015004

CrossRef Full Text | Google Scholar

13. Liu YR, Chen HX, Chen W, Liu X, Zhu SL. Pentaquark and tetraquark states. Prog Part Nucl Phys (2019) 107:237. doi:10.1016/j.ppnp.2019.04.003

CrossRef Full Text | Google Scholar

14. Choi SK, Olse SL, Abe K, Abe T, Adachi I, Sup Ahn B, et al. [Belle collaboration]. Observation of a narrow charmoniumlike state in exclusive $B^{\pm }\to K^{\pm }{\pi }^{+}{\pi }^{-}J/\psi$ decays. Phys Rev Lett (2003) 91:262001. doi:10.1103/physrevlett.91.124101

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Acosta D, Affolder T, Ahn MH, Akimoto T, Albrow MG, Ambrose D, et al. [CDF collaboration]. Observation of the Narrow State $X\left(3872\right)\to J/\psi {\pi }^{+}{\pi }^{-}$ in $\overline{p}p$ Collisions at $\sqrt{s}=1.96TeV$. Phys Rev Lett (2004) 93:072001. doi:10.1103/PhysRevLett.93.072001

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Abazov VM, Abbott B, Abolins M, Acharya BS, Adams DL, Adams M, et al. [D0 collaboration]. Observation and properties of the $X\left(3872\right)$ decaying to $J/\psi {\pi }^{+}{\pi }^{-}$ in $p\overline{p}$ Collisions at $\sqrt{s}=1.96\mathrm{TeV}$. Phys Rev Lett (2004) 93:162002. doi:10.1103/PhysRevLett.93.162002

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Aaltonen T, Amerio S, Amidei D, Anastassov A, Annovi A, Antos A, et al. [CDF collaboration]Observation of the $Y\left(4140\right)$ structure in the $J/\psi \varphi$ Mass Spectrum in $J/\psi \varphi K$ cays. Mod Phys Lett A (2017) 32:1750139. doi:10.1142/S0217732317501395

CrossRef Full Text | Google Scholar

18. Aaij R, Adeva B, Adinolfi M, Ajaltouni Z, Akar S, Albrecht J, et al. [LHCb collaboration]Observation of $J/\psi \varphi$ structures consistent with exotic states from amplitude analysis of $B^{+}\to J/\psi \varphi K^{+}$ decays. Phys Rev Lett (2017) 118:022003. doi:10.1103/PhysRevLett.118.022003

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Ablikim M, Achasov MN, Ai XC, Albayrak O, Ambrose DJ, An FF, et al. [BESIII collaboration]. Observation of a Charged Charmoniumlike Structure in $e^{+}{e}^{-}\to {\pi }^{+}{\pi }^{-}J/\psi$ at $\sqrt{s}=4.26\mathrm{GeV}$. Phys Rev Lett (2013) 110:252001. doi:10.1103/PhysRevLett.110.252001

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Liu ZQ, Shen CP, Yuan CZ, Adachi I, Aihara H, Asner DM, et al. [Belle collaboration]Study of $e^{+}{e}^{-}\to {\pi }^{+}{\pi }^{-}J/\psi$ and observation of a charged charmoniumlike state at belle. Phys Rev Lett (2013) 110:252002. doi:10.1103/PhysRevLett.110.252002

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Bondar A, Garmash A, Mizuk R, Santel D, Kinoshita K, Adachi I, et al. [Belle collaboration]. Observation of Two Charged Bottomoniumlike Resonances in r(5S) decays. Phys Rev Lett (2012) 108:122001. doi:10.1103/PhysRevLett.108.122001

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Voloshin MB. Strange hadrocharmonium. Phys Lett B (2019) 798:135022. doi:10.1016/j.physletb.2019.135022

CrossRef Full Text | Google Scholar

23. Ferretti J, Santopinto E. Hidden-charm and bottom tetra- and pentaquarks with strangeness in the hadro-quarkonium and compact tetraquark models. JHEP (2020) 04:119. doi:10.1007/JHEP04(2020)119

24. Ablikim M, Achasov MN, Adlarson P, Ahmed S, Albrecht M, Aliberti R, et al. [BESIII]. Observation of a near-threshold structure in the $K^{+}$recoil-mass spectra in, $e^{+}{e}^{-}\to K^{+}\left(D_s^{-}{D}^{\text{*}0}+D_s^{\text{*}-}{D}^0\right)$. Phys Rev Lett (2021) 126:102001. doi:10.1103/PhysRevLett.126.102001

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Aaij R, Adeva B, Adinolfi M, Ajaltouni Z, Akar S, Albrecht J, et al. [LHCb collaboration]. Amplitude analysis of $B^{+}\to {J/\psi \varphi K}^{+}$ decays. Phys Rev D (2017) 95:012002. doi:10.1103/PhysRevD.95.012002

CrossRef Full Text | Google Scholar

26. Ferretti J, Santopinto E. Threshold corrections of χc(2P) and χb(3P) states and J/ψρ and J/ψω transitions of the X(3872) in a coupled-channel model. Phys Lett B (2019) 789:550. doi:10.1016/j.physletb.2018.12.052

CrossRef Full Text | Google Scholar

27. Ferretti J, Santopinto E, Anwar MN, Lu Y. Quark structure of the χc(3P) and X(4274) resonances and their strong and radiative. Eur Phys J C (2020) 80:464. doi:10.1140/epjc/s10052-020-8032-5

CrossRef Full Text | Google Scholar

28. Godfrey S, Isgur N. Mesons in a relativized quark model with chromodynamics. Phys Rev D (1985) 32:189. doi:10.1103/physrevd.32.189

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Lü QF, Dong YB. Masses of open charm and bottom tetraquark states in a relativized quark model. Phys Rev D (2016) 94:074007. doi:10.1103/physrevd.94.094041

CrossRef Full Text | Google Scholar

30. Anwar MN, Ferretti J, Santopinto E. Spectroscopy of the hidden-charm $\left[qc\right]\left[\overline{q}\overline{c}\right]$ and $\left[sc\right]\left[\overline{s}\overline{c}\right]$ tetraquarks in the relativized diquark model. Phys Rev D (2018) 98:094015. doi:10.1103/physrevd.98.094015

CrossRef Full Text | Google Scholar

31. Maiani L, Polosa AD, Riquer V. Interpretation of axial resonances in $J/\psi -\varphi$ at the LHCb. Phys Rev D (2016) 94:054026. doi:10.1103/physrevd.94.054026

CrossRef Full Text | Google Scholar

32. Ortega PG, Segovia J, Entem DR, Fernández F. Molecular components in P-wave charmed-strange mesons. Phys Rev D (2016) 94:114018. doi:10.1103/physrevd.94.074037

CrossRef Full Text | Google Scholar

33. Chen HX, Cui EL, Chen W, Liu X, Zhu SL. Understanding the internal structures of X(4140), X(4274), X(4500) and X(4700). Eur Phys J C (2017) 77:160. doi:10.1140/epjc/s10052-017-4737-5

CrossRef Full Text | Google Scholar

34. Oncala R, Soto J. Heavy quarkonium hybrids: spectrum, decay, and mixing. Phys Rev D (2017) 96:014004. doi:10.1103/physrevd.96.014004

CrossRef Full Text | Google Scholar

35. Liu XH. How to understand the underlying structures of X (4140), X (4274), X (4500) and X (4700). Phys Lett B (2017) 766:117. doi:10.1016/j.physletb.2017.01.008

CrossRef Full Text | Google Scholar

36. Geiger P, Isgur N. Quenched approximation in the quark model. Phys Rev D (1990) 41:1595. doi:10.1103/physrevd.41.1595

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Stancu F. Can Y(4140) be a c \bar{c} s \bar{s} tetraquark?. J Phys G: Nucl Part Phys (2010) 37:075017. doi:10.1088/0954-3899/37/7/075017

CrossRef Full Text | Google Scholar

38. Aaij R, Abellan Beteta C, Adeva B, Adinolfi M, Adrover C, Affolder A, et al. [LHCb collaboration]. Search for the $X\left(4140\right)$ state in $B^{+}\to {J/\psi \varphi K}^{+}$ decays. Phys Rev D (2012) 85:091103. doi:10.1103/PhysRevD.85.091103

CrossRef Full Text | Google Scholar

39. Vijande J, Fernández F, Valcarce A. Constituent quark model study of the meson spectra. J Phys G: Nucl Part Phys (2005) 31:481. doi:10.1088/0954-3899/31/5/017

CrossRef Full Text | Google Scholar

40. Segovia J, Yasser AM, Entem DR, Fernández F. $J^{PC}=1^{--}$hidden charm resonances. Phys Rev D (2008) 78:114033. doi:10.1103/physrevd.78.114033

CrossRef Full Text | Google Scholar

41. Aaltonen T, Amerio S, Amidei D, Anastassov A, Annovi A, Antos J, et al. [CDF]. Evidence for a narrow near-threshold structure in the $J/\psi \varphi$ mass spectrum in $B^{+}\to {J/\psi \varphi K}^{+}$. Phys Rev Lett (2009) 102:242002. doi:10.1103/PhysRevLett.102.242002

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Abazov VM, Abbott B, Acharya BS, Adams M, Adams T, Agnew JP, et al. [D0 collaboration]. Search for the $X\left(4140\right)$ state in $B^{+}\to J/\psi \varphi K^{+}$decays with the D0 detector. Phys Rev D (2014) 89:012004. doi:10.1103/PhysRevD.89.012004

CrossRef Full Text | Google Scholar

43. Lees JP, Poireau V, Tisserand V, Grauges E, Palano A, Eigen G, et al. [BaBar collaboration]. Study of $B^{\pm ,0}\to J/\psi K^{+}{K}^{-}{K}^{\pm ,0}$ and search for $B^0\to J/\psi \varphi$ at BaBar. Phys Rev D (2015) 91:012003. doi:10.1103/PhysRevD.91.012003

CrossRef Full Text | Google Scholar

44. Chatrchyan S, Khachatryan V, Sirunyan AM , Tumasyan A, Adam W, Bergauer T, et al. [CMS Collaboration]. Observation of a peaking structure in the $J/\psi \varphi$ mass spectrum from $B^{+}\to {J/\psi \varphi K}^{\pm }$ decays. Phys Lett B (2014) 734:261–81. doi:10.1016/j.physletb.2014.05.055

CrossRef Full Text | Google Scholar

45. Micu L. Decay rates of meson resonances in a quark model. Nucl Phys B (1969) 10:521. doi:10.1016/0550-3213(69)90039-x

CrossRef Full Text | Google Scholar

46. Le Yaouanc A, Oliver L, Pène O, Raynal JC. "Naive" quark-pair-creation model of strong-interaction vertices. Phys Rev D (1973) 8:2223. doi:10.1103/physrevd.8.2223

CrossRef Full Text | Google Scholar

47 Le Yaouanc A, Oliver L, Pène O, Raynal JC. Naive quark-pair-creation model and baryon decays. Phys Rev D (1974) 9:1415. doi:10.1103/physrevd.9.1415

CrossRef Full Text | Google Scholar

48. Roberts W, Silvestre-Brac B. General method of calculation of any hadronic decay in the3 P 0 model. Few-Body Syst (1992) 11:171. doi:10.1007/bf01641821

CrossRef Full Text | Google Scholar

49. Ackleh ES, Barnes T, Swanson ES. On the mechanism of open-flavor strong decays. Phys Rev D (1996) 54:6811. doi:10.1103/physrevd.54.6811

CrossRef Full Text | Google Scholar

50. Barnes T, Close FE, Page PR, Swanson ES. Higher quarkonia. Phys Rev D (1997) 55:4157. doi:10.1103/physrevd.55.4157

CrossRef Full Text | Google Scholar

51. Ferretti J, Galatà G, Santopinto E. Interpretation of the $X\left(3872\right)$ as a charmonium state plus an extra component due to the coupling to the meson-meson continuum. Phys Rev C (2013) 88:015207. doi:10.1103/physrevc.88.015207

CrossRef Full Text | Google Scholar

52. Ferretti J, Santopinto E. Open-flavor strong decays of open-charm and open-bottom mesons in the ³$P_0$ model. Phys Rev D (2018) 97:114020. doi:10.1103/physrevd.97.114020

CrossRef Full Text | Google Scholar

53. Ferretti J, Galatà G, Santopinto E. Quark structure of the $X\left(3872\right)$ and $x_b\left(3P\right)$ resonances. Phys Rev D (2014) 90:054010. doi:10.1103/physrevd.90.054010

CrossRef Full Text | Google Scholar

54. Ferretti J, Galatà G, Santopinto E, Vassallo A. Bottomonium self-energies due to the coupling to the meson-meson continuum. Phys Rev C (2012) 86:015204. doi:10.1103/physrevc.86.015204

CrossRef Full Text | Google Scholar

55. Kalashnikova YS. Coupled-channel model for charmonium levels and an option for $X\left(3872\right)$. Phys Rev D (2005) 72:034010. doi:10.1103/physrevd.72.034010

CrossRef Full Text | Google Scholar

56. Bijker R, Ferretti J, Galatà G, García-Tecocoatzi H, Santopinto E. Strong decays of baryons and missing resonances. Phys Rev D (2016) 94:074040. doi:10.1103/physrevd.94.074040

CrossRef Full Text | Google Scholar

57. Bijker R, Santopinto E. Unquenched quark model for baryons: magnetic moments, spins, and orbital angular momenta. Phys Rev C (2009) 80:065210. doi:10.1103/physrevc.80.065210

CrossRef Full Text | Google Scholar

58. Ferretti J, Santopinto E. In preparation.

59. Kokoski R, Isgur N. Meson decays by flux-tube breaking. Phys Rev D (1987) 35:907. doi:10.1103/physrevd.35.907

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Lee SH, Ko CM. Charmonium mass in nuclear matter. Phys Rev C (2003) 67:038202. doi:10.1103/PhysRevC.67.038202

CrossRef Full Text | Google Scholar

61. Kumar A, Mishra A. D-mesons and charmonium states in hot isospin asymmetric strange hadronic matter. Eur Phys J A (2011) 47:164. doi:10.1140/epja/i2011-11164-6

CrossRef Full Text | Google Scholar

62. Eichten E, Gottfried K, Kinoshita T, Lane KD, Yan TM. Charmonium: the model. Phys Rev D (1978) 17:3090. doi:10.1103/physrevd.17.3090

CrossRef Full Text | Google Scholar

63. Barnes T, Godfrey S, Swanson ES. Higher charmonia. Phys Rev D (2005) 72:054026. doi:10.1103/physrevd.72.054026

CrossRef Full Text | Google Scholar

64. Heikkilä K, Törnqvist NA, Ono S. Heavycc¯andbb¯quarkonium states and unitarity effects. Phys Rev D (1984) 29:110. doi:10.1103/physrevd.29.110

CrossRef Full Text | Google Scholar

65. Heikkilä K, Tornqvist NA, Ono S.Erratum: heavycc¯andbb¯quarkonium states and unitarity effects. Phys Rev D 29, 2136 (1984). doi:10.1103/physrevd.29.2136

CrossRef Full Text | Google Scholar

66. Pennington MR, Wilson DJ. Decay channels and charmonium mass shifts. Phys Rev D (2007) 76:077502. doi:10.1103/physrevd.76.077502

CrossRef Full Text | Google Scholar

67. Ortega PG, Segovia J, Entem DR, Fernandez F. Coupled channel approach to the structure of the $X\left(3872\right)$. Phys Rev D (2010) 81:054023. doi:10.1103/physrevd.81.054023

CrossRef Full Text | Google Scholar

68. Ortega PG, Entem DR, Fernández F. Molecular structures in the charmonium spectrum: theXYZpuzzle. J Phys G: Nucl Part Phys (2013) 40:065107. doi:10.1088/0954-3899/40/6/065107

CrossRef Full Text | Google Scholar

69. Lu Y, Anwar MN, Zou BS. Coupled-channel effects for the bottomonium with realistic wave functions. Phys Rev D (2016) 94:034021. doi:10.1103/physrevd.94.034021

CrossRef Full Text | Google Scholar

70. Lu Y, Anwar MN, Zou BS. How large is the contribution of excited mesons in coupled-channel effects? Phys Rev D (2017) 95:034018. doi:10.1103/physrevd.95.034018

CrossRef Full Text | Google Scholar

71. Ferretti J, Santopinto E. Higher mass bottomonia. Phys Rev D (2014) 90:094022. doi:10.1103/physrevd.90.094022

CrossRef Full Text | Google Scholar