Systemic Risk Caused by the Overlapping Portfolios of Banks Under a Bilateral Network

Frequent financial crises and economic globalization have made systemic risk a growing Research Topic. This paper constructs a dynamic banking system model based on the bank-asset bilateral network. By collecting the balance sheet and portfolio data of 47 Chinese listed banks in 2018, the paper firstly empirically analyses the impact of external shocks, the price-cutting effect, and the proportion of various assets held by banks to their total assets on the systemic risk of the banking system. The risk preference coefficient and systemic shock are then introduced to construct the banks' quantitative portfolio strategy model to study its optimal investment. It has been found that the greater the external shock and the stronger the price-cutting effect, the higher the systemic risk. Moreover, the external shock and price-cutting effect will have a superimposed effect within a specific range, and systemic risk will increase significantly. The asset classes of the Chinese banking system have a different sensitivity to external shocks, among which loan assets are the most sensitive. Further studies reveal an inflection point of risk preference, resulting in banks' expected return “increasing first and then decreasing.” The higher the debt-asset ratio and the stronger the banks' risk tolerance, the more aggressive investment strategies banks can choose to achieve high returns. This paper provides a reference for the banking industry to react to shocks and analyze systemic risk.

Introduction

Affected by global financial crisis, economic globalization, and the rapid development of Internet finance, the current financial environment is increasingly complex. Financial risks are easier to transmit, spread, and accumulate through the internal connections between financial institutions, thus quickly form a systemic risk. Once systemic risk breaks out, it will produce enormous destructive power among financial institutions, and the banking industry is the core of finance. Therefore, the systemic risk of the banking system is one of the main sources of financial crises, and it is also a hot topic of current related research.

The current research on the systemic risk of the banking system mainly focuses on two channels, the direct contagion channel based on the interbank lending market (bank-bank) and the indirect contagion channel based on the portfolios of banks (bank-asset). Under the direct contagion channel, most of the research focuses on the role of risk-sharing and risk contagion played by interbank lending linkages. Most studies have shown that interbank linkages have a dual effect of risk-sharing and risk contagion [Allen and Gale [1]; Leitner [2]; Iori et al. [3]; Nier et al. [4]; Gai and Kapadia [5]; Tedeschi et al. [6]; Georg [7]; Ladley [8]; Deng et al. [9]; Chen et al. [10]; Grilli et al. [11]; Li and Li [12]; Vitali et al. [13]; Calomiris and Carlson [14]]. While some studies have only revealed unilateral effects. Freixas et al. [15] conducted similar research to Allen and Gale [1], the results showed that the interbank linkages play a positive role in risk-sharing. Studies by Brusco and Castiglionesi [16], Bao [17], Wang et al. [18], and Zhou et al. [19] showed that interbank linkages play a role in risk contagion. Besides, Barucca et al. [20] made extended clearing models of interdependent liabilities by considering the uncertainty of banks' external assets, and presented a comprehensive modeling framework for systemic risk in the interbank market. He and Li [21] investigated the systemic risk in the interbank market with different network topologies. They found that network entropy was positively correlated with the effect of systemic risk in the three types of interbank networks. Network entropy in the small-world network was the largest, followed by those in the random and scale-free network. Ramadiah et al. [22] also studied systemic risk in relation to network topology. They considered different realistic network topologies to model shock propagation dynamics and showed that the systemic risk properties of a financial network were extremely sensitive to its network characteristics.

Relevant research under the indirect contagion channel is relatively less, but it has attracted the attention of some researchers. They mainly discuss the impact of changes in asset prices on systemic risk when different banks invest in the same asset class. The studies by Shleifer and Vishny [23], Tsatskis [24], Duarte and Eisenbach [25], Braouezec and Wagalath [26], and Greenwood et al. [27] all focus on financial risk caused by asset prices. Tsatskis [24] proposed a banking network model that focuses on quantifying the impact of asset price changes on systemic risk. However, the research only constructed related models without launching further discussions and practical applications. Duarte and Eisenbach [25] developed a “vulnerability index” for the sale of large bank assets at reduced prices, mainly studying the effects of relevant factors on the “vulnerability index” and also showed that the index could measure the systemic risk of spillovers from reduced prices. Braouezec and Wagalath [26] proposed an asset price-oriented framework and found that the contagion of bank failure under the influence of asset prices was significant. Greenwood et al. [27] had presented a model in which fire sales propagate shocks through bank balance sheets, and the fire sales spillovers were described by a simple linear model. In the latest related research, Tasca et al. [28] investigated the effect of the level of diversification of external assets on the failure probability of the system. Based on a simplified mathematical model, Yao et al. [29] showed that reducing investment portfolio diversification and controlling the interbank lending ratio can reduce systemic risk to a certain extent. Squartini et al. [30] and Gangi et al. [31] used the improved CAPM model and the method of maximizing entropy to reconstruct the bank-asset bilateral financial network, and analyzed the systemic risk caused by the spillover of the price cut.

Besides, Huang et al. [32], Chen et al. [33], Caccioli et al. [34], Levy-Carciente et al. [35], Fang and Zheng [36], Zhang et al. [37], Fan and Liu [38], and Jiang and Fan [39] all built a bank (financial institution)-asset bilateral network model for further study. Huang et al. [32] and Levy-Carciente et al. [35] conducted empirical studies on U.S. commercial banks and Venezuelan banks, respectively, which are based on the bank-asset bilateral network model and found that the models can be used for systemic risk stress testing of the financial system. Chen et al. [33] developed a company-asset bilateral network model based on asset price contagion to analyze systemic risks in financial markets. Similarly, Caccioli et al. [34] constructed a bank-asset bilateral network banking system and investigated the stability characteristics of the banking network under banks' overlapping portfolios. Based on Caccioli et al. [34], Caccioli et al. [40] further proposed a banking network model under the interbank trading channel and the overlapping portfolio channel, empirically studying systemic risks in the banking system under both channels. Jiang and Fan [39] also proposed a model for the interbank market with overlapping portfolios and introduced investment risk to simulate the systemic risk of the banking system. Fang and Zheng [36] used the network model of banks holding common assets to investigate the contagion path of systemic importance. Zhang et al. [37] and Fan and Liu [38] both studied financial risk under the bilateral network based on the financial network model of Caccioli et al. [34], and mainly simulated the impact of different factors in the system. Gualdi et al. [41] proposed a method to detect the most dangerous portfolio overlaps in bank-asset bipartite systems. They found that the similarity of institutional holdings increased significantly just before financial crises or bubble bursts, and stated that the method can be applied to any bipartite network.

The above research primarily analyzed the systemic risk and yielded rich research results. However, there are still some problems in the above work: (1) Empirical research on the systemic risk of the Chinese banking system based on the bank-asset bilateral network model has not yet been studied. We found that Caccioli et al. [34], Zhang et al. [37], and Fan and Liu [38] had carried out simulation analysis based on the bank-asset bilateral network but it did not involve empirical research. Caccioli et al. [40] had only conducted empirical research using Australian banking data for the interbank trading channel, but the overlapping portfolio channel had not been empirically conducted. Huang et al. [32] and Levy-Carciente et al. [35] conducted empirical studies based on the bank-asset bilateral network model. However, both focused on foreign banking systems, and the analysis was taken from the banks' perspective. Empirical research by Fang and Zheng [36] studied the Chinese banking system under the bilateral network, but mainly analyzed the contagion path, and did not study the systemic risk of the Chinese banking system under banks' overlapping portfolio. (2) The current analysis of banks' systemic risk management strategies is from the bank-bank perspective. Gauthier et al. [42], Liao et al. [43], and Fan et al. [44] had built quantitative bank risk management models, primarily studying how to manage systemic risks through the bank's macroprudential capital, and these studies are all interbank channels. The research under the bank-asset channel [Huang et al. [32]; Caccioli et al. [34]; Levy-Carciente et al. [35]] focuses on the impact of different asset classes on systemic risks, and the lack of research on the management of banking systemic risks in bilateral networks. In Levy-Carciente's work, they generated shock scenarios by randomly selecting one asset at a time to depreciate, which is inconsistent with reality and does not take into account the characteristics of the assets (different asset classes may appreciate or depreciate in the same market environment).

Based on the above analysis, this paper builds a banking network system under the bank-asset bilateral network, collects Chinese banks' actual portfolio data, and empirically studies the impact of external shocks, endogenous asset devaluations, and the proportion of various asset classes in the total bank assets on the systemic risk of the Chinese banking system. The model is related to Levy-Carciente et al. [35]. In their paper, Levy-Carciente et al. randomly select an asset to shock, which only considers the impact of asset devaluation when the asset is shocked and focuses on analyzing the bank's systemic risk. Yet there is no relevant research on its risk management based on the bilateral network. Our model extends their work. Unlike Levy-Carciente et al. [35], we construct the Chinese banking system under the bank-asset bilateral network and develop a quantitative investment strategy model. The quantitative investment strategy model presented in this paper has introduced the banks' risk preference and is based on the bilateral network, which is different from previous works [42–44]. Moreover, our model fully considers the evolution of assets in real scenarios, where the value of the asset may suffer losses and rise. Also, a systematic shock method is adopted in our model, whereby all asset classes are shocked at the same time. Furthermore, the existing models mentioned above only consider the systemic risk depending on the bank's default probability. Our investment strategy model takes into account the bank's survivability and expected return to investigate its optimal portfolio strategy.

We apply the bank-asset bilateral network model to 47 listed Chinese banks in 2018 and empirically investigate the systemic risk of the banking system. It shows that loan assets are the most sensitive to external shocks. Moreover, the external shock and the price-cutting effect will have a superimposed effect within a specific range, where systemic risk will increase sharply. This has not been noted by Levy-Carciente et al. [35]. We then use the quantitative investment strategy model to carry out the simulation. It should be noted that our analysis shows that there is an inflection point of risk preference. This means that the bank has an optimal risk preference when investing, so that it can determine its investment strategy based on the risk level of assets. Furthermore, the inflection point is different under different debt-asset ratios. This contributes to the banks' ability to make reasonable investment decisions.

The Model

Banks and assets, bank-bank, asset-asset, and bank-asset options in a complex network system all have complex interrelationships. The three links can form independently of each other, as well as interconnected networks. The interbank and inter-asset networks are composed only of the same type of nodes. In contrast, the bank-asset network comprises two different types of nodes, which have bilateral characteristics and is called a bilateral network.

In the existing research, Huang et al. [32], Chen et al. [33], Caccioli et al. [34], and Levy-Carciente et al. [35] all developed bank (financial institution)-asset bilateral network models by the interconnection between two different types of nodes. Based on the model of Levy-Carciente et al. [35], this paper uses the data of Chinese listed banks to construct a bank-asset bilateral network model of the Chinese banking system, and has revised the method of the asset class being shocked by switching from random shock to systemic shock. To construct the banks' quantitative investment strategy model, different asset classes with different types of risk and return are set up and the banks' risk preference coefficient is introduced. This paper has studied the systemic risks of Chinese banks and analyzed banks' optimal investment.

The Bank-Asset Bilateral Network

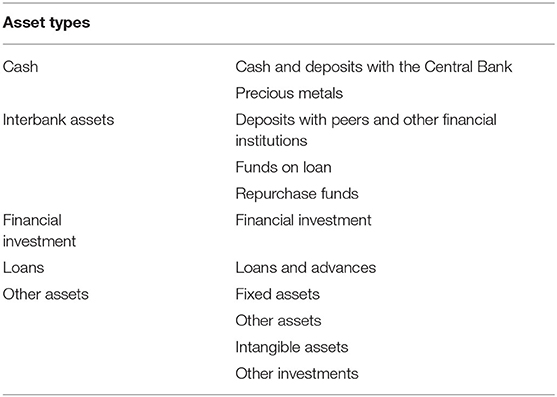
There are two types of nodes in the bank-asset bilateral network, such as bank nodes, and asset nodes. It assumes that there are no links between interbank nodes and the inter-asset nodes. Once a bank invests in a specific type of asset, a linkage between the bank and the asset is created. A bilateral network between a bank and an asset eventually develops through the banks' portfolio. A bank's portfolio contains various assets, such as interbank lending assets, cash, precious metals, fixed assets, credit, etc.

In the bank-asset bilateral network, the dynamic evolution algorithm is constructed as follows:

Step 1: Select one asset class from all asset classes to devalue it;

Step 2: The total assets of all banks held such as shocked assets (the shocked asset in step 1) are updated, and the updated total assets of each bank are compared with their total liabilities. If a bank becomes insolvent, the bank is declared bankrupt;

Step 3: The asset of the default bank is liquidated, and all of its assets are sold in fire sales, these asset classes will depreciate again; at the same time, the total value of the bank assets held in these depreciated asset classes will also have a cascading depreciation;

Step 4: Determine each bank's survival again and execute the above algorithm in sequence until there are no more bank failures.

As shown in Figure 1, firstly, the shock of assets A in Figure 1A depreciates their assets, and the total value of all banks that invest in this asset suffer losses (see bank 1, bank 2…bank i in Figure 1B). Among them, bank 1 defaulted due to insolvency, and the failed bank 1 sold all the assets it held (asset A, asset B. asset E in Figure 1C); similarly, the total value of the bank holding these assets depreciated again (see bank 2…bank i in Figure 1D). Consequently, a bank's failure in the bank-asset bilateral network can trigger chain reactions, resulting in cascading failures.

FIGURE 1

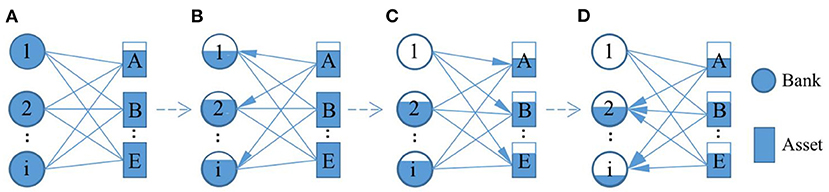
Figure 1. Evolution of bank-asset bilateral network. (A) Represents the asset class A depreciates. (B) Represents the total value of bank 1, bank 2… bank i that invest in asset class A suffers losses. (C) Represents bank 1 defaults, the assets it held asset A, asset B… asset E depreciates. (D) Represents the total value of bank 2… bank i suffers losses.

Dynamic Banking System Model Based on Bilateral Network

In this paper, $B_{i,1},B_{i,2},\dots \stackrel{·}{,}{B}_{i,N}$ is used to represent the various assets held in a bank's portfolio, where the subscript N is the total number of asset classes, and the total assets of bank i are B_i = ∑B_i,m, and L_i is represented by the bank's total liabilities. The total market value of asset class m is defined as A_m = ∑_iB_i,m, so the market share of what bank i invests in asset m is ε_i,m = B_i,m/A_m. Besides, the relative size β of the asset class m throughout the market is defined as β_m = A_m/∑_nA_n. For bank i, the proportion of its investment asset m to its total assets is η_i,m = B_i,m/B_i. According to the Chinese banking system's actual data, this paper can obtain the initial total assets of the banks, the initial total liabilities, the total value of each asset, and the bank-asset investment matrix.

B_i,m,τ represents the value of asset m after τ times of evolution in the model. Its initial value is B_{i, m,0}, then, the total asset of bank i after τ times of evolution in the model can be expressed as B_i,τ = ∑_mB_i,m,τ. In the same way, the total value of asset class m after τ times of evolution is expressed as A_m,τ = ∑_iB_i,m,τ. The total liabilities L_i of bank i are set to be fixed during the evolution of the model. Then an external shock p(p ∈ [0, 1]) is introduced to depreciate a specific asset class, and a non-liquidity parameter α(α ∈ [0, 1]) is introduced to measure the degree of depreciation of assets after a bank's fire sale.

p is an exogenous parameter, which is uncontrollable, and α is an endogenous parameter. Firstly, we select an asset class m′ for external shocks, and the total value of the asset class m′ after the shock is updated to:

$\begin{array}{ll}{A}_{m^{\prime },\tau =1}=p{A}_{m^{\prime },\tau =0.}& (1)\end{array}$

When p = 0.7, it means that the shocked asset class m′ has depreciated by 30%, while p = 0.3 means that the shocked asset has depreciated by 70%. Therefore, the larger the value of p, the smaller the external shock. It should be noted that, except for the shocked asset class, the other asset classes remain unchanged. Then, as long as any bank holds the shocked asset class, the asset class it holds will also be devalued in the same proportion, which can be described as follows:

$\begin{array}{ll}{B}_{i,m^{\prime },1}=p{B}_{i,m^{\prime },0}=B_{i,m^{\prime },0}\frac{A_{m^{\prime },1}}{A_{m^{\prime },0}}& (2)\end{array}$

After suffering a shock, each bank's total assets are recalculated and their updated total assets with their total liabilities are compared. If all the banks are satisfied B_i,1 > L_i, then all the banks survive, and the impact of the shock ends. If one bank is satisfied B_i,1 ≤ L_i, it means that the bank defaults under the shock, and the impact of the shock will continue. The defaulted bank will liquidate the assets and sell them at a reduced price. In the bank-asset bilateral network, any asset class associated with a failed bank is bound to depreciate and its asset class value will be updated as follows:

$\begin{array}{ll}{A}_{m,\tau +1}=A_{m,\tau }-\alpha B_{i,m,\tau .}\forall m,i|B_{i,1}\le L_i& (3)\end{array}$

The parameter α measures the price-cutting effect of a specific asset class. If α = 0, it means that the assets' total value held by the failed bank will not be affected by the fire sale of the failed bank, and will not trigger further cascading failures. If α = 1, it means the assets' total value held by the failed bank is suffering from depreciation, and will lose the total value of all asset classes held by the failed bank. In this case, the effect of the bank's price cuts will be maximized, which could trigger further insolvencies and continue to spread the impact of the shock. At the same time, the depreciation of asset classes will trigger the corresponding depreciation of similar assets held by each bank, which can be described as follows:

$\begin{array}{ll}{B}_{i,m,\tau }=B_{i,m,0}\frac{A_{m,\tau }}{A_{m,0}}.& (4)\end{array}$

The decrease in bank assets in the above equation can lead to more bank bankruptcies. The liquidation of the bank's bankruptcy will further depreciate the asset class and trigger a new round of bankruptcy. The impact of the shock will continue until there are no more bank failures in the system.

Banks' Quantitative Portfolio Strategy Model

The banks' portfolio strategy model is constructed from the asset perspective, as shown in Figure 2. According to the actual asset allocation of the Chinese banking system, banks generally choose to invest in assets with different types of risk and return. Therefore, in the banks' portfolio strategy model, we divide the asset classes into 10 types: {A₁, A₂…A₁₀} (rectangles in Figure 2) and assign different attributes to each asset class. The return rate of the asset class mis S_m, and the corresponding risk loss rate is R_m. At the same time, each bank is set to hold different proportions of various asset classes, as shown in the enlarged circle in Figure 2A. According to the latest bank benchmark interest rate released by the People's Bank of China, the annual interest rate of 1-year cash deposits is 1.5%, while that of 1-year bank loans in the same period is 4.35%. The ratio between the two is ~3. It is assumed that the return rate of the assets in the model is equivalent to the risk loss rate, set S_m = R_m ∈ [0.15, 0.45].

FIGURE 2

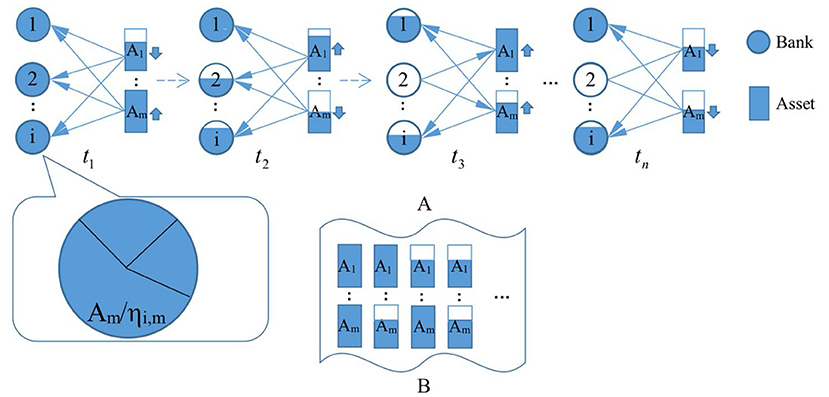
Figure 2. Bank's portfolio strategy model. (A) Represents all asset classes are simultaneously shocked at each time step. (B) Examples of all possible shock events.

Considering that the value of each asset in the banks' portfolio may be affected by the market environment. All asset classes are subject to external shocks at the same time instead of a specific asset class randomly shocked as in section The Bank-Asset Bilateral Network. Thus, the banks' portfolio strategy model adopts a systematic shock method in this section, namely that all asset classes are simultaneously shocked at each time step. As shown in Figure 2A, at the t₁ time step, the asset class A₁ suffers a negative shock, its total assets depreciate; the asset class A_m suffers a positive shock, its total assets increase. At the t₂ time step, the asset class A₁ suffers a positive shock, its total value of assets rebound; the asset class A_m suffers a negative shock, and its total assets depreciate. Likewise, each asset class is simultaneously impacted during the time steps t₃ … t_n, and the total value of the asset changes.

The profitable probability of asset class A_m at each time step is p_m, then its unprofitability probability, namely, a loss is 1 − p_m. Defining a particular external shock as an “event,” there are 2¹⁰ shock events in the model (see Figure 2B, the rectangle is full to indicate profit, not full to indicate loss). According to the “Guidelines for Bank Loan Loss Provision Provisions” issued by the People's Bank of China, the bank's loan loss provision ratio is at least 2% for high-quality loans, and it is up to 100% for poor-quality loans. The bank's average loan loss provision ratio is ~44%. Therefore, for the convenience of research, we set the loss probability of high-risk assets as 0.4 (i.e., the profit probability as 0.6) in our model and the loss probability of low-risk assets as 0.1 (i.e., the profit probability as 0.9). That is p_m ∈ [0.6, 0.9].

Since banks have different risk preferences, banks will have different investment allocation strategies. Moreover, in the empirical research of this paper, we find that the proportion of various assets held by each bank to its total assets has a significant impact on the bank's survival rate. To study the effect of the bank's investment portfolios, we introduce the bank's risk preference coefficient to adjust the bank's portfolio, and thus Equations (5) and (6) are introduced here. We use coefficient θ to represent the banks' risk preferences, θ from small to large, indicating that banks' risk preferences have shifted from steady to radical. When a bank invests asset classA_m, the impact function of each asset held by the bank is as follows:

$\begin{array}{ll}f(p_m,\theta )=\frac{1}{\sqrt{2\pi }}{e}^{\left(-50{(p_m+0.3\theta -0.9)}^2\right)}{p}_m\in \left[0.6,0.9\right],\theta \in \left[0,1\right]& (5)\end{array}$

In Equation (5), we assume that the impact factor of the bank's investment in a specific asset class follows a similar normal distribution. In this model, we have assumed that the profit of high-risk assets is also higher when it is profitable, and the profit of low-risk assets is also lower when it is profitable. Therefore, the impact factor of banks investing in the lowest risk assets is largest whenθ = 0; on the contrary, the impact factor of banks investing in the highest risk assets is largest when θ = 1. p_m is the profitable probability of asset class A_m (i.e., p_m can be used to measure asset risk) and p_m ∈ [0.6, 0.9], which is consistent with the above settings. Besides, 50 in Equation (5) is to make the difference of various assets in the investment portfolio more significant.

The proportion η of each asset held by the banks is expressed as follows:

$\begin{array}{ll}{\eta }_m=\frac{f(p_m,\theta )}{{\displaystyle \sum _{i=1}^M}f(p_i,\theta )}& (6)\end{array}$

In the simulation research of this study, we have explored the optimal asset portfolio ratio by adjusting the bank's risk preference. The optimal value enables the bank to achieve the highest return within the risk tolerance range. However, it does not represent the real value of the scene, and this study only proves that there is an optimal value.

We have set 10 types of assets in the investment strategy model in this paper, and each type of asset may appreciate or depreciate at each time step. Thus, the model defines 2¹⁰ events, and each event includes the appreciation or devaluation of each type of asset. Based on the profitable probability of each asset class, a random shock event for each asset class is generated in the system at the time step t. After the shock, the total value A_m of the asset class m and the value B_i,m of the asset class m held by the bank i are updated according to the event. When the asset value appreciates, it is expressed by Equation (7), when the asset value depreciates, it is expressed by Equation (8).

When the asset is profitable:

$\begin{array}{ll}\{\begin{array}{l}{A}_{m,t+1}=\left(1+S_m\right)A_{m,t},\\ B_{i,m,t+1}=\left(1+S_m\right)B_{i,m,t}.\end{array}& (7)\end{array}$

When assets are at a loss:

$\begin{array}{ll}\{\begin{array}{l}{A}_{m,t+1}=\left(1+R_m\right)A_{m,t},\\ B_{i,m,t+1}=\left(1+R_m\right)B_{i,m,t}.\end{array}& (8)\end{array}$

Where S_m in Equation (7) is the return rate of the asset class m, and R_m in Equation (8) is the corresponding risk loss rate.

Comparing the updated total assets of each bank with its total liabilities; if any bank is insolvent, it will sell its asset portfolio at a lower price, which will trigger further risks. At the same time, the market influence function is introduced in the bankruptcy liquidation of failed banks to measure more precisely the effect of asset price reduction [34]. In their study, Caccioli et al. [34] point out that it is the linear market impact for log-prices in the case of fire sales, so they use an exponential price impact function.

$\begin{array}{ll}g(x_m)=e^{-\partial x_m}& (9)\end{array}$

x_m indicates the ratio of the asset class m to be sold by the failed bank to the total value of the asset class m, and ∂ indicates the sensitivity of asset prices, that is, the degree of fluctuations caused by the fire sale of the asset class m. Caccioli et al. [34] have shown that the parameter ∂ is chosen such that the price drops by 10% when 10% of the asset is liquidated, i.e., ∂ = 1.0536. Based on this, when a bank goes bankrupt and is liquidated, the value of the asset class m after the τ times of price-cutting will change as follows:

$\begin{array}{ll}{A}_{m,\tau +1}=A_{m,\tau }*g(x_{m,\tau })& (10)\end{array}$

x_m,τ indicates that the proportion of asset class m sold at time τ is $x_m$.

We define the expected return E_i of the bank i to measure its profitability under the premise of ensuring its survival, which is defined as follows:

$\begin{array}{ll}{E}_i=P_i*\overline{Pro{f}_i}& (11)\end{array}$

Where $P_i=\frac{S{T}_i}{\lambda }$, P_i is the survival probability of bank i, ST_i is the survival times of bank i in the simulation experiments, λ is the total number of simulation experiments. ${\overline{Prof}}_i$ is the average return of bank i, and the income ${\overline{Prof}}_i$ of bank i is the difference between the value of the total assets of bank i after each simulation and its initial value.

Empirical Results

Data

We have collected the balance sheet data of 47 Chinese listed banks at the end of 2018. It covers five major types of Chinese banks, large state-owned commercial banks, joint-stock commercial banks, city commercial banks, rural commercial banks, and policy banks. It covers most listed banks in China. Therefore, the listed banks' data collected in this paper may reflect the overall asset status of various banks of the banking industry in China.

In this paper, each bank's assets are finally divided into five categories based on their investment attributes and income types, namely cash, interbank assets, financial investment, loans, and other assets. Special assets in the bank's balance sheet are classified according to their nature or classified as other assets. For example, goodwill is an intangible asset and is attributable to other assets; financial leases are investment receivable and are attributable to the financial investment class. Finally, we obtain a summary of the asset classes of Chinese banks in 2018, as shown in Table 1.

TABLE 1

Table 1. Asset classes of Chinese banks.

According to the portfolio of the 47 Chinese listed banks presented in this paper, we have plotted the bank-asset bilateral network of the Chinese banking system, as shown in Figure 3. It should be noted that the interbank assets in Figure 3 refer to the collective name of some assets with common characteristics (such as deposits from interbanks and other financial institutions, buying re-sale funds), rather than the traditional interbank lending assets. Figure 3 shows that in the Chinese banking portfolio, loan assets make up the largest proportion, followed by financial investment assets. The proportion of cash and interbank assets is relatively small, and the two are relatively close, with the other asset class being the lowest. Besides, the six state-owned commercial banks have the largest total assets for bank nodes and hold more loan assets. Among the 12 joint-stock commercial banks, Shanghai Pudong Development Bank, Industrial Bank, Minsheng Bank, and China Merchants Bank have more loan assets than other commercial banks. It should be noted that the network between the bank and the asset is fully connected in this paper.

FIGURE 3

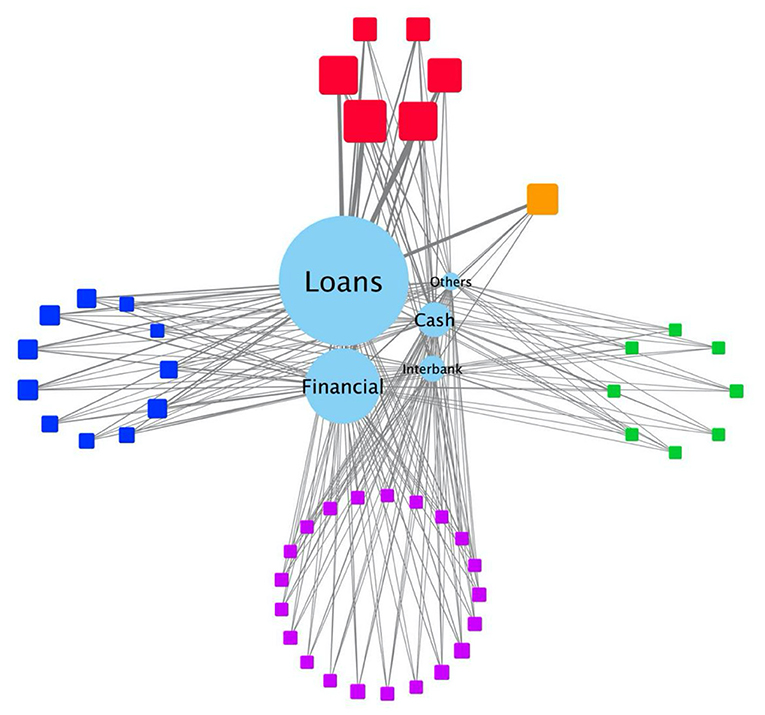
Figure 3. The bank-asset bilateral network of the Chinese banking system. The circle represents the asset class; the rectangle represents the bank class; the size of each node represents the size of its total assets; the thickness of each connecting line represents the total value of each asset class invested by each bank; besides, in the rectangular node: red represents state-owned banks; purple means joint-stock commercial banks; light blue means city commercial banks; dark blue means rural commercial banks; yellow means policy banks.

External Shocks and Price-Cutting Effects

By adjusting the value of p and α to form different external shocks and price-cutting effects, each asset class is shocked to study the survival rate of the banking system under different shocks. We select different asset classes to shock in turn, and conduct multiple experiments by continually adjusting the combined value of p and α when each asset class is shocked. In a single experiment, p and α are the same for all banks-assets. Finally, the results are shown in Figure 4.

FIGURE 4

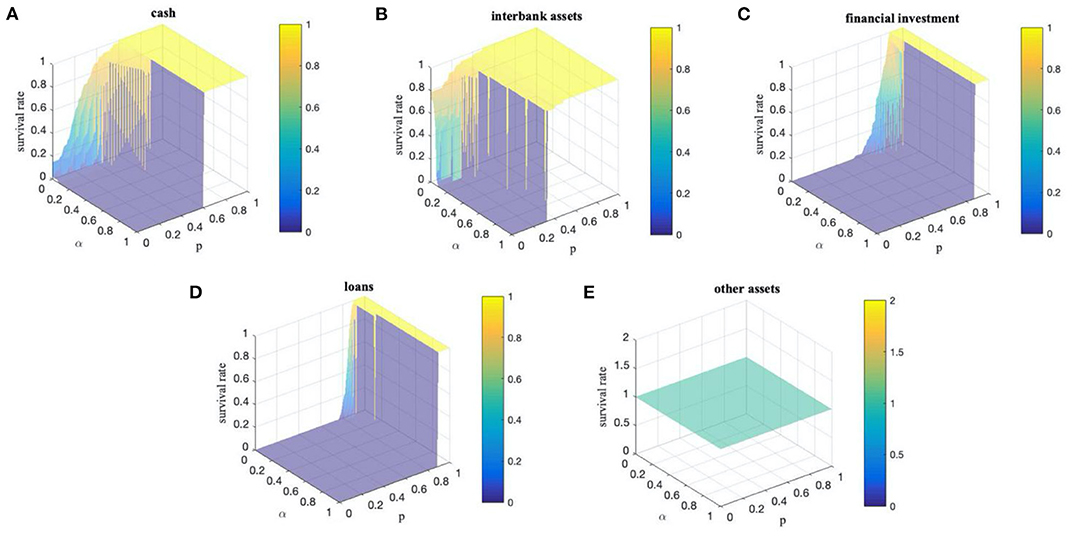
Figure 4. (A–E) The survival rate of the banking system under different values of p and α when cash assets, interbank assets, financial investment assets, loan assets, and other types of assets are shocked, respectively.

It can be seen that when cash assets are shocked (Figure 4A), the survival rate of the banking system gradually increases with the increase of p, and the survival rate is 1 when p > 0.6, i.e., there is no bank default. When p ≤ 0.6, the survival rate of the banking system gradually decreases with the increase of α, and when α > 0.36, for any value of p, the survival rate is 0, i.e., all banks fail, and the whole banking system will collapse. Therefore, generally speaking, when p is large (p > 0.6), the external shock is too small, and no bank fails, so the role of α cannot be reflected; when α is large (α > 0.36), the price-cutting effect is more robust, and changes in external shocks cannot be reflected. When p ≤ 0.6 and α > 0.36, the larger the α, the lower survival rate of the system, and the smaller the p, the lower survival rate of the system. It shows that the external shock and the price-cutting effect are superimposed in this interval, and the larger the external shock, the stronger the price-cutting effect, the more unstable the system. When the interbank assets are shocked (Figure 4B), the impact of p and α on the banking system is similar to the above shock on cash assets. The difference is that the survival rate of the whole banking system is 1 when p > 0.48, and there is no bank default in the system. At that time, the change of α has no effect on the survival rate of the banking system when p > 0.33; while, when p ≤ 0.29 and α ≤ 0.19, the superposition of external shocks and price-cutting effects is more significant. When the financial investment assets are shocked (Figure 4C), the situation is significantly different from the two types of assets mentioned above. At this time, the survival rate of the entire banking system is 0 when p ≤ 0.56, or when p ≤ 0.88 and α > 0.17, indicating that the external shock is large or that the price-cutting effect is strong at this stage, and the banking system is relatively fragile. In contrast, if the survival rate of the banking system is 1 when p ≤ 0.88, all banks in the system survive. It indicates that when the external shock is low, the banking system is stable. Moreover, when 0.56 < p < 0.88 and α ≤ 0.17, the effects of external shocks and price cuts are superimposed. When the loan assets are shocked (Figure 4D), the survival of the banking system is basically the same as that of the above-mentioned shocks on financial assets, except that the boundary value is different in each case. When p ≤ 0.76, or when p ≤ 0.9 and α > 0.25, the survival rate of the banking system is 0, no bank survives. This indicates that the external shock is large or the price-cutting effect is strong at this time, and the banking system is relatively fragile. When p ≥ 0.9, the survival rate of the banking system is 1 and all banks in the system survive, which indicates that the system becomes stable when the external shock is small. And, when 0.76 < p < 0.9 and α ≤ 0.25, the external shock and the price-cutting effect are superimposed. When other types of assets are shocked (Figure 4E), there is no bank default in the system, no matter how p or α changes.

Our analysis suggests that, on the whole, the smaller the p (i.e., the more significant the external impact of assets) and the larger the α (i.e., the stronger the price-cutting effect), the more unstable the banking system will be. When α is large enough, the price-cutting effect will have a significant impact on the stability of the banking system. If p is large, no bank will fail, which means that there will be no price-cutting of assets, so the stability of the banking system does not depend on α; if p is small, the price-cutting sale of assets of the failed bank will lead to the collapse of all banks, that is, the collapse of the entire banking system. Besides, the sensitivity of various assets to external shocks is different. In addition to other assets, loan assets are the most sensitive to external shocks, while interbank assets are the least sensitive. The corresponding ranges of external shocks and price reduction effects are also different.

The Proportion η of Various Assets Held by Banks in the Total Assets of Banks

Based on the research in section External Shocks and Price-Cutting Effects, it is noted that the number of various assets has a particular impact on the stability of the banking system. To explore the influence of the proportion η (various assets held by banks in the total assets of banks) on various banks' stability, we chose the corresponding shock intensity when the banking system is relatively stable to carry out the following research. We select the data when the survival rate of the banking system reaches more than 60% under the shock of each asset class, and the results are shown in Figure 5. Figure 5 shows when each asset class suffers a shock, the proportion of various assets held by banks to the total assets of banks (horizontal axis) and the order of bank default (vertical axis). When the ordinate axis is 0, it represents the bank has not defaulted; when the ordinate axis is 1, it means that the bank defaulted during the first round of shocks, and so forth. Figure 5 indicates that the banks that survived each asset's shock have a substantial similarity in their investment (as can be seen from Figure 5, the nodes representing the surviving banks have a certain degree of aggregation).

FIGURE 5

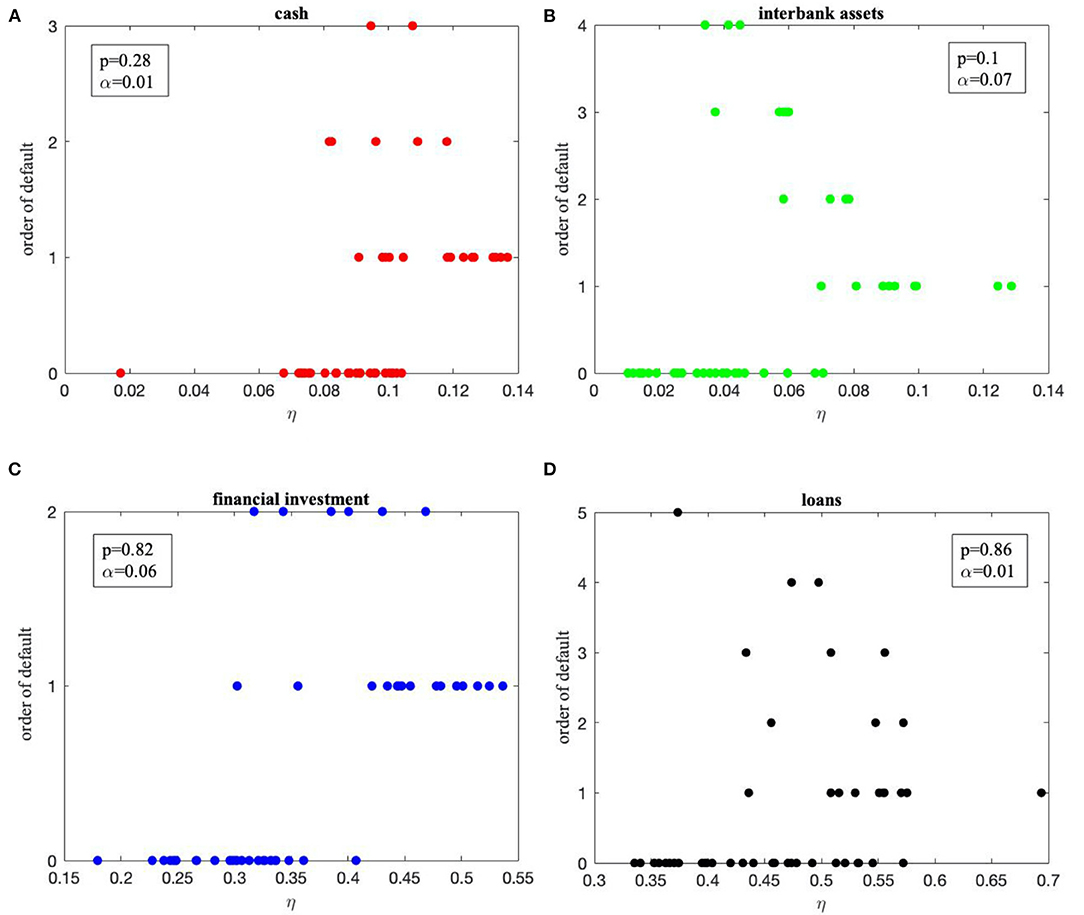
Figure 5. (A–D) The order of default under different values of η when cash assets, interbank assets, financial investment assets, loan assets, and other types of assets are shocked, respectively. The default order is 0 meaning the bank survives.

When shocking cash assets (see Figure 5A), we find that the proportion of cash of surviving banks is mainly around 0.08–0.1, such as large state-owned banks: Bank of Communications; joint-stock commercial banks: China Everbright Bank and China CITIC Bank; city commercial banks: Zhengzhou Bank, Qingdao Bank, and Zhongyuan Bank, etc., and rural commercial banks: Jiangyin Bank, Changshu Bank, and Zhangjiagang Bank. When shocking the interbank assets (see Figure 5B), the proportion of interbank assets of surviving banks mainly clustered around 0.01 and 0.04, such as large state-owned banks: Agricultural Bank and Construction Bank; joint-stock commercial banks: Everbright Bank, China CITIC Bank, and Shanghai Pudong Development Bank Banks; city commercial banks: Ningbo Bank, Guiyang Bank, Qingdao Bank, and Zhengzhou Bank, etc., and rural commercial banks: Jiangyin Bank, Changshu Bank, and Zhangjiagang Bank. When shocking the financial investment assets (see Figure 5C), the proportion of financial investment assets of surviving banks is mainly around 0.3–0.34, such as the large state-owned banks: Agricultural Bank and Bank of Communications; joint-stock commercial banks: Everbright Bank, China Banks, Minsheng Bank and Shanghai Pudong Development Bank; city commercial banks: Chongqing Bank, Gansu Bank, and Xi'an Bank, etc., and rural commercial banks: Wuxi Bank, Jiangyin Bank, Changshu Bank, and Zhangjiagang Bank. When shocking the loan assets (see Figure 5D), the proportion of loan assets of surviving banks is mainly around 0.35 and 0.4, such as city commercial banks: Nanjing Bank, Ningbo Bank, Guiyang Bank, Zhongyuan Bank, Qingdao Bank, Bank of Hangzhou and Bank of Chengdu, etc.

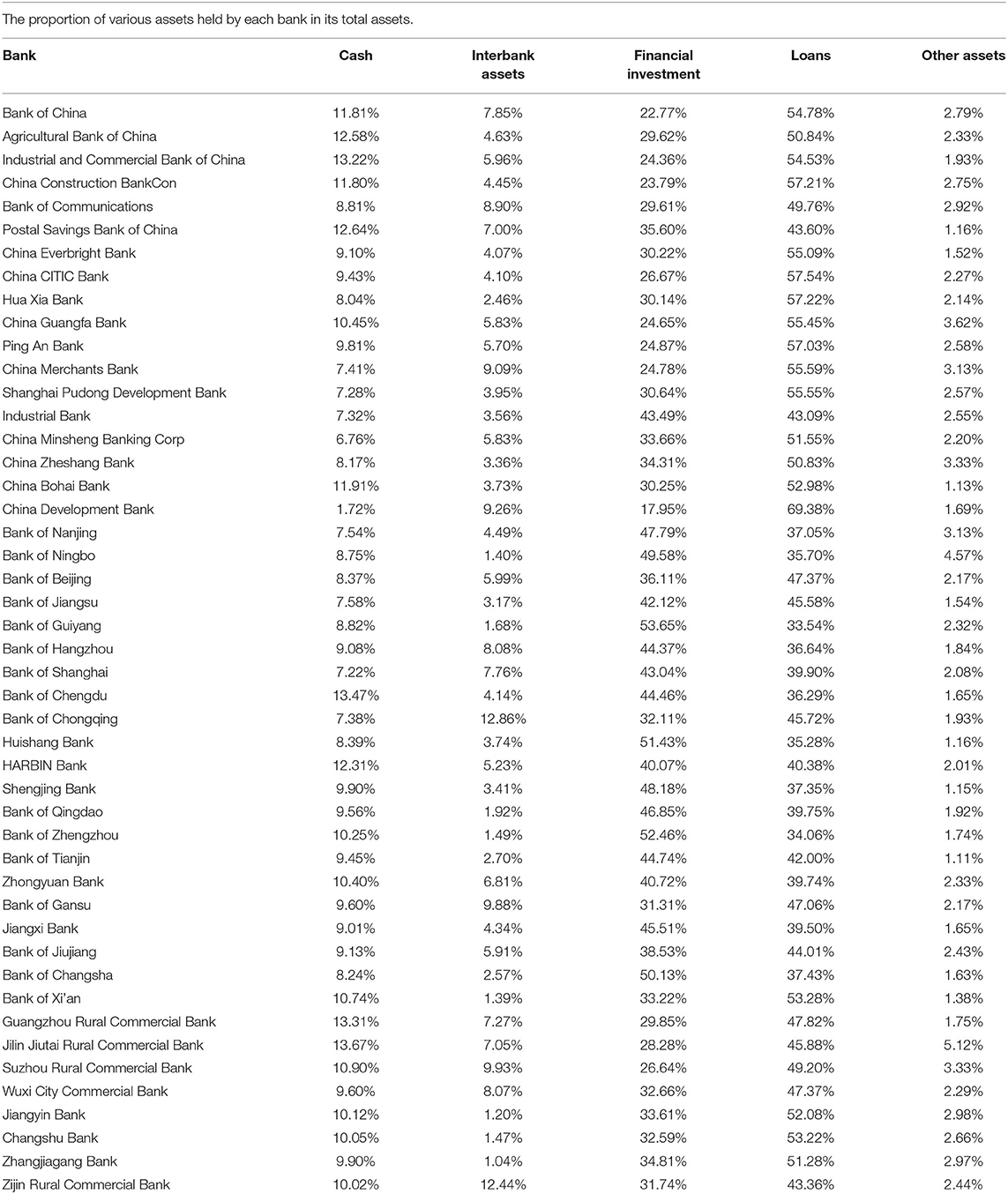
The above results show a particular relationship between the survival of banks and the proportion of corresponding assets invested by banks. Meanwhile, we also found that the four banks, Zhongyuan Bank, Jiangyin Bank, Changshu Bank, and Zhangjiagang Bank, did not fail when each asset class was shocked, indicating the strong robustness of the four banks. Therefore, we analyzed the asset portfolios of the four banks, as shown in Table 2¹. We note that the asset portfolios of the four typical banks exhibit certain similarities, especially Jiangyin Bank, Changshu Bank, and Zhangjiagang Bank, which are highly consistent. Therefore, we propose an optimal portfolio of assets in the banking system, allowing the bank to have high-risk resistance and strong robustness.

TABLE 2

Table 2. The proportion of various assets held by banks in the total assets of banks.

Simulation Analysis

We have developed the banks' quantitative portfolio strategy model based on the results of section The Proportion η of Various Assets Held by Banks in the Total Assets of Banks above. This section further discusses the banks' optimal investment strategy from a portfolio selection perspective.

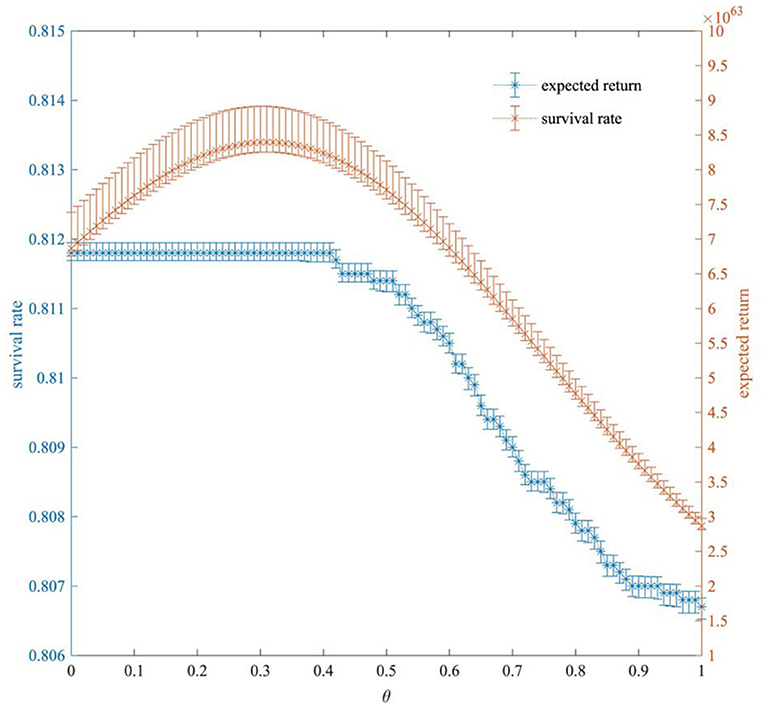
Firstly, we study the expected return and banks' survival rate under banks' different risk preferences θ (θ ∈ [0, 1]). In our model, we set the number of banks as 101, and the difference of risk preference coefficient of each bank is 0.01; the number of asset classes is 10, and each bank holds these 10 types of assets at the same time; the profit probability of each asset is p_m, the return rate when assets are profitable is S_m, and the loss rate when assets are depreciated is R_m; the bank's total liabilities is L = 10,000, and the asset-liability ratio is χ = 1.08 (the average asset-liability ratio of 47 listed banks in the empirical study is 1.08); the total time step of each simulation experiment is 1,024. Finally, the results obtained through more than 10,000 simulation experiments are shown in Figure 6. Figure 6 shows that there is a “turning point” of risk preference. Before the point, each bank's overall expected return shows an upward trend and maintains a relatively high and stable survival rate. After the point, the expected return of the banks decreases significantly, and the survival rate begins to decline.

FIGURE 6

Figure 6. The expected return and survival rate of the bank under different values of θ.

It indicates that when banks' risk preference tends to be conservative and low-risk and low-return assets held by banks account for a relatively large proportion, the banks' survival rate is high. However, it abandons some of the benefits that can result from high-risk and high-return assets. As banks' risk preference changes radically, banks hold more and more high-risk and high-return assets. The banks' expected returns will increase while maintaining strong stability within a specific range. However, as the aggressive process increases, the risk continues to accumulate. Therefore, once the risk preference coefficient has reached the extreme value (0.31 in this experiment), the loss begins to increase due to excessive risk. Rather, the expected return starts to decrease. With the risk preference θ becoming more radical, the stability of the banking system has gradually declined. Overall, we believe there is an optimal risk preference when banks make investment choices. Banks can determine investment strategies based on the risk level of assets to achieve maximum return with reasonable consideration of risk. The simulation results show that the banking system is the most stable and the expected return is the highest when the risk preference coefficient is 0.31.

Since the banking system is heterogeneous in real life, we further investigate the impact of each bank's asset-liability ratio χ on the risk preference. Based on the previous parameter settings, we have simulated and studied the expected return of the bank under different values of θ with various asset-liability ratios. The results are shown in Figure 7. Figure 7 shows that each bank has a “turning point” of risk preference under different asset-liability ratios. As banks' risk preference becomes more and more radical, the expected return of the banking system as a whole shows a tendency to “increase first and then decrease.” At the same time, we find that as banks' asset-liability ratio χ increases, the banks' expected return also rises, and the turning point of risk preference is gradually shifted to the right. That is, as the asset-liability ratio χ increases, the banks' risk preference becomes more and more radical. It shows that a bank with a larger asset-liability ratio has a more robust risk tolerance and can choose more aggressive investment strategies for high returns.

FIGURE 7

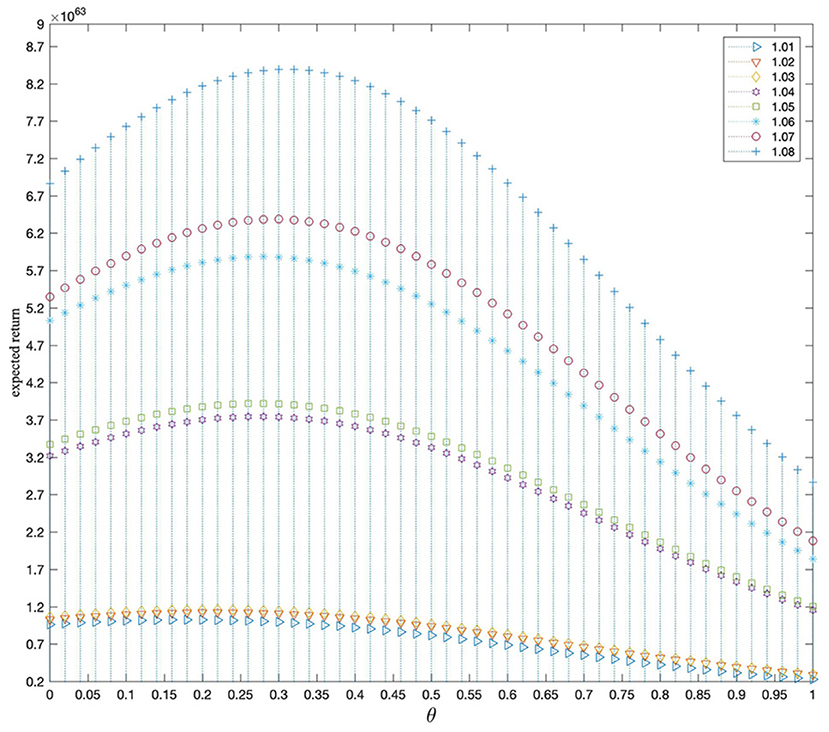
Figure 7. The expected return of the bank under different values of θ with various the asset-liability ratios.

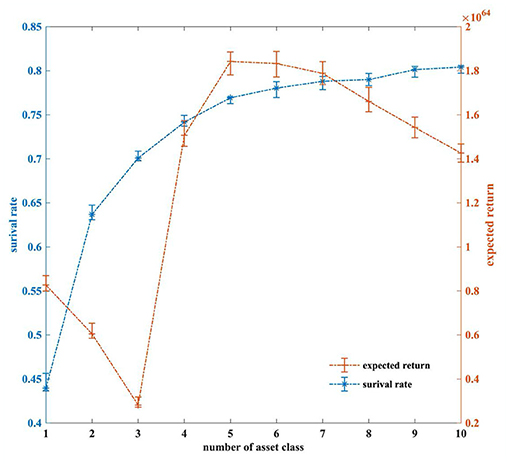
Based on the above research, we have chosen an asset-liability ratio of 1.08, and a risk preference coefficient of 0.31 to further study the dispersion of banking system investments. We have studied the expected return and survival rate of the bank under different asset classes. The results are shown in Figure 8. It turns out that the expected return and the survival rate of banks are different under different investment diversification in the banking system. As banks choose more and more varied assets, their investments become more and more diversified, and the survival rate of banks shows a rising trend. However, the expected return of banks shows a process of first fall, then rise, and then fall.

FIGURE 8

Figure 8. The expected return and survival rate of the bank under different asset classes.

We analyze the fact that as bank investments become increasingly diversified, once risk events occur in a specific asset class, the impact will be reduced correspondingly. The ability of banks to resist risk is becoming increasingly strong, so the probability of survival continues to increase. However, when a bank's investments are relatively concentrated (lower than the first turning point in the expected return), the bank chooses to invest in fewer assets. At this time, investment diversification will have a negative impact on banks. The diversification of bank investments will lead to increased risks, and the investment is not sufficiently diversified. Therefore, when a risk event occurs and causes assets to depreciate, it will not cause the bank to fail, but will still reduce the bank's expected return. When a bank's investment is at a reasonable level (between the two turning points), it reduces asset devaluation. Consequently, the expected return of the bank will continue to rise. When a bank's investment is too diversified (beyond the second turning point), its ability to resist risk is more robust, and the banking system is relatively stable. However, it is too dispersed, makes it impossible to concentrate investment on high-quality assets, and misses the possibility of higher returns, thus leading to a decline in expected returns. Therefore, we propose that banks should consider overall risk resistance and the expected return level to determine the principle of investment diversification, and maximize their returns with a reasonable asset allocation while ensuring stability.

Conclusion

Research on systemic risk under the bank-asset-bank indirect contagion channel is relatively rare. There is no empirical research on the systemic risk of Chinese banks in this channel. This paper used the bank-asset bilateral network to study systemic risk. Moreover, by constructing a quantitative portfolio strategy model for banks, a bank's optimal investment strategy is further explored from the asset class. This paper collects actual data on the balance sheets and portfolios of listed banks in China, obtains the Chinese bank-asset bilateral network, and empirically studies the impact of different external shocks, endogenous asset devaluations, and the proportion of various asset classes in the total bank assets on systemic risk. Based on the banks' quantitative portfolio model, we perform a simulation to study the impact of different banks' risk preferences and investment diversification on systemic risk. In addition, we compare and analyze banks' investment strategies under different asset-liability ratios. The conclusions are as follows:

First, overall, the greater the external shock and the greater the effect of price cuts, the higher the systemic risk. And if the effects of external shocks and price cuts overlap within a specific range, systemic risk has increased dramatically. Loan assets are the most sensitive to external shocks, and interbank assets are the least sensitive in the Chinese bank-asset bilateral network system. Moreover, the higher the proportion of various assets in total assets when subjected to the same external shocks, the greater the impact on the stability of the entire system. The empirical results show that none of the four Chinese listed banks, Zhongyuan Bank, Jiangyin Bank, Changshu Bank, and Zhangjiagang Bank had failed when each asset class was shocked, indicating the strong stability of these banks. Further analysis reveals some similarities between the four banks' portfolios. We believe that the banks' portfolio has a significant impact on the stability of the banking system.

Second, the banks' investment risk preference has a significant impact on systemic risk and investment return. Generally speaking, the more conservative the risk preference, the stronger the stability of the banking system. There is a “turning point” of risk preference in the expected return of banks, and the expected return of each bank “increases first and then decreases” before and after the inflection point. Furthermore, the greater the banks' asset-liability ratio, the stronger their risk tolerance when it comes to choosing more aggressive investment strategies to achieve high returns. The more diversified the banks' investments, the stronger their risk resistance and stability. Meanwhile, there are “two turning points” in the banks' expected return. As bank investments become increasingly dispersed, the expected return of banks first decreases, then increases, and finally decreases. We propose that banks consider their anti-risk capacity and their expected return level to determine investment diversification.

This paper focuses on systemic risk based on the bank-asset bilateral network, without considering the impact of other complex links between banks and the assets of the banking system. In addition, the empirical study on the bilateral network of the Chinese banking system is a fully connected network, which does not explore the systemic risks of banks under other bilateral networks. These issues will continue to be discussed in future work.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

QG performed analyses. QG and HF discussed the results. QG wrote the manuscript. HF approved the submitted version.

Funding

We are grateful for the support from the National Natural Science Foundation of China (71971054) and the Natural Science Foundation of Shanghai (19ZR1402100).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^The investment portfolio data of all 47 banks can be seen in the Appendix. It can be seen that the proportion of various assets held by banks in the total assets of banks is obviously different. And in our study, the proportion of investment portfolio of the four banks that have not failed when each asset class is shocked is the most similar among all banks.

References

1. Allen F, Gale D. Financial contagion. J Polit Econ. (2000) 108:1–33. doi: 10.1086/262109

CrossRef Full Text | Google Scholar

2. Leitner Y. Financial networks: contagion, commitment, and private sector bailouts. J Finan. (2005) 60:2925–53. doi: 10.1111/j.1540-6261.2005.00821.x

CrossRef Full Text | Google Scholar

3. Iori G, Jafarey S, Padilla FG. Systemic risk on the interbank market. J Econ Behav Organ. (2006) 61:525–42. doi: 10.1016/j.jebo.2004.07.018

CrossRef Full Text | Google Scholar

4. Nier E, Yang J, Yorulmazer T, Alentorn A. Network models and financial stability. J Econ Dyn Control. (2007) 31:2033–60. doi: 10.1016/j.jedc.2007.01.014

CrossRef Full Text | Google Scholar

5. Gai P, Kapadia S. Contagion in financial networks. Proc R Soc A Math Phys. (2010) 466:2401–23. doi: 10.1098/rspa.2009.0410

CrossRef Full Text | Google Scholar

6. Tedeschi G, Mazloumian A, Gallegati M, Helbing D. Bankruptcy cascades in interbank market. PLOS ONE. (2012) 7:e52749. doi: 10.1371/journal.pone.0052749

CrossRef Full Text | Google Scholar

7. Georg CP. The effect of the interbank network structure on contagion and common shocks. J Bank Finan. (2013) 37:2216–28. doi: 10.1016/j.jbankfin.2013.02.032

CrossRef Full Text | Google Scholar

8. Ladley D. Contagion and risk-sharing on the inter-bank market. J Econ Dyn Control. (2013) 37:1384–400. doi: 10.1016/j.jedc.2013.03.009

CrossRef Full Text | Google Scholar

9. Deng J, Cao SN, Pan HX, Qin T. Systemic risk contagion based on interbank networks. Comp Syst Compl Sci. (2013) 10:76–85. doi: 10.3969/j.issn.1672-3813.2013.04.010

CrossRef Full Text | Google Scholar

10. Chen Y, Chen DF, Song M. Heterogeneous bank system stability research under complex networks structure. J Syst Eng. (2014) 29:171–81. doi: 10.3969/j.issn.1000-5781.2014.02.004

CrossRef Full Text | Google Scholar

11. Grilli R, Tedeschi G, Gallegati M. Bank interlinkages and macroeconomic stability. Int Rev Econ Finan. (2014) 34:72–88. doi: 10.1016/j.iref.2014.07.002

CrossRef Full Text | Google Scholar

12. Li J, Li HG. Banking systemic risk research by the mechanism of liquidity reallocation. Syst Eng Theor Pract. (2016) 36:1128–35. doi: 10.12011/1000-6788(2016)05-1128-08

CrossRef Full Text | Google Scholar

13. Vitali S, Battiston S, Gallegati M. Financial fragility and distress propagation in a network of regions. J Econ Dyn Control. (2016) 62:56–75. doi: 10.1016/j.jedc.2015.10.003

CrossRef Full Text | Google Scholar

14. Calomiris CW, Carlson M. Interbank networks in the National Banking Era: their purpose and their role in the Panic of 1893. J Financ Econ. (2017) 125:434–53. doi: 10.1016/j.jfineco.2017.06.007

CrossRef Full Text | Google Scholar

15. Freixas X, Parigi BM, Rochet JC. Systemic risk, interbank relations, and liquidity provision by the central bank. J Money Credit Bank. (2000) 32:611–38. doi: 10.2307/2601198

CrossRef Full Text | Google Scholar

16. Brusco S, Castiglionesi F. Liquidity coinsurance, moral hazard, and financial contagion. J Finan. (2007) 62:2275–302. doi: 10.1111/j.1540-6261.2007.01275.x

CrossRef Full Text | Google Scholar

17. Bao QY. Research on the contagion model of bank systemic risk. J Finan Res. (2005) 8:72–84.

Google Scholar

18. Wang XF, Liao KL, Xu JC. The risk contagion effect of inter-bank market from the perspective of complex networks. Econ Perspect. (2015) 3:71–81.

Google Scholar

19. Zhou HL, Gai X, Wu XY. The transmission mechanism of system risk of commercial banks based on a network model of interbank markets. Financ Trade Res. (2015) 5:106–15. doi: 10.19337/j.cnki.34-1093/f.2015.05.014

CrossRef Full Text | Google Scholar

20. Barucca P, Bardoscia M, Caccioli F, D'Errico M, Visentin G, Caldarelli G, et al. Network valuation in financial systems. Math Financ. (2020) 30:1181–204. doi: 10.1111/mafi.12272

CrossRef Full Text | Google Scholar

21. He L, Li SW. Network entropy and systemic risk in dynamic banking systems. Complexity. (2017) 2017:1–7. doi: 10.1155/2017/1852897

CrossRef Full Text | Google Scholar

22. Ramadiah A, Di Gangi D, Sardo DRL, Macchiati V, Minh TP, Pinotti F, et al. Network sensitivity of systemic risk. J Netw Theor Financ. (2019) 5:53–72. doi: 10.21314/JNTF.2019.056

CrossRef Full Text | Google Scholar

23. Shleifer A, Vishny RW. Fire sales in finance and macroeconomics. J Econ Perspect. (2011) 25:29–48. doi: 10.1257/jep.25.1.29

CrossRef Full Text | Google Scholar

24. Tsatskis I. Systemic losses in banking networks: indirect interaction of nodes via asset prices. arXiv preprint arXiv:1203.6778v1 (2012). doi: 10.2139/ssrn.2062174

CrossRef Full Text | Google Scholar

25. Duarte F, Eisenbach TM. Fire-sale Spillovers and Systemic Risk. FRB of New York Staff Report No.645. (2013). doi: 10.2139/ssrn.2340669

CrossRef Full Text | Google Scholar

26. Braouezec Y, Wagalath L. Strategic fire-sales and price-mediated contagion in the banking system. Eur J Oper Res. (2019) 274:1180–97. doi: 10.1016/j.ejor.2018.11.012

CrossRef Full Text | Google Scholar

27. Greenwood R, Landier A, Thesmar D. Vulnerable banks. J Financ Econ. (2015) 115:471–85. doi: 10.1016/j.jfineco.2014.11.006

CrossRef Full Text | Google Scholar

28. Tasca P, Battiston S, Deghi A. Portfolio diversification and systemic risk in interbank networks. J Econ Dyn Control. (2017) 82:96–124. doi: 10.1016/j.jedc.2017.01.013

CrossRef Full Text | Google Scholar

29. Yao H, Wang C, He JM, Li L. Study on the Relationship between investment portfolios diversification and systemic risk. Chin J Manag Sci. (2019) 27:9–18. doi: 10.16381/j.cnki.issn1003-207x.2019.02.002

CrossRef Full Text | Google Scholar

30. Squartini T, Almog A, Caldarelli G, Van Lelyveld I, Garlaschelli D, Cimini G. Enhanced capital-asset pricing model for the reconstruction of bipartite financial networks. Phys Rev E. (2017) 96:032315. doi: 10.1103/PhysRevE.96.032315

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Gangi DD, Lillo F, Pirino D. Assessing systemic risk due to fire sales spillover through maximum entropy network reconstruction. J Econ Dyn Control. (2018) 94:117–41. doi: 10.1016/j.jedc.2018.07.001

CrossRef Full Text | Google Scholar

32. Huang XQ, Vodenska I, Havlin S, Stanley HE. Cascading failures in bi-partite graphs: model for systemic risk propagation. Sci Rep. (2013) 3:1219. doi: 10.1038/srep01219

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Chen C, Iyengar G, Moallemi C. Asset price-based contagion models for systemic risk. Columbia Business School Research Archive (2014).

Google Scholar

34. Caccioli F, Shrestha M, Moore C, Farmer JD. Stability analysis of financial contagion due to overlapping portfolios. J Bank Financ. (2014) 46:233–45. doi: 10.1016/j.jbankfin.2014.05.021

CrossRef Full Text | Google Scholar

35. Levy-Carciente S, Kenett DY, Avakian A, Stanley HE, Havlin S. Dynamical macroprudential stress testing using network theory. J Bank Financ. (2015) 59:164–81. doi: 10.1016/j.jbankfin.2015.05.008

CrossRef Full Text | Google Scholar

36. Fang Y, Zheng ZW. Research on contagion paths of systemic risk in the interbank system: based on network model with common assets holdings. Stud Int Financ. (2016) 350:61–72. doi: 10.16475/j.cnki.1006-1029.2016.06.006

CrossRef Full Text | Google Scholar

37. Zhang Y, Zhu SY, Zhang R, Li HG. Analysis of financial contagion based on overlapping portfolios. J Beijing Norm Univ Nat Sci. (2016) 52:425–9. doi: 10.16360/j.cnki.jbnuns.2016.04.004

CrossRef Full Text | Google Scholar

38. Fan H, Liu CY. Modeling and simulation of financial contagion based on correlated assets portfolio. J Syst Simul. (2019) 31:1062–9. doi: 10.16182/j.issn1004731x.joss.17-0195

CrossRef Full Text | Google Scholar

39. Jiang SS, Fan H. Systemic risk in the interbank market with overlapping portfolios. Complexity. (2019) 2019:1–12. doi: 10.1155/2019/5317819

CrossRef Full Text | Google Scholar

40. Caccioli F, Farmer JD, Foti N, Rockmore DN. Overlapping portfolios, contagion, and financial stability. J Econ Dyn Control. (2015) 51:50–63. doi: 10.1016/j.jedc.2014.09.041

CrossRef Full Text | Google Scholar

41. Gualdi S, Cimini G, Primicerio K, Di Clemente R, Challet D. Statistically validated network of portfolio overlaps and systemic risk. Sci Rep. (2016) 6:39467. doi: 10.1038/srep39467

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Gauthier C, Lehar A, Souissi M. Macroprudential capital requirements and systemic Risk. J Financ Intermed. (2012) 21:594–618. doi: 10.1016/j.jfi.2012.01.005

CrossRef Full Text | Google Scholar

43. Liao S, Sojli E, Tham WW. Managing systemic risk in the Netherlands. Int Rev Econ Financ. (2015) 40:231–45. doi: 10.1016/j.iref.2015.02.012

CrossRef Full Text | Google Scholar

44. Fan H, Keregero CM, Gao QQ. The application of macroprudential capital requirements in managing systemic risk. Complexity. (2018) 2018:1–15. doi: 10.1155/2018/4012163

CrossRef Full Text | Google Scholar

Appendix