Chaos in the Shimizu-Morioka Model With Fractional Order

The investigation of dynamical behaviors for fractional-order chaotic systems is a new trend recently. This article is numerically concerned with the Shimizu-Morioka model with a fractional order. We find that chaos exists in the fractional-order model with order less than three by utilizing the fractional calculus techniques, and some phase diagrams are also constructed.

1 Introduction

In the past twenty years, many scientists paid their attention on the fractional-order chaotic dynamical systems (see Genesio-Tesi system [1], Rabinovich system [2], and Lü system [3] et al.). They presented chaotic attractors indeed occur in the fractional-order model with order less than 3. Sheu and Chen [4] found that the lowest order of the fractional-order Newton-Leipnik system is 2.82. In 2004, Li and Peng [5] discovered the rich dynamical behavior displayed in the fractional-order Chen system such as the fixed points, limit cycles, periodic motions, and chaotic motions.

The original Shimizu-Morioka model [6] is described by the following ordinary differential equation:

$\{\begin{array}{l}\dot{x}=P\left(x,y,z\right)=y\\ \dot{y}=Q\left(x,y,z\right)=x-\tilde{\beta }y-xz\\ \dot{z}=R\left(x,y,z\right)=-\tilde{\alpha }z+x^2\end{array}$(1.1)

where $\left(x,y,z\right)\in {ℝ}^3$ are the state variables and $\tilde{\alpha },\tilde{\beta }$ are positive real parameters. This model has been proposed as a simplified and an alternative model for studying the dynamics of the well-known Lorenz system [7] for large Rayleigh numbers (Ra), in which the complex behavior of the trajectories has been discovered by means of computer simulation. As in the Lorenz model, the Shimizu-Morioka model is invariant, with respect to the substitution $\left(x,y,z\right)\to \left(-x,-y,z\right)$. The model received much attention due to its stability to describe bifurcation of the associated Lorenz-like strange attractors [8], for example, taking $\tilde{\alpha }=0.45$ and $\tilde{\beta }=0.75$ (Figure 1).

FIGURE 1

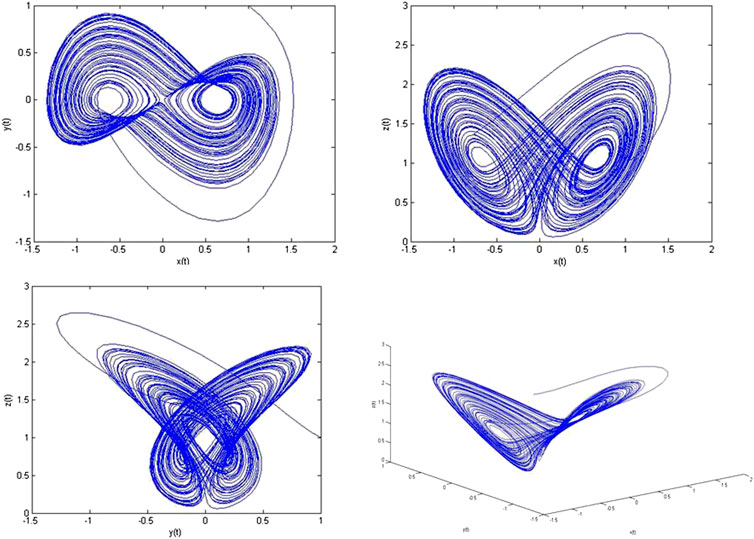
FIGURE 1. Phase portraits of system Eq. 1.1.

Intrigued by the above interesting work, many researchers [9, 10] focused their study on the dynamical behavior analysis of the Shimizu-Morioka model. In particular, articles [11, 12] use feedback control laws and the delay feedback control method [13, 14] to study the local and global stabilization and bifurcation of the Shimizu-Morioka chaotic model.

If the dynamical system of Eq. 1.1 follows

$\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}=-\left(\tilde{\alpha }+\tilde{\beta }\right)<0$(1.2)

then the system is known to be a dissipative one.

In 1992, British scholar Rucklideg studied two-dimensional convection problems of solute gradients and magnetic fields, and introduced the following chaotic system [15]:

$\{\begin{array}{l}\dot{\stackrel{⌣}{x}}=-a\stackrel{⌣}{x}+b\stackrel{⌣}{y}-\stackrel{⌣}{y}\stackrel{⌣}{z}\\ \dot{\stackrel{⌣}{y}}=\stackrel{⌣}{x}\\ \dot{\stackrel{⌣}{z}}=-\stackrel{⌣}{z}+{\stackrel{⌣}{y}}^2\end{array}$(1.3)

where $\left(\stackrel{⌣}{x},\stackrel{⌣}{y},\stackrel{⌣}{z}\right)\in {ℝ}^3$ are the state variables and $a,b$ are the positive real parameters. When $\tilde{\alpha }\ne 0$, by transformation:

$x={\tilde{\alpha }}^{\frac{3}{2}}\stackrel{⌣}{y},y={\tilde{\alpha }}^{\frac{5}{2}}\stackrel{⌣}{x},z={\tilde{\alpha }}^2\stackrel{⌣}{z},t={\tilde{\alpha }}^{-1}\stackrel{⌣}{t}$(1.4)

transformed system Eq. 1.1 to

$\{\begin{array}{l}\dot{\stackrel{⌣}{x}}=-\tilde{\beta }{\alpha }^{-1}\stackrel{⌣}{x}+{\tilde{\alpha }}^{-2}\stackrel{⌣}{y}-\stackrel{⌣}{y}\stackrel{⌣}{z}\\ \dot{\stackrel{⌣}{y}}=\stackrel{⌣}{x}\\ \dot{\stackrel{⌣}{z}}=-\stackrel{⌣}{z}+{\stackrel{⌣}{y}}^2\end{array}$(1.5)

Therefore, system Eq. 1.5 and system Eq. 1.3 are equivalent when $a=-\tilde{\beta }{\tilde{\alpha }}^{-1}$, $b=1/{\tilde{\alpha }}^2$, and $\tilde{\alpha }\ne 0$.

In this article, Section 2 provides a brief review of the fractional-order operator and discretization fractional-order Shimizu-Morioka model using numerical algorithm. In Section 3, the complex dynamical behaviors of the Shimizu-Morioka model with a fractional order are studied numerically in four cases. Finally, conclusions are given in Section 4.

2 Fractional Order Operator and Numerical Algorithm

In this section, we first give out the fractional-order differential operator and the Shimizu-Morioka model with a fractional order. Furthermore, we use the predictor–correctors scheme to discrete the fractional-order Shimizu-Morioka model. Last, we discuss the necessary condition for the existence of chaotic attractors.

There are several definitions of the fractional differential and integral operator, including Grünwald-Letnikov operator, Riemann-Liouville operator, and Caputo operator [16–18]. In this study, we use the following Caputo-type fractional derivative [19].

$D_{\ast }^{\alpha }y\left(x\right)=J^{m-\alpha }{y}^m\left(x\right),\alpha >0$(2.6)

where $m=\left[\alpha \right]$ is the first integer which is not less than α, $y^m$ is the ordinary m-order derivative, $J^{\beta }$ is the β-order Riemann-Liouville integral operator defined by

$J^{\beta }z\left(x\right)=\frac{1}{\Gamma \left(\beta \right)}{\displaystyle {\int }_0^x{\left(x-t\right)}^{\beta -1}z\left(t\right)dt},\beta >0$(2.7)

where $\Gamma \left(\beta \right)$ is the gamma function.

The classical Riemann-Liouville fractional derivative is defined by

$D^{\alpha }y\left(x\right)=\frac{d^m}{d{x}^m}{J}^{m-\alpha }{y}^m\left(x\right)$(2.8)

which requires the homogeneous initial conditions. The main reason why we chose the Caputo-type fractional derivative is that the inhomogeneous initial conditions are also permitted.

The integer-order Shimizu-Morioka model Eq. 1.1 has been extended to the fractional-order Shimizu-Morioka model, which could describe the memory and hereditary properties of the model better. The fractional-order Shimizu-Morioka model is described as follows—in which the standard derivative will be replaced by the fractional-order derivative.

$\{\begin{array}{l}\frac{d^{q_1}x}{d{t}^{q_1}}=y\\ \frac{d^{q_2}y}{d{t}^{q_2}}=x-\tilde{\beta }y-xz\\ \frac{d^{q_3}z}{d{t}^{q_3}}=-\tilde{\alpha }z+x^2\end{array}$(2.9)

where $0<q_1,q_2,q_3\le 1$ and the order is denoted by $q=\left(q_1,q_2,q_3\right)$.

As for model Eq. 2.9, we derive the predictor–correctors scheme which is the generation of Adamas-Bashforth-Moulton one [16, 20]. The following fractional-order differential equation

$D_{\ast }^{\alpha }y\left(t\right)=f\left[t,y\left(t\right)\right],0\le t\le T$

$y^{\left(k\right)}\left(0\right)=y_0^{\left(k\right)},k=\mathrm{0,1},\cdots ,m-1$(2.10)

is equivalent to the Volterra integral equation

$y\left(t\right)={\displaystyle \sum _{k=0}^{\left[\alpha \right]-1}\frac{t^k}{k!}{y}_0^{\left(k\right)}}+\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle {\int }_0^t{\left(t-s\right)}^{\alpha -1}f\left[s,y\left(s\right)\right]ds}$(2.11)

Set $h=T/N$, $t_n=nh$, and $n=\mathrm{0,1},\dots ,N\in {\mathbb{Z}}^{+}$, then (2) can be discretized as follows:

$y_n\left(t_{n+1}\right)={\displaystyle \sum _{k=0}^{\left[\alpha \right]-1}\frac{t_{n+1}^k}{k!}{y}_0^{\left(k\right)}+\frac{h^{\alpha }}{\Gamma \left(\alpha +2\right)}\left\{f\left[t_{n+1},y_h^p\left(t_{n+1}\right)\right]+{\displaystyle \sum _{j=0}^n{a}_{j,n+1}f\left[t_j,y_h\left(t_j\right)\right]}\right\}}$

where

$y_h^p\left(t_{n+1}\right)={\displaystyle \sum _{k=0}^{\left[\alpha \right]-1}\frac{t_{n+1}^k}{k!}{y}_0^{\left(k\right)}}+\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle \sum _{j=0}^n\frac{h^{\alpha }}{\alpha }\left[{\left(n-j+1\right)}^{\alpha }-{\left(n-j\right)}^{\alpha }\right]f\left[t_j,y_h\left(t_j\right)\right]}$

$a_{j,n+1}=\{\begin{array}{l}{n}^{\alpha +1}-\left(n-\alpha \right){\left(n+1\right)}^{\alpha },j=0\\ {\left(n-j+2\right)}^{\alpha +1}+{\left(n-j\right)}^{\alpha +1}-2{\left(n-j+1\right)}^{\alpha +1},1\le j\le n\\ 1,j=n+1\end{array}$

The error estimate is $\underset{j=\mathrm{0,1},\dots ,N}{\max }\left|y\left(t_j\right)-y_h\left(t_j\right)\right|=O\left(h^p\right),p=\min \left(\mathrm{2,1}+\alpha \right)$.

Applying the above formula, system Eq. 2.9 can be discretized as follows:

$\{\begin{array}{l}{x}_{n+1}=x_0+\frac{h^{q_1}}{\Gamma \left(q_1+2\right)}\left(y_{n+1}^p+{\displaystyle \sum _{j=0}^n{\alpha }_{1,j,n+1}{y}_j}\right)\\ y_{n+1}=y_0+\frac{h^{q_2}}{\Gamma \left(q_2+2\right)}\left[x_{n+1}^p-\tilde{\beta }{y}_{n+1}^p-x_{n+1}^p{z}_{n+1}^p+{\displaystyle \sum _{j=0}^n{\alpha }_{2,j,n+1}\left(x_j-\tilde{\beta }{y}_j-x_j{z}_j\right)}\right]\\ z_{n+1}=z_0+\frac{h^{q_3}}{\Gamma \left(q_3+2\right)}\left[-\tilde{\alpha }{z}_{n+1}^p+{\left(x_{n+1}^p\right)}^2+{\displaystyle \sum _{j=0}^n{\alpha }_{3,j,n+1}\left(-\tilde{\alpha }{z}_j+x_j^2\right)}\right]\end{array}$(2.12)

where

$\{\begin{array}{l}{x}_{n+1}^p=x_0+\frac{1}{\Gamma \left(q_1\right)}{\displaystyle \sum _{j=0}^n\frac{h^{q_1}}{q_1}\left[{\left(n-j+1\right)}^{q_1}-{\left(n-j\right)}^{q_1}\right]y_j}\\ y_{n+1}^p=y_0+\frac{1}{\Gamma \left(q_2\right)}{\displaystyle \sum _{j=0}^n\frac{h^{q_2}}{q_2}\left[{\left(n-j+1\right)}^{q_2}-{\left(n-j\right)}^{q_2}\right]\left(x_j-\beta y_j-x_j{z}_j\right)}\\ z_{n+1}^p=z_0+\frac{1}{\Gamma \left(q_3\right)}{\displaystyle \sum _{j=0}^n\frac{h^{q_3}}{q_3}\left[{\left(n-j+1\right)}^{q_3}-{\left(n-j\right)}^{q_3}\right]\left(-\alpha z_j+x_j^2\right)}\end{array}$

and

${\alpha }_{i,j,n+1}=\{\begin{array}{l}{n}^{q_i+1}-\left(n-q_i\right){\left(n+1\right)}^{q_i},j=0\\ {\left(n-j+2\right)}^{q_i+1}+{\left(n-j\right)}^{q_i+1}-2{\left(n-j+1\right)}^{q_i+1},1\le j\le n,i=\mathrm{1,2,3}\\ 1,j=n+1\end{array}$

The fractional-order Shimizu-Morioka model of system Eq. 2.9 discretes to system Eq. 2.12.

Now, we discuss the necessary condition for the existence of chaotic attractors in the fractional-order Shimizu-Morioka model. Set $d^{q_1}x/d{t}^{q_1}=0,d^{q_2}y/d{t}^{q_2}=0,d^{q_3}z/d{t}^{q_3}=0$, we get the following equilibrium points of system Eq. 2.9.

$E_0=\left(\mathrm{0,0,0}\right),E_1=\left(\sqrt{\tilde{\alpha }},\mathrm{0,1}\right)$

The Jacobian matrices at the equilibrium points $E_0$ and $E_1$ are

$J\left(E_0\right)=\left[\begin{array}{ccc}0& 1& 0\\ 1& -\tilde{\beta }& 0\\ 0& 0& -\tilde{\alpha }\end{array}\right],J\left(E_1\right)=\left[\begin{array}{ccc}0& 1& 0\\ 1& -\tilde{\beta }& -\sqrt{\tilde{\alpha }}\\ 0& 0& -\tilde{\alpha }\end{array}\right]$

The eigenvalues at $E_0$ are ${\lambda }_1=-0.45$, ${\lambda }_2=-1.443$, and ${\lambda }_3=0.693$, and the eigenvalues at $E_1$ are ${\lambda }_1=0.1061+0.7912i$, ${\lambda }_2=-1.412$, and ${\lambda }_3=0.1061+0.7912i$. $E_0$ and $E_1$ are saddle points.

Suppose λ is the unstable eigenvalue of the saddle points, then the necessary condition for the fractional-order system Eq. 2.9 to remain chaotic is keeping the eigenvalue λ in the unstable region. By [21], if the eigenvalue λ is in the unstable region, then the following condition is satisfied.

$\left|\arg {\lambda }_i\right|>\frac{q\pi }{2}$

where $\left|\arg {\lambda }_i\right|$ denotes the argument of the eigenvalue λ. That is,

$q>\frac{2}{\pi }\left|\arg {\lambda }_i\right|$

So, the necessary condition for the existence of chaotic attractors in the fractional-order system Eq. 2.9 is

$q>\frac{2}{\pi }\left|\arg {\lambda }_i\right|=\frac{2}{\pi }\arctan \frac{0.7912}{0.1061}=0.9151$

which implied that when $q_i\left(i=\mathrm{1,2,3}\right)>0.9151$, system Eq. 2.9 has chaos, and when $q_i\left(i=\mathrm{1,2,3}\right)<0.9151$, system Eq. 2.9 has no chaos.

3 Numerical Simulations

In what follows, some numerical simulations of system Eq. 2.12 will be studied. We chose the parameters $\tilde{\alpha }=0.45$, $\tilde{\beta }=0.75$, and the initial value $\left(x_0,y_0,z_0\right)=\left(\mathrm{1,1,2}\right)$. The phase portraits and time histories are used to research the dynamical behaviors of system Eq. 2.9. Four cases are considered as follows.

3.1 Commensurate Order $q_1{q}_2{q}_3\alpha$

System Eq. 2.9 is calculated numerically against $\alpha \in \left[0.89,0.99\right]$, while the incremental value of α is 0.01. Figure 2 shows the phase portraits in the $x-y$ space at $q_i\left(i=\mathrm{1,2,3}\right)=0.99,0.92,0.912$, and 0.89, respectively. We find that system Eq. 2.9 behaves chaotically when $\alpha \in \left[0.92,0.99\right]$ is greater than 0.9152; when $\alpha =0.912$ is less than 0.9152, system Eq. 2.9 exhibits periodic motion; and when $\alpha =0.89$, the chaotic motions disappear and the system stabilizes to the fixed point. The numerical simulation results coincide with the necessary conditions for the existence of chaotic attractors that were observed in the last section. The lowest order to yield chaos is 2.76.

FIGURE 2

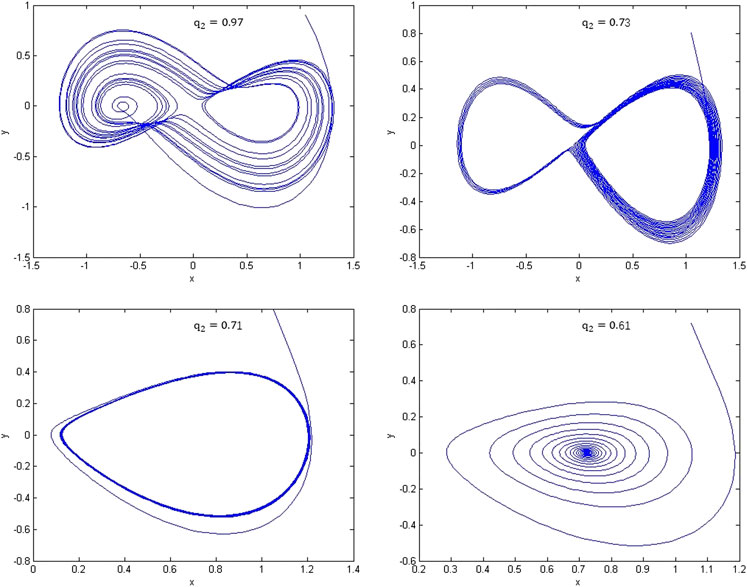
FIGURE 2. Phase portraits of model Eq. 2.9 with $q_i\left(i=\mathrm{1,2,3}\right)=\alpha$.

3.2 $q_1{q}_{3}1$ and Let $q_2$ Vary Less Than one

System Eq. 2.9 is calculated numerically against $\alpha \in \left[0.61,0.97\right]$, while the incremental value of α is 0.01. Figure 3 shows the phase portraits in the $x-y$ space at $q_i\left(i=\mathrm{1,3}\right)=1$, $q_2=0.97,0.73,0.71$, and 0.61, respectively. We find that system Eq. 2.9 behaves chaotically when $\alpha \in \left[0.73,0.97\right]$; when $\alpha =0.71$, system Eq. 2.9 exhibits periodic motion; and when $\alpha =0.61$, the chaotic motions disappear and the system stabilizes to the fixed point.

FIGURE 3

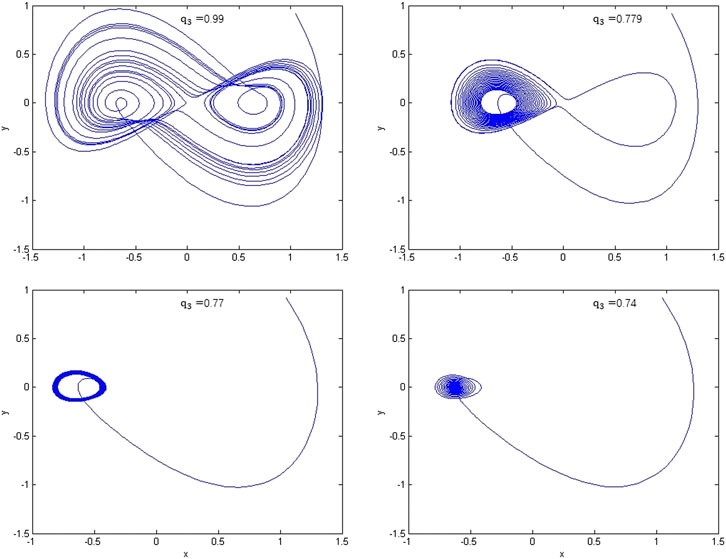
FIGURE 3. Phase portraits of model Eq. 2.9 with $q_1=q_3=1$.

3.3 $q_1{q}_{2}1$ and Let $q_3$ Vary Less Than one

Simulations of system Eq. 2.9 are performed against $\alpha \in \left[0.74,0.99\right]$, while the incremental value of α is 0.01. Figure 4 shows the phase portraits in the $x-y$ space at $q_i\left(i=\mathrm{1,2}\right)=1$, $q_3=0.99,0.779,0.77$, and 0.74, respectively. We find that system Eq. 2.9 behaves chaotically when $\alpha \in \left[0.91,1\right]$; when $\alpha =0.77$, system Eq. 2.9 exhibits periodic motion; and when $\alpha =0.74$, the chaotic motions disappear and the system stabilizes to the fixed point.

FIGURE 4

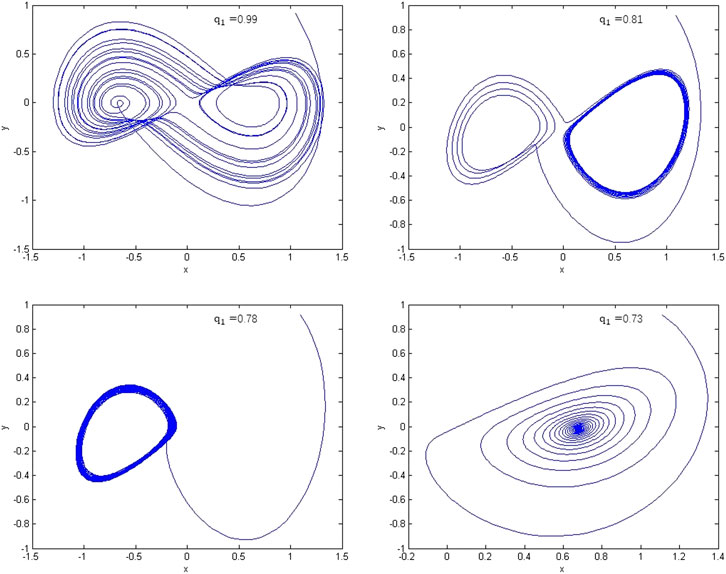
FIGURE 4. Phase portraits of model Eq. 2.9 with $q_1=q_2=1$.

3.4 $q_2{q}_{3}1$ and Let $q_1$ Vary Less Than one

System Eq. 2.9 is calculated numerically against $\alpha \in \left[0.73,0.99\right]$ incrementally. Figure 5 shows the phase portraits in the $x-y$ space at $q_i\left(i=\mathrm{2,3}\right)=1$, $q_1=0.99$, 0.81, $q_1=0.78$, and 0.73, respectively. We find that system Eq. 2.9 behaves chaotically when $\alpha \in \left[0.81,0.99\right]$; system Eq. 2.9 exhibits periodic motion when $\alpha =0.78$; and when $\alpha =0.73$, the chaotic motions disappear and the system stabilizes to the fixed point.

FIGURE 5

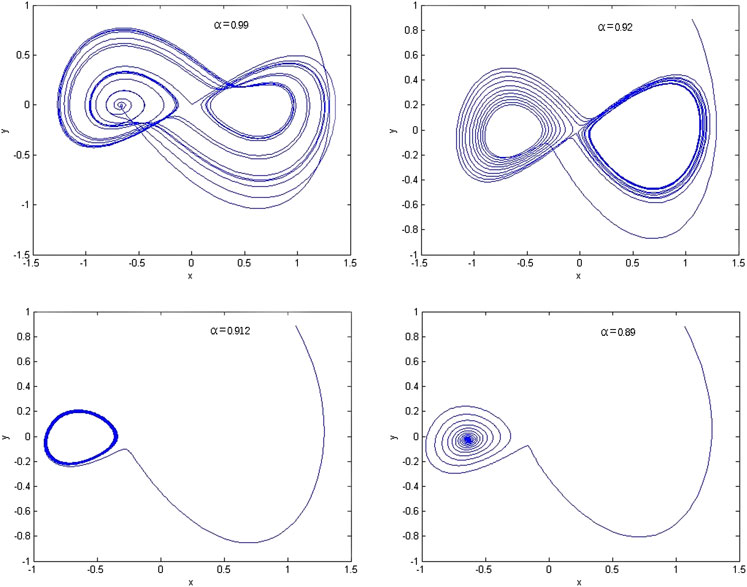
FIGURE 5. Phase portraits of model Eq. 2.9 with $q_2=q_3=1$.

4 Chaos Control

4.1 Theoretical Basis

The following three-dimensional fractional-order system is considered:

$\{\begin{array}{l}\frac{d^{q}x\left(t\right)}{d{t}^q}=f\left(x,y,z\right)\\ \frac{d^{q}y\left(t\right)}{d{t}^q}=g\left(x,y,z\right)\\ \frac{d^{q}z\left(t\right)}{d{t}^q}=h\left(x,y,z\right)\end{array}$(4.13)

where $q\in \left(\mathrm{0,1}\right)$. The Jacobian matrix of system Eq. 4.13 at the equilibrium is

$J=\left[\begin{array}{ccc}\frac{\partial f}{\partial x}& \frac{\partial f}{\partial y}& \frac{\partial f}{\partial z}\\ \frac{\partial g}{\partial x}& \frac{\partial g}{\partial y}& \frac{\partial g}{\partial z}\\ \frac{\partial h}{\partial x}& \frac{\partial h}{\partial y}& \frac{\partial h}{\partial z}\end{array}\right]$(4.14)

The corresponding characteristic equation is

$P\left(\lambda \right)={\lambda }^3+a_1{\lambda }^2+a_2\lambda +a_3$(4.15)

and the discriminant is

$D\left(P\right)=18a_1{a}_2{a}_3+a_1^2{a}_2^2-4a_3{a}_1^3-4a_2^3-27a_3^2$(4.16)

Lemma 4.1. Fractional-order system Eq. 4.13 is locally asymptotically stable if and only if any eigenvalue λ of the Jacobian matrix at the equilibrium satisfies $\left|\arg \left(\lambda \right)\right|>\frac{q\pi }{2}$.

Lemma 4.2. The Routh-Hurwitz criterion [22] of system Eq. 4.13 is as follows:

(i) if $D\left(P\right)>0$, then equilibrium of system Eq. 4.13 is locally asymptotic stability if and only if $a_1>0,a_3>0,a_1{a}_2>a_3$;

(ii) if $D\left(P\right)<0$, $a_1\ge 0,a_2\ge 0,a_3>0$, then system Eq. 4.13 is locally asymptotic stability when the order $q<2/3$; if $D\left(P\right)<0,a_1<0,a_2<0,q>2/3$, then all the eigenvalues of Eq. 4.15 satisfy $\left|\arg \left(\lambda \right)\right|<\frac{q\pi }{2}$;

(iii) if $D\left(P\right)<0,a_1>0,a_2>0,a_1{a}_2=a_3$, then for $0<q\le 1$, system (4.15) is locally asymptotically stable;

(iv) the necessary condition for the local asymptotic stability of the equilibrium of system Eq. 4.13 is $a_3>0$.

4.2 Chaos Control

We will apply feedback control and the fractional Routh-Hurwitz criterion to suppress the three-dimensional fractional Shimizu-Morioka chaotic system. The three-dimensional fractional Shimizu-Morioka chaotic controlled system is described as follows:

$\{\begin{array}{l}\frac{d^{q}x}{d{t}^q}=y+k_1\left(x-\overline{x}\right)\\ \frac{d^{q}y}{d{t}^q}=x-\tilde{\beta }y-xz+k_2\left(y-\overline{y}\right)\\ \frac{d^{q}z}{d{t}^q}=-\tilde{\alpha }z+x^2+k_3\left(z-\overline{z}\right)\end{array}$(4.17)

where $q\in \left(\mathrm{0,1}\right)$, $k_1,k_2,k_3$ are control parameters. $E=\left(\overline{x},\overline{y},\overline{z}\right)$ is the equilibrium of system Eq. 4.13. We will apply linear feedback to stabilize the equilibrium $E_0=\left(\mathrm{0,0,0}\right)$ of system Eq. 4.13. When $\tilde{\alpha }=0.45,\tilde{\beta }=0.75$, the Jacobian matrix of system Eq. 4.17 at $E_0$ is

$J\left(E_1\right)=\left[\begin{array}{ccc}{k}_1& 1& 0\\ 1& k_2-0.75& 0\\ 0& 0& k_3-0.45\end{array}\right]$(4.18)

The corresponding characteristic equation at $E_0$ is

${\lambda }^3+a_1{\lambda }^2+a_2\lambda +a_3=0$(4.19)

and the discriminant is

$D\left(P\right)=18a_1{a}_2{a}_3+a_1^2{a}_2^2-4a_3{a}_1^3-4a_2^3-27a_3^2$(4.20)

where

$\begin{array}{l}{a}_1=\left(0.75-k_1-k_2\right)+\left(0.45-k_3\right)\\ a_2=k_1\left(k_2-0.75\right)-1+\left(0.75-k_1-k_2\right)\left(0.45-k_3\right)\\ a_3=\left(0.45-k_3\right)\left[k_1\left(k_2-0.75\right)-1\right]\end{array}$(4.21)

According to (i) of Lemma 4.2 above, we have the following theorem.

Theorem 4.3. For system Eq. 4.13, when

$k_1<\frac{0.05\left(200k_2{k}_3-200k_3^2-90k_2+30k_3+227\right)}{10k_2-10k_3-3},k_2<k_3+0.3,k_3<-1.55$

the equilibrium $E_0$ is locally asymptotic stability.

5 Conclusion

This article mainly discussed the dynamical behaviors of the fractional-order Shimizu-Morioka model. We find that chaos does exist in the fractional-order model with order less than 3. Future work that requires further consideration regarding this topic includes theoretical analysis of system Eq. 2.9, the largest Lyapunov exponent in the state space, the linear and nonlinear feedback controller, synchronization of this kind of system, and in-depth studies on chaos control for the fractional state.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author/s.

Author Contributions

ZW: conceptualization, methodology, reviewing, and editing. XZ: first draft preparation, and writing: reviewing and editing. All authors contributed to manuscript revision and approved the submitted version.

Funding

This work is supported by the Natural Science Foundation of China (Grant No. 11771001), Provincial Natural Science Research Project of Anhui Colleges (Grant No. KJ2019A0672, KJ2019A0666, and KJ2020A0121), Program for Excellent Young Talents in University of Anhui Province (Grant No. gxyq2017092 and gxyq2018102), Teaching Research Project of Anhui Province (Grant No. 2019jyxm0468), Political Construction of Public Basic Course-Taking Linear Algebra as an Example (Grant No. GJGF202033).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Faieghi MR, Delavari H. Chaos in fractional-order Genesio-Tesi system and its synchronization. Commun Nonlinear Sci Numer Simulation (2012) 17(2):731–41. doi:10.1016/j.cnsns.2011.05.038

CrossRef Full Text | Google Scholar

2. Jin-Man H, Chen F-Q. A new fractional order hyperchaotic rabinovich system and its dynamical behaviors. Int J Non Linear Mech (2017) 95:73–81. doi:10.1016/j.ijnonlinmec.2017.05.013

CrossRef Full Text | Google Scholar

3. Rabah K, Ladaci S, Lashab M. State feedback with fractional pi λ d λ control structure for fractional lü chaos stabilization. in: 2016 8th International Conference on Modelling, identification and control (ICMIC); 2016 Nov 15-17; Algiers, Algeria. New York, NY: IEEE (2016). p. 954–9.

Google Scholar

4. Sheu L-J, Chen H-K, Chen J-H, Tam L-M, Chen W-C, Lin K-T, et al. Chaos in the Newton-Leipnik system with fractional order. Chaos, Solitons and Fractals (2008) 36(1):98–103. doi:10.1016/j.chaos.2006.06.013

CrossRef Full Text | Google Scholar

5. Li C, Peng G. Chaos in Chen’s system with a fractional order. Chaos, Solitons and Fractals (2004) 22(2):443–50. doi:10.1016/j.chaos.2004.02.013

CrossRef Full Text | Google Scholar

6. Shimizu T, Morioka N. On the bifurcation of a symmetric limit cycle to an asymmetric one in a simple model. Phys Lett A (1980) 76(3-4):201–204. doi:10.1016/0375-9601(80)90466-1

CrossRef Full Text | Google Scholar

7. Lorenz EN. Deterministic nonperiodic flow. J Atmos Sci (1963) 20(2):130–41. doi:10.1175/1520-0469(1963)020<0130:dnf>2.0.co;2

CrossRef Full Text | Google Scholar

8. Shil’nikov AL. On bifurcations of the lorenz attractor in the shimizu-morioka model. Physica D: Nonlinear Phenomena (1993) 62(1-4):338–46. doi:10.1016/0167-2789(93)90292-9

CrossRef Full Text | Google Scholar

9. Messias M, Gouveia MRA, Pessoa C. Dynamics at infinity and other global dynamical aspects of Shimizu-Morioka equations. Nonlinear Dyn (2012) 69(1):577–87. doi:10.1007/s11071-011-0288-8

CrossRef Full Text | Google Scholar

10. Tigan G, Turaev D. Analytical search for homoclinic bifurcations in the shimizu-morioka model. Physica D: Nonlinear Phenomena (2011) 240(12):985–9. doi:10.1016/j.physd.2011.02.013

CrossRef Full Text | Google Scholar

11. El-Dessoky MM, Yassen MT, Aly ES. Bifurcation analysis and chaos control in Shimizu-Morioka chaotic system with delayed feedback. Appl Math Comput (2014) 243:283–97. doi:10.1016/j.amc.2014.05.072

CrossRef Full Text | Google Scholar

12. Liao X, Xu F, Wang P, Yu P. Chaos control and synchronization for a special generalized Lorenz canonical system - the SM system. Chaos, Solitons & Fractals (2009) 39(5):2491–508. doi:10.1016/j.chaos.2007.07.029

CrossRef Full Text | Google Scholar

13. Pyragas K, Tamaševičius A. Experimental control of chaos by delayed self-controlling feedback. Phys Lett A (1993) 180(1-2):99–102. doi:10.1016/0375-9601(93)90501-p

CrossRef Full Text | Google Scholar

14. Pyragas K. Continuous control of chaos by self-controlling feedback. Phys Lett A (1992) 170(6):421–8. doi:10.1016/0375-9601(92)90745-8

CrossRef Full Text | Google Scholar

15. Rucklidge AM. Chaos in models of double convection. J Fluid Mech (1992) 237(1):209–29. doi:10.1017/s0022112092003392

CrossRef Full Text | Google Scholar

16. Diethelm K, Ford NJ. Analysis of fractional differential equations. J Math Anal Appl (2002) 265(2):229–48. doi:10.1006/jmaa.2000.7194

CrossRef Full Text | Google Scholar

17. Podlubny I. Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications, Vol. 198. Cambridge, MA: Academic Press (1998).

18. Samko SG, Kilbas AA, Oleg IM. Fractional integrals and derivatives. Theory and Applications. Yverdon, CH: Gordon and Breach (1993). p. 1993.

19. Caputo M. Linear models of dissipation whose Q is almost frequency independent--II. Geophys J Int (1967) 13(5):529–39. doi:10.1111/j.1365-246x.1967.tb02303.x

CrossRef Full Text | Google Scholar

20. Diethelm K. An algorithm for the numerical solution of differential equations of fractional order. Electron Trans Numer Anal (1997) 5(1):1–6.

Google Scholar

21. Matignon D. Stability properties for generalized fractional differential systems. Esaim: Proc (1998) 5:145–58. doi:10.1051/proc:1998004

CrossRef Full Text | Google Scholar

22. Matignon D. Stability results for fractional differential equations with applications to control processing. Comput Eng Syst Appl (1996) 2:963–8.

Google Scholar