Equitable Domination in Vague Graphs With Application in Medical Sciences

Considering all physical, biological, and social systems, fuzzy graph (FG) models serve the elemental processes of all natural and artificial structures. As the indeterminate information is an essential real-life problem, which is mostly uncertain, modeling the problems based on FGs is highly demanding for an expert. Vague graphs (VGs) can manage the uncertainty relevant to the inconsistent and indeterminate information of all real-world problems, in which FGs possibly will not succeed in bringing about satisfactory results. In addition, VGs are a very useful tool to examine many issues such as networking, social systems, geometry, biology, clustering, medical science, and traffic plan. The previous definition restrictions in FGs have made us present new definitions in VGs. A wide range of applications has been attributed to the domination in graph theory for several fields such as facility location problems, school bus routing, modeling biological networks, and coding theory. Concepts from domination also exist in problems involving finding the set of representatives, in monitoring communication and electrical networks, and in land surveying (e.g., minimizing the number of places a surveyor must stand in order to take the height measurement for an entire region). Hence, in this article, we introduce different concepts of dominating, equitable dominating, total equitable dominating, weak (strong) equitable dominating, equitable independent, and perfect dominating sets in VGs and also investigate their properties by some examples. Finally, we present an application in medical sciences to show the importance of domination in VGs.

1 Introduction

Many real-world situations can accessibly be explained by means of a diagram consisting of a set of points together with lines joining certain pairs of these points. Notice that in such diagrams one is mainly interested in whether two given points are joined by a line; the manner in which they are joined is immaterial. A mathematical abstraction of situations of this type gives rise to the concept of a graph. To exemplify the objects and the connection between them, the graph nodes and edges are being employed accordingly. FGs are intended to demonstrate the connection structure among objects so that the concrete object existence (node) and the relationship between two objects (edge) are matters of degree. FG models are advantageous mathematical tools for addressing the combinatorial problems in several fields integrating research, algebra, computing, environmental science, and topology. Owing to the vagueness and ambiguity of natural existence, fuzzy graphical models outperform other graphical models. In 1965, Zadeh [44] proposed fuzzy set (FS) theory as a model for the exemplification of uncertainty and vagueness in real-world systems. FS theory is an exceedingly influential mathematical tool for resolving approximate reasoning-related problems. By defining the VS notion through changing the value of an element in a set with a subinterval of [0,1], Gau and Buehrer [13] introduced the VS theory. More probabilities are illustrated by VSs compared to FSs. A VS is more effective for explaining the false membership degree existence. Many events in the real world provided the incentive for introducing FGs. Kauffman [15] described FGs based on Zadeh’s fuzzy relation [44]. Kosari et al. [16] defined vague graph structure. Fuzzy Graph was introduced by Rosenfeld [32]. Akram et al. [1–6] proposed new definitions on FGs. Mordeson et al. [17–19] studied some results in FGs. Borzooie and Rashmanlou [7–11] analyzed several concepts of VGs. Samanta et al. [33–38] defined fuzzy competition graphs and some bipolar fuzzy graph results. Shao et al. [25, 26, 39–41] introduced new results in FGs and intuitionistic fuzzy graphs. Ramakrishna [24] presented VG concepts and examined their properties. Rashmanlou et al. [27–31] advanced new concepts in VGs.

A VG is a generalized structure of a FG that provides more exactness, adaptability, and compatibility to a system when matched with systems that run on FGs. In addition, a VG is capable of concentrating on determining the uncertainty coupled with the inconsistent and indeterminate information of any real-world problem, where FGs may not lead to adequate results. There exist an extensive array of applications for domination in graph theory in several fields such as school bus routing, facility location problems, and electrical networks. The domination idea was introduced first in the chessboard problem. In 1962, Ore [22] pioneered to apply the expression “domination” for undirected graphs. Somasundaram [42] presented the domination and independent domination in FGs. Gani and Chandrasekaran [20, 21] investigated the fuzzy-DS and independent-DS notion utilizing strong arcs. Cockayne [12] and Hedetniemi [14] described the independent and irredundance domination number in graphs. The domination concept in intuitionistic fuzzy graphs was examined by Parvathi and Thamizhendhi [23]. Talebi and Rashmanlou [43] studied new applications of domination in VGs. Domination in VGs has several uses in different fields. Hence, this study seeks to consider different concepts of dominating, equitable dominating, total equitable dominating, weak (strong) equitable dominating, equitable independent, and perfect dominating sets in VGs and investigate their properties by some examples.

Previously, many emergency patients died due to delays in transportation to the hospital; therefore, we introduce an application in the transportation system to show the importance of domination in VGs.

2 Preliminaries

In this section, to consider the stage for our analysis and to facilitate the following of our discussion, a brief overview of some of the basic definitions is introduced. A graph denotes a pair $G^{\text{*}}=\left(V,E\right)$ satisfying $E\subseteq V\times V$. The elements of V and E are the nodes and edges of the graph $G^{\text{*}}$, correspondingly.

An FG has the form of $\xi =\left(\gamma ,\nu \right)$, where $\gamma :V\to \left[\mathrm{0,1}\right]$ and $\nu :V\times V\to \left[\mathrm{0,1}\right]$ are defined as $\nu \left(ab\right)\le \gamma \left(a\right)\wedge \gamma \left(b\right)$, $\forall a,b\in V$, and ν is a symmetric fuzzy relation on γ and $\wedge$ denotes the minimum.

Definition 2.1. [13] A VS A is a pair $\left(t_A,f_A\right)$on set V where $t_A$ and $f_A$ are used as real valued functions which can be defined on $V\to \left[\mathrm{0,1}\right]$, so that $t_A\left(a\right)+f_A\left(a\right)\le 1$, for all a belongs V. The interval $\left[t_A\left(a\right),1-f_A\left(a\right)\right]$is considered as the vague value of a in A.$G^{\text{*}}$ will be a crisp graph $\left(V,E\right)$ and ζ a VG $\left(A,B\right)$ throughout this article.

Definition 2.2. [13] The support of a vague set $A=\left(t_A,f_A\right)$, denoted by $supp\left(A\right)$, is defined as $supp\left(A\right)=sup{p}^t\left(A\right){{\displaystyle \cup }}^{\text{}}supp{}^f\left(A\right)$, where ${\text{supp}}^t\left(A\right)=\left\{a|t_A\left(a\right)>0\right\}$, $supp{}^f\left(A\right)=\left\{a|f_A\left(a\right)>0\right\}$.

Definition 2.3. [24] A pair $\zeta =\left(A,B\right)$is called a VG on a crisp graph $G^{\text{*}}$ that $A=\left(t_A,f_A\right)$is a VS on V and $B=\left(t_B,f_B\right)$ is a VS on $E\subseteq V\times V$such that $t_B\left(ab\right)\le \text{min}\left(t_A\left(a\right),t_A\left(b\right)\right)$ and $f_B\left(ab\right)\ge \text{max}\left(f_A\left(a\right),f_A\left(b\right)\right)$, for each edge $ab\in E$.

Definition 2.4. [8] Let $\zeta =\left(A,B\right)$be a VG. Then, $\left(i\right)$ the vertex cardinality of ζ is described by $\left|A\right|$ and defined as $\left|A\right|={\displaystyle \sum }_{a_i\in V}\left(t_A\left(a_i\right),f_A\left(a_i\right)\right).$ and $\left(ii\right)$ the edge cardinality of ζ is described by $\left|B\right|$ and defined as

$\left|B\right|={\displaystyle \sum }_{a_i,a_j\in V}\left(t_B\left(a_i{a}_j\right),f_B\left(a_i{a}_j\right)\right).$

Definition 2.5. [8] Let $\zeta =\left(A,B\right)$ be a VG. If $a_i,a_j\in V$, then the t-strength of connectedness between $a_i$ and $a_j$ is defined as $t_B^{\infty }\left(a_i,a_j\right)=\text{sup}\left\{t_B^k\left(a_i,a_j\right)|k=\mathrm{1,2},\dots ,n\right\}$ and f-strength of connectedness is as $f_B^{\infty }\left(a_i,a_j\right)=\text{inf}\left\{f_B^k\left(a_i,a_j\right)|k=\mathrm{1,2},\dots ,n\right\}$. In addition, we have

$t_B^k\left(ab\right)=\text{sup}\left\{t_B\left(a,b_1\right)\wedge t_B\left(b_1,b_2\right)\wedge t_B\left(b_2,b_3\right)\wedge \cdots \wedge t_B\left(b_{k-1},b\right)|\left(a,b_1,b_2,\dots ,b_{k-1},b\right)\in V\right\}.$

and

$f_B^k\left(ab\right)\left(\right)=\text{inf}\left\{f_B\left(a,b_1\right)\vee f_B\left(b_1,b_2\right)\vee f_B\left(b_2,b_3\right)\vee \cdots \vee f_B\left(b_{k-1},b\right)|\left(a,b_1,b_2,\dots ,b_{k-1},b\right)\in V\right\}.$

Definition 2.6. [8] An edge $ab$in a VG $\zeta =\left(A,B\right)$is called strong edge if $t_B\left(ab\right)\ge {\left(t_B\right)}^{\infty }\left(ab\right)$and $f_B\left(ab\right)\le {\left(f_B\right)}^{\infty }\left(ab\right)$.

Definition 2.7. [8] Two nodes $a_i$ and $a_j$ in a VG $\zeta =\left(A,B\right)$ are called to be adjacent if either one of the following conditions holds. $\left(i\right)$$t_B\left(a_i{a}_j\right)>0$ and $f_B\left(a_i{a}_j\right)\ge 0$. $\left(ii\right)$$t_B\left(a_i{a}_j\right)\ge 0$ and $f_B\left(a_i{a}_j\right)>0$, $a_i,a_j\in V$. $\left(iii\right)$ A node a in a VG ζ is called an isolated node if $t_B\left(ab\right)=0$and $f_B\left(ab\right)=0$, $\forall$$b\in V$, $a\ne b$. That is, $N\left(a\right)=\varnothing$.

Definition 2.8. [9] The degree of a node a in a VG ζ is defined as the sum of weights of edges incident to a. It is defined by $d_{\zeta }\left(a\right)=\left({\text{deg}}^t\left(a\right),{\text{deg}}^f\left(a\right)\right)$. The minimum degree of ζ is $\delta \left(\zeta \right)=\text{min}\left\{d_{\zeta }\left(a\right)\right|a\in V\}$. The maximum degree of ζ is $\text{Δ}\left(\zeta \right)=\text{max}\left\{d_{\zeta }\left(a\right)\right|a\in V\}$.

Definition 2.9. [8] Let $\zeta =\left(A,B\right)$be a VG. Suppose that $a,b\in V$; then, a dominates b in ζ if $\exists$a strong edge between a and b.

Definition 2.10. [8] A subset S of V is called a DS in ζ if for each $a\in V-S$, $\exists$$b\in S$so that a dominates b. A DS S of a VG ζ is referred to as a Minimal DS if no proper subset of S is a DS.

Definition 2.11. [8] If ζ is a VG, then the vertex cardinality of $S\subseteq V$ is defined as follows:

$\left|S\right|=\left|{\displaystyle \sum }_{a\in S}\frac{1+t_A\left(a\right)-f_A\left(a\right)}{2}\right|.$

All the basic notations are shown in Table 1.

TABLE 1

TABLE 1. Some basic notations.

3 Domination in VGs

Definition 3.1. Let $\zeta =\left(A,B\right)$be a VG. The equitable neighborhood (EN) of a node $a\in V$, described by $EN\left(a\right)$ and defined as $EN\left(a\right)=\left(E{N}^t\left(a\right),E{N}^f\left(a\right)\right)$, where $E{N}^t\left(a\right)=\{b\in V|b\in N\left(a\right),|{\text{deg}}^t\left(b\right)-{\text{deg}}^t\left(a\right)|\le 1\}$, $t_B\left(ab\right)=\text{min}\left\{t_A\left(b\right),t_A\left(a\right)\right\}$, $E{N}^f\left(a\right)=\{b\in V|b\in N\left(a\right),|{\text{deg}}^f\left(b\right)-{\text{deg}}^f\left(a\right)|\ge 1\}$, $f_B\left(ab\right)=\text{max}\left\{f_A\left(b\right),f_A\left(a\right)\right\}$.

Definition 3.2. The END of a node $a\in V$, denoted by ${\text{deg}}_{EN}\left(a\right)$, is defined as ${\text{deg}}_{EN}\left(a\right)=\left({\text{deg}}_{EN}^t\left(a\right),{\text{deg}}_{EN}^f\left(a\right)\right)$, where ${\text{deg}}_{EN}^t\left(a\right)={\displaystyle \sum }_{b\in EN\left(a\right)}{t}_B\left(ab\right)$and ${\text{deg}}_{EN}^f\left(a\right)={\displaystyle \sum }_{b\in EN\left(a\right)}{f}_B\left(ab\right)$.The minimum END, denoted by ${\delta }_{EN}\left(\zeta \right)$, is defined as ${\delta }_{EN}\left(\zeta \right)=\left({\delta }_{EN}^t\left(\zeta \right),\delta {}_{EN}^f\left(\zeta \right)\right)$, where ${\delta }_{EN}^t\left(\zeta \right)=\text{min}\left\{{\text{deg}}_{EN}^t\left(a\right)\right|a\in V\}$ and $\delta {}_{EN}^f\left(\zeta \right)=\text{min}\{{\text{deg}}_{EN}^f\left(a\right)|a\in V\}$.The maximum END, denoted by ${\text{Δ}}_{EN}\left(\zeta \right)$, is defined as ${\text{Δ}}_{EN}\left(\zeta \right)=\left({\text{Δ}}_{EN}^t\left(\zeta \right),{\text{Δ}}_{EN}^f\left(\zeta \right)\right)$, where ${\text{Δ}}_{EN}^t\left(\zeta \right)=\text{max}\left\{{\text{deg}}_{EN}^t\left(a\right)\right|a\in V\}$ and ${\text{Δ}}_{EN}^f\left(\zeta \right)=\text{max}\left\{{\text{deg}}_{EN}^f\left(a\right)|a\in V\right\}$.

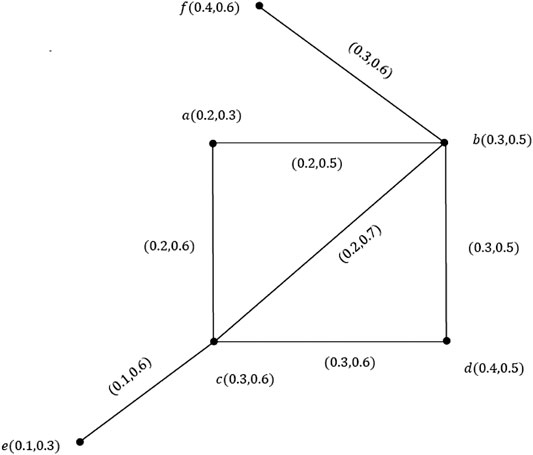
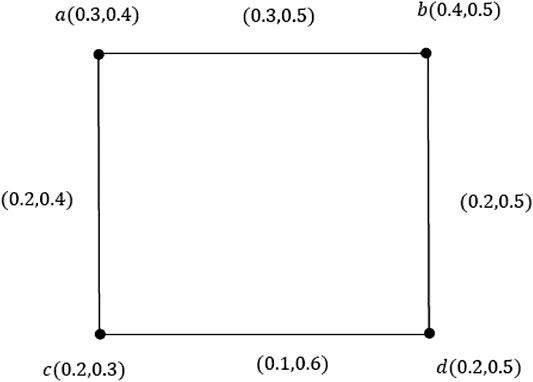
Example 3.3. Let $\zeta =\left(A,B\right)$ be a VG on $V=\left\{a,b,c,d,e,f\right\}$ so that $A=\left(t_A,f_A\right)$ is a vague subset of V, in Table 2, and $B=\left(t_B,f_B\right)$ is a vague subset of $V\times V$ defined in Table 3. The VG is shown in Figure 1. By simple calculation, we have $EN\left(a\right)=\left\{b\right\}$, $EN\left(b\right)=\left\{a,f,d\right\}$, $EN\left(c\right)=\left\{e\right\}$, $EN\left(d\right)=\left\{b\right\}$, $EN\left(e\right)=\left\{c\right\}$, and $EN\left(f\right)=\left\{b\right\}$.The ENDs of nodes are calculated as ${\text{deg}}_{EN}\left(a\right)=\left(0.2,0.5\right)$, ${\text{deg}}_{EN}\left(b\right)=\left(0.8,1.6\right)$, ${\text{deg}}_{EN}\left(c\right)=\left(0.1,0.6\right)$, ${\text{deg}}_{EN}\left(d\right)=\left(0.3,0.5\right)$, ${\text{deg}}_{EN}\left(e\right)=\left(0.1,0.6\right)$, and ${\text{deg}}_{EN}\left(f\right)=\left(0.3,0.6\right)$. The minimum END of VG ζ is ${\delta }_{EN}\left(\zeta \right)=\left(0.1,0.5\right)$ and the maximum END of a VG ζ is ${\text{Δ}}_{EN}\left(\zeta \right)=\left(0.8,1.6\right)$.

TABLE 2

TABLE 2. Vague set A on set V.

TABLE 3

TABLE 3. Vague set B in V×V.

FIGURE 1

FIGURE 1. EN degree of nodes in ζ.

Definition 3.4. Let $\zeta =\left(A,B\right)$ be a VG. A node $b\in V$ is called an EIN in ζ if, for each $a\in V$, $|{\text{deg}}^t\left(a\right)-{\text{deg}}^t\left(b\right)|>1$, $t_B\left(ab\right)<\text{min}\left\{t_A\left(a\right),t_A\left(b\right)\right\}$, and $|{\text{deg}}^f\left(a\right)-{\text{deg}}^f\left(b\right)|<1$, $f_B\left(ab\right)>\text{max}\left\{f_A\left(a\right),f_A\left(b\right)\right\}$, i.e., $EN\left(b\right)=\varnothing$.

Example 3.5.Consider a VG $\zeta =\left(A,B\right)$ on $V=\left\{a,b,c,d,e\right\}$ which is shown in Figure 2.From Figure 2, we have $\text{deg}\left(a\right)=\left(1.3,1.3\right)$, $\text{deg}\left(b\right)=\left(1.2,0.8\right)$, $\text{deg}\left(c\right)=\left(1.4,1.3\right)$, $\text{deg}\left(d\right)=\left(0.2,0.6\right)$, and $\text{deg}\left(e\right)=\left(0.1,0.6\right)$. Since $|{\text{deg}}^t\left(a\right)-{\text{deg}}^t\left(e\right)|>1$, $t_B\left(ae\right)<\text{min}\left\{t_A\left(a\right),t_A\left(e\right)\right\}$, and $|{\text{deg}}^f\left(a\right)-{\text{deg}}^f\left(e\right)|<1$, $f_B\left(ae\right)>\text{max}\left\{f_A\left(a\right),f_A\left(e\right)\right\}$, i.e., $EN\left(e\right)=\varnothing$. Also, $|{\text{deg}}^t\left(c\right)-{\text{deg}}^t\left(d\right)|>1$, $t_B\left(cd\right)<\text{min}\left\{t_A\left(c\right),t_A\left(d\right)\right\}$, and $|{\text{deg}}^f\left(c\right)-{\text{deg}}^f\left(d\right)|<1$, $f_B\left(cd\right)>\text{max}\left\{f_A\left(c\right),f_A\left(d\right)\right\}$, i.e., $EN\left(d\right)=\varnothing$. Hence, e and d are isolated nodes in ζ.

FIGURE 2

FIGURE 2. Equitable isolated node.

Definition 3.6.Let ζ be a VG. A subset $S\subseteq V$ is called an EDS of ζ if for each node $b\in V-S$, $\exists$ a node $a\in S$ so that $ab\in E$, $|{\text{deg}}^t\left(a\right)-{\text{deg}}^t\left(b\right)|\le 1$, $t_B\left(ab\right)=\text{min}\left\{t_A\left(a\right),t_A\left(b\right)\right\}$, and $|{\text{deg}}^f\left(a\right)-{\text{deg}}^f\left(b\right)|\ge 1$, $f_B\left(ab\right)=\text{max}\left\{f_A\left(a\right),f_A\left(b\right)\right\}$. The EDN of ζ, denoted by ${\gamma }_e\left(\zeta \right)$, is defined as the minimum cardinality of an EDS of S.

Definition 3.7.An EDS S of a VG ζ is called a MI-EDS of ζ if for each node $b\in S$, the set $S-\left\{b\right\}$ is not an EDS; i.e., no proper subset of S is an EDS of ζ.

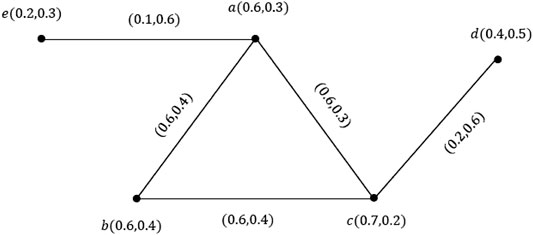
Example 3.8.Consider a VG $\zeta =\left(A,B\right)$, as shown in Figure 3.It is easy to show that the MI-EDS of VG ζ is $S=\left\{a\right\}$. The EDN of ζ is ${\gamma }_e\left(\zeta \right)=0.45$.

FIGURE 3

FIGURE 3. Equitable dominating set of ζ.

Definition 3.9.Let $\zeta =\left(A,B\right)$ be a VG. ζ is called a DEVG if, for each $b\in V$, $\exists$ a node $a\in V$ so that $ab\in supp\left(B\right)$, $|{\text{deg}}^t\left(a\right)-{\text{deg}}^t\left(b\right)|\le 1$, $t_B\left(ab\right)=\text{min}\left\{t_A\left(a\right),t_A\left(b\right)\right\}$, and $|{\text{deg}}^f\left(a\right)-{\text{deg}}^f\left(b\right)|\ge 1$, $f_B\left(ab\right)=\text{max}\left\{f_A\left(a\right),f_A\left(b\right)\right\}$.

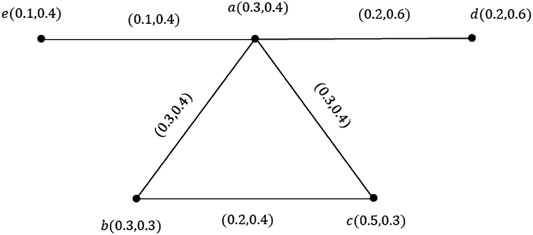
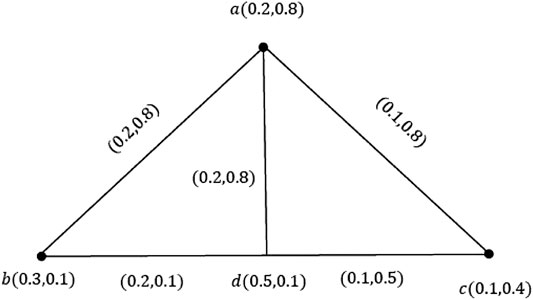
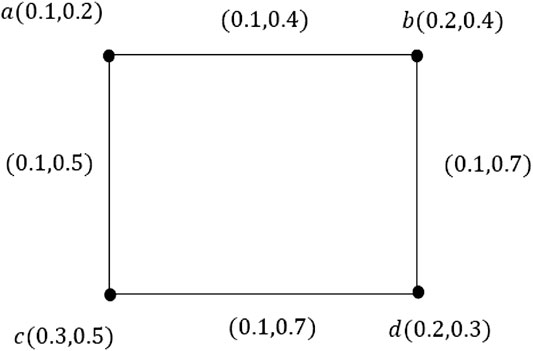
Example 3.10.Consider a VG ζ, as shown in Figure 4. Simple calculations show that ζ is a degree equitable VG.

FIGURE 4

FIGURE 4. Degree equitable VG.

Definition 3.11.A subset $I\subseteq V$ is called an EIS of a VG $\zeta =\left(A,B\right)$ if $|{\text{deg}}^t\left(a\right)-{\text{deg}}^t\left(b\right)|>1$, $t_B\left(ab\right)<\text{min}\left\{t_A\left(a\right),t_A\left(b\right)\right\}$, and $|{\text{deg}}^f\left(a\right)-{\text{deg}}^f\left(b\right)|<1$, $f_B\left(ab\right)>\text{max}\left\{f_A\left(a\right),f_A\left(b\right)\right\}$, for all $a,b\in I$. The EIN of ζ, denoted by ${\gamma }_{ie}\left(\zeta \right)$, is defined as the minimum cardinality of an EIS of ζ.

Definition 3.12.An EIS I is called a MA-EIS of ζ if, for each node $a\in V-I$, the set $I{{\displaystyle \cup }}^{\text{}}\left\{a\right\}$ is not an EIS.

Example 3.13. Consider a VG $\zeta =\left(A,B\right)$ given in Figure 5. It is clear that $S=\left\{a,d\right\}$ is maximal EIS. The EIN is ${\gamma }_{ie}\left(\zeta \right)=1.25$.

FIGURE 5

FIGURE 5. EIS of ζ.

Definition 3.14.Let $\zeta =\left(A,B\right)$ be a VG. For any two nodes $a,b\in V$, a strongly dominates b in ζ if $t_B\left(ab\right)=\text{min}\left\{t_A\left(a\right),t_A\left(b\right)\right\}$, $f_B\left(ab\right)=\text{max}\left\{f_A\left(a\right),f_A\left(b\right)\right\}$, and $de{g}_{\zeta }^t\left(a\right)\ge de{g}_{\zeta }^t\left(b\right)$, $de{g}_{\zeta }^f\left(a\right)\le de{g}_{\zeta }^f\left(b\right)$. Similarly, a weakly dominates b if $t_B\left(ab\right)=\text{min}\left\{t_A\left(a\right),t_A\left(b\right)\right\}$, $f_B\left(ab\right)=\text{max}\left\{f_A\left(a\right),f_A\left(b\right)\right\}$, $de{g}_{\zeta }^t\left(b\right)\ge de{g}_{\zeta }^t\left(a\right)$, and $de{g}_{\zeta }^f\left(b\right)\le de{g}_{\zeta }^f\left(a\right)$.

Definition 3.15.An EDS $S\subseteq V$ is called a weak (strong) EDS of ζ if, for each node $b\in V-S$, $\exists$ at least one node $a\in S$ so that a weakly (strongly) dominates b. The weak (strong) EDN of ζ, denoted by ${\gamma }_{we}\left(\zeta \right)$$\left({\gamma }_{se}\left(\zeta \right)\right)$, is called as the minimum cardinality of a weak (strong) EDS of ζ.

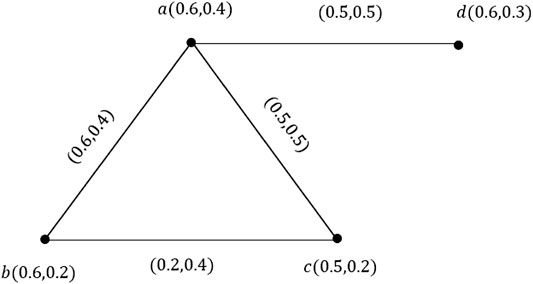
Example 3.16.Consider the VG $\zeta =\left(A,B\right)$ given in Figure 6. It is easy to see that the strong EDSs of ζ are $S_1=\left\{a,b\right\}$ and $S_2=\left\{a,d\right\}$. The strong EDN of ζ is ${\gamma }_{se}\left(\zeta \right)=0.8$.

FIGURE 6

FIGURE 6. Strong EDS of ζ.

Theorem 3.17.Let $\zeta =\left(A,B\right)$ be a VG. An EDS S of ζ is a minimal EDS if and only if, for every $b\in S$, one of the following conditions holds: $\left(i\right)$ b is an isolated node in S, $\left(ii\right)$$EN\left(b\right){{\displaystyle \cap }}^{\text{}}\left(V-S\right)\ne \varnothing$, or $\left(iii\right)$$\exists$ a node $a\in V-S$ so that $EN\left(a\right){{\displaystyle \cap }}^{\text{}}S=\left\{b\right\}$.

Proof. Let ζ be a VG with minimal EDS S; then, for each node $b\in S$, the set $S\text{'}=S-\left\{b\right\}$ is not an EDS. Hence, $\exists$ at least one node $a\in V-S\text{'}$ so that a is not dominated by any node in $S\text{'}$. So, we have two cases.

If $a=b$, then b is an isolated node in S; i.e., b is not neighbor to any node $c\in S$ so that $t_B\left(bc\right)=0=f_B\left(bc\right)$. Thus, $EN\left(b\right){{\displaystyle \cap }}^{\text{}}\left(V-S\right)\ne \varnothing$; that is, every node in S has a neighbor in $V-S$.

If $a\ne b$, i.e., $a\in V-S$, then a is dominated by some node of S but not dominated by any node in $S\text{'}$. Hence, a is neighbor only to one node $b\in S$, so $EN\left(a\right){{\displaystyle \cap }}^{\text{}}S=\left\{b\right\}$.

Conversely, suppose that S is an EDS of a VG ζ and, for every node $b\in S$, one of the given conditions holds. Assume that S is not a MI-EDS, then clearly $\exists$ a node $b\in S$ so that $S-\left\{b\right\}$ is an EDS of ζ. Therefore, b is neighbor to at least one node of set $S-\left\{b\right\}$; i.e., b is not an isolated node in S, and thus condition $\left(i\right)$ is false. In addition, if we get $S\text{'}=S-\left\{b\right\}$ as an EDS of ζ, then each node of $V-S\text{'}$ is neighbor to at least one node in $S\text{'}$. Hence, conditions $\left(ii\right)$ and $\left(iii\right)$ are also false which is a contradiction. ∎

Theorem 3.18.Let $\zeta =\left(A,B\right)$ be a VG with order $o\left(\zeta \right)$, then: $\left(i\right)$${\gamma }_e\left(\zeta \right)\le {\gamma }_{se}\left(\zeta \right)\le o\left(G^{\text{*}}\right)-{\text{Δ}}_{EN}^t\left(\zeta \right)$, $\left(ii\right)$${\gamma }_e\left(\zeta \right)\le {\gamma }_{we}\left(\zeta \right)\le o\left(G^{\text{*}}\right)-{\delta }_{EN}^t\left(\zeta \right)$.

Proof.According to definition, every weak (strong) EDS of a VG ζ is an EDS of ζ, ${\gamma }_e\left(\zeta \right)\le {\gamma }_{se}\left(\zeta \right)$ and ${\gamma }_e\left(\zeta \right)\le {\gamma }_{we}\left(\zeta \right)$. Let a and b be two arbitrary nodes of ζ. If ${\text{deg}}_{EN}^t\left(b\right)={\text{Δ}}_{EN}^t\left(\zeta \right)$ and ${\text{deg}}_{EN}^t\left(a\right)={\delta }_{EN}^t\left(\zeta \right)$, then $V-EN\left(b\right)$ is a strong EDS of ζ and $V-EN\left(a\right)$ is a weak EDS of ζ. Hence, ${\gamma }_{se}\left(\zeta \right)\le |V-EN\left(b\right)|$ and ${\gamma }_{we}^t\left(\zeta \right)\le |V-EN\left(a\right)|$, i.e.,

${\gamma }_{se}\left(\zeta \right)\le o\left(G^{\text{*}}\right)-{\text{Δ}}_{EN}^t\left(\zeta \right)$

and

${\gamma }_{we}\left(\zeta \right)\le o\left(G^{\text{*}}\right)-{\delta }_{EN}^t\left(\zeta \right).$

∎

Theorem 3.19.Let ζ be a VG without single nodes and S be a MI-EDS of ζ; then $V-S$is an EDS of ζ.

Proof.Let ζ be a VG with MI-EDS S; then, for each node $b\in S$, there is at least one node $a\in V-S$ so that $|{\text{deg}}^t\left(a\right)-{\text{deg}}^t\left(b\right)|\le 1$, $t_B\left(ab\right)=\text{min}\left\{t_A\left(a\right),t_A\left(b\right)\right\}$ and $|{\text{deg}}^f\left(a\right)-{\text{deg}}^f\left(b\right)|\ge 1$, $f_B\left(ab\right)=\text{max}\left\{f_A\left(a\right),f_A\left(b\right)\right\}$. Hence, $V-S$ dominates each element of S. So, $V-S$ is an EDS of ζ. ∎

Theorem 3.20. Let ζ be a VG with EIDS I; then I is both a MI-EDS and a MA-EIS of ζ. Conversely, any MA-EIS I of a VG ζ is an EIDS of ζ.

Proof. Let ζ be a VG with EIDS K; then, for each node $b\in V-K$, the set $K{{\displaystyle \cup }}^{\text{}}\left\{b\right\}$ is not an EIS and the set $K-\left\{b\right\}$is not an EDS of ζ. So, K is both a MI-EDS and a MA-EIS of ζ.Conversely, assume that K is a MA-EIS of ζ; then, for each node $b\in V-K$, the set $K{{\displaystyle \cup }}^{\text{}}\left\{b\right\}$ is not an EIS of ζ. Hence, the set K dominates each node $a\in V-K$ and so K is an EDS of ζ. Therefore, K is an EIDS of ζ. ∎

Theorem 3.21.A subset $I\subseteq V$is an EIS and EDS of a VG ζ if and only if I is a MA-EIS of ζ.

Proof.Assume that K is both an EDS and an EIS of a VG ζ. Suppose that K is not a MA-EIS of ζ, then clearly there exists a node $a\in V-K$ so that $K{{\displaystyle \cup }}^{\text{}}\left\{a\right\}$ is an EIS; namely, a is not dominated by any node $b\in K$ that shows K is not an EDS of ζ, a contradiction, so K is a MA-EIS of ζ. Conversely, let K be a MA-EIS of ζ; then, for each node $a\in V-K$, the set $K{{\displaystyle \cup }}^{\text{}}\left\{a\right\}$ is not an EIS of ζ. Hence, the set K dominates each node $a\in V-K$; that is, K is an EDS of ζ. So, K is both an EDS and an EIS of ζ. ∎

Definition 3.22.A total-EDS (TEDS) of a VG $\zeta =\left(A,B\right)$ is a subset $S\subseteq V$if for each node $b\in V$, $\exists$ at least one node $a\in S$ so that $ab\in E\left(\zeta \right)$, $|{\text{deg}}^t\left(a\right)-{\text{deg}}^t\left(b\right)|\le 1$, $t_B\left(ab\right)=\text{min}\left\{t_A\left(a\right),t_A\left(b\right)\right\}$_, and $|{\text{deg}}^f\left(a\right)-{\text{deg}}^f\left(b\right)|\ge 1$, $f_B\left(ab\right)=\text{max}\left\{f_A\left(a\right),f_A\left(b\right)\right\}$. The TEDN of ζ, denoted by ${\gamma }_{te}\left(\zeta \right)$, is defined as the minimum cardinality of a TEDN S.

Definition 3.23.A TEDS S of a VG ζ is called a minimal TEDS if, for each node $b\in S$, the set $S-\left\{b\right\}$is not a TEDS; i.e., no proper subset of S is a TEDS of ζ.

Example 3.24.Consider a VG $\zeta =\left(A,B\right)$, as shown in Figure 7. It is clear that $\left\{a,b\right\}$ and $\left\{b,c\right\}$ are TEDSs of ζ.

FIGURE 7

FIGURE 7. TEDS of ζ.

Theorem 3.25.Let ζ be a VG with no isolated nodes; then ${\gamma }_t\left(\zeta \right)\le {\gamma }_{te}\left(\zeta \right)$.

Proof.As each TEDS of a VG ζ is a total dominating set, so ${\gamma }_t\left(\zeta \right)\le {\gamma }_{te}\left(\zeta \right)$. ∎

Definition 3.26.Let $\zeta =\left(A,B\right)$ be a VG. A subset $S\subseteq V$ is called a PDS of ζ if, for each node $b\in V-S$, there exists exactly one vertex $a\in S$so that a dominates b.

Definition 3.27.A PDS S of a VG ζ is called a minimal PDS if, for each $a\in S$, the set $S-\left\{a\right\}$ is not a PDS in ζ. The minimum cardinality between all MI-PDSs is called the PDN of ζ and it is denoted by ${\gamma }_{pif}\left(\zeta \right)$ or simply ${\gamma }_{pif}$.

Example 3.28.Consider a VG $\zeta =\left(A,B\right)$ given in Figure 8. By simple computation, it is clear that $S=\left\{a,d\right\}$is a MI-PDS. The PDN of ζ is ${\gamma }_{pif}=0.9$.

FIGURE 8

FIGURE 8. VG ξ.

4 The Application of VDS in Medical Sciences

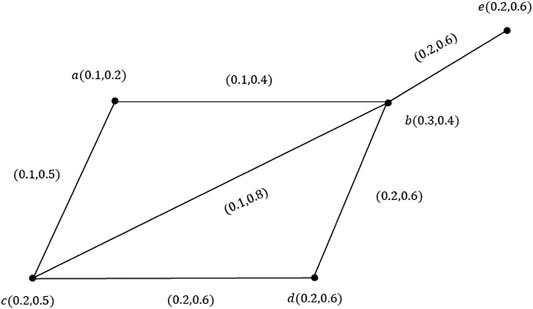
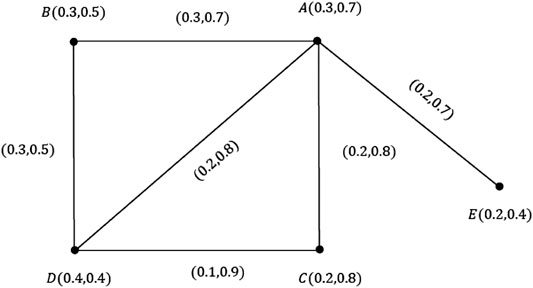
In the past, many emergency patients died due to the delays in transportation to the hospital, but today the number has dropped dramatically. Traffic problems in cities are one of the factors influencing this delay. In addition, the specialization of hospitals has meant that each patient must be transferred to the relevant hospital based on the main complaint, even though this specialized hospital is further away than other available hospitals. Therefore, in this study, we have tried to identify the nearest hospital based on distance, traffic load, and patient complaints. For this purpose, we consider four hospitals located in one city. We show hospitals as B, C, D, and E. In this vague graph, one vertex represents the patient’s home and other vertices are related to the hospitals in the city. The edges indicate the accumulation of cars in the city. (See Figure 9).

FIGURE 9

FIGURE 9. VG ζ.

The node $B\left(0.3,0.5\right)$ means that it has $30\text{\%}$ of the necessary facilities for treating the patient and unfortunately lacks $50\text{\%}$ of the necessary equipment.

The edge $AB$ shows that only $30\text{\%}$ of the patient’s transport route to the hospital by ambulance has a low traffic load, and unfortunately $70\text{\%}$ of the route between these two points has a heavy traffic load during most hours of the day. The EDSs for Figure 8 are as follows:

$S_1=\left\{A,B\right\},$

$S_2=\left\{A,D\right\},$

$S_3=\left\{A,B,C\right\},$

$S_4=\left\{A,B,D\right\},$

$S_5=\left\{A,B,E\right\},$

$S_6=\left\{A,C,D\right\},$

$S_7=\left\{A,D,E\right\},$

$S_8=\left\{B,C,E\right\},$

$S_9=\left\{C,D,E\right\},$

$S_{10}=\left\{A,B,D,E\right\},$

$S_{11}=\left\{A,C,D,E\right\},$

$S_{12}=\left\{B,C,D,E\right\},$

$S_{13}=\left\{A,B,C,E\right\},$

$S_{14}=\left\{A,B,C,D\right\}.$

After calculating the cardinality of $S_1,\cdots ,S_{14}$, we obtain

$\left|S_1\right|=0.7,$

$\left|S_2\right|=0.8,$

$\left|S_3\right|=0.9,$

$\left|S_4\right|=1.2,$

$\left|S_5\right|=1.1,$

$\left|S_6\right|=1,$

$\left|S_7\right|=1.3,$

$\left|S_8\right|=1,$

$\left|S_9\right|=1.1,$

$\left|S_{10}\right|=1.6,$

$\left|S_{11}\right|=1.4,$

$\left|S_{12}\right|=1.5,$

$\left|S_{13}\right|=1.3,$

$\left|S_{14}\right|=\mathrm{1.4.}$

It is obvious that $S_1$ has the smallest size between other DSs; hence, we conclude that it can be the best choice because first there is more free space for the ambulance from the patient’s home to hospital B, so that it can get the patient to the desired location faster, saving time and money. Second, hospital B has more medical services compared to other hospitals. So, the government should invest more on widening roads and controlling traffic between cities so that ambulances can transport patients to the relevant specialized hospitals faster.

5 Conclusion

Considering the precision, elasticity, and compatibility in a system, vague models outweigh the other FGs. The VG concept generally has a large variety of applications in different areas such as computer science, operation research, topology, and natural networks. Domination in graph theory has a wide range of applications in several fields such as facility location problems, school bus routing, and coding theory. Therefore, in this research, we described several concepts of dominating sets, ED, TED, weak (strong) ED, EISs, and PDS, in VGs and also studied their properties incorporating some basic examples. Finally, we introduced an application of domination in the transportation system. Future research will hold the investigation of new concepts of vague planer graphs, vague bridges, vague cycles, and vague competition graphs and represent their applications in medical sciences and social networks.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

All authors have contributed equally to this work. All authors have read and agreed to the possible publication of the manuscript.

Funding

This work was supported by the National Key R&D Program of China (No. 2018YFB1005100).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Akram M, Naz S. Energy of pythagorean fuzzy graphs with Applications. Mathematics (2018) 6:136. doi:10.3390/math6080136

CrossRef Full Text | Google Scholar

2. Akram M, Sitara M. Certain concepts in intuitionistic neutrosophic graph structures. Information (2017) 8:154. doi:10.3390/info8040154

CrossRef Full Text | Google Scholar

3. Akram M, Naz S, Smarandache F. Generalization of maximizing Deviation and TOPSIS Method for MADM in simplified neutrosophic hesitant fuzzy environment. Symmetry (2019) 11:1058. doi:10.3390/sym11081058

CrossRef Full Text | Google Scholar

4. Akram M, Zafar F. Rough fuzzy digraphs with application. J Appl Math Comput (2019) 59:91–127. doi:10.1007/s12190-018-1171-2

CrossRef Full Text | Google Scholar

5. Akram M, Dar JM, Naz S. Pythagorean Dombi fuzzy graphs. J Intell Fuzzy Syst (2020) 6:29–54. doi:10.1007/s40747-019-0109-0

CrossRef Full Text | Google Scholar

6. Akram M, Sarwar M. Transversals of m-polar fuzzy hypergraphs with applications. J Intell Fuzzy Syst (2017) 33:351–64. doi:10.3233/jifs-161668

CrossRef Full Text | Google Scholar

7. Borzooei RA, Rashmanlou H. Ring sum in product intuitionistic fuzzy graphs. J Adv Res Pure Math (2015) 7:16–31. doi:10.5373/jarpm.1971.021614

CrossRef Full Text | Google Scholar

8. Borzooei RA, Rashmanlou H. Domination in vague graphs and its applications. J Intell Fuzzy Syst (2015) 29:1933–40. doi:10.3233/ifs-151671

CrossRef Full Text | Google Scholar

9. Borzooei RA, Rashmanlou H. Degree of vertices in vague graphs. J Appl Math Inform (2015) 33:545–57. doi:10.14317/jami.2015.545

CrossRef Full Text | Google Scholar

10. Borzooei RA, Rashmanlou H, Samanta S, Pal M. Regularity of vague graphs. J Intell Fuzzy Syst (2016) 30:3681–9. doi:10.3233/ifs-162114

CrossRef Full Text | Google Scholar

11. Borzooei RA, Rashmanlou H, Samanta S, Pal M. A Study on fuzzy labeling graphs. J Intell Fuzzy Syst (2016) 6(30):3349–55. doi:10.3233/ifs-152082

CrossRef Full Text | Google Scholar

12. Cockayne EJ, Favaron O, Payan C, Thomason AC. Contribution to the theory of domination and irredundance in graphs. Discret Math (1981) 33(3):249–58. doi:10.1016/0012-365x(81)90268-5

CrossRef Full Text | Google Scholar

13. Gau WL, Buehrer DJ. Vague sets. IEEE Trans Syst Man Cybern (1993) 23:610–4. doi:10.1109/21.229476

CrossRef Full Text | Google Scholar

14. Haynes TW, Hedetniemi S, Slater P. Fundamentals of domination in graphs. Boca Raton: CRC Press (2013).

15. Kaufmann A. Introduction a la Theorie des Sour-Ensembles Flous. Paris, France: Masson et Cie (1973).

16. Kosari S, Rao Y, Jiang H, Liu X, Wu P, Shao Z. Vague graph Structure with Application in medical diagnosis. Symmetry (2017) 12(10):15–82. doi:10.3390/sym12101582

CrossRef Full Text | Google Scholar

17. Mordeson JN, Mathew S. Fuzzy end nodes in fuzzy incidence graphs. New Math Nat Comput (2017) 13(3):13–20. doi:10.1142/s1793005717500028

CrossRef Full Text | Google Scholar

18. Mordeson JN, Mathew S. Human trafficking: source, transit, destination, designations. New Math Nat Comput (2017) 13(3):209–18. doi:10.1142/s1793005717400063

CrossRef Full Text | Google Scholar

19. Mordeson JN, Mathew S, Borzooei RA. Vulnerability and government response to human trafficking: Vague fuzzy incidence graphs. New Math Nat Comput (2018) 14(2):203–19. doi:10.1142/s1793005718500138

CrossRef Full Text | Google Scholar

20. Nagoorgani A, Mohamed SY, Hussain RJ. Point set domination of intuitionistic fuzzy graphs. Int J Fuzzy Math Archive (2015) 7(1):43–9. doi:10.1007/s12190-015-0952-0

CrossRef Full Text | Google Scholar

21. Nagoorgani A, Chandrasekaran VT. Domination in fuzzy graphs. Adv Fuzzy Sets Syst (2006) I(1):17–26. doi:10.1007/s12190-015-0952-0

CrossRef Full Text | Google Scholar

22. Ore O Theory of graphs. Providence: American Mathematical Society Publications (1962)

23. Parvathi R, Thamizhendhi G. Domination in intuitionistic fuzzy graph, proceedings of 14th international Conference on intuiyionistic fuzzy graphs. Notes Intuit Fuzzy Sets (2010) 16(2):39–49. doi:10.1007/3-540-34783-6_15

CrossRef Full Text | Google Scholar

24. Ramakrishna N. Vague graphs. Int J Comput Cogn (2009) 7:51–8. doi:10.1155/2014/525389

CrossRef Full Text | Google Scholar

25. Rao Y, Kosari S, Shao Z. Certain Properties of vague Graphs with a novel application. Mathematics (2020) 8:16–47. doi:10.3390/math8101647

CrossRef Full Text | Google Scholar

26. Rao Y, Kosari S, Shao Z, Cai R, Xinyue L. A Study on Domination in vague incidence graph and its application in medical sciences. Symmetry (2020) 12:18–85. doi:10.3390/sym12111885

CrossRef Full Text | Google Scholar

27. Rashmanlou H, Borzooei RA. Vague graphs with application. J Intell Fuzzy Syst (2016) 30:3291–9. doi:10.3233/ifs-152077

CrossRef Full Text | Google Scholar

28. Rashmanlou H, Samanta S, Pal M, Borzooei RA. A study on bipolar fuzzy graphs. Em J Intell Fuzzy Syst (2015) 28:571–80. doi:10.3233/ifs-141333

CrossRef Full Text | Google Scholar

29. Rashmanlou H, Borzooei RA. Product vague graphs and its applications. J Intell Fuzzy Syst (2016) 30:371–82. doi:10.3233/ifs-152077

CrossRef Full Text | Google Scholar

30. Rashmanlou H, Jun YB, Borzooei RA. More results on highly irregular bipolar fuzzy graphs. Ann Fuzzy Math Inform (2014) 8:149–68. doi:10.1007/978-981-15-8756-6_1

CrossRef Full Text | Google Scholar

31. Rashmanlou H., Borzooei R.A., Shoaib M., Talebi Y., Taheri M., Mofidnakhaei F. New way for finding shortest path problem in a network. Multiple Valued Logic Soft Comput 20205451460. doi:10.1109/icnn.1993.298689

32. Rosenfeld A. In: LA Zadeh, KS Fu, and M Shimura, editors. Fuzzy graphs, fuzzy Sets and their applications. New York, NY, USA: Academic Press (1975). p. 77–95.

33. Samanta S, Pal M. Fuzzy k-competition graphs and pcompetition fuzzy graphs. Fuzzy Inf Eng (2013) 5:191–204. doi:10.1007/s12543-013-0140-6

CrossRef Full Text | Google Scholar

34. Samanta S, Akram M, Pal M. m-step fuzzy competition graphs. J Appl Math Comput (2014) 11:133–9. doi:10.1007/s12190-s12014-s10785-s10782

CrossRef Full Text | Google Scholar

35. Samanta S, Pal M. Irregular bipolar fuzzy graphs. Int J Appl Fuzzy Sets (2012) 2:91–102. doi:10.1109/tfuzz.2014.2387875

CrossRef Full Text | Google Scholar

36. Samanta S, Pal M. Some more results on bipolar fuzzy sets and bipolar fuzzy intersection graphs. J Fuzzy Math (2014) 22:253–62. doi:10.14569/ijarai.2014.030109

CrossRef Full Text | Google Scholar

37. Samanta S, Pal M, Rashmanlou H, Borzooei RA. Vague graphs and strengths. J Intell Fuzzy Syst (2016) 30(6):3675–80. doi:10.3233/ifs-162113

CrossRef Full Text | Google Scholar

38. Sahoo S, Pal M, Rashmanlou H, Borzooei RA. Covering and paired domination in intuitionistic fuzzy graphs. J Intell Fuzzy Syst (2017) 33(6):4007–15. doi:10.3233/jifs-17848

CrossRef Full Text | Google Scholar

39. Shao Z, Kosari S, Rashmanlou H, Shoaib M. New Concepts in intuitionistic fuzzy Graph with Application in water supplier systems. Mathematics (2020) 8:12–41. doi:10.3390/math8081241

CrossRef Full Text | Google Scholar

40. Shao Z, Kosari S, Shoaib M, Rashmanlou H. Certain Concepts of vague graphs with Applications to Medical diagnosis. Front Phys (2020) 8:357. doi:10.3389/fphy.2020.00357

CrossRef Full Text | Google Scholar

41. Shao Z, Li Z, Wu P, Chen L, Zhang X. Multi-factor combination Authentication using fuzzy graph domination model. J Intell Fuzzy Syst (2019) 37:4979–85. doi:10.3233/JIFS-181859

CrossRef Full Text | Google Scholar

42. Somasundaram A, Somasundaram S. Domination in fuzzy graph-I. Patter Recogn Lett (1998) 19(9):787–91.doi:10.1016/S0167-8655(98)00064-6

CrossRef Full Text | Google Scholar

43. Talebi Y, Rashmanlou H. New concepts of domination sets in vague graphs with applications. Int J Comput Sci Mathematics (2019) 10(4):375–89. doi:10.1504/ijcsm.2019.10024350

CrossRef Full Text | Google Scholar

44. Zadeh LA. Fuzzy sets. Inf Control (1965) 8:338–53. doi:10.1016/S0019-9958(65)90241-X

CrossRef Full Text | Google Scholar