Quantum Implications of Non-Extensive Statistics

Exploring the analogy between quantum mechanics and statistical mechanics, we formulate an integrated version of the Quantropy functional. With this prescription, we compute the propagator associated to Boltzmann–Gibbs statistics in the semiclassical approximation as $K=F\left(T\right)\text{exp}\left(i{S}_{cl}/\hslash \right)$. We determine also propagators associated to different nonadditive statistics; those are the entropies depending only on the probability $S_{\pm }$ and Tsallis entropy $S_q$. For $S_{\pm }$, we obtain a power series solution for the probability vs. the energy, which can be analytically continued to the complex plane and employed to obtain the propagators. Our work is motivated by the work of Nobre et al. where a modified q-Schrödinger equation is obtained that provides the wave function for the free particle as a q-exponential. The modified q-propagator obtained with our method leads to the same q-wave function for that case. The procedure presented in this work allows to calculate q-wave functions in problems with interactions determining nonlinear quantum implications of nonadditive statistics. In a similar manner, the corresponding generalized wave functions associated to $S_{\pm }$ can also be constructed. The corrections to the original propagator are explicitly determined in the case of a free particle and the harmonic oscillator for which the semiclassical approximation is exact, and also the case of a particle with an infinite potential barrier is discussed.

1 Introduction

Nonextensive entropies depending only on the probabilities have been obtained in [1]. They belong to a family of nonextensive statistical mechanics, relevant for nonequilibrium systems. Renowned examples are Tsallis ($S_q$) [2, 3] and Sharma-Mital [4]; all of them can be obtained within the framework of Superstatistics [5].

For the entropies depending only on the probability, there are two entropy functionals [1]:

$S_{+}={\displaystyle \sum _l\left(1-p_l^{p_l}\right)},S_{-}={\displaystyle \sum _l\left(p_l^{-p_l}-1\right)}\text{,}$

where the index $l$ runs over the states of the system and $p_l$ denotes the probability of the state $l$. These expressions can be considered as building blocks for nonextensive entropies without parameters. For example, one can consider $S_1=\left(S_{+}+S_{-}\right)/2$. These entropies are noticeably distinct to Boltzmann–Gibbs (BG) entropy for systems with few degrees of freedom; however, when the number of degrees of freedom goes to the thermodynamic limit, they match perfectly with BG statistics Cabo [6]. This is when the probability $p_l$ is small, the leading term in $S_{+}$ and $S_{-}$ expansions is the BG entropy. Therefore, in this limit, BG statistics is recovered. They belong to the class of Superstatistics of [5] with an intensive parameter ${\text{χ}}^2$ distribution found in [1]. These entropies have also been studied in [6–10].

There is a universality of the Superstatistics family [5]. As it has been shown, for several distributions of the temperature, the Boltzmann factor essentially coincides up to the first expansion terms. This has as a consequence that also the entropies associated to these Boltzmann factors have all of them basically the same first corrections to the usual entropy. Furthermore, the three entropies listed here that depend only on the probability are expanded only on the parameter $y=p\text{ln}p$; this is always smaller than 1 giving correction terms to the entropy which at any order are smaller than the previous ones. So, that any function of y proposed as another generalized entropy, depending only on this parameter, when expanded in y will basically coincide with one of the three ones studied here; clearly demanding that the first term in the expansion is $-y$ giving BG entropy. Thus, the entropies $S_{+}$, $S_{-}$, and their linear combinations can be considered as building blocks to compute any possible modified entropies depending only on the probability.

We are motivated by the concept of Quantropy developed by Baez and Pollard [11] and by nonlinear quantum systems with modified wave functions based on Tsallis statistics in [3, 12, 13]. For example, the work [13] developed a nonlinear quantum mechanics with q-mathematics motivated by Tsallis entropy. In recent years, there have also been other interesting developments in the connections of nonextensive entropies and quantum mechanics [14–25]. Also, the work [26] showed extensions of nonlinear quantum equations arising from an effective one particle treatment of many-body physics, such that the nonlinearity represents the interactions, obtaining wave function solutions that are q-distributions and including the harmonic oscillator potential. There exists as well a connection between nonlinear quantum equations and nonlinear diffusion and Fokker–Planck equations [18, 20] that also is noticed in [26]. Moreover, interesting applications of nonextensive entropies to compute statistical and thermodynamical properties of graphene and 2-dimensional quantum structures [27–30] have been developed. We develop a version of Quantropy in terms of the propagator of a quantum mechanical theory. Our generalized propagators could be connected to the appropriate quantum equations. Baez and Pollard’s Quantropy is a functional of the amplitude on the path integral a, with the same functional form as the entropy in terms of the probability $Q=-\underset{X}{{\displaystyle \int }}a\left(x\right)\text{ln}a\left(x\right)dx$. Giving the functional

$\begin{array}{l}{\mathrm{\Phi }}_{\mathrm{BP}}\mathrm{=}-{\displaystyle {\int }_{\mathrm{X}}\mathit{a}\left(\mathit{x}\right)\ln \mathit{a}\left(\mathit{x}\right)}\mathit{dx}-\mathit{\alpha }{\displaystyle {\int }_{\mathit{X}}\mathit{a}\left(\mathit{x}\right)}\mathit{dx}\\ -\mathrm{\lambda }{\displaystyle {\int }_{\mathit{X}}\mathit{a}\left(\mathit{x}\right)\mathit{S}\left(\mathit{x}\right)}\mathit{dx,}\end{array}(1)$

where $\alpha$ and $\text{λ}$ are Lagrange multipliers and $x$ is a path in the space of all possible paths X. From the search of extrema of this functional, restricted to values of a normalized and an average of the action, Baez and Pollard obtained the relation $a=\text{exp}\left(iS/\hslash -1-\alpha \right)$ with $\text{λ}=\frac{1}{i\hslash }$. Then, $a\sim \text{exp}\left(iS/\hslash \right)$ with the normalization fixed by the Lagrange multiplier $\alpha$. This scheme deepens on the relation between Quantum Mechanics and Statistical Physics, which has also been studied in different approaches [31, 32]. For example, in [33], the Fisher Information measure is employed to explore this relation.

In Baez and Pollard’s approach, the energy is mapped to the action S and the temperature to $i\hslash$. We consider the same identification but instead we identify E with the classical action $S_{cl}$. Thus, we consider as the analog of the entropy a functional in terms of the propagator, instead of the amplitude a. This is an extrapolation of the Quantropy [11] to an integration over all classical paths. It is worth to mention that the analog to the microstate in statistical mechanics is a particle path in quantum mechanics. Such that as the partition function in statistical mechanics is the sum over all the microstates, the quantum mechanical analog is the sum over all the paths of the particle (Feynman path integral). The standard expression for the propagator is given semiclassically by $K\sim \text{exp}\left(i{S}_{cl}/\hslash \right)$. We use this fact to define a kind of integrated Quantropy functional now in terms of the propagator for BG statistics, which we extend to the modified statistics $S_{+}$, $S_{-}$, and $S_q$.

This article is organized as follows. In Section 2, we obtain a series expansion for the probabilities versus $\beta E$ for the generalized entropies depending only on the probabilities $S_{+}$ and $S_{-}$. In Section 3, we continue these expansions to the complex plane. In Section 4, we present a version of Quantropy for BG statistics, $S_{+}$ and $S_{-}$ and $S_q$. In Section 5, we study in particular the case of the free particle propagator, obtained from the extrema of the Quantropy in the cases of $S_{+}$ and $S_{-}$ and $S_q$ for $q<1$ and $q>1$. We show that the $K_q$ propagator results exactly in the q-exponential that defines the q-wave function for the free particle [3]. In a similar manner, we argue that the corresponding generalized propagators $K_{+}$ and $K_{-}$ provide us with a procedure to construct ${\text{Ψ}}_{+}$ and ${\text{Ψ}}_{-}$ for the free particle. Our method however gives the possibility to construct $K_q$, $K_{+}$, and $K_{-}$ also for problems with interactions and by this mean to identify the corresponding wave functions. We also provide a way to perform the normalization inspired in Feynman and Hibbs work [34]. Section 6 is devoted to the analysis of the harmonic oscillator, and we exemplify with the case corresponding to $K_{+}$. Finally, in Section 7, we study the $K_{+}$ propagator for the particle in an infinite potential barrier. In Section 8, we summarize our results and present the conclusion. In a Supplementary Appendix we present a numerical study of the propagators.

2 Probability Distributions for Systems with Maximal $S_{+}$ and $S_{-}$

We start by developing a recurrent solution for the probability distribution of the generalized entropy $S_{+}$, introduced in [1]. On the contrary to BG statistics, for a system subjected to $S_{+}$ extremization, probability normalization, and energy conservation, there is not a simple inverse function of the probabilities p vs. the values of the energy state E. We overcome this difficulty by finding a series solution to the extremum equation. There are other possible series solutions, but we discuss here one that has a good convergence. At the end of the section, we give also the probability expansion for the entropy $S_{-}$, which is obtained by an equivalent Ansatz.

The functional to maximize the $S_{+}$ entropy subjected to probability normalization and averaged energy is given by [7, 8]:

${\text{Φ}}_{+}={\displaystyle \sum }_l\left(1-p_l^{p_l}\right)-\text{γ}{\displaystyle \sum }_l{p}_l-\beta {\displaystyle \sum }_l{E}_l{p}_l^{p_l+1}.(2)$

β and γ are Lagrange multipliers and $E_l$ is the energy of the state l, with probability $p_l$. The average values of energy and the normalization value have been omitted for simplicity. The extrema of (2) given by $\frac{\delta {\text{Φ}}_{+}}{\delta p_l}=0$ gives a relation between the energy E and the probabilities p (we have omitted the index l):

$\beta E=\frac{\left(-\text{γ}{p}^{-p}-1-\ln p\right)}{\left(1+p+p\ln p\right)}.(3)$

Notice that we omit the subindex l from the quantities. Setting the Lagrange multiplier $\text{γ}$ to $-1$, we first expand the previous equation around $p=0$ that accounts to consider the expansion around $\text{y}=p\text{ln}p=0$. That is, for the exponential of minus equation (3), one gets

$\begin{array}{c}{e}^{-\beta E}=p-p^2\ln p^2+1/2p^3\left(\ln p^2+2\ln p^3+\ln p^4\right)\\ +1/6p^4\left(-3\ln p^2-8\ln p^3-9\ln p^4-6\ln p^5-\ln p^6\right)\\ +1/24p^5\left(12\ln p^2+44\ln p^3+70\ln p^4+68\ln p^5+42\ln p^6+12\ln p^7+\ln p^8\right)+\dots .\end{array}(4)$

We make the following Ansatz to solve equation (4).

$p=e^{-\beta E}\left(1+{\displaystyle \sum }_{n=1}{c}_n{e}^{-n\beta E}\right),(5)$

where $c_n$ can be functions of $\beta E$. Plugging (5) in (4), to have the LHS equal to the RHS, the coefficients multiplying the powers of $e^{-n\beta E}$ with $n>1$ have to vanish. This gives a recurrent expression for the coefficients $c_n$ which for the first four coefficients is solved as

$\begin{array}{l}{c}_1=x^2,\\ c_2=1/2x^2\left(-1-2x+3x^2\right),\\ c_3=\frac{1}{6}{x}^2\left(3+4x-6x^2-24x^3+16x^4\right),\\ c_4=\frac{1}{24}{x}^2\left(-12-16x+60x^2+116x^3+30x^4-300x^5+125x^6\right).\end{array}(6)$

We have denoted $\beta E$ as x. The coefficients (6) give the following approximate solution for the probabilities versus $\beta E$:

$\begin{array}{c}{p}_{+}=e^{-x}+e^{-2x}{x}^2+\frac{1}{2}{e}^{-3x}{x}^2\left(-1-2x+3x^2\right)\\ +\frac{1}{6}{e}^{-4x}{x}^2\left(3+4x-6x^2-24x^3+16x^4\right)\\ +\frac{1}{24}{e}^{-5x}{x}^2\left(-12-16x+60x^2+116x^3+30x^4-300x^5+125x^6\right)+\dots .\end{array}(7)$

In Figure 1, we compare the exact value of $p$ vs. $\beta E$ with the power series solution (7) till 3rd order and with the Boltzmann distribution $e^{-\beta E}$.

FIGURE 1

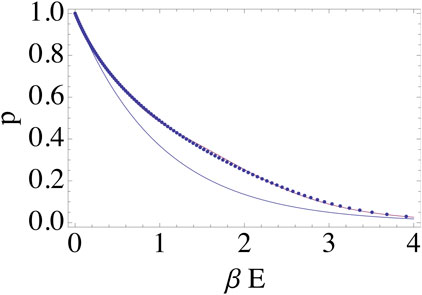
FIGURE 1. Probability versus $\beta E$. The blue line represents the BG statistics distribution. The dots represent the exact dependence in (3), $S_{+}$ statistics distribution, while the continuous red curve overlapping with the dotted line represents the power series solution (7) till order 3, i.e., up to the $e^{-4x}$ correction.

Probability Expansion for the Entropy $S_{-}‐$

Consider the other generalized entropy dependent only on the probabilities $S_{-}$. For this entropy, the functional to extremize ${\text{Φ}}_{-}$ reads

${\text{Φ}}_{-}={\displaystyle \sum }_l\left(p_l^{-p_l}-1\right)-\text{γ}{\displaystyle \sum }_l{p}_l-\beta {\displaystyle \sum }_l{E}_l{p}_l^{1-p_l}.(8)$

$\beta$ and $\text{γ}$ are Lagrange multipliers, and $E_l$ is the energy of the state $l$ and $p_l$ its probability. Finding the extrema of (8) as $\frac{\delta {\text{Φ}}_{-}}{\delta p_l}=0$ and proposing the same Ansatz (5), we obtain a set of equations that can be solved to give the recursive probability solution:

$p_{-}=e^{-x}\left(1-e^{-x}{x}^2+\frac{1}{2}{e}^{-2x}{x}^2\left(-1-2x+3x^2\right)+\frac{1}{6}{e}^{-3x}\left(-3x^2-4x^3+6x^4+24x^5-16x^6\right)\right)....(9)$

3 Modified Amplitude Expansions

In this section, we use the series solutions for the probabilities in terms of the energy obtained in the previous section, to perform an analytic continuation to the complex plane. Considering a as the amplitude of a path, this is a new complex variable substituting the probability $p_l$, and $A$ as the action replacing $\beta E_l$. This identification will allow to study modified Quantropy functionals, for the definition of Baez and Pollard (equation (1)), as well as our definition (18). The usual Quantropy solution will give an exponential $a\sim e^{\frac{iA}{\hslash }}$. In our approach, this would be the propagator $K\sim e^{\frac{i{S}_{cl}}{\hslash }}$. We want to analyze the new statistics $S_{+}$ and $S_{-}$. We will find a functional dependence of a vs. A (K vs. $S_{cl}$) that deviates from the exponential dependence.

The main idea is to complexify first the power expansion solution (7) since the amplitude is a complex number, such that we have a solution to the extrema of the modified Quantropy. The functional to extremize reads

${\text{Φ}}_{BP,+}={{\displaystyle \mathit{\int }}}^{\text{}}\left(1-a{\left(x\right)}^{a\left(x\right)}\right)dx-\alpha {{\displaystyle \mathit{\int }}}^{\text{}}a\left(x\right)dx-\text{λ}\mathit{\int }A\left(x\right)a{\left(x\right)}^{a\left(x\right)+1}dx.(10)$

Finding the extrema of (10) w.r.t. a, i.e., solving $\frac{\delta {\text{Φ}}_{BP,+}}{\delta a\left(x\right)}=0$, one gets

$\frac{A}{i\hslash }=\frac{\left(-\gamma a^{-a}-1-\text{ln}a\right)}{\left(1+a+a\text{ln}a\right)}=F\left(a\left(\frac{A}{i\hslash }\right)\right).(11)$

The range of validity of the propagators expressions depends on the convergence of the imaginary series solution to this equation. The series is obtained by doing the replacement $\beta E$ by $\frac{A}{i\hslash }$ and p by a in (3). Also, the Lagrange multipliers have to be mapped: $\beta$ to $\text{λ}$ and $\text{α}$ to $\text{γ}$. The minus sign gives the right sign after a rotation on the argument of the exponential (similar to a Wick rotation). As the series solution continuation of (7), we obtain the following expression:

$a_{+}\left(\frac{A}{i\hslash }\right)=e^{iA/\hslash }(1-{\frac{A}{\hslash }}^2{e}^{i\left(A/\hslash \right)}-\frac{1}{2}\left(A^2/{\hslash }^2\right)\left(-1+2i\left(A/\hslash \right)-3\left(A^2/{\hslash }^2\right)\right)e^{i2\left(A/\hslash \right)}-\frac{1}{6}\left(A^2/{\hslash }^2\right)\left(3-4i\left(A/\hslash \right)+6\left(A^2/{\hslash }^2\right)-24i\left(A^3/{\hslash }^3\right)+16\left(A^4/{\hslash }^4\right)\right)e^{3i\left(A/\hslash \right)}+\dots ).(12)$

Since A has units of action, the argument of the exponentials and the terms on the expansion are adimensional. Substituting this expression on the constraint equation (11), we obtain the real and imaginary parts of $F\left(a\left(\frac{A}{i\hslash }\right)\right)$. In Figure 2, the relevant difference of the propagators $K_{+}$ obtained employing (12) with respect to the standard one can be observed in the region of $S_{cl}\approx \hslash$.

FIGURE 2

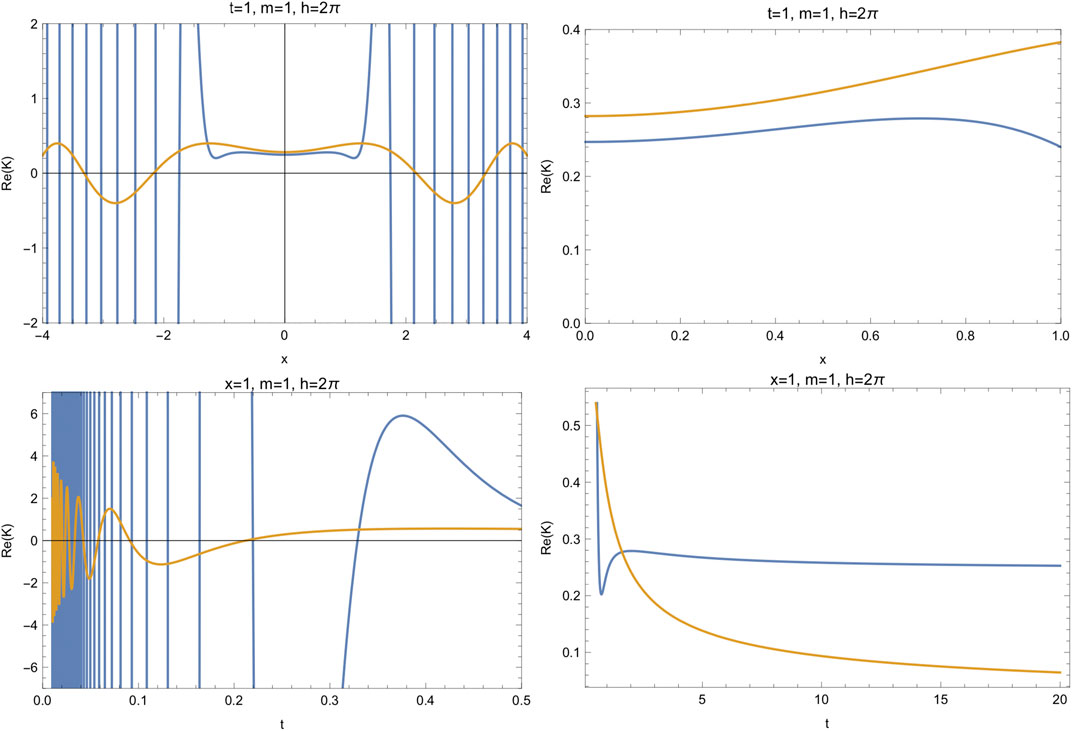
FIGURE 2. Real parts of the modified propagator (blue line) vs. standard propagator (yellow line), for the free particle for the modified statistics $S_{+}$. We set the mass and the Planck constant to unity. The quantum regime is given by $S_{cl}\approx \hslash$. Imposing $S_{cl}\mathrm{\lesssim }\hslash$ which translates for fixed $x=1$ in $t\mathrm{\gtrsim }1/2$, for fixed $t=1$ translates in $x^2\mathrm{\lesssim }2$. Notice that in the quantum regime $S_{cl}\approx \hslash$, there are differences between the standard and the modified propagator. In the classical regime, there are many oscillations caused by the series expansion that should sum up when computing more terms. When $S_{cl}\ll \hslash$, then both results coincide. The difference between the results of the modified propagator and the standard free particle is that the modified propagator result could be interpreted as the particle with an effective potential; this would give a spatially bounded wave function.

Using the parameter $\text{λ}=\frac{1}{i\hslash }$ in (12), the expression for the amplitudes becomes

$\begin{array}{c}{a}_{+}\left(A\right)=e^{-\text{λ}A}(1+{\left(\text{λ}A\right)}^2{e}^{-\text{λ}A}\\ +\frac{1}{2}{\left(\text{λ}A\right)}^2\left(-1-2\text{λ}A+3{\left(\text{λ}A\right)}^2\right)e^{-2\lambda A}\\ +\frac{1}{6}{\left(\text{λ}A\right)}^2(3+4\text{λ}A-6\left(\text{λ}A\right){}^2-24{\left(\text{λ}A\right)}^3+16{\left(\text{λ}A\right)}^4)e^{-3\lambda A}+\dots ).\end{array}(13)$

It is not difficult to observe that all terms of this expansion can be written as derivatives with respect to the parameter λ. If we derive with respect to λ, the usual amplitude we obtain is $\frac{\partial }{\partial \text{λ}}{e}^{-\text{λ}A}=-A{e}^{-\text{λ}A}$. Higher derivates can be written as

${\left(\frac{\text{λ}}{n}\right)}^m\frac{{\partial }^m}{\partial {\text{λ}}^m}{e}^{-n\text{λ}A}={\left(-1\right)}^m{\left(\text{λ}A\right)}^m{e}^{-n\text{λ}A},(14)$

where m and n are positive integers. Thus, we rewrite (3) as

$\begin{array}{c}{a}_{+}=e^{-\text{λ}A}+\frac{{\text{λ}}^2}{4}\frac{{\partial }^2}{\partial {\text{λ}}^2}{e}^{-2\text{λ}A}\\ +\frac{1}{2}\left(-\frac{{\text{λ}}^2}{3^2}\frac{{\partial }^2}{\partial {\text{λ}}^2}+2\frac{{\text{λ}}^3}{3^3}\frac{{\partial }^3}{\partial {\text{λ}}^3}+3\frac{{\text{λ}}^4}{3^4}\frac{{\partial }^4}{\partial {\text{λ}}^4}\right)e^{-3\text{λ}A}\\ +\frac{1}{6}\left(3\frac{{\text{λ}}^2}{4^2}\frac{{\partial }^2}{\partial {\text{λ}}^2}-4\frac{{\text{λ}}^3}{4^3}\frac{{\partial }^3}{\partial {\text{λ}}^3}-6\frac{{\text{λ}}^4}{4^4}\frac{{\partial }^4}{\partial {\text{λ}}^4}+24\frac{{\text{λ}}^5}{4^5}\frac{{\partial }^5}{\partial {\text{λ}}^5}+16\frac{{\text{λ}}^6}{4^6}\frac{{\partial }^6}{\partial {\text{λ}}^6}\right)e^{-4\text{λ}A}+\dots .\end{array}(15)$

One can compute the corrections to any order. Those corrections to the usual amplitude $a_0=e^{iS/\hslash }$ can be interpreted as higher order interactions of the action at different frequencies¹.

Now, one can apply the same method to determine the distribution arising from the Quantropy with statistics $S_{-}$. We also have to perform the extension to the complex plane. The amplitude distribution for the modified Quantropy coming from $S_{-}$ is given by the following:

$a_{-}=e^{i\left(A/\hslash \right)}(1+{\left(A/\hslash \right)}^2{e}^{i\left(A/\hslash \right)}-\frac{1}{2}{\left(A/\hslash \right)}^2\left(-1+2i\left(A/\hslash \right)-3{\left(A/\hslash \right)}^2\right)e^{2i\left(A/\hslash \right)}+\frac{1}{6}\left(3{\left(A/\hslash \right)}^2-4i{\left(A/\hslash \right)}^3+6{\left(A/\hslash \right)}^4-24i{\left(A/\hslash \right)}^5+16{\left(A/\hslash \right)}^6\right)e^{3i\left(A/\hslash \right)}+\dots ).(16)$

4 Quantropy in Terms of the Propagator

In this section, we present as an alternative proposal a kind of integrated version of the Quantropy of [1]. First, we do it for the BG entropy and then for $S_{+},S_{-}$, and $S_q$. The change in distribution probabilities which arise from modified entropies in statistics is now reflected in the quantum arena as modifications to the propagators. The propagators between points in space-time $\left({\mathbf{x}}_a,t_a\right)$ and $\left({\mathbf{x}}_b,t_b\right)$ in quantum mechanics determine the probability amplitude of particles to travel from certain position to another position in a given time. As modified entropies in statistical physics lead to modified probability distributions, distinct probabilities of propagation over all paths from $\left({\mathbf{x}}_a,t_a\right)$ and $\left({\mathbf{x}}_b,t_b\right)$ will arise from a modified Quantropy.

In the work [11], the Quantropy functional associated with BG statistics was formulated, and its maximization leads to the weight on the path integral $a\sim \text{exp}\left(-\text{λ}S\right)$ with $\lambda =1/i\hslash$. We propose another functional, which in a sense constitutes an integrated version of Quantropy. Its maximization leads to the propagator $K\left(x\right)\sim \text{exp}\left(-\text{λ}{S}_{cl}\left(x\right)\right)$. The Wentzel–Kramers–Brillouin (WKB) method [35] allows to compute the wave function in a semiclassical approximation. In a sense, this is linked to our approach, in which we maximize a functional which determines the propagator with a semiclassical approximation in terms of the classical action $S_{cl}$. This is exact for the free particle, the harmonic oscillator as well as for other cases [36, 37]. The procedure is applied to generalized entropy functionals, giving a modified propagator. For the Tsallis statistics, we obtain $K_q\left(x\right)\sim {\text{exp}}_q\left(-\text{λ}{S}_{cl}\left(x\right)\right)$. This structure is the same as the one of the wave function for the free particle of the Tsallis statistic ${\text{Ψ}}_q\left(x\right)={\text{exp}}_q\left(i\left(kx-wt\right)\right)$, which has been proposed as solution of the nonlinear quantum equations of [13]. According to Feynman arguments, one can start with the free particle propagator and determine the corresponding wave function, as discussed in [34]. Thus, our procedure allows to find a propagator which can be identified with the wave function of interest. We should note that the propagator resulting from our procedure will describe not only the free particle but to a good approximation any other problem with its corresponding classical action. Our method should give the wave function solution for the problem of interest.

With the same method, we write functionals for $S_{+}$ and $S_{-}$ and obtain probability distributions; we can write the corresponding Quantropies and obtain the propagators $K_{+}$ and $K_{-}$ and correspondingly extrapolate them to the wave functions ${\text{Ψ}}_{+}$ and ${\text{Ψ}}_{-}$. This would give us the quantum behavior for a given action. The obtained propagators can be related to nonlinear quantum systems studied in the literature [26].

To define our functionals, we use the semiclassical limit to compute the propagator; this is $K\left(x\right)=F\left(a,b\right)e^{\frac{i{S}_{cl}\left(x\right)}{\hslash }}$, denoting the classical action as $S_{cl}\left(x\right)$ and being $F\left(a,b\right)$ a constant depending on the time difference $t_b-t_a$. For the free particle and the harmonic oscillator as well as other physical problems [36, 37], this is an exact result.

For the BG statistics, we define the Quantropy functional:

${\text{Φ}}_0=-{{\displaystyle \mathit{\int }}}^{\text{}}K\left(x\right)\ln K\left(x\right)dx-\alpha {{\displaystyle \mathit{\int }}}^{\text{}}K\left(x\right)dx-\text{λ}{{\displaystyle \mathit{\int }}}^{\text{}}\left(S_{cl}\left(x\right)K\left(x\right)\right)dx.(17)$

The extrema condition $\frac{\delta {\text{Φ}}_0}{\delta K\left(x\right)}=0$ gives as solution the propagator dependence $K\left(x\right)=e^{-1-\alpha -\lambda S_{cl}\left(x\right)}$, with $\lambda =1/i\hslash$, where the normalization constant α determines $F\left(a,b\right)$.

The integrated Quantropy functional for the new $S_{+}$ statistic is studied in [1, 6–10] is given by the following:

${\text{Φ}}_{+}={{\displaystyle \mathit{\int }}}^{\text{}}\left(1-K{\left(x\right)}^{K\left(x\right)}\right)dx-\alpha {{\displaystyle \mathit{\int }}}^{\text{}}K\left(x\right)dx-\text{λ}{{\displaystyle \mathit{\int }}}^{\text{}}\left(S_{cl}\left(x\right)\right)K{\left(x\right)}^{K\left(x\right)+1}dx.(18)$

The extrema condition $\frac{\delta {\text{Φ}}_{+}}{\delta K\left(y\right)}=0$ with functional derivatives leads to the equation:

$\begin{array}{c}0={{\displaystyle \mathit{\int }}}^{\text{}}\left(-\delta \left(x-y\right)K{\left(x\right)}^{K\left(x\right)}\right)\left(\ln K\left(x\right)+1\right)dx-\alpha {{\displaystyle \mathit{\int }}}^{\text{}}\delta \left(x-y\right)dx\\ -\text{λ}\mathit{\int }{S}_{cl}\left(x\right)K{\left(x\right)}^{K\left(x\right)+1}\delta \left(x-y\right)\left(\ln K\left(x\right)+\frac{K\left(x\right)+1}{K\left(x\right)}\right)dx,\end{array}(19)$

and by changing the variable notation y to x, this can be written as

$\text{λ}{S}_{cl}\left(x\right)=\frac{-1-\ln K\left(x\right)-\alpha K{\left(x\right)}^{-K\left(x\right)}}{1+K\left(x\right)+\ln K\left(x\right)}.(20)$

Using our knowledge to solve this type of equation from the statistical physics case, presented in Section 2, this gives for the modified propagator the following series solution:

$K_{+}\left(x\right)=N_{+}{e}^{-\lambda S_{cl}}(1-e^{-\lambda S_{cl}}{\left(\text{λ}{S}_{cl}\right)}^2+e^{-2\text{λ}{S}_{cl}}{\left(\text{λ}{S}_{cl}\right)}^2\left(-1-2\left(\text{λ}{S}_{cl}\right)+3{\left(\text{λ}{S}_{cl}\right)}^2\right)-\frac{1}{6}{e}^{-2S_{cl}\text{λ}}\times \left(-3S_{cl}^2{\text{λ}}^2-4S_{cl}^3{\text{λ}}^3+6S_{cl}^4{\text{λ}}^4+24S_{cl}^5{\text{λ}}^5-16S_{cl}^6{\text{λ}}^6\right)+\dots ).(21)$

where $N_{+}$ is the normalization constant. This is obtained by taking the normalization $\alpha =-1$. A different normalization would change the coefficients in the expansion (21).

The maximization constraint for the new $S_{-}$ statistic is given by

${\text{Φ}}_{-}={{\displaystyle \mathit{\int }}}^{\text{}}\left(K{\left(x\right)}^{-K\left(x\right)}-1\right)dx-\alpha {{\displaystyle {{\displaystyle \mathit{\int }}}^{\text{}}}}^{\text{}}K\left(x\right)dx-\text{λ}{{\displaystyle \mathit{\int }}}^{\text{}}\left(S_{cl}\right)K{\left(x\right)}^{-K\left(x\right)+1}dx.(22)$

The extrema condition $\frac{\delta {\text{Φ}}_{-}}{\delta K\left(x\right)}=0$ gives the equation:

$\text{λ}{S}_{cl}\left(x\right)=\frac{1+\text{ln}K\left(x\right)+\alpha K{\left(x\right)}^{K\left(x\right)}}{1-K\left(x\right)-\text{ln}K\left(x\right)}.(23)$

Using our knowledge of this type of equation from the statistical physics case, we obtain for the modified propagator the series solution:

$K_{-}\left(x\right)=N_{-}{e}^{-\lambda S_{cl}}(1+e^{\left(-\text{λ}{S}_{cl}\right)}{\left(\text{λ}{S}_{cl}\right)}^2-e^{\left(-\text{λ}{S}_{cl}\right)}{\left(\text{λ}{S}_{cl}\right)}^2{\left(-1-2\left(\text{λ}{S}_{cl}\right)+3(\text{λ}{S}_{cl}\right)}^2+\frac{1}{6}{e}^{-2S_{cl}\lambda }\left(-3S_{cl}^2{\text{λ}}^2-4S_{cl}^3{\lambda }^3+6S_{cl}^4{\text{λ}}^4+24S_{cl}^5{\lambda }^5-16S_{cl}^6{\lambda }^6\right)+\dots ),(24)$

$N_{-}$ is the normalization constant. In the case of Tsallis statistics, the functional is given by the following:

${\text{Φ}}_q={{\displaystyle \mathit{\int }}}^{\text{}}\frac{\left(1-K{\left(x\right)}^q\right)}{\left(q-1\right)}dx-\alpha {{\displaystyle \mathit{\int }}}^{\text{}}K\left(x\right)dx-\text{λ}{{\displaystyle {{\displaystyle \mathit{\int }}}^{\text{}}}}^{\text{}}\left(S_{cl}\right)K{\left(x\right)}^{q}dx,(25)$

and the solution to $\frac{\delta {\text{Φ}}_q}{\delta K\left(x\right)}=0$ is

$\begin{array}{c}{K}_q\left(x\right)=N_q{\text{exp}}_q\left(-\text{λ}{S}_{cl}\left(x\right)\right),\\ =N_q{\left(1-\left(1-q\right)\text{λ}{S}_{cl}\right)}^{\frac{1}{1-q}}.\end{array}(26)$

We have still to discuss the normalization of the different Kernels. This q-propagator is related to the q-wave function for the free particle nonlinear quantum mechanics of [3]. We explore this case which has been studied by other means in the literature [3, 13, 24].

5 Free Particle Propagators

In this section, we write a modified propagator up to third order for the free particle in the case of the statistics $S_{+}$, $S_{-}$, and $S_q$ for $q=1-\delta$ and $q=1+\delta$ with $\delta >0$. The values of q less or equal than one are considered in order to compare the different propagators. We determine when the corrections to the usual propagator play an important role which turns to be in the quantum regime characterized by $S_{cl}\approx \hslash$. First, we describe the procedure; then, we describe the normalization; and in the last subsection, we summarize our results.

5.1 Superposition of Kernels

Now, we proceed to describe a generalized Kernel. The generalized complex probability distribution given by expansion (21) can be regarded as a superposition of Kernels. Furthermore, the superposition will carry to the wave functions. In order to normalize the superposition, we consider that the total Kernel expansion integration is the same as the usual (1 for the free particle), as is explicit in the Quantropy functional (4). We show that this coincides with the result for the normalization obtained from propagating the wave function [34]. For the free particle, the unnormalized Kernel is as follows:

$K_0\left(x,t;\mathrm{0,0}\right)={\left(\frac{2\hslash \mathit{ϵ}i\pi }{m}\right)}^{\left(n-1\right)/2}{\left(\frac{1}{n}\right)}^{1/2}\text{exp}\left(\frac{im{x}^2}{2\hslash t}\right),$

where n is the number of divisions of the time interval and ϵ is an infinitesimal time parameter that satisfies $t=\mathit{ϵ}n$. This expression arises from computing the path integral to get the following:

$\begin{array}{c}{K}_0\left(x,t;\mathrm{0,0}\right)={{\displaystyle \mathit{\int }}}^{\text{}}{e}^{iS/\hslash }Dx\\ ={{\displaystyle \mathit{\int }}}^{\text{}}\text{exp}\left(\frac{im}{2\hslash \mathit{ϵ}}{\displaystyle \sum }_n{\left(x_n-x_{n-1}\right)}^2\right)d^{n}x\\ ={\left(\frac{i\pi }{2A}\right)}^{\frac{1}{2}}{\left(\frac{2i\pi }{3A}\right)}^{\frac{1}{2}}{\left(\frac{3i\pi }{4A}\right)}^{\frac{1}{2}}\times \dots \times {\left(\frac{\left(n-1\right)i\pi }{nA}\right)}^{\frac{1}{2}}\text{exp}\left(\frac{iA{\left(x_0-x_n\right)}^2}{n}\right),\end{array}(27)$

with $A=\frac{m}{2\mathit{ϵ}\hslash }$. This calculation is performed dividing the integral in multiple Gaussian integrals (see [34]). The normalization constant is given by $N={\left(\frac{2\pi i\hslash \mathit{ϵ}}{m}\right)}^{-\frac{n}{2}}$; hence, the normalized propagator reads

$K_1\left(x,t;\mathrm{0,0}\right)={\left(\frac{2\hslash ti\pi }{m}\right)}^{-1/2}\text{exp}\left(\frac{im{x}^2}{2\hslash t}\right).(28)$

We define the unnormalized Kernel for the free particle as

$k\left(x,t;1\right)=\text{exp}\left(\frac{im{x}^2}{2\hslash t}\right)=e^{-\text{λ}A},(29)$

and the first two corrections in $K_{+}$ are given by

$\begin{array}{c}k\left(x,t;2\right)={\left(\frac{m{x}^2}{\hslash t}\right)}^2\text{exp}\left(\frac{im{x}^2}{\hslash t}\right)={\left(\text{λ}A\right)}^2\frac{{\partial }^2}{\partial {\text{λ}}^2}{e}^{-\text{λ}A},\\ k\left(x,t;3\right)=-\left(\frac{m^2{x}^4}{8{\hslash }^2{t}^2}+\frac{m^3{x}^6}{8i{\hslash }^3{t}^3}+3\frac{m^4{x}^8}{32{\hslash }^4{t}^4}\right)\times \text{exp}\left(\frac{3im{x}^2}{2\hslash t}\right),\\ =\frac{1}{2}\left(-\frac{{\text{λ}}^2}{3^2}\frac{{\partial }^2}{\partial {\text{λ}}^2}+2\frac{{\text{λ}}^3}{3^3}\frac{{\partial }^3}{\partial \text{λ}}+3\frac{{\text{λ}}^4}{3^4}\frac{{\partial }^4}{\partial {\text{λ}}^4}\right)e^{-3\text{λ}A}.\end{array}$

Thus, the generalized Kernel associated with $S_{+}$ entropy is given by

$K_{+}\left(x,t\right)=N_{+}\left(k\left(x,t;1\right)+k\left(x,t;2\right)+k\left(x,t;3\right)+\dots \right).$

The normalization constant is determined by the requirement ${{{\displaystyle \int }}^{\text{}}}_{-\infty }^{\infty }{K}_{+}\left(x,t\right)dx=1$, and up to the first corrections is given by $N_{+}=\frac{1}{1+3/\left(16\sqrt{2}\right)}=\mathrm{0.883...}$. The reason for this normalization is also understood by an argument presented in the following, motivated by Feynmann and Hibbs procedure [34].

Let us also discuss the normalization of the modified propagator with respect to the usual one, as shown in the standard case [34]. We start considering the original unnormalized Kernel for the free particle computed from the path integral:

$K_{\mathrm{1,0}}\left(x,t;\mathrm{0,0}\right)=2^{\frac{N-1}{2}}{\left(\frac{\pi i\hslash t}{mN}\right)}^{\frac{N-1}{2}}{\left(N\right)}^{-1/2}\text{exp}\left(\frac{im{x}^2}{2\hslash t}\right).$

To determine the normalization constant in the Feynman and Hibbs method, we can apply formulas (2–34) and (4-3) on their book [34] to write the new infinitesimal Kernel between position $x_i$ and $x_{i+1}$, with $\text{Δ}{x}_i=x_{i+1}-x_i$, in a time ϵ as follows:

$\begin{array}{c}{K}_{+}\left(i_{i+1},i\right)=\frac{1}{A}\text{exp}\left(\frac{i\mathit{ϵ}}{\hslash }L\left(\frac{\text{Δ}{x}_i}{\mathit{ϵ}},\frac{x_{i+1}+x_i}{2},\frac{t_{i+1}+t_i}{2}\right)\right),\\ \left(1+{\left(i\mathit{ϵ}/\hslash \right)}^{2}L{\left(\frac{\text{Δ}{x}_i}{\mathit{ϵ}},\frac{x_{i+1}+x_i}{2},\frac{t_{i+1}+t_i}{2}\right)}^2\text{exp}\left(i\mathit{ϵ}L\left(v,\overline{x},\overline{t}\right)/\hslash \right)+\dots \right).\end{array}(30)$

The method consists in writing the wave function at a position x at a time $t+\mathit{ϵ}$ in terms of the wave function at position $y=x+\eta$ at a time t, explicitly

$\begin{array}{c}\psi \left(x,t+\mathit{ϵ}\right)={{{\displaystyle \mathit{\int }}}^{\text{}}}_{-\infty }^{\infty }{K}_{+}\left(x,y,\mathit{ϵ}\right)\psi \left(y,t\right)dy,\\ ={{{\displaystyle \mathit{\int }}}^{\text{}}}_{-\infty }^{\infty }\frac{1}{A}\text{exp}\left(\frac{i\mathit{ϵ}}{\hslash }L\left(\frac{x-y}{\mathit{ϵ}},\frac{x+y}{2},t\right)\right)\times \left(1+\dots \right)\psi \left(y,t\right)dy,\\ ={{{\displaystyle \mathit{\int }}}^{\text{}}}_{-\infty }^{\infty }\frac{1}{A}\text{exp}\left(\frac{i\mathit{ϵ}}{\hslash }L\left(-\frac{\eta }{\mathit{ϵ}},x+\frac{\eta }{2},t\right)\right)\times \left(1+\dots \right)\psi \left(x+\eta ,t\right)d\eta ,\\ ={{{\displaystyle \mathit{\int }}}^{\text{}}}_{-\infty }^{\infty }\frac{1}{A}\text{exp}\left(\frac{im{\eta }^2}{2\hslash \mathit{ϵ}}\right)\text{exp}\left(-\frac{i\mathit{ϵ}V\left(x+\frac{\eta }{2},t\right)}{\hslash }\right)\times \left(1+\dots \right)\psi \left(x+\eta ,t\right)d\eta .\end{array}(31)$

In the quantum standard theory, the normalization constant can be determined by expanding the LHS of (31)$\psi \left(x,t+\mathit{ϵ}\right)=\psi \left(x,t\right)+\mathit{ϵ}{\partial }_t\psi$ and the RHS $\psi \left(x+\eta \right)=\psi \left(x,t\right)+\eta {\partial }_x\psi +\frac{{\eta }^2}{2}{\partial }_x^2\psi$ and $\text{exp}\left(-i\mathit{ϵ}V/\hslash \right)=1-\frac{i\mathit{ϵ}V}{\hslash }+\dots$; then, we compare the leading term ${\mathit{ϵ}}^0$. This implies that

$\frac{1}{A_0}{{{\displaystyle \mathit{\int }}}^{\text{}}}_{-\infty }^{\infty }\text{exp}\left(\frac{im{\eta }^2}{2\hslash \mathit{ϵ}}\right)d\eta =1.(32)$

In a similarly fashion, one gets for the first correction to $K_{+}$ written in (30):

$\frac{1}{A}{{{\displaystyle \mathit{\int }}}^{\text{}}}_{-\infty }^{\infty }\text{exp}\left(\frac{im{\eta }^2}{2\hslash \mathit{ϵ}}\right)\left(1-{\left(\frac{m{\eta }^2}{2\hslash \mathit{ϵ}}\right)}^2{e}^{\frac{im{\eta }^2}{2\hslash \mathit{ϵ}}}+\dots \right)d\eta =1.$

It is worth to mention that the more important contribution to (31) is given for small η′s, as well as in our generalized case. It is necessary to check this argument; in order to verify, let us consider the following integrals:

$\begin{array}{l}{{\displaystyle \mathit{\int }}}^{\text{}}{e}^{iC{w}^2}dw=\sqrt{i\pi /C},{{\displaystyle \mathit{\int }}}^{\text{}}{e}^{iC{w}^2}{w}^{4}dw=\frac{3\sqrt{\pi }}{4{\left(-iC\right)}^{5/2}},\\ {{\displaystyle \mathit{\int }}}^{\text{}}{e}^{iC{w}^2}{w}^{2n+1}dw=0,n\in N.\end{array}$

The first correction gives the following relation:

$A=A_0\left(1+\frac{3}{16\sqrt{2}}+\dots \right).(33)$

The previous normalization factor is a general feature to apply to any potential $V\left(x,t\right)$, in particular is valid for the cases discussed here. A similar expression holds for the normalization of $K_{-}$ normalization, and this will be calculated in the next section.

5.2 Analysis of the Propagators

Here, we summarize the propagators obtained with the normalization methods described in previous subsections. The results for $K_{+}$ can be extrapolated to $K_{-}$ and $K_q$ because the method applied to obtain all of the propagators is the same.

Recall the standard propagator of the free particle from the space-time point $\left(\mathrm{0,0}\right)$ to $\left(x,t\right)$ is given by

$K_1\left(x,t;\mathrm{0,0}\right)=N_0\text{exp}\left(\frac{im{x}^2}{2\hslash t}\right).(34)$

The constant w.r.t. x is as follows: $N_0=\sqrt{\frac{m}{2\pi i\hslash t}}$. For the case of $S_{+}$ and $S_{-}$ statistics, the first two contributions to the modified propagators (21) and (24) read:

$K_{\pm }=N_{\pm }\text{exp}\left(\frac{im{x}^2}{2\hslash t}\right)\times \left(1\mp \text{exp}\left(\frac{im{x}^2}{2\hslash t}\right){\left(\frac{im{x}^2}{2\hslash t}\right)}^2+\dots \right),(35)$

with $N_{+}\sim N_0$. For the Tsallis statics, the associated propagator (26) is given by the expression:

$\begin{array}{c}{K}_q\left(x\right)=N_q{\left(1+\left(q-1\right)\left(\frac{m{x}^2}{2\hslash it}\right)\right)}^{\frac{1}{1-q}}\\ =N_q\text{exp}\left(\frac{im{x}^2}{2\hslash t}\right)\left(1-\left(q-1\right)\left(\frac{m^2{x}^4}{2{\hslash }^2{t}^2}\right)+\dots .\right).\end{array}(36)$

We calculate the normalization constants for $K_{\pm }$ up to the first correction and exactly $K_q$ to get the following:

$N_{+}=\sqrt{\frac{m}{2\pi i\hslash t}}\frac{1}{\left(1+\frac{3}{16\sqrt{2}}+\dots \right)},(37)$

$N_{-}=\sqrt{\frac{m}{2\pi i\hslash t}}\frac{1}{\left(1-\frac{3}{16\sqrt{2}}+\dots \right)},(38)$

$N_q=\sqrt{\frac{m}{2\pi i\hslash t}}\frac{\sqrt{\left(q-1\right)}\text{Γ}\left(\frac{1}{\left(q-1\right)}\right)}{\text{Γ}\left(\frac{1}{\left(q-1\right)}-\frac{1}{2}\right)}.(39)$

In the quantum regime $S_{cl}\approx \hslash$, the differences between the propagators $K_{+},K_{-},K_q$, and $K_0$ are shown in Figures 2–4. In Figure 2 the $K_{-}$ propagator is compared to the usual one. Also, Figure 3 shows a comparision of the $K_{-}$ propagator with the standard one. The last Figure 4 shows a comparison between the propagators for the $S_q$ statistics $K_q$ for $q<1$ and $q>1$ with the usual one. The region of interest is the quantum regime with $S_{cl}\approx \hslash$. Furthermore, in the classical regime, the oscillations of the standard propagator grow averaging to zero as discussed in [34]. Thus, we are interested in comparing the corrections arising from different statistics in the quantum region of interest and, in the plots, the differences between the standard and the modified propagator can be observed. In the classical regime, there are oscillations that should sum up when computing more terms. When $S_{cl}\ll \hslash$, then both results coincide as shown in Figure 5. The modified propagators could be interpreted as describing a particle with an effective potential; this would give a spatially bounded wave function.

FIGURE 3

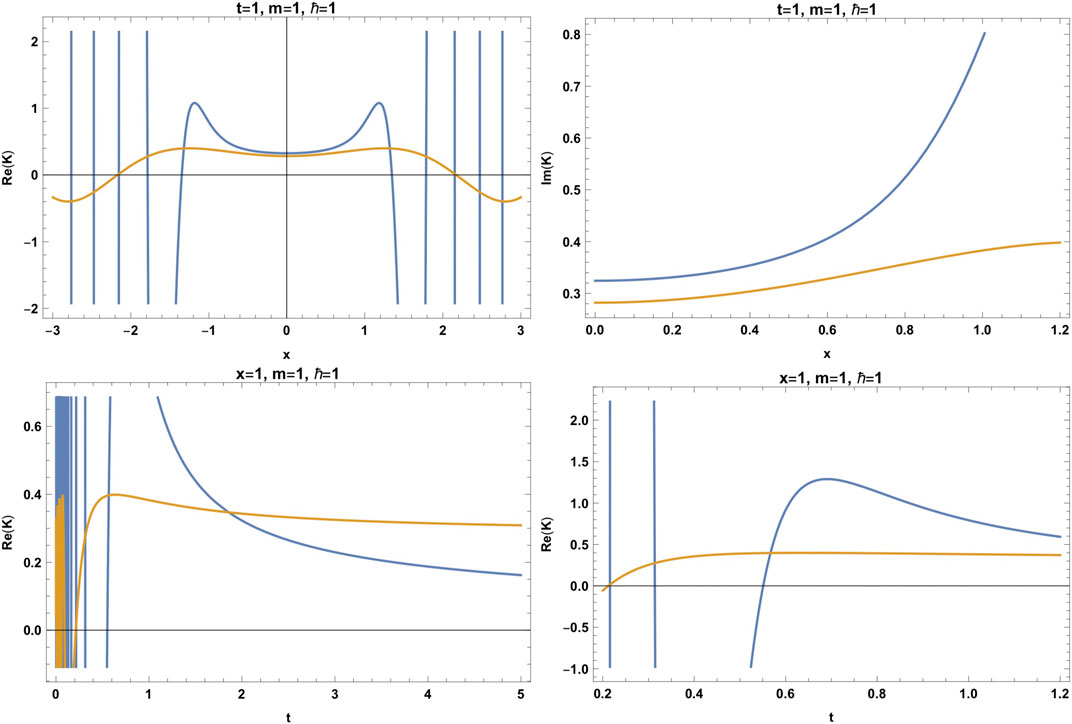
FIGURE 3. Real parts of the modified propagator (blue line) vs. standard propagator (yellow line), for the free particle for the modified statistics $S_{-}$. We set the mass and the Planck constant to unity. Imposing $S_{cl}\mathrm{\lesssim }\hslash$ for fixed $x=1$ translates in $t\mathrm{\gtrsim }1/2$, and for fixed $t=1$ translates in $x^2\mathrm{\lesssim }2$.

FIGURE 4

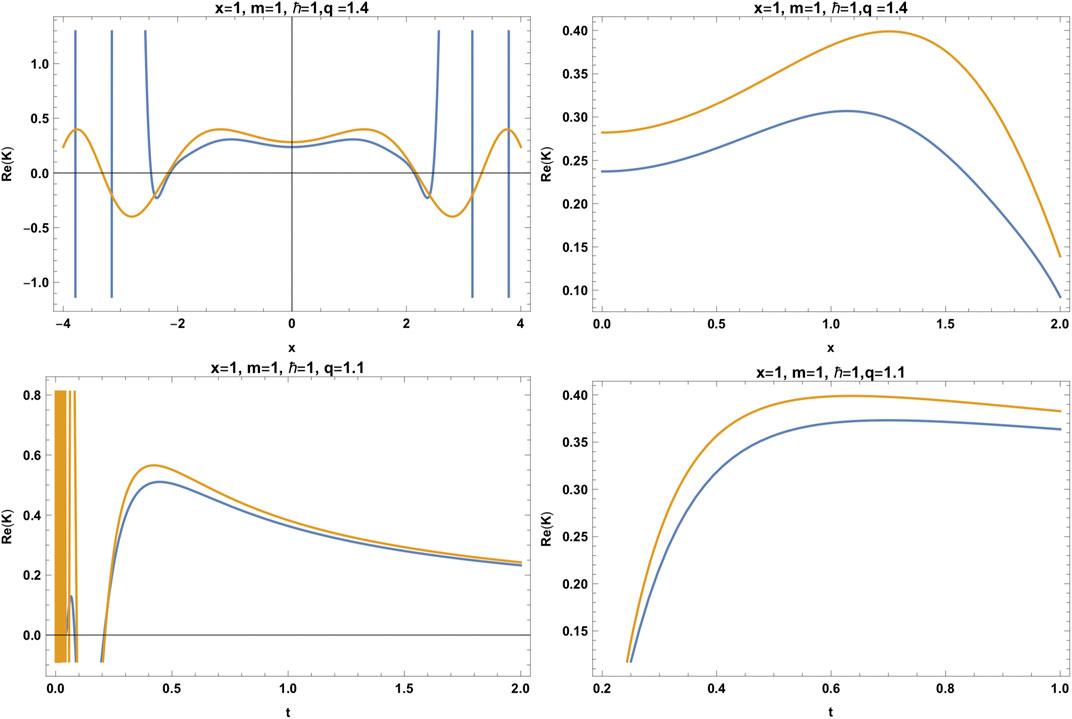
FIGURE 4. Real parts of the modified propagator (blue line) vs. standard propagator (yellow line), for the free particle for the modified statistics of Tsallis for $q=1.1$. We set the mass and the Planck constant to unity. Imposing $S_{cl}\mathrm{\lesssim }\hslash$, it translates for fixed $x=1$ in $t\mathrm{\gtrsim }1/2$ and for fixed $t=1$ translates in $x^2\mathrm{\lesssim }2$.

FIGURE 5

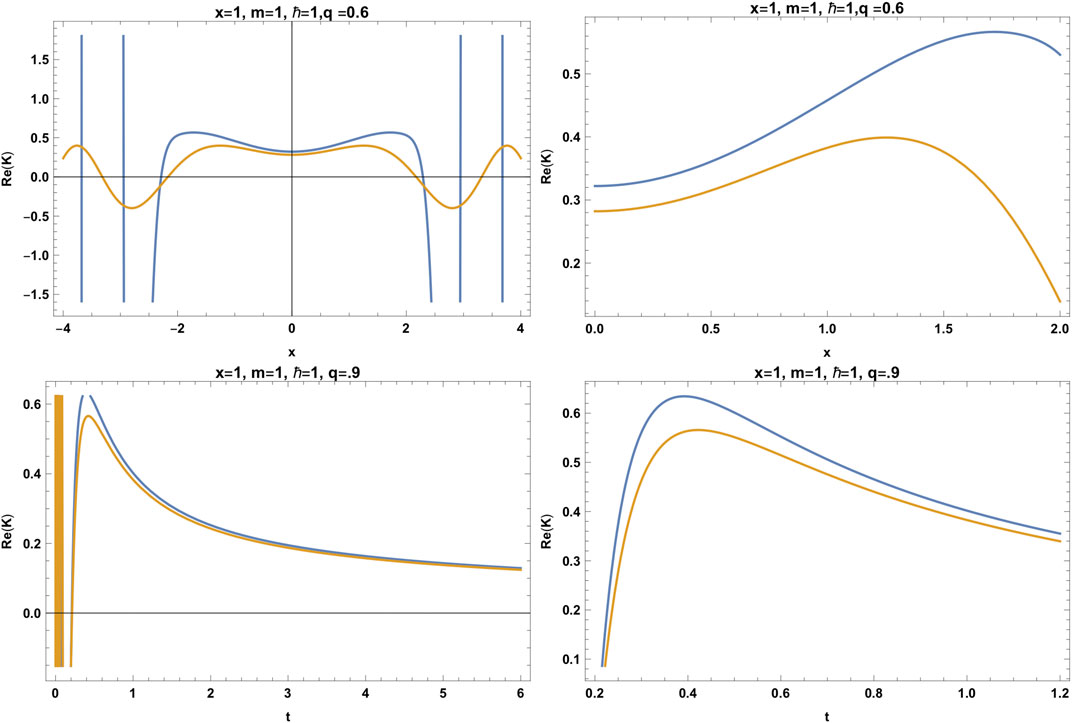
FIGURE 5. Real parts of the modified propagator (blue line) vs. standard propagator (yellow line), for the free particle for the modified statistics of Tsallis for $q=0.9$. We set the mass and the Planck constant to unity. Imposing $S_{cl}\mathrm{\lesssim }\hslash$, it translates for fixed $x=1$ in $t\mathrm{\gtrsim }1/2$ and for fixed $t=1$ translates in $x^2\mathrm{\lesssim }2$.

6 The Harmonic Oscillator

In this section, we apply the formulation of our modified Quantropy of Section 4 for the case of the harmonic oscillator. We compute the modified propagator constructed by a superposition as it was done previously. The extension of quantum systems employing the modified q-statistics has been made only for the case of the free particle [13] with different arguments. Our proposal allows to search the manifestation of nonextensive statistics in nonlinear quantum systems for generic potentials. We illustrate the procedure calculating only $K_{+}$, and the other propagators $K_{-}$ and $K_q$ could be similarly calculated.

For the harmonic oscillator with Lagrangian $\mathrm{ℒ}=\frac{m}{2}{\dot{x}}^2-\frac{m{\omega }^2}{2}{x}^2$, the path integral Kernel reads

$K\left(a,b\right)={\left(\frac{m\omega }{2\pi i\hslash \text{sin}\omega T}\right)}^{1/2}\times \text{exp}\left(\frac{im\omega }{2\hslash \text{sin}\omega T}\left(\left(x_a^2+x_b^2\right)\text{cos}\omega T-2x_a{x}_b\right)\right).$

Next, following a similar procedure as for the free particle, we compute the generalized Kernel and normalize it. The unnormalized Kernel is given by the following:

$K\left(x,t,1\right)=\text{exp}\left(-\frac{1}{2}\text{λ}m\omega \text{cot}\left(\omega t\right)x^2\right).(40)$

Now, we compute the next terms of the Kernel up to third order, which are as follows:

$\begin{array}{c}K\left(x,t,2\right)={\left(\frac{\text{λ}}{2}\right)}^2\frac{{\partial }^2}{\partial {\text{λ}}^2}\text{exp}\left(-2\text{λ}A\right)\\ =\frac{1}{4}{\text{λ}}^2{m}^2{\omega }^2{x}^4\text{exp}\left(-\text{λ}m\omega \text{cot}\left(\omega t\right)x^2\right),\end{array}(41)$

$\begin{array}{c}K\left(x,t,3\right)=\frac{1}{2}\left(-\frac{{\text{λ}}^2}{3^2}{\partial }_{\lambda }^2+2\frac{{\text{λ}}^3}{3^3}{\partial }_{\lambda }^3+3\frac{{\text{λ}}^4}{3^4}{\partial }_{\text{λ}}^4\right)\text{exp}\left(-3\text{λ}A\right)\\ =\left(-\frac{1}{8}{\text{λ}}^2{m}^2{\omega }^2{\text{cot}}^2\left(\omega t\right)x^4-\frac{1}{8}{\text{λ}}^3{m}^3{\omega }^3{\text{cot}}^3\left(\omega t\right)x^6+\frac{3}{32}{\text{λ}}^4{m}^4{\omega }^4{\text{cot}}^4\left(\omega t\right)x^8\right)\\ \times \exp (\frac{-3}{2}\text{λ}m\omega x^2\text{cot}\left(\omega t\right)).\end{array}(42)$

Thus, the total normalized propagator up to third order reads

$K_{+}\left(x,t\right)=\frac{N_{+}}{\sqrt{2\pi }}({\left(\frac{m\omega \text{cot}\left(t\omega \right)}{i\hslash }\right)}^{\frac{1}{2}}\text{exp}\left(\frac{-m\omega x^2\text{cot}\left(t\omega \right)}{2i\hslash }\right)+\frac{1}{4}{\left(\frac{m\omega \text{cot}\left(t\omega \right)}{i\hslash }\right)}^{\frac{5}{2}}{x}^4\text{exp}\left(\frac{-m\omega x^2\text{cot}\left(t\omega \right)}{i\hslash }\right)-\frac{1}{8}[{\left(\frac{m\omega \text{cot}\left(t\omega \right)}{i\hslash }\right)}^{\frac{5}{2}}{x}^4+{\left(\frac{m\omega \text{cot}\left(t\omega \right)}{i\hslash }\right)}^{\frac{7}{2}}{x}^6-\frac{3}{4}{\left(\frac{m\omega \text{cot}\left(t\omega \right)}{i\hslash }\right)}^{\frac{9}{2}}{x}^8\text{exp}\left(\frac{-3m\omega x^2\text{cot}\left(t\omega \right)}{2i\hslash }\right)+\dots )(43)$

where $N_{+}=\frac{1}{\sqrt{\text{cos}\left(\omega T\right)}}\frac{1}{\left(1+\frac{3}{16\sqrt{2}}+\frac{1}{96\sqrt{3}}\right)}$. The relative normalization of the modified propagator with respect to the normalization of the usual propagator is a result obtained in Section 5 [see formulas (31–33)]. This result is universal, i.e., independent of the action. In Figure 6, we compare the propagator for the harmonic oscillator for the standard Quantropy and for the one based on $S_{+}$ and $S_{-}$ statistics. We are interested in the quantum regime given by $S_{cl}\approx \hslash$. There are noticeable effects in that regime. Outside the quantum region, oscillations grow as in the usual case [34]. This behavior occurs in the classical region in which the modified Kernels will also not contribute.

FIGURE 6

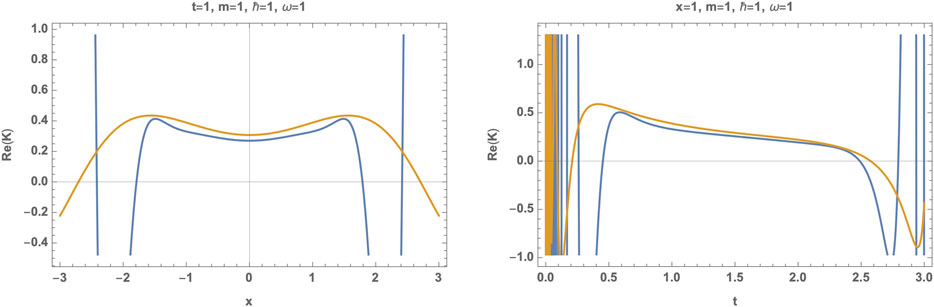
FIGURE 6. We set the units $m=w=\hslash =1$. The left image shows the real parts of the normalized propagators for a fixed time $t=1$, and the region $S_{cl}\mathrm{\lesssim }\hslash$ is given by $\left|x\right|\mathrm{\lesssim }1.765$. The blue line corresponds to the modified propagator $K_{+}$; meanwhile, the yellow one represents the usual propagator $K\left(x,t,1\right)$. The right plot is the comparison between the propagators amplitude for $x=1$ where the blue and the orange are the correction and the usual, respectively, and the quantum region is given by $t\mathrm{\gtrsim }0.464$.

7 Potential Barrier

In this section, we apply the formulation of Quantropy developed previously to compute the propagators associated to a particle in an infinite potential barrier given as follows:

$V\left(x\right)=\{\begin{array}{cc}0& x>0\\ \infty & x\le 0\end{array}.$

The standard unnormalized propagator for this problem is given as follows [38]:

$K\left(x,t;x_0,0\right)=\text{exp}\left[\frac{im}{2\pi \hslash t}{\left(x-x_o\right)}^2\right]-\text{exp}\left[\frac{im}{2\pi \hslash t}{\left(-x-x_o\right)}^2\right],(44)$

where $x_0$ is the initial position. It is important to specify the initial position since the particle cannot be located at $x\le 0$; thus, we set $x_0=\mathit{ϵ}$, where ϵ is a small positive non zero parameter. This allows to make a comparison with the free particle case. Notice that if we set $x_0=0$, the propagator vanishes since the x dependence is quadratic.

Now, we compute the nonlinear propagator associated to the statistics $S_{+}$: $K_{+}\left(x,t;\mathit{ϵ},0\right)$ up to third order, which is given by expression (24). Since our theory is nonlinear, the superposition principle is not valid, i.e., we cannot consider the difference between the propagators of two free particles, like is done for the usual propagator $K\left(x,t;x_0,0\right)$, rather in the semiclassical regime, we consider the logarithm:

$S_{cl}=\frac{\hslash }{i}\text{ln}\left(K\left(x,t;x_0,0\right)\right),(45)$

This allows to substitute $S_{cl}$ into the series expansion (21) $K_{+}\left(x\right)$:

$K_{+}\left(x,t;\mathit{ϵ},0\right)=\left[e^{\frac{im{\left(x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}-e^{\frac{im{\left(-x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}\right]\times [1+\left(e^{\frac{im{\left(x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}-e^{\frac{im{\left(-x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}\right){\ln }^2\left(e^{\frac{im{\left(x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}-e^{\frac{im{\left(-x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}\right)+\frac{1}{2}{\left(e^{\frac{im{\left(x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}-e^{\frac{im{\left(-x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}\right)}^2[3{\ln }^4\left(e^{\frac{im{\left(x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}-e^{\frac{im{\left(-x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}\right)+2{\ln }^3\left(e^{\frac{im{\left(x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}-e^{\frac{im{\left(-x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}\right)-{\ln }^2\left(e^{\frac{im{\left(x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}-e^{\frac{im{\left(-x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}\right)\times ]+\frac{1}{6}{\left(e^{\frac{im{\left(x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}-e^{\frac{im{\left(-x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}\right)}^3[16{\ln }^6\left(e^{\frac{im{\left(x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}-e^{\frac{im{\left(-x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}\right)+24{\ln }^5\left(e^{\frac{im{\left(x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}-e^{\frac{im{\left(-x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}\right)-6{\ln }^4\left(e^{\frac{im{\left(x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}-e^{\frac{im{\left(-x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}\right)-4{\ln }^3\left(e^{\frac{im{\left(x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}-e^{\frac{im{\left(-x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}\right)+3{\ln }^2\left(e^{\frac{im{\left(x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}-e^{\frac{im{\left(-x-\mathit{ϵ}\right)}^2}{2\pi \hslash t}}\right)]].(46)$

Note that the propagator is ill-defined if ϵ is zero. This propagator oscillates faster than the usual propagator in x, and its amplitude is greater. However, the global behavior of both propagators is quite similar, and the oscillations and the amplitude grow as x increases. For the time dependence in both cases, the propagator tends to zero as t grows (see the set of graphics in Figure 7).

FIGURE 7

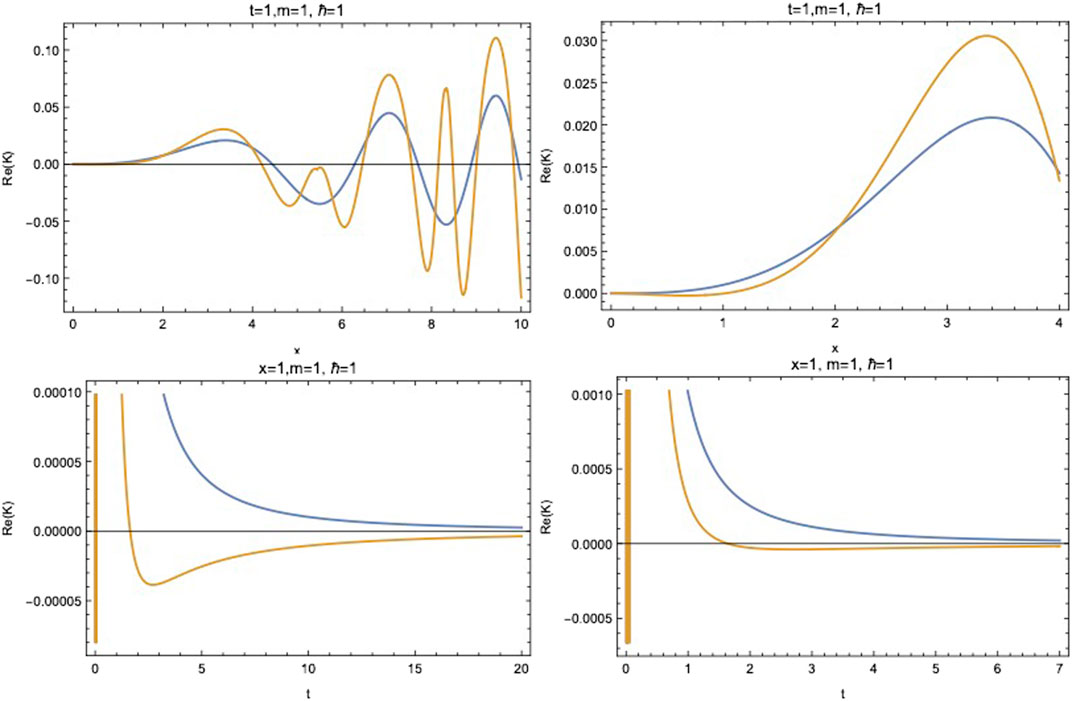
FIGURE 7. We set the units $m=\hslash =1$ and $\mathit{ϵ}=0.01$; the graphic shows the real parts of the modified propagator (blue line) vs. standard propagator (yellow line).

In the usual case, the propagator $K\left(x,t;x_0,0\right)$ has the following interpretation, the first part corresponds to the classical path of the free particle from $\left(x_0,0\right)$ to $\left(x,t\right)$, while the second part corresponds to the classical path of a free particle from $\left(x_0,0\right)$ bouncing off the wall and going to $\left(x,t\right)$. The modified propagator expression suggests a similar interpretation, i.e., the whole propagator can be considered as the sum of both classical paths with the leading terms given by the standard free particle and nonlinear corrections which can be interpreted as an effective potential.

8 Final Remarks

In this work, we explore the novel concept of Quantropy in Quantum Mechanics (Q.M.), which constitutes the analog of the entropy in Statistical Mechanics (S.M.). Mathematically, Quantropy can be regarded as an analytical continuation of entropy, performed under the identification of the energy in S.M. to the action in Q.M., and the identification of the temperature to the Planck constant, the map reads: $E\to S$ and $T\to i\hslash$.

We establish a new definition of Quantropy, with the energy mapped to the classical action $E\to S_{cl}$, i.e., we consider that the main entity is the propagator $K\left(x\right)$ instead of the amplitude $a\left(x\right)$ of the path. Thus, we construct the propagator, a kind of integrated version of the Quantropy $Q_0=-\underset{X}{{\displaystyle \mathit{\int }}}K\left(x\right)\text{ln}K\left(x\right)dx$; in this way, the functional corresponding to the BG under the maximization procedure leads to $K_0\sim \text{exp}\left(i{S}_{cl}/\hslash \right)$.

We applied this concept to find the quantum mechanical implications of modified entropies $S_{+}$, $S_{-}$, and $S_q$, and the associated quantropies lead to generalized propagators, which imply a modified wave functional quantum mechanics (modified Schroedinger equation). Let us point out that the small probabilities limit of modified entropies $S_{+}$ and $S_{-}$ leads to Boltzmann–Gibbs entropy. Similarly in the limit of small path amplitude, one recovers the original Quantropy from the modified functionals. This formalism could be a novel framework to study nonlinear quantum mechanics as those consider in [4, 12, 13]. We also provide an understating of modified propagators associated with Tsallis statistics, leading to wave functions corresponding to q-distributions.

Also, the result for the Tsallis statistics implies a propagator $K_q\sim {\text{exp}}_q\left(i{S}_{cl}/\hslash \right)$, where ${\text{exp}}_q\left(x\right)$ is the q-exponential; this is relevant since it makes contact with the Tsallis result of modified wave function for the free particle, whose solution is ${\psi }_q\sim {\text{exp}}_q\left(i\left(kx-\omega t\right)\right)$. The connection is due to the arguments of [34] in the discussion of the propagator for the free particle $K_0\sim \text{exp}\left(i{S}_{cl}/\hslash \right)$. They show that the propagator $K_0$ corresponds to the free particle wave function ${\psi }_0\sim \text{exp}\left(i\left(kx-\omega t\right)\right)$. Thus, analogously $K_q$ will lead to ${\psi }_q$. As a further work, we need to explore the relations in the case of the modified propagators $K_{+}$ and $K_{-}$. They will give rise to wave functions whose dependencies will be given by ${\text{Ψ}}_{\pm }={\text{exp}}_{\pm }\left(i\left(kx-\omega t\right)\right)$, also for the free particle. In this case, we have a recurrent series solution but we do not have exact expressions for these generalized exponentials. As discussed, our proposal provides also generalized propagators $K_{+},K_{-}$, and $K_q$ for problems with interactions; we illustrated this by considering the $K_{+}$ associated with the harmonic oscillator and the infinite potential barrier.

There are hints from previous studies that the modified entropies considered here can be interpreted as linked with modified effective potentials. Therefore, these modifications to the free particle could be related to a usual quantum mechanics with an effective potential [9]. However, these effects could also lead to nonlinear quantum equations explored in the literature with modified wave functions [3, 12, 13, 26]. Furthermore, what we found here based on the concept of Quantropy could be linked to results for quantum systems in terms of usual entropy vs. the density matrix [10]. A system governed by a modified statistics ($S_{+}$, $S_{-}$ or $S_q$) will lead to modified density-matrix distributions.

Moreover, the modified “propagators” $K_{+},K_{-}$, and $K_q$ actually are strictly no longer standard propagators because they lack the usual propagation property. This means that is not equivalent to propagate the particle from $\left(\mathrm{0,0}\right)$ to $\left(t_2,x_2\right)$, than to first propagate it from $\left(\mathrm{0,0}\right)$ to $\left(t_1,x_1\right)$ and then from $\left(t_1,x_1\right)$ to $\left(t_2,x_2\right)$. This occurs because, for example,

${{\displaystyle \mathit{\int }}}^{\text{}}{K}_{+}\left(\mathrm{0,0};x_1,t_1\right)K_{+}\left(x_1,t_1;x_2,t_2\right)d{x}_1\ne K_{+}\left(\mathrm{0,0};x_2,t_2\right).$

This relates to the fact that in a quantum open systems where these generalized entropies are motivated, the nature of the processes is non-Markovian. Those systems in consideration are modeled with Master Equations (Stochastic) [39]. We consider that this formalism could be a natural framework to study nonlinear quantum mechanics.

We would like to explore further processes where the modified statistics in Quantropy play a central role. This could be done via modified wave functions, which could be interpreted as the usual quantum mechanics with an effective interaction [40] or from nonlinear quantum equations. The modified wave functions will correspond to the modified propagators obtained in this work. In this work, we obtained the modified propagators for the free particle, harmonic oscillator, and the infinite potential barrier associated to the different statistics $K_{+}$, $K_{-}$, and $K_q$, discussing the associated quantum behavior. We would also like to explore in future work the quantum mechanical evolution of other physical systems.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

Here, NB certifies that every author in the present work contributed equally to the research and the writing of the manuscript on the following tasks: conceptualization; formal analysis; funding acquisition; investigation; project administration; resources; software; writing-original draft; and writing-review and editing. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank Alejandro Cabo, Vishnu Jejjala, Oscar Loaiza-Brito, Miguel Sabido, Marco Ortega, Nelsón Flores-Gallegos, and Pablo López-Vázquez for useful discussions and comments. NB thanks PRODEP NPTC UGTO-515 Project, CIIC 181/2019 UGTO Project, CIIC 290/2020 UGTO Project, CIIC 2021 UGTO and CONACYT Project A1-S-37752. RS-S thanks CONACYT and PRODEP NPTC UDG-PTC-1368 Project and the MCFM PROINPEP-University of Guadalajara for supporting this work. OO thanks CONACYT Project 257919 and CIIC 188/2019 UGTO Project. NB, OO and CD thank the support of the University of Guanajuato.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.634547/full#supplementary-material

Footnotes

¹For example, for a massive particle those will be contributions from multiples of the particle mass. For the harmonic oscillator also, there will be contributions with a tower of masses and frequencies.

References

1. Obregón O. Superstatistics and gravitation. Entropy (2010) 12:2067–76. doi:10.3390/e12092067

CrossRef Full Text | Google Scholar

2. Tsallis C. Possible generalization of Boltzmann-Gibbs statistics. J Stat Phys (1988) 52:479–87. doi:10.1007/BF01016429

CrossRef Full Text | Google Scholar

3. Nobre FD, Rego-Monteiro MA, Tsallis C. Nonlinear relativistic and quantum equations with a common type of solution. Phys Rev Lett (2011) 106:140601. doi:10.1103/PhysRevLett.106.140601

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Sharma B, Mital D. New nonadditive measures of inaccuracy. J Math Sci (1975) 10:122–33.

Google Scholar

5. Beck C, Cohen E. Physica A: statistical Mechanics and its applications. Superstatistics (2003) 322:267–275. doi:10.1016/S0378-4371(03)00019-0

6. Cabo Bizet N, Fuentes J, Obregón O. Generalised asymptotic equivalence for extensive and non-extensive entropies. EPL (2019) 128:60004. doi:10.1209/0295-5075/128/60004

7. Obregón O, Gil-Villegas A. Generalized information entropies depending only on the probability distribution. Phys Rev E (2013) 88:062146. doi:10.1103/PhysRevE.88.062146

CrossRef Full Text | Google Scholar

8. Obregón O. Generalized information and entanglement entropy, gravitation and holography. Int J Mod Phys A (2015) 30:1530039. doi:10.1142/s0217751x15300392

CrossRef Full Text | Google Scholar

9. Obregón O, Gil A, Torres J. Computer simulation of effective potentials for generalized Boltzmann-gibbs statistics. J Mol Liq (2017) 248:364–9. doi:10.1016/j.molliq.2017.10.027

CrossRef Full Text | Google Scholar

10. Cabo N, Obregón O. Exploring the gauge/gravity duality of a generalized von neumann entropy. Eur Phys J P (2018) 133:55. doi:10.1140/epjp/i2018-11883-5

CrossRef Full Text | Google Scholar

11. Baez J, Pollard B. Quantropy. Entropy (2015) 17:772–89. doi:10.3390/e17020772

CrossRef Full Text | Google Scholar

12. Nobre FD, Rego-Monteiro MA, Tsallis C. A generalized nonlinear Schrödinger equation: classical field-theoretic approach. Epl (2012a) 97:41001. doi:10.1209/0295-5075/97/41001

CrossRef Full Text | Google Scholar

13. Nobre F, Rego-Monteiro M, Tsallis C. Nonlinear q-generalizations of quantum equations: homogeneous and nonhomogeneous cases-an overview. Entropy (2017) 19:39. doi:10.3390/e19010039

CrossRef Full Text | Google Scholar

14. Batle J, Plastino AR, Casas M, Plastino A. Conditionalq-entropies and quantum separability: a numerical exploration. J Phys A: Math Gen (2002) 35:10311–24. doi:10.1088/0305-4470/35/48/307

CrossRef Full Text | Google Scholar

15. Nobre FD, Rego-Monteiro MA, Tsallis C. A generalized nonlinear Schrödinger equation: classical field-theoretic approach. Epl (2012b) 97:41001. doi:10.1209/0295-5075/97/41001

CrossRef Full Text | Google Scholar

16. Plastino AR, Tsallis C. Nonlinear Schroedinger equation in the presence of uniform acceleration. J Math Phys (2013) 54:041505. doi:10.1063/1.4798999

CrossRef Full Text | Google Scholar

17. Curilef S, Plastino AR, Plastino A. Tsallis' maximum entropy ansatz leading to exact analytical time dependent wave packet solutions of a nonlinear Schrödinger equation. Physica A: Stat Mech its Appl (2013) 392:2631–42. doi:10.1016/j.physa.2012.12.041

CrossRef Full Text | Google Scholar

18. Plastino A, Rocca MC. From the hypergeometric differential equation to a non-linear Schrödinger one. Phys Lett A (2015) 379:2690–3. doi:10.1016/j.physleta.2015.08.015

CrossRef Full Text | Google Scholar

19. Plastino AR, Tsallis C. Dissipative effects in nonlinear klein-gordon dynamics. Epl (2016) 113:50005. doi:10.1209/0295-5075/113/50005

CrossRef Full Text | Google Scholar

20. Plastino A, Rocca MC. Hypergeometric foundations of fokker-planck like equations. Phys Lett A (2016) 380:1900–3. doi:10.1016/j.physleta.2016.03.047

CrossRef Full Text | Google Scholar

21. Pennini F, Ferri G, Plastino A. q-generalization of quantum phase-space representations. Physica A: Stat Mech its Appl (2015) 423:97–107. doi:10.1016/j.physa.2014.12.033

CrossRef Full Text | Google Scholar

22. Majtey A, Plastino AR, Plastino A. New features of quantum discord uncovered by q-entropies. Physica A: Stat Mech its Appl (2012) 391:2491–9. doi:10.1016/j.physa.2011.11.062

CrossRef Full Text | Google Scholar

23. Nobre FD, Plastino AR. A family of nonlinear Schrödinger equations admitting q -plane wave solutions. Phys Lett A (2017) 381:2457–62. doi:10.1016/j.physleta.2017.05.054

CrossRef Full Text | Google Scholar

24. Plastino A, Rocca MC. Quantum q-field theory: q-Schrödinger and q-Klein-Gordon fields. EPL (2017) 118:61004. doi:10.1209/0295-5075/118/61004

CrossRef Full Text | Google Scholar

25. Plastino A, Rocca MC. Tsallis' quantum q-fields. Chin Phys C (2018) 42:053102. doi:10.1088/1674-1137/42/5/053102

CrossRef Full Text | Google Scholar

26. Chavanis P. Generalized euler, smoluchowski and Schrödinger equations admitting self-similar solutions with a tsallis invariant profile. The Eur Phys J Plus (2019) 134:353. doi:10.1140/epjp/i2019-12706-y

CrossRef Full Text | Google Scholar

27. Khordad R, Rastegar Sedehi HR. Magnetic susceptibility of graphene in non-commutative phase-space: extensive and non-extensive entropy. Eur Phys J Plus (2019) 134:133. doi:10.1140/epjp/i2019-12558-5

CrossRef Full Text | Google Scholar

28. Sedehi HRR, Khordad R. Entropy and specific heat of graphene at low and high temperatures under an external magnetic field. Solid State Commun (2020) 313:113911. doi:10.1016/j.ssc.2020.113911

CrossRef Full Text | Google Scholar

29. Khordad R, Bahramiyan H, Rastegar Sedehi HR. Effects of strain, magnetic field and temperature on entropy of a two dimensional gaas quantum dot under spin–orbit interaction. Opt Quan Electronics (2018) 50:294. doi:10.1007/s11082-018-1557-2

CrossRef Full Text | Google Scholar

30. Servatkhah M, Khordad R, Firoozi A, Rastegar Sedehi HR, Mohammadi A. Low temperature behavior of entropy and specific heat of a three dimensional quantum wire: shannon and tsallis entropies. The Eur Phys J B (2020) 93:111. doi:10.1140/epjb/e2020-10034-5

CrossRef Full Text | Google Scholar

31. Abe S, Okuyama S. Similarity between quantum mechanics and thermodynamics: entropy, temperature, and carnot cycle. Phys Rev E (2011) 83:021121. doi:10.1103/PhysRevE.83.021121

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Yokoi Y, Abe S. On quantum-mechanical origin of statistical mechanics. J Phys Conf Ser (2018) 1113:012012. doi:10.1088/1742-6596/1113/1/012012

CrossRef Full Text | Google Scholar

33. Flego SP, Plastino A, Plastino AR. Fisher information, the Hellmann-Feynman theorem, and the Jaynes reciprocity relations. Ann Phys (2011) 326:2533–43. doi:10.1016/j.aop.2011.07.009

CrossRef Full Text | Google Scholar

34. Feynman R, Hibbs A. Quantum mechanics and path integrals international series in the earth and planetary sciences. First Edition. New York, NY: McGraw-Hill College; Edición (1965).

35. Wentzel G. Eine Verallgemeinerung der Quantenbedingungen for die Zwecke der Wellenmechanik. Z Physik (1926) 38:518–29. doi:10.1007/bf01397171

CrossRef Full Text | Google Scholar

36. Stack J. Semiclassical approximation lecture notes in quantum mechanics. Champaign, IL: University of Illinois Urbana-Champaign (2013).

37. Heller E. The semiclassical way to dynamics and spectroscopy. Princeton, NJ: Princeton University Press (2018).

38. Goodman M. Path integral solution to the infinite square well. Am J Phys (1981) 49:843–7. doi:10.1119/1.12720

CrossRef Full Text | Google Scholar

39. de Vega I, Alonso D. Dynamics of non-markovian open quantum systems. Rev Mod Phys (2017) 89:015001. doi:10.1103/RevModPhys.89.015001

CrossRef Full Text | Google Scholar

40. Vignat C, Plastino A, Plastino AR, Sanchez Dehesa J. Quantum potentials with q-Gaussian ground states. Physica A: Stat Mech its Appl (2012) 391:1068–73. doi:10.1016/j.physa.2011.09.031

CrossRef Full Text | Google Scholar