Fractal Pull-in Stability Theory for Microelectromechanical Systems

Tian, Dan; He, Chun-Hui; He, Ji-Huan

doi:10.3389/fphy.2021.606011

BRIEF RESEARCH REPORT article

Front. Phys., 31 March 2021

Sec. Statistical and Computational Physics

Volume 9 - 2021 | https://doi.org/10.3389/fphy.2021.606011

Fractal Pull-in Stability Theory for Microelectromechanical Systems

$\nDan Tian$ Dan Tian¹^*

Chun-Hui He²

Ji-Huan He^3,4^*

¹School of Science, Xi'an University of Architecture and Technology, Xi'an, China
²School of Civil Engineering, Xi'an University of Architecture and Technology, Xi'an, China
³School of Mathematics and Information Science, Henan Polytechnic University, Jiaozuo, China
⁴National Engineering Laboratory for Modern Silk, College of Textile and Clothing Engineering, Soochow University, Suzhou, China

Pull-in instability was an important phenomenon in microelectromechanical systems (MEMS). In the past, MEMS were usually assumed to work in an ideal environment. But in the real circumstances, MEMS often work in dust-filled air, which is equivalent to working in porous media, that's mean fractal space. In this paper, we studied MEMS in fractal space and established the corresponding model. At the same time, we can control the occurrence time and stable time of pull-in by adjusting the value of the fractal index, and obtain a stable pull-in phenomenon.

Introduction

In recent years, Microelectromechanical systems (MEMS) has received extensive attention from scientific researchers. In the operation of MEMS, a pull-in effect will occur. The pull-in voltage analysis of the electrostatic drive device is of great significance to the efficient operation and reliability of the device. Many literatures have conducted a lot of analysis on the dynamic pull-in of MEMS models of linear materials [1–5]. There are many materials used to prepare electrostatic MEMS devices, and among many materials, graphene is considered an excellent material for these devices [6].

Under normal circumstances, the MEMS we consider are in a smooth medium, which can also be called a continuous space. However, with the pollution of the environment, these electronic devices have to work in a porous medium full of particles. Under such conditions, it will inevitably affect the work of electronic devices, and thus also affect the pull-in. So, in this case, we need to analyze MEMS in fractal space. Fractal theory is an excellent tool for dealing with various mathematical problems and some physical phenomena in porous media [7–9]. Because of the diversity application of fractal, it is widely used in various fields [10–22].

In this paper, we analyzed MEMS in the fractal space and established the corresponding fractal model. After that, we explored its impact on pull-in by selecting different fractional derivatives, and realized the effective control of timing for pull-in occurrence, and obtain a stable pull-in condition.

Fractal MEMS Model

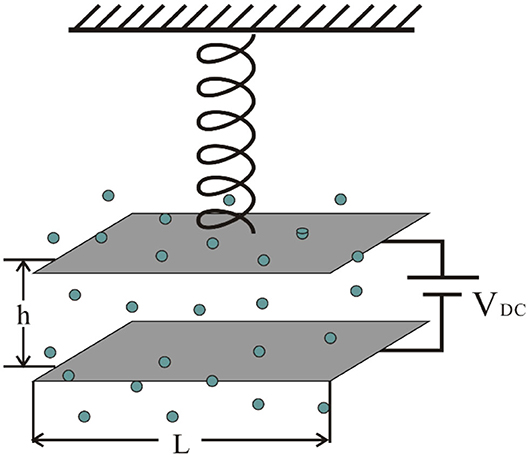
Consider a dual parallel plate model driven by electrostatic forces. The graphene ribbon with a cross-sectional area of A′ is connected to the movable and fixed base components, and the initial distance is h. The movable part is a plate with area A and mass m, as shown in Figure 1. Graphene materials follow the Equation (1) [23, 24],

\begin{array}{l} σ = E ε + D ε^{2} . & (1) \end{array}

where σ, ε, E represent the axial stress, axial strain, Young's modulus, and elastic stiffness constant, respectively. The moving part is affected by the restoring force Frproduced by the axial displacement of the graphene belt and the electrostatic force Fe produced by the applied voltage V. According to Equation (1), Fr and Fe can be write as [1, 6],

\begin{array}{l} F_{r} = - A^{'} E \frac{\tilde{u}}{L} + A^{'} D \frac{\tilde{u}}{L} | \frac{\tilde{u}}{L} |, & (2) \end{array}

\begin{array}{l} F_{e} = \frac{ε_{0} A V^{2}}{2 {(h - ũ)}^{2}} . & (3) \end{array}

Where ε₀ is electric emissivity. Using Newton's second law of motion, the equation of motion of the moving part can be expressed as,

\begin{array}{l} m \frac{d^{2} ũ}{d {\tilde{t}}^{2}} + A^{'} E \frac{ũ}{L} - A^{'} D \frac{\tilde{u}}{L} | \frac{\tilde{u}}{L} | = \frac{ε_{0} A V^{2}}{2 {(h - ũ)}^{2}} . & (4) \end{array}

Equation (4) can be transformed as Equation (5),

\begin{array}{l} u^{″} + u - a u | u | = \frac{k}{{(1 - u)}^{2}} . & (5) \end{array}

Where $u = \frac{ũ}{h}$ , $t = \tilde{t} \sqrt{\frac{A^{'} E}{m L}}$ , $a = \frac{h D}{L E}$ , $k = \frac{ε_{0} A L V^{2}}{2 A^{'} E h^{3}}$ .

FIGURE 1

Figure 1. Graphene MEMS in the porous medium.

In the fractal space, the fractal derivative is defined as [25–29],

\begin{array}{l} D_{F}^{α} h (θ) = \frac{d_{g} (v)}{d_{v}} ∣_{v = j (θ)} & (6) \end{array}

If the Micro-electromechanical system work in the porous medium as shown in Figure 1, we should consider it in fractal place. So, based on Equation (5), the fractal MEMS can be written as,

\begin{array}{l} \frac{d^{2} u}{d t^{2 α}} + u - a u | u | = \frac{k}{{(1 - u)}^{2}} . & (7) \end{array}

We assume the initial conditions are u(0) = 0, u′(0) = 0.

Results and Discussion

In Equation (7), when a and k take different values, it will correspond to different equations. It is worth noting that only in the presence of electrostatic force, that is a = 0, under steady-state conditions, our model is simplified to the well-known Nathan model or parallel plate capacitor model [6].

\begin{array}{l} \frac{d^{2} u}{d t^{2 α}} + u = \frac{k}{{(1 - u)}^{2}} . & (8) \end{array}

The initial conditions are u(0) = 0, u′(0) = 0.

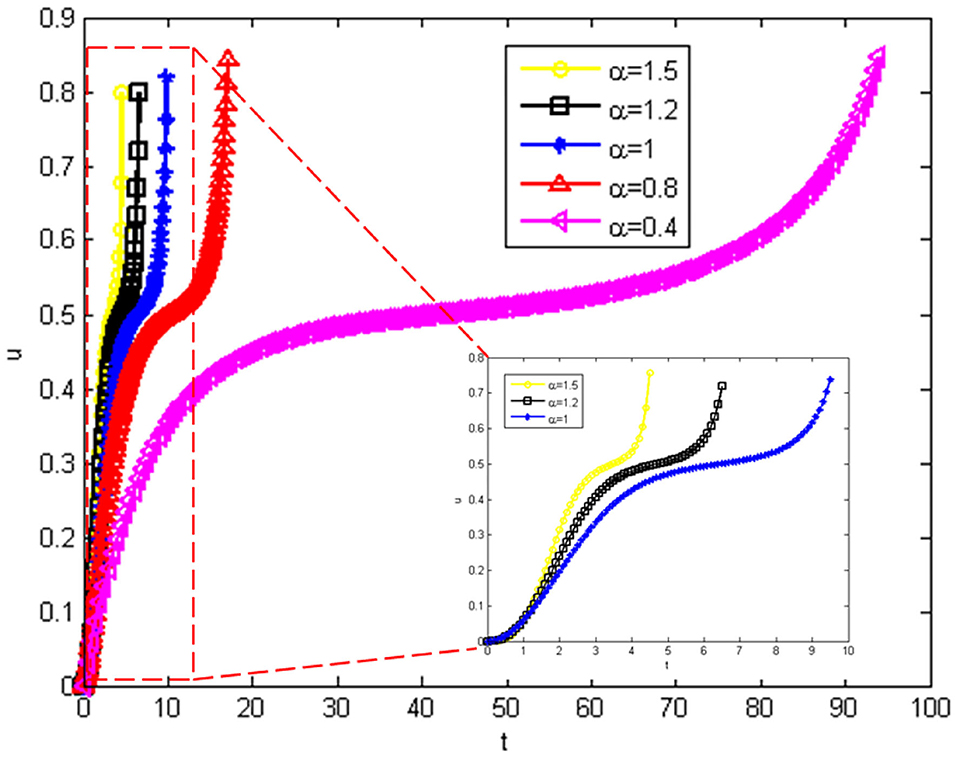
As shown in Figure 2, the numerical solution corresponding to different α in Equation (7) is given. We can see that when k exceeds the critical value, a pull-in phenomenon occurs [1]. Figure 2 shows the Pull-in curve calculated under the three cases of α > 1, α = 1, and α < 1. It can be seen that whenα > 1, Pull-in will happen very soon. From the enlarged picture, it can also be seen that there is a short platform. When α < 1, the occurrence of pull-in will become slower and slower as a decreases. When α = 0.4, a very long platform appears. At this time, relatively speaking, the occurrence of pull-in at α = 1.5 is almost instantaneously. It can be seen that the fractal model of MEMS we have established can control the occurrence time of pull-in and the stable time by adjusting the value of the fractional index.

FIGURE 2

Figure 2. Pull-in instability for different values of α and k = 0.1252.

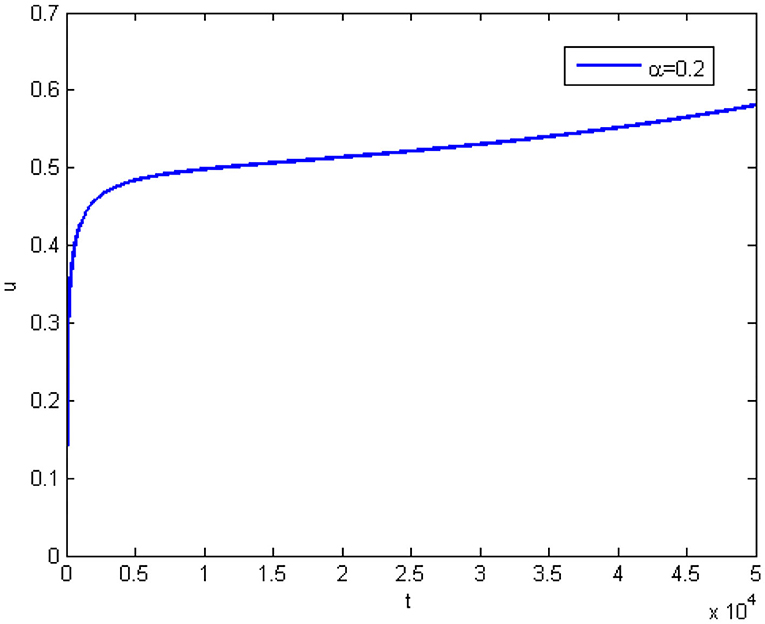
Figure 3 shows the pull-in curve when α = 0.2. It can be seen that the platform at this time has become quite long, which also means that the pull-in is infinitely delayed, which means that we have obtained a stable pull-in. And when it is smaller, the pull-in will be more stable.

FIGURE 3

Figure 3. Pull-in stability for α = 0.2.

Conclusion

In this paper, we studied MEMS which prepared via graphene in fractal space and established a corresponding fractal model. In the fractal space, by discussing different fractional index α, we found that we can control the occurrence and stable time of pull-in by adjusting the fractional index. The fractal model of MEMS we established can broaden the application range of it, which can be used in any discontinuous media. Pull in stability can guide MEMS to work more efficiently.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

DT and C-HH designed the experiments. DT performed data analysis and wrote the paper. J-HH revised the paper. All authors read and contributed to the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Skrzypacz P, Kadyrov S, Nurakhmetov D, We D. Analysis of dynamic pull-in voltage of a graphene MEMS model. Nonlinear Anal Real World Appl. (2019) 45:581–9. doi: 10.1016/j.nonrwa.2018.07.025