- 1Instituto de Física, Universidade Federal Fluminense, Niterói, Brazil
- 2Department of Physics, University of Portland, Portland, OR, United States
We review various theoretical methods that have been used in recent years to calculate dynamical correlation functions of many-body systems. Time-dependent correlation functions and their associated frequency spectral densities are the quantities of interest, for they play a central role in both the theoretical and experimental understanding of dynamic properties. In particular, dynamic correlation functions appear in the fluctuation-dissipation theorem, where the response of a many-body system to an external perturbation is given in terms of the relaxation function of the unperturbed system, provided the disturbance is small. The calculation of the relaxation function is rather difficult in most cases of interest, except for a few examples where exact analytic expressions are allowed. For most of systems of interest approximation schemes must be used. The method of recurrence relation has, at its foundation, the solution of Heisenberg equation of motion of an operator in a many-body interacting system. Insights have been gained from theorems that were discovered with that method. For instance, the absence of pure exponential behavior for the relaxation functions of any Hamiltonian system. The method of recurrence relations was used in quantum systems such as dense electron gas, transverse Ising model, Heisenberg model, XY model, Heisenberg model with Dzyaloshinskii-Moriya interactions, as well as classical harmonic oscillator chains. Effects of disorder were considered in some of those systems. In the cases where analytical solutions were not feasible, approximation schemes were used, but are highly model-dependent. Another important approach is the numericallly exact diagonalizaton method. It is used in finite-sized systems, which sometimes provides very reliable information of the dynamics at the infinite-size limit. In this work, we discuss the most relevant applications of the method of recurrence relations and numerical calculations based on exact diagonalizations. The method of recurrence relations relies on the solution to the coefficients of a continued fraction for the Laplace transformed relaxation function. The calculation of those coefficients becomes very involved and, only a few cases offer exact solution. We shall concentrate our efforts on the cases where extrapolation schemes must be used to obtain solutions for long times (or low frequency) regimes. We also cover numerical work based on the exact diagonalization of finite sized systems. The numerical work provides some thermodynamically exact results and identifies some difficulties intrinsic to the method of recurrence relations.
1 Introduction
Dynamical correlation functions are central to the understanding of time-dependent properties of many-body systems. They appear ubiquitously in the formulation of the fluctuation-dissipation theory, where the response of a system to a weak external perturbation is cast in terms of a time-dependent relaxation function of the unperturbed system [1, 2].
In this article, we are concerned with the recent calculations of such correlation functions. We shall cover two lines of approach, namely the method of recurrence relations and the method of exact diagonalization.
The method of recurrence relations was developed in the early 1980s [3–7] following the ideas of the Mori-Zwanzig projection operator formalism [8, 9]. Essentially one solves the Heisenberg equation of motion for an operator of an interacting system, from which one obtains dynamic correlation functions, a generalized Langevin equation, memory functions, etc. Review articles found in the literature cover the earlier developments [10–12].
On the other hand, exact diagonalization methods have also been used in several areas of physics [13–17]. In this method one numerically determines the eigenvalues and eigenfunctions of a given Hamiltonian of a finite system to find the dynamical correlations of interest. The main drawback is that one is bound by computer limitations and must deal with finite systems. In addition, being a numerical method, it does not provide any new general insight in the form of theorems, etc. Nevertheless, one can obtain surprisingly good results which can be readily extended to the thermodynamic limit. In a way, exact diagonalization complements the method of recurrence relations, especially when solutions become hard to obtain by analytic means. Othertheoretical approaches can be found in Refs. [18–26]. One can also find interesting developments in experiments with cold atoms in optical lattices that mimic the dynamics of some spin systems [27–30].
2 Dynamical Correlation Functions
Consider a system of N elements such as particles, spins, etc., governed by a time-independent Hamiltonian H, in thermal equilibrium with a heat bath at temperature T. For two dynamical variables X and Y of the system, the time-dependent correlation function is given by the average:
where
where
In a classical system, the operators are replaced by classical dynamic variables, the trace by integral over the phase space, and the commutators by Poisson brackets.
For a given variable, the time-dependent correlation function
Its Fourier transform
If we use the integral representation of the Dirac δ-function:
then we obtain
Since the Hamiltonian is time-independent, it follows that
Dynamical correlation functions appear in the relaxation function
where
Time-dependent correlation functions appear in the dynamical structure factor, are related to the inelastic neutron-scattering cross section, where the neutron energy changes upon the scattering process. For a system of interacting spins on a lattice, the dynamic structure factor reads:
where S are spin variables and the sum runs over all the lattice sites.
In light scattering experiments, the scattered intensity is given by the differential cross section, proportional to:
where the form of operator A is system dependent. It also depends on the the particular frequency of the incoming light.
2.1 The Method of Recurrence Relations
The time evolution of a Hermitian operator
where:
Consider a time-independent and Hermitian Hamiltonian H. From now on we will be using a system of units in which
In the method of recurrence relations, the formal solution:
is cast as an orthogonal expansion in a realized Hilbert space
where X, Y
Thus, the time evolution of
where
By choosing the basal vector
with
The
The basal coefficient
The time-dependent coefficients
where
where ϕ is the memory function and
where the coefficients
The memory function
Consider now the Lapace transform
Then RRII can be transformed in the following way:
These equations can be solved for
resulting in a continued fraction. As can be seen from Eq. 14 and the recurrence relation RRII, that the time-dependence actually depends on the recurrants
2.2 The Method of Exact Diagonalization
Given a system governed by a Hamiltonian H, one wishes to numerically determine the time correlation function
where
with the partition function
Another quantity of interest is the moment
Since
where
From the moments, one can use conversion formulas to obtain the recurrants
for
For instance, if the first moments
Conversely, suppose one has the first K known recurrants,
for
In case the first recurrants
Typically, the analytical determination of the recurrants becomes increasingly time consuming. In practice, only a few of them can be obtained to be used in an extrapolation scheme to obtain higher-order recurrants. Several extrapolation schemes have been used. One of the simplest is to set the unknown recurrants to zero, thus truncating the continued fraction for
3 Applications to Interacting Systems
The dynamics of spin chains has attracted a great deal of attention in recent decades. Exact results for the longitudinal dynamics of the one dimensional XY model have been obtained with the Jordan-Wigner transformation [71]. Later, exact results for the transverse time correlation functions of the XY and the transverse Ising chain were obtained at the high temperature limit by using different methods [51, 72–75].
A great deal of progress was achieved in the calculations of the dynamic correlation functions of spin models in one dimension. It was soon recognized that exact solutions using the method of recurrence relations were difficult to obtain, however a notable exception is the classical harmonic oscillator chain where the time correlation functions were obtained exactly [37].
The problem of a mass impurity in the harmonic chain was solved later, and its dynamical correlation functions were found to have the same form as in the quantum electron gas in two dimensions, thus showing that unrelated quantities in these two models displayed the same dynamical behavior, that is, the have dynamic equivalence [76]. It should be mentioned that harmonic oscillator chains have been the subject of a considerable amount of work with the method of recurrence relations [38–46].
The method of recurrence relations provides important insights on how to proceed to obtain reliable approximate solutions. The cornerstone quantity in the dynamics is the recurrant, which is the only quantity that ultimately determines the dynamics of the model. Often it is only possible to determine a few of the recurrants analytically. The calculations become too lenghty so that one must stop at a given order. Thus, an extrapolation method must be devised for the higher order recurrants, which hopefully will have the essential ingredients to produce reliable time-dependent correlation functions for longer times as well as spectral densities with the expected behavior near the origin
The dynamics of the transverse Ising model in two dimensions was studied with the method of recurrence relations [79–82]. The dynamic structure factor of that model compares well to the experimental data of the compound LiTbF4 [83].
The dynamics of spin ladders has also attracted interest from researchers. The dynamical correlation functions were obtained for a two-leg spin ladder with XY interaction along each leg and interchain Ising couplings in a random magnetic field. More recently, the dynamics of a ladder with Ising couplings in the legs and steps as well as four-spin plaquette interactions in a magnetic field [84] have been also investigated.
The dynamical correlations of the Heisenberg model in one dimension have been have been a subject of great interest in the recent decades [13–15, 22, 85]. The method of recurrence relations has been employed in various works [86–92]. In spite of the progress made thus far, the long-time dynamics of the Heisenberg spin model is still an open problem. For instance, there is the standing problem on the power law exponent
There has been a great deal of work that uses exact diagonalization to study the dynamics of spin systems [13, 14]. Earlier works with the Heisenberg model used this technique. Later on, other systems were scrutinized by using exact diagonalization. One of those systems is the Ising model with four-spin interactions in a transverse field. The time correlation function was obtained for one dimensional and infinite temperature [93], where the Gaussian behavior shown in the usual transverse Ising model was ruled out. The effects of disorder on the dynamics of that model were obtained for the cases where the random variables are drawn from bimodal distributions of random couplings and fields [16, 94, 95]. Dynamical correlation functions were also obtained for the system at finite temperatures, ranging from
3.1 Heisenberg Model With Dzyaloshinskii-Moriya Interactions
The dynamical structure factor for a quantum spin Heisenberg chain with Dzyaloshinskii-Moriya (DM) interactions [97, 98] has been investigated by different approaches, such as spin wave theory [99], mean-field [100], and projection operator techniques [101]. The dynamics of the related XY model with DM interactions was also studied by employing Jordan-Wigner fermions [102–104].
The dynamical correlation functions of the spin-1/2 Heisenberg model with DM interactions in a transverse magnetic field was studied recently with the method of recurrence relations. The model Hamiltonian for a one-dimensional chain is given by:
where J is the Heisenberg coupling, D is the Dzyaloshinskii-Moriya interaction, and
The effects of a uniform magnetic field
One crucial point is to determine whether or not the extrapolated recurrants grow indefinitely. The time correlation function of the longitudinal spin component in the
where
Once the recurrants are obtained, the relaxation function and its spectral density can be readily obtained. For the special case without DM interaction, the result shows good agreement with the known results for the XY and Heisenberg models. The full calculation reveals that the effects of the external field are to produce stronger and more rapid oscillations in the relaxation functions, as well as a suppression of the central peak in the spectral density. In addition a peak centered at a well defined frequency appears, which is attributed to an enhancement of the collective mode of spins precessing about the external field. It should be noted that the method of recurrence relations was also used to study the dynamics of the XY model with DM interaction [65].
The effects of disorder in a transverse magnetic field on the dynamical correlation functions are investigated with the bimodal distribution for
The method of recurrence relations is then applied to obtain the dynamical correlation functions for a given realization of disorder [66]. Next, the average over the random fields is performed by using the distribution Eq. 37. This is accomplished by defining the scalar product in the Hilbert space
The time correlation function and its associated spectral density were obtained for
3.2 Random Transverse Ising Model
Consider the
where
The time correlation
where the line indicates that an raverage ove the random variables is performed after the statistical average
where
The inner product in
where A and B are vectors in
The zeroth basis vector
The remaining basis vectors
etc. The vectors
Notice that the couplings and fields are site-dependent.
There are two types of disorder considered in Ref. 106, random fields and random spin couplings. Each case is treated separately. In both cases a simple bimodal distribution is used for the random variable. The field
3.3 Transverse Ising Model With Next-To-Nearest Neighbors Interactions
Consider the transverse Ising model with an additional axial next-nearest-neighbor interaction (transverse ANNNI model) [17]. The Hamiltonian for a chain with L spins can be written as:
where
In the absence of a transverse magnetic field and of thermal fluctuations (
The main quantity of interest is the time-dependent correlation function:
where
The numerical calculations will be performed at the high-temperature limit,
One of the properties of
where the frequency moments are expressed in terms of the trace over iterated commutators:
with
where H is the Hamiltonian and A an operator.
The correlation function is calculated in the Lehman representation. First, we consider the energies
where the moments
The spectral density
After using Eq. 51, the spectral density can be cast in the form:
where
The Dirac δ-function is approximated by a rectangular window of width a and unit area, centered at the zeros of their arguments. The width a, can be adjusted to reduce fluctuations. Another approach could be the use of histograms, such as in Ref. 96. However, the general shape of the spectral density
As a case test, Guimarães et al. [17] consider
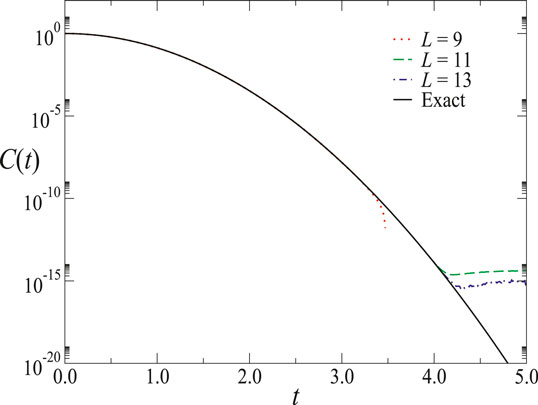
FIGURE 1. Time correlation function of a tagged spin in the TI model when
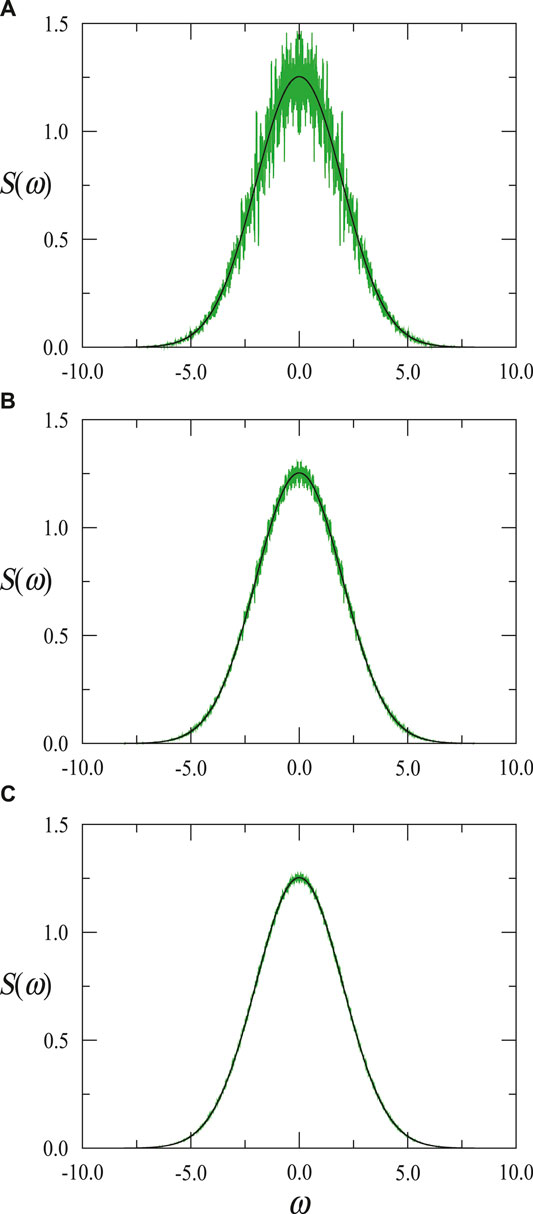
FIGURE 2. Spectral density for the TI model (
In the following, consider the representative cases
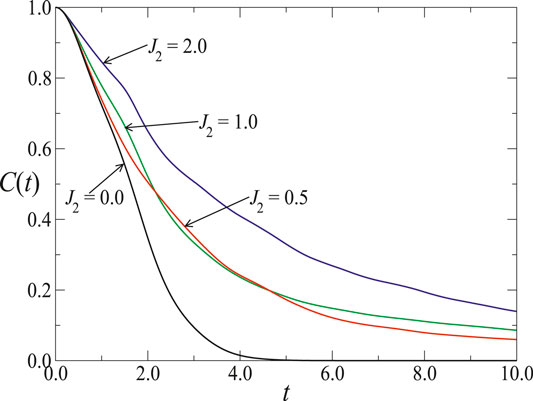
FIGURE 3. Time-dependent correlation function for
In general, the decay of
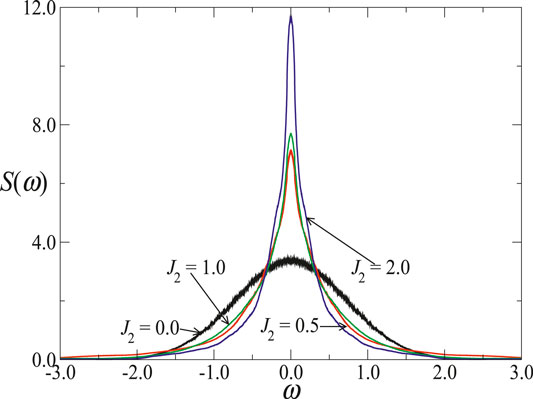
FIGURE 4. Spectral density for
The time correlation function for
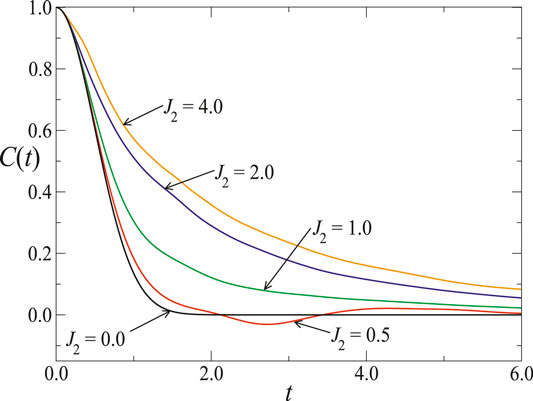
FIGURE 5. Time-dependent correlation function for
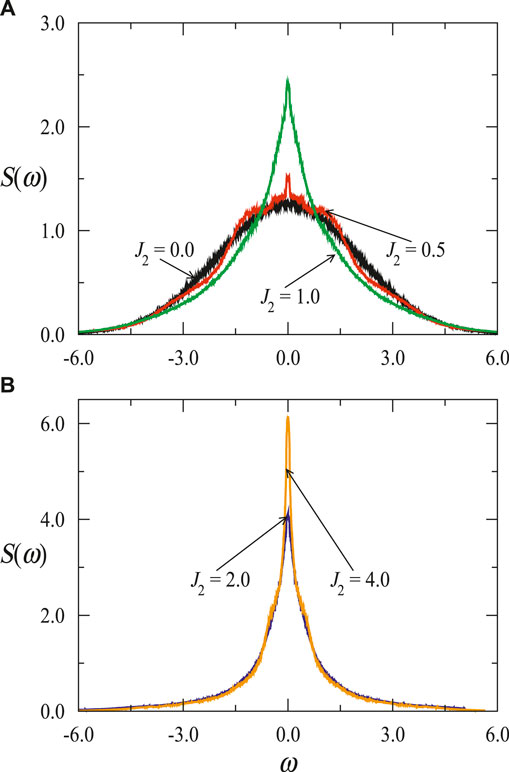
FIGURE 6. Spectral density for
Finally, consider the case where the transverse field is larger (
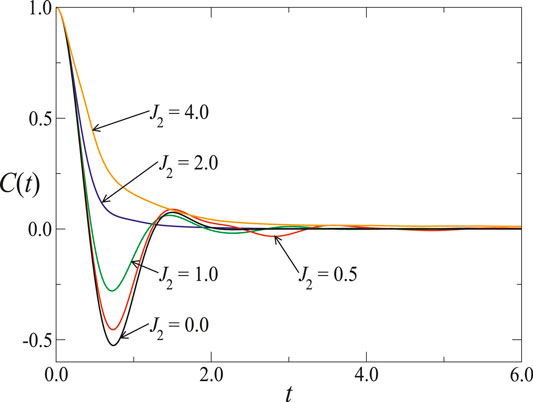
FIGURE 7. Time-dependent correlation function for
Figure 8 depicts the corresponding spectral density
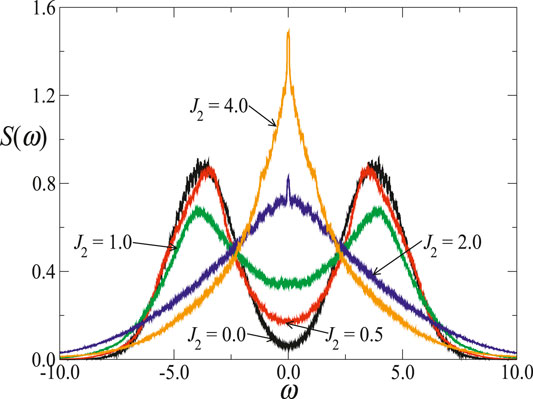
FIGURE 8. Spectral density for the case
The recurrants
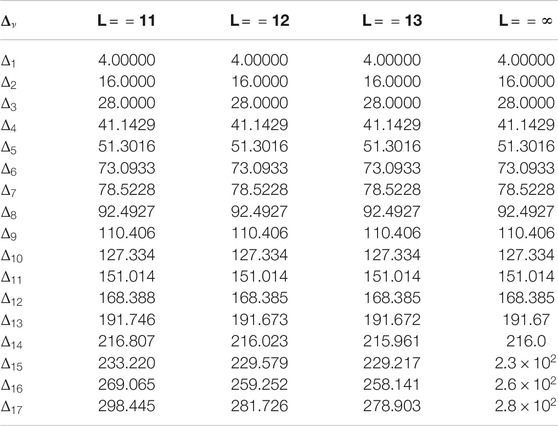
TABLE 1. Recurrants for the transverse ANNNI model, with
The results for the thermodynamic estimates of the recurrants are shown in Figure 9 for
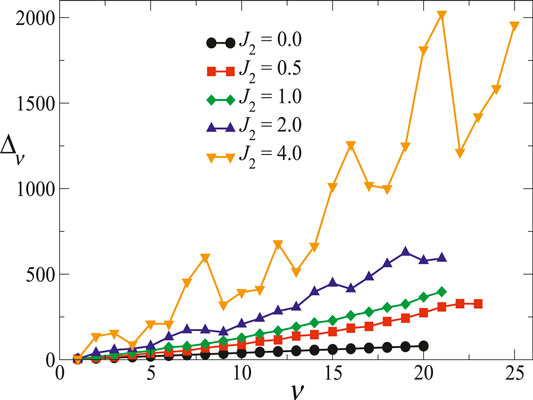
FIGURE 9. Recurrants of the infinite transverse ANNNI model with
4 Summary and Perspectives
The dynamical correlation functions play a crucial role in the fluctuation-dissipation theorem and in the linear response theory. However, the calculation of those quantities is often a very complicated problem in itself. The method of recurrence relations is an exact procedure that allows one to obtain of time correlation functions, spectral densities, and dynamical structure factors. We have shown the main features of the method and the inherent difficulties one might encounter in an attempt to apply to a many-body problem. Another method that is showing great potential is exact diagonalization, a numerical method which relies mostly on computer capabilities. Nevertheless, the two methods can be used together, one complementing the other, to achieve progress in the calculation of dynamical correlation functions.
Author Contributions
The authors JF and OFAB declare that they planned and carried out the elaboration of this work with equal contribution from each author.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by FAPERJ and PROPPI-UFF (Brazilian agencies).
References
1. Callen HB, Welton TA. Irreversibility and generalized noise. Phys Rev E. (1951). 83:34–40. doi:10.1103/PhysRev.83.34
2. Kubo R. The fluctuation-dissipation theorem. Rep Prog Phys. (1966). 29:255. doi:10.1088/0034-4885/29/1/306
3. Lee MH. Orthogonalization processes by recurrence relations. Phys Rev Lett. (1982). 49:1072. doi:10.1103/PhysRevLett.49.1072
4. Lee MH. Solutions of the generalized Langevin equation by a method of recurrence relations. Phys Rev B. (1982). 26:2547. doi:10.1103/PhysRevB.26.2547
5. Lee MH. Derivation of the generalized Langevin equation by a method of recurrence relations. J Math Phys. (1983). 24:2512. doi:10.1063/1.525628
6. Grigolini P, Grosso G, Pastori Parravicini G, Sparpaglione M. Calculation of relaxation functions: a new development within the Mori formalism. Phys Rev B. (1983). 27:7342. doi:10.1103/PhysRevB.27.7342
7. Giordano M, Grigolini P, Leporini D, Marin P. Fast-computational approach to the evaluation of slow-motion EPR spectra in terms of a generalized Langevin equation. Phys Rev A. (1983). 28:2474. doi:10.1103/PhysRevA.28.2474
8. Mori H. A continued-fraction representation of the time-correlation functions. Prog Theor Phys. (1965). 34:399–416. doi:10.1143/PTP.34.399
9. Zwanzig R. Statistical mechanics of irreversibility. In: Britten WE, Downs BW, Downs J, editors Lectures in theoretical physics.. New York, NY: Interscience (1961). p 106–141.
10. Lee MH, Hong J, Florencio J. Method of recurrence relations and applications to many-body systems. Phys Scripta. (1987). T19:498. doi:10.1088/0031-8949/1987/T19B/029
11. Viswanath VS, Müller G. The recursion method - application to many-body dynamics. In: Viswanath GS, Muller GM, editors Lectures notes in physics.. Berlin, Germany: Springer-Verlag (1994). 262 p.
12. Balucani UU, Lee MH, Tognetti V. Dynamical correlations. Phys Rep. (2003). 373:409–492. doi:10.1016/S0370-1573(02)00430-1
13. Sur A, Jasnow D, Lowe IJ. Spin dynamics for the one-dimensional XY model at infinite temperature. Phys Rev B. (1975). 12:3845. doi:10.1103/PhysRevB.12.3845
14. Sur A, Lowe IJ. NMR line-shape calculation for a linear dipolar chain. Phys Rev B. (1975). 12:4597. doi:10.1103/PhysRevB.12.4597
15. Fabricius K, Löw U, Stolze J. Dynamic correlations of antiferromagnetic spin- XXZ chains at arbitrary temperature from complete diagonalization. Phys Rev B. (1997). 55:5833. doi:10.1103/PhysRevB.55.5833
16. Boechat B, Cordeiro C, Florencio J, Sá Barreto FC, de Alcantara Bonfim OF. Dynamical behavior of the random-bond transverse Ising model with four-spin interactions. Phys Rev B. (2000). 61:14327. doi:10.1103/PhysRevB.61.14327
17. Guimarães PRC, Plascak JA, de Alcantara Bonfim OF, Florencio J. Dynamics of the transverse Ising model with next-nearest-neighbor interactions. Phys Rev B. (2015). 92:042115. doi:10.1103/PhysRevE.92.042115
18. Perk JHH, Capel HW. Time-dependent correlation functions in the high-temperature limit for the XY-chain and the Ising-chainin a transverse magnetic field. J Appl Phys. (1979). 50:1771. doi:10.1063/1.327215
19. Pires AST. The memory function formalism in the study of the dynamics of a many body system. Helv Phys Acta. (1988). 61:988–1006. doi:10.5169/seals-115978
20. Plascak JA, Sá Barreto FC, Pires AST. Dynamics of the strong anisotropic three-dimensional Ising model in a transverse field. Phys Rev B. (1983). 27:523. doi:10.1103/PhysRevB.27.523
21. Brandt U, Stolze J. High-temperature dynamics of the anisotropic Heisenberg chain studied by moment methods. Z Phyzik B. (1986). 64:327. doi:10.1007/BF01303603
22. Böhm M, Leschke H. Dynamic spin-pair correlations in a Heisenberg chain at infinite temperature based on an extended short-time expansion. J Phys A. (1992). 25:1043. doi:10.1088/0305-4470/25/5/013
23. Böhm M, Leschke H. Dynamical aspects of spin chains at infinite temperature for different spin quantum numbers. Physica A. (1993). 199:116–131. doi:10.1016/0378-4371(93)90101-9
24. de Alcantara Bonfim OF, Reiter G. Breakdown of hydrodynamics in the classical 1D Heisenberg model. Phys Rev Lett. (1992). 69:367. doi:10.1103/PhysRevLett.69.367
25. Stolze J, Viswanath VS, Müller G. Dynamics of semi-infinite quantum spin chains at T = ∞. Z. Phyzik B (1992). 89:45–55. doi:10.1007/BF01320828
26. Perk JHH, Au-Yang H. New results for the correlation functions of the Ising model and the transverse Ising chain. J Stat Phys. (2009). 135:599–619. doi:10.1007/s10955-009-9758-5
27. Widera A, Gerbier F, F'́olling S, Gericke T, Mandel O, Bloch I. Coherent collisional spin dynamics in optical lattices. Phys Rev Lett. (2005). 95:190405. doi:10.1103/PhysRevLett.95.190405
28. Hild S, Fukuhara T, Schauss P, Zeiher J, Knap M, Demler E, et al. Far-from-equilibrium spin transport in Heisenberg quantum magnets. Phys Rev Lett. (2014). 113:147205. doi:10.1103/PhysRevLett.113.147205
29. Zhang H, Zhai1 Y, Chen X. Spin dynamics in one-dimensional optical lattices. J Phys B Atom Mol Opt Phys. (2014). 47:025301. doi:10.1088/0953-4075/47/2/025301
30. Buyskikh S, Tagliacozzo L, Schuricht D, Hooley CA, Pekker D, Daley AJ. Spin models, dynamics, and criticality with atoms in tilted optical superlattices. Phys Rev Lett. (2019). 123:090401. doi:10.1103/PhysRevLett.123.090401
31. Kubo R. Statistical-mechanical theory of irreversible processes. I. General theory and simple applications to magnetic and conduction problems. J Phys Soc Japan. (1957). 12:570. doi:10.1143/JPSJ.12.570
32. Lee MH. Derivation of the generalized Langevin equation by a method of recurrence relations. J. Math. Phys (1983). 24:2512. doi:10.1063/1.525628
33. Lee MH, Hong J, Sharma NL. Time-dependent behavior of one-dimensional many-fermion models: comparison with two- and three-dimensional models. Phys Rev A. (1984). 29:1561. doi:10.1103/PhysRevA.29.1561
34. Lee MH, Hong J. Recurrence relations and time evolution in the three-dimensional Sawada model. Phys Rev B. (1984). 30:6756. doi:10.1103/PhysRevB.30.6756
35. Sharma NL. Response and relaxation of a dense electron gas in D dimensions at long wavelengths. Phys Rev B. (1992). 45:3552. doi:10.1103/PhysRevB.45.3552
36. Lee MH, Hong J. Time- and frequency-dependent behavior of a two-dimensional electron gas at long wavelengths. Phys Rev B. (1985). 32:7734. doi:10.1103/PhysRevB.32.7734
37. Florencio J, Lee MH. Exact time evolution of a classical harmonic-oscillator chain. Phys Rev A. (1985). 31:3231. doi:10.1103/PhysRevA.31.3231
38. Wierling A, Sawada I. Wave-number dependent current correlation for a harmonic oscillator. Phys Rev A. (2010). 82:051107. doi:10.1103/PhysRevE.82.051107
39. Wierling A. Dynamic structure factor of linear harmonic chain - a recurrence relation approach. Eur Phys J B. (2012). 85:20. doi:10.1140/epjb/e2011-20571-5
40. Yu MB. Momentum autocorrelation function of an impurity in a classical oscillator chain with alternating masses – I General theory. Physica A. (2014). 398:252–63. doi:10.1016/j.physa.2013.11.023
41. Yu MB. Momentum autocorrelation function of an impurity in a classical oscillator chain with alternating masses II. Illustrations. Physica A. (2015). 438:469–86. doi:10.1016/j.physa.2015.06.014
42. Yu MB. Momentum autocorrelation function of a classic diatomic chain. Phys Lett. (2016). 380:3583–7. doi:10.1016/j.physleta.2016.08.042
43. Yu MB. Momentum autocorrelation function of an impurity in a classical oscillator chain with alternating masses III. Some limiting cases. Physica A. (2016). 447:411–21. doi:10.1016/j.physa.2015.12.034
44. Lee MH. Local dynamics in an infinite harmonic chain. Symmetry. (2016). 8:22. doi:10.3390/sym8040022
45. Yu MB. Analytical expressions for momentum autocorrelation function of a classic diatomic chain. Eur Phys J B. (2017). 90:87. doi:10.1140/epjb/e2017-70752-1
46. Yu MB. Cut contribution to momentum autocorrelation function of an impurity in a classical diatomic chain. Eur Phys J B. (2018). 91:25. doi:10.1140/epjb/e2017-80402-3
47. Mokshin AV. Relaxation processes in many particle systems – recurrence relations approach, discontinuity. Interdiscip J Discontinuity Nonlinearity Complexity. (2013). 2:43–56. doi:10.5890/DNC.2012.11.002
48. Mokshin AV. Self-consistent approach to the description of relaxation processes in classical multiparticle systems. Theor Math Phys. (2015). 183:449–77. doi:10.1007/s11232-015-0274-2
49. Sen S. Solving the Liouville equation for conservative systems: continued fraction formalism and a simple application. Physica A. (2006). 360:304–24. doi:10.1016/j.physa.2005.06.047
50. Sawada I. Long-time tails of correlation and memory functions. Physica A. (2002). 315:14–25. doi:10.1016/S0378-4371(02)01231-1
51. Florencio J, Lee MH. Relaxation functions, memory functions, and random forces in the one-dimensional spin-1/2 XY and transverse Ising models. Phys Rev B. (1987). 35:1835. doi:10.1103/PhysRevB.35.1835
52. Florencio J, Lee MH. Memory functions and relaxation functions of some spin systems. Nucl Phys B. (1988). 5A:250–54. doi:10.1016/0920-5632(88)90050-3
53. Sawada I. Dynamics of the s=1/2 alternating chains at T = ∞. Phys Rev Lett. (1999). 83:1668. doi:10.1103/PhysRevLett.83.1668
54. Florencio J, Lee MH, Hong JB. Time dependent transverse correlations in the Ising model in D dimensions. Braz J Phys. (2000). 30:725–30. doi:10.1590/S0103-97332000000400016
55. Nunes MES, Florencio J. Effects of disorder on the dynamics of the XY chain. Phys Rev B. (2003). 68:014406. doi:10.1103/PhysRevB.68.014406
56. Nunes MES, Plascak JA, Florencio J. Spin dynamics of the quantum XY chain and ladder in a random field. Physica A. (2004). 332:1–14. doi:10.1016/j.physa.2003.10.049
57. Plascak JA, Sá Barreto FC, Pires AST, Gonçalves LL. A continued-fraction representation for the one-dimensional transverse Ising model. J Phys C. (1983). 16:49. doi:10.1088/0022-33719/16/1/009
58. Viswanath VS, Müller G. Recursion method in quantum spin dynamics: the art of terminating a continued fraction. J Appl Phys. (1990). 67:5486–8. doi:10.1063/1.345859
59. Müller G, Thomas H, Beck H, Bonner JC. Quantum spin dynamics of the antiferromagnetic linear chain in zero and nonzero magnetic field. Phys Rev B. (1981). 24:1429. doi:10.1103/PhysRevB.24.1429
60. Sawada I. High-energy excitations in aligned dimers. J Chem Phys Solids. (2001). 62:373–6. doi:10.1016/S0022-3697(00)00168-2
61. Sawada I. Dynamics of alternating spin chains and two-leg spin ladders with impurities. Physica B. (2003). 329-333:998–9. doi:10.1016/S0921-4526(02)02176-2
62. Sen S, Cai ZX, Mahanti SD. Dynamical correlations and the direct summation method of evaluating infinite continued fractions. Phys Rev E. (1993). 47:273. doi:10.1103/PhysRevE.47.273
63. Liu ZQ, Kong XM, Chen XS. Effects of Gaussian disorder on the dynamics of the random transverse Ising model. Phys Rev B. (2006). 73:224412. doi:10.1103/PhysRevB.73.224412
64. Yuan XJ, Kong XM, Xu ZB, Liu ZQ. Dynamics of the one-dimensional random transverse Ising model with next-nearest-neighbor interactions. Physica A. (2010). 389:242–8. doi:10.1016/j.physa.2009.08.021
65. Li YF, Kong XM. The dynamics of one-dimensional random quantum XY system with Dzyaloshinskii-Moriya interaction. Chin Phys B. (2013). 22:037502. doi:10.1088/1674-1056/22/3/037502
66. Nunes MES, Silva EM, Martins PHL, Florencio J, Plascak JA. Dynamics of the one-dimensional isotropic Heisenberg model with Dzyaloshinskii-Moriya interaction in a random transverse field. Physica A. (2020). 541:123683. doi:10.1016/j.physa.2019.123683
67. Silva EM. Dynamical class of a two-dimensional plasmonic Dirac system. Phys Rev E. (2015). 92:042146. doi:10.1103/PhysRevE.92.042146
68. Silva EM. Time evolution in a two-dimensional ultrarelativistic-like electron gas by recurrence relations method. Acta Phys Pol B. (2015). 46:1135. doi:10.5506/APhysPolB.46.1135
69. Mokshin AV, Yulmetyev RM, Khusnutdinoff RM, Hänggi P. Analysis of the dynamics of liquid aluminium: recurrent relation approach. J Phys Condens Matter. (2007). 19:046209. doi:1088/0953-8984/19/4/046209
70. Mokshin AV, Galimzyanov BN. Self-consistent description of local density dynamics in simple liquids. The case of molten lithium. J Phys Condens Matter. (2018). 30:085102. doi:10.1088/1361-648X/aaa7bc
71. Niemeijer T. Some exact calculations on a chain of spins 12. Physica. (1967). 36:377–419. doi:10.1016/0031-8914(67)90235-2
72. Brandt U, Jacoby K. Exact results for the dynamics of one-dimensional spin-systems. Z Phyzik B. (1976). 25:181–7. doi:10.1007/BF01320179
73. Brandt U, Jacoby K. The transverse correlation function of anisotropic XY-chains: exact results at T = ∞. Z Phys B. (1977). 26:245–52. doi:10.1007/BF01312930
74. Capel HW, Perk JHH. Autocorrelation function of the x-component of the magnetization in the one-dimensional XY-model. Physica A. (1977). 87:211–42. doi:10.1016/0378-4371(77)90014-0
75. Perk JHH, Capel HW. Transverse correlations in the inhomogenius XY-model at infinite temperature. Physica A. (1968). 92:1–49. doi:10.1016/0378-4371(84)90102-X
76. Lee MH, Florencio J, Hong J. Dynamic equivalence of a two-dimensional quantum electron gas and a classical harmonic oscillator chain with an impurity mass. J Phys A. (1989). 22:L331–L335. doi:10.1088/0305-4470/22/8/005
77. Sen S, Long M, Florencio J, Cai ZX. A unique feature of some simple many body quantum spin systems. J Appl Phys. (1999). 73:5471. doi:10.1063/1.353669
78. Florencio J, Sen S, Cai ZX. Quantum spin dynamics of the transverse Ising model in two dimensions. J Low Temp Phys. (1992). 89:561–4. doi:10.1007/BF00694087
79. Sen S, Long S, Florencio J, Cai ZX. A unique feature of some many-body quantum spin systems. J. Appl Phys. (1993). 73:3471. doi:10.1063/1.353669
80. Sen S, Florencio J, Cai ZX. Long-time dynamics of the transverse Ising model – comparison with data on LiTbF4. Mater Res Soc Symp Proc. (1993). 291:337. doi:10.1557/PROC-291-337
81. Chen SX, Shen YY, Kong XM. Crossover of the dynamical behavior in two-dimensional random transverse Ising model. Phys Rev B. (2010). 82:174404. doi:10.1103/PhysRevB.82.174404
82. Florencio J, Sen S, Cai ZX. Dynamic structure factor of the transverse Ising model in 2-D. J Phys Condens Matter. (1995). 7:1363. doi:10.1088/0953-8984/7/7/017
83. Kotzler J, Neuhaus-Steinmetz H, Froese A, Gorlitz D. Relaxation-coupled order-parameter oscillation in a transverse Ising system. Phys Rev Lett. (1988). 60:647. doi:10.1103/PhysRevLett.60.647
84. Souza WL, Silva EM, Martins PHL. Dynamics of the spin-1/2 Ising two-leg ladder with four-spin plaquette interaction and transverse field. Phys Rev E. (2020). 101:042104. doi:10.1103/PhysRevE.101.042104
85. Khait I, Gazit S, Yao NY, Auerbach A. Spin transport of weakly disordered Heisenberg chain at infinite temperature. Phys Rev B. (2016). 93:224205. doi:10.1103/PhysRevB.93.224205
86. Viswanath VS, Müller G. The recursion method applied to the T = 0 dynamics of the 1D s = 1/2 Heisenberg and XY models. J Appl Phys. (1991). 70:6178. doi:10.1063/1.350036
87. Lee MH. Time evolution, relaxation function, and random force for a single-spin via the method of Mori. Can J Phys. (1983). 61:428–33. doi:10.1139/p83-054
88. Sen S. Relaxation in nonlinear systems, nonconvergent infinite continued fractions and sensitive relaxation processes. Physica A. (2002). 315:150–5. doi:10.1016/S0378-4371(02)01365-1
89. Sen S, Long M. Dynamical correlations in an s = 1/2 isotropic Heisenberg chain at T = ∞. Phys Rev B. (1992). 46:14617. doi:10.1103/PhysRevB.46.14617
90. Bohm M, Viswanath VS, Stolze J, Müller G. Spin diffusion in the one-dimensional s = 1/2 XXZ model at infinite temperature. Phys Rev B. (1994). 49:15669. doi:10.1103/PhysRevB.49.15669
91. Sen S. Relaxation in the s = 1/2 isotropic Heisenberg chain at T = ∞ towards a simple intuitive interpretation. Physica A. (1995). 222:195–204. doi:10.1016/0378-4371(95)00301-0
92. Liu JM, Müller G. Infinite-temperature dynamics of the equivalent-neighbor XYZ model. Phys Rev E. (1990). 42:5854. doi:10.1103/PhysRevA.42.5854
93. Florencio J, de Alcantara Bonfim OF, Sá Barreto EFC. Dynamics of a transverse Ising model with four-spin interactions. Physica A. (1997). 235:523–33. doi:10.1016/S0378-4371(96)00299-3
94. Boechat B, Cordeiro C, de Alcantara Bonfim OF, Florencio J, Sá Barreto FC. Dynamical behavior of the four-body transverse Ising model with random bonds and fields. Braz J Phys. (2000). 30:693–6. doi:10.1590/S0103-97332000000400010
95. de Alcantara Bonfim OF, Boechat B, Cordeiro C, Sá Barreto FC, Florencio J. Dynamics of the Ising chain with four-spin interactions in a disordered transverse magnetic field. J. Phys. Soc. Japan (2001). 70:829–33. doi:10.1143/JPSJ.70.829
96. Florencio J, de Alcantara Bonfim OF. Temperature effects on the dynamics of the 1-D transverse Ising model with four-spin interactions. Physica A. (2004). 344:498–503. doi:10.1016/j.physa.2004.06.020
97. Dzyaloshinskii I. A thermodynamic theory of weak ferromagnetism of antiferromagnetics. J Phys Chem Solid. (1958). 4:241–55. doi:10.1016/0022-3697(58)90076-3
98. Moriya T. Anisotropic superexchange interaction and weak ferromagnetism. Phys Rev. (1960). 120:91. doi:10.1103/PhysRev.120.91
99. Xia Q, Riseborough PS. One-dimensional Dzyaloshinski-Moriya antiferromagnets in an applied field. J Appl Phys. (1988). 63:4141. doi:10.1063/1.340521
100. Lima LS, Pires AST. Spin dynamics in the one-dimensional antiferromagnetic with Dzyaloshinskii-Moriya interaction. J Magn Magn Mater. (2008). 320:2316–18. doi:10.1016/j.jmmm.2008.04.162
101. Pires AST, Gouvêa ME. Dynamics of the one-dimensional quantum antiferromagnet with Dzyaloshinski-Moriya interactions. J Magn Magn Mater. (2000). 212:251–8. doi:10.1016/S0304-8853(99)00758-1
102. Derzhko O, Verkholyak T. Dynamics of the spin-1/2 XY chain with Dzyaloshinskii-Moriya interaction. Physica B. (2005). 359:1403–5. doi:10.1016/j.physb.2005.01.438
103. Derzhko O, Verkholyak T, Krokhmalskii T, Büttner H. Dynamic probes of quantum spin chains with the Dzyaloshinskii-Moriya interaction. Phys Rev B. (2006). 73:214407. doi:10.1103/PhysRevB.73.214407
104. Verkholyak T, Derzhko O, Krokhmalskii T, Stolze J. Dynamic properties of quantum spin chains: simple route to complex behavior. Phys Rev B. (2007). 76:144418. doi:10.1103/PhysRevB.76.144418
105. Nunes MES, Silva EM, Martins PHL, Plascak JA, Florencio J. Effects of a magnetic field on the dynamics of the one-dimensional Heisenberg model with Dzyaloshinskii-Moriya interactions. Phys Rev E. (2018). 98:042124. doi:10.1103/PhysRevE.98.042124
106. Florencio J, Sá Barreto FC. Dynamics of the random one-dimensional transverse Ising model. Phys Rev B. (1999). 60:9555. doi:10.1103/PhysRevB.60.9555
Keywords: dynamical correlation function, relaxation function, time-dependent correlation function, spectral density, recurrence relations, continued fractions, exact diagonalization
Citation: Florencio J and de Alcantara Bonfim OF (2020) Recent Advances in the Calculation of Dynamical Correlation Functions. Front. Phys. 8:557277. doi: 10.3389/fphy.2020.557277
Received: 29 April 2020; Accepted: 02 October 2020;
Published: 26 November 2020.
Edited by:
Fernando A. Oliveira, University of Brasilia, BrazilReviewed by:
Marco G. Mazza, Loughborough University, United KingdomHeng Fan, Institute of Physics (CAS), China
Copyright © 2020 Florencio and de Alcantara Bonfim. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: J. Florencio, amZqQGlmLnVmZi5icg==; O. F. de Alcantara Bonfim, Ym9uZmltQHVwLmVkdQ==
 J. Florencio
J. Florencio O. F. de Alcantara Bonfim2*
O. F. de Alcantara Bonfim2*