On the New Wave Behaviors of the Gilson-Pickering Equation

In this article, we study the fully non-linear third-order partial differential equation, namely the Gilson-Pickering equation. The (1/G′)-expansion method, and the generalized exponential rational function method are used to construct various exact solitary wave solutions for a given equation. These methods are based on a homogeneous balance technique that provides an order for the estimation of a polynomial-type solution. In order to convert the governing equation into a nonlinear ordinary differential equation, a traveling wave transformation has been implemented. As a result, we have constructed a variety of solitary wave solutions, such as singular solutions, compound singular solutions, complex solutions, and topological and non-topological solutions. Besides, the 2D, 3D, and contour surfaces are plotted for all obtained solutions by choosing appropriate parameter values.

1. Introduction

Nonlinear partial differential equations (NLPDEs) are used to represent a variety of nonlinear physical phenomena in different areas of applied sciences like fluid dynamics, plasma physics, optical fibers, and biology. Among the most profitable strategies for examining such nonlinear physical phenomena is to seek for the exact solutions of NLPDEs [1–5]. In recent years, a variety of effective methods have been implemented to investigate the exact solutions of nonlinear partial differential equations, such as Hirota's bilinear method [6], the Adomian decomposition method [7], the exp(−Φ(ξ))-expansion method [8], the sine-Gordon expansion method [9], the Bernoulli sub-equation method [10, 11], the shooting method with the fourth-order Runge-Kutta scheme [12, 13], the generalized exponential rational function method [14–18], the modified exponential function method [19], the modified auxiliary expansion method [20], the homotopy perturbation Sumudu transform method [21], the homotopy perturbation transform method [22, 23], and the fractional homotopy analysis transform method [24].

The third-order nonlinear partial differential equation (NLPDE) was introduced in [25] by Gilson and Pickering as

$\begin{array}{ll}{u}_t-ϵu_{xxt}+2k{u}_x-u{u}_{xxx}-\alpha u{u}_x-\beta u_x{u}_{xx}=0,& (1)\end{array}$

where ε, α, κ, and β are non-zero real numbers. Recently, the Gilson-Pickering equation has been investigated using a variety of methods, such as the (G′/G)-expansion method [26], the anstaz method [27], the (G′/G)-expansion method to tanh, the coth, cot, and the logical forms under certain conditions [28], the Bernoulli sub-equation model [29], a not a knot meshless method [30], and the symmetry method [31].

The core of this paper is to investigate the Gilson-Pickering equation using the (1/G′)-expansion method and the generalized exponential rational function method (GERF).

2. Applications of the Gilson Pickering Equation

This section presents specific instances of the Gilson Pickering equation and their applications. When ε = 1, α = −3, and β = 2, Equation (1) gives the Fuchssteiner-Fokas-Camassa-Holm equation, which is a completely integrable nonlinear partial differential equation that arises at different levels of approximation in shallow water theory [32, 33]. When ε = 0, α = 1, κ = 0, and β = 3, Equation (1) reduces to the Rosenau-Hyman equation (RH), which arises in the study of the influence of nonlinear dispersion on the structure of patterns in liquid drops [34]. When ε = 1, α = −1, κ = 0.5, and β = 3, Equation (1) gives the Fronberg-Whitham (FW), which was developed to analyze the qualitative characteristics of wave breakage and admits a wave of the highest height [35–37].

3. The Basic Concepts of the (1/G′)-Expansion Method

In this section, the fundamental steps of the (1/G′)-expansion method are presented [38, 39]:

Step 1. Let us consider the general form of a two-variable nonlinear partial differential equation (NPDE) as follows:

$\begin{array}{ll}Q(p,p_t,p_x,p_{xx},\dots )=0,& (2)\end{array}$

where p = p(x, t), and Q is a partial differential equation.

Step 2. To convert Equation (2) to a nonlinear ordinary differential equation (NODE), we employ the following wave transformation

$\begin{array}{ll}p(x,t)=P(\eta ),\eta =(x-ht),& (3)\end{array}$

where h is a scalar. After some procedures, Equation (2) reduces to the following NODE:

$\begin{array}{ll}W(P^{\prime },P^{\prime \prime },P^{\prime \prime \prime },\mathrm{...})=0,& (4)\end{array}$

where W is an ordinary differential equation.

Step 3. Assume that Equation (4) has a solution of the form

$\begin{array}{ll}P(\eta )={\displaystyle \sum _{i=0}^m}{a}_i{\left(\frac{1}{G^{\prime }}\right)}^i,& (5)\end{array}$

where a₀, a₁, a₂, …, a_m are scalars to be determined, m is a balance term, and G = G(η) satisfies the following second-order linear ODE:

$\begin{array}{ll}{G}^{″}+\lambda G^{\prime }+\mu =0,& (6)\end{array}$

where λ and μ are scalars.

The solution of Equation (6) is given by

$\begin{array}{ll}G(\eta )=a_0+a_1\left(\frac{1}{-\mu /\lambda +b{\text{e}}^{-\lambda \eta }}\right).& (7)\end{array}$

If we convert the algebraic expression given by Equation (7) to a trigonometric function, we can write it as the following:

$\begin{array}{ll}G(\eta )=a_0+\frac{a_1}{-\frac{\mu }{\lambda }+b\text{ cosh }(\lambda \eta )-b\text{ sinh}(\lambda \eta )}.& (8)\end{array}$

Inserting Equation (6) and its necessary derivatives along with Equation (5) into Equation (4) returns the polynomial of ${\left(\frac{1}{G^{\prime }}\right)}^i$. Summing the ${\left(\frac{1}{G^{\prime }}\right)}^i$ coefficients with the same power and then setting every summation to zero, we get a system of algebraic equations for a_i, i ≥ 0. Eventually, solving this system simply gives the value of the variables. Putting these values of variables with the value of the balance term m into Equation (4), we can get solutions for Equation (2).

4. The Basic Concepts of the GERF

In this section, the basic steps of the GERF are presented.

Step 1. Let us consider that the general form of a nonlinear partial differential equation is given by:

$\begin{array}{ll}Q(p,p_x,p_t,p_{xx},\dots )=0,& (9)\end{array}$

where Q is a partial differential equation.

Suppose that the wave transformation takes the form:

$\begin{array}{ll}p(x,t)=P(\eta ),\eta =x-ht,& (10)\end{array}$

where h is a scalar.

Using Equation (10) in Equation (9), we get the nonlinear ordinary differential equation

$\begin{array}{ll}W(P,P^{\prime },P^{″},\dots )=0,& (11)\end{array}$

where W is an ordinary differential equation.

Step 2. Suppose that the solitary wave solutions of Equation (11) are given by:

$\begin{array}{ll}P(\eta )=A_0+{\displaystyle \sum _{K=1}^m}{A}_K\phi {(\eta )}^K+{\displaystyle \sum _{K=1}^m}{B}_K\phi {(\eta )}^{-K},& (12)\end{array}$

where

$\begin{array}{ll}\phi (\eta )=\frac{r_1{e}^{s_1\eta }+r_2{e}^{s_2\eta }}{r_3{e}^{s_3\eta }+r_4{e}^{s_4\eta }},& (13)\end{array}$

where r_m, s_m (1 ≤ n ≤ 4) are real/complex constants, A₀, A_K, B_K are constants to be determined, and m will be determined by the balance principle.

Step 3. Substituting Equation (12) into Equation (11), we get the polynomials that are dependent on Equation (12). By equating the same order terms, we obtain an algebraic system of equations. With the help of computational programs such as Mathematica, Matlab, and Maple, we solve this system and determine the values of A₀, A_K, B_K. Finally one can easily obtain the nontrivial exact solutions of Equation (11).

5. Mathematical Calculation

In this section, the mathematical calculation of the Gilson-Pickering equation is presented.

Consider the Gilson-Pickering equation (Equation 1) stated in section 1. Inserting the wave transformation

$\begin{array}{ll}u=P(\eta ),\eta =x-ht,& (14)\end{array}$

into Equation (1), the following NODE can be obtained

$\begin{array}{ll}(2k-h)P^{\prime }+ϵh{P}^{‴}-P{P}^{\prime }-\beta P^{\prime }{P}^{\prime }-\alpha P{P}^{\prime }=0,& (15)\end{array}$

where ϵ, β, α, h, and k are non-zero real numbers.

Integrating Equation (15) once with respect to η and assuming that the integration constant is zero, we have.

$\begin{array}{ll}\left(2k-h\right)P+\left(ϵh-P\right)P^{″}+\frac{1-\beta }{2}{\left(P^{\prime }\right)}^2-\frac{\alpha }{2}{P}^2=0.& (16)\end{array}$

6. Implementation of the (1/G′)-Expansion Method

In this section, the application of the (1/G′)-expansion method to the Gilson-Pickering equation is presented.

Applying the balance principle, by taking the nonlinear term P² and the highest derivative P″ in Equation (16) gives m = 2. With m = 2, Equation (5) takes the form

$\begin{array}{ll}P(\eta )=a_0+a_1\left(\frac{1}{G^{\prime }}\right)+a_2{\left(\frac{1}{G^{\prime }}\right)}^2.& (17)\end{array}$

Inserting Equation (17) and its necessary derivatives into Equation (16), returns the polynomial of ${\left(\frac{1}{G^{\prime }}\right)}^i$. Summing the ${\left(\frac{1}{G^{\prime }}\right)}^i$ coefficients with the likely power and then setting every summation to zero, we get a system of algebraic equations. Solving this system simply gives the following families of solutions:

Family 1. When

$\begin{array}{l}{a}_0=-\frac{2(h-2k)}{\alpha },\\ a_1=-\frac{12\sqrt{-(h-2k)\alpha }{(-4k+h(2+\alpha ϵ))}^{3/2}\mu }{{\alpha }^2(-6k+h(3+\alpha ϵ))},\\ a_2=\frac{12{(-4k+h(2+\alpha ϵ))}^2{\mu }^2}{{\alpha }^2(-6k+h(3+\alpha ϵ))},\lambda =-\frac{\sqrt{-(h-2k)\alpha }}{\sqrt{2h-4k+h\alpha ϵ}},\\ \beta =-2,& (18)\end{array}$

we get

$\begin{array}{l}{u}_1(x,t)=\frac{12{\left(-4k+h(2+\alpha ϵ)\right)}^2{\mu }^2}{{\alpha }^2\left(-6k+h(3+\alpha ϵ)\right){\left(-\frac{L\mu }{M}+C_1\text{ cosh }\left(\frac{M\xi }{L}\right)-C_1\text{ sinh }\left(\frac{M\xi }{L}\right)\right)}^2}\\ +\frac{12M{\left(-4k+h(2+\alpha ϵ)\right)}^{3/2}\mu }{{\alpha }^2\left(-6k+h(3+\alpha ϵ)\right)\left(-\frac{L\mu }{M}+C_1\text{ cosh }(\frac{M\xi }{L})-C_1\text{ sinh }\left(\frac{M\xi }{L}\right)\right)}\\ -\frac{2(h-2k)}{\alpha },& (19)\end{array}$

where $M=\sqrt{(-h+2k)\alpha },L=\sqrt{2h-4k+h\alpha ϵ}.$

Family 2. When

$\begin{array}{l}{a}_0=0,a_1=\frac{12h^{3/2}\sqrt{h-2k}{ϵ}^{3/2}\mu }{2k+h(-1+\alpha ϵ)},a_2=\frac{12h^2{ϵ}^2{\mu }^2}{2k+h(-1+\alpha ϵ)},\\ \lambda =\frac{\sqrt{h-2k}}{\sqrt{h}\sqrt{ϵ}},\beta =-2,& (20)\end{array}$

we get

$\begin{array}{l}{u}_2(x,t)=\frac{12h^2{ϵ}^2{\mu }^2}{\left(2k+h(-1+\alpha ϵ)\right){\left(-\frac{\sqrt{h}\sqrt{ϵ}\mu }{\sqrt{h-2k}}+C_1\text{ cosh }(S)-C_1\text{ sinh }(S)\right)}^2}\\ +\frac{12h^{3/2}\sqrt{h-2k}{ϵ}^{3/2}\mu }{\left(2k+h(-1+\alpha ϵ)\right)\left(-\frac{\sqrt{h}\sqrt{ϵ}\mu }{\sqrt{h-2k}}+C_1\text{ cosh }(S)-C_1\text{ sinh }(S)\right)},& (21)\end{array}$

where $S=\frac{\sqrt{h-2k}\xi }{\sqrt{h}\sqrt{ϵ}}$.

Family 3. When

$\begin{array}{l}{a}_0=\frac{4kϵ{\lambda }^2}{\alpha +(2+\alpha ϵ){\lambda }^2},a_2=\frac{(\alpha -{\lambda }^2)(\alpha +(2+\alpha ϵ){\lambda }^2)a_1^2}{24k\alpha ϵ{\lambda }^2},\\ \mu =\frac{(\alpha -{\lambda }^2)(\alpha +(2+\alpha ϵ){\lambda }^2)a_1}{24k\alpha ϵ\lambda },\beta =-2,\\ h=\frac{2k(\alpha +2{\lambda }^2)}{\alpha +(2+\alpha ϵ){\lambda }^2},& (22)\end{array}$

gives

$\begin{array}{l}{u}_3(x,t)=\frac{a_1}{C_1\text{ cosh }(\lambda \xi )-C_1\text{ sinh }(\lambda \xi )-\frac{(\alpha -{\lambda }^2)(\alpha +(2+\alpha ϵ){\lambda }^2)a_1}{24k\alpha ϵ{\lambda }^2}}\\ +\frac{\left(\alpha -{\lambda }^2\right)\left(\alpha +(2+\alpha ϵ){\lambda }^2\right)a_1^2}{24k\alpha ϵ{\lambda }^2{\left(C_1\text{ cosh }(\lambda \xi )-C_1\text{ sinh }(\lambda \xi )-\frac{(\alpha -{\lambda }^2)(\alpha +(2+\alpha ϵ){\lambda }^2)a_1}{24k\alpha ϵ{\lambda }^2}\right)}^2}\\ +\frac{4kϵ{\lambda }^2}{\alpha +(2+\alpha ϵ){\lambda }^2}.& (23)\end{array}$

Family 4. When

$\begin{array}{l}{a}_0=\frac{4kϵ}{1+\alpha ϵ},a_2=0,\beta =-3,\mu =\frac{\text{i}\sqrt{\alpha }(1+\alpha ϵ)a_1}{4kϵ},\\ h=\frac{2k}{1+\alpha ϵ},\lambda =\text{i}\sqrt{\alpha },& (24)\end{array}$

we get

$\begin{array}{ll}{u}_4(x,t)=\frac{4kϵ}{1+\alpha ϵ}+\frac{a_1}{C_1\text{ cos }(\sqrt{\alpha }\xi )-\text{i}{C}_1\text{ sin }(\sqrt{\alpha }\xi )-\frac{(1+\alpha ϵ)a_1}{4kϵ}}.& (25)\end{array}$

Family 5. When

$\begin{array}{l}{a}_0=\frac{\text{i}\sqrt{\alpha }{a}_1}{\mu },a_2=0,\beta =-3,h=\frac{\text{i}\sqrt{\alpha }{a}_1}{2ϵ\mu },\\ k=\frac{\text{i}\sqrt{\alpha }(1+\alpha ϵ)a_1}{4ϵ\mu },\lambda =\text{i}\sqrt{\alpha },& (26)\end{array}$

we get

$\begin{array}{ll}{u}_5(x,t)=\frac{\text{i}\sqrt{\alpha }{a}_1}{\mu }+\frac{a_1}{\frac{\text{i}\mu }{\sqrt{\alpha }}+C_1\text{ cos }(\sqrt{\alpha }\xi )-\text{i}{C}_1\text{ sin }(\sqrt{\alpha }\xi )}.& (27)\end{array}$

Family 6. When

$\begin{array}{l}{a}_0=\frac{12hϵ\mu +3\lambda a_1-\sqrt{-96hϵ\lambda \mu a_1+9{\left(4hϵ\mu +\lambda a_1\right)}^2}}{24\mu },a_2=\frac{\mu a_1}{\lambda },\\ \alpha =\frac{\lambda \left(12hϵ\mu -\lambda a_1+\sqrt{3}\sqrt{48h^2{ϵ}^2{\mu }^2+\lambda a_1\left(-8hϵ\mu +3\lambda a_1\right)}\right)}{2a_1},\\ k=\frac{24h\mu +12hϵ{\lambda }^2\mu -3{\lambda }^3{a}_1+{\lambda }^2\sqrt{-96hϵ\lambda \mu a_1+9{\left(4hϵ\mu +\lambda a_1\right)}^2}}{48\mu },\\ \beta =-2,& (28)\end{array}$

we have

$\begin{array}{l}{u}_6(x,t)=\frac{\mu a_1}{\lambda {\left(-\frac{\mu }{\lambda }+C_1\text{ cosh }(\lambda \xi )-C_1\text{ sinh }(\lambda \xi )\right)}^2}\\ +\frac{a_1}{-\frac{\mu }{\lambda }+C_1\text{ cosh }(\lambda \xi )-C_1\text{ sinh }(\lambda \xi )}\\ +\frac{12hϵ\mu +3\lambda a_1-\sqrt{-96hϵ\lambda \mu a_1+9{\left(4hϵ\mu +\lambda a_1\right)}^2}}{24\mu }.& (29)\end{array}$

7. Implementation of the GERF Method

In this section, the application of the GERF method to the Gilson-Pickering equation is presented.

Applying the balance principle, by taking the nonlinear term P² and the highest derivative P″ in Equation (16) gives m = 2. With m = 2, Equation (12) takes the form

$\begin{array}{ll}P(\eta )=A_0+A_1\phi (\eta )+\frac{B_1}{\phi (\eta )}+A_2\phi {(\eta )}^2+\frac{B_2}{\phi {(\eta )}^2},& (30)\end{array}$

where φ(η) is given by Equation (13). Following the methodology described above in section 4, we obtain the following nontrivial solutions of Equation (1):

Family 1. When r_i = {−2, −1, 1, 1}, s_i = {0, 1, 0, 1}, we get

$\begin{array}{ll}\phi (\eta )=\frac{-2-{\text{e}}^{\eta }}{1+{\text{e}}^{\eta }},& (31)\end{array}$

Case 1.

$\begin{array}{l}{A}_0=\frac{A_1(-1+13\alpha )}{18\alpha },B_1=0,A_2=\frac{A_1}{3},B_2=0,\beta =-2,\\ h=\frac{A_1\left(-2+\alpha +{\alpha }^2\right)}{36\alpha ϵ},k=\frac{A_1(-1+\alpha )(2+\alpha +\alpha ϵ)}{72\alpha ϵ},& (32)\end{array}$

we get

$\begin{array}{l}{u}_7(x,t)=\frac{A_1{\left(-2-{\text{e}}^{x-\frac{A_{1}t(-2+\alpha +{\alpha }^2)}{36\alpha ϵ}}\right)}^2}{3{\left(1+{\text{e}}^{x-\frac{A_{1}t(-2+\alpha +{\alpha }^2)}{36\alpha ϵ}}\right)}^2}\\ \begin{array}{c}+\frac{A_1\left(-2-{\text{e}}^{x-\frac{A_{1}t(-2+\alpha +{\alpha }^2)}{36\alpha ϵ}}\right)}{1+{\text{e}}^{x-\frac{A_{1}t(-2+\alpha +{\alpha }^2)}{36\alpha ϵ}}}+\frac{A_1(-1+13\alpha )}{18\alpha },\end{array}& (33)\end{array}$

Case 2. When

$\begin{array}{l}{A}_0=-\frac{2(h-2k)(-1+13\alpha )}{(-1+\alpha )\alpha },A_1=0,B_1=-\frac{72(h-2k)}{-1+\alpha },\\ A_2=0,B_2=-\frac{48(h-2k)}{-1+\alpha },ϵ-\frac{(h-2k)(2+\alpha )}{h\alpha },\beta =-2,& (34)\end{array}$

we get

$\begin{array}{l}{u}_8(x,t)=-\frac{72\left(1+{\text{e}}^{-ht+x}\right)(h-2k)}{\left(-2-{\text{e}}^{-ht+x}\right)(-1+\alpha )}\\ \begin{array}{c}-\frac{48{\left(1+{\text{e}}^{-ht+x}\right)}^2(h-2k)}{{\left(-2-{\text{e}}^{-ht+x}\right)}^2(-1+\alpha )}-\frac{2(h-2k)(-1+13\alpha )}{(-1+\alpha )\alpha }.\end{array}& (35)\end{array}$

Family 2. When r_i = {−2−i, 2−i, −1, 1}, s_i = {i, −i, i, −i} we get

$\begin{array}{ll}\phi (\eta )=\frac{\text{cos }(\eta )+2\text{ sin }(\eta )}{\text{sin }(\eta )},& (36)\end{array}$

Case 1. When

$\begin{array}{l}{A}_0=\frac{B_1(8-13\alpha )}{60\alpha },A_1=0,A_2=0,B_2=-\frac{5B_1}{4},\beta =-2,\\ h=-\frac{B_1(-8+\alpha )(4+\alpha )}{240\alpha ϵ},k=\frac{B_1(4+\alpha )(8+\alpha (-1+4ϵ))}{480\alpha ϵ},& (37)\end{array}$

we get

$\begin{array}{l}{u}_9(x,t)=\frac{B_1(8-13\alpha )}{60\alpha }-\frac{5B_1\text{sin }{(D)}^2}{4{(\text{cos }(D)+2\text{ sin }(D))}^2}\\ \begin{array}{c}+\frac{B_1\text{sin }(D)}{\text{cos }(D)+2\text{ sin }(D)},\end{array}& (38)\end{array}$

where $D=x+\frac{B_{1}t(-8+\alpha )(4+\alpha )}{240\alpha ϵ}.$

Case 2.

$\begin{array}{l}{A}_0=\frac{A_1(8-13\alpha )}{12\alpha },B_1=0,A_2=-\frac{A_1}{4},B_2=0,\beta =-2,\\ ϵ-\frac{A_1(-8+\alpha )(4+\alpha )}{48h\alpha },k=\frac{1}{24}(12h+A_1(4+\alpha )),& (39)\end{array}$

we get

$\begin{array}{l}{u}_{10}\left(x,t\right)=\frac{A1\left(8-13\alpha \right)}{12\alpha }-A_1\text{ csc }\left(ht-x\right)(\text{cos }\left(ht-x\right)\\ -2\text{ sin }\left(ht-x\right))-\frac{1}{4}{A}_1\text{ csc }{\left(ht-x\right)}^2(\text{cos }\left(ht-x\right)\\ -{2\text{ sin }\left(ht-x\right))}^2.& (40)\end{array}$

Family 3. When r_i = {2, 0, 1, 1}, s_i = {−1, 0, 1, −1}

$\begin{array}{ll}\phi (\eta )=\frac{(\text{cosh }(\eta )-\text{sinh }(\eta ))}{\text{ cosh }(\eta )},& (41)\end{array}$

Case 1. When

$\begin{array}{l}{A}_0=-\frac{A_1(-4+\alpha )}{3\alpha },B_1=0,A_2=-\frac{A_1}{2},B_2=0,\beta =-2,\\ h=-\frac{A_1(-4+\alpha )(8+\alpha )}{24\alpha ϵ},k=-\frac{A_1(-4+\alpha )(8+\alpha +4\alpha ϵ)}{48\alpha ϵ},& (42)\end{array}$

we have

$\begin{array}{l}{u}_{11}\left(x,t\right)=A_{1}Sech\left(D\right)\left(\text{cosh }\left(D\right)-\text{ sinh }\left(D\right)\right)\frac{1}{2}{A}_{1}Sech{\left(D\right)}^2(\text{cosh }\left(D\right)\\ -{\text{ sinh }\left(D\right))}^2-\frac{A_1\left(-4+\alpha \right)}{3\alpha },& (43)\end{array}$

where $D=x+\frac{A_{1}t(-4+\alpha )(8+\alpha )}{24\alpha ϵ}.$

Case 2.

$\begin{array}{l}{A}_0=-\frac{(h-2k)\left(-4+\sqrt{{(-4+\alpha )}^2}+\alpha \right)}{(-4+\alpha )\alpha },B_2=0,\beta =-2,\\ ϵ=-\frac{(h-2k)\left(4\left(-4+\sqrt{{(-4+\alpha )}^2}\right)+{\alpha }^2\right)}{4h\sqrt{{(-4+\alpha )}^2}\alpha },B_1=0,\\ A_1=\frac{6(h-2k)}{\sqrt{{(-4+\alpha )}^2}},A_2=-\frac{3(h-2k)}{\sqrt{{(-4+\alpha )}^2}},& (44)\end{array}$

we get

$\begin{array}{l}{u}_{12}\left(x,t\right)=\frac{6\left(h-2k\right)sech\left(ht-x\right)\left(\text{cosh }\left(ht-x\right)+\text{ sinh }\left(ht-x\right)\right)}{\sqrt{{\left(-4+\alpha \right)}^2}}\\ -\frac{3\left(h-2k\right)sech{\left(ht-x\right)}^2{\left(\text{cosh }\left(ht-x\right)+\text{ sinh }\left(ht-x\right)\right)}^2}{\sqrt{{\left(-4+\alpha \right)}^2}}\\ -\frac{\left(h-2k\right)\left(-4+\sqrt{{\left(-4+\alpha \right)}^2}+\alpha \right)}{\left(-4+\alpha \right)\alpha }.& (45)\end{array}$

8. Result and Discussion

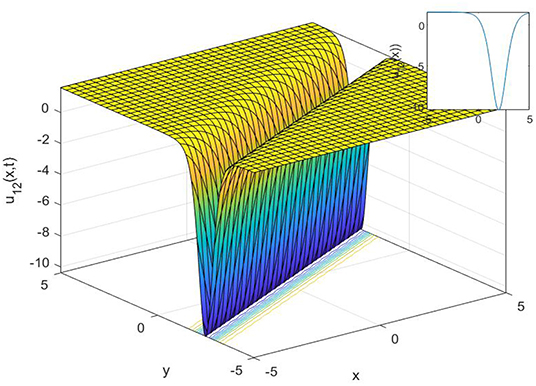
The powerful methods, namely the (1/G′) expansion method and the generalized exponential rational function method, are used to construct various analytical solutions for the Gilson-Pickering equation. Some results of the Gilson-Pickering equation have already been reported in the literature. Fan et al. [28] used (G′/G) and the ansatz method and found the solitary wave solutions to Equation (1). Baskonus [29] investigated the Gilson-Pickering equation by using the first integral method. Zabihi and Saffarian [30] implemented the simplified (G′/G) expansion method to reveal the hyperbolic, trigonometric function, and rational function solutions. Singla and Gupta [31] reported some new complex soliton solutions to Equation (1) with the aid of the Bernoulli sub-equation function method. Camsssa et al. [32] used a not a knot meshless method to obtain numerical solutions to Equation (1). Fuchssteiner and Fokas [33] performed Lie symmetry analysis and found conservation laws for the space-time fractional Gilson-Pickering equation. In this article, we obtained the singular, compound singular, complex, topological, and non-topological wave solutions to the studied equation. It is known that non-topological solutions detect waves with an intensity lower than the background, topological solutions with such a maximum intensity higher than the background, and singular solutions that are waves with discontinuous derivatives.

9. Conclusion

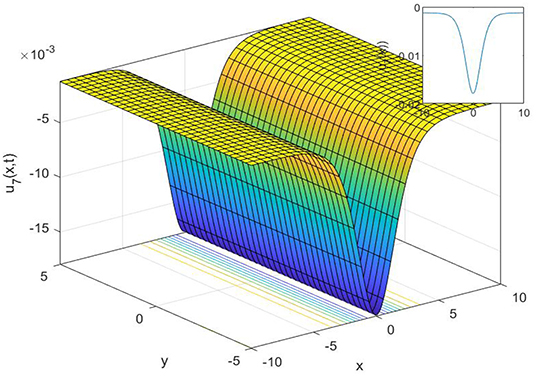
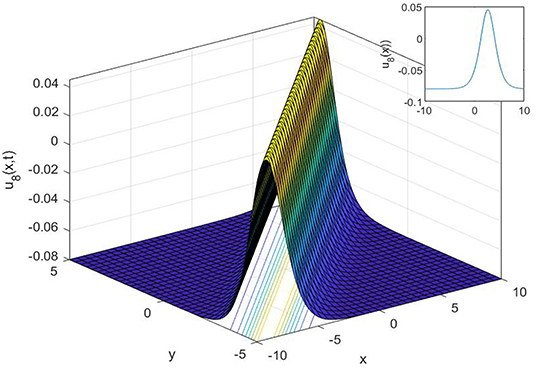
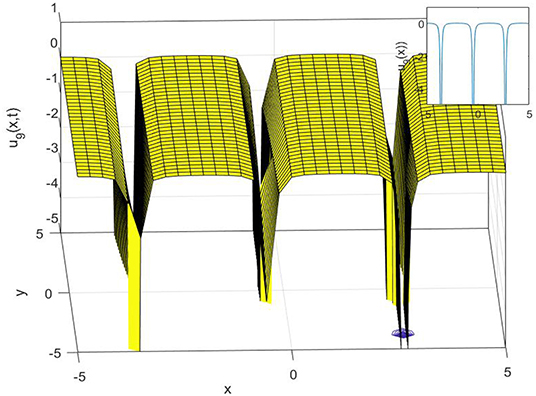
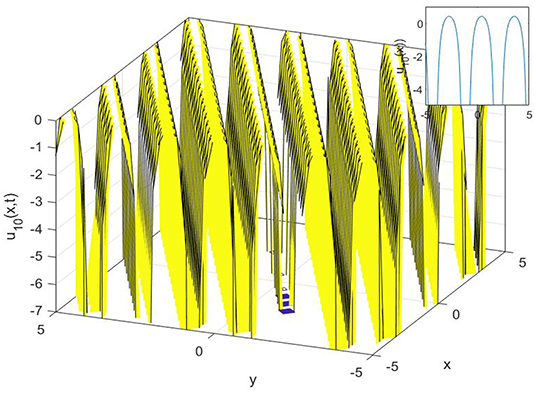
In this study, we have successfully applied the (1/G′) expansion method and the generalized exponential rational function method to find new exact solutions for the Gilson-Pickering equation. In order to convert the governing equation into a NODE, a traveling wave transformation has been implemented. Various analytical solutions of the proposed model have been constructed such as singular solutions, as shown in Figures 1, 2, 3, compound singular solution, as seen in Figure 4, complex solution, as seen in Figure 5, as well as a singular solution, can be shown in Figure 6. The non-topological solution, as shown in Figure 7, topological solutions, as shown in Figure 8, and compound singular solutions, as seen in Figures 9, 10. Also, topological solution and non-topological solution as seen in Figures 11, 12, respectively. Compared with the results reported in Fan et al. [28], Baskonus [29], Zabihi and Saffarian [30], Singla and Gupta [31], Camsssa et al. [32], and Fuchssteiner and Fokas [33], the solutions obtained are novel. Both methods are efficient for solving complex nonlinear partial differential equations, but, by using the generalized exponential rational function method, we can get more solutions than with the (1/G′) expansion method. Furthermore, the 2D, 3D, and contour surfaces are plotted for all obtained solutions by selecting suitable values for the parameters.

FIGURE 1

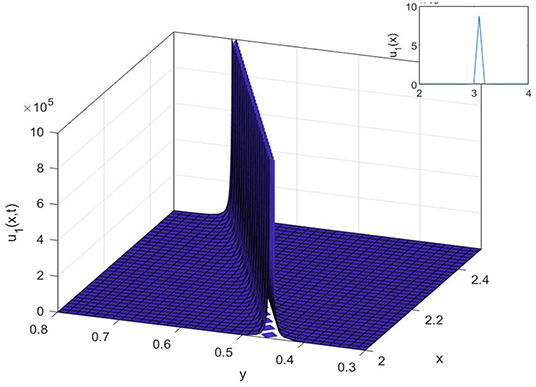
Figure 1. The 3D, 2D, and contour surfaces of Equation (19) when h = 2, k = 2.5, α = 2.6, μ = 0.2, ϵ = 3.5, and C₁ = 0.6.

FIGURE 2

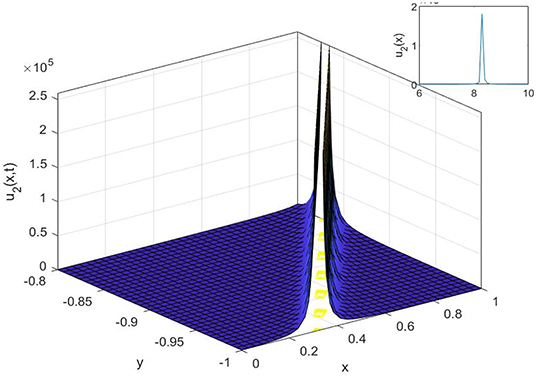
Figure 2. The 3D, 2D, and contour surfaces of Equation (21) using h = 4, k = 0.5, α = 2.6, μ = 0.2, ϵ = 4, and C₁ = 3.

FIGURE 3

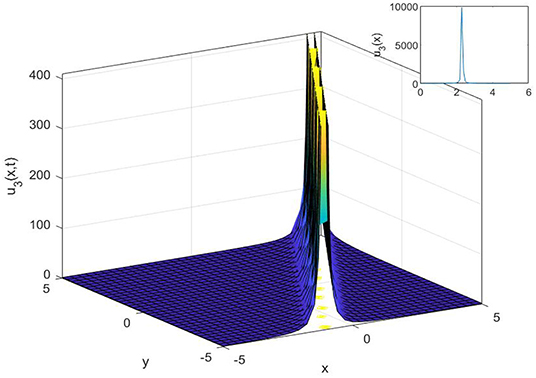
Figure 3. The 3D, 2D, and contour surfaces of Equation (23) using k = 2, α = 5, λ = 1.2, ϵ = 6.6, C₁ = 2, and a₁ = 2.8.

FIGURE 4

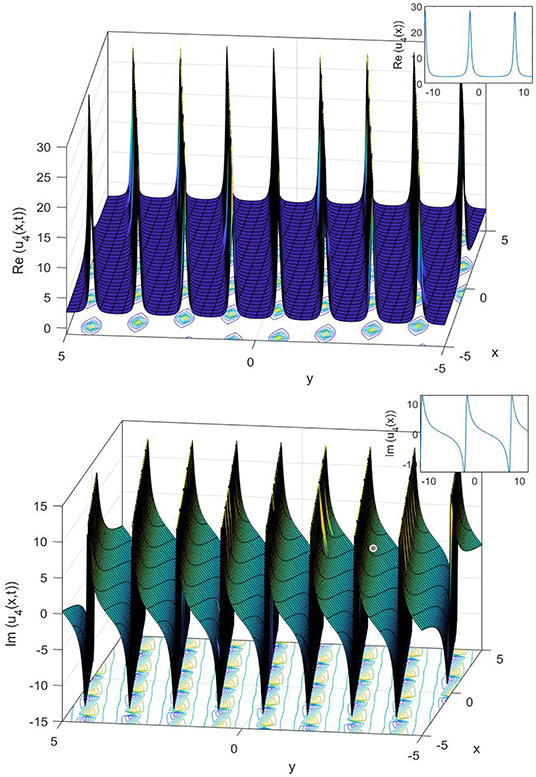
Figure 4. The 3D, 2D, and contour surfaces of Equation (25), using k = 4.5, α = 0.4, ϵ = 0.3, C₁ = 0.2, and a₁ = 0.8.

FIGURE 5

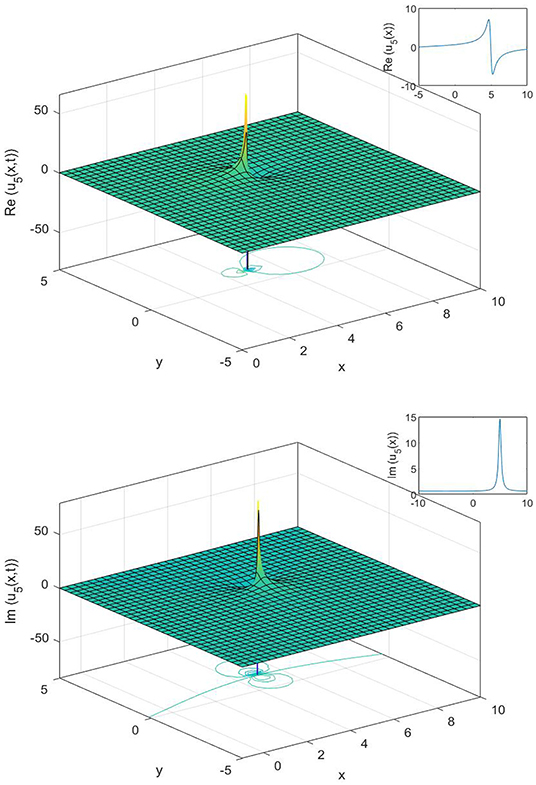
Figure 5. The 3D, 2D, and contour surfaces of Equation (27), using μ = 0.4, α = 0.1, ϵ = 0.5, C₁ = 2, and a₁ = 1.5.

FIGURE 6

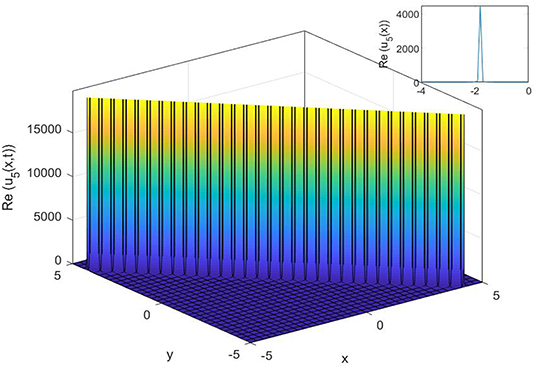
Figure 6. The 3D, 2D, and contour surfaces of Equation (29) using μ = 1.5, α = 0.4, ϵ = 0.1, C₁ = 2, a₁ = 0.4, h = −1, and λ = 0.5.

FIGURE 7

Figure 7. The 3D, 2D, and contour surfaces of Equation (33) using A₁ = 0.2, α = 0.9, and ϵ = 0.6.

FIGURE 8

Figure 8. The 3D, 2D, and contour surfaces of Equation (35) using k = 0.5, α = 25, and h = 2.

FIGURE 9

Figure 9. The 3D, 2D, and contour surfaces of Equation (38) using B₁ = 0.5, α = 4, and ϵ = 2.

FIGURE 10

Figure 10. The 3D, 2D, and contour surfaces of Equation (40) using A₁ = 5, α = 4, and ϵ = 2.

FIGURE 11

Figure 11. The 3D, 2D, and contour surfaces of Equation (43) using A₁ = 5, α = 4, and ϵ = 2.

FIGURE 12

Figure 12. The 3D, 2D, and contour surfaces of Equation (45) using k = 3, α = 5, and h = 2.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

RY and SN suggested the problem first. KA drafted the first version of the problem statement with the help of HD. All authors made several suggestions to make improvements in the problem statement and contributed to the development of solution in their best possible ways.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Osman MS, Abdel-Gawad HI, El Mahdy MA. Two-layer-atmospheric blocking in a medium with high nonlinearity and lateral dispersion. Results Phys. (2018) 8:1054–60. doi: 10.1016/j.rinp.2018.01.040

CrossRef Full Text | Google Scholar

2. Tariq KU, Younis M, Rezazadeh H, Rizvi STR, Osman MS. Optical solitons with quadratic-cubic nonlinearity and fractional temporal evolution. Mod Phys Lett B. (2018) 32:1850317. doi: 10.1142/S0217984918503177

CrossRef Full Text | Google Scholar

3. Osman MS, Ghanbari B, Machado JAT. New complex waves in nonlinear optics based on the complex Ginzburg-Landau equation with Kerr law nonlinearity. Eur Phys J Plus. (2019) 134:20. doi: 10.1140/epjp/i2019-12442-4

CrossRef Full Text | Google Scholar

4. Liu Y, Wen XY, Wang DS. Novel interaction phenomena of localized waves in the generalized (3+ 1)-dimensional KP equation. Comp Math Appl. (2019) 78:1–19. doi: 10.1016/j.camwa.2019.03.005

CrossRef Full Text | Google Scholar

5. Wang DS, Guo B, Wang X. Long-time asymptotics of the focusing Kundu-Eckhaus equation with nonzero boundary conditions. J Diff Equat. (2019) 266:5209–53. doi: 10.1016/j.jde.2018.10.053

CrossRef Full Text | Google Scholar

6. Manafian J. Novel solitary wave solutions for the (3+ 1)-dimensional extended Jimbo-Miwa equations. Comput Math Appl. (2018) 76:1246–60. doi: 10.1016/j.camwa.2018.06.018

CrossRef Full Text | Google Scholar

7. Ismael HF, Ali KK. MHD casson flow over an unsteady stretching sheet. Adv Appl Fluid Mech. (2017) 20:533–41. doi: 10.17654/FM020040533

CrossRef Full Text | Google Scholar

8. Wei G, Ismael HF, Husien AM, Bulut H, Baskonus HM. Optical soliton solutions of the cubic-quartic nonlinear schrödinger and resonant nonlinear schrödinger equation with the parabolic law. Appl Sci. (2020) 10:219. doi: 10.3390/app10010219

CrossRef Full Text | Google Scholar

9. Ali KK, Yilmazer R, Bulut H. Analytical solutions to the coupled Boussinesq-Burgers equations via sine-Gordon expansion method. In: Dutta H, Hammouch Z, Bulut H, Baskonus H, editors. 4th International Conference on Computational Mathematics and Engineering Sciences (CMES-2019). CMES 2019. Advances in Intelligent Systems and Computing, Vol. 1111. Cham: Springer (2020). p. 233–40.

10. Abdulkareem HH, Ismael HF, Panakhov ES, Bulut H. Some novel solutions of the coupled Whitham-Broer-Kaup equations. In: Dutta H, Hammouch Z, Bulut H, Baskonus H, editors. 4th International Conference on Computational Mathematics and Engineering Sciences (CMES-2019). CMES 2019. Advances in Intelligent Systems and Computing, Vol. 1111. Cham: Springer (2020). p. 200–8.

Google Scholar

11. Ismael HF, Bulut H. On the Solitary Wave Solutions to the (2+1)-Dimensional Davey-Stewartson Equations. In: Dutta H, Hammouch Z, Bulut H, Baskonus H, editors. 4th International Conference on Computational Mathematics and Engineering Sciences (CMES-2019). CMES 2019. Advances in Intelligent Systems and Computing, Vol. 1111. Cham: Springer (2020). p. 156–65.

Google Scholar

12. Ismael HF, Arifin NM. Flow and heat transfer in a maxwell liquid sheet over a stretching surface with thermal radiation and viscous dissipation. JP J Heat Mass Transf. (2018) 15:847–66. doi: 10.17654/HM015040847

CrossRef Full Text

13. Ali KK, Varol A. Weissenberg and Williamson MHD flow over a stretching surface with thermal radiation and chemical reaction. JP J Heat Mass Transf. (2019) 18:57–71. doi: 10.17654/HM018010057

CrossRef Full Text | Google Scholar

14. Osman MS, Ghanbari B. New optical solitary wave solutions of Fokas-Lenells equation in presence of perturbation terms by a novel approach. Optik. (2018) 175:328–33. doi: 10.1016/j.ijleo.2018.08.007

CrossRef Full Text | Google Scholar

15. Ghanbari B, Osman MS, Baleanu D. Generalized exponential rational function method for extended Zakharov-Kuzetsov equation with conformable derivative. Mod Phys Lett A. (2019) 34:1950155. doi: 10.1142/S0217732319501554

CrossRef Full Text | Google Scholar

16. Ghanbari B, Baleanu D. A novel technique to construct exact solutions for nonlinear partial differential equations. Eur Phys J Plus. (2019) 134:506. doi: 10.1140/epjp/i2019-13037-9

CrossRef Full Text | Google Scholar

17. Ghanbari B, Nauman R. An analytical method for soliton solutions of perturbed Schrödinger's equation with quadratic-cubic nonlinearity. Mod Phys Lett B. (2019) 33:1950018. doi: 10.1142/S0217984919500180

CrossRef Full Text | Google Scholar

18. Ghanbari B. Abundant soliton solutions for the Hirota-Maccari equation via the generalized exponential rational function method. Mod Phys Lett B. (2019) 33:1950106. doi: 10.1142/S0217984919501069

CrossRef Full Text | Google Scholar

19. Wei G, Ismael HF, Mohammed SA, Baskonus HM, Bulut H. Complex and real optical soliton properties of the paraxial non-linear Schrödinger equation in Kerr media with M-fractional. Front Phys. (2019) 7:197. doi: 10.3389/fphy.2019.00197

CrossRef Full Text | Google Scholar

20. Wei G, Ismael HF, Bulut H, Baskonus HM. Instability modulation for the (2+ 1)-dimension paraxial wave equation and its new optical soliton solutions in Kerr media. Phys Script. (2020) 95:035207. doi: 10.1088/1402-4896/ab4a50

CrossRef Full Text | Google Scholar

21. Goswami A, Singh J, Kumar D. An efficient analytical approach for fractional equal width equations describing hydro-magnetic waves in cold plasma. Phys A. (2019) 524:563–75. doi: 10.1016/j.physa.2019.04.058

CrossRef Full Text | Google Scholar

22. Goswami A, Singh J, Kumar D. Numerical simulation of fifth order KdV equations occurring in magneto-acoustic waves. Ain Shams Eng J. (2018) 9:2265–73. doi: 10.1016/j.asej.2017.03.004

CrossRef Full Text | Google Scholar

23. Kumar D, Singh J, Purohit SD, Swroop R. A hybrid analytical algorithm for nonlinear fractional wave-like equations. Math Model Nat Phenomena. (2019) 14:304. doi: 10.1051/mmnp/2018063

CrossRef Full Text | Google Scholar

24. Bhatter S, Mathur A, Kumar D, Singh J. A new analysis of fractional Drinfeld-Sokolov-Wilson model with exponential memory. Phys A. (2020) 537:122578. doi: 10.1016/j.physa.2019.122578

CrossRef Full Text | Google Scholar

25. Gilson C, Pickering A. Factorization and Painlevé analysis of a class of nonlinear third-order partial differential equations. J Phys A Math Gen. (1995) 28:2871. doi: 10.1088/0305-4470/28/10/017

CrossRef Full Text | Google Scholar

26. Ebadi G, Kara AH, Petkovic MD, Biswas A. Soliton solutions and conservation laws of the Gilson-Pickering equation. Waves Random Comp Media. (2011) 21:378–85. doi: 10.1080/17455030.2011.569036

CrossRef Full Text | Google Scholar

27. Ismail A. Exact and explicit solutions to nonlinear evolution equations using the division theorem. Appl Math Comput. (2011) 217:8134–9. doi: 10.1016/j.amc.2011.02.098

CrossRef Full Text | Google Scholar

28. Fan X, Yang S, Zhao D. Travelling wave solutions for the Gilson-Pickering equation by using the simplified G/G-expansion method. Int J Nonlin Sci. (2009) 8:368–73.

Google Scholar

29. Baskonus HM. Complex soliton solutions to the Gilson-Pickering model. Axioms. (2019) 8:18. doi: 10.3390/axioms8010018

CrossRef Full Text | Google Scholar

30. Zabihi F, Saffarian M. A not-a-knot meshless method with radial basis functions for numerical solutions of Gilson-Pickering equation. Eng Comput. (2018) 34:37–44. doi: 10.1007/s00366-017-0519-9

CrossRef Full Text | Google Scholar

31. Singla K, Gupta RK. Space-time fractional nonlinear partial differential equations: symmetry analysis and conservation laws. Nonlin Dyn. (2017) 89:321–31. doi: 10.1007/s11071-017-3456-7

CrossRef Full Text | Google Scholar

32. Camsssa R, Holm DD, Hyman JM. An integrable shallow water equation with peaked solitons. Phys Rev Lett. (1993) 71:1661–4. doi: 10.1103/PhysRevLett.71.1661

PubMed Abstract | CrossRef Full Text

33. Fuchssteiner B, Fokas AS. Symplectic structure, their biicklund transformations and hereditary symmetries. Physica. (1981) 4:47–66. doi: 10.1016/0167-2789(81)90004-X

CrossRef Full Text | Google Scholar

34. Rosenau P, Hyman J. Compactons: solitons with finite wavelength. Phys Rev Lett. (1993) 93:564–7. doi: 10.1103/PhysRevLett.70.564

CrossRef Full Text | Google Scholar

35. Fornberg B, Whitham G. A numerical and theoretical study of certain nonlinear wave phenomena. Philos Trans R Soc Lond A. (1978) 289:373–404. doi: 10.1098/rsta.1978.0064

CrossRef Full Text | Google Scholar

36. Whitham G. Variational methods and applications to water waves. Proc R Soc Lond A. (1967) 299:6–25. doi: 10.1098/rspa.1967.0119

CrossRef Full Text | Google Scholar

37. Whitham G. Linear and Nonlinear Waves. New York, NY: Wiley (1974).

Google Scholar

38. Yokus A, Doǧan K. Conservation laws and a new expansion method for sixth order Boussinesq equation. In: AIP Conference Proceedings, Vol. 1676. Antalya: AIP Publishing (2015). p. 020062. doi: 10.1063/1.4930488

CrossRef Full Text | Google Scholar

39. Yokus A. An expansion method for finding traveling wave solutions to nonlinear PDEs. Istanbul Ticaret Üniversitesi Fen Bilimleri Dergisi. (2015) 14:65–81.

Google Scholar