- 1Department of Biomedical Engineering, Boston University, Boston, MA, United States
- 2Department of Cognitive Neuroscience, Faculty of Psychology and Neuroscience, Maastricht University, Maastricht, Netherlands
- 3Medical School, University of Nicosia, Nicosia, Cyprus
- 4Center of Neuroscience and Integrative Brain Research (CENIBRE), University of Nicosia, Nicosia, Cyprus
Brain oscillations emerge during sensory and cognitive processes and have been classified into different frequency bands. Yet, even within the same frequency band and between nearby brain locations, the exact frequencies of brain oscillations can differ. These frequency differences (detuning) have been largely ignored and play little role in current functional theories of brain oscillations. This contrasts with the crucial role that detuning plays in synchronization theory, as originally derived in physical systems. Here, we propose that detuning is equally important to understand synchronization in biological systems. Detuning is a critical control parameter in synchronization, which is not only important in shaping phase-locking, but also in establishing preferred phase relations between oscillators. We review recent evidence that frequency differences between brain locations are ubiquitous and essential in shaping temporal neural coordination. With the rise of powerful experimental techniques to probe brain oscillations, the contributions of exact frequency and detuning across neural circuits will become increasingly clear and will play a key part in developing a new understanding of the role of oscillations in brain function.
Main Text
In the mammalian brain, oscillations and synchronization have been found ubiquitously at the level of single neurons, local neural circuits and brain-wide networks, from deep brain nuclei to neocortex and across a variety of species (Buzsáki et al., 2013). The association of oscillatory synchronization with sensory-motor and cognitive processes during sleeping and waking has been well documented. Further, various symptoms are associated with abnormal patterns of synchronization in psychiatric and neurological conditions including epilepsy (da Silva et al., 2003), Parkinson’s disease (Little and Brown, 2014; McGregor and Nelson, 2019) and schizophrenia (Haig et al., 2000; Herrmann and Demiralp, 2005). Unraveling the functions of neuronal oscillatory synchronization has thus been one of the prime objectives of systems neuroscience.
It is common to classify rhythms into broad frequency bands including the delta (2–4 Hz), theta (4–8 Hz), alpha (8–12 Hz), beta (14–25 Hz), and gamma (30–100 Hz) bands. This broad frequency classification has been fruitful in correlating amplitude modulations within specific frequency bands with specific brain regions and/or specific task variables. However, this classification has not enabled a mechanistic interpretation of the range of oscillation frequencies contained within these broad frequency bands, thereby preventing a full understanding of the neural networks that generate the oscillations. Here, we summarize accumulating experimental evidence showing that oscillations within the same broad frequency band may express systematically different frequencies across brain regions and that precise oscillation frequencies are systematically modulated as a function of sensory, motor and cognitive variables. Referring to concepts from synchronization theory (Kopell and Ermentrout, 2002; Pikovsky et al., 2002; Izhikevich, 2007), we then discuss the significance of such systematic tuning of the oscillation frequency for understanding rhythmic coordination and communication in the brain.
The Preferred Oscillation Frequency Is Diverse Across and Within Brain Regions
Although frequency bands have to some extent become associated with specific regions and functions (e.g., gamma with visual processes in low to intermediate visual cortex, and theta with memory processes in hippocampus and frontal lobe), activity in each frequency band can be found in large networks throughout the brain (see Table 1). For example, gamma-band rhythms during visual processing can be found over various visual, parietal and frontal cortical areas (Fries, 2009; Gregoriou et al., 2009; Bastos et al., 2014) as well as subcortical areas (Colgin et al., 2009; Wulff et al., 2009). Another example are theta rhythms which can be co-expressed in different subcortical structures like the hippocampus as well as in cortical regions (Lakatos et al., 2005). These rhythms not only co-occur under similar experimental conditions, but they exhibit marked temporal coordination both within and across brain areas, which changes as a function of sensory stimulus properties, cognition states and animal behavior (Fries, 2005, 2015).
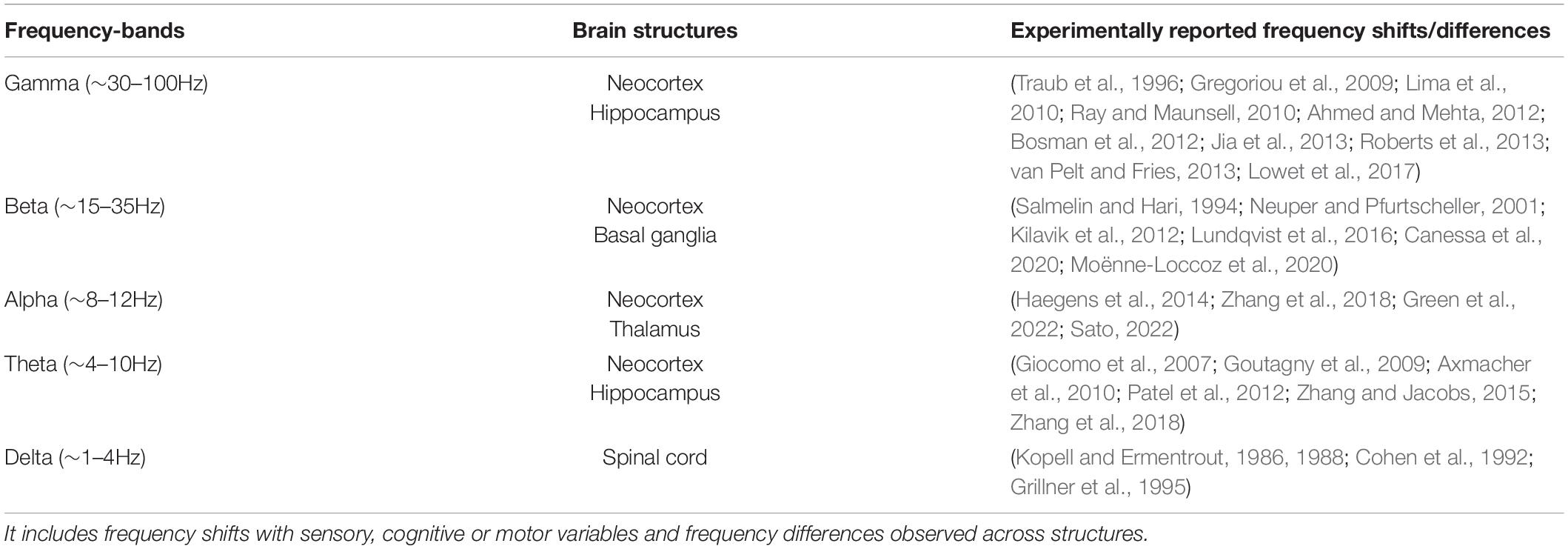
Table 1. A - not exhaustive – overview of observed frequency shifts and differences (detuning) for classically defined frequency bands (delta, theta, alpha, beta, gamma) in the central nervous system.
Intuitively, if oscillatory cycles in one brain region are to coordinate with cycles of another brain region, one assumes that they must share a common frequency. Consistent with this prevalent assumption is the wide use of (spectral) coherence to quantify interactions (Lowet et al., 2016). Coherence however, assumes stationarity of the underlying oscillations (for instance a stable frequency) and linearity of the relationship between them. Any cross-frequency interactions, even across very small frequency differences, are therefore not accounted for in measures of coherence. However, experimental observations showing that neural rhythms across and within brain regions often have somewhat different frequencies show that the stationarity and linearity assumptions required for the calculation of coherence are often violated. For example, small but systematic differences in visual cortical gamma-band rhythms are well documented in the primate visual system. Using a high-density ECoG grid spanning various visual cortical areas in the macaque monkey, Bosman et al. (2012) reported that the preferred gamma frequency was systematically higher (by a few Hz) in V1 than in V4. Different gamma-band frequencies have been also reported between V1 and V2 (Lowet et al., 2018).
Beyond the small differences in gamma frequencies across cortical areas, small differences in preferred frequency can also occur locally within the same cortical area. A gamma-band frequency gradient as a function of eccentricity (fovea to periphery) in V1 has been established (Lima et al., 2010; van Pelt and Fries, 2013; Lowet et al., 2017). In addition, Zhang, (Zhang et al., 2018) has recently observed systematic theta and alpha waves traveling over cortex as recorded by a high-density ECoG array. They found that the direction of the traveling waves was systematically related to frequency gradients over cortical space. Similarly, theta rhythmic resonance in the rodent hippocampal-entorhinal system has also been shown to exhibit specific frequency changes over space (Giocomo et al., 2007; Shay et al., 2012). These different frequency gradients have been hypothesized to be the main cause of observed theta traveling waves occurring across the hippocampus (Zhang and Jacobs, 2015), which has received further experimental support from in vitro recordings (Goutagny et al., 2009).
The Precise Frequency Changes With Sensory and Cognitive Variables
Here, we will provide evidence that oscillation frequency not only differs as a function of anatomical location, but also depends systematically on the animal’s sensation, cognition and behavior (see Table 1).
Gamma-band synchronization is a prime example of oscillations exhibiting marked variability in oscillation frequency, due to a high sensitivity to sensory and cognitive conditions. Various computational studies have shown that the frequency control of the pyramidal-interneuron gamma (PING) mechanism is highly sensitive to the excitation level of excitatory and inhibitory neurons within the PING circuit (Brunel and Wang, 2003; Tiesinga and Sejnowski, 2009; Zachariou et al., 2015), in line with experimental observations showing that increases in gamma frequency are accompanied by increases in firing rate (Ray and Maunsell, 2010; Jia et al., 2013; Roberts et al., 2013). Hence, sensory, cognitive and motor parameters that change the excitability-inhibition balance (Brunel and Wang, 2003; Buzsáki and Wang, 2012) of coordinating neurons will likely also change the oscillation gamma frequency. The dependence of the oscillation frequency on network state is thus expected to be a general property of brain rhythms (Brunel and Wang, 2003; Wang, 2010).
The relation between gamma-band frequency and sensory variables has been increasingly studied over the last decade in primate and human early visual cortex. Gamma-band frequency decreases with increasing stimulus size (Gieselmann and Thiele, 2008; Ray and Maunsell, 2010; Veit et al., 2017), which has been linked to increased recruitment of horizontal inhibition. Striking increases in gamma frequency in V1 as well as V2 have been observed with visual stimulus contrast (Figure 1) with reported shifts of about ∼20 Hz in monkey V1 and ∼10 Hz in human V1 (Roberts et al., 2013; Hadjipapas et al., 2015). Gamma frequency is also modulated as a function of moving speed (Friedman-Hill et al., 2000; Swettenham et al., 2009; Jia et al., 2013), motion direction (Feng et al., 2010), color (Peter et al., 2019) and stimulus complexity (Brunet et al., 2013; Hermes et al., 2015). Importantly, not only is the frequency shift dependent on global stimulus properties, but neuronal groups in nearby locations within area V1 or V2 may express different frequencies depending on the precise stimulus properties in these neural groups’ receptive fields (Gieselmann and Thiele, 2008; Ray and Maunsell, 2010; Lowet et al., 2017, 2018). This indicates that the generative mechanisms of gamma are highly localized. For example, local image contrast can induce distinct gamma frequencies in visual cortical locations with adjacent receptive fields (Ray and Maunsell, 2010; Lowet et al., 2017). In line with these findings, optogenetically increasing the excitability of pyramidal neurons in cat V1 (Area 17) leads to an increase in the gamma frequency (Ni et al., 2016; Lewis et al., 2021). These findings suggest a generic mechanism of how excitatory drive changes the gamma frequency; confirming prior biophysical modeling studies (Traub et al., 1996; Tiesinga and Sejnowski, 2009, 2010).

Figure 1. Gamma frequency shifts in macaque V1 as a function of the basic visual input parameter contrast (single electrode contact example from data published in Roberts et al., 2013 & Hadjipapas et al., 2015). Gamma peak frequency shifts to higher frequencies with visual contrast. The monkey maintained fixation while stimuli were presented away from fixation for > 1 s. Zero on the X-axis represents the presentation onset of the grating stimulus, which remained in the neuronal RFs for the remainder of the trial.
Recent studies have shown that cognitive processes also systematically influence the frequency of rhythms. Visual spatial attention (Bosman et al., 2012) has been observed to shift the V1 gamma band to higher frequencies when the monkey attended the stimulus overlaying the corresponding receptive field, whereas simultaneously recorded unattended V1 locations had a lower frequency. Similar frequency shifts by spatial attention have also been observed in V4 and FEF (Gregoriou et al., 2009). Gamma peak frequency in human MEG has been found to also be predictive of performance in an orientation discrimination task across individuals (Edden et al., 2009). The dependence of the precise oscillation frequency on behavior has also been reported for other frequency bands. For example, the systematic increase of hippocampal theta frequency with locomotion speed (McFarland et al., 1975; Bender et al., 2015; Goyal et al., 2020) has been well documented. Further, the capacity of working memory has been directly linked to the frequency of theta rhythms. Axmacher et al. (2010) showed that subjects with higher working memory load displayed a decrease in their hippocampal theta frequency, in line with a model in which longer theta cycles permit representations of more items (Axmacher et al., 2010). Consistent with this, artificially reducing the theta frequency over parietal cortex using transcranial magnetic stimulation increased the working memory capacity (Wolinski et al., 2018). Another study showed that alpha peak frequency predicts working memory capacity across age span (Clark et al., 2004). These and other studies demonstrate that oscillation frequency is a variable parameter that interacts with basic neural network properties to represent changes in perception and cognition.
The mechanism of frequency regulation, although not largely understood, is likely to depend on the oscillation generation mechanisms, which involve intracellular properties (i.e., bursting) of various cell types, network properties (i.e., synaptic strengths and time constants, the nature of input to the network) as well as involving different neuron transmitters and neuromodulators (i.e., acetylcholine). The generation mechanisms of gamma oscillations have been studied extensively over the last decades using excitatory-inhibitory networks models (PING or ING models), which can reproduce many features of experimentally observed gamma oscillations including shifts of the gamma frequency and the gamma oscillation amplitude (Brunel and Wang, 2003; Tiesinga and Sejnowski, 2010; Roberts et al., 2013; Lowet et al., 2015). In primate visual cortex, increasing visual contrast, a proxy of feedforward excitatory drive (Sclar et al., 1990), is known to increase the frequency of gamma oscillations (Ray and Maunsell, 2010; Jia et al., 2013; Roberts et al., 2013; Hadjipapas et al., 2015; Self et al., 2016). This can be captured well in PING networks, in which excitatory units receives increasing amount of excitatory drive (Traub et al., 1996; Tiesinga and Sejnowski, 2009; Roberts et al., 2013; Lowet et al., 2015; Zachariou et al., 2021). However, the precise change in the frequency depends also on the drive to inhibitory neurons and other network parameters, which often remain unknown (Zachariou et al., 2021). It has also been observed that visual attention can increase the frequency of visual cortical gamma oscillations (Bosman et al., 2012). While this might result from a change in excitatory drive to pyramidal and inhibitory neurons, similar to what occurs for increased contrast, it is likely that the biophysical mechanisms differ. For example, top-down or feedback axonal projections might target different parts of the dendritic tree thus engaging different intracellular dynamics, and might preferentially activate different interneurons and act on different spatial and temporal scales. Further, the role of neuromodulators like acetylcholine might play an important role in behavioral state-dependent changes in oscillation properties, as shown for example in the role of cholinergic modulation of hippocampal theta frequency (Heys et al., 2010; Newman et al., 2013). In addition, it is of note is that differences in the neural mechanisms underlying frequency change can lead to different network effects, which can have implications for the functional significance of the frequency change. For example, enhanced activity of feedback inhibition might reduce the oscillation frequency but increase synchronization (oscillation amplitude) in PING networks. In contrast, while reducing excitatory drive to pyramidal neurons also reduces oscillation frequency, it decreases synchronization.
In summary, various sensory and cognitive factors appear to modulate detuning and may do so by one or most likely several potential mechanisms. One cannot safely conclude from an observed change in detuning which of the potential underlying mechanisms is operating without additional information about the network. Therefore, although experimental manipulations of detuning offer an important route toward understanding the neuronal effect of the manipulation, this understanding requires information about network properties and an assessment of network effects.
Frequency Is Critical for Spatial Synchronization and Phase Relations in Oscillator Networks
Synchronization is often conceptualized as the maintenance of a stable (or at least bounded) phase difference (relation) between two oscillators (Pikovsky et al., 2002). It is intuitive that, in the absence of noise, a pair of frequency-stable oscillations can have a stable phase-relation if their frequencies match. For this to happen, no interaction per se is needed since in the absence of noise the phase-relation will remain constant over time. Alternatively, if a pair of oscillators do not interact and they have a frequency difference, their phase-relation will change continuously with a rate determined by their frequency difference (detuning), a phenomenon termed phase precession. Synchronization as a process, as formulized in the framework of weakly coupled oscillators (Kopell and Ermentrout, 1986, 2002; Strogatz and Stewart, 1993; Izhikevich, 2007), only comes into play when oscillations of different and variable frequencies (detuned oscillators) in different neural groups (oscillators) coordinate around a preferred phase-relation in order to enable neural communication. To achieve this, the phase precession due to the detuning needs to be counteracted through interaction (coupling), which is defined by the so called phase response curve [PRC, for review (Schwemmer and Lewis, 2012)]. Oscillatory interactions lead to phase advances or delays (described by the PRC), which translate to systematic changes of the oscillators’ frequencies that ultimately reduces phase precession. Synchronization will make a slower oscillator speed up when entrained by a faster oscillator and vs. Hence, synchronization essentially involves continuous phase adjustments (deceleration or acceleration) in order to counter-act detuning and thereby balances the oscillations around a preferred phase-relation. This short overview of synchronization highlights that synchronization is a highly non-stationary and non-linear process (Kopell and Ermentrout, 2002; Pikovsky et al., 2002; Izhikevich, 2007) and that frequency detuning has a key role in the process.
Oscillation Frequencies: Natural Frequency and Detuning
In simple physical systems, such as a pendulum, the preferred frequency of an object to oscillate or resonate can be a relative stable property. For example, the pendulum has a characteristic frequency that depends on fixed factors, such as the length of the suspension rope. As we have discussed above, the frequency of neural oscillations can differ between brain areas and can be variable over time depending on sensory, cognitive and motor variables that modulate the underlying neural oscillation generation mechanism.
The frequency of an un-perturbed neural oscillator is called its natural (eigen-, initial or intrinsic) frequency. In practice an oscillator’s natural frequency and its detuning with respect to other oscillators is difficult to measure in a neuroscientific context because the ‘oscillators’ in the living, behaving animal brain are always coupled. In order to observe the natural/intrinsic frequency of an oscillator, it must be decoupled and unperturbed. Here we use two examples to illustrate this. The first illustration pertains to studies of the circadian rhythm: It was observed that the circadian rhythm follows its natural frequency when subjects were decoupled from the day-night rhythm (Strogatz and Stewart, 1993). Thus, without the extrinsic influence of the days turning to nights on a 24-h cycle participants’ sleep/wake and other circadian rhythms were revealed to have an intrinsic frequency of around 25 h. The second example (Figure 2) was reported by Goutagny et al. (2009) in a natural in vitro hippocampal CA1 preparation. Theta rhythms in CA1 between septal and temporal regions were synchronized with nearly matching frequencies. Yet, when an intermediate region between the two recording sites was lesioned, thereby disrupting connectivity, the two CA1 regions started to oscillate at distinct preferred frequencies. Thus, while the observed/expressed frequencies in the original preparation were matched, the natural frequencies were not. The matched frequencies were the result of synchronization taking place.
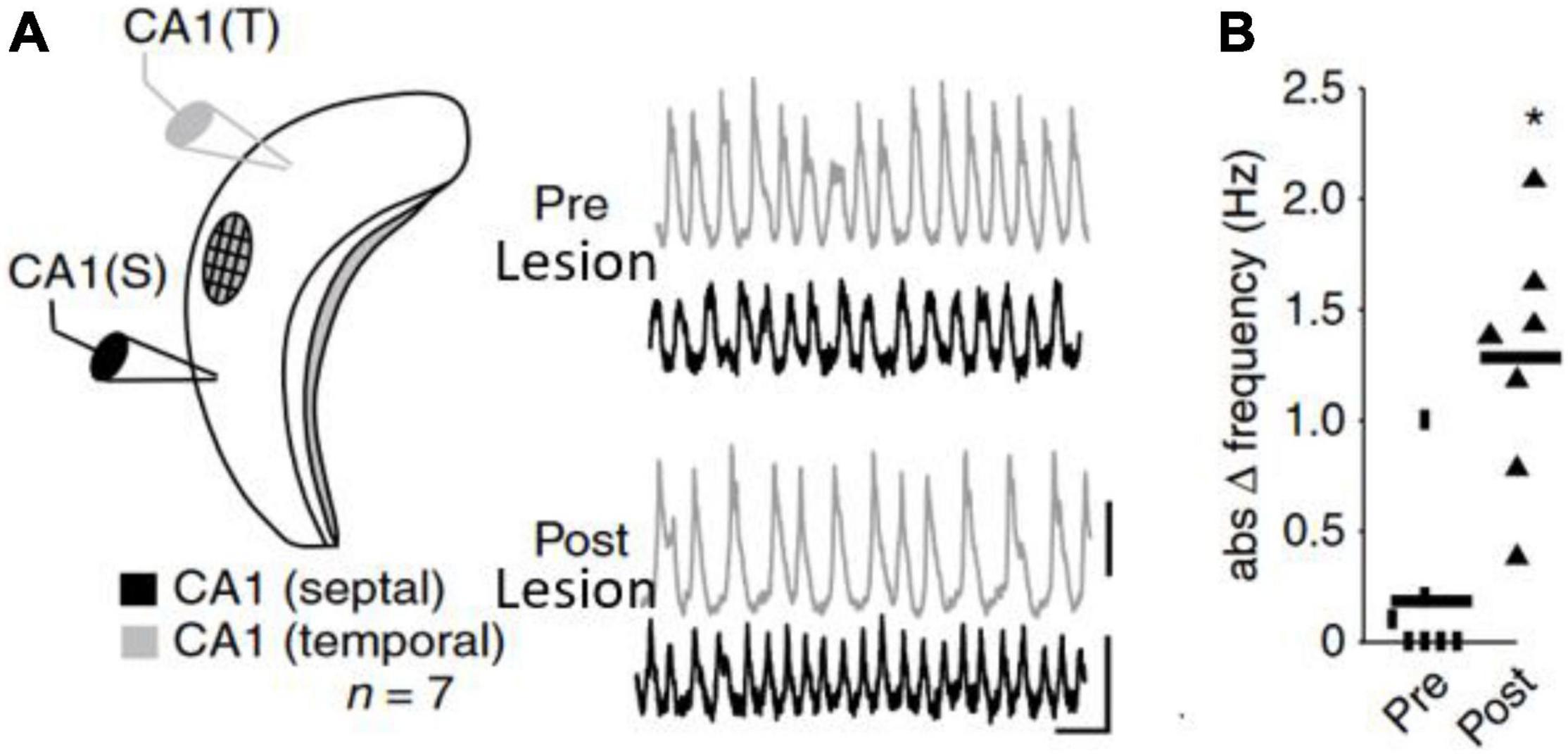
Figure 2. (A,B) In vitro recording from mouse CA1 from Goutagny et al. (2009). (A) Two electrodes in septal and temporal part of CA1 recorded the LFP characterized by theta rhythms. The septal and temporal theta rhythms are synchronized. After lesioning the CA1 in between septal and temporal pole of CA1, the theta rhythms became independent and (B) started to oscillate at different frequencies revealing the underlying frequency difference (detuning). Figures adapted from Goutagny et al. (2009).
As shown above, the natural frequency of brain oscillations and hence detuning can change systematically due to sensory, motor and cognitive variables at short time scales. In noiseless oscillatory systems, detuning is the main obstacle that synchronization has to overcome to achieve phase coordination. However, in biological systems there are additional obstacles as oscillations are commonly highly variable over time and noisy. Apparent random frequency variability is often called phase noise and it limits the ability of oscillators to remain stable at their preferred phase relation. Notably, frequency variability over time can reflect in part the expected features of interacting oscillators, and this aspect of frequency variability is a feature of synchronization, rather than an obstacle. However, phase noise (and hence frequency variability) in addition of randomness may also include other unaccounted systematic (deterministic) complexities like inherent short-term instability of oscillation generation mechanism (e.g., chaotic rhythms) or complexities of the underlying network (due to cross-frequency coupling, or other interactions among multiple rhythms).
The Arnold Tongue(s): The Structure of Synchronization
In an uncoupled system, frequency differences between two oscillators lead to phase precession. Larger frequency differences (detuning) produce faster phase precession. However, in a dynamic system of coupled oscillators, synchronization counteracts phase precession. Synchronization requires moment-to-moment changes of the oscillation frequency. This change of frequency over time is what, from a dynamic perspective, is called interaction. The stronger a pair of oscillators interact, the stronger the frequency modulation becomes, which in turn corresponds to phase advances or delays. This fundamental interplay between the amount of detuning and the amount of interaction is what is reflected in the so-called Arnold tongue (Figure 3). The Arnold tongue describes the regions of synchronization characterized by high phase coordination (phase-locking) in the 2-dimensional space of detuning (drives phase precession) and coupling strength (drives interaction). The region looks like an inverted triangle (hence the term ‘tongue’). For the purpose of this review, we will only consider the synchronization region of 1:1 phase-locking and ignore higher order phase-locking regimes [1:2, 1:3,…, (Pikovsky et al., 2002)].
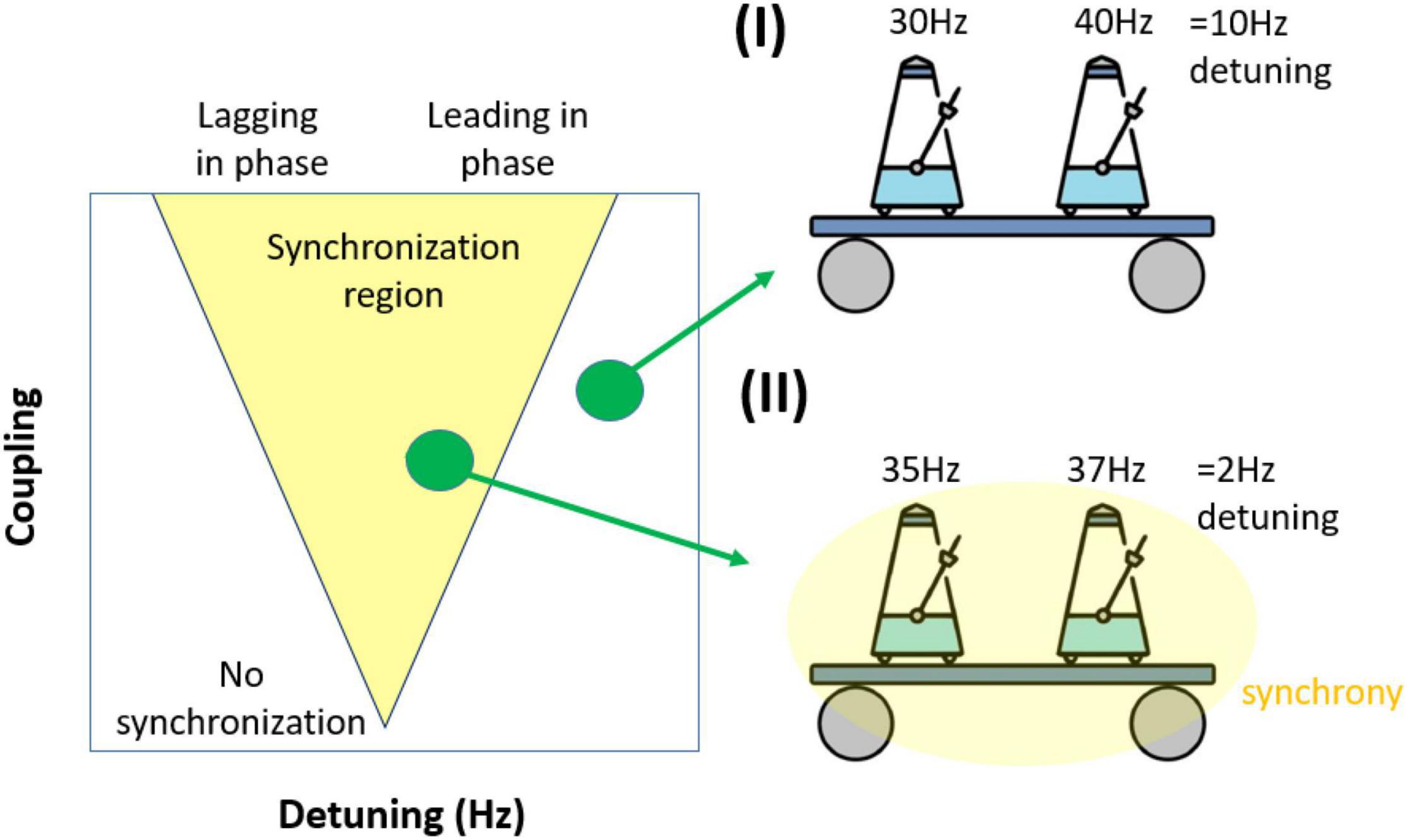
Figure 3. Illustration of how frequency differences (detuning) impact synchronization. (I) Coupled oscillators (metronomes) are not synchronized due to large differences in their preferred frequency. (II) Coupled oscillators are synchronized as they can overcome their smaller frequency difference (detuning). The simplified synchronization region mapped as a function of frequency difference (detuning) and coupling. The triangular synchronization region is called the Arnold tongue. Notably, although the synchronization region will generally be triangular, it will not necessarily be symmetrical, depending on the underlying dynamical system, the connectivity pattern and time delays.
The inverted triangular shape of the Arnold Tongue (Figure 3) shows that to achieve synchronization, the increased phase precession at higher levels of detuning needs to be counter-balanced by increasing coupling. An understanding of how these two forces compete to form the Arnold tongue leads to two important insights. First, if interaction is strong enough to fully counterbalance the detuning, the resultant oscillations frequencies will match. In turn this means that experimentally-measured matched frequencies across brain regions does not necessarily mean that these rhythms also had matching natural frequencies, as was demonstrated by Goutagny et al. (2009) in the in vitro hippocampus recordings (see Figure 2). Second, if interaction is strong enough to counterbalance the detuning, the detuning is converted into a phase difference. Usually, the oscillation with the higher natural frequency will lead the oscillation with the lower natural frequency. These phase differences can emerge without any time-delay in the interaction. Hence, an experimentally measured phase difference can emerge due to synchronization and does not necessarily imply a time-delay in the underlying connectivity. In practice, time delay and detuning will contribute to the observed phase difference in rhythmic neural interactions.
It is important to emphasize that the strongest phase-locking does not necessarily occur at zero detuning, but depends on how the interaction influences the rhythms’ frequencies. The interaction is defined by the underlying phase response curves (PRCs). For example, if synaptic input leads to an acceleration of the down-stream neurons, then it is preferable that the up-stream neurons have a higher frequency compared to the down-stream neurons (Arnold tongue is one-sided). Alternatively, if interaction only leads to deceleration (e.g., inhibition delaying spiking), then the up-stream neurons should have a slower frequency compared to the down-stream neurons. When the interaction has both accelerating and decelerating components (also known as type II PRC compared to type I PRC, [Ermentrout, 1996; Ko and Ermentrout, 2009; Schwemmer and Lewis, 2012)], the detuning between the oscillators will synchronize with positive or negative. The PRC is not a fixed property for a given neural oscillation, but it can change with changes in the underlying intracellular or network properties. A prime example is the well-documented change from mono-phasic type I PRC (either negative or positive) to bi-phasic type II PRC (positive and negative) with cholinergic tone (Stiefel et al., 2008, 2009), which will have dramatic effects on the shape of the Arnold tongue.
According to the theory of weakly coupled oscillators, the amount of detuning that will modulate phase-locking and shift the preferred phase relation depends on the PRC of the oscillations and the coupling strengths between the oscillations. Notably, the amount of detuning that will modulate phase-locking and shift the preferred phase relation does not depend necessarily on the frequency-band of the oscillation; for example, the effect of 1 Hz detuning might be similar whether the oscillation is in the theta range (4–10 Hz) or in the gamma range (30–100 Hz). However, little is known at present about how the PRCs and coupling strength differ between the different brain oscillation bands. Further, it remains unclear whether the amount of frequency variability and phase noise might differ depending on the time scale of brain oscillations.
In spite of the important insights that can be garnered from direct experimental mappings of the Arnold tongue in neural rhythms, studies that do so are still scarce. Yet, two recent studies have been able to map the Arnold tongues experimentally. Notbohm et al. (2016) used flickering visual stimuli at different frequencies and intensities while measuring alpha-range (8–12 Hz) evoked responses in humans. They found a synchronization region between the external oscillatory force provided by the visual stimulus flickering frequency and visual cortical alpha with a shape as expected from an Arnold tongue. Lowet et al. (2017) systematically mapped the synchronization region of simultaneous recorded gamma rhythms from different locations in awake macaque V1 and V2 while changing gamma frequency naturally using local image contrast (Figure 4). An inverted triangular-shaped synchronization region was observed that determined not only the observed phase-locking between gamma-synchronized cortical regions, but also their preferred phase relation.
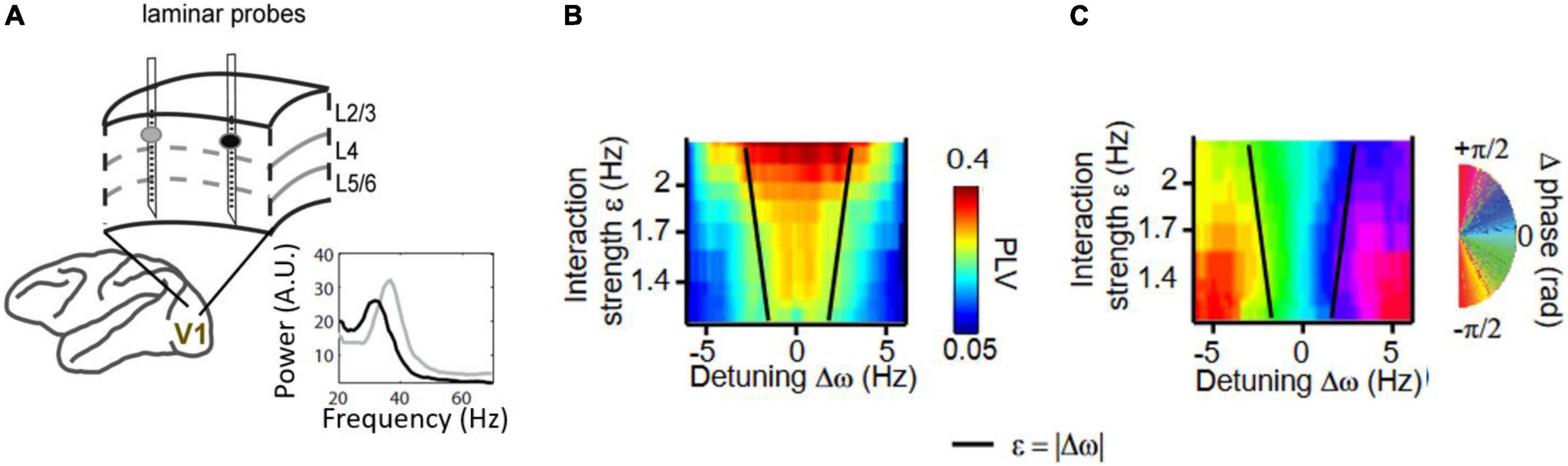
Figure 4. (A) Gamma-band synchronization studied between nearby cortical V1 locations in behaving macaques. Two or three laminar probes to record current source densities (CSD) were inserted in V1 while gratings of spatially variable contrast were shown. Visual contrast is known to modulate the frequency of V1 gamma rhythms. (B) The gamma-band phase-locking value (PLV) was mapped as a function of frequency difference and interaction strength (estimated by cortical distance). The gamma PLV between sites exhibited an Arnold tongue structure. (C) Same as (B) but mapping the preferred phase relation in the gamma range between V1 sites. Preferred phase is defined here as the mean phase difference between two gamma rhythmic V1 signals. Figures adapted from Lowet et al. (2017).
The Neurobiological Functions of Oscillation Frequency Diversity
We have described how frequency diversity of interacting neural rhythms is present across the brain and is modulated by sensation, cognition and behavior. We have also outlined synchronization theory and highlighted that frequency differences among rhythms have important consequences for how they synchronize and what phase-relation they will prefer. In the present section we will discuss more broadly the implications of oscillation frequency shifts for brain function.
Frequency Gradients for Limiting Amount of Neural Synchrony
Flexible regulation and limitation of synchronization in cortical and subcortical brain areas is of critical importance for healthy neural functioning. Abnormal levels of synchronization dynamics of neural activity can have severe negative impact as exemplified for beta rhythms in Parkinson’s disease (Little and Brown, 2014). Frequency diversity in the brain can be viewed as a kind of safety mechanism, which acts to prevent abnormal level of synchronization, and to permit healthy brain function. It is well established that frequency diversity in a network of coupled oscillators (Kuramoto model) reduces global synchronization and shapes clustering (Ermentrout and Kopell, 1984; Chawanya et al., 1993; Strogatz and Stewart, 1993). We have mentioned that there is experimental evidence of systematic frequency gradients in cortical and subcortical areas across different oscillation bands. For example, the preferred gamma frequency decreases as a function of eccentricity (fovea to periphery) in macaque area V1 (Lima et al., 2010). Theta frequency preference in entorhinal cortex and hippocampus show systematic spatial gradients (Shay et al., 2012). In primary sensorimotor cortex the representations of the hand and foot areas exhibit distinct frequencies of beta event related synchronization within the broader beta band (Pfurtscheller et al., 2000; Neuper and Pfurtscheller, 2001). These observations can be seen as supporting the conjecture that slight (but sufficiently large) frequency differences in different network parts are functionally beneficial in the maintenance of related but separate cognitive processes.
Synchronization theory predicts that spatial frequency gradients will limit the extent of neural synchronization, depending on the slope of the frequency gradient and how strongly neurons interact (Figure 5). This is an interplay well represented by the Arnold tongue. Change in frequency preference may be due to differences in intracellular kinetics, different balance of cell types and connectivity properties. While frequency gradients may be implemented through different mechanisms, they might have the same dynamical function: to keep synchronization sufficiently locally and in a healthy regime. For instance, it may be functionally advantageous that when the hand area is activated, that no strong activity is actually propagated through the relatively dense anatomical connections to the foot area. Thus, the limited domain in synchronization serves a representational role by segregating the stimulated area from nearby areas that it is coupled to. Similar considerations apply to the foveal versus peripheral representations in the gamma band mentioned previously. Thus, the targeted absence of synchronization because of large intrinsic frequency differences that cannot be reconciled by the coupling may be utilized functionally.
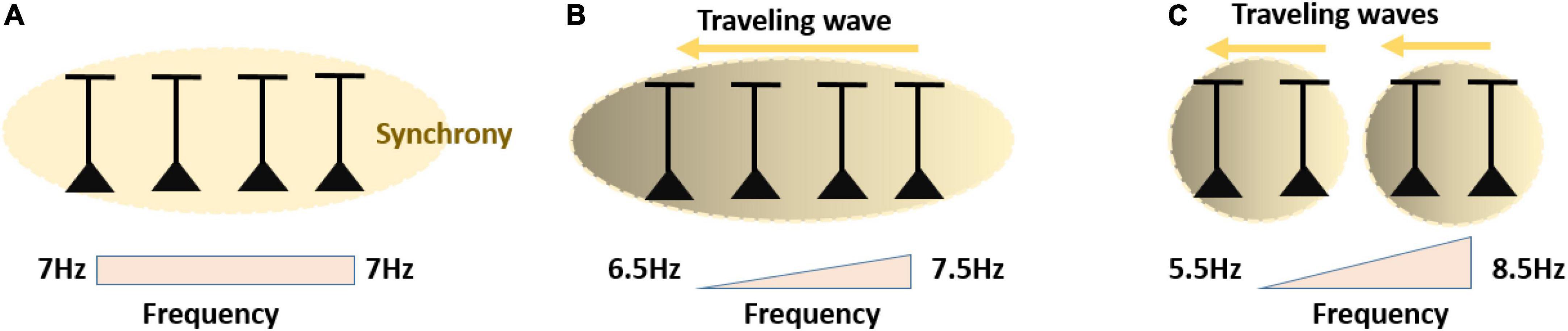
Figure 5. (A) Neurons with matching preferred oscillation frequencies will have a strong tendency to synchronize into one oscillating assembly spiking at same preferred phase. (B) Neurons characterized by a fine frequency gradient will still likely synchronize into one oscillating assembly, yet neurons with slightly higher preferred frequency will spike at an earlier phase. Spatially, this leads to a traveling wave. (C) Neurons characterized by a large frequency gradient, will likely synchronize in distinct sets/clusters of synchronized assemblies oscillating at different frequencies along the gradient. Within the synchronized assemblies, the gradient is converted into phase differences corresponding to local traveling waves.
Frequency Gradients Organize Traveling Waves and Information Flow Within and Across Brain Areas
Synchronization theory predicts that when oscillations synchronize, even if not completely, their initial frequency differences will be converted into a preferred phase relation. For example, in many cases the oscillation with the higher natural frequency will lead in phase. This means that neurons involved in the higher frequency oscillation will fire earlier than neurons involved in the lower frequency oscillation. Applied to a frequency gradient, this results into a traveling wave which spreads down the frequency slope (Ermentrout and Kopell, 1984; Ermentrout and Kleinfeld, 2001). The speed of the traveling waves relates to the slope of the frequency gradient. The existence of traveling waves along human cortex has recently been demonstrated (Zhang et al., 2018). Related work has shown that neural rhythms can be coordinated across different cortical areas in a directed manner. For example, primate cortical gamma rhythmic coordination seems to be organized in a feedforward manner from primary to higher-order visual and associative areas (Bastos et al., 2014). In addition, it has been observed that V1 gamma rhythms have a higher frequency than V4 gamma rhythms (Bosman et al., 2012). This opens the interesting possibility that separate streams of information across cortical hierarchies may be coordinated by specific rhythms with the direction guided by the frequency gradient. Notably, given the fact that hardwired biases in the local frequency can be flexibly influenced by cognitive states or sensory input, a cortical location may switch from follower” to leader” by flipping the frequency gradient. This possibility has been confirmed by Lowet et al. (2017), who showed that a location in V1 displaying a higher gamma frequency due to high-contrast stimulation acted as a leader” compared to a neighboring V1 location displaying a lower frequency due to low-contrast stimulation. More studies are required to test whether by shifting the rhythm’s frequency experimentally, a cortical location can be switched from a follower” to a leader” relative to another cortical area. From a developmental perspective, an inherent frequency gradient from primary to higher-order area might support the development of direct and asymmetric anatomical projections through spike-timing dependent plasticity during maturation (Caporale and Dan, 2008; Lee et al., 2009; Markram et al., 2012).
Flexible Regulation of Synchronization for Sensation and Cognition
The diversity of oscillation frequencies across the brain is not a static property, but is shaped by sensory input, cognition and behavior. Influential theories of how neural synchronization contribute to brain function require that synchronization emerges in a controlled and flexible manner in time and space. Temporal coordination of spike timing has consequences for information coding, signal transmission and plasticity. Whereas neural communication determined by anatomical connectivity is relatively fixed over time, neural synchronization can increase the repertoire of coordination patterns, change flexibly according to behavior and may eventually modify the anatomical connectivity based on experience. This flexibility of synchronization to coordinate neural activity has motivated theories highlighting synchronization as mechanism for sensory segmentation and grouping [Binding by synchrony,” (Singer and Gray, 1995; Eckhorn et al., 2001)] or to selectively route information across cortical areas as needed for visual attention (Fries, 2005, 2009; Akam and Kullmann, 2014).
The appeal of these proposals is that synchronization does not need to follow anatomical connectivity per se, but is able to shape effective” connectivity (Fries, 2009). However, how changes in effective connectivity are implemented in the brain remains largely unknown. From the viewpoint of synchronization theory (and thus the Arnold tongue), there are two main ways: The first is an increase in oscillation amplitude, which ensues from synchronized spikes and would result in a more effective activation of connected down-stream neurons (Fries et al., 2001a). This corresponds to an enhancement of the coupling. Dynamically, an increase in interaction strength means the ability to more strongly modulate the frequency of the receiving rhythm and thereby to influence phase precession. The second way to shape effective connectivity is to modulate the detuning (Figures 6A,B). This facilitates rhythms to reach, maintain or regain their preferred phase relation. Due to the reduced detuning, the rhythms will reach stronger synchronization with the same degree of interaction. Modulation of detuning also has a strong influence on the phase-relation and temporal relationship between rhythms and can set the direction of interaction.
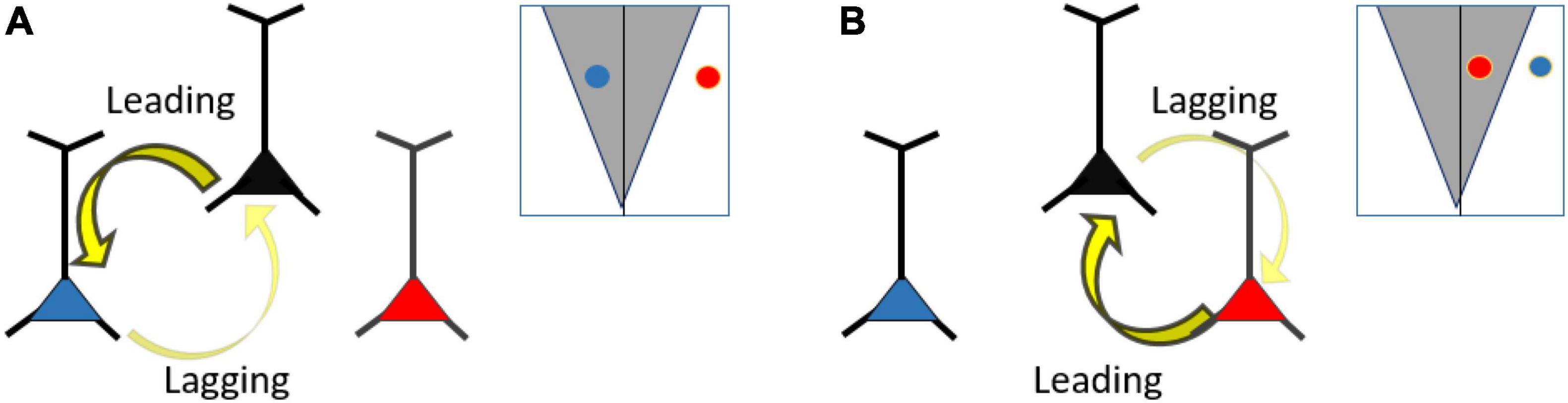
Figure 6. (A) Frequency differences (detuning) regulate information flow. Here, bi-directional connectivity and symmetrical Arnold tongue is assumed. Reducing the detuning between two neurons, such that they fall within the Arnold tongue (the black and blue neuron), will lead to stronger phase entrainment compared to a neuron pair with larger detuning (black and red neuron). The neuron with the higher frequency (black neuron) will lead in phase relative to the slower neuron (blue neuron). (B) Same as (A), but changing the frequency relationship between the blue, black and red neuron. Here, the black and red neurons have a smaller detuning than the black and blue neuron. The red neuron has a higher frequency than the black neuron and thus leading in phase.
Frequency detuning has several key advantages as a mechanism to define effective communication compared to changes in coupling. First, it is a potent mechanism to modulate synchronization. A shift of just a few Hz can make rhythms strongly coordinated or not. Second, it is a potent mechanism to tune the phase-relation (temporal relation). It modulates the time delay between the oscillations without any change in conduction delays. This allows flexible shaping of the precise temporal input pattern - traveling waves in spatial domain - to the down-stream neurons. For example, in the context of selective attention, input arriving earlier might be prioritized relative to later input (Tiesinga and Sejnowski, 2009, 2010). Or the temporal order of neural responses might be of importance for sensory object recognition (Gray and Singer, 1989; Eckhorn et al., 1990; Singer and Gray, 1995; Fries et al., 2001b).
Concluding Remarks
Whether and to what extent frequency differences shape information flow and neural computation in the brain in a causal manner remains to be established. Demonstrating that a particular oscillation is necessary for a neural computation is difficult because experimentally removing an oscillation without affecting various other network properties is normally impossible, given that oscillations are usually emergent network phenomena (Buzsáki, 2006). Nevertheless, this review demonstrates that changes of a few Hz either between brain locations or a moment-to-moment basis, according to stimulus or cognitive conditions, is a property of neuronal oscillations in many frequency bands. Moreover, the precise oscillation frequency can have profound consequences in terms of synchronization properties (correlation, phase relations). Hence, we argue that manipulations of detuning represent a key experimental target to causally infer oscillatory properties without strongly affecting other network properties. Advanced multi-neuron electrophysiological and optical techniques (optogenetics, cellular voltage imaging) in future studies will provide exciting possibilities to measure and target frequency generation in neural oscillations and synchronization during cognition and behavior.
Author Contributions
EL initially drafted the manuscript. All authors contributed to the final manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ahmed, O. J., and Mehta, M. R. (2012). Running speed alters the frequency of hippocampal gamma oscillations. J. Neurosci. 32, 7373–7383. doi: 10.1523/JNEUROSCI.5110-11.2012
Akam, T., and Kullmann, D. M. (2014). Oscillatory multiplexing of population codes for selective communication in the mammalian brain. Nat. Rev. Neurosci. 15, 111–122. doi: 10.1038/nrn3668
Axmacher, N., Henseler, M. M., Jensen, O., Weinreich, I., Elger, C. E., and Fell, J. (2010). Cross-frequency coupling supports multi-item working memory in the human hippocampus. Proc. Natl. Acad. Sci. U. S. A. 107, 3228–3233. doi: 10.1073/pnas.0911531107
Bastos, A. M., Vezoli, J., Bosman, C. A., Schoffelen, J. M., Oostenveld, R., Dowdall, J. R., et al. (2014). Visual Areas Exert Feedforward and Feedback Influences through Distinct Frequency Channels. Neuron 85, 390–401. doi: 10.1016/j.neuron.2014.12.018
Bender, F., Gorbati, M., Cadavieco, M. C., Denisova, N., Gao, X., Holman, C., et al. (2015). Theta oscillations regulate the speed of locomotion via a hippocampus to lateral septum pathway. Nat. Commun. 6:8521. doi: 10.1038/ncomms9521
Bosman, C. A., Schoffelen, J. M., Brunet, N., Oostenveld, R., Bastos, A. M., Womelsdorf, T., et al. (2012). Attentional Stimulus Selection through Selective Synchronization between Monkey Visual Areas. Neuron 75, 875–888. doi: 10.1016/j.neuron.2012.06.037
Brunel, N., and Wang, X.-J. (2003). What determines the frequency of fast network oscillations with irregular neural discharges? I. Synaptic dynamics and excitation-inhibition balance. J. Neurophysiol. 90, 415–430. doi: 10.1152/jn.01095.2002
Brunet, N., Bosman, C. A., Roberts, M., Oostenveld, R., Womelsdorf, T., De Weerd, P., et al. (2013). Visual Cortical Gamma-Band Activity During Free Viewing of Natural Images. Cereb. Cortex 25, 918–926. doi: 10.1093/cercor/bht280
Buzsáki, G., Logothetis, N., and Singer, W. (2013). Scaling Brain Size, Keeping Timing: evolutionary Preservation of Brain Rhythms. Neuron 80, 751–764. doi: 10.1016/j.neuron.2013.10.002
Buzsáki, G., and Wang, X. J. (2012). Mechanisms of gamma oscillations. Annu. Rev. Neurosci. 35, 203–225. doi: 10.1146/annurev-neuro-062111-150444
Canessa, A., Palmisano, C., Isaias, I. U., and Mazzoni, A. (2020). Gait-related frequency modulation of beta oscillatory activity in the subthalamic nucleus of parkinsonian patients. Brain Stimul. 13, 1743–1752. doi: 10.1016/j.brs.2020.09.006
Caporale, N., and Dan, Y. (2008). Spike timing-dependent plasticity: a Hebbian learning rule. Annu. Rev. Neurosci. 31, 25–46. doi: 10.1146/annurev.neuro.31.060407.125639
Chawanya, T., Aoyagi, T., Nishikawa, I., Okuda, K., and Kuramoto, Y. (1993). A model for feature linking via collective oscillations in the primary visual cortex. Biol. Cybern. 68, 483–490. doi: 10.1007/BF00200807
Clark, C. R., Veltmeyer, M. D., Hamilton, R. J., Simms, E., Paul, R., Hermens, D., et al. (2004). Spontaneous alpha peak frequency predicts working memory performance across the age span. Int. J. Psychophysiol. 53, 1–9. doi: 10.1016/j.ijpsycho.2003.12.011
Cohen, A. H., Bard Ermentrout, G., Kiemel, T., Kopell, N., Sigvardt, K. A., and Williams, T. L. (1992). Modelling of intersegmental coordination in the lamprey central pattern generator for locomotion. Trends Neurosci. 15, 434–438. doi: 10.1016/0166-2236(92)90006-T
Colgin, L. L., Denninger, T., Fyhn, M., Hafting, T., Bonnevie, T., Jensen, O., et al. (2009). Frequency of gamma oscillations routes flow of information in the hippocampus. Nature 462, 353–357. doi: 10.1038/nature08573
da Silva, F. L., Blanes, W., Kalitzin, S. N., Parra, J., Suffczynski, P., and Velis, D. N. (2003). Epilepsies as Dynamical Diseases of Brain Systems: basic Models of the Transition Between Normal and Epileptic Activity. Epilepsia 44, 72–83.
Eckhorn, R., Bruns, A., Saam, M., Gail, A., Gabriel, A., and Brinksmeyer, H. J. (2001). Flexible cortical gamma-band correlations suggest neural principles of visual processing. Vis. Cogn. 8, 519–530. doi: 10.1080/13506280143000098
Eckhorn, R., Reitboeck, H. J., Arndt, M., and Dicke, P. (1990). Feature Linking via Synchronization among Distributed Assemblies: simulations of Results from Cat Visual Cortex. Neural Comput. 2, 293–307. doi: 10.1162/neco.1990.2.3.293
Edden, R. A. E., Muthukumaraswamy, S. D., Freeman, T. C. A., and Singh, K. D. (2009). Orientation discrimination performance is predicted by GABA concentration and gamma oscillation frequency in human primary visual cortex. J. Neurosci. 29, 15721–15726. doi: 10.1523/JNEUROSCI.4426-09.2009
Ermentrout, B. (1996). Type I Membranes, Phase Resetting Curves, and Synchrony. Neural Comput. 8, 979–1001. doi: 10.1162/neco.1996.8.5.979
Ermentrout, G. B., and Kleinfeld, D. (2001). Traveling electrical waves in cortex: insights from phase dynamics and speculation on a computational role. Neuron 29, 33–44. doi: 10.1016/s0896-6273(01)00178-7
Ermentrout, G. B., and Kopell, N. (1984). Frequency Plateaus in a Chain of Weakly Coupled Oscillators. SIAM J. Math. Anal. 15, 215–237. doi: 10.1137/0515019
Feng, W., Havenith, M. N., Wang, P., Singer, W., and Nikolić, D. (2010). Frequencies of gamma/beta oscillations are stably tuned to stimulus properties. Neuroreport 21, 680–684. doi: 10.1097/WNR.0b013e32833ae9d1
Friedman-Hill, S., Maldonado, P. E., and Gray, C. M. (2000). Dynamics of striate cortical activity in the alert macaque: i. Incidence and stimulus-dependence of gamma-band neuronal oscillations. Cereb. Cortex 10, 1105–1116. doi: 10.1093/cercor/10.11.1105
Fries, P. (2005). A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends Cogn. Sci. 9, 474–480. doi: 10.1016/j.tics.2005.08.011
Fries, P. (2009). Neuronal gamma-band synchronization as a fundamental proc ess in cortical computation. Annu. Rev. Neurosci. 32, 209–224. doi: 10.1146/annurev.neuro.051508.135603
Fries, P. (2015). Rhythms For Cognition: communication Through Coherence. Neuron 88, 220–235. doi: 10.1016/j.neuron.2015.09.034
Fries, P., Reynolds, J. H., Rorie, A. E., and Desimone, R. (2001a). Modulation of oscillatory neuronal synchronization by selective visual attention. Science 291, 1560–1563. doi: 10.1126/science.1055465
Fries, P., Neuenschwander, S., Engel, A. K., Goebel, R., and Singer, W. (2001b). Rapid feature selective neuronal synchronization through correlated latency shifting. Nat. Neurosci. 4, 194–200. doi: 10.1038/84032
Gieselmann, M. A., and Thiele, A. (2008). Comparison of spatial integration and surround suppression characteristics in spiking activity and the local field potential in macaque V1. Eur. J. Neurosci. 28, 447–459. doi: 10.1111/j.1460-9568.2008.06358.x
Giocomo, L. M., Zilli, E. A., Fransén, E., and Hasselmo, M. E. (2007). Temporal frequency of subthreshold oscillations scales with entorhinal grid cell field spacing. Science 315, 1719–1722. doi: 10.1126/science.1139207
Goutagny, R., Jackson, J., and Williams, S. (2009). Self-generated theta oscillations in the hippocampus. Nat. Neurosci. 12, 1491–1493. doi: 10.1038/nn.2440
Goyal, A., Miller, J., Qasim, S. E., Watrous, A. J., Zhang, H., Stein, J. M., et al. (2020). Functionally distinct high and low theta oscillations in the human hippocampus. Nat. Commun. 11:2469. doi: 10.1038/s41467-020-15670-6
Gray, C. M., and Singer, W. (1989). Stimulus-specific neuronal oscillations in orientation columns of cat visual cortex. Proc. Natl. Acad. Sci. U. S. A. 86, 1698–1702. doi: 10.1073/pnas.86.5.1698
Green, H. L., Dipiero, M., Koppers, S., Berman, J. I., Bloy, L., Liu, S., et al. (2022). Peak Alpha Frequency and Thalamic Structure in Children with Typical Development and Autism Spectrum Disorder. J. Autism Dev. Disord. 52, 103–112. doi: 10.1007/s10803-021-04926-9
Gregoriou, G. G., Gotts, S. J., Zhou, H., and Desimone, R. (2009). High-frequency, long-range coupling between prefrontal and visual cortex during attention. Science 324, 1207–1210. doi: 10.1126/science.1171402
Grillner, S., Deliagina, T., El Manira, A., Hill, R. H., Orlovsky, G. N., Wallén, P., et al. (1995). Neural networks that co-ordinate locomotion and body orientation in lamprey. Trends Neurosci. 18, 270–279. doi: 10.1016/0166-2236(95)80008-P
Hadjipapas, A., Lowet, E., Roberts, M. J., Peter, A., and De Weerd, P. (2015). Parametric variation of gamma frequency and power with luminance contrast: a comparative study of human MEG and monkey LFP and spike responses. Neuroimage 112, 327–340. doi: 10.1016/j.neuroimage.2015.02.062
Haegens, S., Cousijn, H., Wallis, G., Harrison, P. J., and Nobre, A. C. (2014). Inter- and intra-individual variability in alpha peak frequency. Neuroimage 92, 46–55. doi: 10.1016/j.neuroimage.2014.01.049
Haig, A. R., Gordon, E., De Pascalis, V., Meares, R. A., Bahramali, H., and Harris, A. (2000). Gamma activity in schizophrenia: evidence of impaired network binding? Clin. Neurophysiol. 111, 1461–1468. doi: 10.1016/S1388-2457(00)00347-3
Hermes, D., Miller, K. J., Wandell, B. A., and Winawer, J. (2015). Gamma oscillations in visual cortex: the stimulus matters. Trends Cogn. Sci. 19, 57–58. doi: 10.1016/j.tics.2014.12.009
Herrmann, C. S., and Demiralp, T. (2005). Human EEG gamma oscillations in neuropsychiatric disorders. Clin. Neurophysiol. 116, 2719–2733. doi: 10.1016/j.clinph.2005.07.007
Heys, J. G., Giocomo, L. M., and Hasselmo, M. E. (2010). Cholinergic modulation of the resonance properties of stellate cells in layer II of medial entorhinal cortex. J. Neurophysiol. 104, 258–270. doi: 10.1152/jn.00492.2009
Izhikevich, E. M. (2007). Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting. Cambridge: MIT Press.
Jia, X., Xing, D., and Kohn, A. (2013). No consistent relationship between gamma power and peak frequency in macaque primary visual cortex. J. Neurosci. 33, 17–25. doi: 10.1523/JNEUROSCI.1687-12.2013
Kilavik, B. E., Ponce-Alvarez, A., Trachel, R., Confais, J., Takerkart, S., and Riehle, A. (2012). Context-Related Frequency Modulations of Macaque Motor Cortical LFP Beta Oscillations. Cereb. Cortex 22, 2148–2159. doi: 10.1093/cercor/bhr299
Ko, T.-W., and Ermentrout, G. B. (2009). Phase-response curves of coupled oscillators. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 79:16211. doi: 10.1103/PhysRevE.79.016211
Kopell, N., and Ermentrout, G. B. (1986). Symmetry and phaselocking in chains of weakly coupled oscillators. Commun. Pure Appl. Math. 39, 623–660. doi: 10.1002/cpa.3160390504
Kopell, N., and Ermentrout, G. B. (1988). Coupled oscillators and the design of central pattern generators. Math. Biosci. 90, 87–109. doi: 10.1016/0025-5564(88)90059-4
Kopell, N., and Ermentrout, G. B. (2002). Chapter 1 Mechanisms of phase-locking and frequency control in pairs of coupled neural oscillators. Handb. Dyn. Syst. 2, 3–54. doi: 10.1016/S1874-575X(02)80022-4
Lakatos, P., Shah, A. S., Knuth, K. H., Ulbert, I., Karmos, G., and Schroeder, C. E. (2005). An oscillatory hierarchy controlling neuronal excitability and stimulus processing in the auditory cortex. J. Neurophysiol. 94, 1904–1911. doi: 10.1152/jn.00263.2005
Lee, S., Sen, K., and Kopell, N. (2009). Cortical gamma rhythms modulate NMDAR-mediated spike timing dependent plasticity in a biophysical model. PLoS Comput. Biol. 5:e1000602. doi: 10.1371/journal.pcbi.1000602
Lewis, C. M., Ni, J., Wunderle, T., Jendritza, P., Lazar, A., Diester, I., et al. (2021). Cortical gamma-band resonance preferentially transmits coherent input. Cell Rep. 35:109083. doi: 10.1016/j.celrep.2021.109083
Lima, B., Singer, W., Chen, N.-H., and Neuenschwander, S. (2010). Synchronization dynamics in response to plaid stimuli in monkey V1. Cereb. Cortex 20, 1556–1573. doi: 10.1093/cercor/bhp218
Little, S., and Brown, P. (2014). The functional role of beta oscillations in Parkinson’s disease. Parkinsonism Relat. Disord. 20, S44–S48. doi: 10.1016/S1353-8020(13)70013-0
Lowet, E., Gips, B., Roberts, M. J., De Weerd, P., Jensen, O., and van der Eerden, J. (2018). Microsaccade-rhythmic modulation of neural synchronization and coding within and across cortical areas V1 and V2. PLoS Biol. 16:e2004132. doi: 10.1371/journal.pbio.2004132
Lowet, E., Roberts, M., Hadjipapas, A., Peter, A., van der Eerden, J., and De Weerd, P. (2015). Input-Dependent Frequency Modulation of Cortical Gamma Oscillations Shapes Spatial Synchronization and Enables Phase Coding. PLoS Comput. Biol. 11:e1004072. doi: 10.1371/journal.pcbi.1004072
Lowet, E., Roberts, M. J., Bonizzi, P., Karel, J., and De Weerd, P. (2016). Quantifying neural oscillatory synchronization: a comparison between spectral coherence and phase-locking value approaches. PLoS One 11:e0146443. doi: 10.1371/journal.pone.0146443
Lowet, E., Roberts, M. J., Peter, A., Gips, B., and de Weerd, P. (2017). A quantitative theory of gamma synchronization in macaque V1. Elife 6:e26642. doi: 10.7554/eLife.26642
Lundqvist, M., Rose, J., Herman, P., Brincat, S. L., Buschman, T. J., and Miller, E. K. (2016). Gamma and Beta Bursts Underlie Working Memory. Neuron 90, 152–164. doi: 10.1016/j.neuron.2016.02.028
Markram, H., Gerstner, W., and Sjöström, P. J. (2012). Spike-timing-dependent plasticity: a comprehensive overview. Front. Synaptic Neurosci. 4:2. doi: 10.3389/fnsyn.2012.00002
McFarland, W. L., Teitelbaum, H., and Hedges, E. K. (1975). Relationship between hippocampal theta activity and running speed in the rat. J. Comp. Physiol. Psychol. 88, 324–328. doi: 10.1037/h0076177
McGregor, M. M., and Nelson, A. B. (2019). Circuit Mechanisms of Parkinson’s Disease. Neuron 101, 1042–1056. doi: 10.1016/j.neuron.2019.03.004
Moënne-Loccoz, C., Astudillo-Valenzuela, C., Skovgård, K., Salazar-Reyes, C. A., Barrientos, S. A., García-Núñez, X. P., et al. (2020). Cortico-Striatal Oscillations Are Correlated to Motor Activity Levels in Both Physiological and Parkinsonian Conditions. Front. Syst. Neurosci. 14:56. doi: 10.3389/fnsys.2020.00056
Neuper, C., and Pfurtscheller, G. (2001). Evidence for distinct beta resonance frequencies in human EEG related to specific sensorimotor cortical areas. Clin. Neurophysiol. 112, 2084–2097. doi: 10.1016/s1388-2457(01)00661-7
Newman, E. L., Gillet, S. N., Climer, J. R., and Hasselmo, M. E. (2013). Cholinergic Blockade Reduces Theta-Gamma Phase Amplitude Coupling and Speed Modulation of Theta Frequency Consistent with Behavioral Effects on Encoding. J. Neurosci. 33, 19635–19646. doi: 10.1523/JNEUROSCI.2586-13.2013
Ni, J., Wunderle, T., Lewis, C. M., Desimone, R., Diester, I., and Fries, P. (2016). Gamma-rhythmic Gain Modulation (Cold Spring Harbor Labs Journals). Neuron 92, 240–251. doi: 10.1016/j.neuron.2016.09.003
Notbohm, A., Kurths, J., and Herrmann, C. S. (2016). Modification of Brain Oscillations via Rhythmic Light Stimulation Provides Evidence for Entrainment but Not for Superposition of Event-Related Responses. Front. Hum. Neurosci. 10:10. doi: 10.3389/fnhum.2016.00010
Patel, J., Fujisawa, S., Berényi, A., Royer, S., and Buzsáki, G. (2012). Traveling Theta Waves along the Entire Septotemporal Axis of the Hippocampus. Neuron 75, 410–417. doi: 10.1016/j.neuron.2012.07.015
Peter, A., Uran, C., Klon-Lipok, J., Roese, R., Van Stijn, S., Barnes, W., et al. (2019). Surface color and predictability determine contextual modulation of V1 firing and gamma oscillations. Elife 8:e42101. doi: 10.7554/eLife.42101
Pfurtscheller, G., Neuper, C., Pichler-zalaudek, K., and Lopes, F. H. (2000). Do brain oscillations of different frequencies indicate interaction between cortical areas in humans? Neurosci. Lett. 286, 66–68. doi: 10.1016/S0304-3940(00)01055-7
Pikovsky, A., Rosenblum, M., Kurths, J., and Hilborn, R. C. (2002). Synchronization: a Universal Concept in Nonlinear Science. Am. J. Phys. 70:655.
Ray, S., and Maunsell, J. H. R. (2010). Differences in gamma frequencies across visual cortex restrict their possible use in computation. Neuron 67, 885–896. doi: 10.1016/j.neuron.2010.08.004
Roberts, M. J., Lowet, E., Brunet, N. M., Ter Wal, M., Tiesinga, P., Fries, P., et al. (2013). Robust gamma coherence between macaque V1 and V2 by dynamic frequency matching. Neuron 78, 523–536. doi: 10.1016/j.neuron.2013.03.003
Salmelin, R., and Hari, R. (1994). Spatiotemporal characteristics of sensorimotor neuromagnetic rhythms related to thumb movement. Neuroscience 60, 537–550. doi: 10.1016/0306-4522(94)90263-1
Sato, N. (2022). Cortical traveling waves reflect state-dependent hierarchical sequencing of local regions in the human connectome network. Sci. Rep. 12:334. doi: 10.1038/s41598-021-04169-9
Schwemmer, M. A., and Lewis, T. J. (2012). “The theory of weakly coupled oscillators,” in PRCs in Neuroscience: Theory, Experiment and Analysis. Springer Series in Computational Neuroscience, Vol. 6, eds N. W. Schultheiss, A. Prinz, and R. J. Butera (cham: Spinger), 3–31. doi: 10.1007/978-1-4614-0739-3_1
Sclar, G., Maunsell, J. H. R., and Lennie, P. (1990). Coding of image contrast in central visual pathways of the macaque monkey. Vis. Res. 30, 1–10. doi: 10.1016/0042-6989(90)90123-3
Self, M. W., Peters, J. C., Possel, J. K., Reithler, J., Goebel, R., Ris, P., et al. (2016). The Effects of Context and Attention on Spiking Activity in Human Early Visual Cortex. PLoS Biol. 14:e1002420. doi: 10.1371/journal.pbio.1002420
Shay, C. F., Boardman, I. S., James, N. M., and Hasselmo, M. E. (2012). Voltage dependence of subthreshold resonance frequency in layer ii of medial entorhinal cortex. Hippocampus 22, 1733–1749. doi: 10.1002/hipo.22008
Singer, W., and Gray, C. M. (1995). Visual Feature Integration and the Temporal Correlation Hypothesis. Annu. Rev. Neurosci. 18, 555–586. doi: 10.1146/annurev.ne.18.030195.003011
Stiefel, K. M., Gutkin, B. S., and Sejnowski, T. J. (2008). Cholinergic Neuromodulation Changes Phase Response Curve Shape and Type in Cortical Pyramidal Neurons. PLoS One 3:e3947. doi: 10.1371/journal.pone.0003947
Stiefel, K. M., Gutkin, B. S., and Sejnowski, T. J. (2009). The effects of cholinergic neuromodulation on neuronal phase-response curves of modeled cortical neurons. J. Comput. Neurosci. 26, 289–301. doi: 10.1007/s10827-008-0111-9
Strogatz, S. H., and Stewart, I. (1993). Coupled oscillators and biological synchronization. Sci. Am. 269, 102–109. doi: 10.1038/scientificamerican1293-102
Swettenham, J. B., Muthukumaraswamy, S. D., and Singh, K. D. (2009). Spectral properties of induced and evoked gamma oscillations in human early visual cortex to moving and stationary stimuli. J. Neurophysiol. 102, 1241–1253. doi: 10.1152/jn.91044.2008
Tiesinga, P., and Sejnowski, T. J. (2009). Cortical enlightenment: are attentional gamma oscillations driven by ING or PING? Neuron 63, 727–732. doi: 10.1016/j.neuron.2009.09.009
Tiesinga, P. H., and Sejnowski, T. J. (2010). Mechanisms for Phase Shifting in Cortical Networks and their Role in Communication through Coherence. Front. Hum. Neurosci. 4:196. doi: 10.3389/fnhum.2010.00196
Traub, R. D., Whittington, M. A., Colling, S. B., Buzsaki, G., and Jefferys, J. G. (1996). Analysis of gamma rhythms in the rat hippocampus in vitro and in vivo. J. Physiol. 493, 471–484. doi: 10.1113/jphysiol.1996.sp021397
van Pelt, S., and Fries, P. (2013). Visual stimulus eccentricity affects human gamma peak frequency. Neuroimage 78, 439–447. doi: 10.1016/j.neuroimage.2013.04.040
Veit, J., Hakim, R., Jadi, M. P., Sejnowski, T. J., and Adesnik, H. (2017). Cortical gamma band synchronization through somatostatin interneurons. Nat. Neurosci. 20, 951–959. doi: 10.1038/nn.4562
Wang, X. (2010). Neurophysiological and Computational Principles of Cortical Rhythms in Cognition. Physiol. Rev. 90, 1195–1268. doi: 10.1152/physrev.00035.2008
Wolinski, N., Cooper, N. R., Sauseng, P., and Romei, V. (2018). The speed of parietal theta frequency drives visuospatial working memory capacity. PLoS Biol. 16:e2005348. doi: 10.1371/journal.pbio.2005348
Wulff, P., Ponomarenko, A. A., Bartos, M., Korotkova, T. M., Fuchs, E. C., Bähner, F., et al. (2009). Hippocampal theta rhythm and its coupling with gamma oscillations require fast inhibition onto parvalbumin-positive interneurons. Proc. Natl. Acad. Sci. U. S. A. 106, 3561–3566. doi: 10.1073/pnas.0813176106
Zachariou, M., Roberts, M., Lowet, E., de Weerd, P., and Hadjipapas, A. (2015). Contrast-dependent modulation of gamma rhythm in v1: a network model. BMC Neurosci. 16:O10. doi: 10.1186/1471-2202-16-S1-O10
Zachariou, M., Roberts, M., Lowet, E., De Weerd, P., and Hadjipapas, A. (2021). Empirically constrained network models for contrast-dependent modulation of gamma rhythm in V1. Neuroimage 229:117748. doi: 10.1016/j.neuroimage.2021.117748
Zhang, H., and Jacobs, J. (2015). Traveling Theta Waves in the Human Hippocampus. J. Neurosci. 35, 12477–12487. doi: 10.1523/JNEUROSCI.5102-14.2015
Keywords: synchronization, frequency, Arnold tongue, neural circuits, oscillation
Citation: Lowet E, De Weerd P, Roberts MJ and Hadjipapas A (2022) Tuning Neural Synchronization: The Role of Variable Oscillation Frequencies in Neural Circuits. Front. Syst. Neurosci. 16:908665. doi: 10.3389/fnsys.2022.908665
Received: 30 March 2022; Accepted: 23 June 2022;
Published: 08 July 2022.
Edited by:
Conrado Arturo Bosman, University of Amsterdam, NetherlandsReviewed by:
Michal Zochowski, University of Michigan, United StatesChristopher M. Lewis, Max Planck Society, Germany
Copyright © 2022 Lowet, De Weerd, Roberts and Hadjipapas. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Eric Lowet, ZWxvd2V0QG1haWxmZW5jZS5jb20=
†These authors share last authorship
 Eric Lowet
Eric Lowet Peter De Weerd
Peter De Weerd Mark J. Roberts
Mark J. Roberts Avgis Hadjipapas
Avgis Hadjipapas