Loss or gain of function? Effects of ion channel mutations on neuronal firing depend on the neuron type

Introduction: Clinically relevant mutations to voltage-gated ion channels, called channelopathies, alter ion channel function, properties of ionic currents, and neuronal firing. The effects of ion channel mutations are routinely assessed and characterized as loss of function (LOF) or gain of function (GOF) at the level of ionic currents. However, emerging personalized medicine approaches based on LOF/GOF characterization have limited therapeutic success. Potential reasons are among others that the translation from this binary characterization to neuronal firing is currently not well-understood—especially when considering different neuronal cell types. In this study, we investigate the impact of neuronal cell type on the firing outcome of ion channel mutations.

Methods: To this end, we simulated a diverse collection of single-compartment, conductance-based neuron models that differed in their composition of ionic currents. We systematically analyzed the effects of changes in ion current properties on firing in different neuronal types. Additionally, we simulated the effects of known mutations in KCNA1 gene encoding the K_V1.1 potassium channel subtype associated with episodic ataxia type 1 (EA1).

Results: These simulations revealed that the outcome of a given change in ion channel properties on neuronal excitability depends on neuron type, i.e., the properties and expression levels of the unaffected ionic currents.

Discussion: Consequently, neuron-type specific effects are vital to a full understanding of the effects of channelopathies on neuronal excitability and are an important step toward improving the efficacy and precision of personalized medicine approaches.

1. Introduction

The properties and combinations of voltage-gated ion channels are vital in determining neuronal excitability (1–4). However, ion channel function can be disturbed, for instance, through genetic alterations, resulting in altered neuronal firing behavior (2). In recent years, next generation sequencing has led to an increase in the discovery of clinically relevant ion channel mutations and has provided the basis for pathophysiological studies of genetic epilepsies, pain disorders, dyskinesias, intellectual disabilities, myotonias, and periodic paralyzes (1, 2). Ongoing efforts of many research groups have contributed to the current understanding of underlying disease mechanism in channelopathies. However, a complex pathophysiological landscape has emerged for many channelopathies and is likely a reason for limited therapeutic success with standard care.

Ion channel variants are frequently classified in heterologous expression systems as either a loss of function (LOF) or a gain of function (GOF) in the respective ionic current (5–8). This LOF/GOF classification is often directly used to predict the effects on neuronal firing (9–12), which in turn is important for understanding the pathophysiology of these disorders and for identification of potential therapeutic targets (13–16). Experimentally, the effects of channelopathies on neuronal firing are assessed using primary neuronal cultures (17–19) or in vitro recordings from slices of transgenic mouse lines (20–24) but are restricted to a limited number of different neuron types. Neuron types differ in many aspects. They may differ in their composition of ionic currents (25–28) and, therefore, likely respond differently to changes in the properties of a single ionic current. The expression level of an affected gene (29) and relative amplitudes of ionic currents (3, 4, 30–32) indeed dramatically influence the firing behavior and dynamics of neurons. Mutations in different sodium channel genes have been experimentally shown to affect firing in a neuron-type specific manner based on differences in expression levels of the affected gene (29) but also on other neuron-type specific mechanisms (24, 33).

Neuron-type specificity is likely vital for successful precision medicine treatment approaches. For example, Dravet syndrome was identified as the consequence of LOF mutations in encoding the voltage-gated sodium channel Nav1.1. SCN1A (34–36); however, limited success in the treatment of Dravet syndrome persisted (34, 37) in part due to the lack of understanding that inhibitory interneurons and not pyramidal neurons had altered excitability as a result of LOF SCN1A mutations (15, 16).

Taken together, these examples demonstrate the need to study the effects of ion channel mutations in many different neuron types—a daunting if not impossible experimental challenge. In the context of this diversity, simulations of conductance-based neuronal models are a powerful tool bridging the gap between altered ionic currents and firing in a systematic and efficient way. Furthermore, simulations allow to predict the potential effects of drugs needed to alleviate the pathophysiology of the respective mutation (38–40).

In this study, we therefore investigated how the outcome of ionic current kinetic changes on firing depends on neuronal cell type, i.e., on the composition of ionic currents, by (1) characterizing firing responses with two measures, (2) simulating the response of a repertoire of different neuronal models to changes in single current parameters, and (3) bringing more complex changes in this case as they were observed for specific KCNA1 mutations that are associated with episodic ataxia type 1 (39, 41, 42).

2. Materials and methods

All modeling and simulation were done in parallel with custom written Python 3.8 (Python Programming Language; RRID:SCR_008394) software, run on a Cent-OS 7 server with an Intel(R) Xeon (R) E5-2630 v2 CPU.

2.1. Different neuron models

A set of single-compartment, conductance-based neuronal models representing the major classes of cortical and thalamic neurons including regular spiking pyramidal (RS pyramidal; model D), regular spiking inhibitory (RS inhibitory; model B), and fast spiking (FS; model C) neurons were used (4). Additionally, a K_V1.1 current [I_KV1.1; (43)] was added to each of these models (RS pyramidal +K_V1.1; model H, RS inhibitory +K_V1.1; model E, and FS +K_V1.1; model G, respectively). A cerebellar stellate cell model from (44) is used (Cb stellate; model A) in this study. This neuron model was also extended by a K_V1.1 current (43) either in addition to the A-type potassium current (Cb stellate +K_V1.1; model F) or by replacing the A-type potassium current (Cb stellate ΔK_V1.1; model J). A subthalamic nucleus (STN; model L) neuron model as described by (45) was also used. The STN neuron model (model L) was additionally extended by K_V1.1 current (43) either in addition to the A-type potassium current (STN +K_V1.1; model I) or by replacing the A-type potassium current (STN ΔK_V1.1; model K). Model letter naming corresponds to panel lettering in Figure 1. The anatomical origin of each model is shown in Figure 1M. The properties and maximal conductances of each model are detailed in Table 1 and depicted in Figure 2. The gating properties are unaltered from the original Cb stellate (model A) and STN (model L) models (44, 45). For enabling the comparison of models with the typically reported electrophysiological data fitting reported and for the ease of further gating curve manipulations, a modified Boltzmann function was formed as follows:

$\begin{array}{ll}{x}_{\infty }={\left(\frac{1-a}{1+exp\left[\frac{V-V_{1/2}}{k}\right]}+a\right)}^j,& (1)\end{array}$

with slope k, voltage for half-maximal activation or inactivation (V_1/2), exponent j, and persistent current 0 ≤ a ≤ 1 fitted to the original formulism for RS pyramidal (model D), RS inhibitory (model B), and FS (model C) models from (4). The properties of I_KV1.1 were fitted to the mean wild-type biophysical parameters of K_V1.1 described in (39). The fitted gating parameters are detailed in Table 2. Each of the original single-compartment models used here can reproduce physiological firing behavior of the neurons they represent [Figure 1; (4, 44, 45)] and capture key aspects of the dynamics of these neuron types.

FIGURE 1

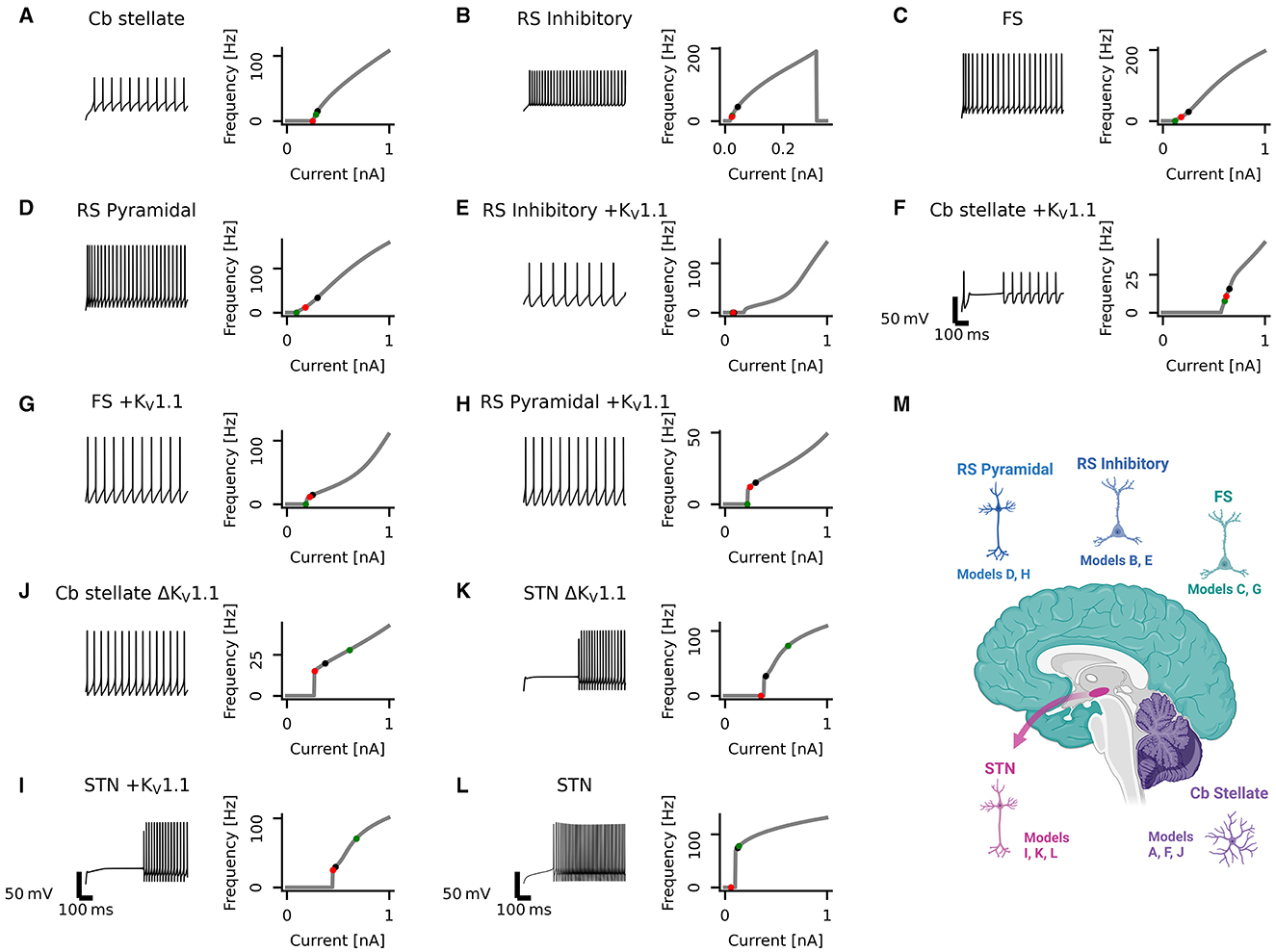
Figure 1. Diversity in neuronal model firing. Spike trains (left), frequency-current (fI) curves (right) for Cb stellate (A), RS inhibitory (B), FS (C), RS pyramidal (D), RS inhibitory +K_V1.1 (E), Cb stellate +K_V1.1 (F), FS +K_V1.1 (G), RS pyramidal +K_V1.1 (H), STN +K_V1.1 (I), Cb stellate ΔK_V1.1 (J), STN ΔK_V1.1 (K), and STN (L) neuron models. Models are sorted qualitatively based on their fI curves. Black markers on the fI curves indicate the current step at which the spike train occurs. The green marker indicates the current at which firing begins in response to an ascending current ramp, whereas the red marker indicates the current at which firing ceases in response to a descending current ramp (see Supplementary Figure 1). A schematic illustrating the anatomical locations of the models is included (M); however, single-compartment models are used for each cell type.

TABLE 1

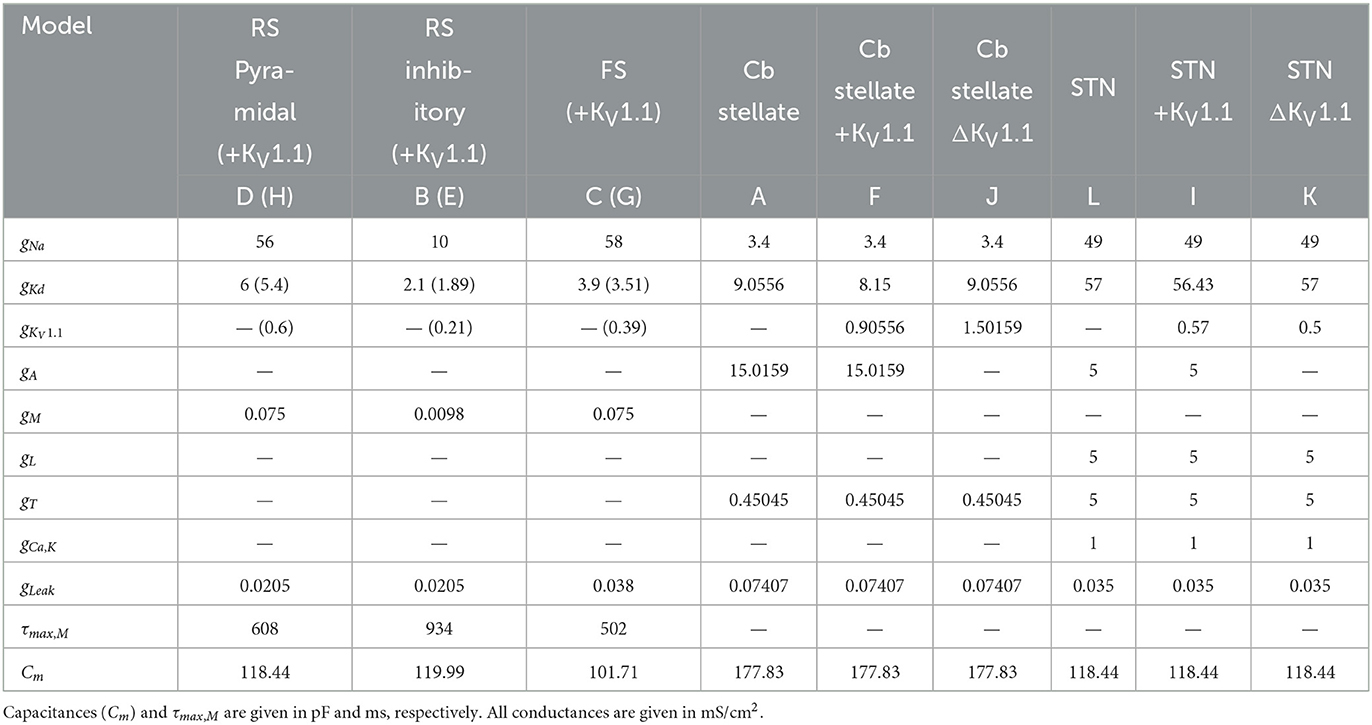
Table 1. Cell properties and conductances of regular spiking pyramidal neuron (RS Pyramidal; model D), regular spiking inhibitory neuron (RS inhibitory; model B), fast spiking neuron (FS; model C) each with additional I_KV1.1 (RS Pyramidal +K_V1.1; model H, RS inhibitory +K_V1.1; model E, FS +K_V1.1; model G, respectively), cerebellar stellate cell (Cb stellate; model A), with additional I_KV1.1 (Cb stellate +K_V1.1; model F) and with I_KV1.1 replacement of I_A (Cb stellate ΔK_V1.1; model J), and subthalamic nucleus neuron (STN; model L), with additional I_KV1.1 (STN +K_V1.1; model I) and with I_KV1.1 replacement of I_A (STN K_V1.1; model K) models.

FIGURE 2

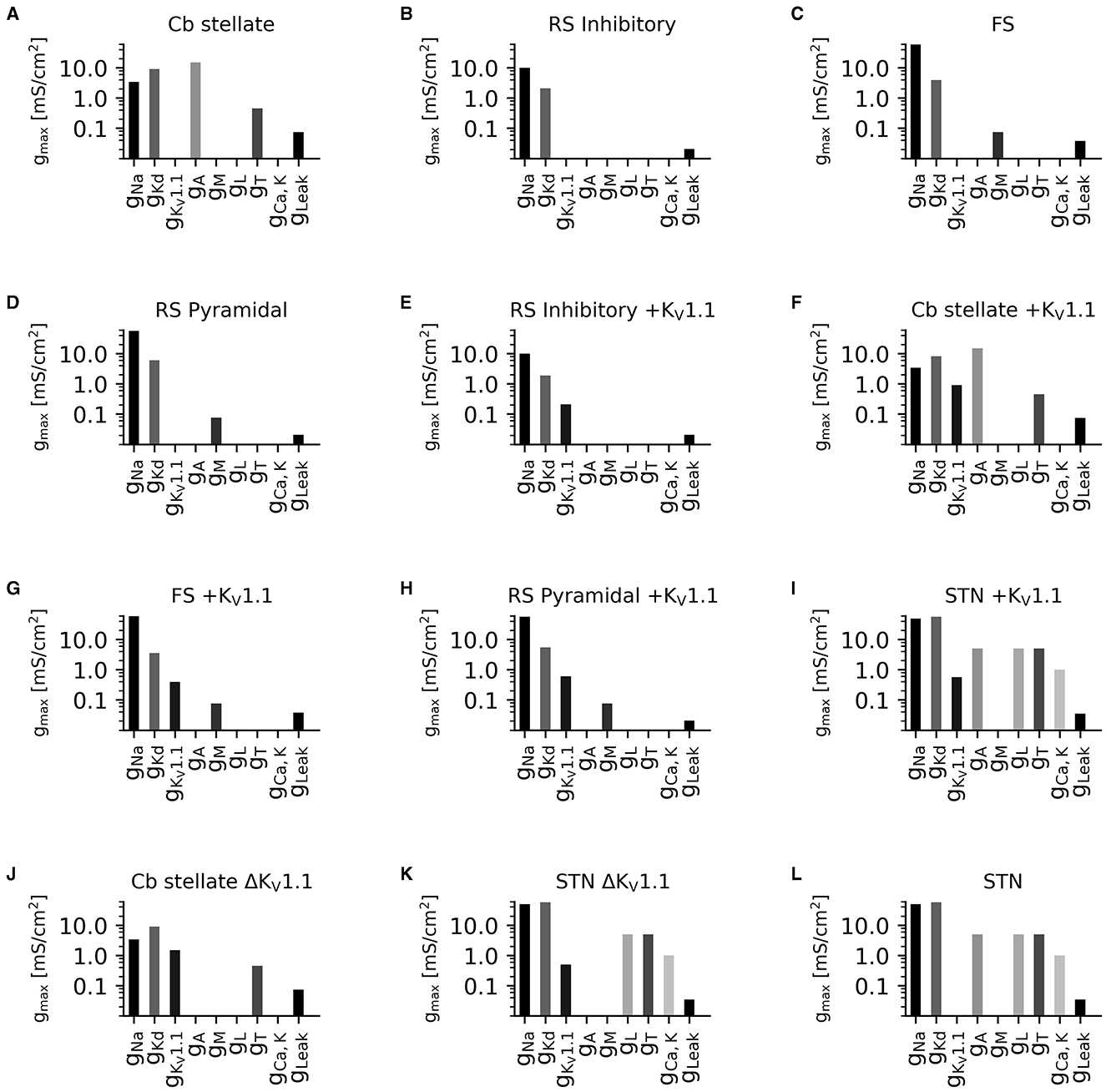
Figure 2. Diversity in neuronal model current composition. Distributions of maximal current conductances (g_max) for Cb stellate (A), RS inhibitory (B), FS (C), RS pyramidal (D), RS inhibitory +K_V1.1 (E), Cb stellate +K_V1.1 (F), FS +K_V1.1 (G), RS pyramidal +K_V1.1 (H), STN +K_V1.1 (I), Cb stellate ΔK_V1.1 (J), STN ΔK_V1.1 (K), and STN (L) neuron models. Models are sorted as in Figure 1.

TABLE 2

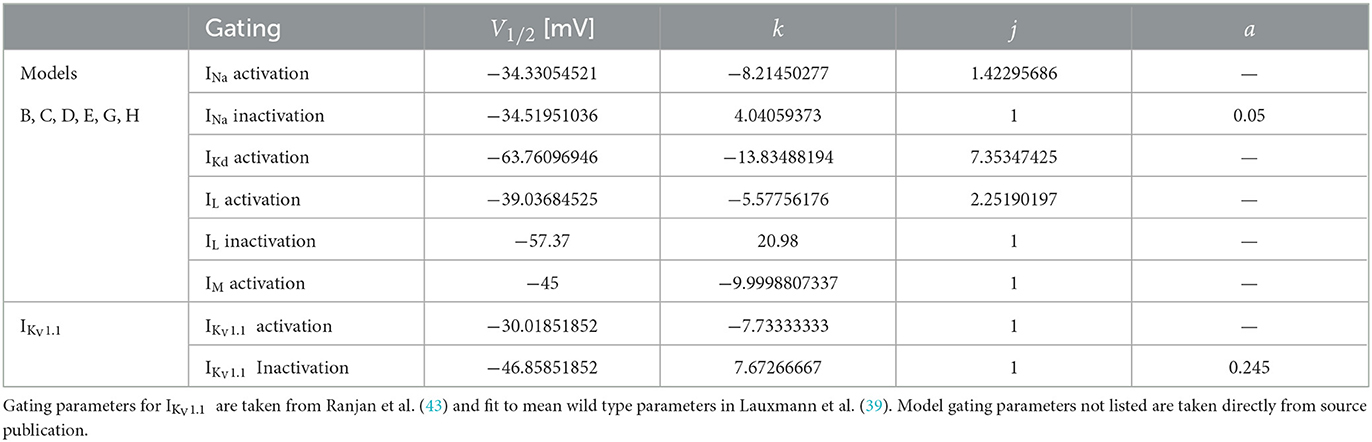
Table 2. For comparability to typical electrophysiological data fitting reported and for ease of further gating curve manipulations, a sigmoid function (Equation 1) with slope k, voltage for half-maximal activation or inactivation (V_1/2), exponent j, and persistent current 0 ≤ a ≤ 1 were fitted for the models originating from Pospischil et al. (4) (models B, C, D, E, G, H) where α_x and β_x are used.

2.2. Firing frequency analysis

The membrane responses to 200 equidistant 2 s long current steps were simulated using the forward Euler method with a Δt = 0.01 ms from a steady state. Current steps ranged from 0 to 1 nA (step size 5 pA) for all models except for the RS inhibitory neuron models, where a range of 0–0.35 nA (step size 1.75 pA) was used to ensure repetitive firing across the range of input currents. For each current step, action potentials were detected as peaks with at least 50 mV prominence, or the relative height above the lowest contour line encircling it, and a minimum interspike interval of 1 ms. The interspike interval was computed and used to determine the instantaneous firing frequencies elicited by the current step. A ramp protocol, consisting of a 2 s ascending ramp followed by a 2 s descending ramp, was also simulated over the same current range to assess model hysteresis. Rheobases assessed from this ramp protocol were not used for subsequent analysis in order to maintain relatability to commonly used experimental measures.

To ensure accurate firing frequencies at low firing rates and reduced spike sampling bias, steady-state firing was defined as the mean firing frequency in a 500 ms window in the last second of the current steps starting at the initial action potential in this last second. Firing characterization was performed in the last second of current steps to ensure steady-state firing is captured, and adaptation processes are neglected in our analysis. Alteration in current magnitudes can have different effects on rheobase and the initial slope of the fI curve (30). For this reason, we quantified neuronal firing using the rheobase as well as the area under the curve (AUC) of the initial portion of the fI curve as a measure of the initial slope of the fI curve (Figure 3A).

FIGURE 3

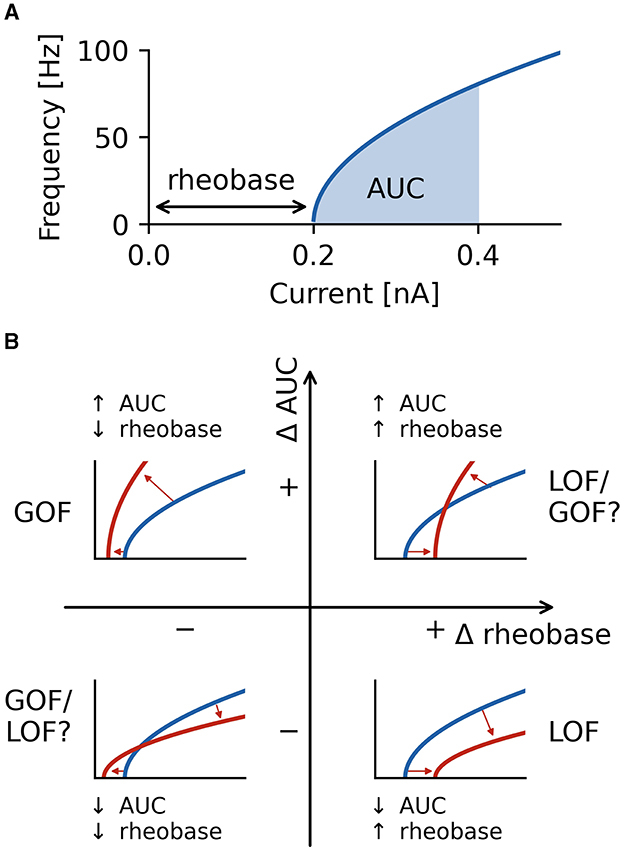
Figure 3. Characterization of firing with AUC and rheobase. (A) The area under the curve (AUC) of the repetitive firing frequency-current (fI) curve. (B) Changes in firing as characterized by ΔAUC and Δrheobase occupy four quadrants separated by no changes in AUC and rheobase. Representative schematic fI curves in red with respect to a reference (or wild type) fI curve (blue) depict the general changes associated with each quadrant. Square root functions are used as fI curves for illustration purposes.

The smallest current at which steady state firing occurred was identified, and the current step interval preceding the occurrence of steady state firing was simulated at higher resolution (100 current steps) to determine the current at which steady state firing began. Firing was simulated with 100 current steps from this current upwards for 1/5 of the overall current range. Over this range, a fI curve was constructed and the integral, or area under the curve (AUC), of the fI curve over this interval was computed with the composite trapezoidal rule and used as a measure of firing rate independent from rheobase.

To obtain the rheobase at a higher current resolution than the fI curve, the current step interval preceding the occurrence of action potentials was explored at higher resolution with 100 current steps spanning the interval (step sizes of 0.05 and 0.0175 pA, respectively). Membrane responses to these current steps were then analyzed for action potentials, and the rheobase was considered the lowest current step for which an action potential was elicited.

All models exhibited tonic steady-state firing with default parameters. In limited instances, variations of parameters elicited periodic bursting; however, these instances were excluded from further analysis.

2.3. Sensitivity analysis and comparison of models

Properties of ionic currents common to all models (I_Na, I_Kd, I_A/I_KV1.1, and I_Leak) were systematically altered in a one-factor-at-a-time sensitivity analysis for all models. The gating curves for each current were shifted (ΔV_1/2) from −10 to 10 mV with an increment of 1 mV. The voltage dependence of the time constant associated with the shifted gating curve was correspondingly shifted. The slope (k) of the gating curves were altered from half to twice the initial slope. Similarly, the maximal current conductance (g) was also scaled from half to twice the initial value. For both slope and conductance alterations, alterations consisted of 21 steps spaced equally on a log₂ scale. We neglected the variation of time constants for the practical reason that estimation and assessment of time constants and changes to them is not straightforward (46, 47).

2.4. Model comparison

Changes in rheobase (Δrheobase) were calculated in relation to the original model rheobase. The contrast of each AUC value (AUC_i) was computed in comparison to the AUC of the unaltered wild type model (AUC_wt):

$\begin{array}{cc}\text{normalized}\Delta \text{AUC}=\frac{AU{C}_i-AU{C}_{wt}}{AU{C}_{wt}}.& (2)\end{array}$

To assess whether the effects of a given alteration on normalized ΔAUC or Δrheobase were robust across models, the correlation between normalized ΔAUC or Δrheobase and the magnitude of the alteration of a current property was computed for each alteration in each model and compared across alteration types. The Kendall's τ coefficient, a non-parametric rank correlation, is used to describe the relationship between the magnitude of the alteration and AUC or rheobase values. A Kendall τ value of −1 or 1 is indicative of monotonically decreasing and increasing relationships, respectively.

2.5. KCNA1 mutations

Known episodic ataxia type 1 associated KCNA1 mutations and their electrophysiological characterization have been reviewed in (39). The mutation-induced changes in I_KV1.1 amplitude and activation slope (k) were normalized to wild-type measurements, and changes in activation V_1/2 were used relative to wild-type measurements. Although initially described as having a lack of fast activation, K_V1.1 displays prominent inactivation at physiologically relevant temperatures (43). The effects of a mutation were also applied to I_A when present as both potassium currents display inactivation. In all cases, the mutation effects were applied to half of the K_V1.1 or I_A under the assumption that the heterozygous mutation results in 50% of channels carrying the mutation. Frequency-current curves for each mutation in each model were obtained through simulation and used to characterize firing behavior as described above. For each model, the differences in mutation AUC to wild type AUC were normalized by wild-type AUC (normalized ΔAUC) and mutation rheobases were compared to wild-type rheobase values (Δrheobase). Pairwise Kendall rank correlations (Kendall τ) were used to compare the correlation in the effects of K_V1.1 mutations on AUC and rheobase between models.

2.6. Code accessibility

The simulation and analysis code including full specification of the models is freely available online at https://github.com/nkoch1/LOFGOF2023.

3. Results

To examine the role of neuron-type specific ionic current environments on the impact of altered ion currents properties on firing behavior, we performed those as follows: (1) firing responses were characterized with rheobase and ΔAUC, (2) a set of neuronal models was used, and properties of channels common across models were altered systematically one at a time, and (3) the effects of a set of episodic ataxia type 1 associated KCNA1 mutations on firing was then examined across different neuronal models with different ionic current environments.

3.1. Variety of model neurons

Neuronal firing is heterogeneous across the CNS, and a set of neuronal models with heterogeneous firing due to different ionic currents is desirable to reflect this heterogeneity. The set of single-compartment, conductance-based neuronal models used here has considerable diversity, as evident in the variability seen across neuronal models both in spike trains and their fI curves (Figure 1). The models chosen for this study all fire tonically and do not exhibit bursting (see Section 2 for details and naming of the models). Models are qualitatively sorted based on their firing curves and labeled model A through L accordingly. Model B ceases firing with large current steps (Figure 1B) indicating depolarization block. Some models, such as models A and B, display type I firing, whereas others such as models J and L exhibit type II firing. Type I firing is characterized by continuous fI curves (i.e., firing rate increases from 0 in a continuous fashion) whereas type II firing is characterized by a discontinuity in the fI curve [i.e., a jump occurs from no firing to firing at a certain frequency; (48, 49)]. The other models used here lie on a continuum between these prototypical firing classifications. Most neuronal models exhibit hysteresis with ascending and descending ramps eliciting spikes at different current thresholds. However, the models I, J, and K have large hysteresis (Figure 1 and Supplementary Figure 1). Different types of underlying current dynamics are known to generate these different firing types and hysteresis (48, 50, 51). This broad range of single-compartmental models represents the distinct dynamics of various neuron types across diverse brain regions but does not take into account differences in morphology or synaptic input.

3.2. Characterization of neuronal firing properties

Neuronal firing is a complex phenomenon, and a quantification of firing properties is required for comparisons across neuron types and between different conditions. In this study, we focus on two aspects of firing that are routinely measured in clinical settings (52): rheobase, the smallest injected current at which the neuron fires an action potential, and the shape of the frequency-current (fI) curve as quantified by the area under the curve (AUC) for a fixed range of input currents above rheobase (Figure 3A). The characterization of the firing properties of a neuron by using rheobase and AUC allows to characterize both a neuron's excitability in the sub-threshold regime (rheobase) and periodic firing in the super-threshold regime (AUC) by two independent measures. Note that AUC is essentially quantifying the slope of a neuron's fI curve.

Using these two measures, we quantified the effects a changed property of an ionic current has on neural firing by the differences in both rheobase, Δrheobase, and in AUC, ΔAUC, relative to the wild type neuron. ΔAUC is in addition normalized to the AUC of the wild type neuron, see Equation (2). Each fI curve resulting from an altered ionic current is a point in a two-dimensional coordinate system spanned by Δrheobase and normalized ΔAUC (Figure 3B). An fI curve similar to the one of the wild type neuron is marked by a point close to the origin. In the upper left quadrant, fI curves become steeper (positive difference of AUC values: +ΔAUC) and are shifted to lower rheobases (negative difference of rheobases: −Δrheobase), unambiguously indicating an increased firing that clearly might be classified as a gain of function (GOF) of neuronal firing. The opposite happens in the bottom right quadrant where the slope of fI curves decreases (−ΔAUC), and the rheobase is shifted to higher currents (+Δrheobase), indicating a decreased, loss of function (LOF) firing. In the lower left (−ΔAUC and −Δrheobase) and upper right (+ΔAUC and +Δrheobase) quadrants, the effects on firing are less clear-cut because the changes in rheobase and AUC have opposite effects on neuronal firing. Changes in a neuron's fI curves in these two quadrants cannot uniquely be described as a gain or loss of excitability.

3.3. Sensitivity analysis

Sensitivity analyses are used to understand how input model parameters contribute to determining the output of a model (53). In other words, sensitivity analyses are used to understand how sensitive the output of a model is to a change in input or model parameters. One-factor-a-time sensitivity analyses involve altering one parameter at a time and assessing the impact of this parameter on the output. This approach enables the comparison of given alterations in parameters of ionic currents across models.

For example, when shifting the half activation voltage V_1/2 of the delayed rectifier potassium current in the model G to more depolarized values, then the rheobase of the resulting fI curves shifted to lower currents −Δrheobase, making the neuron more sensitive to weak inputs, but at the same time, the slope of the fI curves was reduced (−normalized ΔAUC), which resulted in a reduced firing rate (Figure 4A). As a result, the effect of a depolarizing shift in the delayed rectifier potassium current half activation V_1/2 in model G is in the bottom left quadrant of Figure 4B and characterization as LOF or GOF in excitability is not possible. Plotting the corresponding changes in AUC against the change in half activation potential V_1/2 results in a monotonically falling curve (thick orange line in Figure 4B). For each of the many models, we got a different relation between the changes in AUC and the shifts in half maximal potential V_1/2 (thin lines in Figure 4B). To further summarize these different dependencies of the various models, we characterized each of these curves by a single number, the Kendall τ correlation coefficient, a monotonically increasing curve resulted in a Kendall τ close to +1 a monotonously decreasing curve in Kendall τ ≈ −1, and a non-monotonous, non-linear relation in Kendall τ close to zero (compare lines in Figure 4B with dots in black box in Figure 4C).

FIGURE 4

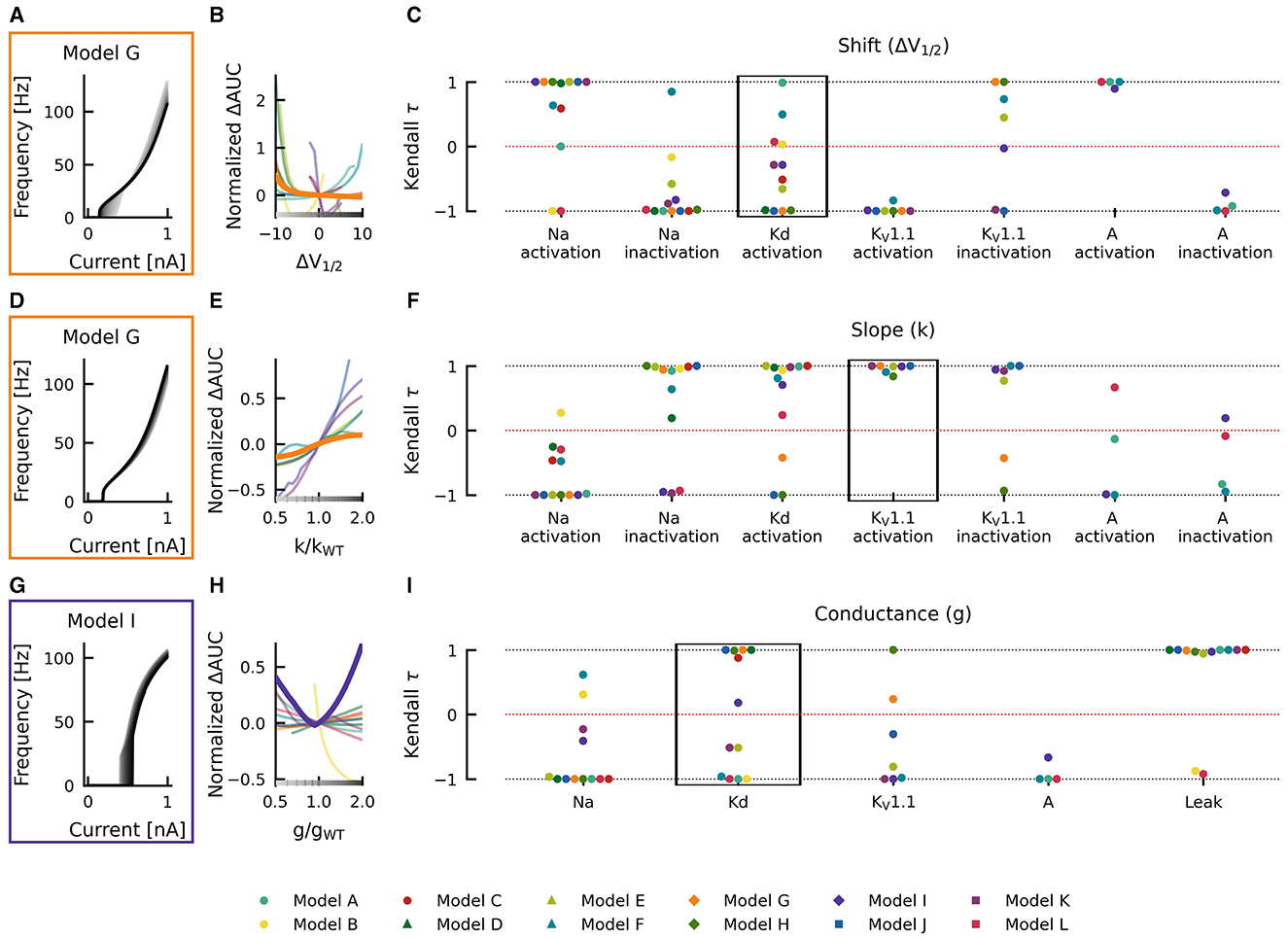
Figure 4. Effects of altered channel kinetics on AUC in various neuron models. The fI curves corresponding to shifts in model G delayed rectifier Kd half activation V_1/2 (A), changes K_V1.1 activation slope factor k in model G (D), and changes in maximal conductance of delayed rectifier K current in the model I (G) are shown. The fI curves from the smallest (gray) to the largest (black) alterations are seen for (A, D, G) in accordance to the grayscale of the x-axis in (B, E, H). The normalized ΔAUC of fI curves is plotted against delayed rectifier K half activation potential [ΔV_1/2; (B)], K_V1.1 activation slope factor k [k/k_WT; (E)], and maximal conductance g of the delayed rectifier Kd current [g/g_WT; (H)] for all models (thin lines) with relationships from the fI curve examples [(A, D, G), respectively] highlighted by thick lines with colors corresponding to the box highlighting each set of fI curves. The Kendall rank correlation (Kendall τ) coefficients between shifts in half maximal potential V_1/2 and normalized ΔAUC (C), slope factor k and normalized ΔAUC (F), as well as maximal current conductances and normalized ΔAUC (I) for each model and current property is computed. The relationships between ΔV_1/2, k/k_WT, and g/g_WT and normalized ΔAUC for the Kendall rank correlations highlighted in the black boxes are depicted in (B, E, H), respectively.

Changes in gating half activation potential V_1/2 and slope factor k as well as the maximum conductance g affected the AUC (Figure 4), but how exactly the AUC was affected usually depended on the specific neuronal model. Increasing the slope factor of the K_V1.1 activation curve, for example, increased the AUC in all models (Kendall τ ≈ +1) but with different slopes (Figures 4D–F). Similar consistent positive correlations could be found for shifts in A-current activation V_1/2. Changes in K_V1.1 half activation V_1/2 and in maximal A-current conductance resulted in negative correlations with the AUC in all models (Kendall τ ≈ −1).

Qualitative differences could be found, for example, when increasing the maximal conductance of the delayed rectifier (Figures 4G–I). In some model neurons, this increased AUC (Kendall τ ≈ +1), whereas in others, AUC was decreased (Kendall τ ≈ −1). In model I, AUC depended in a non-linear way on the maximal conductance of the delayed rectifier, resulting in a Kendall τ close to zero. Even more dramatic qualitative differences between models resulted from shifts of the activation curve of the delayed rectifier, as discussed already above (Figures 4A–C). Some model neurons did almost not depend on changes in Kd-current half activation V_1/2 or showed strong non-linear dependencies, both resulting in Kendall τ close to zero. Many model neurons showed strongly negative correlations, and a few displayed positive correlations with shifting the activation curve of the delayed rectifier.

Changes in gating half activation potential V_1/2 and slope factor k as well as the maximum conductance g affected rheobase (Figure 5). However, in contrast to AUC, qualitatively consistent effects on rheobase across models could be observed. An increase in the maximal conductance of the leak current in model A increased the rheobase (Figure 5G). When these changes were plotted against the change in maximal conductance, a monotonically increasing relationship was evident (thick teal line in Figure 5H). This monotonically increasing relationship was evident in all models (Kendall τ ≈ +1) but with different slopes (thin lines in Figure 5H). Similarly, positive correlations were consistently found across models for maximal conductances of delayed rectifier Kd, K_V1.1, and A-type currents, whereas the maximal conductance of the sodium current was consistently associated with negative correlations (Kendall τ ≈ −1; Figure 5I), i.e., rheobase decreased with increasing maximum conductance in all models.

FIGURE 5

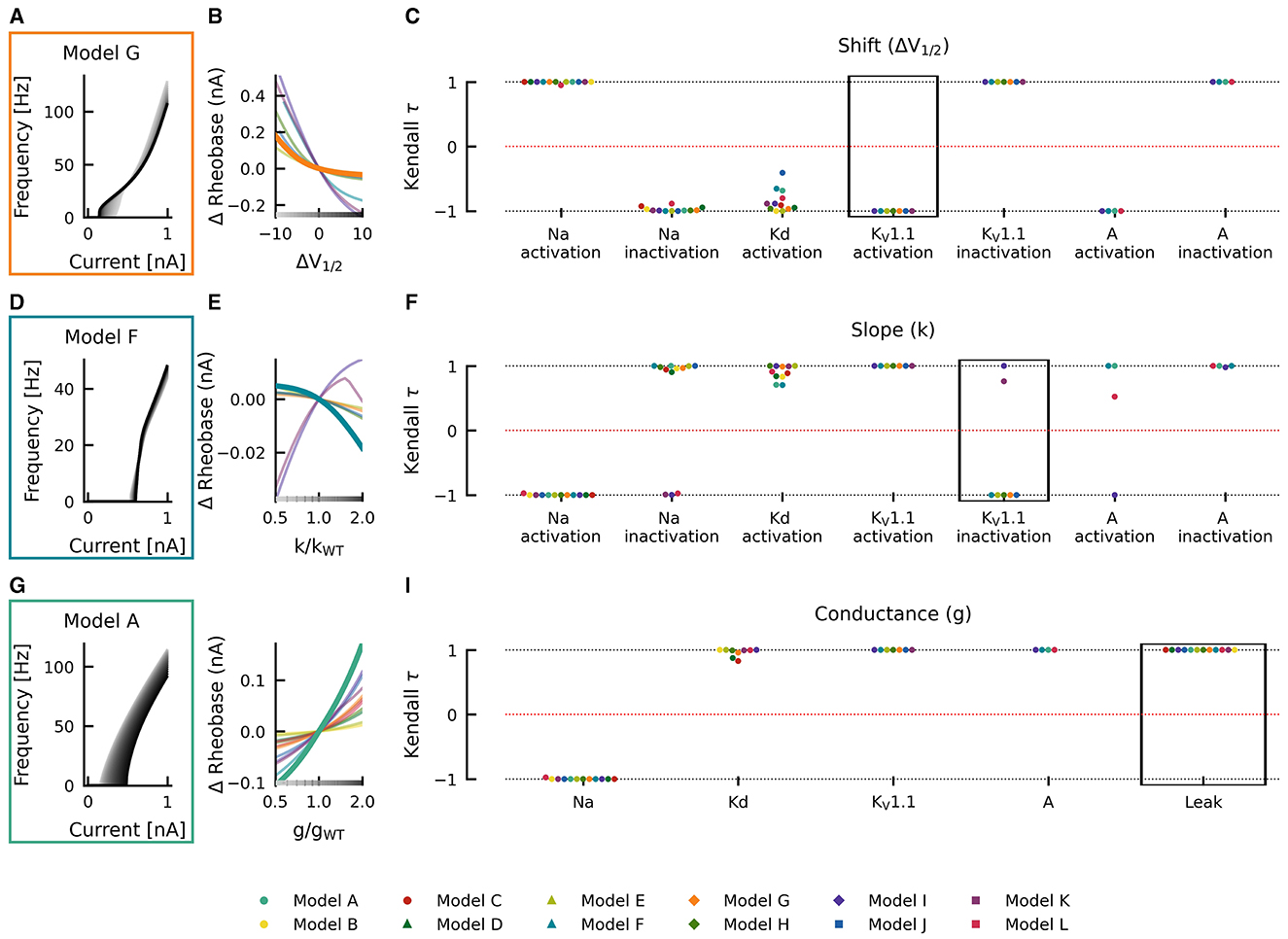
Figure 5. Effects of altered channel kinetics on rheobase. The fI curves corresponding to shifts in model G K_V1.1 activation V_1/2 (A), changes K_V1.1 inactivation slope factor k in model F (D), and changes in maximal conductance of the leak current in model A (G) are shown. The fI curves from the smallest (gray) to the largest (black) alterations are seen for (A, D, G) in accordance to the grayscale of the x-axis in (B, E, H). The Δrheobase of fI curves is plotted against K_V1.1 half activation potential [ΔV_1/2; (B)], K_V1.1 inactivation slope factor k [k/k_WT; (E)], and maximal conductance g of the leak current [g/g_WT; (H)] for all models (thin lines) with relationships from the fI curve examples [(A, D, G), respectively] highlighted by thick lines with colors corresponding to the box highlighting each set of fI curves. The Kendall rank correlation (Kendall τ) coefficients between shifts in half maximal potential V_1/2 and Δrheobase (C), slope factor k and Δrheobase (F) as well as maximal current conductances and Δrheobase (I) for each model and current property is computed. The relationships between ΔV_1/2, k/k_WT, and g/g_WT and Δrheobase for the Kendall rank correlations highlighted in the black boxes are depicted in (B, E, H), respectively.

Although changes in half maximal potential V_1/2 and slope factor k are generally correlated with rheobase, similarly across models, there were some exceptions. Rheobase was affected with both, with positive and negative correlations in different models as a result of changing slope factor of Na⁺-current inactivation (positive: models A–H and J; negative: models I, K, and L), K_V1.1-current inactivation (positive: models I and K; negative: models E–G, J, H), and A-current activation (positive: models A, F and L; negative: model I; Figure 5F). Departures from monotonic relationships also occurred in some models as a result of Kd-current activation V_1/2 (e.g., model J) and slope factor k (models F and G), K_V1.1-current inactivation slope factor k (model K), and A-current activation slope factor k (model L). Thus, identical changes in current gating properties such as the half maximal potential V_1/2 or slope factor k can have differing effects on firing depending on the model in which they occur.

3.4. KCNA1 mutations

Mutations in KCNA1 are associated with episodic ataxia type 1 (EA1) and have been characterized biophysically [as reviewed by (39)]. In the study, they were used as a test case in the effects of various ionic current environments on neuronal firing and on the outcomes of channelopathies. The changes in AUC and rheobase from wild type values for reported EA1 associated KCNA1 mutations were heterogeneous across models containing K_V1.1 but generally showed a decrease in rheobase (Figures 6A–I). Pairwise non-parametric Kendall τ rank correlations between the simulated effects of these K_V1.1 mutations on rheobase were highly correlated across models (Figure 6J), indicating that EA1 associated KCNA1 mutations generally decrease rheobase across diverse neuron types. However, the effects of the K_V1.1 mutations on AUC were more heterogenous as reflected by both weak and strong positive and negative pairwise correlations between models (Figure 6K), suggesting that the effects of ion-channel variant on super-threshold neuronal firing depend both quantitatively and qualitatively on the specific composition of ionic currents in a given neuron.

FIGURE 6

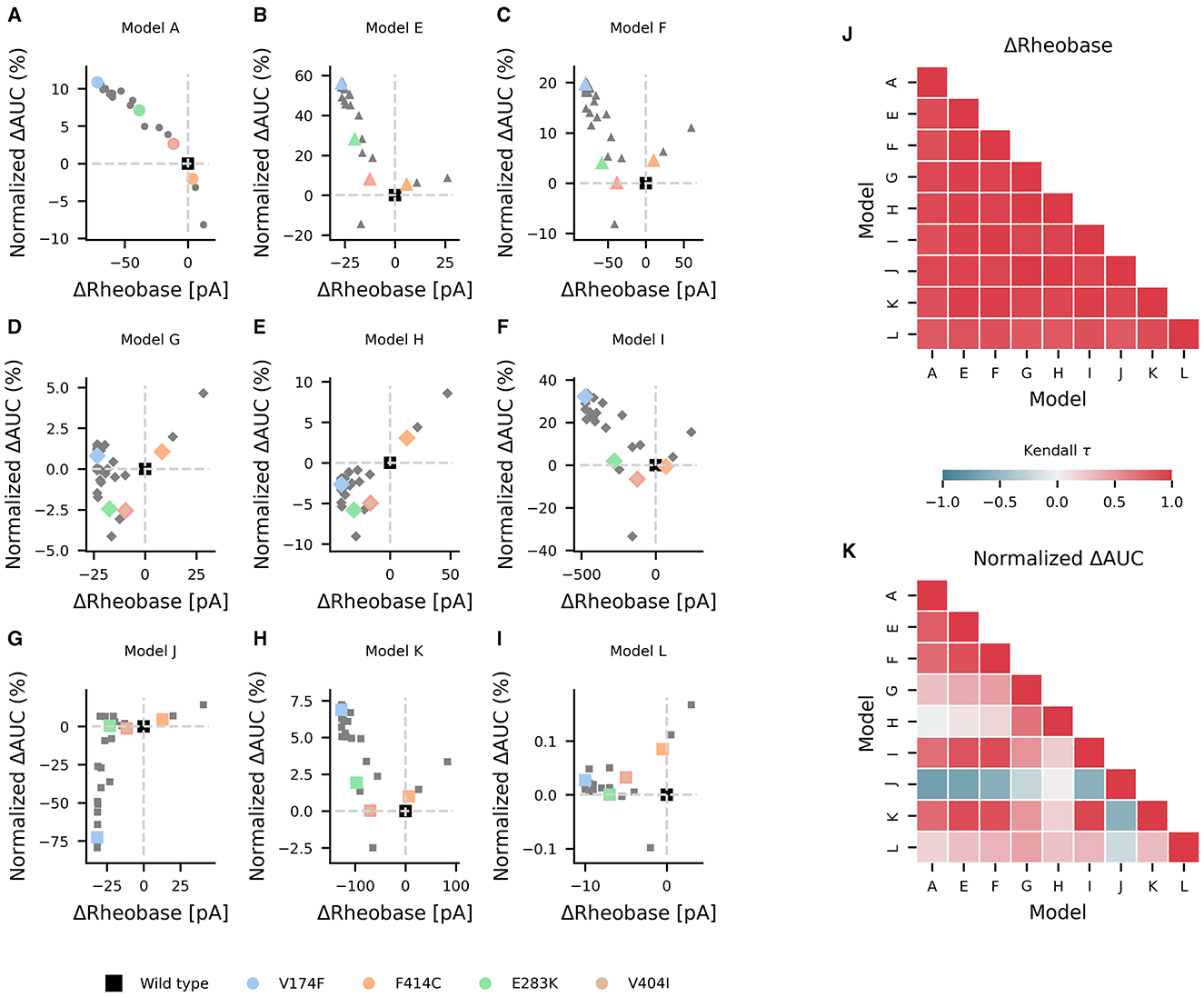
Figure 6. Effects of episodic ataxia type 1 associated KCNA1 mutations on firing. Effects of KCNA1 mutations on AUC (percent change in normalized ΔAUC) and rheobase (ΔRheobase) compared to wild type for model H (A), model E (B), model G (C), model A (D), model F (E), model J (F), model L (G), model I (H), and model K (I). All KCNA1 mutations are marked in gray with the V174F, F414C, E283K, and V404I KCNA1 mutations highlighted in color for each model. Pairwise Kendall rank correlation coefficients (Kendall τ) between the effects of KCNA1 mutations on rheobase and on AUC are shown in (J, K), respectively. A marker shape is indicative of model/firing type, and gray dashed lines denote the quadrants of firing characterization (see Figure 3).

4. Discussion

To compare the effects of ion channel mutations on neuronal firing of different neuron types, we used a diverse set of conductance-based models, that differ in their composition of ionic currents, to systematically characterize the effects of changes in individual channel properties. Additionally, we simulated the effects of specific episodic ataxia type 1 associated (EA1) KCNA1 mutations. Changes to single ionic current properties, as well as known EA1 associated KCNA1 mutations showed consistent effects on the rheobase across neuron types, whereas the effects on the slope of the steady-state fI-curve depended on the neuron type. Our results demonstrate that loss of function (LOF) and gain of function (GOF) on the biophysical level cannot be uniquely transferred to the level of neuronal firing. Thus, the effects caused by different mutations depend on the properties of the other ion channels expressed in a neuron and therefore depend on the channel ensemble of a specific neuron type.

4.1. Firing frequency analysis

Although differences in neuronal firing can be characterized by an area under the curve of the fI curve for a fixed current range, this approach characterizes firing as a mixture of two key features: rheobase and the initial slope of the fI curve. By probing rheobase directly and using an AUC relative to rheobase, we disambiguate these features and enable insights into the effects on rheobase and initial fI curve steepness. This increase in the specificity of our understanding of how ion channel mutations alter firing across neuron types and enable classification is described in Figure 3. Importantly, in cases when ion channel mutations alter rheobase and initial fI curve steepness in ways that oppose effects on firing (upper left and bottom right quadrants of Figure 3B), this disambiguation is important for understanding the outcome of the mutation. In these cases, the regime the neuron is operating in is vital in determining the neuron's firing outcome. If it is in its excitable regime and only occasionally generates an action potential, then the effect on the rheobase is more important. If it is firing periodically with high rates, then the change in AUC might be more relevant.

4.2. Modeling limitations

The single-compartment models used here all capture key aspects of the firing dynamics for their respective neuron. The models fall short of capturing the morphology, complex physiology, biophysics, and heterogeneity of real neurons nor do they take into account subunit stoichiometry, auxiliary subunits, or membrane composition which influence the biophysics of ionic currents (54–57). However, these simplified models allow to study the effect of different compositions of ionic currents on the diversity in firing outcomes of ion channel mutations in isolation.

Our results demonstrate that for exploring possible neuron-type specific effects, variety of currents and dynamics across models is of utmost importance. With this context in mind, the collection of models used here are labeled as models A-L to highlight that the physiological neurons they represent is not of chief concern but rather that the collection of models with different attributes respond heterogeneously to the same perturbation. Additionally, the development of more realistic models is a high priority and will enable neuron-type specific predictions that may aid precision medicine approaches. Thus, weight should not be put on any single predicted firing outcome here in a specific model but rather on the differences in outcomes that occur across the neuron-type spectrum the models used here represent. Further investigation and analysis of the neuron-type effects of ion channel mutations including animal experiments is essential for validation of the results presented here and for furthering the understanding of the effects of channelopathies at multiple levels of scale.

4.3. Neuronal diversity

The nervous system consists of a vastly diverse and heterogeneous collection of neurons with variable properties and characteristics including diverse combinations and expression levels of ion channels which are vital for neuronal firing dynamics.

Advances in high-throughput techniques have enabled large-scale investigation into single-cell properties across the CNS (58) that have revealed large diversity in neuronal gene expression, morphology and neuronal types in the motor cortex (28), neocortex (26, 59), GABAergic neurons in the cortex and retina (60, 61), cerebellum (62), spinal cord (63), visual cortex (64) as well as the retina (65–69).

Diversity across neurons is not limited to gene expression and can also be seen electrophysiologically (28, 59, 64, 65, 67, 70–72) with correlations existing between gene expression and electrophysiological properties (70). At the ion channel level, diversity exists not only between the specific ion channels the different neuron types express but heterogeneity also exists in ion channel expression levels within neuron types (32, 73, 74). As ion channel properties and expression levels are key determinants of neuronal dynamics and firing (30, 75–82) neurons with different ion channel properties and expression levels display different firing properties.

To capture the diversity in neuronal ion channel expression and its relevance in the outcome of ion channel mutations, we used multiple neuronal models with different ionic currents (Figure 2) and underlying firing dynamics (Figure 3).

4.4. Ionic current environments determine the effect of ion channel mutations

To the best of our knowledge, no comprehensive evaluation of how ionic current environment and neuron type affect the outcome of ion channel mutations has been reported. However, comparisons between the effects of such mutations between certain neuron types were described. For instance, the R1648H mutation in SCN1A does not alter the excitability of cortical pyramidal neurons but causes hypoexcitability of adjacent inhibitory GABAergic neurons (24). In the CA3 region of the hippocampus, the equivalent mutation in SCN8A, R1627H, increases the excitability of pyramidal neurons and decreases the excitability of parvalbumin positive interneurons (33). Additionally, the L858H mutation in Na_V1.7, associated with erythromelalgia, has been shown to cause hypoexcitability in sympathetic ganglion neurons and hyperexcitability in dorsal root ganglion neurons (83, 84). The differential effects of L858H Na_V1.7 on firing is dependent on the presence or absence of another sodium channel, namely, the Na_V1.8 subunit (83, 84). These findings, in concert with our findings emphasize that the ionic current environment in which a channelopathy occurs is vital in determining the outcomes of the channelopathy on firing. However, many differences can exist between neuron types at multiple levels of the scale not only in ion channel composition. Despite this complexity, the simulations performed here demonstrate that differential ion channel composition is sufficient to cause neuron-type differences in the effects of ion channel mutations.

Neuron-type specific differences in ionic current properties are important in the effects of ion channel mutations. However, within a neuron-type heterogeneity, in channel expression levels exists, and it is often desirable to generate a population of neuronal models and to screen them for plausibility to biological data in order to capture neuronal population diversity (73, 85). The models we used here are originally generated by characterization of current gating properties and by fitting of maximal conductances to experimental data (4, 43–45). This practice of fixing maximal conductances based on experimental data is limiting as it does not reproduce the variability in channel expression and neuronal firing behavior of a heterogeneous neuron population (86). For example, a model derived from the mean conductance in a neuronal sub-population within the stomatogastric ganglion, the so-called “one-spike bursting” neurons fire three spikes instead of one per burst due to an L-shaped distribution of sodium and potassium conductances (31). Multiple sets of conductances can give rise to the same patterns of activity also termed degeneracy, and differences in neuronal dynamics may only be evident with perturbations (73, 74). The variability in ion channel expression often correlates with the expression of other ion channels (74) and neurons whose behavior is similar may possess correlated variability across different ion channels resulting in stability in the neuronal phenotype (87–89). The variability of ionic currents and degeneracy of neurons may account, at least in part, for the observation that the effect of toxins within a neuronal type is frequently not constant (90–92).

4.5. Effects of KCNA1 mutations

Changes in delayed rectifier potassium currents, analogous to those seen in LOF KCNA1 mutations, change the underlying firing dynamics of the Hodgkin-Huxley model that result in reduced thresholds for repetitive firing and thus contribute to increased excitability (93). Although the Hodgkin-Huxley delayed rectifier lack inactivation, the increase in excitability observed by (93) is in line with our simulation-based predictions of the outcomes of KCNA1 mutations. LOF KCNA1 mutations generally increase neuronal excitability; however, the varying susceptibility on rheobase and different effects on AUC of the fI-curve of KCNA1 mutations across models are indicative that a certain neuron type specific complexity exists. Increased excitability is seen experimentally with K_V1.1 null mice (94, 95), with pharmacological K_V1.1 block (96, 97) and by (93) with simulation-based predictions of KCNA1 mutations. Contrary to these results, Zhao et al. (98) predicted in silico that the depolarizing shifts seen as a result of KCNA1 mutations broaden action potentials and interfere negatively with high frequency action potential firing. However, they varied stimulus duration between different models and therefore comparability of firing rates is lacking in this study.

In our simulations, different current properties alter the impact of KCNA1 mutations on firing as evident in the differences seen in the impact of I_A and I_KV1.1 in the Cb stellate and STN model families on KCNA1 mutation firing. This highlights that not only knowledge of the biophysical properties of a channel but also its neuronal expression and other neuronal channels present is vital for the holistic understanding of the effects of a given ion channel mutation both at the single cell and network level.

4.6. Loss or gain of function characterizations do not fully capture ion channel mutation effects on firing

The effects of changes in channel properties depend in part on the neuronal model in which they occur and can be seen in the variance of correlations (especially in AUC of the fI-curve) across models for a given current property change. Therefore, relative conductances and gating properties of currents in the ionic current environment in which an alteration in current properties occurs play an important role in determining the outcome on firing. The use of LOF and GOF is useful at the level of ion channels to indicate whether a mutation results in more or less ionic current. However, the extension of this thinking onto whether mutations induce LOF or GOF at the level of neuronal firing based on the ionic current LOF/GOF is problematic because of this dependency of neuronal firing changes on the ionic channel environment. Thus, the direct leap from current level LOF/GOF characterizations to effects on firing without experimental or modeling-based evidence, although tempting, should be refrained from and viewed with caution when reported. This is especially relevant in the recent development of personalized medicine for channelopathies, where a patient's specific channelopathy is identified and used to tailor treatments (5, 99–104). In these cases, the effects of specific ion channel mutations are often characterized based on ionic currents in expression systems and classified as LOF or GOF to aid in treatment decisions (5, 38, 103). Although positive treatment outcomes occur with sodium channel blockers in patients with GOF Na_V1.6 mutations, patients with both LOF and GOF Na_V1.6 mutations can benefit from treatment with sodium channel blockers (38). This example suggests that the relationship between effects at the level of ion channels and effects at the level of firing and therapeutics is not linear or evident without further contextual information.

Therefore, the transfer of LOF or GOF from the current to the firing level should be used with caution; the neuron type in which the mutant ion channel is expressed may provide valuable insight into the functional consequences of an ion channel mutation. Experimental assessment of the effects of a patient's specific ion channel mutation in vivo is not generally feasible at a large scale. Therefore, modeling approaches investigating the effects of patient specific channelopathies provide a viable method bridging between characterization of changes in biophysical properties of ionic currents and the firing consequences of these effects. In both experimental and modeling studies on the effects of ion channel mutations on neuronal firing, the specific dependency on neuron type should be considered.

Our simulations demonstrate that the effects of altered ion channel properties on firing is generally influenced by the other ionic currents present in the neuron as illustrated in Figure 7. In channelopathies, the effect of a given ion channel mutation on neuronal firing therefore depends on the neuron type in which those changes occur (24, 33, 83, 84). Although certain complexities of neurons such as differences in neuron-type sensitivities to current property changes, interactions between ionic currents, cell morphology, and subcellular ion channel distribution are neglected here, and it is likely that this increased complexity in vivo would contribute to the neuron-type dependent effects on neuronal firing. The complexity and nuances of the nervous system, including neuron-type dependent firing effects of channelopathies explored here, likely underlie shortcomings in treatment approaches in patients with channelopathies. Accounting for neuron-type dependent firing effects provides an opportunity to improve the efficacy and precision in personalized medicine approaches. Although this is not experimentally feasible, improved modeling and simulation methods to predict neuron-type dependent effects may provide an opportunity to inform therapeutic strategies that are more specific and thus have greater efficacy.

FIGURE 7

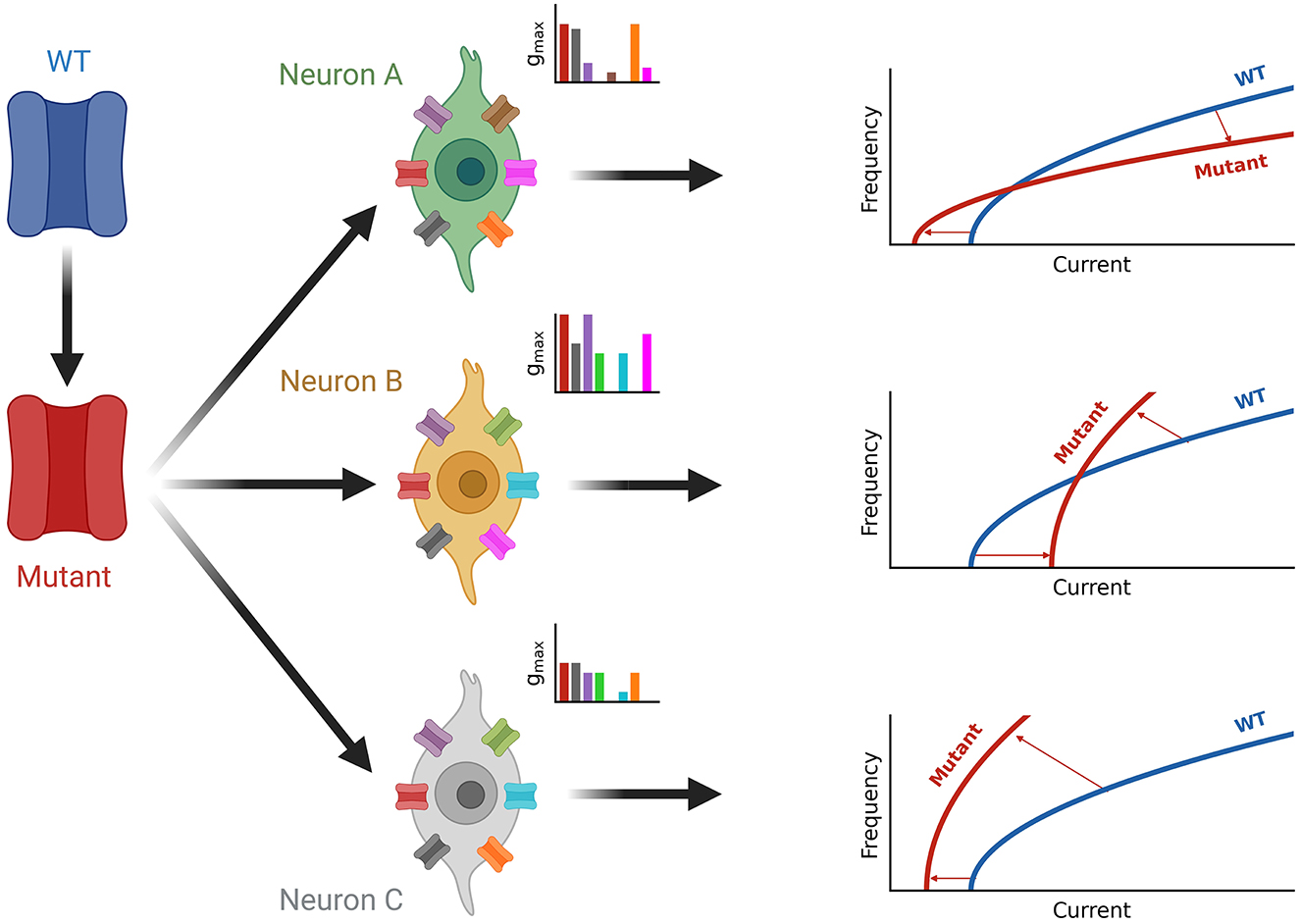
Figure 7. Summary of neuron-type dependence of channelopathies. A wild-type channel (WT, blue) is mutated (Mutant, red) and expressed in different neuron types (green, orange, and gray) each with a unique set of ion channels (see inset axes). The current composition of each neuron determines the effect of firing seen by the shift from the blue wild type fI curve to the red fI curve for the mutated ion channel on the right. Square root functions are used as fI curves for illustration purposes.

With this study, we suggest that neuron-type specific effects are vital to a full understanding of the effects of channelopathies at the level of neuronal firing. Furthermore, we highlight the use of modeling approaches to enable relatively fast and efficient insight into channelopathies.

Data availability statement

The datasets presented in this study can be found in online repositories. The name of the repository and accession number can be found below: GitHub, https://github.com/nkoch1/LOFGOF2023.

Author contributions

NAK, LS, UH, SL, and JB contributed to conception and design of the study. NAK performed simulation and wrote the first draft of the manuscript. NAK and LS analyzed simulation data. All authors wrote sections of the manuscript and contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the German Research Foundation in the Frame of the Research Unit FOR-2715 (DFG, Grants Le1030/15-1/2 and HE 8155/1-2) and the Network for Rare Ion Channel Disorders Treat-ION of the Federal Ministry for Education and Research (BMBF, Grants 01GM1907A and 01GM2210A). SL was supported with an Otfrid-Foerster stipend from the German Society for Epileptology (DGfE).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fneur.2023.1194811/full#supplementary-material

References

1. Bernard G, Shevell MI. Channelopathies: a review. Pediatr Neurol. (2008) 38:73–85. doi: 10.1016/j.pediatrneurol.2007.09.007

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Carbone E, Mori Y. Ion channelopathies to bridge molecular lesions, channel function, and clinical therapies. Pflugers Arch Eur J Physiol. (2020) 472:733–8. doi: 10.1007/s00424-020-02424-y

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Rutecki PA. Neuronal excitability: voltage-dependent currents and synaptic transmission. J Clin Neurophysiol. (1992) 9:195–211.

PubMed Abstract | Google Scholar

4. Pospischil M, Toledo-Rodriguez M, Monier C, Piwkowska Z, Bal T, Frégnac Y, et al. Minimal Hodgkin–Huxley type models for different classes of cortical and thalamic neurons. Biol Cybernet. (2008) 99:427–41. doi: 10.1007/s00422-008-0263-8

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Musto E, Gardella E, Muller RS. Recent advances in treatment of epilepsy-related sodium channelopathies. Eur J Paediatr Neurol. (2020) 24:123–8. doi: 10.1016/j.ejpn.2019.12.009

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Kullmann DM. The neuronal channelopathies. Brain. (2002) 125:1177–95. doi: 10.1093/brain/awf130

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Waxman SG. Channelopathies have many faces. Nature. (2011) 472:173–4. doi: 10.1038/472173a

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Kim HJ, Kang HC. Treatment strategies targeting specific genetic etiologies in epilepsy. J Gen Med. (2021) 18:8–15. doi: 10.5734/JGM.2021.18.1.8

CrossRef Full Text | Google Scholar

9. Niday Z, Tzingounis AV. Potassium channel gain of function in epilepsy: an unresolved paradox. The Neuroscientist. (2018) 24:368–80. doi: 10.1177/1073858418763752

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Wei F, Yan LM, Su T, He N, Lin ZJ, Wang J, et al. Ion channel genes and epilepsy: functional alteration, pathogenic potential, and mechanism of epilepsy. Neurosci Bull. (2017) 33:455–77. doi: 10.1007/s12264-017-0134-1

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Wolff M, Johannesen KM, Hedrich UBS, Masnada S, Rubboli G, Gardella E, et al. Genetic and phenotypic heterogeneity suggest therapeutic implications in SCN2A-related disorders. Brain. (2017) 140:1316–36. doi: 10.1093/brain/awx054

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Masnada S, Hedrich UBS, Gardella E, Schubert J, Kaiwar C, Klee EW, et al. Clinical spectrum and genotype-phenotype associations of KCNA2-related encephalopathies. Brain. (2017) 140:2337–54. doi: 10.1093/brain/awx184

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Orsini A, Esposito M, Perna D, Bonuccelli A, Peroni D, Striano P. Personalized medicine in epilepsy patients. J Transl Genet Genomics. (2018) 2:16. doi: 10.20517/jtgg.2018.14

CrossRef Full Text | Google Scholar

14. Yang Y, Mis MA, Estacion M, Dib-Hajj SD, Waxman SG. NaV1.7 as a pharmacogenomic target for pain: moving toward precision medicine. Trends Pharmacol Sci. (2018) 39:258–75. doi: 10.1016/j.tips.2017.11.010

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Colasante G, Lignani G, Brusco S, Di Berardino C, Carpenter J, Giannelli S, et al. dCas9-based Scn1a gene activation restores inhibitory interneuron excitability and attenuates seizures in Dravet syndrome mice. Mol Therapy. (2020) 28:235–53. doi: 10.1016/j.ymthe.2019.08.018

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Yu FH, Mantegazza M, Westenbroek RE, Robbins CA, Kalume F, Burton KA, et al. Reduced sodium current in GABAergic interneurons in a mouse model of severe myoclonic epilepsy in infancy. Nat Neurosci. (2006) 9:1142–9. doi: 10.1038/nn1754

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Scalmani P, Rusconi R, Armatura E, Zara F, Avanzini G, Franceschetti S, et al. Effects in neocortical neurons of mutations of the Nav1.2 Na+ channel causing benign familial neonatal-infantile seizures. J Neurosci. (2006) 26:10100–9. doi: 10.1523/JNEUROSCI.2476-06.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Smith RS, Kenny CJ, Ganesh V, Jang A, Borges-Monroy R, Partlow JN, et al. Sodium channel SCN3A (NaV1.3) regulation of human cerebra cortical folding and oral motor development. Neuron. (2018) 99:905–13.e7. doi: 10.1016/j.neuron.2018.07.052

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Liu Y, Schubert J, Sonnenberg L, Helbig KL, Hoei-Hansen CE, Koko M, et al. Neuronal mechanisms of mutations in SCN8A causing epilepsy or intellectual disability. Brain. (2019) 142:376–90. doi: 10.1093/brain/awy326

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Mantegazza M, Broccoli V. SCN1A/NaV1.1 channelopathies: mechanisms in expression systems, animal models, and human iPSC models. Epilepsia. (2019) 60:S25–38. doi: 10.1111/epi.14700

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Xie G, Harrison J, Clapcote SJ, Huang Y, Zhang JY, Wang LY, et al. A new Kv1.2 channelopathy underlying cerebellar ataxia. J Biol Chem. (2010) 285:32160–73. doi: 10.1074/jbc.M110.153676

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Lory P, Nicole S, Monteil A. Neuronal Cav3 channelopathies: recent progress and perspectives. Pflugers Arch Eur J Physiol. (2020) 472:831–44. doi: 10.1007/s00424-020-02429-7

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Habib AM, Wood JN, Cox JJ. Sodium channels and pain. In:Schaible HG, , editor. Handbook of Experimental Pharmacology. Berlin; Heidelberg: Springer (2015). p. 39–56.

Google Scholar

24. Hedrich UBS, Liautard C, Kirschenbaum D, Pofahl M, Lavigne J, Liu Y, et al. Impaired action potential initiation in GABAergic interneurons causes hyperexcitable networks in an epileptic mouse model carrying a human NaV1.1 mutation. J Neurosci. (2014) 34:14874–89. doi: 10.1523/JNEUROSCI.0721-14.2014

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Yao Z, Velthoven CTJ, Nguyen TN, Goldy J, Sedeno-Cortes AE, Baftizadeh F, et al. A taxonomy of transcriptomic cell types across the isocortex and hippocampal formation. Cell. (2021) 184:3222–41. doi: 10.1016/j.cell.2021.04.021

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Cadwell CR, Palasantza A, Jiang X, Berens P, Deng Q, Yilmaz M, et al. Electrophysiological, transcriptomic and morphologic profiling of single neurons using Patch-seq. Nat Biotechnol. (2016) 34:199–203. doi: 10.1038/nbt.3445

PubMed Abstract | CrossRef Full Text | Google Scholar

27. BRAIN Initiative Cell Census Network. A multimodal cell census and atlas of the mammalian primary motor cortex. Nature. (2021) 598:86–102. doi: 10.1038/s41586-021-03950-0

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Scala F, Kobak D, Bernabucci M, Bernaerts Y, Cadwell CR, Castro JR, et al. Phenotypic variation of transcriptomic cell types in mouse motor cortex. Nature. (2021) 598:144–50. doi: 10.1038/s41586-020-2907-3

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Layer N, Sonnenberg L, Pardo Gonzalez E, Benda J, Hedrich UBS, Lerche H, et al. Dravet variant SCN1AA1783V impairs interneuron firing predominantly by altered channel activation. Front Cell Neurosci. (2021) 15:754530. doi: 10.3389/fncel.2021.754530

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Kispersky TJ, Caplan JS, Marder E. Increase in sodium conductance decreases firing rate and gain in model neurons. J Neurosci. (2012) 32:10995–1004. doi: 10.1523/JNEUROSCI.2045-12.2012

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Golowasch J, Goldman MS, Abbott LF, Marder E. Failure of averaging in the construction of a conductance-based neuron model. J Neurophysiol. (2002) 87:1129–31. doi: 10.1152/jn.00412.2001

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Barreiro AK, Thilo EL, Shea-Brown E. A-current and type I/type II transition determine collective spiking from common input. J Neurophysiol. (2012) 108:1631–45. doi: 10.1152/jn.00928.2011

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Makinson CD, Dutt K, Lin F, Papale LA, Shankar A, Barela AJ, et al. An Scn1a epilepsy mutation in Scn8a alters seizure susceptibility and behavior. Exp Neurol. (2016) 275:46–58. doi: 10.1016/j.expneurol.2015.09.008

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Claes L, Del-Favero J, Ceulemans B, Lagae L, Van Broeckhoven C, De Jonghe P. De novo mutations in the sodium-channel gene SCN1A cause severe myoclonic epilepsy of infancy. Am J Hum Genet. (2001) 68:1327–32. doi: 10.1086/320609

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Fujiwara T, Sugawara T, Mazaki-Miyazaki E, Takahashi Y, Fukushima K, Watanabe M, et al. Mutations of sodium channel ± subunit type 1 (SCN1A) in intractable childhood epilepsies with frequent generalized tonic-clonic seizures. Brain. (2003) 126:531–46. doi: 10.1093/brain/awg053

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Ohmori I, Ouchida M, Ohtsuka Y, Oka E, Shimizu K. Significant correlation of the SCN1A mutations and severe myoclonic epilepsy in infancy. Biochem Biophys Res Commun. (2002) 295:17–23. doi: 10.1016/S0006-291X(02)00617-4

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Oguni H, Hayashi K, Awaya Y, Fukuyama Y, Osawa M. Severe myoclonic epilepsy in infants–a review based on the Tokyo Women's Medical University series of 84 cases. Brain Dev. (2001) 23:736–48. doi: 10.1016/S0387-7604(01)00276-5

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Johannesen KM, Liu Y, Koko M, Gjerulfsen CE, Sonnenberg L, Schubert J, et al. Genotype-phenotype correlations in SCN8A-related disorders reveal prognostic and therapeutic implications. Brain. (2021) 145:2991–3009. doi: 10.1093/brain/awab321

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Lauxmann S, Sonnenberg L, Koch NA, Bosselmann CM, Winter N, Schwarz N, et al. Therapeutic potential of sodium channel blockers as targeted therapy approach in KCNA1-associated episodic ataxia (EA1) and a comprehensive review of the literature. Front Neurol. (2021) 12:703970. doi: 10.3389/fneur.2021.703970

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Bayraktar E, Liu Y, Sonnenberg L, Hedrich UBS, Sara Y, Eltokhi A, et al. In vitro effects of eslicarbazepine (S-licarbazepine) as a potential precision therapy on SCN8A variants causing neuropsychiatric disorders. Brit J Pharmacol. (2022) 180:1038–55. doi: 10.1111/bph.15981

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Browne DL, Gancher ST, Nutt JG, Brunt ERP, Smith EA, Kramer P, et al. Episodic ataxia/myokymia syndrome is associated with point mutations in the human potassium channel gene, KCNA1. Nat Genet. (1994) 8:136–40. doi: 10.1038/ng1094-136

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Browne DL, Brunt ERP, Griggs RC, Nutt JG, Gancher ST, Smith EA, et al. Identification of two new KCNA1 mutations in episodic ataxia/myokymia families. Hum Mol Genet. (1995) 4:1671–2.

PubMed Abstract | Google Scholar

43. Ranjan R, Logette E, Marani M, Herzog M, Tache V, Scantamburlo E, et al. A kinetic map of the homomeric voltage-gated potassium channel (Kv) family. Front Cell Neurosci. (2019) 13:358. doi: 10.3389/fncel.2019.00358

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Alexander RPD, Mitry J, Sareen V, Khadra A, Bowie D. Cerebellar stellate cell excitability is coordinated by shifts in the gating behavior of voltage-gated Na+ and A-type K+ channels. eNeuro. (2019) 6:ENEURO.0126-19.2019. doi: 10.1523/ENEURO.0126-19.2019

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Otsuka T, Abe T, Tsukagawa T, Song WJ. Conductance-based model of the voltage-dependent generation of a plateau potential in subthalamic neurons. J Neurophysiol. (2004) 92:255–64. doi: 10.1152/jn.00508.2003

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Clerx M, Beattie KA, Gavaghan DJ, Mirams GR. Four ways to fit an ion channel model. Biophys J. (2019) 117:2420–37. doi: 10.1016/j.bpj.2019.08.001

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Whittaker DG, Clerx M, Lei CL, Christini DJ, Mirams GR. Calibration of ionic and cellular cardiac electrophysiology models. WIREs Syst Biol Med. (2020) 12:e1482. doi: 10.1002/wsbm.1482

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Ermentrout B. Type I membranes, phase resetting curves, and synchrony. Neural Comput. (1996) 8:979–1001.

PubMed Abstract | Google Scholar

49. Rinzel J, Ermentrout G. Analysis of neural excitability and oscillations. In:Koch C, Segev I, , editors. Methods in Neuronal Modeling. Cambridge, MA: MIT Press (1989). p. 135–69.

Google Scholar

50. Ermentrout GB, Chow CC. Modeling neural oscillations. Physiol Behav. (2002) 77:629–33. doi: 10.1016/S0031-9384(02)00898-3

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Izhikevich EM. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting. Cambridge, MA: MIT Press (2006).

PubMed Abstract | Google Scholar

52. Bryson A, Hatch RJ, Zandt BJ, Rossert C, Berkovic SF, Reid CA, et al. GABA-mediated tonic inhibition differentially modulates gain in functional subtypes of cortical interneurons. Proc Natl Acad Sci USA. (2020) 117:3192–202. doi: 10.1073/pnas.1906369117

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Saltelli A. Sensitivity analysis for importance assessment. Risk Anal. (2002) 22:579–90. doi: 10.1111/0272-4332.00040

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Al-Sabi A, Kaza S, Dolly JO, Wang J. Pharmacological characteristics of Kv1.1- and Kv1.2-containing channels are influenced by the stoichiometry and positioning of their α aubunits. Biochem J. (2013) 454:101–8. doi: 10.1042/BJ20130297

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Oliver D, Lien CC, Soom M, Baukrowitz T, Jonas P, Fakler B. Functional conversion between A-type and delayed rectifier K+ channels by membrane lipids. Science. (2004) 304:265–70. doi: 10.1126/science.1094113

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Pongs O, Schwarz JR. Ancillary subunits associated with voltage-dependent K+ channels. Physiol Rev. (2010) 90:755–96. doi: 10.1152/physrev.00020.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Rettig J, Heinemann SH, Wunder F, Lorra C, Parcej DN, Oliver Dolly J, et al. Inactivation properties of voltage-gated K+ channels altered by presence of beta-subunit. Nature. (1994) 369:289–94.

PubMed Abstract | Google Scholar

58. Poulin JF, Tasic B, Hjerling-Leffler J, Trimarchi JM, Awatramani R. Disentangling neural cell diversity using single-cell transcriptomics. Nat Neurosci. (2016) 19:1131–41. doi: 10.1038/nn.4366

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Cadwell CR, Scala F, Fahey PG, Kobak D, Mulherkar S, Sinz FH, et al. Cell type composition and circuit organization of clonally related excitatory neurons in the juvenile mouse neocortex. eLife. (2020) 9:e52951. doi: 10.7554/eLife.52951

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Huang ZJ, Paul A. The diversity of GABAergic neurons and neural communication elements. Nat Rev Neurosci. (2019) 20:563–72. doi: 10.1038/s41583-019-0195-4

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Laturnus S, Kobak D, Berens P. A systematic evaluation of interneuron morphology representations for cell type discrimination. Neuroinformatics. (2020) 18:591–609. doi: 10.1007/s12021-020-09461-z

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Kozareva V, Martin C, Osorno T, Rudolph S, Guo C, Vanderburg C, et al. A transcriptomic atlas of mouse cerebellar cortex comprehensively defines cell types. Nature. (2021) 598:214–9. doi: 10.1038/s41586-021-03220-z

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Alkaslasi MR, Piccus ZE, Hareendran S, Silberberg H, Chen L, Zhang Y, et al. Single nucleus RNA-sequencing defines unexpected diversity of cholinergic neuron types in the adult mouse spinal cord. Nat Commun. (2021) 12:2471. doi: 10.1038/s41467-021-22691-2

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Gouwens NW, Sorensen SA, Berg J, Lee C, Jarsky T, Ting J, et al. Classification of electrophysiological and morphological neuron types in the mouse visual cortex. Nat Neurosci. (2019) 22:1182–95. doi: 10.1038/s41593-019-0417-0

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Baden T, Berens P, Franke K, Rosen MR, Bethge M, Euler T. The functional diversity of retinal ganglion cells in the mouse. Nature. (2016) 529:345–50. doi: 10.1038/nature16468

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Voigt AP, Whitmore SS, Flamme-Wiese MJ, Riker MJ, Wiley LA, Tucker BA, et al. Molecular characterization of foveal versus peripheral human retina by single-cell RNA sequencing. Exp Eye Res. (2019) 184:234–42. doi: 10.1016/j.exer.2019.05.001

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Berens P, Euler T. Neuronal diversity in the retina. e-Neuroforum. (2017) 23:93–101. doi: 10.1515/nf-2016-A055

CrossRef Full Text | Google Scholar

68. Yan W, Laboulaye MA, Tran NM, Whitney IE, Benhar I, Sanes JR. Mouse retinal cell atlas: molecular identification of over sixty amacrine cell types. J Neurosci. (2020) 40:5177–95. doi: 10.1523/JNEUROSCI.0471-20.2020

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Yan W, Peng YR, van Zyl T, Regev A, Shekhar K, Juric D, et al. Cell atlas of the human fovea and peripheral retina. Sci Rep. (2020) 10:9802. doi: 10.1038/s41598-020-66092-9

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Tripathy SJ, Toker L, Li B, Crichlow CL, Tebaykin D, Mancarci BO, et al. Transcriptomic correlates of neuron electrophysiological diversity. PLoS Comput Biol. (2017) 13:e1005814. doi: 10.1371/journal.pcbi.1005814

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Gouwens NW, Berg J, Feng D, Sorensen SA, Zeng H, Hawrylycz MJ, et al. Systematic generation of biophysically detailed models for diverse cortical neuron types. Nat Commun. (2018) 9:710. doi: 10.1038/s41467-017-02718-3

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Tripathy SJ, Burton SD, Geramita M, Gerkin RC, Urban NN. Brain-wide analysis of electrophysiological diversity yields novel categorization of mammalian neuron types. J Neurophysiol. (2015) 113:3474–89. doi: 10.1152/jn.00237.2015

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Marder E, Taylor AL. Multiple models to capture the variability in biological neurons and networks. Nat Neurosci. (2011) 14:133–8. doi: 10.1038/nn.2735

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Goaillard JM, Marder E. Ion channel degeneracy, variability, and covariation in neuron and circuit resilience. Annu Rev Neurosci. (2021) 44:335–57. doi: 10.1146/annurev-neuro-092920-121538

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Balachandar A, Prescott SA. Origin of heterogeneous spiking patterns from continuously distributed ion channel densities: a computational study in spinal dorsal horn neurons. J Physiol. (2018) 596:1681–97. doi: 10.1113/JP275240

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Gu H, Chen S. Potassium-induced bifurcations and chaos of firing patterns observed from biological experiment on a neural pacemaker. Sci China Technol Sci. (2014) 57:864–71. doi: 10.1007/s11431-014-5526-0

CrossRef Full Text | Google Scholar

77. Zeberg H, Robinson HPC, Århem P. Density of voltage-gated potassium channels is a bifurcation parameter in pyramidal neurons. J Neurophysiol. (2015) 113:537–49. doi: 10.1152/jn.00907.2013

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Århem P, Blomberg C. Ion channel density and threshold dynamics of repetitive firing in a cortical neuron model. Biosystems. (2007) 89:117–25. doi: 10.1016/j.biosystems.2006.03.015

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Qi Y, Watts AL, Kim JW, Robinson PA. Firing patterns in a conductance-based neuron model: bifurcation, phase diagram, and chaos. Biol Cybernet. (2013) 107:15–24. doi: 10.1007/s00422-012-0520-8

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Gu H, Pan B, Chen G, Duan L. Biological experimental demonstration of bifurcations from bursting to spiking predicted by theoretical models. Nonlinear Dyn. (2014) 78:391–407. doi: 10.1007/s11071-014-1447-5

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Zeberg H, Blomberg C, Århem P. Ion channel density regulates switches between regular and fast spiking in soma but not in axons. PLoS Comput Biol. (2010) 6:e1000753. doi: 10.1371/journal.pcbi.1000753

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Zhou X, Xu Y, Wang G, Jia Y. Ionic channel blockage in stochastic Hodgkin–Huxley neuronal model driven by multiple oscillatory signals. Cogn Neurodyn. (2020) 14:569–78. doi: 10.1007/s11571-020-09593-7

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Waxman SG. Channel, neuronal and clinical function in sodium channelopathies: from genotype to phenotype. Nat Neurosci. (2007) 10:405–9. doi: 10.1038/nn1857

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Rush AM, Dib-Hajj SD, Liu S, Cummins TR, Black JA, Waxman SG. A single sodium channel mutation produces hyper- or hypoexcitability in different types of neurons. Proc Natl Acad Sci USA. (2006) 103:8245–50. doi: 10.1073/pnas.0602813103

PubMed Abstract | CrossRef Full Text | Google Scholar

85. O'Leary T, Marder E. Temperature-robust neural function from activity-dependent ion channel regulation. Curr Biol. (2016) 26:2935–41. doi: 10.1016/j.cub.2016.08.061

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Verma P, Kienle A, Flockerzi D, Ramkrishna D. Computational analysis of a 9D model for a small DRG neuron. J Comput Neurosci. (2020) 48:429–44. doi: 10.1007/s10827-020-00761-6

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Lamb DG, Calabrese RL. Correlated conductance parameters in leech heart motor neurons contribute to motor pattern formation. PLoS ONE. (2013) 8:e79267. doi: 10.1371/journal.pone.0079267

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Soofi W, Archila S, Prinz AA. Co-variation of ionic conductances supports phase maintenance in stomatogastric neurons. J Comput Neurosci. (2012) 33:77–95. doi: 10.1007/s10827-011-0375-3

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Taylor AL, Goaillard JM, Marder E. How multiple conductances determine electrophysiological properties in a multicompartment model. J Neurosci. (2009) 29:5573–86. doi: 10.1523/JNEUROSCI.4438-08.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Khaliq ZM, Raman IM. Relative contributions of axonal and somatic Na channels to action potential initiation in cerebellar Purkinje neurons. J Neurosci. (2006) 26:1935–44. doi: 10.1523/JNEUROSCI.4664-05.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Puopolo M, Raviola E, Bean BP. Roles of subthreshold calcium current and sodium current in spontaneous firing of mouse midbrain dopamine neurons. J Neurosci. (2007) 27:645–56. doi: 10.1523/JNEUROSCI.4341-06.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Ransdell JL, Nair SS, Schulz DJ. Neurons within the same network independently achieve conserved output by differentially balancing variable conductance magnitudes. J Neurosci. (2013) 33:9950–56. doi: 10.1523/JNEUROSCI.1095-13.2013

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Hafez OA, Gottschalk A. Altered neuronal excitability in a Hodgkin-Huxley model incorporating channelopathies of the delayed rectifier potassium channel. J Comput Neurosci. (2020) 48:377–86. doi: 10.1007/s10827-020-00766-1

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Smart SL, Lopantsev V, Zhang CL, Robbins CA, Wang H, Chiu SY, et al. Deletion of the KV1.1 potassium channel causes epilepsy in mice. Neuron. (1998) 20:809–19. doi: 10.1016/S0896-6273(00)81018-1

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Zhou L, Zhang CL, Messing A, Chiu SY. Temperature-sensitive neuromuscular transmission in Kv1.1 null mice: role of potassium channels under the myelin sheath in young nerves. J Neurosci. (1998) 18:7200–15. doi: 10.1523/JNEUROSCI.18-18-07200.1998

PubMed Abstract | CrossRef Full Text | Google Scholar

96. Chi XX, Nicol GD. Manipulation of the potassium channel Kv1.1 and its effect on neuronal excitability in rat sensory neurons. J Neurophysiol. (2007) 98:2683–92. doi: 10.1152/jn.00437.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Morales-Villagran A, Urena-Guerrero ME, Tapia R. Protection by NMDA receptor antagonists against seizures induced by intracerebral administration of 4-aminopyridine. Eur J Pharmacol. (1996) 305:87–93.

PubMed Abstract | Google Scholar

98. Zhao J, Petitjean D, Haddad GA, Batulan Z, Blunck R. A common kinetic property of mutations linked to episodic ataxia type 1 studied in the Shaker Kv channel. Int J Mol Sci. (2020) 21:7602. doi: 10.3390/ijms21207602

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Weber YG, Biskup S, Helbig KL, Von Spiczak S, Lerche H. The role of genetic testing in epilepsy diagnosis and management. Expert Rev Mol Diagn. (2017) 17:739–50. doi: 10.1080/14737159.2017.1335598

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Ackerman MJ, Marcou CA, Tester DJ. Personalized medicine: genetic diagnosis for inherited cardiomyopathies/channelopathies. Rev Esp Cardiol. (2013) 66:298–307. doi: 10.1016/j.rec.2012.12.010

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Helbig I, Ellis CA. Personalized medicine in genetic epilepsies–possibilities, challenges, and new frontiers. Neuropharmacology. (2020) 172:107970. doi: 10.1016/j.neuropharm.2020.107970

PubMed Abstract | CrossRef Full Text | Google Scholar

102. Gnecchi M, Sala L, Schwartz PJ. Precision medicine and cardiac channelopathies: when dreams meet reality. Eur Heart J. (2021) 42:1661–75. doi: 10.1093/eurheartj/ehab007

PubMed Abstract | CrossRef Full Text | Google Scholar

103. Brunklaus A, Feng T, Brunger T, Perez-Palma E, Heyne H, Matthews E, et al. Gene variant effects across sodium channelopathies predict function and guide precision therapy. Brain. (2022) 145:4275–86. doi: 10.1093/brain/awac006

PubMed Abstract | CrossRef Full Text | Google Scholar

104. Hedrich UBS, Lauxmann S, Wolff M, Synofzik M, Bast T, Binelli A, et al. 4-Aminopyridine is a promising treatment option for patients with gain-of-function KCNA2-encephalopathy. Sci Transl Med. (2021) 13:eaaz4957. doi: 10.1126/scitranslmed.aaz4957

PubMed Abstract | CrossRef Full Text | Google Scholar