- RoCAL, Rochester Institute of Technology, Rochester, NY, United States
This invited Review discusses causal learning in the context of robotic intelligence. The Review introduces the psychological findings on causal learning in human cognition, as well as the traditional statistical solutions for causal discovery and causal inference. Additionally, we examine recent deep causal learning algorithms, with a focus on their architectures and the benefits of using deep nets, and discuss the gap between deep causal learning and the needs of robotic intelligence.
1. Introduction
Intelligent robots infer knowledge about the world from sensor perception, estimate status, model the world, and plan and execute tasks. Although intelligent robots have achieved remarkable progress in the past two decades, improving their reliability in the real world remains a challenge. The challenges are rooted in the wide variance of environments and robotic tasks and the uncertainties of the world, sensor observation, models, status, and the execution of tasks.
Robots achieve intelligence through the use of knowledge or methods that learn knowledge from data. Early intelligent robots and some state-of-art applied intelligent robots are programmed with knowledge and rules for making decisions based on dynamic observations. This type of achieved intelligence has predictable performance and is explainable; however, it often lacks adaptiveness as the program complexity grows exponentially with respect to the complexity of tasks. Additionally, robots can use artificial intelligence (AI) algorithms (to learn from data) to achieve intelligence. These methods are considered similar to how humans achieve intelligence and are considered a possible solution that breaks the bottleneck of applicability, scalability, and online learning. However, as today's AI methods demonstrate superior performance in terms of “interpolating” data, these methods still have difficulty in finding knowledge and reasoning.
Humans, or even animals, effortlessly understand the world from an early age and build up prior knowledge quickly to make causal decisions in daily life. We can use the perception of an object's physical properties as an example. Even infants demonstrate instinctual behavior when inspecting a new toy with their hands and eyes in tandem with learning the toy's properties (Smith et al., 2020). Robots, in comparison, still have problems understanding and operating the most commonly used objects in daily life. Although it is clear that causality is critical from low-level visual perception to high-level decision-making, state of art robots rarely establish the causal relationship and utilize it to improve intelligence. However, there are examples of “causal” relationships improving robotic intelligence. For example, simultaneous localization and mapping (SLAM) explicitly utilizes the fact that causal relationships of robot movements causally change observations and use a Bayesian network to improve mapping and localization simultaneously (Thrun et al., 2005).
Causal learning consists of causal discovery and causal inference. Classical causal learning methods include causal discovery, which learns cause-effect relationships, and causal inference, which estimates the level of impact that changes in factors have on each other. Traditional causal learning algorithms mainly use statistical theories and tools. With the development of deep-learning technology, there are trends that use deep learning to improve causal learning with high-dimensional data and big data and trends that use causal learning to improve deep-learning model expandability, extrapolation capability, and explainability. Although these emerging techniques are not developed and have not yet been tested on intelligent robots, they do have great potential to improve robotic intelligence and expand the applicability of intelligent robots. This paper incompletely but systematically reviews causal cognition, causal learning, and deep causal learning, and discusses the need for deep causal learning in robotic intelligence. The rest of the Review is organized as follows: the section “Causal Cognition and Intelligence” briefly introduces causal cognition from the psychological perspective, the section “Causal Learning” presents statistical causal discovery and causal inference, the “Deep Causal Learning” section discusses deep causal learning for robotic intelligence, and the final section presents conclusions.
2. Causal cognition and intelligence
Although there is much debate about the mechanism of cognition, modern physiological studies generally support that the way in which humans cognize causal regularities is more sophisticated than that of any other animal on the planet (Penn and Povinelli, 2007). Causal cognition has major differences with associative learning, as it can improve inferences from non-obvious and hidden causal relationships (Kuhn, 2012). Learning causal relationships is critical for humans (Spelke et al., 1992; Kuhn, 2012), as it confers an important advantage for survival (Legare et al., 2017; Bender and Beller, 2019).
It is clear that to achieve or avoid an outcome, one may want to predict the probability that an effect will occur given that a certain cause of the effect occurs. It remains unclear as to how the input non-causal empirical observations of cues and outcomes yield output values. Studies have shown that causal cognition emerges early in development (Bender and Beller, 2019). Researchers are amazed by how children learn so much about the world so quickly and effortlessly (Gopnik et al., 2004; Sobel and Legare, 2014). Studies have demonstrated that infants as young as 4.5 months register particular aspects of physical causality (Leslie and Keeble, 1987; Spelke et al., 1992; Needham and Baillargeon, 1993; Hespos and Baillargeon, 2001), toddlers recognize various causal relations in the psychological domain, especially about others' desires and intentions (Wellman, 1992; Bonawitz et al., 2010), and preschoolers understand that biological and psychological events can rely on non-obvious hidden causal relations (Gelman and Wellman, 1991; Tooby et al., 1994). Adults use substantive prior knowledge about everyday physics and psychology to make new causal judgments (Ahn et al., 2000).
3. Causal learning
As presented in the previous section, causal learning is associated with human intelligence and has been widely studied. Traditional causal learning uses statistical methods to discover knowledge from data and perform causal inference. These methods are widely used in the field of medical science, economics, epidemiology, etc, but are rarely used in the domain of intelligent robotics (Guo et al., 2020; Yao et al., 2021a).
3.1. Causal discovery
Causal discovery learns the causal structure that represents the causality between observations X, treatments t, and outcomes y.
Traditional causal discovery relies on statistically verifying potential causal relationships or estimating functional equations to establish causal structures. Generally, there are four types of representative algorithms for traditional causal discovery: constraint-based algorithms and the score-based algorithms, which rely on statistical verification, functional causal model-based algorithms, which rely on functional estimation, and hybrid algorithms, which fuse multiple algorithms (Guo et al., 2020).
3.1.1. Constraint-based algorithms
Constraint-based algorithms analyze conditional independence in observation data to identify causal relationships. This family of algorithms often uses statistical testing algorithms to determine the conditional independence of two variables, given their neighbor nodes, then further determine the direction of the causality.
Mathematically, we can use three variables X, Y, and Z to explain constraint-based algorithms. The causal relationship is verified by conditional independence, for example, X ⫫ Y | Z, which is equivalent to zero conditional information I[X; Y | Z] = 0. This is defined as faithfulness in causal learning, as explained in Definition 3.1. If the three variables are discrete, χ2 and G2 can verify the conditional independence based on the contingency table of X, Y, and Z. If the three variables are linear and multivariate Gaussian, we can verify the conditional indecency by a test if the partial correlation is zero. For other circumstances, it often needs extra assumptions to ensure the verification is computationally tractable.
Definition 3.1. (Faithfulness). Conditional independence between a pair of variables, for , can be estimated from a dataset X iff x− d-separates xi and xj in the causal graph .
The conditional independence is symmetric, and additional tests are required to determine the orientations of edges. When X ⊥⊥ Y | Z, there are three possible graphical structures, including two chains (X ← Z ← Y and X → Z → Y) and a fork X ← Z → Y. The determination of which structures are induced based on the adjacency among variables, the background knowledge, etc. When X Y | Z it is a collision structure (X → Z ← Y).
Constraint-based algorithms use assumptions to improve efficiency and effectiveness for causal discovery from data. For example, the Peter-Clark algorithm assumes i.i.d. sampling and no latent confounders, which prunes edges between variables by testing conditional independence based on observation data, and determines and propagates the orients to form the directed acyclic graph (DAG) (Spirtes et al., 2000). The inductive causation algorithm assumes stable distributions (Definition 3.2), tests conditional independence to find the associative relationship between variables, finds collision structures, determines orients based on a variable's adjacency, and propagates directions (Pearl, 2009).
Definition 3.2. (Stable distribution). A distribution is stable if a linear combination of two independent random variables with this distribution has the same distribution, up to location and scale parameters.
Other constraint-based algorithms focus on weakening assumptions, thereby extending causal discovery methods to other distribution families (Sejdinovic et al., 2013; Ramsey, 2014; Glymour et al., 2019), causal discovery from data with unobserved confounders (Spirtes et al., 2013; Guo et al., 2020).
3.1.2. Score-based algorithms
Score-based algorithms learn causal graphs by maximizing the goodness-of-fit test scores of the causal graph G given observation data X (Spirtes et al., 2000). Because these algorithms replace the conditional independence tests with the goodness-of-fit tests, they relax the assumption of faithfulness (Definition 3.1) but often increase computational complexity. This is because the scoring criterion S(X, G) enumerates and scores the possible graphs under parameter adjustments. For example, the popular Bayesian information criterion adopts the score function to find the graph that maximizes the likelihood of observing the data, while the number of parameters and the sample size is regularized, where is the maximum likelihood estimation of the parameters and J and n denote the number of variables and the number of instances, respectively (Schwarz, 1978).
It is not tractable to score all possible causal graphs given observation data because it is NP-hard (Chickering, 1996) and NP-complete (Chickering, 1996). In practice, score-based algorithms use heuristics to find a local optimum (Chickering, 2002; Ramsey et al., 2017). For example, the greedy equivalence search algorithm uses Bayesian-Dirichlet equivalence score SBD:
To score a graph G, where rj and qj signify the numbers of configurations of variable xj and the numbers of configurations of parent set Pa(xj), respectively, Γ(·) denotes the gamma function, Njkl denotes the number of records of xj = k, and Pa(xj) is in the k-th configuration.
Widely used score-based algorithms optimize the searching and scoring process based on assumptions, such as linear-Gaussian models (Fukumizu et al., 2007), discrete data (Heckerman et al., 1995), and sparsity (Zheng et al., 2020). Additionally, there are studies on relaxing the assumptions for causal discovery from non-linear and arbitrarily distributed data (Huang et al., 2018). Compared with constraint-based algorithms, score-based algorithms can compare the output models in the space searched for model selection.
3.1.3. Functional causal models-based algorithms
Functional causal models-based algorithms represent the causal relationship with functional equations (Define 0.0.3).
Definition 3.3 (Functional equation). A functional equation represents a direct causal relation as y = fθ(X, n), where X is the variables that directly impact the outcome y, n is noise with n ⫫ X, and fθ is the general form of a function.
Causal discovery with functional equations can be expressed as sorting causal orders (which variables depend on which) from observation data. We use a linear non-Gaussian acyclic model to explain the process with a simple linear case x = Ax + μ, where x denotes the variable vector, A denotes the adjacency matrix, and μ denotes the noise independent of x. With this representation, the causal discovery is the equivalent of estimating a strictly lower triangle matrix A that determines the unique causal order k(xi), ∀xi ∈ mathbfx, which can be performed in the form of matrix permutation as described by Shimizu et al. (2006).
Functional causal models-based algorithms have demonstrated effectiveness in producing unique causal graphs. For example, the post-non-linear causal model learns the causal relationship that can be represented by a post-non-linear transformation on a non-linear effect of the cause variables and additive noises (Zhang and Hyvarinen, 2012). This algorithm can be further improved with independent component analysis (Taleb and Jutten, 1999) and relaxed by a warped Gaussian process, with the noise modeled by the mixture of Gaussian distributions (Zhang et al., 2015). Compared with the constraint-based and score-based algorithms, functional causal models-based algorithms are able to distinguish between different DAGs from the same equivalent class.
3.1.4. Hybrid algorithms
Hybrid algorithms combine multiple algorithms to overcome problems that exist in constraint-based or score-based algorithms. For example, Tsamardinos et al. (2006) use the max-min parents and children algorithm (constrained-based) to learn the skeleton of the causal graph and uses a Bayesian scoring hill-climbing search (score-based) to determine the orients of edges. Wong et al. (2002) use the conditional independence test to learn the skeleton of the causal graph and use a metric to search good network structures.
3.2. Causal inference
Causal inference is the process of estimating the changes of outcomes y given treatments t. Before we discuss causal inference algorithms, we need to first define the metrics (Definition 3.4) for measuring causal inference. ATE, ATT, CATE, and ITE measure the treatment effects of the population, the treated group, a subgroup of a given feature x, and individuals, respectively.
Definition 3.4. (Treatment Effect).
• Average Treatment Effect (ATE): ATE = E[Y(w = 1) − Y(w = 0)].
• Average Treatment Effect on the Treated Group (ATT): ATT = E[Y(w = 1) | w = 1] − E[Y(w = 0) | w = 1].
• Conditional Average Treatment Effect (CATE): CATE = E[Y(w = 1) | X = x] − E[Y(w = 0)|X = x].
• Individual Treatment Effect (ITE): ITEi = Yi(w = 1) − Yi(w=0).
Causal inference estimates the treatment effects for specific groups. However, the different distributions of groups and the existence of confounders make the task very challenging. According to the methodological differences, existing classical algorithms for addressing these problems can be grouped into reweighting-based algorithms, stratification-based algorithms, batching-based algorithms, and tree-based algorithms.
3.2.1. Reweighting-based algorithms
Reweighting-based algorithms assign appropriate weights to the samples to create pseudo-populations or reweight the covariates to mitigate the differences in the distributions between the treated groups and the control groups. These algorithms are designed to address the selection bias between the treated groups and the control groups.
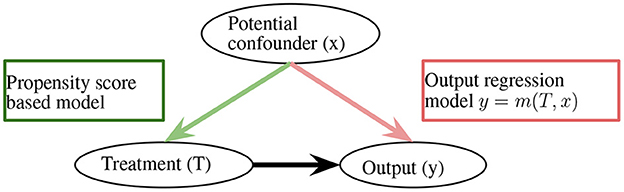
Both sample and covariate reweighting are used to address selection bias. The inverse propensity weighting algorithm is one of the pioneering works on reweighting samples. This algorithm uses propensity scores (Definition 3.5) to find the appropriate weights for samples as r = T/e(x) + (1 − T)/(1 − e(x)), where T is the treatment.
Definition 3.5. (Propensity Score). Propensity score e(x) is the conditional probability of assignment to a particular treatment given a vector of observed covariates e(x) = Pr(T = 1|X = x).
With the reweighting, the ATE is defined as . This method is sufficient for removing bias; however, it heavily relies on the correctness of propensity scores (Robins et al., 1994). Along the lines of propensity score-based sample reweighting, the doubly robust estimator combines the propensity score weighting with the outcome regression to remain unbiased, as long as the propensity score or outcome regression is correct (Figure 1; Robins et al., 1994), the overlap weights algorithm solves the extreme propensity score problem by reducing the weights of the unites that locate in the tails of the propensity score distributions (Li F. et al., 2019).
The covariate reweight algorithms learn sample weights from data through regression. To reweight a covariate, Hainmueller (2012) uses a maximum entropy reweighting scheme to calibrate sample weights to match the moments of the treated group and the control group and minimizes information loss by keeping weights close to the base weights.
Additionally, there are algorithms that balance distributions with both covariate and sample reweighting. The covariate balancing propensity score estimates the propensity score by solving to measure the probability of being treated and the covariate balancing score and improves the empirical performance of propensity score matching (Imai and Ratkovic, 2014). Data-driven variable decomposition (D2VD) balances distribution by automatically decomposing observed variables confounders, adjusted variables, and irrelevant variables (Kuang et al., 2017b). Differentiated confounder balancing (DCB) selects and differentiates confounders and reweights both the sample and the confounders to balance distributions (Kuang et al., 2017a).
3.2.2. Stratification-based algorithms
Stratification-based algorithms split observations into subgroups, which are similar under certain measurements. With subgroups that have balanced distributions, ATE is estimated as . For example, if a model can predict the strata in which subjects always stay in the study regardless of which treatment they were assigned, then the data from this strata is free of selection biases (Frangakis and Rubin, 2002; Jin and Rubin, 2008). The stratification can be performed on samples on the basis of the propensity score to improve the estimation robustness, as explained in the marginal mean weighting through stratification algorithm (Hong, 2010). Additionally, the stratification algorithms can be combined with propensity score-based algorithms to preprocess data to remove imbalances of pre-intervention characteristics (Linden, 2014).
3.2.3. Matching-based algorithms
Matching-based algorithms use specific distance measurements to match samples in the treatment group with ones in the control group to estimate the counterfactuals and reduce the estimation bias of confounders. Matching-based algorithms require the definition of distance metrics and the selection of matching algorithms. Euclidean distances and Mahalanobis distances are commonly used as distance metrics in the original data space, while transformations, such as propensity score-based transformation, and observed outcome information are commonly used in the transformed feature space (Stuart, 2010; Yao et al., 2021a). For matching algorithms, nearest neighbor, Caliper, stratification, and kernel-based methods are all widely adopted (Guo et al., 2020). It is worth noticing that matching-based algorithms can be used in data selection, as well as experimental design and performance. The latter uses matching to identify subjects that have outcomes that should be collected (Kupper et al., 1981; Reinisch et al., 1995), which potentially reduces costs and the difficulty in collecting effective data.
3.2.4. Tree-based methods
A tree structure naturally divides data into disjoint subgroups. Although the subgroups have similar e(x), the estimation of the treatment effect is unbiased. Bayesian additive regression trees (BART), a Bayesian “sum-of-trees” model, is a flexible approach for fitting a variety of regression models while avoiding strong parametric assumptions. With BART, the treatment y is the sum of subgroups as y = g(x; T1, θ1) + ⋯ + g(x; Tn, θn) + σ, where σ is Gaussian white noise (Chipman et al., 2010). Similarly, the classification and regression trees (CART) algorithm also splits data into classes that belong to the response variable. CART is different from BART in that it recursively partitions the data space and fits a simple prediction model for each partition (Loh, 2011). Causal forests ensemble multiple causal trees to achieve a smooth estimation of CATE. Causal forests are based on Breiman's random forest algorithm and maximize the difference across splits in the relationship between an outcome variable and a treatment variable to reveal how treatment effects vary across samples (Wager and Athey, 2018).
4. Deep causal learning
Deep learning (DL) has successfully attracted researchers from all fields as it demonstrates the power and the simplicity of learning from data (Goodfellow et al., 2016). The majority of existing DL algorithms use specialized architecture to establish end-to-end relationships from observation data, e.g., convolutional neural networks (CNN) for data with spatial locality, recurrent neural networks (RNN) for data with sequential or temporal structure, transformers for data with context information, autoencoders for data that need compressed representation, and generative adversarial networks for data that need domain adaption (LeCun and Bengio, 1995; Graves, 2012; Kingma and Welling, 2013; Vaswani et al., 2017; Goodfellow et al., 2020). Despite the remarkable success DL has achieved, some challenges remain, such as model expandability, extrapolation capability, and explainability. Causal learning (CL), on the other hand, discovers knowledge, explains prediction, and has extendable structures, but struggles with high dimensional data and scalability problems. Therefore, complementing DL with CL, and vice versa, can be a way forward. Actually, recent studies have made great progress and have demonstrated the advantages of deep causal learning in that prior knowledge can be used to disentangle modeling problems and reduce data needs (Parascandolo et al., 2018; Bengio et al., 2019; Yang et al., 2020), it has superior performance at extrapolating unseen data (Mart́ınez and Marca, 2019; Pawlowski et al., 2020a), can modularize learning problems, incrementally learns from multiple studies (Kaushik et al., 2019; Singla et al., 2019; Pawlowski et al., 2020b), and demonstrates potential as a solution to artificial general intelligence (Pearl, 2009; Guo et al., 2020).
Below, we introduce some of the representatives in plain language, with a focus on the network architecture and the benefits of using the architecture. Because the algorithms we review share many common characteristics, such as most of them using two or more neural networks and most of the representation learning involving CNN, we categorize the algorithms into the following categories to maximize the uniqueness among the categories.
4.1. Using DL for learning representation
Balancing neural networks and balancing linear regression are pioneering works that use deep neural networks to solve the problem of causal learning from high dimensional data (Johansson et al., 2016). These algorithms learn a representation g : X → ℝd through deep neural networks or feature reweighting and selection, then based on the features g(X), learn the causal effect h : ℝd × T → ℝ. These models learn balanced representations that have similar distributions among the treated and untreated groups and demonstrate effectiveness in cases that have one treatment.
Similarity-preserved individual treatment effect (SITE) uses two networks to preserve local similarity and balances data distributions simultaneously (Yao et al., 2018). The first network is a representation network, which maps the original pretreatment covariate space X into a latent space Z. The second network is a prediction network, which predicts the outcomes based on the latent variable Z. The algorithm uses position-dependent deep metric and middle point distance minimization to enforce two special properties on the latent space Z, including the balanced distribution and preserved similarity. The adaptively similarity-preserved representation learning method for causal effect estimation (ACE) preserves similarity in representation learning in an adaptive way to extract fine-grained similarity information from the original feature space and minimizes the distance between different treatment groups, as well as the similarity loss during the representation learning procedure (Yao et al., 2019a). ACE applies balancing and adaptive similarity preserving (BAS) regularization to the representation space. The BAS regularization consists of distribution distance minimization and adaptive pairwise similarity preservation, thus decreasing the ITE estimation error.
Johansson et al. (2018) presented a theory and an algorithmic framework for learning to predict outcomes of interventions under shifts in design changes in both intervention policy and feature domain. This framework combines representation learning and sample reweighting to balance source and target designs, emphasizing information from the source sample relevant to the target. As a result, this framework relaxes the strong assumption of having a well-specified model or knowing the policy that gave rise to the observed data.
4.2. End-to-end deep causal inference
Shalit et al. (2017) proposed treatment-agnostic representation networks (TARNETs) to estimate ITE based on the Rubin potential outcomes framework under the assumption of strong ignorability. This algorithm uses integral probability metrics to measure distances between distributions and derives explicit bounds for the Wasserstein and maximum mean discrepancy (MMD) distances. Therefore, this algorithm is an end-to-end regularized minimization procedure that fits the balanced representation of the data and a hypothesis for the outcome. Based on this work, Hassanpour and Greiner (2019a) proposed a context-aware importance sampling reweighting scheme to estimate ITEs, which addresses the distributional shift between the source (outcome of the administered treatment appearing in the observed training data) and target (outcome of the alternative treatment) that exists due to selection bias. Perfect matching augments samples within a minibatch with their propensity-matched nearest neighbors to improve inference performance in settings with many treatments (Schwab et al., 2018). Perfect matching is compatible with other architectures, such as the TARNET architecture, and extends these architectures to any number of available treatments. Additionally, perfect matching uses the nearest neighbor approximation of precision in the estimation of heterogenous effects with multiple treatments to select models without requiring access to counterfactual outcomes.
Alaa et al. (2017) modeled the inference of individualized causal effects of a treatment as a multitask learning problem. The algorithm uses a propensity network and a potential outcomes network to estimate ITE (Definition 3.4). The propensity network is a standard feedforward network and is trained separately to estimate the propensity score e(xi) (Definition 3.5) from (xi, ti). By assigning “simple models” to subjects with very high or very low propensity scores (e(xi) close to 0 or 1), and “complex models” to subjects with balanced propensity scores (e(xi) close to 0.5), it alleviates the selection bias problem. The potential outcomes network is a multitask network that models the potential outcomes and as two separate but related learning tasks; therefore, the treatment assignments and the subjects' characteristics are fully utilized.
4.3. Autoencoder-based algorithms
Causal effect variational autoencoder (CEVAE) uses variational autoencoder (VAE) structures to estimate individual treatment effects (Louizos et al., 2017). The algorithm uses an inference network (Figure 2B) and a model network (Figure 2A) to simultaneously estimate the unknown latent space summarizing the confounders and the causal effect, based on latent variable modeling. Because the algorithm uses the two networks to utilize both the causal inference with proxy variables and latent variable modeling, its performance is competitive with the state-of-the-art methods on benchmark datasets and has improved robustness on the problems with hidden confounders.
Figure 2. Causal effect variational autoencoder (Louizos et al., 2017). q(·) is a tractable distribution that approximates the true distribution p(·). X, t, and y are observations, treatments, and outcomes, respectively. (A) Model net. (B) Inference net.
The deep-treat algorithm uses two networks for constructive effective treatment policies by addressing the problems of the biased observed data and unavailable counterfactual information (Atan et al., 2018). The first network is a bias-removing autoencoder, which allows the explicit trade-off between bias reduction and information loss. The second network is a feedforward network, which constructs effective treatment policies on the transformed data.
Task embedding-based causal effect variational autoencoder (TECE-VAE) scales CEVAE with task embedding to estimate the individual treatment effect using observational data for the applications that have multiple treatments (Saini et al., 2019). Additionally, TECE-VAE adopts the encoder-decoder architecture. The encoder network takes input X to generate distribution for z. The decoder network uses z to reconstruct features X, treatments t, and outcomes y. TECE-VAE uses information across treatments and is robust with unobserved treatments.
The conditional treatment-adversarial learning based matching method (CTAM) uses treatment-adversarial learning to effectively filter out the nearly instrumental variables for processing textual covariates (Yao et al., 2019b). CTAM learns the representations of all covariates, which contain text variables, with the treatment-adversarial learning, then performs nearest neighbor matching among the learned representations to estimate the treatment effects. The conditional treatment adversarial training procedure in CTAM filters out the information related to nearly instrumental variables in the representation space; therefore, the treatment discriminator, the representation learner, and the outcome predictor work together in an adversarial learning manner to predict the treatment effect estimation with text covariates. To be more specific, the treatment discriminator is trained to predict the treatment label, while the representation learner works with the outcome predictor to fool the treatment discriminator.
Reducing selection bias-net (RSB-net) uses two networks to address the selection bias problem (Zhang et al., 2019). The first net is an autoencoder that learns the representation. This autoencoder uses a Pearson correlation coefficient (PCC) based on regularized loss and explicitly differentiates the bias variables with the confounders that affect treatments and outcomes and the variables that affect outcomes alone. Therefore, the confounders and the variables affecting outcomes are fed into the second network, which uses the branching structure network to predict outcomes.
The variational sample reweighting (VSR) algorithm uses a variational autoencoder to remove the confounding bias in the applications with bundle treatments (Zou et al., 2020). VSR simultaneously learns the encoder and the decoder by maximizing the evidence lower bound.
4.4. Generative adversarial nets-based algorithms
Generative adversarial nets for the inference of individualized treatment effects (GANITE), as suggested by the name, infer the ITE based on the generative adversarial nets (GANs) framework (Yoon et al., 2018). The algorithm uses a counterfactual generate, G, to generate potential outcome vector ỹ based on features X, treatments t, and factual outcome yf. Then, the generated proxies are passed to an ITE generator that generates potential outcome ŷ based on feature X. As a generative adversarial net (Goodfellow et al., 2020), GANITE uses a discriminator for G, DG, and a discriminator for I, DI to boost the training performance for the generators. DG maps pairs (X, ȳ) to vectors in [0, 1]k with the i−th component to represent the probability that the i−th component of ỹ is the factual outcome. Similarly, DI maps a pair x, y* to [0, 1] representing the probability of y* being from the data .
The causal effect generative adversarial network (CEGAN) utilizes an adversarially learned bidirectional model along with a denoising autoencoder to address the confounding bias caused by the existence of unmeasurable latent confounders (Lee et al., 2018). CEGAN has two networks: a prediction network (consisting of a generator, a prediction decoder, an inference net, and a discriminator), and a reconstruction network (a denoising autoencoder that has an encoder that is used as the generator in the prediction network).
SyncTwin constructs a synthetic twin that closely matches the target in representation to exploit the longitudinal observation of covariates and outcomes (Qian et al., 2021b). SyncTwin uses the sequence-to-sequence architecture with an attentive encoder and an LSTM decoder to learn the representation of temporal covariates and then constructs a synthetic twin to match the target in representations for controlling estimation bias. The reliability of the estimated treatment effect can be assessed by comparing the observed and synthetic pretreatment outcomes.
The generative adversarial de-confounding (GAD) algorithm estimates outcomes of continuous treatments by eliminating the associations between covariates and treatments (Kuang et al., 2021). First, GAD randomly shuffles the value of covariate X into X′ to ensure X′⫫T, where T is the treatments. Second, GAD reweights samples in X so the distribution of X is identical to X′. GAD then eliminates the confounding bias induced by the dependency between T and X.
Adversarial balancing-based representation learning for causal effect inference (ABCEI) uses adversarial learning to balance the distributions of covariates in the latent representation space to estimate the conditional average treatment effect (CATE) (Du et al., 2021). ABCET uses an encoder that is constrained by a mutual information estimator to minimize the information loss between representations and input covariates to preserve highly predictive information for causal effect inference. The generated representations are used for discriminator training, mutual information estimation, and prediction estimation.
4.5. Recurrent neural networks-based algorithms
The recurrent marginal structural network (RMSM) uses recurrent neural networks to forecast a subject's response to a series of planned treatments (Lim, 2018). RMSM uses the encoder-decoder architecture. The encoder learns representations for the subject's current state by using a standard LSTM to predict one-step-ahead outcome given observations of covariates and actual treatments. The decoder forecasts treatment responses on the basis of planned future actions by using another LSTM to propagate the encoder representation forwards in time.
The counterfactual recurrent network (CRN) uses a recurrent neural network-based encoder-decoder to estimate treatment effects over time (Bica et al., 2020b). The encoder uses domain adversarial training to build balancing representations of the patient's history to maximize the loss of the treatment classifier and minimize the loss of the outcome predictor. The decoder updates the outcome predictor to predict counterfactual outcomes of a sequence of future treatments.
The time series deconfounder uses a recurrent neural network architecture with multitask output to leverage the assignment of multiple treatments over time and enable the estimation of treatment effects in the presence of multi-cause hidden confounders (Bica et al., 2020a). The algorithm takes advantage of the patterns in the multiple treatment assignments over time to infer latent variables that can be used as substitutes for the hidden confounders. It first builds a factor model over time and infers latent variables that render the assigned treatments conditionally independent; then, it performs causal inference using these latent variables that act as substitutes for the multi-cause unobserved confounders.
4.6. Transformer-based algorithms
CETransformer uses transformer-based representation learning to address the problems of selection bias and unavailable counterfactual (Guo et al., 2021). CETransformer contains three modules, including a self-supervised transformer for representation learning, which learns the balanced representation, a discriminator network for adversarial learning to progressively shrink the difference between treated and control groups in the representation space, and outcome prediction, which uses the learned representations to estimate all potential outcome representations.
4.7. Multiple-branch networks and subspaces
The dose response network (DRNet) uses neural networks to estimate individual dose-response curves for any number of treatments with continuous dosage parameters (Schwab et al., 2020). DRNet consists of shared base layers, k intermediary treatment layers, and k*E heads for the multiple treatment setting, where k denotes the number of treatments and E defines the dosage resolution. The shared base layers are trained on all samples, the treatment layers are only trained on samples from their respective treatment category, and a head layer is only trained on samples that fall within its respective dosage stratum.
Disentangled representations for counterfactual regression (DR-CFR) disentangles the learning problem by explicitly identifying three categories of features: the ones that only determine treatments, the ones that only determine outcomes, and the confounders that impact both treatments and outcomes (Hassanpour and Greiner, 2019b). Three representation learning networks are trained to identify each of the three categories of factors, and the identified factors are fed into two regression networks to identify two types of treatments and two logistic networks to model the corresponding behavior policy.
Decomposed representations for counterfactual regression (DeR-CFR) disentangles the learning problem by explicitly dividing covariants into instrumental factors, confounding factors, and adjustment factors (Wu A. et al., 2020). DeR-CFR has three decomposed representation networks for learning the three categories of latent factors, has three decomposition and balancing regularizers for confounder identification and balancing of the three categories of latent factors, and has two regression networks for potential outcome prediction.
Neural counterfactual relation estimation (NCoRE) explicitly models cross-treatment interactions to learn counterfactual representations in the combination treatment setting (Parbhoo et al., 2021). NCoRE uses a novel branched conditional neural representation and consists of a variable number of shared base layers with k intermediary treatment layers, which are then merged to obtain a predicted outcome. The shared base layers are trained on all samples and serve to model cross-treatment interactions, and the treatment layers are only trained on samples from their respective treatment category and serve to model per-treatment interactions.
Single-cause perturbation (SCP) uses a two-step procedure to estimate the multi-cause treatment effect (Qian et al., 2021a). The first step augments the observational dataset with the estimated potential outcomes under single-cause interventions. The second step performs covariate adjustment on the augmented dataset to obtain the estimator. Curth and van der Schaar (2021) presented three end-to-end learning strategies for exploiting structural similarities of an individual's potential outcomes under different treatments to obtain better estimates of CATE in finite samples. The three strategies regularize the difference between potential outcome functions, reparametrize the estimators, and automatically learn which information to share between potential outcome functions.
Deep orthogonal networks for unconfounded treatments (DONUT) proposes a regularizer that accommodates unconfoundedness as an orthogonality constraint for estimating ATE (Hatt and Feuerriegel, 2021). The orthogonality constraint is defined as < Y(t) − f(X, t) >, T − E[T|X = x]), where is the inner product.
Subspace learning-based counterfactual inference (SCI) learns in a common subspace, a control subspace, and a treated subspace to improve the performance of estimating causal effect at the individual level (Yao et al., 2021b). SCI learns the control subspace to investigate the treatment-specific information for improving the control outcome inference, learns the treated subspace to retain the treated-specific information for improving the estimation of treated outcomes, and learns common subspace to share information between the control and treated subspaces to extract the cross-treatment information and reduce selection bias.
4.8. Combining DL with statistical regulators and kernels
The varying coefficient neural network (VCNet) puts forward a neural network and a targeted regularization to estimate the average dose-response curve for continuous treatment and to improve finite sample performance (Nie et al., 2021).
Shi et al. (2019) proposed the Dragonnet to exploit the sufficiency of the propensity score for estimation adjustment, and proposed the targeted regularization to induce a bias toward models. The Dragonnet uses a three-headed architecture to provide an end-to-end procedure for predicting propensity score and conditional outcome from covariates and treatment information. The targeted regularization introduces a new parameter and a new regularization term to achieve stable finite-sample behavior and strong asymptotic guarantees on estimation.
Deep kernel learning for individualized treatment effects (DKLITE2) is a deep kernel regression algorithm and posterior regularization framework to avoid learning domain-invariant representations of inputs (Zhang et al., 2020). DKLITE2 works in a feature space constructed by a kernel function to exploit the correlation between inputs and uses a neural network to encode the information content of input variables.
From the above introduction, it is clear that DL architectures are widely used in CL for reducing dimensionality, processing temporal data, balancing distributions, and removing confounding and selection bias. Among the architectures, autoencoder and GAN are particularly popular. From the application perspective, most of the above methods focus on estimating ITE, and the methods for estimating ATE and CATE do exist.
5. Deep causal learning for robotic intelligence
5.1. Challenges in intelligent robotics
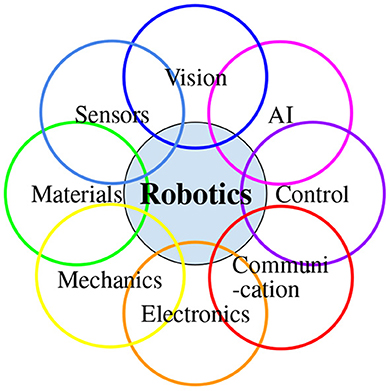
Robotics is challenging. Robots are made up of many different components, including sensors, actuators, and control systems, all of which must work together seamlessly to function properly (Yoshikawa, 1990; Craig, 2005; Smith et al., 2020). Robotic systems are expensive to design, build, and maintain. Additionally, they are subject to regulations, standards, and certifications that need to be adhered to. These challenges require a multidisciplinary approach, combining expertise in areas such as mechanical engineering, electrical engineering, computer science, and cognitive psychology to design and build robots.
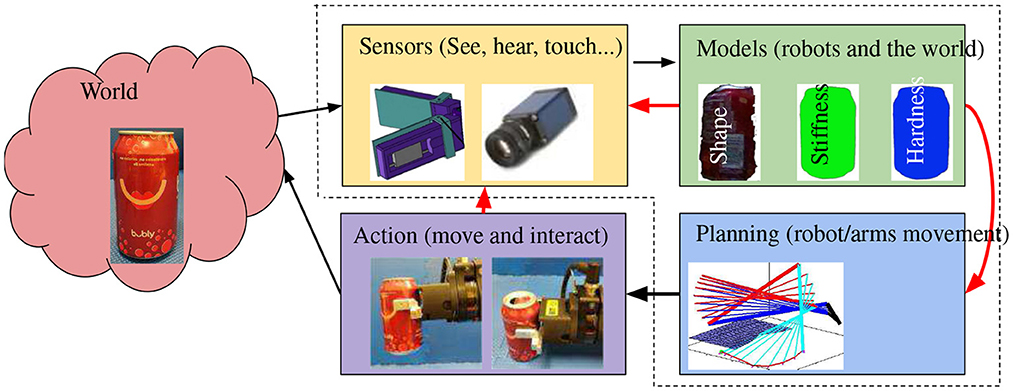
Intelligent robotics is built upon robotics and faces additional challenges as intelligent robots interact with the real world, which is subject to environmental uncertainties, sensory noises, modeling uncertainties, execution errors, and unexpected events (Figure 3). Intelligent robots are multidisciplinary by nature (Figure 4) and interact with humans in the real world, which is full of unexpected events. These facts introduce challenges that are being intensively studied.
∙ Perception: intelligent robots need to be able to perceive and understand their environment to navigate and interact with it. This includes tasks such as object recognition, localization, and mapping, which can be challenging due to the complexity of real-world environments and the presence of noise and uncertainty (Thrun et al., 2005; Li and Olson, 2010; Li et al., 2014, 2018e).
∙ Planning and decision making: robots need to be able to make decisions about how to move and interact with their environment, based on their perception of it. This requires the development of advanced algorithms for planning and decision making, which can be difficult to design and implement in real-world scenarios (Li et al., 2022; Liu et al., 2022a,b; Su et al., 2022b).
∙ Control and actuation: robots need to be able to execute the decisions made by their planning and decision-making systems by controlling their movements and interactions with the environment. This requires the development of robust control systems and actuators, which can be a challenging task, especially in highly dynamic and unpredictable environments (Li et al., 2012b, 2018d; Miyasaka et al., 2020; Qi et al., 2020; Su et al., 2022a).
∙ Interaction with humans: as robots increasingly interact with humans in shared spaces, it is important to ensure that they can understand human behavior and communicate effectively. This requires the development of human-robot interaction (HRI) algorithms and interfaces (Jin et al., 2018; Khan et al., 2018; Zhang et al., 2022).
∙ Understanding domain-specific knowledge: robots need to understand domain knowledge to accomplish tasks, such as robotic surgeries. This is especially challenging while the domain knowledge cannot be formalized as the rules and costs of collecting data are expensive (Li et al., 2017b, 2018a; Saxena et al., 2019). In such applications, robots need to learn from small data and adapt to various tasks (Li et al., 2018b, 2021).
∙ Safety and reliability: ensuring the safety and reliability of robots, especially in critical applications, is a major challenge. This requires the development of robust fault-tolerance and safety mechanisms, as well as rigorous testing and validation of the robot's performance (Li et al., 2013, 2017c; Alemzadeh et al., 2016; Li, 2019; Li Y. et al., 2019).
∙ Scalability: developing robots that can operate effectively in different environments and perform a wide range of tasks is a difficult challenge. This requires the development of modular and scalable robot systems that can adapt to different scenarios (Li et al., 2012a; Li S. et al., 2017; Majumdar et al., 2020).
∙ Ethical and societal concerns: as robots become more advanced and autonomous, there are ethical and societal concerns to be taken into account, such as potential job displacement, privacy, and security issues (Lin et al., 2014; Xu et al., 2022).
5.2. Deep causal learning for intelligent robots
While intelligent robotics has made significant progress in the past two decades, partially benefiting from the development of deep learning, intelligent robots are rarely used in real-world environments. Deep causal learning is a promising solution to the challenges of intelligent robotics in the real world. Deep causal learning infers the causal relationships and can provide a better understanding of the underlying mechanisms that generate the data, which can greatly improve safety and reliability, and make the ethical and societal concerns solvable. Deep causal learning models can be used to identify the most important factors that influence a particular outcome, thus simplifying the understanding of domain-specific knowledge. Deep causal learning can be used to generate counterfactual predictions, which can improve decision making and enable complimentary perception and understanding. Most importantly, deep causal learning extracts the structures of knowledge and enables stackable learning, which improves perception, control, and scalability.
To further explain how deep causal learning can potentially break bottlenecks in intelligent robotics, we use three examples, a low-level visual tracking example, middle-level motion planning, and high-level task planning to illustrate why we believe that deep causal learning has the potential to fundamentally change intelligent robotics.
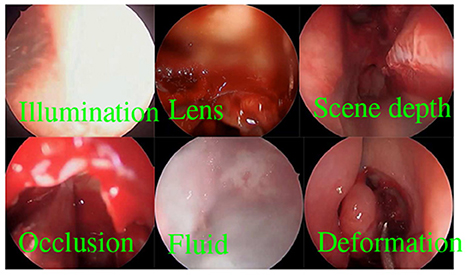
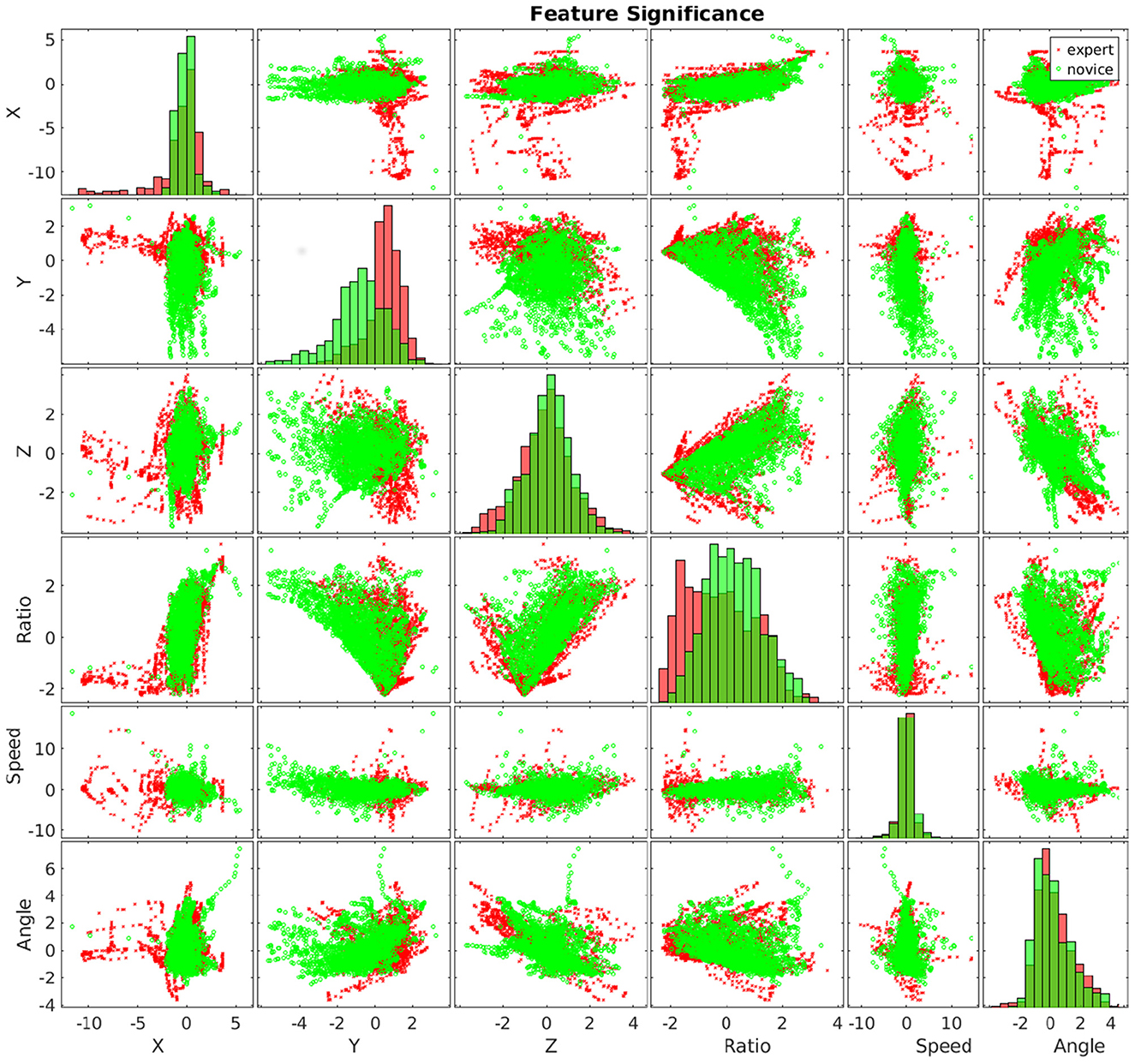
Visual tracking is an important problem in robotics and is widely studied in the fields of computer vision, AI, and the robotics (Figure 5 and Table 1). There are a large number of results that can address the challenges of illumination changes, occlusions, lens blur, drastic scene changes, deformation, etc., particularly for visual tracking in endoscopic surgeries (Qin et al., 2019, 2020; Lin et al., 2020; Recasens et al., 2021). However, visual tracking remains challenging in endoscopic surgeries as all these adverse factors exist simultaneously and deteriorate tracking performance. Meanwhile, these adverse factors, along with the variance of pathology and anatomy, make the need for training data grow beyond our capacity. Therefore, we believe that deep causal learning is needed to disentangle the problems for robots.
Motion planning is widely studied in robotics (LaValle and Kuffner, 2001; Li et al., 2018c). However, in real-world applications, intelligent robots not only need to know where to move to and how to move there but also need to know whether there are other application-specific requirements. For example, it has been well-studied that movement patterns impact surgical outcomes (Figure 6; Harbison et al., 2017; Li et al., 2017a), but it is not trivial to plan motions for a robot for various treatment procedures (Li and Hannaford, 2017, 2018). Therefore, we believe that deep causal learning, which naturally uses graphical structures to represent knowledge, can effectively incorporate domain knowledge with robotic techniques.
Task-level planning involves multiple decision-making and is specific to applications. For example, robotic surgery, as one of the most successful real-world applications of robotic technology, is still fully teleoperated, despite studies showing that many surgical accidents were caused by the incorrect operation of surgical robots (Alemzadeh et al., 2016; Su et al., 2020). Although we believe there are legal and regulatory barriers that prevent the adoption of autonomous technology, we argue that the main problem is that we lack the technology to handle environmental and task variance. For example, robots have problems dynamically adapting to changes and determining the completeness of surgery (Taylor et al., 2016).
6. Conclusion
Deep Causal Learning has recently demonstrated its capability for using prior knowledge to disentangle modeling problems and reduce data needs, improve performance at extrapolating unseen data, modularize learning problems, and incrementally learn from multiple studies. Inspired by these new findings, this Review incompletely but systematically discusses causal cognition, statistical causal learning, deep causal learning, and the need for deep causal learning in intelligent robots and argues that deep causal learning is the new frontier for intelligent robot research.
Author contributions
YL organized the materials, wrote the manuscript, and contributed to the article and approved the submitted version.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ahn, W.-K., Gelman, S. A., Amsterlaw, J. A., Hohenstein, J., and Kalish, C. W. (2000). Causal status effect in children's categorization. Cognition 76, B35-B43. doi: 10.1016/S0010-0277(00)00077-9
Alaa, A. M., Weisz, M., and Van Der Schaar, M. (2017). Deep counterfactual networks with propensity-dropout. arXiv preprint arXiv:1706.05966. doi: 10.48550/arXiv.1706.05966
Alemzadeh, H., Raman, J., Leveson, N., Kalbarczyk, Z., and Iyer, R. K. (2016). Adverse events in robotic surgery: a retrospective study of 14 years of fda data. PLoS ONE 11, e0151470. doi: 10.1371/journal.pone.0151470
Atan, O., Jordon, J., and Van der Schaar, M. (2018). “Deep-treat: learning optimal personalized treatments from observational data using neural networks,” in Proceedings of the AAAI Conference on ArtificialIntelligence. Vol. 32 (New Orleans, LA).
Bârsan, I. A., Liu, P., Pollefeys, M., and Geiger, A. (2018). “Robust dense mapping for large-scale dynamic environments,” in 2018 IEEE International Conference on Robotics andAutomation (ICRA) (Brisbane, QLD: IEEE), 7510–7517.
Bender, A., and Beller, S. (2019). The cultural fabric of human causal cognition. Perspect. Psychol. Sci. 14, 922–940. doi: 10.1177/1745691619863055
Bengio, Y., Deleu, T., Rahaman, N., Ke, R., Lachapelle, S., Bilaniuk, O., et al. (2019). A meta-transfer objective for learning to disentangle causal mechanisms. arXiv preprint arXiv:1901.10912. doi: 10.48550/arXiv.1901.10912
Bica, I., Alaa, A., and Van Der Schaar, M. (2020a). “Time series deconfounder: estimating treatment effects over time in the presence of hidden confounders,” in International Conference on Machine Learning (PMLR) (Vienna; Redmond, WA), 884–895.
Bica, I., Alaa, A. M., Jordon, J., and van der Schaar, M. (2020b). Estimating counterfactual treatment outcomes over time through adversarially balanced representations. arXiv preprint arXiv:2002.04083. doi: 10.48550/arXiv.2002.04083
Bonawitz, E. B., Ferranti, D., Saxe, R., Gopnik, A., Meltzoff, A. N., Woodward, J., et al. (2010). Just do it? investigating the gap between prediction and action intoddlers' causal inferences. Cognition 115, 104–117. doi: 10.1016/j.cognition.2009.12.001
Chen, R. J., Bobrow, T. L., Athey, T., Mahmood, F., and Durr, N. J. (2019). Slam endoscopy enhanced by adversarial depth prediction. arXiv preprint arXiv:1907.00283. doi: 10.48550/arXiv.1907.00283
Chickering, D. M. (1996). “Learning bayesian networks is np-complete,” in Learning From Data (Springer), 121–130.
Chickering, D. M. (2002). Optimal structure identification with greedy search. J. Mach. Learn. Res. 3, 507–554. doi: 10.1162/153244303321897717
Chipman, H. A., George, E. I., and McCulloch, R. E. (2010). Bart: Bayesian additive regression trees. Ann. Appl. Stat. 4, 266–298. doi: 10.1214/09-AOAS285
Craig, J. J. (2005). Introduction to Robotics: Mechanics and Control, Vol. 3. Upper Saddle River, NJ: Pearson Prentice Hall.
Curth, A., and van der Schaar, M. (2021). On inductive biases for heterogeneous treatment effect estimation. Adv. Neural Inf. Process. Syst. 34, 15883–15894.
Davison, A. J., Reid, I. D., Molton, N. D., and Stasse, O. (2007). Monoslam: Real-time single camera slam. IEEE Trans. Pattern Anal. Mach. Intell. 29, 1052–1067. doi: 10.1109/TPAMI.2007.1049
Du, X., Sun, L., Duivesteijn, W., Nikolaev, A., and Pechenizkiy, M. (2021). Adversarial balancing-based representation learning for causal effect inference with observational data. Data Min. Knowl. Discov. 35, 1713–1738. doi: 10.1007/s10618-021-00759-3
Fehr, M., Furrer, F., Dryanovski, I., Sturm, J., Gilitschenski, I., Siegwart, R., et al. (2017). “TSDF-based change detection for consistent long-term dense reconstruction and dynamic object discovery,” in 2017 IEEE International Conference on Robotics andautomation (ICRA) (Singapore: IEEE), 5237–5244.
Frangakis, C. E., and Rubin, D. B. (2002). Principal stratification in causal inference. Biometrics 58, 21–29. doi: 10.1111/j.0006-341X.2002.00021.x
Fukumizu, K., Gretton, A., Sun, X., and Schölkopf, B. (2007). “Kernel measures of conditional dependence,” in Advances in Neural Information Processing Systems, Vol. 20 (Vancouver, BC).
Gelman, S. A., and Wellman, H. M. (1991). Insides and essences: early understandings of the non-obvious. Cognition 38, 213–244. doi: 10.1016/0010-0277(91)90007-Q
Glymour, C., Zhang, K., and Spirtes, P. (2019). Review of causal discovery methods based on graphical models. Front. Genet. 10, 524. doi: 10.3389/fgene.2019.00524
Gomez-Ojeda, R. (2020). Robust visual slam in challenging environments with low-texture and dynamic illumination (Doctoral dissertation). Universidad de Málaga.
Goodfellow, I., Bengio, Y., Courville, A., and Bengio, Y. (2016). Deep Learning, Vol. 1. Cambridge, MA: MIT Press.
Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., et al. (2020). Generative adversarial networks. Commun. ACM 63, 139–144. doi: 10.1145/3422622
Gopnik, A., Glymour, C., Sobel, D. M., Schulz, L. E., Kushnir, T., and Danks, D. (2004). A theory of causal learning in children: causal maps and bayes nets. Psychol. Rev. 111, 3. doi: 10.1037/0033-295X.111.1.3
Graves, A. (2012). “Long short-term memory,” in Supervised Sequence Labelling With Recurrent Neural Networks (Toronto, ON), 37–45.
Guo, R., Cheng, L., Li, J., Hahn, P. R., and Liu, H. (2020). A survey of learning causality with data: problems and methods. ACM Comput. Surveys 53, 1–37. doi: 10.1145/3397269
Guo, Z., Zheng, S., Liu, Z., Yan, K., and Zhu, Z. (2021). “Cetransformer: casual effect estimation via transformer based representation learning,” in Chinese Conference on Pattern Recognition and ComputerVision (PRCV) (Beijing: Springer), 524–535.
Hainmueller, J. (2012). Entropy balancing for causal effects: a multivariate reweighting method to produce balanced samples in observational studies. Political Anal. 20, 25–46. doi: 10.1093/pan/mpr025
Harbison, R. A., Berens, A. M., Li, Y., Bly, R. A., Hannaford, B., and Moe, K. S. (2017). Region-specific objective signatures of endoscopic surgical instrument motion: a cadaveric exploratory analysis. J. Neurol. Surgery B Skull Base 78, 099–104. doi: 10.1055/s-0036-1588061
Hassanpour, N., and Greiner, R. (2019a). “Counterfactual regression with importance sampling weights,” in IJCAI (Macao). 5880–5887.
Hassanpour, N., and Greiner, R. (2019b). “Learning disentangled representations for counterfactual regression,” in International Conference on Learning Representations (New Orleans, LA).
Hatt, T., and Feuerriegel, S. (2021). “Estimating average treatment effects via orthogonal regularization,” in Proceedings of the 30th ACM International Conference onInformation &Knowledge Management (Queensland), 680–689.
Heckerman, D., Geiger, D., and Chickering, D. M. (1995). Learning bayesian networks: the combination of knowledge and statistical data. Mach. Learn. 20, 197–243. doi: 10.1007/BF00994016
Hespos, S. J., and Baillargeon, R. (2001). Reasoning about containment events in very young infants. Cognition 78, 207–245. doi: 10.1016/S0010-0277(00)00118-9
Hong, G. (2010). Marginal mean weighting through stratification: adjustment for selection bias in multilevel data. J. Educ. Behav. Stat. 35, 499–531. doi: 10.3102/1076998609359785
Hsiao, M., and Kaess, M. (2019). “MH-iSAM2: Multi-hypothesis iSAM using bayes tree and hypo-tree,” in 2019 International Conference on Robotics and Automation (ICRA) (Montreal, QC: IEEE), 1274–1280.
Huang, B., Zhang, K., Lin, Y., Schölkopf, B., and Glymour, C. (2018). “Generalized score functions for causal discovery,” in Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (London), 1551–1560.
Imai, K., and Ratkovic, M. (2014). Covariate balancing propensity score. J. R. Stat. Soc. B 76, 243–263. doi: 10.1111/rssb.12027
Jin, H., and Rubin, D. B. (2008). Principal stratification for causal inference with extended partial compliance. J. Am. Stat. Assoc. 103, 101–111. doi: 10.1198/016214507000000347
Jin, L., Li, S., Luo, X., Li, Y., and Qin, B. (2018). Neural dynamics for cooperative control of redundant robot manipulators. IEEE Trans. Ind. Inform. 14, 3812–3821. doi: 10.1109/TII.2018.2789438
Johansson, F., Shalit, U., and Sontag, D. (2016). “Learning representations for counterfactual inference,” in International Conference on Machine Learning (PMLR) (New York, NY), 3020–3029.
Johansson, F. D., Kallus, N., Shalit, U., and Sontag, D. (2018). Learning weighted representations for generalization across designs. arXiv preprint arXiv:1802.08598. doi: 10.48550/arXiv.1802.08598
Kaushik, D., Hovy, E., and Lipton, Z. C. (2019). Learning the difference that makes a difference with counterfactually-augmented data. arXiv preprint arXiv:1909.12434. doi: 10.48550/arXiv.1909.12434
Khan, A. H., Li, S., Zhou, X., Li, Y., Khan, M. U., Luo, X., et al. (2018). Neural &bio-inspired processing and robot control. Front. Neurorobot. 12, 72. doi: 10.3389/fnbot.2018.00072
Kingma, D. P., and Welling, M. (2013). Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114. doi: 10.48550/arXiv.1312.6114
Kuang, K., Cui, P., Li, B., Jiang, M., and Yang, S. (2017a). “Estimating treatment effect in the wild via differentiated confounder balancing,” in Proceedings of the 23rd ACM SIGKDD International Conferenceon Knowledge Discovery and Data Mining (Halifax, NS), 265–274.
Kuang, K., Cui, P., Li, B., Jiang, M., Yang, S., and Wang, F. (2017b). “Treatment effect estimation with data-driven variable decomposition,” in Proceedings of the AAAI Conference on ArtificialIntelligence. Vol. 31 (San Francisco, CA).
Kuang, K., Li, Y., Li, B., Cui, P., Yang, H., Tao, J., et al. (2021). Continuous treatment effect estimation via generative adversarial de-confounding. Data Min. Knowl. Discov. 35, 2467–2497. doi: 10.1007/s10618-021-00797-x
Kuhn, D. (2012). The development of causal reasoning. Wiley Interdisc. Rev. Cogn. Sci. 3, 327–335. doi: 10.1002/wcs.1160
Kupper, L. L., Karon, J. M., Kleinbaum, D. G., Morgenstern, H., and Lewis, D. K. (1981). Matching in epidemiologic studies: validity and efficiency considerations. Biometrics 37, 271–291. doi: 10.2307/2530417
Lamarca, J., Parashar, S., Bartoli, A., and Montiel, J. (2020). Defslam: tracking and mapping of deforming scenes from monocular sequences. IEEE Trans. Robot. 37, 291–303. doi: 10.1109/TRO.2020.3020739
LaValle, S. M., and Kuffner Jr, J. J. (2001). Randomized kinodynamic planning. Int. J. Rob. Res. 20, 378–400. doi: 10.1177/02783640122067453
LeCun, Y., and Bengio, Y. (1995). “Convolutional networks for images, speech, and time series,” in The Handbook of Brain Theory and Neural Networks (New York, NY), 3361.
Lee, C., Mastronarde, N., and van der Schaar, M. (2018). Estimation of individual treatment effect in latent confounder models via adversarial learning. arXiv preprint arXiv:1811.08943. doi: 10.48550/arXiv.1811.08943
Lee, H. S., Kwon, J., and Lee, K. M. (2011). “Simultaneous localization, mapping and deblurring,” in 2011 International Conference on Computer Vision (Barcelona: IEEE),1203–1210.
Legare, C. H., Sobel, D. M., and Callanan, M. (2017). Causal learning is collaborative: examining explanation and exploration in social contexts. Psychon. Bull. Rev. 24, 1548–1554. doi: 10.3758/s13423-017-1351-3
Leslie, A. M., and Keeble, S. (1987). Do six-month-old infants perceive causality? Cognition 25, 265–288. doi: 10.1016/S0010-0277(87)80006-9
Li, F., Thomas, L. E., and Li, F. (2019). Addressing extreme propensity scores via the overlap weights. Am. J. Epidemiol. 188, 250–257. doi: 10.1093/aje/kwy201
Li, Q., Qi, W., Li, Z., Xia, H., Kang, Y., and Cheng, L. (2022). Fuzzy based optimization and control of a soft exo-suit for compliant robot-human-environment interaction. IEEE Trans. Fuzzy Syst. 2022, 3185450. doi: 10.1109/TFUZZ.2022.3185450
Li, S., Cui, H., Li, Y., Liu, B., and Lou, Y. (2012a). Decentralized control of collaborative redundant manipulators with partial command coverage via locally connected recurrent neural networks. Neural Comput. Appl. 23, 1051–1060. doi: 10.1007/s00521-012-1030-2
Li, S., He, J., Li, Y., and Rafique, M. U. (2017). Distributed recurrent neural networks for cooperative control of manipulators: a game-theoretic perspective. IEEE Trans. Neural Netw. Learn. Syst. 28, 415–426. doi: 10.1109/TNNLS.2016.2516565
Li, S., Li, Y., Liu, B., and Murray, T. (2012b). “Model-free control of lorenz chaos using an approximate optimal control strategy,” in Communications in Nonlinear Science and Numerical Simulation (London).
Li, Y. (2019). Trends in control and decision-making for human-robot collaboration systems. IEEE Control Syst. Mag. 39, 101–103. doi: 10.1109/MCS.2018.2888714
Li, Y., Bly, R., Humphreys, I., Whipple, M., Hannaford, B., and Moe, K. (2018a). Surgical motion based automatic objective surgical completeness assessment in endoscopic skull base and sinus surgery. J. Neurol. Surgery B 79, P193. doi: 10.1055/s-0038-1633812
Li, Y., Bly, R., Whipple, M., Humphreys, I., Hannaford, B., and Moe, K. (2018b). Use endoscope and instrument and pathway relative motion as metricfor automated objective surgical skill assessment in skull base and sinus surgery. J. Neurol. Surgery B 79, A194. doi: 10.1055/s-0038-1633609
Li, Y., Bly, R. A., Harbison, R. A., Humphreys, I. M., Whipple, M. E., Hannaford, B., et al. (2017a). Anatomical region segmentation for objective surgical skill assessment with operating room motion data. J. Surgery B 369, 1434–1442.
Li, Y., and Hannaford, B. (2017). Gaussian process regression for sensorless grip force estimation of cable-driven elongated surgical instruments. IEEE Robot. Autom. Lett. 2, 1312–1319. doi: 10.1109/LRA.2017.2666420
Li, Y., and Hannaford, B. (2018). “Soft-obstacle avoidance for redundant manipulators with recurrent neural network,” in Intelligent Robots and Systems (IROS), 2018 IEEE/RSJ International Conference on (Madrid: IEEE), 1–6.
Li, Y., Hannaford, B., Humphreys, I., Moe, K. S., and Bly, R. A. (2021). “Learning surgical motion pattern from small data in endoscopic sinus and skull base surgeries,” in Robotics and Automation (ICRA), 2021 IEEE InternationalConference on (Xi'an: IEEE), 1–6.
Li, Y., Hannaford, B., and Rosen, J. (2019). The raven open surgical robotic platforms: a review and prospect. Acta Polytech. Hungarica 16, 8. doi: 10.12700/APH.16.8.2019.8.2
Li, Y., Harbison, R. A., Bly, R. A., Humphreys, I. M., Hannaford, B., and Moe, K. (2017b). Atlas based anatomical region segmentation for minimally invasive skull base surgery objective motion analysis. J. Neurol. Surgery B 78, A146. doi: 10.1055/s-0037-1600670
Li, Y., Li, S., and Ge, Y. (2013). A biologically inspired solution to simultaneous localization and consistent mapping in dynamic environments. Neurocomputing 104, 170–179. doi: 10.1016/j.neucom.2012.10.011
Li, Y., Li, S., and Hannaford, B. (2018c). A model based recurrent neural network with randomness for efficient control with applications. IEEE Trans. Ind. Inform. 15, 2054–2063. doi: 10.1109/TII.2018.2869588
Li, Y., Li, S., and Hannaford, B. (2018d). A novel recurrent neural network control scheme for improving redundant manipulator motion planning completeness. IEEE Int. Conf. Robot. Autom. 2018, 2956–2961. doi: 10.1109/ICRA.2018.8461204
Li, Y., Li, S., Miyasaka, M., Lewis, A., and Hannaford, B. (2017c). “Improving control precision and motion adaptiveness for surgical robot with recurrent neural network,” in Intelligent Robots and Systems (IROS), 2017 IEEE/RSJInternational Conference on (IEEE) (Vancouver, BC: IEEE), 1–6.
Li, Y., Li, S., Song, Q., Liu, H., and Meng, M. Q.-H. (2014). Fast and robust data association using posterior based approximatejoint compatibility test. IEEE Trans. Ind. Inform. 10, 331–339. doi: 10.1109/TII.2013.2271506
Li, Y., and Olson, E. B. (2010). A general purpose feature extractor for light detection and ranging data. Sensors 10, 10356–10375. doi: 10.3390/s101110356
Li, Y., Zhang, J., and Li, S. (2018e). STMVO: biologically inspired monocular visual odometry. Neural Comput. Appl. 29, 215–225. doi: 10.1007/s00521-016-2536-9
Lim, B. (2018). “Forecasting treatment responses over time using recurrent marginal structural networks,” in Advances in Neural Information Processing Systems, Vol. 31 (Montréal, QC).
Lin, P., Abney, K., and Bekey, G. A. (2014). Robot Ethics: The Ethical and Social Implications oF Robotics. Cambridge, MA: MIT Press.
Lin, S., Qin, F., Li, Y., Bly, R. A., Moe, K. S., and Hannaford, B. (2020). “LC-GAN: Image-to-image translation based on generative adversarialnetwork for endoscopic images,” in 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (Las Vegas, NV: IEEE), 2914–2920.
Linden, A. (2014). Combining propensity score-based stratification and weighting to improve causal inference in the evaluation of health care interventions. J. Eval. Clin. Pract. 20, 1065–1071. doi: 10.1111/jep.12254
Liu, X., Jiang, W., Su, H., Qi, W., and Ge, S. S. (2022a). A control strategy of robot eye-head coordinated gaze behavior achieved for minimized neural transmission noise. IEEE/ASME Trans. Mechatron. 2022, 592. doi: 10.1109/TMECH.2022.3210592
Liu, X., Li, X., Su, H., Zhao, Y., and Ge, S. S. (2022b). “The opening workspace control strategy of a novel manipulator-driven emission source microscopy system,” in ISA Trans (Hong Kong).
Loh, W.-Y. (2011). Classification and regression trees. Wiley Interdisc. Rev. 1, 14–23. doi: 10.1002/widm.8
Louizos, C., Shalit, U., Mooij, J. M., Sontag, D., Zemel, R., and Welling, M. (2017). “Causal effect inference with deep latent-variable models,” in Advances in Neural Information Processing Systems, Vol. 30 (Long Beach, CA).
Lurie, K. L., Angst, R., Zlatev, D. V., Liao, J. C., and Bowden, A. K. E. (2017). 3D reconstruction of cystoscopy videos for comprehensive bladder records. Biomed. Opt. Express. 8, 2106–2123. doi: 10.1364/BOE.8.002106
Ma, R., Wang, R., Pizer, S., Rosenman, J., McGill, S. K., and Frahm, J.-M. (2019). “Real-time 3D reconstruction of colonoscopic surfaces for determining missing regions,” in International Conference on Medical Image Computing andComputer-Assisted Intervention (Shenzhen: Springer), 573–582.
Mahmoud, N., Cirauqui, I., Hostettler, A., Doignon, C., Soler, L., Marescaux, J., et al. (2016). “Orbslam-based endoscope tracking and 3d reconstruction,” in International Workshop on Computer-Assisted and Roboticendoscopy (Athens: Springer), 72–83.
Mahmoud, N., Hostettler, A., Collins, T., Soler, L., Doignon, C., and Montiel, J. (2017). Slam based quasi dense reconstruction for minimally invasive surgery scenes. arXiv preprint arXiv:1705.09107. doi: 10.48550/arXiv.1705.09107
Majumdar, A., Hall, G., and Ahmadi, A. A. (2020). Recent scalability improvements for semidefinite programming with applications in machine learning, control, and robotics. Ann. Rev. Control Robot. Auton. Syst. 3, 331–360. doi: 10.1146/annurev-control-091819-074326
Martínez Á, P., and Marca, J. V. (2019). “Explaining visual models by causal attribution,” in 2019 IEEE/CVF International Conference on Computer Vision (Seoul: IEEE).
Milford, M. J., and Wyeth, G. F. (2012). “Seqslam: visual route-based navigation for sunny summer days and stormy winter nights,” in 2012 IEEE International Conference on Robotics Andautomation (Saint Paul, MN: IEEE), 1643–1649.
Miyasaka, M., Haghighipanah, M., Li, Y., Matheson, J., Lewis, A., and Hannaford, B. (2020). Modeling cable-driven robot with hysteresis and cable-pulley network friction. IEEE/ASME Trans. Mechatron. 25, 1095–1104. doi: 10.1109/TMECH.2020.2973428
Mur-Artal, R., Montiel, J., and Tardós, J. D. (2015). Orb-slam: a versatile and accurate monocular slam system. IEEE Trans. Robot. 31, 1147–1163. doi: 10.1109/TRO.2015.2463671
Mur-Artal, R., and Tardós, J. D. (2015). “Probabilistic semi-dense mapping from highly accurate feature-based monocular slam,” in Robotics: Science and Systems, Vol. 2015 (Rome).
Needham, A., and Baillargeon, R. (1993). Intuitions about support in 4.5-month-old infants. Cognition 47, 121–148. doi: 10.1016/0010-0277(93)90002-D
Nie, L., Ye, M., Liu, Q., and Nicolae, D. (2021). Vcnet and functional targeted regularization for learning causal effects of continuous treatments. arXiv preprint arXiv:2103.07861. doi: 10.48550/arXiv.2103.07861
Okatani, T., and Deguchi, K. (1997). Shape reconstruction from an endoscope image by shape from shading technique for a point light source at the projection center. Comput. Vis. Image Understand. 66, 119–131. doi: 10.1006/cviu.1997.0613
Parascandolo, G., Kilbertus, N., Rojas-Carulla, M., and Schölkopf, B. (2018). “Learning independent causal mechanisms,” in International Conference on Machine Learning (PMLR) (Vienna), 4036–4044.
Parbhoo, S., Bauer, S., and Schwab, P. (2021). Ncore: neural counterfactual representation learning for combinations of treatments. arXiv preprint arXiv:2103.11175. doi: 10.48550/arXiv.2103.11175
Pawlowski, N., Castro, D. C., and Glocker, B. (2020a). Deep structural causal models for tractable counterfactual inference. arXiv preprint arXiv:2006.06485. doi: 10.48550/arXiv.2006.06485
Pawlowski, N., Coelho de Castro, D., and Glocker, B. (2020b). Deep structural causal models for tractable counterfactual inference. Adv. Neural Inf. Process. Syst. 33, 857–869.
Penn, D. C., and Povinelli, D. J. (2007). Causal cognition in human and nonhuman animals: a comparative, critical. Annu. Rev. Psychol. 58, 97–118. doi: 10.1146/annurev.psych.58.110405.085555
Péntek, Q., Hein, S., Miernik, A., and Reiterer, A. (2018). Image-based 3d surface approximation of the bladder using structure-from-motion for enhanced cystoscopy based on phantom data. Biomed. Eng. Biomedizinische Technik 63, 461–466. doi: 10.1515/bmt-2016-0185
Pepperell, E., Corke, P., and Milford, M. (2016). Routed roads: Probabilistic vision-based place recognition for changing conditions, split streets and varied viewpoints. Int. J. Rob. Res. 35, 1057–1179. doi: 10.1177/0278364915618766
Qi, Y., Jin, L., Li, H., Li, Y., and Liu, M. (2020). Discrete computational neural dynamics models for solving time-dependent sylvester equations with applications to robotics and mimo systems. IEEE Trans. Ind. Inform. 16, 6231–6241. doi: 10.1109/TII.2020.2966544
Qian, Z., Curth, A., and van der Schaar, M. (2021a). Estimating multi-cause treatment effects via single-cause perturbation. Adv. Neural Inf. Process. Syst. 34, 23754–23767.
Qian, Z., Zhang, Y., Bica, I., Wood, A., and van der Schaar, M. (2021b). Synctwin: treatment effect estimation with longitudinal outcomes. Adv. Neural Inf. Process. Syst. 34, 3178–3190.
Qin, F., Li, Y., Su, Y.-H., Xu, D., and Hannaford, B. (2019). “Surgical instrument segmentation for endoscopic vision with data fusion of cnn prediction and kinematic pose,” in 2019 International Conference on Robotics and Automation (ICRA) (IEEE) (Montreal, QC: IEEE), 9821–9827.
Qin, F., Lin, S., Li, Y., Bly, R. A., Moe, K. S., and Hannaford, B. (2020). Towards better surgical instrument segmentation in endoscopic vision:multi-angle feature aggregation and contour supervision. IEEE Robot. Autom. Lett. 5, 6639–6646. doi: 10.1109/LRA.2020.3009073
Ramsey, J., Glymour, M., Sanchez-Romero, R., and Glymour, C. (2017). A million variables and more: the fast greedy equivalence search algorithm for learning high-dimensional graphical causal models, with an application to functional magnetic resonance images. Int. J. Data Sci. Anal. 3, 121–129. doi: 10.1007/s41060-016-0032-z
Ramsey, J. D. (2014). A scalable conditional independence test for nonlinear, non-gaussian data. arXiv preprint arXiv:1401.5031. doi: 10.48550/arXiv.1401.5031
Recasens, D., Lamarca, J., Fácil, J. M., Montiel, J., and Civera, J. (2021). Endo-depth-and-motion: reconstruction and tracking in endoscopic videos using depth networks and photometric constraints. IEEE Robot. Autom. Lett. 6, 7225–7232. doi: 10.1109/LRA.2021.3095528
Reinisch, J. M., Sanders, S. A., Mortensen, E. L., and Rubin, D. B. (1995). In utero exposure to phenobarbital and intelligence deficits in adultmen. JAMA 274, 1518–1525. doi: 10.1001/jama.1995.03530190032031
Robins, J. M., Rotnitzky, A., and Zhao, L. P. (1994). Estimation of regression coefficients when some regressors are notalways observed. J. Am. Stat. Assoc. 89, 846–866. doi: 10.1080/01621459.1994.10476818
Saini, S. K., Dhamnani, S., Ibrahim, A. A., and Chavan, P. (2019). “Multiple treatment effect estimation using deep generative model with task embedding,” in The World Wide Web Conference (San Francisco, CA), 1601–1611.
Saputra, M. R. U., Markham, A., and Trigoni, N. (2018). Visual slam and structure from motion in dynamic environments: a survey. ACM Comput. Surveys 51, 1–36. doi: 10.1145/3177853
Saxena, R. C., Friedman, S., Bly, R. A., Otjen, J., Alessio, A. M., Li, Y., et al. (2019). Comparison of micro-computed tomography and clinical computed tomography protocols for visualization of nasal cartilage before surgical planning for rhinoplasty. JAMA Facial Plast Surg. 21, 237–243. doi: 10.1001/jamafacial.2018.1931
Schwab, P., Linhardt, L., Bauer, S., Buhmann, J. M., and Karlen, W. (2020). Learning counterfactual representations for estimating individual dose-response curves. Proc. AAAI Conf. Artif. Intell. 34, 5612–5619. doi: 10.1609/aaai.v34i04.6014
Schwab, P., Linhardt, L., and Karlen, W. (2018). Perfect match: a simple method for learning representations for counterfactual inference with neural networks. arXiv preprint arXiv:1810.00656. doi: 10.48550/arXiv.1810.00656
Schwarz, G. (1978). Estimating the dimension of a model. Ann. Stat. 6, 461–464. doi: 10.1214/aos/1176344136
Sejdinovic, D., Sriperumbudur, B., Gretton, A., and Fukumizu, K. (2013). Equivalence of distance-based and rkhs-based statistics in hypothesis testing. Ann. Stat. 41, 2263–2291. doi: 10.1214/13-AOS1140
Seok Lee, H., and Mu Lee, K. (2013). “Dense 3D reconstruction from severely blurred images using a single moving camera,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Portland, OR: IEEE), 273–280.
Shalit, U., Johansson, F. D., and Sontag, D. (2017). “Estimating individual treatment effect: generalization bounds and algorithms,” in International Conference on Machine Learning (PMLR) (Sydney, NSW), 3076–3085.
Shi, C., Blei, D., and Veitch, V. (2019). “Adapting neural networks for the estimation of treatment effects,” in Advances in Neural Information Processing Systems, Vol. 32 (Vancouver, BC).
Shimizu, S., Hoyer, P. O., Hyvärinen, A., Kerminen, A., and Jordan, M. (2006). A linear non-gaussian acyclic model for causal discovery. J. Mach. Learn. Res. 7, 2003–2030.
Singla, S., Pollack, B., Chen, J., and Batmanghelich, K. (2019). Explanation by progressive exaggeration. arXiv preprint arXiv:1911.00483. doi: 10.48550/arXiv.1911.00483
Smith, E., Calandra, R., Romero, A., Gkioxari, G., Meger, D., Malik, J., et al. (2020). 3D shape reconstruction from vision and touch. Adv. Neural Inf. Process. Syst. 33, 14193–14206.
Sobel, D. M., and Legare, C. H. (2014). Causal learning in children. Wiley Interdisc. Rev. Cogn. Sci. 5, 413–427. doi: 10.1002/wcs.1291
Soper, T. D., Porter, M. P., and Seibel, E. J. (2012). Surface mosaics of the bladder reconstructed from endoscopic videofor automated surveillance. IEEE Trans. Biomed. Eng. 59, 1670–1680. doi: 10.1109/TBME.2012.2191783
Spelke, E. S., Breinlinger, K., Macomber, J., and Jacobson, K. (1992). Origins of knowledge. Psychol. Rev. 99, 605. doi: 10.1037/0033-295X.99.4.605
Spirtes, P., Glymour, C. N., Scheines, R., and Heckerman, D. (2000). Causation, Prediction, and Search. Vancouver, BC: MIT Press.
Spirtes, P. L., Meek, C., and Richardson, T. S. (2013). Causal inference in the presence of latent variables and selectionbias. arXiv preprint arXiv:1302.4983. doi: 10.48550/arXiv.1302.4983
Stuart, E. A. (2010). Matching methods for causal inference: A review and a look forward. Stat. Sci. 25, 1. doi: 10.1214/09-STS313
Su, H., Hou, X., Zhang, X., Qi, W., Cai, S., Xiong, X., et al. (2022a). Pneumatic soft robots: challenges and benefits. Actuators 11, 92. doi: 10.3390/act11030092
Su, H., Qi, W., Chen, J., and Zhang, D. (2022b). Fuzzy approximation-based task-space control of robot manipulators with remote center of motion constraint. IEEE Trans. Fuzzy Syst. 30, 1564–1573. doi: 10.1109/TFUZZ.2022.3157075
Su, Y.-H., Munawar, A., Deguet, A., Lewis, A., Lindgren, K., Li, Y., et al. (2020). “Collaborative robotics toolkit (crtk):open software framework forsurgical robotics research,” in 2020 Fourth IEEE International Conference on Robotic Computing (IRC) (Taichung: IEEE), 1–8.
Taleb, A., and Jutten, C. (1999). Source separation in post-nonlinear mixtures. IEEE Trans. signal Process. 47, 2807–2820. doi: 10.1109/78.790661
Tateno, K., Tombari, F., Laina, I., and Navab, N. (2017). “CNN-SLAM: real-time dense monocular slam with learned depth prediction,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Honolulu, HI: IEEE), 6243–6252.
Taylor, R. H., Menciassi, A., Fichtinger, G., Fiorini, P., and Dario, P. (2016). “Medical robotics and computer-integrated surgery,” in Springer Handbook of Robotics (Baltimore, MD: Springer), 1657–1684.
Tooby, J., Leslie, A. M., Sperber, D., Caramazza, A., Hillis, A. E., Leek, E. C., et al. (1994). Mapping the Mind: Domain Specificity in Cognition and Culture. Cambridge, MA: Cambridge University Press.
Tsamardinos, I., Brown, L. E., and Aliferis, C. F. (2006). The max-min hill-climbing bayesian network structure learning algorithm. Mach. Learn. 65, 31–78. doi: 10.1007/s10994-006-6889-7
Turan, M., Almalioglu, Y., Araujo, H., Konukoglu, E., and Sitti, M. (2017). A non-rigid map fusion-based direct slam method for endoscopic capsule robots. Int. J. Intell. Robot. Appl. 399–409. doi: 10.1007/s41315-017-0036-4
Vasconcelos, F., Mazomenos, E., Kelly, J., and Stoyanov, D. (2019). “RCM-SLAM: visual localisation and mapping under remote centre of motion constraints,” in 2019 International Conference on Robotics and Automation (ICRA) (Montreal, QC: IEEE), 9278–9284.
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., et al. (2017). “Attention is all you need,” in Advances in Neural Information Processing Systems, Vol. 30 (Long Beach, CA).
Visentini-Scarzanella, M., Sugiura, T., Kaneko, T., and Koto, S. (2017). Deep monocular 3d reconstruction for assisted navigation in bronchoscopy. Int. J. Comput. Assist. Radiol.Surgery 12, 1089–1099. doi: 10.1007/s11548-017-1609-2
Wager, S., and Athey, S. (2018). Estimation and inference of heterogeneous treatment effects using random forests. J. Am. Stat. Assoc. 113, 1228–1242. doi: 10.1080/01621459.2017.1319839
Wen, S., Zhao, Y., Liu, X., Sun, F., Lu, H., and Wang, Z. (2020). Hybrid semi-dense 3D semantic-topological mapping from stereo visual-inertial odometry slam with loop closure detection. IEEE Trans. Vehicular Technol. 69, 16057–16066. doi: 10.1109/TVT.2020.3041852
Whelan, T., Salas-Moreno, R. F., Glocker, B., Davison, A. J., and Leutenegger, S. (2016). Elasticfusion: real-time dense slam and light source estimation. Int. J. Rob. Res. 35, 1697–1716. doi: 10.1177/0278364916669237
Williams, B., Klein, G., and Reid, I. (2007). “Real-time slam relocalisation,” in 2007 IEEE 11th International Conference on Computer Vision (Rio de Janeiro: IEEE), 1–8.
Wimbauer, F., Yang, N., von Stumberg, L., Zeller, N., and Cremers, D. (2021). “Monorec: semi-supervised dense reconstruction in dynamic environments from a single moving camera,” in Proceedings of the IEEE/CVF Conference on Computer Visionand Pattern Recognition (Nashville, TN: IEEE), 6112–6122.
Wong, M. L., Lee, S. Y., and Leung, K. S. (2002). “A hybrid approach to discover bayesian networks from databases using evolutionary programming,” in 2002 IEEE International Conference on Data Mining, 2002.Proceedings (Maebashi City: IEEE), 498–505.
Wu, A., Kuang, K., Yuan, J., Li, B., Wu, R., Zhu, Q., et al. (2020). Learning decomposed representation for counterfactual inference. arXiv preprint arXiv:2006.07040. doi: 10.48550/arXiv.2006.07040
Wu, Y., Zhang, Y., Zhu, D., Feng, Y., Coleman, S., and Kerr, D. (2020). “EAO-SLAM: monocular semi-dense object slam based on ensemble data association,” in 2020 IEEE/RSJ International Conference on Intelligent Robotsand Systems (IROS) (Las Vegas, NV: IEEE), 4966–4973.
Xu, Y., Su, H., Ma, G., and Liu, X. (2022). A novel dual-modal emotion recognition algorithm with fusing hybrid features of audio signal and speech context. Complex Intell. Syst. 1–13. doi: 10.1007/s40747-022-00841-3
Yang, M., Liu, F., Chen, Z., Shen, X., Hao, J., and Wang, J. (2020). Causalvae: Structured causal disentanglement in variational autoencoder. arXiv preprint arXiv:2004.08697. doi: 10.48550/arXiv.2004.08697
Yang, S., Song, Y., Kaess, M., and Scherer, S. (2016). “Pop-up slam: semantic monocular plane slam for low-texture environments,” in 2016 IEEE/RSJ International Conference on Intelligent Robotsand Systems (IROS) (Daejeon: IEEE), 1222–1229.
Yao, L., Chu, Z., Li, S., Li, Y., Gao, J., and Zhang, A. (2021a). A survey on causal inference. ACM Trans. Knowl. Discov. Data 15, 1–46. doi: 10.1145/3444944
Yao, L., Li, S., Li, Y., Huai, M., Gao, J., and Zhang, A. (2018). “Representation learning for treatment effect estimation from observational data,” in Advances in Neural Information Processing Systems, Vol. 31 (Montréal, QC).
Yao, L., Li, S., Li, Y., Huai, M., Gao, J., and Zhang, A. (2019a). “ACE: Adaptively similarity-preserved representation learning for individual treatment effect estimation,” in 2019 IEEE International Conference on Data Mining (ICDM) (Beijing: IEEE), 1432–1437.
Yao, L., Li, S., Li, Y., Xue, H., Gao, J., and Zhang, A. (2019b). “On the estimation of treatment effect with text covariates,” in International Joint Conference on Artificial Intelligence (Macao).
Yao, L., Li, Y., Li, S., Huai, M., Gao, J., and Zhang, A. (2021b). “SCI: subspace learning based counterfactual inference for individual treatment effect estimation,” in Proceedings of the 30th ACM International Conference onInformation and Knowledge Management (Queensland), 3583–3587.
Yoon, J., Jordon, J., and Van Der Schaar, M. (2018). “Ganite: estimation of individualized treatment effects using generative adversarial nets,” in International Conference on Learning Representations (Vancouver, BC).
Yu, C., Liu, Z., Liu, X.-J., Xie, F., Yang, Y., Wei, Q., et al. (2018). “DS-SLAM: a semantic visual slam towards dynamic environments,” in 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (Madrid: IEEE), 1168–1174.
Zhang, D., Wu, Z., Chen, J., Zhu, R., Munawar, A., Xiao, B., et al. (2022). Human-robot shared control for surgical robot based on context-aware sim-to-real adaptation. arXiv preprint arXiv:2204.11116. doi: 10.1109/ICRA46639.2022.9812379
Zhang, K., and Hyvarinen, A. (2012). On the identifiability of the post-nonlinear causal model. arXiv preprint arXiv:1205.2599.
Zhang, K., Wang, Z., Zhang, J., and Schölkopf, B. (2015). On estimation of functional causal models: general results and application to the post-nonlinear causal model. ACM Trans. Intell. Syst. Technol. 7, 1–22. doi: 10.1145/2700476
Zhang, Y., Bellot, A., and Schaar, M. (2020). “Learning overlapping representations for the estimation of individualized treatment effects,” in International Conference on Artificial Intelligence and Statistics (PMLR) (Palermo), 1005–1014.
Zhang, Z., Lan, Q., Ding, L., Wang, Y., Hassanpour, N., and Greiner, R. (2019). Reducing selection bias in counterfactual reasoning for individual treatment effects estimation. arXiv preprint arXiv:1912.09040. doi: 10.48550/arXiv.1912.09040
Zheng, X., Dan, C., Aragam, B., Ravikumar, P., and Xing, E. (2020). “Learning sparse nonparametric dags,” in International Conference on Artificial Intelligence and Statistics (PMLR) (Palermo), 3414–3425.
Keywords: deep causal learning, robotic perception, complementary perception, robotics, intelligence
Citation: Li Y (2023) Deep causal learning for robotic intelligence. Front. Neurorobot. 17:1128591. doi: 10.3389/fnbot.2023.1128591
Received: 20 December 2022; Accepted: 30 January 2023;
Published: 22 February 2023.
Edited by:
Hang Su, Fondazione Politecnico di Milano, ItalyReviewed by:
Wen Qi, Politecnico di Milano, ItalyXiaorui Liu, Qingdao University, China
Yantao Shen, University of Nevada, United States
Jing Luo, Wuhan University of Technology, China
Jing Xu, Tsinghua University, China
Copyright © 2023 Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yangming Li, 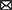 eWFuZ21pbmcubGlAcml0LmVkdQ==
eWFuZ21pbmcubGlAcml0LmVkdQ==
 Yangming Li
Yangming Li