Wrinkling of Elastic Cylinders With Material Properties Varying in Radial Direction

Although the instability of graded elastic cylinders has been analyzed by many researchers, most of them focused on the core-shell cylinders and film-substrate structures with inhomogeneous Young’s modulus. For a radially graded elastic cylinder subjected to the axial compression, the variation of Poisson’s ratio may result in the radial and circumferential stresses and thereby affects the critical condition of instability. By assuming linear elasticity with nonlinear kinematics, the governing equation for the incremental stress field is developed for instability analysis of the cylinder with radially graded material properties (Young’s modulus and Poisson’s ratio). Considering the arbitrariness of material properties, the state space technique is implemented and a semi-analytical solution is acquired. The obtained solution is validated by the finite element results. Numerical examples show that the critical condition of instability for graded elastic cylinders is related to whether Poisson’s ratio is assumed to be constant.

1 Introduction

The morphology characteristics caused by surface instability are often observed in nature and biological tissues, such as fruits, vegetables, animal brains, human guts (Dai and Liu, 2014; Budday et al., 2014; Balbi et al., 2015), and have been exploited for a broad range of applications, e.g., testing of mechanical properties for ultrathin films (Stafford et al., 2004), active surfaces (Tokarev and Minko, 2009), micro-optics (Harrison et al., 2004), microfluidic devices (Sugiura et al., 2007), and soft electronics and actuators (Rogers, et al., 2010; Yang et al., 2010). Due to curiosity about the natural phenomena and motivation of the development and utilization based on these configurations, the intrinsic mechanism of surface instability has attracted much attention of a large number of researchers over the last decades.

For the surface wrinkling instability, there are many previous works on core-shell cylinders and film-substrate structures. The pioneering work on film-substrate structures originated from the delamination analysis of such systems with a large unbounded flaw under compressive stress (Evans and Hutchinson, 1984; Hutchinson and Suo, 1992). The instability of an elastic film on a viscous substrate was then studied profoundly (Sridhar, et al., 2001; Huang and Suo, 2002a; Huang and Suo, 2002b). The relevant analyses of stiff films on compliant substrates were later presented ceaselessly in a large numbers. Huang et al. (2005) provided a nonlinear analysis of a film bonded to a substrate with finite thickness. Using the finite deformation theory, Song et al. (2008) studied the mechanics of thin buckled films on compliant substrates and obtained an analytical solution. Jia et al. (2012) investigated the wrinkling problem of a bilayer film on a soft substrate via theoretical analysis and finite element simulations. Xu et al. (2015) studied the occurrence and evolution of 3D instability patterns in thin films on hyperelastic substrates based on a fully nonlinear 3D finite element model. In comparison with the film-substrate structure, the stability analysis of cylindrical shells with soft cores was considered earlier by Seide (1962) using Donnell’s equations. About the same time a theoretical solution for the determination of buckling characteristics was presented for a long cylinder shell with a solid or elastic soft core under axial compression with the sinusoidal buckling assumption (Yao, 1962). Inspired by optimization of natural structures, Karam and Gibson (1995) theoretically analyzed the buckling of core-shell structures and found that the buckling resistance of a hollow cylindrical shell could be improved significantly by infilling a compliant elastic core. Hutchinson and He (2000) addressed the buckling of cylindrical sandwich shells with foamed metal cores for the optimal design for structural weight and carrying capacity, and a similar comprehensive analysis was provided by Dawson and Gibson (2007). By energy method, Arani et al. (2007) studied the elastic axisymmetric buckling of a thin simply supported cylindrical shell with an elastic core under axial compression. To further investigate the effect of the filled core rigidity and thickness on the buckling behavior, Ye et al. (2011) developed a simple formula to predict the critical buckling stress by using the Rayleigh–Ritz approximation. Based on the nonlinear Donnell-Mushtari-Vlassov shell theory, Zhao et al. (2014) investigated surface wrinkling of a core-shell cylinder along the axial and circumferential directions. Recently, the axisymmetric and non-axisymmetric mode transitions in the post-buckling regime in axially compressed core–shell cylinders were investigated based on a nonlinear 3D finite element model (Xu and Potier-Ferry, 2016) and nonlinear shell finite element (Lavrencic et al., 2020).

The aforementioned literature only involves the film-substrate and core-shell systems with uniform substrates and cores. In nature and some engineering problems, the material properties of substrates and cores are commonly inhomogeneous, and thus the surface wrinkling of such systems is necessary to be studied. However, the inhomogeneity of materials makes it difficult to obtain a completely analytical solution. In the past few years, some theoretical researches on surface instability have been devoted to graded elastic materials. Cao et al. (2012a) derived the critical condition of wrinkling for a stiff thin layer on a semi-infinite substrate with the power-law and exponential grading moduli, respectively. For elastic layers with material properties varying from the surface to the interior, a semi-analytical solution was obtained by the theoretical analysis combined with the finite element method (Lee et al., 2008) and the state space method (Wu et al., 2014); similar semi-analytical solutions for onset of surface instability of elastic cylinders with radially graded Young’s modulus were performed by Jia et al. (2014) and Han et al. (2017). Based on Floquet’s principle, most recently an explicit semi-analytical isogeometric analysis method was suggested for predicting wrinkling instability of a stiff film on a graded compliant cylinder (Li et al., 2020). We note in the existing studies that Poisson’s ratio in graded elastic layers and cylinders was commonly assumed to be a constant. In practice, however, for a radially graded elastic cylinder subjected to the axial compression, the variation of Poisson’s ratio may result in radial and circumferential stresses, which must affect the critical condition of instability.

In addition to be directly subjected to compression, surface instability of film-substrate or core-shell systems may be induced by swelling or growing, and surface stability of soft elastic layers may be also influenced by surface tension (Kang and Huang, 2010a; Wang, 2020). Upon swelling in a solvent, the surface of thin hydrogel layers on rigid substrates may become unstable and further evolves into various morphologies (Guvendiren et al., 2009; Guvendiren et al., 2010; Kang and Huang, 2010b; Wu et al., 2017). The tubular organ of animals, such as esophagus, can be seen as cylindrical bilayers with the stiffer outer layer (muscle) and softer inner layer (mucosa). When the inner mucosa grows, the outer muscle restricts its expansion, eventually leading to wrinkling, folding or creasing on the inner surface of mucosa (Jin et al., 2011; Li et al., 2011; Razavi et al., 2016). Similar instability was also found on the outer surface of core-shell cylinders as the outer shell grows or swells on a stiff core Cao et al. (2012b). The surface instability related to growth and swelling has been adequately studied in the past 10 years.

In this paper, we focus on an inhomogeneous elastic cylinder and assume that both Young’s modulus and Poisson’s ratio vary arbitrarily in the radial direction. A state space method is employed to investigate the onset of wrinkling for elastic cylinders under axial compression. The effects of the variation of Poisson’s ratio on stress distribution and critical condition of instability are discussed. The rest of this paper is arranged as follows. In Section 2, the instability theory of elastic cylinders is introduced. The solution of stress field in fundamental state is obtained by using the state space method in Section 3. In Section 4, the instability analysis for elastic cylinders with material properties varying arbitrarily in the radial direction is carried out and the critical condition of instability is presented. Two instability examples, a cylinder covered by a bilayer and a homogeneous cylinder with a linearly graded stiff layer, are discussed in Section 5. Concluding remarks are presented in Section 6.

2 Instability Theory of Elastic Cylinders

An elastic hollow inhomogeneous cylinder with traction free surfaces is considered as shown in Figure 1A, where a Cartesian coordinate system is set up with the reference coordinates X₁ and X₂ at one cross-section and X₃ along the axis of the cylinder. The inner and outer radii of the cylinder in the stress-free state are A and B, respectively. When subjected to an axial compression, the compressive stress inside the cylinder may cause surface or internal instability of the cylinder. Prior to surface or internal instability, the compressed cylinder is seen as in the fundamental state with the inner and outer radii a and b (Figure 1B), and the corresponding current coordinates are denoted as (x₁, x₂, x₃).

FIGURE 1

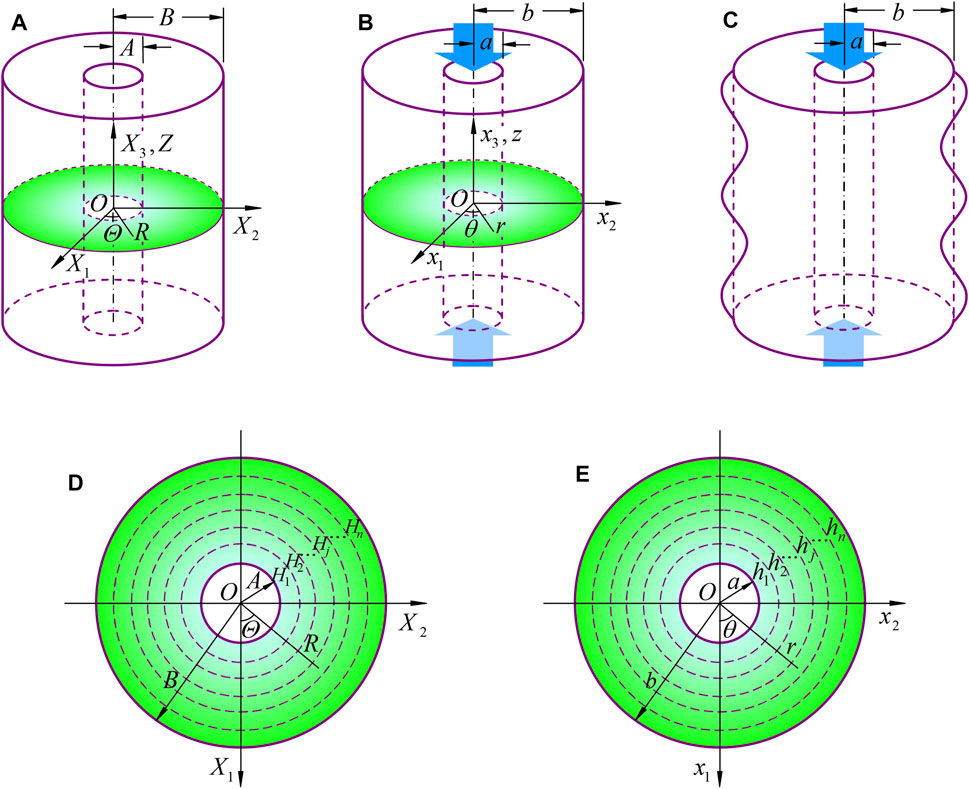
FIGURE 1. Schematic illustrations for an elastic hollow cylinder: (A) in the stress-free reference state; (B) in the fundamental state subjected to axial compression; (C) in the axial wrinkling state; (D) and (E) divided into n cylindrical subshells in the reference and fundamental states for the state space analysis.

In the present study, we consider an elastic cylinder with material properties varying in the radial direction, especially emphasizing the influence of Poisson’s ratio on stress distribution and structural stability. The material is assumed to be linear elastic and isotropic with a quadratic strain energy density function in terms of Green-Lagrange strain:

$W=\frac{1}{2}{C}_{IJKL}{E}_{IJ}{E}_{KL}(1)$

where E_IJ = (F_kIF_kJ − δ_IJ)/2, F_kJ = ∂x_k/∂X_J, δ_IJ is the Kronecker delta, and the elastic modulus C_IJKL is a function of X₁ and X₂ and possesses the isotropic symmetry. The first and second Piola–Kirchhoff stresses P_iJ and S_IJ are accordingly in the Cartesian coordinate system as (Wu et al., 2014)

$P_{iJ}=F_{iK}{S}_{KJ},S_{IJ}=C_{IJKL}{E}_{KL}(2)$

In the fundamental state, the equilibrium equation is

$P_{iJ,J}=0(3)$

and the boundary conditions at the inner and outer surfaces are

$P_{iJ}{N}_J=0,\mathrm{at}\sqrt{X_1^2+X_2^2}=A\mathrm{and}\mathrm{B}(4)$

where the notation ( )_,J stands for differentiation with respect to X_J in the reference state, N_J represents the direction cosine of the outer normal relative to the coordinate X_J; the Einstein summation convention is implied over repeated indices unless noted otherwise.

Under the axial compression, the imposed axial nominal strain ε₀ = F₃₃–1 is identical everywhere in the fundamental state. In the process of instability analysis, it is assumed that an incremental displacement Δu_i (i = 1, 2, 3) occurs from the fundamental state, then the corresponding incremental stress field must satisfy the following equilibrium equation and boundary conditions:

$\Delta P_{iJ,J}=(F_{iK}\Delta S_{KJ}+S_{KJ}\Delta F_{iK}){,}_J=0(5)$

$\Delta P_{iJ}{N}_J=0,\mathrm{at}\sqrt{X_1^2+X_2^2}=A\mathrm{and}\mathrm{B}(6)$

where $\Delta F_{kJ}=F_{iJ}\Delta u_{k,i}$, $\Delta S_{IJ}=C_{IJKL}\Delta E_{KL}$, $\Delta E_{IJ}=\frac{1}{2}(F_{kI}{F}_{iJ}+F_{iI}{F}_{kJ})\Delta u_{k,i}$.

Assuming that the strain in the fundamental state is small, we have $F_{iK}\approx {\delta }_{iK}$ and the equilibrium Eq. 5 and boundary condition (6) may be translated as that

$\Delta P_{ij,j}={(C_{ijkl}\Delta u_{k,l}+P_{kj}\Delta u_{i,k})}_{,j}=0(7)$

$\Delta P_{ij}{n}_j=0,\mathrm{at}\sqrt{x_1^2+x_2^2}=a\text{and}b(8)$

where ( )_,j denotes differentiation with respect to x_j in the current state, and n_j represents the direction cosine of the outer normal relative to the coordinate x_j.

Considering axisymmetry of the problem, the cylindrical coordinates in the reference state (R, Θ, Z) and in the current state (r, θ, z) are applied as shown in Figure 1. With the coordinate transformation from the Cartesian coordinates to the cylindrical coordinates, the equilibrium Eq. 3 in the fundamental state for radially graded elastic cylinders can be converted into the following form:

$\frac{\partial P_{rR}}{\partial R}+\frac{P_{rR}-P_{\theta \Theta }}{R}=0(9)$

where

$P_{rR}=C_{rRRR}\frac{\partial u_R}{\partial R}+C_{rR\mathit{\Theta \Theta }}\frac{u_R}{R}+C_{rRZZ}{\epsilon }_0(10)$

$P_{\theta \Theta }=C_{\theta \Theta RR}\frac{\partial u_R}{\partial R}+C_{\theta \Theta \mathit{\Theta \Theta }}\frac{u_R}{R}+C_{\theta \Theta ZZ}{\epsilon }_0(11)$

with u_R representing the radial displacement component. The axial stress in the fundamental state is then determined by

$P_{zZ}=C_{zZRR}\frac{\partial u_R}{\partial R}+C_{zZ\Theta \Theta }\frac{u_R}{R}+C_{zZZZ}{\epsilon }_{\text{0}}(12)$

The boundary condition (4) becomes

$P_{rR}=0,\mathrm{at}\mathit{R}\mathrm{=}\mathit{A}\mathrm{and}\mathit{B}(13)$

In general, Poisson’s ratio changes with the change of Young’s modulus of graded elastic materials. Poisson’s ratio commonly changes very little and thus it is often approximated as a constant for convenience. When the radially graded elastic cylinder is subjected to axial compression, the axial compressive stress is generated definitely. However, the radial and circumferential stresses do not necessarily occur, which depend on Poisson’s ratio. If Poisson’s ratio remains constant in the radial direction, transversely homogeneous strain generates and no radial and circumferential stresses occur. In contrast, if Poisson’s ratio varies in the radial direction, the radial and circumferential strains are inhomogeneous and corresponding stresses must be produced, which will inevitably affect the axial and circumferential stabilities of cylindrical structures. The instability analysis for Poisson’s ratio fixed as a constant has been carried out by many researchers (Jia et al., 2014; Han et al., 2017). In the present study, we assume that Poisson’s ratio varies in the radial direction as that of Young’s modulus. By the coordinate transformation, the equilibrium equation of the incremental stress field in Eq. 7 can be converted into the following form in the cylindrical coordinate system:

$\frac{\partial \Delta P_{rr}}{\partial r}+\frac{\partial \Delta P_{r\theta }}{r\partial \theta }+\frac{\partial \Delta P_{rz}}{\partial z}+\frac{\Delta P_{rr}-\Delta P_{\theta \theta }}{r}=0(14)$

$\frac{\partial \Delta P_{\theta r}}{\partial r}+\frac{\partial \Delta P_{\theta \theta }}{r\partial \theta }+\frac{\partial \Delta P_{\theta z}}{\partial z}+\frac{\Delta P_{\theta r}+\Delta P_{r\theta }}{r}=0(15)$

$\frac{\partial \Delta P_{zr}}{\partial r}+\frac{\partial \Delta P_{z\theta }}{r\partial \theta }+\frac{\partial \Delta P_{zz}}{\partial z}+\frac{\Delta P_{zr}}{r}=0(16)$

where

$\Delta P_{rr}=(C_{rrrr}+P_{rr})\frac{\partial \Delta u_r}{\partial r}+C_{rr\theta \theta }\left(\frac{\partial \Delta u_{\theta }}{r\partial \theta }+\frac{\Delta u_r}{r}\right)+C_{rrzz}\frac{\partial \Delta u_z}{\partial z}(17)$

$\Delta P_{\theta \theta }=C_{\theta \theta rr}\frac{\partial \Delta u_r}{\partial r}+(C_{\theta \theta \theta \theta }+P_{\theta \theta })\left(\frac{\partial \Delta u_{\theta }}{r\partial \theta }+\frac{\Delta u_r}{r}\right)+C_{\theta \theta zz}\frac{\partial \Delta u_z}{\partial z}(18)$

$\Delta P_{zz}=C_{zzrr}\frac{\partial \Delta u_r}{\partial r}+C_{zz\theta \theta }\left(\frac{\partial \Delta u_{\theta }}{r\partial \theta }+\frac{\Delta u_r}{r}\right)+(C_{zzzz}+P_{zz})\frac{\partial \Delta u_z}{\partial z}(19)$

$\Delta P_{r\theta }=C_{r\theta \theta r}\frac{\partial \Delta u_{\theta }}{\partial r}+(C_{r\theta r\theta }+P_{\theta \theta })\left(\frac{\partial \Delta u_r}{r\partial \theta }-\frac{\Delta u_{\theta }}{r}\right)(20)$

$\Delta P_{\theta r}=(C_{\theta r\theta r}+P_{rr})\frac{\partial \Delta u_{\theta }}{\partial r}+C_{\theta rr\theta }\left(\frac{\partial \Delta u_r}{r\partial \theta }-\frac{\Delta u_{\theta }}{r}\right)(21)$

$\Delta P_{\theta z}=C_{\theta zz\theta }\frac{\partial \Delta u_z}{r\partial \theta }+(C_{\theta z\theta z}+P_{zz})\frac{\partial \Delta u_{\theta }}{\partial z}(22)$

$\Delta P_{z\theta }=(C_{z\theta z\theta }+P_{\theta \theta })\frac{\partial \Delta u_z}{r\partial \theta }+C_{z\theta \theta z}\frac{\partial \Delta u_{\theta }}{\partial z}(23)$

$\Delta P_{zr}=(C_{zrzr}+P_{rr})\frac{\partial \Delta u_z}{\partial r}+C_{zrrz}\frac{\partial \Delta u_r}{\partial z}(24)$

$\Delta P_{rz}=C_{rzzr}\frac{\partial \Delta u_z}{\partial r}+(C_{rzrz}+P_{zz})\frac{\partial \Delta u_r}{\partial z}(25)$

The boundary condition of the incremental stress field in Eq. 8 becomes

$\Delta P_{rr}=\Delta P_{\theta r}=\Delta P_{zr}=0,\text{at}r=a\text{and}b(26)$

Equations 9–12 and Eqs 14–25 constitute the governing equations of instability analysis for radially graded elastic cylinders, which together with the boundary conditions (13) and (26) lead to an eigenvalue problem. If there is a nontrivial solution for the incremental displacement field, the critical condition for onset of instability is obtained successfully.

It should be noted that if the cylindrical structure is a solid cylinder, the boundary condition (13) at R = A needs to be replaced with

$u_R=0,\text{at}R=0(27)$

and the boundary condition (26) at r = a replaced with

$\Delta P_{\theta r}=\Delta P_{zr}=0\text{and}\Delta u_r=0,\text{at}r=0(28)$

3 Solution of Stress Field in Fundamental State

Considering arbitrariness of the material properties varying in the radial direction, it is impossible to obtain the analytical solution of stress field in the cylinder, and the state space technique is thereby employed in this paper.

From Eq. 10, we have

$\frac{\partial u_R}{\partial R}=-\frac{\lambda }{\lambda +2\mu }\frac{u_R}{R}+\frac{1}{\lambda +2\mu }{P}_{rR}-\frac{\lambda }{\lambda +2\mu }{\epsilon }_{\text{0}}(29)$

Substituting Eq. 29 into Eq. 11 and then into Eq. 9, we get

$\frac{\partial P_{rR}}{\partial R}=\frac{4(\lambda +\mu )\mu }{\lambda +2\mu }\frac{u_R}{R^2}-\frac{2\mu }{\lambda +2\mu }\frac{P_{rR}}{R}+\frac{2\lambda \mu }{\lambda +2\mu }\frac{{\epsilon }_{\text{0}}}{R}(30)$

and the circumferential and axial nominal stresses are, respectively,

$P_{\theta \Theta }=\frac{4(\lambda +\mu )\mu }{\lambda +2\mu }\frac{u_R}{R}+\frac{\lambda }{\lambda +2\mu }{P}_{rR}+\frac{2\lambda \mu }{\lambda +2\mu }{\epsilon }_0(31)$

$P_{zZ}=\frac{2\lambda \mu }{\lambda +2\mu }\frac{u_R}{R}+\frac{\lambda }{\lambda +2\mu }{P}_{rR}+\frac{4(\lambda +\mu )\mu }{\lambda +2\mu }{\epsilon }_0(32)$

where λ and μ are Lame’s constants of isotropic elasticity, relating to Young’s modulus E and Poisson’s ratio ν as follows:

$\lambda =\frac{E\nu }{(1+\nu )(1-2\nu )},\mu =\frac{E}{2(1+\nu )}(33)$

Combining Eqs 29, 30, a set of inhomogeneous differential equations are obtained in a matrix form as

$\frac{\partial }{\partial R}\left\{\begin{array}{c}{u}_R\\ P_{rR}\end{array}\right\}=\mathbf{D}\left\{\begin{array}{c}{u}_R\\ P_{rR}\end{array}\right\}+\mathbf{K}(34)$

where the coefficient matrix D and the inhomogeneous item K are, respectively,

$\mathbf{D}=\left[\begin{array}{cc}-\frac{\lambda }{\lambda +2\mu }\frac{1}{R}& \frac{1}{\lambda +2\mu }\\ \frac{4(\lambda +\mu )\mu }{\lambda +2\mu }\frac{1}{R^2}& -\frac{2\mu }{\lambda +2\mu }\frac{1}{R}\end{array}\right],\mathbf{K}=\left(\begin{array}{c}-\frac{\lambda }{\lambda +2\mu }\\ \frac{2\lambda \mu }{\lambda +2\mu }\frac{1}{R}\end{array}\right){\epsilon }_0,(35)$

Since the coefficient matrix and inhomogeneous item in Eq. 35 contain the radial coordinate R and the radially varying material parameters, the analytical solution to Eq. 34 cannot be obtained directly. For this reason, we first divide the hollow cylinder into n subshells and number them from the inner subshell to the outer subshell. The thickness of the ith subshell is denoted by H_i ($i=$ 1, 2, ⋅⋅⋅, n) as illustrated in Figure 1D, and its inner and outer radii are $R_{i-1}$ and $R_i$, respectively. Thus there are $R_i=A+H_1+H_2+\cdots +H_i$, $R_0=A$ and $R_n=B$. The material parameters are accordingly dispersed into each subshell as piecewise constant functions E_i, ν_i. In each subshell, the material parameters are assumed as their corresponding values at its mid-surface, i.e., $E_i=E[(R_{i-1}+R_i)/2]$ and ${\nu }_i=\nu [(R_{i-1}+R_i)/2]$. When $n\to \infty$ and $H_i\to 0$, the virtual laminated cylinder with material properties varying as piecewise constant functions infinitely approaches the originally graded cylinder. Taking $R=(R_{i-1}+R_i)/2$ in Eq. 35, a set of the first-order inhomogeneous differential equations with constant coefficients for the ith subshell, i.e. the state equation, are obtained as

$\frac{\partial }{\partial R}\left\{\begin{array}{c}{u}_{Ri}\\ P_{rRi}\end{array}\right\}={\mathbf{D}}_i\left\{\begin{array}{c}{u}_{Ri}\\ P_{rRi}\end{array}\right\}+{\mathbf{K}}_i(36)$

The relation between the state vectors at outer surface and the inner surface of the ith subshell is determined as

$\left\{\begin{array}{c}{u}_{Ri}\left(R_i\right)\\ P_{rRi}\left(R_i\right)\end{array}\right\}={\text{e}}^{{\mathbf{D}}_i{H}_i}\left\{\begin{array}{c}{u}_{Ri}\left(R_{i-1}\right)\\ P_{rRi}\left(R_{i-1}\right)\end{array}\right\}+{\displaystyle {\int }_{R_{i-1}}^{R_i}{\text{e}}^{{\mathbf{D}}_i(R_i-\xi )}{\mathbf{K}}_i\text{d}\xi }(37)$

Thanks to the continuity of the state vector across all interfaces between the adjacent subshells, the relationship between the state vectors at the outer and inner surfaces of the cylinder can be acquired as

$\left\{\begin{array}{c}{u}_{Rn}\left(R_n\right)\\ P_{rRn}\left(R_n\right)\end{array}\right\}={\displaystyle \prod _{i=n}^1{\text{e}}^{{\mathbf{D}}_i{H}_i}}\left\{\begin{array}{c}{u}_{R1}\left(R_0\right)\\ P_{rR1}\left(R_0\right)\end{array}\right\}+{\displaystyle \sum _{j=1}^{n-1}{\displaystyle \prod _{i=n}^{j+1}{\text{e}}^{{\mathbf{D}}_i{H}_i}}}{\displaystyle {\int }_{R_{j-1}}^{R_j}{\text{e}}^{{\mathbf{D}}_j(R_j-\xi )}{\mathbf{K}}_j\text{d}\xi }+{\displaystyle {\int }_{R_{n-1}}^{R_n}{\text{e}}^{{\mathbf{D}}_n(R_n-\xi )}{\mathbf{K}}_n\text{d}\xi }(38)$

By using the boundary condition (13), i.e.

$P_{rR1}\left(R_0\right)=P_{rRn}\left(R_n\right)=0(39)$

or Eq. 27 together with Eq. 13 at R = B, i.e.

$u_{R1}\left(0\right)=0and{P}_{rRn}\left(R_n\right)=0(40)$

the state variables at the inner and outer surfaces are subsequently obtained as functions of the axial strain ε₀, and u_Ri and P_rRi ($i=1,2,\cdots ,n$) at any interface may be calculated successively by Eq. 37. The other two stress components P_θΘi and P_zZi are in turn computed from Eqs 31, 32. As a result, all displacement and stress components in fundamental state are determined as functions of ε₀.

4 Instability Analysis

To acquire the critical condition of instability for cylinders with material properties varying arbitrarily in the radial direction, the virtual dividing model in the prior section is still demanded in the following solving process.

From Eqs 14–25, we can get the differentiations of incremental displacements and stresses with respect to the radial coordinate r as follows:

$\frac{\partial \Delta u_r}{\partial r}=-\frac{\lambda }{\lambda +2\mu +P_{rr}}\left(\frac{\partial \Delta u_{\theta }}{r\partial \theta }+\frac{\Delta u_r}{r}\right)-\frac{\lambda }{\lambda +2\mu +P_{rr}}\frac{\partial \Delta u_z}{\partial z}+\frac{1}{\lambda +2\mu +P_{rr}}\Delta P_{rr}(41)$

$\frac{\partial \Delta u_{\theta }}{\partial r}=-\frac{\mu }{\mu +P_{rr}}\left(\frac{\partial \Delta u_r}{r\partial \theta }-\frac{\Delta u_{\theta }}{r}\right)+\frac{1}{\mu +P_{rr}}\Delta P_{\theta r}(42)$

$\frac{\partial \Delta u_z}{\partial r}=-\frac{\mu }{\mu +P_{rr}}\frac{\partial \Delta u_r}{\partial z}+\frac{1}{\mu +P_{rr}}\Delta P_{zr}(43)$

$\frac{\partial \Delta P_{rr}}{\partial r}=\left(\lambda +2\mu +P_{\theta \theta }-\frac{{\lambda }^2}{\lambda +2\mu +P_{rr}}\right)\frac{\Delta u_r}{r^2}-\left(\mu +P_{\theta \theta }-\frac{{\mu }^2}{\mu +P_{rr}}\right)\frac{{\partial }^2\Delta u_r}{r^2\partial {\theta }^2}+\left(\lambda -\frac{{\lambda }^2}{\lambda +2\mu +P_{rr}}\right)\frac{\partial \Delta u_z}{r\partial z}-\left(\mathrm{1-}\frac{\lambda }{\lambda +2\mu +P_{rr}}\right)\frac{\Delta P_{rr}}{r}-\frac{\mu }{\mu +P_{rr}}\frac{\partial \Delta P_{\theta r}}{r\partial \theta }-\frac{\mu }{\mu +P_{rr}}\frac{\partial \Delta P_{zr}}{r\partial \theta }-\left(\mu +P_{zz}-\frac{{\mu }^2}{\mu +P_{rr}}\right)\frac{{\partial }^2\Delta u_r}{\partial z^2}+\left(\lambda +3\mu +2P_{\theta \theta }-\frac{{\lambda }^2}{\lambda +2\mu +P_{rr}}-\frac{{\mu }^2}{\mu +P_{rr}}\right)\frac{\partial \Delta u_{\theta }}{r^2\partial \theta }(44)$

$\frac{\partial \Delta P_{\theta r}}{\partial r}=-\left(\lambda +3\mu +2P_{\theta \theta }-\frac{{\lambda }^2}{\lambda +2\mu +P_{rr}}-\frac{{\mu }^2}{\mu +P_{rr}}\right)\frac{\partial \Delta u_r}{r^2\partial \theta }+\left(\mu +P_{\theta \theta }-\frac{{\mu }^2}{\mu +P_{rr}}\right)\frac{\Delta u_{\theta }}{r^2}-\left(\lambda +2\mu +P_{\theta \theta }-\frac{{\lambda }^2}{\lambda +2\mu +P_{rr}}\right)\frac{{\partial }^2\Delta u_{\theta }}{r^2\partial {\theta }^2}-(\mu +P_{zz})\frac{{\partial }^2\Delta u_{\theta }}{\partial z^2}-\left(\lambda +\mu -\frac{{\lambda }^2}{\lambda +2\mu +P_{rr}}\right)\frac{{\partial }^2\Delta u_z}{r\partial \theta \partial z}-\frac{\lambda }{\lambda +2\mu +P_{rr}}\frac{\partial \Delta P_{rr}}{r\partial \theta }-\left(1+\frac{\mu }{\mu +P_{rr}}\right)\frac{\Delta P_{\theta r}}{r}(45)$

$\frac{\partial \Delta P_{zr}}{\partial r}=-\left(\lambda -\frac{{\lambda }^2}{\lambda +2\mu +P_{rr}}\right)\frac{\partial \Delta u_r}{r\partial z}-\left(\lambda +\mu -\frac{{\lambda }^2}{\lambda +2\mu +P_{rr}}\right)\frac{\partial \Delta u_{\theta }}{r\partial \theta \partial z}-(\mu +P_{\theta \theta })\frac{{\partial }^2\Delta u_z}{r^2\partial {\theta }^2}-\left(\lambda +2\mu +P_{zz}-\frac{{\lambda }^2}{\lambda +2\mu +P_{rr}}\right)\frac{{\partial }^2\Delta u_z}{\partial z^2}-\frac{\lambda }{\lambda +2\mu +P_{rr}}\frac{\partial \Delta P_{rr}}{\partial z}-\frac{1}{r}\Delta P_{zr}(46)$

With the assumption of small strain in the fundamental state, we have $P_{rr}\approx P_{rR}$, $P_{\theta \theta }\approx P_{\theta \mathit{\Theta }}$, and $P_{zz}\approx P_{zZ}$, they are functions of the axial strain ${\epsilon }_0$ and determined by the state space method in Section 3. According to Eqs 41–46, the incremental displacements and stresses may be assumed to predict the axial and circumferential instabilities as

$\Delta u_r=U_r\left(r\right)\cos {\omega }_1\theta \cos {\omega }_2,z\Delta u_{\theta }=U_{\theta }\left(r\right)\sin {\omega }_1\theta \cos {\omega }_{2}z,\Delta u_z=U_z\left(r\right)\cos {\omega }_1\theta \sin {\omega }_{2}z(47)$

$\Delta P_{rr}=T_r\left(r\right)\cos {\omega }_1\theta \cos {\omega }_{2}z,\Delta P_{\theta r}=T_{\theta }\left(r\right)\sin {\omega }_1\theta \cos {\omega }_{2}z,\Delta P_{zr}=T_z\left(r\right)\cos {\omega }_1\theta \sin {\omega }_{2}z(48)$

where ω₁ and ω₂ refer to the wave number along the circumferential and axial directions, respectively. Substituting Eqs 47, 48 into Eqs 41–46, we obtain a set of homogeneous differential equations in the matrix form as

$\frac{\mathrm{d}\mathbf{G}\left(r\right)}{\mathrm{d}r}=\mathbf{MG}\left(r\right)(49)$

where the state vector G(r) = [U_r(r) U_θ(r) U_z(r) T_r(r) T_θ(r) T_z(r)]^T, and M is a 6×6 coefficient matrix with the following nonzero elements:

$\begin{array}{l}{M}_{11}=-\frac{1}{r}\frac{\lambda }{\lambda +2\mu +P_{rr}},M_{12}=-\frac{1}{r}\frac{\lambda {\omega }_1}{\lambda +2\mu +P_{rr}},M_{13}=-\frac{\lambda {\omega }_2}{\lambda +2\mu +P_{rr}},M_{14}=\frac{1}{\lambda +2\mu +P_{rr}}\\ M_{21}=\frac{1}{r}\frac{\mu {\omega }_1}{\mu +P_{rr}},M_{22}=\frac{1}{r}\frac{\mu }{\mu +P_{rr}},M_{25}=\frac{1}{\mu +P_{rr}},M_{31}=\frac{\mu {\omega }_2}{\mu +P_{rr}},M_{36}=\frac{1}{\mu +P_{rr}}\\ M_{41}=\frac{1}{r^2}\left[\left(\lambda +2\mu +P_{\theta \theta }-\frac{{\lambda }^2}{\lambda +2\mu +P_{rr}}\right)+\left(\mu +P_{\theta \theta }-\frac{{\mu }^2}{\mu +P_{rr}}\right){\omega }_1^2\right]+\left(\mu +P_{zz}-\frac{{\mu }^2}{\mu +P_{rr}}\right){\omega }_2^2\\ M_{42}=\frac{1}{r^2}\left(\lambda +3\mu +2P_{\theta \theta }-\frac{{\lambda }^2}{\lambda +2\mu +P_{rr}}-\frac{{\mu }^2}{\mu +P_{rr}}\right){\omega }_1,M_{43}=\frac{1}{r}\left(\lambda -\frac{{\lambda }^2}{\lambda +2\mu +P_{rr}}\right){\omega }_2\\ M_{44}=-\frac{1}{r}\left(1-\frac{\lambda }{\lambda +2\mu +P_{rr}}\right),M_{45}=-\frac{1}{r}\frac{\mu }{\mu +P_{rr}}{\omega }_1,M_{46}=-\frac{\mu }{\mu +P_{rr}}{\omega }_2\\ M_{51}=\frac{1}{r^2}\left(\lambda +3\mu +2P_{\theta \theta }-\frac{{\lambda }^2}{\lambda +2\mu +P_{rr}}-\frac{{\mu }^2}{\mu +P_{rr}}\right){\omega }_1\\ M_{52}=\frac{1}{r^2}\left[\left(\mu +P_{\theta \theta }-\frac{{\mu }^2}{\mu +P_{rr}}\right)+\left(\lambda +2\mu +P_{\theta \theta }-\frac{{\lambda }^2}{\lambda +2\mu +P_{rr}}\right){\omega }_1^2\right]+(\mu +P_{zz}){\omega }_2^2\\ M_{53}=\frac{1}{r}\left(\lambda +\mu -\frac{{\lambda }^2}{\lambda +2\mu +P_{rr}}\right){\omega }_1{\omega }_2,M_{54}=\frac{1}{r}\frac{\lambda }{\lambda +2\mu +P_{rr}}{\omega }_1,M_{55}=-\frac{1}{r}\left(1+\frac{\mu }{\mu +P_{rr}}\right)\\ M_{61}=\frac{1}{r}\left(\lambda -\frac{{\lambda }^2}{\lambda +2\mu +P_{rr}}\right){\omega }_2,M_{62}=\frac{1}{r}\left(\lambda +\mu -\frac{{\lambda }^2}{\lambda +2\mu +P_{rr}}\right){\omega }_1{\omega }_2\\ M_{63}=\frac{1}{r^2}(\mu +P_{\theta \theta }){\omega }_1^2+\left(\lambda +2\mu +P_{zz}-\frac{{\lambda }^2}{\lambda +2\mu +P_{rr}}\right){\omega }_2^2,M_{64}=\frac{\lambda }{\lambda +2\mu +P_{rr}}{\omega }_2,M_{66}=-\frac{1}{r}\end{array}$

Taking $E=E_i$, $\nu ={\nu }_i$, and $r=(r_i+r_{i-1})/2$ in the coefficient matrix M, the state equation for the i^th subshell can be obtained as

$\frac{\mathrm{d}{\mathbf{G}}_i\left(r\right)}{\mathrm{d}r}={\mathbf{M}}_i{\mathbf{G}}_i\left(r\right)(50)$

Integrating two sides of Eq. 50, the state vector of the outer surface relating to that of the inner surface is derived as

${\mathbf{G}}_i\left(r_i\right)={\mathbf{N}}_i\left(h_i\right){\mathbf{G}}_i\left(r_{i-1}\right)={\text{e}}^{M_i{h}_i}{\mathbf{G}}_i\left(r_{i-1}\right)\left(\mathrm{no}\mathrm{Summation}\mathrm{over}\mathit{i}\right),(51)$

By means of the continuity of the state vector across all interfaces, the relationship between the state vectors for the outer and inner surfaces of the whole cylinder is determined as

${\mathbf{G}}_n\left(r_n\right)=\mathbf{N}{\mathbf{G}}_1\left(r_0\right)(52)$

where $\mathbf{N}={\displaystyle \prod _{i=n}^1{\mathbf{N}}_i\left(h_i\right)}$.

Corresponding to Eq. 52, the boundary condition Eqs 26, 28 can be rewritten as that

$T_{rn}\left(r_n\right)=T_{\theta n}\left(r_n\right)=T_{zn}\left(r_n\right)=0,T_{r1}\left(r_0\right)=T_{\theta 1}\left(r_0\right)=T_{z1}\left(r_0\right)=0(53)$

and

$U_{r1}\left(0\right)=0,T_{\theta 1}\left(0\right)=T_{z1}\left(0\right)=0(54)$

Since the coefficient matrix M_i includes the wave numbers ω₁ and ω₂, and the stress components P_rRi, P_θΘi, and P_zZi ($i=1,2,\cdots ,n$) are functions of the axial strain ε₀, the relationship between the state vector G_n (r_n) and G₁ (r₀) by Eq. 52 therefore depends on ω₁, ω₂ and ε₀. Using the boundary conditions Eqs 53, 54, the critical strain for onset of instability of radially graded elastic cylinders can be found and eventually written in the following form:

${\epsilon }_{\text{c}}=f({\omega }_1,{\omega }_2,E_i,{\nu }_i;i=1,2,\cdots ,n)(55)$

5 Results and Discussion

For a validation of the present study, we first analyze the stress distribution for a graded elastic cylinder under axial compression, and then discuss the critical condition of instability for a soft homogeneous cylinder covered by a bilayer or including a linearly graded stiff layer, respectively. The numerical simulation is computed by the finite element analysis code ABAQUS. The stress field and the critical condition of instability for graded elastic cylinders with a varied Poisson’s ratio are addressed and compared to that with a fixed Poisson’s ratio.

5.1 Validation of Stress Field in Fundamental State

For a radially graded elastic cylinder subjected to axial compression, from the theoretical analysis we know that the radial and circumferential stresses will be induced due to the variation of Poisson’s ratio. Consider a solid cylinder with the outer radius B = 100 mm, both Young’s modulus and Poisson’s ratio are assumed to vary linearly in the radial direction, i.e.

$y=y_0+(y_B-y_0)\frac{R}{R_B}(56)$

where y stands for Young’s modulus E or Poisson’s ratio ν, y₀ and y_B represent E or ν at R = 0 and B, respectively.

Figure 2 depicts the radial displacement u_R, radial stress P_rR, circumferential stress P_θΘ, and axial stress P_zZ as functions of the radial coordinate R for a solid cylinder with E₀ = 1 MPa and E_B = 100 MPa, comparing with the numerical results by ABAQUS. From Figure 2, it is observed that the present results are in excellent agreement with the results by ABAQUS. Figures 2A,D reveal that both the varied Poisson’s ratio (ν₀ = 0.45 and ν_B = 0.35) and the fixed one (ν₀ = 0.4 and ν_B = 0.4) have little effectiveness on the radial displacement and the axial stress. However, the variation of Poisson’s ratios has significant influence on the radial and circumferential stresses (Figures 2B,C). When Poisson’s ratio is varied and ranges from 0.45 to 0.35, the radial and circumferential compressive stresses increase firstly and then decrease in the radial direction. The radial stress is consistently compressive within the cylinder and equal to zero at the surface, satisfying the traction free boundary condition, whereas the circumferential stress turns to be tensile as $r>60\text{mm}$, and the maximum tensile stress reaches 0.035 MPa. Comparatively, when Poisson’s ratio is fixed as 0.4, the radial and circumferential stresses are equal or very close to zero, consisting with the theoretical analysis results. During the following instability analyses, Poisson’s ratio is assumed to be varied, and thus the radial and circumferential stresses will affect the critical condition of instability.

FIGURE 2

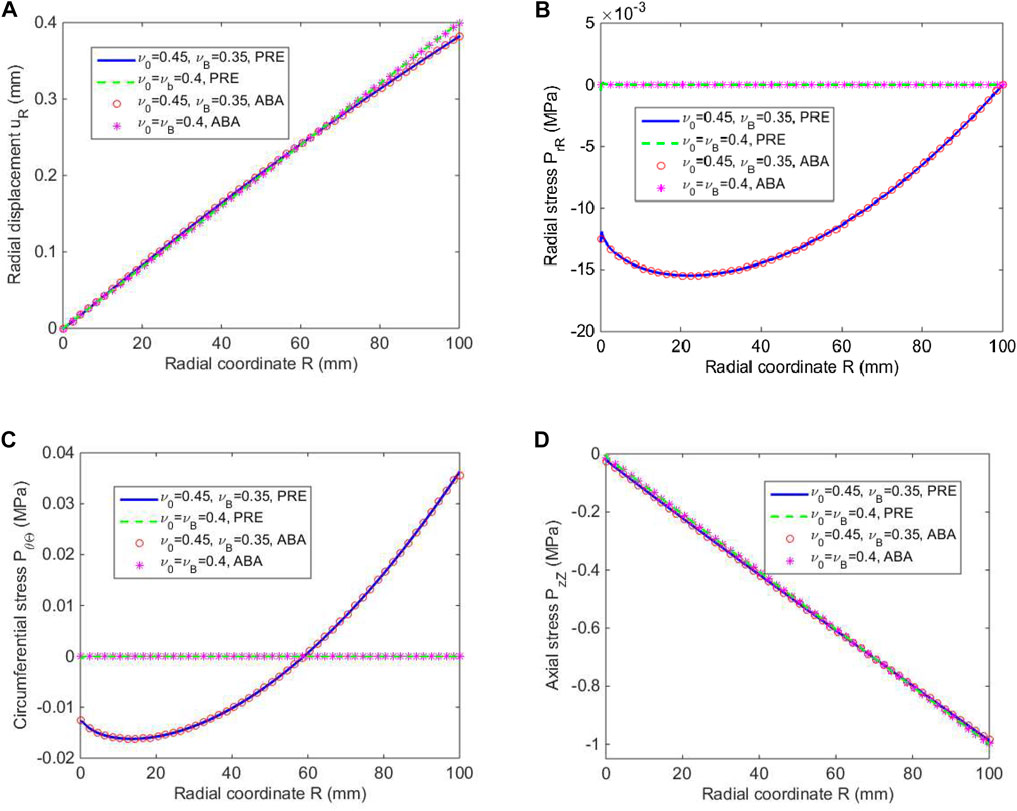
FIGURE 2. (A) Radial displacement, (B) radial stress, (C) circumferential stress, and (D) axial stress varying in the radial direction, obtained by the present method (PRE), for a solid cylinder under an axial strain ε₀ = −0.01, in comparison with the results by ABAQUS (ABA).

5.2 Surface Instability for a Cylinder Covered by a Bilayer

As an example for surface instability analysis for a graded elastic cylinder, we consider a soft cylinder covered by a bilayer as shown in Figure 3. Similar to the example in Jia et al. (2014) and Han et al. (2017), the radius of the inner soft cylinder is h_s = 90 mm, the thicknesses of the surface shell and the intermediate shell are h_f = 1 mm and h_i = 10 mm, respectively. Young’s moduli for the surface shell and the inner cylinder are E_f = 1 GPa and E_s = 1 MPa. However, in this paper Poisson’s ratios for three different layers are not fixed as 0.4. We here assume that Poisson’s ratios for the surface shell and the inner cylinder to be ν_f = 0.4 and ν_s = 0.48, and that for the intermediate shell varies with its Young’s modulus and is given by

${\nu }_{\text{i}}={\nu }_{\text{s}}+\frac{E_{\text{i}}-E_{\text{s}}}{E_{\text{f}}-E_{\text{s}}}({\nu }_{\text{f}}-{\nu }_{\text{s}})(57)$

where E_i is Young’s module for the intermediate shell.

FIGURE 3

FIGURE 3. A cross-section of a soft cylinder covered by a bilayer.

The critical strain for onset of surface instability ε_c and the corresponding wavelength ${\lambda }_{\text{c}}=2\pi /{\omega }_{\text{c}}$, normalized by h_f, are plotted in Figure 4 for such a cylinder with the modulus ratio of the intermediate shell to the soft cylinder E_i/E_s varying from 1 to 1,000, and the varied Poisson’s ratio ν_i from 0.48 to 0.4 according to Eq. 57. In comparison with the results by Han et al. (2017) in which Poisson’s ratio is fixed as ν_i = ν_f = ν_s = 0.4, it is found that the critical strain for the varied Poisson’s ratio is very close to that for the fixed one, and their corresponding critical wavelengths are also close to each other in most part of the interval of modulus ratio. Both of the critical wavelengths for the two cases have a sudden rise. The sudden rise point for the varied Poisson’s ratio happens at E_i/E_s = 11.502, the dimensionless wavelength increases from 24.7 to 37.1, different from E_i/E_s = 17.025 for the fixed Poisson’s ratio with the dimensionless wavelength from 18.0 to 57.5. Obviously, the increase amplitude of the wavelength for the varied Poisson’s ratio is greatly reduced in comparison with that for the fixed one. The results show that the radial and circumferential stresses induced by the variation of Poisson’s ratio inside the cylinder have little effect on the critical strain, but have some effect on the critical wavelength, especially on the point of critical wavelength switching for such a system.

FIGURE 4

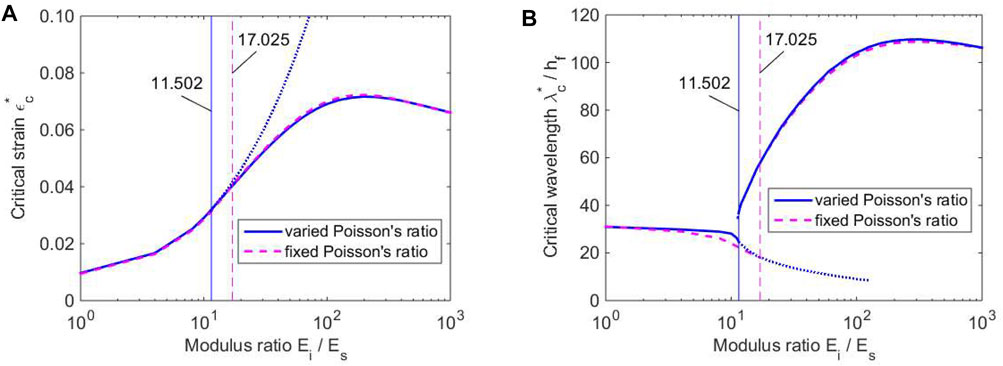
FIGURE 4. (A) The critical strain and (B) the corresponding wavelength for a soft cylinder covered by a bilayer with a varied Poisson’s ratio in the intermediate shell, in comparison with the results with a fixed Poisson’s ratio (Han et al., 2017).

It should be noted that during searching for the critical stain, there are two local minimums for the candidate of the critical strain ε_c, corresponding to a short wavelength and a long wavelength (see Han et al., 2017). The smaller local minimum strain and the corresponding wavelength are the true critical strain and critical wavelength. The dotted lines in Figures 4A,B illustrate the bigger local minimum strain and the corresponding wavelength for the system with varied Poisson’s ratio at a possible metastable state of surface instability.

To verify the correctness of the theoretical solution, we select two computation models with two different lengths for numerical simulation: one has the length 162.8 mm with a varied Poisson’s ratio, equivalent to four times of the wavelength at E_i/E_s = 12.0; the other has 175.28 mm with a fixed Poisson’s ratio, equivalent to three times of the wavelength at E_i/E_s = 17.5. Figures 5A,B present the surface wrinkling patterns for the cylinder with a varied Poisson’s ratio, and their modulus ratios are E_i/E_s = 11.0 and 12.0, respectively. Figures 5C,D provide the surface wrinkling patterns for the cylinder with a fixed Poisson’s ratio and their E_i/E_s = 16.5 and 17.5. It can be found that the wave numbers are 6.5 in Figures 5A, 4 in Figure 5B, respectively, indicating that the modulus ratio for critical wavelength switching must be within 11.0 and 12.0 for the varied Poisson’s ratio. In Figures 5C,D, the wave numbers are 8.5 and 3, respectively, illustrating that the modulus ratio for critical wavelength switching is within 16.5 and 17.5 for the fixed Poisson’s ratio. The numerical simulation manifests that the modulus ratios 11.502 and 17.025, predicted for critical wavelength switching by the theoretical analysis, are correct and enough accurate.

FIGURE 5

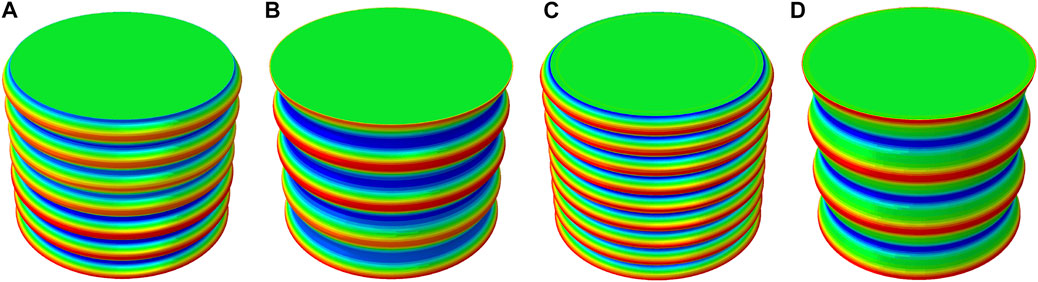
FIGURE 5. Wrinkling patterns for a soft cylinder covered by a bilayer: (A) and (B) for the system with a varied Poisson’s ratio and the modulus ratios E_i/E_s = 11.0 and 12.0, respectively; (C) and (D) for the system with a fixed Poisson’s ratio and E_i/E_s = 16.5 and 17.5, respectively.

5.3 Instability of a Homogeneous Cylinder With a Linearly Graded Stiff Layer

Next we consider a homogeneous soft hollow cylinder containing a linearly graded stiff layer with the thickness h_g = 1 mm as shown in Figure 6. The inner and outer radii of the cylinder are A = 40 mm and B = 100 mm, Young’s modulus and Poisson’s ratio are E_h = 1 MPa and ν_h = 0.48 for the homogeneous soft material, respectively. Young’s modulus and Poisson’s ratio of the stiff layer are assumed to be linear in the radial direction, and the maximum Young’s modulus is denoted as E_m, corresponding Poisson’s ratio as ν_m. In the numerical analysis, the stiff layer is considered to be the inner layer (Figure 6A), the middle layer (Figure 6B), and the outer layer (Figure 6C) of the cylinder, respectively. For the first case, Young’s modulus and Poisson’s ratio of the stiff layer vary linearly from E_m and ν_m at R = 40 mm to E_h and ν_h at R = 41 mm; for the second case, from E_h and ν_h at R = 69.5 mm to E_m and ν_m at R = 70 mm, and then to E_h and ν_h at R = 70.5 mm; for the third case, from E_h and ν_h at R = 99 mm to E_m and ν_m at R = 100 mm.

FIGURE 6

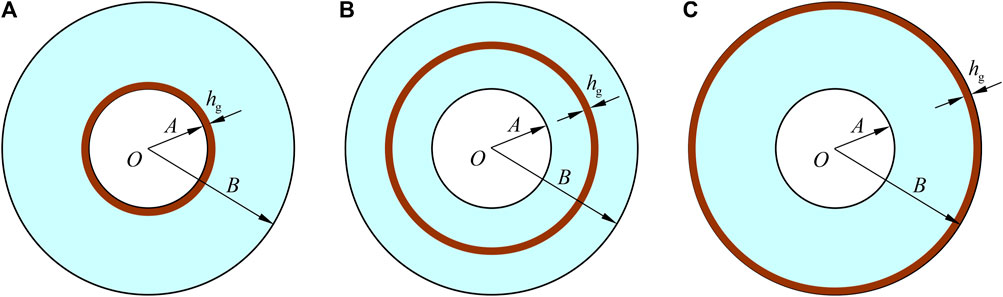
FIGURE 6. Cross-sections of a homogeneous soft hollow cylinder containing a linearly graded stiff (A) inner layer, (B) middle layer, and (C) outer layer with the thickness h_g.

Figure 7 presents the critical strain and the corresponding wavelength versus the modulus ratio E_m/E_h ranging from 10² to 10⁵ for soft cylinders with an inner, a middle, and an outer stiff layers. ν_m = 0.4 and ν_m = ν_h = 0.48 are used for the stiff layer with the varied Poisson’s ratio and fixed Poisson’s ratio, respectively. It is seen that the critical strains for the stiff cylinder with varied and fixed Poisson’s ratios are very close to each other in each case and even indistinguishable, while the critical wavelength for varied Poisson’s ratio is obviously less than that for the fixed Poisson’s ratio, showing that the change of Poisson’s ratio mainly affects the critical wavelength. In addition, from the results for the three different cases we can find that the critical strain of the cylinder with an outer stiff layer is always less than that with an inner or a middle stiff layer, and the corresponding wavelength is greater than that of the other two cases overall. For the cylinders with an inner stiff layer and a middle one, there is an intersection point for both the critical strain and the corresponding wavelength.

FIGURE 7

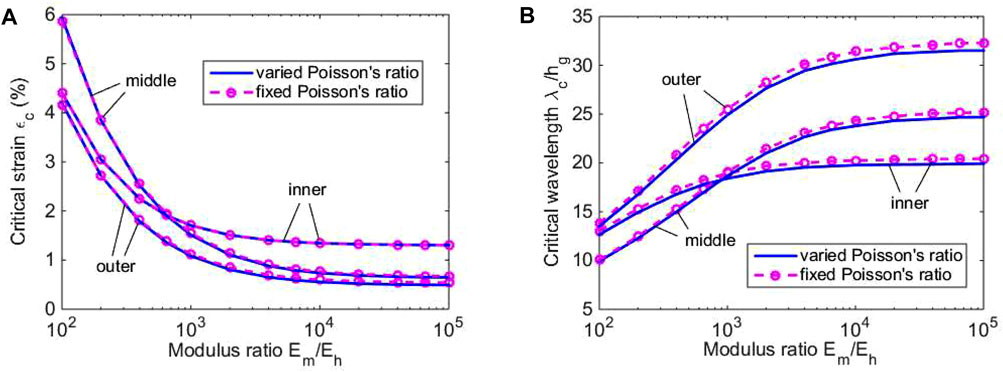
FIGURE 7. (A) The critical strain and (B) the corresponding wavelength for soft cylinders with a linearly graded stiff layer as the inner, the middle, and the outer layers.

Finally we provide three numerical simulations for the homogeneous hollow cylinders with an inner, a middle, and an outer stiff layers, respectively, as shown in Figure 8. As predicted in Figure 7B, there is an intersection point near the modulus ratio E_m/E_h = 10³ for the critical wavelengths of the first and second cases. The exact dimensionless wavelengths at E_m/E_h = 10³ for the three cases are 18.41, 18.68, and 24.91, respectively. Thus, there is an approximate common multiple for the three wavelengths, such as 74.73. In the numerical simulation, the lengths of cylinders are selected as 74.73 mm, equivalent to about three times the critical wavelength for the cylinder with an outer stiff layer, four times for the cylinder with an inner stiff layer or a middle one. From the profiles of the numerical simulations in Figure 8, it can be clearly identified that there are four, four, and three wave numbers at the inner surface, middle face, and outer surface of the cylinder.

FIGURE 8

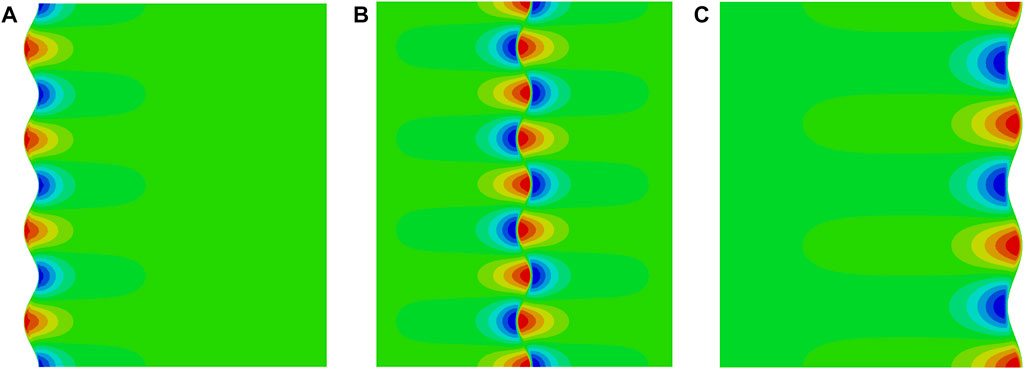
FIGURE 8. Numerical simulations of instability for a hollow soft cylinder with: (A) an inner stiff layer, (B) a middle stiff layer, and (C) an outer stiff layer. The modulus ratio of the stiff layer E_m/E_h = 10³, and Poisson’s ratio ν_m = 0.4 and ν_h = 0.48.

It should be mentioned that in the above example analyses, the circumferential instability has not been found. In the practical numerical calculation, the critical strains for axial and circumferential instabilities are obtained by taking wave number ω₁ = 0 and ω₂ = 0 in Eq. 55, respectively. The critical strain for onset of circumferential instibility is found to be much greater than that of axial instability. Therefore, axial instability always occurs earlier than circumferential instability for the cylinder subjected to axial compression. We note that the circumferential instability has been investigated in Zhao et al. (2014) and Xu and Potier-Ferry (2016) for a stiff film on a soft cylinder. In their works, the postbuckling was analyzed and the circumferential instability was found to commonly occur after the formation of axial wrinkling. By further analysis, we can realize that when the cylinder wrinkles, the circumferential compressive stress at the trough of the axial wrinkling turns to be larger and larger with increasing of the axial deformation. Hence, it is not hard to understand that the circumferential instability always starts at the trough of the axial wrinkling. The relative postbuckling analysis for graded elastic cylnders is left for further studies.

6 Concluding Remarks

The critical condition for onset of instability of elastic cylinders was analyzed for their Young’s modulus and Poisson’s ratio varying in the radial direction. When the cylinder is subjected to an axial loading, the radial and circumferential stresses will be produced simultaneously due to the variation of Poisson’s ratio, and thus both the axial and the circumferential instabilities may be caused individually. A semi-analytical solution was obtained for the prediction of instability in both the axial and the circumferential directions. The critical strain for onset of the circumferential instability is much greater than that of the axial instability, and consequently the axial wrinkling often occurs before the circumferential instability. For a soft cylinder covered by a bilayer with varied and fixed Poisson’s ratios, the numerical results manifest that their critical strains are very close to each other, but their modulus ratios for critical wavelength switching are different obviously. For the soft cylinder with a linearly graded stiff layer, the critical wavelength for the varied Poisson’s ratio is slightly smaller than that for the fixed one. Numerical examples show that the critical condition is different for the radially graded elastic cylinder as its Poisson’s ratio is assumed to be varied or fixed as a constant. The results obtained may provide valuable reference for the design and evaluation of the relevant cylindrical structures.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

ZW contributed to the conception and design of the study. CZ performed the numerical analysis and prepared the first draft of the manuscript. All authors equally contributed to the manuscript revision, reading, and approved the submitted version.

Funding

This work is financed by the National Natural Science Foundation of China (Grant No. 11572108).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

ZW and CZ gratefully acknowledge Prof. Rui Huang of the University of Texas at Austin for the insightful discussions.

References

Arani, A. G., Golabi, S., Loghman, A., and Daneshi, H. (2007). Investigating Elastic Stability of Cylindrical Shell with an Elastic Core under Axial Compression by Energy Method. J. Mech. Sci. Technol. 21 (7), 983–996. doi:10.1007/BF03027648

CrossRef Full Text | Google Scholar

Balbi, V., Kuhl, E., and Ciarletta, P. (2015). Morphoelastic Control of Gastro-Intestinal Organogenesis: Theoretical Predictions and Numerical Insights. J. Mech. Phys. Solids 78, 493–510. doi:10.1016/j.jmps.2015.02.016

CrossRef Full Text | Google Scholar

Budday, S., Steinmann, P., and Kuhl, E. (2014). The Role of Mechanics during Brain Development. J. Mech. Phys. Solids 72, 75–92. doi:10.1016/j.jmps.2014.07.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Cao, Y.-P., Jia, F., Zhao, Y., Feng, X.-Q., and Yu, S.-W. (2012a). Buckling and Post-buckling of a Stiff Film Resting on an Elastic Graded Substrate. Int. J. Solids Struct. 49 (13), 1656–1664. doi:10.1016/j.ijsolstr.2012.03.004

CrossRef Full Text | Google Scholar

Cao, Y.-P., Li, B., and Feng, X.-Q. (2012b). Surface Wrinkling and Folding of Core-Shell Soft Cylinders. Soft Matter 8 (2), 556–562. doi:10.1039/c1sm06354e

CrossRef Full Text | Google Scholar

Dai, H.-H., and Liu, Y. (2014). Critical Thickness Ratio for Buckled and Wrinkled Fruits and Vegetables. Epl 108 (4), 44003. doi:10.1209/0295-5075/108/44003

CrossRef Full Text | Google Scholar

Dawson, M. A., and Gibson, L. J. (2007). Optimization of Cylindrical Shells with Compliant Cores. Int. J. Solids Struct. 44 (3−4), 1145–1160. doi:10.1016/j.ijsolstr.2006.06.009

CrossRef Full Text | Google Scholar

Evans, A. G., and Hutchinson, J. W. (1984). On the Mechanics of Delamination and Spalling in Compressed Films. Int. J. Solids Struct. 20, 455–466. doi:10.1016/0020-7683(84)90012-x

CrossRef Full Text | Google Scholar

Guvendiren, M., Burdick, J. A., and Yang, S. (2010). Solvent Induced Transition from Wrinkles to Creases in Thin Film Gels with Depth-wise Crosslinking Gradients. Soft Matter 6 (22), 5795–5801. doi:10.1039/c0sm00317d

CrossRef Full Text | Google Scholar

Guvendiren, M., Yang, S., and Burdick, J. A. (2009). Swelling-induced Surface Patterns in Hydrogels with Gradient Crosslinking Density. Adv. Funct. Mat. 19 (19), 3038–3045. doi:10.1002/adfm.200900622

CrossRef Full Text | Google Scholar

Han, L., Zhan, C., Liu, Y., and Wu, Z. (2017). A State Space Solution for Onset of Surface Instability of Elastic Cylinders with Radially Graded Young's Modulus. Int. J. Solids Struct. 126-127, 8–16. doi:10.1016/j.ijsolstr.2017.07.025

CrossRef Full Text | Google Scholar

Harrison, C., Stafford, C. M., Zhang, W., and Karim, A. (2004). Sinusoidal Phase Grating Created by a Tunably Buckled Surface. Appl. Phys. Lett. 85 (18), 4016–4018. doi:10.1063/1.1809281

CrossRef Full Text | Google Scholar

Huang, R., and Suo, Z. (2002b). Instability of a Compressed Elastic Film on a Viscous Layer. Int. J. Solids Struct. 39 (7), 1791–1802. doi:10.1016/S0020-7683(02)00011-2

CrossRef Full Text | Google Scholar

Huang, R., and Suo, Z. (2002a). Wrinkling of a Compressed Elastic Film on a Viscous Layer. J. Appl. Phys. 91 (3), 1135–1142. doi:10.1063/1.1427407

CrossRef Full Text | Google Scholar

Huang, Z. Y., Hong, W., and Suo, Z. (2005). Nonlinear Analyses of Wrinkles in a Film Bonded to a Compliant Substrate. J. Mech. Phys. Solids 53 (9), 2101–2118. doi:10.1016/j.jmps.2005.03.007

CrossRef Full Text | Google Scholar

Hutchinson, J. W., and He, M. Y. (2000). Buckling of Cylindrical Sandwich Shells with Metal Foam Cores. Int. J. Solids Struct. 37 (46−47), 6777–6694. doi:10.1016/S0020-7683(99)00314-5

CrossRef Full Text | Google Scholar

Hutchinson, J. W., and Suo, Z. (1992). Mixed Mode Cracking in Layered Materials. Adv. Appl. Mech. 29, 63. doi:10.1016/S0065-2156(08)70164-9

CrossRef Full Text | Google Scholar

Jia, F., Cao, Y.-P., Liu, T.-S., Jiang, Y., Feng, X.-Q., and Yu, S.-W. (2012). Wrinkling of a Bilayer Resting on a Soft Substrate under In-Plane Compression. Philos. Mag. 92 (12), 1554–1568. doi:10.1080/14786435.2011.652691

CrossRef Full Text | Google Scholar

Jia, F., Cao, Y.-P., Zhao, Y., and Feng, X.-Q. (2014). Buckling and Surface Wrinkling of an Elastic Graded Cylinder with Elastic Modulus Arbitrarily Varying along Radial Direction. Int. J. Appl. Mech. 06, 1450003. doi:10.1142/S1758825114500033

CrossRef Full Text | Google Scholar

Jin, L., Cai, S., and Suo, Z. (2011). Creases in Soft Tissues Generated by Growth. Epl 95 (6), 64002. doi:10.1209/0295-5075/95/64002

CrossRef Full Text | Google Scholar

Kang, M. K., and Huang, R. (2010a). Effect of Surface Tension on Swell-Induced Surface Instability of Substrate-Confined Hydrogel Layers. Soft Matter 6 (22), 5736–5742. doi:10.1039/c0sm00335b

CrossRef Full Text | Google Scholar

Kang, M. K., and Huang, R. (2010b). Swell-induced Surface Instability of Confined Hydrogel Layers on Substrates. J. Mech. Phys. Solids 58, 1582–1598. doi:10.1016/j.jmps.2010.07.008

CrossRef Full Text | Google Scholar

Karam, G. N., and Gibson, L. J. (1995). Elastic Buckling of Cylindrical Shells with Elastic Cores-I. Analysis. Int. J. Solids Struct. 32, 1259–1283. doi:10.1016/0020-7683(94)00147-o

CrossRef Full Text | Google Scholar

Lavrenčič, M., Brank, B., and Brojan, M. (2020). Multiple Wrinkling Mode Transitions in Axially Compressed Cylindrical Shell-Substrate in Dynamics. Thin-Walled Struct. 150, 106700. doi:10.1016/j.tws.2020.106700

CrossRef Full Text | Google Scholar

Lee, D., Triantafyllidis, N., Barber, J. R., and Thouless, M. D. (2008). Surface Instability of an Elastic Half Space with Material Properties Varying with Depth. J. Mech. Phys. Solids 56 (3), 858–868. doi:10.1016/j.jmps.2007.06.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, B., Cao, Y.-P., Feng, X.-Q., and Gao, H. (2011). Surface Wrinkling of Mucosa Induced by Volumetric Growth: Theory, Simulation and Experiment. J. Mech. Phys. Solids 59 (4), 758–774. doi:10.1016/j.jmps.2011.01.010

CrossRef Full Text | Google Scholar

Li, C., Han, Q., and Wang, Z. (2020). Semi-analytical Isogeometric Analysis for Wrinkling Instability of Stiff Films Bonded to Cylindrical Modulus-Graded Compliant Substrates. Compos. Struct. 235, 111787. doi:10.1016/j.compstruct.2019.111787

CrossRef Full Text | Google Scholar

Razavi, M. J., Pidaparti, R., and Wang, X. (2016). Surface and Interfacial Creases in a Bilayer Tubular Soft Tissue. Phys. Rev. E 94 (2), 022405. doi:10.1103/PhysRevE.94.022405

PubMed Abstract | CrossRef Full Text | Google Scholar

Rogers, J. A., Someya, T., and Huang, Y. (2010). Materials and Mechanics for Stretchable Electronics. Science 327, 1603–1607. doi:10.1126/science.1182383

PubMed Abstract | CrossRef Full Text | Google Scholar

Seide, P. (1962). The Stability under Axial Compression and Lateral Pressure of Circular-Cylindrical Shells with a Soft Elastic Core. J. Aerosp. Sci. 29, 851–862. doi:10.2514/8.9619

CrossRef Full Text | Google Scholar

Song, J., Jiang, H., Liu, Z. J., Khang, D. Y., Huang, Y., Rogers, J. A., et al. (2008). Buckling of a Stiff Thin Film on a Compliant Substrate in Large Deformation. Int. J. Solids Struct. 45 (10), 3107–3121. doi:10.1016/j.ijsolstr.2008.01.023

CrossRef Full Text | Google Scholar

Sridhar, N., Srolovitz, D. J., and Suo, Z. (2001). Kinetics of Buckling of a Compressed Film on a Viscous Substrate. Appl. Phys. Lett. 78, 2482–2484. doi:10.1063/1.1368180

CrossRef Full Text | Google Scholar

Stafford, C. M., Harrison, C., Beers, K. L., Karim, A., Amis, E. J., Vanlandingham, M. R., et al. (2004). A Buckling-Based Metrology for Measuring the Elastic Moduli of Polymeric Thin Films. Nat. Mater 3 (8), 545–550. doi:10.1038/nmat117510.1038/nmat1175

PubMed Abstract | CrossRef Full Text | Google Scholar

Sugiura, S., Sumaru, K., Ohi, K., Hiroki, K., Takagi, T., and Kanamori, T. (2007). Photoresponsive Polymer Gel Microvalves Controlled by Local Light Irradiation. Sensors Actuators A Phys. 140 (2), 176–184. doi:10.1016/j.sna.2007.06.024

CrossRef Full Text | Google Scholar

Tokarev, I., and Minko, S. (2009). Stimuli-responsive Hydrogel Thin Films. Soft matter 5 (3), 511–524. doi:10.1039/b813827c

CrossRef Full Text | Google Scholar

Wang, L. (2020). Axisymmetric Instability of Soft Elastic Tubes under Axial Load and Surface Tension. Int. J. Solids Struct. 191-192, 341–350. doi:10.1016/j.ijsolstr.2020.01.015

CrossRef Full Text | Google Scholar

Wu, Z., Bouklas, N., Liu, Y., and Huang, R. (2017). Onset of Swell-Induced Surface Instability of Hydrogel Layers with Depth-wise Graded Material Properties. Mech. Mater. 105, 138–147. doi:10.1016/j.mechmat.2016.11.005

CrossRef Full Text | Google Scholar

Wu, Z., Meng, J., Liu, Y., Li, H., and Huang, R. (2014). A State Space Method for Surface Instability of Elastic Layers with Material Properties Varying in Thickness Direction. J. Appl. Mech. 81 (8), 081003. doi:10.1115/1.4027464

CrossRef Full Text | Google Scholar

Xu, F., Koutsawa, Y., Potier-Ferry, M., and Belouettar, S. (2015). Instabilities in Thin Films on Hyperelastic Substrates by 3D Finite Elements. Int. J. Solids Struct. 69-70, 71–85. doi:10.1016/j.ijsolstr.2015.06.007

CrossRef Full Text | Google Scholar

Xu, F., and Potier-Ferry, M. (2016). On Axisymmetric/diamond-like Mode Transitions in Axially Compressed Core-Shell Cylinders. J. Mech. Phys. Solids 94, 68–87. doi:10.1016/j.jmps.2016.04.025

CrossRef Full Text | Google Scholar

Yang, S., Khare, K., and Lin, P.-C. (2010). Harnessing Surface Wrinkle Patterns in Soft Matter. Adv. Funct. Mat. 20 (16), 2550–2564. doi:10.1002/adfm.201000034

CrossRef Full Text | Google Scholar

Yao, J. C. (1962). Buckling of Axially Compressed Long Cylindrical Shell with Elastic Core. J. Appl. Mech. 29 (2), 329–334. doi:10.1115/1.3640550

CrossRef Full Text | Google Scholar

Ye, L., Lu, G., and Ong, L. S. (2011). Buckling of a Thin-Walled Cylindrical Shell with Foam Core under Axial Compression. Thin-Walled Struct. 49 (1), 106–111. doi:10.1016/j.tws.2010.08.011

CrossRef Full Text | Google Scholar

Zhao, Y., Cao, Y., Feng, X.-Q., and Ma, K. (2014). Axial Compression-Induced Wrinkles on a Core-Shell Soft Cylinder: Theoretical Analysis, Simulations and Experiments. J. Mech. Phys. Solids 73, 212–227. doi:10.1016/j.jmps.2014.09.005

CrossRef Full Text | Google Scholar