Neural network-based performance prediction of marine UHPC with coarse aggregates

In order to improve bearing capacity and service life of marine structure using marine UHPC with coarse aggregate (UHPC-CA), it is necessary to reasonably predict the performance of UHPC-CA. The performance of UHPC-CA was predicted in this paper based on five prediction models: multiple linear regression, multiple nonlinear regression, traditional neural network (T-BP), principal component approach neural network (PCA-BP), and improved neural network based on genetic algorithm (GA-BP). Seven influencing factors were taken as input, such as coarse aggregate type, coarse aggregate content, steel fiber type, steel fiber content, water-binder ratio, rubber particle sand replacement rate and curing system. Mechanical and long-term performance of UHPC-CA were taken as outputs. The results show that artificial neural network can be applied to predict performance of UHPC-CA with multi-parameter input and multi-index output. In terms of the prediction accuracy of mechanical properties and long-term performance of UHPC-CA, the order is GA-BP > PCA-BP > T-BP > multiple nonlinear regression > multiple linear regression. The GA-BP neural network has the highest goodness of fit for the prediction of mechanical properties and long-term performance of UHPC-CA, which is 93.87%, 37.34%, 5.13% and 3.21% averagely higher than that of multiple linear regression, multiple nonlinear regression, T-BP and PCA-BP, respectively. Furthermore, GA-BP neural network has the lowest error index for each performance prediction. MAE, MSE and RMSE are 18.13%, 77.26% and 52.31% lower than PCA-BP on average.

1 Introduction

Due to the harsh service environment and serious corrosion, marine structures often fail to reach the expected service life (Li et al., 2020; Alexander and Beushausen, 2019; ASTM C1856/C1856M-17.2017, 2024; Martin-Perez et al., 2000; Yi et al., 2020; Zhang, 2024). Since the advent of UHPC-CA, it has partially replaced traditional concrete as the building material for marine structures with its high strength, high performance and excellent durability (Du et al., 2021; Bajaber and Hakeem, 2020; Huang et al., 2024; Shafieifar et al., 2017; Zhang, 2022). With the objective to application of UHPC-CA in marine structures, it is extremely important to realize the efficient and accurate prediction of the performance of UHPC-CA.

The performance prediction of cement-based materials such as UHPC has always been a hot topic. The most commonly used methods for UHPC performance prediction are mainly empirical formulas or simulation models by means of indoor experiments, numerical analysis, etc. Ou et al. (2021) established the semi-empirical equations considering the effect of water-cement ratio and aggregate content on the compressive strength of UHPC by referring to the semi-empirical formulas of others. Xue et al. (2018) predicted and analyzed the sevice life of UHPC by using mathematical formulas based on specific test data. Liu et al. (2021) established the empirical formula of shrinkage and creep of UHPC based on the test results of shrinkage and creep of UHPC 1080 days. Wu and Huang (2024) optimized the dynamic Catboost regression formula and established the prediction model of UHPC compressive and flexural strength. Liu et al. (2022) established relationship between the volume content of steel fiber and polypropylene fiber and the strength of UHPC, and proposed a prediction model by nonlinear formula. However, the application range of the formula prediction method is limited, and its prediction accuracy is relatively low. Furthermore, prediction methods above stated cannot achieve multi-parameter input and multi-index output. It is necessary to further establish an accurate and reliable prediction model.

Artificial neural networks has been extensively used to predict the properties of materials with its powerful learning, adaptation, generalization and fault-tolerance capabilities. Arriagada et al. (2002) trained a neural network model to learn the performance parameters in a planar SOFC, and found that the neural network model showed a good congruence with the physical model. Yang (2003) used the maximum particle size of gravel, cement grade, slump, water, cement, sand and stone as the input parameters of the model, and established a multi-parameter input BP network prediction model for 28 days strength of concrete. Es-Samlali et al. (2024) developed high-performance neural network model to accurately predict the ultimate properties of asphalt mixes incorporating steel slag. However, it has been less applied in the field of UHPC. Chen et al. (2020) established a neural network training model by combining the existing test data, which can be applied to predict the compressive strength of UHPC. Xu et al. (2023) constructed a deep neural network model based on the uniaxial compression test results of 144 specimens, which can be used to predict the full residual stress-strain response of UHPC. Lee et al. (2023) employed an artificial neural network to predict the compression strength of UHPC with lateral restraint limit states. Farouk and Jinsong (2022) predicted the bond strength of UHPC-NSC interface by two kinds of methods, such as artificial neural network and multiple linear regression. The reliability of the artificial neural network prediction model is proved. Zhang et al. (2017) examined the influence law of the dosing of cementitious materials such as fly ash and silica fume on the mechanical properties of UHPC using artificial neural network model. Artificial neural network models have been proved to exhibit excellent stability and prediction ability after sufficient data training.

The above researches have an essential role in promoting the application of artificial neural network in the field of UHPC. However, there is still a lack of intelligent performance prediction methods that can realize multi-parameter input and multi-index output of UHPC-CA. This makes it difficult to realize efficient and accurate prediction of the performance of UHPC-CA.

To address the above problems, this paper compared and analyzed the prediction results of five prediction models: multiple linear regression, multiple nonlinear regression, T-BP, PCA-BP and GA-BP. An optimal prediction model for the performance prediction of UHPC-CA was established, which can realize multi-parameter input and multi-index output of UHPC-CA. It provides a basis for the application of UHPC-CA in marine structures.

2 Predictive modeling

In this paper, the univariate linear equation and quadratic model were used to establish the multivariate linear model and multivariate nonlinear model, respectively. The artificial neural network method was used to establish the T-BP neural network model, the PCA-BP neural network model, and the GA-BP neural network model.

The data of this survey were based on the measured data of related performance tests of UHPC-CA, which were sorted out as the original samples (show in Supplementary Appendix). The compressive strength, flexural strength and split tensile strength were tested by a 3,000 kN electro-hydraulic servo universal testing machine produced by MTS Co., Ltd. The specifications used are “Fundamental characteristics and test methods of ultra-high performance concrete (T/CBMF 37-2018)” and “Specification for reactive powder concrete (GB/T 31387-2015)” in China. The abrasion resistance test was carried out by underwater steel ball method. The specification used is “Test code for hydraulic concrete (DL/T 5150-2001)”. The chloride ion diffusion test was carried out by using the chloride ion penetration resistance three-in-one tester produced by Beijing Nelder Company. The specification used is “Standard for test methods of long-term performance and durability of ordinary concrete (GBT50082-2009)” in China. The input parameters of the prediction model include seven, such as coarse aggregate type, coarse aggregate content, steel fiber type, steel fiber content, water-binder ratio, rubber particle sand replacement rate, and curing system (shown in Schedule 1). The output indicators of the prediction model are three mechanical performance indicators (compressive strength, splitting tensile strength, flexural strength) and two long-term performance indicators (abrasion resistance, chloride ion erosion resistance). The particle size of aggregates is 5–10 mm, and the appearance and geometry of aggregates is irregular spherical particles. Due to the particularity of the anti-chloride ion erosion test, in which electroconductive steel fiber would cause failure of anti-chloride ion erosion test. Therefore, the input parameters of the chloride ion diffusion coefficient prediction model do not include steel fiber content or steel fiber type (Han et al., 2018; Han, 2007; Wang et al., 2021; Zhang L. Z. et al., 2023; Song and Hwang, 2004).

In this paper, the mixture ratio of UHPC is obtained according to the Modified Andreasen and Andersen model, the specific formula is as follows (Equation 1):

$P\left(D\right)=\frac{D^q-D_{\max }^q}{D_{\max }^q-D_{\min }^q}(1)$

P (D) is the percentage of particles with particle size less than D in the mixed particles; D is particle size, mm; D_max is the maximum particle size in the mixed particles, mm; D_min is the minimum particle size in the mixed particles, mm; q is the distribution modulus, and q is 0.23 in this paper.

According to the above mix design theory, the mass ratio of cement: silica fume: fly ash in UHPC matrix is determined to be 7:2:1, the basic cement-sand ratio is 1.0, and the mass of water reducing agent is 2% of the cementitious material.

2.1 T-BP neural network modeling

The T-BP neural network is mainly composed of input layer, hidden layer and output layer (Krogh, 2008; Haykin, 1998; Ryu et al., 2011). After several predictions, the key parameters such as hidden layer number, neuron number, activation function and training parameters were determined. To prevent the risk of over-fitting, the regularization parameter of the layer was set in the TensorFlow deep learning framework. We added a Dropout layer to the layer of the neural network and set the dropping rate to prevent the co-adaptability between neurons, which can improve the generalization ability of neural network models. The algorithm flow chart of T-BP neural network is shown in Figure 1.

Figure 1

Figure 1. T-BP neural network prediction model algorithm flow.

According to Li et al. (2012), Cui and Jing (2019), this paper built a T-BP neural network prediction model of UHPC-CA. After several times of fittings, the number of nodes in the hidden layer of the model for the mechanical properties was 15. The number of nodes in the hidden layer of the chloride ion diffusion coefficient was 12. The construction of mechanical properties and abrasion resistance model needed 90 sets of test results from the original sample (shown in Schedule 2), of which 72 sets were set as training sets and 18 sets were set as test sets. The construction of chloride ion diffusion coefficient model was based on 105 sets of test results of the original sample (shown in Schedule 3), of which 84 sets were set as training sets and 21 sets were set as test sets. The input parameters of the model were coarse aggregate type, coarse aggregate content, steel fiber type, steel fiber content, water-binder ratio, rubber particle replacement rate, and curing system. Therefore, the number of neurons in the input layer was set to 7. The number of neurons in the hidden layer was calculated according to the empirical formula (Parichatprecha and Nimityongskul, 2009). After calculation, the number of hidden layer neurons was 15. The output parameters of this prediction model were compressive strength, splitting tensile strength, flexural strength, abrasion resistance and chloride ion erosion resistance. Therefore, the number of neurons in the output layer was 5. This model transfer function used tansig function which transferring data from input layer to the implicit layer. Another transfer function used purelin function which transferring data from implicit layer to the output layer. The learning rate of the model was set to 0.01. The number of training times was 5,000. The minimum error of the target was 10⁻⁶. The maximum number of confirmed failures was designed to 5. The number of steps displayed at intervals was 10.

2.2 PCA-BP neural network modeling

The crucial of PCA-BP neural network modeling is the determination of the number of principal components. The algorithm flow is shown in Figure 2.

Figure 2

Figure 2. PCA-BP neural network prediction model algorithm flow.

According to the calculation method of literature (Zhang et al., 2019; Xiaofeng et al., 2017; Zou et al., 2009; Song and Kwon, 2009), the histogram of the contribution rate of each principal component was obtained. The UHPC mechanical properties and abrasion resistance performance indexes originally had 7 principal components. Referring to the previous experience (Huang, 2009), the first 5 principal components of the cumulative contribution rate were selected as the principal component variables of the PCA-BP model. The chloride ion erosion resistance originally had 5 principal components. The first 4 principal components of the contribution rate were selected as the principal component variables. The data set after dimensionality reduction was divided into training set and test set. Among them, 80% are training sets and 20% are test sets. We added the L1 regularization term and Dropout layer to the layer of the neural network and set the dropping rate to prevent the risk of over-fitting.

2.3 GA-BP neural network modeling

The establishment of GA-BP neural network model includes three steps: BP neural network structure determination, genetic algorithm optimization and neural network prediction (Zhang L. et al., 2023; Khan, 2012; Jin et al., 2019; Wang et al., 2016). We added the L1 regularization term and Dropout layer to the layer of the neural network and set the dropping rate to prevent the risk of over-fitting. The algorithm flow is shown in Figure 3.

Figure 3

Figure 3. GA-BP neural network prediction model algorithm flow.

The determination of neural network structure was the same as the T-BP model. The data initialization coding adopted real coding. The calculation formula of fitness function adopted empirical formula (Nachaoui et al., 2021). The selection, crossover and mutation operations were based on the literature (Yu, 2011). The genetic algorithm training parameter population number, maximum iteration number, crossover probability and mutation probability of the GA-BP neural network model were 30, 50, 0.8 and 0.2, respectively.

3 Evaluation of model prediction results

The established models for mechanical properties and long-term performance of UHPC-CA were trained by 72–84 sets of data from the original samples and were verified by 18–21 sets of data from the original samples. The prediction accuracy of five models was assessed in terms of discreteness of model prediction results, error fitting between expected and actual values and statistical indexes of prediction model. Mean absolute error (MAE), mean square error (MSE), root mean square error (RMSE) and fitting correlation (R²) were selected as the statistical indexes of prediction models (Zhang et al., 2016; Taskinen and Yliruusi, 2003).

3.1 Analysis of prediction results of multiple linear and multiple nonlinear regression prediction models

3.1.1 Mechanical properties and abrasion resistance

The compressive strength, flexural strength, splitting tensile strength and abrasion resistance data of the data set were subjected to multiple linear and multiple nonlinear regression. The multiple linear prediction equation and multiple nonlinear regression parameter vector of the prediction model for mechanical properties and abrasion resistance were obtained, as shown in Schedule 4. The multivariate nonlinear regression modulus refers to the matrix composed of the coefficients of all independent variables in the quadratic model. The multiple linear and multiple nonlinear regression fitting curves of mechanical properties and abrasion resistance of UHPC-CA are shown in Figures 4, 5.

Figure 4

Figure 4. Multivariate linear fitting results of mechanical properties and abrasion resistance.

Figure 5

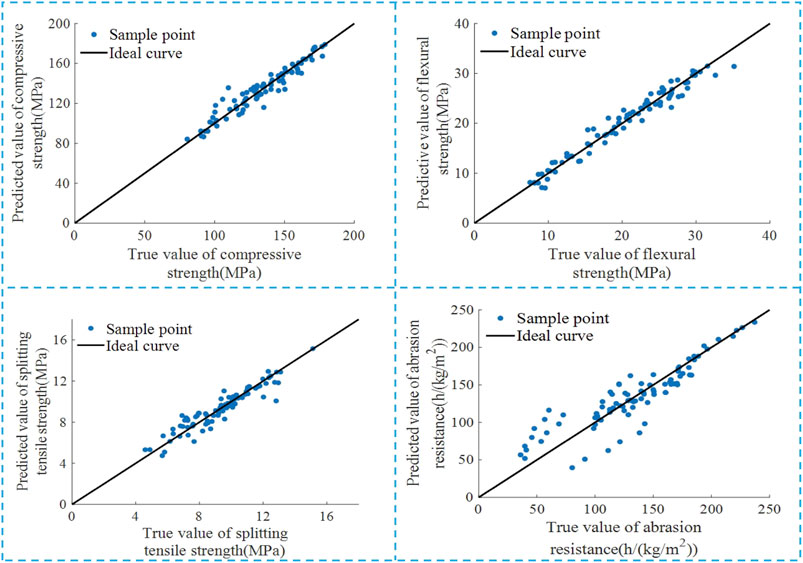
Figure 5. Multivariate nonlinear fitting results of mechanical properties and abrasion resistance. (A) Compressive strength. (B) Flexural strength. (C) Splitting tensile strength. (D) Abrasion resistance.

As can be seen in Figures 4, 5: The scatter points of the predicted value and the true value of the linear regression model are roughly distributed on both sides of the straight line with a slope of 1, but the discreteness is large. The predicted value and the true scatter distribution of the nonlinear regression model are more concentrated. The discreteness of the nonlinear regression model is significantly smaller than that of the linear regression prediction model.

The linear and nonlinear statistical indexes of mechanical properties and abrasion resistance of UHPC-CA are shown in Table 1. The goodness of fit and significance level of the linear regression prediction model for the mechanical properties and abrasion resistance of UHPC-CA are at a low level. R² value is less than 0.80, and F values are 45.6, 31.7, 26 and 19.5. Compared with the multiple linear regression prediction model: ①The goodness of fit of the nonlinear regression prediction model for each performance index is significantly improved. The R² of each performance index is increased by 16.08%, 31.48%, 28.42% and 27.10%, respectively. However, the significance level of compressive strength and abrasion resistance is reduced, and the reduction range is low. ②Each error index is remarkably reduced. The MAE, MSE, and RMSE of compressive strength are reduced by 45%, 56.06%, and 33.76%, respectively. In general, the prediction accuracy of the multivariate nonlinear model in predicting the mechanical properties and abrasion resistance of UHPC-CA is better than that of the multivariate linear model.

Table 1

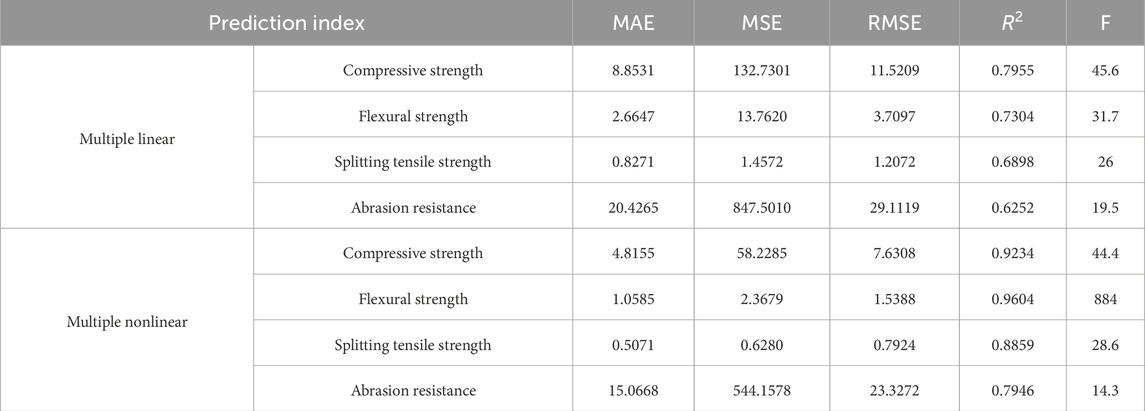
Table 1. Linear and nonlinear regression statistical indexes for mechanical properties and abrasion resistance.

3.1.2 Chloride ion erosion resistance

The chloride ion diffusion coefficient data of the data set were subjected to multiple linear and multiple nonlinear regression. The multiple linear regression equation and the multiple nonlinear regression parameter vector of the prediction model were obtained as shown in Schedule 4.

The multiple linear and nonlinear regression fitting results of chloride ion diffusion coefficient of UHPC-CA are shown in Figure 6. The discreteness of sample points in the multivariate linear and nonlinear regression prediction models of chloride ion diffusion coefficient of UHPC-CA is relatively large. Most of them are irregularly distributed on the left side of the straight line with a slope of 1, and fewer sample points fall on the other side.

Figure 6

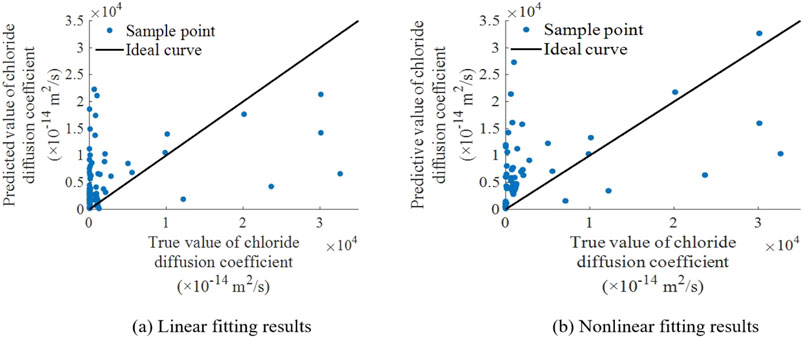
Figure 6. Multivariate linear and nonlinear fitting results of chloride ion erosion resistance. (A) Linear fitting results. (B) Nonlinear fitting results.

The statistical indexes of linear and nonlinear regression models for chloride ion corrosion resistance of UHPC-CA are shown in Table 2. ①The goodness of fit and significance level of the linear regression prediction model are at a very low level. The F value and R² are 6.13 and 0.2363, respectively. ②The goodness of fit of the nonlinear regression prediction model is 67.92% higher than that of the linear model, and the significance level is 24.96% lower than that of the linear model. The F value and R² value are 4.6 and 0.3968, respectively. Therefore both linear and nonlinear regression prediction models have poor accuracy in predicting chloride diffusion coefficients of UHPC-CA and the prediction results are not referential.

Table 2

Table 2. Linear and nonlinear regression statistical indexes for chloride ion erosion resistance.

3.2 Analysis of prediction results of T-BP neural network

3.2.1 Mechanical properties and abrasion resistance

The prediction results of T-BP neural network model for mechanical properties and abrasion resistance of UHPC-CA are shown in Figure 7. The T-BP neural network model can make a reasonable prediction for mechanical properties and abrasion resistance of UHPC-CA. However, there are still some results with large errors in the prediction process. It indicates that there is a certain lack of stability and generalization ability of the T-BP neural network prediction model for the mechanical properties and abrasion resistance of UHPC-CA.

Figure 7

Figure 7. Prediction results of T-BP neural network model for performance of UHPC-CA.

The regression fitting diagram of the true value and the model prediction value of the sample data of the mechanical properties and abrasion resistance of UHPC-CA is shown in Figure 8. The sample points of the T-BP neural network model for the mechanical properties and abrasion resistance of UHPC-CA are mostly regularly distributed on both sides of the straight line. The predictive model straight line for compressive strength has a high degree of coincidence with the ideal model straight line. However, the predictive model straight lines for the other three strengths do not overlap with the ideal model straight line. Compared with the multivariate linear and multivariate nonlinear fitting results, the fitting accuracy of the T-BP neural network model is significantly improved.

Figure 8

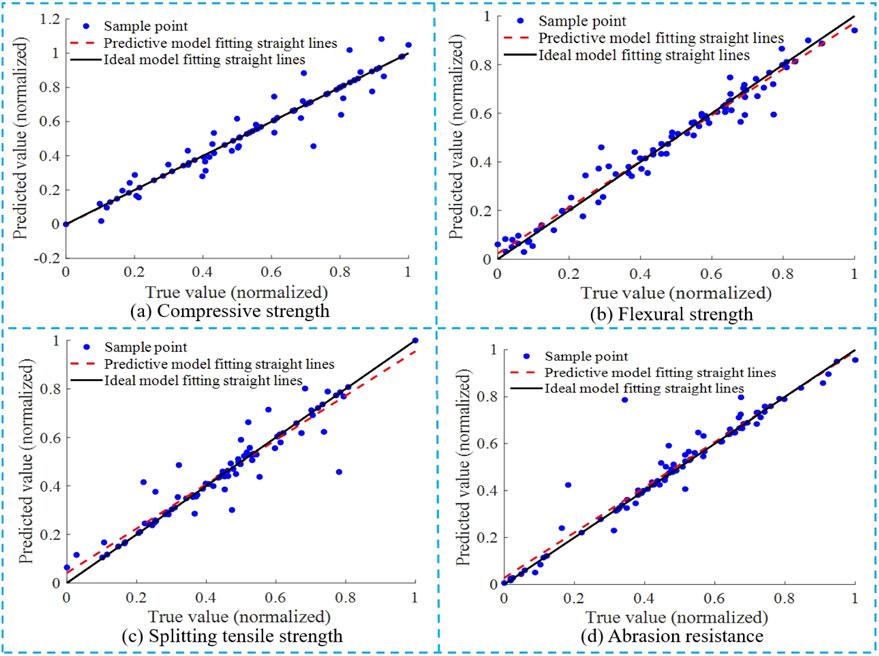
Figure 8. Regression fitting diagram of T-BP neural network model for performance of UHPC-CA. (A) Compressive strength. (B) Flexural strength. (C) Splitting tensile strength. (D) Abrasion resistance.

The statistical indexes of T-BP neural network model for mechanical properties and abrasion resistance of UHPC-CA are shown in Table 3. ①The goodness of fit of the model is significantly higher than that of the linear and nonlinear prediction models. The R² values of compressive strength, flexural strength, splitting tensile strength and abrasion resistance are 17.32%, 32.22%, 31.56% and 34.56% higher than the linear prediction model, and 1.07%, 5.6%, 2.43% and 11.54% higher than the R² values of the nonlinear prediction model. ②The MAE, MSE and RMSE are significantly smaller than the relevant statistical indexes of the linear and nonlinear regression prediction models. In the prediction of compressive strength, the error index is reduced by 60.56%, 70.29%,45.49% respectively compared with the linear model, and 27.50%, 32.27% and 17.70% respectively compared with the nonlinear model. Therefore, the T-BP neural network model is more suitable for the prediction of mechanical properties and abrasion resistance of UHPC-CA than linear and nonlinear models.

Table 3

Table 3. Statistical indexes of T-BP neural network model for performance of UHPC-CA.

3.2.2 Chloride ion erosion resistance

The prediction results of T-BP neural network model for chloride diffusion coefficient of UHPC-CA are shown in Figure 10. Analysis shows: The prediction of the model is not good enough in predicting the chloride diffusion coefficients of UHPC-CA. There is a serious over-prediction phenomenon in the prediction results, which will cause the predicted value to be much smaller than the normal value range. Because the neural network algorithm has a local optimal problem, it cannot achieve global optimization. The initial weights and thresholds value of BP algorithm based on MATLAB program are randomly generated. Different initial weights may lead to non-convergence or overfitting of the network.

The regression fitting diagram of the true value and the predicted value of the sample data of the T-BP neural network model for chloride diffusion coefficient of UHPC-CA are shown in Figure 9. Although the fitting curve of the prediction model can basically coincide with the fitting line of the ideal model, most of the sample points are deviated from the straight line. The fitting effect of the T-BP neural network model for chloride diffusion coefficient of UHPC-CA is not optimal.

Figure 9

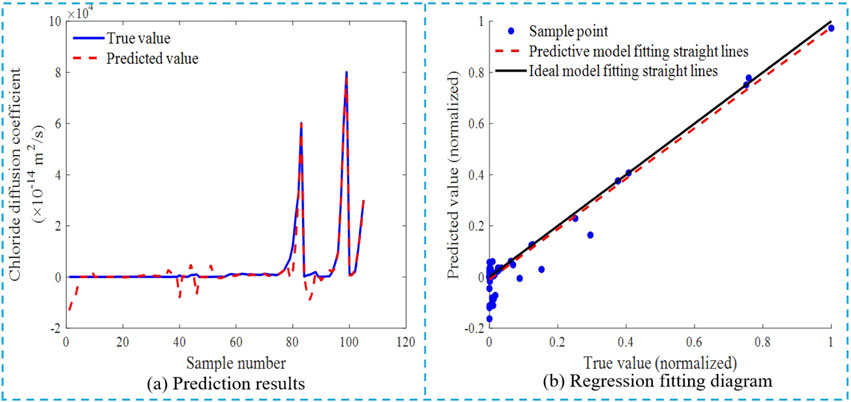
Figure 9. Prediction results and regression fitting diagram of T-BP neural network model for chloride diffusion coefficient. (A) Prediction results. (B) Regression fitting diagram.

The statistical indexes of T-BP neural network model for chloride ion corrosion resistance of UHPC-CA are shown in Table 4. ①The goodness of fit of the model is effectively improved compared with the linear and nonlinear prediction models. Its R² is 3.96 times and 2.35 times of the linear and nonlinear prediction model R², respectively. ②The values of MAE, MSE and RMSE are 1,431.6729, 9,972,531.7 and 3,157.9315, respectively, which are significantly lower than those of linear and nonlinear models. The MAE, MSE, and RMSE are 74.29%, 92.09%, and 71.89% lower than the linear model, and are 74.9%, 90.79%, and 69.66% lower than the nonlinear model. Therefore, the prediction accuracy for chloride ion corrosion resistance of T-BP neural network model is higher than that of linear and nonlinear models. However, the prediction stability and generalization need to be improved.

Table 4

Table 4. Statistical indexes of T-BP neural network model for chloride diffusion coefficient of UHPC-CA.

3.3 Analysis of PCA-BP neural network prediction results

3.3.1 Mechanical properties and abrasion resistance

The prediction results of PCA-BP neural network model for mechanical properties and abrasion resistance of UHPC-CA are shown in Figure 10. It can be seen from the figure that the PCA-BP neural network model has better prediction results for the compressive strength, flexural strength, splitting tensile strength and abrasion resistance. Most of the true values are very close to the predicted values. The calculation efficiency and accuracy of the PCA-BP neural network model are also higher than those of the T-BP neural network model.

Figure 10

Figure 10. Prediction results of PCA-BP neural network model for performance of UHPC-CA.

The regression fitting diagram of the true value and the predicted value of the PCA-BP neural network model for mechanical properties and abrasion resistance of UHPC-CA after normalization is shown in Figure 11. As can be seen in the figure: The PCA-BP prediction model curve of flexural strength and abrasion resistance is in good agreement with the ideal model curve. The prediction model curve of compressive strength and splitting tensile strength is poorly fitted with the ideal model curve, with a few sample values disperse outside the two straight lines. Therefore, the PCA-BP neural network model predicts the flexural strength and abrasion strength of UHPC-CA better. However, the accuracy of the prediction of the compressive strength and splitting tensile strength of UHPC-CA needs to be enhanced.

Figure 11

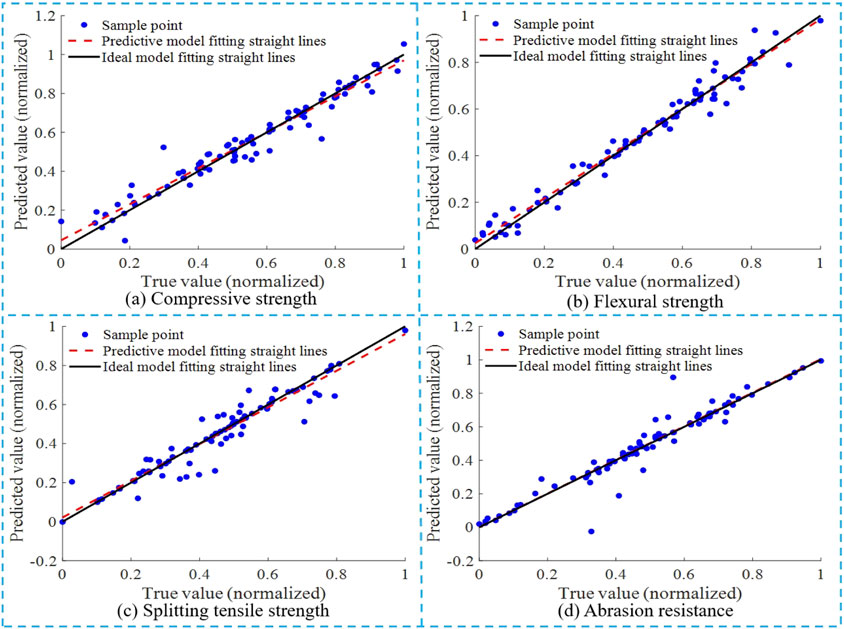
Figure 11. Regression fitting diagram of PCA-BP neural network model for performance of UHPC-CA. (A) Compressive strength. (B) Flexural strength. (C) Splitting tensile strength. (D) Abrasion resistance.

The statistical indexes of PCA-BP neural network model for mechanical properties and abrasion resistance of UHPC-CA are shown in Table 5. ①The goodness of fit of the model for compressive strength, flexural strength, splitting tensile strength and abrasion resistance is greater than 0.90, which is 1.79%, 0.48%, 0.46% and 3.19% higher than that of T-BP, respectively. ②Compared with the T-BP neural network model, the average error of the compressive strength and splitting tensile strength of the model is slightly higher. Errors of the other performance parameters are significantly reduced. The MAE, MSE and RMSE of the abrasion resistance are only 58.54%, 75.11% and 86.33% of the T-BP neural network model, respectively. In summary, the prediction accuracy for mechanical properties and abrasion resistance of PCA-BP model is higher than that of T-BP model.

Table 5

Table 5. Statistical indexes of PCA-BP neural network model for performance of UHPC-CA.

3.3.2 Chloride ion erosion resistance

The prediction results of PCA-BP neural network model for chloride diffusion coefficient of UHPC-CA are shown in Figure 13. It can be seen from the figure that the PCA-BP neural network model has poor prediction results for the chloride ion diffusion coefficient of UHPC-CA. Several predicted values are out of the normal chloride ion diffusion coefficient range.

The regression fitting diagram of the true value and the predicted value of the PCA-BP neural network model for chloride diffusion coefficient of UHPC-CA after normalization are shown in Figure 12. As can be seen from the figure, the predictive model curves fit well with the ideal model curves, although there are several sample data with a large degree of deviation.

Figure 12

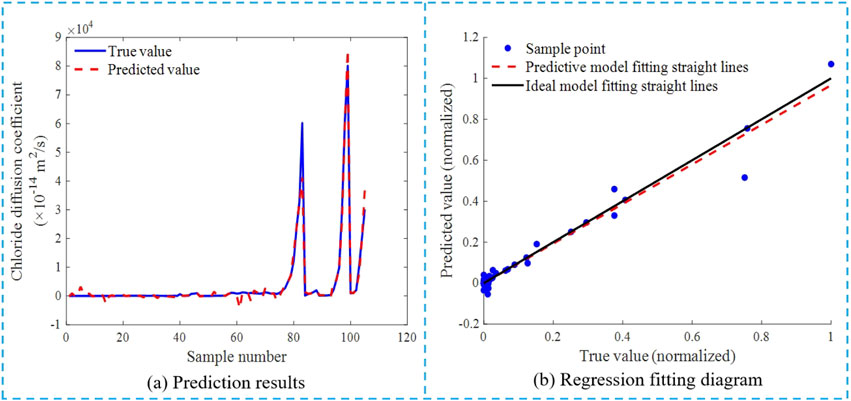
Figure 12. Prediction results and regression fitting diagram of PCA-BP neural network model for chloride diffusion coefficient. (A) Prediction results. (B) Regression fitting diagram.

The statistical indexes of PCA-BP neural network model for chloride ion corrosion resistance of UHPC-CA are shown in Table 6. ①The goodness of fit R² of the model is 0.9665, which is 3.27% higher than that of the T-BP model for chloride ion corrosion resistance of UHPC-CA. ②The MAE, MSE and RMSE are 810.8747, 5,220,356.2 and 2,284.8099, respectively, which were 43.36%, 47.65% and 27.65% lower than those of the T-BP neural network prediction model. Therefore, the prediction effect of PCA-BP neural network on chloride diffusion coefficient is better than that of T-BP neural network.

Table 6

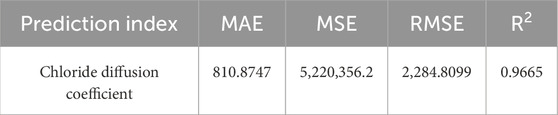
Table 6. Statistical indexes of PCA-BP neural network model for chloride ion erosion resistance of UHPC-CA.

3.4 Analysis of GA-BP neural network prediction results

3.4.1 Mechanical properties and abrasion resistance

The prediction results of GA-BP neural network model for mechanical properties and abrasion resistance of UHPC-CA are shown in Figure 13. As can be seen from the figure, the GA-BP neural network model has excellent prediction effect for the compressive strength, flexural strength, splitting tensile strength and abrasion resistance of UHPC-CA. Compared with the prediction results of T-BP and PCA-BP models, the prediction accuracy is significantly improved.

Figure 13

Figure 13. Prediction results of GA-BP neural network model for performance of UHPC-CA.

Figure 14 is the regression fitting diagram of the true value and the predicted value of the GA-BP neural network model for mechanical properties and abrasion resistance of UHPC-CA after normalization. Analysis of Figure 14 shows that the predicted model curves of each performance indicators fit well with the ideal model curves. The sample points are regularly distributed on both sides of the two straight lines, and most of the sample values fall on the fitted straight line. It demonstrates that the GA-BP model after genetic algorithm has excellent prediction ability on the mechanical properties and abrasion resistance of UHPC-CA.

Figure 14

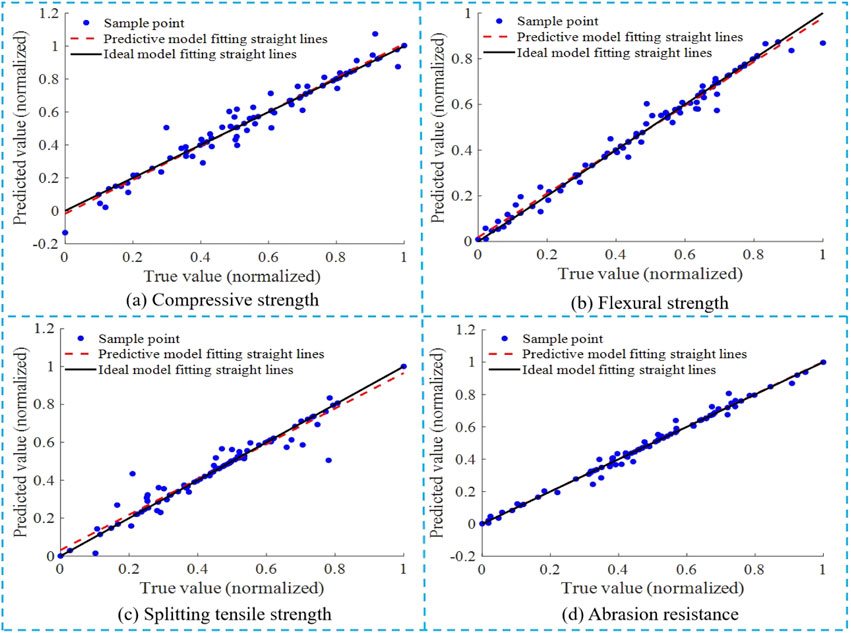
Figure 14. Regression fitting diagram of GA-BP neural network model for performance of UHPC-CA. (A) Compressive strength. (B) Flexural strength. (C) Splitting tensile strength. (D) Abrasion resistance.

The statistical indexes of GA-BP neural network model for mechanical properties and abrasion resistance of UHPC-CA are shown in Table 7. ①The goodness of fit of the model for mechanical properties and abrasion resistance is greater than 0.93, which is 3.32%, 1.69%, 3.00% and 11.62% higher than that of T-BP, and 1.51%, 1.16%, 2.53% and 8.17% higher than that of PCA-BP, respectively. ②The prediction error indexes of the model for all performance parameters are significantly lower than T-BP model and PCA-BP model. The MAE, MSE and RMSE values of each performance prediction decreased by 34.25%, 53.29% and 34.81% on average compared with T-BP neural network, and decreased by 32.73%, 45.18% and 28.94% on average compared with PCA-BP neural network.

Table 7

Table 7. Statistical indexes of GA-BP neural network model for performance of UHPC-CA.

3.4.2 Chloride ion erosion resistance

The prediction results of the GA-BP neural network model for chloride diffusion coefficients of UHPC-CA are shown in Figure 15. It can be seen from the figure that the prediction effect of GA-BP neural network model is better than that of T-BP model and PCA-BP model, but it still shows instability and relatively higher errors. The reason for this result, on the one hand, there are many factors involved in the prediction, and the rationality of the neural network model lacks more data to verify. On the other hand is that the current input parameters might not comprehensively capture all the factors affecting chloride diffusion, potentially reducing the reliability of the predictions for this parameter.

Figure 15

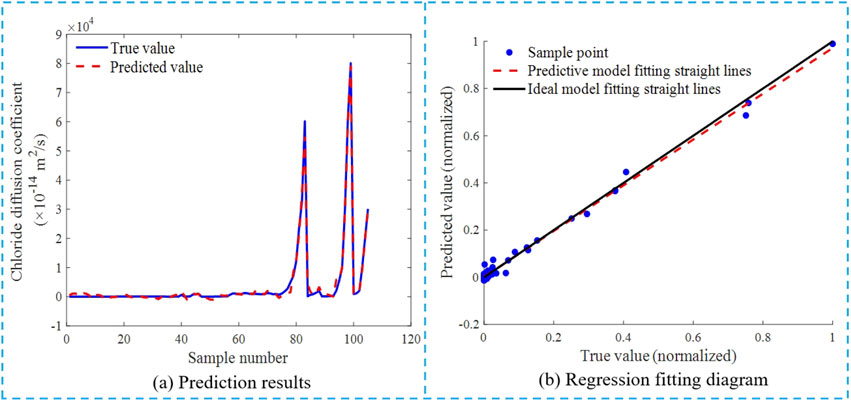
Figure 15. Prediction results and regression fitting diagram of GA-BP neural network model for chloride diffusion coefficient. (A) Prediction results. (B) Regression fitting diagram.

The regression fitting diagram of the GA-BP neural network model for chloride ion diffusion coefficient of UHPC-CA sample content value and model prediction value after normalization is shown in Figure 16. It can be seen from the figure that the fitting degree of the prediction model is very high. The prediction model is in good agreement with the ideal model curve, and the sample values are almost completely distributed on two straight lines. It shows that the predicted model successfully captures the characteristics of the actual data and it has a very good prediction effect for the chloride diffusion coefficient of UHPC-CA.

Figure 16

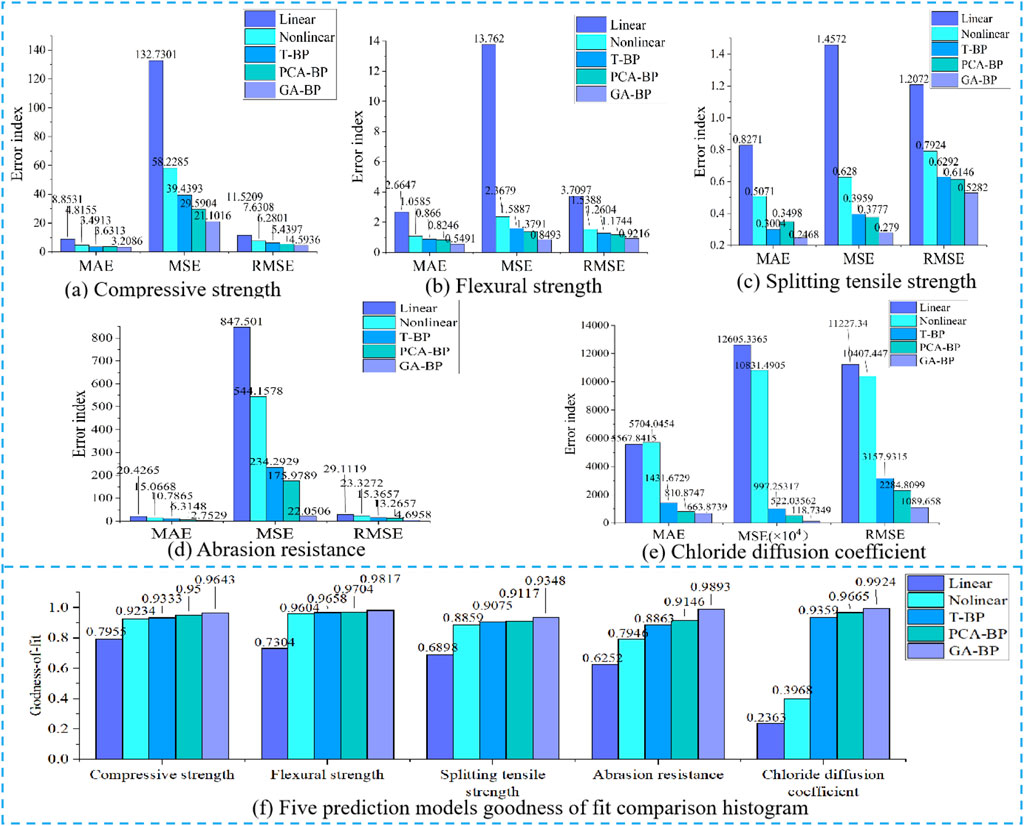
Figure 16. Five prediction models error index and goodness of fit comparison histogram. (A) Compressive strength. (B) Flexural strength. (C) Splitting tensile strength. (D) Abrasion resistance. (E) Chloride diffusion coefficient. (F) Five prediction models goodness of fit comparison histogram.

Table 8 shows the table of statistical indexes of the GA-BP neural network modeling for chloride erosion resistance of UHPC-CA. ①The goodness of fit R² of the model is 0.9924, close to 1, which is 6.04% and 2.68% higher than that of T-BP and PCA-BP models, respectively. ②The MAE, MSE and RMSE are 663.87, 1,187,349.7 and 1,089.6558, respectively, which are 18.13%, 77.26% and 52.31% lower than those of PCA-BP model. Therefore, the GA-BP model is more suitable for predicting the chloride ion diffusion coefficient than the T-BP and PCA-BP models.

Table 8

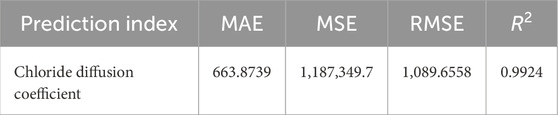
Table 8. Statistical indexes of GA-BP neural network model for chloride diffusion coefficients of UHPC-CA.

3.5 Comparative analysis of the five prediction models

3.5.1 Prediction results of the five models

From the analysis of the prediction results, the neural network model are better than the statistical regression model. However, the predictions exhibit instability and errors, even with the GA-BP model. This indicates that the neural network has limitations in the performance prediction of UHPC-CA. The limitations of the neural network are as follows: ①The neural network is a black box method, which is difficult to make any explanation for the results obtained. ②There is no standard method to determine the structure of neural network, and it is difficult to establish the most suitable prediction model. ③Neural network prediction needs more data to verify, and the size of dataset affects the prediction accuracy to a certain extent. ④The neural network algorithm has the risk of overfitting, and different initial weights will cause the network not to converge or fall into the local extreme point. ⑤The generalization ability across different datasets needs to be improved.

3.5.2 Statistical indexes of the five models

The goodness of fit and the error index of the five prediction models are shown in Schedule 5 and Schedule 6. Figure 16 is the five prediction models error index and goodness of fit comparison histogram. Analysis shows: The results of the five prediction models on the prediction of UHPC-CA varies greatly. The prediction models of UHPC-CA were ranked according to the prediction accuracy and error value as follows: GA-BP > PCA-BP > T-BP > Nonlinear regression > Linear regression. The GA-BP prediction model has the optimal prediction effect, with the minimum MAE, MSE, RMSE, and the maximum R². The GA-BP neural network has the highest goodness of fit for the prediction of mechanical properties and long-term performance of UHPC-CA, which is 93.87%, 37.34%, 5.13% and 3.21% averagely higher than that of multiple linear regression, multiple nonlinear regression, T-BP and PCA-BP, respectively. Furthermore, GA-BP neural network has the lowest error index for each performance prediction. MAE, MSE and RMSE are 18.13%, 77.26% and 52.31% lower than PCA-BP on average. In summary, the GA-BP model with genetic evolution has stable and high-precision prediction results, which can be used to effectively predict the performance of UHPC-CA.

4 Discussion

(1) The model studied in this paper requires multi-parameter input and multi-index output. Seven influencing factors were taken as input, such as coarse aggregate type, coarse aggregate content, steel fiber type, steel fiber dosage, water-binder ratio, rubber particle sand replacement rate and curing system. Five performance indexes were taken as output, such as compressive strength, flexural strength, splitting tensile strength, abrasion resistance and chloride diffusion coefficient. For the existing literature, we did not find a dataset in which these input parameters and output indexes have been used simultaneously. In the current literature about UHPC performance prediction, there are large datasets for any index studied in this paper. However, these single-index datasets have different sample ratio, test condition and curing condition. Therefore, the existing large datasets cannot be applied to the model of multi-parameter input and multi-index output in this paper. In order to solve the above problems, we made 90 groups of samples for mechanical properties and abrasion resistance test, and 105 groups of samples for chloride ion diffusion coefficient test, and nearly 500 groups of test data were used for model training and verification. In future study, we will carry out more experiments to expand the dataset to verify the accuracy of the model.

(2) In this article, we pay more attention to the prediction accuracy and error of the five prediction models, and judge the quality of the prediction results by the goodness of fit R² and the error indexes. The neural network is regarded as a black box, and it is difficult to explain the relationship between input parameters and output indicators from aspects of physical and mechanical. For multivariate linear and nonlinear models, it is difficult to obtain the physical meaning of each coefficient because there are too many independent variables involved. In general, the five models in this paper can only provide reference for predicting the performance of UHPC, and the parameters involved in the model have no physical and mechanical interpretation.

5 Conclusion

(1) The traditional multiple linear and nonlinear regression equation prediction models are not suitable for the prediction of mechanical properties and long-term performance of UHPC-CA. It cannot achieve the prediction requirement of multi-parameter input and multi-index output. It has significant limitations in terms of low prediction accuracy and single prediction function.

(2) The T-BP model based on artificial neural network has higher prediction accuracy for UHPC-CA than linear and nonlinear regression models. The goodness of fit of T-BP model is significantly higher than that of linear and nonlinear models. The R² value of mechanical properties and long-term performance are 17.32%, 32.22%, 31.56%, 34.56% and 296.06% higher than linear prediction model, and 1.07%, 5.6%, 2.43%, 11.54% and 135.86% higher than nonlinear model, respectively. The error index of T-BP model is significantly lower than that of linear and nonlinear models.

(3) The PCA-BP model is more suitable for the performance prediction of UHPC-CA than the traditional T-BP model. The R² value of mechanical properties and long-term performance is 1.79%, 0.48%, 0.46%, 3.9%, 3.27% and higher than that of T-BP, respectively. However, the average error of compressive strength and splitting tensile strength is slightly higher, and the rest are significantly reduced. For instance, the MAE, MSE and RMSE of chloride ion erosion resistance are 43.37%, 47.65% and 27.65% lower than those of T-BP model, respectively.

(4) The GA-BP model performs very well in predicting the performance of UHPC-CA. It can be seen from the prediction results that the GA-BP model has high stability and small variation of the fitting curve. In the model training, the genetic algorithm optimizes the initial weights and thresholds of the neural network, and R2 is more stable. The goodness of fit of the model for mechanical properties and long-term performance is greater than 0.93, which is 3.32%, 1.69%, 3.00%, 11.62% and 6.04% higher than that of T-BP, and 1.51%, 1.16%, 2.53%, 8.17% and 2.68% higher than that of PCA-BP, respectively. The error indexes of all performance parameters are significantly lower than those of T-BP model and PCA-BP model. The MAE, MSE and RMSE values of each performance prediction decreased by 34.25%, 53.29% and 34.81% on average compared with T-BP neural network, and decreased by 32.73%, 45.18% and 28.94% on average compared with PCA-BP neural network.

(5) According to the prediction accuracy and error value, the prediction model of UHPC-CA is ranked as follows: GA-BP > PCA-BP > T-BP > Nonlinear regression > Linear regression.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

YL: Data curation, Software, Validation, Writing–original draft, Writing–review and editing, Conceptualization. DC: Investigation, Writing–review and editing, Visualization. DW: Methodology, Supervision, Writing–review and editing. CL: Writing–review and editing. AW: Writing–review and editing. CW: Writing–review and editing. DK: Writing–review and editing. CX: Writing–review and editing. SH: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Key Research and Development Project (2022YFB2603000), the National Natural Science Foundation of China (52179120, 52171267, 51909270 and 51909147), and the Fundamental Research Funds for the Central Universities (23CX07013A).

Conflict of interest

Authors DC, CL, CW, DK, and CX were employed by The Seventh Engineering Co., Ltd., of CCCC First Highway Engineering Co. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2025.1550991/full#supplementary-material

References

Alexander, M., and Beushausen, H. (2019). Durability, service life prediction, and modelling for reinforced concrete structures – review and critique. Cem. Concr. Res. 122, 17–29. doi:10.1016/j.cemconres.2019.04.018

CrossRef Full Text | Google Scholar

Arriagada, J., Olausson, P., and Selimovic, A. (2002). Artificial neural network simulator for SOFC performance prediction. J. Power Sources 112 (1), 54–60. doi:10.1016/s0378-7753(02)00314-2

CrossRef Full Text | Google Scholar

ASTM C1856/C1856M-17.2017 (2024). Standard practice for fabricating and testing specimens of ultra-high performance concrete.

Google Scholar

Bajaber, M. A., and Hakeem, I. Y. (2020). UHPC evolution, development, and utilization in construction: a review. J. Mater. Res. Technol. 10, 1058–1074. doi:10.1016/j.jmrt.2020.12.051

CrossRef Full Text | Google Scholar

Chen, Q., Ma, R., and Jiang, Z. W. (2020). Compressive strength prediction and mix design of UHPC based on GA-BP neural network. J. Build. Mater. 23 (01), 176–183+191. (in Chinese). doi:10.3969/j.issn.1007-9629.2020.01.027

CrossRef Full Text | Google Scholar

Cui, K. J. X., and Jing, X. (2019). Research on prediction model of geotechnical parameters based on BP neural network. Neural Comput. and Appl. 31, 8205–8215. doi:10.1007/s00521-018-3902-6

CrossRef Full Text | Google Scholar

Du, J., Meng, W., Khayat, K. H., Bao, Y., Guo, P., Lyu, Z., et al. (2021). New development of ultra-high-performance concrete (UHPC). Compos. Part B Eng. 224 (9), 109220. doi:10.1016/j.compositesb.2021.109220

CrossRef Full Text | Google Scholar

Es-Samlali, L., El Haloui, Y., Oudrhiri-Hassani, F., Tlidi, A., and bekri, A. (2024). Performance assessment of sustainable asphalt concrete using steel slag, with an artificial neural network prediction of asphalt concrete behavior. Case Stud. Constr. Mater. 21, e03877. doi:10.1016/j.cscm.2024.e03877

CrossRef Full Text | Google Scholar

Farouk, A. I. B., and Jinsong, Z. (2022). Prediction of interface bond strength between ultra-high-performance concrete (UHPC) and normal strength concrete (NSC) using a machine learning approach. Arabian J. Sci. Eng. 47 (4), 5337–5363. doi:10.1007/s13369-021-06433-6

CrossRef Full Text | Google Scholar

Han, S. H. (2007). Influence of diffusion coefficient on chloride ion penetration of concrete structure. Constr. and Build. Mater. 21 (2), 370–378. doi:10.1016/j.conbuildmat.2005.08.011

CrossRef Full Text | Google Scholar

Han, Z., Jian, L., Jie, X., Bo, M., Li, J., and Tang, B. (2018). Research on anti-chloride ion penetration property of crumb rubber concrete at different ambient temperatures. Constr. Build. Mater. 189, 42–53. doi:10.1016/j.conbuildmat.2018.08.193

CrossRef Full Text | Google Scholar

Haykin, S. (1998). Neural networks: a comprehensive foundation. 3rd Edition. Macmillan.

Google Scholar

Huang, C. X., Zhang, Q. S., Liu, J., Zhang, L. Z., Wang, X., and Pei, Y. (2024). Rheological properties of quick-setting slurry considering heat exchange in high temperature fractured rock mass and its application. Constr. Build. Mater. 438, 137221. doi:10.1016/j.conbuildmat.2024.137221

CrossRef Full Text | Google Scholar

Huang, Y. B. (2009). Advances in artificial neural networks-methodological development and application. Algorithms 2.3, 973–1007. doi:10.3390/algor2030973

CrossRef Full Text | Google Scholar

Jin, B. L. M., Li, S., Hu, B., and Liu, M. (2019). A survey on projection neural networks and their applications. Appl. Soft Comput. 76, 533–544. doi:10.1016/j.asoc.2019.01.002

CrossRef Full Text | Google Scholar

Khan, M. I. (2012). Predicting properties of high performance concrete containing composite cementitious materials using artificial neural networks. Automation Constr. 22 (Mar), 516–524. doi:10.1016/j.autcon.2011.11.011

CrossRef Full Text | Google Scholar

Krogh, A. (2008). What are artificial neural networks? Nat. Biotechnol. 26 (2), 195–197. doi:10.1038/nbt1386

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, S. S. Y., Hiew, S. Y., and Raman, S. N. (2023). Data-driven ultimate condition prediction of UHPC columns subjected lateral confinement using Artificial Neural Network (ANN) approach. J. Phys. Conf. Ser. 2521.1, 012010. doi:10.1088/1742-6596/2521/1/012010

CrossRef Full Text | Google Scholar

Li, J., Cheng, J. H., and Shi, J. Y. (2012). Brief introduction of back propagation (BP) neural network algorithm and its improvement. Berlin Heidelberg: Springer Berlin Heidelberg Springer.

CrossRef Full Text | Google Scholar

Li, J. Q., Wu, Z. M., Shi, C. J., Yuan, Q., and Zhang, Z. (2020). Durability of ultra-high performance concrete–A review. Constr. Build. Mater. 255, 119296. doi:10.1016/j.conbuildmat.2020.119296

CrossRef Full Text | Google Scholar

Liu, J., Zhang, B., Li, Y., Zhao, B., and Deng, Y. (2022). Modeling and analysis of fiber-reinforced high-performance concrete strength prediction based on nonlinear programming. Constr. Build. Mater. 322, 126421. doi:10.1016/j.conbuildmat.2022.126421

CrossRef Full Text | Google Scholar

Liu, L. M., Fang, Z., and Liu, F. C. (2021). Shrinkage and creep test and prediction of UHPC under indoor environment. China J. Highw. Transp. 34 (08), 35–44. doi:10.19721/j.cnki.1001-7372.2021.08.003

CrossRef Full Text | Google Scholar

Martin-Perez, B., Zibara, H., Hooton, R. D., and Thomas, M. (2000). A Study of the effect of chloride binding on service life predictions. Cem. Concr. Res. 30 (8), 1215–1223. doi:10.1016/s0008-8846(00)00339-2

CrossRef Full Text | Google Scholar

Nachaoui, M., Afraites, L., and Laghrib, A. (2021). A regularization by denoising super-resolution method based on genetic algorithms. Signal Process. Image Commun. 99, 116505. doi:10.1016/j.image.2021.116505

CrossRef Full Text | Google Scholar

Ou, Y. X., Shi, C. J., and Shi, J. H. (2021). Prediction of compressive mechanical properties and elastic modulus of ultra-high performance concrete. J. Chin. Ceram. Soc. 49 (02), 296–304. doi:10.14062/j.issn.0454-5648.20200286

CrossRef Full Text | Google Scholar

Parichatprecha, R., and Nimityongskul, P. (2009). Analysis of durability of high performance concrete using artificial neural networks. Constr. Build. Mater. 23 (2), 910–917. doi:10.1016/j.conbuildmat.2008.04.015

CrossRef Full Text | Google Scholar

Ryu, G. S., Kang, S. T., Park, J. J., Koh, K. T., and Kim, S. W. (2011). Evaluation of fundamental UHPC properties according to the shape of steel fiber. Key Eng. Mater. 452. 717–720. doi:10.4028/www.scientific.net/kem.452-453.717

CrossRef Full Text | Google Scholar

Shafieifar, M., Farzad, M., and Azizinamini, A. (2017). Experimental and numerical study on mechanical properties of ultra high performance concrete (UHPC). Constr. Build. Mater. 156 (15), 402–411. doi:10.1016/j.conbuildmat.2017.08.170

CrossRef Full Text | Google Scholar

Song, H. W., and Kwon, S. J. (2009). Evaluation of chloride penetration in high performance concrete using neural network algorithm and micro pore structure. Cem. and Concr. Res. 39 (9), 814–824. doi:10.1016/j.cemconres.2009.05.013

CrossRef Full Text | Google Scholar

Song, P. S., and Hwang, S. (2004). Mechanical properties of high-strength steel fiber-reinforced concrete. Constr. and Build. Mater. 18 (9), 669–673. doi:10.1016/j.conbuildmat.2004.04.027

CrossRef Full Text | Google Scholar

Taskinen, J., and Yliruusi, J. (2003). Prediction of physicochemical properties based on neural network modelling. Adv. Drug Deliv. Rev. 55, 1163–1183. doi:10.1016/s0169-409x(03)00117-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, S., Zhang, N., Wu, L., and Wang, Y. (2016). Wind speed forecasting based on the hybrid ensemble empirical mode decomposition and GA-BP neural network method. Renew. Energy 94, 629–636. doi:10.1016/j.renene.2016.03.103

CrossRef Full Text | Google Scholar

Wang, X. C., Xiao, F., Zhang, Q., Zhou, A., and Liu, R. (2021). Grouting characteristics in rock fractures with rough surfaces: apparatus design and experimental study. Measurement 184, 109870. doi:10.1016/j.measurement.2021.109870

CrossRef Full Text | Google Scholar

Wu, Y., and Huang, H. (2024). Predicting compressive and flexural strength of high-performance concrete using a dynamic Catboost Regression model combined with individual and ensemble optimization techniques. Mater. Today Commun. 38, 108174. doi:10.1016/j.mtcomm.2024.108174

CrossRef Full Text | Google Scholar

Xiaofeng, X., Xibing, L. I., and Xueyi, S. (2017). Prediction of height of water flowing fractured zone based on PCA-BP neural networks model. China Saf. Sci. J.

Google Scholar

Xu, L., Yang, Y., Zhang, Y., Xue, Y., Yu, Y., and Hao, N. (2023). Estimation of stress–strain constitutive model for ultra-high performance concrete after high temperature with an deep neural network based method. Constr. Build. Mater. 408, 133690. doi:10.1016/j.conbuildmat.2023.133690

CrossRef Full Text | Google Scholar

Xue, H., Ma, X. W., and Qi, J. M. (2018). Life cycle prediction of ultra-high performance concrete under freeze-thaw environment. Low. Temp. Build. Technol. 40 (01), 21–23. doi:10.13905/j.cnki.dwjz.2018.01.006

CrossRef Full Text | Google Scholar

Yang, Z. Y. (2003). Prediction model of common concrete strength by BP artificial neural network. J. Chang Univ. ( Nat. Sci. Ed. ) 03, 50–52. doi:10.1142/S0252959903000104

CrossRef Full Text | Google Scholar

Yi, Z. S. C., Zhu, D., Guo, S., Zhang, Z., and Shi, C. (2020). A review on the deterioration and approaches to enhance the durability of concrete in the marine environment. Cem. and Concr. Compos. 113, 103695. doi:10.1016/j.cemconcomp.2020.103695

CrossRef Full Text | Google Scholar

Yu, S. J. (2011). An optimizing BP neural network algorithm based on genetic algorithm. Artif. Intell. Rev. Int. Sci. Eng. J. 36, 2. doi:10.4028/www.scientific.net/KEM.452-453.717

CrossRef Full Text | Google Scholar

Zhang, J., Zhao, Y., and Li, H. (2017). Experimental investigation and prediction of compressive strength of ultra-high performance concrete containing supplementary cementitious materials. Adv. Mater. Sci. Eng. 2017, 1–8. doi:10.1155/2017/4563164

CrossRef Full Text | Google Scholar

Zhang, L., Wang, F., and Sun, T. (2016). A constrained optimization method based on BP neural network. Neural Computing and Applications. 29, 413–421. doi:10.1007/2Fs00521-016-2455-9

CrossRef Full Text | Google Scholar

Zhang, L., Zhang, J., Ren, P., Ding, L., Hao, W., et al. (2023b). Analysis of energy consumption prediction for office buildings based on GA-BP and BP algorithm. Case Stud. Therm. Eng. 50, 103445. doi:10.1016/j.csite.2023.103445

CrossRef Full Text | Google Scholar

Zhang, L. Z. (2022). Permeation grouting diffusion mechanism of quick setting grout. Tunn. Undergr. space Technol. Jun, 124. doi:10.1016/j.tust.2022.104449

CrossRef Full Text | Google Scholar

Zhang, L. Z. (2024). Characteristics of slurry-water mixing region in fractured rock mass grouting process: experimental study. Constr. Build. Mater. May 10, 427.

Google Scholar

Zhang, L. Z., Xu, H., Qingsong, Z., Yuntian, C., and Jun, L. (2023a). Rheological characteristics of cement-sodium silicate grout in its fluid–solid phase transition process. Constr. Build. Mater. 362, 129443. doi:10.1016/j.conbuildmat.2022.129443

CrossRef Full Text | Google Scholar

Zhang, Y., Chen, B., Pan, G., and Zhao, Y. (2019). A novel hybrid model based on VMD-WT and PCA-BP-RBF neural network for short-term wind speed forecasting. Energy Convers. Manag. 195 (SEP), 180–197. doi:10.1016/j.enconman.2019.05.005

CrossRef Full Text | Google Scholar

Zou, J., Han, Y., and So, S. S. (2009). Overview of artificial neural networks. Methods Mol. Biol. 458 (458), 15–23. doi:10.1007/978-1-60327-101-1_2

PubMed Abstract | CrossRef Full Text | Google Scholar