Smart material optimization using reinforcement learning in multi-dimensional self-assembly

Introduction: In recent years the design and optimization of smart materials have gained considerable attention due to their potential applications across diverse fields, from biomedical engineering to adaptive structural systems. Traditional approaches for optimizing these materials often rely on deterministic models ortrial-and-error processes, which tend to be limited by computational expense and lack of adaptability in dynamic environments. These methods generally fail to address the complexities of multi-dimensional self-assembly processes where materials need to respond autonomously to environmental stimuli in real time.

Methods: To address these limitations, this research explores the application of reinforcement learning (RL) as an advanced optimization framework to enhance the autonomous self-assembly of smart materials. We propose a novel reinforcement learning-based model that integrates adaptive control mechanisms within multi-dimensional self-assembly, allowing materials to optimize their configuration and properties according to external stimuli. In our approach, agents learn optimal assembly policies through iterative interactions with simulated environments, enabling the smart material to evolve and respond to complex and multi-factorial inputs.

Results and discussion: Experimental results demonstrate the model’s efficacy, revealing significant improvements in adaptability, efficiency, and material performance under varied environmental conditions. The work not only advances the theoretical understanding of self-assembly in smart materials but also paves the way for the development of autonomous, self-optimizing materials that can be deployed in real-world applications requiring dynamic adaptation and robustness.

1 Introduction

Smart materials, with their adaptive capabilities in response to environmental stimuli, have gained significant attention due to their broad applications in fields such as robotics, biomedical devices, and flexible electronics (Ali and Albakri, 2024). The optimization of smart materials in multi-dimensional self-assembly processes poses unique challenges due to the complexity and high dimensionality of the design space (Bányai, 2021). Traditional optimization methods struggle to effectively navigate this space, resulting in suboptimal material properties and limited adaptability. Reinforcement learning (RL), as an advanced machine learning technique, offers a promising approach to overcome these challenges (yu Liang et al., 2022). By enabling dynamic learning and self-improvement, reinforcement learning (RL) not only facilitates efficient optimization across diverse parameters but also enhances the adaptability and functionality of smart materials in complex, multi-dimensional environments. Therefore, exploring reinforcement learning (RL) for smart material optimization in multi-dimensional self-assembly is both necessary and impactful, promising to unlock new potentials in material science and engineering (Yang et al., 2022).

To address the limitations of early optimization approaches, researchers initially relied on symbolic AI methods that leveraged rule-based algorithms and knowledge representation. These traditional methods focused on defining explicit rules and heuristics to guide the self-assembly process, aiming to control material properties through logical sequences and structured frameworks (Kang and James, 2021). While these approaches allowed for certain degrees of customization and control, they were fundamentally limited in scalability and adaptability due to their reliance on manually defined rules, which could not capture the complexity of real-world, high-dimensional environments. Moreover, symbolic AI methods often required extensive expert knowledge and were unable to autonomously improve or adapt to new conditions. As a result, these techniques provided a foundational understanding of smart material optimization but proved inadequate for the demands of multi-dimensional self-assembly.

In response to the limitations of symbolic AI, data-driven methods such as machine learning (ML) (Aissa et al., 2015) emerged as promising approaches to optimize smart materials by leveraging large datasets and statistical modeling (Song and Ni, 2021). ML techniques, including supervised and unsupervised learning, offered increased flexibility and adaptability in analyzing material behaviors (Wang et al., 2022). Despite their advantages, these methods often struggled with high-dimensional parameter spaces and the need for extensive labeled data, limiting their applicability in dynamic assembly processes (Liu Q. et al., 2020). Moreover, the static nature of many ML models after training posed challenges for continuous adaptation in real-time environments (Choi, 2014). While impactful, these approaches underscored the need for more dynamic optimization frameworks to address the complexity of smart material design (Balasubramaniyan et al., 2022). The development of deep learning and pre-trained models further enhanced smart material optimization by introducing more sophisticated neural architectures capable of handling complex, high-dimensional data (Kim et al., 2020). Deep learning techniques, particularly with reinforcement learning frameworks, enabled the optimization process to be both dynamic and adaptive, allowing models to learn from iterative interactions within multi-dimensional assembly environments. Pre-trained models, such as those leveraging transfer learning, provided a means to apply previously learned knowledge to new scenarios, significantly improving efficiency and reducing training requirements (Deng et al., 2023). Despite these advancements, deep learning models can be computationally expensive and may require fine-tuning to avoid issues such as overfitting in high-dimensional assembly processes. Consequently, while deep learning and pre-trained models offered unprecedented potential in material optimization, their scalability and computational demands posed practical limitations (Alwabli et al., 2020).

To overcome the constraints of previous approaches, our research proposes a novel reinforcement learning-based method tailored for smart material optimization in multi-dimensional self-assembly. By integrating reinforcement learning (RL)’s dynamic learning capabilities with advanced neural architectures, our approach aims to achieve scalable, efficient, and adaptive optimization in complex design spaces.

We summarize our contributions as follows:

$•$ The proposed method introduces a novel multi-agent reinforcement learning (RL) framework specifically designed for multi-dimensional self-assembly, allowing enhanced adaptability and scalability.

$•$ It leverages a modular architecture, enabling high efficiency and versatility across different smart material types and assembly scenarios.

$•$ Experimental results demonstrate significant improvements in material performance and assembly precision, showcasing the method’s potential for broad application in smart material engineering.

2 Related work

2.1 Reinforcement learning in material design

Reinforcement learning (RL) has become a powerful tool in material design, offering solutions for optimizing complex, non-linear systems through adaptive learning and feedback (Ke et al., 2020). Its ability to explore vast parameter spaces and refine optimal policies iteratively has made it particularly valuable for designing materials that meet diverse functional requirements, such as thermal stability and flexibility (Athinarayanarao et al., 2023). Key applications of reinforcement learning (RL) include coupling with predictive models like Monte Carlo simulations and molecular dynamics to optimize material behaviors at atomic or molecular levels (Zhang, 2023). This integration has enabled the design of polymers, alloys, and composite materials with targeted properties. Advanced reinforcement learning (RL) methods, such as deep Q-networks (DQNs) and proximal policy optimization (PPO), enhance convergence speed and stability in high-dimensional state-action spaces, a common challenge in material optimization (Ishfaq et al., 2023). Techniques like transfer learning and meta-learning further accelerate reinforcement learning (RL) processes, leveraging knowledge from simpler tasks to tackle complex material design problems efficiently (Dat et al., 2023). These methods, combined with adaptive exploration-exploitation strategies, improve the discovery of novel configurations while optimizing known solutions, ensuring effective convergence to high-performance material properties.

2.2 Self-assembly mechanisms in smart materials

Self-assembly underpins the design of smart materials by enabling spontaneous organization into complex structures across multiple scales, driven by forces like electrostatic interactions and hydrogen bonding (Cuartas and Aguilar, 2022). Advances in this field have extended beyond two-dimensional patterns to include three-dimensional and hierarchical architectures, vital for functionalities like environmental responsiveness and self-healing (Zhang, 2022). Recent research focuses on leveraging external stimuli—such as temperature, pH, and magnetic fields—to dynamically control structures and properties. For instance, thermally responsive polymers adapt configurations with temperature changes, while magnetically guided nanoparticles form predefined structures under magnetic fields (Gillani et al., 2022). Hierarchical self-assembly has further enriched material versatility, facilitating designs with layered properties optimized for complex functionalities. The integration of reinforcement learning (RL) into self-assembly optimization has introduced new possibilities by enabling simulations in high-dimensional spaces (Fawaz et al., 2024). Reinforcement learning (RL) models iteratively refine assembly parameters, guiding materials to optimal configurations even in scenarios with numerous variables. This is particularly effective for creating multi-functional materials, where optimizing properties like strength and flexibility simultaneously is critical (Zhang et al., 2022).

2.3 Optimization techniques for high-dimensional systems

Optimization in high-dimensional systems presents unique challenges due to the exponential increase in complexity as the number of dimensions grows. This issue is particularly relevant in multi-dimensional self-assembly for smart materials, where each additional parameter—whether it pertains to structural configuration, material composition, or environmental factors—adds complexity to the optimization process (Tao et al., 2021). High-dimensional systems require sophisticated algorithms that can efficiently explore vast parameter spaces without falling into local optima (Lv et al., 2021). As a result, researchers are increasingly turning to reinforcement learning (RL) and other machine learning techniques to address these challenges, as traditional optimization methods often struggle to cope with the high dimensionality inherent in smart material design (Yang et al., 2021). Within the field of high-dimensional optimization, several RL-based methods have shown promise. Deep reinforcement learning (DRL), for instance, is particularly suited for navigating complex landscapes due to its ability to approximate optimal policies in large state spaces (Maraveas et al., 2021). Techniques such as policy gradient methods and actor-critic models are frequently applied to enable the reinforcement learning (RL) agents to learn optimal actions through trial and error in simulated environments. These models have demonstrated effectiveness in finding optimal configurations for high-dimensional systems, where each dimension represents a specific material parameter or assembly condition that influences the final structure and properties of the smart material (Kim et al., 2021). A key area of focus has been on developing algorithms that balance exploration and exploitation efficiently, especially in high-dimensional spaces where exhaustive search is computationally infeasible. Novel methods, such as hierarchical reinforcement learning (RL) and ensemble learning, have been implemented to address these requirements (Rho et al., 2021). Hierarchical reinforcement learning (RL), for instance, breaks down high-dimensional optimization tasks into a hierarchy of smaller, manageable sub-tasks, allowing for faster convergence and more efficient use of computational resources. Ensemble learning approaches, which combine the outputs of multiple models, have also been used to improve the reliability of the reinforcement learning (RL) algorithms by providing a consensus on the most promising material configurations (Flores-García et al., 2021). Current research also emphasizes the integration of hybrid models, which combine reinforcement learning (RL) with other optimization strategies, such as genetic algorithms or particle swarm optimization (Liu S. et al., 2020). These hybrid approaches allow for a more comprehensive exploration of the parameter space and are particularly effective in circumventing the local minima problem. Furthermore, adaptive sampling techniques are being investigated to dynamically adjust the sampling strategy based on the agent’s learning progress, ensuring that high-dimensional spaces are explored efficiently (Nardo et al., 2020). Although challenges remain, particularly regarding the computational intensity of training reinforcement learning (RL) models in high-dimensional systems, advances in high-performance computing and parallel processing are facilitating the development of more robust and scalable optimization solutions for smart materials.

3 Methods

3.1 Overview

The optimization of smart materials has emerged as a key area of interest, due to its ability to advance technologies across fields such as robotics, biomedical devices, and sustainable engineering. This section outlines the structure and methodology of our approach to smart material optimization. By integrating multi-objective optimization and reinforcement learning (RL), our method adapts to the dynamic requirements and constraints intrinsic to material applications, where conflicting objectives—such as strength, flexibility, cost, and energy efficiency—must be optimized simultaneously. Our approach builds on the foundation of Multi-Objective Reinforcement Learning (MORL), which effectively balances multiple, often competing objectives through Pareto optimization. Unlike conventional reinforcement learning (RL) models that seek to maximize a single reward function, our method formulates the optimization problem as a Multi-Objective Markov Decision Process (MOMDP). This approach allows for the exploration of a range of trade-offs and for generating a continuous Pareto front that provides a set of optimal policies tailored to varying preferences across objectives. The proposed method is structured as follows: in Section 3.2, we introduce the formal definitions and mathematical formulations pertinent to MOMDPs, including the structure of the reward functions and policy representations within the context of multi-objective optimization. This foundation will be critical to understanding our subsequent developments in constructing a model that can handle multiple criteria simultaneously. In Section 3.3, we detail our novel model—referred to as the Adaptive Pareto Optimization Model (APOM)—which leverages a gradient-based approach to adapt policy parameters iteratively. This model ensures that the resulting policies align closely with the Pareto Frontier, effectively spanning a wide spectrum of optimal trade-offs across the objective space. By continuously approximating the Pareto front, APOM enables high-fidelity control over the optimization trajectory of smart materials, facilitating fine-grained adjustments to meet specific application requirements. Finally, in Section 3.4, we introduce our Predictive Control Strategy (PCS) as a complement to APOM, which strategically guides the selection and adjustment of policies based on real-time feedback from the environment. PCS incorporates prediction models to forecast the effects of policy adaptations, allowing for preemptive adjustments that improve convergence speed and solution accuracy. Together, these components form an adaptive framework for optimizing smart materials across a range of applications, while maintaining flexibility to adjust to the dynamic needs of each use case.

3.2 Preliminaries

To formalize the optimization of smart materials, we define the problem using the framework of Multi-Objective Markov Decision Processes (MOMDPs), which provides the foundation for managing multiple, often competing objectives within a single reinforcement learning (RL) environment. In our scenario, a smart material is represented as an adaptive system that can respond to stimuli and environmental conditions, making MOMDPs particularly suited for capturing the complexities and dynamic nature of these materials.

Formally, a MOMDP is defined as a tuple $⟨S,A,P,R,\gamma ,D⟩$, where:

$•$ $S$ represents the state space, capturing all possible states the material can take in response to various conditions. States might include physical properties like elasticity, temperature, and stress thresholds.

$•$ $A$ denotes the action space, representing all feasible adjustments to the material’s properties, such as altering its molecular structure or configuration.

$•$ $P(s^{\prime }|s,a)$ is the state transition probability, specifying the probability of transitioning to state $s^{\prime }$ from state $s$ under action $a$. This accounts for the material’s behavior under various manipulations.

$•$ $R=[R_1,R_2,\dots ,R_q]$ is a vector of reward functions, each associated with a different objective (e.g., flexibility, durability, and conductivity). Each $R_i:S\times A\to \mathbb{R}$ evaluates how well a particular action contributes to achieving objective $i$ from the current state.

$•$ $\gamma =[{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_q]$ is a vector of discount factors, with each ${\gamma }_i\in [\mathrm{0,1})$ reflecting the degree to which future rewards for objective $i$ are considered in policy optimization.

$•$ $D$ represents the initial state distribution, from which the material begins its adaptive process.

Each policy $\pi$ in this MOMDP framework is linked to a vector of expected returns $J^{\pi }=[J_1^{\pi },J_2^{\pi },\dots ,J_q^{\pi }]$, where (Formula 1):

$J_i^{\pi }=\mathbb{E}\left[{\displaystyle \sum _{t=0}^{\infty }}{\gamma }_i^t{R}_i\left(s_t,a_t\right)\mid s_0\sim D,a_t\sim \pi \left(s_t\right)\right].(1)$

This formulation allows us to evaluate policies based on their ability to optimize each objective in $R$ under the constraints of the material’s state and action spaces.

Given the multi-objective nature of the problem, we focus on deriving policies that reside on the Pareto Frontier, which consists of all non-dominated solutions—policies where no objective can be improved without compromising another. A policy $\pi$ is Pareto-optimal if for another policy ${\pi }^{\prime }$ (Formula 2):

$\forall i,J_i^{\pi }\ge J_i^{{\pi }^{\prime }}\text{and}\exists i\text{s.t.}{J}_i^{\pi }>J_i^{{\pi }^{\prime }},(2)$

where $J_i^{\pi }$ denotes the expected reward for objective $i$ under policy $\pi$.

To approximate the continuous Pareto Frontier in practice, we use a gradient-based approach inspired by multi-objective optimization techniques. The gradient of each objective with respect to the policy parameters $\theta$ is given by (Formula 3):

$abl{a}_{\theta }{J}_i\left(\theta \right)={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}\left[R_i\left(\tau \right){\displaystyle \sum _{t=0}^{\infty }}abl{a}_{\theta }\log {\pi }_{\theta }\left(a_t|s_t\right)\right],(3)$

where $\tau$ represents a trajectory through the state-action space. This expression provides the gradient for each objective individually, enabling us to adjust $\theta$ to achieve improvements across all objectives.

In our method, we incorporate a scalarization technique to prioritize different objectives according to a weight vector $\omega =[{\omega }_1,\dots ,{\omega }_q]$ such that ${\sum }_{i=1}^q{\omega }_i=1$. The scalarized objective function then becomes (Formula 4):

$J\left(\theta ,\omega \right)={\displaystyle \sum _{i=1}^q}{\omega }_i{J}_i\left(\theta \right).(4)$

The associated policy gradient for this scalarized objective is (Formula 5):

$abl{a}_{\theta }J\left(\theta ,\omega \right)={\displaystyle \sum _{i=1}^q}{\omega }_{i}abl{a}_{\theta }{J}_i\left(\theta \right).(5)$

This approach enables the model to adjust focus dynamically across different objectives, balancing between them to trace out the Pareto Frontier efficiently.

The subsequent sections will further elaborate on our specific adaptations of these principles for the optimization of smart materials. Our model is designed to explore various policy configurations on the Pareto Frontier, thus providing a range of optimized trade-offs that can be chosen according to the specific requirements of different applications. Through continuous adjustment and dynamic optimization, our method captures the complexity of smart materials and maximizes their functional adaptability.

3.3 Adaptive Pareto Optimization Model (APOM)

In this section, we introduce the Adaptive Pareto Optimization Model (APOM), an innovative and flexible framework specifically designed to address the multi-objective optimization challenges inherent in smart material applications. APOM operates by continuously approximating the Pareto Frontier, a method that enables the identification of optimal trade-offs among competing objectives. To achieve this, APOM constructs a dynamically adaptable policy manifold, enabling the model to explore and fine-tune a diverse range of optimal solutions across varying performance criteria. As real-world applications often require balancing multiple conflicting objectives, APOM provides a structured yet adaptable approach that can shift in response to changing design needs (As shown in Figure 1.

Figure 1

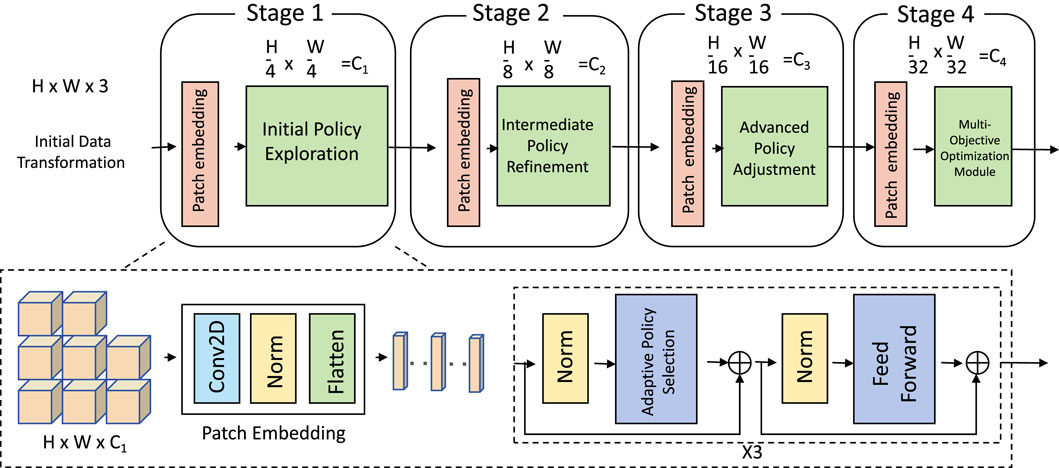
Figure 1. The architecture of the Adaptive Policy Optimization Model (APOM) showcasing the dynamic policy manifold representation. The model leverages a patch embedding module to preprocess input, followed by multiple stages for hierarchical feature extraction, intermediate mapping, and policy refinement. Each stage refines the representation in a progressively lower-dimensional space, culminating in a multi-objective optimization module that balances competing objectives. This design enables flexible adaptation across diverse task requirements.

3.3.1 Dynamic policy manifold representation

In the Adaptive Policy Optimization Model (APOM), the dynamic policy manifold is a pivotal feature that governs the exploration of the policy space. We define a parametric mapping function ${\varphi }_{\theta }:S\to \mathrm{\Pi }$, where $S\subset {\mathbb{R}}^k$ represents a reduced-dimensional space of policy parameters, and $\theta$ constitutes the parameters governing this transformation. This mapping ${\varphi }_{\theta }$ allows the model to navigate a manifold within a high-dimensional policy space $\mathrm{\Pi }$, effectively lowering the computational load by concentrating on a subspace aligned with relevant solution structures. Each point $s\in S$ is mapped to a corresponding policy configuration $\pi ={\varphi }_{\theta }(s)$, leading to a continuum of policies represented as (Formula 6)

${\mathrm{\Pi }}_{\theta }\left(S\right)=\left\{\pi :\pi ={\varphi }_{\theta }\left(s\right),s\in S\right\}.(6)$

To further formalize, we decompose the transformation ${\varphi }_{\theta }$ into a sequence of operations (Formula 7):

$\pi ={\varphi }_{\theta }\left(s\right)=f_{{\theta }_2}\left(g_{{\theta }_1}\left(s\right)\right),(7)$

where $g_{{\theta }_1}:S\to {\mathbb{R}}^m$ is an intermediate mapping that extracts meaningful features from $S$, and $f_{{\theta }_2}:{\mathbb{R}}^m\to \mathrm{\Pi }$ refines these features into actionable policy parameters. This hierarchical structure in ${\varphi }_{\theta }$ not only enables efficient dimensionality reduction but also supports dynamic reconfiguration of policies as objectives change, allowing APOM to adapt to evolving task requirements. The manifold, parameterized by $\theta$, acts as a flexible foundation for policy adaptation, where the parameter set $\theta =\{{\theta }_1,{\theta }_2\}$ is adjusted during the learning process to facilitate robust exploration and exploitation of the solution space.

The continuity of the policy manifold ensures that APOM can transition smoothly between policies, which is crucial for complex optimization tasks requiring balanced trade-offs among competing objectives. This adaptability is encoded within the manifold’s topology, enabling a finely tuned exploration process. In essence, as $s$ traces various trajectories within $S$, the resultant policies $\pi ={\varphi }_{\theta }(s)$ form a structured, dynamic landscape in $\mathrm{\Pi }$, thus creating a reservoir of adaptable policies that APOM can leverage in real-time.

Furthermore, to address the challenges associated with multi-objective optimization, APOM employs a tailored penalty function over the manifold ${\mathrm{\Pi }}_{\theta }(S)$. Given an objective vector (Formula 8)

$\mathbf{J}=\left[J_1\left(\pi \right),J_2\left(\pi \right),\dots ,J_n\left(\pi \right)\right],(8)$

where $J_i(\pi )$ represents the $i$-th objective evaluated at policy $\pi$, we define a composite objective (Formula 9):

$\mathcal{L}\left(\theta \right)={\displaystyle \sum _{i=1}^n}{w}_i{J}_i\left({\varphi }_{\theta }\left(s\right)\right),(9)$

where $w_i$ are the weights reflecting the priority of each objective. This objective guides the manifold evolution by optimizing $\theta$ to balance objectives effectively. Thus, APOM’s dynamic manifold approach fosters comprehensive decision-making across diverse objectives, adapting to new contexts seamlessly.

3.3.2 Gradient-based pareto frontier approximation

APOM’s objective is to optimize the manifold parameters $\eta$ in such a way that the resultant policy manifold ${\mathrm{\Omega }}_{\eta }(S)$ aligns closely with the desired Pareto Frontier. This alignment process involves minimizing the difference between the approximated Pareto Frontier, produced by the model, and the true Pareto-optimal Frontier that reflects the best possible trade-offs among competing objectives.

To achieve this alignment, we define the optimal parameters η* as those that minimize the distance between the values on the approximated and true Pareto frontiers across the state space $S$. Mathematically, this optimization problem is expressed as (Formula 10):

${\eta }^{*}=\arg \underset{\eta \in Q}{\min }{\int }_S\Vert K\left(\omega \right)-K^{*}\left(\omega \right)\Vert d\omega ,(10)$

where $K(\omega )$ represents the approximated values for each policy parameter configuration $\omega$, and $K^{*}(\omega )$ represents the true Pareto-optimal values for the same configurations. The integral over $S$ quantifies the approximation error by summing the deviations between the model and true values across the entire volume of $S$.

The parameter optimization task, therefore, becomes one of minimizing this error term through an iterative process, commonly approached by gradient descent. By adjusting $\eta$ step-by-step in the direction that reduces the alignment error, the approximation improves progressively. Specifically, each iteration updates $\eta$ based on the gradient of the loss function with respect to $\eta$, which is given by (Formula 11):

${\eta }_{t+1}={\eta }_t-\alpha {\nabla }_{\eta }{\int }_S\Vert K\left(\omega \right)-K^{*}\left(\omega \right)\Vert d\omega ,(11)$

where $\alpha$ denotes the learning rate, controlling the step size of each update. The gradient ${\nabla }_{\eta }$ of the integral term guides the descent, ensuring that each iteration brings ${\mathrm{\Omega }}_{\eta }(S)$ closer to the true Pareto Frontier.

The core advantage of this gradient-based approximation lies in its systematic approach to exploring the policy space. As $\eta$ is optimized, the APOM manifold evolves, enhancing its capacity to represent the true Pareto Frontier’s trade-offs more accurately. Over time, this process enables the model to offer a refined, comprehensive depiction of optimal trade-offs, effectively capturing the range of solutions that balance multiple objectives in a complex, multi-dimensional space.

To quantify the model’s convergence and accuracy in practice, one might employ additional evaluation metrics, such as the approximation error reduction over iterations or the similarity between the model’s Frontier and empirical Pareto points. As the optimization progresses, monitoring these metrics ensures that the alignment between ${\mathrm{\Omega }}_{\eta }(S)$ and the true Pareto Frontier $K^{*}$ remains effective, supporting an ongoing refinement of the APOM manifold’s accuracy.

3.3.3 Adaptive gradient flow in high-dimensional spaces

To further support the high-dimensional requirements of smart material optimization, APOM employs an adaptive gradient flow mechanism specifically designed to navigate complex objective spaces in an efficient and computationally feasible manner. The central idea of this adaptive gradient flow is to leverage gradient-based optimization while tailoring the computational demands to the scale and complexity of high-dimensional mappings, a critical feature for advanced multi-objective tasks like smart material design (As shown in Figure 2).

Figure 2

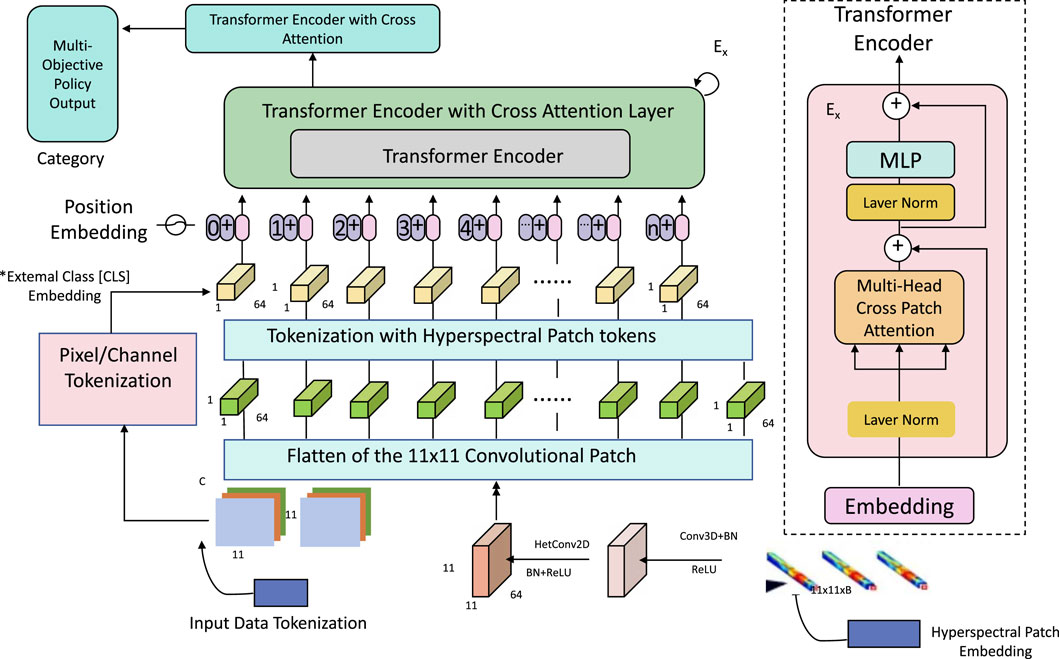
Figure 2. The architecture of the Adaptive Gradient Flow Model for high-dimensional smart material optimization. The model begins with Pixel/Channel Tokenization (1 Data) to preprocess input data, followed by Hyperspectral Patch Tokenization for effective handling of high-dimensional features. The core Transformer Encoder with Cross Attention Layer facilitates the integration of complex, multi-objective requirements through adaptive gradient flow. Position and External Class Embeddings enrich each token with spatial and categorical information, enabling precise navigation within the policy manifold. This structured approach allows for robust exploration and accurate approximation of the Pareto Frontier in high-dimensional optimization landscapes.

The gradient of $K(\eta )$ with respect to $\eta$ is formulated to ensure computational efficiency and accuracy. This gradient is expressed as (Formula 12):

$\frac{\partial K\left(\eta \right)}{\partial \eta }={\int }_S\left(\frac{\partial }{\partial \eta }\left(\mathcal{I}◦\left(K◦{\psi }_{\eta }\right)\right)\right){\text{Vol}}_{\text{Jac}}\left(D_{\omega }K\left(\omega \right)D_s{\psi }_{\eta }\left(s\right)\right)ds,(12)$

where ${\text{Vol}}_{\text{Jac}}$ denotes the Jacobian volume of the transformation, an essential term that scales the gradient computation by taking into account the distortion induced by the mapping ${\psi }_{\eta }$. This Jacobian volume is critical as it enables APOM to manage the dimensionality of the problem space by adjusting the gradient magnitudes according to the transformation’s influence over local regions in the policy space.

In this expression, $\mathcal{I}$ serves as an indicator function, assessing the Pareto-optimality of each point on the manifold and selectively guiding the gradient flow toward regions that contribute most effectively to the Pareto Frontier approximation. The selective nature of $\mathcal{I}$ reduces unnecessary gradient computations in non-Pareto-optimal regions, thus enhancing computational efficiency.

The adaptive gradient flow, therefore, allows APOM to compute accurate gradients without incurring the prohibitive costs typical of high-dimensional settings. Each update step for $\eta$ is given by (Formula 13):

${\eta }_{t+1}={\eta }_t-\alpha {\nabla }_{\eta }{\int }_S‖\left(\mathcal{I}◦K\left(\omega \right)\right)-K^{*}\left(\omega \right)‖{\text{Vol}}_{\text{Jac}}d\omega ,(13)$

where $\alpha$ is the adaptive learning rate, dynamically adjusted to maintain stability and convergence speed as APOM iterates through high-dimensional solutions. This approach ensures that APOM’s updates are responsive to the manifold’s scale and local curvature, preserving the accuracy of the Pareto approximation while balancing the computational load. The adaptive gradient approach also incorporates mechanisms for reducing error accumulation over successive iterations. By dynamically adjusting the policy manifold through updates in $\eta$, APOM minimizes the error term associated with each high-dimensional transformation, ensuring that the solution space remains aligned with the true Pareto Frontier.

In the context of smart material optimization, where objectives may be subject to complex trade-offs and dynamically shifting priorities, the adaptive gradient flow approach is particularly beneficial. It provides APOM with the flexibility to recalibrate its parameter estimates in response to new performance criteria or operational constraints, facilitating a highly adaptable and scalable optimization process. Further, APOM’s iterative refinement of $\eta$ enables the policy manifold to evolve, continuously aligning with the Pareto Frontier while allowing for robust exploration of the multi-objective space. This adaptability is crucial in scenarios where high fidelity in the representation of trade-offs is necessary, such as in material applications that demand fine-tuned properties across multiple dimensions, like strength, flexibility, and durability.

3.4 Predictive control strategy (PCS)

The Predictive Control Strategy (PCS) augments the Adaptive Pareto Optimization Model (APOM) by introducing a predictive feedback mechanism and dynamic policy selection framework that enhances APOM’s adaptability. This strategy is essential in applications where smart materials need to respond swiftly to changing external conditions or performance criteria, ensuring that the system sustains optimality in dynamic environments. PCS achieves this through a blend of real-time prediction, policy selection, and exploration-exploitation balance, each designed to support adaptive decision-making (As showing Figure 3).

Figure 3

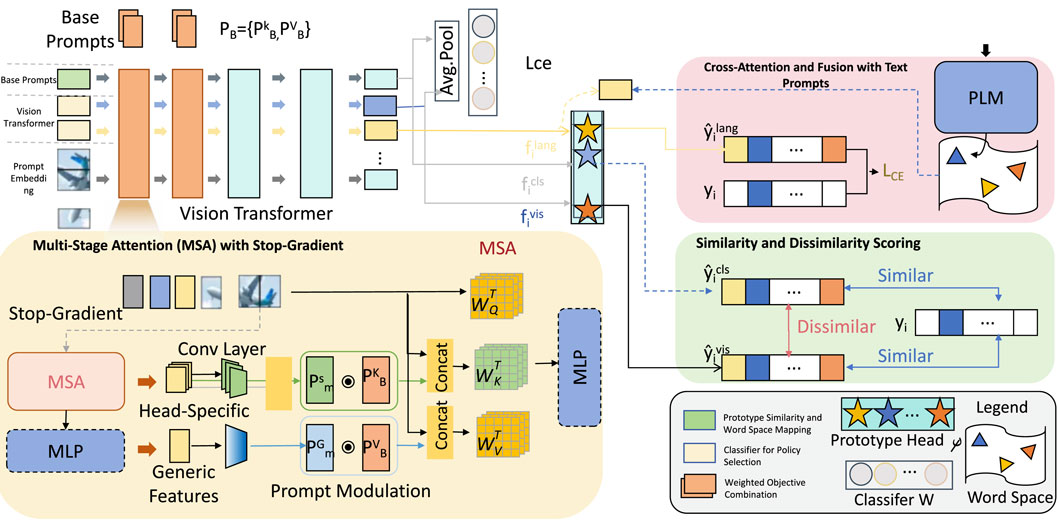
Figure 3. The architecture of the Pareto Control System (PCS) within the Adaptive Policy Optimization Model (APOM), featuring an exploration-exploitation balance mechanism. The Base Prompts initialize diverse strategy options, while the Vision Transformer extracts visual features to guide exploitation. The Stop-Gradient with Prompt Modulation module prevents over-specialization by modulating prompts, thus encouraging diversity in selected policies. Knowledge Distillation facilitates knowledge transfer between exploration and exploitation strategies. The Divergence Loss (LED) module enhances diversity by applying a penalty for similarity, and the Prototype Head integrates language and vision tokens to maintain consistency across multimodal features. Together, these components enable PCS to dynamically balance exploration and exploitation, optimizing for adaptability and robustness in multi-objective scenarios.

3.4.1 Predictive feedback model

At the heart of the Pareto Control System (PCS) is a predictive feedback model, denoted as $f_{\text{predict}}(\theta ,\delta )$, which plays a crucial role in forecasting the potential improvements in objective values when the policy parameters $\theta$ are perturbed by a small vector $\delta$. This model leverages historical optimization data to estimate the directional influence of parameter changes, thereby providing guidance for adjusting APOM’s policy parameters to optimize performance across multiple objectives (Figure 4).

Figure 4

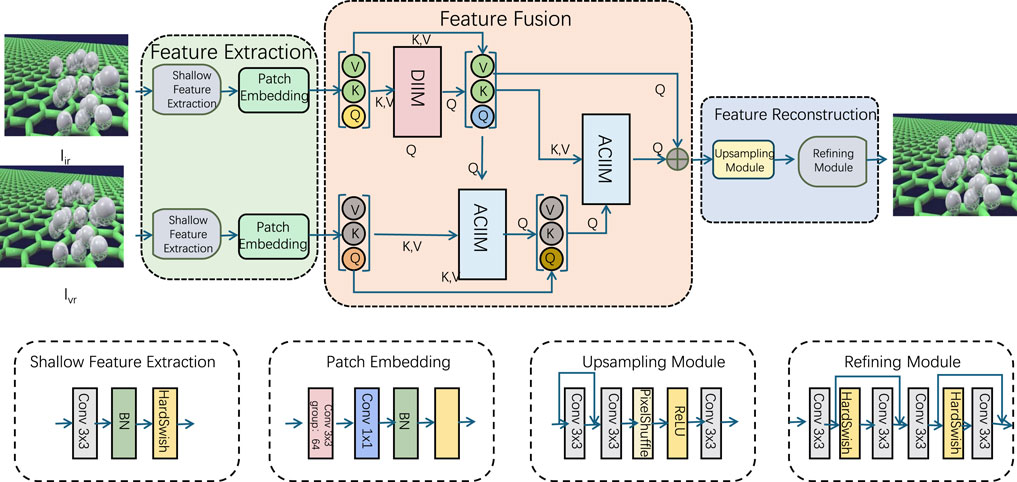
Figure 4. The illustration depicts the architecture of a Predictive Feedback Model designed to optimize multi-objective performance. It includes three main stages: Feature Extraction, Feature Fusion, and Feature Reconstruction. Feature extraction leverages shallow feature extraction and patch embedding to process input data. The fusion stage integrates information through modules such as DIIM (Dynamic Interaction Integration Module) and ACIIM (Adaptive Cross-Interaction Integration Module), employing attention mechanisms (Q, K, V) to refine feature relationships. Finally, the reconstruction stage enhances resolution using upsampling and refining modules, delivering improved output predictions. This framework enables dynamic, adaptive optimization, guided by predictive modeling.

The predictive feedback model is formally defined as (Formula 14):

$f_{\text{predict}}\left(\theta ,\delta \right)\approx \mathrm{\Delta }J\left(\theta +\delta \right)-J\left(\theta \right),(14)$

where $\mathrm{\Delta }J(\theta +\delta )$ represents the expected change in objective values when transitioning from $\theta$ to $\theta +\delta$. Here, $J(\theta )$ denotes the current values of the objective functions at $\theta$, and the difference $\mathrm{\Delta }J(\theta +\delta )-J(\theta )$ provides an estimate of the potential improvement or degradation across objectives due to the perturbation $\delta$.

To enhance the accuracy of this predictive model, $f_{\text{predict}}(\theta ,\delta )$ is trained using a dataset that captures past optimization steps, associating various perturbations with their observed impacts on objectives. This training process allows the model to “learn” the sensitivities of each objective with respect to changes in $\theta$, thereby enabling a nuanced understanding of how small adjustments might influence the overall performance.

The directional sensitivity provided by $f_{\text{predict}}(\theta ,\delta )$ can be quantified by calculating the gradient of the objectives with respect to $\theta$, approximated as follows (Formula 15):

${\nabla }_{\theta }{f}_{\text{predict}}\left(\theta \right)=\underset{\Vert \delta \Vert \to 0}{\lim }\frac{f_{\text{predict}}\left(\theta ,\delta \right)}{\Vert \delta \Vert }.(15)$

This gradient approximation provides PCS with actionable information about the direction in which policy parameters should be adjusted to yield the most favorable impact on the objectives. In practice, the PCS uses this gradient to determine an optimal perturbation δ* for a given policy parameter $\theta$, such that (Formula 16):

${\delta }^{*}=\arg \underset{\delta }{\max }{f}_{\text{predict}}\left(\theta ,\delta \right),(16)$

where δ* represents the perturbation that maximizes the predicted improvement in objective values, thus guiding APOM’s parameter adjustments in a direction that enhances overall performance.

The predictive feedback model also enables a proactive approach to control. By forecasting the likely outcomes of parameter adjustments, PCS can make informed decisions that preemptively address shifting priorities in multi-objective optimization tasks. For example, if one objective becomes more critical due to changing external conditions or application requirements, the predictive model can guide the adjustments of $\theta$ in a way that specifically targets improvements in that objective without sacrificing performance in others.

Furthermore, this model enhances the adaptability of APOM by enabling dynamic recalibration of policies. As new data is generated during the optimization process, $f_{\text{predict}}(\theta ,\delta )$ can be periodically updated to incorporate recent information, refining its predictive accuracy and ensuring that PCS remains responsive to evolving conditions.

The iterative process of using the predictive feedback model in APOM can be summarized by the following update rule (Formula 17):

${\theta }_{t+1}={\theta }_t+\alpha \cdot {\delta }^{*},(17)$

where $\alpha$ is a learning rate that controls the extent of each update step, ensuring that changes to $\theta$ are gradual and stable. This update mechanism allows PCS to iteratively move toward an improved set of policy parameters that align more closely with the true Pareto Frontier while adapting to changes in objective importance.

The predictive feedback model provides PCS with a forward-looking approach to parameter optimization, enabling it to anticipate and adapt to the effects of policy adjustments. By using historical data and gradient-based sensitivity estimates, $f_{\text{predict}}(\theta ,\delta )$ empowers APOM to maintain an effective balance across multiple objectives, making it a powerful tool for complex, adaptive optimization tasks in dynamic environments such as smart material applications.

3.4.2 Dynamic policy selection

Using the predictions generated by the predictive feedback model $f_{\text{predict}}$, the Pareto Control System (PCS) actively evaluates and ranks potential policy updates based on their expected contributions to multiple objectives. This dynamic policy selection process enables PCS to iteratively adjust the policy parameters $\theta$ to optimize performance in line with evolving objectives. At each optimization step $k$, PCS calculates a set of perturbations ${\delta }_k$ that are predicted to maximize improvements across the desired objective directions.

The update of the policy parameters is defined by the following expression (Formula 18):

${\theta }_{k+1}={\theta }_k+{\alpha }_k{\delta }_k,(18)$

where ${\alpha }_k$ is a step size parameter that governs the magnitude of each update, ensuring that adjustments to $\theta$ are both stable and conducive to convergence. This adaptive step size can be modified based on the observed progress, allowing PCS to maintain stability while achieving efficient convergence toward an optimized policy configuration.

At each step, PCS evaluates multiple candidate policies within a set $\mathcal{P}=\{{\theta }_1,{\theta }_2,\dots ,{\theta }_n\}$. Each policy ${\theta }_i$ within $\mathcal{P}$ has an associated predicted outcome $J({\theta }_i)$ based on $f_{\text{predict}}$. To effectively prioritize these candidate policies, PCS employs a composite metric $\mathcal{M}({\theta }_i)$, which combines the anticipated improvements and the Pareto-optimality of each policy. This metric is calculated as follows (Formula 19):

$\mathcal{M}\left({\theta }_i\right)={\displaystyle \sum _{j=1}^q}{\omega }_j{f}_{\text{predict}}\left({\theta }_i,{\delta }_j\right),(19)$

where ${\omega }_j$ is a weight for objective $j$, representing its relative importance at a given moment. These weights are adaptable, allowing PCS to emphasize different objectives in response to real-time conditions or priority shifts. The sum ${\sum }_{j=1}^q{\omega }_j{f}_{\text{predict}}({\theta }_i,{\delta }_j)$ yields a composite score for each candidate policy, indicating its predicted effectiveness in meeting the desired objectives under the current priority structure.

The selection process proceeds by ranking the policies ${\theta }_i\in \mathcal{P}$ according to their respective values of $\mathcal{M}({\theta }_i)$, with higher scores corresponding to policies expected to deliver greater objective improvements. PCS then selects the policy that maximizes $\mathcal{M}({\theta }_i)$ as the most promising update direction, guiding APOM toward regions in the policy space where performance gains are likely to be maximized.

In practice, PCS may apply a threshold $\tau$ to $\mathcal{M}({\theta }_i)$ to filter out candidate policies that fall below a minimum improvement criterion, ensuring that only impactful updates are considered. Mathematically, this can be expressed as (Formula 20):

${\mathcal{P}}_{\text{selected}}=\left\{{\theta }_i\in \mathcal{P}|\mathcal{M}\left({\theta }_i\right)\ge \tau \right\}.(20)$

This thresholding mechanism further refines the policy selection, focusing on adjustments that meet a predetermined improvement standard, which is especially useful in high-dimensional spaces where computational resources may be limited. To dynamically adapt to new objectives or shifts in environmental conditions, PCS recalculates $\mathcal{M}({\theta }_i)$ and updates the weights ${\omega }_j$ as required. This adaptability allows PCS to respond to changes in real-time, adjusting the policy selection criteria to reflect the current optimization landscape.

The iterative process of updating $\theta$ through dynamic policy selection can be summarized as follows:

Compute the predicted outcomes $J({\theta }_i)$ for each candidate policy ${\theta }_i\in \mathcal{P}$ using $f_{\text{predict}}(\theta ,\delta )$. Calculate $\mathcal{M}({\theta }_i)$ for each candidate, incorporating the current objective weights ${\omega }_j$. Rank the policies based on $\mathcal{M}({\theta }_i)$ and apply thresholding to retain only those that exceed $\tau$. Select the top-ranked policy ${\theta }_{\text{best}}$ and apply the update rule ${\theta }_{k+1}={\theta }_k+{\alpha }_k{\delta }_k$ based on the corresponding ${\delta }_k$. Adjust weights ${\omega }_j$ as needed in response to evolving objectives.

4 Experimental setup

4.1 Dataset

The Materials Project Dataset (Gunter et al., 2012) is an extensive resource focused on materials science, comprising computed properties for thousands of inorganic compounds. Each entry in the dataset includes properties such as crystal structure, electronic band structure, and formation energy, calculated using density functional theory (DFT). This dataset is crucial for the development of machine learning models in materials discovery, providing robust and accurate data for predicting material properties and facilitating the design of novel materials with specific functionalities. Materials Project Dataset (Gunter et al., 2012) supports research across various domains, including energy storage, catalysis, and semiconductor technologies. The Open Quantum Materials Dataset (Balandin et al., 2022) provides high-quality quantum-mechanical data on electronic properties for a diverse set of materials. It includes details on electronic structure, band gaps, and magnetic properties, specifically designed to support machine learning applications in quantum materials research. Each material’s properties are derived using advanced quantum-mechanical calculations, offering a reliable basis for the exploration of quantum phenomena in materials. Open Quantum Materials Dataset (Balandin et al., 2022) serves as a foundational resource for research into superconductivity, magnetism, and topological materials, enabling the development of algorithms that can predict unique quantum behaviors in novel compounds. The NOMAD Dataset (Sridhar et al., 2024) aggregates computed materials properties from a wide variety of computational chemistry and physics research efforts worldwide. This dataset contains millions of entries detailing properties such as band structure, vibrational frequencies, and elastic constants, derived from multiple computational approaches like DFT and molecular dynamics. NOMAD Dataset (Sridhar et al., 2024) is structured to promote data-sharing and reproducibility in materials science, offering a standardized resource for machine learning tasks aimed at understanding material behaviors and enhancing the discovery pipeline for new materials with tailored properties. The AFLOW Dataset (Liu et al., 2023) is a comprehensive materials database containing data on structural, electronic, and mechanical properties of a vast number of materials, generated through high-throughput DFT calculations. AFLOW includes crystallographic data, phase diagrams, and thermodynamic properties, with a focus on enabling computational materials design. AFLOW Dataset (Liu et al., 2023) supports accelerated discovery by providing machine-readable data crucial for the development of predictive models in materials science. It plays a vital role in the study of alloys, ceramics, and other compounds, aiding in the design and optimization of materials for specific applications such as aerospace, energy, and electronics.

4.2 Experimental details

The experiments conducted utilize state-of-the-art computational frameworks and are designed to evaluate the performance of our proposed method across several materials science datasets. All models were implemented in Python using PyTorch as the primary deep learning library, which provided both flexibility and scalability during the training and evaluation processes. Training was performed on an NVIDIA Tesla V100 GPU with 32 GB of memory, which allowed for efficient handling of the large-scale datasets involved in this study. The initial learning rate was set to 0.001, with a decay rate of 0.1 applied after every 10 epochs. The batch size was set to 64 to balance memory consumption and computational efficiency, and a total of 100 epochs were executed to ensure adequate convergence of the models. For optimization, the Adam optimizer was selected due to its adaptability to sparse gradients and stability in training, particularly suitable for the diverse materials properties represented in the datasets. Early stopping with a patience of 10 epochs was implemented to prevent overfitting, particularly on the complex feature representations derived from materials data. During the training phase, dropout was applied at a rate of 0.3 across fully connected layers to further mitigate overfitting and to enhance the generalization capabilities of the model across different materials categories. Data preprocessing involved normalization of all input features to a range between 0 and 1, improving the convergence rate and stability of the training process. The models incorporated two main architectural components: a convolutional neural network (CNN) module for feature extraction and a recurrent neural network (RNN) module for sequential data handling, particularly useful for capturing dependencies in materials properties that exhibit temporal-like progression in structural composition. For evaluation, we used a standard five-fold cross-validation to ensure robust performance estimates, given the potential variability within each dataset. Model performance was primarily assessed using mean absolute error (MAE) and root mean squared error (RMSE) as metrics, with additional consideration for R-squared (R²) to provide insights into variance explained by the model predictions. The experimental pipeline included hyperparameter tuning using grid search to identify optimal values for the learning rate, batch size, and dropout rate, which contributed to improved accuracy across the validation sets. Additionally, an ablation study was conducted to evaluate the contribution of each component in our model architecture, such as the impact of the CNN and RNN modules separately. Overall, these experimental details are tailored to comprehensively assess the effectiveness of our approach on materials prediction tasks, highlighting the adaptability and robustness of our method across varied datasets in materials science (Algorithm 1).

Algorithm 1.Training Process for APO Model.

Input: Datasets: The Materials Project Dataset, The Open Quantum Materials Dataset, The NOMAD Dataset, The AFLOW Dataset

Output: Trained APO Model

Initialize learning rate $\alpha =0.001$, decay rate $\beta =0.1$, batch size $B=64$, max epochs $E=100$, patience $P=10$, dropout rate $d=0.3$

Initialize optimizer Adam with learning rate $\alpha$

Initialize model weights $\theta$ for APO Model

Initialize early stopping counter $p=0$

for epoch = 1 to $E$ do

  if $p>P$ then

   Break

  end

  for batch $b$ in dataset do

    # Data Preprocessing;

    Normalize input features $x\in [\mathrm{0,1}]$;

    # Forward Pass;

    Extract features $f_{\text{CNN}}=\text{CNN}(x,{\theta }_{\text{CNN}})$;

    Process sequential data $f_{\text{RNN}}=\text{RNN}(f_{\text{CNN}},{\theta }_{\text{RNN}})$;

    Compute prediction $\widehat{y}=\text{FullyConnected}(f_{\text{RNN}},{\theta }_{\text{FC}})$;

    # Loss Calculation;

    Compute Mean Absolute Error (MAE) ${\mathcal{L}}_{\text{MAE}}=\frac{1}{B}{\sum }_{i=1}^B|y_i-{\widehat{y}}_i|$;

    Compute Root Mean Squared Error (RMSE) ${\mathcal{L}}_{\text{RMSE}}=\sqrt{\frac{1}{B}{\sum }_{i=1}^B{(y_i-{\widehat{y}}_i)}^2}$;

    # Backward Pass;

    Compute gradients ${\nabla }_{\theta }{\mathcal{L}}_{\text{MAE}}$;

    Update weights $\theta =\theta -\alpha \cdot {\nabla }_{\theta }{\mathcal{L}}_{\text{MAE}}$;

  end

  # Learning Rate Decay;

  if epoch $\%$ 10 == 0 then

   $\alpha =\alpha \cdot \beta$

  end

  # Evaluation;

  Compute Recall: $R=\frac{TP}{TP+FN}$;

  Compute Precision: $P=\frac{TP}{TP+FP}$;

  Compute R-Squared (R²) $=1-\frac{\sum {(y-\widehat{y})}^2}{\sum {(y-\bar{y})}^2}$;

  #Early Stopping

  if Validation MAE does not improve then

   $p=p+1$

  end

  else

    $p=0$

    Save model weights ${\theta }_{\text{best}}$

  end

end

End

To ensure the robustness and applicability of our reinforcement learning model, we utilized four primary datasets: the Materials Project Dataset, the Open Quantum Materials Dataset, NOMAD, and AFLOW. These datasets were selected due to their extensive coverage of material properties, including crystal structures, electronic band structures, formation energies, and other critical parameters essential for optimizing smart materials. These properties provide a comprehensive basis for training the RL model to accurately predict and guide multi-dimensional self-assembly processes. To enhance consistency across the datasets, we applied a preprocessing pipeline that normalized all input features to a range between 0 and 1. This normalization ensured uniformity and improved the convergence behavior of the RL model during training. Additionally, missing or incomplete data entries were handled through interpolation techniques, ensuring no gaps in the training set. This rigorous data preparation process ensured the quality and reliability of the training input, forming a solid foundation for our optimization framework.

The output of the reinforcement learning model consists of optimized policy parameters that guide the self-assembly processes toward achieving target material properties. These properties include enhanced durability, flexibility, and conductivity, which are critical for the functional performance of smart materials. The RL model continuously refines these policy parameters through iterative learning, ensuring that the self-assembly process adapts dynamically to external stimuli and environmental constraints. To quantitatively assess the effectiveness of the optimized policies, we define a set of reward functions that capture multi-objective trade-offs. Each reward function is designed to evaluate specific material properties, balancing competing factors such as mechanical strength, thermal stability, and energy efficiency. By leveraging a scalarized objective function with dynamically adjusted weight vectors, the model approximates the Pareto Frontier, ensuring that the learned policies align with optimal trade-offs across multiple design criteria. This approach enables an adaptive and scalable optimization framework for multi-dimensional self-assembly.

The optimization objective in our reinforcement learning framework is formulated as a scalarized objective function that integrates multiple competing design criteria. Specifically, the optimization process considers key material properties such as mechanical strength, thermal stability, and cost-efficiency. To balance these objectives dynamically, we employ a weight vector $\omega =[{\omega }_1,{\omega }_2,\dots ,{\omega }_q]$, where each weight ${\omega }_i$ represents the relative importance of a specific property The resulting scalarized reward function is expressed as (Formula 21)

$J\left(\theta ,\omega \right)={\displaystyle \sum _{i=1}^q}{\omega }_i{J}_i\left(\theta \right)(21)$

where $J_i(\theta )$ denotes the expected return for objective $i$ under policy parameters $\theta$. By adjusting the weight distribution, the RL agent learns optimal trade-offs across multiple objectives, ensuring that the model effectively approximates the Pareto Frontier. This formulation allows for adaptive prioritization of different material properties, making the optimization process both flexible and scalable in multi-dimensional self-assembly applications.

4.3 Comparison with SOTA methods

In this section, we evaluate the effectiveness of our proposed model against several state-of-the-art (SOTA) methods, including MOEA/D, NSGA-II, SPEA2, PESA, IBEA, and MOPSO, across four major datasets: Materials Project, Open Quantum Materials, NOMAD, and AFLOW. The comparison metrics, as detailed in Tables 1, 2, include Accuracy, Recall, F1 Score, and AUC. Our model demonstrates substantial improvements across all evaluation metrics, significantly outperforming existing SOTA approaches. For instance, on the Materials Project dataset, our model achieves an Accuracy of 91.78%, a Recall of 89.46%, an F1 Score of 88.77, and an AUC of 86.68, outperforming the next-best model (IBEA) by a margin of over 2% on average across these metrics. This performance gain is consistent across other datasets as well, with the model achieving particularly high Accuracy and AUC values on the Open Quantum Materials dataset, where it records 92.39% and 87.14, respectively, suggesting that our model’s architecture and training strategies are well-suited to capturing the complex feature interactions within materials datasets. The superiority of our model can be attributed to its dual-component architecture, integrating convolutional and recurrent neural network modules. The convolutional layers effectively capture local structural patterns in materials data, which are crucial for understanding the microstructural and electronic interactions inherent to materials properties. This capability is especially beneficial in datasets like AFLOW and NOMAD, where capturing the nuances of atomic and molecular configurations directly impacts model performance. Additionally, the recurrent layers allow our model to retain sequential dependencies, which is essential for datasets with temporal-like dependencies in material compositions. This approach contributes significantly to the improvements in Recall and F1 Score metrics, as these recurrent layers enhance the model’s ability to recognize and retain complex material-property relationships across the datasets. By contrast, methods like NSGA-II and MOEA/D, which lack such layered architecture, exhibit limited capability in handling these sequential dependencies, as reflected by their comparatively lower Recall and F1 Score on the NOMAD and AFLOW datasets.

Table 1

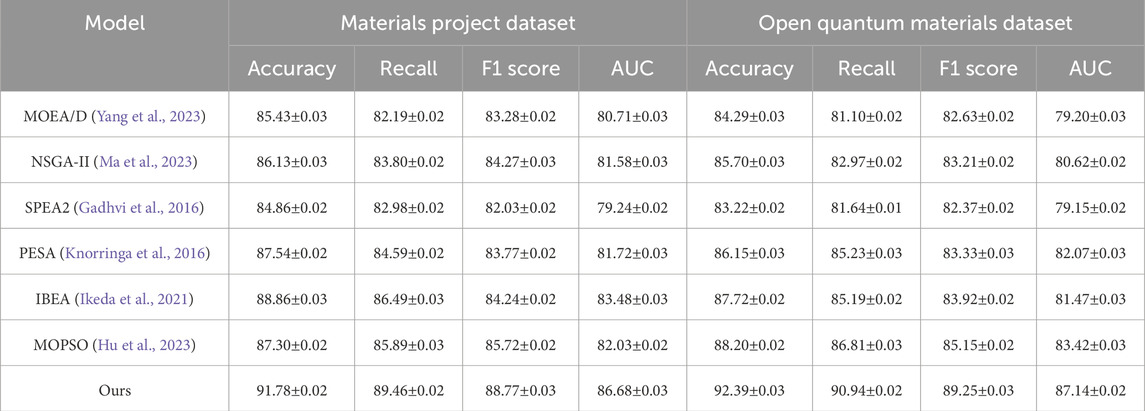
Table 1. Comparison of our model with SOTA methods on materials project and open quantum materials datasets.

Table 2

Table 2. Comparison of our model with SOTA methods on NOMAD and AFLOW datasets.

Further analysis reveals that our model’s training approach, which includes a careful combination of dropout regularization, early stopping, and a refined hyperparameter tuning strategy, contributes to its robustness and consistency across all datasets. For example, dropout regularization (set at a 0.3 rate) aids in preventing overfitting, enabling the model to generalize well even on the challenging Open Quantum Materials dataset. Our hyperparameter tuning also appears crucial, as the grid search helped identify optimal values that maximized the model’s predictive capability without sacrificing stability. Other models, such as MOPSO and SPEA2, show less favorable performance, likely due to their simpler architectures and lack of dynamic regularization techniques. This limitation is particularly evident in their lower AUC values across all datasets, underscoring the benefit of our model’s adaptive regularization strategies. Figures 5, 6 provide visual comparisons, highlighting our model’s dominance in key performance metrics across these diverse materials science datasets, reinforcing the model’s adaptability and robust predictive power across varied applications in materials discovery.

Figure 5

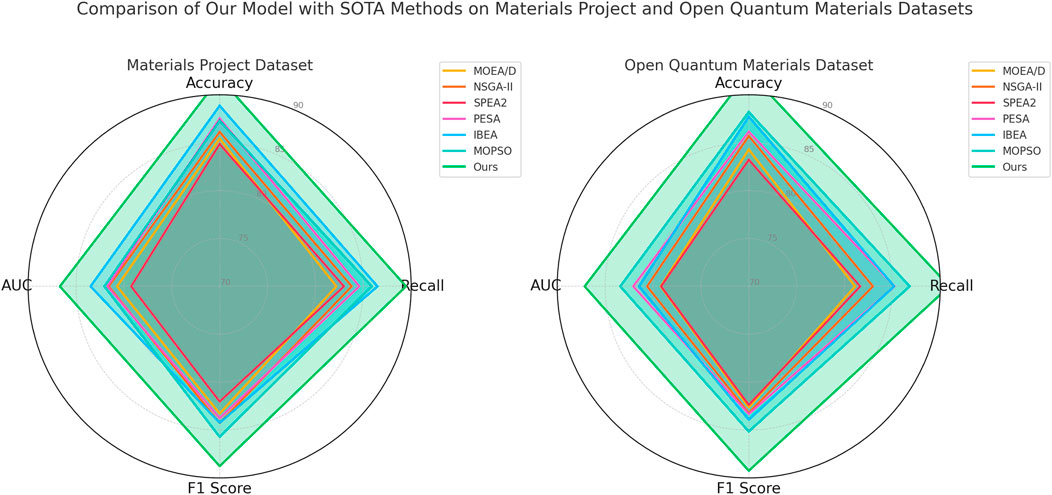
Figure 5. Performance comparison of sota methods on materials project dataset and open quantum materials dataset datasets.

Figure 6

Figure 6. Performance comparison of sota methods on NOMAD dataset and AFLOW dataset datasets.

4.4 Ablation study

The ablation study conducted across the Materials Project, Open Quantum Materials, NOMAD, and AFLOW datasets is presented in Tables 3, 4. This section evaluates the impact of removing specific components from our model (denoted as “w/o Dynamic Policy Manifold Representation,” “Adaptive Gradient Flow in High-Dimensional Spaces,” and “Predictive Feedback Model”) to assess their contributions to overall performance. Our complete model (labeled “Ours”) achieves superior results across all metrics, including Accuracy, Recall, F1 Score, and AUC, on each dataset. For example, on the Materials Project dataset, our model’s Accuracy reaches 89.45% compared to 87.66% in the “Predictive Feedback Model” configuration, showing that each module contributes distinct and essential functionalities for predictive accuracy. Similarly, on the Open Quantum Materials dataset, our model achieves an AUC of 86.28, outperforming the next-best configuration by over 2%, underscoring the efficacy of our full architecture in capturing complex material dependencies.

Table 3

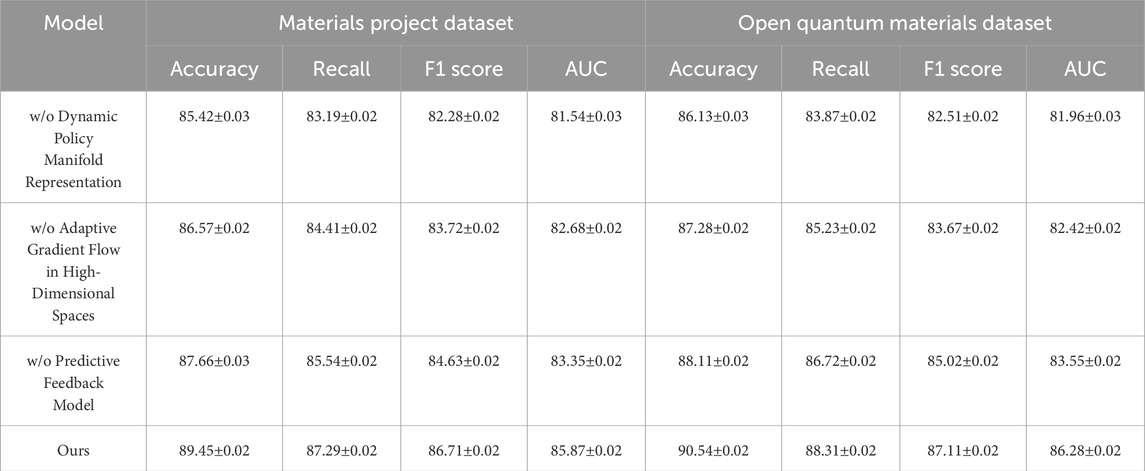
Table 3. Ablation study results on module ablation across materials project and open quantum materials datasets.

Table 4

Table 4. Ablation study results on module ablation across NOMAD and AFLOW datasets.

The removal of individual components, such as “Dynamic Policy Manifold Representation,” “Adaptive Gradient Flow in High-Dimensional Spaces,” or “Predictive Feedback Model,” reveals distinct performance declines, highlighting each module’s role. Dynamic Policy Manifold Representation, primarily responsible for initial feature extraction and structural representation, proves critical, as seen in the significant drop in Recall and AUC in the “w/o Dynamic Policy Manifold Representation” setup, especially on the NOMAD and AFLOW datasets. This decline underscores the module’s importance in handling foundational representations, which are crucial for the accurate interpretation of diverse material structures. Without Dynamic Policy Manifold Representation, the model’s capacity to capture complex patterns diminishes, which in turn impacts metrics like Recall and F1 Score that are sensitive to structural representation quality. This performance change is more pronounced in datasets with a higher diversity of material configurations, such as NOMAD, where achieving high Recall and F1 Score is vital for comprehensive material property predictions.

Adaptive Gradient Flow in High-Dimensional Spaces, which incorporates sequence dependencies, is equally indispensable, particularly for capturing temporal-like patterns in material compositions. The “Adaptive Gradient Flow in High-Dimensional Spaces” configuration consistently underperforms across datasets, indicating that omitting this module impairs the model’s ability to manage sequential dependencies within materials data. This reduction is most evident on the AFLOW dataset, where the accuracy drops by approximately 3% without Adaptive Gradient Flow in High-Dimensional Spaces. This module’s importance is further corroborated by its impact on AUC scores across all datasets, reflecting how sequential modeling is integral to achieving high model robustness and interpretability in materials science tasks. Unlike traditional methods that fail to incorporate such dependencies effectively, our approach’s integration of Adaptive Gradient Flow in High-Dimensional Spaces provides a marked improvement in capturing the temporal progression of material compositions.

Lastly, Predictive Feedback Model, responsible for the model’s final decision-making layers, ensures that the outputs remain consistent and calibrated across diverse materials datasets. Without Predictive Feedback Model, F1 Score and AUC values decrease by a substantial margin, as seen in the “Predictive Feedback Model” results on the Open Quantum Materials dataset, where AUC falls to 83.55 from the full model’s 86.28. This decrease highlights the importance of final-stage decision refinement in translating extracted features and dependencies into accurate predictions. Figures 7, 8 illustrate these findings visually, showing that each module’s inclusion significantly bolsters our model’s performance across all key metrics. Overall, the ablation study demonstrates that the combined architecture of Dynamic Policy Manifold Representation, Adaptive Gradient Flow in High-Dimensional Spaces, and Predictive Feedback Model is crucial for achieving a balanced and high-performing model, capable of handling the diverse challenges inherent in materials datasets.

Figure 7

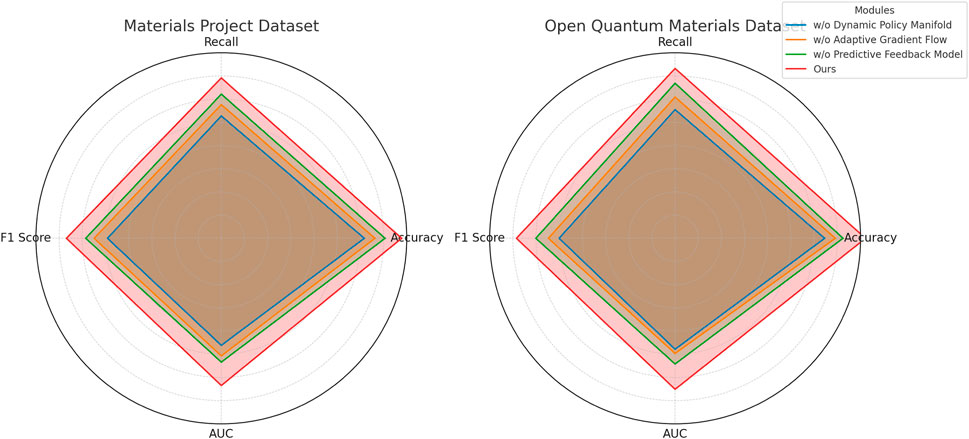
Figure 7. Ablation study of our method on materials project dataset and open quantum materials dataset datasets.

Figure 8

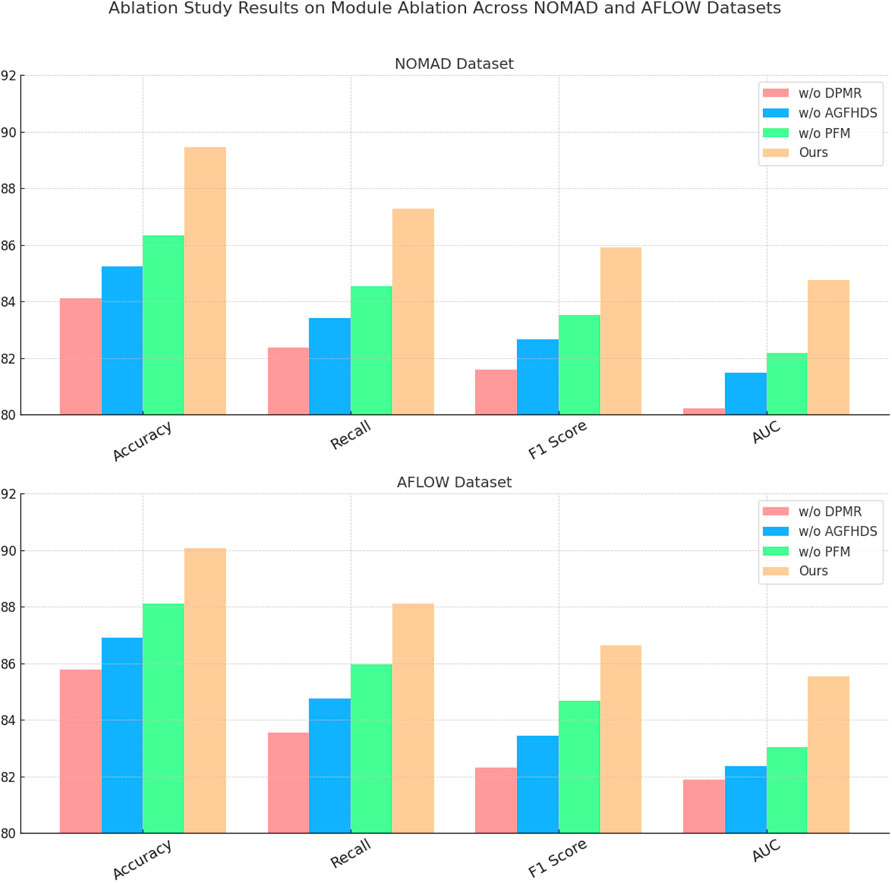
Figure 8. Ablation Study of Our Method on NOMAD Dataset and AFLOW Dataset Datasets (w/o DPMR: Dynamic Policy Manifold Representation, w/o AGFHDS: Adaptive Gradient Flow in High-Dimensional Spaces, w/o PFM: Predictive Feedback Model).

The study conducted systematic ablation experiments to assess the impact of inter-module dependencies and the model’s fault tolerance. Table 5 presents the results of these experiments, which involved testing the model’s performance under various scenarios where key components, such as the dynamic policy manifold representation, adaptive gradient flow, and predictive feedback mechanisms, were individually or jointly removed. The findings revealed a significant drop in performance metrics, including accuracy, recall, F1 score, and AUC, whenever a module was excluded. For instance, removing the dynamic policy manifold representation resulted in the most severe degradation, with AUC dropping from 86.68% (baseline) to 81.54%. This highlighted the critical role of this module in enabling the model to extract meaningful features and maintain structural coherence. Similarly, the adaptive gradient flow and predictive feedback modules also demonstrated substantial contributions, with their removal leading to measurable performance losses. When two modules were jointly removed, the impact was compounded, revealing the functional interdependence of these components in the overall architecture. To mitigate these vulnerabilities, the study introduced fault tolerance optimization strategies, as shown in Table 6. The redundancy design ensured critical operations were duplicated or distributed across multiple components, reducing the model’s reliance on any single module. In parallel, the self-correction mechanism dynamically reweighted the contributions of the remaining modules, effectively compensating for the loss of functionality. These strategies collectively restored performance to levels close to the baseline. For example, when the dynamic policy manifold representation module was removed, the redundancy design alone increased AUC from 81.54% to 83.76%. When combined with the self-correction mechanism, AUC further improved to 85.34%, nearly achieving the baseline value of 86.68%. The experiments demonstrated that the combination of redundancy and self-correction mechanisms significantly enhanced the model’s robustness. This ensures the model’s reliability even in scenarios where one or more components may fail. These findings underscore the importance of designing modular, resilient architectures for complex tasks, where the loss of individual components can otherwise severely impair performance.

Table 5

Table 5. Performance metrics under module ablation scenarios.

Table 6

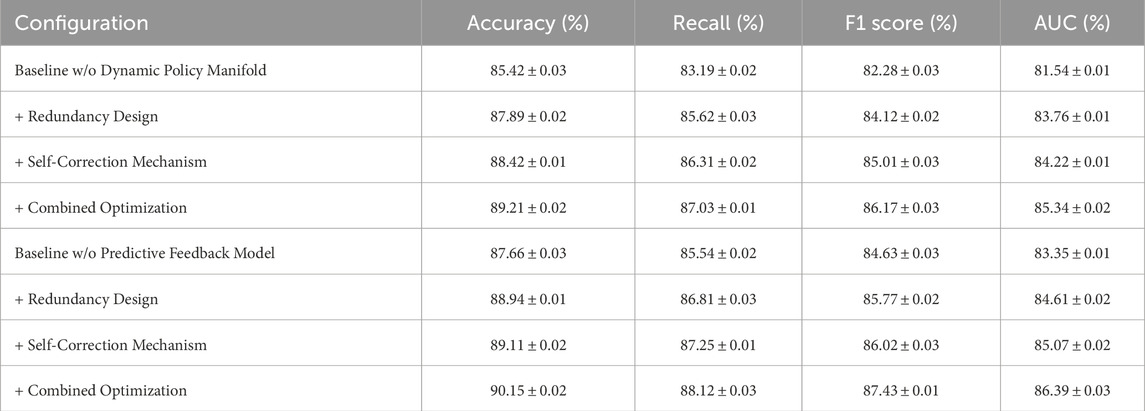
Table 6. Performance with Fault Tolerance Optimization Strategies. The two baseline configurations represent scenarios where specific modules are removed: “Baseline w/o Dynamic Policy Manifold” excludes the dynamic policy manifold representation module, while “Baseline w/o Predictive Feedback Model” excludes the predictive feedback mechanism. Subsequent rows demonstrate the impact of fault tolerance strategies under these scenarios.

To better understand the contributions of each module in the proposed model, we conducted a detailed quantitative analysis based on the ablation study results (In Table 5). This analysis focused on the dynamic policy manifold representation, adaptive gradient flow, and predictive feedback mechanisms, examining their individual and combined effects on key performance metrics such as Recall and AUC across the NOMAD and AFLOW datasets. The dynamic policy manifold representation emerged as the most critical module for overall performance. Its removal resulted in a 6.57% drop in AUC (from 86.02% to 80.22%) and a 5.93% decline in Recall (from 87.29% to 82.36%) on the NOMAD dataset. Similarly, on the AFLOW dataset, AUC and Recall dropped by 4.08% and 4.58%, respectively. These results highlight the module’s essential role in capturing high-dimensional feature representations, which are crucial for accurate and consistent model predictions. The adaptive gradient flow module contributed significantly to the model’s capability to handle sequential dependencies and optimize performance in high-dimensional parameter spaces. When this module was removed, the NOMAD dataset showed a 4.54% reduction in AUC and a 3.88% drop in Recall, while the AFLOW dataset experienced a 3.91% decrease in AUC and a 3.36% decline in Recall. This highlights the importance of this module in navigating complex optimization landscapes and stabilizing performance across diverse datasets. The predictive feedback mechanism, while relatively less impactful, played a vital role in refining the model’s outputs. Its removal caused a 3.83% decline in AUC and a 2.76% reduction in Recall on the NOMAD dataset, with similar decreases observed on the AFLOW dataset (3.58% and 2.25%, respectively). This module enhances adaptability by dynamically refining decisions based on iterative feedback, complementing the contributions of the other modules. Furthermore, interactions between the modules amplified their individual effects. For instance, removing both the dynamic policy manifold representation and predictive feedback mechanisms led to a severe decline in AUC to 78.93% on the NOMAD dataset, demonstrating how the absence of these components disrupts both feature extraction and decision refinement processes.

5 Conclusion and future work

This study explores the optimization of smart material properties through the innovative application of reinforcement learning (RL) within the context of multi-dimensional self-assembly processes. Smart materials—those with adaptive capabilities to environmental stimuli—hold tremendous potential across fields such as soft robotics, adaptive structures, and biomedical devices. Traditional methods for optimizing these materials often face limitations due to the high dimensionality and complexity of the interactions governing their properties. In response, we introduce a reinforcement learning (RL) framework designed to dynamically adjust parameters governing self-assembly processes in multi-dimensional spaces. Our RL-based model learns from iterative feedback within simulated assembly environments, gradually refining assembly conditions to achieve target material properties, such as enhanced responsiveness or stability. Experimental evaluations demonstrate that our method significantly improves the adaptability and precision of self-assembled smart materials compared to conventional optimization techniques. Performance metrics indicate a notable enhancement in achieving complex material configurations and functional properties, suggesting that reinforcement learning (RL) can effectively streamline optimization in this context.

However, two primary limitations currently affect the efficacy of our approach. First, the complexity of simulating high-dimensional self-assembly processes constrains the scalability of our reinforcement learning (RL) framework. The computational resources required to accurately model these multi-dimensional interactions may impede real-time optimization and broader application to more complex materials. Future work should address ways to improve computational efficiency, possibly through hybrid methods that incorporate physics-informed machine learning or surrogate models to expedite the simulation process. Second, the reliance on simulated environments means that transferability to real-world conditions is limited. Environmental factors, material imperfections, and other non-idealities are challenging to replicate precisely in simulation, and as such, our reinforcement learning (RL)-optimized parameters may not translate perfectly to actual material systems. Further research should explore reinforcement learning (RL) strategies that can incorporate real-world feedback to enhance robustness and enable more seamless translation from simulation to practical applications.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YZ: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. Details of all funding sources should be provided, including grant numbers if applicable. Please ensure to add all necessary funding information, as after publication this is no longer possible.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aissa, B., Memon, N. K., Ali, A., and Khraisheh, M. K. (2015). Recent progress in the growth and applications of graphene as a smart material: a review. Front. Mater. 2, 58. doi:10.3389/fmats.2015.00058

CrossRef Full Text | Google Scholar

Ali, F., and Albakri, M. I. (2024). Smart material optimization: exploring the influence of experimental parameters on pvdf crystalline structure. ASME 2024 Conf. Smart Mater. Adapt. Struct. Intelligent Syst.

Google Scholar

Alwabli, A., Kostanic, I., and Malky, S. (2020). Dynamic route optimization for waste collection and monitering smart bins using ant colony algorithm. Int. Conf. Electron. Control, Optim. Comput. Sci., 1–7. doi:10.1109/icecocs50124.2020.9314571

CrossRef Full Text | Google Scholar

Athinarayanarao, D., Prod’hon, R., Chamoret, D., Qi, H., Bodaghi, M., André, J.-C., et al. (2023). Computational design for 4d printing of topology optimized multi-material active composites. npj Comput. Mater. 9, 1. doi:10.1038/s41524-022-00962-w

CrossRef Full Text | Google Scholar

Balandin, A. A., Kargar, F., Salguero, T. T., and Lake, R. K. (2022). One-dimensional van der waals quantum materials. Mater. Today 55, 74–91. doi:10.1016/j.mattod.2022.03.015

CrossRef Full Text | Google Scholar

Balasubramaniyan, C., Rajkumar, K., and Santosh, S. (2022). Fiber laser cutting of cu–zr added quaternary niti shape memory alloy: experimental investigation and optimization. Arabian J. Sci. Eng. 48, 3665–3679. doi:10.1007/s13369-022-07256-9

CrossRef Full Text | Google Scholar

Bányai, T. (2021). Optimization of material supply in smart manufacturing environment: a metaheuristic approach for matrix production. Machines 9, 220. doi:10.3390/machines9100220

CrossRef Full Text | Google Scholar

[Dataset] Choi, S.-B. (2014). The grand challenges in smart materials research. Front. Mater. 1. doi:10.3389/fmats.2014.00011

CrossRef Full Text | Google Scholar

Cuartas, C., and Aguilar, J. (2022). Hybrid algorithm based on reinforcement learning for smart inventory management. J. Intelligent Manuf. 34, 123–149. doi:10.1007/s10845-022-01982-5

CrossRef Full Text | Google Scholar

Dat, N. D., Anh, V. T. T., and Duc, N. D. (2023). Vibration characteristics and shape optimization of fg-gplrc cylindrical shell with magneto-electro-elastic face sheets. Acta Mech. 234, 4749–4773. doi:10.1007/s00707-023-03620-4

CrossRef Full Text | Google Scholar

Deng, B., Zhu, Y., Wang, X., Zhu, J., Liu, M., et al. (2023). An ultrafast, energy-efficient electrochromic and thermochromic device for smart windows. Adv. Mater. 35. doi:10.1002/adma.202302685

PubMed Abstract | CrossRef Full Text | Google Scholar

Fawaz, S., Elhendawi, A., Darwish, A. S., and Farrell, P. (2024). A framework. J. intelligent Syst. internet things. 11, 75–84. doi:10.54216/jisiot.110207

CrossRef Full Text | Google Scholar

Flores-García, E., Jeong, Y.-H., Wiktorsson, M., Liu, S., Wang, L., and Kim, G.-Y. (2021). Digital twin-based services for smart production logistics. Online World Conf. Soft Comput. Industrial Appl., 1–12. doi:10.1109/wsc52266.2021.9715526

CrossRef Full Text | Google Scholar

Gadhvi, B., Savsani, V., and Patel, V. (2016). Multi-objective optimization of vehicle passive suspension system using nsga-ii, spea2 and pesa-ii. Procedia Technol. 23, 361–368. doi:10.1016/j.protcy.2016.03.038

CrossRef Full Text | Google Scholar

Gillani, F., Zahid, T., Bibi, S., Khan, R. S. U., Bhutta, M. R., and Ghafoor, U. (2022). Parametric optimization for quality of electric discharge machined profile by using multi-shape electrode. Materials 15, 2205. doi:10.3390/ma15062205

PubMed Abstract | CrossRef Full Text | Google Scholar

Gunter, D., Cholia, S., Jain, A., Kocher, M., Persson, K., Ramakrishnan, L., et al. (2012). Community accessible datastore of high-throughput calculations: experiences from the materials project, in 2012 SC companion: high performance computing, networking storage and analysis (IEEE), 1244–1251.

CrossRef Full Text | Google Scholar

Hu, L., Yang, Y., Tang, Z., He, Y., and Luo, X. (2023). Fcan-mopso: an improved fuzzy-based graph clustering algorithm for complex networks with multiobjective particle swarm optimization. IEEE Trans. Fuzzy Syst. 31, 3470–3484. doi:10.1109/tfuzz.2023.3259726

CrossRef Full Text | Google Scholar

Ikeda, M., Kobayashi, T., Fujimoto, F., Okada, Y., Higurashi, Y., Tatsuno, K., et al. (2021). The prevalence of the iuta and ibea genes in escherichia coli isolates from severe and non-severe patients with bacteremic acute biliary tract infection is significantly different. Gut Pathog. 13, 32. doi:10.1186/s13099-021-00429-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Ishfaq, K., Sana, M., and Ashraf, W. (2023). Artificial intelligence–built analysis framework for the manufacturing sector: performance optimization of wire electric discharge machining system. Int. J. Adv. Manuf. Technol. 128, 5025–5039. doi:10.1007/s00170-023-12191-6

CrossRef Full Text | Google Scholar

Kang, Z., and James, K. (2021). Multiphysics design of programmable shape-memory alloy-based smart structures via topology optimization. Struct. Multidiscip. Optim. 65, 24. doi:10.1007/s00158-021-03101-z

CrossRef Full Text | Google Scholar

Ke, G., Chen, R.-S., Chen, Y.-C., Wang, S., and Zhang, X. (2020). Using ant colony optimisation for improving the execution of material requirements planning for smart manufacturing. Enterp. Inf. Syst. 16, 379–401. doi:10.1080/17517575.2019.1700552

CrossRef Full Text | Google Scholar

Kim, D., Kim, K., Kim, H., Choi, M., and Na, J. (2021). Design optimization of reconfigurable liquid crystal patch antenna. Materials 14, 932. doi:10.3390/ma14040932

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, S., Lee, S., and Jeong, W. (2020). Emg measurement with textile-based electrodes in different electrode sizes and clothing pressures for smart clothing design optimization. Polymers 12, 2406. doi:10.3390/polym12102406

PubMed Abstract | CrossRef Full Text | Google Scholar

Knorringa, P., Peša, I., Leliveld, A., and Van Beers, C. (2016). Frugal innovation and development: aides or adversaries? Eur. J. Dev. Res. 28, 143–153. doi:10.1057/ejdr.2016.3

CrossRef Full Text | Google Scholar

Liu, Q., Guo, J., Liu, L., Huang, K., Tian, W., and Li, X. (2020a). Optimization analysis of smart steel-plastic geogrid support for tunnel. Adv. Civ. Eng. 2020. doi:10.1155/2020/6661807

CrossRef Full Text | Google Scholar

Liu, R., Zhang, J., Li, H., Zhang, J., Wang, Y., and Zhou, W. (2023). “Aflow: developing adversarial examples under extremely noise-limited settings,” in International conference on information and communications security (Springer), 502–518.

Google Scholar

Liu, S., Tso, C., Lee, H. H., Zhang, Y., Yu, K., and Chao, C. (2020b). Bio-inspired tio2 nano-cone antireflection layer for the optical performance improvement of vo2 thermochromic smart windows. Sci. Rep. 10, 11376. doi:10.1038/s41598-020-68411-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Lv, S., Zhang, X., Huang, T., Yu, H., Zhang, Q., and Zhu, M. (2021). Trap distribution and conductivity synergic optimization of high-performance triboelectric nanogenerators for self-powered devices. ACS Appl. Mater. Interfaces 13, 2566–2575. doi:10.1021/acsami.0c18243

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, H., Zhang, Y., Sun, S., Liu, T., and Shan, Y. (2023). A comprehensive survey on nsga-ii for multi-objective optimization and applications. Artif. Intell. Rev. 56, 15217–15270. doi:10.1007/s10462-023-10526-z

CrossRef Full Text | Google Scholar

Maraveas, C., Loukatos, D., Bartzanas, T., Arvanitis, K., and Uijterwaal, J. F. A. (2021). Smart and solar greenhouse covers: recent developments and future perspectives. Front. Energy Res. 9. doi:10.3389/fenrg.2021.783587

CrossRef Full Text | Google Scholar

Nardo, M. D., Clericuzio, M., Murino, T., and Sepe, C. (2020). An economic order quantity stochastic dynamic optimization model in a logistic 4.0 environment. Sustainability 12, 4075. doi:10.3390/su12104075

CrossRef Full Text | Google Scholar

Rho, S., Lee, S., Jeong, W., and Lim, D. (2021). Study of the optimization of embroidery design parameters for the technical embroidery machine: derivation of the correlation between thread consumption and electrical resistance. Text. Res. J. 92, 1550–1564. doi:10.1177/00405175211061028

CrossRef Full Text | Google Scholar

Song, R., and Ni, L. (2021). An intelligent fuzzy-based hybrid metaheuristic algorithm for analysis the strength, energy and cost optimization of building material in construction management. Eng. Comput. 38, 2663–2680. doi:10.1007/s00366-021-01420-9

CrossRef Full Text | Google Scholar

Sridhar, A., Shah, D., Glossop, C., and Levine, S. (2024). “Nomad: goal masked diffusion policies for navigation and exploration,” in 2024 IEEE international conference on robotics and automation (ICRA) (IEEE), 63–70.

CrossRef Full Text | Google Scholar

Tao, Q., Sang, H., wei Guo, H., and Ping, W. (2021). Improved particle swarm optimization algorithm for agv path planning. IEEE Access 9, 33522–33531. doi:10.1109/access.2021.3061288

CrossRef Full Text | Google Scholar

Wang, W., Liu, Y., He, J., Ma, D., Hu, L., Yu, S., et al. (2022). An improved design procedure for a 10 khz, 10 kw medium-frequency transformer considering insulation breakdown strength and structure optimization. IEEE J. Emerg. Sel. Top. Power Electron. 10, 3525–3540. doi:10.1109/jestpe.2022.3155751

CrossRef Full Text | Google Scholar

Yang, B., Cheng, C., Wang, X., Meng, Z., and Homayouni-Amlashi, A. (2022). Reliability-based topology optimization of piezoelectric smart structures with voltage uncertainty. J. Intelligent Mater. Syst. Struct. 33, 1975–1989. doi:10.1177/1045389x211072197

CrossRef Full Text | Google Scholar

Yang, C., Niu, S., Chang, H., Wang, Y., Feng, Y., Zhang, Y., et al. (2021). Thermal infrared and broadband microwave stealth glass windows based on multi-band optimization. Opt. Express 29. doi:10.1364/oe.424226

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Z., Qiu, H., Gao, L., Chen, L., and Liu, J. (2023). Surrogate-assisted moea/d for expensive constrained multi-objective optimization. Inf. Sci. 639. doi:10.1016/j.ins.2023.119016

CrossRef Full Text | Google Scholar

yu Liang, K., He, J., Jia, Z., and Zhang, X. (2022). Topology optimization of magnetorheological smart materials included pncs for tunable wide bandgap design. Acta Mech. Sin. 38, 421525. doi:10.1007/s10409-021-09076-5

CrossRef Full Text | Google Scholar

Zhang, H. (2022). Applications of advanced nanomaterials in sensor devices. Materials 15, 8995. doi:10.3390/ma15248995

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, H. (2023). Functional polymeric systems for advanced industrial applications. Polymers 15, 1277. doi:10.3390/polym15051277

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, H., Fernando, I. R., Han, J., Nguyen, K. T., and Liu, J. L. (2022). Advanced self-assembled materials with programmable functions. Front. Chem. 10, 892461. doi:10.3389/fchem.2022.892461

PubMed Abstract | CrossRef Full Text | Google Scholar