Prediction and prevention of concrete chloride penetration: machine learning and MICP techniques

The chloride migration coefficient (CMC) of concrete is crucial for evaluating its durability. This study develops ensemble models to predict the CMC of concrete, addressing the limitations of traditional, labor-intensive laboratory tests. We developed three ensemble models: an inverse variance-based model, an Artificial Neural Network (ANN)-based model, and a tree-based model using the random forest regression algorithm. These models were trained on a dataset comprising 843 concrete mix proportions from existing literature. Results indicate that ensemble models outperform single models such as ANN and Support Vector Regression (SVR) in predicting CMC, with the combined random forest and ANN model showing the highest accuracy. Sensitivity analysis using Shapley Additive Explanations (SHAP) reveals that the CMC is most influenced by the water-to-cement ratio and curing age. Additionally, we designed a graphical user interface (GUI) to facilitate the practical application of our models. This research offers a robust methodology for evaluating concrete durability and potential for extending the prediction to other concrete properties.

1 Introduction

Reinforced concrete structures in marine environments are prone to deteriorate due to the ingress of chloride ions. The intrusion of chloride ions leads to the corrosion of steel reinforcement, subsequently diminishing the durability and service life of marine concrete structures (Zuquan et al., 2018; Du, 2020; Zhang, 2023). In general, concrete exhibits high alkaline conditions, aid in creating a protective coating on the surface of steel rods, thereby slowing down the occurrence of corrosion. However, once the chloride concentration surrounding the reinforcement bar exceeds a specific threshold, depassivation (the breakdown of the protective layer) transpires, leading to corrosion and consequently diminishing the safety, functionality, and longevity of the structure (Sirivivatnanon et al., 2023). Therefore, it is crucial to accurately predict and evaluate the behavior of chloride ion penetration in concrete.

Traditional methods are usually based on experimental measurements to assess the chloride mitigation coefficients (CMC) in concrete. Several laboratory techniques have been developed to determine the CMC of concrete. According to ASTM C1556–11, and NT Build 443 (Junior, 2021), bulk diffusion trials are extensive experiments where concrete samples are subjected to a chloride solution for an extended period. However, these procedures are often impractical due to their labor-intensive and time-consuming nature. An accelerated approach for assessing the chloride diffusion coefficient is outlined in the Nordic standard NT Build 492 (Build, 1999), where chlorides infiltrate the concrete at high speeds under an applied electric field. This migration coefficient is not directly comparable to chloride diffusion coefficients obtained from other methods. While the NT Build 492 test yields fast results, it is typically conducted 28 days after concrete production to allow for curing and demands a skilled operator. Consequently, experimental evaluation of concrete diffusion coefficients for each project is challenging due to the substantial time and resources involved. Hence, it is crucial to develop models that calculate the CMC for specific concretes, considering all relevant parameters.

Considerable efforts have been devoted in recent years to developing phenomenological and physically-based models for predicting CMC, taking into account factors related to concrete mix composition. For example, Chidiac and Shafikhani (Chidiac et al., 2019) introduced a phenomenological model that incorporates the tortuosity factor, aggregate volume fraction, porosity, chloride diffusivity of cement paste, compressive strength, cement content, and supplementary cementitious material content to quantify effective chloride diffusion in concrete Riding et al., 2013. A concrete apparent diffusion coefficient estimation model was proposed, which includes various supplementary cement materials (SCM), with several relationships used to calculate the diffusion coefficient. Bogas & Gomes (Bogas et al., 2015). presented empirical expressions for determining the diffusion coefficient as a function of the water-to-cement ratio. The existing models often overlook key factors that define concrete microstructure. Their accuracy and applicability vary significantly across different scenarios due to reliance on various assumptions and experimental databases. The increasing use of supplementary cementitious materials (SCMs) and chemical admixtures further limits their effectiveness in predicting diffusion coefficients reliably. Therefore, it is crucial to develop methods that account for all governing parameters.

Creating an advanced CMC prediction model that considers all influential parameters is challenging. Concrete permeability depends on numerous factors that are difficult to mathematically represent without making several assumptions. To address these challenges, developing a CMC prediction model using state-of-the-art machine learning algorithms could be more effective. Machine learning algorithms excel at solving complex problems involving numerous variables without making assumptions. In recent years, in many aspects of materials science, machine learning has made significant progress., including the prediction of the performance of materials, the design of new materials, etc. However, few studies are found on prediction of CMC of concrete considering various influential factors such as supplementary cementitious materials and chemical admixtures, etc (Pallapothu et al., 2023; Qian and Du, 2023).

In this study, we propose machine learning approaches for predicting the CMC of concrete. These machine learning models are trained using a large amount of concrete CMC data from published literature, including information on concrete mix ratio, age, and environmental conditions. Compared to the traditional physical model-based approach, our method has higher flexibility and generalization ability, and can better adapt to the complex behavior of chloride ion penetration in concrete under different conditions.

2 Data description

2.1 Data collection

CMC of concrete is an indicator to assess its ability to resist chloride ion attack in chloride salt environments, which is an important cause of corrosion of reinforcements and deterioration of durability of concrete structures. Concrete is a porous, non-homogeneous composite material into which chloride ions enter mainly through hydrostatic pressure, capillary adsorption and free diffusion (Audenaert et al., 2010; Elfmarkova et al., 2015; Taffese et al., 2022; Pontes et al., 2023). Hydrostatic pressure is usually found in environments where there is a water pressure difference, such as the deep sea, following Darcy’s law. Capillary adsorption, on the other hand, occurs when the internal pores of the concrete are not saturated and chloride ions enter the concrete through the capillary voids. Free diffusion is usually driven by a concentration gradient and can be categorized as either steady state or unsteady state. Under steady state diffusion, the concentration distribution is independent of time and conforms to Fick’s first law; whereas, in practical engineering, the chloride ion diffusion is more affected by time and the concentration varies with time, which conforms to the unsteady state diffusion process of Fick’s second law.

There are many factors affecting chloride ion diffusion in concrete, the most important of which are water cement ratio, sand rate, mineral admixture, admixtures, age of curing and experimental age. The key input variables include the water-to-binder ratio (W/B), which is the ratio of the weight of water to the weight of binder in the concrete mix and significantly affects porosity and permeability. Cement age (CM-Age) refers to the age of the cementitious material in days since mixing, impacting the hydration process and reducing permeability over time. Water content (W), measured in kilograms per cubic meter, affects workability and hydration, influencing final porosity and permeability. Coarse aggregate content (Ca), also measured in kilograms per cubic meter, affects the interfacial transition zone and overall permeability. Superplasticizer (SP) is a chemical admixture that enhances workability without increasing water content, reducing the water-to-cement ratio and decreasing porosity. Fly ash (FA) is a supplementary cementitious material that improves packing density and reduces permeability through pozzolanic reactions. Silica fume (SF) is another supplementary material that refines pore structure and enhances matrix density, significantly reducing permeability. Lastly, air-entraining agent (AEA) introduces microscopic air bubbles into the concrete, improving freeze-thaw durability but potentially increasing permeability if not used properly. These explanations provide a clear understanding of each variable’s role and impact on the predicted chloride migration coefficient of concrete. We hope these additions address the reviewer’s concerns and improve the manuscript’s clarity and readability.

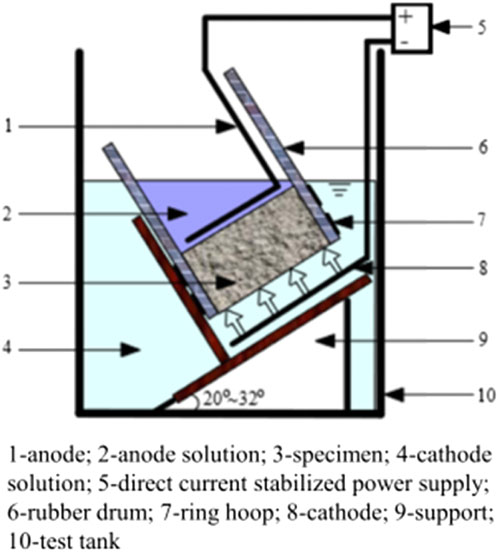
According to Nordic standard NT Build 492 (Sua-iam et al., 2024), the transport of negatively charged chloride ions towards the anode can be accelerated through the application of an electric field. Although this method does not fully replicate the actual process of chloride ion penetration in structures, it offers a rapid means to compare the chloride ion resistance between concrete specimens and standard specimens. The diffusion coefficient determined by this method is referred to as the “non-steady-state migration coefficient” or Dnssm. The RCM method is a non-steady-state electromigration-based testing technique (Tang et al., 2011). The specimen is placed between two solutions and an external electric field is applied. Under the influence of the external electric field, the chloride ions present in the cathode solution gradually diffuse into the interior of the sample. After a period of electromigration testing, the specimen is split along its axis, and a silver nitrate solution is sprayed onto the newly created section. The depth of chloride ion penetration within the specimen is measured using white silver chloride precipitates, from which the chloride ion diffusion coefficient in concrete is calculated. The test apparatus is shown in Figure 1. The specific calculation formula is shown in equation Eq. 1.

$D_{nssm}=2.872\times 10^{-6}\frac{Th\left(x_d-\alpha \sqrt{x_d}\right)}{t}(1)$

$D_{nssm}$: Chloride diffusion coefficients measured by the RCM method (m²/s); T: Average of initial and final anode electrolyte temperatures(K); h: Specimen height(m); x_d: depth of chloride ions in the specimen(m); t: test time(s); ɑ:feature variable-(3.338 × 10⁻³ $\surd Th$)

Figure 1

Figure 1. The test apparatus of RCM.

For the collection of data, source references were made according to the following criteria.

• Academic authority: literature was selected from well-known academic journals, conference proceedings or published by professional academic institutions, so that the collected experimental data have a high degree of academic credibility.

• Feasibility of the research methodology: the literature describes the design of the experiment, sample preparation, testing methods and other information as accurately as possible, so that other researchers can reproduce the results of the experiment.

• Data diversity and completeness: The type and scope of data covered in the literature should be taken into account, and literature with diverse data should be selected, which may include information on the physical properties of concrete, its chemical composition, and its engineering applications.

• Availability of data: The data provided in the literature can be used for further analysis and research. The data should be presented in suitable formats and units with detailed data descriptions and documentation so that other researchers can effectively use and understand the data.

• Updatability of data: Priority is given to the most recent data sources, especially literature published within the last few years, to reflect the latest progress and trends in the current field of concrete research, so that the machine learning model can be more adapted to the current situation and the new concrete model in the longer term future.

Ultimately this study has collected a comprehensive data set from peer-reviewed papers included in reputed journals. The dataset contains 843 experiments (Hao-bo and Guo-zhi, 2004; Audenaert et al., 2010; Jain and Neithalath, 2011; Liu et al., 2011; Marks et al., 2012; Maes et al., 2013; Bogas et al., 2015; Elfmarkova et al., 2015; Liu and Zhang, 2015; Marks et al., 2015; Real et al., 2015; Ferreira et al., 2016; Park et al., 2016; Rajaie and Mahmoud, 2016; Van Noort et al., 2016; Choi et al., 2017; Liu et al., 2017; Naito et al., 2020; Shiu and Yang, 2020; Pontes et al., 2021; Sell Junior et al., 2021) that investigated the unsteady state migration coefficients (𝐷𝑛𝑠𝑠𝑚) of various types of concrete. The data were collected from articles published in international journals. The raw data stores information about the concrete mixture, including its flow and hardening characteristics. During data preprocessing, the data selected from the raw data were used to create four machine learning based models (Models I, II, III, and IV), which are presented in separate worksheets.

2.2 Data pre-processing

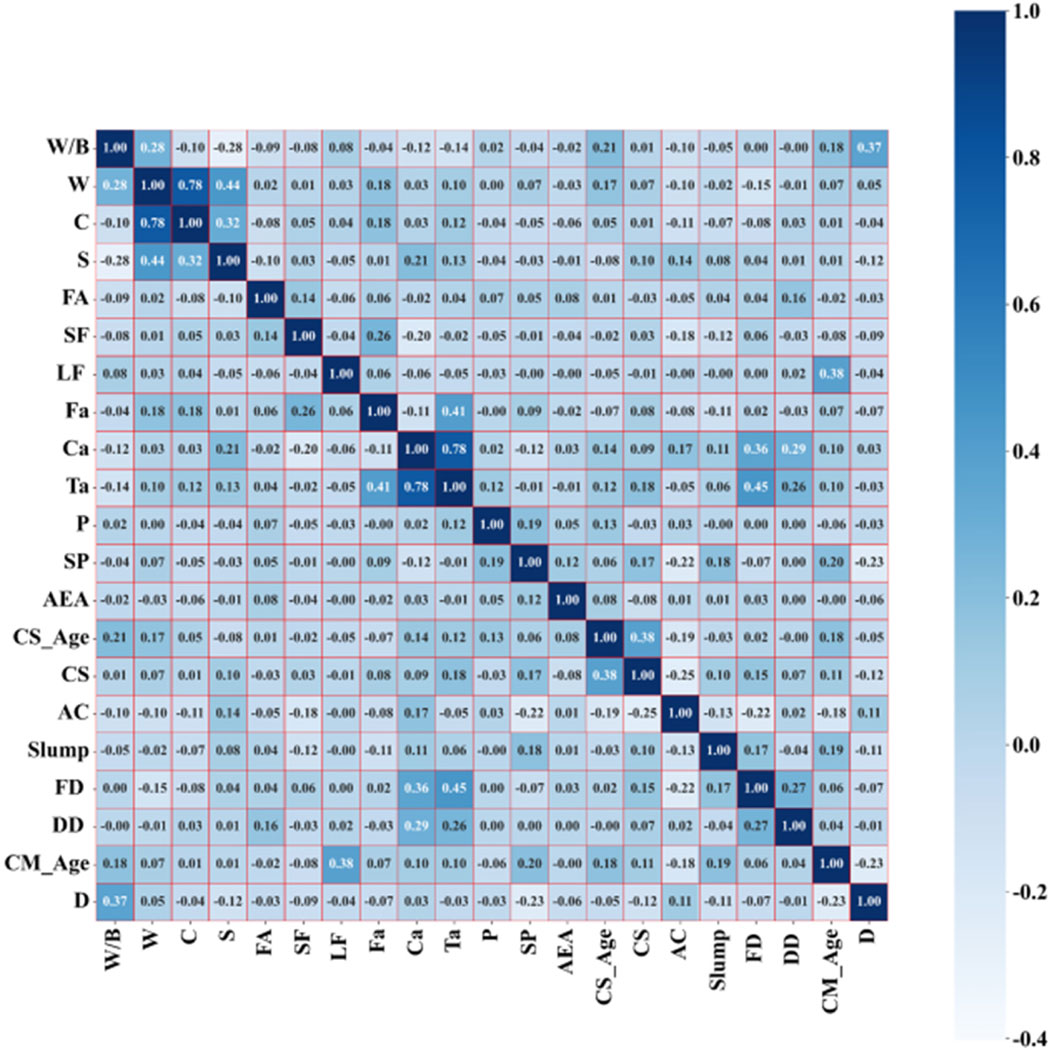
In machine learning modeling, the interdependence between the selected input parameters can lead to poor interpretation, resulting in the “multicollinearity problem.” It is stated that the correlation coefficient between every two parameters involved in the modeling should be less than 0.80 for the model to be reliable (Hall, 1999; Garg and Tai, 2013; Jebli et al., 2021; Chan et al., 2022). In this study, the correlation coefficients between two input parameters were calculated for all the selected input parameters and the results are shown in Figure 2 below. From the results, it can be seen that the correlation coefficients (both positive and negative) between different input parameters are significantly less than 0.80, which reduces the risk of multicollinearity problems and meets the modeling requirements. At the same time, it has been shown that the minimum ratio of database size to the number of input variables should be at least 3:5 when modeling using machine learning, and other performance criteria are satisfied so that the model built can be used as a general model. The relationship between database size and input variables involved in this study satisfies the requirements for building a generalized model.

Figure 2

Figure 2. Correlation matrix of input variables.

Preprocessing steps included normalization using min-max normalization to ensure equal contribution from each variable and handling missing values through mean imputation for variables with few missing entries and regression imputation for those with significant missing data. These steps ensured the dataset was clean, consistent, and suitable for training the machine learning models.

3 Methodology

3.1 Machine learning algorithms

This study compares both ensemble models and single models for prediction of CMC of concrete (Gandomi et al., 2012; Gandomi and Roke, 2015; Feng et al., 2021). Artificial Neural Networks (ANN) and Support Vector Regression (SVR) are single type models, and ensemble models includes Random Forest Regression (RFR), the inverse variance-based ensemble model (HEM-IV), and the Artificial Neural Network-based ensemble model (HEM-ANN). The description of the models are as follows.

3.1.1 ANN

Artificial Neural Networks (ANN) are mathematical models inspired by biological neural networks (Agatonovic-Kustrin et al., 2000; Krenker et al., 2011; Dongare et al., 2012; Eluyode et al., 2013; Abdolrasol et al., 2021). The network is made up of layers of interconnected nodes, which include an input layer, one or more hidden layers, and an output layer. Each connection between nodes is assigned a weight, denoted as $w_{ij}$, where i is the index of the input neuron and j is the index of the output neuron. The output $x_j$ of neuron j in a layer is determined by the weighted sum of the inputs $y_j$ passed through an activation function f (Eq. 2):

$y_j=f\left({\sum }_i{w}_{ij}{x}_j\right)(2)$

The activation function introduces non-linearity into the network, allowing it to learn complex relationships in the data. Training the network involves adjusting the weights to minimize a loss function, often using algorithms like backpropagation. ANNs are highly flexible and capable of capturing complex nonlinear relationships between input variables and the target variable. They can learn from large datasets and improve prediction accuracy through deep learning techniques.

3.1.2 SVR

Support Vector Regression (SVR) is a type of Support Vector Machine (SVM) that is used for regression tasks (Gunn, 1998; Basak et al., 2007; Awad et al., 2015). In contrast to traditional regression techniques that seek to minimize the discrepancy between predicted and observed values, SVR focuses on finding a function that deviates from the actual values by a value no greater than a specified margin (𝜖). The objective of SVR is to determine a hyperplane that best fits the data while maximizing the margin. This is achieved by solving the following optimization problem (Eq. 3):

${\mathit{min}}_{\mathit{w},b,\xi ,,{\xi }^{*}}\frac{1}{2}{‖\mathit{w}‖}^2+C{\sum }_{i=1}^n\left({\xi }_i+{\xi }_i^{*}\right)(3)$

subject to the constraints (Eq. 4):

$\left\{\begin{array}{l}{y}_i-\left(\mathit{w}·x_i+b\right)\le ϵ+{\xi }_i\\ \left(\mathit{w}·x_i+b\right)-y_i\le ϵ+{\xi }_i^{*}\\ \left({\xi }_i,{\xi }_i^{*}\ge 0\right.\end{array}\right.(4)$

The weight vector is denoted by w and the bias is represented by b, ${\xi }_i$ and ${\xi }_i^{*}$ are slack variables representing the degree of deviation from the margin, and C is a regularization parameter that determines the trade-off between the flatness of the regression function and the amount up to which deviations larger than 𝜖ϵ are tolerated. SVR is effective in high-dimensional spaces and is robust to outliers, making it a powerful tool for various regression applications.

3.1.3 RFR

Random Forest Regression (RFR) is a method of ensemble learning that involves using utilizing multiple decision trees can enhance predictive accuracy and mitigate overfitting. Each tree in the forest is built from a random subset of the training data, and its predictions the final output is generated by averaging the values. The random selection of both data samples and features for each tree ensures a diverse set of models, enhancing robustness. The prediction for a given input x in a random forest is given by (Eq. 5):

$\widehat{y}=\frac{1}{M}{\sum }_{m=1}^M{T}_m\left(\mathbf{x}\right)(5)$

where 𝑀 is the quantity of trees in the forest and T_m(x) is the prediction of the mth tree. The method can handle a large number of input variables and provides estimates of feature importance, making it a versatile and powerful tool for regression tasks across various domains.

3.1.4 HEM method

Ensemble learning, a technique combing ML algorithms to enhance predictive outcomes by bolstering stability and precision (Che et al., 2011; Yohannese et al., 2018; Rosellini et al., 2020; Saadaari et al., 2020), was employed in this investigation. Two distinct methods for amalgamating ML algorithms, HEM-IV and HEM-ANN, were utilized. RF, SVR, and ANN yield diverse prediction outcomes owing to their distinct algorithms, even when the same dataset and sampling technique are employed: Y1 (RF), Y2 (SVR), and Y3 (ANN). By combining Y1, Y2, and Y3 through a linear combination, HEM-IV derives the final prediction result Y. The coefficients for HEM-IV are established using the root mean square error (RMSE) is a widely utilized metric for evaluating performance ML models (Nevitt et al., 2000; Botchkarev, 2018; Botchkarev, 2019; Schratz et al., 2019; Naser and Alavi, 2020). The HEM-IV model is represented by the following equations (Eq. 6):

$\begin{array}{ll}\hfill Y& =Y_1\frac{\frac{1}{RMS{E}_{RF}}}{\frac{1}{RMS{E}_{RF}}+\frac{1}{RMS{E}_{SVR}}+\frac{1}{RMS{E}_{ANN}}}\hfill \\ \hfill & +Y_2\frac{1/RMS{E}_{SVR}}{\frac{1}{RMS{E}_{RF}}+\frac{1}{RMS{E}_{SVR}}+1/RMS{E}_{ANN}}\hfill \\ \hfill & +Y_3\frac{1/RMS{E}_{ANN}}{\frac{1}{RMS{E}_{RF}}+\frac{1}{RMS{E}_{SVR}}+1/RMS{E}_{ANN}}\hfill \end{array}(6)$

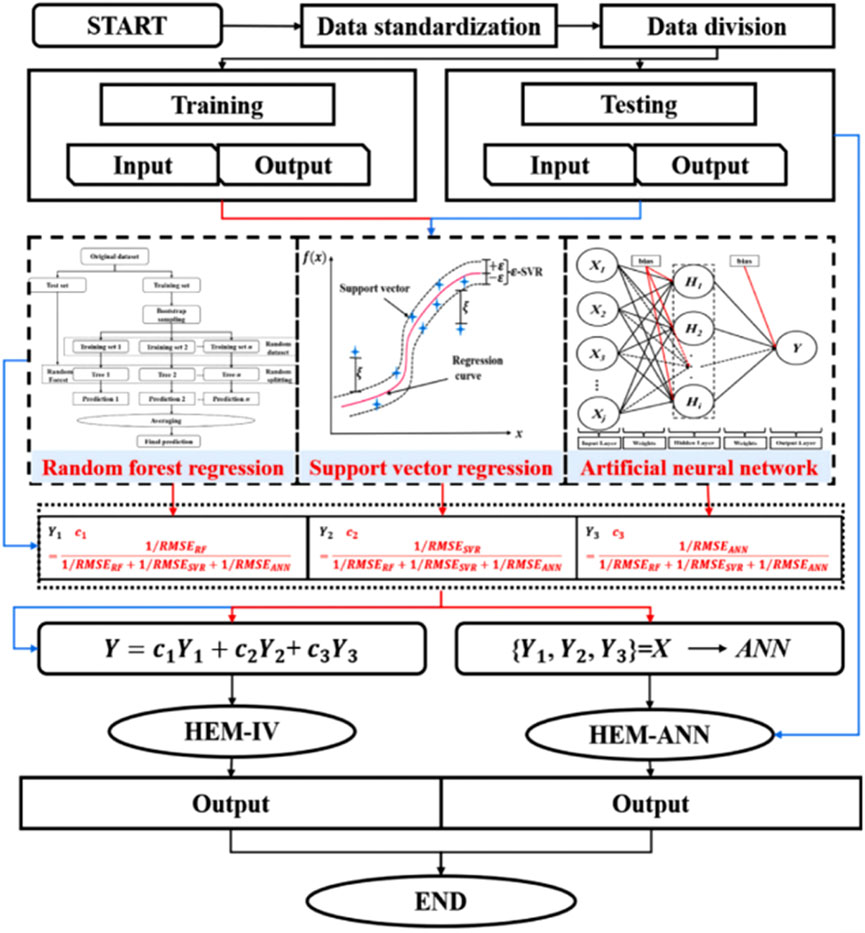
For HEM-ANN, the prediction results (Yi) of the three individual ML models from the training set are utilized as new input variables to train HEM-ANN, forming the training set Xtrain. This process leads to the development of the hybrid ensemble learning model HEM-ANN. Figure 3 depicts the workflow of these hybrid ensemble models. This approach leverages the strengths of each individual model, reduces prediction errors, and improves overall accuracy.

Figure 3

Figure 3. Construction of the ensemble learning models.

3.2 Hyperparameter tuning

The selection and tuning of hyperparameters is crucial in the process of constructing and developing ML models. Hyperparameters are parameters set before model training; they control the learning process and complexity of the model, and directly affect the performance and accuracy of the model (Cawley et al., 2007; Probst et al., 2019; Yang and Shami, 2020). Since different datasets and problems require different model configurations, choosing appropriate hyperparameter values becomes critical. It is known that determining the optimal hyperparameter values undertaking a complex and time-consuming process, given the wide array of tasks involved.hyperparameter values is often large and their interactions are complex, and hence it is difficult to find the optimal solution by simple trial and error methods. To solve this problem, researchers have proposed various methods to automate and optimize the hyperparameter selection process. These include the use of empirical formulas to guide parameter selection, e.g., grid search, stochastic search, Bayesian optimization, etc., and the use of techniques such as cross-validation to evaluate model performance (Bergstra et al., 2012; Strumberger, 2019; Alibrahim and Ludwig, 2021). These methods can help researchers find the optimal hyperparameter configurations more efficiently and improve model performance and accuracy.

In this study, the hyperparameter tuning of the ML models were tuned through the Firefly Algorithm (FIA) (RAJESWARI and BASHU; Naser, 2021; Xu et al., 2016). FIA is a nature-inspired optimization technique used for tuning hyperparameters of ML models by mimicking the behavior of fireflies. The key idea is that each firefly represents a potential solution, and their attractiveness is determined by their brightness, which corresponds to the quality of the solution. Fireflies move towards brighter ones, thereby exploring the solution space effectively. The brightness of a firefly I is related to the objective function f(x) that needs to be maximized or minimized. The movement of a firefly i towards another more attractive firefly 𝑗 is given by (Eq. 7):

${\mathbf{x}}_i^{t+1}={\mathbf{x}}_i^t+{\beta }_0{e}^{-\gamma r_{ij}^2}\left({\mathbf{x}}_j^t-{\mathbf{x}}_i^t\right)+\alpha \left(rand-0.5\right)(7)$

where ${\mathbf{x}}_i^t$ is location of fireflies 𝑖 at time t, β₀ is the attractiveness at 𝑟 = 0, 𝛾 is the light absorption coefficient, r_ij is the distance between fireflies i and j, α is the randomization parameter, and rand is a random number uniformly distributed in (0,1). This iterative process continues until convergence criteria are met, effectively tuning the hyperparameters to optimize the performance of machine learning models.

The tuning of the hyperparameters was carried out on a training set that included 70% of all the example data. FA searched for the best hyperparameters on 90% of the training set and carried out the computation of the corresponding RMSEs on the remaining 10%. The best hyperparameters were obtained after convergence occurred (i.e., when the RMSEs were no longer decreasing). Finally, the predictive performance of the model is performed on a test dataset containing 30% of the data points, which is not related to the training dataset but is only used for the evaluation of the model’s correlation performance. If it appears that there exists a model that fits well on both the training and test sets, then minimal overfitting has occurred. Figure 4 shows the overall process of predicting the 𝐷𝑛𝑠𝑠𝑚 for concrete using a tree-based model.

Figure 4

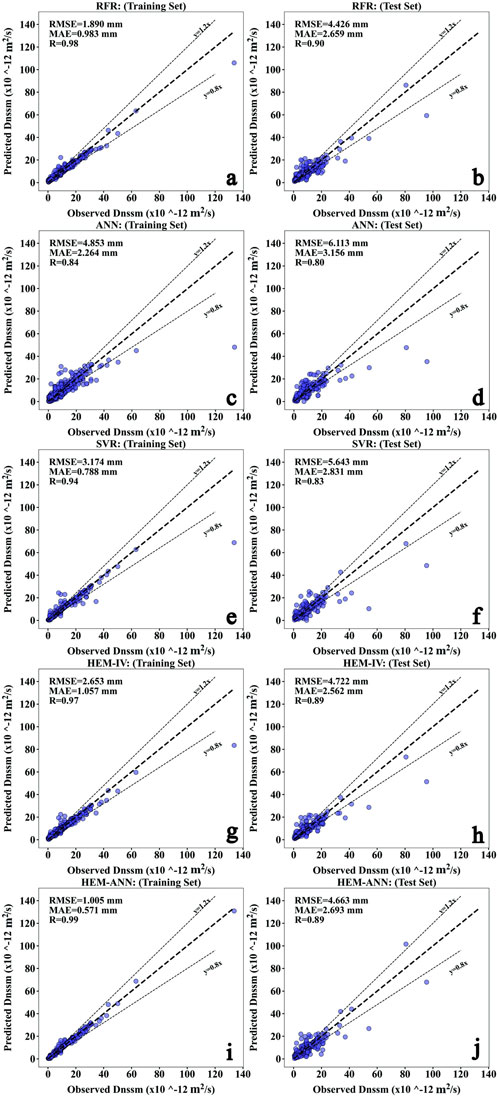
Figure 4. Predicted versus observed values for different models on the training and test sets: (A,B) RFR, (C,D) ANN, (E,F) SVR, (G,H) HEM-IV, (I,J) HEM-ANN.

For initial configuration, the HEM-IV combines predictions from RFR, SVR, and ANN, weighted by the inverse of their MSE. The HEM-ANN uses predictions from these base models as inputs to an additional ANN, structured with an input layer of 3 neurons, two hidden layers with 10 and 5 neurons respectively using ReLU activation, and an output layer with 1 neuron using a linear activation function. It is trained with the Adam optimizer, a learning rate of 0.001, MSE as the loss function, over 100 epochs with a batch size of 32. The RFR consists of 100 trees with a maximum depth of 30, minimum samples split of 2, minimum samples leaf of 1, bootstrap enabled, and uses MSE as the criterion for split quality.

3.3 Model evaluation

Relationship coefficients (R), the mean absolute error (MAE) and the root mean square error (RMSE) were employed for assessment. model in this study (Tikhamarine et al., 2020).

Relationship Coefficient (R), also known as the correlation coefficient, it quantifies the intensity and alignment of the linear correlation between estimated and observed values. It ranges from −1 to 1, where 1 indicates a perfect positive correlation, −1 indicates a perfect negative correlation, and 0 indicates no correlation (Eq. 8).

$R=\frac{{\sum }_{i=1}^n\left(y_i-\overline{y}\right)\left({\widehat{y}}_i-\overline{\widehat{y}}\right)}{\sqrt{{\sum }_{i=1}^n{\left(y_i-\overline{y}\right)}^2{\sum }_{i=1}^n{\left({\widehat{y}}_i-\overline{\widehat{y}}\right)}^2}}(8)$

The Mean Absolute Error (MAE) calculates the average size of the errors between predicted and actual values, regardless of their direction. It is calculated as (Eq. 9):

$MAE=\frac{1}{n}{\sum }_{i=1}^n\left|\left({\widehat{y}}_i-{\overline{\widehat{y}}}_i\right)\right|(9)$

The Root Mean Square Error (RMSE) is a widely utilized metric that quantifies the square root of the average squared deviation between predicted and actual values. It is given by (Eq. 10):

$RMSE=\sqrt{\frac{1}{n}{\sum }_{i=1}^n{\left({\widehat{y}}_i-{\overline{\widehat{y}}}_i\right)}^2}(10)$

In the above equations, $y_i$ are the actual values, ${\widehat{y}}_i$ are the predicted values, and the variable n represents the number of observations.

4 Findings and analysis

4.1 Prediction results of different ML models

Figure 3 plots the correlation between the forecasted Dnssm values the real values of Dnssm are each model on the training and testing subsets. It can be seen that most of the data points in the five models are closely spread out on either side of the line y = x straight line, and all of them can be fitted relatively accurately. The R-values of the measured and predicted values of the five models are 0.98, 0.84, 0.94, 0.965, 0.994, respectively, while the RMSEs of the models on the training set are 1.89, 4.853, 3.174, 2.653, 1.005, among which the RFR and HEM-ANN models have the best fitting of the measured and fitted values among the five models, and the data points of their were more closely distributed.

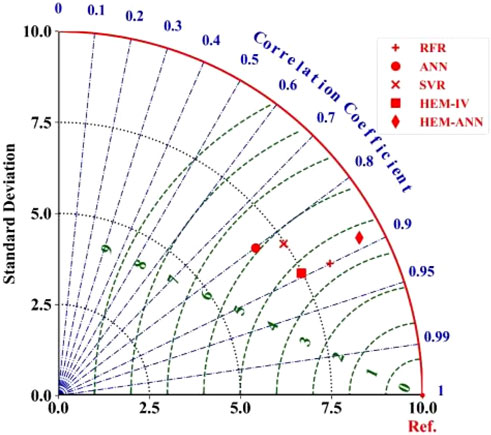
In order to verify the prediction accuracy and generalization ability of the models, the five established machine learning models are used to perform simulation tests on the test set data in the database that are not involved in modeling. It can be seen that the accuracy of the prediction ensemble models is greater than that of singe models, among which, the ensemble model RF has the best prediction performance with R and RMSE on the test of 0.9 and 4.4, respectively. To further validate the predictive ability of the models, the performance of each model was further compared using a Taylor diagram as shown in Figure 5. A Taylor diagram is a visual representation representation used to display the performance of different models in terms of their standard deviation, the three measures being referred to are standard deviation, correlation coefficient, and root mean square error (RMSE). (Despotovic et al., 2016; Alam et al., 2021; Soleimani, 2021). The radial distance from the origin represents the standard deviation of the models, the angular coordinate represents the correlation coefficient between the model output and the reference data, and the concentric dashed curves represent the RMSE values. The reference data is located at the point on the x-axis labeled “Ref.” with a standard deviation of 10.0, correlation coefficient of 1.0, and RMSE of 0. Models closer to the reference point on the x-axis have higher correlation coefficients and lower RMSE values, indicating better performance, and those with smaller radial distances have standard deviations closer to the reference data, indicating better performance in capturing variability. For example, ensemble models show higher performance with higher correlation coefficients and a standard deviations close to the reference, while single models like SVR and ANN have lower correlation coefficients and higher standard deviations, indicating poorer performance. The Taylor diagram provides a comprehensive visual comparison of model performance relative to the data that is used for referencing.

Figure 5

Figure 5. Taylor diagram comparison of models.

4.2 Variable importance

To further understand how the key features of the inputs affect the output of the model, the Shapley Additive exPlanations (SHAP) values of the features of interest were obtained with the best performed model (RF) (Halamickova et al., 1995; Zhang et al., 2018). Figure 6A shows the average SHAP values of different input features for Dnssm of plain concrete. In which various features are arranged in descending order of importance. It can be seen that among the many features, W/B, CM-Age and W are the input variables that affect the Dnssm to a higher extent, while AEA has the lowest influence. Therefore, in order to achieve a more superior resistance to chloride penetration in the preparation of concrete, more attention should be paid to these variables.

Figure 6

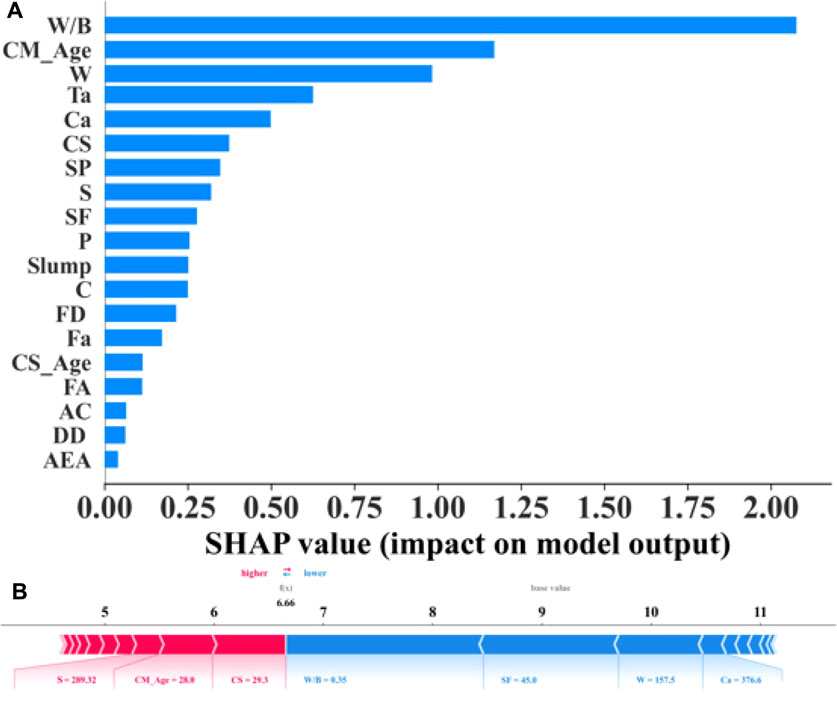
Figure 6. (A) Variable importance with SHAP analysis, and (B) local interpretations of the first sample for predicting Dnssm.

Figure 5B shows the local interpretation of the first sample in predicting Dnssm. The provided SHAP plot visually represents the contribution of various features to a single prediction made by a machine learning model. The base value, around 6.66, is the average model output across the training dataset, serving as the starting point for the explanation. Features pushing the prediction higher are shown in red, while those pushing it lower are in blue. For example, “Speed = 289.32,” “CM_Age = 28.0,” and “CS = 29.3” contribute positively, increasing the prediction, whereas “W/B = 0.35,” “SF = 45.0,” “W = 157.5,” and “Ca = 376.6” contribute negatively, decreasing the prediction. The length of each bar indicates the magnitude of the feature’s impact, with longer bars signifying a more significant influence.

4.3 Sensitivity analysis

The Dnssm value is predicted using the RF model when changing a certain input variable while other input variables are fixed to their average values. By this way, the sensitivity of the output variable to the change of input variables is calculated. From the effects of the input feature variables on Dnssm are broadly categorized into three groups: one group is to make the Dnssm trend significantly higher, such as the features (W/B, Ca, DD, etc.); one group is to make the Dnssm trend significantly lower, such as the features (Spreed, CM-Age, CS, SF, etc.), and the last group is to make no large fluctuation in the Dnssm trend, such as the features (CS-Age, P, SP, AEA, etc.).

4.3.1 Variables positively influencing the Dnssm

The variables positively influencing Dnssm include W/B, Ca, DD, Ta, C, W, DD, LF, as shown in Figure 7. It is observed that an increase in the W/B ratio (after 0.34) increases the Dnssm significantly. The possible reason is that higher W/B ratio may lead to the formation of more pores and voids this results in enhanced chloride ion penetration in the concrete (Win et al., 2004; Wang et al., 2016), while the increase of binder (cement) results more hydrates and densifies the matrix, decreasing the Dnssm (Figure 7D). The amount of coarse aggregate (Ca) in concrete significantly influences chloride penetration by affecting permeability, porosity, and the interfacial transition zone (ITZ) (Figure 7B). In addition, a higher aggregate content may lead to microcracks due to differential shrinkage and thermal stresses, offering pathways for chlorides (Kozul and Darwin, 1997; Grassl et al., 2010; Zhang et al., 2020; Zhang et al., 2023). Figures 7H–L represent the ITZ of concrete with different lightweight coarse aggregate (LWA) dosages ranging from 0% (0 kg) to 100% (692 kg) (Mangalathu et al., 2020). It can be seen that larger ITZ and more micro cracks are observed with the increase in LWA, which enhances the chloride ion transport to some extent.

Figure 7

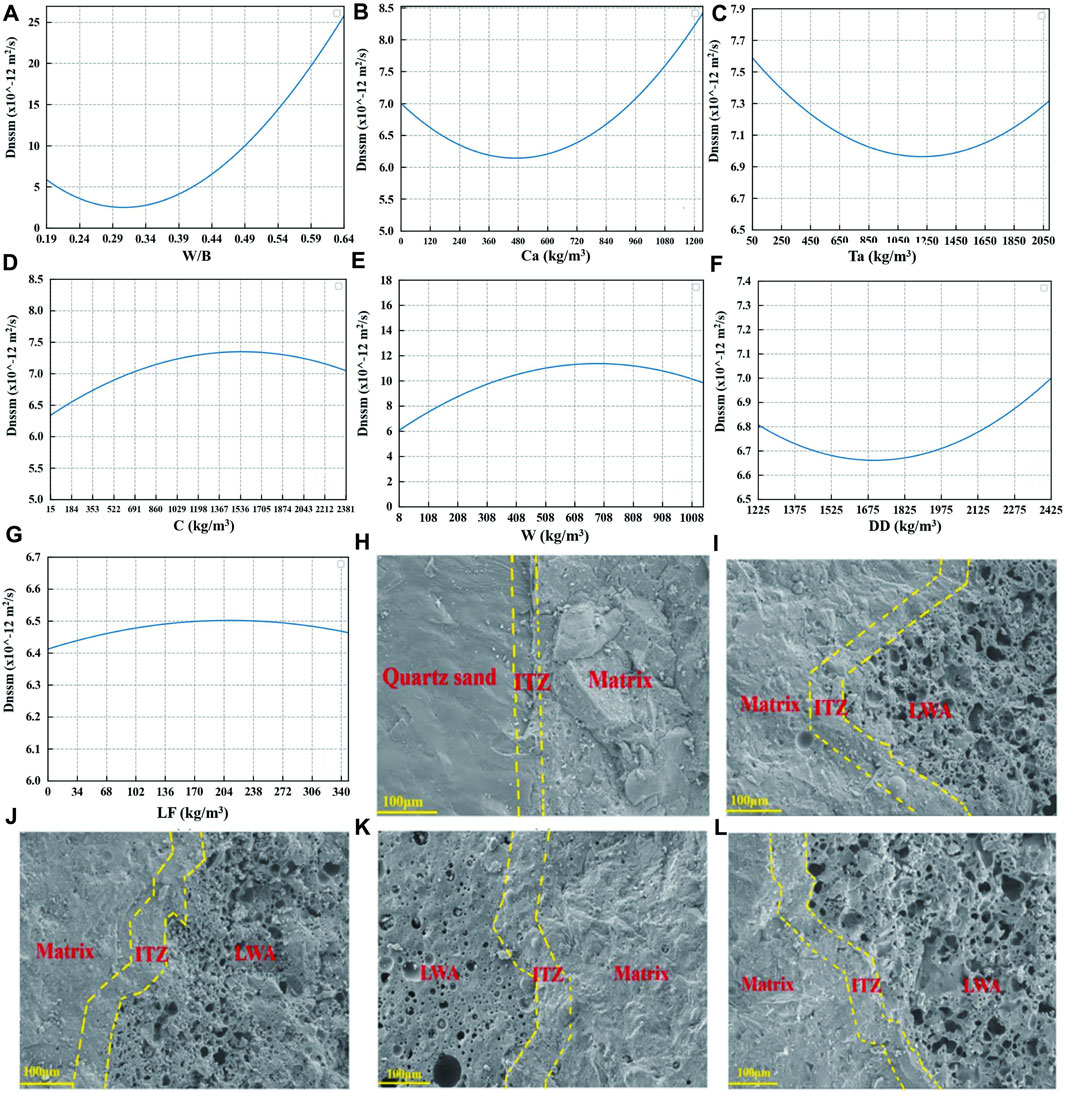
Figure 7. Sensitivity of Dnssm to change of (A) W/B, (B) Ca, (C) Ta, (D) C, (E) W, (F) DD, (G) LF, and (H–L) ITZ of concrete with increase in LWA.

It should be noted that higher loads applied to the concrete may lead to the formation of microcracks within the concrete, these pathways could serve as channels for chloride ions to enter, leading to an elevated permeability coefficient for chloride ions. (Figure 7G). Higher ambient Temperature (Ta) may result in faster water loss from the concrete, which may exacerbate the pore structure of the concrete and increase chloride ion penetration (Figure 7C) (Powers, 1947; Cawley and Talbot, 2010; Liu et al., 2011; Zeng et al., 2012; Lyngdoh et al., 2022).

4.3.2 Variables negatively influencing the Dnssm

The variables positively influencing Dnssm include CM_Age, CS, SP, Fa, AC, FA, as shown in Figure 8. It is not unexpected that as the CM_Age of concrete increases, its hydration reaction will continue, producing more hydration products to fill the pores of concrete, improving the compactness and densification of concrete, thus reducing the infiltration of chloride ions (Lee et al., 2012; Franus et al., 2015; Huang et al., 2019); This is verified by Figures 8H–K showing the SEM images of fly ash concrete at different curing ages. It can be seen that the number of hydrates inside the concrete gradually increased and the tiny pores gradually decreased with curing age.

Figure 8

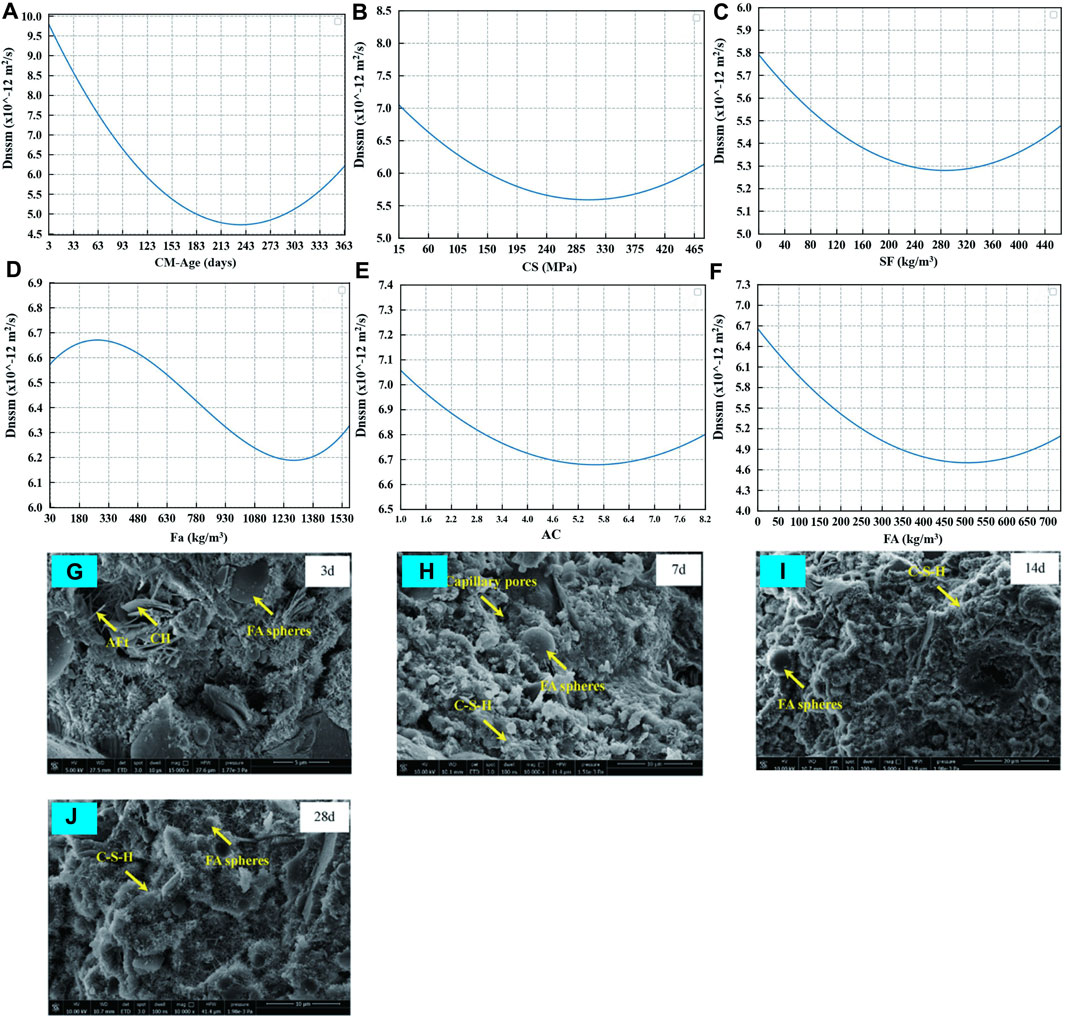
Figure 8. Sensitivity of Dnssm to the change of (A) CM_Age, (B) CS, (C) SF, (D) Fa, (E) AC, (FA) FA, and microstructure of fly ash concrete at (G) 3d, (H) 7d, (I) 14d and (J) 28d.

The addition of a certain amount of supplementary cementitious materials (SCMs) such as SF (Figure 8D) and Fa (Figure 8E) improve the packing density of the cement paste, fill voids, and refine the pore structure, thereby decreasing the connectivity of capillary pores through which chlorides can penetrate. They also contribute to the pozzolanic reaction, consuming calcium hydroxide and forming additional calcium silicate hydrate, which further densifies the matrix and reduces porosity. Moreover, SCMs enhance the chloride binding capacity of concrete by forming additional compounds that can chemically bind chlorides, thereby reducing the free chloride ions available for corrosion processes (Gjørv et al., 1979; Li et al., 2015). The increase in variables SP, FA and AC in a certain amount all increase the density of concrete, thus reducing the chloride penetration (Standard, 1996; Kozul and Darwin, 1997; Zhao et al., 2014; Simčič et al., 2015).

4.4 GUI design

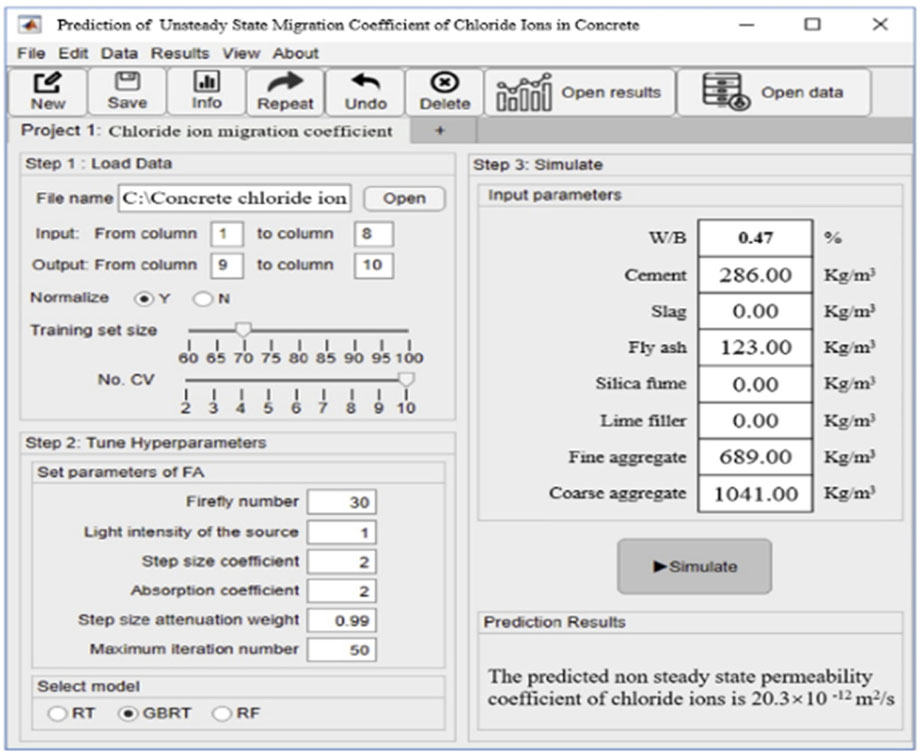
In order to enable more scholars to use the model to predict the chloride permeability coefficients of concrete in an easy way, we designed a graphical user interface (GUI) in the environment of MATLAB. The screenshot of its operation interface is shown in Figure 9 below. By using this GUI, users can more easily and quickly use the system to load training data, select the type of tree-based model, adjust hyperparameters, insert different input variables, and compare the prediction results of different models.

Figure 9

Figure 9. Model user interface diagram.

The GUI is designed to simplify the process for researchers and practitioners who may not be familiar with the underlying machine learning algorithms. By using the GUI, users can easily input various concrete mix parameters, select the type of predictive model (e.g., ANN, SVR, RFR, HEM-IV, or HEM-ANN), and adjust hyperparameters. The GUI then processes these inputs and provides a prediction of the CMC, along with visualizations of the results. This interface enhances accessibility and usability, making the advanced predictive capabilities of our models available to a broader audience without requiring extensive technical knowledge. It also supports comparative analysis by allowing users to view and compare the predictions from different models, thereby aiding in the selection of the most suitable model for their specific needs.

4.5 Prevention of concrete chloride penetration with MICP

As mentioned above, curing environments are the input variables that affect the Dnssm to a higher extent. These variables influence the concrete chloride penetration by influencing the inner pores and cracks in concrete. Therefore, by reducing or healing the newly generated cracks in concrete with microbially induced calcium carbonate precipitation (MICP) techniques, the chloride penetration can be prevented. This study will explore the curing environments together with the bacteria on the chloride penetration of concrete.

The bacteria used in our study are applied as a surface treatment to the concrete specimens, rather than being mixed with the cement and water. Surface treatment allows for targeted healing of exposed cracks, is simpler, and may be more cost-effective; however, it has limited penetration and durability may be compromised over time. Mixing bacteria with cement and water ensures uniform distribution and internal healing, enhancing durability and providing continuous self-healing, but it is more complex, potentially more expensive, and might affect concrete properties. Our study chose surface treatment for its simplicity and effectiveness in demonstrating MICP in reducing chloride penetration. Future research could explore combining both methods to maximize the benefits of bacterial self-healing in concrete structures.

Throughout this study, the main bacterial agent used was Sporosarcina pasteurii PTCC 1645 (DSM 33), a calcium carbonate-producing bacterium. Lyophilized bacteria were activated under sterile conditions using a suspension with a bacterial concentration of 10⁷ cells/mL. According to ACI-211, the concrete mixes were designed to reach a UCS of 25 MPa at 28 days with cement, water, coarse aggregate and fine aggregate of 373.8 kg/m³, 206.5 kg/m³, 739.3 kg/m³, and 993.5 kg/m³, respectively. The specimens were surface treated with bacterial suspension for 48 h before testing.

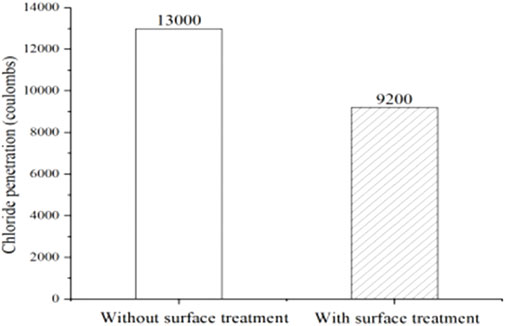
From Figure 10, the untreated sample shows a chloride penetration of 13,000 coulombs, while the treated sample shows a reduced penetration of 9,200 coulombs. This significant reduction of 3,800 coulombs demonstrates the effectiveness of microbial surface treatment in minimizing chloride penetration. Consequently, applying microbial surface treatment can enhance the durability and longevity of concrete structures exposed to chloride environments.

Figure 10

Figure 10. Influence of microbial surface treatment on the chloride penetration of concrete.

5 Conclusion

The study began by creating an ensemble model based on machine learning to forecast the chloride permeability coefficients of concrete. The effects of different input variables on the Dnssm values were analyzed by SHAP analysis. The results are summarized as follows:

(1) Five machine learning models—Random Forest Regression (RFR), Artificial Neural Networks (ANN), Support Vector Regression (SVR), Inverse Variance-Based Ensemble Model (HEM-IV), and Artificial Neural Network-Based Ensemble Model (HEM-ANN)—were used to predict the Dnssm of concrete with different mix ratios. The ensemble models demonstrated higher prediction accuracy than the single models. Specifically, the RFR model achieved an R-value of 0.98 and an RMSE of 1.89 on the training set, while the HEM-ANN model achieved an R-value of 0.994 and an RMSE of 1.005, indicating superior performance in fitting the data.

(2) The most important variable affecting the chloride migration coefficient of concrete is the water-to-binder ratio (W/B). Carefully adjusting this variable can significantly reduce the micropores in concrete, thereby decreasing chloride penetration.

(3) Variables such as W/B, coarse aggregate content (Ca), dry density (DD), ambient temperature (Ta), cement content (C), water content (W), and lime filler (LF) positively influence the Dnssm, whereas cement age (CM-Age), compressive strength (CS), superplasticizer (SP), fly ash (Fa), and air content (AC) negatively influence the Dnssm of concrete. These findings emphasize the importance of optimizing the combination of materials and curing processes to enhance the durability of concrete structures in chloride-rich environments. Additionally, microbial surface treatment can effectively reduce chloride penetration in concrete.

Based on the positive findings of this study, future research should aim to enhance the dataset by including a wider variety of mix ratios and environmental conditions to improve the overall applicability and strength of the ensemble model. Additionally, exploring advanced machine learning techniques, such as deep learning and hybrid models, could further enhance prediction accuracy and provide deeper insights into the complex interactions between input variables. While W/B was identified as the most critical variable, future studies should optimize this parameter by examining various admixtures and supplementary cementitious materials to fine-tune the concrete’s microstructure. Investigating the impact of nano-materials and advanced curing techniques on reducing micropores and enhancing durability is also a promising direction.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.

Author contributions

LL: Conceptualization, Data curation, Investigation, Methodology, Writing–original draft. LS: Conceptualization, Investigation, Software, Writing–original draft. BG: Data curation, Methodology, Supervision, Writing–review and editing. RC: Formal Analysis, Project administration, Resources, Visualization, Writing–review and editing. XW: Resources, Supervision, Validation, Writing–review and editing. TZ: Project administration, Supervision, Validation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The research was supported by Tianjin Transportation Science and Technology Development Plan Project (2023–31) and Tianjin Binhai New Area Urban Investment Construction Development Co., Ltd. (2023-CJ).

Conflict of interest

Author LL was employed by Tianjin Municipal Engineering Design and Research Institute Co., Ltd. Author LS was employed by Tianjin Binhai New Area Urban Investment Construction Development Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdolrasol, M. G., Hussain, S. M. S., Ustun, T. S., Sarker, M. R., Hannan, M. A., Mohamed, R., et al. (2021). Artificial neural networks based optimization techniques: a review. Artif. neural Netw. based Optim. Tech. A Rev. 10 (21), 2689. doi:10.3390/electronics10212689

CrossRef Full Text | Google Scholar

Agatonovic-Kustrin, S., Beresford, R. J. J. o.p., and analysis, b. (2000). Basic concepts of artificial neural network (ANN) modeling and its application in pharmaceutical research. J. Pharm. Biomed. Anal. 22 (5), 717–727. doi:10.1016/s0731-7085(99)00272-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Alam, M. S., Sultana, N., and Hossain, S. Z. J. A. S. C. (2021) Bayesian optimization algorithm based support vector regression analysis for estimation of shear capacity of FRP reinforced concrete members, 105.107281

CrossRef Full Text | Google Scholar

Alibrahim, H., and Ludwig, S. A. (2021). “Hyperparameter optimization: comparing genetic algorithm against grid search and bayesian optimization,” in 2021 IEEE congress on evolutionary computation (CEC) (IEEE).

CrossRef Full Text | Google Scholar

Audenaert, K., Yuan, Q., and De Schutter, G. (2010). On the time dependency of the chloride migration coefficient in concrete. Constr. Build. Mat. 24 (3), 396–402. doi:10.1016/j.conbuildmat.2009.07.003

CrossRef Full Text | Google Scholar

Awad, M., et al. (2015). Support vector regression, 67–80.

CrossRef Full Text | Google Scholar

Basak, D., et al. Support vector regression. 2007. 11(10): p. 203–224.

Google Scholar

Bergstra, J., and Bengio, Y. J. J. o.m.l.r., Random search for hyper-parameter optimization. 2012. 13(2).

Google Scholar

Bogas, J. A., Gomes, A. J. C., and Composites, C. (2015) Non-steady-state accelerated chloride penetration resistance of structural lightweight aggregate concrete, 60, 111–122.

CrossRef Full Text | Google Scholar

Botchkarev, A. J. a.p.a. (2018). Performance metrics (error measures) in machine learning regression, forecasting and prognostics: properties and typology.

Google Scholar

Botchkarev, A. J. I. J. o.I. (2019). A new typology design of performance metrics to measure errors in machine learning regression algorithms. A new typology Des. Perform. metrics Meas. errors Mach. Learn. Regres. algorithms 14, 045–076. doi:10.28945/4184

CrossRef Full Text | Google Scholar

Build, N. (1999). Concrete, mortar and cement-based repair materials: chloride migration coefficient from non-steady-state migration experiments. 492.

Google Scholar

Cawley, G. C., and Talbot, N. L. (2007). Preventing over-fitting during model selection via bayesian regularisation of the hyper-parameters 8(4).

Google Scholar

Cawley, G. C., and Talbot, N. L. J. T. J. o.M. L. R. (2010). On over-fitting in model selection and subsequent selection bias in performance evaluation, 11, 2079–2107.

Google Scholar

Chan, J.Y.-L., Leow, S. M. H., Bea, K. T., Cheng, W. K., Phoong, S. W., Hong, Z. W., et al. (2022). Mitigating the multicollinearity problem and its machine learning approach: a review. Mitigating multicollinearity problem its Mach. Learn. approach a Rev. 10 (8), 1283. doi:10.3390/math10081283

CrossRef Full Text | Google Scholar

Che, D., Liu, Q., Rasheed, K., and Tao, X. (2011). Decision tree and ensemble learning algorithms with their applications in bioinformatics. Adv. Exp. Med. Biol. 696, 191–199. doi:10.1007/978-1-4419-7046-6_19

PubMed Abstract | CrossRef Full Text | Google Scholar

Chidiac, S., Shafikhani, M. J. C., and Materials, B. (2019). Phenomenological model for quantifying concrete chloride diffusion coefficient, 224, 773–784.

CrossRef Full Text | Google Scholar

Choi, Y. C., et al. (2017). Modelling of chloride diffusivity in concrete considering effect of aggregates, 136, 81–87.

CrossRef Full Text | Google Scholar

Despotovic, M., et al. (2016). Evaluation of empirical models for predicting monthly mean horizontal diffuse solar radiation 56, 246–260.

CrossRef Full Text | Google Scholar

Dongare, A., et al. (2012). Introduction to artificial neural network 2(1), 189–194.

Google Scholar

Du, F. (2020) Chloride ions migration and induced reinforcement corrosion in concrete with cracks: a comparative study of current acceleration and natural marine exposure, 263. 120099.

CrossRef Full Text | Google Scholar

Elfmarkova, V., et al. (2015) Determination of the chloride diffusion coefficient in blended cement mortars. 78, 190–199.

CrossRef Full Text | Google Scholar

Eluyode, O., Akomolafe, D. T., and Research, S. (2013). Comparative study of biological and artificial neural networks 2(1), 36–46.

Google Scholar

Feng, D.-C., Cetiner, B., Azadi Kakavand, M. R., and Taciroglu, E. (2021). Data-driven approach to predict the plastic hinge length of reinforced concrete columns and its application. J. Struct. Eng. (N. Y. N. Y). 147 (2), 04020332. doi:10.1061/(asce)st.1943-541x.0002852

CrossRef Full Text | Google Scholar

Ferreira, R., et al. (2016). Effect of metakaolin on the chloride ingress properties of concrete, 20, 1375–1384.

CrossRef Full Text | Google Scholar

Franus, W., Panek, R., and Wdowin, M. (2015). “SEM investigation of microstructures in hydration products of portland cement,” in 2nd international multidisciplinary microscopy and microanalysis congress: proceedings of InterM, october 16-19, 2014 (Springer).

CrossRef Full Text | Google Scholar

Gandomi, A. H., Babanajad, S. K., Alavi, A. H., and Farnam, Y. (2012). Novel approach to strength modeling of concrete under triaxial compression. J. Mat. Civ. Eng. 24 (9), 1132–1143. doi:10.1061/(asce)mt.1943-5533.0000494

CrossRef Full Text | Google Scholar

Gandomi, A. H., and Roke, D. A. J. A. i.E. S. (2015) Assessment of artificial neural network and genetic programming as predictive tools, 88, 63–72.

CrossRef Full Text | Google Scholar

Garg, A., and Tai, K. J. I. J. o.M. (2013). Comparison of statistical and machine learning methods in modelling of data with multicollinearity. Comp. Stat. Mach. Learn. methods Model. data multicollinearity 18 (4), 295–312. doi:10.1504/ijmic.2013.053535

CrossRef Full Text | Google Scholar

Gjørv, O., Vennesland, Ø. J. C., and Research, C. (1979). Diffusion of chloride ions from seawater into concrete. Cem. Concr. Res. 9 (2), 229–238. doi:10.1016/0008-8846(79)90029-2

CrossRef Full Text | Google Scholar

Grassl, P., Wong, H. S., and Buenfeld, N. R. (2010). Influence of aggregate size and volume fraction on shrinkage induced micro-cracking of concrete and mortar. Cem. Concr. Res. 40 (1), 85–93. doi:10.1016/j.cemconres.2009.09.012

CrossRef Full Text | Google Scholar

Gunn, S. R. J. I. t.r., Support vector machines for classification and regression. 1998. 14(1): p. 5–16.

Google Scholar

Halamickova, P., Detwiler, R. J., Bentz, D. P., and Garboczi, E. J. (1995). Water permeability and chloride ion diffusion in Portland cement mortars: relationship to sand content and critical pore diameter. Cem. Concr. Res. 25 (4), 790–802. doi:10.1016/0008-8846(95)00069-o

CrossRef Full Text | Google Scholar

Hall, M. A. (1999). Correlation-based feature selection for machine learning. The University of Waikato.

Google Scholar

Hao-bo, H., and Guo-zhi, Z. J. (2004) Assessment on chloride contaminated resistance of concrete with non-steady-state migration method, 19, 6–8.

CrossRef Full Text | Google Scholar

Huang, X., et al. (2019) The effect of supplementary cementitious materials on the permeability of chloride in steam cured high-ferrite Portland cement concrete, 197, 99–106.

CrossRef Full Text | Google Scholar

Jain, J., and Neithalath, N. J. M. C. (2011). Electrical impedance analysis based quantification of microstructural changes in concretes due to non-steady state chloride migration. Mat. Chem. Phys. 129 (1-2), 569–579. doi:10.1016/j.matchemphys.2011.04.057

CrossRef Full Text | Google Scholar

Jebli, I., et al. (2021) Prediction of solar energy guided by pearson correlation using machine learning, 224.120109

CrossRef Full Text | Google Scholar

Junior, J. R. H. (2021) Comparison of test methods to determine resistance to chloride penetration in concrete: sensitivity to the effect of fly ash, 277.122265

CrossRef Full Text | Google Scholar

Kozul, R., and Darwin, D. (1997). Effects of aggregate type, size, and content on concrete strength and fracture energy. University of Kansas Center for Research, Inc.

Google Scholar

Krenker, A., et al. (2011). Introduction to the artificial neural networks, 1–18.

Google Scholar

Lee, C.-L., et al. (2012) Establishment of the durability indices for cement-based composite containing supplementary cementitious materials, 37, 28–39.

CrossRef Full Text | Google Scholar

Li, L.-y., et al. (2015) Numerical simulation of chloride penetration in concrete in rapid chloride migration tests, 63, 113–121.

CrossRef Full Text | Google Scholar

Liu, J., et al. (2017) Understanding the effect of curing age on the chloride resistance of fly ash blended concrete by rapid chloride migration test, 196, 315–323.

CrossRef Full Text | Google Scholar

Liu, X., Chia, K. S., and Zhang, M. H. (2011). Water absorption, permeability, and resistance to chloride-ion penetration of lightweight aggregate concrete. Constr. Build. Mat. 25 (1), 335–343. doi:10.1016/j.conbuildmat.2010.06.020

CrossRef Full Text | Google Scholar

Liu, X., and Zhang, M. H. (2015). A model to estimate the durability performance of both normal and light-weight concrete. Constr. Build. Mat. 80, 255–261. doi:10.1016/j.conbuildmat.2014.11.033

CrossRef Full Text | Google Scholar

Lyngdoh, G. A., Zaki, M., Krishnan, N. A., and Das, S. (2022). Prediction of concrete strengths enabled by missing data imputation and interpretable machine learning. Predict. Concr. strengths enabled by missing data imputation interpretable Mach. Learn. 128, 104414. doi:10.1016/j.cemconcomp.2022.104414

CrossRef Full Text | Google Scholar

Maes, M., et al. (2013) Resistance of concrete with blast-furnace slag against chlorides, investigated by comparing chloride profiles after migration and diffusion, 46, 89–103.

CrossRef Full Text | Google Scholar

Mangalathu, S., Hwang, S.-H., and Jeon, J.-S. J. E. S. (2020). Failure mode and effects analysis of RC members based on machine-learning-based SHapley Additive exPlanations (SHAP) approach. Eng. Struct. 219, 110927. doi:10.1016/j.engstruct.2020.110927

CrossRef Full Text | Google Scholar

Marks, M., Glinicki, M. A., and Gibas, K. J. M. (2015). Prediction of the chloride resistance of concrete modified with high calcium fly ash using machine learning 8(12), 8714–8727. doi:10.3390/ma8125483

PubMed Abstract | CrossRef Full Text | Google Scholar

Marks, M., Jozwiak-Niedzwiedzka, D., and Glinicki, M. A. (2012) Automatic categorization of chloride migration into concrete modified with CFBC ash 9(5), 375–387. doi:10.12989/cac.2012.9.5.375

CrossRef Full Text | Google Scholar

Naito, C., et al. (2020) Chloride migration characteristics and reliability of reinforced concrete highway structures in Pennsylvania, 231.117045

CrossRef Full Text | Google Scholar

Naser, M., and Alavi, A. J. a.p.a. (2020). Insights into performance fitness and error metrics for machine learning.

Google Scholar

Naser, M. J. (2021). Observational analysis of fire-induced spalling of concrete through ensemble machine learning and surrogate modeling. J. Mat. Civ. Eng. 33 (1), 04020428. doi:10.1061/(asce)mt.1943-5533.0003525

CrossRef Full Text | Google Scholar

Nevitt, J., and Hancock, G. R. (2000) Improving the root mean square error of approximation for nonnormal conditions in structural equation modeling. 68(3), 251–268. doi:10.1080/00220970009600095

CrossRef Full Text | Google Scholar

Pallapothu, S. N. R. G., Pancharathi, R. K., and Janib, R. J. E. A. o.A. I. (2023) Predicting concrete strength through packing density using machine learning models. 126, 107177.

CrossRef Full Text | Google Scholar

Park, J.-I., et al. (2016). Diffusion decay coefficient for chloride ions of concrete containing mineral admixtures.

Google Scholar

Pontes, J., Bogas, J. A., Real, S., and Silva, A. (2021). The rapid chloride migration test in assessing the chloride penetration resistance of normal and lightweight concrete. Appl. Sci. (Basel). 11 (16), 7251. doi:10.3390/app11167251

CrossRef Full Text | Google Scholar

Pontes, J., et al. (2023) The rapid chloride migration test as a method to determine the chloride penetration resistance of concrete in marine environment. 404. 133281.

CrossRef Full Text | Google Scholar

Powers, T. C. (1947). A discussion of cement hydration in relation to the curing of concrete. Portland Cement Association Chicago.

Google Scholar

Probst, P., Wright, M. N., and Boulesteix, A. (2019). Hyperparameters and tuning strategies for random forest. WIREs Data Min. Knowl. 9 (3), e1301. doi:10.1002/widm.1301

CrossRef Full Text | Google Scholar

Qian, C., and Du, W. J. J. o.B. E. (2023) Analysis method of apparent quality of fair-faced concrete based on convolutional neural network machine learning, 80. 108154

CrossRef Full Text | Google Scholar

Rajaie, H., and Mahmoud, S. (2016). Practical evaluation of rapid tests for assessing the Chloride resistance of concretes containing Silica Fume.

Google Scholar

Real, S., et al. (2015) Chloride migration in structural lightweight aggregate concrete produced with different binders, 98, 425–436.

CrossRef Full Text | Google Scholar

Riding, K. A., Thomas, M. D., and Folliard, K. J. J. A. M. J., Apparent diffusivity model for concrete containing supplementary cementitious materials. 2013. 110(6): p. 705–714.

Google Scholar

Rosellini, A. J., Liu, S., Anderson, G. N., Sbi, S., Tung, E. S., and Knyazhanskaya, E. (2020). Developing algorithms to predict adult onset internalizing disorders: an ensemble learning approach. J. Psychiatr. Res. 121, 189–196. doi:10.1016/j.jpsychires.2019.12.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Saadaari, F. S., Mireku-Gyimah, D., and Olaleye, B. M. J. G. M. J. (2020). Development of a stope stability prediction model using ensemble learning techniques - a case study. Dev. a Stope Stab. Predict. Model. Using Ensemble Learn. Tech. - A Case Study 20 (2), 18–26. doi:10.4314/gm.v20i2.3

CrossRef Full Text | Google Scholar

Schratz, P., et al. (2019) Hyperparameter tuning and performance assessment of statistical and machine-learning algorithms using spatial data, 406, 109–120.

CrossRef Full Text | Google Scholar

Sell Junior, F. K., et al. (2021) Experimental assessment of accelerated test methods for determining chloride diffusion coefficient in concrete, 14.e14407.

CrossRef Full Text | Google Scholar

Shiu, R.-W., and Yang, C.-C. J. J. o.M. S. (2020). Technology. Eval. Migr. Charact. opc slag Concr. rapid chloride Migr. test 28 (2), 1.

Google Scholar

Simčič, T., et al. (2015) Chloride ion penetration into fly ash modified concrete during wetting–drying cycles, 93, 1216–1223.

Google Scholar

Sirivivatnanon, V., Xue, C., and Khatri, R. (2023). Long-term reinforcement corrosion in low carbon concrete with a high volume of SCMs exposed to NaCl solutions and field marine environment. Constr. Build. Mat. 393, 132071. doi:10.1016/j.conbuildmat.2023.132071

CrossRef Full Text | Google Scholar

Soleimani, F. (2021). “Analytical seismic performance and sensitivity evaluation of bridges based on random decision forest framework,” in Structures (Elsevier).

CrossRef Full Text | Google Scholar

Standard, A. (1996). Standard practice for selecting proportions for normal, heavyweight, and mass concrete. ACI Man. Concr. Pract., 1–38.

Google Scholar

Strumberger, I. (2019). “Designing convolutional neural network architecture by the firefly algorithm,” in 2019 international young engineers forum (YEF-ECE) (IEEE).

CrossRef Full Text | Google Scholar

Sua-iam, G., and Makul, N. J. C. S. i.C. M., Characteristics of non-steady-state chloride migration of self-compacting concrete containing recycled concrete aggregate made of fly ash and silica fume. 2024. 20: p. e02877, doi:10.1016/j.cscm.2024.e02877

CrossRef Full Text | Google Scholar

Taffese, W. Z., Espinosa-Leal, L. J. C., and Materials, B. (2022) A machine learning method for predicting the chloride migration coefficient of concrete. 348. 128566

CrossRef Full Text | Google Scholar

Tang, L., Nilsson, L.-O., and Basheer, P. M. (2011). Resistance of concrete to chloride ingress: testing and modelling. CRC Press.

Google Scholar

Tikhamarine, Y., Malik, A., Pandey, K., Sammen, S. S., Souag-Gamane, D., Heddam, S., et al. (2020). Monthly evapotranspiration estimation using optimal climatic parameters: efficacy of hybrid support vector regression integrated with whale optimization algorithm. Environ. Monit. Assess. 192, 696–719. doi:10.1007/s10661-020-08659-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Van Noort, R., et al. (2016) Long-term chloride migration coefficient in slag cement-based concrete and resistivity as an alternative test method, 115, 746–759.

CrossRef Full Text | Google Scholar

Wang, H.-L., et al. (2016) Characteristics of concrete cracks and their influence on chloride penetration, 107, 216–225.

CrossRef Full Text | Google Scholar

Win, P. P., Watanabe, M., and Machida, A. (2004). Penetration profile of chloride ion in cracked reinforced concrete. Cem. Concr. Res. 34 (7), 1073–1079. doi:10.1016/j.cemconres.2003.11.020

CrossRef Full Text | Google Scholar

Xu, Z., Hou, Z., Han, Y., and Guo, W. (2016). A diagram for evaluating multiple aspects of model performance in simulating vector fields. Geosci. Model. Dev. 9 (12), 4365–4380. doi:10.5194/gmd-9-4365-2016

CrossRef Full Text | Google Scholar

Yang, L., and Shami, A. J. N. (2020). On hyperparameter optimization of machine learning algorithms: theory and practice. Hyperparam. Optim. Mach. Learn. algorithms Theory Pract. 415, 295–316. doi:10.1016/j.neucom.2020.07.061

CrossRef Full Text | Google Scholar

Yohannese, C. W., et al. (2018). “Ensembles based combined learning for improved software fault prediction: a comparative study,” in International conference on intelligent systems & knowledge engineering.

Google Scholar

Zeng, Q., Li, K., Fen-chong, T., and Dangla, P. (2012). Pore structure characterization of cement pastes blended with high-volume fly-ash. Cem. Concr. Res. 42 (1), 194–204. doi:10.1016/j.cemconres.2011.09.012

CrossRef Full Text | Google Scholar

Zhang, G., et al. (2023) Relationship between chloride ion permeation resistance of ultra-high performance concrete and lightweight aggregate ratio, 76.107360

CrossRef Full Text | Google Scholar

Zhang, J., et al. (2018). Eff. pore Struct. gas permeability chloride diffusivity Concr. 163, 402–413.

CrossRef Full Text

Zhang, J., et al. (2020) Multi-objective optimization of concrete mixture proportions using machine learning and metaheuristic algorithms, 253.119208

CrossRef Full Text | Google Scholar

Zhang, M. (2023). Research on the critical chloride content of reinforcement corrosion in marine concrete—a review.

Google Scholar

Zhao, J., et al. (2014). Influ. freeze–thaw cycle curing time chloride ion penetration Resist. Sulphoaluminate Cem. Concr. 53, 305–311.

CrossRef Full Text

Zuquan, J., Xia, Z., Tiejun, Z., and Jianqing, L. (2018). Chloride ions transportation behavior and binding capacity of concrete exposed to different marine corrosion zones. Constr. Build. Mat. 177, 170–183. doi:10.1016/j.conbuildmat.2018.05.120

CrossRef Full Text | Google Scholar