Application of Artificial Neural Networks for Corrosion Behavior of Ni–Zn Electrophosphate Coating on Galvanized Steel and Gene Expression Programming Models

Zn–Ni electrophosphate coating is one of the most commonly used materials in industrial applications. The corrosion resistance of this coating is very important in order to achieve the minimum corrosion current of the Zn–Ni electrophosphate coating. This study described a new reliability simulation framework to determine the corrosion behavior of coating using a gene artificial neural network (ANN) to estimate the corrosion current of the coating. The input parameters of the model are temperature, pH of electroplating bath, current density, and Ni²⁺ concentration, and corrosion current defined as output. The effectiveness and accuracy of the model were checked by utilizing the absolute fraction of variance (R² = 0.9999), mean absolute percentage error (MAPE = 0.0171), and root mean square error (RMSE= 0.0002). This is determined using the genetic algorithm (GA) and the optimum practice condition.

Introduction

Hot-dip galvanization is an efficient safety measure of steel against the corrosion of atmospheric corrosion, but it cannot offer adequate protection of the steel substrates against the corrosion substance produced in the atmosphere (Lin et al., 2008; Tsai et al., 2010; Su and Lin, 2014). In general, the surface modification treatment is applied to galvanized steel for greater protection of zinc-coated steel from corrosion. Phosphating, which has been used extensively in a wide variety of industries, is one of the major processes of chemical conversion for applications such as corrosion prevention, paint primers, wear prevention, metal forming lubricants, electrical insulation, and even decoration (Xu and Lin, 2007; Li et al., 2020). The highest operating temperatures of the most traditional phosphating baths mentioned in the literature are 90–98°C. A high level of energy consumption is the biggest problem for the use of a high temperature bath, which is a huge crisis nowadays. In addition, due to the development of a scale that contributes to excessive heating of the bath solution, the application and retaining of the heating coils is difficult, and thus a repeated replacement is needed (Darband et al., 2016a). The overheating of bath solution, allowing an early conversion of primary phosphate into tertiary phosphate before the metal is treated, is another issue in this case. These reasons increase the free acidity of the bath and thus delay the precipitation of the coating of phosphates. The low-temperature phosphating processes have become more promising and successful due to the high cost of energy in the high-temperature bath. However, the phosphating bath at low temperatures is slow, and certain techniques must be used to accelerate. In order to facilitate the phosphating process, chemical, electrochemical, and mechanical methods are used. The chemical methods are most widely used in many industries. However, the chemical accelerators such as nitrite are poisonous and have a detrimental effect on the environment and human health, and it is desirable to be eliminated from the bath composition and replaced with some replacements such as electrochemical accelerator (Huang et al., 2021; Zhang et al., 2021).

In many industries, the chemical processes are most commonly used. However, chemical accelerators such as nitrite are toxic and have a harmful effect on the environment. So, it is required to restrict the use of these hazardous chemicals by replacing the electrochemical accelerator (Datta and Chattopadhyay, 2013; Ashtiani and Shahsavari, 2016; Coşkun and Karahan, 2018; Huang et al., 2021; Zhu et al., 2021). The electrochemical methods using cathodic and anodic treatments for accelerating phosphating processes become popular these days for their low operating temperature, high speed of coating, and improved coating properties. So, experimental parameters will affect the structural and chemical properties as well as electroplating efficiency during electrodeposition of an electrophosphating coating. Typical methods and measurements make it very difficult to analyze the results of these deposition parameters and to consider the relations between the performance characteristics.

The use of the artificial neural network (ANN) and the genetic algorithm is an engineering technique to improve process variables. The ANN is one of the important non-linear strategies to simulate the complicated behavior of materials (Datta and Chattopadhyay, 2013; Zhu et al., 2021). This method can learn and simulate the experiential information through weight and bias in the neuron, but cannot determine the optimal condition and may be hindered at the local minimum.

Genetic algorithms (GA) are used to find the optimum solution(s) for a computational problem that maximizes or minimizes a certain function. Genetic algorithms are also called as evolutionary computation, which mimic biological reproductive and selection processes in order to find the “fittest” lst solutions. Artificial intelligence (AI) techniques such as ANN and gene expression programming (GEP) are important in many areas of physical, chemical, and mathematical science (Coşkun and Karahan, 2018). The ANN method offers a modern technique for predicting material deterioration in different conditions. The ANN is a technology for artificial intelligence to simulate human brain biological processes (Kim et al., 2009; Ashtiani and Shahsavari, 2016). The system consists of one-way signal flow channels of interconnected operators. Samples are obtained with a distributed code that forms a non-linear, feasible framework. It is also environmentally self-adapting to react rationally to the different inputs (Evis and Arcaklioglu, 2011; Zeraati and Khayati, 2018). ANN models have few drawbacks of local minima, and to prevent local minima, which leads to false convergence of the ANN model, a derivative-free optimization algorithm should be added in the ANN algorithm training process (Gandomi and Roke, 2015). There are a lot of studies about the applications of GEP in the literature for different engineering problems (Karahan and Özdemir, 2015). The combination of regression strategies and systematic design of experiment is an efficient alternative approach for providing the experimental data in a new popular model approach such as GEP. ANN and GEP can capture complex interactions among input/output variables in a system without using prior knowledge about the nature of these interactions. Isleem et al. reported a database based on the ANN for predicting the hardening and softening behavior of glass fiber-reinforced polymers (Isleem et al., 2021). Finke et al. have developed anticorrosion behavior of coating based on the ANN (Finke et al., 2021). Hu et al. reported on the corrosion behavior of Mo–V–Cr–Ni steel using an ANN model to predict polarization curves in deep-sea environments without the need for experiments (Hu et al., 2019).

To the best of our knowledge, very few studies are reported about ANN and GEP together to compare the expected results and explain the research protocol (Karahan et al., 2013; Gandomi and Roke, 2015; Golafshani et al., 2015; Karahan and Özdemir, 2015; Xu et al., 2015). The purpose of this study was to assess the oxidation behavior of Ni base alloys using particle swarm optimization (PSO)-ANN and GEP models.

Due to their flexibility in general regression processes, the present study was conducted using combined GA–ANN to determine an appropriate process for zinc–nickel electrophosophate coating on galvanized steel conditions.

Materials Production and Processing

The thickening of zinc covering on a steel layer of galvanized stain was 10 μm, and the dimension of hot-dip galvanized steel with a dimension (50 × 20 × 2 mm) was used in this experiment. It was ultrasonically degassed for 12 min in acetone, and then washed with deionized water for 20 s in 4% sulfuric acid. A dip into a titanium phosphate solution (1 g/L) for 1 min was used to enable the samples. Finally, prepared specimens were immersed in a cell-contained phosphating solution under different coating conditions.

Constant direct current was used for electrophosphating cells using a galvanostat. Table 1 indicates the chemical composition and operating conditions of the bath (Darband et al., 2016a; Darband et al., 2016b).

TABLE 1

TABLE 1. Experimental conditions.

In this analysis, anodes of stainless steel were used. Two sets of galvanized steel substrates have been mounted on both ends. The area under the review was one square centimeter, and the remainder was sealed. The cell for corrosion measurement comprises three electrodes, namely, the operating electrode, stainless steel plate, and reference saturated calomel electrode (SCE). The potentiodynamic polarization experiments were performed with a scanning speed of 1 mV/S ranging from - 300 mV (relating to the open circuit potential) to +300 mV. The corrosion current density (i_corr) was evaluated using the linear polarization method.

Artificial Neural Network

The ANN, in particular the structure of the brain, is influenced by biological neural networks. An ANN model includes elements such as inputs and works in a manner that creates a relation between the elements in an approximation to what a brain is doing in other words, it works by learning the connection between input and output data (Laugier and Richon, 2003). A connected neuron formula in terms of weight is reported as Eq. 1:

$x={\displaystyle \sum _{i=1}^p{w}_{i}x}+b,(1)$

Herein, b represents the bias of neurons, p represents the number of elements, and w_i represents the weight of the input vector (a_i). Each neuron receives sum of the weight inputs with bias and is used from the activation function to validate its output signal, as Eq. 2:

$f\left(x\right)=\beta \left({\displaystyle \sum _{i=1}^p{w}_{i}nx}+b\right),(2)$

where $\beta$ represents the transfer function of the neuron. Some of the most common transfer functions are log-sigmoid (Logsig), tan-sigmoid (Tansig), and linear transfer function (Purelin), followed by Eqs 2–4.

$\beta \left(x\right)=\frac{1}{1+\exp \left(-x\right)},(3)$

$\beta \left(x\right)=\frac{1}{1+\exp \left(-2x\right)}-1,(4)$

$\beta \left(x\right)=x,(5)$

Figure 1 schematically shows these transfer function. Feed-forward back-propagation is one of the most common strategies for training of the ANN. This approach enables us to present effective solutions for engineering applications, especially in material science (Rashidi et al., 2012; Varol et al., 2013; Vettivel et al., 2013).

FIGURE 1

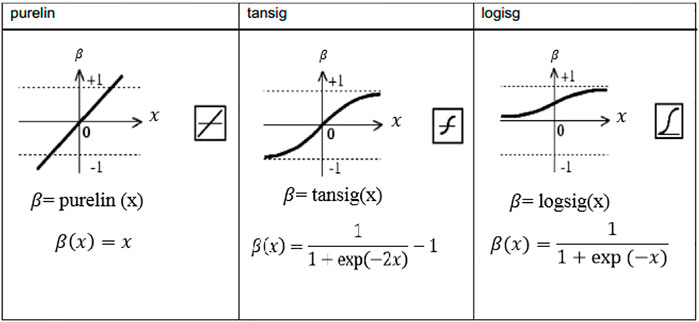
FIGURE 1. Schematical representation of transfer functions (Mozaffari et al., 2017).

Detailed explanations of the functions of hidden and output layers are descripted in the work by Ates (2007); Asadi et al. (2012); Varol et al. (2013). In the modeling step, we predicted the minimal root mean square error (RMSE) and mean absolute percentage error (MAPE) of the training and testing sets. RMSE and MAPE can be determined using Eqs 6, 7.

$RMSE=\sqrt{\frac{1}{\mathrm{N}}{{\displaystyle \sum _1^N\left(y_p-y_a\right)}}^2,}(6)$

$\text{MAPE}=\frac{1}{\mathrm{N}}{\displaystyle \sum _1^N\left(\frac{\left|y_a-y_p\right|}{y_a}\times 100\right)},(7)$

where $y_p$ is the real value, $y_a$ is the model prediction value, and N is the number of testing data (Canakci et al., 2015; Wu et al., 2021).

GA

As Darwin’s theory explains, the GA is a random global method of search and optimization which mimics natural biological evolution. Using a population of individuals, the GA examines all regions of the solution space (Hou et al., 2007; Zaki et al., 2015; Jamshidi et al., 2016; Dashtian and Zare-Dorabei, 2017).

PSO

PSO is one of the most popular population-based stochastic optimization algorithms (Yusup et al., 2012). In recent years, the PSO method has received a great deal of attention as it can efficiently converge to the optimization value and has excellent robustness (Kennedy and Eberhart, 1995; Li et al., 2008). The pseudo-code of standard PSO is shown in Figure 2.

FIGURE 2

FIGURE 2. Pseudo-code of standard PSO.

The aim of the current study was to determine the most appropriate values for the weights and bias of NN (i.e., optimized NN) based on the PSO algorithm (Nouiri et al., 2018). Then, we used the optimized NN as a fitness function of PSO to obtain the best values for our futures.

GEP

According to the literature, the use of AI, for example, the adaptive neuron fuzzy inference system (ANFIS), and the ANN in combination with optimization techniques, for example, the GA, simulated annealing (SA), are powerful techniques for modification and simulation of engineering phenomena (Mansouri and Kisi, 2015; Jafari et al., 2017; Mansouri et al., 2018). One of the most relevant methodologies for AI is called GEP, that is, an advanced combination of GA and genetic programming (GP) ideas to improve their accuracy (Ferreira, 2006; Zhang et al., 2007). GEP, similar to GA and GP, employed the fitness values as the criteria for the selection of individual’s population and using the genetic variation operator to determine the best relationship within inputs and output variables. Finally, the GEP is able to depict the relationship between input and output as an expression tree (ET) or mathematical function. These functions enable us to calculate the output at various practical conditions with acceptable accuracy (Martí et al., 2013; Hoseinian et al., 2017; Jafari and Mahini, 2017).

ETs are combined from constants, functions, operators, and input variables with their nodes and terminals. A mathematical function is responsible to connect each other ETs as shown in Figure 3 (Hosseinzadeh et al., 2014).

FIGURE 3

FIGURE 3. Typical representation of linear string and their GEP model.

Figure 4 illustrates the GEP operators, schematically. As shown, the generation of chromosomes in a random manner is the first stage of GEP. In the second stage, the validation of each individual population is investigated by the use of fitness functions as the criteria. The generation of new output is performed by the usage of reproduction, crossover, and mutation operators in GEP.

FIGURE 4

FIGURE 4. Schematical representation of GEP flowchart (Ferreira, 2006).

During the regeneration stages, functions with lower performance are omitted after the adoption of the algorithm. Selection and combination of most appropriate data from parents were carried out using a swamp randomly selected section of two trees. Mutation is responsible to investigate the non-local properties during simulation (Okhovat and Mousavi, 2012; Khalaj et al., 2013; Zadshakoyan and Pourmostaghimi, 2013).

Results and Discussion

In this study, a feed-forward neural network with a back-propagation algorithm is used to simulate the process. The output of each neuron in the feed-forward technique is simply linked with the next layer. This strategy consists of one or more hidden layers and has one output layer. To increase the performance of evolution, all input data were normalized in the range 0–1. Hidden layers control the network by using a non-linear transfer function to learn linear or non-linear behavior between inputs and outputs. Normalizing is performed using Eq. 6 (Asadi et al., 2012):

$X_n=\frac{X-X_{\min }}{X_{\max }-X_{\min }},(8)$

where X_max and X_min are the highest and lowest limits, respectively. In this work, the back-propagation used by a network that has an input layer with its operating condition factor neurons (Table 1) and an output layer that has one neuron (i_corr); 47 experimental result patterns used to train the ANN model are seen in Table 2, and the remainder is used for research. As shown in Table 3, by consideration of regression as the criteria, “Logsig” and “Purelin” are the best functions for hidden and output layers, respectively.

TABLE 2

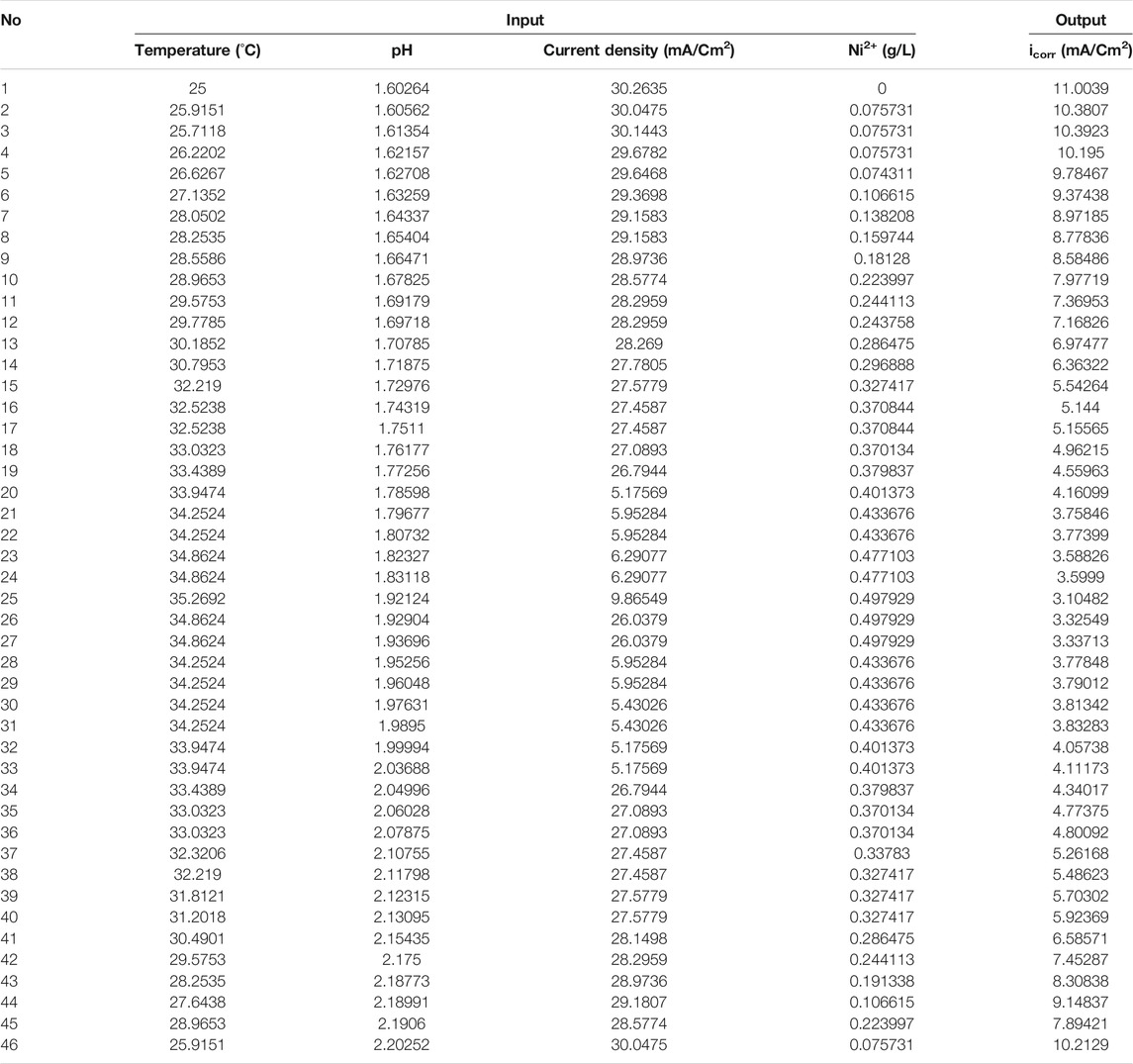
TABLE 2. Experimental data descriptions for GEP models (Darband et al., 2016a; Darband et al., 2016b).

TABLE 3

TABLE 3. Amount of regressions for different ANN structures.

In Figure 7, it can be observed that different ANN models with different neurons in the hidden layer provide higher R² of 0.9999, lower RMSE of 0.0002, and MAPE of 0.0171. Hence, this 3-3-1 topology is used in further analysis in this study, as shown in Figure 3.

The comparison between experimental and expected data is shown in Figure 5. The correlation coefficient for the training and evaluation processes is also 0.9999 and 0.9985, respectively. Neural network results confirmed high precision in the experimental data.

FIGURE 5

FIGURE 5. Result of ANN models: (A) R², (B) RMSE, and (C) MAPE.

The close linear pattern between the ANN predicts the values for the performance parameters, and the experimental dataset shows the adjacency of the model (Jiménez-Come et al., 2020). In order to determine the relative value of each input parameter, the sensitivity analyses have been performed. The aim of the study was to reduce the number of input parameters if the output of the model proves negligible. The elimination of input parameters would minimize excessive data processing, leading to a reduction in costs. A step-by-step procedure was performed for the trained ANN in order to continuously adjust each parameter of the input. In this study, we have selected different rates (5 and 10). As a result of changing the input parameter, the percentage of each input parameter was modified to the output. Eq. 9 has measured the sensitivity of each input parameter (Liu et al., 2017).

${\mathrm{S}}_{\mathrm{i}}=\frac{1}{\mathrm{N}}{\displaystyle \sum _1^n\left(\frac{\%\text{Change}\text{in}\text{output}}{\%\text{Change}\text{in}\text{input}}\right)}\times 100,(9)$

where the level of sensitivity related to input is represented by S_i (%), and N = 47 is the number of datasets.

Changes in the hardness of each input variable are shown in Figure 6. As shown, the magnitude of operating conditions such as pH, temperature, Ni²⁺, and current density has more positive impact on the corrosion current density (i_corr) of products.

FIGURE 6

FIGURE 6. Schematical representation of the ANN model.

The corrosion current of Ni–Zn electrophosphate coating is a function of temperature. The corrosion current decreased as the temperature increased.

Only tiny needlelike crystals shaped on a substrate surface at room temperature do not cover the entire region. In general, the development of phosphate coating includes nucleation and growth phases. As the nucleation stage occurs at low temperatures, the tiny needles are formed, but the growth kinetics at this temperature is too low, and thus the growth process cannot be completed. As can be observed, the kinetic energy of the growth stage is high enough to complete the growth process by raising the temperature to 43°C, thereby increasing the corrosion current (Zhang et al., 2016; Lu et al., 2021).

The corrosion current increases slightly when the pH increases from 1.8 to 2.2 and increases greatly up to 2.2. Increasing of corrosion current with increase of pH is related to the porosity of coating and thus decreasing of resistance of corrosion.

As the current density is increased to 22 mA/cm², further increase in the current density is directly dependent on corrosion current. This increase in the current density results from a high over potential, and this leads to an increased nucleation rate. The increasing value of the current density also leads to Ni–Zn electrophosphate coating (Benea et al., 2009). It displays the effect of Ni²⁺ concentration on the corrosion current of Ni–Zn electrophosphate coating. The corrosion current of coating decreases when the Ni²⁺ concentration in the bath is increased. However, an increase in the excess of 1 g/L does not cause further loss of corrosion current and become constant.

The presence of nickel ions in the bath decreases the size of phosphate coatings and improves the corrosion behavior of phosphate coatings. The improvement of corrosion resistance of phosphate coating in the presence of Ni²⁺ is due to the fact that nickel ions in the phosphatization bath is a place for nucleation of phosphate crystals which acts and reduces the size of phosphate coating seeds.

Genetic algorithms have been used for the choosing of a single point crossover and the roulette wheel. Each individual was developed using an ANN model to determine the fitness function. The crossover probability, mutation probability, starting population, and generation size have been chosen to be 0.8, 0.2, 50, and 100, respectively. According sensitivity analysis and GA simulation predicted the combination sintering temperature 8.35°C, pH 9.93, current density 8.64 mA/cm², and Ni²⁺ 9.09 g/L to give the optimum corrosion current density (i_corr) of 1.61 mA/cm². Experiments in various setups were performed to test the results, and the results are described in Table 3. The experimentally obtained optimum fitness function was determined by number 1 closer to GA’s predicted conditions. The validity of the simulated results is conclusively confirmed.

The practical parameters of each GEP model are abbreviated in Table 4. The maximum number of genes chosen is equal to 4 to prevent an increase in complexity. Since 1 gene has a very weak performance, the number of genes chosen is equal to 3. The head size is changed continuously from 10 at first to 11. MAPE is more appropriate than RMSE for fitness function.

TABLE 4

TABLE 4. Proposed optimum condition by GA.

Table 5 abbreviates the statistical characteristics of GEP models. Accordingly, R² values for the training phase change between 0.9913–0.9981. As shown in Figure 7 the minimum value of MAPE and RMSE are 0.0435 and 0.1040, respectively, for training data.

TABLE 5

TABLE 5. Different parameters of GEP.

FIGURE 7

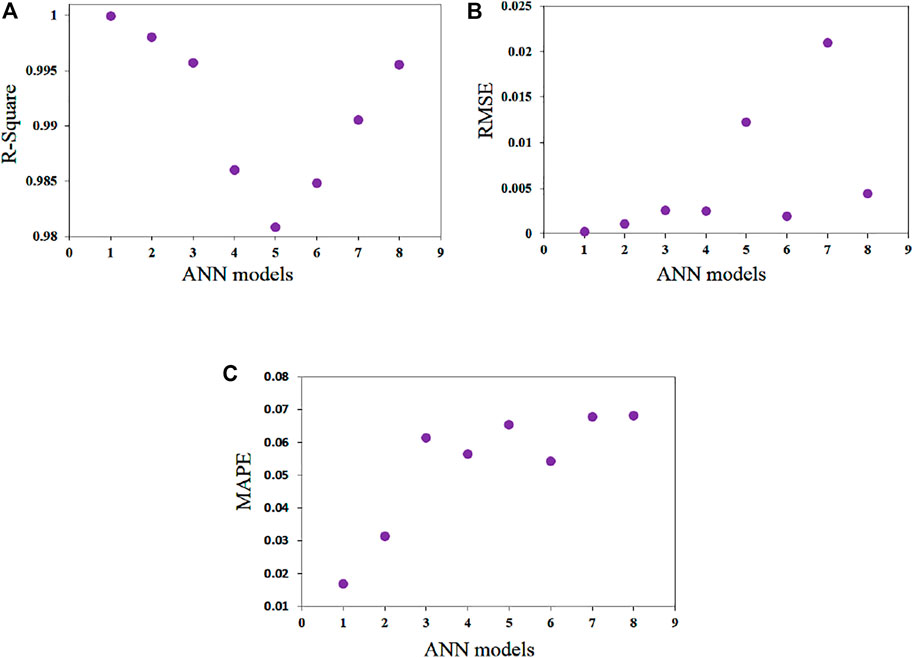
FIGURE 7. (A) Training data and (B) testing data using regression analysis of predicted and experimental hardness.

In Table 6, the best GEP model is GEP-2 with linking function addition, head size 10, and number of genes about 4. Changing the linking function to multiplication with the same head size and number of genes in the GEP-6 model shows the best model is GEP-2 with 30 chromosomes. Table 7 shows the differed chromosomes, head size, and genes number for GEP-2 models. The R², RMSE, and MAPE of different models of GEP-2 are shown in Figure 8.

TABLE 6

TABLE 6. Statistics of GEP models.

TABLE 7

TABLE 7. Statistical data and parameters for selected GEP model.

FIGURE 8

FIGURE 8. Significances of input variables in mechanical properties.

The best GEP model is Model 1 as shown in Table 7, according to R² values. In Figure 9, this model expression tree is provided for the four subgenes of the proposed model.

FIGURE 9

FIGURE 9. Result of GEP models: (A) R², (B) RMSE, and (C) MAPE.

As shown in Figure 10, the expression tree of the GEP-2 and formulation of this shows

$y=\cos \frac{\left({\left(d_3\times 9.55\right)}^2/\left(d_2-\log \left(d_2\right)\right)\right)}{\cos \left(d_3\right)}+\cos \left(d_2+{242.79}^2\right)+{\left(\frac{d_3-4.03}{\left(6.34/d_0+d_0+\sqrt{5.15}\right)}\right)}^2,$

$d_0=pH,d_2=\text{Current}\text{density}{d}_3=\mathrm{N}{i}^{2+} .$

FIGURE 10

FIGURE 10. Expression tree of the GEP-2.

Conclusion

The ANN model with one hidden layer with three neurons in the hidden layer is a useful method for the prediction of operating conditions to the corrosion current density (i_corr). The combined GA–ANN algorithm was an effective model for optimizing i_corr parameters to the minimum of operating conditions. Sensitivity analysis showed that Ni²⁺ concentration and temperature are the most significant parameter, and Ni²⁺ concentration is the most important parameter.

This study proposed the most appropriate models by the employment of GEP for the estimation of operating conditions to the minimum corrosion current density (i_corr). One type of function, that is, monotonic and non-monotonic, has been used within GEP. Then, by consideration of the lowest value of MAPE as the criteria, the best models were selected. The combination of sintering temperature 8.35°C, pH 9.93, current density 8.64 mA/cm², and Ni²⁺ 9.09 g/L predicted by GA simulation and sensitivity analysis would result in an optimal corrosion current density (icorr) of 1.61 mA/cm². In summary, the GEP models had a relatively high accuracy for the prediction of friction factor of multi-stage counter-current fluidized bed reactor, by consideration of the process parameters, operating conditions to the minimum corrosion current density (i_corr).

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

We consciously assure that this manuscript is our own original work, which has not been previously published elsewhere. It is not currently being considered for publication elsewhere and also reflects its analysis in a truthful and in complete manner. We have properly given credits to the meaningful contributions of co-authors. The results are appropriately placed in the context of prior and existing research. All sources used are properly disclosed (correct citation). All authors have been personally and actively involved in substantial work leading to the manuscript, and will take public responsibility for its content.

Author Contributions

MZ: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, resources, software, validation, visualization, writing—original draft. HA: writing—formal analysis and writing—revising draft. PG: formal analysis and writing—revising draft. NS: conceptualization, data curation, formal analysis, investigation, methodology, resources, supervision, validation, visualization, writing—original draft, and writing—review and editing. GS: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing—original draft, and writing—review and editing.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors are thankful to Bam University of Medical Sciences.

References

Asadi, P., Givi, M. K. B., Rastgoo, A., Akbari, M., Zakeri, V., and Rasouli, S. (2012). Predicting the Grain Size and Hardness of AZ91/SiC Nanocomposite by Artificial Neural Networks. Int. J. Adv. Manuf Technol. 63, 1095–1107. doi:10.1007/s00170-012-3972-z

CrossRef Full Text | Google Scholar

Ashtiani, H. R. R., and Shahsavari, P. (2016). A Comparative Study on the Phenomenological and Artificial Neural Network Models to Predict Hot Deformation Behavior of AlCuMgPb alloy. J. Alloys Compd. 687, 263–273. doi:10.1016/j.jallcom.2016.04.300

CrossRef Full Text | Google Scholar

Ates, H. (2007). Prediction of Gas Metal Arc Welding Parameters Based on Artificial Neural Networks. Mater. Des. 28, 2015–2023. doi:10.1016/j.matdes.2006.06.013

CrossRef Full Text | Google Scholar

Benea, L., Wenger, F., Ponthiaux, P., and Celis, J. P. (2009). Tribocorrosion Behaviour of Ni-SiC Nano-Structured Composite Coatings Obtained by Electrodeposition. Wear 266, 398–405. doi:10.1016/j.wear.2008.04.018

CrossRef Full Text | Google Scholar

Canakci, A., Varol, T., and Ozsahin, S. (2015). Artificial Neural Network to Predict the Effect of Heat Treatment, Reinforcement Size, and Volume Fraction on AlCuMg alloy Matrix Composite Properties Fabricated by Stir Casting Method. Int. J. Adv. Manuf Technol. 78, 305–317. doi:10.1007/s00170-014-6646-1

CrossRef Full Text | Google Scholar

Coşkun, M. İ., and Karahan, İ. H. (2018). Modeling Corrosion Performance of the Hydroxyapatite Coated CoCrMo Biomaterial Alloys. J. Alloys Compd. 745, 840–848. doi:10.1016/j.jallcom.2018.02.253

CrossRef Full Text | Google Scholar

Darband, G. B., Afshar, A., and Aliabadi, A. (2016). Zn-Ni Electrophosphating on Galvanized Steel Using Cathodic and Anodic Electrochemical Methods. Surf. Coat. Technol. 306, 497–505. doi:10.1016/j.surfcoat.2015.12.089

CrossRef Full Text | Google Scholar

Darband, G. B., Afshar, A., and Rabani, M. (2016). Effect of Treatment Time and Temperature on Microstructure and Corrosion Behavior of Zn-Ni Electrophosphate Coating. J. Alloys Compd. 688, 596–604. doi:10.1016/j.jallcom.2016.07.032

CrossRef Full Text | Google Scholar

Dashtian, K., and Zare-Dorabei, R. (2017). Synthesis and Characterization of Functionalized Mesoprous SBA-15 Decorated with Fe3O4 Nanoparticles for Removal of Ce(III) Ions from Aqueous Solution: ICP-OES Detection and central Composite Design Optimization. J. Colloid Interf. Sci. 494, 114–123. doi:10.1016/j.jcis.2017.01.072

PubMed Abstract | CrossRef Full Text | Google Scholar

Datta, S., and Chattopadhyay, P. P. (2013). Soft Computing Techniques in Advancement of Structural Metals. Int. Mater. Rev. 58, 475–504. doi:10.1179/1743280413y.0000000021

CrossRef Full Text | Google Scholar

Evis, Z., and Arcaklioglu, E. (2011). Artificial Neural Network Investigation of Hardness and Fracture Toughness of Hydroxylapatite. Ceramics Int. 37, 1147–1152. doi:10.1016/j.ceramint.2010.10.037

CrossRef Full Text | Google Scholar

Ferreira, C. (2006). Gene Expression Programming: Mathematical Modeling by an Artificial Intelligence. Berlin/Heidelberg, Germany: Springer.

Google Scholar

Finke, A., Escobar, J., Munoz, J., Petit, M., and Technology, C. (2021). Prediction of Salt spray Test Results of Micro Arc Oxidation Coatings on AA2024 Alloys by Combination of Accelerated Electrochemical Test and Artificial Neural Network. Surf. Coat. Technol. 421, 127370. doi:10.1016/j.surfcoat.2021.127370

CrossRef Full Text | Google Scholar

Gandomi, A. H., and Roke, D. A. (2015). Assessment of Artificial Neural Network and Genetic Programming as Predictive Tools. Adv. Eng. Softw. 88, 63–72. doi:10.1016/j.advengsoft.2015.05.007

CrossRef Full Text | Google Scholar

Golafshani, E. M., Rahai, A., and Sebt, M. H. (2015). Artificial Neural Network and Genetic Programming for Predicting the Bond Strength of GFRP Bars in concrete. Mater. Struct. 48, 1581–1602. doi:10.1617/s11527-014-0256-0

CrossRef Full Text | Google Scholar

Hoseinian, F. S., Faradonbeh, R. S., Abdollahzadeh, A., Rezai, B., and Soltani-Mohammadi, S. (2017). Semi-autogenous Mill Power Model Development Using Gene Expression Programming. Powder Technol. 308, 61–69. doi:10.1016/j.powtec.2016.11.045

CrossRef Full Text | Google Scholar

Hosseinzadeh, F., Sarpoolaki, H., and Hashemi, H. (2014). Precursor Selection for Sol-Gel Synthesis of Titanium Carbide Nanopowders by a New Intuitionistic Fuzzy Multi-Attribute Group Decision-Making Model. Int. J. Appl. Ceram. Technol. 11, 681–698. doi:10.1111/ijac.12108

CrossRef Full Text | Google Scholar

Hou, T.-H., Su, C.-H., and Liu, W.-L. (2007). Parameters Optimization of a Nano-Particle Wet Milling Process Using the Taguchi Method, Response Surface Method and Genetic Algorithm. Powder Technol. 173, 153–162. doi:10.1016/j.powtec.2006.11.019

CrossRef Full Text | Google Scholar

Hu, Q., Liu, Y., Zhang, T., Geng, S., and Wang, F. (2019). Modeling the Corrosion Behavior of Ni-Cr-Mo-V High Strength Steel in the Simulated Deep Sea Environments Using Design of experiment and Artificial Neural Network. J. Mater. Sci. Technol. 35, 168–175. doi:10.1016/j.jmst.2018.06.017

CrossRef Full Text | Google Scholar

Huang, Y., An, C., Zhang, Q., Zang, L., Shao, H., Liu, Y., et al. (2021). Cost-effective Mechanochemical Synthesis of Highly Dispersed Supported Transition Metal Catalysts for Hydrogen Storage. Nano Energy 80, 105535. doi:10.1016/j.nanoen.2020.105535

CrossRef Full Text | Google Scholar

Isleem, H. F., Tayeh, B. A., Alaloul, W. S., Musarat, M. A., and Raza, A. (2021). Artificial Neural Network (ANN) and Finite Element (FEM) Models for GFRP-Reinforced Concrete Columns under Axial Compression. Materials 14, 7172. doi:10.3390/ma14237172

PubMed Abstract | CrossRef Full Text | Google Scholar

Jafari, M. M., Soroushian, S., and Khayati, G. R. (2017). Hardness Optimization for Al6061-MWCNT Nanocomposite Prepared by Mechanical Alloying Using Artificial Neural Networks and Genetic Algorithm. J. Ultrafine Grained Nanostructured Mater. 50, 23–32. doi:10.7508/JUFGNSM.2017.01.04

CrossRef Full Text | Google Scholar

Jafari, S., and Mahini, S. S. (2017). Lightweight concrete Design Using Gene Expression Programing. Construction Building Mater. 139, 93–100. doi:10.1016/j.conbuildmat.2017.01.120

CrossRef Full Text | Google Scholar

Jamshidi, M., Ghaedi, M., Dashtian, K., Hajati, S., and Bazrafshan, A. A. (2016). Sonochemical Assisted Hydrothermal Synthesis of ZnO: Cr Nanoparticles Loaded Activated Carbon for Simultaneous Ultrasound-Assisted Adsorption of Ternary Toxic Organic Dye: Derivative Spectrophotometric, Optimization, Kinetic and Isotherm Study. Ultrason. Sonochem. 32, 119–131. doi:10.1016/j.ultsonch.2016.03.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiménez-Come, M. J., Martín, M. D. L. L., Matres, V., and Baladés, J. D. M. (2020). The Use of Artificial Neural Networks for Modelling Pitting Corrosion Behaviour of EN 1.4404 Stainless Steel in marine Environment: Data Analysis and New Developments. Corrosion Rev. 38. doi:10.1515/corrrev-2019-0095

CrossRef Full Text | Google Scholar

Karahan, İ. H., and Özdemir, R. (2015). A Comparison for Grain Size Calculation of Cu-Zn Alloys with Genetic Programming and Neural Networks. Acta Physica Pol. A 128, B427–B431. doi:10.12693/aphyspola.128.b-427

CrossRef Full Text | Google Scholar

Karahan, İ. H., Ozdemir, R., and Erkayman, B. (2013). A Comparison of Genetic Programming and Neural Networks; New Formulations for Electrical Resistivity of Zn-Fe Alloys. Appl. Phys. A. 113, 459–476. doi:10.1007/s00339-013-7544-3

CrossRef Full Text | Google Scholar

Kennedy, J., and Eberhart, R. (1995). “Particle Swarm Optimization,” in Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 Nov.-1 Dec. 1995.

Google Scholar

Khalaj, G., Nazari, A., Khoie, S. M. M., Khalaj, M. J., and Pouraliakbar, H. (2013). Chromium Carbonitride Coating Produced on DIN 1.2210 Steel by Thermo-Reactive Deposition Technique: Thermodynamics, Kinetics and Modeling. Surf. Coat. Technol. 225, 1–10. doi:10.1016/j.surfcoat.2013.02.030

CrossRef Full Text | Google Scholar

Kim, J. H., Reddy, N. S., Yeom, J. T., Hong, J. K., Lee, C. S., and Park, N.-K. (2009). Microstructure Prediction of Two-phase Titanium alloy during Hot Forging Using Artificial Neural Networks and FE Simulation. Met. Mater. Int. 15, 427–437. doi:10.1007/s12540-009-0427-7

CrossRef Full Text | Google Scholar

Laugier, S., and Richon, D. (2003). Use of Artificial Neural Networks for Calculating Derived Thermodynamic Quantities from Volumetric Property Data. Fluid phase equilibria 210, 247–255. doi:10.1016/s0378-3812(03)00172-9

CrossRef Full Text | Google Scholar

Li, J. G., Yao, Y. X., Gao, D., Liu, C. Q., and Yuan, Z. J. (2008). Cutting Parameters Optimization by Using Particle Swarm Optimization (PSO). Appl. Mech. Mater. 10, 879–883. doi:10.4028/www.scientific.net/AMM.10-12.879

CrossRef Full Text | Google Scholar

Li, Y., Macdonald, D. D., Yang, J., Qiu, J., and Wang, S. (2020). Point Defect Model for the Corrosion of Steels in Supercritical Water: Part I, Film Growth Kinetics. Corrosion Sci. 163, 108280. doi:10.1016/j.corsci.2019.108280

CrossRef Full Text | Google Scholar

Lin, B.-L., Lu, J.-T., and Kong, G. (2008). Effect of Molybdate post-sealing on the Corrosion Resistance of Zinc Phosphate Coatings on Hot-Dip Galvanized Steel. Corrosion Sci. 50, 962–967. doi:10.1016/j.corsci.2007.12.002

CrossRef Full Text | Google Scholar

Liu, G., Jia, L., Kong, B., Guan, K., and Zhang, H. (2017). Artificial Neural Network Application to Study Quantitative Relationship between Silicide and Fracture Toughness of Nb-Si Alloys. Mater. Des. 129, 210–218. doi:10.1016/j.matdes.2017.05.027

CrossRef Full Text | Google Scholar

Lu, Z., Zhang, F.-Y., Fu, H., Ding, H., and Chen, L.-Q. (2021). Rotational Nonlinear Double-Beam Energy Harvesting. Smart Mater. Structures 31, 210–218. doi:10.1088/1361-665X/ac4579

CrossRef Full Text | Google Scholar

Mansouri, I., Gholampour, A., Kisi, O., and Ozbakkaloglu, T. (2018). Evaluation of Peak and Residual Conditions of Actively Confined concrete Using Neuro-Fuzzy and Neural Computing Techniques. Neural Comput. Applic 29, 873–888. doi:10.1007/s00521-016-2492-4

CrossRef Full Text | Google Scholar

Mansouri, I., and Kisi, O. (2015). Prediction of Debonding Strength for Masonry Elements Retrofitted with FRP Composites Using Neuro Fuzzy and Neural Network Approaches. Composites B: Eng. 70, 247–255. doi:10.1016/j.compositesb.2014.11.023

CrossRef Full Text | Google Scholar

Martí, P., Shiri, J., Duran-Ros, M., Arbat, G., De Cartagena, F. R., and Puig-Bargués, J. (2013). Artificial Neural Networks vs. Gene Expression Programming for Estimating Outlet Dissolved Oxygen in Micro-irrigation Sand Filters Fed with Effluents. Comput. Electron. Agric. 99, 176–185. doi:10.1016/j.compag.2013.08.016

CrossRef Full Text | Google Scholar

Mozaffari, S., Li, W., Thompson, C., Ivanov, S., Seifert, S., Lee, B., et al. (2017). Colloidal Nanoparticle Size Control: Experimental and Kinetic Modeling Investigation of the Ligand-Metal Binding Role in Controlling the Nucleation and Growth Kinetics. Nanoscale 9, 13772–13785. doi:10.1039/c7nr04101b

PubMed Abstract | CrossRef Full Text | Google Scholar

Nouiri, M., Bekrar, A., Jemai, A., Niar, S., and Ammari, A. C. (2018). An Effective and Distributed Particle Swarm Optimization Algorithm for Flexible Job-Shop Scheduling Problem. J. Intell. Manuf 29, 603–615. doi:10.1007/s10845-015-1039-3

CrossRef Full Text | Google Scholar

Okhovat, A., and Mousavi, S. M. (2012). Modeling of Arsenic, Chromium and Cadmium Removal by Nanofiltration Process Using Genetic Programming. Appl. Soft Comput. 12, 793–799. doi:10.1016/j.asoc.2011.10.012

CrossRef Full Text | Google Scholar

Rashidi, A. M., Hayati, M., and Rezaei, A. (2012). Application of Artificial Neural Network for Prediction of the Oxidation Behavior of Aluminized Nano-Crystalline Nickel. Mater. Des. 42, 308–316. doi:10.1016/j.matdes.2012.06.011

CrossRef Full Text | Google Scholar

Su, H.-Y., and Lin, C.-S. (2014). Effect of Additives on the Properties of Phosphate Conversion Coating on Electrogalvanized Steel Sheet. Corrosion Sci. 83, 137–146. doi:10.1016/j.corsci.2014.02.002

CrossRef Full Text | Google Scholar

Tsai, C.-Y., Liu, J.-S., Chen, P.-L., and Lin, C.-S. (2010). A Two-step Roll Coating Phosphate/molybdate Passivation Treatment for Hot-Dip Galvanized Steel Sheet. Corrosion Sci. 52, 3385–3393. doi:10.1016/j.corsci.2010.06.020

CrossRef Full Text | Google Scholar

Varol, T., Canakci, A., and Ozsahin, S. (2013). Artificial Neural Network Modeling to Effect of Reinforcement Properties on the Physical and Mechanical Properties of Al2024-B4c Composites Produced by Powder Metallurgy. Composites Part B: Eng. 54, 224–233. doi:10.1016/j.compositesb.2013.05.015

CrossRef Full Text | Google Scholar

Vettivel, S. C., Selvakumar, N., and Leema, N. (2013). Experimental and Prediction of Sintered Cu-W Composite by Using Artificial Neural Networks. Mater. Des. 45, 323–335. doi:10.1016/j.matdes.2012.08.056

CrossRef Full Text | Google Scholar

Wu, X., Liu, Z., Yin, L., Zheng, W., Song, L., Tian, J., et al. (2021). A Haze Prediction Model in Chengdu Based on LSTM. Atmosphere 12, 1479. doi:10.3390/atmos12111479

CrossRef Full Text | Google Scholar

Xu, C., Rangaiah, G. P., and Zhao, X. S. (2015). Application of Artificial Neural Network and Genetic Programming in Modeling and Optimization of Ultraviolet Water Disinfection Reactors. Chem. Eng. Commun. 202, 1415–1424. doi:10.1080/00986445.2014.952813

CrossRef Full Text | Google Scholar

Xu, Y.-Y., and Lin, B.-L. (2007). Effect of Silicate Pretreatment, post-sealing and Additives on Corrosion Resistance of Phosphated Galvanized Steel. Trans. Nonferrous Met. Soc. China 17, 1248–1253. doi:10.1016/s1003-6326(07)60257-x

CrossRef Full Text | Google Scholar

Yusup, N., Zain, A. M., and Hashim, S. Z. M. (2012). Overview of PSO for Optimizing Process Parameters of Machining. Proced. Eng. 29, 914–923. doi:10.1016/j.proeng.2012.01.064

CrossRef Full Text | Google Scholar

Zadshakoyan, M., and Pourmostaghimi, V. (2013). Genetic Equation for the Prediction of Tool-Chip Contact Length in Orthogonal Cutting. Eng. Appl. Artif. Intelligence 26, 1725–1730. doi:10.1016/j.engappai.2012.10.016

CrossRef Full Text | Google Scholar

Zaki, M. R., Varshosaz, J., and Fathi, M. (2015). Preparation of agar Nanospheres: Comparison of Response Surface and Artificial Neural Network Modeling by a Genetic Algorithm Approach. Carbohydr. Polym. 122, 314–320. doi:10.1016/j.carbpol.2014.12.031

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeraati, M., and Khayati, M. (2018). Optimization of Micro Hardness of Nanostructure Cu-Cr-Zr Alloys Prepared by the Mechanical Alloying Using Artificial Neural Networks and Genetic Algorithm. J. Ultrafine Grained Nanostructured Mater. 51, 183–192. doi:10.22059/JUFGNSM.2018.02.11

CrossRef Full Text | Google Scholar

Zhang, L., Wang, L., Zhang, Y., Wang, D., Guo, J., Zhang, M., et al. (2021). The Performance of Electrode Ultrafiltration Membrane Bioreactor in Treating Cosmetics Wastewater and its Anti-fouling Properties. Environ. Res. 206, 112629. doi:10.1016/j.envres.2021.112629

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Q., Zhou, C., Xiao, W., and Nelson, P. C. (2007). “Improving Gene Expression Programming Performance by Using Differential Evolution,” in Proceedings of the Sixth International Conference on Machine Learning and Applications (ICMLA 2007), Cincinnati, OH, USA, December 2007 (Piscataway, New Jersey, United States: IEEE), 31–37. doi:10.1109/icmla.2007.62

CrossRef Full Text | Google Scholar

Zhang, X., Tang, Y., Zhang, F., and Lee, C.-S. (2016). A Novel Aluminum-Graphite Dual-Ion Battery. Adv. Energ. Mater. 6, 1502588. doi:10.1002/aenm.201502588

CrossRef Full Text | Google Scholar

Zhu, H., Zhu, J., Zhang, Z., and Zhao, R. (2021). Crossover from Linear Chains to a Honeycomb Network for the Nucleation of Hexagonal Boron Nitride Grown on the Ni (111) Surface. The J. Phys. Chem. C 48, 26542–26551. doi:10.1021/acs.jpcc.1c09334

CrossRef Full Text | Google Scholar