
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater. , 28 September 2022
Sec. Computational Materials Science
Volume 9 - 2022 | https://doi.org/10.3389/fmats.2022.1010049
This article is part of the Research Topic Computational Modeling for Nuclear Materials View all 5 articles
The total ionizing dose (TID) effect is one of the main causes of the performance degradation/failure of semiconductor devices under high-energy γ-ray irradiation. In special, the concentration of doubly-hydrogenated oxygen vacancy (a case study of
More and more new semiconductor materials are widely used as the core electronic components of sensors, detectors, radar and so on. In extreme service environments, semiconductor devices are inevitably affected by harsh radiation effects. All kinds of high-energy particles will cause serious ionization or displacement damage to semiconductors, then lead to the degradation/failure of the electrical performance of semiconductor devices, and pose adverse effects on the safety and lifetime of the entire electronic systems (Benton and Benton, 2001).
As early as 1964, Hughes and Giroux conducted a preliminary study (Hughes and Giroux, 1964) on the performance degradation of semiconductor devices (MOS) under the total ionizing dose (TID). They found that TID-induced performance degradation is due to the additional charge generated in the oxide layer (SiO2) rather than on the surface. In subsequent decades, a large number of experimental studies of ionizing irradiation showed that the key mechanism of the performance degradation induced by the TID is the formation of oxide charged defects (Not) in the gate oxide region (Hughes, 1965a; Hughes, 1965b; Kooi, 1965; Zaininger, 1966). Therefore, identification of neutral defects in SiO2 before irradiation and exploration of the evolution of charged defects after irradiation are the basis for studying the TID effect of MOS devices.
In 1956, Robert used electron paramagnetic resonance (EPR) for the first time to measure radiation-induced defects in crystalline or amorphous SiO2 (Weeks, 1963) and found two basic types of oxygen vacancies in SiO2, including deep (
The pre-existing concentration of defects in SiO2 is still known little. Density functional theory (DFT) calculations suggest that relative concentrations of different pre-existing trap species, and order of magnitude estimates of the actual concentration of defects have been suggested by etch-back experiments of irradiated oxides (Devine et al., 1993). It is found that the initial concentration of doubly-hydrogenated oxygen vacancy before irradiation is relatively high, while its charged concentration after irradiation is the lowest among the oxide charged defects (Rowsey et al., 2011a). In the process of ionizing irradiation, the evolution process of doubly-hydrogenated oxygen vacancy and its specific contribution to the TID effect are still unclear. It is thus urgent to establish a dynamic model of the TID effect that includes the dynamic of doubly-hydrogenated oxygen vacancy to reveal their influence mechanism.
In this paper, a one-dimensional (1-D) dynamics model of mobile particles and fixed defects in the oxide layer (SiO2) of typical silicon MOS devices is developed to systematically study the influence of doubly-hydrogenated oxygen vacancy on the TID effect. This work provides theoretical guidance by controlling the concentration of doubly-hydrogenated oxygen vacancy for the radiation-hardening-by-design (RHBD) techniques of semiconductor devices.
The model framework is shown in Figure 1. First, the initial distribution of defects can be determined by EPR measurements (Lenahan and Conley, 1998; Lu et al., 2002). The reaction events and rate coefficients between mobile particles and defects are mainly given by the DFT calculations (Rowsey et al., 2011a; Rowsey et al., 2011b). Then, with this information, the continuity equations of mobile particles and fixed defects can be described based on the rate theory. In addition, the Poisson equation is established to determine the spatial electric field distribution. Finally, the finite difference method is employed to solve the ordinary differential equations (ODEs). The evolution and distribution of oxide charged defects and electric fields can thus be obtained by this model.
Continuity equation
The continuity Eq. 1 in Figure 1, where
The generation rate of e-h pairs induced by ionizing irradiation is given as follows (Oldham, 2000),
where G0 represents the density of e-h pairs per unit ionizing dose, Y is the survival rate of the e-h pairs after initial recombination, which is set to be 0.01 for SiO2 under γ-ray irradiation (Shaneyfelt et al., 1991), and R is the dose rate (rad/s).
The reaction rates of mobile particles with fixed defects are determined by the rate theory, which is proportional to the reactant concentrations. Comprehensively considering all reaction events, the total reaction rate of the particle i is given by (Xu et al., 2018),
where the j, m and n are termed as the other reactants, and the α and β represent the forward and reverse reaction rate coefficients, respectively.
Since the fixed defect is immobile and has no additional generation, the continuity equation includes only the reaction term (
Since deep- and shallow-level defects cannot be transformed into each other, we only consider the dynamics of deep-level defects (
For oxygen vacancy (
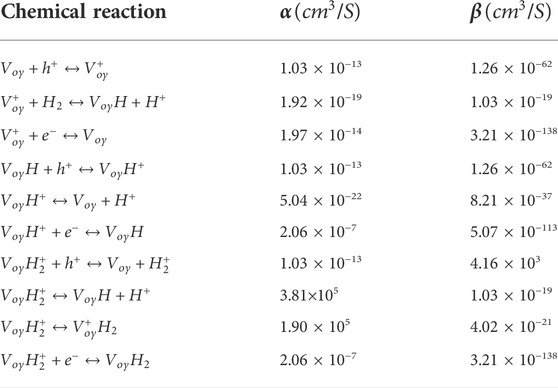
TABLE 1. Chemical reaction and rate coefficients (Bunson et al., 2000; Rowsey et al., 2012; Patrick et al., 2015; Sharov et al., 2022).
The accumulation of the charged defects results in the formation of a built-in electric field in the oxide layer. The electric field can be solved by Poisson’s equation as below (Esqueda et al., 2012; Jafari et al., 2015),
where,
An important parameter is the density of Not, with units of cm−2, which can be integrated from the distribution of each oxide charged defect as (Esqueda et al., 2011),
where Lox is the thickness of the oxide layer, and x refers to the distance from the Gate.
The finite difference method with a uniform spatial grid is adopted for solving the partial differential equations (PDEs). Here the lsoda solver of the C version (Whitbeck, 1991) is employed to solve the corresponding ODEs. The key to using the finite difference method to solve the above time and space related problems is the setting of appropriate initial values and boundary conditions. The initial concentration of charged defects and charged particles is set to 0. In the 1-D model, there are two boundaries of Gate/SiO2 and Si/SiO2 in contact with the SiO2 layer. The mobile particles can flow freely at both boundaries, so the first kind of boundary conditions are adopted. In addition, we specify that the electrostatic potential is continuous at all boundaries (Xu et al., 2018).
This section presents the evolution and distribution of defects in the SiO2 layer of an NPN-type MOS capacitor (Lox = 200 nm) irradiated by γ-rays of
The simulated density of oxide charged defects (Not) is compared with the experimental ones (Tuttle et al., 2010) to verify our model. Figure 2 shows the time evolution of the density of Not, under the time of
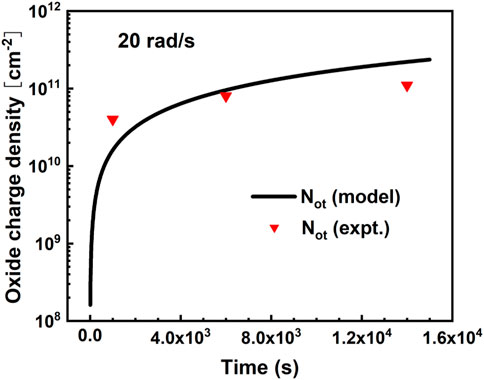
FIGURE 2. Comparison of the evolution of Not with the experiment for the MOS capacitor with a 200 nm SiO2 layer under 5 V bias.
In the following, we studied the key factors of the oxide charged defects for the TID effect, such as their composition, distribution and evolution. Figure 3A shows the distributions of different oxide charged defects under the TID of 10 krad with the dose rate of 10 rad/s at 300 K.
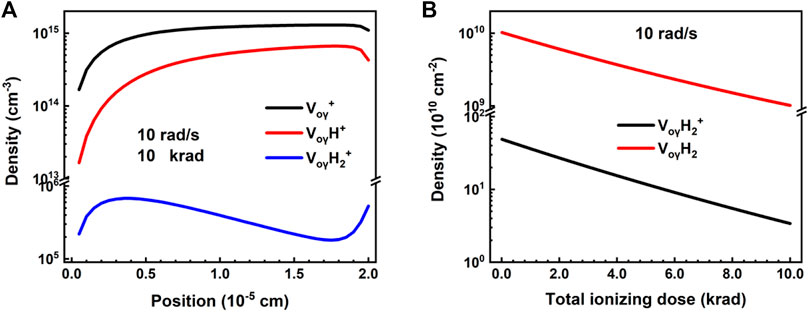
FIGURE 3. Distributions of (A) different oxide charged defects under the TID of 10 krad, and (B) evolution of
Also as shown in Figure 3A, with increasing the distance from the Gate, the densities of
As given above,
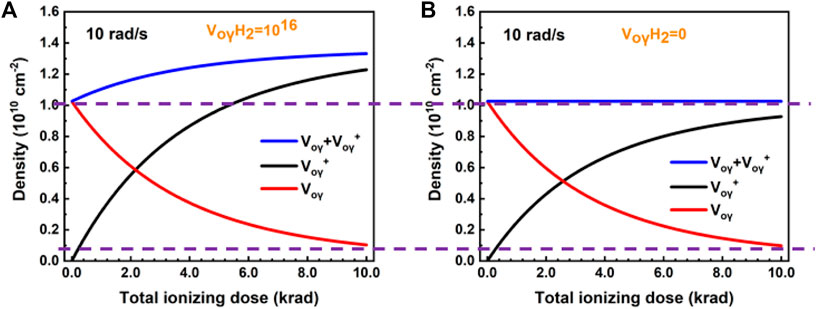
FIGURE 4. Evolution of
We also simulated the densities of
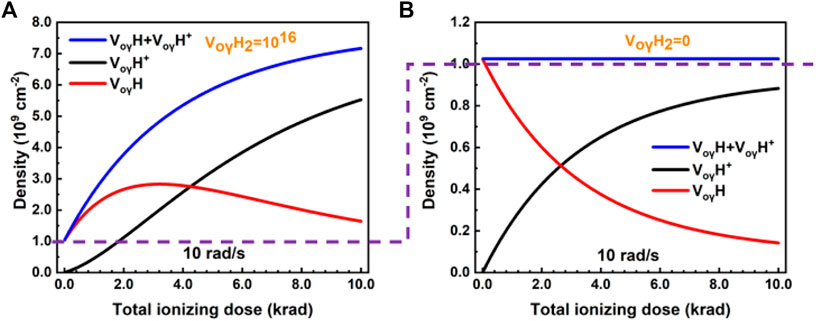
FIGURE 5. Evolution of
It has been known that the TID effect of devices is closely related to the electric field near the Si/SiO2 interface (
According to Eq. 8, when the gate voltage (
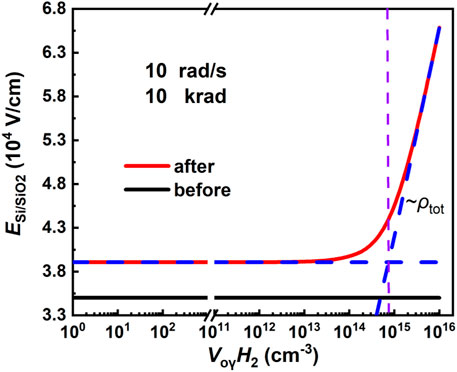
FIGURE 6. Electric fields at the Si/SiO2 interface with increasing the density of
In summary,
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
GL: Methodology, Software, Data Curation, Formal analysis, Writing—Original Draft. JL: Methodology, Formal analysis, Software, Writing—Review and; Editing. QZ: Writing—Review and; Editing. YL: Formal analysis, Writing—Review and; Editing, Funding acquisition.
This work was supported by the National Natural Science Foundation of China (Grant No. 11975018), the National MCF Energy R&D Program (Grant No. 2018YEF0308100), and the Outstanding member of Youth Innovation Promotion Association CAS (Grant No. Y202087). Some of the calculations were performed at the Center for Computational Science of CASHIPS, the ScGrid of Supercomputing Center, and the Computer Network Information Center of the Chinese Academy of Sciences. This research work was also supported by the Tianhe-2JK computing time award of the Beijing Computational Science Research Center (CSRC).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Benton, E. R., and Benton, E. V. (2001). Space radiation dosimetry in low-Earth orbit and beyond. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 184, 255–294. doi:10.1016/s0168-583x(01)00748-0
Blöchl, P. E. (2000). First-principles calculations of defects in oxygen-deficient silica exposed to hydrogen. Phys. Rev. B 62, 6158–6179. doi:10.1103/physrevb.62.6158
Bunson, P. E., Ventra, M. D., Pantelides, S. T., Fleetwood, D. M., and Schrimpf, R. D. (2000). Hydrogen-related defects in irradiated SiO2. IEEE Trans. Nucl. Sci. 47, 2289–2296. doi:10.1109/23.903767
Conley, J. F., and Lenahan, P. M. (1993). Room temperature reactions involving silicon dangling bond centers and molecular hydrogen in amorphous SiO2 thin films on silicon. Appl. Phys. Lett. 62, 40–42. doi:10.1063/1.108812
Devine, R. A. B., Mathiot, D., Warren, W. L., Fleetwood, D. M., and Aspar, B. (1993). Point defect generation during high temperature annealing of the Si-SiO2 interface. Appl. Phys. Lett. 63, 2926–2928. doi:10.1063/1.110275
Esqueda, I. S., Barnaby, H. J., and Adell, P. C. (2012). Modeling the effects of hydrogen on the mechanisms of dose rate sensitivity. IEEE Trans. Nucl. Sci. 59, 701–706. doi:10.1109/tns.2012.2195201
Esqueda, I. S., Barnaby, H. J., Adell, P. C., Rax, B. G., Hjalmarson, H. P., McLain, M. L., et al. (2011). Modeling low dose rate effects in shallow trench isolation oxides. IEEE Trans. Nucl. Sci. 58, 2945–2952. doi:10.1109/tns.2011.2168569
Hughart, D. R., Schrimpf, R. D., Fleeteood, D. M., Rowsey, N. L., Law, M. E., Tuttle, B. R., et al. (2012). The effects of proton-defect interactions on radiation-induced interface-trap formation and annealing. IEEE Trans. Nucl. Sci. 59, 3087–3092. doi:10.1109/tns.2012.2220982
Hughart, D. R., Schrimpf, R. D., Fleetwood, D. M., Chen, X. J., Barnaby, H. J., Holbert, K. E., et al. (2009). The effects of aging and hydrogen on the radiation response of gated lateral PNP bipolar transistors. IEEE Trans. Nucl. Sci. 56, 3361–3366. doi:10.1109/tns.2009.2034151
Hughart, D. R., Schrimpf, R. D., Fleetwood, D. M., Tuttle, B. R., and Pantelides, S. T. (2011). Mechanisms of interface trap buildup and annealing during elevated temperature irradiation. IEEE Trans. Nucl. Sci. 58, 2930–2936. doi:10.1109/tns.2011.2171364
Hughes, H. L. (1965). Radiation effects on evacuated and gas encapsulated commercially available silicon planar transistors. Bull. Am. Phys. Soc. 9, 655.
Hughes, H. L. (1965). Surface effects of space radiation on silicon devices. IEEE Trans. Nucl. Sci. 12, 53–63. doi:10.1109/tns.1965.4323924
Jafari, H., Feghhi, S. A. H., and Boorboor, S. (2015). The effect of interface trapped charge on threshold voltage shift estimation for gamma irradiated MOS device. Radiat. Meas. 73, 69–77. doi:10.1016/j.radmeas.2014.12.008
Kooi, E. (1965). Influence of X-ray irradiations on the charge distribution of metal-oxide-silicon structures. Philips Res. Rept. 20, 306.
Lenahan, P. M., and Conley, J. F. (1998). What can electron paramagnetic resonance tell us about the Si/SiO2 system. J. Vac. Sci. Technol. B 16, 2134–2153. doi:10.1116/1.590301
Lenahan, P. M., and Dressendorfer, P. V. (1984). Hole traps and trivalent silicon centers in metal/oxide/silicon devices. J. Appl. Phys. 55, 3495–3499. doi:10.1063/1.332937
Lu, Z. Y., Nicklaw, C. J., Fleetwood, D. M., Schrimpf, R. D., and Pantelides, S. T. (2002). Structure, properties, and dynamics of oxygen vacancies in amorphous SiO2. Phys. Rev. Lett. 89, 285505. doi:10.1103/physrevlett.89.285505
Oldham, T. R. (2000). Ionizing radiation effects in MOS oxides. World Scientific Programming. Singapore.
Patrick, E., Rowsey, N., and Law, M. E. (2015). Total dose radiation damage: A simulation framework. IEEE Trans. Nucl. Sci. 62, 1650–1657. doi:10.1109/tns.2015.2425226
Rowsey, N. L., Law, M. E., Schrimpf, R. D., Fleetwood, D. M., Tuttle, B. R., and Pantelides, S. T. (2011). A quantitative model for ELDRS and H2 degradation effects in irradiated oxides based on first principles calculations. IEEE Trans. Nucl. Sci. 58, 2937–2944. doi:10.1109/tns.2011.2169458
Rowsey, N. L., Law, M. E., Schrimpf, R. D., Fleetwood, D. M., Tuttle, B. R., and Pantelides, S. T. (2011). Radiation-induced oxide charge in low- and high-H2 environments. IEEE Trans. Nucl. Sci. 59, 51–53. doi:10.1109/TNS.2012.2183889
Rowsey, N. L., Law, M. E., Schrimpf, R. D., Fleetwood, D. M., Tuttle, B. R., and Pantelides, S. T. (2012). Radiation-induced oxide charge in low- and high-H2 environments. IEEE Trans. Nucl. Sci. 59, 755–759. doi:10.1109/tns.2012.2183889
Shaneyfelt, M. R., Fleetwood, D. M., and Hughes, K. L. (1991). Charge yield for cobalt-60 and 10-keV X-ray irradiations of MOS devices. IEEE Trans. Nucl. Sci. 38, 1187–1194. doi:10.1109/23.124092
Sharov, F. V., Moxim, S. J., Haase, G. S., Hughart, D. R., McKay, C. G., and Lenahan, P. M. (2022). Probing the atomic scale mechanisms of time dependent dielectric breakdown in Si/SiO2 MOSFETs. IEEE Trans. Device Mate. Reliab. 22, 322–331. doi:10.1109/TDMR.2022.3186232
Tuttle, B. R., Hughart, D. R., Schrimpf, R. D., Fleetwood, D. M., and Pantelides, S. T. (2010). Defect interactions of H2 in SiO2: Implications for ELDRS and latent interface trap buildup. IEEE Trans. Nucl. Sci. 57, 3046–3053. doi:10.1109/TNS.2010.2086076
Walle, C. G. V., and Tuttle, B. R. (2000). Microscopic theory of hydrogen in silicon devices. IEEE Trans. Electron Devices 47, 1779–1786. doi:10.1109/16.870547
Weeks, R. A. (1963). Paramagnetic spectra of E02 centers in crystalline quartz. Phys. Rev. 130, 570–576. doi:10.1103/physrev.130.570
Whitbeck, M. (1991). React - Program to solve kinetic equations for chemical systems. Desert Research Institute.Reno, Nevada.
Xu, J. J., Ma, Z. C., Li, H. L., Song, Y., Zhang, L. B., and Lu, B. Z. (2018). A multi-time-step finite element algorithm for 3-D simulation of coupled drift-diffusion reaction process in total ionizing dose effect. IEEE Trans. Semicond. Manufact. 31, 183–189. doi:10.1109/tsm.2017.2779058
Keywords: total ionizing dose effect, dynamic modeling, doubly-hydrogenated oxygen vacancy, microscopic mechanism, MOS devices
Citation: Lu G, Liu J, Zheng Q and Li Y (2022) Influence of doubly-hydrogenated oxygen vacancy on the TID effect of MOS devices. Front. Mater. 9:1010049. doi: 10.3389/fmats.2022.1010049
Received: 02 August 2022; Accepted: 07 September 2022;
Published: 28 September 2022.
Edited by:
Weiliang Wang, Sun Yat-sen University, ChinaReviewed by:
Zexiang Deng, Guilin University of Aerospace Technology, ChinaCopyright © 2022 Lu, Liu, Zheng and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yonggang Li, eWdsaUB0aGVvcnkuaXNzcC5hYy5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.