
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater. , 10 January 2020
Sec. Ceramics and Glass
Volume 6 - 2019 | https://doi.org/10.3389/fmats.2019.00342
This article is part of the Research Topic Glasses for Energy Applications View all 9 articles
Physical storage of gaseous hydrogen under high-pressure in glassy micro-containers such as spheres and capillaries is a promising concept for enhancing safety and the volumetric capacity of mobile hydrogen storage systems. As very low permeation through the container wall is required for storage of compressed hydrogen, development of glasses of minimal hydrogen permeability is needed. For this purpose, one has to understand better the dependence of hydrogen permeability on glass structure. The paper points out that minimizing the accessible free volume is a sound strategy to minimize hydrogen permeability. Based on previously measured and comprehensive literature data, it is shown that permeation is independently controlled by ionic porosity and network modifier content. Thus, ionic porosity in modified and fully polymerized networks can be decreased equally to the lowest hydrogen permeability among the glasses under study. Applying this concept, a drop of up to 30,000 with respect to the permeation of hydrogen molecules through silica glass is attainable.
Although gravimetric energy density of hydrogen gas (142 MJ kg−1) is at least three times larger than that of liquid hydrocarbons like conventional fuel, it suffers from low volumetric storage capacity (Schlapbach and Züttel, 2001). Compressed hydrogen in form of onboard tanks and portable devices would offer a cost-effective and sustainable near-term solution of hydrogen storage due to its low infrastructure impact and small carbon footprint involved with the effective production of hydrogen in its gaseous state by water electrolysis or water splitting. Despite the overall attractiveness of pressurized hydrogen gas storage, there remain striking issues in selection of safe and lightweight encapsulation materials. As metals suffer from material embrittlement and cracking well-below its initial yield stress and polymers cannot offer low enough permeation rates, oxidic glasses are found to be promising candidates for cost-effective, safe, and long-term storage of pressurized hydrogen in micro containers such as hollow microspheres and capillaries (Zhevago, 2016). Hence, the usage of glass capillary arrays has received progressive attention in recent years, not least because of the well-established manufacturing process (precise redrawing tubes) but due to closed-packed (honeycomb) polymer coated structuring options in combination with a rapid refueling capability (Zhevago and Glebov, 2007; Holtappels et al., 2011; Prewitz et al., 2018).
Compressed hydrogen storage in glass micro-containers demands for low permeation through the container wall and for successful development of glass compositions for which the product of hydrogen solubility and diffusion coefficient is minimal. Besides low permeability, a strong performance of the glass during hot shaping, which is expressed mainly in the form of a sufficient workability and a small crystallization tendency, as well as during service, where chemical process robustness is important, have to be taken into account before implementing new compositions into storage applications (Prewitz et al., 2018). With respect to permeation, accessibility of free volume of the network structure has been shown to be closely linked to the fundamental migration and solubility processes. For silica glass, predictions from noble gas solubility experiments under ambient conditions (Shackelford and Masaryk, 1978; Nakayama and Shackelford, 1990), high-pressure regimes (Shelby, 1976) and from molecular dynamics simulations (Chan and Elliott, 1991) result in a log-normal distribution of interstitial sites varying in size from 0.1 to 0.4 nm. Following the free volume approach, gas solubility and diffusion is then proportional to the fraction of the total interstitial volume that is connected to the main network and large enough for occupation (Shackelford, 2014).
Experimental studies, which are limited to fused silica and commercial borosilicate glasses (Johnson and Burt, 1922; Barrer, 1934; Altemose, 1961; Lee et al., 1962; Laska and Doremus, 1969; Laska et al., 1969; Morimoto et al., 1992; Shelby, 1996; Kurita et al., 2002), alkali-alkaline earth silicate glasses (Barton and Morain, 1970) and aluminoborosilicate glasses (Ried et al., 2014) show that isothermal permeability can vary up to three orders of magnitude. The underlying principles in the correlations between glass composition, accessible free volume and hydrogen permeation are still unclear. Only recently, a first attempt limited to hydrogen diffusivity was made by drawing a distinction between free volume reductions in modified and in fully polymerized networks (Welter et al., 2019).
The present paper picks up the threads that minimizing the accessible volume is a sound strategy to hinder migration and solubility of hydrogen molecules. Therefore, a broader data base is analyzed and a special focus is placed on the contributions in decreasing the total free volume that results from network modifying by creation of non-bridging oxygen (NBO = oxygen that is part of a tetrahedron but not shared with a second one. It forms the ionic bonds with the modifiers) and filling (“stuffing”) polymerized (NBO-free) silicate networks by introducing charge balanced network formers like aluminum and boron tetrahedra.
Generally, permeation of hydrogen gas molecules through the thin wall (thickness d) of a glass capillary or hollow sphere of area A is proportional to the product of hydrogen solubility and diffusion coefficients. For the steady state (the directional flux is constant with time for t ≥ d2/6D; Barrer, 1941), the H2 permeation can be approximated using Fick's first law (Shelby, 1996):
where dQ/dt is the permeation rate (mol s−1), Δp is the pressure difference (Pa) between inner and outer surface of the wall and S; D, P are the coefficients of hydrogen solubility (mol m−3 Pa−1), diffusion (m2 s−1) and permeation (mol m−1 Pa−1 s−1), respectively. Equation (1) assumes Henry's law (physical dissolution), and that coefficients are independent on concentration. Solubility, diffusivity and permeability depend strongly on temperature. Within narrow temperature ranges, permeability obeys an Arrhenius type dependence, which can be expressed as:
where P0 is the maximum hydrogen permeation at infinite temperature, also named permeation constant (mol m−1 Pa−1 s−1), EP is the activation energy (J mol−1) for permeation, T is the temperature (K) and R is the gas constant (8.314 J mol−1 K−1). If broader temperature ranges are analyzed, a slight temperature dependence of the activation energy of Equation (2) becomes evident. Under these conditions, temperature dependence of gas permeability in glass is best described by Shelby and Keeton (1974) and (Shelby, 1977a):
Tsugawa et al. (1976) introduced a first empirical correlation between hydrogen permeation and glass composition. They were following a similar compositional approach for helium permeation (Altemose, 1961), which was based on the finding that for commercial borosilicate glasses EP decreases with increasing fraction of network former, whereas P0 is constant with composition. Under these constraints, Equation (2) is given by (Tsugawa et al., 1976):
where P is in units of mol m−1 Pa−1 s−1and G is the total molar fraction (%) of network forming SiO2, P2O5, B2O3, and Al2O3. Analysis of the available data shows that Equation (4) can only serve as an approximate of the hydrogen permeation through silicate glasses (Figure 1). Worthy of note here is that P0 and EP differ considerably among compositions of similar network former fraction. This finding gives clear evidence that permeation, which reflects both, solubility and diffusivity, is not solely governed by G. Although P0 strongly scatters, Figure 1 indicates that P0 and EP tend to decrease with increasing G.
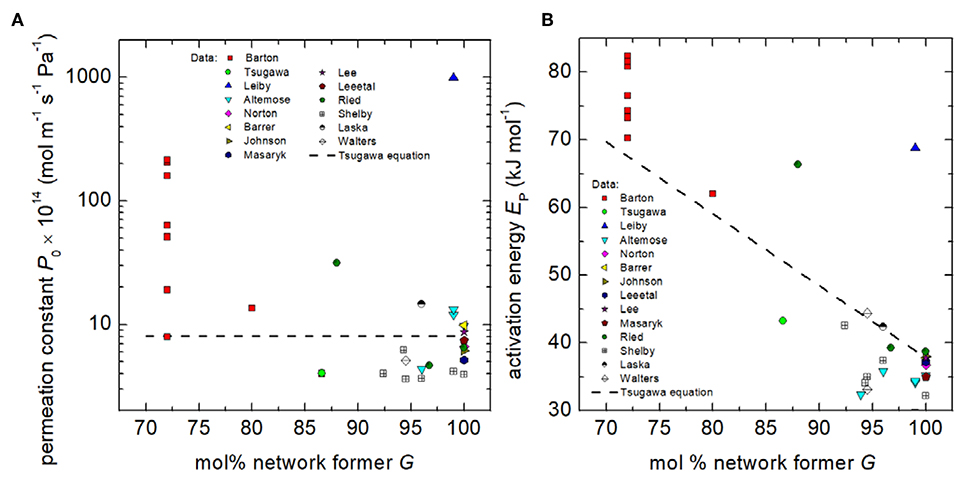
Figure 1. Permeation constant P0 (A) and activation energy EP (B) of hydrogen and deuterium permeation vs. the molar percentage of network formers G. Data: Barton (Barton and Morain, 1970), Tsugawa (Tsugawa et al., 1976), Leiby (Leiby and Chen, 1960), Altemose (Altemose, 1961, 1962; Shelby, 1996), Norton (Norton, 1953), Barrer (Barrer, 1934), Johnson (Johnson and Burt, 1922), Lee et al. (Lee et al., 1962), Lee (Lee, 1963), Massaryk (Masaryk, 1968), Ried (Ried et al., 2014), Shelby (Shelby, 1974b, 1977a, 1996), Laska (Laska et al., 1969), and Walters (Walters, 1970). Dashed line represents Tsugawa's compositional dependence [Equation (4)].
In order to assess to which extent solubility S and diffusivity D could interfere in different types of glasses as P = SD and EP = ED + ES, the activation energies for diffusivity and solubility, ED and ES, are plotted in Figure 2. For that purpose, data of hydrogen, deuterium, and noble gases were analyzed for glasses containing non-bridging oxygen (NBO) and those, which are nominal NBO-free. Therefore, the degree of depolymerization in glasses was determined for each composition by the ratio of non-bridging oxygen over tetrahedra cations (NBO/T). NBO/T is calculated considering the molar content of network modifier oxides, e.g., (Na2O + CaO + K2O + MgO) and all network forming oxides, e.g., (SiO2, Al2O3, B2O3). For commercial aluminoborosilicate glasses, we can assume that all aluminum and boron are four-fold coordinated and stabilized by modifier ions. Then, NBO/T is given as:
As a result, Figure 2 reveals different behavior of NBO-bearing and NBO-free glasses. In case of NBO-bearing glasses, the activation energy of solubility, ES, ranges between −5 and +20 KJ mol−1 and that of diffusion, ED, between +25 and +50 KJ mol−1. No correlation between ED and ES, however, is seen. One can state that more activation energy is needed to solve gas atoms or molecules as in case of NBO-free glasses. For the latter, ES is mostly negative varying between +5 and −20 KJ mol−1, whereas ED more strongly varies between +20 and +120 KJ mol−1. In contrast to NBO-bearing glasses, for (NBO/T = 0) ED and ES correlates according to
(Es and ED in kJ mol−1), indicating that similar fundamental (thermally activated) processes for occupation and migration of gases are active. However, a negative ES means that S decreases with temperature and that hydrogen molecules are likely to be dissolved in NBO-free glasses. This would imply stronger glass-gas interactions. The decrease in ES with increasing G can also explain the similar trend shown in Figure 1B.
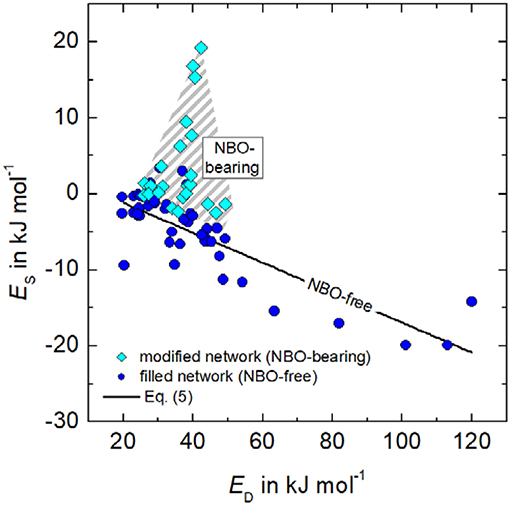
Figure 2. Relationship between the activation energies of solubility Es and diffusivity ED for He, Ne, Ar, H2, and D2 of silica, alkali silicate, lead silicate, alkali-alkaline earth silicate, borosilicate, aluminoborosilicate, and aluminosilicate glasses. Data: (Shelby, 1973, 1974a, 1996; Shelby and Eagan, 1976; Ried et al., 2014).
Volumetric properties of glasses can be accessed from density and chemical composition. Firstly, one can calculate the molar volume VM (based on 1 mol oxygen atoms) as
where xi, Mi and ni are being, respectively, the mol fraction, the molar mass of the oxide i and the number of oxygen atoms in the oxide i with AjOk chemical formula. Secondly, VM can be utilized to determine the total free volume Vfree and ionic porosity IP (Carroll and Stolper, 1993). Vfree and IP are, respectively, the part and fraction of the molar volume not occupied by individual atoms, which are given by:
and
where Vi = 4π Na ( )/3 is the ionic volume the oxide i with AjOk chemical formula. NA is the Avogadro constant and rA, rO are ionic radii using, 66 pm (LiV), 102 pm (NaVI), 151 pm (KVIII), 166 (RbX), 188 pm (CsXII), 66 pm (MgV), 100 pm (CaVI), 118 pm (SrVI), 142 pm (BaVIII), 74 pm (ZnVI), 140 pm (PbX), 11 pm (BIV), 39 pm (AlIV), 26 pm (SiIV), 17 pm (PIV), and 135 pm (OII) (Shannon, 1976).
Figure 3A shows the isothermal permeability of hydrogen/deuterium molecules at 473 K as a function of the ionic porosity at that temperature. In order to allow for analysis on a broader data basis, permeation of helium atoms was included (Figure 3B). Overall, it is very clear that permeation of helium and hydrogen seems to follow the expected trend, i.e., a positive correlation with ionic porosity is evident. On the other hand, a network of high connectivity seems to be more effective in reducing permeability as the data points of fully polymerized network structures (NBO-free) are mainly located on the right hand side of the hatched areas of Figure 3.
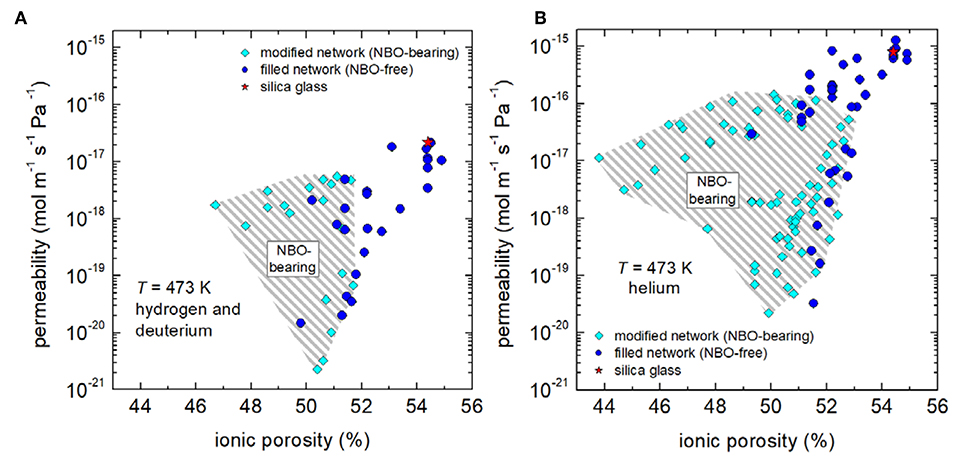
Figure 3. Isothermal hydrogen/deuterium (A) and helium (B) permeability vs. ionic porosity. Data are from the compositions collected by Shelby (1996) (commercial silica and borosilicate glasses), Shelby (1973), Shelby (1974a), Shelby (1977b), Shelby and Lapp (1993), Lapp and Shelby (1997) (binary alkali silicate glasses), Ried et al. (2014) (aluminosilicate and borosilicate glasses), Tsugawa et al., 1976) (alkali-alkaline earth silicate glasses), Shelby and Eagan (1976), Shelby (1977b), Welter et al. (2019), Marzok (2019) (aluminosilicate glasses). Mean value for silica glass is labeled with a red star. Note that for calculation of VM at 473 K available data of thermal expansion were utilized [SciGlass (http://www.akosgmbh.de/sciglass/sciglass.htm)].
Further, one can analyse that permeability is higher for helium atoms than for hydrogen molecules. Both data sets are shifted in by a factor of approximately 36, with regard to the mean value for silica glass (labeled by a red star in Figure 3). It is quite understandable that this difference can be traced back to the difference in the kinetic diameter of hydrogen, which is about 11% larger than that of helium dH2 = 298 pm (Chambers et al., 1998), dHe = 260 pm (Matteucci et al., 2006).
Furthermore, the data sets of Figure 3 seem to follow self-similar pattern (hatched areas), which will be utilized to access volumetric dependencies with the following master-curve concept. For that reason, dimensionless ratios (the so-called “reduced permeability”) were calculated for isothermal conditions by dividing permeability through the respective value [2.2 × 10−17 mol m−1 Pa−1 s−1 (H2/D2) and 8.0 × 10−16 mol m−1 Pa−1 s−1 (He)] for silica glass. Figure 4 shows that reduced permeability declines in fully polymerized (NBO-free) glasses and depolymerized (NBO-bearing) glasses by up to four and a half orders of magnitude. It becomes clear that stuffing the network by charge compensating cations in fully polymerized networks is a viable option for considerably reducing hydrogen permeability. Particularly, these glasses are favorable when comparing their process properties as they offer a smaller crystallization tendency and a higher workability then NBO-bearing compositions.
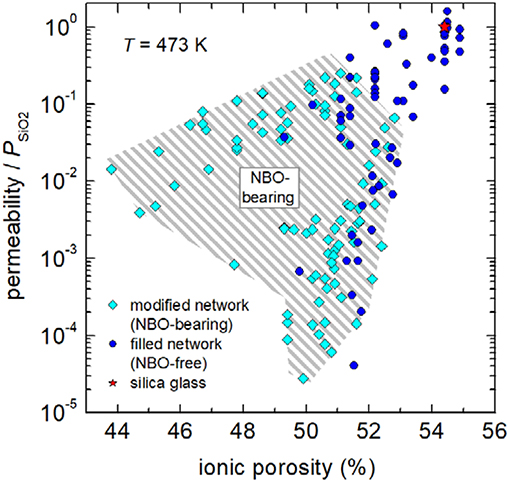
Figure 4. Reduced permeability P/PSiO2 vs. ionic porosity at 473 K. Gray hatched area indicate NBO-bearing compositions. Data: see caption of Figure 3.
Figure 5 shows the dependence of reduced permeability on ionic porosity for fully polymerized glasses and depolymerized glasses in separate figures. Grouping the NBO-free glasses by network former (Figure 5A) reveals that charge balancing of tetrahedral boron is less effective in decreasing reduced permeability. In particular, technical borosilicate glasses are only capable to decrease the permeability of silica by a factor <100. In contrast, when tetrahedral aluminum is stabilized by modifier ions, available data show that reduced permeability is strongly declined. Factors up to 104.5 in reduction are found for lithium and sodium aluminosilicate glasses. It is interesting to note that stabilization of mixed network formers (aluminoborosilicate glass) lead to an intermediate position between borosilicate and aluminosilicate compositions. On the other hand, if network modifiers are present in excess, they depolymerize the network and compensate charges of NBOs instead of tetrahedral coordinated aluminum and boron. In this case, reduction of free volume and with it the drop in reduced permeability depends on the nature of the modifier cation (Figure 5B). High-field strength cations such as Li+, which strongly attract NBOs, lead to a relative low reduction in ionic porosity but to a relative strong decrease in permeation, whereas low-field strength cations such as K+, Rb+ and Cs+, which are less effective to attract NBOs, result in stronger reduction of free volume but less decrease in permeation. The compositional dependence becomes clearer if one follows the iso-NBO/T lines. For NBO/T = 1 (in technology called disilicate compositions) on can find that lithium ions reduce permeation by a factor of 30,000, sodium ions by 1,800, and potassium ions only by 250 with respect to the permeation through silica glass. Figure 5B shows further that for Na+-modified glasses, which includes the mixed modifier float glass of high technical importance, the dependence of reduced permeability on ionic porosity is only slightly weaker than for binary lithium silicates glasses.
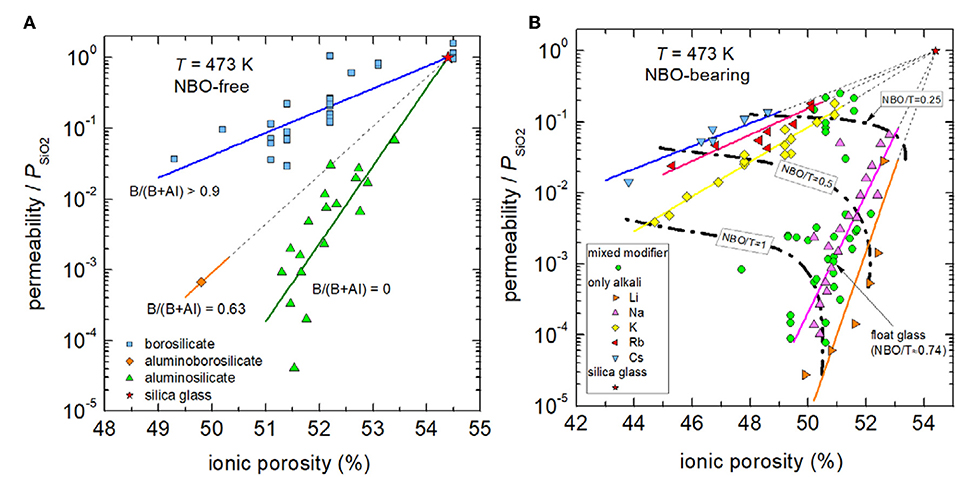
Figure 5. Reduced permeability P/PSiO2 vs. ionic porosity of fully polymerized (A) and depolymerized (B) glasses at 473 K. Solid lines are intended as visual guides to indicate compositional trends of borosilicate glasses (blue), aluminoborosilicate glasses (orange), and aluminosilicate glasses (green) in (A) as well as those of binary silicate glasses of cesium (blue), rubidium (red), potassium (yellow), sodium (magenta), and lithium (orange) in (B). Dashed dotted lines in part B indicate compositions of NBO/T = 0.25, 0.5, and 1. The black arrow due to technical importance emphasizes the data point of soda-lime float glass. Data: see caption of Figure 3. Note that data for pure silica glasses, titania silicate glasses, and demixed silicate glasses with SiO2-rich matrices are not shown.
The analysis of available data show that assuming a simplistic effect of either ionic porosity or network modifier content fails to predict hydrogen permeability in silicate glasses. Fully polymerized (NBO-free) glasses, which are stuffed with Li+ and Na+ ions for charge balancing network forming tetrahedral aluminum as well as depolymerized (NBO-bearing) lithium and sodium silicate glasses, both ranging between 50 and 51.5% ionic porosity, seem to offer low hydrogen permeability that is up to 30,000 times lower than that of silica glass. This finding indicates that, the local network connectivity may control hydrogen permeability more strongly than ionic porosity.
The datasets generated for this study are available on request to the corresponding author.
TW, UM, and SR produced the manuscript. JD and RM contributed to the critical revision and direction of the manuscript.
The authors received funding by Deutsche Forschungsgemeinschaft (DFG) through grants DE598/20 and MU963/11.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Altemose, V. O. (1961). Helium diffusion through glass. J. Appl. Phys. 32, 1309–1316. doi: 10.1063/1.1736226
Barrer, R. M. (1934). The mechanism of activated diffusion through silica glass. J. Chem. Soc. 136, 378–386. doi: 10.1039/jr9340000378
Barton, J. L., and Morain, M. (1970). Hydrogen diffusion in silicate glasses. J. Non-Cryst. Solids 3, 115–126. doi: 10.1016/0022-3093(70)90107-9
Carroll, M. R., and Stolper, E. M. (1993). Noble gas solubilities in silicate melts and glasses new experimental results for argon and the relationship between solubility and ionic porosity. Cosmochim. Geochim. Acta 57, 5039–5051. doi: 10.1016/0016-7037(93)90606-W
Chambers, A., Park, C., Baker, R. T. K., and Rodriguez, N. M. (1998). Hydrogen storage in graphite nanofibers. J. Phys. Chem. B 102, 4253–4256. doi: 10.1021/jp980114l
Chan, S. L., and Elliott, S. R. (1991). Theoretical study of the interstice statistics of the oxygen sublattice in vitreous SiO2. Phys. Rev. B 43, 4423–4432. doi: 10.1103/PhysRevB.43.4423
Holtappels, K., Beckmann-Kluge, M., Gebauer, M., and Eliezer, D. (2011). Pressure resistance of glass capillaries for hydrogen storage. Mater. Testing 53, 14–18. doi: 10.3139/120.110195
Johnson, J. B., and Burt, R. C. (1922). The passage of hydrogen through quartz glass. J. Opt. Soc. Am. 6, 734–734. doi: 10.1364/JOSA.6.000734
Kurita, N., Fukatsu, N., Otsuka, H., and Ohashi, T. (2002). Measurements of hydrogen permeation through fused silica and borosilicate glass by electrochemical pumping using oxide protonic conductor. Solid State Ionics, 146, 101–111. doi: 10.1016/S0167-2738(01)00989-4
Lapp, J. C., and Shelby, J. E. (1997). Helium permeation, diffusion and solubility in sodium galliosilicate glasses. Phys. Chem. Glasses 38, 256–259.
Laska, H. M., and Doremus, R. H. (1969). Effect of stress on the permeation of helium through borosilicate glass. J. Chem. Phys. 51, 1934–1938. doi: 10.1063/1.1672281
Laska, H. M., Doremus, R. H., and Jorgensen, P. J. (1969). Permeation, diffusion, and solubility of deuterium in Pyrex glass. J. Chem. Phys. 50, 135–137. doi: 10.1063/1.1670770
Lee, R. W. (1963). Diffusion of hydrogen in natural and synthetic fused quartz. J. Phys. Chem. 38, 448–455. doi: 10.1063/1.1733679
Lee, R. W., Frank, R. C., and Swets, D. E. (1962). Diffusion of hydrogen and deuterium in fused quartz. J. Chem. Phys. 36, 1062–1071. doi: 10.1063/1.1732632
Leiby, C. C., and Chen, C. L. (1960). Diffusion coefficients, solubilities, and permeabilities for He, Ne, H2, and N2 in Vycor Glass. J. Appl. Phys. 31, 268–274. doi: 10.1063/1.1735556
Masaryk, J. S. (1968). Permeation in fused silica (M. S. Thesis), University of California, Berkeley, Berkeley, CA, United States.
Matteucci, S., Yampolskii, Y., Freeman, B. D., and Pinnau, I. (2006). “Transport of gases and vapors in glassy and rubbery polymers”. in. Materials Science of Membranes for Gas and Vapor Separation, eds Y. Yampolskii, B. D. Freeman, and I. Pinnau (Hoboken, NJ: John Wiley and Sons), 1–47. doi: 10.1002/047002903X.ch1
Morimoto, Y., Igarashi, T., Sugahara, H., and Nasu, S. (1992). Analysis of gas release from vitreous silica. J. Non-Cryst. Solids 139, 35–46. doi: 10.1016/S0022-3093(05)80803-8
Nakayama, G. S., and Shackelford, J. F. (1990). Solubility and diffusivity of argon in vitreous silica. J. Non-Cryst. Solids 126, 249–254. doi: 10.1016/0022-3093(90)90826-8
Norton, F. J. (1953). Helium diffusion through glass. J. Am. Ceram. Soc. 36, 90–96. doi: 10.1111/j.1151-2916.1953.tb12843.x
Prewitz, M., Gaber, M., Müller, R., Marotztke, C., and Holtappels, K. (2018). Polymer coated glass capillaries and structures for high-pressure hydrogen storage: permeability and hydrogen tightness. Int. J. Hydro. Energ. 43, 5637–5644. doi: 10.1016/j.ijhydene.2017.12.092
Ried, P., Gaber, M., Müller, R., and Deubener, J. (2014). Hydrogen permeability of a barium-aluminoborosilicate glass – a methodical approach. J. Non-Cryst. Solids 394–395, 43–49. doi: 10.1016/j.jnoncrysol.2014.04.006
Schlapbach, L., and Züttel, A. (2001). Hydrogen-storage materials for mobile applications. Nature 414, 353–358. doi: 10.1038/35104634
Shackelford, J. F. (2014). Gas solubility and diffusion in oxide glasses – implications for nuclear waste forms. Proc. Mater. Sci. 7, 278–285. doi: 10.1016/j.mspro.2014.10.036
Shackelford, J. F., and Masaryk, J. S. (1978). The interstitial structure of vitreous silica. J. Non-Cryst. Solids 30, 127–134. doi: 10.1016/0022-3093(78)90061-3
Shannon, R. D. (1976). Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A 32, 751–767. doi: 10.1107/S0567739476001551
Shelby, J. E. (1973). Effect of phase separation on helium migration in sodium silicate glasses. J. Am. Ceram. Soc. 56, 263–266. doi: 10.1111/j.1151-2916.1973.tb12484.x
Shelby, J. E. (1974a). Helium diffusion and solubility in K2O-SiO2 glasses. J. Am. Ceram. Soc. 57, 260–263. doi: 10.1111/j.1151-2916.1974.tb10883.x
Shelby, J. E. (1974b). Helium, deuterium and neon migration in a common borosilicate glass. J. Appl. Phys. 45, 246–2149. doi: 10.1063/1.1663560
Shelby, J. E. (1976). Pressure dependence of helium and neon solubility in vitreous silica. J. Appl. Phys. 47, 135–139. doi: 10.1063/1.322359
Shelby, J. E. (1977a). Molecular diffusion and solubility of hydrogen isotopes in vitreous silica. J. Appl. Phys. 48, 3387–3394. doi: 10.1063/1.324180
Shelby, J. E. (1977b). Helium migration in lithium aluminosilicate glasses. J. Appl. Phys. 48, 1497–1502. doi: 10.1063/1.323868
Shelby, J. E., and Eagan, R. J. (1976). Helium migration in sodium aluminosilicate glasses. J. Am. Ceram. Soc. 59, 420–425. doi: 10.1111/j.1151-2916.1976.tb09509.x
Shelby, J. E., and Keeton, S. C. (1974). Temperature dependence of gas diffusion in glass. J. Appl. Phys. 45, 1458–1460. doi: 10.1063/1.1663433
Shelby, J. E., and Lapp, J. C. (1993). Helium and deuterium migration in alkali silicate glasses. Phys. Chem. Glasses 34, 227–231.
Tsugawa, R. T., Moen, I., Roberts, P. E., and Souers, P. C. (1976). Permeation of helium and hydrogen from glass-microsphere laser targets. J. Appl. Phys. 47, 1987–1993. doi: 10.1063/1.322924
Walters, L. C. (1970). Permeabilities of helium and deuterium through a borosilicate glass. J. Am. Ceram. Soc. 53, 288–289. doi: 10.1111/j.1151-2916.1970.tb12102.x
Welter, T., Marzok, U., Deubener, J., Reinsch, S., and Müller, R. (2019). Hydrogen diffusivity in sodium aluminosilicate glasses. J. Non-Cryst. Solids 521:119502. doi: 10.1016/j.jnoncrysol.2019.119502
Zhevago, N. K. (2016). “Other methods for the physical storage of hydrogen,” in Compendium of Hydrogen Energy, Vol. 2, eds R. B. Gupta, A. Basile, and T. Nejat Veziroglu (Woodhead Publishing Series in Energy), 189–218. doi: 10.1016/B978-1-78242-362-1.00008-0
Keywords: hydrogen storage, glass, permeability, solubility, diffusivity, ionic porosity
Citation: Welter T, Müller R, Deubener J, Marzok U and Reinsch S (2020) Hydrogen Permeation Through Glass. Front. Mater. 6:342. doi: 10.3389/fmats.2019.00342
Received: 01 October 2019; Accepted: 17 December 2019;
Published: 10 January 2020.
Edited by:
Yong Gyu Choi, Korea Aerospace University, South KoreaReviewed by:
Stefan Karlsson, RISE Glass section, RISE Research Institutes of Sweden, SwedenCopyright © 2020 Welter, Müller, Deubener, Marzok and Reinsch. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Joachim Deubener, am9hY2hpbS5kZXViZW5lckB0dS1jbGF1c3RoYWwuZGU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.