Improved identification and tracking of three-dimensional eddies in the Southern Ocean utilizing 3D-U-Res-Net

Oceanic mesoscale eddies are prevalent throughout the global ocean, playing a critical role in material and energy transport while significantly influencing climate change. Accurate characterization of their three-dimensional structures and movement is essential for a quantitative analysis of their transport processes. Traditional eddy detection algorithms have lower successful detection rate and with more limitations, so they fall short in the complex and dynamic ocean environment. The rising trend of applying artificial intelligence (AI) algorithms, due to their efficiency, precision, and automation, addresses this challenge. This study employs the 3D-U-Res-Net algorithm to identify the three-dimensional structures of mesoscale eddies in the Southern Ocean using GLORYS12V1 data from 2011 to 2020. A vector geometry-based eddy detection algorithm (VG) initially identified 1587292 eddy snapshots in the Southern Ocean (2011–2019), which were used for training the 3D-U-Res-Net algorithm. Data from 2020 served as the ground truth and validation set. The successful detection rate of 3D-U-Res-Net algorithm is 100%, which means that it identified all 135734 eddy snapshots from the VG dataset in 2020. For eddy tracking, the VG algorithm counted 18168 eddy tracks, whereas the 3D-U-Res-Net counted 18559, reflecting a 2.15% bias. To reduce uncertainty, eddies with lifespans shorter than two weeks were excluded. The average lifespans and traveling distances for eddies detected by the 3D-U-Res-Net (VG) algorithm were 29.35 (29.61) days and 77.78 (37.60) km, respectively, with the 3D-U-Res-Net identifying eddies with longer traveling distances. The mean radius of eddies detected by the VG algorithm was 43.16 km, while the 3D-U-Res-Net detected eddies with a mean radius of 43.74 km, a 0.58 km increase. We categorized eddies into four three-dimensional structures: bowl-shaped, cone-shaped, lens-shaped, and cylindrical. The VG algorithm identified these structures in proportions of 32%, 31%, 25%, and 12%, respectively, whereas the 3D-U-Res-Net algorithm found 19.48%, 19.58%, 0.04%, and 60.9%, respectively. The 3D-U-Res-Net identified more cylindrical eddies and was approximately ten times faster than the VG algorithm. Overall, this algorithm has good performance and higher efficiency. It is an attempt of using AI for oceanic research, and more works can be carried out in the future.

1 Introduction

As a complex phenomenon in the ocean, mesoscale eddies not only play a vital role in the transport of heat and energy, but also regulate the biogeochemical cycles (Chelton et al., 2007; Dong et al., 2014). Moreover, they exert considerable influence on local near-surface winds and precipitation (Frenger et al., 2013). Compared to the background mean currents, mesoscale eddies have larger velocities. Moreover, eddies can penetrate and influence deep layers (Cao et al., 2022). It is typical for mesoscale eddies to be accompanied by a range of anomalies in sea surface height and sea surface temperature, which in turn have an influence on the global climate. Figure 1 shows topography of the Southern Ocean, with the black dotted line indicating the mean position of the Antarctic Circumpolar Current ACC (He et al., 2023). The Southern Ocean, as a vast marine region surrounding the Antarctic continent, exhibits distinctive characteristics. The ACC exhibits a strong eastward flow (Chapman et al., 2020), which effectively impedes the exchange of seawater between the northern and southern sides of the ACC and significantly affects global climate change (Rintoul and Garabato, 2013). There are numerous mesoscale eddies in the Southern Ocean, particularly in the area where the ACC interacts with the surrounding topography. These eddies are pivotal in maintaining the thermohaline balance of the Southern Ocean (Morrow et al., 2010; Patel et al., 2019), and also transport nutrients and chemicals in the vertical direction by inducing Ekman pumping, thereby changing their horizontal local distribution (Moreau et al., 2017). On the other hand, temperature anomalies within eddies are intimately associated with extreme temperature events. As temperature anomalies within eddies intensify, eddies may be an important driver of extreme temperatures on surface marine heatwaves (He et al., 2023). According to Griffies et al. (2015), transient climate change, which is typically defined by changes in global mean surface temperature, is fundamentally linked to how the ocean transports heat both vertically and laterally, with mesoscale eddies playing a critical role in this process. On the other hand, as can be seen in line 51, eddies also have some influence on global climate change. Therefore, accurately identifying and tracking mesoscale eddies in the Southern Ocean will facilitate the exploration of the essential characteristics of the eddies, as well as deepen our understanding of the air-sea interactions, and the response to global climate change in the Southern Ocean.

Figure 1

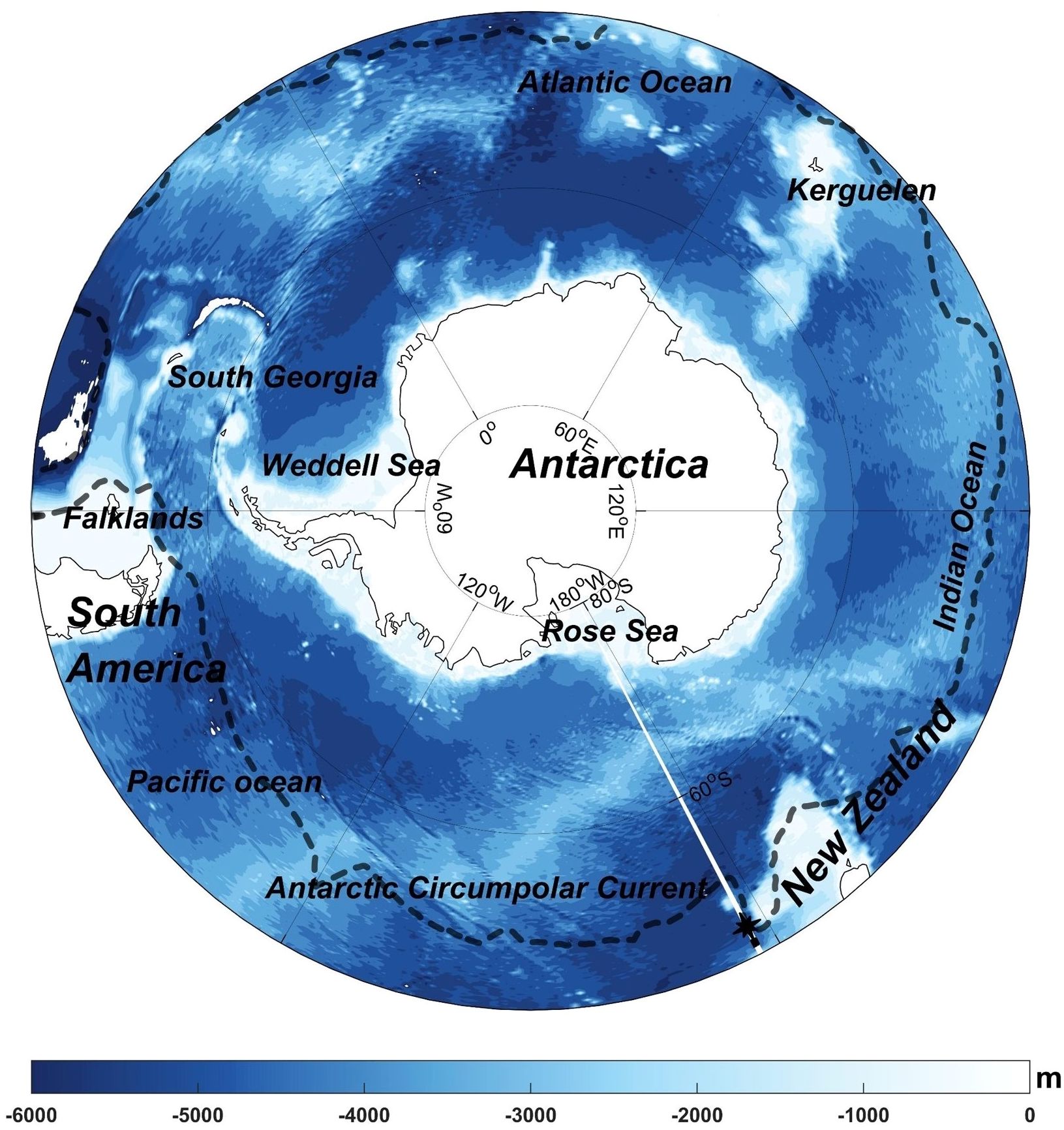
Figure 1. A bathymetric topographic map of the Southern Ocean. The black dotted line represents the mean position of the ACC as reported by He et al. (2023).

Earlier than 1970s, eddies are observed by in situ observation, so they heavily reliant on experts’ experience with high cost and limited acquisition of observational data. In recent years, with the increase in satellite remote sensing observations and the development of ocean numerical models, the research on eddies has become increasingly in-depth. Consequently, automated eddy detection methods are required for the detection of larger sea areas over longer time spans (Duo et al., 2019)). There are several eddy detection algorithms, among them, the winding angle algorithm (W-A), the Okubo-Weiss (OW) parameter method, and the vector geometry-based eddy detection algorithm (VG) are commonly used (Xing and Yang, 2021; Hammoud et al., 2023). The W-A algorithm detects eddies by identifying the extreme values of sea level anomaly (SLA) and then selects closed SLA streamlines by calculating the winding angle (Sadarjoen and Post, 2000). The OW parameter algorithm identifies eddies based on comparing relative importance of vorticity to total deformation rate (Okubo, 1970; Weiss, 1991; Chang and Oey, 2014). The formula is $W=S_{sh}^2+S_{st}^2-{\xi }^2$, where $S_{sh}$ and $S_{st}$ represent the shear and strain deformation, respectively, and $\xi$ is the vertical component of vorticity. Then set a negative threshold $W_0$ and compare with this threshold. The VG algorithm is developed based on the vector geometry characteristics of the eddies’ flow field (Nencioli et al., 2010). It defines the eddies’ centers through four different constraints, then takes the maximum closed stream function contour as each eddie’s boundary, and performs eddies tracking. Previous assessments of these three most widely used algorithms in the South China Sea have found that the O-W algorithm has an average successful detection rate of only 51.9%, making it unsuitable for tracking long-lived eddies in this region. Additionally, the W-A algorithm can only detect eddies with radii greater than 1° (Xing and Yang, 2021). In contrast, the VG algorithm is capable of identifying smaller eddies and boasts the lowest average suspicious tracking rate, at just 1.1%. Compared to eddies in mid-latitude regions, those in the Southern Ocean have smaller radii and shorter lifetimes, which makes the VG algorithm the most suitable for comparison with AI algorithms in this area. Using traditional algorithms to detect eddies need studies to adjust thresholds in different region. For AI algorithm, it trained by eddies’ graphical features, available anywhere in the world ocean and no need to adjust different threshold. Accordingly, the development of more versatile methods for the detection of oceanic mesoscale eddies is required.

In recent years, as artificial intelligence has developed rapidly, studies have come to recognize the feasibility of applying AI algorithms to eddies studies (Lguensat et al., 2018b). Compared with traditional eddy detection algorithms, deep learning can learn the characteristics of eddies without excessive parameter settings, is smarter in eddy detection and tracking (Liu et al., 2022). This method can learn the characteristics of eddies without human intervention, facilitating the identification and tracking of vortices in marine environments. Huang et al. (2017) applied DeepEddy to synthetic aperture radar (SAR) images, the results showed that using the DeepEddy model achieved an accuracy of 96.88% in identifying 136 eddies identified on ENVISAT and ERS-2 SAR images. Xu et al. (2019) employed the Pyramid Scene Parsing Network (PSPNet) to detect mesoscale eddies in the ocean. Their findings revealed that the PSPNet is more effective than the VG algorithm in detecting a greater number of eddies, particularly smaller ones. Lguensat et al. (2018a) proposed an automatic eddy recognition network, termed EddyNet. This algorithm was based on the U-Net structure and was divided into two parts: encoder and decoder. To prevent over-fitting, a dropout layer was added between the pooling layer and the convolution layer. This allows for regularization, enhancing the algorithm’s performance. Zhao et al. (2023) proposed a novel eddy detection algorithm, which is also based on the U-Net network, but integrated the pyramid segmentation attention module (PSA) and the spatial pyramid pooling (ASPP) module. The sea level anomaly data (SLA) and sea surface temperature (SST) were employed as inputs into the algorithm. The PSA module can take into account both spatial and channel attention modules, and the addition of the ASPP module facilitates the acquisition of multi-scale features through enhanced learning. Furthermore, the research compared several popular eddy identification algorithms, including UNet, EddyNet, Swin-UNet, and DeepLabV3+. The findings of the study indicate that their algorithm performs better than the other four algorithms.

Mesoscale eddies have the capacity to transport oxygen and nutrients, regulate the reproduction of plankton, and thus exert an influence on fisheries (Zhang et al., 2016; Marez et al., 2019). Conversely, mesoscale eddies dominate the ocean kinetic energy, especially in the upper flow field above the thermocline depth. In this region, they play a key role in the transport of water mass, heat, and other air-sea interaction fluxes (Zhang et al., 2024). However, the satellite altimeter data currently widely used in mesoscale eddy detection and identification has insufficient spatial resolution and the inability to discern signals from depths below the surface. Additionally, there is a dearth of deep learning algorithms for three-dimensional eddies research (Huang et al., 2021; Chen et al., 2021). This has resulted in a paucity of research on the three-dimensional structure of eddies using artificial intelligence algorithms. Huang et al. (2021) used a three-dimensional neural network based on the residual network (ResNet) to classify and enumerate the vertical structure of eddies. The results demonstrated that this algorithm is effective in identifying three-dimensional ocean eddies and exhibits robust classification performance. Used 3D eddies dataset detected by HYCOM as the training set, Feng et al. (2023) proposed an algorithm based on 3D-EddyNet, for the idenfication of three-dimensional eddies in the ocean. The algorithm employed three-dimensional convolution to capture the characteristics of the eddies, thereby obtaining their three-dimensional structures. Based on previous studies, these structures were classified into three different steep types, bowl-shaped, lens-shaped and cone-shaped. Liu et al. (2024) likewise introduced a novel deep learning model, 3D-EddyNet, for reconstructing the 3D thermohaline structure of mesoscale eddies. And the 3D-EddyNet model was optimized by adjusting the image size, introducing a convolutional block attention module and incorporating the physical parameters of the eddy. The results show that the model is able to accurately represent the three-dimensional thermohaline eddy structure in both vertical and horizontal directions and is able to infer the three-dimensional eddy structure in the absence of Argo profile data. Xu et al. (2024) proposed 3D-U-Res-Net to identify three-dimensional eddies in the northwest Pacific. The 3D-U-Res-Net combines the advantages of 3D-UNet and ResNet networks, enabling more effective identification of three-dimensional ocean eddies.

The Southern Ocean plays a key role in the global climate system, and the densely distributed mesoscale eddies are crucial in the transport of heat and carbon in the Southern Ocean, which also has a significant impact on improving climate models and climate predictions. To gain a deeper understanding of the mesoscale eddies in the Southern Ocean, it is crucial to accurately and efficiently extract the three-dimensional characteristics of the eddies. We used the 3D-U-Res-Net algorithm compared to other deep learning algorithms. This model is based on the 3D-UNet and adds a ResNet in order to avoid potential information loss during the training process. The algorithm is capable of learning eddy features more effectively and captures more effective information through the use of residual connections than single 3D-UNet. With this network, we managed to automatically detect and categorize three-dimensional mesoscale eddies. For a detailed introduction to 3D-U-Res-Net, please refer to the method introduction in the section 2. The network was utilized to automatically detect and categorize three-dimensional mesoscale eddies. For a comprehensive overview of the 3D-U-Res-Net methodology, please refer to the method introduction in Section 2.

The remainder of this paper is organized as follows: Section 2 presents the data and methods employed in the study. Section 3 analyzes the results, while Section 4 summarizes the main findings of the study.

2 Data and methods

2.1 Data

The GLORYS12V1 data is a high-resolution global physical ocean and sea ice reanalysis product, produced by Mercator Ocean International in the context of the Copernicus Marine Environment Monitoring Service (CMEMS, Global Ocean Physics Reanalysis | Copernicus Marine Service). This dataset integrates a variety of data types, including satellite observations and in-situ measurements, and uses advanced data assimilation techniques to accurately simulate ocean dynamic changes. The temporal resolution is 1 day, and the horizontal spatial resolution is 1/12°×1/12°, with a regular rectangular projection in latitude and longitude (Lellouche et al., 2018). The dataset is divided vertically into 50 unequal layers, ranging from 0 to 5500 m. It provides global ocean temperature, salinity, ocean currents, sea level height, mixed layer depth, and sea ice parameters since 1993. The overall evaluation of GLORYS12V1 shows that the model has a good level of performance in characterizing and simulating ocean physical processes and is capable of accurately capturing the main interannual climate variability signals of the ocean and sea ice (Jean-Michel et al., 2021). GLORYS12V1 demonstrates notable advantages in controlling water mass properties, sea ice coverage and its low-frequency variability (Jean-Michel et al., 2021). This work employs sea temperature, current field, and sea surface height data at a depth of 0-700 m, spanning the period from 2011 to 2020, to study the Southern Ocean (-180°W -180°E, 45°S -65°S). Furthermore, the data were interpolated vertically, from a depth of 0.5 m to 700 m, with an interval of 100 m per layer, resulting in eight layers: 0.5m, 100m, 200m, 300m, 400m, 500m, 600m, 700m.

Moreover, the AVISO (Archiving Validation and Interpretation of Satellite Oceanographic data) geostrophic current anomaly data is also used for comparison with GLORYS12V1. The data is obtained from the CMEMS. The temporal resolution of AVISO is 1 day, and the horizontal spatial resolution is 1/4°×1/4°.

The “Mesoscale Eddy Trajectory Atlas” (META) product can be accessed via the AVISO website (Global mesoscale eddy trajectory product (altimetry.fr)). Eddies in this dataset are identified through the spatially high-pass filtered daily SLA of AVISO, which is regarded as the most comprehensive eddy dataset and is provided by Chelton et al. (2011). The dataset provides a comprehensive set of global eddy characteristics, including eddy track, location, radius, amplitude, rotation speed, and polarity. For further details regarding this eddy dataset, please consult Chelton et al. (2011) and Pegliasco et al. (2022).

2.2 Methods

2.2.1 The vector geometry-based (VG) eddy detection algorithm

The VG algorithm was initially developed by Nencioli et al. (2010). The versatility and precision of the VG algorithm make it a versatile tool for eddy detection in a wide range of applications. This algorithm has been applied globally to regions such as Lanai Island in Hawaii (Dong et al., 2009), the subtropical North Pacific Ocean (Liu et al., 2012), the South China Sea (Lin et al., 2015), and the Northwest Pacific (Wang et al., 2020). The VG algorithm, based on the characteristics of the velocity field, firstly accurately defines the eddy center through four constraints. The first constraint is that the velocity components in the east-west direction on either side of the eddy center must be opposite, and their magnitudes must increase with distance from the center. The second constraint is that the velocity components in the north-south direction must also be opposite on either side of the eddy center, and their magnitudes must increase with distance from the center. The third constraint is that the point of minimum velocity is taken as the eddy center. The fourth constraint is that the velocity vector directions around the eddy center must be consistent. Once the centers of the eddies have been identified, the boundary of each eddy is calculated using the outermost closed stream-function contour. Additionally, eddies with the same polarity are tracked on the subsequent day. For a comprehensive overview of this methodology, please refer to Nencioli et al. (2010). In this study, the velocity data from the GLORYS12V1 dataset are employed as the input and the VG algorithm is utilized to detect eddies at 8 layers ranging from 0.5 to 700 m. Subsequently, a Southern Ocean eddy dataset is generated, containing information on the radius, position, trajectory, polarity and lifetime of the eddies at various depths.

The eddy tracking method is to track the identified transient eddy throughout its lifetime. The tracking process is initiated on the first day, with the eddy center being determined via consecutive time steps in order to trace the eddy tracks. At the eddy center established at time t, a search for the same type of eddy in the search area at time t + 1 should be conducted. Once the center at the next day is determined, the search proceeds until the same type of eddy cannot be identified at a certain day. In this paper, we set the radius of the search area to be 60 km. In the event that multiple eddies of the same type are identified within a given area, the eddy situated closest to the center is selected as the subsequent eddy position. For more details on the tracking algorithm, please refer to the paper by Nencioli et al. (2010).

The 8-layer eddy dataset is employed to construct a three-dimensional eddy dataset. It is assumed that the tilt of each eddy’s center does not exceed one-quarter of its radius in the subsequent layer. We commence our investigation at the surface layer and proceed to identify any eddies exhibiting the same polarity in the subsequent layers, extending down to a depth of 700 meters. If an eddy with the same polarity (cyclone/anticyclone) and on the same day is found in the next deeper layer, it is considered the same eddy at different depths. This process continues until a layer is reached where no eddy with the same characteristics is found. At this point, the previous layer to represent the deepest extent of the eddy. Further details regarding the 3D eddy detection algorithm can be found in Dong et al. (2012) and Lin et al. (2015). The aforementioned method allows for the acquisition of a three-dimensional dataset of eddies.

2.2.2 The 3D-U-Res-Net

The traditional eddy detection algorithms are computationally intensive and time-consuming. To address this issue, this study adopts a new network architecture based on deep learning, namely 3D-U-Res-Net (Xu et al., 2024). This network combines the advantages of the 3D-UNet (Çiçek et al., 2016) and the ResNet (He et al., 2016), thereby enabling more efficient integration of cross-channel and spatial correlations. The specific structure of the 3D-U-Res-Net is shown in Figure 2. The network is composed of 7 modules. The initial module consists of a convolutional layer, a dropout layer with a rate of 0.5, and the activation function (ReLU). The final module consists of a convolutional layer and the Softmax activation function. The Softmax function is employed to compare the network output with the annotated data, thereby reducing the weight of frequently appearing unnecessary background, and weight the features of the annotated data. This facilitates more effective learning of the requisite features and reduces errors. Apart from these two modules, the remaining modules utilize residual connections. This connection effectively addresses the issues of gradient disappearance and gradient explosion, enhancing our ability to learn image features, increasing the feature extraction ability of the 3D-UNet, and improving accuracy. Additionally, residual connections facilitate smoother information transmission, reduce information loss during the transmission process, accelerate the training process, and improve the performance and learning ability of the network (Xiao et al., 2020).

Figure 2

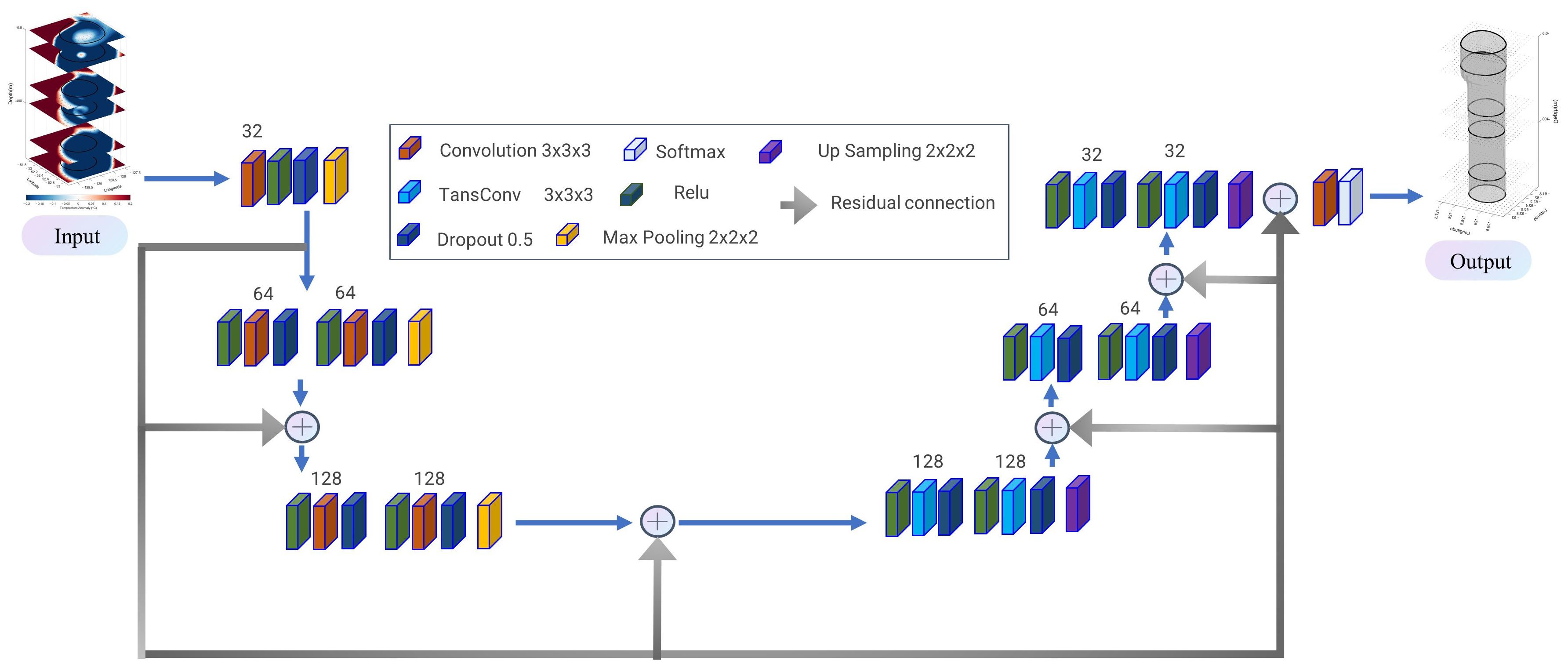
Figure 2. Basic structure diagram of the 3D-U-Res-Net. According to the order of the squares appearing in the diagram are: convolution, ReLU layer, dropout layer, max pooling layer, transpose convolution layer, upsampling module, softmax module. The gray quiver represents a residual connection.

ADDITIThe network is comprised of two primary components: the encoder and the decoder, with a convolution kernel size of 3×3×3 and a pooling step of 2×2×2. The left side of Figure 2 shows the encoder, which is composed of three modules. With the exception of the initial module, each module performs two consecutive rounds of convolution, followed by a 0.5 rate dropout layer and the ReLU activation function, with a max pooling layer at the end of each module to extract key information. Concurrently, the number of convolutional filters is doubled, and information from different layers is concatenated through residual connections. Subsequently, the extracted information is conveyed to the decoder section, which is situated on the right side of the network and is comprised of four modules. With the exception of the final module, the remaining three modules are similar to those in the encoder. These include two consecutive rounds of ReLU activation functions, transposed convolution, and a dropout layer. Finally, a sampling module is employed to aggregate the obtained information. In the residual connections, information from different layers is merged using transposed convolution and upsampling. This approach allows the final convolutional and activating function module to generate a feature map of the same size as the input image.

2.3 Data and method evaluation

2.3.1 Evaluation of GLORYS12 dataset

In order to assess the dependability of the GLORYS12V1 dataset, the eddy kinetic energy (EKE) of 2020 in both GLORYS12V1 and AVISO datasets are compared. The time-mean EKE is then computed as:

$$EKE=\frac{1}{2}(u^{\prime 2}+v^{\prime 2})$$

where ‘$u^{\prime }$’ represents east-west velocity anomaly and ‘$v^{\prime }$’ represents north-south velocity anomaly. The EKE is obtained by subtracting the mean value from 2020. The spatial distribution pattern of EKE obtained from GLORYS12V1 is consistent with the altimeter data (Figure 3), indicating that a high value of EKE is generally between the Subantarctic Front and the Polar Front (Belkin and Gordon, 1996; Zhang et al., 2021). Because the presence of heightened frontal and eddy instabilities, thus the value of EKE is greater near the front. But there are still some inconsistencies between Figures 3A, B, such as the EKE calculated by GLORYS12V1 being significantly larger than AVISO’s around 60-70 ° S, showing higher EKE zonal stripes distribution. Quantitatively, the mean EKE of GLORYS12V1 is 219.48 ${\text{cm}}^2/{\text{s}}^2$, while that calculated by AVISO is 160.39 ${\text{cm}}^2/{\text{s}}^2$, resulting in a higher EKE intensity of 59.09 ${\text{cm}}^2/{\text{s}}^2$. Because the GLORYS12V1 dataset has higher spatial resolution (triple times) compared to the geostrophic current flow field of AVISO, and EKE calculated through geostrophic velocity of AVISO, which may lead to miss some non-geostrophic effects, result in higher EKE values and capture of smaller scale ocean eddies, fronts and filaments in GLORYS12V1. This difference indicates that the GLORYS12V1 dataset is more effective in capturing mesoscale ocean dynamic and can more accurately reflect the energy distribution and flow characteristics within the ocean (Lin et al., 2023). Therefore, it is reasonable to utilize the flow field data from GLORYS12V1 for the detection of three-dimensional eddies.

Figure 3

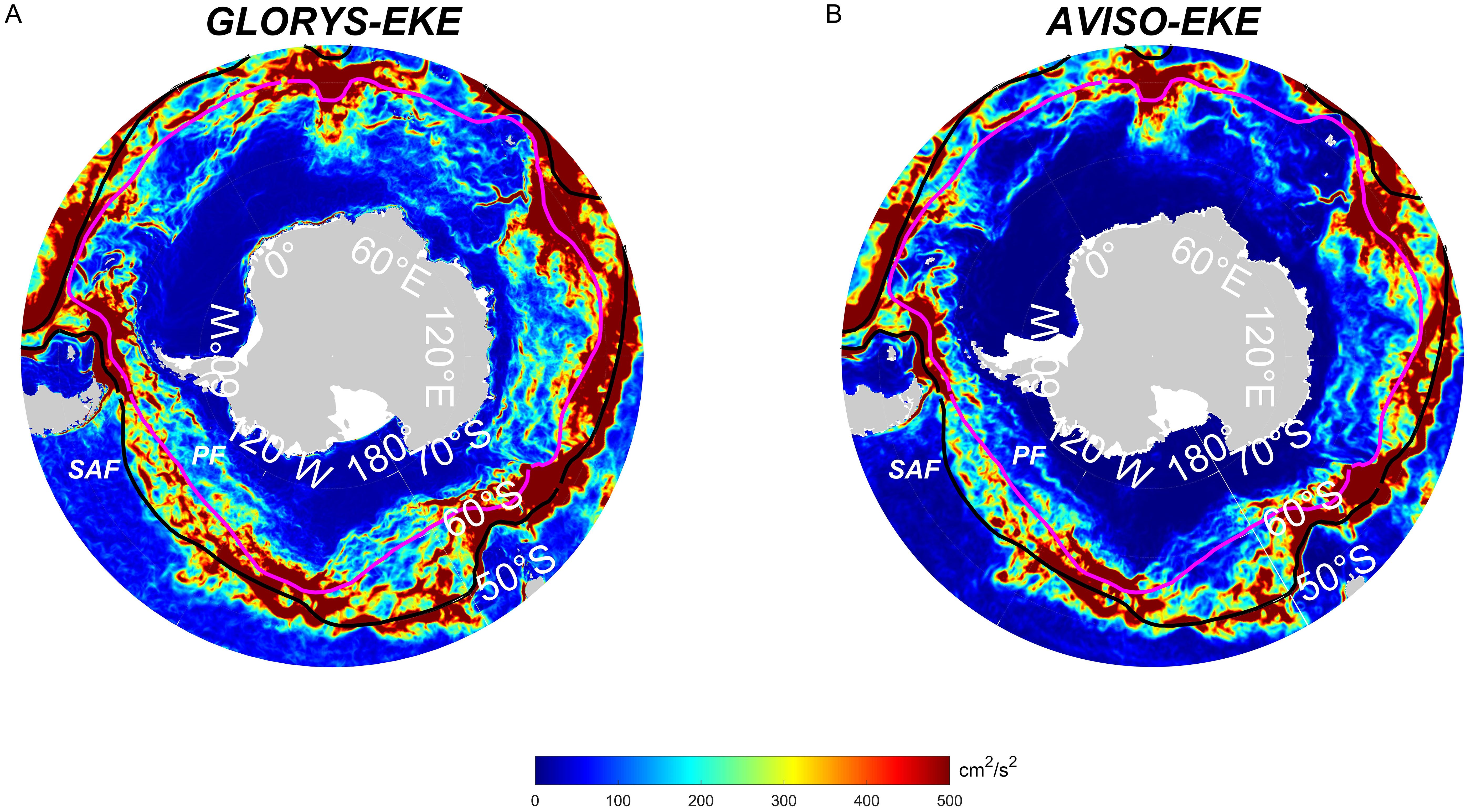
Figure 3. Distribution of the 2020 mean EKE in the Southern Ocean for both GLORYS12V1 and AVISO data. (A) EKE distribution from GLORYS12V1. (B) EKE distribution from AVISO. The black and pink solid lines represent the Subantarctic Front and the Polar Front, respectively.

2.3.2 Evaluation of VG algorithm

To validate the efficacy of VG algorithm and eddy tracking method, we conducted a comparative analysis with the “Mesoscale Eddy Trajectory Atlas” (META, Chelton et al., 2011; Pegliasco et al., 2021). The surface eddy lifetimes of the Southern Ocean during 2020 are selected for comparison. To refine the eddy tracking process and mitigate external disturbances, we imposed some constraint conditions. Given the spatial resolution of 1/12° provided by the GLORYS12V1 dataset, we implemented an initial filtering step, discarding all eddies with an average radius less than 20 km. This measure aims to eliminate potential instabilities or misidentifications of small-scale eddies that could arise due to resolution limitations. Furthermore, to ensure the robustness of the eddy tracking outcomes and the continuity of their dynamical evolution, we further refined the dataset, retaining only eddies with lifespans exceeding two weeks for subsequent statistical analysis. As shown in Figure 4, the META dataset contains 10066 such eddies, while the VG algorithm identified 14022. Specifically, the VG algorithm detected the highest number of eddies with a lifespan of less than 60 days, accounting for 77.21% of the total, whereas the META dataset showed a corresponding proportion of 71.37%. Both datasets exhibit a similar distribution pattern, with a sharp decline in the number of eddies with lifespans exceeding 180 days, the VG algorithm identified 106 such eddies, compared to 284 in the META dataset. In summary, the VG algorithm demonstrates a reasonable consistency with the META dataset in terms of the number and lifespan distribution of detected eddies, particularly excelling in the identification of short-lived eddies. Conversely, the META tends to capture a greater number of long-lived eddies. Overall, the VG algorithm effectively tracks eddy trajectories, making it well-suited for application in this study.

Figure 4

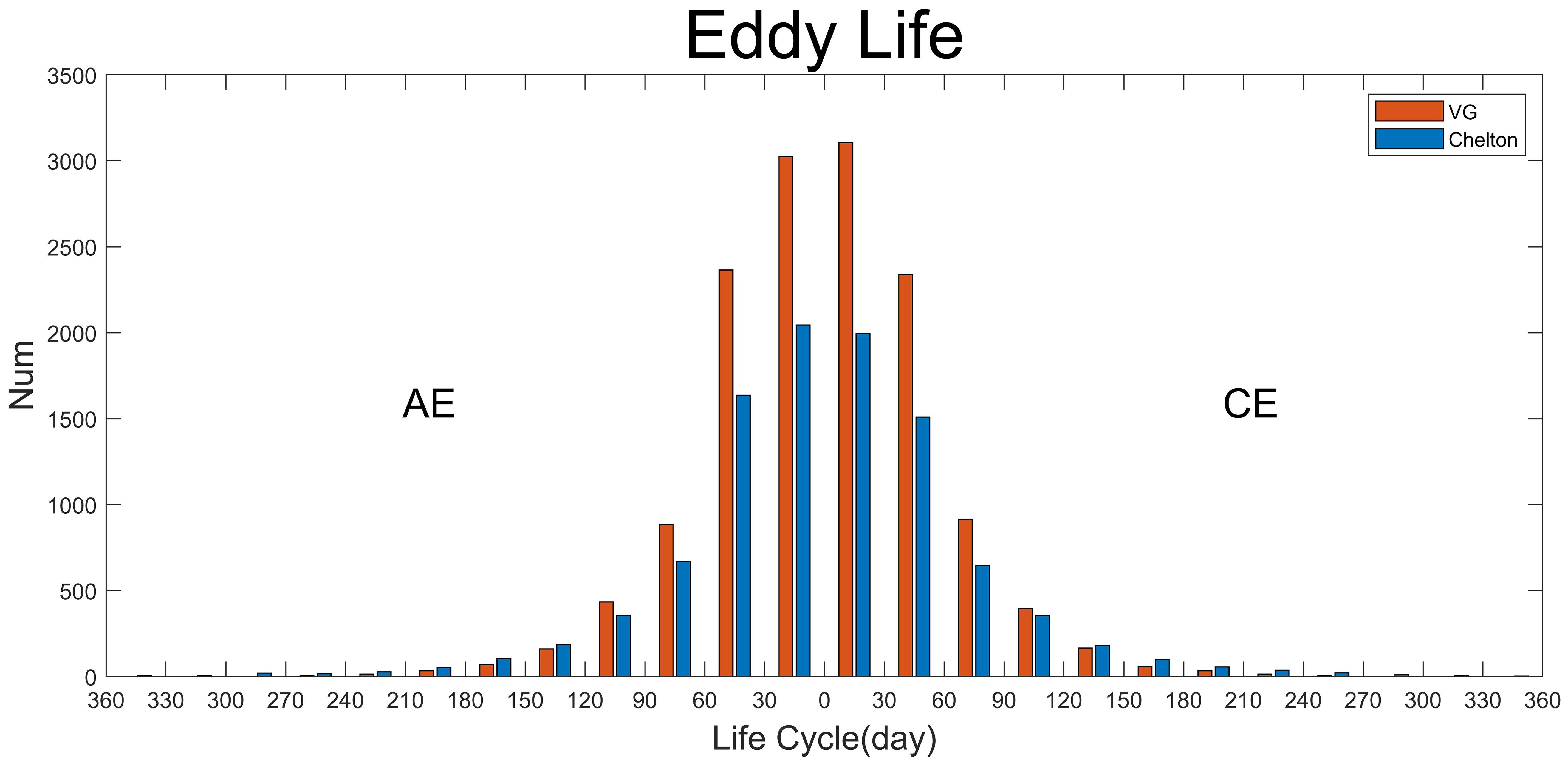
Figure 4. A comparison of eddy lifetime distribution based on the META (the blue bars) and VG algorithms (the orange bars).

3 Results

3.1 Eddy numbers, lifespans and propagation

Since the spatial resolution of the GLORYS12V1 data is 1/12°, eddies smaller than 20 km are excluded from the analysis. Additionally, compared to mid-latitude regions, Southern Ocean eddies are observed to be smaller and deeper (Frenger et al., 2015). To obtain more accurate three-dimensional characteristics of eddies, we also excluded those of shallower and weaker eddies, retaining only those that reach a depth of 700 m. After applying the thresholds of > 20 km and eddies’ depth equal to 700 m, a total of 1587292 eddies were detected from 2011–2019. These eddies were used as the training set. Each 3D eddy was individually divided into a grid of 32×32×8 for longitude, latitude and depth, respectively. The velocities are normalized to a range between -1 and 1 for each layer, with cyclones and anticyclones labeled. The data from 2020 serves as the validation set. The extensive sample training data helps us better extract eddy features and improve the performance of the 3D-U-Res-Net. Compared to the 3D eddies’ snapshots in the northwest Pacific (Xu et al., 2024), we also tracked the eddies to determine their lifetimes and their positions throughout the entirety of their lifespans.

The application of the 3D-U-Res-Net algorithm resulted in the detection of 135734 eddies in 2020, the same number identified by the VG algorithm. The eddies detected by the VG algorithm are used as the ground truth. Figure 5 shows a snapshot of the eddies in the Southern Ocean on September 29, 2020. The dots of different sizes represent different radius scales, including 20-40 km, 40-60 km, 60-80 km, and larger than 80 km. The results show that the 3D-U-Res-Net algorithm identified all eddies on that day, most of the eddies are located near the Subantarctic Front and the Polar Front, which is consistent with previous studies (Frenger et al., 2015). Further observation revealed that although the 3D-U-Res-Net algorithm correctly identified all eddies, the radius differed between the two algorithms. The VG algorithm identified 62 eddies larger than 80 km, whereas the 3D-U-Res-Net algorithm identified only 30 large eddies. This may be because the 3D-U-Res-Net algorithm smooths the edges of the eddies. However, it is worth noting that, using the same computer, it took 10 days to identify 2020 eddies using the VG algorithm, whereas the 3D-U-Res-Net algorithm accomplished the task in only one day, thus saving 10 times the time and greatly improving the efficiency of eddy current detection.

Figure 5

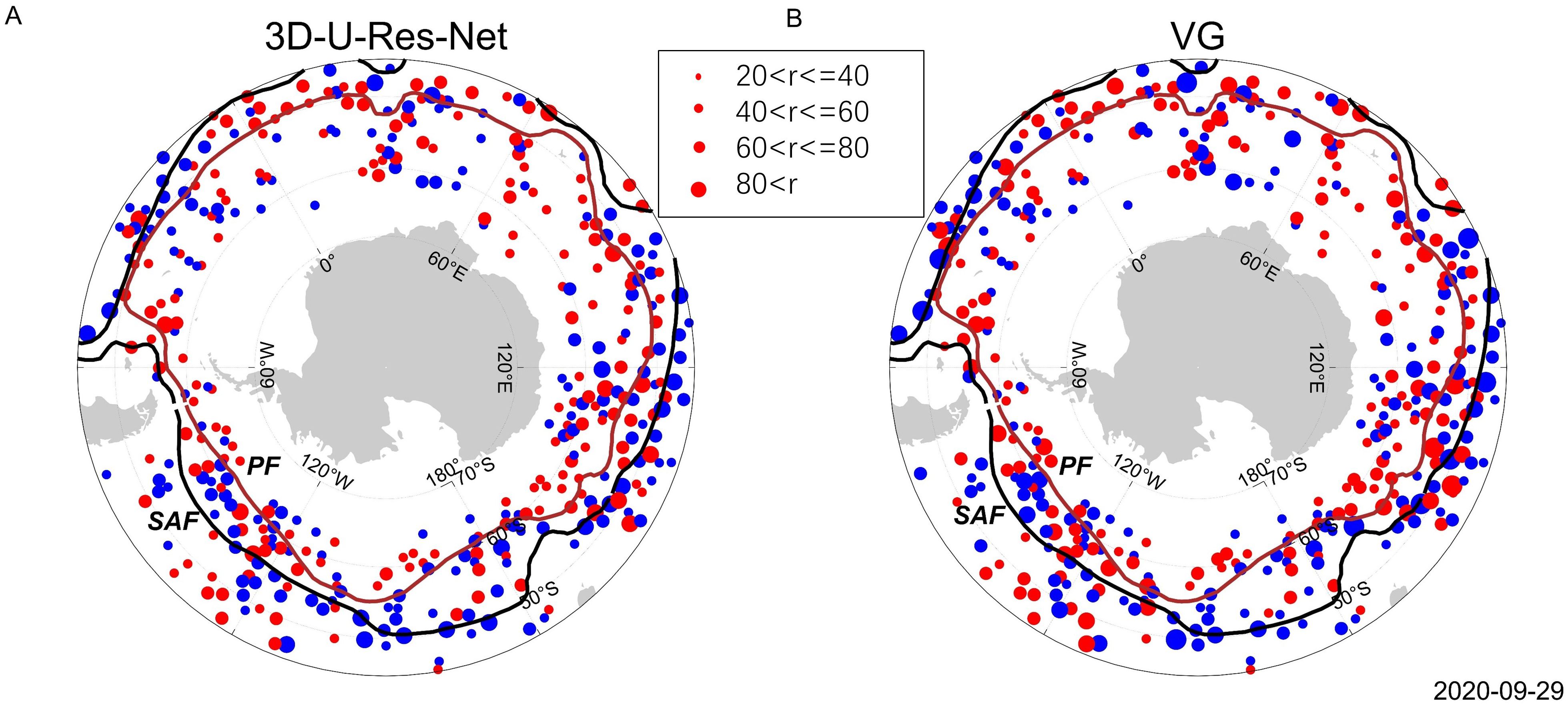
Figure 5. The eddy snapshots for September 29, 2020 in the Southern Ocean. (A) Distribution of 3D-U-Res-Net eddy snapshots. (B) Distribution of eddy snapshots for the VG algorithm. The blue solid dots indicate cyclonic eddies and red solid dots represent anticyclonic eddies. The solid points are categorized into four different radius scales: 20-40km, 40-60km, 60-80km, and greater than 80km. The black and red lines represent the two major fronts in the Southern Ocean: the Subantarctic Front and the Polar Front.

In the year 2020, the VG algorithm is employed to track a total of 18168 eddies, including 8917 anticyclonic eddies and 9251 cyclonic eddies. The 3D-U-Res-Net algorithm identified 18559 eddies, comprising 9092 anticyclonic eddies and 9467 cyclonic eddies. The 3D-U-Res-Net algorithm identified 391 more eddies than the VG algorithm. There are the greatest number of eddies with lifetimes less than 20 days, the 3D-U-Res-Net algorithm amounting to 16973, while the VG algorithm identified 16566 with the same lifespans. Among the eddies with lifetimes exceeding 20 days, the 3D-U-Res-Net algorithm detected slightly fewer, amounting to 1466, compared to 1485 for the VG algorithm. Furthermore, the majority of eddies have a life cycle of less than 20 days. The VG algorithm accounts for 91.18% of the eddies with lifetimes fewer than 20 days, while the 3D-U-Res-Net algorithm accounts for 91.45% of the eddies. Figures 6A, B shows the distribution of the number of eddies in the Southern Ocean for both algorithms. The screening of eddies with a lifetime greater than two weeks resulted in 2400 eddies identified by the VG algorithm and 2387 by the 3D-U-Res-Net algorithm, with a slight predominance of eddies identified by the VG algorithm. The spatial distributions of eddies detected by the two algorithms is consistent. To further analyze the quantitative differences between the two methods, we counted the lifetimes and moving distances of the eddies, as illustrated in Figures 6C, D. Comparing the distribution of lifespans, the eddy lifespans obtained by both methods are fairly consistent, with no significant difference in the number of anticyclonic and cyclonic eddies. Furthermore, the majority of these lifespans are under 30 days. As the lifespans increase, the number of eddies shows a consistent decreasing trend. With regard to the moving distances shown in Figure 6D, the VG algorithm tracked a greater number of eddy trajectories concentrated within 40 km than the 3D-U-Res-Net algorithm. In addition, with regard to trajectories exceeding 80 km, the 3D-U-Res-Net algorithm identified a greater number of eddies. The average traveling distances of the 3D algorithm is 77.78 km, while the average traveling distances of the VG algorithm is 37.60 km. These findings demonstrate the good recognition capability of the 3D-U-Res-Net algorithm.

Figure 6

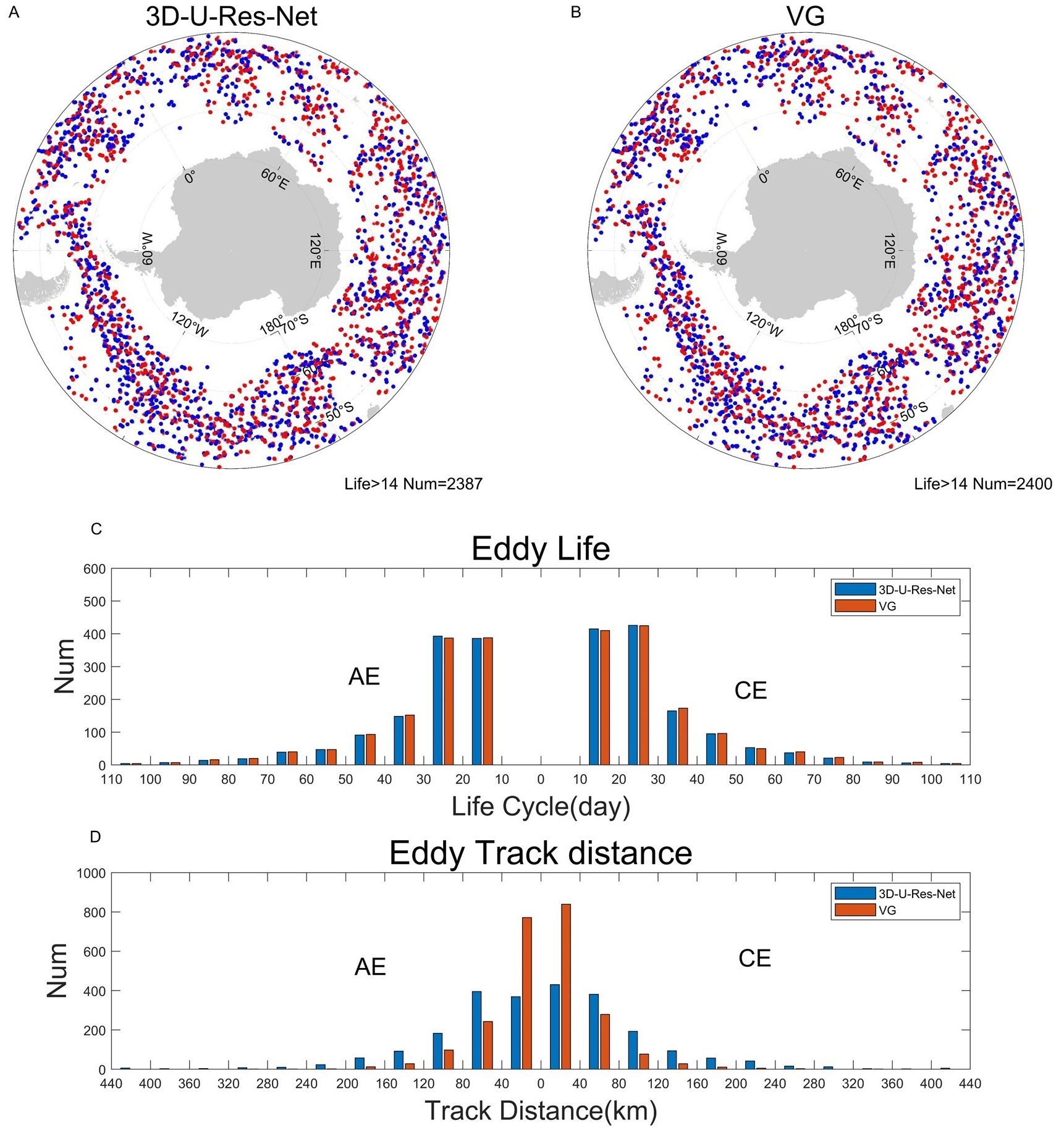
Figure 6. The spatial distribution, the mean lifetime and moving distances of eddies in the Southern Ocean during the year of 2020. A threshold of more than 14 days is used for eddies here. (A) Distribution of eddy trajectories from the 3D-U-Res-Net algorithm. (B) Distribution of eddy trajectories from the VG algorithm. The red points represent anticyclonic eddies and the blue points represent cyclonic eddies. The origin indicates the generated position of the eddy and the asterisk indicates the terminated position of the eddy. (C) A comparison of eddy lifetime distributions based on the 3D-U-Res-Net (the blue bars) and VG algorithms (the orange bars). (D) The same as (C), but for eddy traveling distances. The distribution of the number of anticyclonic eddies is displayed on the left side of the figure, while the distribution of the number of cyclonic eddies is displayed on the right. .

3.2 Eddy radius and 3D shapes

In order to ascertain the distinctions between the 3D-U-Res-Net and the VG algorithm in capturing the three-dimensional structure of eddies, a random selection was made of two eddy examples, one cyclonic and one anticyclonic. The cyclonic eddy example was generated on August 13. As shown in Figures 7A, B, both algorithms are capable of discerning the three-dimensional structure of the cyclone. Compared to the VG algorithm, the eddy radius obtained by the 3D-U-Res-Net is larger and the shapes are more closely aligned with the characteristics of temperature anomaly. The quantitative comparison of cyclone by the two methods shows that the average radius of the cyclone obtained by the VG algorithm from the surface to 700 m is 24.40 km, with a maximum radius of 25.92 km located at a depth of 700 m. Meanwhile, the average radius of the eddy obtained by the 3D-U-Res-Net is 29.66 km, with a maximum radius of 31.83 km located at a depth of 100 m. Notably, the anticyclonic eddy obtained by both algorithms on August 30 exhibited a greater degree of similarity in their 3D structures, as shown in Figures 7C, D. The average radius of the anticyclonic eddy obtained by the VG algorithm is 45.86 km, with a maximum radius of 49.11 km, located at the surface. In comparison, the 3D-U-Res-Net algorithm obtained the anticyclone with an average radius of 43.34 km and a maximum radius of 43.69 km at a depth of 700 m. Thus, 3D-U-Res-Net is accurate for the identification of three-dimensional structures.

Figure 7

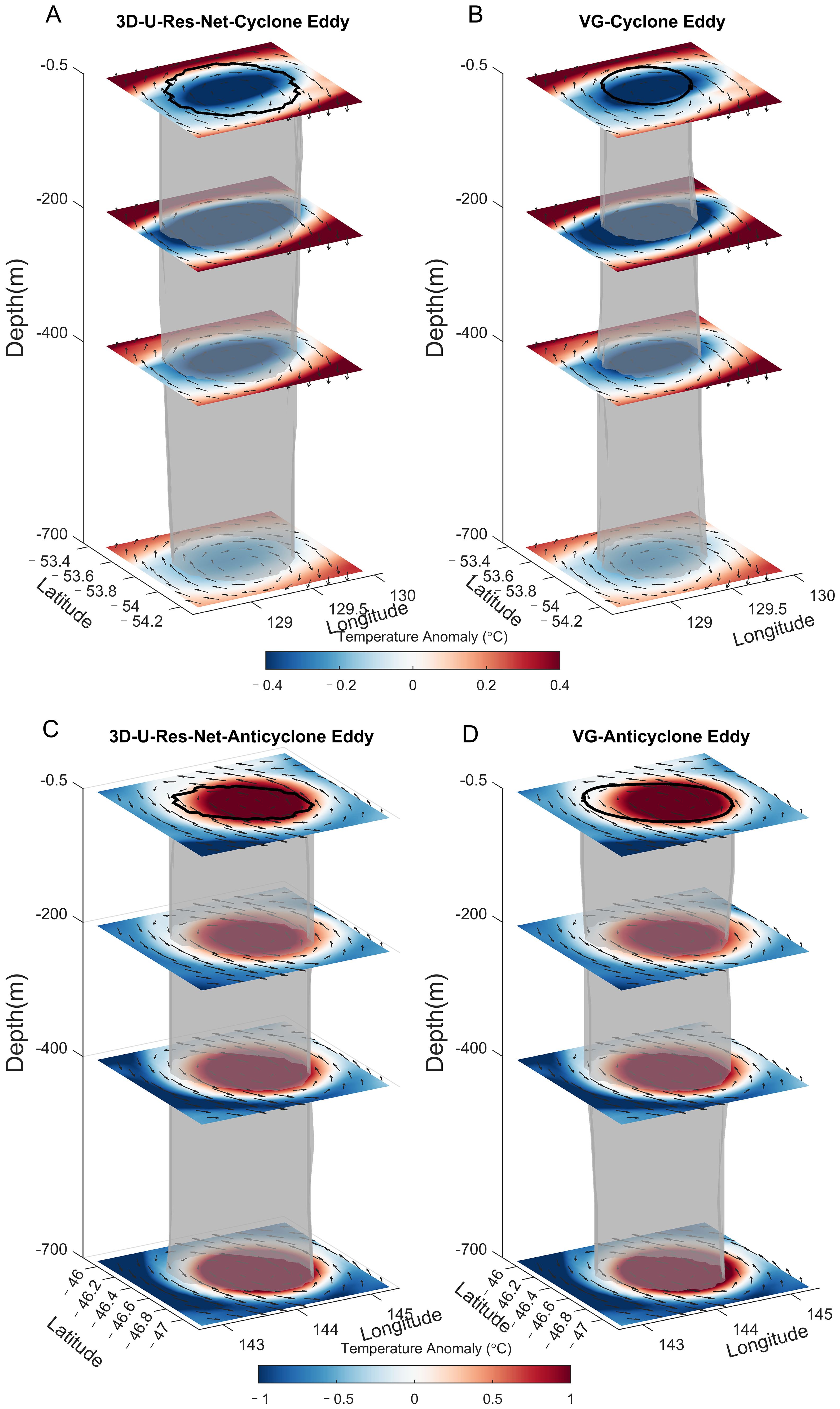
Figure 7. Three-dimensional eddy structures are identified through the VG algorithm and 3D-U-Res-Net. (A) Cyclonic eddy detected by the 3D-U-Res-Net on August 13, 2020. (B) same as (A), but detected using the VG algorithm. (C) Anticyclonic eddy is detected by the 3D-U-Res-Net on August 30, 2020. (D) same as (C), but detected using the VG algorithm. The background colors represent the temperature anomaly, the surface black solid lines indicated the eddies’ surface boundaries, the gray and transparent shapes represented the three-dimensional structures of the eddies, and the gray arrows indicated the velocity flow field.

Additionally, to verify the differences and advantages of the 3D-U-Res-Net algorithm compared to the VG algorithm through a more comprehensive and systematic quantitative analysis, the eddy radius distributions obtained by the two algorithms are examined and contrasted, as shown in Figure 8. The analysis revealed some discrepancies in the resulting data. Most of the eddies identified by the 3D-U-Res-Net algorithm are within the range of 30-60 km. Specifically, 90.4% of anticyclonic eddies and 87.8% of cyclonic eddies are situated within this interval. In the VG algorithm, 83.2% and 84.2% of anticyclonic and cyclonic eddies are between 30 and 60 km. The eddies identified by the 3D-U-Res-Net algorithm were observed to be of a smaller magnitude. For eddies with radii greater than 70 km, the 3D-U-Res-Net algorithm identified anticyclones and cyclones at a rate of 3.3% and 4.6%, respectively, compared to anticyclone and cyclone percentages of 8.3% and 7.6% with the VG algorithm.

Figure 8

Figure 8. (A) Radius distributions from the VG and 3D-U-Res-Net algorithms. Blue represents the VG algorithm and red represents the 3D algorithm. The radius distribution of the anticyclone is shown on the left and that of the cyclone on the right. (B) Vertical distribution of the radius of the anticyclonic eddy, red for the 3D algorithm and blue for the VG algorithm. (C) Vertical distribution of cyclonic eddy radii, red for the 3D algorithm and blue for the VG algorithm. (D) Comparison of the vertical radius of eddies from the two algorithms: the red solid line represents the 3D-U-Res-Net algorithm, and the blue solid line represents the VG algorithm.

A comparison of the radius distribution in the vertical direction, as shown in Figures 8B–D, reveals that the average vertical radius of both anticyclone and cyclone eddies demonstrates a declining trend with increasing depth, as observed using the VG algorithm. The average radius of anticyclonic eddies obtained from the VG algorithm is 44.11 km, while the average radius from the 3D algorithm is 42.62 km. As shown in Figure 8B, the 3D algorithm exhibits the smallest eddy radius at the surface; however, this radius increases with depth. Within the depth range of 100 m to 600 m, the eddy radius remains relatively stable, but it begins to increase again at 700 m, exceeding that of the VG algorithm at the deepest point. In contrast, the radius of anticyclonic eddies from the VG algorithm shows a trend of first increasing and then decreasing with depth. At 700 m, its radius is slightly smaller than that of the 3D algorithm, but the difference between the two is minimal. The average radius of cyclonic eddies obtained from the VG algorithm is 43.39 km, while that from the 3D algorithm is 43.67 km. As illustrated in Figure 8C, the radii of the two methods are very close, with noticeable differences only at the 100 m and 700 m depths. Figure 8D illustrates further discrepancies between the 3D-U-Res-Net algorithm results and the VG algorithm. At depths above 600 m, the 3D-U-Res-Net algorithm eddy radius is smaller than the radius of the VG algorithm. However, this trend reverses below 600 m. At a depth of 700 m, the 3D-U-Res-Net algorithm eddy radius is slightly larger than that of the VG algorithm, with the overall mean radius differing by a mere 0.58 km. The discrepancy may be attributed to the upper eddy features exhibiting relatively unstable, which the 3D-U-Res-Net algorithm smoothing the eddy boundary features, thereby resulting in a slightly smaller eddy radius. As depth increases, eddies tend to stabilize gradually, potentially resulting in an increase in eddy radius over depth. As the depth increases, the flow field becomes weaker. The VG algorithm identifies eddies by using the flow field, while the 3D algorithm learns labels to recognize them. This may result in the radius identified by the 3D algorithm being larger than that identified by the VG algorithm at greater depths.

According to previous research, the three-dimensional structure of ocean eddies can be categorized into three different kinds of 3D shapes based on the distribution of their eddy radii at different depths. These categories are bowl-shaped, cone-shaped, and lens-shaped (Lin et al., 2015). The bowl-shaped eddy has the largest radius at the surface, the cone-shaped eddy exhibits the largest radius at the bottom, and the lens-shaped eddy has the largest radius in the middle. Figures 9A–C shows typical cases of three eddy types identified and classified using 3D-U-Res-Net algorithm. As illustrated in the figure, the center of cyclones and anticyclones is characterized by an evident low-temperature (or high-temperature) core area. During the identification process, a fourth type of 3D eddy structure is defined, namely the cylindrical eddy. For this type of eddy, the difference between the maximum and minimum radii are less than one-tenth of the average radius (Figure 9D). This indicates that this type of eddy has a relatively stable radius distribution throughout all depth layers, and resemble a complete cylindrical shape.

Figure 9

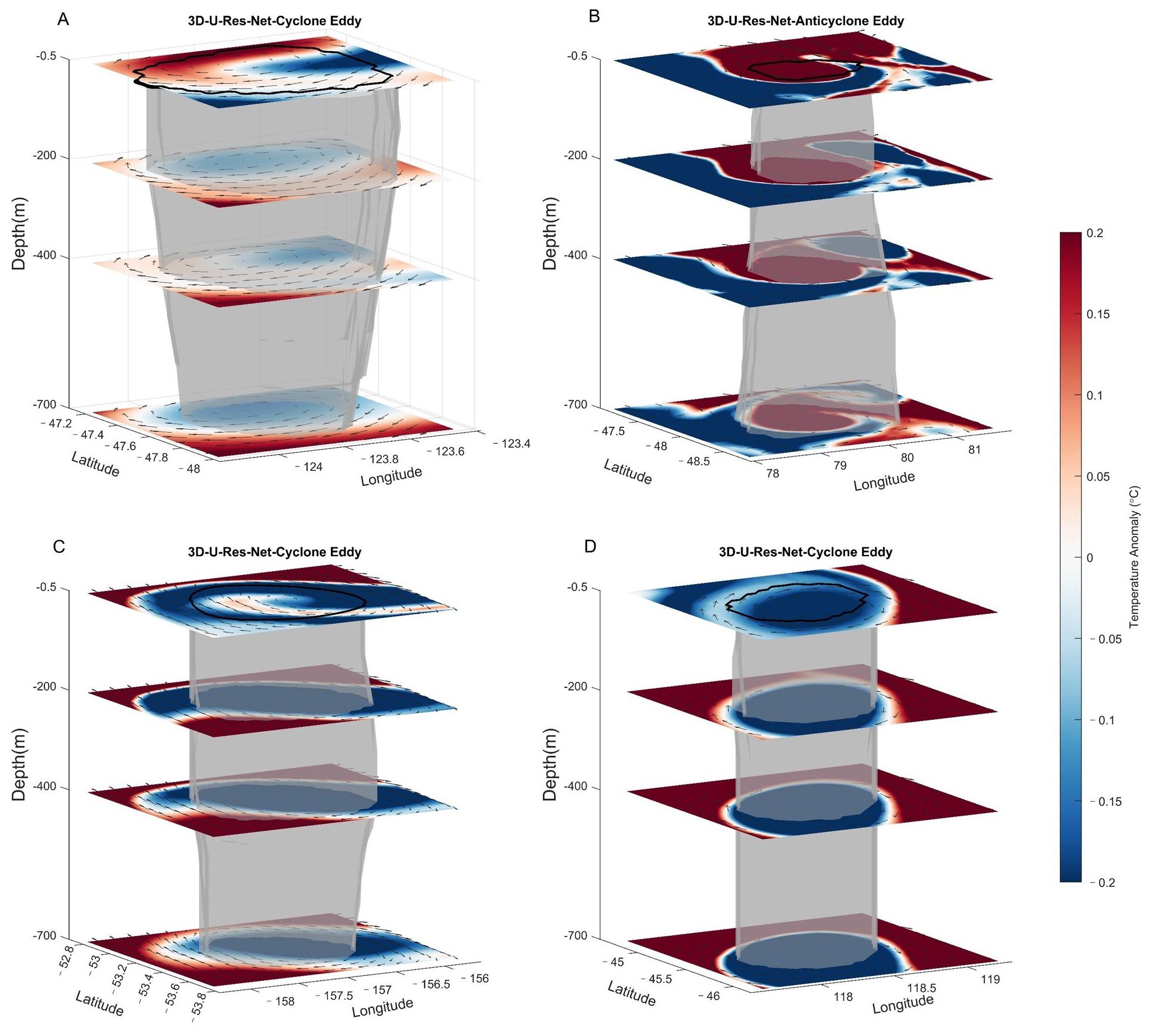
Figure 9. Four distinct types of three-dimensional eddies. (A) Bowl-shaped cyclonic eddies observed on May 7, 2020. (B) A representative example of a cone-shaped anticyclonic eddy observed on May 8, 2020. (C) An individual example of a lens-shaped anticyclonic eddy observed on February 19, 2020. (D) An individual example of a cylindrical cyclonic eddy observed on January 24, 2020. The background field is the temperature anomaly field, the black solid lines indicate the eddy surface contour lines, the gray shapes indicate the eddy boundary, and the gray arrows indicate the velocity flow field.

In order to ascertain the similarities and differences between the two algorithms used to identify the three-dimensional eddies, a statistical analysis is conducted on the number of four different types of eddies (Figure 10). The distribution of anticyclonic and cyclonic eddies is relatively similar in both algorithms. The results of the 3D-U-Res-Net algorithm indicate the number of cylindrical eddies is the most prevalent, while the number of bowl-shaped eddies and cone-shaped eddies is relatively similar, and the number of lens-eddy is minimal. In contrast, the results of the VG algorithm show that the number of cylindrical eddies is relatively low, while the number of the other three eddies is relatively balanced. They account for 32%, 31%, 25%, and 12%, respectively, in the VG algorithm. The percentages of the various types in the 3D-U-Res-Net algorithm were 19.48%, 19.58%, 0.04%, and 60.9%, respectively. In the VG algorithm, the bowl-shaped eddies have the largest proportion of cyclonic eddy, reaching 31.4%, while the cylindrical eddy accounts for 11.98% of anticyclone eddy. In contrast, the 3D-U-Res-Net algorithm results show that bowl-shaped eddies account for 20.86% of the cyclones, while cylinder -shaped eddies have a significant proportion of 64.26%. In the 3D algorithm, the proportion of anticyclones and cyclones of a lens-shaped eddies is only 0.05% and 0.02%, much lower than the VG algorithm of 25.47% and 24.32%. These findings suggest that the 3D-U-Res-Net algorithm is more effective at identifying cylinder -shaped eddies, thereby confirming that the 3D-U-Res-Net algorithm is capable of consistently generating three-dimensional eddy structures during the recognition process. Figure 8B illustrates that the eddy radius is markedly large at depths of 100 m and 700 m, while the radius at intermediate depths is relatively small. This is a contributing factor to the relatively low percentage of lens-shaped eddies compared to the other three types of eddies. However, the method does not correctly identifies lens-shaped, which is one of its shortcomings.

Figure 10

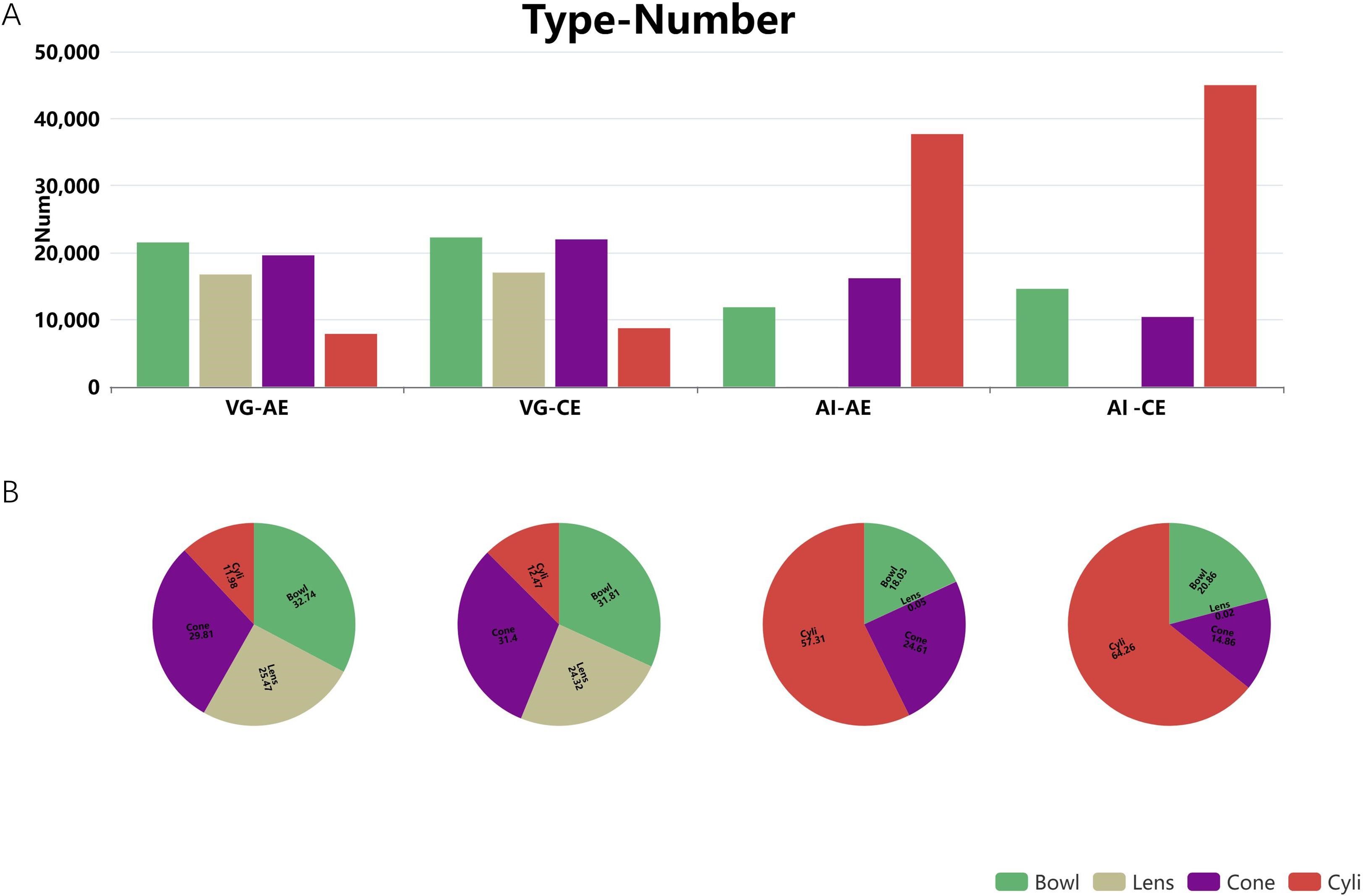
Figure 10. (A) Histogram distribution of the number of four 3D types of eddies. (B) The pie chart illustrates the percentage of the four 3D types of eddies, from left to right, for the VG algorithm anticyclone, VG algorithm cyclone, 3D-U-Res-Net algorithm anticyclone, and 3D-U-Res-Net algorithm cyclone, respectively. The green and gray represents bowl-shaped eddies and lens-shaped eddies, respectively, while the purple and orange represents cone-shaped eddies and cylinder -shaped eddies, respectively.

4 Conclusions

This study utilizes an innovative 3D eddy intelligent recognition algorithm, namely the 3D-U-Res-Net algorithm. The integration of the 3D-UNet and the ResNet enables the extraction and identification of three-dimensional eddy characteristics in complex ocean environment with greater intelligence and efficacy. The GLORYS12V1 dataset spanning the period from 2011 to 2020 is employed in this study. Based on the VG algorithm, a total of 1587292 eddies are identified and used as training sets. These data are then input into the 3D-U-Res-Net for training. Additionally, 135734 eddies identified by the VG algorithm in 2020 are utilized as a validation set. For eddy number, the 3D-U-Res-Net algorithm is able to successfully identify all eddies, meanwhile simultaneously demonstrating the potential to reduce the time required for eddy identification by a factor of 10. The eddies are tracked, and it is determined that a total of 18168 eddies are tracked using the VG algorithm and 18559 eddies are tracked using the 3D-U-Res-Net algorithm. The VG algorithm identify 8917 anticyclonic eddies and 9251 cyclonic eddies. The 3D-U-Res-Net algorithm identify 9092 anticyclonic and 9467 cyclonic eddies, respectively. The 3D-U-Res-Net algorithm tracks a little bit greater number of eddies than the VG algorithm. For eddy lifespan, the majority of eddies obtained by the two algorithms have lifetimes of less than 20 days, with 91.18% for the VG algorithm and 91.45% for the 3D-U-Res-Net algorithm. Eddies with a lifespan exceeding two weeks are selected for statistical analysis. The average lifespan of eddies for the 3D-U-Res-Net and VG algorithms are 29.35 and 29.61 days, respectively. The distribution of eddy lifetimes exhibits a similar pattern for both algorithms, with only a slight discrepancy in the number of eddies observed. The mean traveling distances for the 3D-U-Res-Net and VG algorithms are 77.78 and 37.60 km, respectively. With regard to the trajectories and distances traveled by eddies, those detected by the 3D-U-Res-Net algorithm are observed to have greater ranges. The trajectories of the VG algorithm exhibit a higher number of eddies up to 40 km, while the 3D-U-Res-Net algorithm has a lower number of eddies. The eddies identified by the 3D-U-Res-Net algorithm can be tracked to eddies with a longer trajectory.

A comparison of the eddy radii across different layers reveals that the eddy radii identified by the 3D-U-Res-Net algorithm are larger in the surface and bottom layers. In the depth range from the sea surface to 600 m, the mean eddy radius identified by the 3D-U-Res-Net is smaller compared to that identified by the VG algorithm. Below 600 m, the mean eddy radius identified by the 3D-U-Res-Net is larger. The average eddy radius detected by the 3D-U-Res-Net algorithm is 0.58 km smaller than that detected by the VG algorithm. Eddies are classified into four distinct types based on their radii distribution: bowl-shaped, cone-shaped, lens-shaped, and cylindrical. The identified three-dimensional eddies exhibited greater structural similarity, including the discovery of a new type termed ‘cylindrical eddy,’ which constituted 60.9% of all detected eddies. This proportion is five times higher than that observed with the VG algorithm. The number of lens-shaped eddies is small, representing only 0.04% of the total. The number of bowl-shaped eddies is comparable to that of cone-shaped eddies, with respective counts of 26441 and 26577, respectively. In contrast, the VG algorithm identified the highest numbers of bowl-shaped and cone-shaped eddies, with counts of 43435 and 42078, respectively. The number of lens-shaped eddies is 33933, while the number of cylindrical eddies is the lowest, comprising 12% of the total with a count of 16288.

Overall, the 3D-U-Res-Net algorithm effectively identifies three-dimensional eddies in the ocean and significantly reduces processing time compared to the VG algorithm, thereby saving considerable time and effort. Additionally, in eddy tracking, the 3D-U-Res-Net algorithm captures eddies with longer trajectories and tends to identify more stable eddy structures in three dimensions. However, this comes with a drawback: smoothing out eddy structures may lead to fewer detections of other types of eddies, such as lens-shaped eddies. The 3D-U-Res-Net algorithm identified more cylindrical eddies, resulting in some differences from the VG algorithm, which reflects a limitation of the 3D-U-Res-Net algorithm. The 3D-U-Res-Net algorithm determines eddy boundaries by learning annotations at grid points, and since calibration values at these points may be slightly lower than the actual eddy boundaries, this could lead to radius discrepancies. Furthermore, due to the stability of eddies in the Southern Ocean, the structural differences in three-dimensional eddies may inherently be smaller. Currently, our understanding of this model remains limited, and how to optimize its performance is not yet clear. We hope to continuously conduct experimental training to uncover underlying reasons and improve model performance. The present study focused exclusively on eddies with a depth of 700 m in the Southern Ocean region. It is expected that in the subsequent research activities, this method will be applied to investigate eddies of different depths and extended to different sea areas. This will undoubtedly facilitate our comprehension of the three-dimensional structure of eddies, promote the research process of eddy dynamics mechanisms, and is of extremely critical significance for in-depth exploration of ocean eddies.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

CL: Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review & editing. XL: Conceptualization, Data curation, Formal analysis, Funding acquisition, Resources, Software, Supervision, Validation, Writing – original draft, Writing – review & editing. GX: Data curation, Methodology, Software, Supervision, Writing – review & editing. GH: Data curation, Formal analysis, Software, Supervision, Validation, Writing – review & editing. YL: Data curation, Formal analysis, Supervision, Validation, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was funded by Southern Marine Science and Engineering Guangdong Laboratory (Zhuhai), grant number SML2020SP007 and SML2021SP207; the Innovation Group Project of Southern Marine Science and Engineering Guangdong Laboratory (Zhuhai), grant number 311020004 and 311022001; the National Natural Science Foundation of China, grant number 42206005; the open fund of State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, MNR, grant number QNHX2309; General scientific research project of Zhejiang Provincial Department of Education, grant number Y202250609; the Open Foundation from Marine Sciences in the First-Class Subjects of Zhejiang, grant number OFMS006.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Belkin I. M., Gordon A. L. (1996). Southern Ocean fronts from the Greenwich meridian to Tasmania. J. Geophysical Research: Oceans 101, 3675–3696. doi: 10.1029/95JC02750

Crossref Full Text | Google Scholar

Cao L., Zhang D., Guo Q., Zhan J. (2022). “Ocean mesoscale eddies identification based on YOLOF,” in In IGARSS 2022-2022 IEEE International Geoscience and Remote Sensing Symposium, Vol. 2022. 1177–1180 (Kuala Lumpur, Malaysia: IEEE).

Google Scholar

Chang Y. L., Oey L. Y. (2014). Analysis of STCC eddies using the Okubo–Weiss parameter on model and satellite data. Ocean Dynamics 64, 259–271. doi: 10.1007/s10236-013-0680-7

Crossref Full Text | Google Scholar

Chapman C. C., Lea M. A., Meyer A., Sallée J. B., Hindell M. (2020). Defining Southern Ocean fronts and their influence on biological and physical processes in a changing climate. Nat. Climate Change 10, 209–219. doi: 10.1038/s41558-020-0705-4

Crossref Full Text | Google Scholar

Chelton D. B., Schlax M. G., Samelson R. M. (2011). Global observations of nonlinear mesoscale eddies. Prog. oceanography 91, 167–216. doi: 10.1016/j.pocean.2011.01.002

Crossref Full Text | Google Scholar

Chelton D. B., Schlax M. G., Samelson R. M., de Szoeke R. A. (2007). Global observations of large oceanic eddies. Geophysical Res. Lett. 34, 87–101. doi: 10.1029/2007GL030812

Crossref Full Text | Google Scholar

Chen X., Chen G., Ge L., Huang B., Cao C. (2021). Global oceanic eddy identification: A deep learning method from argo profiles and altimetry data. Front. Mar. Sci. 8, 646926. doi: 10.3389/fmars.2021.646926

Crossref Full Text | Google Scholar

Çiçek Ö., Abdulkadir A., Lienkamp S. S., Brox T., Ronneberger O. (2016). “3D U-Net: learning dense volumetric segmentation from sparse annotation,” in Lecture Notes in Computer Science ((LNIP, volume 9901)) Medical Image Computing and Computer-Assisted Intervention–MICCAI 2016: 19th International Conference, Athens, Greece, October 17-21, 2016. Springer, Cham. 424–432, Proceedings, Part II 19.

Google Scholar

Dong C., Lin X., Liu Y., Nencioli F., Chao Y., Guan Y., et al. (2012). Three-dimensional oceanic eddy analysis in the Southern California Bight from a numerical product. J. Geophysical Research: Oceans 117, C00H14. doi: 10.1029/2011JC007354

Crossref Full Text | Google Scholar

Dong C., Mavor T., Nencioli F., Jiang S., Uchiyama Y., McWilliams J. C., et al. (2009). An oceanic cyclonic eddy on the lee side of Lanai Island, Hawai’i. J. Geophysical Research: Oceans 114, C10008. doi: 10.1029/2009JC005346

Crossref Full Text | Google Scholar

Dong C., McWilliams J. C., Liu Y., Chen D. (2014). Global heat and salt transports by eddy movement. Nat. Commun. 5, 3294. doi: 10.1038/ncomms4294

PubMed Abstract | Crossref Full Text | Google Scholar

Duo Z., Wang W., Wang H. (2019). Oceanic mesoscale eddy detection method based on deep learning. Remote Sens. 11, 1921. doi: 10.3390/rs11161921

Crossref Full Text | Google Scholar

Feng P., Fu Z., Hu L., Wu S., Wang Y., Zhang F. (2023). 3D-eddyNet: A novel approach for identifying three-dimensional morphological features of mesoscale eddies in the ocean. J. Mar. Sci. Eng. 11, 1779. doi: 10.3390/jmse11091779

Crossref Full Text | Google Scholar

Frenger I., Gruber N., Knutti R., Münnich M. (2013). Imprint of Southern Ocean eddies on winds, clouds and rainfall. Nat. Geosci. 6, 608–612. doi: 10.1038/ngeo1863

Crossref Full Text | Google Scholar

Frenger I., Münnich M., Gruber N., Knutti R. (2015). Southern O cean eddy phenomenology. J. Geophysical Research: Oceans 120, 7413–7449. doi: 10.1002/2015JC011047

Crossref Full Text | Google Scholar

Griffies S. M., Winton M., Anderson W. G., Benson R., Delworth T. L., Dufour C. O., et al. (2015). Impacts on ocean heat from transient mesoscale eddies in a hierarchy of climate models. J. Climate 28, 952–977. doi: 10.1175/JCLI-D-14-00353.1

Crossref Full Text | Google Scholar

Hammoud M. A. E. R., Zhan P., Hakla O., Knio O., Hoteit I. (2023). Semantic segmentation of mesoscale eddies in the arabian sea: A deep learning approach. Remote Sens. 15, 1525. doi: 10.3390/rs15061525

Crossref Full Text | Google Scholar

He Q., Zhan W., Cai S., Du Y., Chen Z., Tang S., et al. (2023). Enhancing impacts of mesoscale eddies on Southern Ocean temperature variability and extremes. Proc. Natl. Acad. Sci. 120, e2302292120. doi: 10.1073/pnas.2302292120

PubMed Abstract | Crossref Full Text | Google Scholar

He K., Zhang X., Ren S., Sun J. (2016). “Deep residual learning for image recognition,” in Proceedings of the IEEE conference on computer vision and pattern recognition. arXiv:1512.03385. 770–778.

Google Scholar

Huang D., Du Y., He Q., Song W., Liotta A. (2017). “DeepEddy: A simple deep architecture for mesoscale oceanic eddy detection in SAR images,” in 2017 IEEE 14th International Conference on Networking, Sensing and Control (ICNSC). 673–678 (Calabria, Italy: IEEE).

Google Scholar

Huang B., Ge L., Chen X., Chen G. (2021). Vertical structure-based classification of oceanic eddy using 3-D convolutional neural network. IEEE Trans. Geosci. Remote Sens. 60, 1–14. doi: 10.1109/TGRS.2021.3103251

Crossref Full Text | Google Scholar

Jean-Michel L., Eric G., Romain B. B., Gilles G., Angélique M., Marie D., et al. (2021). The Copernicus global 1/12 oceanic and sea ice GLORYS12 reanalysis. Front. Earth Sci. 9, 698876. doi: 10.3389/feart.2021.698876

Crossref Full Text | Google Scholar

Lellouche J. M., Le Galloudec O., Greiner E., Garric G., Regnier C., Drevillon M., et al. (2018). “The Copernicus Marine Environment Monitoring Service global ocean 1/12 physical reanalysis GLORYS12V1: description and quality assessment,” in 20th EGU General Assembly, EGU2018 Proceedings from the conference, 4-13 April. EGU: Vienna, Austria. p. 19806.

Google Scholar

Lguensat R., Rjiba S., Mason E., Fablet R., Sommer J. (2018a). Convolutional neural networks for the segmentation of oceanic eddies from altimetric maps. Remote Sens 1, 1–16. doi: 10.13140/RG.2.2.23386.90564

Crossref Full Text | Google Scholar

Lguensat R., Sun M., Fablet R., Tandeo P., Mason E., Chen G. (2018b). “EddyNet: A deep neural network for pixel-wise classification of oceanic eddies,” in IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium. 1764–1767 (Valencia, Spain: IEEE). doi: 10.48550/arXiv.1711.03954

Crossref Full Text | Google Scholar

Lin X., Dong C., Chen D., Liu Y., Yang J., Zou B., et al. (2015). Three-dimensional properties of mesoscale eddies in the South China Sea based on eddy-resolving model output. Deep Sea Res. Part I: Oceanographic Res. Papers 99, 46–64. doi: 10.1016/j.dsr.2015.01.007

Crossref Full Text | Google Scholar

Lin X., Zhao H., Liu Y., Han G., Zhang H., Liao X. (2023). Ocean eddies in the Drake Passage: Decoding their three-dimensional structure and evolution. Remote Sens. 15, 2462. doi: 10.3390/rs15092462

Crossref Full Text | Google Scholar

Liu Y., Dong C., Guan Y., Chen D., McWilliams J., Nencioli F. (2012). Eddy analysis in the subtropical zonal band of the North Pacific Ocean. Deep Sea Res. Part I: Oceanographic Res. Papers 68, 54–67. doi: 10.1016/j.dsr.2012.06.001

Crossref Full Text | Google Scholar

Liu Y., Wang H., Jiang F., Zhou Y., Li X. (2024). Reconstructing three-dimensional thermohaline structures for mesoscale eddies using satellite observations and deep learning. IEEE Trans. Geosci. Remote Sensing 62. doi: 10.1109/TGRS.2024.3373605

Crossref Full Text | Google Scholar

Liu Y., Wang H., Li X. (2022). “A Deep Learning-Based Mesoscale Eddy Subsurface Temperature Inversion Model,” in IGARSS 2022-2022 IEEE International Geoscience and Remote Sensing Symposium (IEEE), 6884–6886. doi: 10.1109/IGARSS46834.2022.9883558

Crossref Full Text | Google Scholar

Marez C., L’Hégaret P., Morvan M., Carton X. (2019). On the 3D structure of eddies in the Arabian Sea. Deep Sea Res. Part I: Oceanographic Res. Papers 150, 103057. doi: 10.1016/j.dsr.2019.06.003

Crossref Full Text | Google Scholar

Moreau S., Penna A. D., Llort J., Patel R., Langlais C., Boyd P. W., et al. (2017). Eddy-induced carbon transport across the Antarctic Circumpolar Current. Global Biogeochemical Cycles 31, 1368–1386. doi: 10.1002/2017GB005669

Crossref Full Text | Google Scholar

Morrow R., Ward M. L., Hogg A. M., Pasquet S. (2010). Eddy response to Southern Ocean climate modes. J. Geophysical Research: Oceans 115, 10030. doi: 10.1029/2009JC005894

Crossref Full Text | Google Scholar

Nencioli F., Dong C., Dickey T., Washburn L., McWilliams J. C. (2010). A vector geometry–based eddy detection algorithm and its application to a high-resolution numerical model product and high-frequency radar surface velocities in the Southern California Bight. J. atmospheric oceanic Technol. 27, 564–579. doi: 10.1175/2009JTECHO725.1

Crossref Full Text | Google Scholar

Okubo A. (1970). “Horizontal dispersion of floatable particles in the vicinity of velocity singularities such as convergences,” in Deep sea research and oceanographic abstracts, vol. 17. (Elsevier), 445–454.

Google Scholar

Patel R. S., Phillips H. E., Strutton P. G., Lenton A., Llort J. (2019). Meridional heat and salt transport across the subantarctic front by cold-core eddies. J. Geophysical Research: Oceans 124, 981–1004. doi: 10.1029/2018JC014655

Crossref Full Text | Google Scholar

Pegliasco C., Delepoulle A., Busche C., Morrow R., Faugère Y., Dibarboure G. (2021). “A New Global Mesoscale Eddy Trajectories Atlas Derived from Altimetry: Presentation and Future Evolutions,”, vol. 2021. (AGU Fall Meeting Abstracts: AGU Fall Meeting Abstracts), OS12A–OS104.

Google Scholar

Pegliasco C., Delepoulle A., Mason E., Morrow R., Faugère Y., Dibarboure G. (2022). META3. 1exp: A new global mesoscale eddy trajectory atlas derived from altimetry. Earth System Sci. Data 14, 1087–1107. doi: 10.5194/essd-14-1087-2022

Crossref Full Text | Google Scholar

Rintoul S. R., Garabato A. C. N. (2013). “Dynamics of the Southern Ocean circulation,” in International geophysics, vol. 103. (Academic Press), 471–492.

Google Scholar

Sadarjoen I. A., Post F. H. (2000). Detection, quantification, and tracking of vortices using streamline geometry. Comput. Graphics 24, 333–341. doi: 10.1016/S0097-8493(00)00029-7

Crossref Full Text | Google Scholar

Wang H., Liu D., Zhang W., Li J., Wang B. (2020). Characterizing the capability of mesoscale eddies to carry drifters in the northwest Pacific. J. Oceanology Limnology 38, 1711–1728. doi: 10.1007/s00343-019-9149-y

Crossref Full Text | Google Scholar

Weiss J. (1991). The dynamics of enstrophy transfer in two-dimensional hydrodynamics. Physica D. Nonlinear Phenomena 48, 273–294. doi: 10.1016/0167-2789(91)90088-Q

Crossref Full Text | Google Scholar

Xiao Z., Liu B., Geng L., Zhang F., Liu Y. (2020). Segmentation of lung nodules using improved 3D-UNet neural network. Symmetry 12, 1787. doi: 10.3390/sym12111787

Crossref Full Text | Google Scholar

Xing T., Yang Y. (2021). Three mesoscale eddy detection and tracking methods: Assessment for the South China Sea. J. Atmospheric Oceanic Technol. 38, 243–258. doi: 10.1175/JTECH-D-20-0020.1

Crossref Full Text | Google Scholar

Xu G., Cheng C., Yang W., Xie W., Kong L., Hang R., et al. (2019). Oceanic eddy identification using an AI scheme. Remote Sens. 11, 1349. doi: 10.3390/rs11111349

Crossref Full Text | Google Scholar

Xu G., Xie W., Lin X., Liu Y., Hang R., Sun W., et al. (2024). Detection of three-dimensional structures of oceanic eddies using artificial intelligence. Ocean Model. 2024, 102385. doi: 10.1016/j.ocemod.2024.102385

Crossref Full Text | Google Scholar

Zhang Y., Chambers D., Liang X. (2021). Regional trends in Southern Ocean eddy kinetic energy. J. Geophysical Research: Oceans 126, e2020JC016973. doi: 10.1029/2020JC016973

Crossref Full Text | Google Scholar

Zhang Z., Tian J., Qiu B., Zhao W., Chang P., Wu D., et al. (2016). Observed 3D structure, generation, and dissipation of oceanic mesoscale eddies in the South China Sea. Sci. Rep. 6, 24349. doi: 10.1038/srep24349

PubMed Abstract | Crossref Full Text | Google Scholar

Zhang Z., Wang G., Wang H., Liu H. (2024). Three-dimensional structure of oceanic mesoscale eddies. Ocean-Land-Atmosphere Res. 3, 0051. doi: 10.34133/olar.0051

Crossref Full Text | Google Scholar

Zhao N., Huang B., Zhang X., Ge L., Chen G. (2023). Intelligent identification of oceanic eddies in remote sensing data via Dual-Pyramid UNet. Atmospheric Oceanic Sci. Lett. 16, 100335. doi: 10.1016/j.aosl.2023.100335

Crossref Full Text | Google Scholar