Phytoplankton carbon to chlorophyll a model development: a review

The cellular carbon content and chlorophyll a (Chl a) concentration are two of the most significant indices for assessing phytoplankton biomass. Recording and monitoring these biomasses are essential tasks in phytoplankton research, and the carbon-to-chlorophyll a (C:Chl a) ratio serves as a crucial conversion tool between them. Although the C:Chl a ratio varies widely, it is influenced by external environmental factors, making modeling studies of C:Chl a particularly important. This paper provides an overview of the historical development of the C:Chl a model, beginning with early empirical models and progressing to the development of mechanistic models. This discussion is followed by an examination of existing gaps and future challenges in current C:Chl a modeling, particularly the potential underestimation of carbon biomass in existing C:Chl a models for dinoflagellates exhibiting multiple growth strategies. Finally, it is suggested that future C:Chl a models should strive to achieve a balance between reliability and applicability.

1 Introduction

Unicellular phytoplankton are significant contributors to ocean productivity, accounting for approximately half of global primary production (Worden et al., 2015; Levine and Leles, 2021). They play a crucial role in global biogeochemical cycles and climate change (Falkowski, 1994; Boyce et al., 2010; Litchman et al., 2015; Behrenfeld et al., 2016). Phytoplankton metabolic processes significantly influence global marine carbon and oxygen production. In addition to regulating food web dynamics, phytoplankton are responsible for cycling essential biological elements such as carbon and nitrogen (Litchman et al., 2015; Behrenfeld et al., 2016).

Phytoplankton in the surface ocean convert dissolved carbon and nutrients into organic matter, which is then transported downward through sinking particles. This process creates a biological pump that reduces atmospheric CO₂ concentrations (DeVries et al., 2012; Agustí et al., 2015; Tréguer et al., 2018). Understanding the elemental composition of marine photoautotrophic phytoplankton is crucial for studying global ecosystems and Earth’s climate (Falkowski, 2012; Schoo et al., 2013; Kwiatkowski et al., 2018). Several studies on phytoplankton conducted in recent years have demonstrated that community structure, composition, and diversity significantly influence phytoplankton stoichiometry (Tréguer et al., 2018; McCain et al., 2021). This stoichiometry, in turn, reflects the quality of the food supply and the pathways of energy transfer in tropical ecosystems (Sardans et al., 2021).

Because of its widespread presence in all phytoplankton taxa, including both prokaryotes and eukaryotes, chlorophyll a (Chl a) concentration is one of the most commonly used indicators of phytoplankton biomass. The measurement of chlorophyll concentration is conducted using various methods, such as spectrophotometry (Ergun et al., 2004), fluorescence (Kruskopf and Flynn, 2006), and high-performance liquid chromatography (Moorhouse et al., 2018). Chl a measurements, in addition to being convenient and continuously operable, can be conducted remotely using satellite remote sensing methods. Remote sensing of ocean water color is an effective monitoring tool for the simultaneous observation of phytoplankton distribution at the sea surface on a large scale and for the detection of phytoplankton blooms (Dierssen, 2010; Kaymaz and Ates, 2018; He et al., 2020). However, there were differences in Chl a concentrations among taxonomic groups. Letelier et al. (1993) summarized seven distinct taxonomic groups of Chl a algorithms based on diagnostic pigments specific to each algal group. The Chl a concentration of Bacillariophytes was primarily determined by fucoxanthin, while the Chl a concentration of Dinoflagellates exhibited a linear correlation with peridinin. The Chl a concentration of Cyanobacteria was influenced by zeaxanthin and chlorophyll b (Chl b). Additionally, the Chl a concentration of Chrysophytes was linearly correlated with 19′-butanoyloxyfucoxanthin, and the Chl a concentration of Prymnesiophytes was linearly correlated with 19′-hexanoyloxyfucoxanthin. The Chl a concentration of Prasinophytes was linearly correlated with prasinoxanthin, and the Chl a concentration of Prochlorococcus spp. was determined by both Chl b and prasinoxanthin. It is important to note that the phytoplankton community counts also included both mixotrophic and heterotrophic dinoflagellates that do not contain Chl a. In addition, because changes in Chl a concentration may not be influenced by phytoplankton carbon biomass, Chl a concentrations do not fully represent phytoplankton biomass (Jackson et al., 2017; Sathyendranath et al., 2020).

To address the limitations of Chl a as an indicator of biomass, scientists have employed alternative biological indicators, with biological carbon being the most widely used. Carbon is typically found in high concentrations relative to other elements, and importantly, biomass measured using biocarbon markers can be directly linked to the carbon cycle (Graff et al., 2012). However, unlike Chl a, directly measuring phytoplankton carbon content is quite challenging. Currently, our techniques do not permit direct monitoring of phytoplankton carbon biomass over large areas of the ocean. Traditionally, phytoplankton carbon biomass has been estimated from cell volume through microscopic counts, which are then converted to carbon per cell. This information is subsequently used to determine the distribution and variation of carbon biomass throughout the community (Menden-Deuer and Lessard, 2000). However, the methods of microscopic counting and estimating cell volume for biomass still have limitations. Some species, such as diatoms, possess a large cell volume that is primarily occupied by a vacuole, which may lead to an overestimation of their cell carbon content (Hansen and Visser, 2019).

To estimate the carbon content of phytoplankton based on its Chl a concentration, a conversion factor known as the phytoplankton carbon to Chl a ratio (C: Chl a), has been established (Strickland, 1960). This conversion requires quantifying the C:Chl a ratios, as they are essential for relating Chl a concentration to carbon biomass. However, the C:Chl a ratio in phytoplankton is not constant; it varies not only between species but is also significantly influenced by external environmental factors such as light, nutrients, and temperature (Geider et al., 1997; Behrenfeld et al., 2002; Wang et al., 2009; Li et al., 2010). Therefore, the accuracy with which ecosystem models can predict the C:Chl a ratio in natural ecosystems is one of the fundamental challenges in contemporary ocean carbon cycle research (Armstrong, 2006). Phytoplankton cells under nutrient-deficient or senescent conditions exhibited a higher C: Chl a ratio compared to healthy phytoplankton cells, and this ratio was significantly influenced by environmental factors. Lorenzen (1968) found that the C:Chl a ratio of phytoplankton was positively correlated with light intensity. Eppely determined the C: Chl a of phytoplankton in two areas within the La Jolla Sea Area and found that the C: Chl a in the saturated nutrient area was about 22-28 g C g Chl a^-1, whereas it was higher in the oligotrophic area, about 91-105 g C g Chl a^-1 (Eppley, 1968). Like higher plants, phytoplankton convert solar energy into chemical energy and inorganic matter into storable organic matter through photosynthesis. Factors such as light and temperature can influence this photosynthetic process, thereby altering the carbon to chlorophyll a ratio in phytoplankton. Additionally, nutrients, trace elements, and other factors can affect the composition of materials within phytoplankton cells.

In early phytoplankton modeling studies, the relationship between phytoplankton growth rates and various environmental factors was often analyzed separately. Light is the environmental factor most frequently utilized in modeling, and several models have been developed to describe the light dependence of growth and photosynthetic rates. These include modifications of the Monod equation, hyperbolic tangent functions, and Poisson functions (Jassby and Platt, 1976; Aiba, 1982; Yun and Park, 2003; García-Malea et al., 2006; Costache et al., 2013). For nutrients, the Monod equation is commonly used to describe the external nutrient dependence of phytoplankton growth rates, while the Droop equation illustrates the relationship between growth rates and cellular quotas of limiting nutrients (Morel, 1987; Sunda et al., 2009; Mei et al., 2011; Edwards et al., 2012; Thomas et al., 2017). Under equilibrium growth conditions, the Monod and Droop equations align with each other and with Michaelis-Menten nutrient uptake kinetics (Geider et al., 1998). Additionally, various equations describe the relationship between growth rate and temperature (Kremer et al., 2017); however, this relationship is typically represented using an exponential function or the Arrhenius equation (Ahlgren, 1987; Blackford et al., 2004; Taucher and Oschlies, 2011; Sherman et al., 2016; Barton et al., 2020).

A substantial body of laboratory experiments has demonstrated the reliability of these early models in describing the dependence of phytoplankton growth and photosynthesis on environmental factors (Burmaster, 1979; Megard et al., 1984; Sukenik et al., 1987, 1991; Grima et al., 1996; Xin et al., 2010). However, these models are only applicable under the constraints of balanced growth, which necessitates that nutrient uptake, light capture, and carbon fixation be strictly coupled (Eppley, 1980). Furthermore, when phytoplankton are limited by a combination of environmental factors, early modeling efforts lacked consensus on how to integrate these factors concerning growth rates and develop new descriptive equations (Rodhe, 1978; Droop, 1983). Some authors have stated that phytoplankton growth processes are limited by a single factor (Rodhe, 1978), while other researchers have demonstrated that there is a multiplicative interaction between light and nutrient limitations (Droop, 1983).Phytoplankton dynamic models have been extensively utilized in marine biological and global marine ecological models (Moore et al., 2001; Fennel and Boss, 2003; Faugeras et al., 2004; Li et al., 2010; Schourup-Kristensen et al., 2014; Álvarez et al., 2018). However, research has demonstrated that the outputs of these models are not entirely reliable, and that time-series changes in Chl a, phytoplankton carbon biomass, and C:Chl a ratios do not align consistently with observations (Lefevre et al., 2003; Doney et al., 2009). Therefore, in addition to model simulation studies, there is also a need for evaluation studies to assess the actual performance of the models.

This paper introduces the C:Chl a model and reviews the history of the development of this type of model and highlights the characteristics of each of these models. There is limited understanding of how light, nutrients and temperature interact together to regulate large-scale changes in phytoplankton C:Chl a in the ocean. The purpose of this study is to describe the research ideas of C:Chl a models from empirical to mechanistic models and to explore their gaps by summarizing the existing C:Chl a models. Then, the gaps and future challenges facing C:Chl a models are discussed in terms of particular limiting circumstances and species differences. Finally, the balance between reliability and applicability of the model is emphasized.

2 C:Chl a model development: from empirical to mechanistic models

Similar to most biological models, early C: Chl a models were based on a substantial amount of laboratory experimental data, with empirical models derived through linear or nonlinear fitting to this data. These empirical models typically describe C: Chl a as a function of one or more environmental factors. They are characterized by their simplicity and convenience, allowing for rapid transformation to obtain C: Chl a when the parameters of the culture environment are specified.

2.1 Empirical models

2.1.1 Geider empirical model (1987)

In early models of phytoplankton physiology, C:Chl a (θ) was an important variable (Kiefer and Mitchell, 1983; Geider et al., 1986), but its fundamental role was implicit in the model (Steele, 1962; Eppley and Sloan, 1966; Shuter, 1979). Geider (1987) provided an empirical model for the variation of C:Chl a with light and temperature for microalgae and cyanobacteria under nutrient-sufficient conditions based on from laboratory experiments data. The results show that under nutrient-sufficient conditions, it is possible to describe most of the variation in θ using functions of light intensity, temperature and four coefficients.

By summarizing experiments with 13 phytoplankton (Table 1), Geider found that the light dependence of C:Chl a can be expressed as a linear function when a single phytoplankton species is at constant temperature and under nutrient-sufficient conditions:

Table 1

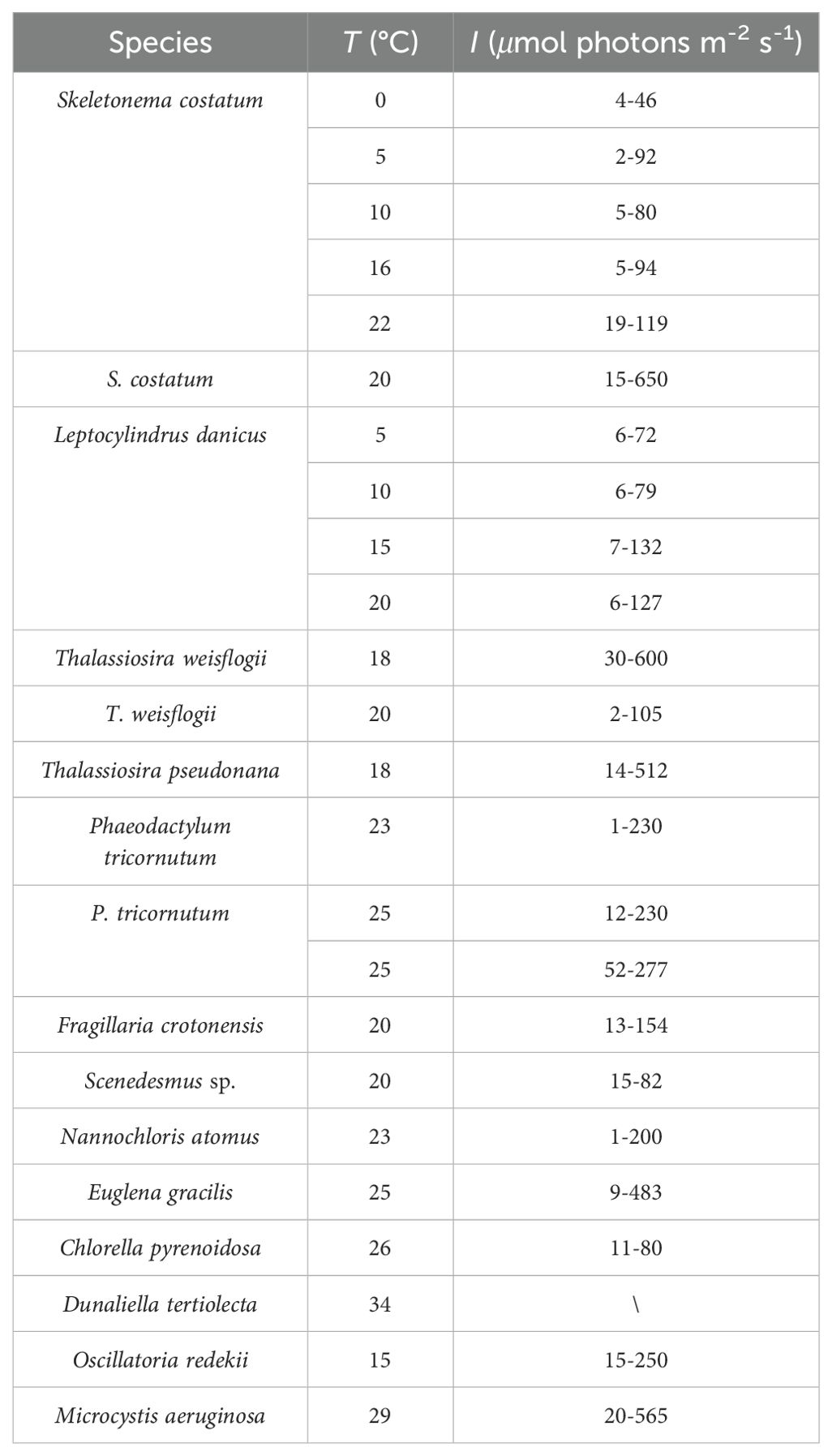
Table 1. Microalgae species and culture conditions summarized by Geider (1987).

$\begin{array}{ll}\theta ={\theta }_0+ϵ·I& \text{(1.1-1)}\end{array}$

where θ is the C: Chl a ratio (g C g Chl a^-1), I is the photon flux density (μmol photons m^-2 s^-1). θ₀ is the value of θ at I = 0, and ϵ is the empirical regression coefficient in g C g Chl a^-1 m² s μmol photons^-1. The intercept θ₀ varied from 6 to 40 g C g Chl a^-1. The slope ϵ varied over a wide range from 0.04 to 1.9 g C g Chl a^-1 m² s μmol photons^-1.

Geider found a linear decrease in θ₀ as the temperature increased from 15°C to 30°C. In addition, the regression coefficient ϵ has a negative exponential relationship with temperature (T):

$\begin{array}{ll}ϵ=1.85\ast \text{exp}(-0.126T)& \text{(1.1-2)}\end{array}$

Combining Equations 1.1-1 and 1.1-2, the change in θ can be described in terms of light and temperature:

$\begin{array}{ll}\theta =(a-bT)+cI\text{exp}(-dT)& \text{(1.1-3)}\end{array}$

where the 4 regression coefficients a = 43.4, b = 1.14, c = 1.85, and d = 0.126, respectively. The variation of θ with light at three temperature conditions (5°C, 15°C and 25°C) was predicted using Equation 1.1-3. The results showed that the tendency of θ becoming larger with increasing light was more obvious at low temperatures. In addition, θ was larger at low temperatures, which is consistent with the results of several studies (Eppley, 1971; Li, 1980; William and Morris, 1982). This phenomenon is widespread in nature (Berry and Bjorkman, 1980; Lapointe et al., 1984), and it is exacerbated by increased light (Liu et al., 2021).This is due to the fact that at low temperatures, phytoplankton can suffer from low-temperature chlorosis due to chlorophyll loss (Eppley, 1971).

Geider empirical model revealed a relationship between C: Chl a (θ), light intensity and temperature in microalgae. It was possible to describe changes in θ using a single function of temperature and light intensity, independent of species. However, because the study included only a few species and limited observations at low temperatures, this empirical model has limited applicability.

2.1.2 Cloern model (1995)

In the previous section, Geider proposed a model for the light-temperature dependence of C: Chl a under nutrient-sufficient conditions, but much of the ocean is oligotrophic, so the model is not applicable in these regions. Cloern proposed a new empirical equation that describes much of the variation in Chl: C ratios expressed by phytoplankton of laboratory experiments. The modeling approach differs from that of Geider (1987), which incorporates an explicit link between nutrient-limited growth rates and Chl: C. The Cloern model is based on a theory describing the link between biochemical components and phytoplankton growth proposed by previous modeling studies (Laws and Bannister, 1980; Kiefer and Mitchell, 1983; Laws and Chalup, 1990).

Cloern summarized data from 12 published studies, most of which were conducted under different light-limited or nutrient-limited conditions and reported temperature T (°C), irradiance I (mol quanta m^-2 d^-1), photoperiod, nutrient-limited growth rate μ′ (d^-1) and Chl: C, to obtain an empirical equation applicable to temperate coastal waters:

$\begin{array}{ll}\text{Chl:C}=0.003+0.0154·\exp (0.050T)·\exp (-0.059I)·\mu \text{'}& \text{(1.2-1)}\end{array}$

Cloern model possessed three features: Firstly, Chl: C possesses a minimum value of about 0.003 mg Chl a (mg C)^-l. Secondly, Chl: C is linearly related to μ′ when light and temperature are stable (Laws and Bannister, 1980; Sakshaug et al., 1989; Chalup and Laws, 1990). Third, the linear relationship between Chl:C and μ′ changes with light. For mixed waters, I is related to the depth of the mixing layer, H (Cullen, 1990):

$\begin{array}{ll}\begin{array}{l}I=(1/H)·{\displaystyle {\int }_0^H{I}_{\phi }}\exp (-kz)\text{ d}z\\ =(I_{\phi }/kH)·[1-\exp (-kH)]\end{array}& \text{(1.2-2)}\end{array}$

I_ϕ is the daily irradiance below the surface. The Monod equation was used to describe the limitation of growth rate μ′ by nutrients:

$\begin{array}{ll}\mu \text{'}=N/(K_N+N)& \text{(1.2-3)}\end{array}$

N is the limiting nutrient concentration, and K_N is the half-saturation constant, i.e., the nutrient concentration at which the growth rate reaches 1/2 of its maximum, which also represents μ′ sensitivity to changes in nutrient concentration. Combining the three equations gives an equation that is directly described by light, temperature and nutrient concentration together:

$\begin{array}{ll}\text{Chl:C}=0.003+0.0154·\exp (0.050T)·\exp \left\{-0.059(I_{\phi }/kH)·[1-\exp (-kH)]\right\}·[N/(K_N+N)]& \text{(1.2-4)}\end{array}$

Although the Cloern empirical model is sufficient to describe most of the variability in phytoplankton Chl:C in the steady state of laboratory experiments (Figure 1), a considerable number of questions remain unanswered. Examples include the P-I parameters (Harding et al., 1981), the dynamics of photoadaptation (Lewis et al., 1984), and differential adaptations between different phytoplankton taxa (Chan, 1980).

Figure 1

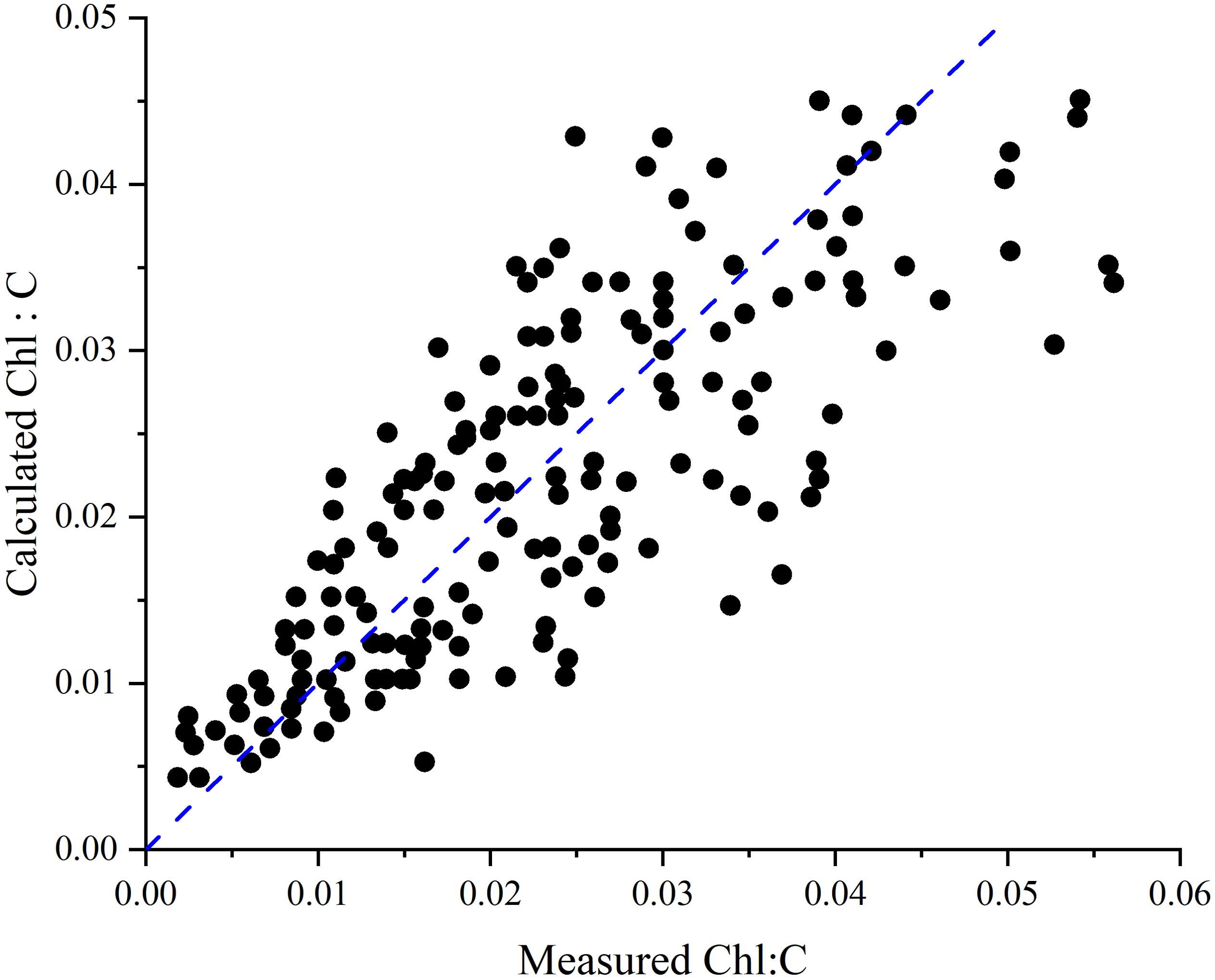
Figure 1. Comparison of predicted and measured Chl:C from the Cloern model. The dashed line indicates a 1:1 relationship.

2.1.3 Shortcomings of empirical models

Although the empirical model initially fit the data well, it was limited to laboratory experiments that overlooked the biological processes of phytoplankton, such as photosynthesis, chlorophyll synthesis, and respiration. This limitation hindered the understanding of how environmental factors specifically affect the physiological state of phytoplankton. In more complex growth environments, the empirical model’s fitting results become unsatisfactory, indicating that it is not suitable for estimating the C:Chl a ratio of phytoplankton communities in natural waters. Consequently, more comprehensive mechanistic modeling approaches are necessary to address the challenges associated with modeling C:Chl a.

2.2 Mechanism models

The natural environment is often in a dynamic state of flux, and the cellular chemistry of phytoplankton changes in response to changes in the environment, an adjustment known as acclimation. Typically, environmental acclimation that regulate phytoplankton growth and physiology include principally light, nutrients and temperature. There have been several studies on the individual modeling of these factors on phytoplankton growth or photosynthesis (Jassby and Platt, 1976; McCarthy, 1981; Li, 1980; Droop, 1983; Morel, 1987). In natural environment, phytoplankton growth is often co-regulated by multiple factors, and models of single-factor dependence are not fully applicable.

In both procaryotic and eukaryotic phytoplankton, photoacclimation involves the down-regulation of pigment synthesis at high irradiance (Falkowski and LaRoche, 1991; Alderkamp et al., 2011; McKew et al., 2013). Two of the most widely used indicators of the state of phytoplankton photoacclimation are Chl a: C (η) and Chl a-specific light-saturated photosynthetic rate (Geider, 1993). Geider et al. (1996) described a dynamic model of phytoplankton growth and photoacclimation under nutrient-sufficient conditions. The main features of the model are that it explicitly describes the role of the ratio of photosynthesis to light harvesting in regulating the biosynthesis of light-harvesting pigments, shows how light acclimation arises from the dynamic partitioning between intracellular carbon pools, and accounts for equilibrium growth and transient responses to changes in irradiance. Subsequently, Geider et al. (1997) proposed an improvement, with a new model providing an analysis of the response of η to irradiance in equilibrium growth, and the limiting effects of nutrient limitation and temperature on the rate of light-saturated photosynthesis were incorporated into the model.

2.2.1 Geider initial model (1997)

C:Chl a has a wide range (Taylor et al., 1997; Wang et al., 2009; Jakobsen and Markager, 2016) but is highly regulated by irradiance, nutrient effectiveness, and temperature (Goldman, 1980; Geider, 1987, 1993; Cloern et al., 1995). Geider initially built a dynamic model that C:Chl a under different conditions of irradiance, nutrient-limitation and temperature. Changes in Chl a depend on the ratio of energy supplied by light absorption and photosynthetic energy conversion to the energy required for growth.

The light dependence of photosynthesis (P-I curve) in traditional studies is usually described as a saturation function (Jassby and Platt, 1976). Geider built on this to establish a light (I) dependence function for the carbon-specific photosynthetic rate (P^C):

$\begin{array}{ll}{P}^C=P_{\text{m}}^C\left[1-\exp \left(\frac{-{\alpha }^{\text{Chl}}I\eta }{P_{\text{m}}^C}\right)\right]& \text{(2.1-1)}\end{array}$

where η is Chl a:C, P^C is the carbon-specific photosynthetic rate, α^Chl is the Chl a-specific initial slope of the P-I curve, and P^C_m is the carbon-specific light saturated photosynthetic rate. Changes in η were assumed to depend on the relative changes in the rates of net Chl a synthesis and net carbon fixation. The net rate of carbon fixation (dC/dt) is derived from the difference between photosynthetic and respiration rates (Equation 2.1-2). The net rate of Chl a accumulation (dChl/dt) is derived from the difference between synthesis and degradation rates (Equation 2.1-3):

$\begin{array}{ll}\frac{\text{d}C}{\text{d}t}=P^{C}C-R^{C}C& \text{(2.1-2)}\end{array}$

$\begin{array}{ll}\frac{\text{dChl}}{\text{d}t}={\rho }_{\text{Chl}}{P}^{C}C-R^{\text{Chl}}\text{Chl}& \text{(2.1-3)}\end{array}$

R^C and R^Chl are the degradation rate constants for carbon and Chl a, respectively, and ρ_Chl is the ratio of Chl a synthesis to carbon fixation, which can be expressed as:

$\begin{array}{ll}{\rho }_{\text{Chl}}={\eta }_{\text{m}}\left(\frac{P^C}{{\alpha }^{\text{Chl}}I\eta }\right)& \text{(2.1-4)}\end{array}$

η_m is the Chl a:C maximum. Combining Equations 2.1-1 to 2.1-4 yields a light-dependent function of η:

$\begin{array}{ll}\eta =\frac{{\eta }_{\text{m}}}{1+\left(\frac{{\alpha }^{\text{Chl}}I{\eta }_{\text{m}}}{2P_{\text{m}}^C}\right)}& \text{(2.1-5)}\end{array}$

For temperature and nutrient limitation, Geider assumed that both factors affect only the light-saturated photosynthetic rate, the temperature dependence of P^C_m was described using the Arrhenius equation (Li, 1980), and the nutrient limitation of P^C_m was described as the Monod equation (Morel, 1987), with the combined effect of the two factors regarded as a multiplicative function of temperature and nutrient effectiveness:

$\begin{array}{ll}{P}_{\text{m}}^C(T,N)=P_{\text{ref}}^C\left(\frac{N}{N+K_N}\right)\times \text{exp}\left[-\frac{E_a}{R}\left(\frac{1}{T}-\frac{1}{T_{\text{ref}}}\right)\right]& \text{(2.1-6)}\end{array}$

P^C_m(T, N) is the light-saturated photosynthetic rate at a given temperature and nutrient concentration. T is the temperature, T_ref is the reference temperature of 293 K, P^C_ref is the reference value of P^C_m under nutrient-sufficient conditions at the temperature of T_ref, N denotes the nutrient concentration, K_N is the half-saturation constant of growth, and E_a/R is the slope of the curve of the Arrhenius equation.

Geider initial model was a more simplified model, and although based on intracellular sources and losses of carbon and chlorophyll, there were still some parts that were not included (e.g., excretion of DOC, biosynthesis consumption of C) in order to make the model easy to use.

2.2.2 Geider model (1998)

Based on previous work (Geider et al., 1996; Geider et al., 1997), Geider developed a more complete model of the C:Chl mechanism, which will be referred to simply as the Geider model (Geider et al., 1998) (Table 2). The Geider model was based on the adaptation of phytoplankton growth and physiology to light, nutrient concentration, and temperature, and treats nutrient uptake and photosynthesis rates as a function of environmental factors and cell chemical composition (Chl:C and N:C). Multiple environmental variables together determine the instantaneous rates of light utilization, carbon assimilation, Chl synthesis and nutrient assimilation (Table 3).

Table 2

Table 2. The equations of Geider Model (1998).

Table 3

Table 3. The variables of Geider Model (1998).

The Geider model is based on three features of the phytoplankton adaptation process. First, it includes the down-regulation of pigment content at high irradiance and/or when growth rates are limited by nutrient availability or temperature (Falkowski and LaRoche, 1991; Geider et al., 1996). Second, it includes the accumulation of energy-storing polymers when growth rates are light-saturated and/or nutrient-limited, and the subsequent release of these polymers when light is limited or nutrients are replenished (Foy and Smith, 1980). Third, it includes feedbacks between nitrogen and carbon metabolism. This model differs from previous equilibrium growth steady-state models (Bannister, 1979; Shuter, 1979; Kiefer and Mitchell, 1983; Laws et al., 1983; Geider et al., 1997) in that it explicitly takes into account the time-dependence of biomass and pigment accumulation under non-equilibrium growth steady-state conditions and incorporates both nitrogen limitation and N:C ratio changes are included.

The Geider model is based on phytoplankton mass balances of carbon (C), nitrogen (N) and chlorophyll a (Chl) (Equations 2.2-1, 2.2-2, 2.2-3). The light dependence of photosynthesis is considered as a Poisson function (Equation 2.2-4), nutrient uptake rates are described using the Michaelis-Menten function (Equation 2.2-6), and temperature affects light-saturated photosynthesis, maximum nutrient uptake rate, and maintenance respiration rate through the Arrhenius relationship (Equation 2.2-10).

In the Geider model, the constants that maintain C respiration, N remineralization and Chl degradation are assumed to be equal. In the Geider model, the carbon-specific light-saturated photosynthetic rate depends on the nitrogen status inside the cell (Equation 2.2-5), and the carbon-specific light-limited photosynthetic rate depends on the Chl: C ratio (Equation 2.2-4). The synthesis of Chl a requires nitrogen assimilation (Equation 2.2-3), and the maximum rate of nitrogen assimilation is regulated by the nitrogen status inside the cell (Equation 2.2-7). Chl a synthesis is down-regulated when the rate of light absorption exceeds the photon utilization rate of carbon fixation (Equation 2.2-3), and the extent of the down-regulation depends on the imbalance between the rates of light absorption and photosynthesis (Equation 2.2-8). Respiration rate is linked to the rate of nitrogen assimilation through the cost of biosynthesis (Equation 2.2-1).

The Geider model provides a more complete dynamic model of phytoplankton physiology based on the sources and destinations of elements within the phytoplankton than previous models. The introduction of dynamic regulation of nitrogen in addition to carbon and Chl a has linked pigment synthesis to nitrogen assimilation in the model. The Geider model is the first representative model in C:Chl modeling research, and it provides a foundation idea for future C:Chl modeling research.

2.2.3 Pahlow model (2013)

In the Geider model, the nutrient dependence of nutrient uptake rates is described using the Michaelis-Menten equation (MM equation), but the MM equation is still flawed. For two limiting nutrients, nitrogen (Rhee, 1974) and phosphorus (Droop, 1974; Rhee, 1974), the MM equation is unable to describe the steady-state uptake response over a wide range of concentrations with constant half-saturation constants, K_s, and nutrient uptake saturation rates, V_max. Therefore, scientists have proposed a new hypothesis - optimal uptake (OU) kinetics. Optimal uptake (OU) kinetics assumes that there is a physiological trade-off between the efficiency of nutrient contact at the cell surface (A_s) and the maximum rate of nutrient assimilation (V_max,s). The main idea is that phytoplankton change the number of their surface uptake sites (or ion channels), which determine the time scale of nutrient encounters, and the number of internal enzymes, which assimilate the nutrients after they have been encountered. Nitrogen is recognized as a key resource for partitioning between these two uses, as both uptake sites and enzymes are predominantly composed of proteins and therefore require large amounts of nitrogen (Pahlow, 2005).

Based on this assumption, Pahlow proposed an optimality-based model for phytoplankton (hereafter referred to as the Pahlow model). In the Pahlow model, phytoplankton cells are assumed to transiently optimize the Chl a and N content of their cells for maximum net growth, i.e., the net accumulation of carbon fixation minus the energy cost of photosynthesis and nutrient uptake. The N of the Pahlow model is divided into three components: nutrient acquisition, light-trapping organs and structural proteins (Figure 2).

Figure 2

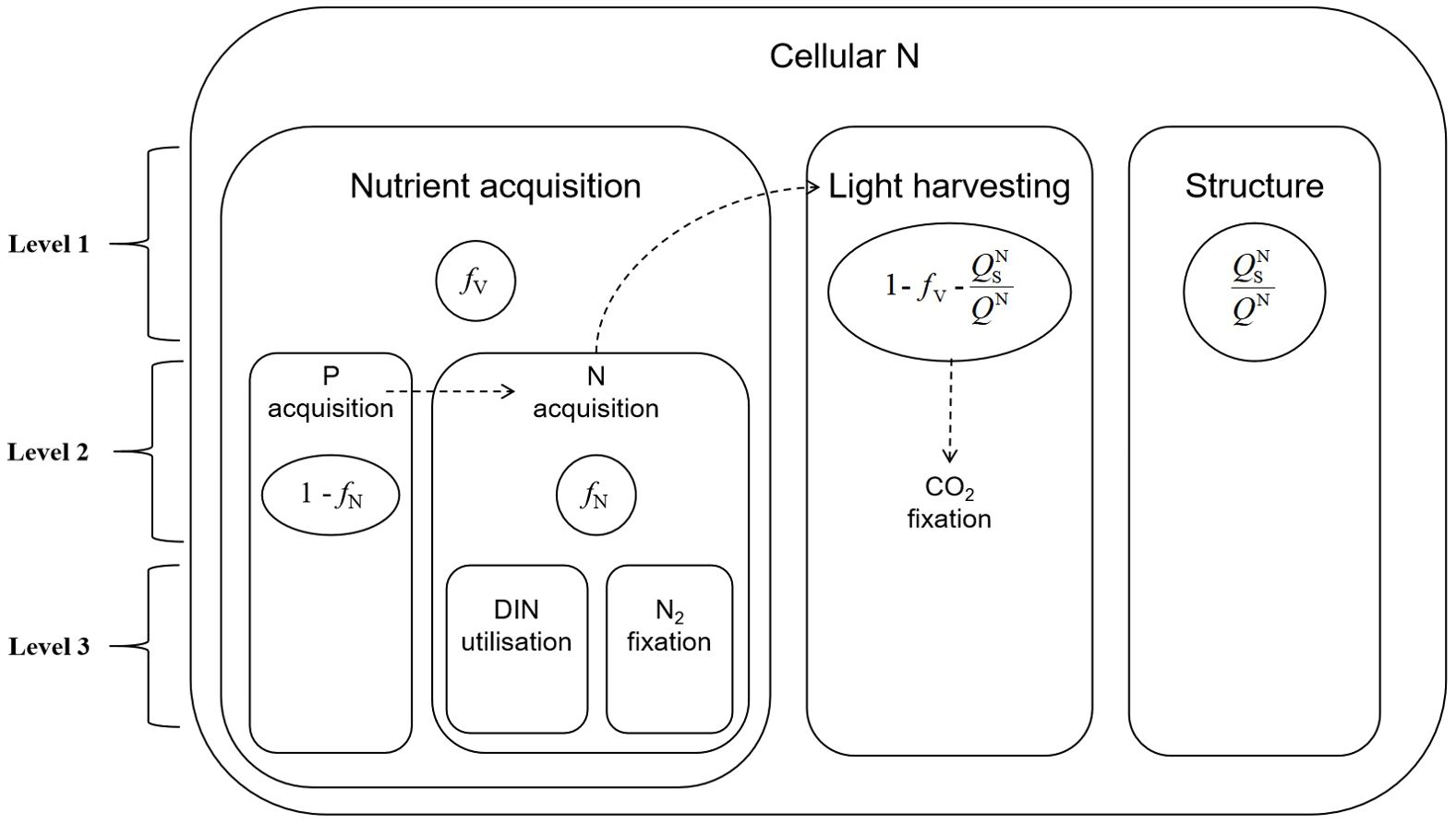
Figure 2. Three levels of nitrogen partitioning in the Pahlow model. Level 1 includes nutrient acquisition (ƒ_V), structural proteins (Q^N_s/Q^N) and light harvesting (1-ƒ_V-Q^N_s/Q^N). Level 2 divides nutrient acquisition into P acquisition (1-ƒ_N) and N acquisition (ƒ_N). Level 3 divides dissolved inorganic nitrogen (DIN) uptake and N2 fixation.

The Pahlow model has three optimization levels without considering P limitation. The first is to optimize the Chl:C ratio (${\stackrel{\wedge }{\eta }}_0$) within the chloroplasts such that net photosynthesis is maximised. ${\stackrel{\wedge }{\eta }}_0$ can be obtained by solving the gradient function of net photosynthesis of a chloroplast with respect to ${\stackrel{\wedge }{\eta }}_0$:

$\begin{array}{ll}{\stackrel{\wedge }{\eta }}_0=\frac{1}{{\zeta }^{chl}}+\frac{V_0^C}{{\alpha }^{chl}I}\left\{1-W_0\left[\left(1+\frac{R_M^{chl}}{L_d{V}_0^C}\right)e^{\left(1+\frac{{\alpha }^{chl}I}{{\zeta }^{chl}{V}_0^C}\right)}\right]\right\} \text{if} I>I_0& \text{(2.3-1)}\end{array}$

$${\stackrel{\wedge }{\eta }}_0=\eta \text{min if }I>I_0$$

where I is irradiance (W m^-2), α^chl is the chlorophyll-specific initial slope of the photosynthesis-irradiance (P-I) curve, and ζ^chl is the cost coefficient of photosynthesis. $R_M^{chl}$ is the maintenance cost of Chl. L_d is the length of the day. W₀ is the zero branch of the Lambert-W function. η_min is the minimum chlorophyll-to-carbon ratio. I₀ is the threshold light level for chlorophyll synthesis.

$\begin{array}{ll}{I}_0=\frac{{\zeta }^{chl}{R}_M^{chl}}{L_d{\alpha }^{chl}}& \text{(2.3-2)}\end{array}$

The second level of optimization is to balance the energy allocation between photosynthesis and nitrogen uptake. The net relative growth of a cell is equal to the net photosynthesis of the whole cell minus the respiratory cost of nitrogen uptake. The optimal cellular nitrogen quota, Q^N, can be calculated by solving the gradient function of net relative growth against the nitrogen uptake allocation factor (f_V):

$\begin{array}{ll}{Q}^N=Q_S^N\left[1+\sqrt{1+\frac{1}{Q_S^N\left(\frac{{\widehat{\mu }}^I}{{\widehat{V}}^N}+{\zeta }^N\right)}}\right]& \text{(2.3-3)}\end{array}$

where $Q_S^N$ is the nitrogen quota for structural proteins, which is half of the minimum nitrogen quota ($Q_0^N$). ${\widehat{V}}^N$ is the potential nutrient uptake rate. ${\widehat{\mu }}^I$ is the light-dependent growth rate after accounting for photosynthesis and chlorophyll maintenance. ζ^N stands for the cost of nitrogen assimilation. f_V can be calculated as:

$\begin{array}{ll}{f}_{\text{V}}=\frac{Q_S^N}{Q^N}-{\zeta }^N(Q^N-2Q_S^N)& \text{(2.3-4)}\end{array}$

Chl:C (η) for the whole cell can be calculated as.

$\begin{array}{ll}\eta ={\widehat{\eta }}_0\left(1-\frac{Q_S^N}{Q^N}-f_{\text{V}}\right)& \text{(2.3-5)}\end{array}$

The third dimension of optimization concerns the trade-off between nutrient uptake at the cell surface and nutrient assimilation within the cell (Pahlow, 2005; Smith et al., 2009). The potential nutrient uptake rate (${\widehat{V}}^N$) is calculated as.

$\begin{array}{ll}{\widehat{V}}^N=\frac{V_0^{N}N}{\frac{V_0^N}{A_0^N}+2\sqrt{\frac{V_0^{N}N}{A_0^N}}+N}& \text{(2.3-6)}\end{array}$

where $V_0^N$ is the maximum potential nitrogen uptake rate. $A_0^N$ is the maximum potential affinity. N is the nitrogen concentration in the environment.

The success of the Pahlow model is demonstrated by the fact that it provided the first theoretical derivation of the well-known Droop quota model (Pahlow and Oschlies, 2013) and has been extensively validated (Fernández-Castro et al., 2016; Smith et al., 2016) with laboratory datasets (Pahlow et al., 2013) and ocean observations (Arteaga et al., 2014). However, the Pahlow model is still flawed, and under low light conditions, the prediction of Chl a:C by the Pahlow model may be lower than the actual value (Chen and Smith, 2018).

2.3 Applications of several models

Several C:Chl a models are also used in a wide range of applications, from indoor incubation to parts of the ocean, and in global ocean (Table 4). For the empirical models, most of them have been applied in various sea areas, especially the Cloern model (Pondaven et al., 1999; Kettle, 2009; Omta et al., 2009; Itoh et al., 2015; Kooi et al., 2017), due to the advantage of ease of use of empirical models, which can be directly used for estimation. For mechanism models, mostly global ocean and biogeochemical models are applicable, due to the fact that mechanistic models cover phytoplankton biological processes and are closely linked to the ocean carbon cycle. Because the Pahlow model describes the nutrient uptake of phytoplankton cells more rationally, the Pahlow model has begun to gradually replace the Geider model in recent studies (Arteaga et al., 2016; Masuda et al., 2021; Sasai et al., 2022; Kerimoglu et al., 2023).

Table 4

Table 4. Application of several types of models.

3 Future development challenges

3.1 Light

Light is one of the most crucial external factors in phytoplankton modeling, particularly in carbon-to-chlorophyll (C:Chl) modeling. This is because light directly influences carbon fixation and plays a key role in regulating chlorophyll a synthesis. However, there are still aspects of light research that require further exploration.

Most of the data used to validate the models come from laboratory experiments, which are primarily conducted under constant irradiance using artificial light sources. In contrast, the only light source for phytoplankton growth in the natural environment is sunlight, whose intensity varies continuously throughout the day and with depth in the water column. Since the C:Chl model is intended for application in natural environments, this limitation reduces the applicability of laboratory experiment data for the model.

In addition, photoinhibition is a phenomenon that cannot be overlooked. Microalgal cells undergo three processes depending on light intensity (Figure 3). When irradiance exceeds saturating light levels, the photosynthetic system becomes impaired, leading to a decrease in the photosynthetic rateos phenomenon known as photoinhibition (Marshall et al., 2000). Due to light attenuation, most of the seawater is in a photo-restricted state, with only a small portion experiencing photoinhibition. However, as mentioned in the introduction, the application of the C:Chl a model necessitates the integration of satellite remote sensing data, which measures Chl a from the ocean’s surface layer, the region most significantly affected by photoinhibition. Álvarez et al. (2018) developed a preliminary C:Chl a model that incorporates photoinhibition by including the photoinhibition term function proposed by Platt et al. (1980). Nevertheless, the photoinhibition resulting from the transient inactivation of PSII or the reduction of its absorption cross-section remains inadequately explained.

Figure 3

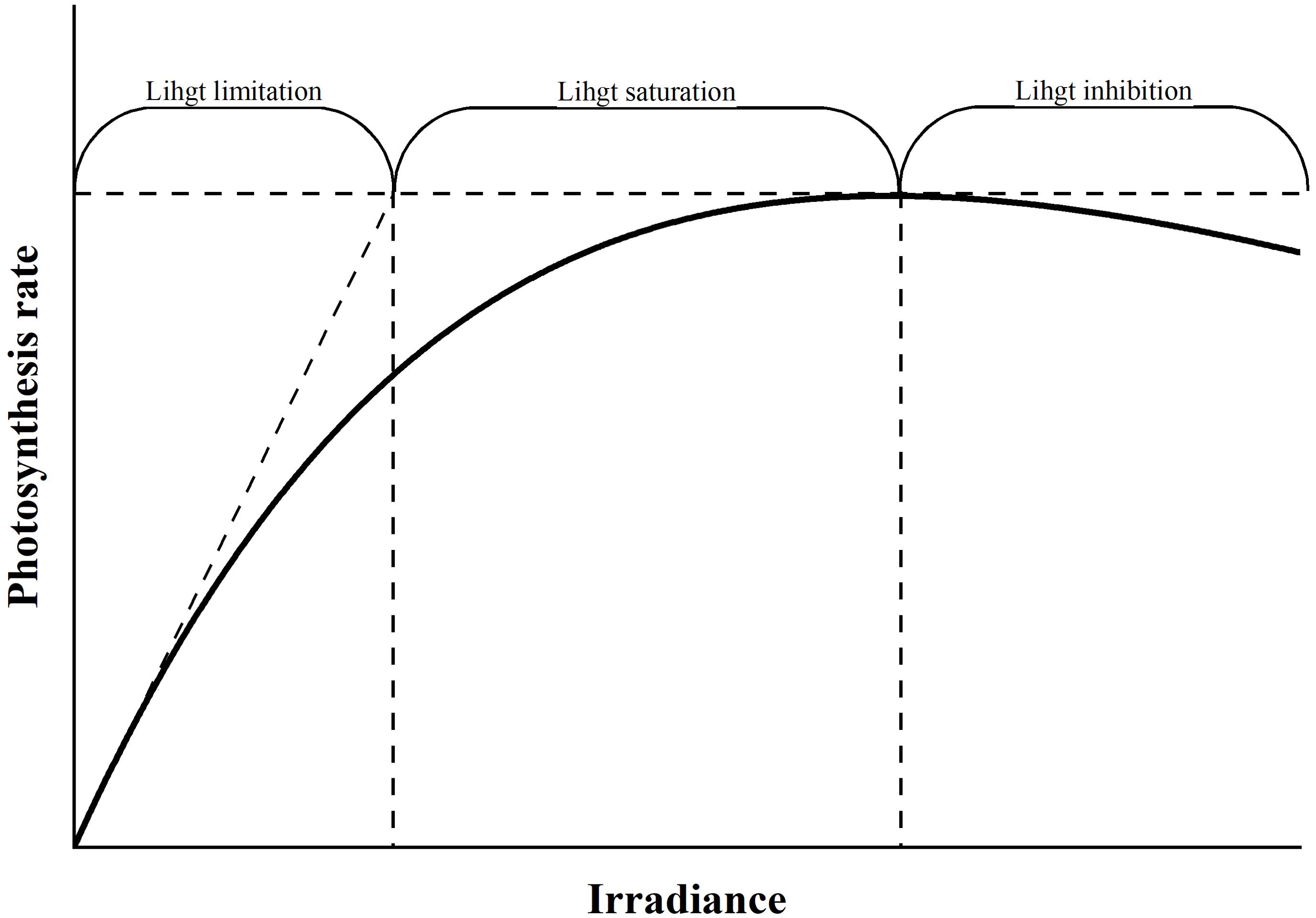
Figure 3. Schematic diagram of the P-I curve. Phytoplankton cells undergo 3 stages of increasing light: (1) light limitation, (2) light saturation, and (3) light photoinhibition.

3.2 Nutrients

Currently, nutrient uptake is often described using either the Monod equation or the Pahlow model. Chen and Smith (2018) compared these two models and found that the assumption of a trade-off between photosynthesis and nutrient uptake in the Pahlow model was useful, suggesting that optimal uptake dynamics should be considered in marine biogeochemical models. In the Monod model, only one nutrient is assumed to be limiting for other nutrients such as phosphorus, silicon, and iron. However, Browning and Moore (2023) conducted a global analysis of nutrient limitation in marine phytoplankton and discovered that surface seawater is often close to a state of nutrient co-limitation. Although the Pahlow model incorporates phosphorus uptake, its computational steps are quite cumbersome, making it challenging to obtain a reliable and user-friendly nutrient uptake component for the C:Chl a model.

3.3 Temperature

In most cases, the role of temperature is incorporated into the model in a multiplicative form. The temperature dependence of phytoplankton growth has been demonstrated by Bernard and Rémond (2012), showing that the growth rate of phytoplankton increases gradually with rising temperatures up to an optimum level, after which it decreases sharply when temperatures exceed this optimum (Figure 4). This sharp decline is attributed to the inactivation of enzymes or denaturation of proteins at elevated temperatures, leading to metabolic disorders and potentially algal cell death (Renaud et al., 2002; Ras et al., 2013; Serra-Maia et al., 2016). The Arrhenius equation, while a useful model for representing growth rates at low temperatures, has a limited temperature range in which it is applicable and fails to account for the declining portion of the thermal growth curve. In the Geider model, temperature is assumed to influence only the light-saturated photosynthetic rate (see Section 2.1). Additionally, some ecosystem models treat the respiration rate as a constant, typically set at 0.01 d^-1 (Schourup-Kristensen et al., 2014). Notably, the impact of temperature on respiration is more significant compared to its effect on photosynthesis (Barton et al., 2020). Furthermore, temperature also influences enzyme activity, indicating that reactive processes such as nutrient uptake may be affected by temperature fluctuations. However, nutrient limitation can inhibit the temperature dependence of phytoplankton metabolism (Marañón et al., 2018).

Figure 4

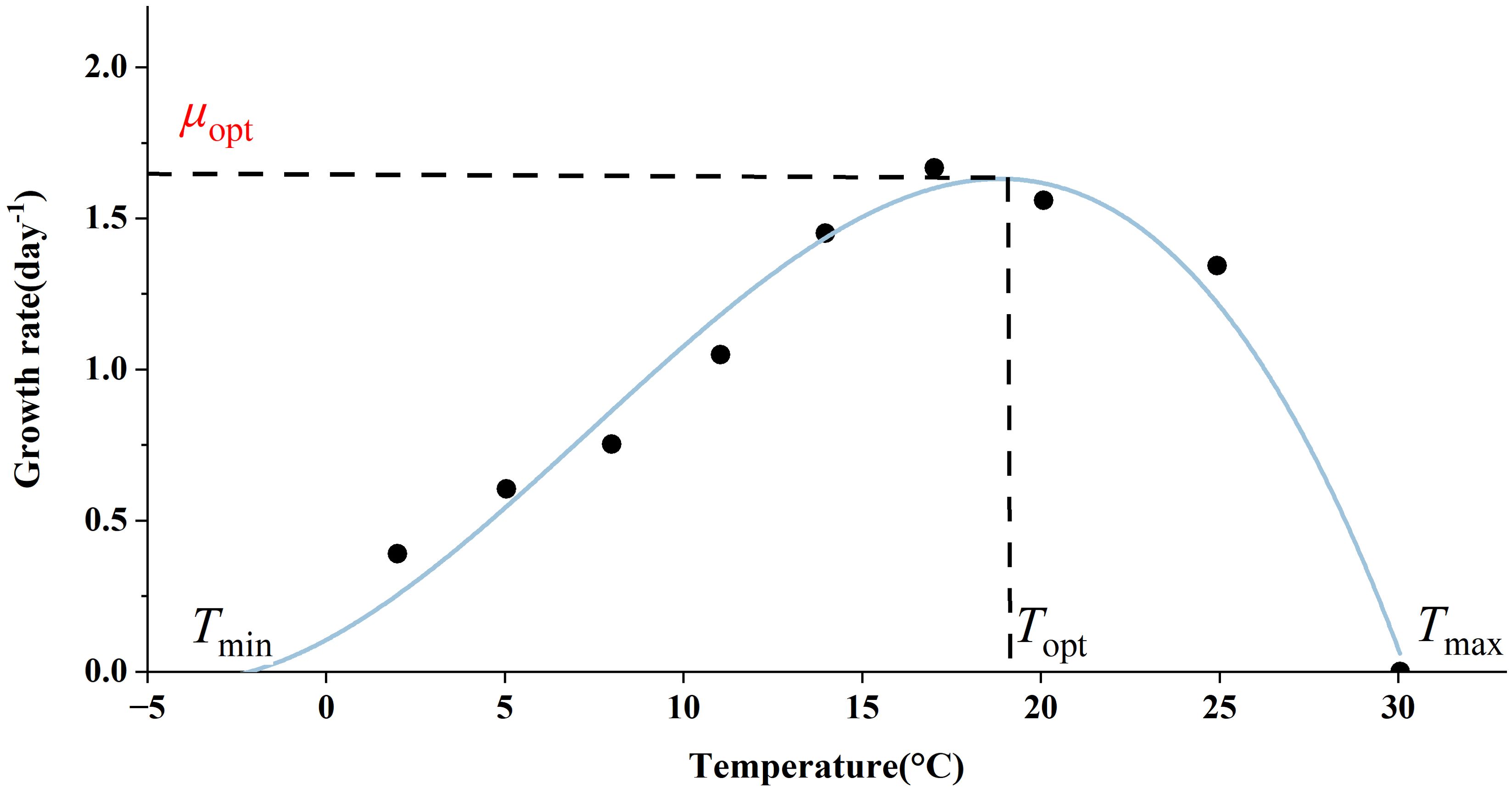
Figure 4. Thermal growth curves of microalgae as exemplified by Astrionella formosa (from Bernard and Rémond, 2012).

In addition to its effects on phytoplankton cells at the microscopic level, temperature also influences the stratification of the water column, resulting in changes to the vertical distribution of phytoplankton (Berger et al., 2010; Hordoir and Meier, 2012). Over time, seasonal variations in temperature significantly impact phytoplankton communities. In previous studies, the influence of temperature has been regarded as secondary to that of light and nutrients. However, in light of rising global and ocean temperatures, the significance of temperature must be emphasized.

3.4 Communities

The impact of phytoplankton species has largely been overlooked in current C:Chl modeling studies, as these models typically estimate the carbon biomass of the entire phytoplankton community across various marine environments. However, certain specific cases warrant consideration, including mixotrophic, methanotrophs, and heterotrophs. Most dinoflagellates are mixotrophic and play a dominant role in several marine ecosystems (Burkholder et al., 2008; Taylor et al., 2008; Zhang et al., 2013; Stoecker et al., 2017; Jeong et al., 2021). Cohen et al. (2021) demonstrated that dinoflagellates are a significant component of the microbial community in the Pacific Ocean, exhibiting high relative abundance across a trophic gradient. Unlike other phytoplankton, dinoflagellates exhibit a diverse range of trophic strategies, including autotrophy, heterotrophy, and mixotrophy (Cohen et al., 2021). This diversity suggests that the C:Chl model may underestimate carbon biomass by not adequately accounting for dinoflagellate mixotrophy when assessing the phytoplankton community dominated by these organisms. It is unclear how much the carbon biomass acquired by dinoflagellates through heterotrophy impacts the total carbon biomass of the entire phytoplankton community.

3.5 Improved methodology

Currently, mechanistic models, such as the Geider model and the Pahlow model, are widely utilized in biogeochemical modeling studies due to the cycling processes within phytoplankton that involve elements such as carbon (C) and nitrogen (N). However, there are still aspects of the Geider model that can be enhanced. Firstly, for photosynthetic processes (Equations 2.1-1, 2.2-4), a photoinhibition term can be incorporated (Platt et al., 1980).

$\begin{array}{ll}{P}^C=P_m^C·\left[1-\exp \left(\frac{-{\alpha }^{Chl}I\eta }{P_m^C}\right)\right]·\exp \left(\frac{-{\beta }^{Chl}I\eta }{P_m^C}\right)& \text{(3.5-1)}\end{array}$

where β^Chl represents the empirical photoinhibition parameter. The inclusion of this term enables the Geider model to provide a more accurate estimation of phytoplankton carbon biomass in the ocean’s surface waters. Additionally, for nutrient uptake, optimal uptake kinetics are more appropriate than the Monod or Droop equations (Pahlow, 2005):

$\begin{array}{ll}{V}_{\text{OU}}=\frac{1}{{(f_A{A}_{0,S}S)}^{-1}+{[(1-f_A)V_{0,S}]}^{-1}}& \text{(3.5-2)}\end{array}$

f_A is the proportion of the total nitrogen pool allocated to the cell surface, and (1 - f_A) is the proportion assigned to intracellular enzymes. A_0,S and V_0,S are the potential affinity maximum value and maximum uptake rate for nutrient S, respectively. Thirdly, irreversible damage caused by high temperatures can be described using the modified Arrhenius equation (Grimaud et al., 2017):

$\begin{array}{ll}{T}_{\text{function}}=k_r\text{exp}\left(\frac{T_A}{T_{\text{ref}}}-\frac{T_A}{T}\right)& \text{(3.5-3)}\end{array}$

where T_ref is the reference temperature, T_A is the Arrhenius temperature (i.e., the slope of the straight line in the Arrhenius plot), and k_r is the reaction rate at T_ref. Currently, there is no superior method to exclude the effects of mixotrophic or heterotrophic dinoflagellates in natural phytoplankton taxa. Additionally, more culture experiments, such as mixed incubations of diatoms and dinoflagellates, are necessary to summarize potential empirical relationships.

3.6 Special events

There are several episodic and special events in the oceans that can alter the phytoplankton community and, consequently, its biomass. Phytoplankton blooms frequently occur in both lakes and oceans, some of which are harmful algal blooms (HABs) driven by coastal upwelling or significant anthropogenic nutrient enrichment (Pitcher et al., 2010; Richlen et al., 2010; Andersen et al., 2017; López-Cortés et al., 2019). Research indicates that the frequency and distribution of these blooms are expected to increase with future climate change (Dai et al., 2023). Therefore, it is possible to develop a specialized C:Chl a model for algal blooms and to analyze later whether it is feasible to predict the likelihood of blooms based on C:Chl a ratios. The Southern Ocean is commonly characterized as a high-nutrient, low-chlorophyll (HNLC) region, a phenomenon attributed to the limitation of trace element iron (Broecker, 1992). Current projections of carbon biomass for the global ocean primarily rely on Monod dynamics or optimal uptake dynamics that describe nitrogen limitation. However, for the HNLC region, C:Chl a modeling that accounts for iron limitation is essential.

4 Conclusion

The key to the transition of the C:Chl a model from a simple empirical framework to a dynamically regulated mechanistic model lies in a fundamental shift in modeling concepts. Initially, empirical models were primarily characterized by values of C:Chl a. While there was some consideration of the individual or combined effects of environmental factors (Figure 5A), the relationship between these factors and C:Chl a was direct, with only specific regression coefficients influencing C:Chl a. Consequently, the primary purpose of the empirical models was to investigate the mathematical relationships derived from the regression results. Thus, the aim of these models was to explore the mathematical connections within the regression findings. There has been significant advancement in the theory of mechanistic models, including the Geider model, which is based on cellular elemental sources and destinations, and the Pahlow model, which focuses on optimal uptake kinetics. Both models are grounded in the cellular physiological regulation of phytoplankton (Figure 5B). The regulatory role of environmental factors is more clearly defined in these models.

Figure 5

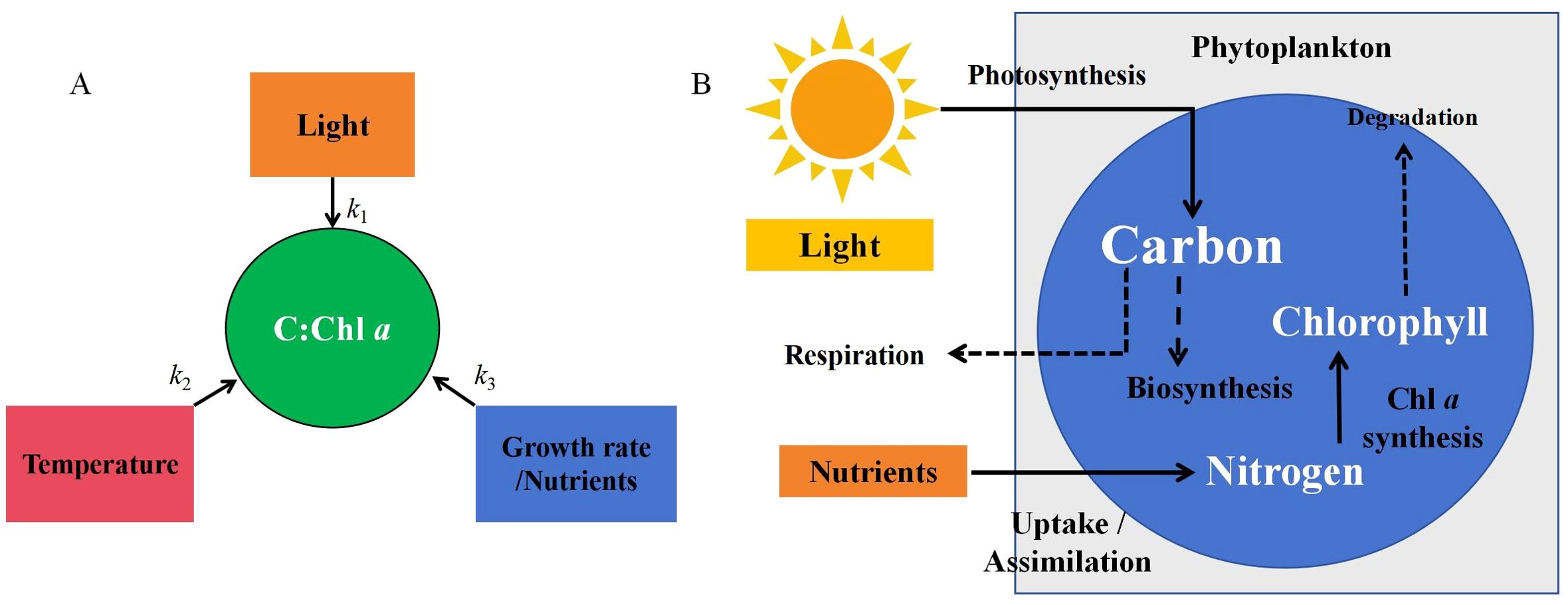
Figure 5. Ideas for building empirical (A) and mechanistic (B) models. The empirical model is based on the regression relationship between environmental factors and C:Chl a and the mechanistic model is based on the cellular physiology of phytoplankton.

This paper reviews the C:Chl a models that have been commonly applied to date, which primarily consider the combined effects of light, temperature, and nutrients on phytoplankton biological processes. However, these considerations are not comprehensive. C:Chl a models that incorporate photodamage still fail to explain the photoinhibition caused by the transient inactivation of PSII or the reduction of its absorption cross-section. While optimality absorption kinetics may offer a more plausible explanation, its computational steps are significantly more complex. The impact of temperature is likely underestimated and should be more thoroughly considered in the context of global warming. Additionally, since dinoflagellates exhibit multiple trophic strategies, new models may need to be incorporated when dinoflagellates are dominant to minimize the underestimation of carbon biomass.

In addition to the necessity of being as comprehensive as possible to encompass all types of scenarios and enhance the reliability of the output results, the modeling process should not be overly complex. For instance, while the Pahlow model’s optimality-based assumption makes it superior to the Monod equation in describing the nutrient uptake of phytoplankton cells, it is rarely employed in marine biogeochemical modeling due to its complicated computational requirements. Consequently, the model’s structure should remain straightforward and user-friendly.

Author contributions

JS: Funding acquisition, Writing – review & editing. JG: Writing – original draft.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was financially supported by the National Key K&D Program of China (2019YFC1407800) and Ministry of Education of the People’s Republic of China Changjiang Scholar Program (T2014253) to Jun Sun. This research was also supported by National Natural Science Foundation of China (No. 41876134) and “CUG Scholar” Scientific Research Funds at China University of Geosciences (Wuhan) (No. 2020087).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agustí S., González-Gordillo J. I., Vaqué D., Estrada M., Cerezo M. I., Salazar G., et al. (2015). Ubiquitous healthy diatoms in the deep sea confirm deep carbon injection by the biological pump. Nat. Commun. 6, 7608. doi: 10.1038/ncomms8608

PubMed Abstract | Crossref Full Text | Google Scholar

Ahlgren G. (1987). Temperature functions in biology and their application to algal growth constants. Oikos 49 (2), 177–190. doi: 10.2307/3566025

Crossref Full Text | Google Scholar

Aiba S. (1982). Growth kinetics of photosynthetic microorganisms. Adv. Biochem. Engineering/Biotechnology 23, 85–156. doi: 10.1007/3540116982_3

Crossref Full Text | Google Scholar

Alderkamp A. C., Garcon V., de Baar H. J. W., Arrigo K. R., et al. (2011). Short-term photoacclimation effects on photoinhibition of phytoplankton in the Drake Passage (Southern Ocean). Deep Sea Res. Part I: Oceanogr. Res. Papers 58, 943–955. doi: 10.1016/j.dsr.2011.07.001

Crossref Full Text | Google Scholar

Álvarez E., Thoms S., Völker C. (2018). Chlorophyll to carbon ratio derived from a global ecosystem model with photodamage. Global Biogeochem. Cycles 32, 799–816. doi: 10.1029/2017GB005850

Crossref Full Text | Google Scholar

Andersen J. H., Carstensen J., Conley D. J., Dromph K., Fleming-Lehtinen V., Gustafsson B. G., et al. (2017). Long-term temporal and spatial trends in eutrophication status of the Baltic Sea. Biol. Rev. 92, 135–149. doi: 10.1111/brv.12221

Crossref Full Text | Google Scholar

Armstrong R. A. (2006). Optimality-based modeling of nitrogen allocation and photoacclimation in photosynthesis. Deep Sea Res. Part II: Topical Stud. Oceanogr. 53, 513–531. doi: 10.1016/j.dsr2.2006.01.020

Crossref Full Text | Google Scholar

Arteaga L., Pahlow M., Oschlies A. (2014). Global patterns of phytoplankton nutrient and light colimitation inferred from an optimality-based model. Global Biogeochem. Cycles 28, 648–661. doi: 10.1002/2013GB004668

Crossref Full Text | Google Scholar

Arteaga L., Pahlow M., Oschlies A. (2016). Modeled Chl: C ratio and derived estimates of phytoplankton carbon biomass and its contribution to total particulate organic carbon in the global surface ocean. Global Biogeochem. Cycles 30, 1791–1810. doi: 10.1002/2016GB005458

Crossref Full Text | Google Scholar

Bannister T. T. (1979). Quantitative description of steady state, nutrient-saturated algal growth, including adaptation. Limnol. Oceanogr. 24, 76–96. doi: 10.4319/lo.1979.24.1.0076

Crossref Full Text | Google Scholar

Barton S., Jenkins J., Buckling A., Schaum C. E., Smirnoff N., Raven J. A., et al. (2020). Evolutionary temperature compensation of carbon fixation in marine phytoplankton. Ecol. Lett. 23, 722–733. doi: 10.1111/ele.13469

PubMed Abstract | Crossref Full Text | Google Scholar

Behrenfeld M. J., Marañón E., Siegel D. A., Hooker S. B. (2002). Photoacclimation and nutrient-based model of light-saturated photosynthesis for quantifying oceanic primary production. Mar. Ecol. Prog. Ser. 228, 103–117. doi: 10.3354/meps228103

Crossref Full Text | Google Scholar

Behrenfeld M. J., O’Malley R. T., Boss E. S., Westberry T., Graff J. R., Halsey K. H., et al. (2016). Revaluating ocean warming impacts on global phytoplankton. Nat. Climate Change 6, 323–330. doi: 10.1038/nclimate2838

Crossref Full Text | Google Scholar

Berger S. A., Diehl S., Stibor H., Trommer G., Ruhenstroth M. (2010). Water temperature and stratification depth independently shift cardinal events during plankton spring succession. Global Change Biol. 16, 1954–1965. doi: 10.1111/j.1365-2486.2009.02134.x

Crossref Full Text | Google Scholar

Bernard O., Rémond B. (2012). Validation of a simple model accounting for light and temperature effect on microalgal growth. Biores. Technol. 123, 520–527. doi: 10.1016/j.biortech.2012.07.022

Crossref Full Text | Google Scholar

Berry J., Bjorkman O. (1980). Photosynthetic response and adaptation to temperature in higher plants. Annu. Rev. Plant Physiol. 31, 491–543. doi: 10.1146/annurev.pp.31.060180.002423

Crossref Full Text | Google Scholar

Blackford J. C., Allen J. I., Gilbert F. J. (2004). Ecosystem dynamics at six contrasting sites: a generic modelling study. J. Mar. Syst. 52, 191–215. doi: 10.1016/j.jmarsys.2004.02.004

Crossref Full Text | Google Scholar

Boyce D. G., Lewis M. R., Worm B. (2010). Global phytoplankton decline over the past century. Nature 466, 591–596. doi: 10.1038/nature09268

PubMed Abstract | Crossref Full Text | Google Scholar

Broecker W. S. (1992). The great ocean conveyor. Global warming: Phys. facts 247, 129–161. doi: 10.1063/1.41925

Crossref Full Text | Google Scholar

Browning T. J., Moore C. M. (2023). Global analysis of ocean phytoplankton nutrient limitation reveals high prevalence of co-limitation. Nat. Commun. 14, 5014. doi: 10.1038/s41467-023-40774-0

PubMed Abstract | Crossref Full Text | Google Scholar

Burkholder J. A. M., Glibert P. M., Skelton H. M. (2008). Mixotrophy, a major mode of nutrition for harmful algal species in eutrophic waters. Harmful algae 8, 77–93. doi: 10.1016/j.hal.2008.08.010

Crossref Full Text | Google Scholar

Burmaster D. E. (1979). The unsteady continuous culture of phosphate-limited Monochrysis lutheri Droop: experimental and theoretical analysis. J. Exp. Mar. Biol. Ecol. 39, 167–186. doi: 10.1016/0022-0981(79)90012-1

Crossref Full Text | Google Scholar

Chalup M. S., Laws E. A. (1990). A test of the assumptions and predictions of recent microalgal growth models with the marine phytoplankter Pavlova lutheri. Limnol. Oceanogr. 35, 583–596. doi: 10.4319/lo.1990.35.3.0583

Crossref Full Text | Google Scholar

Chan A. T. (1980). Comparative physiological study of marine diatoms and dinoflagellates in relation to irradiance and cell size. II. Relationship between photosynthesis, growth, and carbon/chlorophyll a ratio 1, 2. J. phycology 16, 428–432. doi: 10.1111/j.1529-8817.1980.tb03056.x

Crossref Full Text | Google Scholar

Chen B., Smith S. L. (2018). Optimality-based approach for computationally efficient modeling of phytoplankton growth, chlorophyll-to-carbon, and nitrogen-to-carbon ratios. Ecol. Model. 385, 197–212. doi: 10.1016/j.ecolmodel.2018.08.001

Crossref Full Text | Google Scholar

Cloern J. E., Grenz C., Vidergar-Lucas L. (1995). An empirical model of the phytoplankton chlorophyll: carbon ratio-the conversion factor between productivity and growth rate. Limnol. Oceanogr. 40, 1313–1321. doi: 10.4319/lo.1995.40.7.1313

Crossref Full Text | Google Scholar

Cohen N. R., McIlvin M. R., Moran D. M., Held N. A., Saunders J. K., Hawco N. J., et al. (2021). Dinoflagellates alter their carbon and nutrient metabolic strategies across environmental gradients in the central Pacific Ocean. Nat. Microbiol. 6, 173–186. doi: 10.1038/s41564-020-00814-7

PubMed Abstract | Crossref Full Text | Google Scholar

Costache T. A., Acien Fernandez F. G., Morales M. M., Stamatin I., Molina E. (2013). Comprehensive model of microalgae photosynthesis rate as a function of culture conditions in photobioreactors. Appl. Microbiol. Biotechnol. 97, 7627–7637. doi: 10.1007/s00253-013-5035-2

PubMed Abstract | Crossref Full Text | Google Scholar

Coyle K. O., Hermann A. J., Hopcroft R. R. (2019). Modeled spatial-temporal distribution of productivity, chlorophyll, iron and nitrate on the northern Gulf of Alaska shelf relative to field observations. Deep Sea Res. Part II: Topical Stud. Oceanogr. 165, 163–191. doi: 10.1016/j.dsr2.2019.05.006

Crossref Full Text | Google Scholar

Cullen J. J. (1990). On models of growth and photosynthesis in phytoplankton. Deep Sea Res. Part A. Oceanogr. Res. Papers 37, 667–683. doi: 10.1016/0198-0149(90)90097-F

Crossref Full Text | Google Scholar

Dai Y., Yang S., Zhao D., Hu C., Xu W., Anderson D. M., et al. (2023). Coastal phytoplankton blooms expand and intensify in the 21st century. Nature 615, 280–284. doi: 10.1038/s41586-023-05760-y

PubMed Abstract | Crossref Full Text | Google Scholar

DeVries T., Primeau F., Deutsch C. (2012). The sequestration efficiency of the biological pump. Geophys. Res. Lett. 39, 13. doi: 10.1029/2012GL051963

Crossref Full Text | Google Scholar

Dierssen H. M. (2010). Perspectives on empirical approaches for ocean color remote sensing of chlorophyll in a changing climate. Proc. Natl. Acad. Sci. 107, 17073–17078. doi: 10.1073/pnas.0913800107

Crossref Full Text | Google Scholar

Doney S. C., Lima I., Moore J. K., Lindsay K., Behrenfeld M. J., Westberry T. K., et al. (2009). Skill metrics for confronting global upper ocean ecosystem-biogeochemistry models against field and remote sensing data. J. Mar. Syst. 76, 95–112. doi: 10.1016/j.jmarsys.2008.05.015

Crossref Full Text | Google Scholar

Droop M. R. (1974). The nutrient status of algal cells in continuous culture. J. Mar. Biol. Assoc. United Kingdom 54, 825–855. doi: 10.1017/S002531540005760X

Crossref Full Text | Google Scholar

Droop M. R. (1983). 25 years of algal growth kinetics a personal view. Botanica Marina. 26 (3), 99–112. doi: 10.1515/botm.1983.26.3.99

Crossref Full Text | Google Scholar

Edwards K. F., Thomas M. K., Klausmeier C. A., Litchman E. (2012). Allometric scaling and taxonomic variation in nutrient utilization traits and maximum growth rate of phytoplankton. Limnol. Oceanogr. 57, 554–566. doi: 10.4319/lo.2012.57.2.0554

Crossref Full Text | Google Scholar

Eppley R. W. (1968). An incubation method for estimating the carbon content of phytoplankton in natural samples. Limnol. Oceanogr. 13, 574–582. doi: 10.4319/lo.1968.13.4.0574

Crossref Full Text | Google Scholar

Eppley R. W. (1971). Temperature and phytoplankton growth in the sea. Fishery Bull. 70, 1063.

Google Scholar

Eppley R. W. (1980). “Estimating phytoplankton growth rates in the central oligotrophic oceans,” in Primary productivity in the sea (Springer US, Boston, MA), 231–242.

Google Scholar

Eppley R. W., Sloan P. R. (1966). Growth rates of marine phytoplankton: correlation with light absorption by cell chlorophyll a. Physiol. Plant. 19, 47–59. doi: 10.1111/j.1399-3054.1966.tb09073.x

Crossref Full Text | Google Scholar

Ergun E., Demirata B., Gumus G., Apak R. (2004). Simultaneous determination of chlorophyll a and chlorophyll b by derivative spectrophotometry. Anal. bioanal. Chem. 379, 803–811. doi: 10.1007/s00216-004-2637-7

PubMed Abstract | Crossref Full Text | Google Scholar

Falkowski P. G. (1994). The role of phytoplankton photosynthesis in global biogeochemical cycles. Photosynth. Res. 39, 235–258. doi: 10.1007/BF00014586

PubMed Abstract | Crossref Full Text | Google Scholar

Falkowski P. (2012). Ocean science: the power of plankton. Nature 483, S17–S20. doi: 10.1038/483S17a

PubMed Abstract | Crossref Full Text | Google Scholar

Falkowski P. G., LaRoche J. (1991). Acclimation to spectral irradiance in algae. J. Phycol. 27, 8–14. doi: 10.1111/j.0022-3646.1991.00008.x

Crossref Full Text | Google Scholar

Faugeras B., Bernard O., Sciandra A., Lévy M. (2004). A mechanistic modelling and data assimilation approach to estimate the carbon/chlorophyll and carbon/nitrogen ratios in a coupled hydrodynamical-biological model. Nonlinear Process. Geophys. 11, 515–533. doi: 10.5194/npg-11-515-2004

Crossref Full Text | Google Scholar

Fennel K., Boss E. (2003). Subsurface maxima of phytoplankton and chlorophyll: Steady-state solutions from a simple model. Limnol. Oceanogr. 48, 1521–1534. doi: 10.4319/lo.2003.48.4.1521

Crossref Full Text | Google Scholar

Fernández-Castro B., Pahlow M., Mouriño-Carballido B., Maranon E., Oschlies A. (2016). Optimality-based Trichodesmium diazotrophy in the North Atlantic subtropical gyre. J. Plankton Res. 38, 946–963. doi: 10.1093/plankt/fbw047

Crossref Full Text | Google Scholar

Foy R. H., Smith R. V. (1980). The role of carbohydrate accumulation in the growth of planktonic Oscillatoria species. Br. Phycol. J. 15, 139–150. doi: 10.1080/00071618000650161

Crossref Full Text | Google Scholar

Gallegos C. L., Vant W. N. (1996). An incubation procedure for estimating carbon-to-chlorophyll ratios and growth-irradiance relationships of estuarine phytoplankton. Mar. Ecol. Prog. Ser. 138, 275–291. doi: 10.3354/meps138275

Crossref Full Text | Google Scholar

García-Malea M. C., Acién F. G., Fernández J. M., Cerón M. C., Molina E. (2006). Continuous production of green cells of Haematococcus pluvialis: modeling of the irradiance effect. Enzyme microb. Technol. 38, 981–989. doi: 10.1016/j.enzmictec.2005.08.031

Crossref Full Text | Google Scholar

Geider R. J. (1987). Light and temperature dependence of the carbon to chlorophyll a ratio in microalgae and cyanobacteria: implications for physiology and growth of phytoplankton. New Phytol. 106 (1), 1–34. doi: 10.1111/j.1469-8137.1987.tb04788.x

Crossref Full Text | Google Scholar

Geider R. J. (1993). Quantitative phytoplankton physiology: implications for primary production and phytoplankton growth[C]//ICES Mar. Sci. Symp. 197, 52–62.

Google Scholar

Geider R. J., MacIntyre H. L., Kana T. M. (1996). A dynamic model of photoadaptation in phytoplankton. Limnol. Oceanogr. 41, 1–15. doi: 10.4319/lo.1996.41.1.0001

Crossref Full Text | Google Scholar

Geider R. J., MacIntyre H. L., Kana T. M. (1997). Dynamic model of phytoplankton growth and acclimation: responses of the balanced growth rate and the chlorophyll a: carbon ratio to light, nutrient-limitation and temperature. Mar. Ecol. Prog. Ser. 148, 187–200. doi: 10.3354/meps148187

Crossref Full Text | Google Scholar

Geider R. J., Maclntyre H. L., Kana T. M. (1998). A dynamic regulatory model of phytoplanktonic acclimation to light, nutrients, and temperature. Limnol. oceanogr. 43, 679–694. doi: 10.4319/lo.1998.43.4.0679

Crossref Full Text | Google Scholar

Geider R. J., Platt T., Raven J. A. (1986). Size dependence of growth and photosynthesis in diatoms: a synthesis. Mar. Ecol. Prog. Ser. 30, 93–104. doi: 10.3354/meps030093

Crossref Full Text | Google Scholar

Goldman J. C. (1980). “Physiological processes, nutrient availability, and the concept of relative growth rate in marine phytoplankton ecology,” in Primary productivity in the sea (Springer US, Boston, MA), 179–194.

Google Scholar

Graff J. R., Milligan A. J., Behrenfeld M. J. (2012). The measurement of phytoplankton biomass using flow-cytometric sorting and elemental analysis of carbon. Limnol. Oceanogr.: Methods 10, 910–920. doi: 10.4319/lom.2012.10.910

Crossref Full Text | Google Scholar

Grima E. M., Sevilla J. M. F., Pérez J. A. S., Camacho F. G. (1996). A study on simultaneous photolimitation and photoinhibition in dense microalgal cultures taking into account incident and averaged irradiances. J. Biotechnol. 45, 59–69. doi: 10.1016/0168-1656(95)00144-1

Crossref Full Text | Google Scholar

Grimaud G. M., Mairet F., Sciandra A., Bernard O. (2017). Modeling the temperature effect on the specific growth rate of phytoplankton: a review. Rev. Environ. Sci. Bio/Technol. 16, 625–645. doi: 10.1007/s11157-017-9443-0

Crossref Full Text | Google Scholar

Hansen A. N., Visser A. W. (2019). The seasonal succession of optimal diatom traits. Limnol. Oceanogr. 64, 1442–1457. doi: 10.1002/lno.11126

Crossref Full Text | Google Scholar

Harding L. W., Meeson B. W., Prézelin B. B., Sweeney B. M. (1981). Diel periodicity of photosynthesis in marine phytoplankton. Mar. Biol. 61, 95–105. doi: 10.1007/BF00386649

Crossref Full Text | Google Scholar

He J., Chen Y., Wu J., Stow D. A., Christakos G. (2020). Space-time chlorophyll-a retrieval in optically complex waters that accounts for remote sensing and modeling uncertainties and improves remote estimation accuracy. Water Res. 171, 115403. doi: 10.1016/j.watres.2019.115403

PubMed Abstract | Crossref Full Text | Google Scholar

Henson S. A., Dunne J. P., Sarmiento J. L. (2009). Decadal variability in North Atlantic phytoplankton blooms. J. Geophys. Res.: Oceans 114. doi: 10.1029/2008jc005139

Crossref Full Text | Google Scholar

Hordoir R., Meier H. E. M. (2012). Effect of climate change on the thermal stratification of the Baltic Sea: a sensitivity experiment. Climate Dynam. 38, 1703–1713. doi: 10.1007/s00382-011-1036-y

Crossref Full Text | Google Scholar

Itoh S., Yasuda I., Saito H., Tsuda A., Komatsu K. (2015). Mixed layer depth and chlorophyll a: Profiling float observations in the Kuroshio–Oyashio Extension region. J. Mar. Syst. 151, 1–14. doi: 10.1016/j.jmarsys.2015.06.004

Crossref Full Text | Google Scholar

Jackson T., Sathyendranath S., Platt T. (2017). An exact solution for modeling photoacclimation of the carbon-to-chlorophyll ratio in phytoplankton. Front. Mar. Sci. 4, 283. doi: 10.3389/fmars.2017.00283

Crossref Full Text | Google Scholar

Jakobsen H. H., Markager S. (2016). Carbon-to-chlorophyll ratio for phytoplankton in temperate coastal waters: Seasonal patterns and relationship to nutrients. Limnol. Oceanogr. 61, 1853–1868. doi: 10.1002/lno.10338

Crossref Full Text | Google Scholar

Jassby A. D., Platt T. (1976). Mathematical formulation of the relationship between photosynthesis and light for phytoplankton. Limnol. oceanogr. 21, 540–547. doi: 10.4319/lo.1976.21.4.0540

Crossref Full Text | Google Scholar

Jeong H. J., Kang H. C., Lim A. S., Jang S. H., Lee K., Lee S. Y., et al. (2021). Feeding diverse prey as an excellent strategy of mixotrophic dinoflagellates for global dominance. Sci. Adv. 7, eabe4214. doi: 10.1126/sciadv.abe4214

PubMed Abstract | Crossref Full Text | Google Scholar

Kaymaz ŞM., Ates E. (2018). Estimating chlorophyll-a concentration using remote sensing techniques. Ann. Rev. Res. 4, 555633.

Google Scholar

Kerimoglu O., Pahlow M., Anugerahanti P., Smith S. L.. (2023). FABM-NflexPD 2.0: testing an instantaneous acclimation approach for modeling the implications of phytoplankton eco-physiology for the carbon and nutrient cycles. Geosci. Model. Dev. 16, 95–108. doi: 10.5194/gmd-16-95-2023

Crossref Full Text | Google Scholar

Kettle H. (2009). Using satellite-derived backscattering coefficients in addition to chlorophyll data to constrain a simple marine biogeochemical model. Biogeosciences 6, 1591–1601. doi: 10.5194/bg-6-1591-2009

Crossref Full Text | Google Scholar

Kiefer D. A., Mitchell B. G. (1983). A simple, steady state description of phytoplankton growth based on absorption cross section and quantum efficiency 1. Limnol. Oceanogr. 28, 770–776. doi: 10.4319/lo.1983.28.4.0770

Crossref Full Text | Google Scholar

Kooi M., Nes E. H., Scheffer M., Koelmans A. A. (2017). Ups and downs in the ocean: effects of biofouling on vertical transport of microplastics. Environ. Sci. Technol. 51, 7963–7971. doi: 10.1021/acs.est.6b04702

PubMed Abstract | Crossref Full Text | Google Scholar

Kremer C. T., Thomas M. K., Litchman E. (2017). Temperature-and size-scaling of phytoplankton population growth rates: Reconciling the Eppley curve and the metabolic theory of ecology. Limnol. oceanogr. 62, 1658–1670. doi: 10.1002/lno.10523

Crossref Full Text | Google Scholar

Kruskopf M., Flynn K. J. (2006). Chlorophyll content and fluorescence responses cannot be used to gauge reliably phytoplankton biomass, nutrient status or growth rate. New Phytol. 169, 525–536. doi: 10.1111/j.1469-8137.2005.01601.x

PubMed Abstract | Crossref Full Text | Google Scholar

Kwiatkowski L., Aumont O., Bopp L., Ciais P. (2018). The impact of variable phytoplankton stoichiometry on projections of primary production, food quality, and carbon uptake in the global ocean. Global Biogeochem. Cycles 32, 516–528. doi: 10.1002/2017GB005799

Crossref Full Text | Google Scholar

Lapointe B. E., Tenore K. R., Dawes C. J. (1984). Interactions between light and temperature on the physiological ecology of Gracilaria tikvahiae (Gigartinales: Rhodophyta) I. growth, photosynthesis and respiration. Mar. Biol. 80, 161–170. doi: 10.1007/BF02180183

Crossref Full Text | Google Scholar

Laws E. A., Bannister T. T. (1980). Nutrient-and light-limited growth of Thalassiosira fluviatilis in continuous culture, with implications for phytoplankton growth in the ocean 1. Limnol. Oceanogr. 25, 457–473. doi: 10.4319/lo.1980.25.3.0457

Crossref Full Text | Google Scholar

Laws E. A., Chalup M. S. (1990). A microalgal growth model. Limnol. oceanogr. 35, 597–608. doi: 10.4319/lo.1990.35.3.0597

Crossref Full Text | Google Scholar

Laws E. A., Redalje D. G., Karl D. M., Chalup M. S. (1983). A theoretical and experimental examination of the predictions of two recent models of phytoplankton growth. J. Theor. Biol. 105, 469–491. doi: 10.1016/0022-5193(83)90188-1

Crossref Full Text | Google Scholar

Lefevre N., Taylor A. H., Gilbert F. J., Geider R. J. (2003). Modeling carbon to nitrogen and carbon to chlorophyll a ratios in the ocean at low latitudes: Evaluation of the role of physiological plasticity. Limnol. Oceanogr. 48, 1796–1807. doi: 10.4319/lo.2003.48.5.1796

Crossref Full Text | Google Scholar

Letelier R. M., Bidigare R. R., Hebel D. V., Ondrusek M., Winn C. D., Karl D. M. (1993). Temporal variability of phytoplankton community structure based on pigment analysis. Limnol. Oceanogr. 38, 1420–1437. doi: 10.4319/lo.1993.38.7.1420

Crossref Full Text | Google Scholar

Levine N. M., Leles S. G. (2021). Marine plankton metabolisms revealed. Nat. Microbiol. 6, 147–148. doi: 10.1038/s41564-020-00856-x

PubMed Abstract | Crossref Full Text | Google Scholar

Lewis M. R., Cullen J. J., Plantt T. (1984). Relationships between vertical mixing and photoadaptation of phytoplankton: similarity criteria. Mar. Ecol. Prog. Ser. 15, 141–149. doi: 10.3354/meps015141

Crossref Full Text | Google Scholar

Li W. K. W. (1980). Temperature adaptation in phytoplankton: cellular and photosynthetic characteristics. Primary productivity sea 11, 259–279. doi: 10.1007/978-1-4684-3890-1_15

Crossref Full Text | Google Scholar

Li Q. P., Franks P. J. S., Landry M. R., Goericke R., Taylor A. G. (2010). Modeling phytoplankton growth rates and chlorophyll to carbon ratios in California coastal and pelagic ecosystems. J. Geophys. Res.: Biogeosci. 115 (G4). doi: 10.1029/2009jg001111

Crossref Full Text | Google Scholar

Liu X., Liu Y., Noman M. A., Thangaraj S., Sun J. (2021). Physiological changes and elemental ratio of Scrippsiella trochoidea and Heterosigma akashiwo in different growth phase[J]. Water 13 (2), 132. doi: 10.3390/w13020132

Crossref Full Text | Google Scholar

Litchman E., de Tezanos Pinto P., Edwards K. F., Klausmeier C. A., Kremer C. T., Thomas M. K., et al. (2015). Global biogeochemical impacts of phytoplankton: a trait-based perspective. J. Ecol. 103, 1384–1396. doi: 10.1111/jec.2015.103.issue-6

Crossref Full Text | Google Scholar

López-Cortés D. J., Núñez Vázquez E. J., Dorantes-Aranda J. J., Band-Schmidt C. J., Hernández-Sandoval F. E., Bustillos-Guzmán J. J., et al. (2019). The state of knowledge of harmful algal blooms of Margalefidinium polykrikoides (aka Cochlodinium polykrikoides) in Latin America. Front. Mar. Sci. 6, 463. doi: 10.3389/fmars.2019.00463

Crossref Full Text | Google Scholar

Lorenzen C. J. (1968). Carbon/chlorophyll relationships in an upwelling area. Limnol. Oceanogr. 13, 202–204. doi: 10.4319/lo.1968.13.1.0202

Crossref Full Text | Google Scholar

Losa S. N., Dutkiewicz S., Losch M., Oelker J., Soppa M. A., Trimborn S., et al. (2019). On modeling the Southern Ocean phytoplankton functional types. Biogeosci. Discuss. 2019, 1–37. doi: 10.5194/bg-2019-289

Crossref Full Text | Google Scholar

Marañón E., Lorenzo M. P., Cermeño P., Mouriño-Carballido B. (2018). Nutrient limitation suppresses the temperature dependence of phytoplankton metabolic rates. ISME J. 12, 1836–1845. doi: 10.1038/s41396-018-0105-1

PubMed Abstract | Crossref Full Text | Google Scholar

Marshall H. L., Geider R. J., Flynn K. J. (2000). A mechanistic model of photoinhibition. New Phytol. 145, 347–359. doi: 10.1046/j.1469-8137.2000.00575.x

Crossref Full Text | Google Scholar

Masuda Y., Yamanaka Y., Smith S. L., Hirata T., Nakano H., Oka A, et al. (2021). Photoacclimation by phytoplankton determines the distribution of global subsurface chlorophyll maxima in the ocean. Commun. Earth Environ. 2, 128. doi: 10.1038/s43247-021-00201-y

Crossref Full Text | Google Scholar

McCain J. S. P., Tagliabue A., Susko E., Achterberg E. P., Allen A. E., Bertrand E. M., et al. (2021). Cellular costs underpin micronutrient limitation in phytoplankton. Sci. Adv. 7, eabg6501. doi: 10.1126/sciadv.abg6501

PubMed Abstract | Crossref Full Text | Google Scholar

McCarthy J. J. (1981). The kinetics of nutrient utilization. Can. Bull. Fish. Aquat. Sci. 210, 211–233.

Google Scholar

McKew B. A., Davey P., Finch S. J., Hopkins J., Lefebvre S. C., Metodiev M. V., et al. (2013). The trade-off between the light-harvesting and photoprotective functions of fucoxanthin-chlorophyll proteins dominates light acclimation in Emiliania huxleyi (clone CCMP 1516). New Phytol. 200, 74–85. doi: 10.1111/nph.2013.200.issue-1

PubMed Abstract | Crossref Full Text | Google Scholar

Megard R. O., Tonkyn D. W., Senft W. H. (1984). Kinetics of oxygenic photosynthesis in planktonic algae. J. Plankton Res. 6, 325–337. doi: 10.1093/plankt/6.2.325

Crossref Full Text | Google Scholar

Mei Z. P., Finkel Z. V., Irwin A. J. (2011). Phytoplankton growth allometry and size dependent C: N stoichiometry revealed by a variable quota model. Mar. Ecol. Prog. Ser. 434, 29–43. doi: 10.3354/meps09149

Crossref Full Text | Google Scholar

Menden-Deuer S., Lessard E. J. (2000). Carbon to volume relationships for dinoflagellates, diatoms, and other protist plankton. Limnol. oceanogr. 45, 569–579. doi: 10.4319/lo.2000.45.3.0569

Crossref Full Text | Google Scholar

Moore J. K., Doney S. C., Kleypas J. A., Glover D. M., Fung I. Y. (2001). An intermediate complexity marine ecosystem model for the global domain. Deep Sea Res II Top Stud Oceanogr 49 (1-3), 403–462.

Google Scholar

Moorhouse H. L., Read D. S., McGowan S., Wagner M., Roberts C., Armstrong L. K., et al. (2018). Characterisation of a major phytoplankton bloom in the River Thames (UK) using flow cytometry and high performance liquid chromatography. Sci. total Environ. 624, 366–376. doi: 10.1016/j.scitotenv.2017.12.128

PubMed Abstract | Crossref Full Text | Google Scholar

Morel F. M. M. (1987). Kinetics of nutrient uptake and growth in phytoplankton 1. J. phycology 23, 137–150. doi: 10.1111/j.0022-3646.1987.00137.x

Crossref Full Text | Google Scholar

Omta A. W., Llido J., Garçon V., Kooijman S. A. L. M., Dijkstra H. A. (2009). The interpretation of satellite chlorophyll observations: The case of the Mozambique Channel. Deep Sea Res. Part I: Oceanogr. Res. Papers 56, 974–988. doi: 10.1016/j.dsr.2009.01.011

Crossref Full Text | Google Scholar

Pahlow M. (2005). Linking chlorophyll-nutrient dynamics to the Redfield N: C ratio with a model of optimal phytoplankton growth. Mar. Ecol. Prog. Ser. 287, 33–43. doi: 10.3354/meps287033

Crossref Full Text | Google Scholar

Pahlow M., Dietze H., Oschlies A. (2013). Optimality-based model of phytoplankton growth and diazotrophy. Mar. Ecol. Prog. Ser. 489, 1–16. doi: 10.3354/meps10449

Crossref Full Text | Google Scholar

Pahlow M., Oschlies A. (2013). Optimal allocation backs Droop’s cell-quota model. Mar. Ecol. Prog. Ser. 473, 1–5. doi: 10.3354/meps10181

Crossref Full Text | Google Scholar

Pitcher G. C., Figueiras F. G., Hickey B. M., Moita M. T. (2010). The physical oceanography of upwelling systems and the development of harmful algal blooms. Prog. oceanogr. 85, 5–32. doi: 10.1016/j.pocean.2010.02.002

PubMed Abstract | Crossref Full Text | Google Scholar

Platt T., Gallegos C. L., Harrison W. G. (1980). Photoinhibition of photosynthesis in natural assemblages of marine phytoplankton.

Google Scholar

Pondaven P., Ruiz-Pino D., Druon J. N., Fravalo C., Tréguer P. (1999). Factors controlling silicon and nitrogen biogeochemical cycles in high nutrient, low chlorophyll systems (the Southern Ocean and the North Pacific): Comparison with a mesotrophic system (the North Atlantic). Deep Sea Res. Part I: Oceanogr. Res. Papers 46, 1923–1968. doi: 10.1016/s0967-0637(99)00033-3

Crossref Full Text | Google Scholar

Ras M., Steyer J. P., Bernard O. (2013). Temperature effect on microalgae: a crucial factor for outdoor production. Rev. Environ. Sci. bio/technol. 12, 153–164. doi: 10.1007/s11157-013-9310-6

Crossref Full Text | Google Scholar

Renaud S. M., Thinh L. V., Lambrinidis G., Parry D. L. (2002). Effect of temperature on growth, chemical composition and fatty acid composition of tropical Australian microalgae grown in batch cultures. Aquaculture 211, 195–214. doi: 10.1016/S0044-8486(01)00875-4

Crossref Full Text | Google Scholar

Rhee G. Y. (1974). Phosphate uptake under nitrate limitation by scenedesmus sp. and its ecological implications 1. J. Phycol. 10, 470–475. doi: 10.1111/j.0022-3646.1974.00470.x

Crossref Full Text | Google Scholar

Richlen M. L., Morton S. L., Jamali E. A., Rajan A., Anderson D. M. (2010). The catastrophic 2008–2009 red tide in the Arabian gulf region, with observations on the identification and phylogeny of the fish-killing dinoflagellate Cochlodinium polykrikoides. Harmful algae 9, 163–172. doi: 10.1016/j.hal.2009.08.013

Crossref Full Text | Google Scholar

Rodhe W. (1978). Algae in culture and nature: With 1 figure and 5 tables in the text. Internationale Vereinigung für Theoretische und Angewandte Limnol.: Mitt. 21, 7–20. doi: 10.1080/05384680.1978.11903945

Crossref Full Text | Google Scholar

Ross O. N., Geider R. J. (2009). New cell-based model of photosynthesis and photo-acclimation: accumulation and mobilisation of energy reserves in phytoplankton. Mar. Ecol. Prog. Ser. 383, 53–71. doi: 10.3354/meps07961

Crossref Full Text | Google Scholar

Sakshaug E., Andresen K., Kiefer D. A. (1989). A steady state description ofgrowth and light absorption in the marine planktonic diatom Skeletonema costatum. Limnol. Oceanogr. 34, 198–205. doi: 10.4319/lo.1989.34.1.0198

Crossref Full Text | Google Scholar

Sardans J., Janssens I. A., Ciais P., Obersteiner M., Peñuelas J. (2021). Recent advances and future research in ecological stoichiometry. Perspect. Plant Ecol. Evol. System. 50, 125611. doi: 10.1016/j.ppees.2021.125611

Crossref Full Text | Google Scholar

Sasai Y., Smith S. L., Siswanto E., Sasaki H., Nonaka M. (2022). Physiological flexibility of phytoplankton impacts modelled chlorophyll and primary production across the North Pacific Ocean. Biogeosciences 19, 4865–4882. doi: 10.5194/bg-19-4865-2022

Crossref Full Text | Google Scholar

Sathyendranath S., Platt T., Kovač Ž., Dingle J., Jackson T., Brewin R. J., et al. (2020). Reconciling models of primary production and photoacclimation. Appl. Optics 59, C100–C114. doi: 10.1364/AO.386252

Crossref Full Text | Google Scholar

Schoo K. L., Malzahn A. M., Krause E., Boersma M. (2013). Increased carbon dioxide availability alters phytoplankton stoichiometry and affects carbon cycling and growth of a marine planktonic herbivore. Mar. Biol. 160, 2145–2155. doi: 10.1007/s00227-012-2121-4

Crossref Full Text | Google Scholar

Schourup-Kristensen V., Sidorenko D., Wolf-Gladrow D. A., Völker C. (2014). A skill assessment of the biogeochemical model REcoM2 coupled to the Finite Element Sea Ice–Ocean Model (FESOM 1.3). Geosci. Model. Dev. 7, 2769–2802. doi: 10.5194/gmd-7-2769-2014

Crossref Full Text | Google Scholar

Serra-Maia R., Bernard O., Gonçalves A., Bensalem S., Lopes F. (2016). Influence of temperature on Chlorella vulgaris growth and mortality rates in a photobioreactor. Algal Res. 18, 352–359. doi: 10.1016/j.algal.2016.06.016

Crossref Full Text | Google Scholar

Sherman E., Moore J. K., Primeau F., Tanouye D. (2016). Temperature influence on phytoplankton community growth rates. Global Biogeochem. Cycles 30, 550–559. doi: 10.1002/2015GB005272

Crossref Full Text | Google Scholar

Shuter B. A. (1979). model of physiological adaptation in unicellular algae. J. Theor. Biol. 78, 519–552. doi: 10.1016/0022-5193(79)90189-9

PubMed Abstract | Crossref Full Text | Google Scholar

Smith S. L., Pahlow M., Merico A., Acevedo-Trejos E., Sasai Y., Yoshikawa C., et al. (2016). Flexible phytoplankton functional type (FlexPFT) model: size-scaling of traits and optimal growth. J. Plankton Res. 38, 977–992. doi: 10.1093/plankt/fbv038

Crossref Full Text | Google Scholar

Smith S. L., Yamanaka Y., Pahlow M., Oschlies A. (2009). Optimal uptake kinetics: physiological acclimation explains the pattern of nitrate uptake by phytoplankton in the ocean. Mar. Ecol. Prog. Ser. 384, 1–12. doi: 10.3354/meps08022

Crossref Full Text | Google Scholar

Steele J. H. (1962). Environmental control of photosynthesis in the sea. Limnol. oceanogr. 7, 137–150. doi: 10.4319/lo.1962.7.2.0137

Crossref Full Text | Google Scholar

Stoecker D. K., Hansen P. J., Caron D. A., Mitra A. (2017). Mixotrophy in the marine plankton. Annu. Rev. Mar. Sci. 9, 311–335. doi: 10.1146/annurev-marine-010816-060617

Crossref Full Text | Google Scholar

Strickland J. D. H. (1960). Measuring the production of marine phytoplankton. Fish. Res. Bd. Canada Bull. 122, 172.

Google Scholar

Sukenik A., Falkowski P. G., Bennett J. (1987). Potential enhancement of photosynthetic energy conversion in algal mass culture. Biotechnol. bioengineering 30, 970–977. doi: 10.1002/bit.260300808

Crossref Full Text | Google Scholar

Sukenik A., Levy R. S., Levy Y., Falkowski P. G., Dubinsky Z. (1991). Optimizing algal biomass production in an outdoor pond: a simulation model. J. Appl. phycology 3, 191–201. doi: 10.1007/BF00003577

Crossref Full Text | Google Scholar

Sunda W. G., Shertzer K. W., Hardison D. R. (2009). Ammonium uptake and growth models in marine diatoms: Monod and Droop revisited. Mar. Ecol. Prog. Ser. 386, 29–41. doi: 10.3354/meps08077

Crossref Full Text | Google Scholar

Taucher J., Oschlies A. (2011). Can we predict the direction of marine primary production change under global warming? Geophys. Res. Lett. 38. doi: 10.1029/2010gl045934

Crossref Full Text | Google Scholar

Taylor A. H., Geider R. J., Gilbert F. J. H. (1997). Seasonal and latitudinal dependencies of phytoplankton carbon-to-chlorophyll a ratios: results of a modelling study. Mar. Ecol. Prog. Ser. 152, 51–66. doi: 10.3354/meps152051

Crossref Full Text | Google Scholar

Taylor F. J. R., Hoppenrath M., Saldarriaga J. F. (2008). Dinoflagellate diversity and distribution. Biodivers. Conserv. 17, 407–418. doi: 10.1007/s10531-007-9258-3

Crossref Full Text | Google Scholar

Thomas M. K., Aranguren-Gassis M., Kremer C. T., Gould M. R., Anderson K., Klausmeier C. A., et al. (2017). Temperature–nutrient interactions exacerbate sensitivity to warming in phytoplankton. Global Change Biol. 23, 3269–3280. doi: 10.1111/gcb.2017.23.issue-8

Crossref Full Text | Google Scholar

Tréguer P., Bowler C., Moriceau B., Dutkiewicz S., Gehlen M., Aumont O., et al. (2018). Influence of diatom diversity on the ocean biological carbon pump. Nat. Geosci. 11, 27–37. doi: 10.1038/s41561-017-0028-x

Crossref Full Text | Google Scholar

Wang X. J., Behrenfeld M., Le Borgne R., Murtugudde R., Boss E. (2009). Regulation of phytoplankton carbon to chlorophyll ratio by light, nutrients and temperature in the Equatorial Pacific Ocean: a basin-scale model. Biogeosciences 6, 391–404. doi: 10.5194/bg-6-391-2009

Crossref Full Text | Google Scholar

William K. W. L., Morris I. (1982). Temperature adaptation in Phaeodactylum tricornutum Bohlin: photosynthetic rate compensation and capacity. J. Exp. Mar. Biol. Ecol. 58, 135–150. doi: 10.1016/0022-0981(82)90125-3

Crossref Full Text | Google Scholar

Worden A. Z., Follows M. J., Giovannoni S. J., Wilken S., Zimmerman A. E., Keeling P. J. (2015). Rethinking the marine carbon cycle: factoring in the multifarious lifestyles of microbes. Science 347, 1257594. doi: 10.1126/science.1257594

PubMed Abstract | Crossref Full Text | Google Scholar

Xin L., Hong-Ying H., Ke G., Ying-Xue S. (2010). Effects of different nitrogen and phosphorus concentrations on the growth, nutrient uptake, and lipid accumulation of a freshwater microalga Scenedesmus sp. Biores. Technol. 101, 5494–5500. doi: 10.1016/j.biortech.2010.02.016

Crossref Full Text | Google Scholar

Yun Y. S., Park J. M. (2003). Kinetic modeling of the light-dependent photosynthetic activity of the green microalga Chlorella vulgaris. Biotechnol. Bioeng. 83, 303–311. doi: 10.1002/bit.10669

PubMed Abstract | Crossref Full Text | Google Scholar

Zhang Q. C., Song J. J., Yu R. C., Yan T., Wang Y. F., Kong F. Z., et al. (2013). Roles of mixotrophy in blooms of different dinoflagellates: implications from the growth experiment. Harmful Algae 30, 10–26. doi: 10.1016/j.hal.2013.08.003

Crossref Full Text | Google Scholar