- 1College of Geography and Environmental Science, Henan University, Kaifeng, China
- 2Henan Industrial Technology Academy of Spatio-Temporal Big Data, Henan University, Zhengzhou, China
- 3Henan Key Laboratory of General Aviation Technology, School of Electronics and Information, Zhengzhou University of Aeronautics, Zhengzhou, China
- 4Research Center for UAV Technology, Lantian Laboratory, Anyang, China
- 5School of Information and Electronics, Beijing Institute of Technology, Beijing, China
- 6Hubei Key Laboratory of Intelligent Robot, Wuhan Institute of Technology, Wuhan, China
- 7School of Computer Science and Technology, Xinjiang University, Urumqi, China
Timely and accurate monitoring of typical coastal targets using remote sensing technology is crucial for maintaining marine ecological stability. Hyperspectral target detection technology proves to be an effective tool in extracting various typical materials along the coastline. Traditional target detection methods using spectral domain information can effectively retain the intrinsic properties of the material. However, it is difficult to effectively recognize targets in homogeneous regions by using only spectral domain information, which may lead to insufficient utilization of spatial information. In this study, a detector based on signal-to-noise ratio fusion constrained energy minimization with low-rank sparse decomposition (SFLRSD) is proposed. This detector improves the separability of background and target by obtaining spatial domain information from hyperspectral images and fusing spectral domain information. First, total variation regularization and fractional Fourier transform are applied to process spatial and spectral domain information, respectively. The constrained energy minimization (CEM) detector is used to improve the separability between the target and background of the processed data. Then, the background and anomalies are represented as low-rank and sparse components, respectively, using low-rank sparse matrix factorization. This transforms the model solution into a covariance matrix problem, which is then solved using marginal distance difference (MDD) to isolate anomalous parts. Subsequently, the anomaly parts are fused with CEM detector results, weighted by their respective signal-to-noise ratios. This detection model leverages unified hyperspectral image features, enhancing spectral discreteness of anomalous targets and backgrounds. Finally, experiments on custom created hyperspectral dataset show that the proposed method outperforms other baseline methods in terms of visualization and quantitative performance. In this paper, we not only propose a new hyperspectral target detection method, but we also collect three typical marine litter of different materials by means of airborne hyperspectral remote sensing and construct four hyperspectral datasets in a real environment. All the simulation experiments in this paper are conducted in these four datasets.
1 Introduction
Artificial items of various material types, such as plastic bottles, metal cans, and fabrics, as well as the wooden debris by meteorological phenomena such as storms, are often left behind on human-activated coastlines or riverbanks. Litter of various materials are harmful to marine ecosystems. Efficient and accurate monitoring of coastal scattering is of great significance for ecological environment and coastal defense safety (Yang et al., 2023; Zhou et al., 2023a; Li et al., 2024). With the development and maturity of unmanned aerial vehicle (UAV) technology, it plays an increasingly critical role in the field of high-resolution data collection at low altitude. Currently, airborne remote sensing (RS) technology enriches the ways of satellite data acquisition and provides better support for the information extraction from RS images. Moreover, satellite RS (Zhong et al., 2021; Sun et al., 2023; Gong et al., 2024; Yin et al., 2023a; Yin et al., 2023b), UAVs, video surveillance, and traditional ground manual inspection methods constitute a comprehensive technical system for the inspection and monitoring of the water coastline (Li et al., 2021; Li L. et al., 2023; Zhang, 2023; Zhou et al., 2023b).
Hyperspectral remote sensing is a powerful ground-based observation technology, different from traditional remote sensing technology, hyperspectral imagery (HSI) integrates spectral and spatial information and is a kind of three-dimensional image data (Bioucas-Dias et al., 2013; Zhao et al., 2023a), which can obtain detailed spectral information of objects or materials by detecting hundreds of narrow bands (Hu et al., 2023). In the water shoreline, hyperspectral remote sensing technology is usually applied to detect and monitor garbage and other environmental pollutants (Dierssen et al., 2021), which mainly utilizes the information of continuous spectral bands collected by hyperspectral imagers, which can identify and differentiate the spectral characteristics of garbage and natural wetland environment (Karaca et al., 2013). Therefore, the increasing popularity and influence of the new remote sensing method of detecting shoreline litter, such as oceans and seas, through drone-borne hyperspectral remote sensing has become a necessary choice in remote sensing for both academia and industry. This technique has also been successfully used in the fields of mapping of coastal zones, monitoring of vegetation growth, estimation of vegetation biomass, extraction of geologic information, and monitoring of river and lake shoreline litter (Ma et al., 2008; Li et al., 2012; Liu et al., 2014; Liu et al., 2019; Tong et al., 2016; Bajjouk et al., 2020; Li et al., 2022) and has become a continuing research hotspot in the field of remote sensing.
With the rapid development of remote sensing technology, in 2012, researchers and scholars have used remote sensing technology for detecting water surface litter, using a variety of airborne equipment and achieved good detection results (Veenstra and Churnside, 2012), Mace (2012) proposed the idea of modeling analysis methods combined with remote sensing technology for monitoring the sea area where plastic litter accumulates. Freitas et al. (2022) collected airborne hyperspectral remote sensing to acquire a hyperspectral imaging dataset of marine litter, which contains different plastic targets and other litter targets, and evaluated the detection and classification of plastic materials in an unsupervised manner with unknown spectral response of the plastic materials, and the results showed that the overall accuracy of the classification of all categories of marine litter in the dataset reached 98.71%. Zeng et al. (2019) constructed a classification network of Multi-Scale Convolutional Neural Network (MSCNN) using aerial hyperspectral remote sensing and combining it with the latest deep learning techniques to solve the problem of monitoring large-scale garbage, which further combined with image segmentation techniques to realize the accurate extraction of the location of large-scale garbage and its size. Freitas et al. (2021) developed a remote hyperspectral imaging system for monitoring the concentration of marine litter, which adopts the form of aerial hyperspectral remote sensing to collect marine litter, and uses random forest and support vector machine to monitor marine litter automatically, and the results show a high detection accuracy. Balsi et al. (2021) developed an automated procedure for identifying and distinguishing different types of large plastic litter in the coastal environment using UAV-mounted hyperspectral imaging, and the effectiveness of the procedure was verified through a field survey carried out along the coast of Sassari, Italy. Serranti et al. (2018) proposed a new method based on hyperspectral imaging for analyzing microplastic litter in the ocean, which is capable of obtaining detailed information about plastic particles, including number, size, shape, and polymer type, from individual images. With the development of hyperspectral imaging technology, in the field of plastic waste identification, hyperspectral imaging is commonly used to identify polymer-based litter (Hu et al., 2013; Bonifazi et al., 2015a; Bonifazi et al., 2015b; Luciani et al., 2015; Serranti et al., 2015).
In general, hyperspectral target detection algorithms are divided into two main categories: anomaly detection and target detection (Zhao et al., 2020; Zhao et al., 2022). Target detection for hyperspectral images can be regarded as a binary classification task aiming to categorize pixels as targets or backgrounds. Hyperspectral match detection relies on the a priori information of the target spectra by comparing the deviations of the image pixel spectra from the target spectra and converting these deviations into characterization metrics, and then using statistical methods to set thresholds to achieve target pixel identification. In contrast, hyperspectral anomaly detection is a type of target detection that does not require any a priori spectral information, but instead utilizes mathematical or physical models to identify target pixels that are significantly different compared to surrounding pixels.
Recently, some researchers have analyzed and studied hyperspectral spectra in the transform domain. In hyperspectral image processing, Li et al. (2012) proposed a spectral similarity measure based on Fourier transform (FT). In order to balance the differences between high-frequency and low-frequency components, the method uses the target spectral features as normalization factors. The above transform only analyzes the spectral in the frequency domain, and the fractional Fourier transform (FrFT) can better deal with non-stationary signals compared with the conventional FrFT (Chen et al., 2014). Currently, FrFT has been used in some remote sensing image processing. Tao et al. (2019) proposed an anomaly detection algorithm with fractional Fourier entropy RX (FrFE-RX) and used it as a feature extraction method to obtain intermediate features between spectral and Fourier domains. Zhao X. et al. (2021) used FrFT to project the raw spectral information into the fractional domain and designed a new adaptive constrained energy minimization (FACEM) detector.
In recent years, low-rank sparse matrix decomposition (LRaSMD) (Du et al., 2016; Li et al., 2020) has been paid attention by many research scholars in the field of hyperspectral anomalous target detection due to its complete theoretical knowledge and operability. In the low-rank sparse representation assuming that the background data are located in multiple low-rank subspaces, Xu et al. (2015) proposed a background dictionary training method to separate the outlier pixels by training the background dictionary. Robust principal component analysis (RPCA) significantly enhances the robustness of anomaly detection by treating the background and anomaly targets of hyperspectral data as low-rank and sparse components, respectively, and combining them with the RX (Reed-Xiaoli) algorithm for anomaly detection of the sparse component (Sun et al., 2014). Yao et al. (2022) proposed a nonconvex regularized approximation model based on low-rank sparse matrix factorization (LRSNCR) based on RPCA, which is closer to the original problem than the RPCA model, replacing the low-rank and sparse terms of the matrices with the WNNM (weighted kernel paradigm minimization method) and Capped l2,1-norm, respectively, and gave an effective optimization algorithm. Zhao et al. (2023b) proposed a time-series target detection based on spectral perception and spatial-temporal tensor decomposition.
Hyperspectral image processing methods based on tensor analysis are used in hyperspectral image target detection due to their ability to maximize the original structure of the hyperspectral image. Zhang et al. (2008) proposed a tensor-based spatial target recognition algorithm for hyperspectral images. Liu et al. (2016) designed a new tensor hyperspectral target detection framework “Tensor Matched Subspace Detector (MSD)” integrates tensor well into traditional target detection algorithms, in which hyperspectral data is stored in the form of a kind of third-order tensor to jointly utilize the information of multidimensional data. Zhao et al. (2019) designed a detection method for solving anomalous targets by localized Mahalanobis distances based on tensor decomposition, where anomalies and noise are excluded from each factor matrix after the decomposition to filter out the clean background according to the definition of tensor Tucker decomposition, and finally Mahalanobis distances are used to calculate the degree of anomalies using the sliding double-window method in the original and background image datasets, respectively. Huang et al. (2019) designed a hyperspectral remote sensing image change detection method based on a restricted Boltzmann machine with a third-order tensor, and obtained good anomaly detection results. The tensor space-based detection model can analyze and represent the spatial features of hyperspectral image data more conveniently, and can improve the detection effect very significantly on the basis of traditional methods.
He et al. (2015) proposed a total variation regularization low-rank matrix decomposition method by incorporating total variation regularization into the low-rank matrix decomposition framework. The method combines the denoising model with simultaneous constraints of total variation regularization and low-rank matrix decomposition, which can effectively retain the spatial edge information while removing the noise. The necessity of sparse low-rank simultaneous use for denoising hyperspectral images is demonstrated. Due to the atmospheric interference and signal response, almost all of the acquired HSIs are inevitably polluted by various noises to different degrees (Rasti et al., 2021; Xu et al., 2022). The noise pollution destroys both initial spectral and spatial features in HSI. On the one hand, if we discard all these noisy HSI in subsequent applications, it will lead to severe data waste (Zhang et al., 2021). On the other hand, if we ignore these noise pollution problems and directly utilize them for subsequent applications, it will also disturb the interpretation algorithms (Bruzzone and Persello, 2009; Zhang et al., 2018). For instance, many works manifest that the noise pollution problem results in reducing HSI classification accuracy. However, it is hard to suppress the mixed noise in HSI through hardware improvement (Kerekes and Baum, 2003; Xiao et al., 2023). Therefore, removing noise in HSI via denoising algorithms is indispensable before HSI interpretation and applications (Yuan et al., 2015; Xie et al., 2023). Cheng and Wang (2019) incorporated the graph and total variation (TV) regularization into the LRR optimization (GTVLRR). Zhao C. et al. (2021) utilized a novel enhanced TV with an endmember background dictionary (EBD) for HSI anomaly detection, which decreased the impact of anomaly components in mixed pixels. Cheng and Wang (2020) fused TV and sparsity-inducing decomposition regularizations to facilitate the separation. Wang et al. (2023) proposed a joint anomaly detection and noise removal paradigm called DSR-ADNR, which develops a double subspace representation method to obtain both denoised and detection results simultaneously. Yuan et al. (2012) propose a hyperspectral image denoising algorithm employing a spectral-spatial adaptive total variation (TV) model, in which the spectral noise differences and spatial information differences are both considered in the process of noise reduction. To reduce the computational load in the denoising process, the split Bregman iteration algorithm is employed to optimize the spectral-spatial hyperspectral TV model and accelerate the speed of hyperspectral image denoising.
This paper mainly focuses on the detection of small and scattered typical material objects in the waterside shoreline environment, and creates a hyperspectral dataset by collecting hyperspectral data of typical material objects in the shoreline in the field. Then the proposed low rank sparse decomposition algorithm based on target saliency fusion is utilized for target detection experiments to provide technical support for ecological environmental protection. The main contributions of this paper are as follows:
(1) Acquisition and creation of hyperspectral dataset of typical material objects in the waterside shoreline environment.
(2) The spatial and spectral domains of hyperspectral images are processed using total variation (TV) regularization and FrFT, respectively, and a new constrained energy minimization (CEM) detector based on the fusion of spatial and spectral information is proposed.
(3) The background and anomalies are represented as low-rank and sparse components using low-rank sparse matrix decomposition technique, respectively, and the anomalous part is obtained by converting the model solution into a problem of solving the covariance matrix through the Marginal distance difference. Then, a target detector is proposed based on a signal-to-noise ratio (SNR) fusion CEM model. This model aims to automatically fuse the results of low-rank and sparse decomposition by utilizing the SNR fusion CEM technique. Finally, experiments on the four self-constructed hyperspectral datasets created show that the proposed method has better detection performance than other methods and can better separate background and anomaly.
2 Methodology
By taking advantage of the feature of spectral unity of hyperspectral images, the spatial domain of hyperspectral images is processed with total variation (TV) regularization for noise reduction, which can preserve the edge information of the images and promote the segmentation smoothness of the images. Then the spectral domain of the hyperspectral image is feature extracted by fractional Fourier transform (FrFT) to enhance the spectral difference between the anomalous target and the background, and then CEM is used to further improve the separability of the target and the background, and to comprehensively utilize the spatial spectral information of the image to improve the detection effect. Subsequently, the background and the anomaly are represented as low-rank and sparse components, respectively, using the low-rank sparse matrix decomposition technique, and then the anomaly part is obtained by converting the model solution into a problem of solving the covariance matrix through the Marginal distance difference. Finally, the obtained anomaly part and the CEM detector processing results can be fused by their respective signal-to-noise ratio (SNR) as the weighting coefficients to obtain superior target detection results, and the framework of the hyperspectral target detection based on spatial spectral domain transform fused low-rank sparse decomposition (SFLRSD) method is shown in Figure 1.
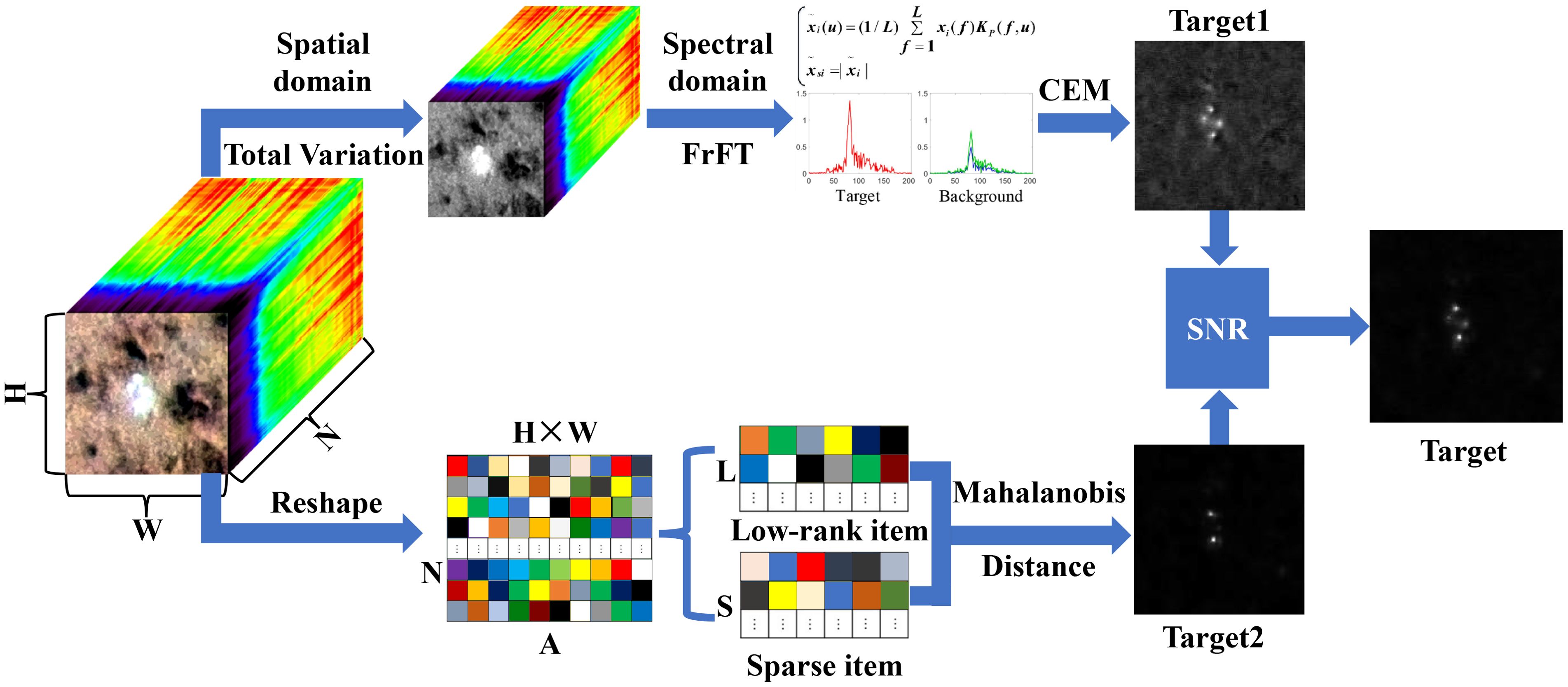
Figure 1. Framework of hyperspectral target detection method based on saliency fusion low-rank sparse decomposition (SFLRSD).
2.1 Constrained energy minimization detector based on fusion space spectral information
2.1.1 Spatial domain data processing based on total variation regularization
Total variation (TV) regularization is frequently employed in the process of converting hyperspectral images from three-dimensional (3D) cube images to two-dimensional (2D) matrices. This technique is used to maintain the local spatial information of the image segmentation, while also achieving smoothing effects and removing some of the noise that may be introduced during the conversion process. Therefore, when target detection is performed on hyperspectral images, the spatial domain of the hyperspectral image can first be processed using the TV (Osher et al., 2005), which preserves the edge information of the image and promotes segmental smoothing of the image in order to improve the estimation of the background portion.
Since spatially adjacent pixels can be represented as linear combinations of background atoms, the spatial regularization constraints can be expressed in terms of linear combination coefficients, i.e., low-rank coefficients xi and xj (Niu and Wang, 2016). For any point in the hyperspectral image, the TV regularizer is represented as shown in Equation 1 (Sun et al., 2022).
Where, U denotes the set of points in the spatial neighborhood of each pixel point.
Introducing the linear operators Gh and Gv in the horizontal and vertical directions (Iordache et al., 2012), in the two-dimensional image , Nx and Ny denote the two-dimensional image width and height, respectively, then the horizontal direction operator Gh and the vertical direction operator Gv are shown in Equations 2 and 3.
For the three-dimensional image, the operations of Equations 2 and 3 are performed for each band in turn. As a result, a linear operator representation of the horizontal and vertical directions of the hyperspectral image is obtained as shown in Equations 4 and 5.
Rewrite Equation 1 as Equation 6.
Where, l1,1 -parameters is defined as the sum of l1-parameters of each column of the matrix. Equation 6 represents the superposition of vectors in the horizontal and vertical directions.
2.1.2 The fractional Fourier transform based spectral domain data processing
Traditional hyperspectral target detection methods are based on the concept that background pixels can be represented by their spatial neighborhood, while target pixels cannot be represented by their spatial neighborhood. However, these methods do not consider transform domain information and are greatly affected by non-stationary noise. Consequently, the constructed background model remains influenced by targets and does not fully utilize background information. Although some hyperspectral target detection algorithms for deep feature extraction have recently been proposed by experts and scholars in combination with deep learning, they all have the disadvantages of high computational complexity and low target detection performance. However, the Fourier transform (FT) can effectively extract features in the spectral and transform domains, and by adjusting the order, it can reveal the characteristics of the signal in the time domain, the frequency domain, and the time-frequency domain. In the optimal order domain, similar signals exhibit significant energy aggregation, which shows excellent performance for applications such as noise suppression and target detection (Chen et al., 2014).
The FrFT is a Fourier transform method that uses linear frequency modulation (FM) orthogonal basis to replace the traditional complex exponential orthogonal basis, which realizes the comprehensive acquisition of spectral information between the frequency domain and the spectral domain by changing the order. In hyperspectral target detection, by using the optimal order of the FrFT, the essential features of the image can be extracted in the intermediate domain, highlighting the differences in spectral features between the target and the background.
For L-band, the spectral vector N hyperspectral image RL×1, xi (i=1,2,…,N) is any one of the points, and the spectra are normalized by rearranging all the spectra of the hyperspectral image into a matrix (L×N): X = [x1, x2, …, xN] as shown in Equation 7.
The center pixels D (d1,d2,…,dn) of some a priori targets are selected from the hyperspectral image and the average of these pixels is calculated as shown in Equation 8.
Where, n denotes the number of a priori targets. The hyperspectral dataset is projected into the fractional domain after TV smoothing of the hyperspectral image and the known targets. The formula for FrFT is calculated as shown in Equation 9.
Where, L is the number of hyperspectral bands; n represents an integer; f and u represent indices; ϕ represents the rotation angle; and p represents the fractional order. Aϕ is calculated as shown in Equation 11.
Where, denotes the original spectral at p=0. When p=1, is the FT of the original spectral. is a complex number, and in order to utilize the phase information, the magnitude needs to be calculated as shown in Equation 12.
Where, is obtained by calculating size.
2.1.3 Constrained energy minimization model with fused spatial information
Let the observation dataset S={x1,x2,…,xN}, where xi=(xi1,xi2,…,xiL)T, 1 ≤ i ≤ N is a dataset pixel vector, N is the number of pixels, and L is the number of bands in the hyperspectral image. The CEM is a FIR linear filter which is represented by an l-dimensional vector that minimizes the energy of the output under certain conditions, which are constrained as shown in Equation 13.
Where, d is the target spectral vector of the dataset, w is the filter; and c is an arbitrary scalar, usually 1. Assuming that the input xi to the FIR filter produces an output of yi, yi is computed as shown in Equation 14.
Where, yi is the output of the linear filter and xi is the input pixel spectral vector. Therefore, the average output energy produced by the observation data set S is shown in Equations 15 and 16.
Where, Xl×l is the autocorrelation matrix of the observed data set S. Therefore, the design of the FIR linear filtering algorithm can be considered as a CEM problem as shown in Equation 17.
If the Lagrange multiplier method is used to solve the above problem, the FIR linear filter w is shown in Equation 18.
Then, the CEM is shown in Equation 19.
Substituting into observation dataset S, the observation dataset is thus replaced by , and thus the detection result D1= is obtained by the calculations in Equation 13 through Equation 19.
2.2 Detection model based on SNR fusion of CEM and low-rank sparse matrix decomposition
2.2.1 Low-rank sparse matrix solution based on fast approximation algorithm
In the field of hyperspectral imaging analysis, it is well known that anomalous pixels account for a very small proportion of the overall image, and the vast majority of pixels are background. The spectral vectors of the background pixels can be linearly characterized by their neighboring pixels due to their high interdependence, and these background pixels can reveal the regularity of their statistical distributions more accurately in a contracted, low-dimensional subspace. However, the target pixels in anomaly detection exhibit a high degree of unpredictability and randomness, presenting obvious sparse distribution characteristics, in contrast to the dense background pixels. On this basis, the spectra of the background pixels mostly originate from a mixture of several common substances, and thus can be considered to be drawn from several low-dimensional subspace samples, which leads to a low-rank distribution of the dimensionality of the background. Relying on this low-rank nature, hyperspectral target detection algorithms utilizing low-rank and sparse matrix decomposition techniques have been proposed. The core idea behind such methods lies in conceptualizing the hyperspectral data set as a high-dimensional information matrix and separating the background from the anomalous targets through matrix decomposition methods to achieve effective recognition of anomalies.
In hyperspectral anomaly detection, to realize the separation of anomalous and background components, the acquisition of effective anomalous components can be achieved by low-rank sparse representation and matrix decomposition strategies (Yu, 2023). The matrix decomposition method usually decomposes the hyperspectral data into three parts: background, anomaly and noise, and the model can be expressed as shown in Equation 20.
Where, D∈RB×N is the acquired hyperspectral data (B denotes the number of bands and N is the overall number of pixels), L is the low-rank background, S is the sparse target, and N is the interference noise. Applying constraints to the background and the anomalous targets yields as shown in Equation 21.
Where, is the Frobenius paradigm, is the matrix rank, is the matrix cardinality value, r is the upper limit of the degree of matrix low-rank, and k is the upper limit of the degree of matrix sparsity. The cardinality value k of S denotes the amount of sparsity and is often referred to as the l0 norm. The solution can be performed by alternating L and S, L and S are updated as shown in Equation 22.
Where, t is the time, from which the L and S values were obtained.
The raw hyperspectral image data cube (HSI) has spatial and spectral dimensions H × W × B, which can be rearranged into a two-dimensional matrix of size B × N, where B represents the number of spectral bands, H and W represent the height and width of the image scene, respectively, and N denotes the total number of pixels in the entire image scene. The spectral features of the neighboring image elements of the material in the HSI data are highly correlated, so each spectral vector can be approximated as a linear combination of several basis vectors. Background images are usually considered to have low-rank properties. On the other hand, due to the low spatial resolution of HSI, the anomalies of interest in the HSI data usually have low probability and represent only a small portion of the entire image scene, which indicates the sparse nature of the anomalies.
In recent years, experts and scholars have proposed many optimization methods for low-rank sparse models, mainly focusing on developing fast approximations and meaningful decompositions. Zhou and Tao (2011) proposed a fast approximation algorithm (Go Decomposition, GoDec) to solve the low-rank background component and sparse target component. In addition, the GoDec algorithm explores the low-rank sparse structure and can consider additive noise simultaneously. The BRP-based GoDec problem can be solved by minimizing the decomposition error under rank and sparsity constraints by writing Eq. (20) as X = B + S + N. Where, B denotes the low-rank background component, S denotes the sparse target component, and N denotes the noise, and the modeling problem of GoDec is specified as shown in Equation 23.
Where, r is the upper limit of the rank of B, which can be set according to the main background end elements, and k is the upper limit of the base of S, which is called the l0-paradigm of S. The optimization problem in Equation 23 can be transformed into solving the following two subproblems alternately until convergence as shown in Equations 24 and 25.
Low-order approximation theory is used to solve the subproblems in Equation 24, assuming as shown in Equation 26.
Where, A1∈RB×r and A2∈RN×r are random matrices. Where A1 can be obtained by the Matlab randn function which generates random matrices conforming to a standard normal distribution and A2 can be obtained by A2=Y1=XA1. The rank r approximation of X∈RB×N based on BRP is shown in Equation 27.
For the subproblems in Equation 25, St is updated by the item-by-item hard-thresholding method of X–Bt-1 as shown in Equation 28.
Where, PΩ(·) is the projection of the matrix onto the set Ω, and Ω is a nonzero subset of the first kN largest elements of |X–Bt-1|.
2.2.2 Low-rank sparse decomposition target detector based on mahalanobis distance
After solving for the low-rank and sparse components of the matrix using GoDec respectively, the low rank and sparse matrices are then separated using the Mahalanobis distance method, where the low-rank background matrix captures the global background information and the sparse matrix contains the anomaly information, thus separating the background from the anomaly. Therefore, the statistical features of the background can be obtained from the background matrix, and then the detection model can be created by applying the Mahalanobis distance difference using the statistical features. The detector can be represented as shown in Equation 29.
Where, μb is the mean of the input background data and Гb is the covariance matrix of the input background data. μb and Гb can be estimated from the recovered background component B = [B1, …,BN] as shown in Equations 30 and 31.
The characteristic decomposition of the background covariance matrix Гb is shown in Equation 32.
Where, is the eigenvector matrix, A=diag(λ1λ2,…,λB) is the eigenvalue matrix and . The inverse covariance matrix is shown in Equation 33.
Due to insufficient training samples, the inverse matrix of the background covariance matrix is usually rank-lossy, especially in localized methods, when there exists a certain eigenvalue that is too small and makes significantly higher. Therefore, the inverse background covariance matrix can be estimated from the first r largest eigenvalues of the background component vectors and their corresponding eigenvectors as shown in Equation 34.
In target detection, SNR is commonly used to measure the ratio between the intensity of the detected target and the intensity of the background noise, which is often used to describe the quality and clarity of the detection. The SNR of the CEM and the low-rank sparse matrix decomposition detection results are calculated separately, and then the feature vectors of the two are multiplied by their respective SNRs and then summed up to obtain the final detection results as shown in Equation 35.
Where, SNR1 is the D1 signal-to-noise ratio and SNR2 is the D2 signal-to-noise ratio. Table 1

Table 1. CEM method incorporating spatial spectral information combined with low-rank sparse matrix decomposition algorithm.
3 Hyperspectral datasets
3.1 Hyperspectral data set acquisition
3.1.1 Acquisition of experimental systems
The study area and experimental environment are as shown in Figure 2.
The data in this paper are constructed through UAV hyperspectral remote sensing experimental acquisition, and the experiment adopts the UAV hyperspectral image acquisition system of UAV + hyperspectral imager. The system consists of a UAV platform and an airborne hyperspectral imager, and the UAV platform adopts a multi-rotor UAV for hovering and route planning flight. The airborne hyperspectral imager is a dedicated airborne hyperspectral imager with a two-axis gimbal, which can realize two-axis anti-shaking stabilization to reduce the jitter of the screen when collecting data.
(1) Unmanned airborne platform. The UAV platform used for the experimental data collection in this project is DJI M300 RTK multi-rotor UAV, with a built-in RTK module that can realize centimeter-level positioning.
(2) Airborne hyperspectral imager. The hyperspectral imager used in this experiment is Cubert-X20P airborne hyperspectral imager, with a spectral range of 350nm~1000nm, covering visible and some near-infrared spectral bands, and the resolution of the hyperspectral image is 1886×1886pix. The microcomputer contains the control software program for the hyperspectral camera, and by connecting the Cubert-X20P airborne hyperspectral imager to the DJI M300 RTK UAV, the hyperspectral imager can be powered by the UAV power supply system.
3.1.2 Data acquisition experiments
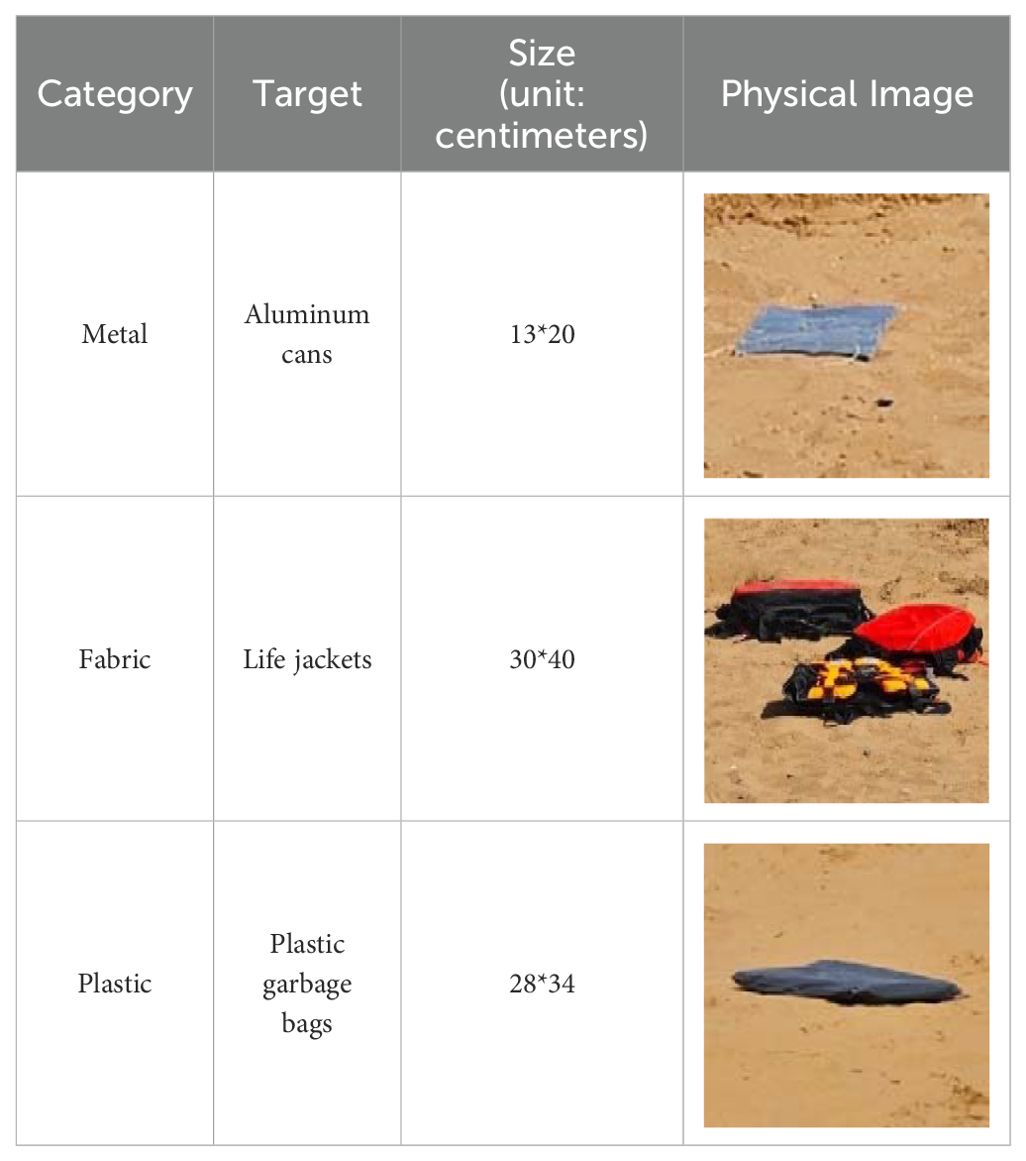
(1) Collecting target object statistics. After the previous research in the experimental area, it was found that the typical garbage in the environment of the experimental area contains materials such as metal, fabric and plastic. Accordingly, in the collection experiment of this study, three types of typical targets, namely metal, fabric, and plastic, were collected. The statistics of typical target types are presented in Table 2.
In order to create as realistic a hyperspectral database as possible of typical material objects in shoreline environments, the environments for this acquisition experiment were sandy beaches and water surfaces.
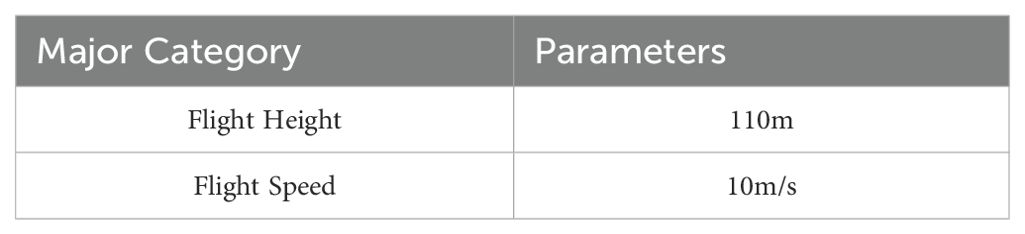
(2) Hyperspectral image data acquisition. Different types of material objects were collected using a UAV-mounted hyperspectral imager with a spectral range of 350 to 1000 nm and an image resolution of 1886 × 1886pixels. The datasets were collected under sunny weather conditions from 10:30 to 16:30, thus ensuring sufficient sunlight and the integrity of the hyperspectral imager’s acquisition bands (Cheng et al., 2022). In order to ensure the consistency of the quality of the datasets and reduce the operational error of each dataset during acquisition, the UAV routes were therefore first set up before acquisition, of which the main parameters of the routes are shown in Table 3.
3.2 Creating datasets
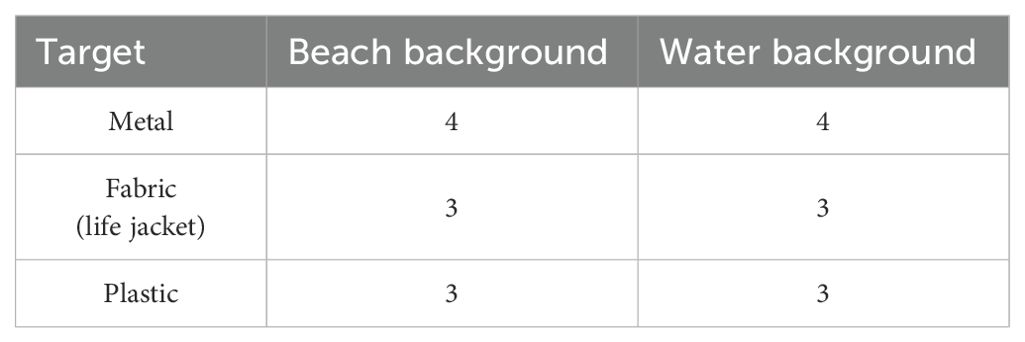
Through field acquisition experiments, the created datasets are typical material targets in a real shoreline environment, where the acquisition height is 110 meters. In order to eliminate the influence of invalid bands, the culled bands were 450-950nm, totaling 126 valid bands. The resolution of the hyperspectral images in the dataset is 150×150 pixels, and the spatial resolution (GSD) is 3.73cm. In order to ascertain the feasibility and robustness of the proposed algorithm, the datasets comprised two backgrounds and three material targets. Figure 3 illustrates the four datasets that were constructed. Figures 3A, B illustrate the hyperspectral images collected under the beach background, while Figures 3C, D) depict the hyperspectral images collected under the water background. In total, there are four datasets, each collected under a different background. The next experiments will be conducted on these four datasets. Table 4 presents the statistical data regarding the number of targets for the three materials in the two contexts.
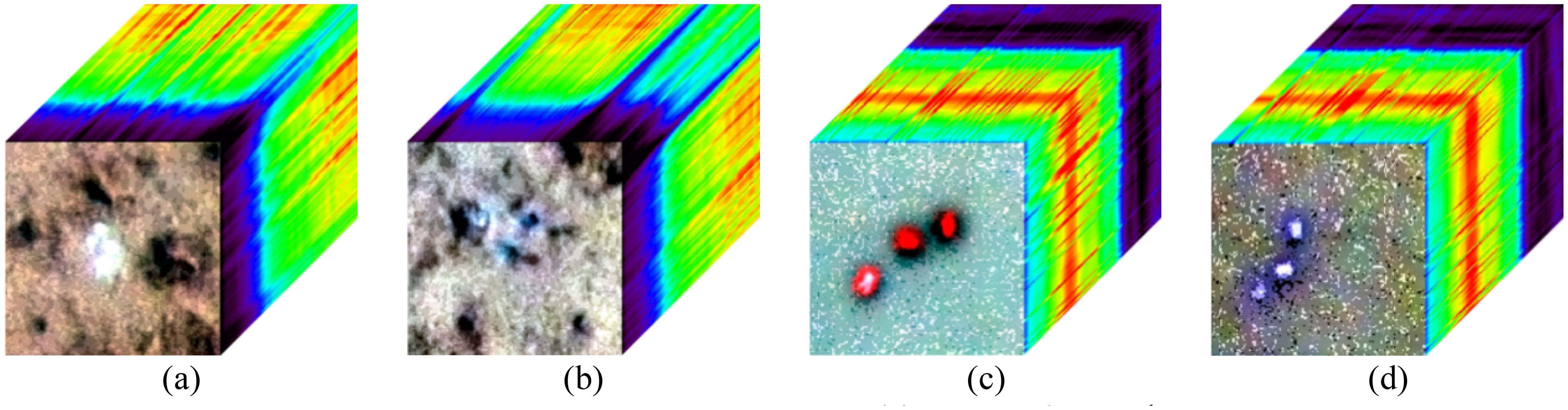
Figure 3. The pseudo-color 3D cube image of the four datasets. (A) Dataset-A: metal material for beach background. (B) Dataset-B: plastic material for beach background. (C) Dataset-C: fabric (life jacket) material for water background. (D) Dataset-D: plastic material for water background.
4 Experiments and results
In this section, the applicability of our proposed SFLRSD model for hyperspectral image target detection is illustrated by analyzing and discussing the experimental results. The algorithms and processes in this paper were implemented using MATLAB language in a PC that was powered by Windows 10 and Core i7-11800H CPU @2.30GHz by Intel with 32 GB RAM.
Secondly, five hyperspectral target detection methods are selected in this paper as comparative methods to verify the detection performance of the proposed method, including CEM (Harsanyi, 1993), ACE (Pieper et al., 2011), LSMAD (Zhang et al., 2015), LRSNCR (Yao et al., 2022), TD-IEEPST (Sun et al., 2024). All five comparison methods are set up in accordance with the parameters of the original text to optimize their performance.
4.1 Detection performance
The evaluation criteria for hyperspectral image (HSI) target detection results used in this section contain both qualitative and quantitative aspects. Qualitatively using the difference between the target brightness and background contrast, as a visual display of the detection results, generally the larger the target image element percentage, the brighter its corresponding image element the better the detection effect. Quantitative evaluation indexes of detection effect are receiver operating characteristic (ROC) curve, ROC area under the curve (AUC) value (Hou et al., 2021) and AUC values the signal to noise probability ratio (AUCSNPR) (Chang, 2020; Li Z. et al., 2023).
(1) ROC curve. The ROC curve is an index for quantifying target detection and evaluating the technical performance ofB hyperspectral images based on the real information about the location of anomalies in the hyperspectral images, which quantitatively analyzes the performance of the target detection method by comparing the detection value with the reference information of the anomalous target. Generally, in the ROC curve, the horizontal axis is the false alarm rate (FAR) and the vertical axis is the detection rate (PD). The false alarm rate (FAR) and detection rate (PD) are defined as shown in Equations 36 and 37.
Where, Nfd symbolizes the background pixel counts that are incorrectly judged as anomaly pixel counts and Na symbolizes the total counts of pixels in HSI. Ncd represents the detected anomaly pixel counts and Nt represents the total counts of anomaly target pixel in the HSI.
(2) AUC value. When the ROC curves of two target detection algorithms intersect or are closely adjacent to each other, it indicates that these algorithms have mutual advantages and disadvantages in terms of detection probability at different false alarm probability levels, which makes it difficult to directly discriminate the advantages and disadvantages of the algorithms by the ROC curves. In this case, in order to accurately compare the detection performance, the AUC (area under the ROC curve) value can be used as a comprehensive evaluation index. The AUC value represents the area of the region between the ROC curve and the false alarm probability axis, and the closer its value is to 1, the better the performance of the algorithm is, and in the ideal case, the AUC value reaches the maximum value of 1. The AUC is calculated as shown in Equation 38.
Where, FROC represents the ROC curve function.
(3) AUCSNPR value. A recent study (Chang, 2020) deeply analyzed the evaluation tools for hyperspectral target detection and proposed AUCSNPR to evaluate background suppressibility. AUCSNPR is calculated based on the 3-D ROC curve. In addition to PD and FAR, the 3-D ROC curve introduces the segmentation threshold τ as the third variable, which is sampled from the anomaly score map with max-min normalization. A 3-D ROC curve can generate three 2D ROC curves, which take (PD, FAR), (PD, τ), and (FAR, τ) as variables, respectively. Similar to Equation 38, the AUC value under the 2D ROC curve (PD, τ) is calculated as shown in Equation 39.
And the AUC value under the 2D ROC curve (FAR, τ) is calculated as shown in Equation 40.
Then, the AUCSNPR value is calculated as shown in Eq. (41).
A larger AUCSNPR value means a better background suppressibility of hyperspectral target detection methods.
4.2 Analysis of detection performance
In this section, the detection performance of the proposed hyperspectral target detection algorithms is analyzed through four sets of comparative experiments, starting with a visual detection result analysis, where the six methods are tested in each of the four different datasets (Dataset-A, Dataset-B, Dataset-C, and Dataset-D). Figures 4–7 show the detection plots of the different methods on each dataset, the brighter the pixel in the plot, it also means the higher the chance of being the target pixel.

Figure 4. Detection maps by Dataset-A. (A) Pseudo-color image for Dataset-A. (B) Ground truth image for Dataset-A. (C) CEM. (D) ACE. (E) LSMAD. (F) LRSNCR. (G) TD-IEEPST. (H) SFLRSD.

Figure 5. Detection maps by Dataset-B. (A) Pseudo-color image for Dataset-B. (B) Ground truth image for Dataset-B. (C) CEM. (D) ACE. (E) LSMAD. (F) LRSNCR. (G) TD-IEEPST. (H) SFLRSD.

Figure 6. Detection maps by Dataset-C. (A) Pseudo-color image for Dataset-C. (B) Ground truth image for Dataset-C. (C) CEM. (D) ACE. (E) LSMAD. (F) LRSNCR. (G) TD-IEEPST. (H) SFLRSD.

Figure 7. Detection maps by Dataset-D. (A) Pseudo-color image for Dataset-D. (B) Ground truth image for Dataset-D. (C) CEM. (D) ACE. (E) LSMAD. (F) LRSNCR. (G) TD-IEEPST. (H) SFLRSD.
The visualized detection results of the various algorithms on the four datasets are shown in Figures 4–7. Figure 4 illustrates the detection results for Dataset-A, where the ACE algorithm detects all the targets but its suppression of the background is not as good as that of the SFLRSD algorithm. The CEM algorithm also detects all the targets but again its suppression of the background is not as good as the SFLRSD algorithm. The TD-IEEPST algorithm also detected all targets, but it also had many false targets, and was the algorithm with the most misdetected targets among the comparison algorithms. Although the LSMAD and LRSNCR algorithms suppress the background well, they both detect only some of the targets, and are the algorithms with the most missed targets. Our SFLRSD algorithm not only detects all the targets but also has the most superior suppression of the background. Therefore, in the detection results of Dataset-A, our proposed SFLRSD algorithm has the best detection results. Figure 5 demonstrates the detection results of Dataset-B, in which the ACE and CEM algorithms can obviously detect two targets, but are not good for the third target, especially the third target of the CEM algorithm is almost mixed with the background. The TD-IEEPST, LSMAD and LRSNCR algorithms almost completely confuse the target with the background, and it is difficult to distinguish the target from the background, and these three algorithms have poor detection results. It can be seen that our SFLRSD algorithm is able to detect the three targets completely, and the detection effect is also good, and the suppression of the background is also the best. Figure 6 shows the detection results of Dataset-C. The ACE and CEM algorithms are only able to detect two targets, especially the CEM algorithm has more obvious miss detection. The TD-IEEPST algorithm is able to detect all targets obviously, but the suppression of the background is very poor and there are some false detections. The LSMAD and LRSNCR algorithms have good suppression of the background, but they both detect only some of the targets. Our SFLRSD algorithm not only detects all targets, but also suppresses the background well. Figure 7 shows the detection results for Dataset-D. The ACE, CEM and TD-IEEPST algorithms are able to detect all the targets, but the suppression of the background is poor, especially the TD-IEEPST algorithm detects a large amount of background as a target. Although LSMAD can suppress the background well, it only detects one target, and there is a serious leakage. The LRSNCR algorithm not only suffers from the problem of missed detection, but also has poor background suppression. It can be seen that our SFLRSD algorithm is able to detect all targets and also suppresses the background well, with the best detection effect. Therefore, by comparing the detection results on the four datasets, our proposed algorithm has the best detection results, which is not only able to detect all targets, but also able to suppress the background well.
Our algorithm achieves the best detection results because we first perform full variational regularization noise reduction in the spatial domain of the hyperspectral image to remove the noise due to equipment, environment, etc., and promote image smoothness. The spectral discreteness of the anomalous target from the background is then enhanced using fractional order Fourier transform. We then fused the results of target detection and anomaly detection using a signal-to-noise ratio-based approach, which fuses the advantages of both while removing the disadvantages of both, and is able to enhance the separation of the target from the background and improve the detection rate.
Therefore, by comparing the detection results of the SFLRSD algorithm for the four datasets, it can be concluded that the SFLRSD algorithm is more effective in detecting the water surface targets than the beach environment, which may be due to the presence of more materials of similar material in the beach environment generating a higher number of mixed image elements. Relatively less clutter exists in the water surface environment, but the stronger reflection of sunlight from the water surface also leads to a decrease in the detection effect.
Figure 8 shows the ROC curves for four datasets using different methods, where SFLRSD is the corresponding ROC curve of the proposed method. As shown in Figure 8A, the ROC curve of the proposed algorithm has a clear trend and is always at the top, wrapping around the other curves, and the PD value of the SFLRSD algorithm is larger than the other schemes at the beginning, and after that, the proposed algorithm still has a high probability of detection and a low FAR. As shown in Figure 8B, the SFLRSD algorithm has a smoother curve when the FAR is small and keeps wrapping the other curves at the top, and the PD value is much larger than the other algorithms at the same FAR. As shown in Figure 8C, LSMAD is at the top when the FAR is small, and then it is intertwined with SFLRSD and then covered by SFLRSD, after which the SFLRSD algorithm has been at the top wrapping the other curves. As shown in Figure 8D, when the FAR is small, SFLRSD has a large PD value, while the other algorithms have smaller PD values, and the SFLRSD curve has been at the top wrapping the other curves. The ROC curves of our method almost always wrap around the ROC curves of the other methods and cover them, with SFLRSD having a higher PD and lower FAR. Therefore, the proposed method performs much better than the other methods on the ROC curve.
Table 5 lists Table II lists the PD values of the six comparison algorithms when FAR is 0.1. The PD values of SFLRSD are 1.0000, 0.9960, 1.0000, and 1.0000 for the four datasets when FAR is 0.1, respectively. The optimal PD values of the remaining algorithms in the four different datasets are 0.9735, 0.9840, 0.8322, and 0.9615, respectively. These values are poor relative to the AUC values of SFLRSD. Table 6 lists Table II lists the FAR values of the six comparison algorithms when PD is 0.9. The FAR values of SFLRSD are 0.0023, 0.0123, 0.0048, and 0.0009 for the four datasets when PD is 0.9, respectively. The remaining algorithms have the smallest FARs of 0.0067, 0.0273, 0.0102, and 0.0202, respectively. These values are large relative to the FAR of SFLRSD. These results demonstrate the effectiveness of the proposed SFLRSD.
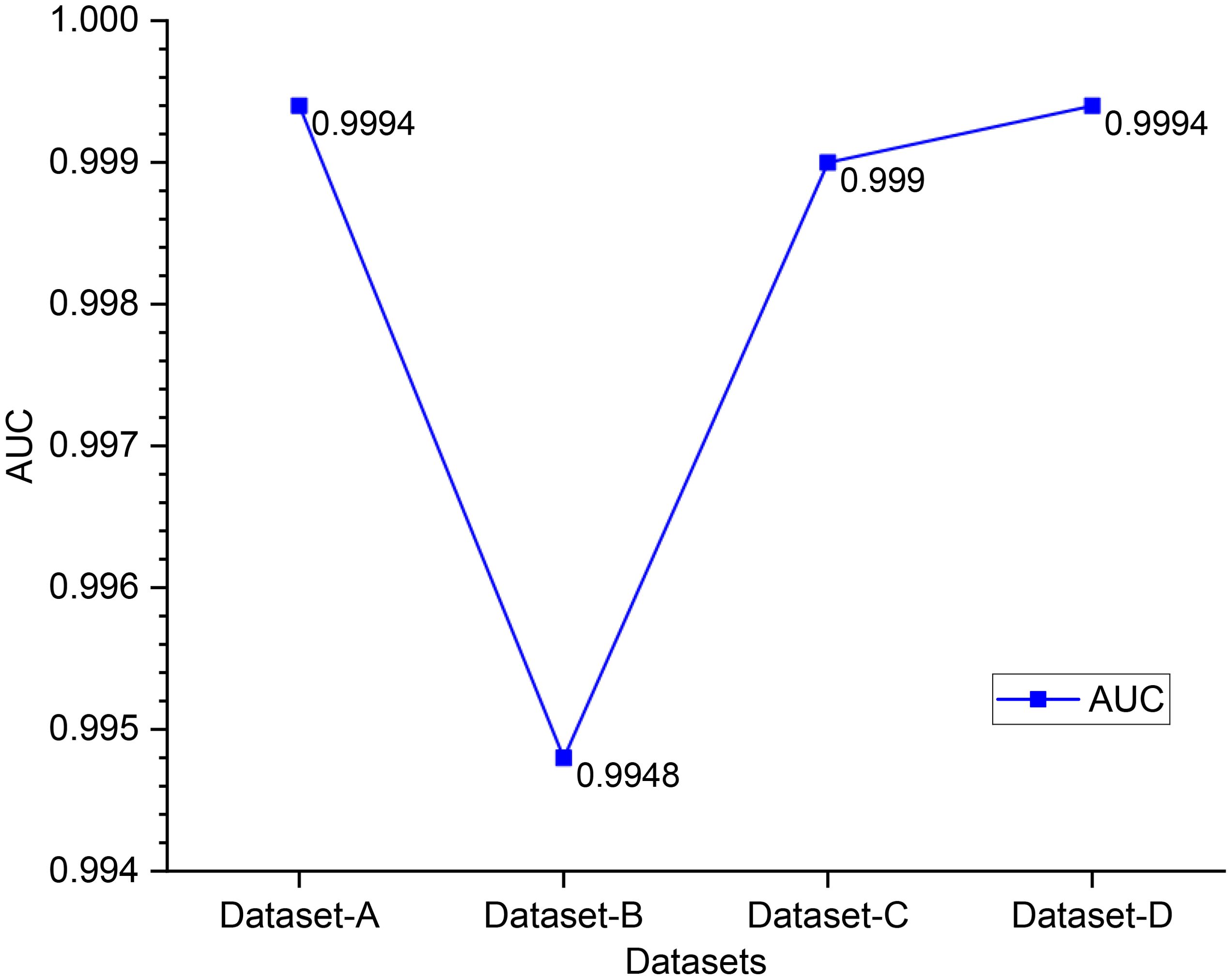
Table 7 lists the AUC values of the objective indices obtained for each dataset using different methods for anomaly detection, and SFLRSD in the table is the ROC value corresponding to the proposed method. The AUCs of the proposed SFLRSD on the four datasets are 0.9994, 0.9948, 0.9990, 0.9994, respectively. In addition, the second largest AUCs on the four datasets are 0.9977, 0.9881, 0.9969, 0.9868, which are not higher than that of our method.
Table 8 lists the AUCSNPR values of the six comparison algorithms. The AUCSNPR values of SFLRSD are 17.5761, 19.4009, 25.7517, and 20.5797 for these four datasets, respectively. The optimal AUCSNPR values of the remaining algorithms in the four different datasets are 13.8463, 13.8959, 17.8302, and 12.1180, respectively. These values are poor relative to the AUCSNPR values of SFLRSD.
The AUC values of our SFLRSD algorithm on the four datasets are presented in Figure 9. A comparison of these values reveals that the detection performance in the same background decreases as the size of the target increases. A comparison of the AUC values of the same target in different backgrounds indicates that the AUC value of the water background dataset is greater than that of the beach background. Consequently, it can be posited that the detection performance of the SFLRSD algorithm is contingent upon not only the size of the target, but also the complexity of the background in the dataset.
In order to further evaluate the algorithms suppression of background and separation of target, we added Box Plot to evaluate and explain the separability between target and background of the algorithm SFLRSD proposed in this paper and the comparison algorithm. In Box Plot, we use blue and red color to represent the background and target, respectively, and the height of the blue box and the red box indicates the suppression of the background and target by different algorithms (the values of the background and target). In hyperspectral target detection, the lower the blue box is, the more severely the background is suppressed. The distance between the red box and the blue box indicates how well the algorithm separates the background and the target, the larger the interval, the better the separation of the target, which means that the algorithm has a better separation. Figure 10 gives a box-and-line plot of the separation between the target and the background based on the detection values, which reveals the separability of the target and background pixels to measure the detection performance. As shown in Figure 10A, the SFLRSD algorithm is able to highlight the target while suppressing the background better and the distance between the red and blue rectangles is larger than the other comparative methods, which suggests that SFLRSD can separate the anomalies from the background better and more convincingly. As shown in the box line plots of the other three datasets in Figures 10B–D, it can be seen that the proposed SFLRSD can easily identify the desired target from the background.
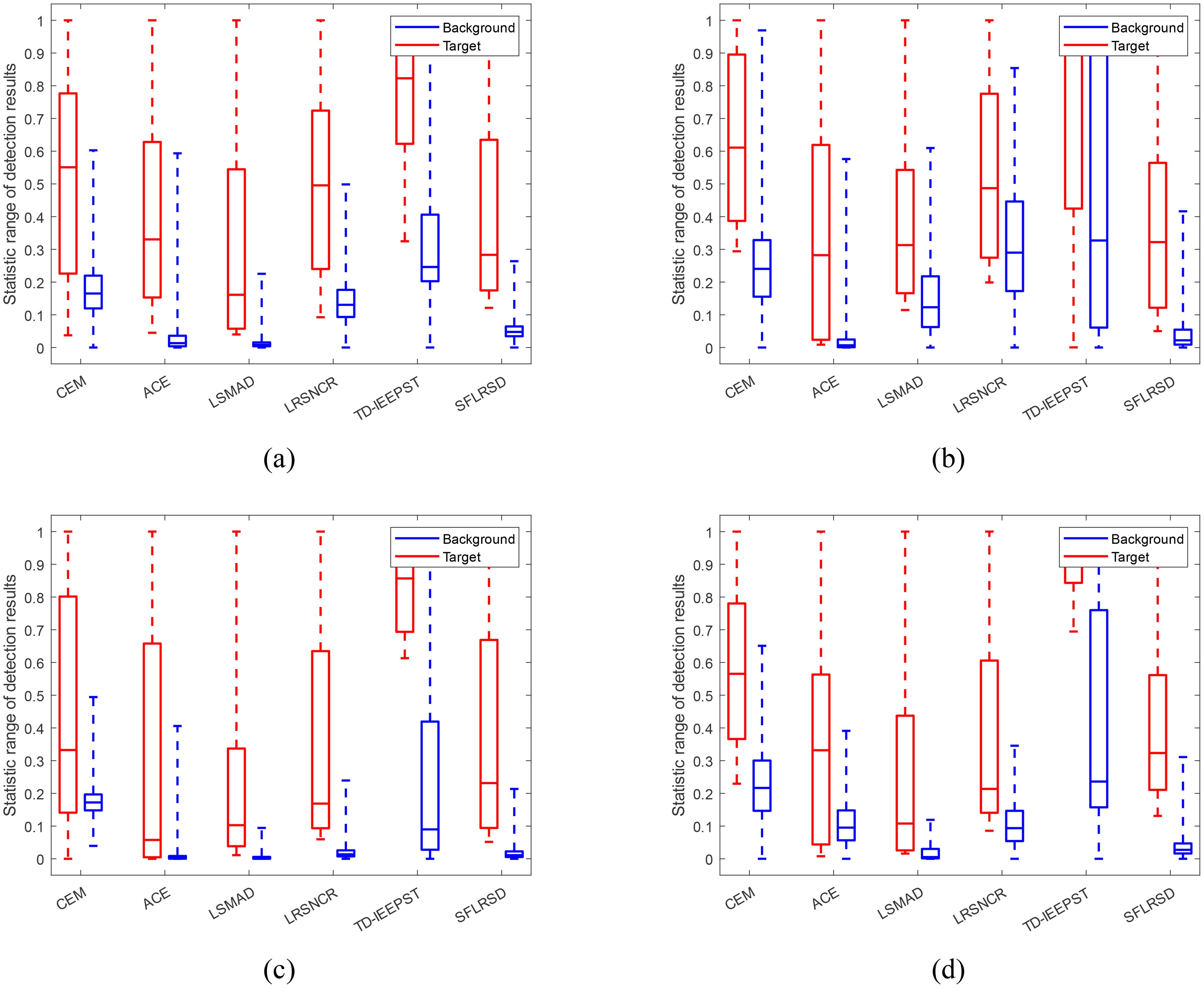
Figure 10. Statistical separability comparison for four datasets. (A) Dataset-A. (B) Dataset-B. (C) C Dataset-C. (D) Dataset-D.
In order to analyze the experimental results in more detail, we also used a three-dimensional receiver operating characteristic curve (3D ROC) analysis. Chang (2020) developed an effective 3D ROC analysis-based evaluation tool, which extends the traditional ROC analysis by including the threshold τ as an additional independent parameter to represent a 3D ROC curve as a function of three parameters, detection rate (PD), false alarm rate (PF), and τ. As a result, a 3D ROC curve can be generated by a triplet parameter vector specified by (PD, PF, τ) and it can also be used to two ROC curves of (PD, τ), and (PF, τ), and the ideal values of (PD, τ) and (PF, τ) are 1 and 0, respectively. Figure 11 shows the 3D ROC curves for four datasets using different methods, where SFLRSD is the corresponding 3D ROC curve of the proposed method. As can be seen from Figure 11, the SFLRSD algorithm performs better with high PD and low PF in all the datasets. This corresponds to the ROC curves, AUC values, and AUCSNPR values, which indicates that our algorithm has a high detection rate and a low false alarm rate.
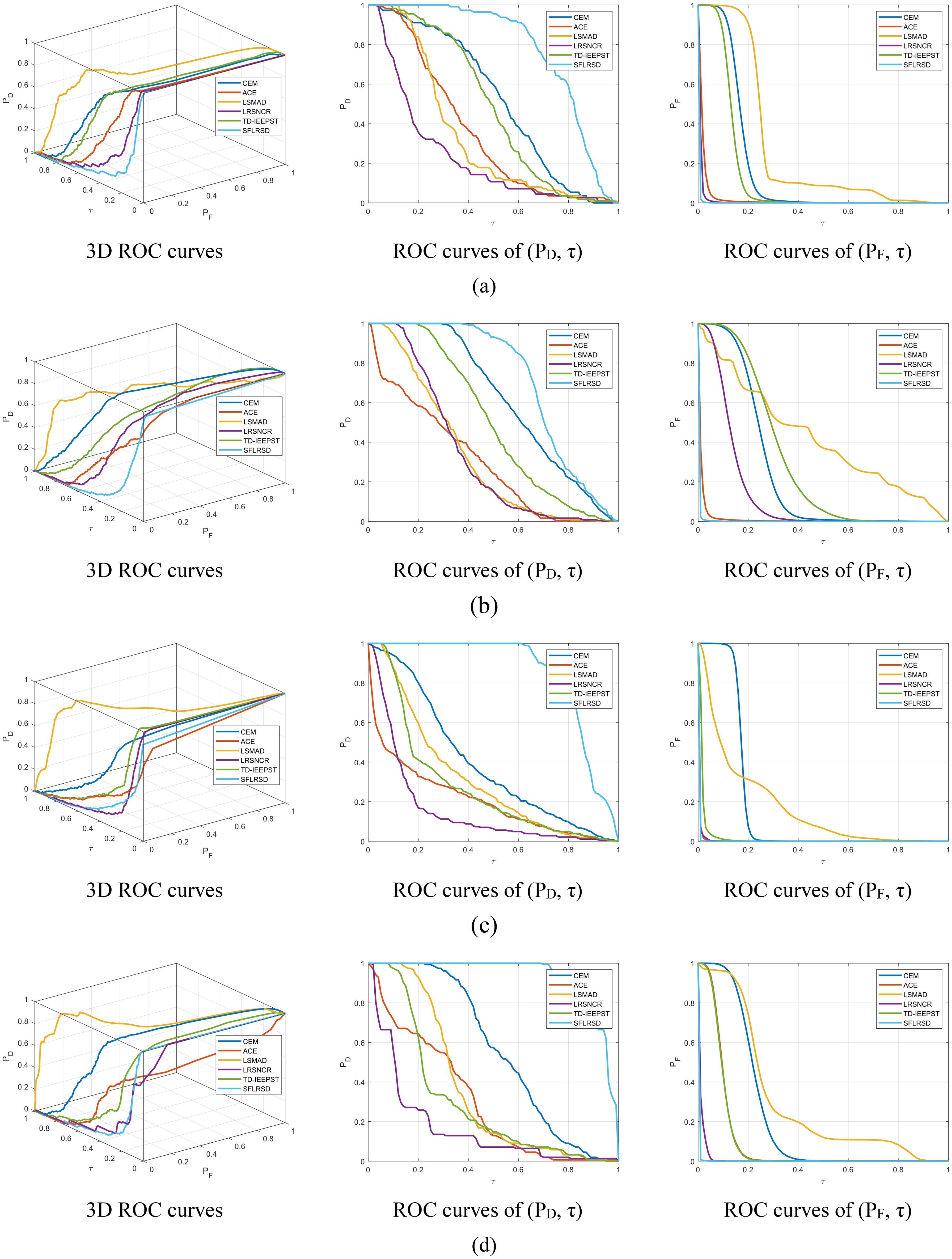
Figure 11. The 3D ROC for four datasets. (A) Dataset-A. (B) Dataset-B. (C) Dataset-C. (D) B Dataset-D.
We counted the running time of the six algorithms on the four datasets, as shown in Table 9. Table 9 shows that our SFLRSD algorithm runs for 18.7269s, 18.6818s, 19.0549s, and 18.9280s on the four datasets, and the comparison algorithms run for the longest time of 17.7754s, 16.7303s, 22.3435s, and 17.6235s, respectively. Our algorithm has the longest running time on most of the datasets, so it can be concluded that the computational efficiency of our algorithm is not the best compared to the comparison algorithms, and this is something we need to improve.
5 Conclusions
In this paper, we used aerial hyperspectral remote sensing to collect hyperspectral images of typical material targets in shoreline environments to create four hyperspectral datasets in beach and water environments. We propose to present a hyperspectral target detection algorithm based on target saliency fusion with low-rank sparse decomposition. The research content of this paper can not only provide some theoretical basis for the monitoring of coastal scattered garbage, but also provide a new method and new ideas. First, processing the spatial domain information and spectral domain information separately not only preserves the edge information of the image and promotes image segmentation smoothness, but also enhances the spectral distinctiveness of the anomalous target from the background. Then, a target detection model based on SNR fusion CEM with low-rank sparse decomposition is proposed, which can make full use of the spectral information as well as obtain excellent targets. In order to verify the robustness and feasibility of the proposed algorithm, comparison experiments are conducted on four datasets created by the waterside shoreline environment, and after analyzing the visual detection results, the proposed algorithm is able to detect the target on all datasets. After comparing the remaining five algorithms, the experimental results show that the proposed method has the highest AUC value and obvious background suppression and target extraction ability in all datasets. Meanwhile, there are still some shortcomings, which need to continue further exploration and research. The iterative optimization speed of our algorithm may be less dominant, so shortening the running time or speeding up the convergence speed is an important aspect worth improving. The number of targets collected in this paper is small, and the dataset needs to continue to accumulate and expand.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding authors.
Author contributions
SZ: Conceptualization, Data curation, Writing – original draft, Writing – review & editing. YL: Data curation, Formal analysis, Methodology, Writing – original draft, Writing – review & editing. XZ: Investigation, Methodology, Writing – original draft, Writing – review & editing. JW: Project administration, Resources, Writing – original draft. WL: Data curation, Writing – original draft. ML: Data curation, Writing – original draft.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was supported by the Scientific and Technological project in Henan Province (grant number 232102320258), the Open Fund Projects of Henan Key Laboratory of General Aviation Technology (grant number ZHKF-230211), the Hubei Key Laboratory of Intelligent Robot (grant number HBIR202308), and the Fund of Henan Province Collaborative Innovation Center of Aeronautics and Astronautics Electronic Information Technology.
Acknowledgments
We would like to express our sincere appreciation to the editor and reviewers who provided valuable comments to help improve this paper. We also appreciate the assistance provided by all researchers involved in this study. Additionally, we are grateful to the researchers who provided comparative methods.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bajjouk T., Jauzein C., Drumetz L., Dalla Mura M., Duval A., Dubois S. F. (2020). Hyperspectral and lidar: complementary tools to identify benthic features and assess the ecological status of sabellaria alveolata reefs. Front. Mar. Sci. 7. doi: 10.3389/fmars.2020.575218
Balsi M., Moroni M., Chiarabini V., Tanda G. (2021). High-resolution aerial detection of marine plastic litter by hyperspectral sensing. Remote Sens. 13, 1557. doi: 10.3390/rs13081557
Bioucas-Dias J. M., Plaza A., Camps-Valls G., Scheunders P., Nasrabadi N., Chanussot J. (2013). Hyperspectral remote sensing data analysis and future challenges. IEEE Geosci. Remote Sens. magazine 1, 6–36. doi: 10.1109/MGRS.2013.2244672
Bonifazi G., Palmieri R., Serranti S. (2015a). Hyperspectral imaging applied to end-of-life (EOL) concrete recycling. tm-Technisches Messen 82, 616–624. doi: 10.58895/ksp/1000044906-12
Bonifazi G., Palmieri R., Serranti S. (2015b). “Short wave infrared hyperspectral imaging for recovered post-consumer single and mixed polymers characterization,” in Image sensors and imaging systems 2015, vol. Vol. 9403. (San Francisco, California, USA: SPIE), 165–176. doi: 10.1117/12.2081362
Bruzzone L., Persello C. (2009). A novel approach to the selection of spatially invariant features for the classification of hyperspectral images with improved generalization capability. IEEE Trans. Geosci. Remote Sens. 47, 3180–3191. doi: 10.1109/TGRS.2009.2019636
Chang C. I. (2020). An effective evaluation tool for hyperspectral target detection: 3D receiver operating characteristic curve analysis. IEEE Trans. Geosci. Remote Sens. 59, 5131–5153. doi: 10.1109/TGRS.2020.3021671
Chen S., Zhang S., Zhao H., Chen Y. (2014). A new chirp scaling algorithm for highly squinted missile-borne SAR based on FrFT. IEEE J. Selected Topics Appl. Earth Observations Remote Sens. 8, 3977–3987. doi: 10.1109/JSTARS.2014.2360192
Chen X. L., Liu N. B., Wang G. Q., Guan J., He Y. (2014). Gaussian short-time fractional fourier transform based detection algorithm of target with micro-motion at sea. Acta Electronica Sin. 42, 971–977. doi: 10.3969/j.issn.0372-2112.2014.05.021
Cheng D., Chen L., Lv C., Guo L., Kou Q. (2022). Light-guided and cross-fusion U-Net for anti-illumination image super-resolution. IEEE Trans. Circuits Syst. Video Technol. 32, 8436–8449. doi: 10.1109/TCSVT.2022.3194169
Cheng T., Wang B. (2019). Graph and total variation regularized low-rank representation for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 58, 391–406. doi: 10.1109/TGRS.2019.2936609
Cheng T., Wang B. (2020). Total variation and sparsity regularized decomposition model with union dictionary for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 59, 1472–1486. doi: 10.1109/TGRS.2020.3004478
Dierssen H. M., Ackleson S. G., Joyce K. E., Hestir E. L., Castagna A., Lavender S., et al. (2021). Living up to the hype of hyperspectral aquatic remote sensing: science, resources and outlook. Front. Environ. Sci. 9. doi: 10.3389/fenvs.2021.649528
Du L., Wu Z., Xu Y., Liu W., Wei Z. (2016). “Kernel low-rank representation for hyperspectral image classification,” in 2016 IEEE international geoscience and remote sensing symposium (IGARSS) (Beijing, China: IEEE), 477–480. doi: 10.1109/IGARSS.2016.7729118
Freitas S., Silva H., Silva E. (2021). Remote hyperspectral imaging acquisition and characterization for marine litter detection. Remote Sens. 13, 2536. doi: 10.3390/rs13132536
Freitas S., Silva H., Silva E. (2022). Hyperspectral imaging zero-shot learning for remote marine litter detection and classification. Remote Sens. 14, 5516. doi: 10.3390/rs14215516
Gong X., Hou Z., Wan Y., Zhong Y., Zhang M., Lv K. (2024). Multispectral and SAR image fusion for multi-scale decomposition based on least squares optimization rolling guidance filtering. IEEE Trans. Geosci. Remote Sens. 62, 1–20. doi: 10.1109/TGRS.2024.3353868
He W., Zhang H., Zhang L., Shen H. (2015). Total-variation-regularized low-rank matrix factorization for hyperspectral image restoration. IEEE Trans. Geosci. Remote Sens. 54, 178–188. doi: 10.1109/TGRS.2015.2452812
Hou Z., Li W., Li L., Tao R., Du Q. (2021). Hyperspectral change detection based on multiple morphological profiles. IEEE Trans. Geosci. Remote Sens. 60, 1–12. doi: 10.1109/TGRS.2021.3090802
Hu S., Hou R., Ming L., Meifang S., Chen P. (2023). A hyperspectral image reconstruction algorithm based on RGB image using multi-scale atrous residual convolution network. Front. Mar. Sci. 9. doi: 10.3389/fmars.2022.1006452
Hu B., Serranti S., Fraunholcz N., Di Maio F., Bonifazi G. (2013). Recycling-oriented characterization of polyolefin packaging waste. Waste Manage. 33, 574–584. doi: 10.1016/j.wasman.2012.11.018
Huang F., Yu Y., Feng T. (2019). Hyperspectral remote sensing image change detection based on tensor and deep learning. J. Visual Communication Image Representation 58, 233–244. doi: 10.1016/j.jvcir.2018.11.004
Iordache M. D., Bioucas-Dias J. M., Plaza A. (2012). Total variation spatial regularization for sparse hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 50, 4484–4502. doi: 10.1109/TGRS.2012.2191590
Karaca A. C., Ertürk A., Güllü M. K., Elmas M., Ertürk S. (2013). “Automatic waste sorting using shortwave infrared hyperspectral imaging system,” in 2013 5th workshop on hyperspectral image and signal processing: evolution in remote sensing (WHISPERS) (Gainesville, FL, USA: IEEE), 1–4. doi: 10.1109/WHISPERS.2013.8080744
Kerekes J. P., Baum J. E. (2003). Hyperspectral imaging system modeling. Lincoln Lab. J. 14, 117–130. Available at: https://api.semanticscholar.org/CorpusID:12014588.
Li L., Li W., Du Q., Tao R. (2020). Low-rank and sparse decomposition with mixture of gaussian for hyperspectral anomaly detection. IEEE Trans. Cybernetics 51, 4363–4372. doi: 10.1109/TCYB.2020.2968750
Li L., Ma H., Jia Z. (2021). Change detection from SAR images based on convolutional neural networks guided by saliency enhancement. Remote Sens. 13, 3697. doi: 10.3390/rs13183697
Li L., Ma H., Jia Z. (2022). Multiscale geometric analysis fusion-based unsupervised change detection in remote sensing images via FLICM model. Entropy 24, 291. doi: 10.3390/e24020291
Li L., Ma H., Jia Z. (2023). Gamma correction-based automatic unsupervised change detection in SAR images via FLICM model. J. Indian Soc. Remote Sens. 51, 1077–1088. doi: 10.1007/s12524-023-01674-4
Li L., Ma H., Zhang X., Zhao X., Lv M., Jia Z. (2024). Synthetic aperture radar image change detection based on principal component analysis and two-level clustering. Remote Sens. 16, 1861. doi: 10.3390/rs16111861
Li Z., Wang Y., Xiao C., Ling Q., Lin Z., An W. (2023). You only train once: Learning a general anomaly enhancement network with random masks for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 61, 1–18. doi: 10.1109/TGRS.2023.3258067
Li Z. Z., Yang R. H., Dang F. X., Du P. J., Zhang X. F., Tan B. X., et al. (2012). “A review on the geological applications of hyperspectral remote sensing technology,” in 2012 4th workshop on hyperspectral image and signal processing: evolution in remote sensing (WHISPERS) (Shanghai, China: IEEE), 1–4. doi: 10.1109/whispers.2012.6874235
Liu Y., Gao G., Gu Y. (2016). Tensor matched subspace detector for hyperspectral target detection. IEEE Trans. Geosci. Remote Sens. 55, 1967–1974. doi: 10.1109/TGRS.2016.2632863
Liu S., Shan T., Tao R., Zhang Y. D., Zhang G., Zhang F., et al. (2014). Sparse discrete fractional fourier transform and its applications. IEEE Trans. Signal Process. 62, 6582–6595. doi: 10.1109/TSP.2014.2366719
Liu Y., Sun D., Hu X., Liu S., Gan F., Ge S. (2019). Observation capability and application prospect of the advanced hyperspectral imager. Aerospace Shanghai S2), 99–105. doi: 10.19328/j.cnki.1006-1630.2019.S.016
Luciani V., Bonifazi G., Rem P., Serranti S. (2015). Upgrading of PVC rich wastes by magnetic density separation and hyperspectral imaging quality control. Waste Manage. 45, 118–125. doi: 10.1016/j.wasman.2014.10.015
Ma G. X., Xue Y. Q., Li G. F. (2008). Satellite remote sensing for haze monitoring in Pearl River delta region. Sci. Technol. Rev. 26, 72–76. doi: 10.3321/j.issn:1000-7857.2008.16.016
Mace T. H. (2012). At-sea detection of marine debris: overview of technologies, processes, issues, and options. Mar. pollut. Bull. 65, 1–653doi: 10.1016/j.marpolbul.2011.08.042
Niu Y., Wang B. (2016). Hyperspectral anomaly detection based on low-rank representation and learned dictionary. Remote Sens. 8, 289. doi: 10.3390/rs8040289
Osher S., Burger M., Goldfarb D., Xu J., Yin W. (2005). An iterative regularization method for total variation-based image restoration. Multiscale Modeling Simulation 4, 460–489. doi: 10.1137/040605412
Pieper M. L., Manolakis D., Lockwood R., Cooley T., Armstrong P., Jacobson J. (2011). “Hyperspectral detection and discrimination using the ACE algorithm,” in Imaging spectrometry XVI, vol. Vol. 8158. (San Diego, California, USA: SPIE), 92–103. doi: 10.1117/12.893950
Rasti B., Chang Y., Dalsasso E., Denis L., Ghamisi P. (2021). Image restoration for remote sensing: Overview and toolbox. IEEE Geosci. Remote Sens. Magazine 10, 201–230. doi: 10.1109/MGRS.2021.3121761
Serranti S., Luciani V., Bonifazi G., Hu B., Rem P. C. (2015). An innovative recycling process to obtain pure polyethylene and polypropylene from household waste. Waste Manage. 35, 12–20. doi: 10.1016/j.wasman.2014.10.017
Serranti S., Palmieri R., Bonifazi G., Cózar A. (2018). Characterization of microplastic litter from oceans by an innovative approach based on hyperspectral imaging. Waste Manage. 76, 117–125. doi: 10.1016/j.wasman.2018.03.003
Sun F., Li X., Zhao Li, Yu S. (2022). Anomaly detection algorithm based on FrFT transform and total variation regularization. J. ZheJiang Univ. (Engineering Science) 56, 1276–1284. doi: 10.3785/j.issn.1008-973X.2022.07.002
Sun W., Liu C., Li J., Lai Y. M., Li W. (2014). Low-rank and sparse matrix decomposition-based anomaly detection for hyperspectral imagery. J. Appl. Remote Sens. 8, 083641–083641. doi: 10.1117/1.JRS.8.083641
Sun L., Wang Q., Chen Y., Zheng Y., Wu Z., Fu L., et al. (2023). CRNet: Channel-enhanced remodeling-based network for salient object detection in optical remote sensing images. IEEE Trans. Geosci. Remote Sens. 61, 1–14. doi: 10.1109/TGRS.2023.3305021
Sun X., Zhuang L., Gao L., Gao H., Sun X., Zhang B. (2024). A point-set topology-based information entropy estimation method for hyperspectral target detection. IEEE Trans. Geosci. Remote Sens. 62, 1–17. doi: 10.1109/TGRS.2024.3400321
Tao R., Zhao X., Li W., Li H. C., Du Q. (2019). Hyperspectral anomaly detection by fractional fourier entropy. IEEE J. Selected Topics Appl. Earth Observations Remote Sens. 12, 4920–4929. doi: 10.1109/JSTARS.2019.2940278
Tong Q. X., Zhang B., Zhang L. F. (2016). Current progress of hyperspectral remote sensing in China. J. Remote Sens. 20, 689–707. doi: 10.11834/JRS.20166264
Veenstra T. S., Churnside J. H. (2012). Airborne sensors for detecting large marine debris at sea. Mar. pollut. Bull. 65, 63–68. doi: 10.1016/j.marpolbul.2010.11.018
Wang M., Hong D., Zhang B., Ren L., Yao J., Chanussot J. (2023). Learning double subspace representation for joint hyperspectral anomaly detection and noise removal. IEEE Trans. Geosci. Remote Sens. 61, 1–17. doi: 10.1109/TGRS.2023.3261964
Xiao Y., Yuan Q., Jiang K., He J., Wang Y., Zhang L. (2023). From degrade to upgrade: Learning a self-supervised degradation guided adaptive network for blind remote sensing image super-resolution. Inf. Fusion 96, 297–311. doi: 10.1016/j.inffus.2023.03.021
Xie Z., Duan P., Liu W., Kang X., Wei X., Li S. (2023). Feature consistency-based prototype network for open-set hyperspectral image classification. IEEE Trans. Neural Networks Learn. Syst. 35 (7), 9286–9296. doi: 10.1109/TNNLS.2022.3232225
Xu H., Li Q., Chen J. (2022). Highlight removal from a single grayscale image using attentive GAN. Appl. Artif. Intell. 36, 1988441. doi: 10.1080/08839514.2021.1988441
Xu Y., Wu Z., Li J., Plaza A., Wei Z. (2015). Anomaly detection in hyperspectral images based on low-rank and sparse representation. IEEE Trans. Geosci. Remote Sens. 54, 1990–2000. doi: 10.1109/TGRS.2015.2493201
Yang J., Hu Y., Zhang J., Ma Y., Li Z., Jiang Z. (2023). Identification of marine oil spill pollution using hyperspectral combined with thermal infrared remote sensing. Front. Mar. Sci. 10. doi: 10.3389/fmars.2023.1135356
Yao W., Li L., Ni H., Li W., Tao R. (2022). Hyperspectral anomaly detection based on improved RPCA with non-convex regularization. Remote Sens. 14, 1343. doi: 10.3390/rs14061343
Yin L., Wang L., Li T., Lu S., Tian J., Yin Z., et al. (2023a). U-Net-LSTM: time series-enhanced lake boundary prediction model. Land 12, 1859. doi: 10.3390/land12101859
Yin L., Wang L., Li T., Lu S., Yin Z., Liu X., et al. (2023b). U-Net-STN: A novel end-to-end lake boundary prediction model. Land 12, 1602. doi: 10.3390/land12081602
Yu S. (2023). Research on hyperspectral anomaly detection methods based on intrinsic component representation. ZheJiang Univ. 7, 1–109. doi: 10.27461/d.cnki.gzjdx.2023.000842
Yuan Q., Zhang L., Shen H. (2012). Hyperspectral image denoising employing a spectral-spatial adaptive total variation model. IEEE Trans. Geosci. Remote Sens. 50, 3660–3677. doi: 10.1109/TGRS.2012.2185054
Yuan Y., Zheng X., Lu X. (2015). Spectral-spatial kernel regularized for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 53, 3815–3832. doi: 10.1109/TGRS.2014.2385082
Zeng D., Zhang S., Chen F., Wang Y. (2019). Multi-scale CNN based garbage detection of airborne hyperspectral data. IEEE Access 7, 104514–104527. doi: 10.1109/ACCESS.2019.2932117
Zhang X. (2023). River ecological protection and restoration using multi-source remote sensing data. Mobile Networks Appl. 28, 1–12. doi: 10.1007/s11036-023-02169-9
Zhang Y., Du B., Zhang L., Wang S. (2015). A low-rank and sparse matrix decomposition-based mahalanobis distance method for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 54, 1376–1389. doi: 10.1109/TGRS.2015.2479299
Zhang Q., Wang H., Plemmons R. J., Pauca V. P. L. (2008). Tensor methods for hyperspectral data analysis: a space object material identification study. JOSA A 25, 3001–3012. doi: 10.1364/JOSAA.25.003001
Zhang Q., Yuan Q., Li J., Wang Y., Sun F., Zhang L. (2021). Generating seamless global daily AMSR2 soil moisture (SGD-SM) long-term products for the years 2013-2019. Earth System Sci. Data 13, 1385–1401. doi: 10.5194/essd-13-1385-2021
Zhang Q., Yuan Q., Li J., Yang Z., Ma X. (2018). Learning a dilated residual network for SAR image despeckling. Remote Sens. 10, 196. doi: 10.3390/rs10020196
Zhao X., Hou Z., Wu X., Li W., Ma P., Tao R. (2021). Hyperspectral target detection based on transform domain adaptive constrained energy minimization. Int. J. Appl. Earth Observation Geoinformation 103, 102461. doi: 10.1016/j.jag.2021.102461
Zhao C., Li C., Feng S., Jia X. (2021). Enhanced total variation regularized representation model with endmember background dictionary for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 60, 1–12. doi: 10.1109/TGRS.2021.3128183
Zhao X., Li W., Zhang M., Tao R., Ma P. (2020). Adaptive iterated shrinkage thresholding-based lp-norm sparse representation for hyperspectral imagery target detection. Remote Sens. 12, 3991. doi: 10.3390/rs12233991
Zhao X., Liu K., Gao K., Li W. (2023a). Hyperspectral time-series target detection based on spectral perception and spatial-temporal tensor decomposition. IEEE Trans. Geosci. Remote Sens. 61, 1–12. doi: 10.1109/TGRS.2023.3307071
Zhao C., Zhang L., Cheng B. (2019). A local Mahalanobis-distance method based on tensor decomposition for hyperspectral anomaly detection. Geocarto Int. 34, 490–503. doi: 10.1080/10106049.2017.1408701
Zhao X., Zhang M., Li W., Gao K., Tao R. (2023b). A sparse representation and cauchy distance combination graph for hyperspectral target detection. Remote Sens. Lett. 14, 1218–1226. doi: 10.1080/2150704X.2023.2282399
Zhao X., Zhao W., C. and Tao R. (2022). “Hyperspectral target detection based on weighted cauchy distance graph and local adaptive collaborative representation,” in IEEE transactions on geoscience and remote sensing. IEEE: IEEE Transactions on Geoscience and Remote Sensing, vol. 60, 1–13. doi: 10.1109/TGRS.2022.3169171
Zhong Y., Wang X., Wang S., Zhang L. (2021). Advances in spaceborne hyperspectral remote sensing in China. Geo-spatial Inf. Sci. 24, 95–120. doi: 10.1080/10095020.2020.1860653
Zhou T., Tao D. (2011). “Godec: Randomized low-rank & sparse matrix decomposition in noisy case,” in Proceedings of the 28th International Conference on Machine Learning. Bellevue, Washington, USA: International Conference on Machine Learning. Available at: http://hdl.handle.net/10453/19145.
Zhou G., Xu J., Hu H., Liu Z., Zhang H., Xu C., et al. (2023a). Off-axis four-reflection optical structure for lightweight single-band bathymetric LiDAR. IEEE Trans. Geosci. Remote Sens. 61, 1–17. doi: 10.1109/TGRS.2023.3298531
Keywords: marine ecology, remote sensing, target detection, hyperspectral imagery, spatial fusion, low-rank sparsity
Citation: Zhao S, Lv Y, Zhao X, Wang J, Li W and Lv M (2024) Coastline target detection based on UAV hyperspectral remote sensing images. Front. Mar. Sci. 11:1452737. doi: 10.3389/fmars.2024.1452737
Received: 21 June 2024; Accepted: 06 September 2024;
Published: 02 October 2024.
Edited by:
Fengqin Yan, Institute of Geography Science and Natural Resources (CAS), ChinaReviewed by:
Jiangtao Peng, Hubei University, ChinaLi Hengjian, University of Jinan, China
Songyi Xiao, Chinese Academy of Sciences (CAS), China
Minghua Wang, Chinese Academy of Sciences (CAS), China
Muhammad Yasir, China University of Petroleum, Qingdao, China
Copyright © 2024 Zhao, Lv, Zhao, Wang, Li and Lv. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yali Lv, OTA2MDkzNTkwQHFxLmNvbQ==; Xiaobin Zhao, eGlhb2JpbnpoYW9AYml0LmVkdS5jbg==; Jiayao Wang, d3JvbmdwdUAxNjMuY29t
 Song Zhao
Song Zhao Yali Lv
Yali Lv Xiaobin Zhao
Xiaobin Zhao Jiayao Wang1,2*
Jiayao Wang1,2* Wei Li
Wei Li Ming Lv
Ming Lv