Design and experiment of cone disk centrifugal shellfish seeding device

This paper designed a centrifugal shellfish seeding device with a conical disc structure to improve the seeding efficiency and uniformity of the centrifugal shellfish seeding device. The dynamic model of the shellfish seedling moving on the conical disk is established, and the main parameters affecting the shellfish seedling’s movement characteristics are determined as the cone angle of the impeller, the speed of the impeller, and the offset angle of the blade. Using the EDEM software and the shellfish seedlings blanking rate as the influencing factors, a single factor simulation test was performed. The research found that the variation trend of shellfish seedlings distribution in a single statistical area gradually decreased along the horizontal direction of both sides, with the origin being the center of the seedling sowing device. Test orthogonal rotation simulations using the variation coefficient of seedlings distribution uniformity and the effective job width as evaluation indicators. Use Design Expert software to optimize the structure of the seedling sowing device based on the test results, and determine the optimal structure with the maximum width and the minimum variation coefficient as constraints: the impeller cone angle is 7.72°, and the blade offset angle is -0.9°. Use the above-mentioned seeding device for simulation and actual seeding testing. The simulation results show that when the impeller speed is 750r/min and the blanking rate is 0.65kg/s, the variation coefficient of seedlings distribution uniformity and the effective job width are 12.84% and 24.98m, respectively, while the actual test results are 13.77% and 23.25m, respectively. The object of the seeding performance test was commonly used size shellfish seedlings of the Philippines clam. The results showed that the impeller speed, blanking rate, quadratic term of shellfish seedling size, quadratic term of blanking rate, and interactive term of impeller speed and blanking rate had significant effects on the variation coefficient of the distribution uniformity of shellfish seedlings (P<0.01). Shellfish seedling size, impeller speed, and interactive term of impeller speed and blanking rate all had a significant impact on job width (P<0.01). The results of this study provide a reference for the mechanized design of shellfish seeding.

1 Introduction

Shellfish are the biological species with the highest proportion of marine aquaculture production in China, living in shallow seas and intertidal tidal mudflats containing sediment, and are cultivated on a large scale by fishermen due to their high edible and economic value (Fishery Administration Bureau of Ministry of Agriculture and Rural Affairs, 2021). However, due to the unique working conditions, seedlings are still primarily sown manually at this stage (National Fisheries Technology Extension Station, 2008; Yuan et al., 2014), posing issues such as high labor intensity, low operational efficiency, and a high crushing rate of shellfish seedlings. The traditional artificial seeding method is no longer capable of meeting the production requirements of large-scale shellfish farming. The use of mechanized seedling sowing devices can significantly improve seedling sowing efficiency, reduce shellfish damage, and lower labor costs (Liu et al., 2014; Liu et al., 2020).

Currently, mechanical seeding methods include grooved wheel type, drag type, air suction type, and so on (Keith et al., 2000; Yuan et al., 2018; Li et al., 2019). These methods, however, cannot meet the actual needs of a shellfish seeding operation. In comparison to the preceding scheme, the centrifugal seeding device has the advantages of a simple structure, a wide operating range, and high operational efficiency. The specific centrifugal seeding implementation scheme can refer to the operation mode of centrifugal fertilization and seeding in agriculture (Lv et al., 2016; Liu et al., 2017; Yang et al., 2019). In terms of centrifugal fertilization, Dintwa et al. (2004) established the particle flow model of centrifugal fertilizer applicator, analyzed the movement of particles on the rotating disk, deduced the motion equation of particles on the centrifugal flat disk and cone disk, and provided a theoretical basis for centrifugal fertilizer applicator design optimization. Coetzee et al (Coetzee and Lombard, 2011). used discrete element modeling to investigate the effect of disc speed, blanking position, blanking rate, and blade angle on fertilization results, and they found that discrete element modeling simulation can accurately predict the actual operation situation. Artur (2015) investigated the effect of disc speed, fertilizer feed position, and blade angle on fertilizer spatial distribution. It was demonstrated that changing the working parameters can influence the distribution results in order to adapt to different work requirements. In China, Yongguang Hu et al. (2016) designed a tea garden fertilizer spreader and investigated the effects of the fertilizer spreader’s walking speed, number of centrifugal disc blades, and blade offset angle on the fertilizer spreader’s operating performance during the fertilization process. Yinyan Shi et al. (2018) created a surface variable fertilizer spreader with a centrifugal uniform fertilizer cover and investigated the effects of fertilizer discharge flow, disc speed, and travel speed on the spreader’s performance. Guozhong Zhang et al. (2021) created a lotus root field centrifugal side-throwing fertilizer spreader. By developing a model, the main influencing factors were identified as fertilizer spreader rotation speed, blade inclination Angle, and blade deflection Angle, and the effects of fertilizer spreader rotation speed, blade inclination Angle, blade deflection Angle, and fertilizer feeding rate on the working performance of the fertilizer spreader were investigated.

In the research of shellfish bottom seeding device, Frederick et al. (1977) developed a centrifugal oyster seeding device in the research of shellfish bottom seeding device, which transported oyster seedlings from the cabin to the centrifugal plate at the stern of the ship via the conveyor belt and then spread them by the centrifugal plate. Keith et al. (2000) created an air suction bottom sowing clam pulling seedling device that can be moved on the seabed by divers or traction devices, and the seedlings can be spread from the silo to the seabed via suction. In China, Wei Huang et al. (2022) created a centrifugal beach shellfish seeding device. The number of blades, centrifugal disk speed, and traveling speed were found to be the factors influencing the variation coefficient of distribution of shellfish seedlings through simulation analysis and beach test verification. Gang Mu et al. (2019) created a beachside shellfish seeding machine that could seed shellfish seedlings at a distance and quantitatively based on the variety, size, and geology of the beachside, effectively reducing seedling injury, increasing seedling survival, and greatly improving seeding efficiency. Zhe Li et al. (2019) invented a suspension type seedling release device that can prevent seedlings from being carried by ocean currents to sea areas unsuitable for shellfish seedling growth, effectively improve shellfish seedling survival rates, and avoid a large number of shellfish seedlings concentrated in a specific location, which is conducive to the spread and reproduction of shellfish seedlings. Jian Liang et al. (2021) invented a portable wind-swept shellfish seeding machine that ejects seedlings from the seeding port via the air flow generated by the fan, achieving automatic seedling seeding and addressing issues such as low efficiency, high labor intensity, high cost, and uneven seeding of shellfish in tidal flats. Chunting Yuan et al. (2018) invented a bottom-seeding device for benthic shellfish seedlings in shallow sea, addressing the issue of seedlings being washed away from the set area due to the influence of waves, tides, and other factors.

The current shellfish bottom sowing device, on the other hand, has a small operation area and poor seeding uniformity, making it unsuitable for large-scale shellfish breeding on the beach. In order to address the existing issues, this paper designed a cone disk centrifugal shellfish seeding device for use on the beach. The main factors influencing the movement of shellfish seedlings were determined by analyzing the movement of shellfish particles. EDEM discrete element software was used to simulate the seeding process. The structural parameters of the seeding device were optimized based on simulation results, and the operating parameters of the seeding device were optimized based on actual seeding test results, with the goal of providing a reference for the design of mechanized shellfish seeding devices.

2 Structure and working principle of centrifugal seeding device

Figure 1 depicts the centrifugal seeding device developed in this paper, which consists primarily of a hopper, blanking device, conical seeding tray, frame, and other components. 1. Hopper and blanking device 2. Switch and speed regulating mechanism 3. Guard board 4. Shelter plate 5. Hook 6. Generator box 7. Electric motor 8. Conical seeding tray 9. Blanking port 10. Slide rail 11. Belt pulley 12. Frame

FIGURE 1

Figure 1 Centrifugal seeding device.

The shellfish seedlings fall to the surface of the conical seeding tray through the blanking device due to gravity in the hopper. The shellfish seedlings are subjected to centrifugal force and Coriolis force while rotating with the blade, gradually move to the blade’s edge, and are thrown out of the conical impeller disk at a certain speed before being sown in the operation area.

3 Design of key components

3.1 Design of hopper and blanking device

Figure 2 depicts the design of the hopper. The upper half of the hopper is a cuboid, whereas the lower half is an asymmetric construction. To avoid shellfish seedling arching in the hopper, the angle of repose on one side is greater than the angle of repose of the shellfish seedling accumulation, the upper section is 1500mm long, 1100mm wide, and 300mm high, the lower half is 400mm high, and the hopper volume is 833L. The interior is lined with 4mm thick EVA material, which acts as a cushion when the shellfish seedlings fall and keeps them from breaking. Figure 2 depicts the blanking device, to adjust the blanking rate of shellfish seedlings, the opening between the blanking baffle and the chute is controlled by a motor and gear transmission mechanism. The blanking opening is 20cm wide and designed as a square, use formula (1) to calculate the flow rate of the blanking port ω relation with blanking opening width D₀ and seedling size D (Yi,; Qin et al., 1966; Chen et al., 2019).

FIGURE 2

Figure 2 Hopper and blanking control device.

$\begin{array}{ll}\omega =c{\rho }_B{(D_0-KD)}^{2.5}& (1)\end{array}$

Wherein, ρ_B is the density of shellfish seedlings (non bulk density), c and K are dimensionless parameters, their values depend on the shape and friction of the shellfish seedlings, generally 0.5<c<0.7, 1.2<K<3.

When c is 0.6 and K is 2, ω=5.56kg/s=20016kg/h, that is, when the width of the blanking opening is 20cm, 20t can be sown per hour when the blanking opening is fully open.

3.2 Design of conical seeding mechanism

The conical seeding tray, as shown in Figure 3, is primarily made up of a conical impeller disc with a diameter of 600mm and a blade with a length of 310mm. It is 3D printed with resin and internally covered with 4mm EVA material. The shellfish will rotate with the conical impeller’s blade as a result of centrifugal force as it rotates, and when the blade reaches the edge of the impeller plate, it will be thrown from the plate. It will eventually spread to the working area after a certain amount of time.

FIGURE 3

Figure 3 Conical seeding mechanism.

The impeller disc has a conical structure to increase the operation efficiency and job width, a protection cover is added inside the conical disc to prevent shellfish from falling to the bottom of the cone plate and causing blockage. To gather the shellfish seedlings, the upper end of the blade is bent in the direction of rotation. The blade offset angle can be adjusted to change the sowing area and range.

4 Motion analysis of shellfish seedling on impeller disk

Establish a radius of R and a cone angle of α_d, as shown in Figure 4. Straight blades extend directly to the edge of the impeller disk and are offset from the pitch radius r_p. Shellfish seedlings are fed into the impeller disk of the seeding device through the blanking port at the bottom of the hopper. The blanking port’s inner diameter is r_i, its outer diameter is r_o, and the range angle is Φ. The blanking port’s initial angle is Ψ. The impeller disk is installed on the traction device, the traction device’s speed is v_s, and the disk’s angular velocity is ω.

FIGURE 4

Figure 4 Schematic diagram of conical impeller disk. (A) Top view (B) Cross section C−C.

Figure 5 shows the trajectory of the shellfish seedlings randomly falling on a certain position on the impeller disk through the initial angle (Ψ<Φ_L<Ψ+Φ) and radius (r_i<r_L<r_o) to define the initial position of the seedlings. Where r_L is the radius from the center of the disc when the seedlings fall, θ_L is the angle at which the seedlings fall, θ_p is the angle of the shellfish when the impeller disk moves to different positions, Ψ is the initial angle of the blanking port, Φ is the angle of the blanking port, r_i is the inner diameter of the blanking port, r_o is the outer diameter of the blanking port, R is the radius of the disc, and v_tot is the exit velocity of the shellfish seedling at the edge of the disc. The particles of shellfish seedlings are placed in a specific position (R, θ_p) disengage the bladed disc.

FIGURE 5

Figure 5 Top view of the trajectory of shells on the impeller disk.

Figure 6 illustrates the velocity analysis of a shellfish seedling moving on an impeller disk. Where α_tot is the angle between the horizontal plane and the exit direction of the seedling; β_tot is the angle between the driving direction and the ejection direction of the seedling on the horizontal plane; v_s is the motion speed relative to the ground; v_v is the velocity component of v_tot in the vertical direction; v_o is the exit velocity of shellfish seedling under the static state of the bladed disc (v_s=0); v_h is the horizontal component of the exit velocity of the shellfish seedling under the static state of the impeller disk; v_toth is the total horizontal component of the exit velocity of the shellfish seedling under the unsteady state of the impeller disk; ω is the angular velocity when the disc rotates; θ_L is the angle of the initial position of the shellfish seedling on the impeller disk relative to the driving direction; θ_p is the angle of the seedling position relative to the initial position; α_o is the included angle between the vertical line of the particle outlet direction and the ground (horizontal plane) under the stable state of the impeller disk; α_tot is the total vertical angle of the exit direction of the shellfish seedling relative to the ground under the unsteady state of the impeller disk; β_o is the horizontal outlet angle of the shellfish seedling under the stable state of the impeller disk; β_tot is the total horizontal exit angle of the shellfish seedling under the unstable state.

FIGURE 6

Figure 6 Speed analysis of shellfish on the impeller disc.

The rebound between the blade and the shellfish seedling is not taken into account in the process of establishing the motion equation, assuming that the shellfish seedling maintains contact with the blade at all times from dropping on the impeller disk to exiting the impeller disk. Figure 7 depicts the top view and front view of the shellfish seedling under stress study on the conical impeller disk. Where r_p is the blade pitch radius, R is the diameter of the impeller disk, and r is the distance between the shellfish seedling and the horizontal direction of the rotation center, ω is the angular velocity of impeller disk rotation.

FIGURE 7

Figure 7 Analysis of the force of shellfish on the impeller disk.

The shellfish seedling on the conical impeller disk are mainly subjected to centrifugal force F_c, gravity F_g, Coriolis force F_co and friction force F_f. In the Figure 7, the axis of the conical impeller disk serves as the origin of the (XYZ) coordinate system, which is constructed along the surface of the blade and the conical disk. If we establish the force balance equation along the X-axis, we can obtain:

$\begin{array}{ll}F=F_c\cos \alpha \cos \beta -F_g\sin \alpha \cos \beta -F_f& (2)\end{array}$

In which case the pitch angle β is:

$\begin{array}{ll}\beta =\arcsin (\frac{r_p}{r})& (3)\end{array}$

When the blade offset direction is opposite to the impeller disk rotation direction, r_p> 0, and when the blade offset direction is the same as the impeller disk rotation direction, r_p< 0. The cone angle α_d is the included angle between the blade and the horizontal plane when the blade is placed radially. The friction force between the shellfish seedling and the blade and the friction between the shellfish seedling and the conical blade disc adds up to the force operating on the shellfish seedling.

$\begin{array}{ll}{F}_f={\mu }_d(F_g\cos \alpha +F_c\sin \alpha )+{\mu }_v(F_g\sin \alpha \sin \beta +F_{co}-F_c\sin \beta )& (4)\end{array}$

Where μ_d is the coefficient of friction between the blade and the shellfish seedling and μ_v is the coefficient of friction between the seedling shellfish and the cone impeller disk. The vector representations of Coriolis force and centrifugal force are as follows:

$\begin{array}{ll}{F}_c=m{\omega }^{2}r\widehat{r}& (5)\end{array}$

$\begin{array}{ll}{F}_{co}=2m(\omega \times v)=2m\omega \cos \alpha \frac{\text{d}x}{\text{d}t}\widehat{\text{y}}& (6)\end{array}$

The analytical expression of gravity is:

$\begin{array}{ll}{F}_g=mg& (7)\end{array}$

Where g is the acceleration of gravity, $\widehat{r}$ and $\widehat{y}$ is the unit vector in the radial and Y directions. By substituting formula (5) ~ (7) into formula (4), the equation of motion of the shellfish seedling on the conical impeller disk can be written:

$\begin{array}{ll}\begin{array}{l}\frac{{\text{d}}^{2}x}{\text{d}{t}^2}+2{\mu }_{\text{v}}\omega \cos \alpha \frac{\text{d}x}{\text{d}t}-{\omega }^{2}r(\cos \alpha \cos \beta +{\mu }_v\sin \beta -{\mu }_d\sin \alpha )\\ +g(\sin \alpha \cos \beta +{\mu }_d\cos \alpha +{\mu }_v\sin \alpha \sin \beta )=0\end{array}& (8)\end{array}$

The aforementioned analysis shows that the impeller speed ω, impeller cone angle α, and blade offset angle β all have an impact on the motion trajectory of the shellfish seedling on the impeller disc.

5 Discrete element simulation optimization test

The EDEM discrete element simulation software was used to perform single factor experiments and rotation orthogonal combination experiments, analyze the influence of different parameters on the working performance of the centrifugal seeding device, perform response surface analysis and variance analysis on the simulation results, and optimize the seeding device’s key parameters.

5.1 Parameter setting of simulation model

Only import the three-dimensional model of the key component conical seeding mechanism in EDEM to reduce the amount of simulation calculation. The conical seeding mechanism is made of resin material. To prevent the shellfish particles from leaving the calculation domain during simulation, the shellfish bearing surface in EDEM software is set to 30m×50m; the seeding mechanism is 1m away from the bearing surface; and the contact between the shellfish and the shellfish is Hertz-Mindlin (no slip). Because the EDEM only contains regular spherical particle models, it is necessary to scan the three-dimensional model of the clam and import it, and then use multiple spherical particles to fill to create the simulation model of the clam. Reference (Huang, 2022) specifies the simulation parameters of the clam: Poisson’s ratio 0.35, density 1367kg/m³, elastic modulus 8.2MPa. Poisson’s ratio of resin material is 0.38, density is 1.117g/cm³, and elastic modulus is 1GPa; the elastic recovery coefficient between particles is 0.1, the static friction coefficient is 0.36, and the dynamic friction coefficient is 0.01; the elastic recovery coefficient, static friction coefficient and dynamic friction coefficient between particles and conical seeding mechanism are 0.15, 0.266 and 0.157 respectively.

5.2 Statistics of simulation data

After the simulation is completed, a statistical grid perpendicular to the seeding direction is established in the EDEM post-processing, and the grid size is 1m × 30m, the sowing direction is defined as vertical, and at the same time, the distribution variation coefficient of the shellfish seedlings in this direction is taken as the seedings uniformity index. The quality of the shellfish seedlings in each row is counted, and the distribution variation coefficient is calculated, and the variation coefficient and the effective width are used to assess how well the seeding device operates. As shown in Figure 8. Taking the center of the seedling sowing device as the origin, the distribution of shellfish seedlings in a single statistical area gradually decreases along the horizontal direction on both sides, and the distance between the two sides of a single statistical area that reaches the highest peak and half of the seedlings fall is defined as the effective job width.

FIGURE 8

Figure 8 Shellfish seeding simulation diagram.

The calculation formula of coefficient of variation Cv is

$\begin{array}{ll}Cv=\frac{S}{\overline{m}}\times 100\%& (24)\end{array}$

In formula

$\begin{array}{ll}S=\sqrt{\frac{{\displaystyle \sum _{i=1}^n{(m_i-\overline{m})}^2}}{n-1}}& (25)\end{array}$

$\begin{array}{ll}\overline{m}=\frac{1}{n}·{\displaystyle \sum _{i=1}^n{m}_i}& (26)\end{array}$

Where, S is the standard deviation of shellfish seedlings quality, g; m_i is the mass of shellfish seedlings in the statistical area of line i, g; $\overline{m}$is the average quality of shellfish seedlings in the statistical area, g; n is the number of grid lines in the statistical area.

5.3 Single factor simulation test

To investigate the distribution characteristics of shellfish seedlings after sowing and the influence of a single factor on the distribution law of shellfish seedlings, a single factor simulation test was first performed to change the value of the single factor to be investigated, while the values of the other factors remained constant at the middle value. For results statistics, the rotation center’s position was defined as the origin of the coordinate axis.

5.3.1 Effect of impeller speed on the distribution of shellfish seedlings

Set the test conditions as follows: the impeller cone angle is 10°, the blade offset angle is 0°, and the blanking rate is 0.7kg/s. In order to prevent the crushing rate of the shellfish seedlings from being too high due to excessive rotating speed, the range of the rotating speed of the impeller disk is 500~900 r/min, and the increment is 100 r/min. Figure 9A) displays the measured transverse distribution of shellfish seedlings. At low speeds, the dispersion of shellfish seedlings is limited and rather dense. The width, distribution range, and variation coefficient of the regularity of the dispersion of shellfish seedlings all steadily rise with an increase in impeller speed. The explanation behind this is that when the impeller speed increases, the distribution of shellfish seedlings becomes more uniform, the distance and width of sowing increase, and the initial speed at which shellfish seedlings leave the blade edge increases.

FIGURE 9

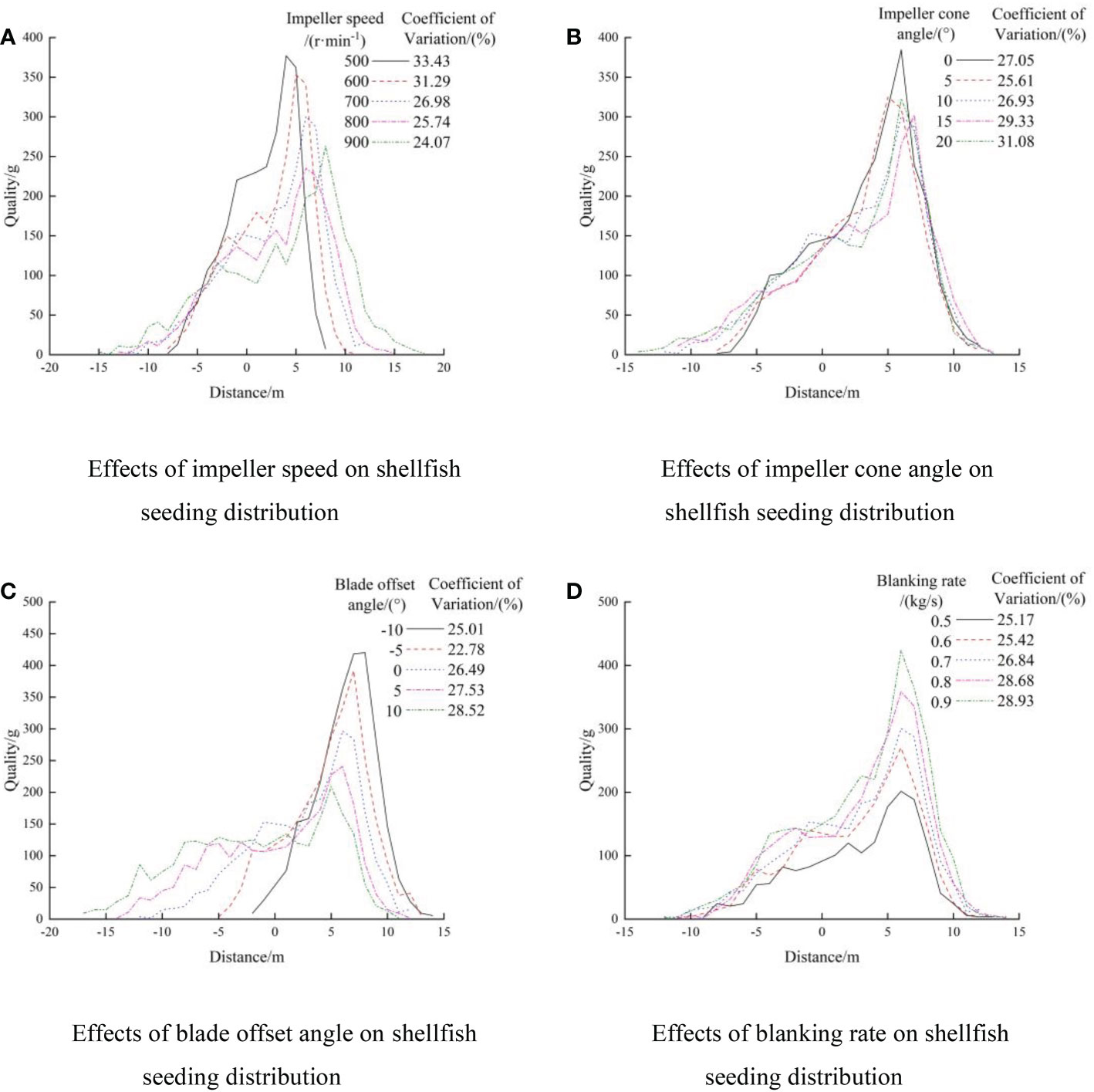
Figure 9 Effects of single factor on shellfish seeding distribution. (A) Effects of impeller speed on shellfish (B) Effects of impeller cone angle on seeding distribution shellfish seeding distribution (C) Effects of blade offset angle on shellfish (D) Effects of blanking rate on shellfish seeding distribution seeding distribution.

5.3.2 Effect of impeller cone angle on the distribution of shellfish seedlings

Set the test conditions as follows: rotating speed is 700r/min, blade offset angle is 0°, blanking rate is 0.7kg/s, impeller cone angle within the range of 0°~20°, and increment is 5°. Figure 9B) displays the shellfish seedlings distribution. The breadth of shellfish seedlings gradually grows as the impeller cone angle increases, and the variation coefficient of the evenness of the distribution of shellfish seedlings first declines and then increases. In order to make the distribution of shellfish seedlings more uniform, the distribution coefficient of variation can be decreased by altering the cone angle.

5.3.3 Effect of blade offset angle on the distribution of shellfish seedlings

Set the test conditions as follows: rotating speed is 700r/min, impeller cone angle is 10°, blanking rate is 0.7kg/s, blade offset angle value range -10°~10°, and the increment is 5°. Figure 9C) displays the dispersion status of shellfish seedlings. The coefficient of variance of shellfish seedlings distribution uniformity drops initially and subsequently increases. The direction of shellfish seedings is mostly affected by the blade offset angle. With a blade offset angle of -10° to 10°, the seedings direction progressively shifts from the right to the left side of the rotation center, and the width gradually rises. As a result, this factor can be used to adjust the direction and width of shellfish seedings.

5.3.4 Effect of blanking rate on the distribution of shellfish seedlings

Set the test conditions as follows: rotating speed is 700r/min, impeller cone angle is 10°, blade offset angle is 0°, blanking rate value range 0.5~0.9kg/s, increment is 0.1kg/s. Figure 9D) displays the shellfish seedlings distribution. When all other elements are held constant, as the blanking rate rises, the width stays the same, the peak value gradually rises, and the variation coefficient of the uniformity of the distribution of shellfish seedlings gradually rises. The simulation findings demonstrate that as the degree of blanking grows, the concentration of shellfish seedlings in the distribution region steadily rises.

5.4 Rotary orthogonal combination test

5.4.1 Orthogonal combination test of rotation of conical impeller disc

The effects of impeller speed n, impeller cone angle α, blade offset angle β, blanking rate v, and their interaction terms on the distribution coefficient of variation Cv and width L were examined in order to optimize the performance of the seeding device. The rotary orthogonal combination test was also carried out. According to the definition of American ASAE (, ; Geneva (Switzerland) International Organization for Standardization’s scientific contributions, 1984; Jones et al., 2008), the effective width is defined as the distance between the statistical region where the distribution quality of shellfish seedlings is half of the peak quality and the seeding device. Prepare a four factor five horizontal rotation orthogonal combination test and optimize the results for structural parameters (Ren, 2009; Xu and He, 2010). The test arm length should be set to 2. Table 1 displays the level coding table, whereas Table 2 displays the test scheme and results.

TABLE 1

Table 1 Factor level coding table.

TABLE 2

Table 2 Test scheme and results.

5.4.2 Analysis of test results

Use Design-8.0.6 software to conduct regression analysis on the test results, and remove the non significant items about the evaluation indicators in turn. The results of variance analysis are shown in Table 3 and Table 4.

TABLE 3

Table 3 ANOVA of coefficient of variation of shellfish distribution.

TABLE 4

Table 4 ANOVA of job width.

The lack of fit term of the variance analysis of the distribution coefficient of variation of shellfish seedlings is 0.1640>0.05, and the lack of fit term is not significant, it shows that the model can accurately capture the impact of numerous factors on the distribution coefficient of variation. The distribution of shellfish seedlings’ variation coefficient Cv and different affecting factors are modeled by the following regression equation:

$\begin{array}{ll}{C}_{\text{v}}=13.43-1.52\text{n}+7.63\alpha +1.77\beta +2.81\text{v}+2.24\alpha \beta +1.30\alpha \text{v}+2.61{\alpha }^2& (27)\end{array}$

The lack of fit term of variance analysis of job width is 0.1626 > 0.05, which is not significant, demonstrating the model’s ability to accurately depict the influence law of several factors on job width. The following is the regression equation between job width L and different affecting factors:

$\begin{array}{ll}\begin{array}{l}L=22.64+1.80\text{n}+3.90\alpha +0.68\beta +0.29\text{v}+0.67\text{n}\alpha -0.71\alpha \text{v}-0.67{\alpha }^2\\ -1.41{\beta }^2-0.57{\text{v}}^2\end{array}& (28)\end{array}$

5.4.3 Interaction analysis

Response surface analysis was performed on the interaction items with significant impact on the evaluation indicators using Design expert 8.0.6 software, as shown in Figure 10.

FIGURE 10

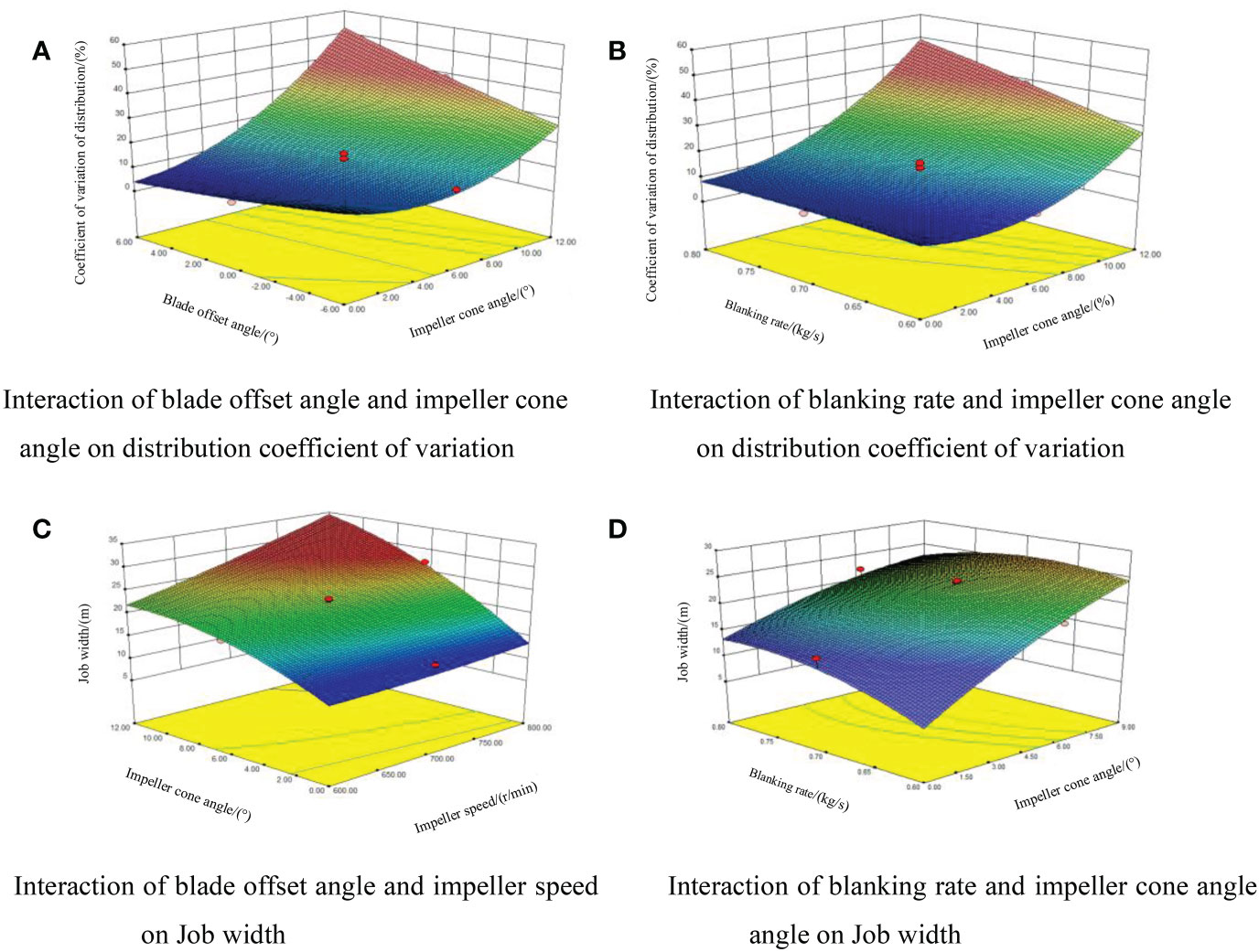
Figure 10 Response surface diagram. (A) Interaction of blade offset angle and impeller cone (B) Interaction of blanking rate and impeller cone angle angle on distribution coefficient of variation on distribution coefficient of variation (C) Interaction of blade offset angle and impeller speed (D) Interaction of blanking rate and impeller cone angle on Job width angle on Job width.

When the rotating speed of the impeller is 700r/min and the blanking rate is 0.70kg/s, the response surface of the blade offset angle and the cone angle of the impeller to the variation coefficient of the seedlings distribution is shown in Figure 10A). When the blade offset angle of the impeller is fixed, the cone angle of the impeller is directly proportional to the variation coefficient of the distribution of shellfish seedlings; when the cone angle of the impeller is fixed, the blade offset angle is directly proportional to the variation coefficient of the distribution of shellfish seedlings.

When the blade offset angle is 0° and the blanking rate is 0.70kg/s, the response surface of the impeller cone angle and impeller speed to the job width is shown in Figure 10C). The speed of the impeller is proportional to the job width when the cone angle of the impeller is fixed; and the cone angle of the impeller is proportionate to the job width when the speed of the impeller is fixed.

When the speed of the impeller is 700r/min and the offset angle of the blade is 0°, the response surface of the blanking rate and the cone angle of the impeller to the variation coefficient of the seedlings distribution and the job width is shown in Figure 10B, D). When the cone angle of the impeller is fixed, the blanking rate is directly proportional to the variation coefficient of the shellfish seedlings distribution and inversely proportional to the job width. When the blanking rate is constant, the cone angle of the impeller is proportional to the variation coefficient of the seedlings distribution and the job width.

5.4.4 Parameter optimization

The results of the variance and response surface analyses show that the influence of various factors on the distribution variation coefficient of shellfish seedlings is greater than the influence of the operating width. To optimize the operating parameters, the central composite response surface design of Design Expert software is used. The operating efficiency and seeding effect are thoroughly examined. The optimization goals are to minimize the distribution variation coefficient and maximize the effective operating width. When the impeller speed is 750 r/min, the blanking rate is 0.65kg/s, the impeller cone angle is 7.72°and the blade offset angle is -0.9°, the distribution variation coefficient is 12.84% and the job width is 24.98m.

6 Performance test of seeding device

In order to verify the operation performance of the seeding device, a 30 * 30m experimental site is arranged for bench test and whole machine test. The test scenario is shown in Figure 11.

FIGURE 11

Figure 11 Test site. (A) Bench test (B) Whole machine test.

6.1 Bench test

Install the blade on the conical impeller, the impeller taper is 7.72°, and the blade offset angle is -0.9°, according to the results of optimization of the above simulation parameters. Prepare a bench for the actual seeding test. The shellfish seedlings are used clam seedlings from the Philippines, which are classified as large, medium, or small based on shell length. Table 5 shows its physical characteristics after measurement.

TABLE 5

Table 5 Physical characteristics of shellfish seedlings.

6.1.1 Single size shellfish seedling test

The verification test was performed with medium-sized shellfish seedlings at the same impeller speed and blanking rate, as shown in Figure 12A). The simulation time is the same as the actual seeding time, and the measurement is repeated three times. The results revealed that the average measured mean value of the distribution variation coefficient of shellfish seedlings was 13.77%, the effective job width was 23.25 m, and the errors with the simulation results were respectively 7.24% and 6.92%, and the crushing rate of shellfish seedlings was less than 3%. According to the analysis, the main causes of the above errors are stone inclusion in shellfish seedlings, measurement errors of structure and operation parameters, and the influence of air resistance in the actual seeding process.

FIGURE 12

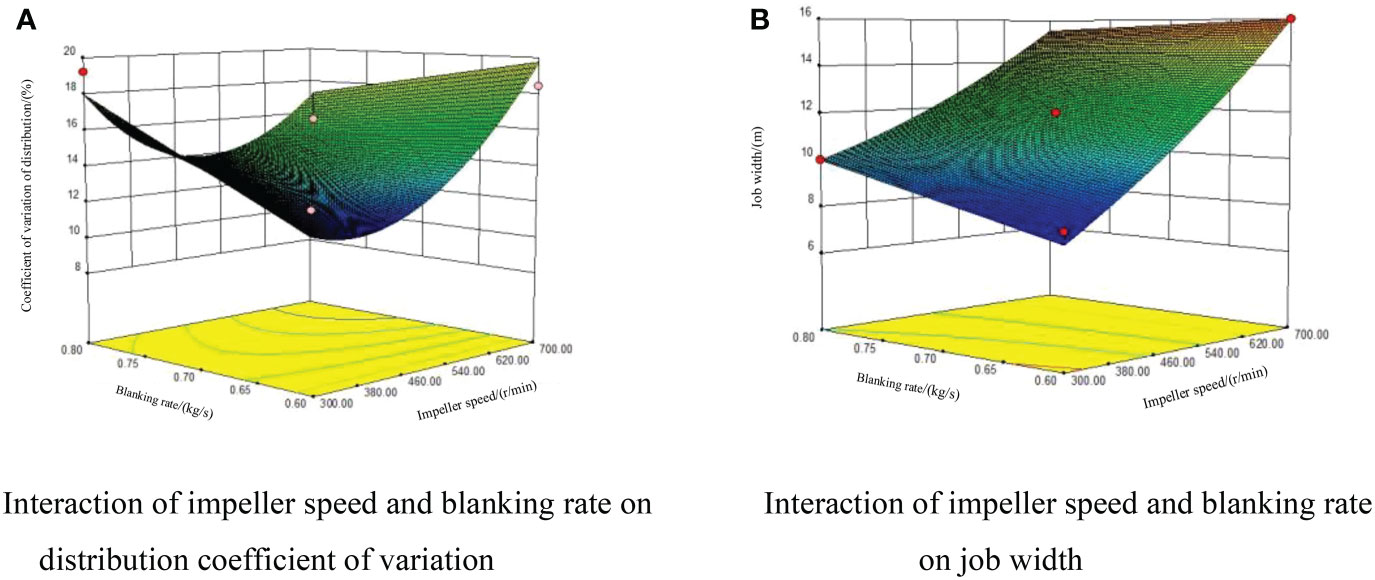
Figure 12 Response surface diagram. (A) Interaction of impeller speed and blanking rate on (B) Interaction of impeller speed and blanking rate distribution coefficient of variation on job width.

6.1.2 Different shellfish seedlings working performance test

In order to study the actual operation performance of the seeding device under the same operating parameters, the three factor and three horizontal rotation orthogonal combination tests were carried out with the shellfish seedling size A, impeller speed n and blanking rate τ as the factors, the distribution variation coefficient Cv and width L as the influencing indexes. The level coding table is shown in Table 6. The bench test scheme and results are shown in Table 7.

TABLE 6

Table 6 Factor level coding table.

TABLE 7

Table 7 Bench test scheme and results.

6.1.3 Analysis of test results

Use Design-8.0.6 software to conduct regression analysis on the test results, and remove the non-significant items about the evaluation indicators in turn. The results of variance analysis are shown in Tables 8 and 9.

TABLE 8

Table 8 ANOVA of coefficient of variation of shellfish distribution.

TABLE 9

Table 9 ANOVA of job width.

The lack of fit term of the variance analysis of the distribution coefficient of variation of shellfish seedlings is 0.3987>0.05, and the lack of fit term is not significant, it shows that the model can better reflect the influence of various influencing factors on the distribution coefficient of variation. The variation coefficient of seedlings distribution uniformity is significantly affected by impeller speed, blanking rate, the quadratic term of seedling size, the quadratic term of blanking rate, and the interaction term of impeller speed and blanking rate. The regression equation describing the relationship between the variation coefficient Cv of shellfish seedlings distribution and the influencing factors is given:

$\begin{array}{ll}Cv=12.97+0.3987A-2.24n-3.13\tau -2.66n\tau +2.55A^2+3.23{\tau }^2& (29)\end{array}$

The lack of fit term of variance analysis of job width is 0.5017 > 0.05, which is not significant, demonstrating that the model can better reflect the influence of various influencing factors on job width. The shellfish seedling size, impeller speed, impeller speed and blanking rate all have a significant impact on the job width. The regression equation for the relationship between width L and various factors is:

$\begin{array}{ll}L=11.78-0.75A+3.50n+0.50\tau -0.75n\tau +0.47n^2& (30)\end{array}$

6.1.4 Interaction analysis

Figure 12A) displays the impeller speed and blanking rate reaction surfaces to the shellfish seedlings distribution variation coefficient while the shellfish seedling size remain constant. The blanking rate is directly proportional to the seedlings distribution’s variation coefficient when the impeller speed is constant; when the blanking rate is constant, the impeller speed is inversely proportional to the seedlings distribution’s variation coefficient.

Figure 12B) displays the impeller speed and blanking rate reaction surface to job width when the shellfish seedling size will not change. The blanking rate is proportional to the job width when the impeller speed is constant; when the blanking rate is constant, the impeller speed is also proportional to the job width.

6.2 Whole machine test

Place the seeding device at the tail of the traction device and drive at an even speed to simulate the offshore seeding operation, as shown in Figure 12B). At this time, the impeller disk is 1.5m above the ground. The seeding process begins when the traction device’s tail enters the site 4m and ends when the vehicle’s tail drives out of the site 4m. The mass of shellfish seedlings in the unit grid was counted after each test, and the distribution variation coefficient Cv was calculated.

Four factor and three level orthogonal experiments were carried out to investigate the effect of travel speed on distribution coefficient of variation. Table 10 shows the factor level coding table; Table 11 shows the whole machine test scheme and results. The size of R in the analysis results in Table 10 shows that the influence on the distribution variation coefficient Cv in the traveling process is in the order of shellfish seedling size, blanking rate, travel speed, and impeller speed.

TABLE 10

Table 10 Factor level coding table.

TABLE 11

Table 11 Whole machine test scheme and results.

7 Conclusion

1) This paper designed a cone disc centrifugal shellfish seedling sowing device on the beach to improve the breadth and evenness of shellfish seedlings. The main factors influencing the force and movement of a single shellfish seedling on the cone disc were determined by analyzing its movement characteristics. The results of a single factor simulation test revealed that the distribution of shellfish seedlings in a single statistical area decreased gradually along the horizontal direction of both sides, with the origin being the center of the seeding device.

2) The rotary orthogonal combination test was performed with four factors and five levels. The design expert software was used to perform variance analysis and response surface analysis on the test results. The results showed that the interaction between the impeller cone angle and the blade offset angle, the impeller cone angle and the blanking rate had a significant effect, and the quadratic term of the impeller cone angle had an extremely significant effect on the distribution variation coefficient of shellfish seedlings (P<0.01). The interaction between the impeller speed and the impeller cone angle, the impeller cone angle and the blanking rate, and the quadratic term of the impeller cone angle, the blade offset angle, and the blanking rate all have a significant effect on the job width (P<0.05).

3) Design Expert software’s central composite response surface design was chosen. The optimization objectives were the lowest coefficient of variation and the greatest effective width. The impeller cone angle and the blade offset angle were 7.72° and - 0.9°, respectively, after optimization. The impeller with the critical parameters was installed in the seeding device, and the simulation optimization test was run. The coefficient of variation was 12.84%, and the effective operating width was 24.98m. The bench verification test revealed that the average values of the above indicators are 13.77% and 23.25 m, respectively, and the errors with the simulation results are 7.24% and 6.92%. The crushing rate is less than 3%, which meets the requirements for beach shellfish seeding.

4) On the seeding device, seedlings from the Philippines of three commonly used specifications were tested. The test results showed that the seedling spreader’s rotation speed had a wide range of adaptability, the job width increased and the coefficient of variation of uniformity decreased under high-speed rotation of the seedling tray, and the seeding effect was better; however, the breaking rate of medium seedlings and small seedlings is higher under high rotating speed of the seedling tray, so they are not suitable for operation under high rotating speed. The test results can be used to select operation parameters for shellfish seedlings of various specifications.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

HBZ, XL, GZ, GM contributed to the conception and design of thepaper and give modification suggestions. PL wrote the manuscript. HNZ draw the graph. WH carry out statistical analysis. All authors contributed to the article and approved the submitted version.

Funding

This research was funded by National Key R&D Program of China(2019YFD0900701); Education Department of Liaoning Province (LJKMZ20221112); Science and Technology Innovation Fund of Dalian(2021JJ12SN33); Key Laboratory of Environment Controlled Aquaculture (Dalian Ocean University) Ministry of Education (202212).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Artur P. (2015). The impact of structural and operational parameters of the centrifugal disc spreader on the spatial distribution of fertilizer. Agric. Agric. Sci. Proc. 7, 215–222. doi: 10.1016/j.aaspro.2015.12.021

CrossRef Full Text | Google Scholar

(2006). American Society of agricultural and biological engineers procedure for measuring distribution uniform and calibrating granular broadcast spreaders.

Google Scholar

Chen H., Nan J., Gao H., Wang M. (2019). Study on the relationship between velocity of particulate matter and beverloo formula[J]. Univ. Phys. 38 (9), 6. doi: 10.16854/j.cnki.1000-0712.180687

CrossRef Full Text | Google Scholar

Coetzee C. J., Lombard S. G. (2011). Discrete element method modelling of a centrifugal fertiliser spreader. Biosyst. Eng. 109 (4), 308–325. doi: 10.1016/j.biosystemseng.2011.04.011

CrossRef Full Text | Google Scholar

Dintwa E., Liedekerke Van P., Olieslagers R., Tijskens E., Ramon H. (2004). Model for simulation of particle flow on a centrifugal fertiliser spreader. Biosyst. Eng. 87 (4), 407–415. doi: 10.1016/j.biosystemseng.2003.12.009

CrossRef Full Text | Google Scholar

Fishery Administration Bureau of Ministry of Agriculture and Rural Affairs (2021). 2021 China fisheries statistical yearbook (Beijing: China Agricultural Press), 17–57.

Google Scholar

Frederick L., Garrett J., Frederick L., Gordon B. M. (1977). Apparatus for planting seed oysters: US4052961, Vol. 10. 11.

Google Scholar

Geneva (Switzerland) International Organization for Standardization’s scientific contributions (1984). Equipment for distributing fertilizers-test methods-part 2: Fertilizer distributors in lines.

Google Scholar

Huang W. (2022). Design and experimental study of centrifugal shellfish seeding equipment (Dalian Ocean University). doi: 10.16535/j.cnki.dlhyxb.2021-270

CrossRef Full Text | Google Scholar

Huang W., Li X., Mu G., Zhang G., Bai Y., Zhang H., et al. (2022). Design and experiment of centrifugal shoal shellfish seeding device. J. Dalian Ocean Univ. 37 (02), 320–328.

Google Scholar

Hu Y., Yang Y., Xiao H., Li P. (2016). Simulation and parameter optimization of centrifugal fertilizer spreader for tea plants. Trans. Chin. Soc. Agric. Machinery 47 (5), 77–82. doi: 10.6041/j.issn.1000-1298.2016.05.011

CrossRef Full Text | Google Scholar

Jones J. R., Hayden L. G., Yule I. J. (2008). A statistical comparison of international fertiliser spreader test methods-confidence in bout width calculations. Powder Technology 184 (3), 337–351. doi: 10.1016/j.powtec.2007.09.004

CrossRef Full Text | Google Scholar

Keith W., Rob J., Doug S., Fred L., Reinhold S. (2000). Machine for planting shellfish seedings: US6082303, Vol. 07. 04.

Google Scholar

Liang J., Li Y., Liang S., Guo Y., Shun X., You H., et al. (2021). A portable windswept shellfish seeding machine: CN213404549 U, Vol. 06. 11.

Google Scholar

Liu C., Li Y., Song J., Ma T., Wang M., Wang X., et al. (2017). Performance analysis and test of centrifugal disc fertilizer spreader based on EDEM. Trans. Chin. Soc. Agric. Eng. 33 (14), 32–39. doi: 10.11975/j.issn.1002-6819.2017.14.005

CrossRef Full Text | Google Scholar

Liu W., Zhang H., Li X., Zhang G., Zhang Q., Qu S., et al. (2020). Analysis of biomechanical properties of juvenile Manila clam for mechanization sowing. J. Dalian Ocean Univ. 35 (3), 455–461. doi: 10.16535/j.cnki.dlhyxb.2019-241

CrossRef Full Text | Google Scholar

Liu Y., Zheng J., Qiu T. (2014). Research and development status and trend of shellfish facility breeding engineering. Fishery modernization 41 (05), 1–5. doi: 10.3969/j.issn.1007-9580.2014.05.001

CrossRef Full Text | Google Scholar

Li Z., Xu G., Xu K., Zhang H. (2019). Towed seedling release device: CN110089463A, Vol. 08. 06.

Google Scholar

Lv J., Shang Q., Yang Y., et al. (2016). Performance analysis and test of tapered disc fertilizer sprinkling device. Trans. Chin. Soc. Agric. Eng. 32 (11), 16–24. doi: 10.11975/j.issn.1002-6819.2016.11.003

CrossRef Full Text | Google Scholar

Mu G., Wei X., Li X., Li Z., Li J., Liu Z., et al. (2019). Mud flat shellfish seedling planting machine: CN208768735U, Vol. 04. 23.

Google Scholar

National Fisheries Technology Extension Station (2008). Healthy cultivation technology of shellfish in tidal flats. Chin. Aquat. products 6), 52–53.

Google Scholar

Qin J., Chen H., Tu Z., Cui X. (1966). The flow of solid particles through the orifice. J. Chem. Eng. 2), 115–123.

Google Scholar

Ren L. (2009). Regression design and optimization (Beijing: Science Press).

Google Scholar

Shi Y., Chen M., Wang X., Morice O. O., Li C., Ding W., et al. (2018). Design and experiment of a variable rice surface fertilizer spreader with centrifugal uniform fertilizer cover. Trans. Chin. Soc. Agric. Machinery 49 (03), 86–93+113. doi: 10.6041/j.issn.1000-1298.2018.03.010

CrossRef Full Text | Google Scholar

Xu X., He M. (2010). Experimental Design and application of Design-Expert and SPSS. (Beijing: Science Press).

Google Scholar

Yang L., Chen L., Zhang J., Shun H., Liu H., Li M., et al. (2019). Test and analysis of uniformity of centrifugal disc spreading. Trans. Chin. Soc. Agric. Machinery 50 (sup 1), 108–114. doi: 10.6041/j.issn.1000-1298.2019.S0.018

CrossRef Full Text | Google Scholar

Yi M. (1973). Flow of solid particles through orifice-gravity flow and negative pressure differential flow of granular material through vertical and inclined pipe orifice. Chem. Eng. 1973 (1), 2–17.

Google Scholar

Yuan C., Liu Q., Liu Y. (2018). Shallow seabed sowing device for de-mersal shellfish larvae and using method of shallow seabed sowing device: CN105900878B. Vol. 08. 03.

Google Scholar

Yuan H., Shen H., Wang L., Shi L. (2014). Ecological culture technology of Philippine clam beach. Aquatic science and technology information 1, 54–56.

Google Scholar

Zhang G., Wang Y., Liu H., Ji C., Hou Q., Zhou Y., et al. (2021). Design and experiments of the centrifugal side throwing fertilizer spreader for lotus root fields. Trans. Chin. Soc. Agric. Eng. 37 (19), 11.

Google Scholar