
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mar. Sci. , 31 May 2022
Sec. Marine Fisheries, Aquaculture and Living Resources
Volume 9 - 2022 | https://doi.org/10.3389/fmars.2022.918449
This article is part of the Research Topic Nutrition, Disease, Environmental Stress, and Microorganisms in Crustacean Aquaculture View all 16 articles
Environmental problems such as organic pollution and eutrophication caused by highly intensive mariculture activities constrain the sustainable and healthy development of industry. Therefore, it is necessary to quantify the nutrient dynamics of aquaculture animals in order to reduce the risk of environmental pollution. In this study, a discontinuous individual growth model of Portunus trituberculatus in an intensive mariculture pond of P. trituberculatus–Penaeus japonicus–Sinonovacula constricta was constructed based on a dynamic energy budget theory combined with the index of condition factor. This model better predicted the growth and molting behavior of P. trituberculatus, and an acceptable fit was obtained through model parameterization using the Add-my-Pet (AmP) method (mean relative error = 0.058, symmetric mean squared error = 0.007). Ten molts were simulated over 180 days and generally coincided with the recorded molt time points. Based on this model and P. trituberculatus populations, the dynamic processes of carbon, nitrogen, and phosphorus in ingestion, respiration, excretion, feces, residual feed, dead crabs, seeding, molt, and harvest were simulated. The carbon, nitrogen, and phosphorus ingested during the 180-day culture period were 4,938.57 kg ha-1, 1,255.88 kg ha-1, and 244.16 kg ha-1, respectively. Carbon, nitrogen, and phosphorus removal by harvest accounted for 1.06%, 1.03% and 0.62% of the total ingestion, respectively, while carbon, nitrogen, and phosphorus removal by dead crabs accounted for 6.84%, 6.63%, and 4.04%, respectively, and carbon, nitrogen, and phosphorus released from residual feed into the water accounted for 41.43% of the total feed. The accurate simulation of molting behavior and nutrient dynamics in this study provides a theoretical basis for molting risk prevention and environmental stress assessment of P. trituberculatus and provides basic modules and data support for the construction of the integrated mariculture ecosystem model.
In order to secure fish supplies and reduce the global food crisis caused by the COVID-19 epidemic, intensive farming activities continue to increase around the world (Trottet et al., 2021). Intensive aquaculture involves high-density stocking and feeding of exogenous feed. The residual feed, feces, and excretion can have adverse effects on the aquaculture water bodies and the surrounding aquatic environment (e.g., water eutrophication, reduction of aquatic plant, and animal diversity) (Folke et al., 1988; Roy et al., 2020), and may also lead to food safety problems (e.g., drug residues and spread of pathogens) (Fan et al., 2011). Due to overfishing and resource decline in China, the degree of intensive mariculture of P. trituberculatus is increasing and the annual yield exceeds 100,000 tons (China Fishery Statistics Yearbook, 2022). In order to reduce the negative impact of intensive aquaculture activities on the environment, improve aquaculture yield and ecological benefits, and maintain sustainable development of the industry, it is necessary to construct a reasonable integrated multi-trophic aquaculture model for P. trituberculatus (Largo et al., 2016; Knowler et al., 2020).
As a method of long-term stable integrated aquaculture, polyculture of crab, shrimp, and shellfish reduces eutrophication and purifies water through shrimp and shellfish feeding on residual bait and feces, and shellfish filtering phytoplankton and suspended matter (Gao et al., 2008; Chang et al., 2020). In order to improve the complementarity between allotment species and main animals in terms of food and ecological niches, it is necessary to understand the growth of the animals and their impact on the environment during the aquaculture process (Reid et al., 2020). The assessment of the environmental impact of P. trituberculatus aquaculture has been reported in numerous papers (Zhang et al., 2015; Feng et al., 2018), but their feeding and metabolic activities have been neglected and nutrient dynamics have not been quantified well enough to accurately guide farm production. Continuous monitoring of the physiological dynamics of aquatic animals in the field is time-consuming and laborious. Because of this, individual growth models, which can reproduce the dynamics of each physiological activity in combination with environmental conditions, may be useful tools (Reid et al., 2020; Dong et al., 2022).
A dynamic energy budget (DEB) model is an individual growth model based on the physical and chemical properties of energy metabolism, which can reflect the universal laws of biological energy metabolism (Kooijman, 1986). The model not only quantifies the energy used for growth and the energy distribution throughout the life history stages (including shell and gonadal development) but can also be easily applied to the study of different species and waters (Ren and Ross, 2001; Kooijman, 2010; Sousa et al., 2010). DEB models are increasingly applied to aquatic bioenergetics and population dynamics studies to provide guidance for aquaculture and fisheries management (Spillman et al., 2008; Ren and Schiel, 2008; Orestis et al., 2019). They have been used to study some crustaceans, including the molting behavior of swimming crab Liocarcinus depurator, which provides the basis for their application to P. trituberculatus in this study (Campos et al., 2009; Talbot et al., 2019; Yang et al., 2020). However, the previous DEB model for P. trituberculatus only simulated growth during a single molt period, which has limited application in real production (Talbot et al., 2019).
The purpose of this study was to establish a DEB model for P. trituberculatus and simulate its nutrient (carbon, nitrogen, and phosphorus) dynamics based on the model, with the goal of providing important information for environmental assessment and integrated mariculture model management of P. trituberculatus in an intensive mariculture pond. In addition, we discussed the possibility of applying the model to carbon sink value estimation and ecosystem modeling in the future.
The DEB model describes the energy allocation process of biological growth and reproduction as having three parts: 1) structural body (V), which is related to body length, metabolism, and structural maintenance; 2) storage energy (E), which is the assimilated energy that first enters a reserve compartment; and 3) energy for development and reproduction (ER), which determines reproduction (Kooijman, 1986). Individuals ingest food in an amount proportional to the surface area of the organism and it is then converted into reserves through digestion and absorption at a constant efficiency. Stored energy comes from these reserves and is used for growth, reproduction, and maintenance of life activities based on the k-rule (Kooijman, 2010). The maintenance of structural material takes priority over growth and growth stops when food is insufficient and reserves are low.
Most standard DEB models assume continuous growth in structural volume but crustaceans are molt-growing species that initiate molting when nutrient accumulation and growth and development reach a certain level. This makes application of the DEB model to crustaceans somewhat challenging. Two key pieces of information are required to understand crustacean molt dynamics: the molt increment (MI) (i.e., the magnitude of the increase in size at molt) and the intermolt period (IP) (i.e., the length of time between two successive molts) (Chang et al., 2012). The primary factor influencing crustacean molting is the number of nutrients accumulated in the body (Abuhagr et al., 2014), and this can be assessed via indicators such as body weight and condition factors (Roberto and Defeo, 2002; Sharawy et al., 2019). MI and IP can be obtained from the pre- and post-molt lengths predicted by the DEB model if a threshold for nutrient accumulation at the start of the molt is available. In this study, we used condition factor (CF) (i.e., the ratio of body weight to the third power of carapace width) as an indicator of nutrient accumulation in P. trituberculatus to initiate molting, extending the DEB model for carapace width growth simulation (Table 1). When CF does not reach the molting threshold (kCF), body weight will increase with the aquaculture period but carapace width will not grow. When CF reaches the molting threshold, molting occurs and the carapace width grows to the width simulated by the DEB model. According to observed data, the kCF was 45% for the first 40 days and 30% for days 40 – 180.

Table 1 Equations describing the discontinuous individual growth model of the swimming crab Portunus trituberculatus.
The parameters of the swimming crab DEB model were estimated according to the Add-my-Pet (AmP) procedure (Marques et al., 2019). The data required for parameterization included zero-variate data, univariate data, and pseudo-data. Zero-variate and univariate data were obtained from previous studies and surveys.
The physiological rate in the DEB model is temperature dependent and follows the Arrhenius relationship. The Arrhenius temperature (TA) can be obtained from physiological experimental data describing the relationship between respiration and temperature and was estimated to be 6270 K (Dai et al., 2014; see Figure A1). Zero variate data related to the development and reproduction of P. trituberculatus were mainly obtained from fishery surveys along the Chinese coast (Dong, 2012). Univariate data for carapace width- wet weight, carapace width-age, and wet weight-age were obtained from pond aquaculture observation (Gao et al., 2016; Che et al., 2019).
Based on the completeness scale proposed by Lika et al. (2011), we assigned a completeness score of 2.5 to the data available for P. trituberculatus. Mean relative error (MRE) and symmetric mean squared error (SMSE) were used to assess the overall goodness of fit. The goodness-of-fit of model predictions were assessed by estimating the relative error for each zero-variate data point and univariate data set (Marques et al., 2019).
The experimental P. trituberculatus–Penaeus japonicus–Sinonovacula constricta integrated multi-trophic aquaculture pond used in this study was located in Zhoushan City, Zhejiang Province, China (24°35′N, 112°7′E), and was 1.33 ha in area, with an average water depth of 1.2 m during the study period. P. trituberculatus with a carapace width of 0.74 ± 0.05 cm were stocked to a density of 7.5 kg·ha-1. The experiment was carried out over 180 d, from June 2020 to November 2021. The water temperature in the pond was recorded continuously by a water temperature recorders (HOBO-MX2201, America). During the experiment, iced trash fish were provided daily at 17:50 and the feed level was recorded. Water was changed 1-2 times per month. The salinity range was 14.5 to 19.0. The water temperatures and feed levels are shown in Figure A2.
Carbon (C) and nitrogen (N) content in crab feed and feces were determined using an elemental analyzer. The samples were digested using the HClO4-H2SO4 method. The phosphorus (P) content in feed and feces was determined using a flow injection analyzer. The energy content of the crab feed was determined using a PARR1281 oxygen bomb calorimeter.
After seeding, the growth and molting of crabs in the pond were monitored twice daily and the molting time was recorded. After molt, 30 – 50 crabs were removed and their wet weight, carapace width, and shell weight were measured. The C, N, and P contents of ground and mixed crabs were analyzed using method described above.
The simulation of nutrients dynamics associated with P. trituberculatus included the dynamic processes of ingestion, respiration, excretion, and feces, as well as the nutrient content of seeding, residual feed, dead crab release, molt, and harvest. The simulation of dynamic physiological processes takes into account the general temperature dependence of chemical (enzymatic) processes (Gillooly et al., 2001). Nutrient quantification based on the DEB model was scaled up to the population level based on the aquaculture density of the swimming crabs. The population density of P. trituberculatus was calculated as:
where MN represents the density of the swimming crabs (ind ha-1), and δr represents their mortality (0.0253 d-1).
The ingestion rate (Jx) of P. trituberculatus has been calculated using the individual growth model (Table 1). The food intake of P. trituberculatus was calculated according to equation (2):
where Jx represents the ingestion rate, which is calculated based on the DEB model and ENfood represents the energy content of the crab feed (20.08 J mg-1). The intake of C, N, and P by P. trituberculatus were calculated as (kg ha-1 d-1):
where Cfood, Nfood, and Pfood represent the C, N, and P contents of the crab feed (36.61%, 9.31%, and 1.81%, respectively).
In intensive aquaculture, exogenous feed is typically provided in large quantities and adjusted to the culture period. The unconsumed food was calculated according to equation (6):
where Foodw represents the daily crab feeding level (kg d -1 ha-1). The C, N, and P content of unconsumed food (kg d -1 ha-1) were calculated as:
Swimming crabs also affect the environment through respiration and excretion. Respiration rate is proportional to the catabolic rate (Pc, J d-1), (Pouvreau et al., 2006). The amount of C released through respiration by P. trituberculatus was calculated as (kg ha-1 d-1):
where η is a constant for converting oxygen to energy equivalents and equals 14.3 J mg−1 O2 (Gnaiger and Forstner, 1983) and 0.375 is the ratio of molecular weights used to transform O2 in C. The amount of N and P released through excretion was calculated as (kg ha-1 d-1):
where JmgC is the ratio of carbon to energy value of the crab feed (55 J mg C-1).represents the ratio of nitrogen and carbon in crab (0.247 mg N mg C-1) and represents the ratio of phosphorus and nitrogen in excreta (0.0653 mg P mg N-1).P. trituberculatus feces is the main source of nutrients in pond sediment. The fecal wastes were calculated as (kg ha-1 d-1):
where ae represents the assimilation efficiency (0.8). The amount of C, N, and P released into the pond by the crab feces was calculated as (kg ha-1 d-1):
Dead crabs need to be removed daily to prevent them from remaining decomposing in the water column and causing deterioration of the water quality. Based on their mortality rate, the C, N, and P contents of dead P. trituberculatus were calculated as (kg ha-1):
where Ccrab, Ncrab, and Pcrab represent the C, N, and P contents of the crab (6.16%, 1.52%, and 0.18%, respectively).
Nitrogen and phosphorus levels in the water are also influenced by P. trituberculatus molting. Ten molts were simulated in this study, and the amounts of N and P released during each molt were estimated using the following equations (kg ha-1):
where δS represents the ratio of shell weight to body weight (9.82%). Nshell and Pshell represent the N and P contents of crab shells (7.15% and 0.55%, respectively).
The C, N, and P contents of P. trituberculatus seeding and harvest were calculated as (kg ha-1):
where MN0 and WW0 represent the density and wet weight of crab at the time of seeding, respectively. MN180 and WW180 represent the density and wet weight of crab at the time of harvest, respectively.
The results of the predicted zero-variate values for swimming crab based on the AmP procedure are listed in Table 2. The DEB parameters were estimated at a reference temperature of 20°C (Table 3). The parameter estimation resulted in acceptable goodness-of-fit with MRE = 0.058 and SMSE = 0.007. The model underestimated the age at birth and life span and overestimated the length at end acceleration and ultimate length. The predicted value of the ultimate reproduction rate was in general agreement with the observed value. (http://www.bio.vu.nl/thb/deb/deblab/add_my_pet/entries_web/Portunus_trituberculatus/Portunus_trituberculatus_res)

Table 2 Zero-variate data used for estimating parameters of the swimming crab Portunus trituberculatus DEB model. Observed data and relative error (RE) are specified.
Simulated and observed growth conditions and the molting behavior of swimming crabs from June to November are shown in Figure 1. The simulation was generally consistent with the observed results, indicating that the model accurately simulated the variation in wet weight and carapace width of P. trituberculatus. Ten molts were simulated over 180 days and this was equal to the number of molts observed and generally coincided with the recorded molt time points. The simulated molting cycle time lengthened with each stage, from 4 days for juvenile crabs in stages I – II (Observed days: 4), 12 days for juveniles in stages V – VI (Observed days: 11), and 38 days for adults in stages X – XI (Observed days: 36) (Figure 1A).
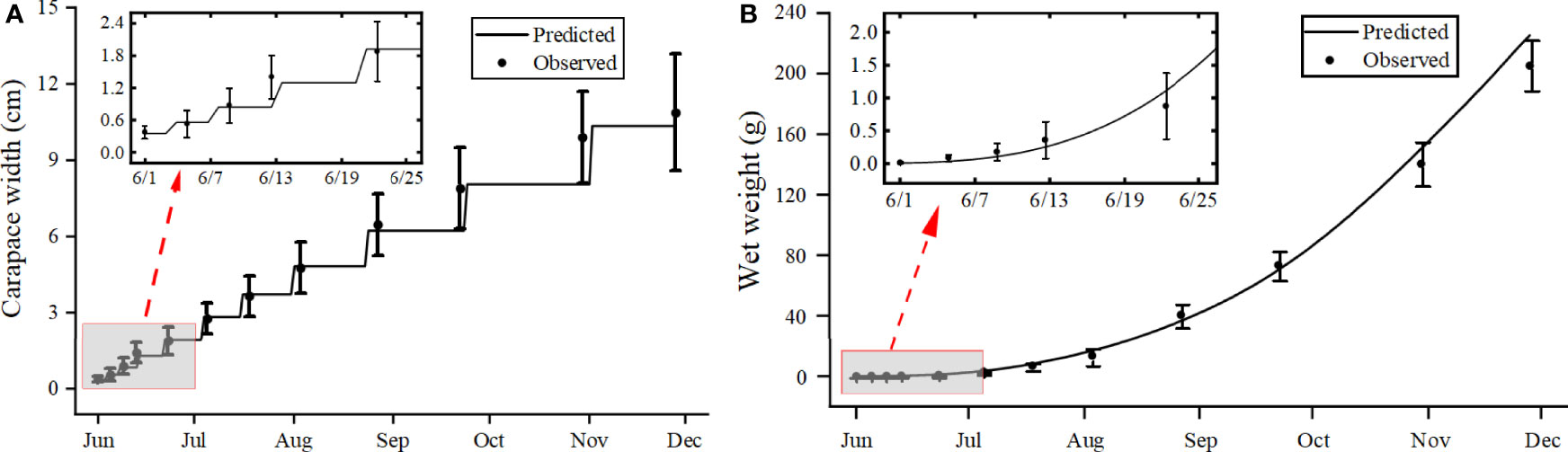
Figure 1 Comparison of observations (circles with bars for standard deviation) and simulations (lines) of carapace width (A) and wet weight (B) of the swimming crab Portunus trituberculatus.
The simulation of nutrients dynamics associated with P. trituberculatus aquaculture (ingestion, respiration, excretion and feces) is shown in Figure 2. The dynamics of C, N, and P involved showed an overall trend of rising and then falling, with a maximum in August. In addition, the trend fluctuated significantly in August due to the high temperature.
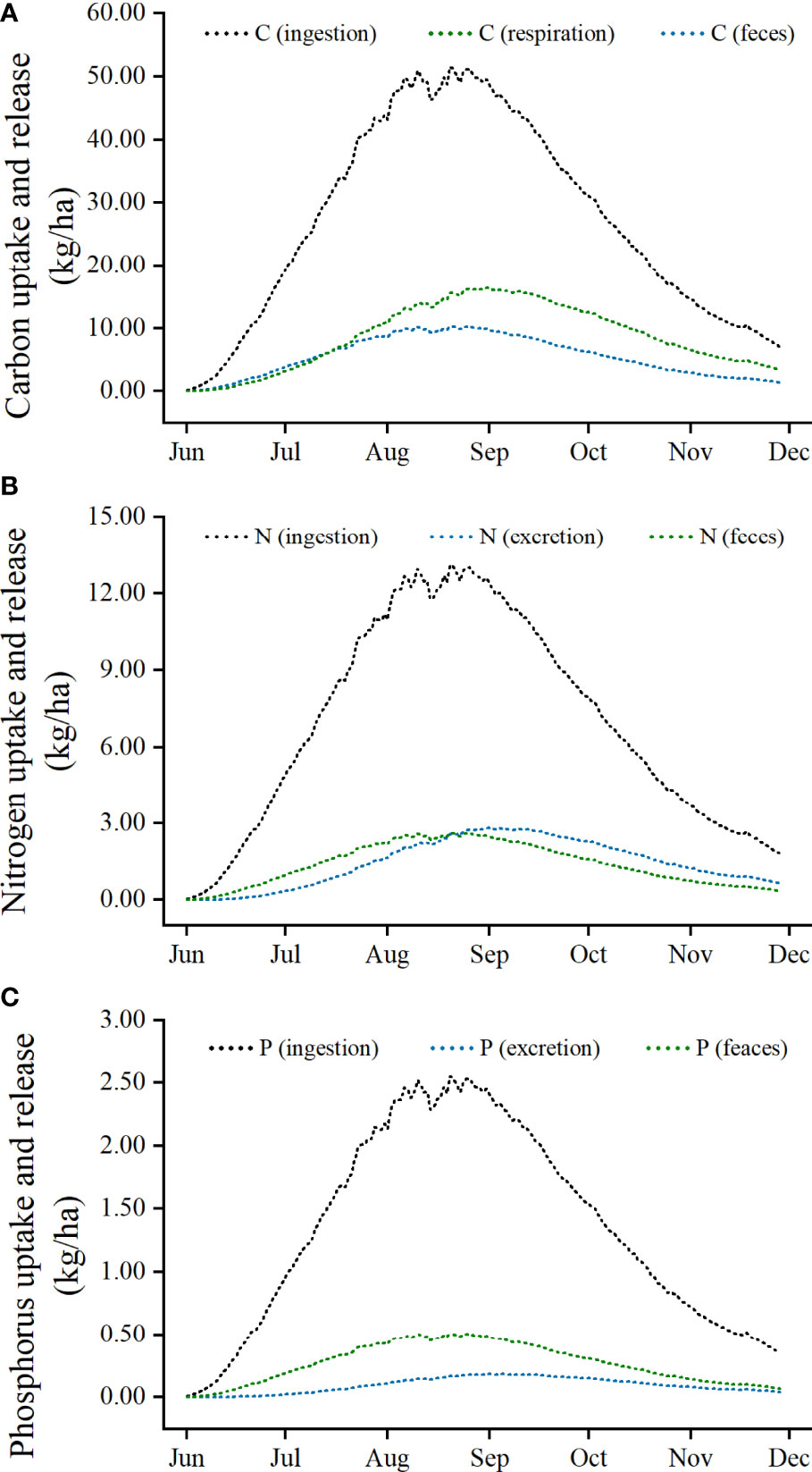
Figure 2 Simulation of carbon (A), nitrogen (B), and phosphorus (C) dynamics associated with Portunus trituberculatus aquaculture.
The C, N, and P released during molts are shown in Table 4. The highest N and P release occurred during the ninth molt, and prior to the last molt, N and P release increased with the number of molts. The total amount of nitrogen and phosphorus released during the last five molts was close to 90% of the total release.
Figure 3 shows the C, N, and P fluxes associated with P. trituberculatus aquaculture over the six months rearing cycle including seeding and harvest. The C, N, and P introduced at seeding were 0.46 kg ha-1, 0.11 kg ha-1 and 0.01 kg ha-1, respectively. The C, N, and P ingested during the 180-day culture period were 4,938.57 kg ha-1, 1,255.88 kg ha-1, and 244.16 kg ha-1, respectively, of which approximately 1.06%, 1.03%, and 0.62% were removed by harvest and 6.84%, 6.63%, and 4.04% were removed by dead crabs. Overall, 44.46% of the N and 28.43% of the P were released as excretion, feces, and molts. The C, N, and P released from the residual feed accounted for 41.43% of the total feed. The C, N, and P released into the water (excluding dead crabs and harvest) during the 180-day aquaculture period were 4,480.53 kg ha-1, 1,446.60 kg ha-1, and 242.09 kg ha-1, respectively.
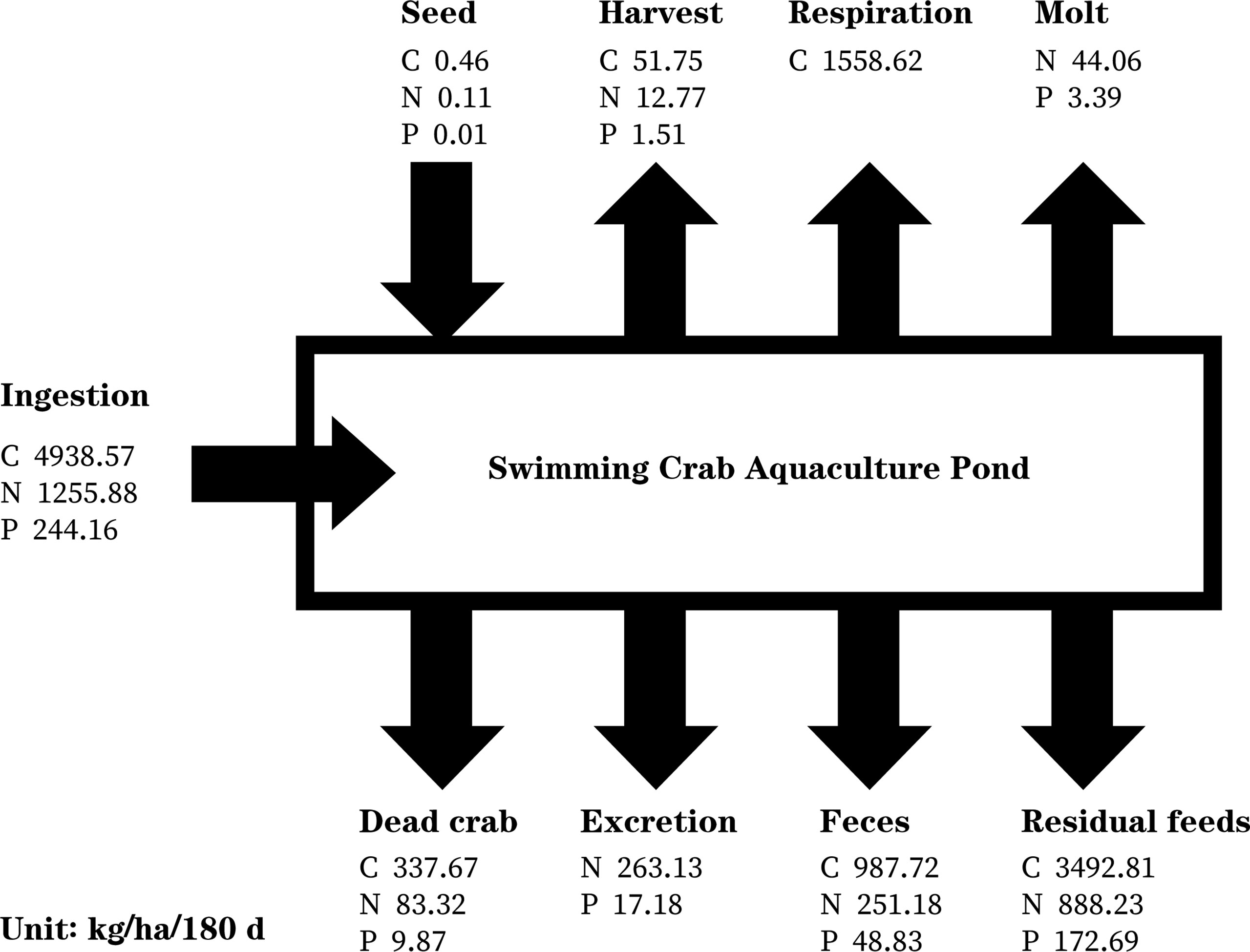
Figure 3 Carbon (C), nitrogen (N), and phosphorus (P) budgets associated with Portunus trituberculatus aquaculture over the six months rearing cycle.
Traditionally, the parameterization of the DEB model relies on a large number of physiological experiments on individuals held in standard conditions including controlled temperature (Ren and Schiel, 2008; Serpa et al., 2013). As an economically important farmed crab in China, studies on P. trituberculatus have focused on biological surveys, genetic breeding, and farming techniques (Lv et al., 2014; Wang et al., 2018; Duan et al., 2021), lacking sufficient physiological information (e.g., starvation experiments). The AmP procedure allows us to estimate parameters for a species for which limited physiological data is available (Lika et al., 2011; Ren et al., 2020) because it allows us to estimate model parameters according to biological (zero-variate data) and growth characteristics (univariate data). Complete zero-variate data include age, length at birth, weight, maturation temperature, lifespan, ultimate length, and ultimate weight. Inadequate accumulation of relevant knowledge may affect the accuracy of some of these parameters (Marques et al., 2018). Another advantage of the AmP method is that MRE and SMSE can be used to check the veracity of the data (Marques et al., 2019) and the simulated and predicted values of the parameters in this study show a high match (Table 2), indicating that the model parameters are reasonable and valid.
More than 1,000 papers have been published on DEB theory (https://www.zotero.org/groups/500643/deb_library/library), which is widely used in aquaculture for finfish, bivalves, shrimp (Cheng et al., 2018; Dambrine et al., 2020; Yang et al., 2020), and swimming crab L. depurator (Talbot et al., 2019). This study showed that the DEB model can be applied to P. trituberculatus in integrated aquaculture ponds (Figure 1). The DEB model predicts individual growth based on food and water temperature dynamics. In the DEB model, food condition f (range: 0 – 1) is used to represent food availability (density and mass), whereas typically the unstable food condition of bivalves, which is usually set to a fixed value in models of finfish, shrimp, and other cast-feeding farming animals, is used (Campos et al., 2009; Ren et al., 2020). This study included values of f ranging from the lowest food scenario (f = 0) to arbitrary feeding (f = 1), and the results show that the most growth occurred at f = 1, indicating adequate and high-quality feed in the experimental pond (Haberle et al., 2020). DEB theory uses the Arrhenius equation to describe the effect of changing temperature on the rate of individual physiological responses (Kooijman, 2010). P. trituberculatus is a eurythermic species but temperature changes have a large effect on its metabolism (Lu et al., 2015). Although the water temperature in the experimental ponds fluctuated within 10°C, the temperature dependence function of the P. trituberculatus DEB model showed a significant difference in August (high temperature: 29.1 – 30.70 °C) and November (low temperature: 21.70 – 24.40 °C) (Figure A3).
The molting period of crustaceans is often accompanied by unstable ingestion and metabolism, cannibalism, and other phenomena (Su et al., 2019). During the molting period, good feed and water quality and nutrient supplementation can help ensure a successful molt. This makes molting prediction an important prerequisite for crustacean aquaculture management (Lemos and Weissman, 2020; Liu et al., 2021). The application of a discontinuous growth model based on mathematical functions and probability statistics to P. trituberculatus showed satisfactory results (Wang, 2017). The discontinuous growth and periodic loss of calcified structures due to molt make a growth modeling approach based on individual physiological and ecological characteristics inappropriate for crustaceans and most studies ignore molting behavior (Campos et al., 2009; Yang et al., 2020). In the swimming crab DEB model, Talbot et al. (2019) substituted wet weight for structural volume and established a logical relationship with physiological rates in the standard model to complete molt predictions within a single molt cycle. As a comprehensive index to determine the physiological and nutritional states of animals, the condition factor has been used as an important predictor of molt in crustaceans such as penaeid shrimp (Farfantepenaeus aztecus, F. brasiliensis, F. duorarum, and F. notialis), brown shrimp (Crangon crangon) and Chinese mitten crab (Eriocheir sinensis) (Roberto and Defeo, 2002; Chen et al., 2016; Sharawy et al., 2019). The results of this study showed that the growth model of P. trituberculatus could accurately predict molt (Figure 1A), but molt was also influenced by the environment (temperature, precipitation, etc.). Because these environmental factors are uncontrollable outside of experimental settings, the stability of the model needs further validation. In addition, shell mineralization in shrimp and crabs can play a role in carbon sequestration (Troell et al., 2009), and the successful simulation of molting behavior can provide a reference for carbon sink value estimation of crustaceans.
By using the ecologically complementary habits of different farming organisms and making full use of system materials and energy, the integrated aquaculture model helps to improve economic efficiency and reduce farming pollution (Troell et al., 2003). In China, the shrimp-crab and shrimp-crab-shellfish integrated aquaculture model has become the main farming model for P. trituberculatus. However, the existing studies on intensive ponds of P. trituberculatus have focused on the overall static carbon, nitrogen, and phosphorus budget and have not quantified nutrient dynamics associated with the aquaculture process (Dong et al., 2013; Zhang et al., 2016). Considering that the simulation of nutrient dynamics at the population level is more meaningful than at the individual level, this study combined the DEB model with the crab density to model the population dynamics of P. trituberculatus (Figure A3) and simulated the related nutrient dynamic processes (Figure 2). The patterns of carbon, nitrogen, and phosphorus uptake and release caused by the ingestion and metabolism of the swimming crabs in the experiment were determined by density changes and fluctuated in July and August due to the frequency of hot weather in summer that reduced physiological activity (Lu et al., 2015).
The assessment of the carbon, nitrogen, and phosphorus budget in the ecosystem is an effective method to evaluate nutrient utilization, energy conversion efficiency and pollution levels in aquaculture ponds (Guo et al., 2017). The results showed that ≤ 8% of the carbon, nitrogen, and phosphorus in feed was converted to swimming crab (including harvested and dead crabs), with most of the remainder being released into the aquaculture environment in the form of excretion, feces, and molts. Meanwhile, 41% of the nutrients in the feed were not consumed by P. trituberculatus and was discharged into the aquaculture water environment in the form of residual feed, resulting in 4,480.53 kg ha-1, 1,446.60 kg ha-1 and 242.09 kg ha-1 of carbon, nitrogen, and phosphorus being retained in the water. Aquaculture discharges can raise the nutrient load of nearby waters and lead to water eutrophication (Herbeck et al., 2013). We have combined Japanese shrimp and razor clams in the P. trituberculatus aquaculture system to improve food resource utilization, increase farm production, and reduce the negative environmental impact of farming activities. Of course, assessing the carrying capacity and proportion of farming organisms in an integrated aquaculture system requires long-term dynamic simulation and analysis. In a follow-up study, we will couple the simulation of P. trituberculatus nutrient dynamics to an ecosystem model for ecosystem-level assessment of carrying capacity and environmental pollution to provide scientific and precise management information for integrated aquaculture activities.
The discontinuous growth model established in this study will accurately relay the growth and molting behavior of P. trituberculatus, and provide support for a series of techniques such as seeding, feeding, water quality control, and molting management in intensive mariculture. The assessment of nutrient dynamics, in combination with population dynamics and physiological activities, can provide technical guidance for integrated aquaculture practices and help achieve environmental and economic sustainability. This model can not only be used independently for mariculture assessment but can also be combined into an ecological model of an integrated multi-trophic aquaculture ecosystem in order to assess the potential impacts of aquaculture on a larger spatial scale.
The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.
SD, XX, and FL designed the experiments and wrote the manuscript. LY and HS performed the experiments. FW supervised and validated the manuscript. All authors contributed to the article and approved the submitted version.
This study was funded by the National Key Research and Development Program of China (2019YFD0900402) and the Yellow River Delta Industry Leading Talents Project.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2022.918449/full#supplementary-material
Abuhagr A. M., Blindert J. L., Nimitkul S., Zander I. A., LaBere S. M., Chang S. A., et al. (2014). Molt Regulation in Green and Red Color Morphs of the Crab Carcinus Maenas: Gene Expression of Molt-Inhibiting Hormone Signaling Components. J. Exp. Biol. 217, 976–808. doi: 10.1242/jeb.093385
Campos J., Veer H., Freitas V., Kooijman S. (2009). Contribution of Different Generations of the Brown Shrimp Crangon Crangon (L.) in the Dutch Wadden Sea to Commercial Fisheries: A Dynamic Energy Budget Approach. J. Sea. Res. 62, 106–113. doi: 10.1016/j.seares.2009.07.007
Chang Z. Q., Neori A., He Y. Y., Li J. T., Qiao L., Preston S. I., et al. (2020). Development and Current State of Seawater Shrimp Farming, With an Emphasis on Integrated Multi-Trophic Pond Aquaculture Farms, in China - a Review. Rev. Aquacult. 12, 2544–2558. doi: 10.1111/raq.12457
Chang Y. J., Sun C. L., Chen Y., Yeh S. Z. (2012). Modelling the Growth of Crustacean Species. Rev. Fish. Biol. Fisher. 22, 157–187. doi: 10.1007/s11160-011-9228-4
Che J., Liu M. M., Hou W. J., Dong Z. G., Yang S., Cheng Y. X., et al. (2019). Growth and Gonadal Development of Pond-Reared Male Swimming Crab, Portunus Trituberculatus. Chin. J. Zool. 54, 347–361. doi: 10.13859/j.cjz.201903005
Cheng M., Tan A., Rinaldi A., Giacoletti A., Sarà G., Williams G. A. (2018). Predicting Effective Aquaculture in Subtropical Waters: A Dynamic Energy Budget Model for the Green Lipped Mussel, Perna Viridis. Aquaculture 495, 749–756. doi: 10.1016/j.aquaculture.2018.04.008
Chen J., Yue W. C., Chen X. W., Ci Y. J., Huang Z., Wang J., et al. (2016). Observation on Individual Molting, Growth and Association Analysis With Relative Gene Expression in Chinese Mitten Crab (Eriocheir Sinensis). Chin. J. Zool. 51, 1059–1070. doi: 10.13859/j.cjz.201606014
China Fishery Statistics Yearbook. (2022). Department of Agriculture, Fisheries Bureau. China Fishery Statistics Yearbook. Beijing, China: Agricultural Press.
Dai C., Wang F., Fang Z. H., Dong S. L. (2014). Effects of Temperature on the Respiratory Metabolism and Activities of Related Enzymes of Swimming Crab Portunus Trituberculatus. Prog. Fish. Sci. 35, 90–96. doi: 10.3969/j.issn.1000-7075.2014.02.013
Dambrine C., Huret M., Woillez M., Pecquerie L., Allal F., Servili A., et al. (2020). Contribution of a Bioenergetics Model to Investigate the Growth and Survival of European Seabass in the Bay of Biscay E English Channel Area. Ecol. Model. 423, 109007. doi: 10.1016/j.ecolmodel.2020.109007
Dong Z. G. (2012). The Study on Morphology, Biochemistry, Molecular Phylogeography and Genetic Diversity of the Swimming Crab Along Portunus Trituberculatus China Coast (Ph.D. Dissertation. Shanghai: Shanghai Ocean University).
Dong J., Tian X. L., Dong S. L., Zhang K., Feng J., He R. P. (2013). Study on Nitrogen and Phosphorus Budget in Polyculture Systems of Litopenaeus Vannamei and Portunus Trituberculatus. Periodic. Ocean. Univ. China 43, 16–24. doi: 10.16441/j.cnki.hdxb.2013.12.003
Dong S. P., Wang F., Zhang D. X., Yu L. Y., Pu W. J., Shang Y. K. (2022). Growth Performance and Ecological Services Evaluation of Razor Clams Based on Dynamic Energy Budget Model. J. Environ. Manage. 306, 114392. doi: 10.1016/j.jenvman.2021.114392
Duan H. B., Mao S., Xia Q., Ge H. X., Liu M. M., Li W. Q., et al. (2021). Comparisons of Growth Performance, Gonadal Development and Nutritional Composition Among Monosex and Mixed-Sex Culture Modes in the Swimming Crab (Portunustrituberculatus). Aquac. Res. 52, 3403–3414. doi: 10.1111/are.15185
Fan L. M., Wu W., Hu G. D., Qu J. H., Meng S. L., Qiu L. P., et al. (2011). Preliminary Exploration on Assessment of Intensive Pond Ecosystem Health. Chin. Agric. Sci. Bull. 27, 395–399. doi: 10.1016/S1671-2927(11)60313-1
Feng J., Tian X. L., Dong S. L., He R. P., Zhang K., Zhang D. X., et al. (2018). Comparative Analysis of the Energy Fluxes and Trophic Structure of Polyculture Ecosystems of Portunus Trituberculatus Based on Ecopath Model. Aquaculture 496, 185–196. doi: 10.1016/j.aquaculture.2018.07.020
Folke C., Kautsky N., Berg H., Jansson Å., Troell M. (1988). The Ecological Footprint Concept for Sustainable Seafood Production—a Review. Ecol. Appl. 8, 63–71. doi: 10.1016/j.aquaculture.2018.07.020
Gao T. L., Wang Y. F., Bao X. N., Ren Z. M., Mu C. K., Wang C. L. (2016). Study on the Characteristics of Molting and Growth of Portunus Trituberculatus Cultured in Single Individual Basket. J. Biol. 33, 41–46. doi: 10.3969/j.issn.2095-1736.2016.03.041
Gao Q. F., Xu W. Z., Liu X. S., Cheung S. G., Shin P. K. S. (2008). Seasonal Changes in C, N and P Budgets of Green-Lipped Mussels Perna Viridis and Removal of Nutrients From Fish Farming in Hong Kong. Mar. Ecol. Prog. Ser. 353, 137–146. doi: 10.3354/meps07162
Gillooly J. F., Brown J. H., West G. B., Savage V. M., Charnov E. L. (2001). Effects of Size and Temperature on Metabolic Rate. Science 293, 2248–2251. doi: 10.1126/science.1061967
Gnaiger E., Forstner H. (1983). Polarographic Oxygen Sensors: Aquatic and Physiological Applications (Berlin: Springer), XII, 370 pp.
Guo K., Zhao W., Jiang Z. Q., Dong S. L. (2017). A Study of Organic Carbon, Nitrogen and Phosphorus Budget in Jellyfish-Shellfish-Fish-Prawn Polyculture Ponds. Aquac. Res. 48, 68–76. doi: 10.1111/are.12861
Haberle J., Marn N., Gecek S., Klanjek S. (2020). Dynamic Energy Budget of Endemic and Critically Endangered Bivalve Pinna Nobilis: A Mechanistic Model for Informed Conservation. Ecol. Model 434, 109207. doi: 10.1016/j.ecolmodel.2020.109207
Herbeck L. S., Unger D., Wu Y., Jennerjahn T. C. (2013). Effluent, Nutrient and Organic Matter Export From Shrimp and Fish Ponds Causing Eutrophication in Coastal and Back-Reef Waters of NE Hainan, Tropical China. Cont. Shelf. Res. 57, 92–104. doi: 10.1016/j.csr.2012.05.006
Knowler D., Chopin T., Martinez-Espineira R., Neori A., Nobre A., Noce A., et al. (2020). The Economics of Integrated Multi-Trophic Aquaculture: Where are We Now and Where Do We Need to Go? Rev. Aquacult. 12, 1–16. doi: 10.1111/raq.12399
Kooijman S. A. L. M. (1986). “Population Dynamics on the Basis of Budgets,” in The Dynamics of Physiologically Structured Populations, 68. Eds. Metz J. A. J., Diekmann O. (Heidelberg/Berlin/NY: Springer-Verlag), 266–297.
Kooijman S. A. L. M. (2010). Dynamic Energy Budget Theory for Metabolic Organisation (Cambridge: Cambridge University Press).
Largo D. B., Diola A. G., Marababol M. S. (2016). Development of an Integrated Multi-Trophic Aquaculture (IMTA) System for Tropical Marine Species in Southern Cebu, Central Philippines. Aquacult. Rep. 3, 67–76. doi: 10.1016/j.aqrep.2015.12.006
Lemos D., Weissman D. (2020). Moulting in the Grow-Out of Farmed Shrimp: A Review. Rev. Aquacult. 13, 5–17. doi: 10.1111/raq.12461
Lika K., Kearney M. R., Freitas V., van der Veer H. W., van der Meer J., Wijsman J. W. M., et al. (2011). The “Covariation Method” for Estimating the Parameters of the Standard Dynamic Energy Budget Model I: Philosophy and Approach. J. Sea. Res. 66, 270–277. doi: 10.1016/j.seares.2011.07.010
Liu S., Wang X., Bu X., Zhang C., Chen L. (2021). Influences of Dietary Vitamin D3 on Growth, Antioxidant Capacity, Immunity and Molting of Chinese Mitten Crab (Eriocheir Sinensis) Larvae. J. Steroid. Biochem. 210, 105862. doi: 10.1016/j.seares.2011.09.004
Lu Y. L., Wang F., Dong S. L. (2015). Energy Response of Swimming Crab Portunus Trituberculatus to Thermal Variation: Implication for Crab Transport Method. Aquaculture 441, 64–71. doi: 10.1016/j.aquaculture.2015.02.022
Lv J. J., Liu P., Gao B. Q., Wang Y., Wang Z., Chen P., et al. (2014). Transcriptome Analysis of the Portunus Trituberculatus: De Novo Assembly, Growth-Related Gene Identification and Marker Discovery. PloS One 9, e94055. doi: 10.1371/journal.pone.0094055
Marques G. M., Augustine S., Lika K., Pecquerie L., Domingos T., Kooijman S. A. L. M. (2018). The Amp Project: Comparing Species on the Basis of Dynamic Energy Budget Parameters. Plos. Comput. Biol. 14, e1006100. doi: 10.1371/journal.pone.0094055
Marques G. M., Lika K., Augustine S., Pecquerie L., Kooijman S. A. L. M. (2019). Fitting Multiple Models to Multiple Data Sets. J. Sea. Res. 143, 48–56. doi: 10.1016/j.seares.2018.07.004
Orestis S. Z., Nikos P., Konstadia L. (2019). A DEB Model for European Sea Bass (Dicentrarchus Labrax): Parameterisation and Application in Aquaculture. J. Sea. Res. 143, 262–271. doi: 10.1016/j.seares.2018.05.008
Pouvreau S., Bourlès Y., Lefebvre S., Gangnery A., Alunno-Bruscia M. (2006). Application of a Dynamic Energy Budget Model to the Pacific Oyster, Crassostrea Gigas, Reared Under Various Environmental Conditions. J. Sea. Res. 56, 156–167. doi: 10.1016/j.seares.2006.03.007
Reid G. K., Lefebvre S., Filgueira R., Robinson S. M. C., Broch O. J., Dumas A., et al. (2020). Performance Measures and Models for Open-Water Integrated Multi-Trophic Aquaculture. Rev. Aquacult. 12, 47–75. doi: 10.1111/raq.12304
Ren J. S., Jin X. S., Yang T., Kooijman S., Shan X. J. (2020). A Dynamic Energy Budget Model for Small Yellow Croaker Larimichthys Polyactis: Parameterisation and Application in its Main Geographic Distribution Waters. Ecol. Model. 427, 109051. doi: 10.1016/j.ecolmodel.2020.109051
Ren J. S., Ross A. H. (2001). A Dynamic Energy Budget Model of the Pacific Oyster Crassostrea Gigas. Ecol. Model. 142, 105–120. doi: 10.1016/S0304-3800(01)00282-4
Ren J. S., Schiel D. R. (2008). A Dynamic Energy Budget Model: Parameterisation and Application to the Pacific Oyster Crassostrea Gigas in New Zealand Waters. J. Exp. Mar. Biol. Ecol. 361, 42–48. doi: 10.1016/j.jembe.2008.04.012
Roberto P. C., Defeo O. (2002). Morphometric Relationships of Penaeid Shrimps in a Coastal Lagoon: Spatio-Temporal Variability and Management Implications. Estuar. Coast. 25, 282–287. doi: 10.1007/BF02691315
Roy K., Vrba J., Kaushik S. J., Mraz J. (2020). Feed-Based Common Carp Farming and Eutrophication: Is There a Reason for Concern? Rev. Aquacult. 12, 1–23. doi: 10.1111/raq.12407
Serpa D., Ferreira P. P., Ferreira H., Fonseca L., Dinis M. T., Duarte P. (2013). Modelling the Growth of White Seabream (Diplodus Sargus) and Gilthead Seabream (Sparus Aurata) in Semi-Intensive Earth Production Ponds Using the Dynamic Energy Budget Approach. J. Sea. Res. 76, 135–145. doi: 10.1016/j.seares.2012.08.003
Sharawy Z. Z., Hufnagl M., Temming A. (2019). A Condition Index Based on Dry Weight as a Tool to Estimate in-Situ Moult Increments of Decapod Shrimp: Investigating the Effects of Sex, Year and Measuring Methods in Brown Shrimp (Crangon Crangon). J. Sea. Res. 152, 101762. doi: 10.1016/j.seares.2019.05.004
Sousa T., Domingos T., Poggiale J. C., Poggiale J. C., Kooijman S. A. L. M. (2010). Dynamic Energy Budget Theory Restores Coherence in Biology. Philos. T. R. Soc. B. 365, 3413–3428. doi: 10.1098/rstb.2010.0166
Spillman C. M., Hamilton D. P., Hipsey M. R., Imberger J. (2008). A Spatially Resolved Model of Seasonal Variations in Phytoplankton and Clam (Tapes Philippinarum) Biomass in Barbamarco Lagoon, Italy. Estuar. Coast. Shelf. S. 79, 187–203. doi: 10.1016/j.ecss.2008.03.020
Su X., Liu J., Wang F., Wang Q., Liu D. (2019). Effect of Temperature on Agonistic Behavior and Energy Metabolism of the Swimming Crab (Portunus Trituberculatus). Aquaculture 516, 734573. doi: 10.1016/j.aquaculture.2019.734573
Talbot S. E., Widdicombe S., Hauton C., Bruggeman J. (2019). Adapting the Dynamic Energy Budget (DEB) Approach to Include non-Continuous Growth (Moulting) and Provide Better Predictions of Biological Performance in Crustaceans. ICES. J. Mar. Sci. 76, 192–205. doi: 10.1093/icesjms/fsy164
Troell M., Halling C., Neori A., Chopin T., Buschmann A. H., Kautsky N., et al. (2003). Integrated Mariculture: Asking the Right Questions. Aquaculture 226, 59–90. doi: 10.1016/S0044-8486(03)00469-1
Troell M., Joyce A., Chopin T., Neori A., Buschmann A. H., Fang J. G. (2009). Ecological Engineering in Aquaculture — Potential for Integrated Multi-Trophic Aquaculture (IMTA) in Marine Offshore Systems. Aquaculture 297, 1–9. doi: 10.1016/j.aquaculture.2009.09.010
Trottet A., George C., Drillet G., Lauro F. M. (2021). Aquaculture in Coastal Urbanized Areas: A Comparative Review of the Challenges Posed by Harmful Algal Blooms. Crit. Rev. Env. Sci. Tec. 1—42. doi: 10.1080/10643389.2021.1897372
Wang X. G. (2017). Growth Characteristics of Portunus Trituberculatus in Zhejiang Fishing Ground (M. Sc. Dissertation. Zhejiang: Zhejiang Ocean University).
Wang Y. B., Gao L., Chen Y. X. (2018). Assessment of Portunus (Portunus) Trituberculatus (Mier) Stock in the Northern East China Sea. Indian. J. Fish. 65, 28–35. doi: 10.21077/ijf.2018.65.4.81039-03
Yang T., Ren J. S., Kooijman S., Shan X., Gorfine H. (2020). A Dynamic Energy Budget Model of Fenneropenaeus Chinensis With Applications for Aquaculture and Stock Enhancement. Ecol. Model. 431, 109186. doi: 10.1016/j.ecolmodel.2020.109186
Zhang K., Tian X. L., Dong S. L., Dong J., Feng J., He R. P., et al. (2015). Nitrogen and Phosphorus Budgets of Polyculture System of Portunus Trituberculatus, Litopenaeus Vanname and Ruditapes Philippinarum. Periodic. Ocean. Univ. China 45, 44–53. doi: 10.16441/j.cnki.hdxb.20140063
Keywords: intensive mariculture pond, nutrient dynamic simulation, discontinuous growth model, Portunus trituberculatus populations, molt, condition factor
Citation: Dong S, Xu X, Lin F, Yu L, Shan H and Wang F (2022) A Discontinuous Individual Growth Model of Swimming Crab Portunus trituberculatus and Its Application in the Nutrient Dynamic Simulation in an Intensive Mariculture Pond. Front. Mar. Sci. 9:918449. doi: 10.3389/fmars.2022.918449
Received: 12 April 2022; Accepted: 03 May 2022;
Published: 31 May 2022.
Edited by:
Yangfang Ye, Ningbo University, ChinaReviewed by:
Yongxu Cheng, Shanghai Ocean University, ChinaCopyright © 2022 Dong, Xu, Lin, Yu, Shan and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fang Wang, d2FuZ2ZhbmcyNDlAb3VjLmVkdS5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.