The Identification and Prediction of Mesoscale Eddy Variation via Memory in Memory With Scheduled Sampling for Sea Level Anomaly

Ocean mesoscale eddies are ubiquitous in world ocean and account for 90% oceanic kinetic energy, which dominate the upper ocean flow field. Accurately predicting the variation of ocean mesoscale eddies is the key to understand the oceanic flow field and circulation system. In this article, we propose to make an initial attempt to explore spatio-temporal predictability of mesoscale eddies, employing deep learning architecture, which primarily establishes Memory In Memory (MIM) for sea level anomaly (SLA) prediction, combined with the existing mesoscale eddy detection. Oriented to the western Pacific ocean (125°−137.5°E and 15°−27.5°N), we quantitatively investigate the historic daily SLA variability at a 0.25° spatial resolution from 2000 to 2018, derived by satellite altimetry. We develop the enhanced MIM prediction strategies, equipped with Gated Recurrent Unit (GRU) and spatial attention module, in a scheduled sampling manner, which overcomes the gradient vanishing and complements to strengthen spatio-temporal features for long-term dependencies. At the early stage, the real value SLA input guides the model training process for initialization, while the scheduled sampling intentionally feeds the newly predicted value, to resolve the distribution inconsistency of inference. It has been demonstrated in our experiment results that our proposed prediction scheme outperformed the state-of-art approaches for SLA time series, with MAPE, RMSE of the 14-day prediction duration, respectively, 5.1%, 0.023 m on average, even up to 4.6%, 0.018 m for the effective sub-regions, compared to 19.8%, 0.086 m in ConvLSTM and 8.3%, 0.040 m in original MIM, which greatly facilitated the mesoscale eddy prediction. This proposed scheme will be beneficial to understand of the underlying dynamical mechanism behind the predictability of mesoscale eddies in the future, and help the deployment of ARGO, glider, AUV and other observational platforms.

Introduction

Ocean mesoscale eddies, the rotating vortices with typical horizontal scales of tens to hundreds km and timescales on the order of weeks to months, are ubiquitous in world ocean. They induce significant transport of water mass, heat, salt, dissolved CO₂, and other important oceanic tracers, which may have profound climatological impact (Bryden and Brady, 1989; Martin and Richards, 2001; McGillicuddy et al., 2007; Chelton et al., 2011a; Chen et al., 2011; Sarangi, 2012; Frenger, 2013; Dong et al., 2014; Zhang Y. et al., 2014; Zhang Z. G. et al., 2014, 2017; Zhang et al., 2016; Ma et al., 2019; Yang et al., 2019; Tian et al., 2020; Zhang and Qiu, 2020; Martínez-Moreno et al., 2021; Thoppil et al., 2021). The mesoscale eddies account for 90% oceanic kinetic energy and dominate the upper ocean flow field (Pascual et al., 2006; Wunsch, 2007; Martínez-Moreno et al., 2021). Accurately predicting the variation of ocean mesoscale eddies is the key to understand the oceanic flow field and circulation system. That could provide opportunities to potentially identify the underlying patterns and mechanism associated with mesoscale eddies, as well as the related physical and biogeochemical impact. It could also help to guide the deployment of Array for Real-time Geostrophic Oceanography (ARGO), ocean glider, or Autonomous Underwater Vehicles (AUV), and when the observational missions are involved mesoscale eddies (Chaigneau et al., 2011; Zhang et al., 2013; Dong et al., 2017; Gourdeau et al., 2017; Shu et al., 2019; Chen et al., 2021).

For decades, there have been intensive attention working on the predictability of mesoscale eddy. The existing techniques could be roughly divided into the numerical methods, mathematical statistics, and machine learning approaches. Robinson et al. (1984) and Robinson and Leslie (1985) first predicted the evolution of eddies during 2-week periods in the north-east Pacific off California, encouraging a lot the prospects of mesoscale eddy forecast. Ocean dynamical models have long been used to predict mesoscale eddies (Rienecker et al., 1987). Masina and Pinardi (1994) presented a quasi-geostrophic numerical model with a set of initial fields for mesoscale assimilation around the Middle Adriatic Sea, to make a 30-day dynamical prediction of the mesoscale flow field. Shriver et al. (2007) performed a 30-day forecast with the increased forecast resolution from 1/16° to 1/32°, based on the Navy Layered Ocean Model (NLOM), and compared to ocean water color images of the Northwest Arabian Sea and Gulf of Oman, with the median eddy center location error 29 km of 80% reliability.

Progresses have been made with data assimilation scheme and the increase of resolution. It has been reported that the daily forecast errors of eddy center positions in the northwestern Arabian Sea and the Gulf of Oman could be 44–68 km with the 1/12° global HYCOM model, and have reached to 22.5–37 km with the 1/32° NLOM model (Hurlburt et al., 2008). Eddy resolving, non-assimilative models are insufficient for accurate prediction of evolving mesoscale eddies and fronts due to mismatches in the initial locations (Thoppil et al., 2021). Data assimilation could provide the initial conditions for forecast but does not compensate for the shortcomings of most models (Li et al., 2019). In addition, these kinds of approaches tend to be very time-consuming and computation resource dependent, which brings great challenges to simultaneously perform ocean mesoscale eddy prediction in high accuracy with higher efficiency.

Recently, machine learning framework has been increasingly applied into mesoscale eddy prediction (Elman, 1990; Hochreiter and Schmidhuber, 1997; Grigorievskiy et al., 2014; Box et al., 2015). Li et al. (2019) have built one predictive model for mesoscale eddy propagation trajectory with the multiple linear regression, based on 5 years of satellite altimeter data in the northern South China Sea (NSCS), demonstrated its forecast skills over a 4-week window, relating oceanic parameters about the effects of β and mean flow advection, and the accuracy was sensitive to eddy polarity and the forecast season. Ma et al. (2019) proposed an improved Convolutional Long Short-Term Memory (ConvLSTM) network for mesoscale eddy forecast, to reconstruct the spatio-temporal characteristics of the sea level anomaly (SLA), combined with an SLA-based eddy detection algorithm, and the predicted eddies are closer to eddies detected from AVISO SLA data, compared with the Hybrid Coordinate Ocean Model data set (HYCOM). Wang et al. (2020) have predicted mesoscale eddy properties and propagation trajectories with Long Short-Term Memory (LSTM) and extra trees (ET), showing superior performances with the root mean square error (RMSE) of the meridional displacement from 23.8 to 37.2 km, and the zonal displacement from 28.8 to 47.2 km, for 1–4 week prediction duration.

Due to the great success of deep learning, all kinds of most emerging and advanced algorithms have been developed and made progresses in the context, in learning the deterministic spatial correlations and temporal dependencies (Röske, 1997; Sertel et al., 2008; Niedzielski and Miziński, 2013), from Deep Belief Networks (DBN) (Hinton et al., 2006), Deep Convolutional Neural Networks (CNN) (Karpathy et al., 2014), AlexNet (Krizhevsky et al., 2012) to recent Generative Adversarial Networks (GAN) (Goodfellow et al., 2014), Deep Residual Networks (ResNet) (He et al., 2016) and Dense Convolutional Network (DenseNet) (Huang et al., 2017). Among them, the deep architecture of the Recurrent Neural Networks (RNN), which could model the sequences at the arbitrary length by applying a transition function to all its hidden layer states in a recursive manner, and capture all information stored in sequence in the previous element, has been proven to be quite effective in prediction (Lipton, 2015; Braakmann-Folgmann et al., 2017). Long Short Term Memory (LSTM) has been designed by adjusting the structure of the hidden neurons, based on a series of memory cells recurrently connected through layers to capture and retain the long-term dependencies, not only suppressing the disappearing gradient problem, but also enhancing the capability in predicting multi-step ahead into the future (Zhang et al., 2017; Wang et al., 2018; Shi and Yeung, 2018; Nian et al., 2021). Wang et al. (2019b) revolutionarily proposed Memory In Memory (MIM) networks to exploit the differential signals between the adjacent recurrent states to model the non-stationary and approximately stationary properties in spatio-temporal dynamics with two cascaded, self-renewed memory modules, by stacking multiple MIM blocks, potentially handle higher-order non-stationarity time series prediction.

Meanwhile, there have been a large number of mesoscale eddy identification algorithms that could be developed to indirectly act on predicting mesoscale eddy activities (Wu, 2014; Yi et al., 2014; Du et al., 2019; Duo et al., 2019; Moschos et al., 2020), which could be primarily divided into four types, the physical based algorithms (Okubo, 1970; Weiss, 1991; Isern-Fontanet et al., 2003; Morrow et al., 2004; Chelton et al., 2007; Chaigneau et al., 2008), the geometrical based algorithms (Sadarjoen and Post, 2000; Nencioli et al., 2010), the hybrid algorithms (Halo et al., 2014; Mkhinini et al., 2014; Le Vu et al., 2018), and sea surface height (SSH) based algorithms (Fang and Morrow, 2003; Chelton et al., 2011b; Mason et al., 2014; Laxenaire et al., 2018), including Okubo-Weiss (O-W), Vector-Geometry (V-G), and Winding-Angle (W-A) algorithms, etc. Chelton et al. (2011b) investigated mesoscale eddy variability in the global ocean within 16 years of SSH observations comprising approximately 1.15 million eddy observations, suggested the prevalence of coherent mesoscale features are readily apparent, and proposed an automated procedure to identify and track mesoscale features based on their SSH signatures, which yields 35,891 long-lived eddies, with an average life cycle of 32 weeks and an average propagation distance of 550 km, the mean amplitude and a speed-based radius scale 8 cm and 90 km. Liu et al. (2016) proposed parallel identification of mesoscale eddies by simplifying the recognition process and SLA contour search range, characterized the eddy structure with radius, amplitude, eddy core, and closed SLA contour by maximum average geostrophic velocity. Tian et al. (2020) put forward the parallel eddy identification and tracking algorithm, validated by Argo float trajectory and drifter trajectory data, where the vectorized contour line-based boundaries enabled the centroid core to be computed with high accuracy and the most stable properties of eddies have been chosen as a set of dimensionless similarity parameters.

At present, the advances in remote sensing technologies have enabled the acquisition of global observation to be more accessible in ocean mesoscale eddy detection, tracking, prediction tasks. Mesoscale eddies have been investigated both intensively and extensively with long-term time series (Oey et al., 2005; Wang et al., 2015; Świerczyńska et al., 2016; Fablet et al., 2017; Imani et al., 2017; Fu et al., 2019), e.g., sea surface height, salinity, temperature, SLA, etc. The initialization of ocean dynamic state through assimilation underpins prediction with the optimal statistical estimation from the numerical models and the sparse ocean interior information (Thoppil et al., 2021). It has been reported that the current generation of the operational products has received prediction skills of median SSH with at least 5–10 cm RMSE calculation from model-driven methods (Smedstad et al., 2002; Martin et al., 2007; Drévillon et al., 2008; Chassignet et al., 2009; Cornillon et al., 2009; Metzger et al., 2010, Metzger et al., 2014; Thoppil et al., 2021).

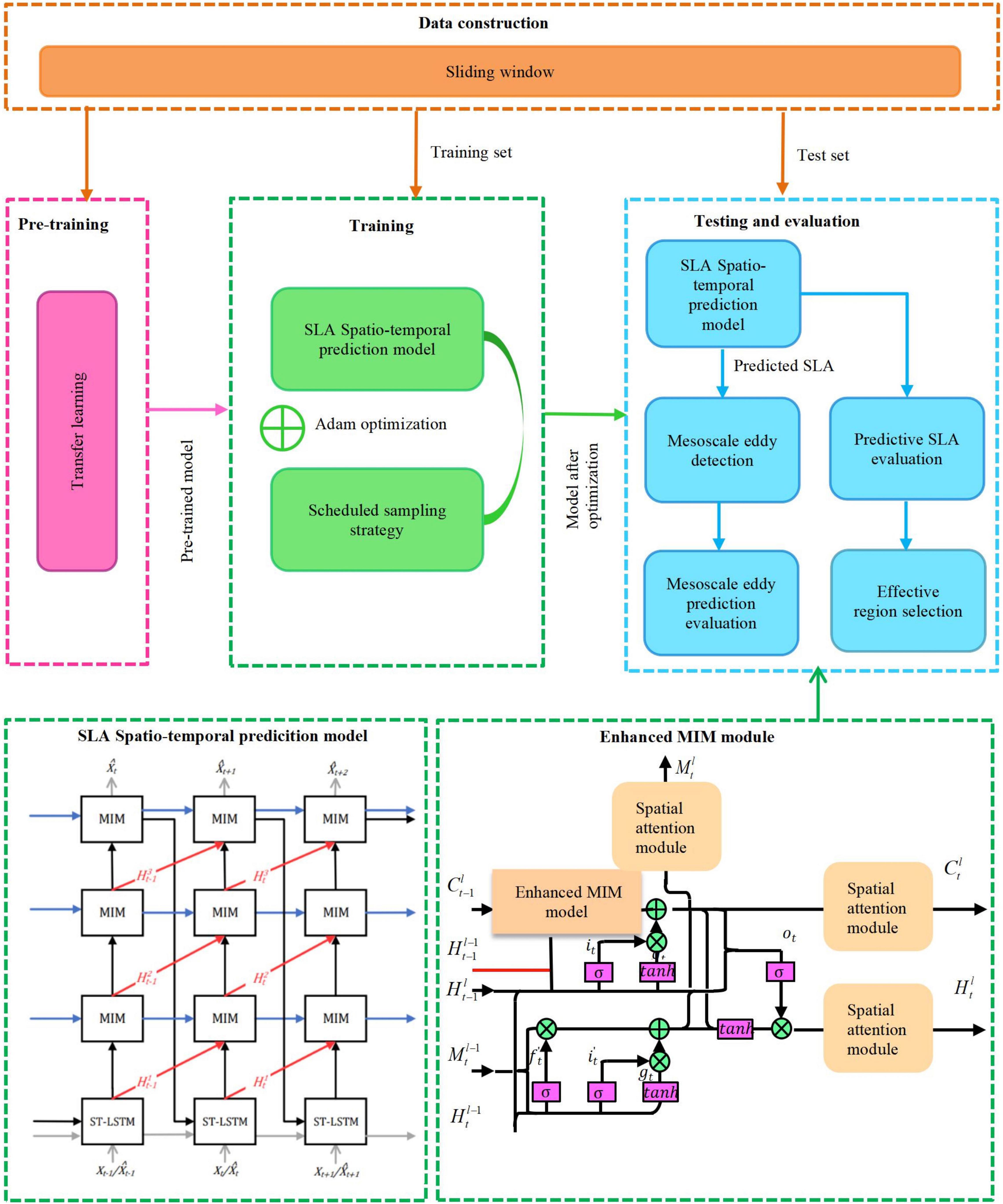
In this article, we make an attempt to develop mesoscale eddy prediction strategies with their SLA time series, combined with the existing mesoscale eddy detection algorithm, as is shown in Figure 1. The overall framework of our proposed mesoscale eddy prediction is made up of correlative steps, including model construction, pre-training, optimization, transfer learning, performance evaluation. One deep learning based model has been constructed to explore the mechanism of SLA prediction process, by means of an enhanced MIM with scheduled sampling (Bengio et al., 2015). In view of the availability in most mesoscale eddy identification and tracking algorithms, we primarily focus on how to establish SLA prediction with higher accuracy and efficiency. We incorporate the Gated Recurrent Unit (GRU) (Cho et al., 2014; Chung et al., 2014) and the spatial attention (Jaderberg et al., 2015; Zhu et al., 2019) into original MIM architecture, in order to balance the computation complexity and prediction accuracy, and strengthen feature extraction with spatio-temporal variability characteristics in SLA. We adopt scheduled sampling to solve the inconsistency of input distribution. At the early stage of training, the real value input leads to a reasonable state from a randomly initialized state, and as the training progresses, it gradually involves the newly generated value to feed into the model.

FIGURE 1

Figure 1. Overall flow chart of the mesoscale eddy prediction system.

The remainder of the article is organized as follows: Section “Data” describes the study area and the access of SLA time series referred. Section “Sea Level Anomaly Prediction With Enhanced Memory In Memory and Scheduled Sampling” outlines the architecture of our SLA prediction network with the enhanced MIM and scheduled sampling, including the basics in MIM, GRU and spatial attention module, Section “Mesoscale Eddy Detection With Sea Level Anomaly Prediction” introduces mesoscale eddy detection algorithm. Section “Simulation Experiment and Result Analysis” quantitatively and systematically evaluates the performance of our proposed spatio-temporal prediction model for mesoscale eddy variation, and exhibits the experimental results. Finally, the conclusion is drawn in section “Conclusion.”

Data

The SLA product in our study, retrieved from Archival Verification and Interpretation of Satellite Oceanographic Data (AVISO), hosted at the Copernicus Climate Change Service Center (C3S)¹, is defined as the water height above the average sea level, composed of gridded sea height with a 0.25° Mercator projection covering between 0°E–360°E and 90°S–90°N from 1993 to 2020, processed and generated by Data Unification and Altimeter Combination System (DUACS) (Taburet et al., 2019), in the optimally interpolated mapping procedure, through the use of multiple altimetry satellites (ERS-1/2, Topex/Poseidon, ENVISAT, and Jason-1/2) and uniform calibration standards. In addition, the centered processing time window and verification process increase the stability and accuracy of sea level variables, and adapt to mesoscale eddy applications, enabling the retrieval of long-term ocean variability. The average reference value for SLA is calculated for two decades, and the coverage region could reach the global scope, its spatial resolution is 0.25° latitude, and the temporal resolution is daily. Our study area is located in the western Pacific ocean (125°−137.5°E and 15°−27.5°N), as is shown in Figure 2, represented in green rectangle, where the propagation paths of mesoscale eddies in 2000–2018 and corresponding density distribution are also listed, with cyclonic eddies in red and anticyclonic eddies in blue.

FIGURE 2

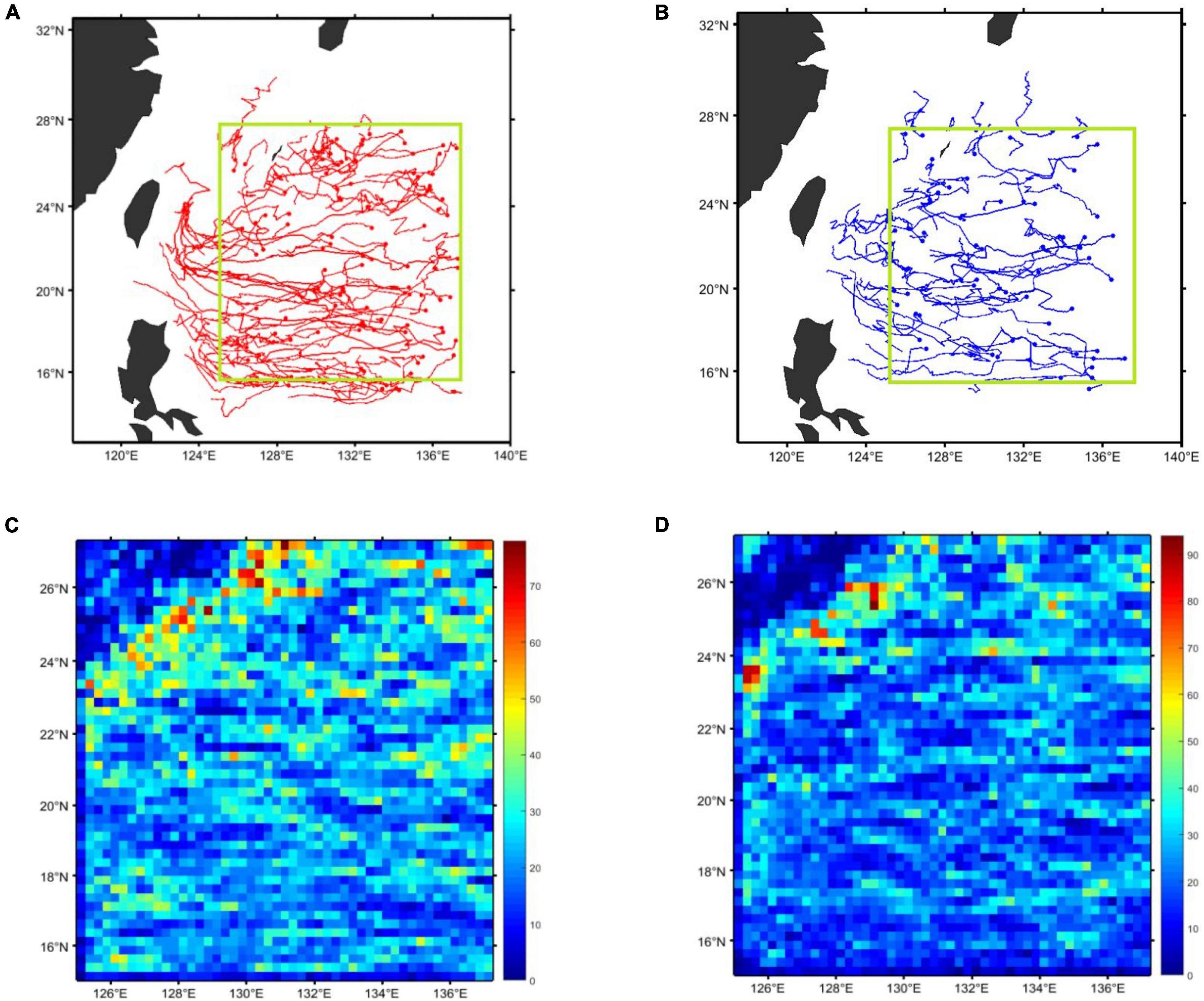
Figure 2. Propagation paths and density distribution of mesoscale eddies in the study area. (A) Propagation paths of cyclonic eddies. (B) Propagation paths of anticyclonic eddies. (C) Density distribution of cyclonic eddies. (D) Density distribution of anticyclonic eddies.

Sea Level Anomaly Prediction With Enhanced Memory in Memory and Scheduled Sampling

The intrinsic attributes of mesoscale eddies, including the variation of the amplitude, the rotation speed, and the radius, are significantly involved in the time-varying processes. SLA time series could reflect those variability correlative with origins of mesoscale eddies to their evolution and propagation in manifold forms. According to Cramér’s decomposition (Cramér, 1961), the non-stationary SLA time series could be decomposed into deterministic, time-variant polynomial, plus a zero-mean stochastic term. The original MIM is to propose to exploit the differential operation between adjacent recurrent states so as to adapt the non-stationary and approximately stationary properties in spatio-temporal dynamics with two cascaded, self-renewed memory modules. Here we elaborate on one enhanced MIM strategy, equipped with GRU and spatial attention module, to discern non-stationary link toward SLA prediction through scheduled sampling, from the low-level features including spatial correlations or temporal dependencies, to high-level properties like accumulation, deformation, or dissipation.

Memory in Memory With Gated Recurrent Unit and Spatial Attention

In order to implement SLA prediction with long-term dependencies, we first develop one enhanced MIM mechanism, with GRU and spatial attention module, which makes a trade-off between model complexity and prediction accuracy for SLA time series highly associated with spatio-temporal variability of mesoscale eddies. Such deep learning scheme first applies the basic idea of stacking multiple MIM blocks to potentially handle the predictability of higher-order non-stationarity in SLA time series. Since over-differentiation for SLA prediction may inevitably lead to loss, the forget gate is replaced with two embedded long short-term memory in MIM, with the differential operation between adjacent hidden states in a loop path, so that one basic MIM consists of non-stationary module (MIM-N) and stationary module (MIM-S), which has been proved to be superior to basic Spatiotemporal LSTM (ST-LSTM) (Wang et al., 2017) and ConvLSTM (Shi et al., 2015) in prediction performance (Wang et al., 2019a). Second, due to the high computational requirement in the entire MIM network architecture, we propose to simplify the model size of the original MIM for SLA prediction, with the update gate and reset gate inspired by GRU unit, which enables to manage the long-term flow, with much less calculation and parameter size, refines the model construction into a lightweight level. Third, the spatio-temporal variation of SLA time series appears with the variable location, while the convolutional recursive structure in deep learning framework is position-invariant at every moment. We further focus on constructing one spatial attention mechanism to refrain from the connection structure mismatching within the convolution operation for the enhanced MIM scheme. More details could be found in our Supplementary Material.

Model Construction for Sea Level Anomaly Prediction

The overall model construction for SLA prediction is shown in Figure 3, by stacking three enhanced MIM blocks and one ST-LSTM layer, with the diagonal state transition paths for differentiation is in red arrows, the horizontal transition paths of the memory cells in blue arrows, and the zigzag state transition paths in black arrows, to capture higher orders of non-stationarity signals, gradually stationarize the spatio-temporal process and make the time series more predictable. The ST-LSTM layer extracts spatial and temporal representations simultaneously in a unified memory cell and conveys the memory both vertically across layers and horizontally over states. When inputting into MIM-N module, we adaptively decide to forget or remember the differentiation or cell state with gating mechanism. If the differentiation disappears, indicating that non-stationary dynamics would not be prominent, MIM-S will reuse the original cell state. On the contrary, MIM-S covers the cell state and focuses more on non-stationary component, while repeatedly differentiating may lead to the stationary process.

FIGURE 3

Figure 3. Overall predictive model construction.

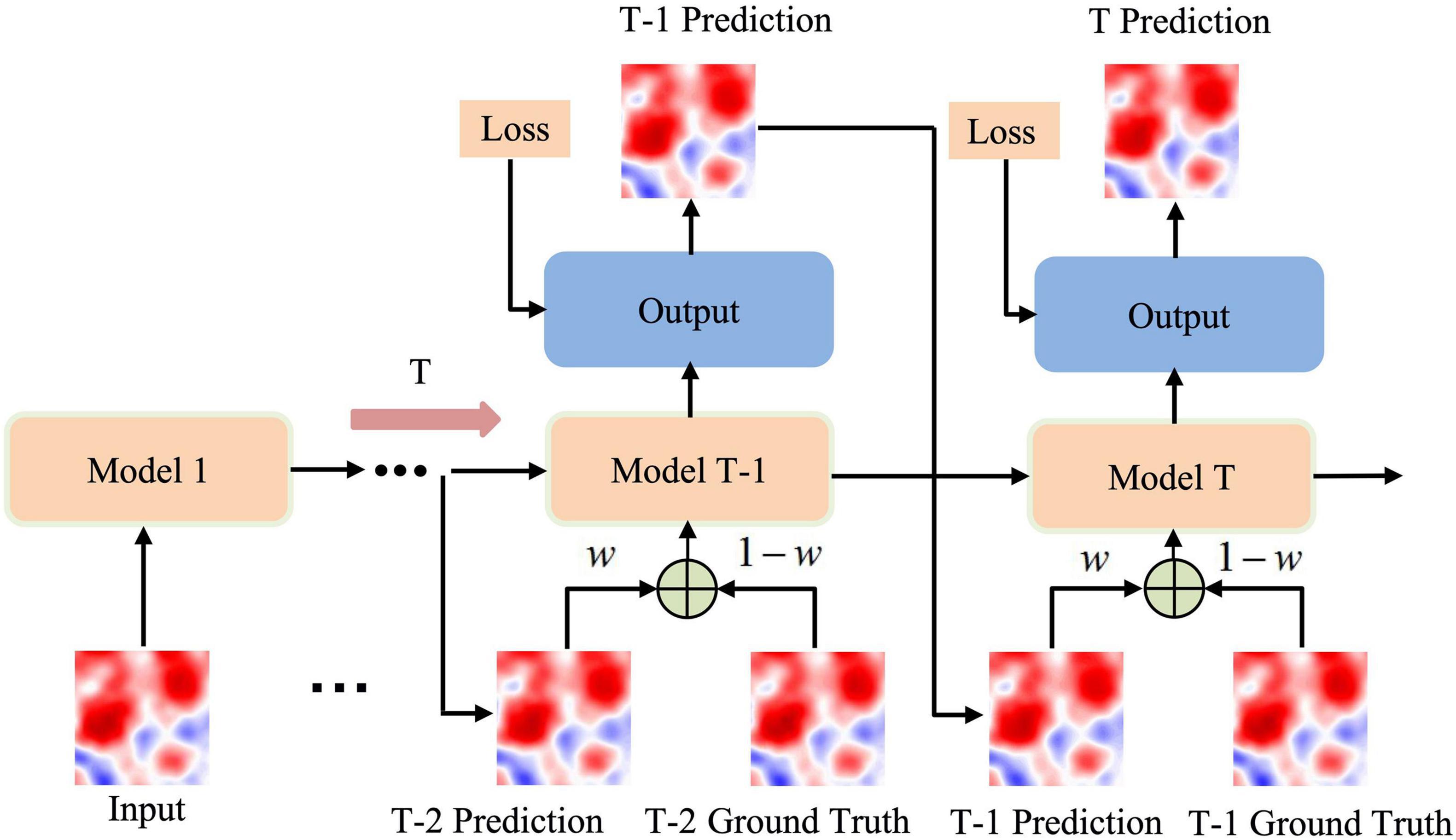
For the SLA multi-step prediction, the training process in the original MIM consists of maximizing the likelihood of each output given the current recurrent state and the previous input. The error accumulation problem sharply occurs as the prediction time steps proceed, partially due to the unbalanced scale between the training and test samples. We employ the learning strategy of scheduled sampling for SLA prediction in the context of reinforcement learning, to gently change the training process from a fully guided scheme with the ground truth, toward a less guided scheme which mostly makes use of the already generated prediction instead. The enhanced MIM model is hereby designed to learn how to recognize the discrepancy and force itself to correct error accumulation, by deciding whether the ground truth or the predicted output value behaves as the input for the next step. In virtue of such adversarial learning, we would expect to pursue a probably better balance in modeling between the training and inference stages more consistently for SLA prediction. In response to the resulting convergence at the low speed, we assigned a summed weight for both the ground truth and predicted output value, instead of the probability, to improve the scheduled sampling strategy, as is shown in Figure 4. The superposition only happens from the time t to be predicted, not the time step at the origin. The weight of superposition indicates the proportion that the predicted output value takes, at the initial stage of insufficient training, it tends to be set relatively low. As the model parameters are thoroughly learned, it will gradually increase, and finally completely depend on the predicted output value. In this way, we could combine the two candidates as a fused input with the dynamic weight coefficient, to improve the capacity of long-term dependencies for SLA prediction.

FIGURE 4

Figure 4. Framework of the improved Scheduled Sampling.

Mesoscale Eddy Detection With Sea Level Anomaly Prediction

The existing SSH based mesoscale eddy identification and tracking algorithms have been essentially well suited to mesoscale eddy detection from noisy SSH (Chelton et al., 2011b). In this article, we directly employ the above algorithm to conduct the mesoscale eddy identification in aid of SLA variation prediction. The eddy identification procedure strives to achieve threshold-free mesoscale eddy detection without the differentiation of the SSH field and with no smoothing beyond that inherent in the SSH fields of the AVISO Reference Series, obviating the need to differentiate the SSH fields and avoiding the associated deleterious effects of noise that are problematic in numerous previous studies.

Simulation Experiment and Results Analysis

In our simulation experiment, we retrieved the records of SLA time series from AVISO, ranging from 2000 to 2018, to benefit for our prediction tasks of mesoscale eddies. Due to the advancement of multi-satellite altimeter sensing techniques, we applied SLA time series after 2000, as the fused observation has been collected with consistently high temporal and spatial resolutions in quality. The experimental steps and result analysis, such as the construction of SLA dataset, the optimization strategy in the enhanced MIM architecture with scheduled sampling, including the pre-training of transfer learning, the solution in over-fitting, and model selection of hyperparameters, as well as the prediction performance evaluation, will be involved here.

Dataset Creation for Sea Level Anomaly Prediction

We tried to devote to predict SLA time series of the next 14 days at most, with our proposed mechanism, provided with the known SLA time series available 14 days before. Owing to the scarcity of records for deep learning, we considered the segmentation and data augmentation techniques for SLA time series. The certain sliding window of a 14-day prediction duration has been defined, with a time step of 1 day long, as is shown in Figure 5A. If we arbitrarily shift this window on SLA time series and stop at any location along the time domain, there will be 14-day input in red rectangle and 14-day expected output in blue rectangle for the enhanced MIM architecture.

FIGURE 5

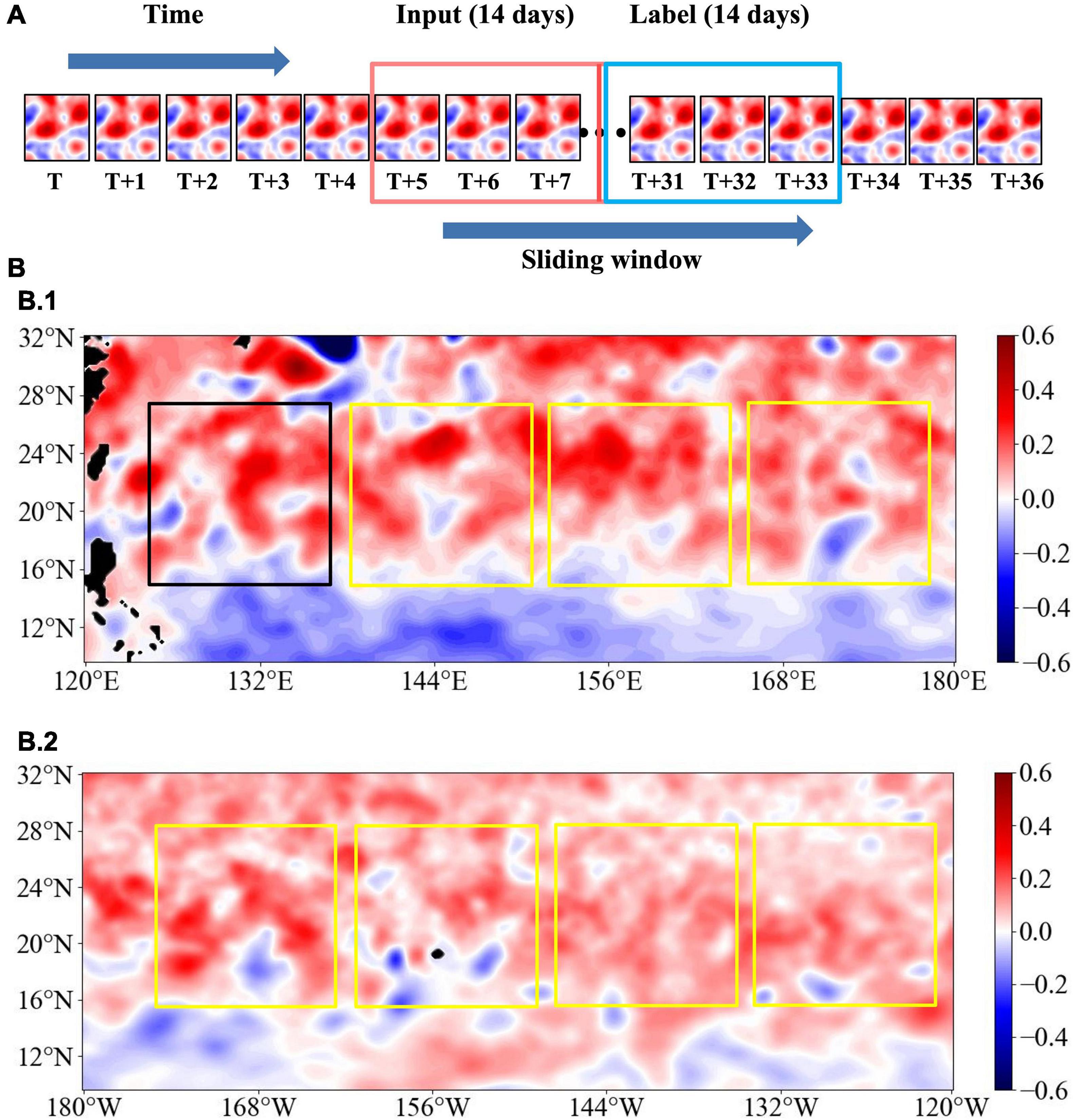
Figure 5. Data segmentation and augmentation for SLA time series. (A) Segmentation with sliding window. (B) Augmentation of SLA time series for transfer learning.

In view of the fact that the deep learning model in this article requires a large amount of high-quality labeled data, pre-training and fine-tuning in transfer learning are commonly used techniques to solve the problem of low data volume and improve the training speed and generalization ability of the model. Since it is of great importance to implementing deep learning with sufficient samples in appropriate models, we introduced a large number of extra SLA time series for transfer learning, respectively from the regions located at the same latitude of our study area, as is shown in Figure 5B, with our study area in black rectangle, and the other regions in yellow rectangle.

In this way, the total number of all the SLA time series segments in our study area for the 14-day prediction duration from 2000 to 2018 is 6,400, of 50×50 in size, and then we divided the original time series segment datasets into three types individually, 4,000 selected from the even years between and including 2000 and 2018 for training, 1,200 selected from the odd years between and including 2001 and 2007 for cross-validation, and 1,200 selected from the odd years between and including 2009 and 2017 for testing. Meanwhile, 45,000 extra samples from other seven regions at the same latitude, have been taken to facilitate transfer learning in the enhanced MIM architecture with scheduled sampling for a higher prediction accuracy.

During our transfer learning, we first established SLA prediction in a source task for the eight regions together, related to a large amount of training samples, to feed into the enhanced MIM architecture with scheduled sampling and develop the source model, then reused the pre-trained model with the learned parameters to initialize the model in our target task for the study area, and finally fine-tuned the previous model for further optimization.

Model Construction, Configuration, Selection

The configuration of supercomputing solutions during the model building, training and testing process, is as follows, NVIDIA TITAN Xp Graphics Card and GeForce GTX 1080Ti Graphics Cards, Intel Core i5-2410M CPU, with main frequency 2.3 GHZ, 32 GB Memory Cards, Ubuntu 16.04 operating system, Tensorflow1.3.0 Deep learning framework, Python3.5 interpreter, data science libraries including NumPy and Pandas, and netCDF data viewers.

For the enhanced MIM architecture, all of the input and output SLA sequences were of 50×50 size. The best Adam optimizer has been adopted for optimization, among which β₁ and β₂ were, respectively, 0.95 and 0.9995, the learning rate was initially set to 10⁻³−10⁻⁴, until we determined to be 3e⁻⁴ for transfer learning, with the fine-tuning process 3e⁻⁵. We have chosen the loss function by the root mean square error of L2 regularization, and also added one Batch Normalization (BN) layer (Ioffe and Szegedy, 2015) and parameter clipping to prevent overfitting. The parameter clipping C value was 0.01; the initialization utilized the Xavier method, designed for the tanh activation function, and the parameter matrix initialization was as follows:

$w_{ij}\text{∼}U(-\frac{1}{\sqrt{n}},\frac{1}{\sqrt{n}})(1)$

Where w_ij refers to the weight parameter matrix from the ith layer to the jth layer that obeys a uniform probabilistic distribution U, with n the total number of network parameters in the enhanced MIM architecture. For the model selection, we have conducted a series of hyperparameter evaluation experiments in comparison. As a basic hyperparameter, too large a batch size leads to poor generalization ability and easily causes Out of Memory (OOM), and too small a batch causes unstable convergence. We have combined the local computational resources and prior knowledge to provide three alternative values: 4, 8, and 16. At the same time, for the number of filters about the feature map channels, too few could lead to under-fitting, too many might bring over-fitting, and OOM problem. We adopted three alternative values: 16, 32, and 64, with the size of the convolution kernel.

As a commonly used parameter tuning technique, grid search has been used to combine all parameter possibilities to select our optimal model, and the average percentage error of multiple parameter combination and selection for the 14-day prediction duration has been listed in Table 1. It could be seen from the experimental results that when the number of filters and batch size are (64, 8) and (64, 4), there occurred OOM in deep learning. Since both the batch size and the number of filters had a great impact on memory, we had to look for their trade-off with higher prediction performance. The relatively optimal parameter combination in bold was to choose the filter number 32 and the batchsize 8, and for the dual GPU, the batchsize of each GPU was 4.

TABLE 1

Table 1. Hyperparameter grid search.

Quantitative Metrics for Sea Level Anomaly Prediction

We employ Mean Absolute Percentage Error (MAPE) and Root Mean Square Error (RMSE) metrics to quantify the prediction performances with the reference SLA maps.

Mean Absolute Percentage Error is initially defined as follows,

$MAPE=\frac{1}{m}\sum _{k=1}^m\left|\frac{(y_{i,j}^k-{\widehat{y}}_{i,j}^k)}{y_{i,j}^k}\right|\times 100\%(2)$

Where $y_{i,j}^k$ stands for the kth actual value at the spatial location (i,j) and ${\widehat{y}}_{i,j}^k$ is the kth predicted value, m refers to the number of samples.

Root Mean Square Error can be expressed as follows,

$RMS{E}_{i,j}=\sqrt{\frac{1}{m}\sum _{k=1}^m{(y_{i,j}^k-{\widehat{y}}_{i,j}^k)}^2}(3)$

Where ${\widehat{y}}_{i,j}^k$ is the kth actual value at the spatial location (i,j) and ${\widehat{y}}_{i,j}^k$ is the corresponding kth predicted value, mrefers to the number of samples.

Optimization Strategies in Enhanced Memory in Memory Architecture

We further tried to evaluate the prediction performance of the enhanced MIM architecture with scheduled sampling.

First, we have verified whether our proposed model would be effectively extract the possibly non-stationary features of SLA time series. As is shown in Figure 6A, compared to the original MIM framework, as the time increased gradually in such 14-day prediction duration, the prediction performance did not change sharply, but rather smoothly, regarding to the average percentage error.

FIGURE 6

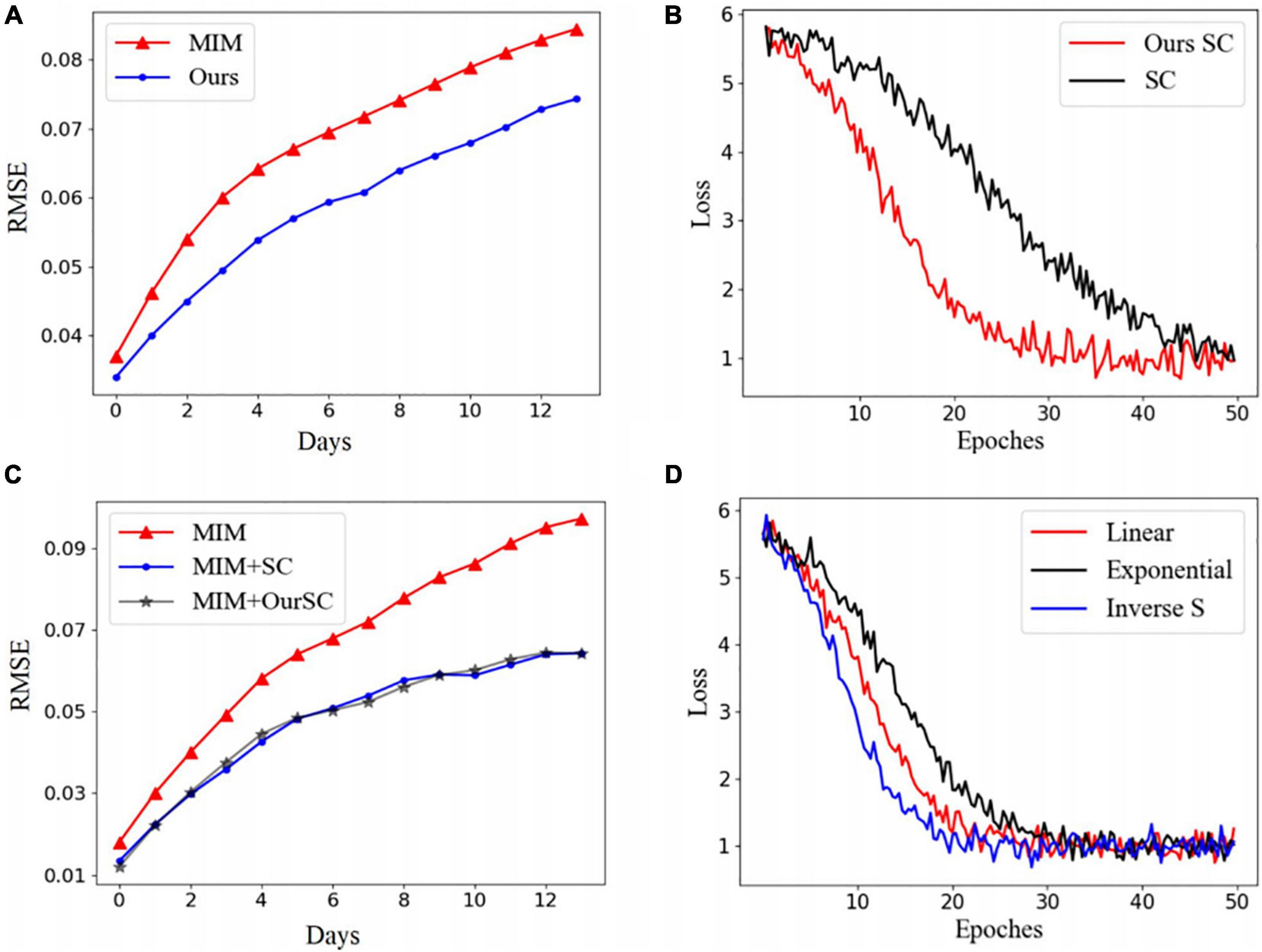
Figure 6. Prediction performance evaluation in enhanced MIM model with scheduled sampling (SC). (A) 14-day prediction performance comparison between original MIM and our enhanced scheme. (B) Comparison between our improved scheduled sampling (SC) with the classical one. (C) The enhanced MIM combining with the different scheduled sampling (SC) strategies. (D) Comparison in weight adjustment means.

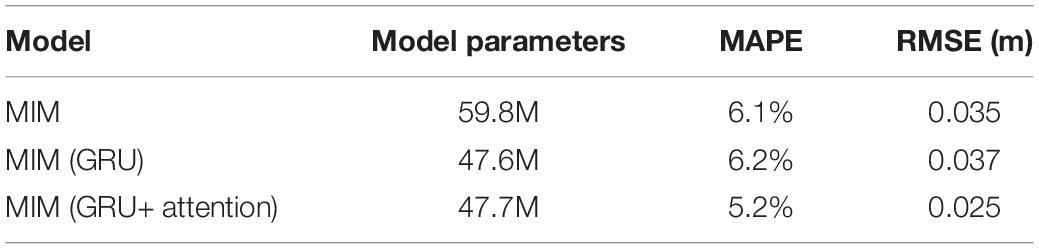
We further quantitatively investigated how much extent the progress of the prediction performance could benefit from the improvement of GRU and attention mechanism in our enhanced MIM model individually. The performance verification for each step is listed in Table 2, in terms of spatio-temporal averaged MAPE and RMSE. GRU simplified the calculation and reduced the storage of intermediate state at the cost of lower accuracy, and after the spatial attention module being added, by dynamically adjusting the weight in space, the fixed position of the convolution parameters was updated, and the prediction accuracy has been indeed improved.

TABLE 2

Table 2. Model performance verification.

We also examined the stacking number of the enhanced MIM modules as 2, 3, and 4, with spatio-temporal averaged MAPE and RMSE, as is shown in Table 3, and among them, three stacking MIM modules performed best, indicating its learning ability in high-order non-stationary features. Stacking too few MIM modules would lead to the insufficient non-stationary modeling capabilities, while MIM modules stacked too deep would probably bring difficulty in training and slow down the convergence.

TABLE 3

Table 3. Number of stacking layers.

Second, we have made comparison of our improved scheduled sampling with the classical one regarding to the losses during training, in the context of enhanced MIM framework, as is shown in Figure 6B, where the improved scheduled sampling made the model converge faster at the early stage of training.

In the enhanced MIM framework, the fused scheduled sampling outperformed to the traditional training and classical scheduled sampling, did significantly improve the error accumulation in multi-step prediction problem, achieved almost the comparable effects as the classical one, but accelerated the early convergence speed greatly, as is shown in Figure 6C.

We also carried out the comparative experiments to the weight update means as the number of training epochs increased, between the linear, exponential and inverse S-shaped function, as is shown in Figure 6D, where there have been no obviously differences in three functions for prediction accuracy, and the inverse S-shaped function tended to be more conducive to convergence, so we adopted by default.

Our transfer learning could be regarded as model optimization process, and we have considered the assessment of transfer learning by the convergence speed and prediction accuracy, in terms of the spatio-temporal averaged MAPE and RMSE, as is listed in Table 4. The pre-training model would make the whole training process much faster, at a smaller learning rate, compared to the training from scratch, indicating the transfer learning in bold accelerated the progress of the SLA prediction in our study, and the prediction accuracy have also improved through transfer learning.

TABLE 4

Table 4. Transfer learning with convergence speed and performance evaluation.

Performance Evaluation for Sea Level Anomaly Prediction

Overall Prediction Assessment

Furthermore, after individual evaluation in the performance improvement step by step, we made an overall assessment and comparison with the classic ConvLSTM, ConvLSTM with scheduled sampling (SC), and the original MIM model. In order to ensure the evaluation at the same level, all the models have adopted a four-layer network structure, with the most appropriate hyperparameters for our computational resources. It should be noted that neither the classic ConvLSTM nor the original MIM have not made any improvements in training strategies such as the scheduled sampling and transfer learning mechanisms.

After optimization, the overall predication performance of the four models is illustrated in Table 5, in terms of the spatio-temporal averaged MAPE and RMSE. It has been demonstrated that our proposed scheme in bold achieved better 14-day prediction performances, compared to that of classic ConvLSTM and the original MIM, as well as ConvLSTM with SC. The prediction results of classic ConvLSTM and ConvLSTM with SC tended to be noisy and less good in depicting the edges, both the proposed scheme and the original MIM behaved better at the early stage, and the former was more superior for the long-term prediction when the time proceeded, with a smooth SLA variation of distinct edges. The example prediction results of three models, including the classic ConvLSTM, the original MIM, and our proposed scheme, for a 14-day prediction duration, have been visualized in Figure 7A, with the effective sub-region location in yellow rectangle.

TABLE 5

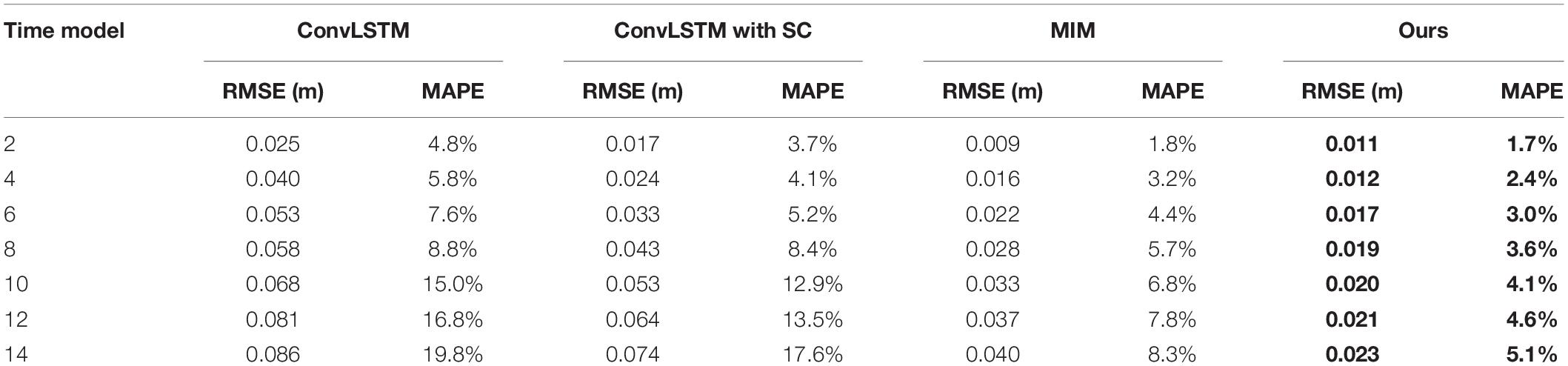
Table 5. Performance comparison among classical ConvLSTM, original MIM, ConvLSTM with scheduled sampling (SC), and the proposed scheme.

FIGURE 7

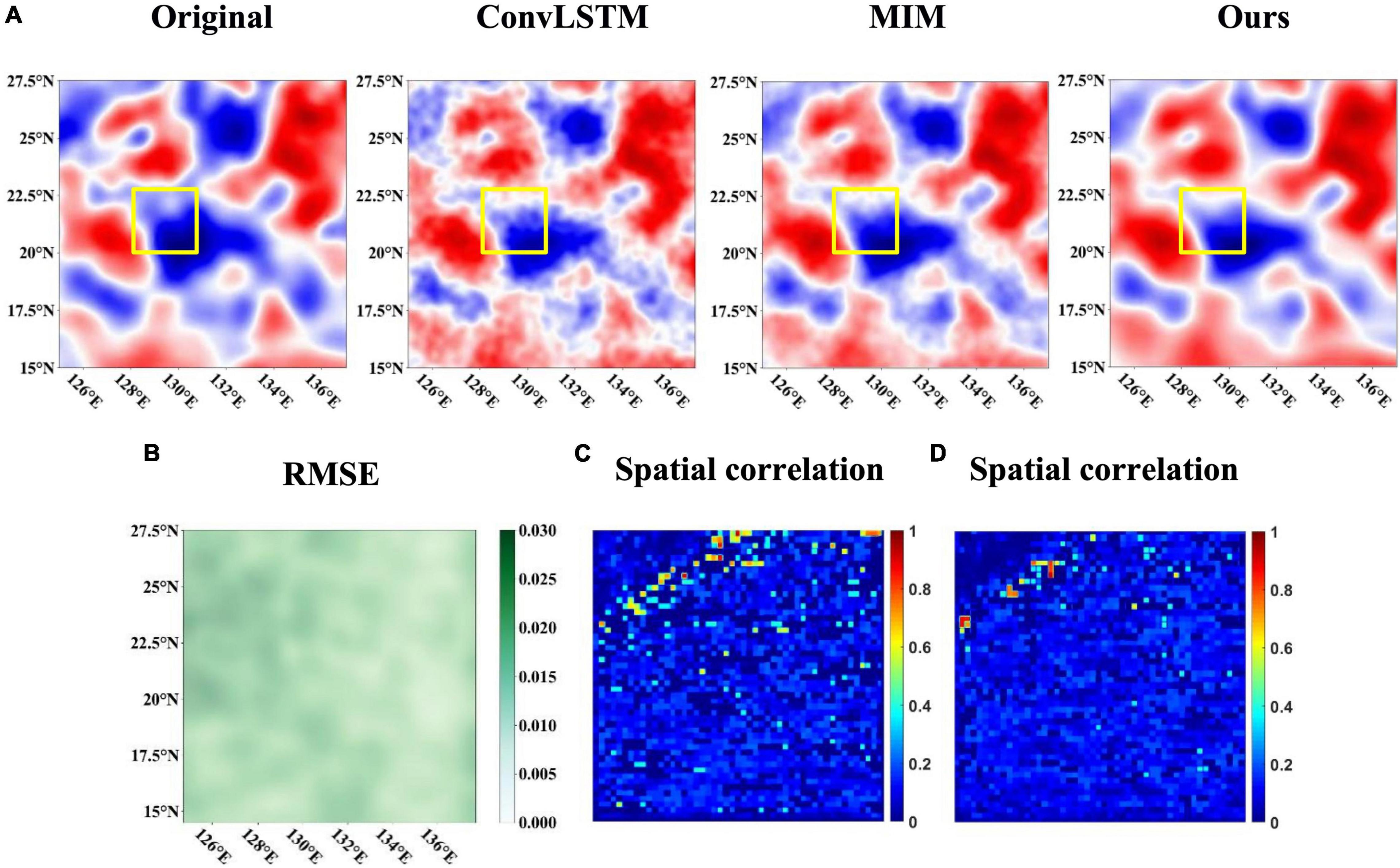
Figure 7. Example SLA prediction results and pointwise prediction performance for a 14-day prediction duration. (A) The example SLA prediction results from the classic ConvLSTM, the original MIM, and our proposed scheme. (B) RMSE spatial distribution for example SLA prediction with our proposed scheme. (C) Spatial correlation map between RMSE and cyclonic density distribution. (D) Spatial correlation map between RMSE and anticyclonic density distribution.

Meanwhile, we have also designed to randomly divide the entire dataset of all the SLA time series segments for training, verification, and test, and basically achieved as good performance as the above one in most cases under the deep learning architecture, showing no significant prediction preferences. Generally, the above experiment design basically provided the relatively reasonable prediction performances, reflected the uniform distributed attributes of SLA records, and promoted the generalization capacity for both even and odd years, with the reduction of the repeated learning within years.

Pointwise and Increment Evaluation

The pointwise prediction performance of the above example SLA time series has also been calculated, as is shown in Figure 7B, with the prediction error distribution of 14 days listed here. It could be seen from the experiment results that due to the spatio-temporal correlation in SLA time series, the edges approach to the higher prediction error as some of the edges come from non-study areas. The insufficient input of the edges could lead to the inaccuracy for the edge prediction, and the higher error would pass on gradually in the iterative prediction process, and make the high error region of the edge gradually expand. In addition, the spatial correlation map between RMSE and the average density distribution in Figures 2C,D has been depicted, with Figure 7C for cyclonic eddies and Figure 7D for anticyclonic eddies. From the perspectives of average density distribution, the regions with higher density of mesoscale eddies tended to obtain higher errors, implying the existing sensitivity to the strong nonlinearity degrees of mesoscale eddy variation.

We also carried out the increment evaluation from the mean SLA in the first 14 days to SLA in the next 7 days or 14 days, with both the ground truth and the predicted values. The increment prediction evaluation results for one example SLA time series segment, randomly selected from April 30, 2015 to May 27, 2015, have been shown in Figure 8, where the first and second rows respectively refer to the results for the 7-day and 14-day prediction duration, with the ground truth on the left and the predicted values on the right, and the effective sub-region located in black rectangle.

FIGURE 8

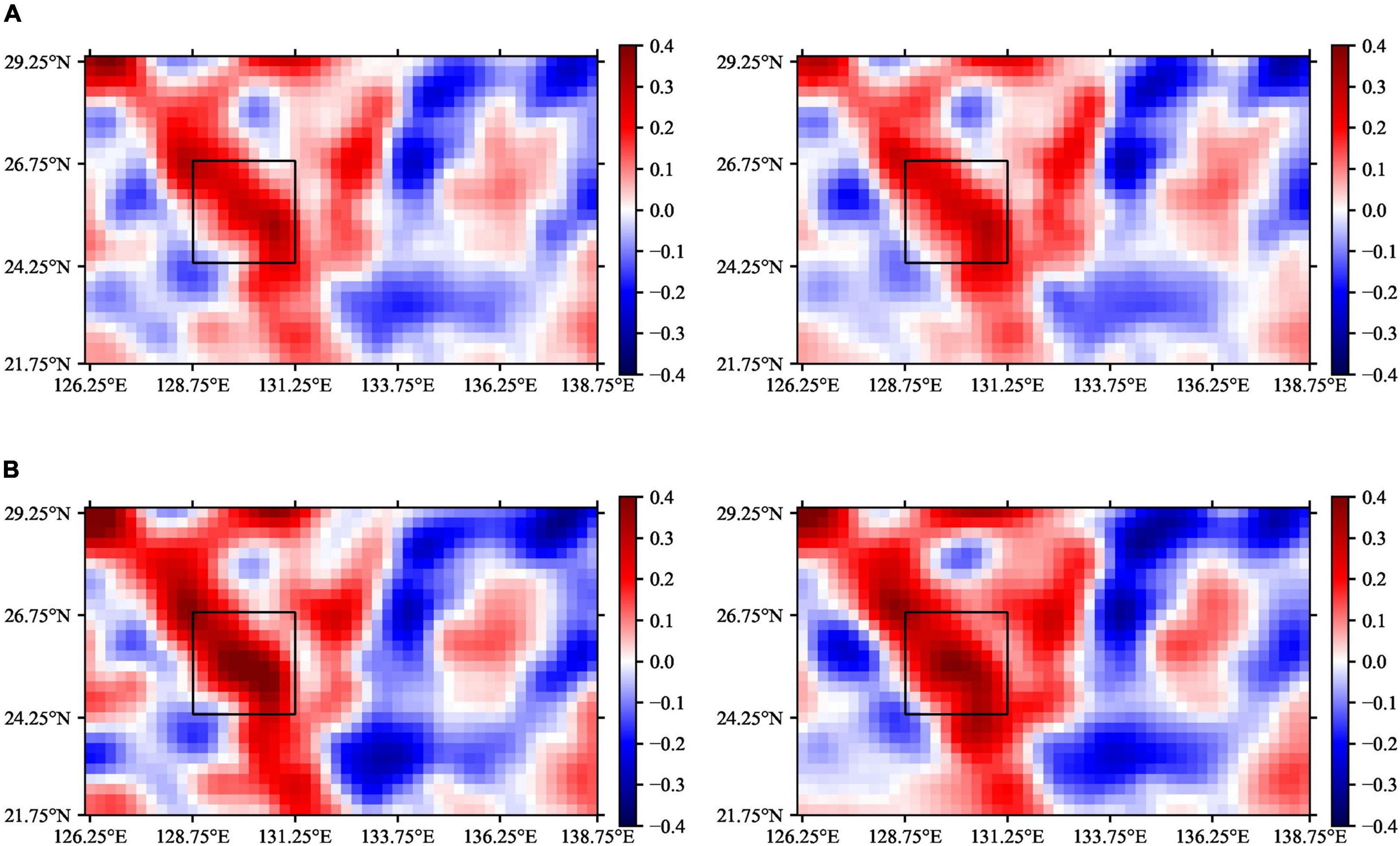
Figure 8. Increment prediction evaluation and effective sub-region selection. (A) Increment prediction evaluation in the 7-day duration, with SLA ground truth on the left and the predicted values on the right. (B) Increment prediction evaluation in the 14-day duration, with SLA ground truth on the left and the predicted values on the right.

Effective Sub-Region Performance

The prediction performance of the edges within SLA time series would be most probably less good than that of the central location. We assumed there was an effective sub-region included in each SLA record at each time step, considering the prediction duration and the eddy propagation direction from east to west, and the most important SLA variation in the effective sub-region would be all covered without missing. We further evaluated our prediction performances within the effective sub-regions.

The quantitative evaluation of prediction performance for only the effective sub-regions have been illustrated in Table 6. It has been demonstrated from our experimental results that our proposed scheme outperformed the state-of-the-art learning-based models for SLA time series, with MAPE, RMSE of the 14-day prediction duration, respectively, 5.1%, 0.023 m on average, even up to 4.6%, 0.018 m for the effective sub-regions, compared to 19.8%, 0.086 m in ConvLSTM, 17.6%, 0.073 m in ConvLSTM with SC, and 8.3%, 0.040 m in original MIM.

TABLE 6

Table 6. Effective sub-region assessment.

The definition of edges refers to the margins away from the center of SLA records. In practice, we could divide the research area into multiple effective sub-regions, and train multiple models separately, and finally stitch the prediction results to avoid the poor edge effects. Or after determining the research area, we could extend the ranges of SLA records to ensure that all the effective sub-regions we are interested in are all included after edge elimination.

Performance Evaluation for Mesoscale Eddy Prediction

Mesoscale Eddy Identification

After the spatio-temporal prediction of SLA time series, we could further feed the predicted SLA output through mesoscale eddy detection, to acquire the estimated properties of the mesoscale eddy trajectories, including the amplitude, the rotation speed, the radius, and location, etc.

With the development of the existing mesoscale eddy detection algorithms, as long as we enable to provide more reliable SLA prediction results, we could expect the prediction of mesoscale eddy variation to be reasonably inferred during the evolution and propagation. Figures 9A,B shows one example mesoscale eddy prediction result in aid of SLA prediction, where on the left, the arbitrarily selected 14-day SLA time series have been fed into the enhanced MIM to predict the next 14th day, and the corresponding ground truth of the 28th day from the beginning of the SLA time series has been illustrated on the right, combined with the mesoscale eddy detection results, with the cyclonic center in red and the anti-cyclonic center in white. Among them, we could see that most of the mesoscale eddies have been predicted relatively accurately in a 14-day prediction duration. Although there were still two anti-cyclonic and one cyclonic missing, for those larger vortices, almost all of them could be predicted, while for the smaller vortices, the prediction performances tended to be poor. Meanwhile, the location of the mesoscale eddies was almost visually well estimated.

FIGURE 9

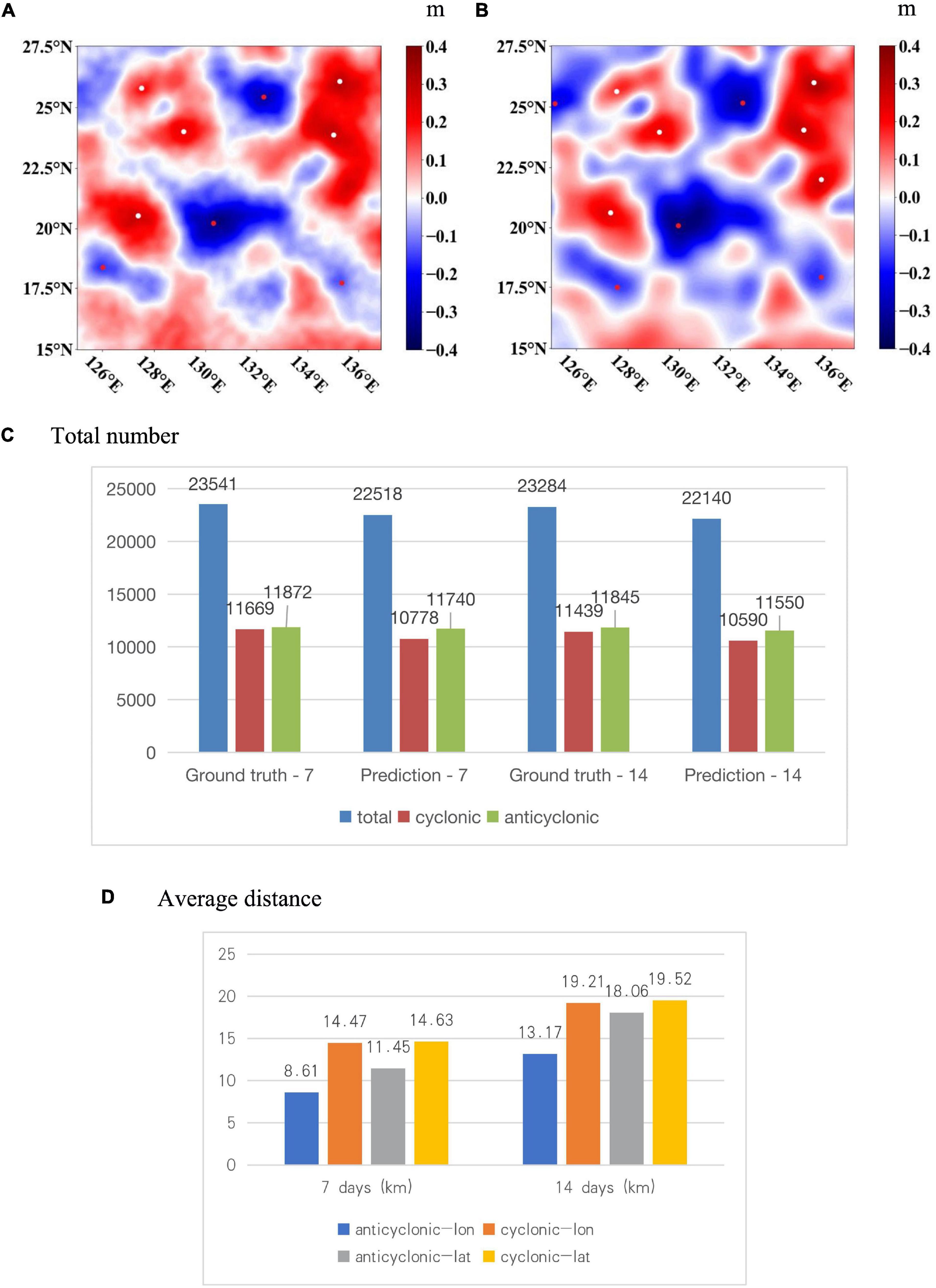
Figure 9. The example mesoscale eddy prediction result and the 7-day and 14-day mesoscale eddy prediction statistics in our study area. (A) Mesoscale eddy detection result from SLA prediction, with the cyclonic center in red and the anti-cyclonic center in white. (B) Mesoscale eddy detection result from SLA ground truth, with the cyclonic center in red and the anti-cyclonic center in white. (C) The number of the detected mesoscale eddies with SLA prediction and SLA ground truth. (D) The average spatial distance in longitude and latitude between the detected center position of mesoscale eddy with SLA prediction and that from SLA ground truth.

Overall Prediction Statistics

We further made an integrated statistics for mesoscale eddy prediction within the 7-day and 14-day duration in our study area, as is shown in Figures 9C,D. In Figure 9C, the total number of the detected mesoscale eddies from SLA prediction is listed on the left, with the corresponding ground truth as the ideal predictive references on the right, and both the number of the cyclonic and anticyclonic eddies have been, respectively displayed. In Figure 9D, the average spatial distance between all the detected center position of mesoscale eddies with SLA prediction and ground truth have been calculated with regard to the geographic latitude and longitude, for both cyclonic and anticyclonic eddies.

The noticeable asymmetry has been discovered between the cyclonic and anticyclonic eddies regarding to the number of the detected mesoscale eddies and the average spatial distance in latitude and longitude. It has been demonstrated from Figure 9C that the predicted number of anticyclonic and cyclonic eddies, respectively, decreased by 1.11 and 7.64%, 2.49 and 7.42%, compared to the ground truth, for the 7-day and 14-day of prediction duration, indicating that the prediction error of the number of anticyclonic eddies tends to be less in the study area. In the 7-day prediction duration, the number of anticyclonic and cyclonic eddies for the SLA ground truth, respectively, accounts for 50.5% and 49.5% in total, while the predicted number accounts for 52.1% and 47.9%. In comparison, the predicted proportion of anticyclonic eddies increased by 1.6%, and the predicted proportion of cyclonic eddies decreased by 1.6%. In the 14-day prediction duration, the number of anticyclonic and cyclonic eddies for the SLA ground truth, respectively, accounts for 50.9% and 49.1% in total, while the predicted number accounts for 52.2% and 47.8%. In comparison, the predicted proportion of anticyclonic eddies increased by 1.8%, and the predicted proportion of cyclonic eddies decreased by 1.8%. All of the above has shown the tendency of better prediction performances for anticyclonic eddies in our study area.

It has also been illustrated from Figure 9D that, in the 7-day prediction duration, the average meridional distances of the predicted mesoscale eddy centers from SLA prediction and SLA ground truth for anticyclonic and cyclonic eddies are 8.61 and 14.47 km, respectively, with a difference of 5.86 km, and the average zonal distances for anticyclonic and cyclonic eddies are, respectively, 11.45 and 14.63 km, with a difference of 3.18 km. The average spatial displacement of mesoscale eddy centers is 17.41 km, with 11.54 and 13.04 km, respectively, from longitude and latitude. The RMSE calculation of the mesoscale eddy centers from SLA prediction and SLA ground truth is 21.43 km, with the meridional and zonal displacement, respectively, 14.51 and 15.77 km, for 7-day prediction duration. In the 14-day prediction duration, the average meridional distances of the predicted mesoscale eddy centers from SLA prediction and SLA ground truth for anticyclonic and cyclonic eddies have reached 13.17 and 19.21 km, with a difference of 6.04 km, and the average zonal distances for anticyclonic and cyclonic eddies are, respectively, 18.06 and 19.52 km, with a difference of 1.46 km. The average spatial displacement of mesoscale eddy centers is 24.8 km, with 16.19 and 18.19 km, respectively, from longitude and latitude. The RMSE calculation of the mesoscale eddy centers from SLA prediction and SLA ground truth is 29.8 km, with the meridional and zonal displacement, respectively, 20.78 and 21.36 km, for 14-day prediction duration. The average spatial distance of anticyclonic eddies seemed smaller than that of cyclonic eddies to the mesoscale eddy center detection from SLA ground truth, and their differences tend to be more significant for the meridional distances.

The average relative error of the predicted mesoscale eddy radius, amplitude, total number in our study area has also been quantitatively investigated, with the relative error 6.8 and 8.8% for mesoscale eddy radius, 6.9 and 10.8% for mesoscale eddy amplitude, 4.35 and 4.91% for the total number of mesoscale eddies, of the 7-day and 14-day prediction duration.

Predictive Analytics With Decomposition

We tried to decompose the predicted mesoscale eddies into three subsets with regard to the evenly distributed ranges of the radius values, i.e., less than 55 km, 55–85 km, more than 85 km, and examined the detection rate distribution across the subset, respectively, reaching 80.1% and 64.1%, 92.6% and 85.1%, 94.5% and 90.9% in each subset, for the 7-day and 14-day of prediction duration. The subset with smaller average radius, i.e., 61.25% of the average radius over all the predicted mesoscale eddies, is more likely to be ignored in some cases.

The number of the cyclonic and anticyclonic eddies distribution across the above three subsets has also been investigated, respectively, coming to 2869 and 2707, 3856 and 4021, 4053 and 5012 in each subset, for the 7-day of prediction duration, and 2644 and 2527, 3885 and 4013, 4061 and 5010 in each subset, for the 14-day of prediction duration.

Similarly, we divided the predicted mesoscale eddies into another three subsets with regard to the distributed ranges of the amplitude values, i.e., less than 2.9 cm, 2.9–4.7 cm, more than 4.7 cm, and the number of the cyclonic and anticyclonic eddies distribution across the three subsets have been examined, respectively, reaching 2592 and 2385, 3114 and 3346, 5072 and 6009 in each subset, for the 7-day of prediction duration, and 2453 and 2294, 3348 and 3339, 4989 and 5917 in each subset, for the 14-day of prediction duration.

It has also been shown from the experimental results that there tended to be more anticyclonic eddies in the larger radius subset and the stronger amplitude subset in our study area, while the cyclonic eddies that gathered in the subset with smaller radius and amplitude are more likely to be ignored, resulting in the different errors between cyclonic and anticyclonic eddies.

The effective sub-regions could be applicable to the edge position mesoscale eddies, while for small mesoscale eddies and mesoscale eddy edges, more efforts still need to be done as the predictability depends much on SLA prediction, and the appropriate eddy detection and tracking techniques. There exhibited the possible declines in the total number, radius, amplitude of the predicted mesoscale eddies, compared to the ground truth, implying that the predictability of small mesoscale eddies and mesoscale eddy edges might be relatively weak.

Proposal for More Diagnostics

We have also made an initial attempt to explore the spatial Fourier spectra and the gradient of the example SLA prediction from Figure 9A, as is shown in Supplementary Figure 1. In the future, in addition to RMSE and MAPE, we will try to look into the performance evaluation by applying more diagnostics, in terms of energetics, velocity, and vorticity derived fields, e.g., the power spectral density calculation, which would potentially capture both the intensity and phase of SLA spatio-temporal variation, and might be in turn more helpful to resolve the spatial scale estimation for mesoscale eddy multi-step prediction.

By now, we focus on daily mesoscale eddy distribution prediction, not referring to the link of the adjoining daily predictive results and the aligning propagation trajectory tracking, so the lifetime of the mesoscale eddies has not been prepared to be available. We will try to develop the mesoscale eddy tracking capacities with the application of deep learning techniques in the future, which may be more helpful to further improve the prediction of small mesoscale eddies and mesoscale eddy edges, and accurately determine the scope of our prediction model in applications.

Moreover, the mesoscale eddy identification and tracking algorithm mentioned above refers to Eulerian with SLA snapshots (Mason et al., 2014; Faghmous et al., 2015; Conti et al., 2016). There are probably still limitations such as the excess eddy merging and prematurely terminating trajectories that need to be considered (Faghmous et al., 2015). The Lagrangian based eddy detection algorithms have also been suggested its effectivity, specially for mesoscale eddy evolution and its properties (Vortmeyer-Kley et al., 2016; Prants et al., 2017). Prants et al. (2017) proposed the Lagrangian methodology to distinguish whether the origin and history of water masses in mesoscale eddies came from the main currents in Kuroshio-Oyashio confluence zone, showing a good qualitative correspondence, compared with in situ measurements. Vortmeyer-Kley et al. (2016) proposed a vorticity based heuristic Euler-Lagrangian descriptor utilizing the idea of Lagrangian coherent structures, showing closer lifetime estimation to analytical results and its robustness with respect to certain types of noise in eddy detection from observation.

Although the most common mesoscale eddy identification and tracking methodology is to analyze altimetry-based sea-level gridded products, Amores et al. (2018) analyzed up to what extent sea-level gridded products characterize mesoscale eddies with a special focus on the North Atlantic Ocean and the Mediterranean Sea, which suggested that gridded products might largely underestimate the density of eddies. The main reason behind is possibly that the spatial resolution is not enough to capture the small-scale eddies, and the unresolved structures are aliased into larger structures, showing an unrealistic number of large eddies with overestimated amplitudes. In the future, we will elaborate more on assessing the predictability of mesoscale eddies at multiple scales, from altimetry-based sea-level gridded products, assisted with potential insights into mesoscale eddy categories from the satellite observations at a higher resolution, e.g., chlorophyll products.

Conclusion

In this article, we make an initial attempt to capture the spatio-temporal predictability of mesoscale eddies, by employing deep learning architecture, which primarily establishes MIM model for SLA prediction. In order to implement deep learning algorithms, sufficient samples and appropriate models are always fundamental requirements. Therefore, we quantitatively investigate the historic daily SLA maps of 27 years AVISO data in the selected region (125°−137.5°E and 15°−27.5°N), develop enhanced MIM prediction strategies on NVIDIA Titan Xp GPU, equipped with GRU and spatial attention module, in a scheduled sampling manner. Owing to the input scarcity in deep learning, transfer learning has been conducted to SLA time series in those regions located at the same latitude as our study area, through data segmentation and augmentation techniques. Inspired by GRU, the gating mechanism of MIM-N and MIM-S modules has been improved to balance the model complexity and prediction accuracy, overcoming the gradient vanishing and explosion problem when learning long-term dependencies, and the spatial attention module has been complemented to strengthen feature extraction toward spatio-temporal variability in SLA time series, thus refraining from the connection structure mismatching within the convolution operation. At the early stage of training, the real value input of the known SLA time series guides the model from a randomly initialization to a more reasonable state, as the training progresses, scheduled sampling will be deeply involved to intentionally feed into the model with the newly predicted value as the input, providing opportunities in tackling the input distribution inconsistency between training and inference. It has been demonstrated in our experiment results that our proposed prediction scheme outperformed most of the state-of-arts approaches for SLA time series, in terms of MAPE and RMSE, achieved superior prediction performances for the long-term dependency, with MAPE, RMSE of the 14-day prediction duration, respectively, 5.1%, 0.023 m in our developed model, compared to 19.8%, 0.086 m in classic ConvLSTM and 8.3%, 0.040 m in original MIM, over the comparable structure configuration. The visualization of the pointwise error and the increment prediction to SLA time series also suggest the highly consistent variation to the altimeter observations, which greatly facilitated the mesoscale eddy prediction during its evolution and propagation process, in aid of classical mesoscale eddy detection. When assessing the concerning sub-region in SLA time series, the 14-day prediction performance could reach up to 4.6% and 0.018 m on average. This proposed scheme will be beneficial to understand of the underlying dynamical mechanism behind the predictability of mesoscale eddies in the future, and help the deployment of ARGO, glider, AUV and other observational platforms.

Data Availability Statement

The AVISO satellite altimeter database can be accessed on the (https://www.aviso.altimetry.fr/en/data.html).

Author Contributions

RN designed the study, analyzed and interpreted the data, drafted the manuscript, and made final consent about the manuscript to be published. YC performed the main experimental work and drafted the manuscript. ZZ has brought up the conception of the study and provided guidance on the data analysis and interpretation. HH and JW assisted in the experimental work and helped the statistic of data. QY assisted in the experimental work and acquisition of data. XG helped to guide the experimental methods and data analysis. YQ and HY helped to draft the manuscript. BH discussed and helped the experiments. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Key R&D Program (2019YFC1408304), National Natural Science Foundation of China (42022041), National Natural Science Foundation of China (41876001), National Key R&D Program (2016YFC0301400), National High-Tech R&D 863 Program (2014AA093410), National Natural Science Foundation of China (31202036), National Program of International S&T Cooperation (2015DFG32180), National Science & Technology Pillar Program (2012BAD28B05), and National Natural Science Foundation of China (41376140).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to acknowledge the team member Jie Wang for his help in data analysis.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2021.753942/full#supplementary-material

Footnotes

1. ^ Climate Data Store: https://cds.climate.copernicus.eu/

References

Amores, A., Jordà, G., Arsouze, T., and Le Sommer, J. (2018). Sommer up to what extent can we characterize ocean eddies using present-day gridded altimetric products? J. Geophys. Res. 123, 7220–7236. doi: 10.1029/2018JC014140

CrossRef Full Text | Google Scholar

Bengio, S., Vinyals, O., Jaitly, N., and Shazeer, N. (2015). “Scheduled sampling for sequence prediction with recurrent neural networks,” in Proceedings of the Advances in Neural Information Processing Systems (Montreal, QC), 1171–1179. doi: 10.5555/2969239.2969370

PubMed Abstract | CrossRef Full Text | Google Scholar

Box, G. E. P., Jenkins, G. M., Reinsel, G. C., and Ljung, G. M. (2015). Time Series Analysis: Forecasting and Control. Hoboken, NJ: John Wiley & Sons. doi: 10.2307/3008255

CrossRef Full Text | Google Scholar

Braakmann-Folgmann, A., Roscher, R., Wenzel, S., Uebbing, B., and Kusche, J. (2017). Sea level anomaly prediction using recurrent neural networks. arXiv [Preprint]. arXiv:1710.07099

Google Scholar

Bryden, H. L., and Brady, E. C. (1989). Eddy momentum and heat fluxes and their effect on the circulation of the equatorial Pacific Ocean. J. Mar. Res. 47, 55–79. doi: 10.1357/002224089785076389

CrossRef Full Text | Google Scholar

Chaigneau, A., Gizolme, A., and Grados, C. (2008). Mesoscale eddies off Peru in altimeter records: identification algorithms and eddy spatio-temporal patterns. Prog. Oceanogr. 79, 106–119. doi: 10.1016/j.pocean.2008.10.013

CrossRef Full Text | Google Scholar

Chaigneau, A., Texier, M. L., Eldin, G., Grados, C., and Pizarro, O. (2011). Vertical structure of mesoscale eddies in the eastern South Pacific Ocean: a composite analysis from altimetry and Argo profiling floats. J. Geophys. Res. 116:C11025. doi: 10.1029/2011JC007134

CrossRef Full Text | Google Scholar

Chassignet, E. P., Hurlburt, H. E., Metzger, E. J., Smedstad, O. M., Cummings, J., Halliwell, G. R., et al. (2009). US GODAE: global ocean prediction with the HYbrid coordinate ocean model (HYCOM). Oceanography 22, 64–75. doi: 10.5670/oceanog.2009.39

CrossRef Full Text | Google Scholar

Chelton, D. B., Gaube, P. M. G., Early, J. J., and Samelson, R. M. (2011a). The influence of nonlinear mesoscale eddies on near-surface oceanic chlorophyll. Science 334, 328–332. doi: 10.1126/science.1208897

PubMed Abstract | CrossRef Full Text | Google Scholar

Chelton, D. B., Schlax, M. G., and Samelson, R. M. (2011b). Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 91, 167–216. doi: 10.1016/j.pocean.2011.01.002

CrossRef Full Text | Google Scholar

Chelton, D. B., Schlax, M. G., Samelson, R. M., and de Szoeke, R. A. (2007). Global observations of large oceanic eddies. Geophys. Res. Lett. 34:L15606. doi: 10.1029/2007GL030812

CrossRef Full Text | Google Scholar

Chen, G., Hou, Y., and Chu, X. (2011). Mesoscale eddies in the South China Sea: mean properties, spatiotemporal variability, and impact on thermohaline structure. J. Geophys. Res. 116:C06018. doi: 10.1029/2010JC006716

CrossRef Full Text | Google Scholar

Chen, X., Chen, G., Ge, L., Huang, B., and Cao, C. (2021). Global oceanic eddy identification: a deep learning method from Argo profiles and altimetry data. Front. Mar. Sci. 8:646926. doi: 10.3389/fmars.2021.646926

CrossRef Full Text | Google Scholar

Cho, K., Merrienboer, B. V., Gülçehre, Ç, Bahdanau, D., Bougares, F., Schwenk, H., et al. (2014). “Learning phrase representations using RNN encoder-decoder for statistical machine translation,” in Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha.

Google Scholar

Chung, J., Gülçehre, Ç, Cho, K., and Bengio, Y. (2014). Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv [Preprint]. arXiv:1412.3555

Google Scholar

Conti, D., Orfila, A., Mason, E., Sayol, J. M., Simarro, G., and Balle, S. (2016). An eddy tracking algorithm based on dynamical systems theory. Ocean Dyn. 66, 1415–1427. doi: 10.1007/s10236-016-0990-7

CrossRef Full Text | Google Scholar

Cornillon, P., Weisberg, R., Barth, A., He, R., Werner, F., and Wilkin, J. (2009). U.S. GODAE: global ocean prediction with the hybrid coordinate ocean model (HYCOM). Oceanography 22, 64–75.

Google Scholar

Cramér, H. (1961). “On some classes of nonstationary stochastic processes,” in Proceedings of the Berkeley Symposium on Mathematical Statistics and Probability, Vol. 2, (Los Angeles, CA: University of Los Angeles Press), 57–78.

Google Scholar

Dong, C., McWilliams, J. C., Liu, Y., and Chen, D. (2014). Global heat and salt transports by eddy movement. Nat. Commun. 5:3294. doi: 10.1038/ncomms4294

PubMed Abstract | CrossRef Full Text | Google Scholar

Dong, D., Brandt, P., Chang, P., Schutte, F., Yang, X., Yan, J., et al. (2017). Mesoscale eddies in the Northwestern Pacific Ocean: three-dimensional eddy structures and heat/salt transports. J. Geophys. Res. Oceans 122, 9795–9813. doi: 10.1002/2017JC013303

CrossRef Full Text | Google Scholar

Drévillon, M., Bourdallé-Badie, R., Derval, C., Lellouche, J. M., Rémy, E., Tranchant, B., et al. (2008). The GODAE/Mercator-ocean global ocean forecasting system: results, applications and prospects. J. Oper. Oceanogr. 1, 51–57. doi: 10.1080/1755876X.2008.11020095

CrossRef Full Text | Google Scholar

Du, Y., Song, W., He, Q., Huang, D., Liotta, A., and Su, C. (2019). Deep learning with multi-scale feature fusion in remote sensing for automatic oceanic eddy detection. Inf. Fusion 49, 89–99. doi: 10.1016/j.inffus.2018.09.006

CrossRef Full Text | Google Scholar

Duo, Z., Wang, W., and Wang, H. (2019). Oceanic mesoscale eddy detection method based on deep learning. Remote Sens. 11:1921. doi: 10.3390/rs11161921

CrossRef Full Text | Google Scholar

Elman, J. L. (1990). Finding structure in time. Cogn. Sci. 14, 179–211. doi: 10.1207/s15516709cog1402_1

CrossRef Full Text | Google Scholar

Fablet, R., Viet, P. H., and Lguensat, R. (2017). “Data-driven models for the spatio-temporal interpolation of satellite-derived SST fields,” in IEEE Transactions on Computational Imaging, Vol. 3, (Piscataway, NJ: IEEE), 647–657. doi: 10.1109/TCI.2017.2749184

CrossRef Full Text | Google Scholar

Faghmous, J. H., Frenger, I., Yao, Y., Warmka, R., Lindell, A., and Kumar, V. (2015). A daily global mesoscale ocean eddy dataset from satellite altimetry. Sci. Data 2:150028. doi: 10.1038/sdata.2015.28

PubMed Abstract | CrossRef Full Text | Google Scholar

Fang, F., and Morrow, R. (2003). Evolution, movement and decay of warm-core Leeuwin Current eddies. Deep Sea Res. II 50, 2245–2261. doi: 10.1016/S0967-0645(03)00055-9

CrossRef Full Text | Google Scholar

Frenger, I. (2013). On Southern Ocean Eddies and Their Impacts on Biology and the Atmosphere. Ph.D. thesis. Zürich: ETH Zurich.

Google Scholar

Fu, Y., Zhou, X., Sun, W., and Tang, Q. (2019). Hybrid model combining empirical mode decomposition, singular spectrum analysis, and least squares for satellite-derived sea-level anomaly prediction. Int. J. Remote Sens. 40, 7817–7829. doi: 10.1080/01431161.2019.1606959

CrossRef Full Text | Google Scholar

Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., et al. (2014). “Generative adversarial nets,” in Proceedings of the NIPS, Montreal, Canada.

Google Scholar

Gourdeau, L., Verron, J., Chaigneau, A., Cravatte, S., and Kessler, W. (2017). Complementary use of glider data, altimetry, and model for exploring mesoscale eddies in the tropical Pacific Solomon Sea. J. Geophys. Res. Oceans 122, 9209–9229.

Google Scholar

Grigorievskiy, A., Miche, Y., Ventelä, A.-M., Séverin, E., and Lendasse, A. (2014). Long-term time series prediction using OP-ELM. Neural Netw. 51, 50–56. doi: 10.1016/j.neunet.2013.12.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Halo, I., Backeberg, B., Penven, P., Ansorge, I., Reason, C., and Ullgren, J. (2014). Eddy properties in the Mozambique channel: a comparison between observations and two numerical ocean circulation models. Deep Sea Res. II 100, 38–53. doi: 10.1016/j.dsr2.2013.10.015

CrossRef Full Text | Google Scholar

He, K., Zhang, X., Ren, S., and Sun, J. (2016). “Deep residual learning for image recognition,” in Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (Las Vegas, NV), 770–778.

Google Scholar

Hinton, G. E., Osindero, S., and Teh, Y. W. (2006). A fast learning algorithm for deep belief nets. Neural Comput. 18, 1527–1554. doi: 10.1162/neco.2006.18.7.1527

PubMed Abstract | CrossRef Full Text | Google Scholar

Hochreiter, S., and Schmidhuber, J. (1997). “LSTM can solve hard long time lag problems,” in Advances in Neural Information Processing Systems, eds M. C. Mozer, M. I. Jordan, and T. Petsche (Cambridge MA: MIT Press), 473–479. doi: 10.5555/2998981.2999048

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, G., Liu, Z., Van Der Maaten, L., and Weinberger, K. Q. (2017). “Densely connected convolutional networks,” in Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, 2261–2269.

Google Scholar

Hurlburt, H., Chassignet, E., Cummings, J., Kara, A., Metzger, E., Shriver, J., et al. (2008). “Eddy resolving global ocean prediction,” in Eddy-Resolving Ocean Modeling: Geophysical Monograph Series, eds M. Hecht and H. Hasumi (Washington DC: American Geophysical Union), 353–381.

Google Scholar

Imani, M., Chen, Y. C., You, R. J., Lan, W. H., Kuo, C. Y., Chang, J. C., et al. (2017). Spatiotemporal prediction of satellite altimetry sea level anomalies in the tropical Pacific Ocean. IEEE Geosci. Remote Sens. Lett. 14, 1126–1130. doi: 10.1109/LGRS.2017.2699668

CrossRef Full Text | Google Scholar

Ioffe, S., and Szegedy, C. (2015). “Batch normalization: accelerating deep network training by reducing internal covariate shift,” in Proceedings of the 32nd International Conference on Machine Learning, Lille.

Google Scholar

Isern-Fontanet, J., García-Ladona, E., and Font, J. (2003). Identifification of marine eddies from altimetric maps. J. Atmos. Ocean. Technol. 20, 772–778. doi: 10.1175/1520-0426200320<772:IOMEFA<2.0.CO;2

CrossRef Full Text | Google Scholar

Jaderberg, M., Simonyan, K., and Zisserman, A. (2015). “Spatial transformer networks,” in Advances in Neural Information Processing Systems, Vol. 28, eds C. Cortes, N. D. Lawrence, D. D. Lee, M. Sugiyama, and R. Garnett, (Red Hook, NY: Curran Associates, Inc.), 2017–2025.

Google Scholar

Karpathy, A., Toderici, G., Shetty, S., Leung, T., Sukthankar, R., and Fei-Fei, L. (2014). “Large-scale video classification with convolutional neural networks,” in Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, 1725–1732.

Google Scholar

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). “Imagenet classification with deep convolutional neural networks,” in Advances in Neural Information Processing Systems, eds F. Pereira, C. J. C. Burges, L. Bottou, and K. Q. Weinberger (Red Hook, NY: Curran Associates, Inc.), 1097–1105. doi: 10.1145/3065386

CrossRef Full Text | Google Scholar

Laxenaire, R., Speich, S., Blanke, B., Chaigneau, A., Pegliasco, C., and Stegner, A. (2018). Anticyclonic eddies connecting the western boundaries of Indian and Atlantic Oceans. J. Geophys. Res. Oceans 123, 7651–7677.

Google Scholar

Le Vu, B., Stegner, A., and Arsouze, T. (2018). Angular momentum eddy detection and tracking algorithm (AMEDA) and its application to coastal eddy formation. J. Atmos. Oceanic Technol. 35, 739–762. doi: 10.1175/JTECH-D-17-0010.1

CrossRef Full Text | Google Scholar

Li, J., Wang, G., Xue, H., and Wang, H. (2019). A simple predictive model for the eddy propagation trajectory in the northern South China Sea. Ocean Sci. 15, 401–412. doi: 10.5194/os-15-401-2019

CrossRef Full Text | Google Scholar

Lipton, Z. C. (2015). A critical review of recurrent neural networks for sequence learning. arXiv [Preprint]. arXiv:1506.00019

Google Scholar

Liu, Y., Chen, G., Sun, M., Liu, S., and Tian, F. (2016). A parallel SLA-based algorithm for global mesoscale eddy identification. J. Atmos. Ocean. Technol. 33, 2743–2754. doi: 10.1175/JTECH-D-16-0033.1

CrossRef Full Text | Google Scholar

Ma, C., Li, S., Wang, A., Yang, J., and Chen, G. (2019). Altimeter observation-based eddy nowcasting using an improved Conv-LSTM network. Remote Sens. 11:783. doi: 10.3390/rs11070783

CrossRef Full Text | Google Scholar

Martin, A. P., and Richards, K. J. (2001). Mechanisms for vertical nutrient transport within a North Atlantic mesoscale eddy. Deep Sea Res. II Top. Stud. Oceanogr. 48, 757–773. doi: 10.1016/S0967-0645(00)00096-5

CrossRef Full Text | Google Scholar

Martin, M. J., Hines, A., and Bell, M. J. (2007). Data assimilation in the FOAM operational short-range ocean forecasting system: a description of the scheme and its impact. Q. J. R. Meteorol. Soc. 133, 981–995. doi: 10.1002/qj.74

CrossRef Full Text | Google Scholar

Martínez-Moreno, J., Hogg, A. M., England, M. H., Constantinou, N. C., Kiss, A. E., and Morrison, A. K. (2021). Global changes in oceanic mesoscale currents over the satellite altimetry record. Nat. Clim. Chang. 11, 397–403. doi: 10.1038/s41558-021-01006-9

CrossRef Full Text | Google Scholar

Masina, S., and Pinardi, N. (1994). Mesoscale data assimilation studies in the Middle Adriatic Sea. Cont. Shelf Res. 14, 1293–1310. doi: 10.1016/0278-4343(94)90049-3

CrossRef Full Text | Google Scholar

Mason, E., Pascual, A., and McWilliams, J. C. (2014). A new sea surface height-based code for oceanic mesoscale eddy tracking. J. Atmos. Oceanic Technol. 31, 1181–1188. doi: 10.1175/JTECH-D-14-00019.1

CrossRef Full Text | Google Scholar

McGillicuddy, D. J., Anderson, L. A., Bates, N. R., Bibby, T. S., Buesseler, K., Carlson, C. A., et al. (2007). Eddy/wind interactions stimulate extraordinary mid-ocean plankton blooms. Science 316, 1021–1026. doi: 10.1126/science.1136256

PubMed Abstract | CrossRef Full Text | Google Scholar

Metzger, E. J., Hurlburt, H. E., Wallcraft, A. J., Shriver, J. F., and Townsend, T. L. (2010). Validation test report for the global ocean forecast system V3.0-1/12 deg HYCOM-NCODA: phase II. US Navy operational global ocean and Arctic ice prediction systems. Oceanography 27, 32–43.

Google Scholar

Metzger, E. J. Smedstad, O. M., Thoppil, P. G., Hurlburt, H. E., Cummings, J. A., Wallcraft, A. J., et al. (2014). US Navy operational global ocean and Arctic ice prediction systems. Oceanogr. 27, 32–43. doi: 10.5670/oceanog.2014.66

CrossRef Full Text | Google Scholar

Mkhinini, N., Coimbra, A. L. S., Stegner, A., Arsouze, T., Taupier-Letage, I., and Béranger, K. (2014). Longlived mesoscale eddies in the eastern Mediterranean Sea: analysis of 20 years of AVISO geostrophic velocities. J. Geophys. Res. Oceans 119, 8603–8626. doi: 10.1002/2014JC010176

CrossRef Full Text | Google Scholar

Morrow, R., Birol, F., Griffin, D., and Sudre, J. (2004). Divergent pathways of cyclonic and anticyclonic ocean eddies. Geophys. Res. Lett. 31:L24311. doi: 10.1029/2004GL020974

CrossRef Full Text | Google Scholar

Moschos, E., Schwander, O., Stegner, A., and Gallinari, P. (2020). “Deep-SST-eddies: a deep learning framework to detect oceanic eddies in sea surface temperature images,” in Proceedings of the ICASSP 2020 – 2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, 4307–4311. doi: 10.1109/ICASSP40776.2020.9053909

CrossRef Full Text | Google Scholar

Nencioli, F., Dong, C., Dickey, T., Washburn, L., and Mcwilliams, J. C. (2010). A vector geometry-based eddy detection algorithm and its application to a high-resolution numerical model product and high-frequency radar surface velocities in the Southern California bight. J. Atmos. Ocean. Technol. 27, 564–579. doi: 10.1175/2009JTECHO725.1

CrossRef Full Text | Google Scholar

Nian, R., Yuan, Q., He, H., Geng, X., Su, C., He, B., et al. (2021). The identification and prediction in abundance variation of atlantic cod via long short-term memory with periodicity, time–frequency co-movement, and lead-lag effect across sea surface temperature, sea surface salinity, catches, and prey biomass from 1919 to 2016. Front. Mar. Sci. 8:665716. doi: 10.3389/fmars.2021.665716

CrossRef Full Text | Google Scholar

Niedzielski, T., and Miziński, B. (2013). Automated system for near-real time modelling and prediction of altimeter-derived sea level anomalies. Comput. Geosci. 58, 29–39. doi: 10.1016/j.cageo.2013.04.022

CrossRef Full Text | Google Scholar

Oey, L. Y., Ezer, T., Forristall, G., Cooper, C., DiMarco, S., and Fan, S. (2005). An exercise in forecasting loop current and eddy frontal positions in the Gulf of Mexico. Geophys. Res. Lett. 32:L12611. doi: 10.1029/2005GL023253

CrossRef Full Text | Google Scholar

Okubo, A. (1970). Horizontal dispersion of flfloatable particles in the vicinity of velocity singularities such as convergences. Deep Sea Res. Oceanogr. Abstr. 17, 445–454. doi: 10.1016/0011-7471(70)90059-8

CrossRef Full Text | Google Scholar

Pascual, A., Faugere, Y., Larnicol, G., and Traon, P. Y. L. (2006). Improved description of the ocean mesoscale variability by combining four satellite altimeters. Geophys. Res. Lett. 33:L02611. doi: 10.1029/2005GL024633

CrossRef Full Text | Google Scholar

Prants, S. V., Budyansky, M. V., and Uleysky, M. Y. (2017). Lagrangian simulation and tracking of the mesoscale eddies contaminated by Fukushima-derived radionuclides. Ocean Sci. 13, 453–463. doi: 10.5194/os-13-453-2017

CrossRef Full Text | Google Scholar

Rienecker, M. M., Mooers, C. N., and Robinson, A. R. (1987). Dynamical interpolation and forecast of the evolution of mesoscale features off Northern California. J. Phys. Oceanogr. 17, 1189–1213. doi: 10.1175/1520-04851987017<1189:DIAFOT<2.0.CO;2

CrossRef Full Text | Google Scholar

Robinson, A. R., Carton, J. A., Mooers, C. N. K., Walstad, L. J., Carter, E. F., Rienecker, M. M., et al. (1984). A real-time dynamical forecast of ocean synoptic/mesoscale eddies. Nature 309, 781–783. doi: 10.1038/309781a0

CrossRef Full Text | Google Scholar

Robinson, A. R., and Leslie, W. G. (1985). Estimation and prediction of oceanic eddy fields. Prog. Oceanogr. 14, 485–510. doi: 10.1016/0079-6611(85)90024-2

CrossRef Full Text | Google Scholar

Röske, F. (1997). Sea level forecasts using neural networks. Dtsch. Hydrogr. Z. 49, 71–99. doi: 10.1007/BF02765119

CrossRef Full Text | Google Scholar

Sadarjoen, I. A., and Post, F. H. (2000). Detection, quantifification, and tracking of vortices using streamline geometry. Comput. Graph. 24, 333–341. doi: 10.1016/S0097-8493(00)00029-7

CrossRef Full Text | Google Scholar

Sarangi, R. K. (2012). Observation of oceanic eddy in the Northeastern Arabian sea using multisensor remote sensing data. Int. J. Oceanogr. 2012:531982.

Google Scholar

Sertel, E., Cigizoglu, H. K., and Sanli, D. U. (2008). Estimating daily mean sea level heights using artificial neural networks. J. Coast. Res. 24, 727–734. doi: 10.2112/06-742.1

CrossRef Full Text | Google Scholar

Shi, X., Chen, Z., Wang, H., Yeung, D., Wong, W., and Woo, W. (2015). “Convolutional LSTM network: a machine learning approach for precipitation nowcasting,” in Proceedings of the 29th Annual Conference on Neural Information Processing Systems (NIPS 2015), Montreal, QC. doi: 10.5555/2969239.2969329

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, X., and Yeung, D. (2018). Machine learning for spatiotemporal sequence forecasting: a survey. arXiv [Preprint]. arXiv:1808.06865

Google Scholar

Shriver, J. F., Hurlburt, H. E., Smedstad, O. M., Wallcraft, A. J., and Rhodes, R. C. (2007). 1/32 real-time global ocean prediction and value-added over 1/16 resolution. J. Mar. Syst. 65, 3–26. doi: 10.1016/j.jmarsys.2005.11.021

CrossRef Full Text | Google Scholar

Shu, Y., Chen, J., Li, S., Wang, Q., Yu, J., and Wang, D. (2019). Field-observation for an anticyclonic mesoscale eddy consisted of twelve gliders and sixty-two expendable probes in the northern South China Sea during summer 2017. Sci. China Earth Sci. 62, 451–458. doi: 10.1007/s11430-018-9239-0

CrossRef Full Text | Google Scholar

Smedstad, O. M., Hurlburt, H. E., Metzger, E. J., Rhodes, R. C., Shriver, J. F., Wallcraft, A. J., et al. (2002). “An operational real-time eddy-resolving 1/16/spl deg/global ocean nowcast/forecast system,” in Proceedings of the OCEANS ‘02 MTS/IEEE, Vol. 2, Biloxi, MI, 769–774. doi: 10.1109/OCEANS.2002.1192067

CrossRef Full Text | Google Scholar

Świerczyńska, M., Miziński, B., and Niedzielski, T. (2016). Comparison of predictive skills offered by prognocean, prognocean plus and MyOcean real-time sea level forecasting systems. Ocean Eng. 113, 44–56. doi: 10.1016/j.oceaneng.2015.12.023

CrossRef Full Text | Google Scholar

Taburet, G., Sanchez-Roman, A., Ballarotta, M., Pujol, M.-I., Legeais, J.-F., Fournier, F., et al. (2019). DUACS DT2018: 25 years of reprocessed sea level altimetry products. Ocean Sci. 15, 1207–1224. doi: 10.5194/os-15-1207-2019

CrossRef Full Text | Google Scholar

Thoppil, P. G., Frolov, S., Rowley, C. D., Reynolds, C. A., Jacobs, G., Joseph Metzger, E., et al. (2021). Ensemble forecasting greatly expands the prediction horizon for ocean mesoscale variability. Commun. Earth Environ. 2:89. doi: 10.1038/s43247-021-00151-5

CrossRef Full Text | Google Scholar

Tian, F., Wu, D., Yuan, L., and Chen, G. (2020). Impacts of the efficiencies of identification and tracking algorithms on the statistical properties of global mesoscale eddies using merged altimeter data. Int. J. Remote Sens. 41, 2835–2860. doi: 10.1080/01431161.2019.1694724

CrossRef Full Text | Google Scholar

Vortmeyer-Kley, R., Gräwe, U., Ulrike Feudel, U. (2016). “Detecting and tracking eddies in oceanic flow fields: A vorticity based Euler-Lagrangian method,” in Proceedings of the Nonlinear Processes in Geophysics Discussions, Vienna: EGU General Assembly.

Google Scholar

Wang, X., Wang, H., Liu, D., and Wang, W. (2020). The prediction of oceanic mesoscale eddy properties and propagation trajectories based on machine learning. Water 12:2521. doi: 10.3390/w12092521

CrossRef Full Text | Google Scholar

Wang, Y., Gao, Z., Long, M., Wang, J., and Philip, S. Y. (2018). “Predrnn++: towards a resolution of the deep-in-time dilemma in spatiotemporal predictive learning,” in Proceedings of the 35th International Conference on Machine Learning, PMLR, Vol. 80, Stockholm, 5123–5132.

Google Scholar

Wang, Y., Jiang, L., Yang, M., Li, L., Long, M., and Fei-Fei, L. (2019b). “Eidetic 3D LSTM: a model for video prediction and beyond,” in Proceedings of the 2019 ICLR 19/5/6 - 19/5/9, New Orleans, LA.

Google Scholar

Wang, Y., Zhang, J., Zhu, H., Long, M., Wang, J., and Yu, P. S. (2019a). “Memory in memory: a predictive neural network for learning higher-order non-stationarity from spatiotemporal dynamics,” in Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, 9146–9154. doi: 10.1109/CVPR.2019.00937

Google Scholar

Wang, Y., Long, M., Wang, J., Gao, Z., and Yu, P. S. (2017). “Predrnn: recurrent neural networks for predictive learning using spatiotemporal LSTMS,” in Proceedings of the 31st International Conference on Neural Information Processing Systems, (Red Hook, NY: Curran Associates Inc.), 879–888. doi: 10.5555/3294771.3294855

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., Li, Q., Sun, L., Li, S., Yang, Y., and Liu, S. (2015). The most typical shape of oceanic mesoscale eddies from global satellite sea level observations. Front. Earth Sci. 9, 202–208. doi: 10.1007/s11707-014-0478-z

CrossRef Full Text | Google Scholar

Weiss, J. (1991). The dynamics of enstrophy transfer in two-dimensional hydrodynamics. Phys. D 48, 273–294. doi: 10.1016/0167-2789(91)90088-Q

CrossRef Full Text | Google Scholar

Wu, Q. (2014). Region-shrinking: a hybrid segmentation technique for isolating continuous features, the case of oceanic eddy detection. Remote Sens. Environ. 153, 90–98. doi: 10.1016/j.rse.2014.07.026

CrossRef Full Text | Google Scholar

Wunsch, C. (2007). “The past and future ocean circulation from a contemporary perspective,” in Ocean Circulation: Mechanisms and Impacts-Past and Future Changes of Meridional Overturning, Geophys. Monogr. Ser., Vol. 173, eds A. Schmittner, J. C. H. Chiang, and S. Hemming (Washington, DC: AGU), 53–74. doi: 10.1111/brv.12327

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Q., Nikurashin, M., Sasaki, H., Sun, H., and Tian, J. (2019). Dissipation of mesoscale eddies and its contribution to mixing in the northern South China Sea. Sci. Rep. 9:556. doi: 10.1038/s41598-018-36610-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Yi, J., Du, Y., He, Z., and Zhou, C. (2014). Enhancing the accuracy of automatic eddy detection and the capability of recognizing the multi-core structures from maps of sea level anomaly. Ocean Sci. 10:39. doi: 10.5194/os-10-39-2014

CrossRef Full Text | Google Scholar

Zhang, J., Zheng, Y., and Qi, D. (2017). “Deep spatio-temporal residual networks for citywide crowd flows prediction,” in Proceedings of the AAAI Conference on Artificial Intelligence (San Francisco, CA: Association for the Advancement of Artificial Intelligence). doi: 10.5555/3298239.3298479

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, J., Zheng, Y., Qi, D., Li, R., Yi, X., and Li, T. (2018). Predicting citywide crowd flows using deep spatio-temporal residual networks. Artif. Intell. 259, 147–166. doi: 10.1016/j.artint.2018.03.002

CrossRef Full Text | Google Scholar

Zhang, Y., Liu, Z., Zhao, Y., Wang, W., Li, J., and Xu, J. (2014). Mesoscale eddies transport deep-sea sediments. Sci. Rep. 4:5937. doi: 10.1038/srep05937

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Z. G., Wang, W., and Qiu, B. (2014). Oceanic mass transport by mesoscale eddies. Science 345, 322–324. doi: 10.1126/science.1252418

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Z., and Qiu, B. (2020). Surface chlorophyll enhancement in mesoscale Eddies by submesoscale spiral bands. Geophys. Res. Lett. 47:e2020GL088820.

Google Scholar

Zhang, Z., Tian, J., Qiu, B., Zhao, W., Chang, P., Wu, D., et al. (2016). Observed 3D Structure, generation, and dissipation of oceanic mesoscale eddies in the South China Sea. Sci. Rep. 6:24349. doi: 10.1038/srep24349

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Z., Zhang, Y. X., Wang, W., and Huang, R. X. (2013). Universal structure of mesoscale eddies in the ocean. Geophys. Res. Lett. 40, 3677–3681. doi: 10.1002/grl.50736

CrossRef Full Text | Google Scholar

Zhang, Z. G., Zhang, Y., and Wang, W. (2017). Three-compartment structure of subsurface-intensified mesoscale eddies in the ocean. J. Geophys. Res. 122, 1653–1664. doi: 10.1002/2016JC012376

CrossRef Full Text | Google Scholar

Zhang, Z. W., Qiu, B., Tian, J., Zhao, W., and Huang, X. (2018). Latitude-dependent finescale turbulent shear generations in the Pacific tropical-extratropical upper ocean. Nat. Commun. 9, 1–13. doi: 10.1038/s41467-018-06260-8

CrossRef Full Text | Google Scholar

Zhu, X., Cheng, D., Zhang, Z., Lin, S. C., and Dai, J. (2019). “An empirical study of spatial attention mechanisms in deep networks,” in Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, 6687–6696. doi: 10.1109/ICCV.2019.00679

CrossRef Full Text | Google Scholar