A Biophysical Model and Network Analysis of Invertebrate Community Dispersal Reveals Regional Patterns of Seagrass Habitat Connectivity

Introduction

A key challenge in marine ecology and conservation science is to identify the spatial scale of biodiversity patterns and the relative role of the complex oceanographic processes that may influence these patterns. This requires moving beyond the study of biodiversity in single habitat patches to instead considering the seascape as a mosaic of habitat patches connected by dispersal (Boström et al., 2011; Pittman et al., 2011). Dispersal, a foundational process in metacommunity theory, has been shown to be a key driver determining diversity patterns at local and regional scales (Kneitel and Miller, 2003; Loreau et al., 2003; Mouquet and Loreau, 2003; Massol et al., 2017; Thompson et al., 2020). In coastal systems, the diversity of a region or any habitat within the region can depend on the spatial arrangement of habitats and the variation among organisms’ abilities to move between them (Cowen and Sponaugle, 2009; Boström et al., 2010). Therefore, understanding the ecological consequences of movement requires spatially explicit knowledge of functional connectivity – how dispersal behavior and habitat configuration combine to influence the movement of an individual across the seascape (Kindlmann and Burel, 2008; Kool et al., 2013).

Spatially explicit movement information facilitates the analysis of dispersal patterns as a network in the context of meta-population/community theory (Hanski, 2001; Leibold and Chase, 2018), which can reveal emergent spatial properties of the seascape and focal communities that would otherwise not be evident without a network perspective (Urban et al., 2009). A disconnected network would indicate isolated communities that do not interact, whereas a highly connected network of habitat patches may operate as a single regional community. Furthermore, identifying patches of habitat that are central, in terms of how they link populations in other patches through dispersal and colonization, indicates areas of habitat that may provide stepping stones that are important for maintaining regional connectivity and thus maintaining biodiversity patterns (Saura et al., 2014; Albert et al., 2017). A network analysis can also identify clusters of patches based on higher levels of ecological exchange within than outside the cluster (Thomas et al., 2014; Gilarranz et al., 2017). This can identify dispersal barriers and subsequently reveal the spatial scale of metapopulations or provide a first prediction of the scale of metacommunities in the absence of local biological and environmental influences on persistence. These and other seascape-scale patterns that have consequences for biodiversity only emerge from a network approach that can consider movement rates among many patches simultaneously.

Marine connectivity research has primarily focused on the connectivity of coral reefs or pelagic species, but the connectivity of other patchy nearshore habitat types and the species that disperse among them remains poorly understood (Bryan-Brown et al., 2017). Seagrass, like coral, provides foundational biogenic habitat for a high level of biodiversity (Orth et al., 1984), including communities of epifaunal invertebrates (Heck and Thoman, 1984; Duffy et al., 2015). The patchy distribution of seagrass meadows across the seascape may create the structure for a metacommunity of seagrass-associated species that are connected by animal movement (Bell, 2006; Boström et al., 2006; Whippo et al., 2018). There are a variety of life histories present in this community which results in a range of dispersal abilities. These species may move as larvae, juveniles or adults through mostly passive transportation in ocean currents and settle on distant meadows of seagrass (Boström et al., 2010). Dispersal and connectivity have been suggested as one of the important drivers of local and regional biodiversity patterns in eelgrass-associated communities (France and Duffy, 2006; Yamada et al., 2014; Whippo et al., 2018; Stark et al., 2020). These inferences were based on spatial biodiversity patterns and in the absence of oceanographically informed estimates of potential connectivity. Consequently, spatially explicit dispersal information is essential to gain further insight into how these communities are structured across spatially heterogeneous seascapes.

In the nearshore seascape, connectivity patterns are determined by physical oceanographic processes (e.g., tidal, wind, and freshwater forcing), dispersal ecology (dispersal and post settlement survival), and the physical arrangement of habitat (Werner et al., 2007). A biophysical model that incorporates hydrodynamic models and biological properties can be an effective tool for predicting movement pathways and quantifying connectivity between habitats in the form of probabilities linking a matrix of habitat (Siegel et al., 2003; Treml et al., 2012; Sunday et al., 2014; Schill et al., 2015; Wren et al., 2016). However, modeling nearshore dynamics is difficult compared to pelagic studies. While we know the broad-scale movement of ocean currents adjacent to the coast of a continent (e.g., California current, Alaska current), predicting connectivity for spatially complex coastal areas and for species with low dispersal abilities requires high resolution hydrodynamic models and spatial habitat data (Werner et al., 2007).

A biophysical model for nearshore habitat would allow for the quantification of connectivity at the smaller spatial and temporal scales relevant to ecological processes. While genetic studies can support inferences of connectivity from parentage analysis, logistical constraints limit the spatial scope of these studies (D’Aloia et al., 2015; Bode et al., 2019), they may only be applicable at very large scales (Riginos et al., 2019), and regional genetic structure may not reflect the levels of connectivity that influence the population dynamics that maintain biodiversity at the community level. For example, in areas influenced by past glaciation, genetic structure may still be detectable from historical gene flow patterns and may not reflect current pathways of exchange (Hedgecock et al., 2003; Sunday et al., 2014; Selkoe et al., 2016). However, biophysical modeling can still predict what may be considered weak connections but genetically significant dispersal events (e.g., one migrant per generation), as even minimal levels of gene flow can homogenize populations (Waples, 1998; Jenkins and Stevens, 2018). Therefore, “ecological connectivity” is the level of exchange of individuals that can influence population and community dynamics at non-evolutionary time scales (Treml et al., 2012). In addition, an ecological connectivity analysis based on a biophysical modeling approach can supply the information most relevant to conservation and the design of a network of connected protected areas, such as population rescue effects, source sink dynamics, and trophic dynamics (Burgess et al., 2014; Guzman et al., 2019).

The objective of this study is to quantify potential connectivity among communities inhabiting seagrass (Zostera marina) habitat on the British Columbia (BC) coast of Canada in the form of the functional connectivity that is generated by the varying dispersal abilities of different species of the seagrass associated epifaunal invertebrate community. We expect that asymmetric ocean currents, dispersal ability, and the spatial arrangement of habitat create patterns of connectivity that vary spatially across the region. We use a biophysical modeling and network analysis approach to answer the following questions: (1) To what degree is an invertebrate community, consisting of multiple life-history strategies, likely connected by dispersal among seagrass meadows? (2) Do increases in dispersal potential result in higher habitat connectivity? (3) Which seagrass meadows are important for maintaining network connectivity, and does habitat location and/or size determine this importance? (4) Do coastal topography and water currents create distinct clusters of meadows likely to be ecologically connected? Together, these questions allow us to assess patterns of connectivity across spatial scales and for multiple taxa.

Materials and Methods

We used a biophysical modeling approach to simulate dispersal and estimate potential connectivity of the community of seagrass associated invertebrate fauna (i.e., “community connectivity”; Table 1). The model consists of five components: (1) seascape physical structure information, (2) invertebrate community trait data that influences dispersal ability, (3) hydrodynamic model results that contain ocean current velocities, (4) an individual-based particle tracking model (IBM) to estimate dispersal trajectories with the influence of dispersal traits, (5) and a network and cluster detection analysis to interpret the connectivity of the dispersal trajectories in an ecological context (Figure 1).

TABLE 1

Table 1. Glossary of key terms.

FIGURE 1

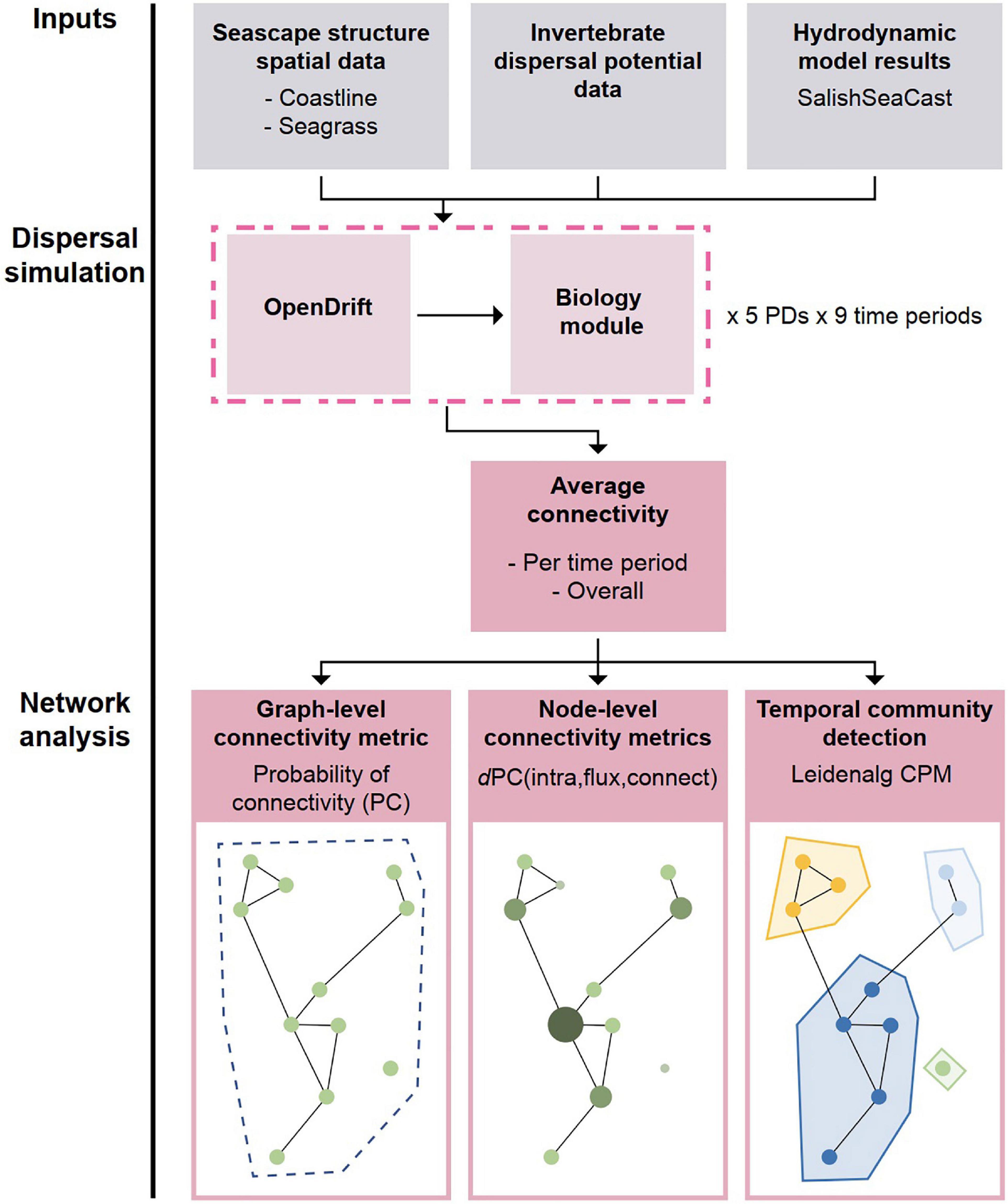
Figure 1. Flow chart of the biophysical model and network analysis. Seascape structure data, dispersal trait data, and hydrodynamic model results are used in the OpenDrift dispersal simulation. The biology module applies settlement and mortality to the resulting trajectories and creates weighted and directional connections. The drift simulations are run for up to 60 days and for 9 date ranges. We then average the connectivity for different pelagic propagule durations (PD). Finally, we calculate connectivity metrics on the entire graph for the Salish Sea and for each meadow (node), and we detect connectivity-defined communities across time. Graphics: Sylvia Heredia.

Study System

We focused on the Salish Sea region of the BC and Washington coast. The Salish Sea is a semi-enclosed system bounded by Vancouver Island, and connected to the Pacific Ocean through the Juan de Fuca Strait in the south and narrow channels to the north (Figure 2). The topographic complexity and glacial history of BC’s coastline, that likely influence species distributions (Pielou, 1991), creates unique challenges for modeling and as a result nearshore connectivity is poorly understood. In this region, there are also two important climatic changes that drive strong seasonal differences in hydrodynamics and have ecological relevance: (1) the spring transition between Aleutian Low and North Pacific High pressure dominance over the northeast Pacific that suppresses winter storm activity resulting in phytoplankton blooms (Kathleen Collins et al., 2009; Bakri and Jackson, 2019), and (2) the summer freshet, dominated by the undammed Fraser River that increases the stratification and reduces the residence time of the surface layer (Pawlowicz et al., 2007).

FIGURE 2

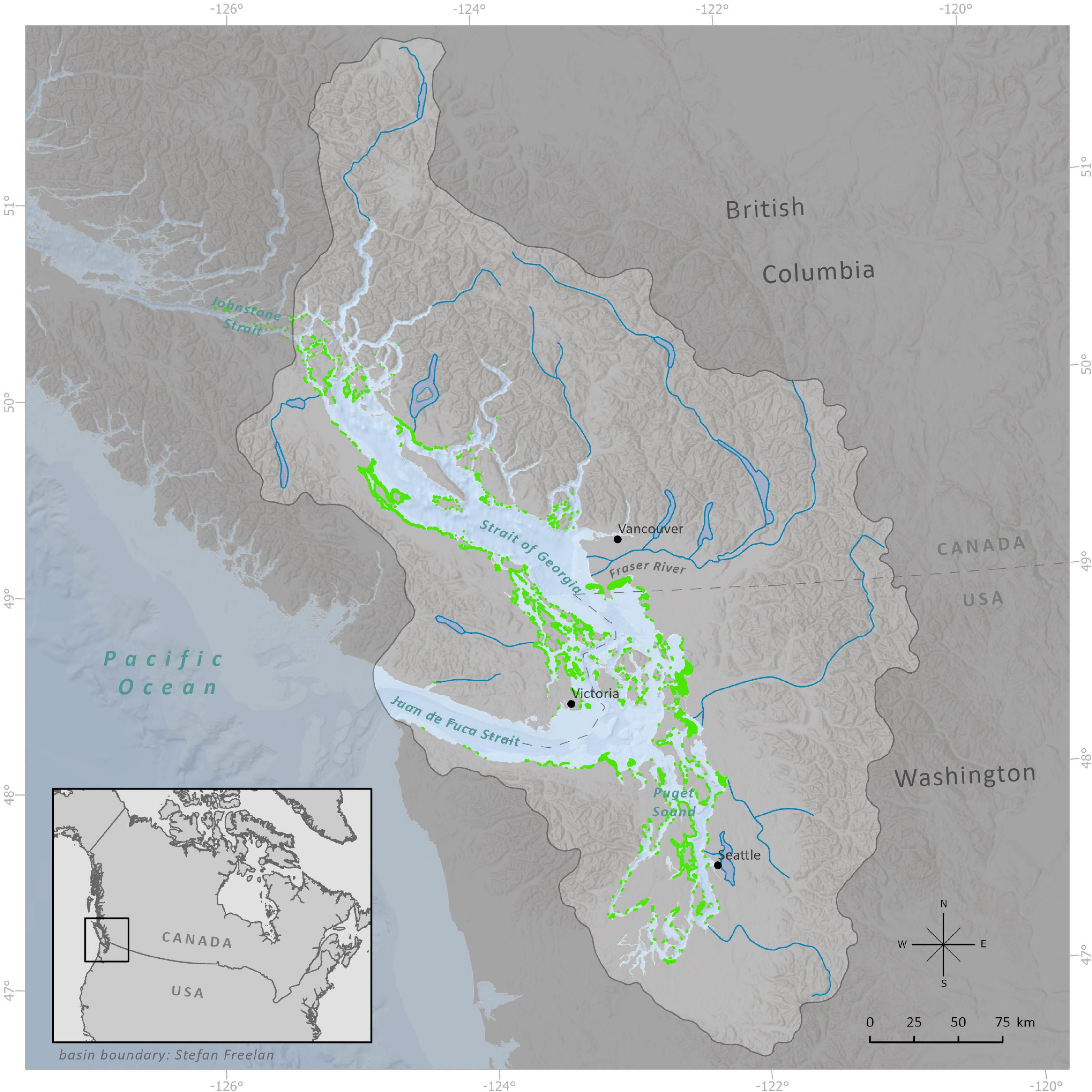
Figure 2. The Salish Sea and seagrass meadows. The basin boundary and major rivers are highlighted to show the significant freshwater inputs in this estuarine system. The SalishSeaCast oceanographic model extends from Puget Sound in the south to Johnstone Strait in the north, with open boundaries to the Pacific Ocean at Johnstone Strait and Juan de Fuca Strait. The model has a near-uniform grid spacing of 440 m × 500 m and a 1-h temporal resolution. Seagrass meadows range in size from <0.001 to 50 km², with a total area of 519 km². Seagrass polygon size is exaggerated in this map for visualization.

The dominant habitat-forming seagrass is eelgrass (Z. marina) which is patchily distributed along the entire coast of BC in sheltered intertidal and subtidal areas. Eelgrass occurs to a maximum depth of 10 m depending on turbidity (Christiaen et al., 2015) and can form meadows that range in size from a few seasonally intermittent shoots to more permanent meadows greater than 30 km² (Murphy G. E. P. et al., 2021). As a primary producer and coastal habitat forming species, eelgrass provides habitat and a productive algal food source for multiple trophic levels (Heck et al., 2008; Amundrud et al., 2015; Duffy et al., 2015; Huang et al., 2015). Eelgrass has also been identified as an ecological conservation priority for current marine conservation planning efforts in BC (Gale et al., 2019; Rubidge et al., 2020).

Eelgrass provides biogenic habitat for a variety of epifaunal and infaunal invertebrates. Common taxa include Amphipoda, Isopoda, Decapoda, Polychaeta, and Bivalvia, and may include the full life cycle of a species or just the juvenile or adult stages. While not all species within these groups are eelgrass habitat specialists, together they constitute a unique assemblage distinct from communities in the surrounding substrates, and we are focusing on their probabilities of connecting spatially distinct habitat as a possible route of dispersal. In general, most species in this community are direct developers or planktotrophic/lecithotrophic, and they are semi-mobile or sessile as adults (Boström et al., 2010). In addition to larval drifting, pelagic dispersal may also occur by rafting on seagrass and epiphytic algae which has been shown as a viable mode of transport for small invertebrates and can enable kilometer-scale dispersal for sessile species (Worcester, 1994; Brooks and Bell, 2001). Reproductive eelgrass shoots can remain buoyant for up to 26 days (Harwell and Orth, 2002; Källström et al., 2008). While species with a multi-day pelagic larval phase may have the greatest dispersal distance potential, species that are direct developers may still make short movements through rafting that can be more influential to population dynamics than longer distance low probability dispersal (Johannesson, 1988). Therefore, we included all sampled species in the community regardless of development type and mobility.

Seascape Structure Spatial Data

The first component of the biophysical model is the structural data of the seascape, consisting of coastline and seagrass spatial data. A coastline vector dataset was derived from a 1:20,000 scale provincial government dataset which provided the sufficient detail to represent nearshore features. Small islands (<0.01 km²) were removed to reduce the complexity of the dataset. Eelgrass spatial data was obtained from multiple government and non-governmental sources, which used a variety of survey methods. While the dataset achieves near coastwide coverage, only presences were consistently documented and there are likely areas of incomplete sampling effort which means there are likely meadows that exist that are not included in our analysis. However, much of the data have been ground truthed, and we are confident that most major meadows are included. The seagrass dataset was simplified to more closely match the resolution of the oceanographic model (0.5 km). Primarily, this involved aggregating seagrass polygons that were within 100 m of each other.

Parameterize Model With Dispersal Trait Values

To simulate the dispersal of the seagrass invertebrate community we compiled dispersal related traits from a literature search for 63 species that were identified in biodiversity surveys of meadows along the coast of BC (Whippo et al., 2018; Stark et al., 2020). We considered the potential pelagic propagule duration (PD) and a daily mortality rate in the biophysical model. PD is inclusive of larval drift, adult movement, and rafting (Shanks, 2009). In addition, all species were assumed to have a settlement behavior trait, which simply means that they will settle if they drift over suitable seagrass habitat (see Figure 3 for a diagram of processes that influence connectivity). We binned PD values into five levels, and to achieve equal width bins we used values of eⁿ days, where n = 0, 1, 2, 3, 4, which we rounded to 1, 3, 7, 21, and 60 days on a linear scale (Supplementary Figure 1). Although some species have a PD longer than 60 days, early testing showed that the coastal boundary constraints of the Salish Sea prevent most larvae from drifting longer than 60 days before stranding. For species that do not have a planktonic larval phase, we considered them capable of rafting on seagrass debris, which can remain buoyant for up to 3 weeks (Harwell and Orth, 2002; Källström et al., 2008).

FIGURE 3

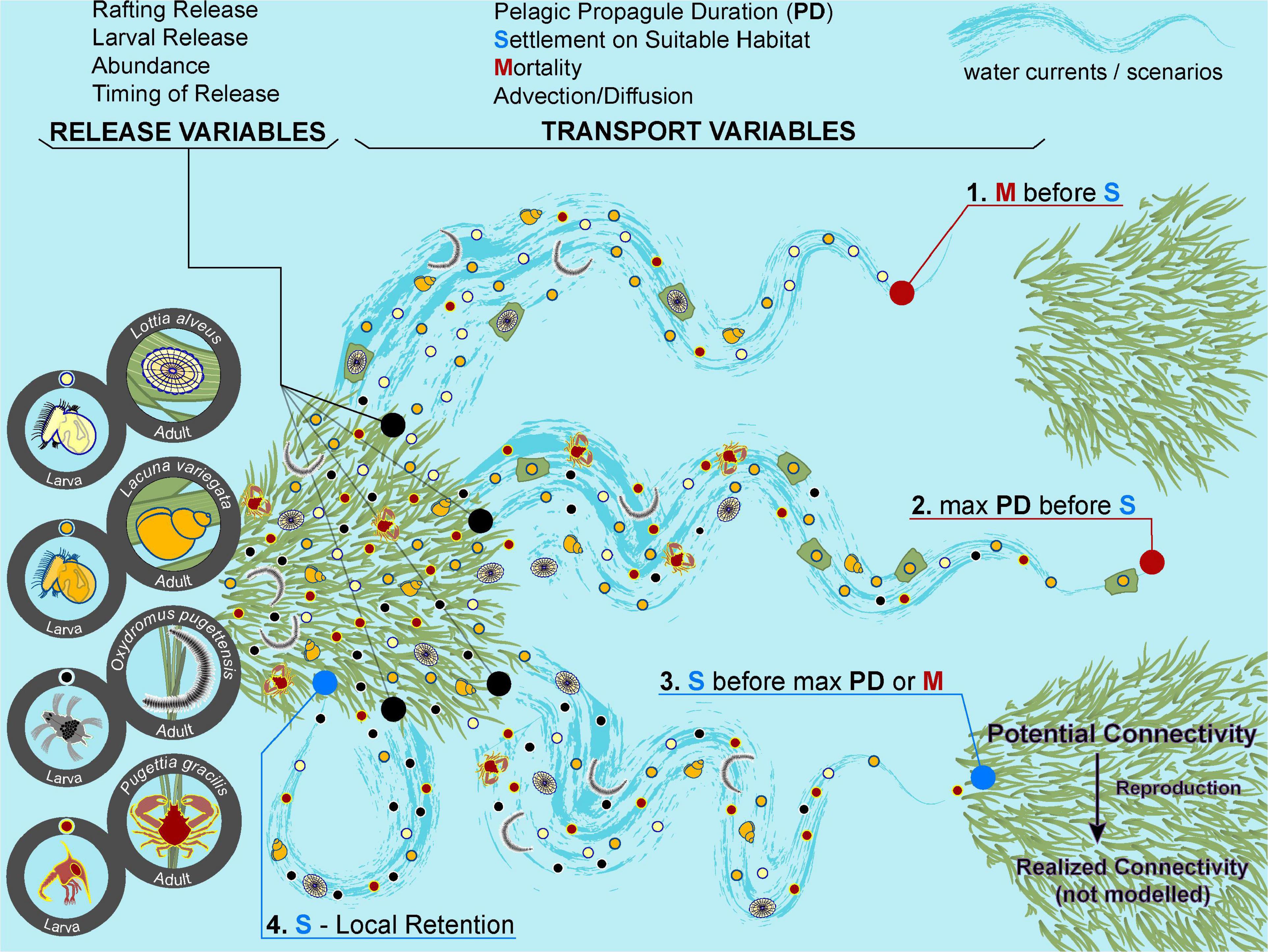
Figure 3. Examples of dispersal scenarios and the processes that contribute to connectivity. Each numbered scenario represents a potential fate of a particle. Four representative species are shown, but a scenario is not specific to any one species. In a simulation, particles are released from a seagrass meadow. RELEASE VARIABLES: The timing of release varies by year, season, and hour within a tidal cycle. The abundance released is proportional to meadow size. Particles can drift as pelagic larvae or by rafting on seagrass as a juvenile or adult (if rafting, pelagic duration = 21 days). TRANSPORT VARIABLES: During transport, particles are advected and diffused by the hydrodynamic model and they experience a 15% daily mortality rate (randomly applied), thus reducing density and abundance through time. When a particle drifts over another seagrass meadow, it settles and is removed from the simulation. If a particle encounters the coastline, it strands and is unable to drift further. A particle can drift for as long as its pelagic propagule duration (PD). We do not model any swimming behavior, but for our species it is negligible compared to the advection speeds. SCENARIOS: In scenario 1, the particles experience mortality before reaching suitable habitat. In scenario 2, a particle reaches its maximum PD before drifting over any suitable habitat. In scenario 3, a particle reaches suitable habitat before experiencing mortality or reaching its max PD. Reaching this stage is considered “potential connectivity.” Full “realized connectivity” requires the individual to reproduce to establish a genetic connection. In our simulations, we only model up to potential connectivity. In scenario 4, a particle is advected back to its meadow of origin. Graphics: Sylvia Heredia.

We applied a single instantaneous mortality rate for all species due to a lack of information for individual species. Frequently used rates of invertebrate larvae mortality range between 0.15 and 0.23 day^–1 depending on methodology (Rumrill, 1990). White et al. (2014) revisited the Rumrill (1990) data and estimated mortality rates of <0.15 day^–1 using a different methodology. Therefore, we used 0.15 day^–1 to ensure that an adequate mortality rate was still represented for all species but that it was not set unrealistically high.

We did not include active or directed swimming behavior in the biophysical model. There is limited information on swimming speed of invertebrate larvae for many of these species. In addition, the sustained swimming speeds of small larvae are usually much less than current speeds (Orth, 1992; Daigle et al., 2016). Therefore, we make the assumption that modeling passive dispersal as influenced by advection and diffusion is adequate when considering large-scale movements.

Hydrodynamic Model

The hydrodynamic fields used to force the dispersal simulations were obtained from the SalishSeaCast configuration of the Nucleus for European Modelling of the Ocean, a finite-difference, hydrostatic, community ocean model (Gurvan et al., 2017). SalishSeaCast is described in detail by Soontiens et al. (2016), Soontiens and Allen (2017), and Olson et al. (2020). Briefly, the configuration uses approximately 0.5 km horizontal resolution and 40 z-coordinate layers ranging in thickness from 1 m near the surface to 27 m at depth. Hourly surface wind and meteorological forcing fields are sourced from the 2.5 km High Resolution Deterministic Prediction System maintained by Environment and Climate Change Canada (ECCC; Milbrandt et al., 2016). Runoff at 150 rivers is prescribed using monthly watershed climatologies (Morrison et al., 2012) along with daily observations from the ECCC Fraser River flow gage at Hope, BC. Oceanic forcing of temperature, salinity, and eight tidal constituents is implemented at open boundaries in Juan de Fuca Strait and Johnstone Strait.

SalishSeaCast is optimized for the Strait of Georgia and reproduces extensive observations of water level (Soontiens et al., 2016) and temperature and salinity (Olson et al., 2020) in that portion of the domain with competitive skill relative to similar models of the region (e.g., Khangaonkar et al., 2018). This skill was achieved through careful tuning of tides, bathymetry, and sub-grid scale physics to accurately resolve several important features of the circulation, including mixing over sills and annual flushing of the deep Strait of Georgia (Soontiens and Allen, 2017). While the SalishSeaCast velocity fields have not been directly evaluated against observations, the lack of significant temperature and salinity bias in the presence of strong spatial gradients suggests that near-surface currents are statistically accurate. Aside from model tuning, this accuracy is primarily owed to the high-resolution wind forcing as wind is a dominant driver of surface currents along with rivers and tides (Halverson and Pawlowicz, 2016).

We used hourly current velocities from the SalishSeaCast model for 3 years (2011, 2014, and 2017). Within each year we considered three distinct time periods that may have ecological significance: January–March (winter), May–July (spring), and August–October (summer). Pawlowicz et al. (2019) noted distinct differences in circulation between winter and summer as a result of differences in freshwater inputs and upwelling over the outer shelf. In addition, peak seagrass reproduction occurs during August, followed by senescence in the fall when shoots are most likely to break (Källström et al., 2008), which may be a time when more rafting occurs. Only the surface layer of the model was used for our dispersal simulations. We justify this assumption because seagrass is a shallow subtidal habitat and we are interested in successful connections between meadows and not the fate of particles that sink.

Despite the high resolution of the model, there were still areas of the Salish Sea too narrow to be resolved (e.g., inlets, passages). The hydrodynamic model criteria requires a modeled area to be at least two grid points wide, and narrow areas were either widened or not considered (Soontiens et al., 2016). Therefore, we removed seagrass meadows that overlap with any narrow area not considered in the hydrodynamic model. This resulted in the removal of only 24 out of 994 meadows.

Dispersal Simulation

The dispersal of eelgrass-associated invertebrates was simulated using the Python-based framework OpenDrift – an IBM for Lagrangian particle tracking (Dagestad et al., 2018). In addition to the Forward–Euler numerical integration scheme provided by OpenDrift, we wrote a custom module to incorporate PD, mortality, and settlement. The basic description of a simulation is as follows: for each of the nine experimental time periods (3 seasons × 3 years), particles are released simultaneously from all seagrass meadows every 4 h for the first 2 weeks to account for tidal variation, they are tracked as they are advected and diffused across the seascape, daily mortality is applied by randomly selecting particles and removing them from the simulation, if a particle drifts over another seagrass meadow or returns to the same meadow it is considered settled and removed from the simulation, the simulation is run until the end of the PD or until all particles have settled or stranded on the coast (Figure 3). These simulations model potential connectivity (transport and settlement only), whereas realized connectivity requires the individual to reproduce and establish a genetic connection.

The number of particles released per meadow scales with meadow area and release locations are spaced evenly within a meadow. In total, 3.8 million particles were released per period, which was sufficient to capture the variation of particle destinations while scaling within the computing resources available. The position of particles was updated every 30 s in the simulation. A 1.5 m²/s diffusion rate (K) was used to represent the effect of subgrid-scale turbulent motions on particle displacement. We implemented this diffusion using a statistical relationship between K and the particle velocity variance V²

$$\overline{V^2}=\frac{2K}{dt}$$

where dt is the time step (LaCasce, 2008). A random walk was then applied to the particle displacements using a Gaussian distribution defined by the velocity variance.

Network Analysis

We conducted a network analysis to answer our first three questions on quantifying and characterizing potential connectivity. Network methods analyze connections resulting from the dispersal simulation in graphical form to study their topological relationships and uncover spatial patterns of connectivity. With a graphical approach, seagrass meadows are nodes and dispersal connections are edges in a graph, which are directional and weighted by connection probability (Minor and Urban, 2007). Connection probabilities were calculated as the percentage of particles released from the origin meadow that settle on a destination meadow.

To answer our first question on the connection probabilities of whole seagrass invertebrate communities, we averaged connectivity across PD scenarios and across time to move from population-level to community-level estimates of connectivity. This approach is useful for characterizing the functional role of habitat to multi-species patterns of movement (Melià et al., 2016; D’Aloia et al., 2017). In the averaging scheme, we weighted connections by how common they were across all PD scenarios and time periods. For example, if a connection between two meadows was made in just the 60-day PD scenario in only 1 of the 9 time periods, then it would be considered less important to overall community connectivity than a connection made at multiple PD levels and in every time period.

To answer our second question on the relationship between dispersal ability and overall habitat connectivity, we calculated the Probability of Connectivity (PC) metrics from the Conefor software package for each PD level (Saura and Torné, 2009; Saura and Rubio, 2010). PC incorporates dispersal probabilities and weights them by an additional patch attribute, typically area, to calculate a measurement of “habitat availability,” indicating how well connected (i.e., available for movement) the entire system is. By incorporating patch area, we start with the assumption that a patch itself provides area for movement, which may be important for seagrass-associated invertebrates with limited dispersal abilities. Then, any connections made between patches add to the area available for an organism to move between. For instance, a connection probability of 10% between two large patches connects more habitat than the same strength connection between two smaller patches. Thus, the intraconnectivity of a network provides a baseline measurement of connectivity to compare to the additional area made accessible by interconnectivity. This allows us to move beyond simply knowing a quantity of nodes connected which may not be as informative for understanding the importance of a patch to the overall network. An additional benefit of considering intraconnectivity is to avoid characterizing isolated meadows as having no functional role in supporting animal movement, and therefore in supporting community diversity.

By weighting connections by area as the patch attribute in the PC calculation, we are using area as a proxy for intrapatch movement. However, we also intend area to be a general proxy for other patch importance metrics that may scale with area, but non-linearly, such as habitat quality, local retention, and species diversity (Minor and Urban, 2007; Saura and Rubio, 2010; Pereira et al., 2011; Engelhard et al., 2017). Since our patch areas spanned 7 orders of magnitude with a right-skewed distribution, we log-transformed areas to achieve a normal distribution of patch areas, so as not to overweight the importance of large patches or deem small patches as completely insignificant to the multiple functional roles that they may play in influencing connectivity patterns.

To answer our third question on characterizing the contribution of individual seagrass meadows to the overall connectivity, we calculated the change in PC (dPC) when that meadow is removed, indicating the importance of that node to contributing to and maintaining connectivity. We calculated dPC for each dispersal scenario and averaged the results. dPC is comprised of three component parts: intra, flux, and connector. These components represent the different ways a node can contribute to connectivity. They are non-overlapping properties of the network and provide a more comprehensive assessment of connectivity than just considering traditional connectivity metrics separately (e.g., betweenness centrality, node degree). Intra represents the intra-connectivity of a patch (i.e., the area available for within patch movement and local retention). Flux represents how much a patch is connected to other patches by considering all the area-weighted connections in and out of that patch. Connector measures how much a patch is included in the multi-step paths between other patches and therefore acting as a stepping-stone to link the system.

Together, these metrics show the different ways that a seagrass patch can contribute to the overall connectivity of the network (Saura and Rubio, 2010). Given that we are interested in dispersal as a fundamental ecological process, it was important to use ecologically relevant metrics that have both a structural and functional basis and relate pattern and process (Pittman, 2018). The PC metric and its component parts allow us to interpret the functional role of seagrass habitat connectivity patterns in the context of the invertebrate dispersal process.

Cluster Detection

To answer our fourth question on identifying distinct clusters of connected seagrass habitat that may arise from topography and ocean currents, we used “community detection” methods. Community detection algorithms identify clusters of nodes that are strongly connected to each other and weakly connected to other nodes in the network (a “community” refers to a graphical property and not an ecological community of species, to avoid confusion with an ecological community, we refer to a graph theoretical “community” as a cluster). This allows us to quantify the spatial scale of dispersal between interacting clusters and potentially identifies ecologically distinct regions.

We used the CPM function in the Leidenalg Python package to identify meadow clusters of varying clustering strength (Traag et al., 2019). CPM gives the user control over a resolution parameter that sets a threshold of connectivity for community membership. Maintaining control over the resolution parameter allows for different ecological interpretations of the network clustering, as opposed to just identifying the one mathematically optimal partitioning which may not be ecologically interpretable. For instance, setting a low threshold value will select for large clusters which will identify where the strongest barriers to dispersal are in the system as only very rare connections would connect clusters. Alternatively, setting a high threshold value will select fewer nodes per cluster and identify the strongest connected clusters of nodes, but the boundaries of a cluster are more permeable (Thomas et al., 2014).

We used a temporal cluster detection method to identify meadows potentially clustered across time periods (Mucha et al., 2010; Traag et al., 2019). Using this multidimensional method, nodes could take on membership in multiple clusters which allowed us to identify how variable seagrass meadow clusters are through time. To implement this method, the user provides “interslice” weightings to indicate how similar the overall connectivity results between time periods should be considered. Knowing that hydrodynamics vary seasonally in the Salish Sea with less interannual variation, and with evidence that community composition and abundance for meadows can vary seasonally (Lefcheck et al., 2016a; Whippo et al., 2018), we chose to focus on seasonal variation. Therefore, we weighted our interslices so that between-season membership could vary more compared to year-to-year variation. This allows the seasonal dynamics to be more prevalent.

We followed similar methodology to Thomas et al. (2014) and calculated a range of temporal cluster configurations by varying the connectivity probability threshold. To identify potentially unique configurations from this range, we plotted the amount of connectivity occurring between clusters against the connectivity threshold. At threshold values where the connectivity between clusters plateaus or scales inconsistently, this indicates a stable configuration where a barrier allows the connectivity within the cluster to increase but not the connectivity between clusters (Supplementary Figure 2). For the configurations at the plateaus, we then calculated the weighted connectivity length scale for each cluster (see Table 1) and compared these values between clusters. This comparison assesses if connectivity probability scales with distance consistently across the region. Configurations with highly varying weighted connection lengths among detected clusters indicate unique dispersal patterns that may be the result of spatially distinct hydrodynamic/topographic features that are only evident at that resolution.

Ultimately, our approach analyzes connectivity at three graphical levels: a graph-wide level (PC metric), a node level (dPC metric), and a regional cluster level (temporal community detection) (Figure 1). The multi-level approach allows us to assess multi-species dispersal as it relates to the Salish Sea, individual seagrass meadows, and to sub-regional dynamics (i.e., sub-sections of the Salish Sea).

Results

Community-Level Connectivity

An overall average of community connectivity probabilities is presented when averaged by PD and through time (Figure 4), which highlights the relative importance of a connection to all species in the community. The biophysical model predicted many possible connections and few isolated meadows, but the probability of most connections was low. Connection probabilities ranged from 0.0001 to 84% (median: 0.03%, mean: 3.9%), and connection probability got weaker as distance between meadows increased (Figure 5). Dispersal was not limited to immediately adjacent meadows. While the strongest connections were made among meadows nearby on the same section of coastline, there was significant cross-basin movement (Figure 4). Only 35 of 970 meadows were completely isolated throughout all simulations and these were primarily located in sheltered channels or bays. Most of these isolated meadows were in Johnstone Strait toward the northern end of the model domain and therefore may not be isolated if the model boundary was extended. The meadows in the north are technically not part of the Salish Sea.

FIGURE 4

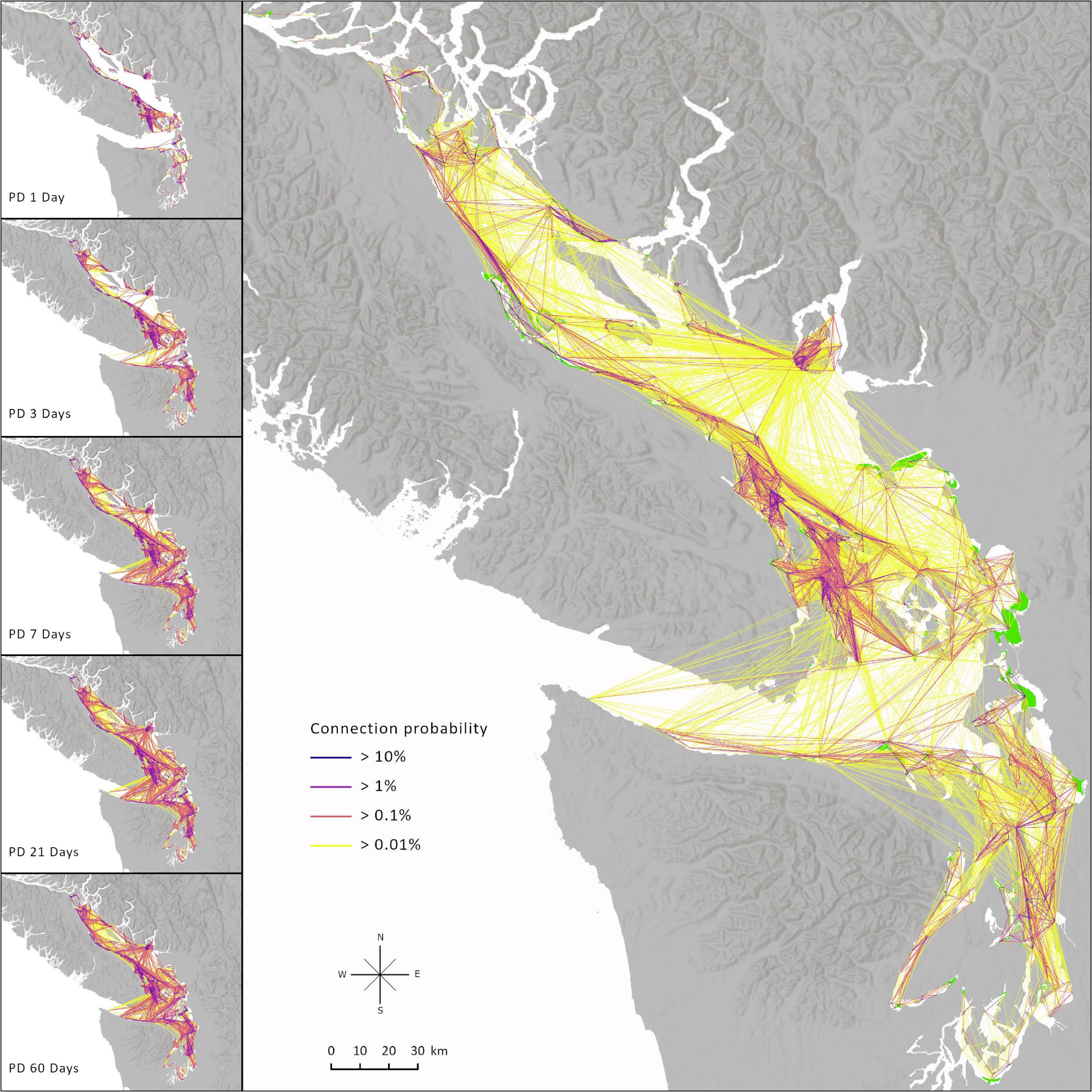
Figure 4. Averaged community connectivity and individual pelagic propagule duration (PD) level connectivity. Connection probability is the percentage of particles released from the origin meadow that successfully settled on another meadow. The individual PD scenarios are for one period to show differences of connectivity for one run of the model. The overall connectivity results from averaging the PD scenarios within each period and then averaging across all time periods. Most connections will decrease in probability because not all connections were common among PDs and time periods. This prevents weighting the network toward higher dispersing species and it represents community connectivity.

FIGURE 5

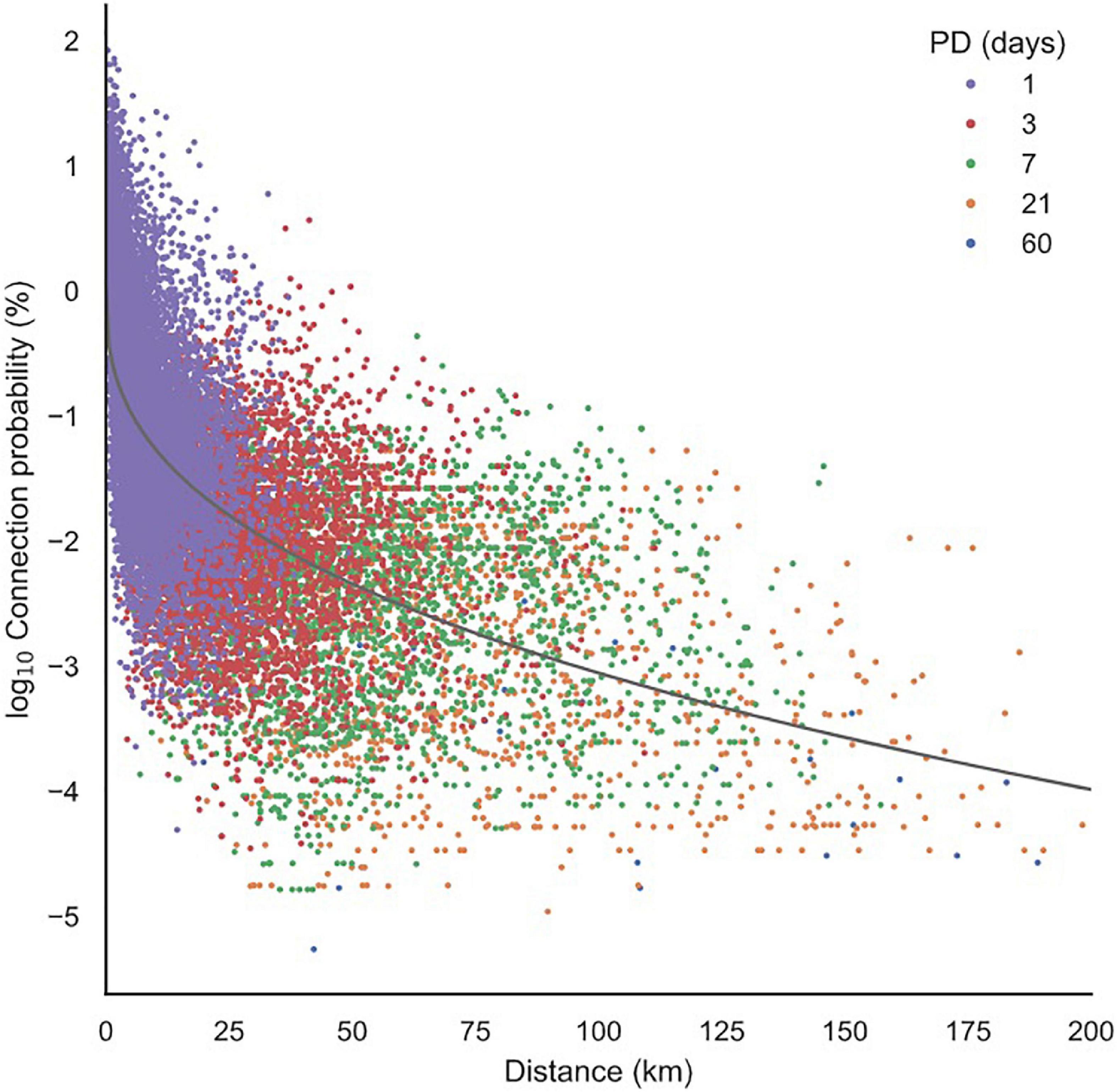
Figure 5. The relationship of connection probability and distance. Probability decreased with increasing distance. Each point represents a directional connection between seagrass meadows. Connection probability is the percentage of particles released from the origin meadow that successfully settled on another meadow. An exponential curve was fitted to the data, y = -0.52 × 0.38, R² = 0.46. Connections are symbolized by the pelagic propagule duration (PD) interval in which the connection was made. Generally, longer distance connections are made by species with longer PDs.

In all iterations of the simulation, >99% of particles either (1) settled on another seagrass meadow, (2) were retained by the source meadow, (3) stranded on the coastline, (4) or were selected for mortality. The remainder of active particles after 60 days were at the model boundary at the exit of Juan de Fuca Strait. This indicates that the Salish Sea operates as a mostly closed system when considering regular ecological exchange for nearshore habitat.

Dispersal Potential and Habitat Connectivity

We used the graph-wide metric, PC, to answer the question of how overall connectivity of the network changes with dispersal potential. We compared the percentages of connectivity that are attributable to interconnectivity, as intraconnectivity (i.e., the total seagrass area of the network) is the same for all dispersal abilities and provides a baseline of connected area (Figure 6). The relatively small amount of area attributable to inter-meadow movement (∼4.0–4.7%) is due to the low dispersal probabilities connecting most meadows. The total area made available from inter-meadow movement increased with PD, as species that were able to drift longer were able to travel further to reach more meadows, but a limit was reached at higher values. 1-day of dispersal resulted in the largest increase in interconnectivity (4.0%), and most habitat connectivity was achieved by 3 days of dispersal time (4.6%). After 1 day, increases in PD resulted in only small increases in habitat availability because the new connections established were relatively weak (Figure 5). This indicates that there is a limitation to longer distance dispersal most likely caused by the constraints of the Salish Sea topography. Lastly, although differences in connectivity between seasons were minimal (∼0.2–0.4%), connectivity was consistently lower in the winter than in the spring/summer.

FIGURE 6

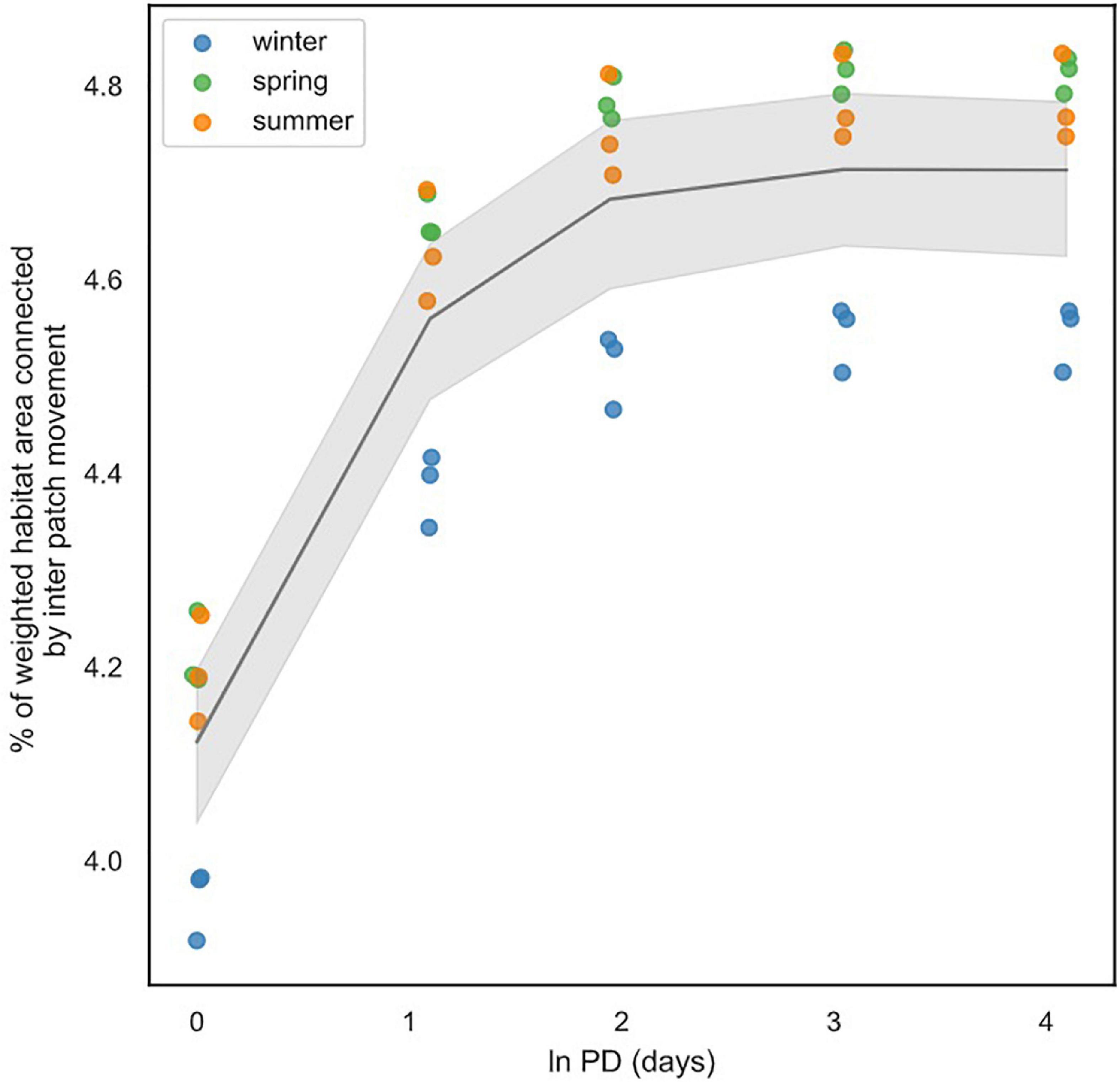
Figure 6. The percent of weighted habitat area (as derived from the PC metric) connected by inter-meadow movement for each PD. For reference, 100% interconnectivity would occur if the particles from every meadow settled on another meadow. The natural log of the pelagic duration (PD) levels (i.e., 1, 3, 7, 21, and 60 days) is used to display the data in equal intervals. The black line is the mean and the gray shading indicates the 95% confidence interval.

Meadow-Level Connectivity and Importance

To answer our third question about which meadows contribute most to connectivity patterns, we used the dPC metric and its component parts (intra, flux, and connect) to estimate each meadow’s contribution as well as its functional role in the type of connectivity it maintains. In the Salish Sea, the meadows with the highest dPC values were primarily large meadows. This is expected when the system is connected by mostly low dispersal probabilities and most of the connectivity is represented by the intraconnectivity of meadows. However, the flux and connect values still combined to influence the overall dPC score, indicating that a meadow’s position in a network can influence its importance (Figure 7).

FIGURE 7

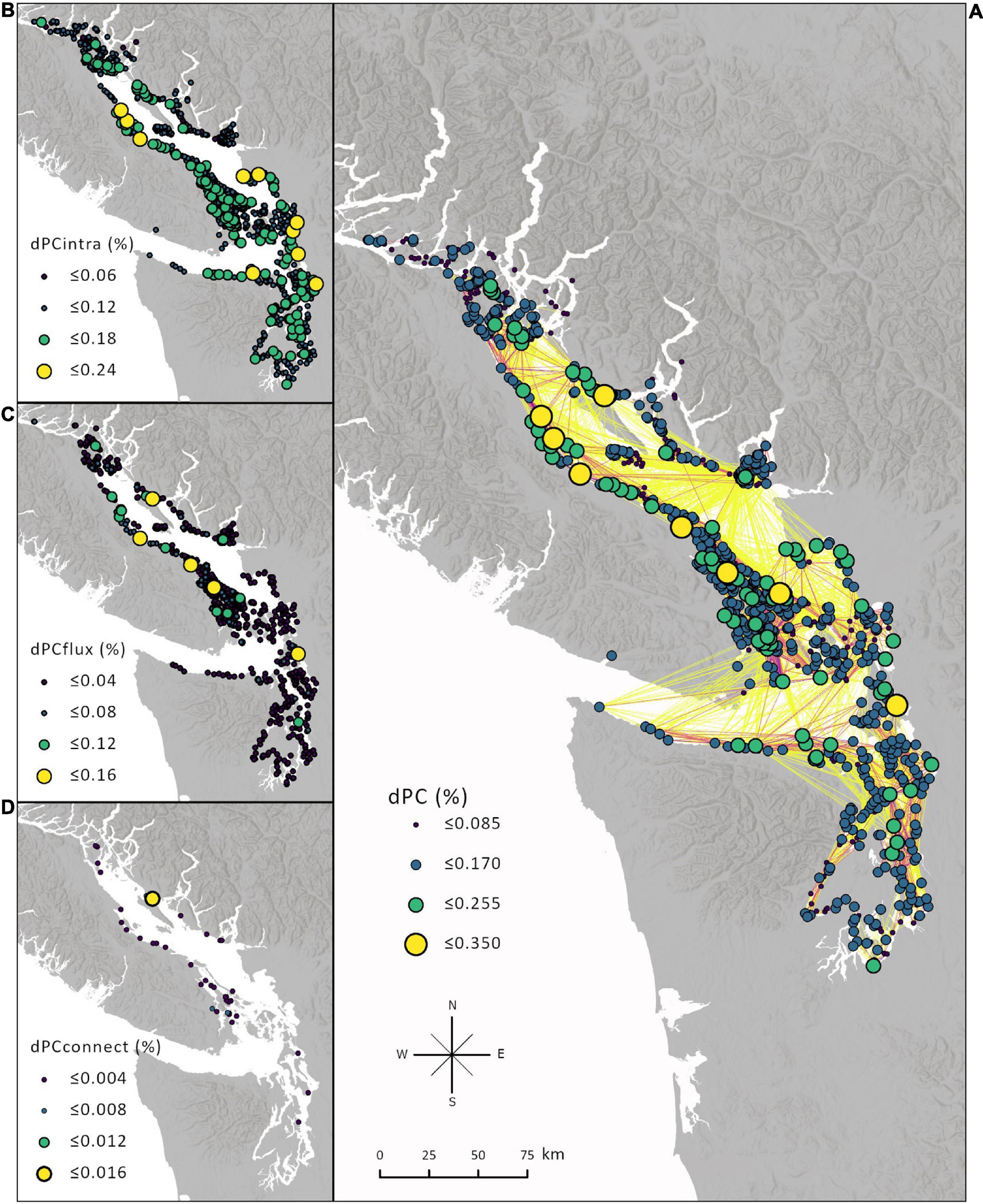
Figure 7. (A) dPC of each node. The change in the PC metric that results from removing a node indicates the importance of that node to maintaining the connectivity of the network. dPC considers intra meadow movement (dPCintra) and inter meadow movement (dPCflux and dPCconnect). Generally, (B) intra scales with the area of the meadow, (C) flux indicates how well the meadow is connected to other meadows, (D) and connect places more emphasis on the topological position of the meadow and its use as a stepping stone. Only meadows greater than 0.001 are shown for flux and connect. The range of values is different for each component and equal intervals are used to symbolize which nodes stand out for that component.

With so many meadows in the network and with dispersal among them on relatively short (days) time scales, our analysis suggests that the overall connectivity patterns are robust to excluding any one meadow from the system. A meadow’s connect value plays the smallest role in a meadow’s importance due to no one meadow standing out as a sole stepping-stone connecting groups of meadows (Figure 7D). In addition, the meadows with the most flux are not necessarily the largest (which would be expected because they release the most particles), indicating that dispersal is restricted to some degree (Figure 7C). If there were no barriers to movement (e.g., asymmetric currents, land barriers), then flux would scale with area.

Meadow Clustering

Using temporal cluster detection and the relationship between intra and inter cluster connectivity (Supplementary Figure 2), we uncovered unique and stable configurations, of which we present two configurations that may provide ecologically relevant information (Figure 8). In Figure 8A, the connection probability required for cluster membership is extremely low (∼10^–4). This results in large clusters with minimal movement between them (0.4% of total connectivity), indicating where strong barriers to dispersal may exist.

FIGURE 8

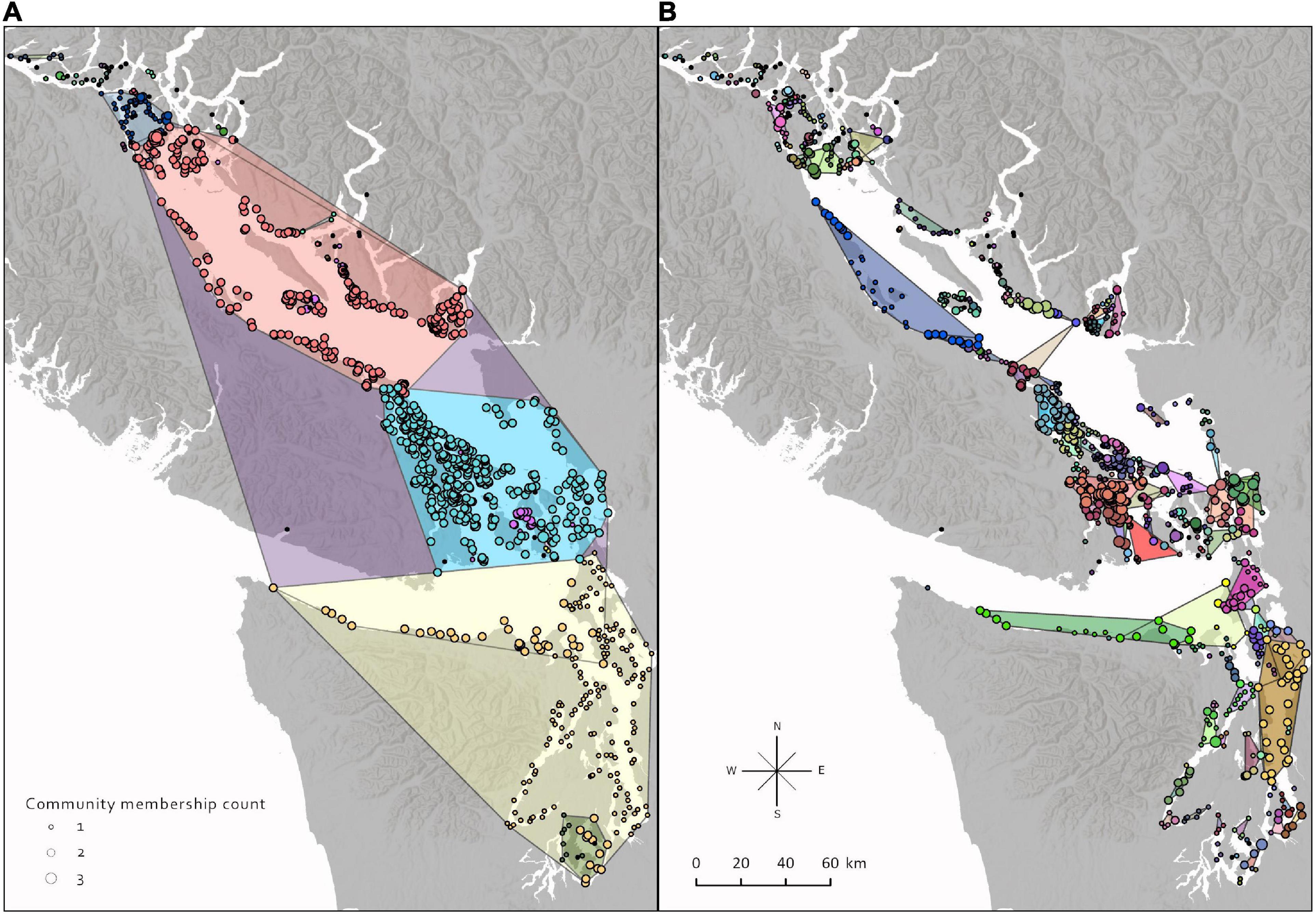
Figure 8. Two seagrass network community configurations obtained from the temporal community detection analysis. A node can be a part of multiple communities through time as connectivity changes seasonally, and therefore some of the polygon boundaries overlap. Configurations were obtained by varying the threshold of connectivity probability required for community membership, and then calculating among community connectivity characteristics to select two configurations that potentially have ecological significance. (A) A low connectivity threshold results in large communities and indicates where barriers to dispersal occur between groups of meadows within the Salish Sea. (B) A higher threshold results in smaller communities but a higher certainty of where regular exchange occurs.

In Figure 8B, the connection probability required for cluster membership is high (∼10^–1), which creates smaller clusters. The connectivity of these clusters is more certain, but the boundaries are more permeable (11.3% of total connectivity). This resolution level showed the most variation in average weighted connectivity lengths between clusters indicating unique dispersal patterns that may be the result of spatially distinct hydrodynamic/topographic features that are only evident at this resolution.

In both configurations, a node can be part of up to three different clusters because the temporal community detection analysis was set up so that dynamics could vary between three seasons. In both configurations, many nodes on the boundaries of their clusters will vary in membership. Even with high barriers to dispersal (Figure 8A), nodes have membership in more than 1 cluster due to the strong seasonal changes in connectivity. In Figure 8B, while many of the nodes are part of more than one cluster, this is mostly due to a cluster being subset into different parts and not as much from large-scale boundary overlap.

Discussion

Scales of Connectivity Analysis

We posed four questions to characterize seascape patterns of connectivity from the local to regional scale. This involved analyzing connectivity at three spatial scales: the entire Salish Sea (PC metric), individual meadows (dPC metric), and clusters of meadows (temporal community detection). By using ecologically relevant metrics, we can interpret the functional role of an individual seagrass meadow or characterize the entire network in the context of dispersal ability, thus relating pattern to process across scales.

The individual and averaged PD results (Figures 4–6) quantify community-level connectivity and describe how connectivity increases with PD. The establishment of many connections after just 1 day of dispersal indicates that the relevant spatial scale for understanding seagrass community dynamics extends beyond an individual meadow scale since most species in any given meadow can likely reach other meadows. In an open system with more symmetric movement and without mortality, we would expect PC to continue to increase linearly with PD. However, we find that most connectivity is established by 3 days. Beyond this level, the topography of the Salish Sea and mortality restrict longer distance movement and most of the connectivity established is through weak connections. Pawlowicz et al. (2019) also found that the mean time to drifter stranding was 3.5 days and was not very sensitive to source location. Lastly, at each PD level, connectivity was consistently lower in the winter than in the spring/summer. Pawlowicz et al. (2019) estimated that water traveling from the Fraser River to the Pacific takes 23 days in the summer and 53 days in winter. This is driven by changes in coastal upwelling and freshwater inflow.

The node level analysis reveals the different roles that individual seagrass meadows play in maintaining network connectivity and allows us to rank meadows by their contribution to connectivity (Figure 7). We can understand our results by comparing them to two predictions for species with varying dispersal abilities. (1) A species with a very low dispersal ability would primarily rely on intrapatch movement and local retention, whereas a species with a very high dispersal ability could make a direct connection to every patch and the network would essentially act as one large patch. Thus, in both scenarios the largest area patches would be selected as the most important for low and high dispersing species. (2) At intermediate levels of dispersal where a network is not uniformly connected, the topological position of a node (e.g., stepping stone meadows) becomes more important to maintaining connectivity (Saura and Rubio, 2010). We found that the Salish Sea is not lacking in connections, although most connections have a low probability. Therefore, large meadows are mostly selected as important, but the spatial position of a meadow is also important, as the flux and connector values combined to influence importance (Figure 7). This is to be expected since we are considering a community of species with a range of dispersal abilities, and stepping-stones and flux quantity may matter to overall connectivity at the low-intermediate level of dispersal ability.

Lastly, we identified clusters of nodes where hydrodynamics and topography create distinct clusters of connectivity. This allowed us to characterize connectivity at a sub-regional level. There are limitations to interpreting connectivity at the regional and local scales depending on the relative scale of analysis. Therefore, it is useful to also know the sub-regional clustering of meadows to narrow research and management considerations. For instance, a field study may need to know where regular exchange occurs to compare populations inside or outside of these subregions. In addition, to underpin marine spatial management, one may be interested in where potential barriers to dispersal exist to designate planning subregions.

The Biophysical Modeling Approach for Understanding Ecological Connectivity

We used a multi-species individual-based biophysical modeling approach to quantify the connectivity of seagrass habitat in the Salish Sea. By using an IBM, we were able to obtain spatially explicit movement information, which allowed us to uncover the actual pathways of movement. By basing our study on a spatially distinct habitat type, we were able to build understanding of the seascape-scale dynamics of an invertebrate community that would otherwise be difficult to track and characterize if not linked to habitat. In addition, by classifying the seascape as a series of transfer probabilities, we not only uncovered direct individual movement, but from this we can also predict the probabilities of multi-generational stepping-stone movement among multiple patches (Crandall et al., 2012; Hock and Mumby, 2015).

We found the extent of the Salish Sea to be an appropriate spatial scale for assessing ecologically relevant connectivity with a biophysical model. The fates of most particles indicate that the Salish Sea is mostly operating as a closed system. However, a small percentage of particles would have exited the system at Juan de Fuca Strait (∼<0.005%). This amount is trivial when considering population dynamics, but it may be relevant to understanding connectivity at evolutionary time scales (Treml et al., 2012). A drift card study found similar patterns (Pawlowicz et al., 2019). When cards were released from various locations the majority stranded within the Salish Sea. However, a few cards were found on the west coast of Vancouver Island and four cards were found 6 months later in Alaska, although mortality and drift time makes this an extremely unlikely scenario for a real organism.

Seagrass Metacommunity Dynamics

Our study is a necessary first step toward uncovering the spatially explicit scale that seagrass communities are functionally connected. Our results complement recent studies of seagrass-associated invertebrate communities in BC that have investigated the drivers of observed spatial biodiversity patterns. In the absence of direct estimates of connectivity that can include oceanographic currents, these studies have inferred dispersal limitation from comparisons of community composition over Euclidean distances. Stark et al. (2020) found low turnover in community composition over 1,000 km of coastline which suggests that dispersal is not limiting the presence of species in seagrass meadows in this region and that most meadows are likely connected by dispersal at least often enough to rescue populations from stochastic extinction. While our results show low probabilities for long distance connections, we found a large number of possible short-distance connections and few completely isolated meadows. Therefore, much of the Salish Sea could be connected through multi-generational stepping-stone dispersal to connect distant meadows, which could explain the community composition patterns found in Stark et al. (2020). Additionally, Stark et al. (2020) found that the subset of taxa present in all sampled meadows represented multiple dispersal strategies, and no one strategy dominated cosmopolitan taxa. Our results are consistent with this finding in that any species that can disperse as larvae or rafting on debris for at least 1+ days could connect most of the Salish Sea through stepping-stone dispersal, and generalists utilizing other habitat types could potentially accomplish this even more efficiently. Another study in BC found that a salinity gradient correlated with abundance patterns of common species (Whippo et al., 2018). However, this gradient did not explain patterns for all groups of species, and some meadows in close proximity and with similar environments had significantly different community compositions. Whippo et al. (2018) speculated that varying dispersal rates influenced by directional hydrodynamics could be structuring these patterns. While our study area did not extend to Barkley Sound, we did find that connection probability can vary substantially (0.0001–99%) over short distances (0–30 km; the maximum distance between meadows in Whippo et al., 2018), suggesting that not all meadows in close proximity are equally connected. Our study provides the first estimates of dispersal for these eelgrass associated organisms that reflect the water currents of the region, going beyond previous, less direct inferences about the possible scales of dispersal limitation in this system (Whippo et al., 2018; Stark et al., 2020). Together, these studies imply that regional biodiversity processes, in addition to local habitat conditions, likely play a role in eelgrass biodiversity.

Our results can be used to generate predictions concerning how the spatiotemporal variation in species’ dispersal patterns structure local and regional diversity. These predictions can then be tested with empirical data from field sampling and genetic analysis to indicate if other processes besides those included in the biophysical model are influencing successful dispersal and settlement. While transport is an important part of connectivity (Cowen and Sponaugle, 2009), it is still largely unknown how exchange at the spatial and temporal scale in our model relate to observed biodiversity patterns. Upon arrival in a patch, local environmental conditions and biotic interactions may determine if an individual can actually settle and persist. For instance, biodiversity patterns in seagrass have been shown to be structured by salinity (Whippo et al., 2018), water temperature, seagrass cover, algal biomass (Murphy C. E. et al., 2021), and metrics of fragmentation (Yeager et al., 2019). In addition, microsite selection may occur among nearby meadows (e.g., within a bay) suggesting that transport alone does not determine the final location of an individual (Orth, 1992). A necessary future research direction will be to link transport quantities, abiotic conditions and biotic interactions using metacommunity modeling (e.g., Thompson et al., 2020) to understand realized patterns of seagrass biodiversity.

Lastly, our temporal clustering data can be used when considering the complexities of the shifting spatial scale of metacommunity dynamics through time. Due to environmental variation through time, a static analysis of a metacommunity may not adequately link processes to observed patterns (Stier et al., 2019; Jabot et al., 2020). Seasonal changes to abiotic conditions may alter biotic interactions and reproduction rates which may influence dispersal rates for select species, thus changing community composition through time. While the variation in our clusters is only the result of changing physical ocean dynamics, they once again provide a first prediction for how aspects of the abiotic environment may influence the spatial scale of a metacommunity.

Conservation and Management Applications

A multi-scale, multi-species approach is necessary for the effective management of natural resources across a seascape (Guichard et al., 2004; Pittman, 2018). Dispersal in the context of seagrass habitat requires us to think beyond a single-patch approach to conservation and consider that the true objective may be managing ecological communities through space and time. Functional connectivity is one of the primary design principles for marine protected areas (Aichi Biodiversity Target 11). Reserves that are connected through functional linkages create redundancy and resilience for important ecosystems, communities, and populations. This ensures that the flow of materials, individuals, and genes is considered across scales (Carr et al., 2017). In BC, eelgrass is a conservation priority that has been targeted for inclusion in the MPA network planning process (Rubidge et al., 2020; Martone et al., 2021), and our connectivity results can be included in future planning efforts for designing a nearshore reserve.

Additional management-related applications of our biophysical model include predicting the consequences of disturbance (e.g., climate change, pollution, habitat loss, and invasive species) on connectivity patterns. Through changes in temperature, climate change can alter larval development and mortality rates (O’Connor et al., 2007; Lawlor and Arellano, 2020), thus reducing functional connectivity and potentially preventing a species from tracking their environment (Gerber et al., 2014). The parameters in our model can be altered to predict the potential outcome. Pollution can also create barriers to dispersal through increased mortality during dispersal (Puritz and Toonen, 2011), and identifying reductions in connectivity will be crucial for understanding the broader regional effects to what may initially seem like a localized problem (Jonsson et al., 2020). In addition, seagrass worldwide is being lost at an alarming rate (Waycott et al., 2009; Dunic et al., 2021), and the consequences of habitat loss for biodiversity will depend on the specific connectivity characteristics of the remaining habitat (Thompson et al., 2016). By quantifying the contribution of each meadow or set of meadows to network connectivity, we can predict the consequences of losing a seagrass meadow. Lastly, the degree of direct connectivity and modularity of a network can determine how fast an invasive species with passive dispersal can spread. Variance in connectivity and a high degree of clustering can slow the spread of an invasive (Morel-Journel et al., 2018). Currently in the Salish Sea, the spread of the invasive European green crab among seagrass meadows will provide an interesting case study.

Limitations

The interpretive power of the biophysical model could be improved by addressing some of its key assumptions and limitations. (1) We assume passive surface dispersal, and although we believe surface movement captures successful transport between coastal shallow areas, the absolute quantities could be improved with 3D hydrodynamic data and vertical swimming behavior. This would also address the influence that vertical migration may have on connectivity (Metaxas and Saunders, 2009; Snauffer et al., 2014), because diel vertical movement may alter the distance traveled during pelagic dispersal (Paris et al., 2007; Daigle et al., 2016). (2) We assumed that the quality of all seagrass habitat was equal, and that abundance of individuals scaled with area. Future iterations of the model could recognize differences in meadow characteristics and the implications for invertebrate abundance and reproduction. (3) We used a constant daily mortality rate due to a lack of data, but other rates and distributions may more accurately model mortality (e.g., Weibull distribution; Treml et al., 2015). (4) We did not include larval precompetency values (the minimum required time of development before larvae can settle), although the functionality to do so was included in the model. Data on the precompetency period for most species do not exist. While this increases the uncertainty of the timing of settlement on suitable habitat, we found that most settlement occurred in conjunction with coastal stranding. Therefore, the spatial position would remain accurate and only the exact timing of successful settlement would be uncertain. (5) Due to a lack of species-specific data, we assumed that rafting on seagrass and algal debris is a primary mode of passive dispersal for species without a pelagic life-stage. However, for many of these species the exact mode of transport between seagrass meadows is largely unknown (Lefcheck et al., 2016b). (6) The spatial scale of the hydrodynamic model does not match the scale of the smallest meadows (∼30 × 30 m). Although velocities are interpolated between points, a higher resolution model would be beneficial for reducing uncertainty in these areas. (7) We only modeled potential transport and settlement. A full measure of connectivity requires an individual surviving and reproducing in its destination meadow. Our dispersal results could be combined with population modeling to predict successful connectivity. (8) Lastly, we modeled connectivity between just seagrass habitat. Not all the species we considered are seagrass specialists and some may utilize other habitat types for movement. We view our results as providing a baseline of minimum movement required for seagrass habitat to be connected, but the model could be improved by including other habitat types in the simulation (e.g., kelp).

The model is also limited by the difficulty in validating the results. Physical oceanography studies can partially validate the accuracy of movement by comparing drifter tracks in the Salish Sea to simulated data (Pawlowicz et al., 2019). However, validation of ecological connectivity is more difficult. Genetic similarity data have been used to validate differences in connectivity across large scales (Sunday et al., 2014), but at the spatial scale of the Salish Sea, differences in allele frequencies may not be sufficient to detect differences in regular ecological exchange (Waples, 1998; Riginos et al., 2019). Despite the difficulty in validating our results, we feel we have adequately accounted for the variation that may be present in the system by releasing a large number of particles, incorporating a diffusion value, and averaging across seasons and years.

Data Availability Statement

The code and datasets generated for this study are available at https://doi.org/10.5281/zenodo.5177779. The velocity fields from the SalishSeaCast model are available at https://salishsea.eos.ubc.ca/erddap/index.html.

Author Contributions

JC, ER, and MIO conceived of and designed the study. JC wrote the manuscript with input, direction, and review from ER, MIO, BM, and CF. BM provided code for the analysis and technical direction for the simulations. CF compiled species trait data and provided direction on the theoretical context of the study. JC ran the simulations and analyzed the data. All authors contributed to the article and approved the submitted version.

Funding

This research is sponsored by the NSERC Canadian Healthy Oceans Network and its Partners: Department of Fisheries and Oceans Canada and INREST (representing the Port of Sept-Îles and City of Sept-Îles). It is also funded through the Fisheries and Oceans Canada Strategic Program for Ecosystem-based Research and Assessment (SPERA).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Knut-Frode Dagestad for his technical support with Opendrift, Vincent Traag for his support with the Leidenalg package, and Susan Allen and Mike Foreman for providing early direction on the use of hydrodynamic models. We also thank Patrick Thompson and Matt Whalen for their review of the manuscript, and Sylvia Heredia for the graphic design.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2021.717469/full#supplementary-material

References

Albert, C. H., Rayfield, B., Dumitru, M., and Gonzalez, A. (2017). Applying network theory to prioritize multispecies habitat networks that are robust to climate and land-use change. Conserv. Biol. 31, 1383–1396. doi: 10.1111/cobi.12943

PubMed Abstract | CrossRef Full Text | Google Scholar

Amundrud, S. L., Srivastava, D. S., and O’Connor, M. I. (2015). Indirect effects of predators control herbivore richness and abundance in a benthic eelgrass (Zostera marina) mesograzer community. J. Anim. Ecol. 84, 1092–1102. doi: 10.1111/1365-2656.12350

PubMed Abstract | CrossRef Full Text | Google Scholar

Bakri, T., and Jackson, P. (2019). Statistical and synoptic analyses of offshore wind variations. Int. J. Climatol. 39, 3201–3217. doi: 10.1002/joc.6012

CrossRef Full Text | Google Scholar

Bell, S. S. (2006). “Seagrasses and the Metapopulation Concept: Developing a Regional Approach to the Study of Extinction, Colonization, and Dispersal,” in Marine Metapopulations, eds J. P. Kritzer and P. F. Sale (Elsevier Inc.), 387–408. doi: 10.1016/B978-0-12-088781-1.50014-5

CrossRef Full Text | Google Scholar

Bode, M., Leis, J. M., Mason, L. B., Williamson, D. H., Harrison, H. B., Choukroun, S., et al. (2019). Successful validation of a larval dispersal model using genetic parentage data. PLoS Biol. 17:e3000380. doi: 10.1371/journal.pbio.3000380

PubMed Abstract | CrossRef Full Text | Google Scholar

Boström, C., Jackson, E. L., and Simenstad, C. A. (2006). Seagrass landscapes and their effects on associated fauna: A review. Estuar. Coast. Shelf Sci. 68, 383–403. doi: 10.1016/j.ecss.2006.01.026

CrossRef Full Text | Google Scholar

Boström, C., Pittman, S. J., Simenstad, C., and Kneib, R. T. (2011). Seascape ecology of coastal biogenic habitats: Advances, gaps, and challenges. Mar. Ecol. Prog. Ser. 427, 191–217. doi: 10.3354/meps09051

CrossRef Full Text | Google Scholar

Boström, C., Törnroos, A., and Bonsdorff, E. (2010). Invertebrate dispersal and habitat heterogeneity: Expression of biological traits in a seagrass landscape. J. Exp. Mar. Bio. Ecol. 390, 106–117. doi: 10.1016/j.jembe.2010.05.008

CrossRef Full Text | Google Scholar

Brooks, R. A., and Bell, S. S. (2001). Mobile corridors in marine landscapes: Enhancement of faunal exchange at seagrass/sand ecotones. J. Exp. Mar. Bio. Ecol. 264, 67–84. doi: 10.1016/S0022-0981(01)00310-0

CrossRef Full Text | Google Scholar

Bryan-Brown, D. N., Brown, C. J., Hughes, J. M., and Connolly, R. M. (2017). Patterns and trends in marine population connectivity research. Mar. Ecol. Prog. Ser. 585, 243–256. doi: 10.3354/meps12418

CrossRef Full Text | Google Scholar

Burgess, S., Nickols, K., Griesemer, C., Barnett, L. A., Dedrick, A., Satterthwaite, E., et al. (2014). Beyond connectivity: how empirical methods can quantify population persistence to improve marine protected area design: supplementary Information. Ecol. Soc. Am. 24, 8. doi: 10.1890/13-0710.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Carr, M. H., Robinson, S. P., Wahle, C., Davis, G., Kroll, S., Murray, S., et al. (2017). The central importance of ecological spatial connectivity to effective coastal marine protected areas and to meeting the challenges of climate change in the marine environment. Aquat. Conserv. Mar. Freshw. Ecosyst. 27, 6–29. doi: 10.1002/aqc.2800

CrossRef Full Text | Google Scholar

Christiaen, B., Ferrier, L., Dowty, P., Gaeckle, J., and Berry, H. (2015). Puget Sound Seagrass Monitoring Report. Available online at: https://sites.google.com/a/psemp.org/psemp/home (accessed August 14, 2018).

Google Scholar

Cowen, R. K., and Sponaugle, S. (2009). Larval Dispersal and Marine Population Connectivity. Ann. Rev. Mar. Sci. 1, 443–466. doi: 10.1146/annurev.marine.010908.163757

PubMed Abstract | CrossRef Full Text | Google Scholar

Crandall, E. D., Treml, E. A., and Barber, P. H. (2012). Coalescent and biophysical models of stepping-stone gene flow in neritid snails. Mol. Ecol. 21, 5579–5598. doi: 10.1111/mec.12031

PubMed Abstract | CrossRef Full Text | Google Scholar

Dagestad, K. F., Röhrs, J., Breivik, O., and Ådlandsvik, B. (2018). OpenDrift v1.0: A generic framework for trajectory modelling. Geosci. Model Dev. 11, 1405–1420. doi: 10.5194/gmd-11-1405-2018

CrossRef Full Text | Google Scholar

Daigle, R. M., Chasse, J., and Metaxas, A. (2016). The relative effect of behaviour in larval dispersal in a low energy embayment. Prog. Oceanogr. 144, 93–117. doi: 10.1016/j.pocean.2016.04.001

CrossRef Full Text | Google Scholar

D’Aloia, C. C., Bogdanowicz, S. M., Francis, R. K., Majoris, J. E., Harrison, R. G., and Buston, P. M. (2015). Patterns, causes, and consequences of marine larval dispersal. Proc. Natl. Acad. Sci. U. S. A. 112, 13940–13945. doi: 10.1073/pnas.1513754112

PubMed Abstract | CrossRef Full Text | Google Scholar

D’Aloia, C. C., Daigle, R. M., Côté, I. M., Curtis, J. M. R., Guichard, F., and Fortin, M. J. (2017). A multiple-species framework for integrating movement processes across life stages into the design of marine protected areas. Biol. Conserv. 216, 93–100. doi: 10.1016/j.biocon.2017.10.012

CrossRef Full Text | Google Scholar

Duffy, J. E., Reynolds, P. L., Boström, C., Coyer, J. A., Cusson, M., Donadi, S., et al. (2015). Biodiversity mediates top-down control in eelgrass ecosystems: A global comparative-experimental approach. Ecol. Lett. 18, 696–705. doi: 10.1111/ele.12448

PubMed Abstract | CrossRef Full Text | Google Scholar

Dunic, J. C., Brown, C. J., Connolly, R. M., Turschwell, M. P., and Côté, I. M. (2021). Long-term declines and recovery of meadow area across the world’s seagrass bioregions. Glob. Chang. Biol. 15, 15684. doi: 10.1111/gcb.15684

PubMed Abstract | CrossRef Full Text | Google Scholar

Engelhard, S. L., Huijbers, C. M., Stewart-Koster, B., Olds, A. D., Schlacher, T. A., and Connolly, R. M. (2017). Prioritising seascape connectivity in conservation using network analysis. J. Appl. Ecol. 54, 1130–1141. doi: 10.1111/1365-2664.12824

CrossRef Full Text | Google Scholar

France, K. E., and Duffy, E. (2006). Diversity and dispersal interactively affect predictability of ecosystem function. Nature 441, 1139–1143. doi: 10.1038/nature04729

PubMed Abstract | CrossRef Full Text | Google Scholar

Gale, K. S., Frid, A., Lee, L., McCarthy, J.-B., Robb, C., Rubidge, E., et al. (2019). A framework for identification of ecological conservation priorities for marine protected area (MPA) network design and its application in the Northern Shelf Bioregion. DFO Can. Sci. Advis. Secr. 2018, 186.

Google Scholar

Gerber, L. R., Mancha-Cisneros, M. D. M., O’Connor, M. I., and Selig, E. R. (2014). Climate change impacts on connectivity in the ocean: Implications for conservation. Ecosphere 5, art33. doi: 10.1890/ES13-00336.1

CrossRef Full Text | Google Scholar

Gilarranz, L. J., Rayfield, B., Liñán-Cembrano, G., Bascompte, J., and Gonzalez, A. (2017). Effects of network modularity on the spread of perturbation impact in experimental metapopulations. Science (80-.). 357, 199–201. doi: 10.1126/science.aal4122

PubMed Abstract | CrossRef Full Text | Google Scholar

Guichard, F., Levin, S., Hastings, A., and Siegel, D. A. (2004). Toward a dynamic metacommunity approach to marine reserve theory. Bioscience 54, 1003–1011.

Google Scholar

Gurvan, M., Bourdallé-Badie, R., Bouttier, P.-A., Bricaud, C., Bruciaferri, D., Calvert, D., et al. (2017). NEMO ocean engine. ^∗city pub.

Google Scholar

Guzman, L. M., Germain, R. M., Forbes, C., Straus, S., O’Connor, M. I., Gravel, D., et al. (2019). Towards a multi-trophic extension of metacommunity ecology. Ecol. Lett. 22, 19–33. doi: 10.1111/ele.13162

PubMed Abstract | CrossRef Full Text | Google Scholar

Halverson, M., and Pawlowicz, R. (2016). Tide, wind, and river forcing of the surface currents in the fraser river plume. Atmos. Ocean 54, 131–152. doi: 10.1080/07055900.2016.1138927

CrossRef Full Text | Google Scholar

Hanski, I. (2001). Spatially realistic theory of metapopulation ecology. Nature 2001, 372–381. doi: 10.1007/s001140100246

PubMed Abstract | CrossRef Full Text | Google Scholar

Harwell, M. C., and Orth, R. J. (2002). Long-distance dispersal potential in a marine macrophyte. Ecology 83, 3319–3330.

Google Scholar

Heck, K. L., Carruthers, T. J. B., Duarte, C. M., Randall Hughes, A., Kendrick, G., Orth, R. J., et al. (2008). Trophic transfers from seagrass meadows subsidize diverse marine and terrestrial consumers. Ecosystems 11, 1198–1210. doi: 10.1007/s10021-008-9155-y

CrossRef Full Text | Google Scholar

Heck, K. L., and Thoman, T. A. (1984). The nursery role of seagrass meadows in the upper and lower reaches of the Chesapeake Bay. Estuaries 7, 70–92. doi: 10.2307/1351958

CrossRef Full Text | Google Scholar

Hedgecock, D., Barber, P. H., and Edmands, S. (2003). Genetic Approaches to Measuring Connectivity. Oceanography 20, 70–79. doi: 10.1073/pnas.0401921101

PubMed Abstract | CrossRef Full Text | Google Scholar

Hock, K., and Mumby, P. J. (2015). Quantifying the reliability of dispersal paths in connectivity networks. J. R. Soc. Interface 12, 20150013. doi: 10.1098/rsif.2015.0013

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, A. C., Essak, M., and O’Connor, M. I. (2015). Top-down control by great blue herons Ardea herodias regulates seagrass-associated epifauna. Oikos 124, 1492–1501. doi: 10.1111/oik.01988

CrossRef Full Text | Google Scholar

Jabot, F., Laroche, F., Massol, F., Arthaud, F., Crabot, J., Dubart, M., et al. (2020). Assessing metacommunity processes through signatures in spatiotemporal turnover of community composition. Ecol. Lett. 23, 1330–1339. doi: 10.1111/ele.13523

PubMed Abstract | CrossRef Full Text | Google Scholar

Jenkins, T. L., and Stevens, J. R. (2018). Assessing connectivity between MPAs: Selecting taxa and translating genetic data to inform policy. Mar. Policy 94, 165–173. doi: 10.1016/j.marpol.2018.04.022

CrossRef Full Text | Google Scholar

Johannesson, K. (1988). The paradox of Rockall: why is a brooding gastropod (Littorina saxatilis) more widespread than one having a planktonic larval dispersal stage (L. littorea)? Mar. Biol. 99, 507–513. doi: 10.1007/BF00392558

CrossRef Full Text | Google Scholar

Jonsson, P. R., Hammar, L., Wåhlström, I., Pålsson, J., Hume, D., Almroth-Rosell, E., et al. (2020). Combining seascape connectivity with cumulative impact assessment in support of ecosystem-based marine spatial planning. J. Appl. Ecol. 1–11. doi: 10.1111/1365-2664.13813

CrossRef Full Text | Google Scholar

Källström, B., Nyqvist, A., Åberg, P., Bodin, M., and André, C. (2008). Seed rafting as a dispersal strategy for eelgrass (Zostera marina). Aquat. Bot. 88, 148–153. doi: 10.1016/j.aquabot.2007.09.005

CrossRef Full Text | Google Scholar

Kathleen Collins, A., Allen, S. E., and Pawlowicz, R. (2009). The role of wind in determining the timing of the spring bloom in the Strait of Georgia. Can. J. Fish. Aquat. Sci. 66, 1597–1616. doi: 10.1139/F09-071

PubMed Abstract | CrossRef Full Text | Google Scholar

Khangaonkar, T., Nugraha, A., Xu, W., Long, W., Bianucci, L., Ahmed, A., et al. (2018). Analysis of Hypoxia and Sensitivity to Nutrient Pollution in Salish Sea. J. Geophys. Res. Ocean. 123, 4735–4761. doi: 10.1029/2017JC013650

CrossRef Full Text | Google Scholar

Kindlmann, P., and Burel, F. (2008). Connectivity measures: A review. Landsc. Ecol. 23, 879–890. doi: 10.1007/s10980-008-9245-4

CrossRef Full Text | Google Scholar

Kneitel, J. M., and Miller, T. E. (2003). Dispersal Rates Affect Species Composition in Metacommunities of Sarracenia purpurea Inquilines. Am. Nat. 162, 165–171.

Google Scholar

Kool, J. T., Moilanen, A., and Treml, E. A. (2013). Population connectivity: Recent advances and new perspectives. Landsc. Ecol. 28, 165–185. doi: 10.1007/s10980-012-9819-z

CrossRef Full Text | Google Scholar

LaCasce, J. H. (2008). Statistics from Lagrangian observations. Prog. Oceanogr. 77, 1–29. doi: 10.1016/j.pocean.2008.02.002

CrossRef Full Text | Google Scholar

Lawlor, J. A., and Arellano, S. M. (2020). Temperature and salinity, not acidification, predict near-future larval growth and larval habitat suitability of Olympia oysters in the Salish Sea. Sci. Rep. 10, 1–15. doi: 10.1038/s41598-020-69568-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Lefcheck, J. S., Marion, S. R., Lombana, A. V., and Orth, R. J. (2016a). Faunal communities are invariant to fragmentation in experimental seagrass landscapes. PLoS One 11:1–24. doi: 10.1371/journal.pone.0156550

PubMed Abstract | CrossRef Full Text | Google Scholar

Lefcheck, J. S., Marion, S. R., and Orth, R. J. (2016b). Restored Eelgrass (Zostera marina L.) as a Refuge for Epifaunal Biodiversity in Mid-Western Atlantic Coastal Bays. Estuaries and Coasts 40, 1–13. doi: 10.1007/s12237-016-0141-x

CrossRef Full Text | Google Scholar

Leibold, M. A., and Chase, J. M. (2018). Metacommunity Ecology. Princeton, NJ: Princeton University Press, 59.

Google Scholar

Loreau, M., Mouquet, N., and Gonzalez, A. (2003). Biodiversity as spatial insurance in heterogeneous landscapes. Proc. Natl. Acad. Sci. 100, 12765–12770. doi: 10.1073/pnas.2235465100

PubMed Abstract | CrossRef Full Text | Google Scholar

Martone, R. G., Gale, K., Martone, R. G., Robb, C. K., Gale, K. S. P., Frid, A., et al. (2021). Design Strategies for the Northern Shelf Bioregional Marine Protected Area Network Canadian Science Advisory Secretariat, science advisory Report, 1919-5087; 2019/026.

Google Scholar

Massol, F., Altermatt, F., Gounand, I., Gravel, D., Leibold, M. A., and Mouquet, N. (2017). How life-history traits affect ecosystem properties: effects of dispersal in meta-ecosystems. Oikos 126, 532–546. doi: 10.1111/oik.03893

CrossRef Full Text | Google Scholar

Melià, P., Schiavina, M., Rossetto, M., Gatto, M., Fraschetti, S., and Casagrandi, R. (2016). Looking for hotspots of marine metacommunity connectivity: a methodological framework. Sci. Rep. 6, 23705. doi: 10.1038/srep23705

PubMed Abstract | CrossRef Full Text | Google Scholar

Metaxas, A., and Saunders, M. (2009). Quantifying the “ Bio- ” Components in Biophysical Models of Larval Transport in Marine Benthic Invertebrates: Advances and Pitfalls. Biol. Bull. 216, 257–272. doi: 10.2307/25548159

CrossRef Full Text | Google Scholar

Milbrandt, J. A., Bélair, S., Faucher, M., Vallée, M., Carrera, M. L., and Glazer, A. (2016). The pan-canadian high resolution (2.5 km) deterministic prediction system. Weather Forecast. 31, 1791–1816. doi: 10.1175/WAF-D-16-0035.1

CrossRef Full Text | Google Scholar

Minor, E. S., and Urban, D. L. (2007). Graph theory as a proxy for spatially explicit populations models in conservation planning. Ecol. Appl. 17, 1771–1782.

Google Scholar

Morel-Journel, T., Assa, C. R., Mailleret, L., and Vercken, E. (2018). Its all about connections: hubs and invasion in habitat networks. Ecol. Lett. 22, 13192. doi: 10.1111/ele.13192

PubMed Abstract | CrossRef Full Text | Google Scholar

Morrison, J., Foreman, M. G. G., and Masson, D. (2012). A method for estimating monthly freshwater discharge affecting British Columbia coastal waters. Atmos. Ocean 50, 1–8. doi: 10.1080/07055900.2011.637667

CrossRef Full Text | Google Scholar

Mouquet, N., and Loreau, M. (2003). Community Patterns in Source-Sink Metacommunities. Am. Nat. 162, 544–557. doi: 10.1086/378857

PubMed Abstract | CrossRef Full Text | Google Scholar

Mucha, P. J., Richardson, T., Macon, K., Porter, M. A., and Onnela, J.-P. (2010). Community Structure in Time-Dependent, Multiscale, and Multiplex Networks. Science (80-.). 328, 876–878. doi: 10.1126/science.1184819

PubMed Abstract | CrossRef Full Text | Google Scholar

Murphy, C. E., Orth, R. J., and Lefcheck, J. S. (2021). Habitat Primarily Structures Seagrass Epifaunal Communities: a Regional-Scale Assessment in the Chesapeake Bay. Estuaries and Coasts 44, 442–452. doi: 10.1007/s12237-020-00864-4

CrossRef Full Text | Google Scholar

Murphy, G. E. P., Dunic, J. C., Adamczyk, E. M., Bittick, S. J., Côté, I. M., Cristiani, J., et al. (2021). From coast to coast to coast: ecology and management of seagrass ecosystems across Canada. Facets 6, 1–41. doi: 10.1139/facets-2020-0020

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Connor, M. I., Bruno, J. F., Gaines, S. D., Halpern, B. S., Lester, S. E., Kinlan, B. P., et al. (2007). Temperature control of larval dispersal and the implications for marine ecology, evolution, and conservation. Proc. Natl. Acad. Sci. U. S. A. 104, 1266–1271. doi: 10.1073/pnas.0603422104

PubMed Abstract | CrossRef Full Text | Google Scholar

Olson, E. M., Allen, S. E., Do, V., Dunphy, M., and Ianson, D. (2020). Assessment of Nutrient Supply by a Tidal Jet in the Northern Strait of Georgia Based on a Biogeochemical Model. J. Geophys. Res. Ocean. 125, 1–25. doi: 10.1029/2019JC015766

CrossRef Full Text | Google Scholar

Orth, R. J. (1992). “A Perspective on Plant-Animal Interactions in Seagrasses: Physical and Biological Determinats influencing Plant and Animal Abundance,” in Plant-Animal Interactions in the Marine Benthos, eds D. M. John, S. J. Hawkins, and J. H. Price (Oxford : Clarendon Press), 147–164.

Google Scholar

Orth, R. J., Heck, K. L., and van Montfrans, J. (1984). Faunal communities in seagrass beds: A review of the influence of plant structure and prey characteristics on predator-prey relationships. Estuaries 7, 339–350. doi: 10.2307/1351618

CrossRef Full Text | Google Scholar

Paris, C. B., Chérubin, L. M., and Cowen, R. K. (2007). Surfing, spinning, or diving from reef to reef: Effects on population connectivity. Mar. Ecol. Prog. Ser. 347, 285–300. doi: 10.3354/meps06985

CrossRef Full Text | Google Scholar

Pawlowicz, R., Hannah, C., and Rosenberger, A. (2019). Lagrangian observations of estuarine residence times, dispersion, and trapping in the Salish Sea. Estuar. Coast. Shelf Sci. 225, 106246. doi: 10.1016/j.ecss.2019.106246

CrossRef Full Text | Google Scholar

Pawlowicz, R., Riche, O., and Halverson, M. (2007). The circulation and residence time of the Strait of Georgia using a simple mixing-box approach. Atmos. Ocean 45, 173–193. doi: 10.3137/ao.450401

CrossRef Full Text | Google Scholar

Pereira, M., Segurado, P., and Neves, N. (2011). Using spatial network structure in landscape management and planning: A case study with pond turtles. Landsc. Urban Plan. 100, 67–76. doi: 10.1016/j.landurbplan.2010.11.009

CrossRef Full Text | Google Scholar

Pielou, E. (1991). After the ice age: The return of life to glaciated North America 1991. Chicago, LI: University of Chicago Press.

Google Scholar

Pittman, S. J. (2018). Seascape Ecology. Hoboken, NJ: Wiley-Blackwell.

Google Scholar

Pittman, S. J., Kneib, R. T., and Simenstad, C. A. (2011). Practicing coastal seascape ecology. Mar. Ecol. Prog. Ser. 427, 187–190. doi: 10.3354/meps09139

CrossRef Full Text | Google Scholar

Puritz, J. B., and Toonen, R. J. (2011). Coastal pollution limits pelagic larval dispersal. Nat. Commun. 2, 226. doi: 10.1038/ncomms1238

PubMed Abstract | CrossRef Full Text | Google Scholar

Riginos, C., Hock, K., Matias, A. M., Mumby, P. J., van Oppen, M. J. H., and Lukoschek, V. (2019). Asymmetric dispersal is a critical element of concordance between biophysical dispersal models and spatial genetic structure in Great Barrier Reef corals. Divers. Distrib. 25, 1684–1696. doi: 10.1111/ddi.12969

CrossRef Full Text | Google Scholar

Rubidge, E., Jeffery, S., Gregr, E. J., Gale, K. S. P., and Frid, A. (2020). Assessment of nearshore features in the Northern Shelf Bioregion against criteria for determining Ecologically and Biologically Significant Areas (EBSAs). Report number 2020/023.

Google Scholar

Rumrill, S. S. (1990). Natural mortality of marine invertebrate larvae. Ophelia 32, 163–198. doi: 10.1080/00785236.1990.10422030

CrossRef Full Text | Google Scholar

Saura, S., and Bodin, Ö, and Fortin, M. J. (2014). EDITOR’S CHOICE: Stepping stones are crucial for species’ long-distance dispersal and range expansion through habitat networks. J. Appl. Ecol. 51, 171–182. doi: 10.1111/1365-2664.12179

CrossRef Full Text | Google Scholar

Saura, S., and Rubio, L. (2010). A common currency for the different ways in which patches and links can contribute to habitat availability and connectivity in the landscape. Ecography 33, 523–537. doi: 10.1111/j.1600-0587.2009.05760.x

CrossRef Full Text | Google Scholar

Saura, S., and Torné, J. (2009). Conefor Sensinode 2.2: A software package for quantifying the importance of habitat patches for landscape connectivity. Environ. Model. Softw. 24, 135–139. doi: 10.1016/j.envsoft.2008.05.005

CrossRef Full Text | Google Scholar

Schill, S. R., Raber, G. T., Roberts, J. J., Treml, E. A., Brenner, J., and Halpin, P. N. (2015). No reef is an island: Integrating coral reef connectivity data into the design of regional-scale marine protected area networks. PLoS One 10:1–24. doi: 10.1371/journal.pone.0144199

PubMed Abstract | CrossRef Full Text | Google Scholar

Selkoe, K. A., D’Aloia, C. C., Crandall, E. D., Iacchei, M., Liggins, L., Puritz, J. B., et al. (2016). A decade of seascape genetics: Contributions to basic and applied marine connectivity. Mar. Ecol. Prog. Ser. 554, 1–19. doi: 10.3354/meps11792

CrossRef Full Text | Google Scholar

Shanks, A. L. (2009). Pelagic larval duration and dispersial distance revisited. Biol. Bull. 216, 373–385. doi: 10.2307/25548167

CrossRef Full Text | Google Scholar

Siegel, D. A., Kinlan, B. P., Gaylord, B., and Gaines, S. D. (2003). Lagrangian descriptions of marine larval dispersion. Mar. Ecol. Prog. Ser. 260, 83–96. doi: 10.3354/meps260083

CrossRef Full Text | Google Scholar

Snauffer, E. L., Masson, D., and Allen, S. E. (2014). Modelling the dispersal of herring and hake larvae in the Strait of Georgia for the period 2007-2009. Fish. Oceanogr. 23, 375–388. doi: 10.1111/fog.12072

CrossRef Full Text | Google Scholar

Soontiens, N., and Allen, S. E. (2017). Modelling sensitivities to mixing and advection in a sill-basin estuarine system. Ocean Model. 112, 17–32. doi: 10.1016/j.ocemod.2017.02.008

CrossRef Full Text | Google Scholar

Soontiens, N., Allen, S. E., Latornell, D., Le Souëf, K., Machuca, I., Paquin, J.-P., et al. (2016). Storm Surges in the Strait of Georgia Simulated with a Regional Model. Atmosphere-Ocean 54, 1–21. doi: 10.1080/07055900.2015.1108899

CrossRef Full Text | Google Scholar

Stark, K., Thompson, P., Yakimishyn, J., Lee, L., Adamczyk, E., Hessing-Lewis, M., et al. (2020). Beyond a single patch: local and regional processes explain diversity patterns in a seagrass epifaunal metacommunity. Mar. Ecol. Prog. Ser. 655, 91–106. doi: 10.3354/meps13527

CrossRef Full Text | Google Scholar

Stier, A. C., Lee, S. C., and O’Connor, M. I. (2019). Temporal variation in dispersal modifies dispersal-diversity relationships in an experimental seagrass metacommunity. Mar. Ecol. Prog. Ser. 613, 67–76. doi: 10.3354/meps12908

CrossRef Full Text | Google Scholar

Sunday, J. M., Popovic, I., Palen, W. J., Foreman, M. G. G., and Hart, M. W. (2014). Ocean circulation model predicts high genetic structure observed in a long-lived pelagic developer. Mol. Ecol. 23, 5036–5047. doi: 10.1111/mec.12924

PubMed Abstract | CrossRef Full Text | Google Scholar

Thomas, C. J., Lambrechts, J., Wolanski, E., Traag, V. A., Blondel, V. D., Deleersnijder, E., et al. (2014). Numerical modelling and graph theory tools to study ecological connectivity in the Great Barrier Reef. Ecol. Modell. 272, 160–174. doi: 10.1016/j.ecolmodel.2013.10.002

CrossRef Full Text | Google Scholar

Thompson, P. L., Guzman, L. M., De Meester, L., Horváth, Z., Ptacnik, R., Vanschoenwinkel, B., et al. (2020). A process-based metacommunity framework linking local and regional scale community ecology. Ecol. Lett. 23, 1314–1329. doi: 10.1111/ele.13568

PubMed Abstract | CrossRef Full Text | Google Scholar

Thompson, P. L., Rayfield, B., and Gonzalez, A. (2016). Loss of habitat and connectivity erodes species diversity, ecosystem functioning, and stability in metacommunity networks. Ecography 40, 98–108. doi: 10.1111/ecog.02558

CrossRef Full Text | Google Scholar

Traag, V. A., Waltman, L., and van Eck, N. J. (2019). From Louvain to Leiden: guaranteeing well-connected communities. Sci. Rep. 9, 1–12. doi: 10.1038/s41598-019-41695-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Treml, E. A., Ford, J. R., Black, K. P., and Swearer, S. E. (2015). Identifying the key biophysical drivers, connectivity outcomes, and metapopulation consequences of larval dispersal in the sea. Mov. Ecol. 3, 17. doi: 10.1186/s40462-015-0045-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Treml, E. A., Roberts, J. J., Chao, Y., Halpin, P. N., Possingham, H. P., and Riginos, C. (2012). Reproductive output and duration of the pelagic larval stage determine seascape-wide connectivity of marine populations. Integr. Comp. Biol. 52, 525–537. doi: 10.1093/icb/ics101

PubMed Abstract | CrossRef Full Text | Google Scholar

Urban, D. L., Minor, E. S., Treml, E. A., and Schick, R. S. (2009). Graph models of habitat mosaics. Ecol. Lett. 12, 260–273. doi: 10.1111/j.1461-0248.2008.01271.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Waples, R. S. (1998). Separating the wheat from the chaff: Patterns of genetic differentiation in high gene flow species. J. Hered. 89, 438–450. doi: 10.1093/jhered/89.5.438

CrossRef Full Text | Google Scholar

Waycott, M., Duarte, C. M., Carruthers, T. J. B., Orth, R. J., Dennison, W. C., Olyarnik, S., et al. (2009). Accelerating loss of seagrasses across the globe threatens coastal ecosystems. Proc. Natl. Acad. Sci. 106, 12377–12381. doi: 10.1073/pnas.0905620106

PubMed Abstract | CrossRef Full Text | Google Scholar

Werner, F. E., Cowen, R. K., and Paris, C. B. (2007). Coupled Biological and Physical Models. Oceanography 20, 54–69. doi: 10.1016/S0967-0645(00)00079-5

CrossRef Full Text | Google Scholar

Whippo, R., Knight, N. S., Prentice, C., Cristiani, J., Siegle, M. R., and O’Connor, M. I. (2018). Epifaunal diversity patterns within and among seagrass meadows suggest landscape-scale biodiversity processes. Ecosphere 9, e02490. doi: 10.1002/ecs2.2490

CrossRef Full Text | Google Scholar

White, J. W., Morgan, S. G., and Fisher, J. L. (2014). Planktonic larval mortality rates are lower than widely expected. Ecology 95, 3344–3353. doi: 10.1890/13-2248.1

CrossRef Full Text | Google Scholar

Worcester, S. E. (1994). Adult rafting versus larval swimming: dispersal and recruitment of a botryllid ascidian on eelgrass. Mar. Biol. 121, 309–317. doi: 10.1007/BF00346739

CrossRef Full Text | Google Scholar

Wren, J. L. K., Kobayashi, D. R., Jia, Y., and Toonen, R. J. (2016). Modeled population connectivity across the Hawaiian archipelago. PLoS One 11:1–25. doi: 10.1371/journal.pone.0167626

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamada, K., Tanaka, Y., Era, T., and Nakaoka, M. (2014). Environmental and spatial controls of macroinvertebrate functional assemblages in seagrass ecosystems along the Pacific coast of northern Japan. Glob. Ecol. Conserv. 2, 47–61. doi: 10.1016/j.gecco.2014.08.003

CrossRef Full Text | Google Scholar

Yeager, L. A., Geyer, J. K., and Fodrie, F. J. (2019). Trait sensitivities to seagrass fragmentation across spatial scales shape benthic community structure. J. Anim. Ecol. 88, 1743–1754. doi: 10.1111/1365-2656.13067

PubMed Abstract | CrossRef Full Text | Google Scholar