End-to-end deep learning pipeline for real-time Bragg peak segmentation: from training to large-scale deployment

X-ray crystallography reconstruction, which transforms discrete X-ray diffraction patterns into three-dimensional molecular structures, relies critically on accurate Bragg peak finding for structure determination. As X-ray free electron laser (XFEL) facilities advance toward MHz data rates (1 million images per second), traditional peak finding algorithms that require manual parameter tuning or exhaustive grid searches across multiple experiments become increasingly impractical. While deep learning approaches offer promising solutions, their deployment in high-throughput environments presents significant challenges in automated dataset labeling, model scalability, edge deployment efficiency, and distributed inference capabilities. We present an end-to-end deep learning pipeline with three key components: (1) a data engine that combines traditional algorithms with our peak matching algorithm to generate high-quality training data at scale, (2) a modular architecture that scales from a few million to hundreds of million parameters, enabling us to train large expert-level models offline while deploying smaller, distilled models at the edge, and (3) a decoupled producer-consumer architecture that separates specialized data source layer from model inference, enabling flexible deployment across diverse computing environments. Using this integrated approach, our pipeline achieves accuracy comparable to traditional methods tuned by human experts while eliminating the need for experiment-specific parameter tuning. Although current throughput requires optimization for MHz facilities, our system's scalable architecture and demonstrated model compression capabilities provide a foundation for future high-throughput XFEL deployments.

1 Introduction

X-ray free electron lasers (XFEL) serial crystallography has revolutionized structural biology by enabling radiation damage-free structural determination through the diffraction-before-destruction approach (Neutze et al., 2000; Chapman et al., 2006, 2011). Time-resolved serial femtosecond crystallography at facilities like the Linac Coherent Light Source (LCLS) has led to many breakthrough studies in understanding biochemical reactions at femtosecond resolution (Aquila et al., 2012; Kupitz et al., 2014; Nango et al., 2016; Pande et al., 2016; Young et al., 2016; Suga et al., 2017; Kern et al., 2018; Ibrahim et al., 2020; Suga et al., 2020). The crystallography pipeline begins with Bragg peak finding, a critical first step that underpins subsequent analyses. Accurate peak finding directly impacts crystal indexing, which determines the crystal orientation and unit cell parameters. These results then feed into peak integration to measure reflection intensities, followed by merging and scaling procedures to obtain structure factors necessary for final structure determination. The precision of this entire workflow hinges on the initial peak finding step, making robust and efficient peak detection crucial for high-quality structural analysis.

Bragg peak finding algorithms have seen several key developments. Early template matching approaches (Wilkinson et al., 1988) struggled with efficiency and low signal-to-noise ratio (SNR) peaks, while region-growing techniques (Bolotovsky et al., 1995; Barty et al., 2014) faced challenges with XFEL data, particularly for weak peaks at higher scattering angles. Notable progress came with the Robust Peak Finder (RPF) (Hadian-Jazi et al., 2017, 2021), which implemented the Modified Selective Statistical Estimator (MSSE) method, offering improved automation and parallel processing capabilities. Current software solutions like Cheetah (Barty et al., 2014), DIALS (Winter et al., 2018), and Psocake (Yoon, 2020) have integrated various peak finding approaches, with recent developments exploring neural network-based methods. However, these neural network approaches, such as BraggNet (Ronneberger et al., 2015) and BraggNN (Liu et al., 2021), while promising, have been limited to analyzing single peaks within small windows, leaving room for advancement in multiple peak detection capabilities across large area detectors.

The advancement of XFEL facilities toward higher repetition rates has created an urgent need for more sophisticated crystallography processing solutions. While existing peak finding algorithms have served the crystallography community well and can potentially be optimized for MHz data rates, they rely heavily on manual parameter tuning and exhaustive grid searches across multiple experiments. This requirement for expert intervention can create significant delays in the analytical pipeline and become increasingly impractical as facilities advance toward MHz-scale operations. Neural networks trained with human supervision at scale offer a data-driven alternative, eliminating the need for manual parameter optimization while maintaining expert-level performance. However, the key challenge lies in scaling these end-to-end solutions to handle diverse experimental conditions, detector configurations, and biochemical samples while maintaining robust performance.

In this work, we develop an end-to-end deep learning pipeline for real-time Bragg peak segmentation without human expert intervention through three key developments: an automated dataset generation pipeline, a flexible model architecture supporting both large-scale training and model distillation for efficient edge deployment, and a decoupled producer-consumer architecture for scaling the inference. The pipeline eliminates hours of manual parameter tuning while achieving a 37.5% indexing yield that exceeds expert-tuned methods (36.4%). When deployed on 40 GPUs, our system processes 183 1920-by-1920 images per second, surpassing current LCLS data rates (120 Hz). While further optimization is needed for MHz-scale operations, our architecture demonstrates robust performance even under extreme model compression (from 673 to 16M parameters) and enables independent scaling of data ingestion and processing components.

2 Methods

2.1 PeakNet data engine

The Data Engine implements a self-improving workflow that combines traditional crystallographic analysis tools with deep learning to automate high-quality dataset generation. Figure 1 provides a schematic overview of our pipeline, illustrating how diffraction patterns flow through peak finding using established software (Psocake or Cheetah), crystal indexing via CrystFEL (White et al., 2012), and peak matching before entering the distributed labeling system. While the circular workflow design enables continuous system improvement through iterative training dataset curation and model refinement, the current work focuses on demonstrating the initial implementation using our first comprehensive training dataset.

Figure 1

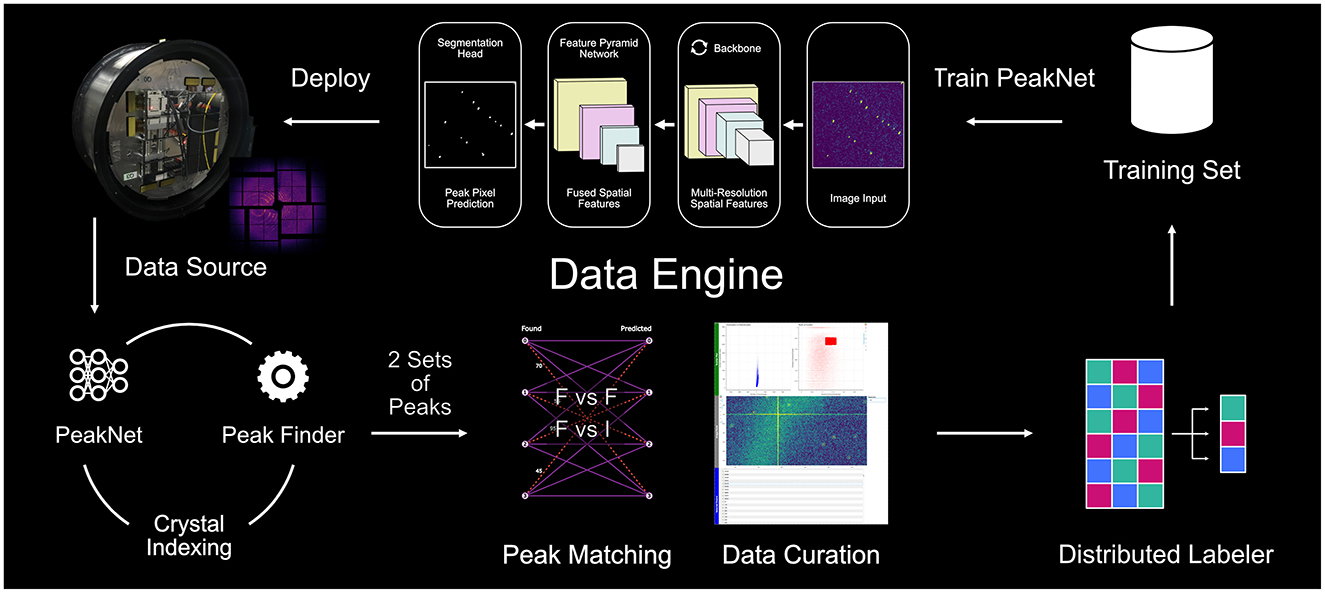
Figure 1. Schematic overview of the data engine, our automated training data generation pipeline. Diffraction patterns are processed through parallel peak finding paths, matched by solving a set-matching problem, and curated based on quality metrics. The selected images are feed into the distributed labeling for segmentation mask generation. The circular workflow enables continuous system improvement through iterative data collection and model refinement.

2.1.1 Data labeling workflow

The data labeling process begins with traditional peak finding and indexing using established crystallographic tools. Diffraction patterns are processed using Psocake or Cheetah peak finder, followed by CrystFEL for indexing, generating both CrystFEL-compatible HDF5 files and CrystFEL stream files containing peak information. The system's key innovation lies in PeakDiff, an algorithm that validates peaks by solving a set matching problem between found and predicted peaks using scipy's linear_sum_assignment implementation (Virtanen et al., 2020). Figure 2 visualizes the results of this peak matching process, showing how the algorithm establishes correspondences between peaks detected by Psocake (yellow squares) and PeakNet (red triangles). The cyan circles highlighting successful matches demonstrate the algorithm's ability to quantitatively evaluate consistency between arbitrary sets of peak positions, whether they come from different detection methods, crystal indexing predictions, or other sources.

Figure 2

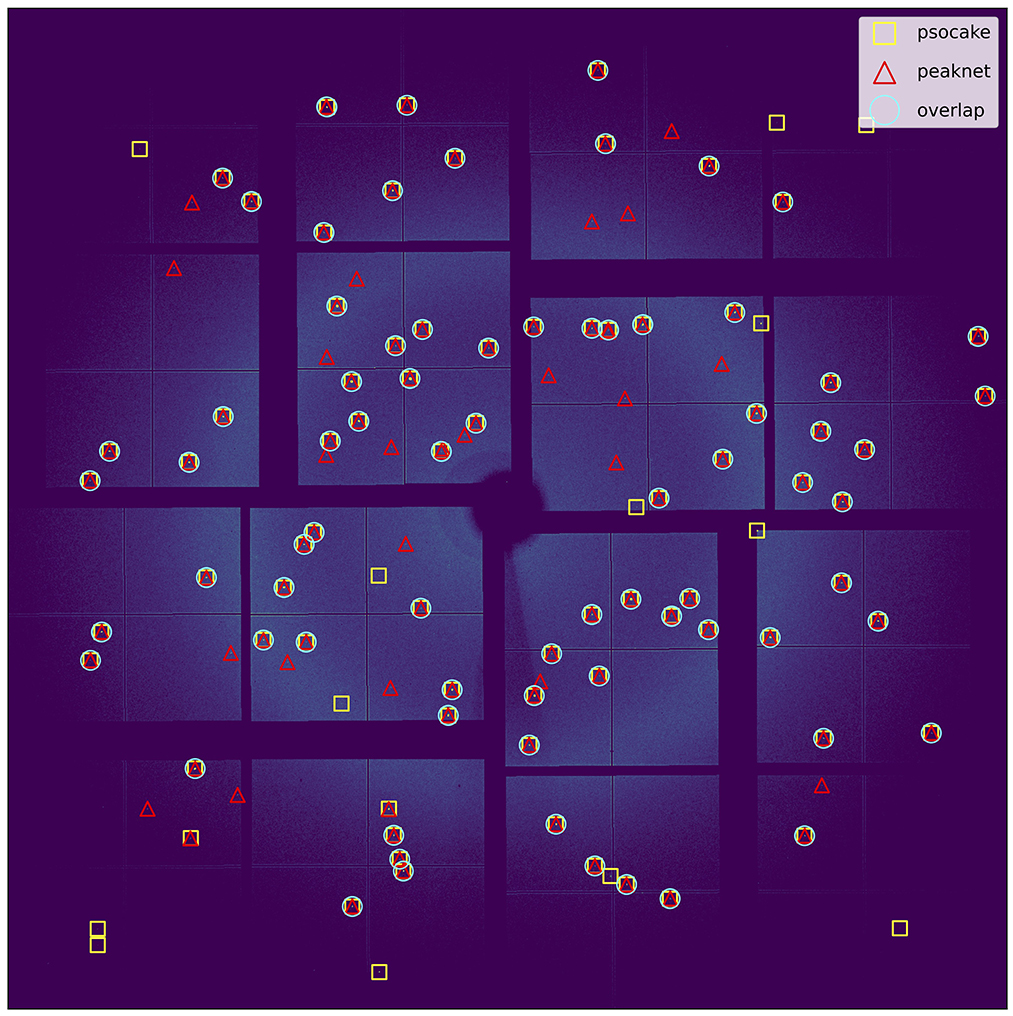
Figure 2. Visualization of peak matching results using a set matching algorithm. The algorithm solves a linear sum assignment problem to establish correspondences between any two sets of peak positions. In this example, peaks detected by Psocake (yellow squares) and PeakNet (red triangles) are matched, with cyan circles indicating successfully matched peak pairs. This matching approach provides a quantitative basis for evaluating consistency between arbitrary sets of peak positions, whether they come from different detection methods, crystal indexing predictions, or other sources.

Quality metrics for pattern selection are derived from the peak matching results, with recall measured as the ratio of overlapping peaks to predicted peaks, and precision as the ratio of overlapping peaks to detected peaks. It's important to note that low recall values are expected in crystallography, as many theoretically predicted peaks from crystal indexing may not be visible in the diffraction pattern due to experimental factors such as weak diffraction intensities, limited detector sensitivity, or crystal quality. As a result, high-precision patterns, indicating strong agreement between detected and predicted peaks, are prioritized for inclusion in the training dataset. However, the selection process also considers peak quantity thresholds to avoid biasing the dataset toward trivial cases. Figure 3 illustrates this selection process, showing the relationship between found and predicted peaks, as well as the precision-recall distribution used to identify high-quality diffraction patterns. This balanced approach ensures the initial training set comprises well-indexed images with representative peak distributions, while maintaining the capability to incorporate more challenging cases through iterative curation with the Data Engine.

Figure 3

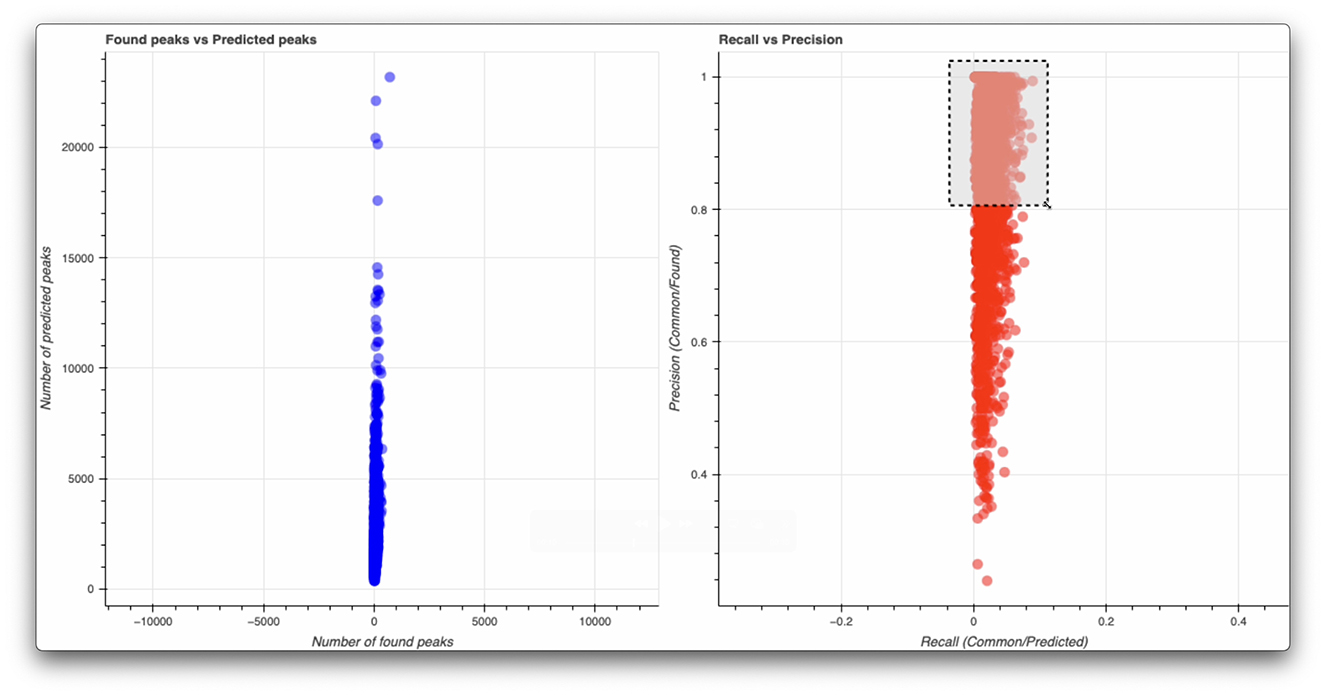
Figure 3. Analysis of peak detection quality metrics for dataset curation. (Left) Comparison between the number of found peaks using traditional peak finding algorithms and predicted peaks from crystal indexing, showing the correlation and distribution of peak counts across the dataset. The clustering around the diagonal indicates good agreement between detection and prediction methods, while outliers represent potential false positives or missed peaks. (Right) Precision-recall analysis for image selection, where precision represents the ratio of overlapping peaks to detected peaks, and recall is the ratio of overlapping peaks to predicted peaks. The dashed box highlights the high-precision region (precision >0.8) used to prioritize images for inclusion in the training dataset. This selection strategy ensures the initial training set comprises well-indexed images while maintaining sufficient diversity in peak distributions.

2.1.2 Segmentation label generation

For semantic segmentation training, pixel-level labels are generated using a distributed peak profile fitting pipeline. The Data Engine identifies high-quality diffraction patterns by matching detected and predicted peaks. For each candidate peak, detailed fitting, as shown in Figure 4, is performed on a small window (typically 9 × 9 pixels) centered on its position extracted from the detector image.

Figure 4

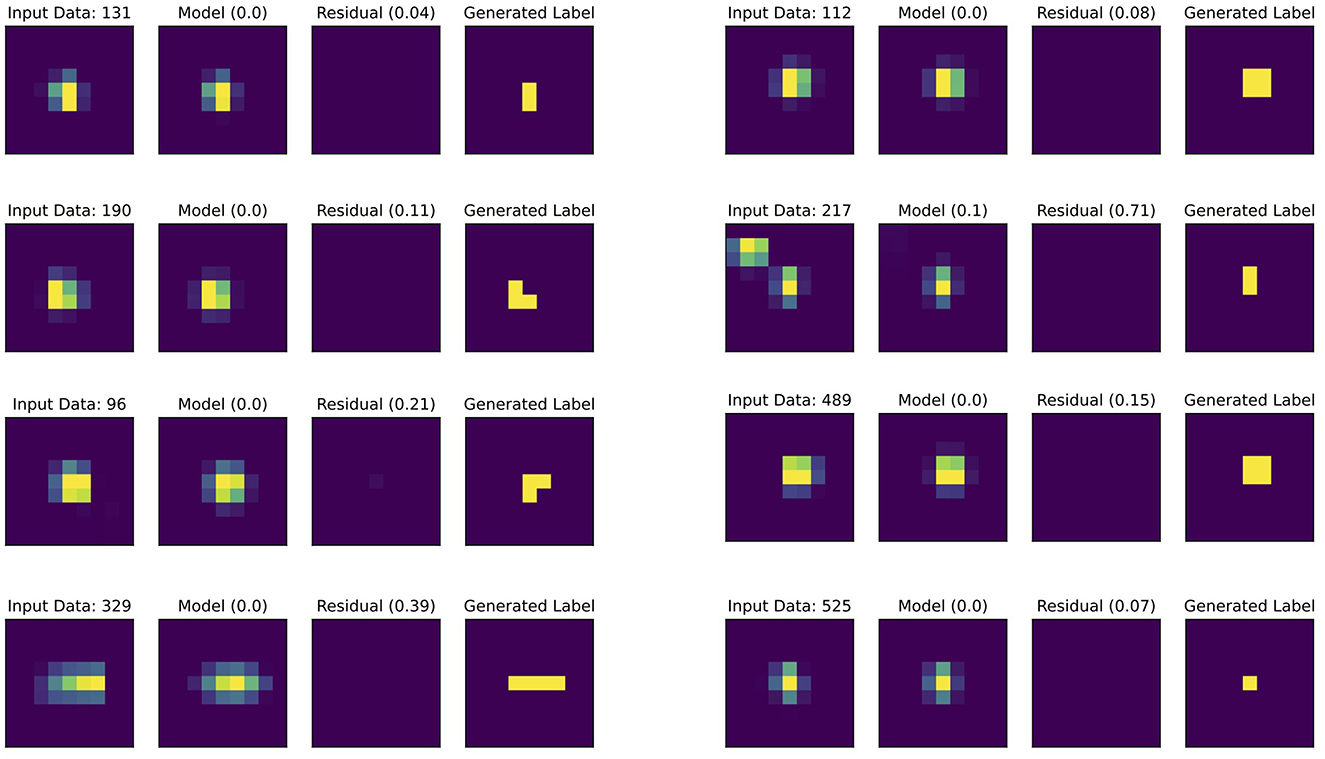
Figure 4. Peak fitting workflow for generating segmentation labels. Each set shows: Input Data (detector image window), Model (fitted 2D pseudo-Voigt function with ${\chi }_{\mathrm{\text{red}}}^2$), Residual (with RMSD values), and Generated Label (binary segmentation mask). Eight different peaks demonstrate the fitting process across varying peak intensities and shapes.

The peak fitting employs a two-dimensional pseudo-Voigt profile that combines Gaussian and Lorentzian components with a planar background:

$\begin{array}{l}I(y,x)=A[\eta L(y,x)+(1-\eta )G(y,x)]+ay+bx+c\end{array}$

where A is the amplitude, η is the mixing parameter between Lorentzian (L) and Gaussian (G) components, and (a, b, c) define the planar background. The Gaussian and Lorentzian components are given by:

$\begin{array}{l}G(y,x)=exp\left(-\frac{{(y-c_y)}^2}{2{\sigma }_y^2}-\frac{{(x-c_x)}^2}{2{\sigma }_x^2}\right)\end{array}$

$\begin{array}{l}L(y,x)=\frac{1}{1+\frac{{(y-c_y)}^2}{{\gamma }_y^2}+\frac{{(x-c_x)}^2}{{\gamma }_x^2}}\end{array}$

Here, (c_y, c_x) represent the peak center coordinates in the y and x directions, σ_y and σ_x represent the standard deviations of the Gaussian component in the y and x directions, while γ_y and γ_x are the half-width at half-maximum parameters of the Lorentzian component in the respective directions, controlling the peak width and shape in each dimension.

The fitting is implemented using the lmfit package (Newville et al., 2024), which provides robust non-linear least squares optimization with parameter bounds and constraints. To mitigate the influence of high-intensity pixels, the residuals (model − data) are weighted by $1/\sqrt{I+1}$ where I is the pixel intensity.

Peak filtering employs reduced chi-square (${\chi }_{\mathrm{\text{red}}}^2$) statistics for quality assessment. The resulting binary masks undergo a final validation step where peaks exceeding specified reduced chi-square thresholds are rejected to ensure label quality.

To handle the computational demands of processing millions of peaks, the fitting pipeline is distributed across compute nodes using Ray Core (Moritz et al., 2018). The system implements a two-level elastic task scheduling: at the top level, diffraction patterns are processed in configurable batches (e.g., 40 frames per batch) with a fixed number of concurrent batch tasks (e.g., 80 parallel batches). Within each batch, individual peak fitting tasks are dynamically scheduled based on available resources. This hierarchical scheduling approach efficiently handles the variable processing times of different peaks, a common challenge in crystallography where peak complexity varies significantly. In our implementation, processing 40,000 peaks achieved a throughput of ~600 peaks per second when distributed across 200 CPU cores (20 cores × 10 nodes). This distributed approach enables efficient processing of large-scale datasets while maintaining consistent label quality across diverse peak characteristics.

2.2 Model architecture and supervised pre-training

2.2.1 Modules in the architecture

The PeakNet architecture, as illustrated in the model component of Figure 1, employs a scalable, modular design to accommodate both large-scale pre-training and efficient edge deployment scenarios. The network follows a three-component structure: (1) a swappable convolutional neural network (CNN) backbone for multi-scale feature extraction, (2) a bidirectional feature pyramid network (BiFPN) (Tan et al., 2020) for feature fusion, and (3) a prediction head for peak segmentation. This modular approach allows each component to be independently optimized or replaced while maintaining the overall pipeline structure, enabling systematic exploration of different architectural configurations without disrupting the end-to-end workflow.

The backbone utilizes the RegNet design principles (Radosavovic et al., 2020), which provide a systematic approach to model scaling through carefully balanced network depth, width, and group width hyperparameters. This design choice enables systematic exploration of the accuracy-efficiency trade-off space while maintaining architectural consistency. The backbone extracts hierarchical features at multi-spatial scales, creating a rich representation of the crystallographic diffraction patterns. Specifically, we adopt the ConvNeXtV2 (Woo et al., 2023) model as the CNN backbone, which scales from 3.7M to 658M parameters, and utilize the 658M parameter backbone for the supervised pre-training.

The feature fusion stage implements a BiFPN, which enhances information flow through bidirectional connections between different feature scales. This component is independently scalable in both width and depth (e.g. stack multiple BiFPN blocks), offering increased flexibility for adjusting model capacity. This approach preserves the network's capability to capture both local and global peak features effectively. Our implementation adopts a modified BiFPN architecture where layer normalization replaces batch normalization throughout the network, eliminating the need for tracking running statistics during training. This modification ensures the model's inference behavior depends solely on its learned parameters rather than on accumulated training statistics, resulting in more deterministic and reliable deployment.

The prediction head employs a dual-pathway architecture optimized for precise peak segmentation. The first pathway operates on downsampled feature maps for efficient segmentation of large peaks, while the second pathway implements learnable upsampling to generate full-resolution peak predictions that can be as precise as a single pixel. Each pathway is made of a single layer, minimizing computational overhead while maintaining high localization accuracy. The prediction head's architecture remains constant across different model scales, ensuring consistent output characteristics regardless of the backbone and BiFPN configurations.

This modular and scalable architecture enables systematic exploration of the model capacity spectrum, from high-capacity models suitable for pre-training to efficient variants optimized for real-time edge deployment at XFEL facilities.

2.2.2 Supervised pre-training

Training utilized a focal loss function with alpha-balanced cross-entropy to address class imbalance inherent in crystallographic data, where Bragg peaks typically occupy a small fraction of detector pixels. The focal loss is defined as:

$\begin{array}{ll}FL(p_t)=-{\alpha }_t{(1-p_t)}^{\gamma }log(p_t)& (1)\end{array}$

where p_t is the model's estimated probability for the target class, α_t is the alpha-balancing factor for class t, and γ is the focusing parameter. We employed class-specific alpha values (α_peak = 0.75, α_background = 0.25) to account for the predominance of background pixels, with γ = 2 to down-weight well-classified examples and focus training on challenging cases.

The Data Engine enables continuous model improvement through iterative dataset curation and refinement. At the time of this manuscript's preparation, we pre-trained the model using supervised learning on PeakNet-20k, an in-house dataset of ~20,000 diffraction patterns curated through the Data Engine. This dataset represents diverse experimental conditions, including various detector configurations, sample types, crystal qualities and beam conditions. To enhance the model's robustness to real-world scenarios, we also incorporated challenging cases such as patterns with detector artifacts and malfunctioning pixel areas. As the Data Engine continues to process new experimental data, the dataset's quality and diversity will grow, enabling further improvements in model performance.

Supervised pre-training utilizes a ConvNeXtV2 backbone with 658M parameters, complemented by four BiFPN blocks contributing an additional 14M parameters. Pre-training was implemented using Fully Sharded Data Parallel (FSDP) on a single-node system equipped with 10 NVIDIA L40S GPUs, with the software infrastructure designed to scale to larger computational clusters as needed. To preserve spatial information integrity, pre-training was conducted on fully assembled diffraction patterns. To accommodate varying detector sizes, we implemented a standardized pad-and-crop procedure, normalizing all input images to 1, 920 × 1, 920 pixels, followed by z-standardization on a per-image basis. While individual samples were processed with a batch size of one, gradient accumulation was performed every 20 iterations to simulate the effects of a larger batch. The pre-training also employed a base learning rate of 3 × 10⁻⁴ with cosine decay scheduling and 20 warm-up iterations. To ensure training stability, gradient norm clipping was enforced at a threshold of 1.0.

2.2.3 Model distillation for edge deployment and distributed inference

2.2.3.1 Distillation

Model distillation was employed to transfer the capabilities of the large-scale teacher model to a more compact student model suitable for edge deployment. To optimize the distillation process, pre-activation feature maps were generated for the entire PeakNet-20k dataset using the teacher model and cached to disk, eliminating the need for repeated teacher inference during training. The cached feature maps were then processed to produce activation maps through a temperature-scaled softmax activation, while segmentation labels were further derived using argmax operations.

The distillation framework incorporates three complementary loss functions: mean squared error (MSE) loss between teacher and student feature maps, Kullback-Leibler (KL) divergence loss between activation maps, and focal loss for segmentation map prediction. Given teacher logits z_t and student logits z_s, the total loss is computed as:

$\begin{array}{ll}{L}_{\text{total}}={\text{λ}}_{\text{mse}}{L}_{\text{mse}}+{\text{λ}}_{\text{kl}}{L}_{\text{kl}}+{\text{λ}}_{\text{focal}}{L}_{\text{focal}},& (2)\end{array}$

where λ_mse = 0.4, λ_kl = 0.4, and λ_focal = 0.2 are weighting coefficients for each loss component.

The mean squared error loss $L_{\mathrm{\text{mse}}}$ directly supervises feature map alignment and is given by:

$\begin{array}{ll}{L}_{\text{mse}}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(z_t^{(i)}-z_s^{(i)}\right)}^2,& (3)\end{array}$

where N is the number of feature map elements. This loss ensures that the student model learns feature representations similar to those of the teacher model at a fine-grained level.

Knowledge transfer is further facilitated through the Kullback-Leibler divergence loss $L_{\mathrm{\text{kl}}}$, which minimizes the difference between the teacher's and student's probability distributions after temperature scaling. The KL divergence loss is defined as:

$\begin{array}{ll}{L}_{\text{kl}}=T^2·\text{KL}(p_t(T)||p_s(T)),& (4)\end{array}$

where the temperature-scaled softmax probabilities for the teacher and student models are expressed as:

$\begin{array}{ll}{p}_t(T)=\sigma \left(\frac{z_t}{T}\right),& (5)\end{array}$

$\begin{array}{ll}{p}_s(T)=\sigma \left(\frac{z_s}{T}\right),& (6)\end{array}$

with σ(·) denoting the softmax function. The temperature scaling factor T = 2.0 softens the probability distributions, which is critical for transferring knowledge from the teacher to the student (Hinton et al., 2015). The scaling factor T² is applied to preserve appropriate gradient magnitudes during backpropagation. In alignment with PyTorch's built-in KLDivLoss, the spatial dimensions H and W of the feature maps are reshaped into the batch dimension to properly account for the spatial structure of the feature maps. The KL divergence loss is calculated using the batchmean reduction method, which averages the loss over the batch size.

The focal loss $L_{\mathrm{\text{focal}}}$ provides additional supervision using pseudo-labels derived from the teacher model's activation map, as detailed in Section 2.2.2. These “fake” hard labels are generated by applying an argmax operation to the teacher's activation map, selecting the most likely class at each spatial location. Unlike “true” hard labels from ground truth segmentation annotations (which are not used in our current distillation framework), these teacher-derived labels reflect the teacher model's predictions and are therefore subject to its limitations and biases.

This composite loss function enables the student model to learn both fine-grained feature representations and decision boundaries from the teacher while maintaining robust peak segmentation performance. The empirical weights λ_mse, λ_kl, and λ_focal were chosen to balance feature-level supervision ($L_{\mathrm{\text{mse}}}$), soft target learning ($L_{\mathrm{\text{kl}}}$), and “fake” hard target regularization ($L_{\mathrm{\text{focal}}}$).

Model distillation was performed using Fully Sharded Data Parallel (FSDP) with Zero2 sharding strategy on a system with 10 NVIDIA L40s GPUs. While the smaller student models could theoretically be trained using standard data parallel approaches, we kept using FSDP for code base consistency between teacher and student training, with only optimizer states and gradients being sharded in the distillation process. To maintain consistency with the teacher model training, we applied the same standardized pad-and-crop procedure for 1920 × 1920 pixel images and per-image z-standardization. The distillation process utilized a batch size of 4 with gradient accumulation every 10 steps to balance memory constraints with effective batch statistics. Training employed a base learning rate of 3 × 10⁻⁴ with cosine decay scheduling to 1 × 10⁻⁷ over 3,200 steps. Convergence was typically observed after ~1,400 steps, as indicated by stabilization of the composite distillation loss. Additionally, we maintained the same gradient norm clipping threshold of 1.0 as used in teacher model training to ensure training stability.

2.2.3.2 Inference

The inference pipeline implements a producer-consumer architecture using Ray Core (Moritz et al., 2018). Data flows from Psana, our specialized LCLS data source infrastructure, through distributed queues to inference workers and then through a second queue to HDF5 file writers. Each GPU runs one model instance, with configurable batch processing for optimized throughput.

Final peak finding results are persisted in CrystFEL-compatible HDF5 format, with aggregation to optimize I/O performance. The system enables parallel processing across multiple nodes and GPUs, with planned enhancements for dynamic load balancing and fault recovery in future Ray-based implementations. Monitoring capabilities track queue depths, GPU utilization, and processing throughput, enabling real-time performance optimization and system maintenance.

3 Results and discussion

3.1 Evaluation framework

We evaluate the effectiveness of Bragg peak finding algorithms in crystallography through their impact on downstream structure determination processes. Our evaluation framework centers on three complementary metrics that capture different aspects of pipeline performance. The hit rate, defined as the ratio of potential crystal diffraction patterns to total collected images, indicates detection sensitivity. However, high hit rates alone can be misleading or even detrimental, potentially overwhelming storage systems and computational resources with poor-quality patterns. The indexing rate, measuring the proportion of hit images that are successfully indexed, reveals how reliably the identified peaks contribute to structure determination when processed through identical indexing methods and parameter configurations. In fact, a high hit rate combined with a low indexing rate often indicates that the system is producing many false positives, identifying non-crystallographic features as Bragg peaks. Finally, the indexing yield, computed as the product of hit rate and indexing rate, provides a holistic measure of the pipeline's efficiency in converting raw detector images into indexed crystal structures.

3.2 Performance analysis on recent LCLS data

We evaluated our pipeline using a recent “road runner” (Roedig et al., 2017) crystallography experimental run at the Macromolecular Femtosecond Crystallography (MFX) instrument in LCLS, processing 77,023 detector images using an Epix10ka2M detector. To ensure fair comparison, all peak finding approaches fed into identical indexing pipelines with consistent parameters.

3.2.1 Baseline and teacher model performance

The traditional approach, utilizing expert-tuned parameters in established crystallographic software, achieved an indexing yield of 36.38% through a hit rate of 50.02% and indexing rate of 72.73%. This baseline represents a carefully optimized configuration that typically requires several hours of trials and errors to converge on optimal parameter settings when working with new sample types, crystal quality or detector configurations, even with experienced crystallographers. While this manual optimization process can be expedited when working with familiar samples and detectors where approximate parameters are known, the time investment required for each new experimental configuration represents a significant bottleneck that our neural network approach eliminates.

Our large-scale teacher model (658M parameters backbone) matched the baseline's overall effectiveness while operating at a different balance point. The model achieved a higher indexing yield (37.50%) with more aggressive hit finding (54.32% hit rate) while maintaining a reasonable indexing rate (69.03%). This improvement in indexing yield, the key metric for overall pipeline efficiency, suggests that the model successfully learns to identify peaks that are more consistently useful for crystal indexing. Figure 5 visualizes how the model processes a raw diffraction pattern (Figure 5A) to generate precise peak segmentation (Figure 5B) through its learned feature representations for crystallographic peaks (Figure 5C) and non-peak features (Figure 5D).

Figure 5

Figure 5. Visualization of the PeakNet pipeline's image processing and feature extraction capabilities on an example X-ray diffraction pattern. (A) Raw diffraction pattern from an Epix10ka2M detector showing characteristic Bragg peaks, with an inset highlighting the detailed peak distribution and detector panel boundaries. (B) Final segmentation output from the model, where bright spots indicate identified Bragg peaks. (C) Bragg peak activation map showing the model's learned feature representations for crystallographic peaks, with brighter regions indicating higher activation values. (D) Non-Bragg-peak activation map highlighting the model's ability to identify non Bragg peak features such as panel gaps and background noise. The complementary nature of the activation maps (C, D) demonstrates the model's ability to differentiate between genuine Bragg peaks and other features, which is crucial for reliable peak segmentation in challenging experimental conditions.

3.2.2 Student model analysis

Model distillation revealed systematic trends across student models of varying capacities (Table 1). Model compression consistently led to increased hit rates but decreased indexing rates, suggesting reduced capacity impacts Bragg peak discrimination of high-quality and marginal diffraction patterns. Student1 (tiny backbone, four BiFPN blocks) achieved the most practical balance with a 32.15% indexing yield, maintaining selective hit finding (40.12%) with strong indexing performance (80.13%).

Table 1

Table 1. Performance comparison of different model configurations on a crystallography dataset with 77,023 images.

Notably, Student3, trained exclusively on Epix10ka2M detector data, demonstrated how training on detector specific data can partially mitigate compression trade-offs, achieving a 32.90% indexing yield despite increased hit sensitivity (68.51%). In contrast, highly compressed models (Student4, Student5) showed concerning behavior with extremely high hit rates (>95%) but poor indexing rates (~34%), indicating degraded Bragg peak quality discrimination.

3.2.3 Unit cell parameter analysis

The distributions of indexed unit cell parameters, as shown in Figure 6, provide strong quantitative validation of our deep learning approach. All models, including the heavily compressed student variants, preserve the characteristic sharp peaks centered at the expected values seen in human expert processing. The human reference establishes baseline distributions with cell lengths a = 40.07 ± 3.91Å, b = 70.90 ± 0.50Å, c = 91.10 ± 0.28Åand angles α = β = γ = 90.0° with standard deviations of 0.2°, 0.3°, and 0.3°, respectively.

Figure 6

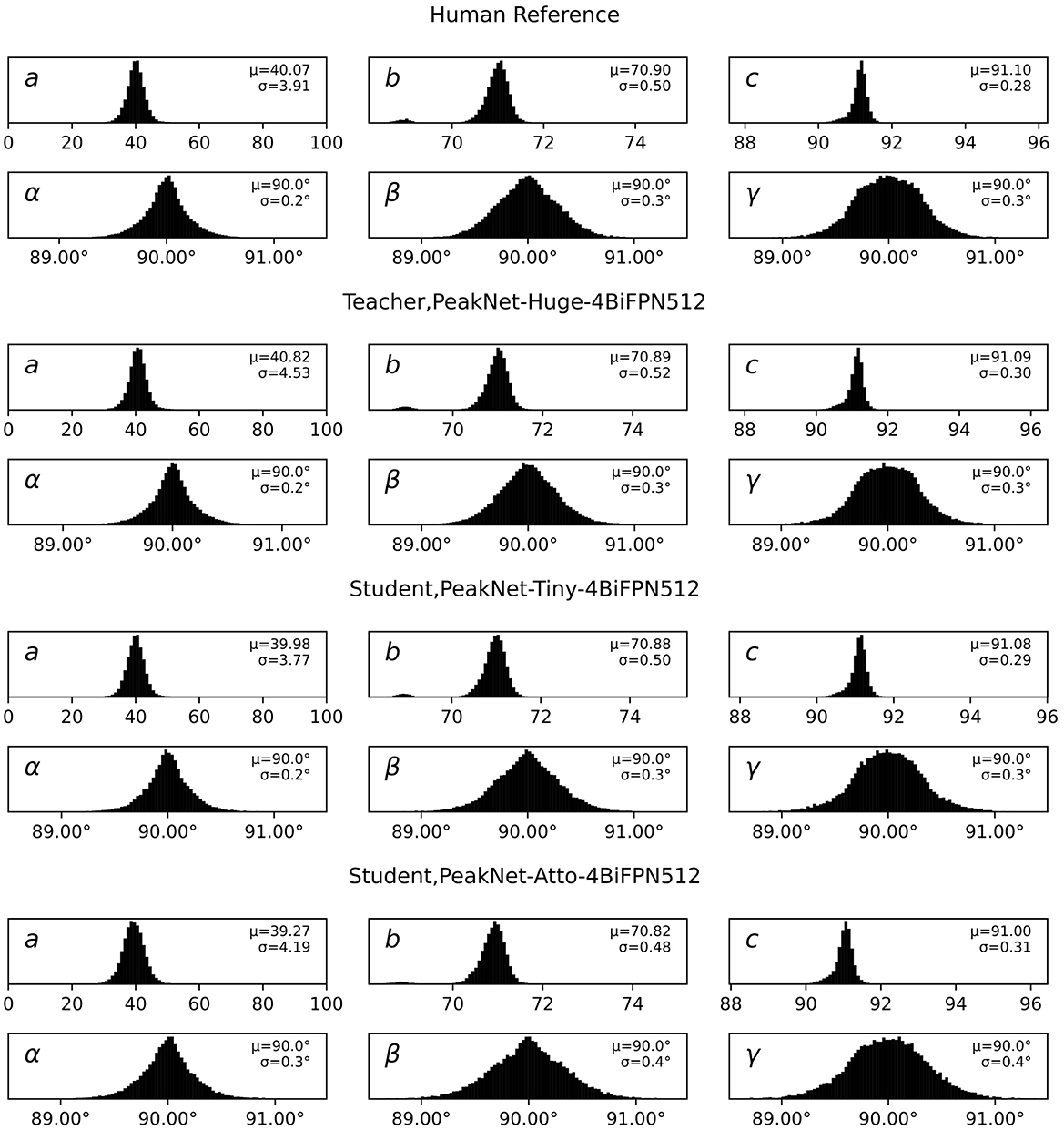
Figure 6. Distribution of unit cell parameters (lengths a, b, c and angles α, β, γ) from crystal indexing across different peak finding approaches. The plots show remarkably consistent distributions between human expert processing (top row) and subsequent model variants, with mean (μ) and standard deviation (σ) values annotated for each parameter. Both teacher (second row) and student models (third and fourth rows) maintain tight distributions around expected values, with the teacher model showing marginally sharper peaks particularly in the angle parameters. The atto-backbone student model exhibits slightly increased variability in angular parameters (σ up to 0.4°) while maintaining accurate mean values, demonstrating successful knowledge transfer even under extreme model compression.

The teacher model demonstrates remarkable consistency with these reference values, showing only minimal deviations in the mean values (a = 40.82 ± 4.53Å, b = 70.89 ± 0.52Å, c = 91.09 ± 0.30Å) and maintaining identical angular precision (α = β = γ = 90.0 ± 0.2-0.3°). Both student models maintain this high level of accuracy, with the tiny backbone variant showing slight parameter shifts (a = 39.98 ± 3.77Å, b = 70.88 ± 0.50Å, c = 91.08 ± 0.29Å) and the atto backbone exhibiting marginally increased variability (a = 39.27 ± 4.19Å, b = 70.82 ± 0.48Å, c = 91.00 ± 0.31Å) while preserving the expected 90° angles with only minor increases in angular uncertainty (up to 0.4° for γ).

This consistency across cell parameters, particularly the preservation of tight distributions around physically expected values, confirms that our models are identifying genuine Bragg peaks that enable accurate crystal indexing rather than spurious features that happen to pass the indexing step. The slightly broader distributions in student models, especially visible in the a-axis parameters, suggest a modest degradation in peak quality discrimination, consistent with the lower indexing rates observed in Table 1. However, the effect remains minimal enough to maintain reliable crystal indexing performance across all model variants.

3.2.4 Architecture impact analysis

Our systematic exploration of model architectures revealed several key insights about scaling behavior and performance characteristics. The choice of backbone significantly influences the operating point balance, with the huge backbone (Teacher) achieving optimal indexing yield (37.50%) through balanced operation (54.32% hit rate, 69.03% indexing rate). The tiny backbone configuration (Student1) demonstrates more conservative behavior with lower hit rate (40.12%) but higher indexing rate (80.13%), while the atto backbone maintains practical indexing yields (~32%) when optimized for specific detector configurations despite its minimal size.

BiFPN block count emerges as a critical factor in maintaining Bragg peak discrimination capabilities. Student models with 4 BiFPN blocks maintain high indexing rates (>74%) with controlled hit rates, while 2-block variants show degraded discrimination with indexing rates below 50% and a tendency toward over-sensitive Bragg peak detection evidenced in the elevated hit rate. This pattern suggests that reduced feature fusion capacity significantly impacts the model's ability to distinguish genuine Bragg peaks, even with identical backbones.

3.2.5 Implications for deployment strategy

Our analysis reveals several key considerations for practical deployment. While smaller models enable faster inference, their tendency toward detecting more peaks per image results in high hit rates but lower indexing rates, potentially creating downstream processing bottlenecks that offset speed advantages. Furthermore, maintaining adequate BiFPN capacity appears more critical than backbone size for preserving discrimination capabilities. The promising performance of detector-specific distillation (e.g., Student3) suggests the value of implementing systematic testing frameworks to evaluate model performance across different detector configurations. Such evaluation frameworks could help identify cases where detector-specific fine-tuning might complement our primary strategy of distillation using diverse, multi-detector datasets.

3.3 Visual results

We present two sets of visualizations to demonstrate both the model's feature extraction capabilities and the effectiveness of our model distillation approach.

Figure 7 shows a collection of 12 representative diffraction pattern segments, with each panel displaying the original detector image alongside its corresponding non-Bragg-peak activation map, Bragg peak activation map, and final segmentation result. The activation maps reveal the model's ability to differentiate between crystallographic peaks and other features, with particularly robust performance in challenging scenarios such as detector panel gaps, varying peak densities, and strong background features.

Figure 7

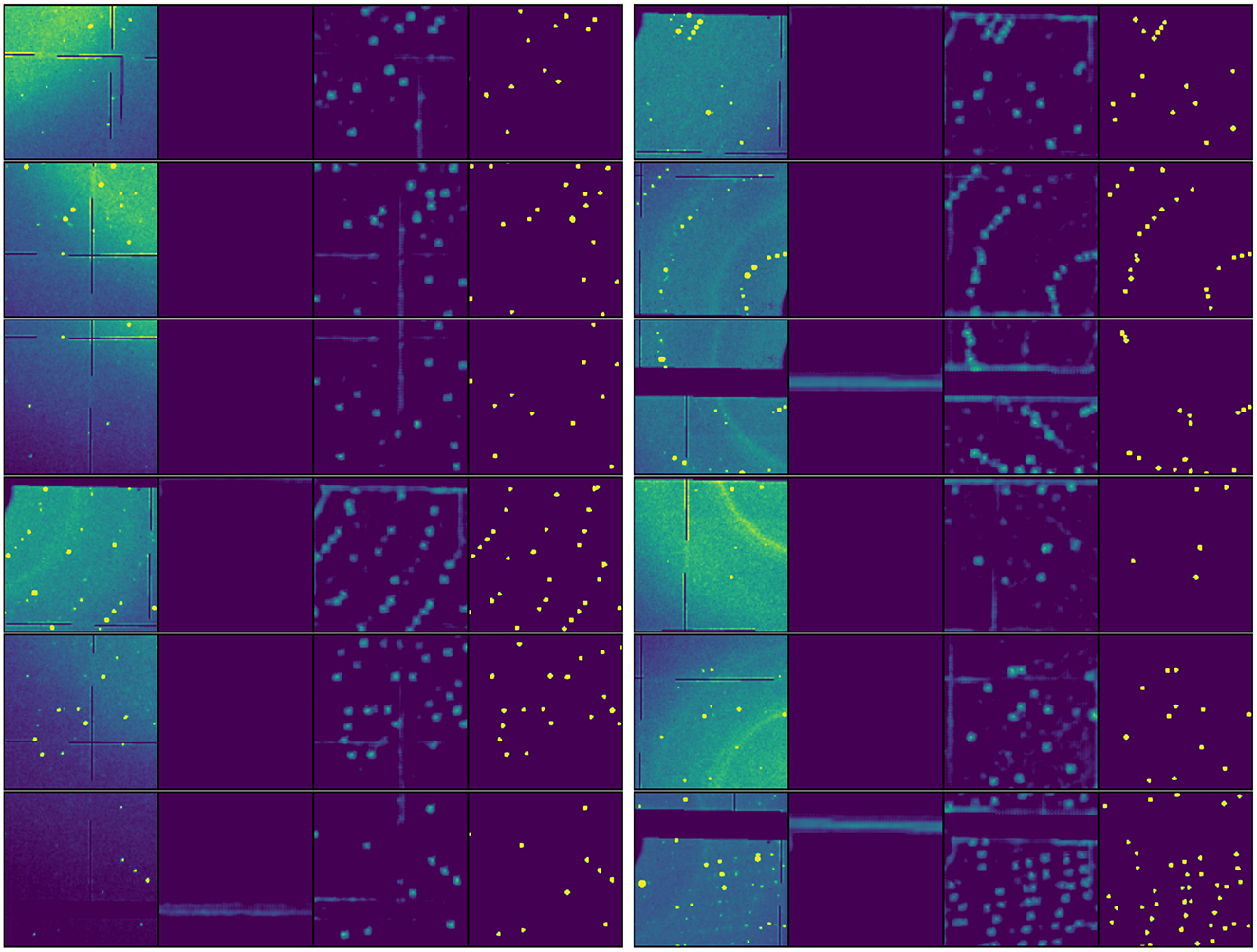
Figure 7. Feature extraction visualization across diverse diffraction patterns. Each panel shows a quartet visualization of: original detector image (leftmost), non-Bragg-peak activation map, Bragg peak activation map, and final segmentation result (rightmost, yellow areas). The 12 random patterns demonstrate the model's ability to handle varying experimental conditions including different peak densities, detector panel gaps, and background intensities.

Figure 8 provides a comparative analysis of model distillation outcomes through four sets of triplet visualizations arranged in a 2 × 2 grid. Each triplet shows results from the teacher model (top row), tiny-backbone student (middle row), and atto-backbone student (bottom row) applied to identical input patterns. This comparison reveals several key insights into the effects of model compression. The teacher model consistently produces sharper, more concentrated activation patterns for Bragg peaks, while student models exhibit progressively more diffuse activations as model capacity decreases. Nevertheless, both student models maintain reliable peak discrimination capabilities, as evidenced by the consistency of their final segmentation results across most cases. The visualization of challenging scenarios, particularly near detector artifacts and panel boundaries, illustrates how model compression affects robustness. In these complex regions, the atto-backbone occasionally exhibits uncertainty where the teacher model remains decisive, though it still maintains acceptable peak detection performance. These visualizations support our quantitative findings regarding the trade-offs between model size and performance, while demonstrating that even highly compressed student models retain core peak detection capabilities through effective model distillation.

Figure 8

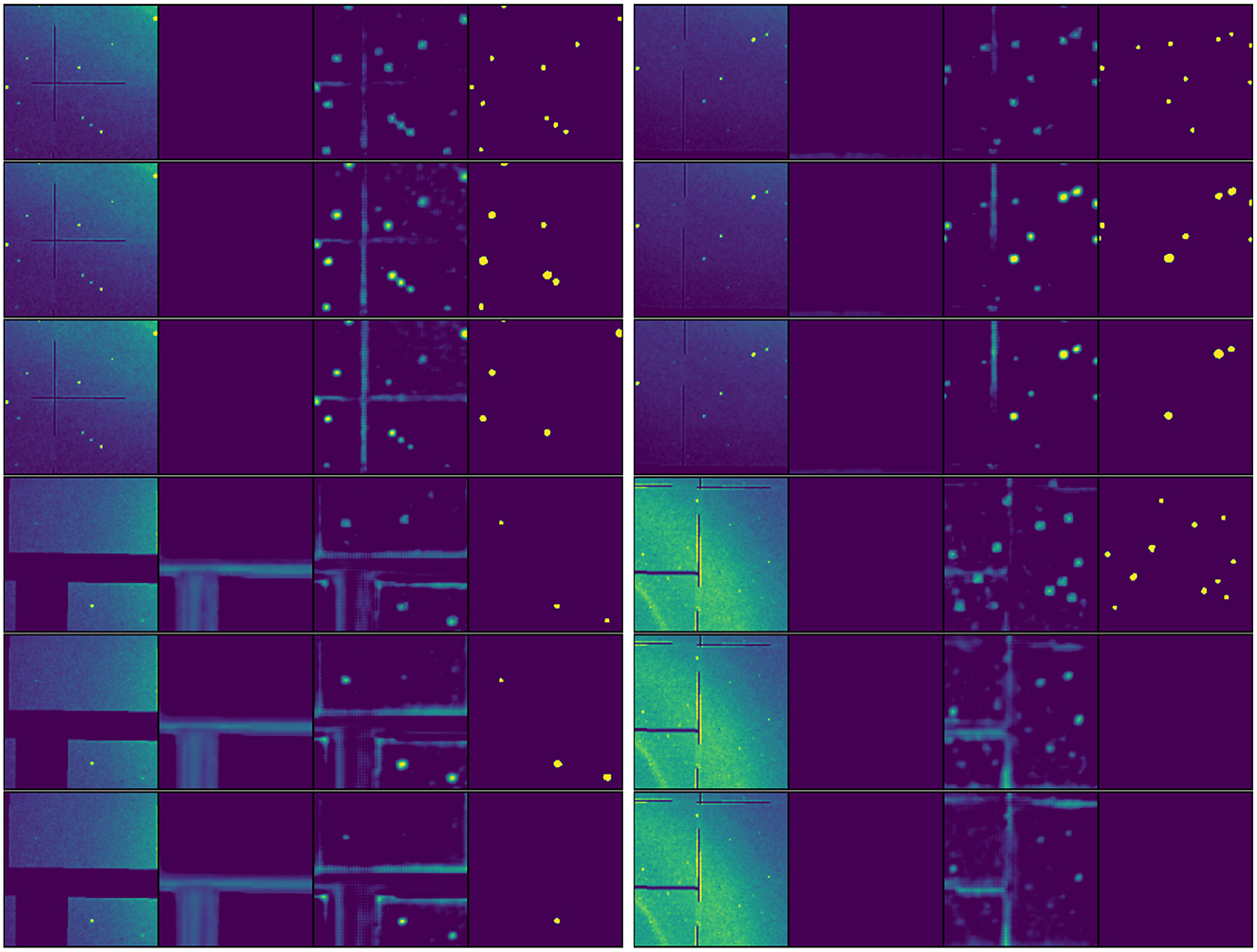
Figure 8. Comparative visualization of model distillation results. Four sets of diffraction patterns (arranged in a 2 × 2 grid) are shown, each processed by three model variants: teacher model (top row), tiny-backbone student (middle row), and atto-backbone student (bottom row). Each row shows the quartet visualization format: original image, non-Bragg-peak activation map, Bragg peak activation map, and final segmentation. Note how activation patterns become more diffuse with reduced model capacity, while maintaining consistent peak identification in the final segmentation. The selection of patterns includes various challenging scenarios such as detector artifacts and panel boundaries to demonstrate robustness across model compression levels.

3.4 Inference runtime analysis

We evaluated the inference pipeline's performance using a dataset of 77,023 Epix10ka2M detector images across two distinct computing environments. The baseline CPU implementation was tested on a system with dual-socket AMD EPYC 7713 64-Core processors (3.7 GHz max frequency, 32MB L3 cache per CCX). The GPU-accelerated pipeline was evaluated on a cluster equipped with AMD EPYC 9454 48-Core processors (3.8 GHz max frequency) and NVIDIA L40S GPUs.

The performance characteristics across model variants (Table 2) reveal the trade-offs between model capacity and inference speed. While the teacher model offers highest accuracy, the atto-backbone student achieves 71% higher throughput at 183 images per second while maintaining acceptable peak detection quality, as discussed in Section 3.2.

Table 2

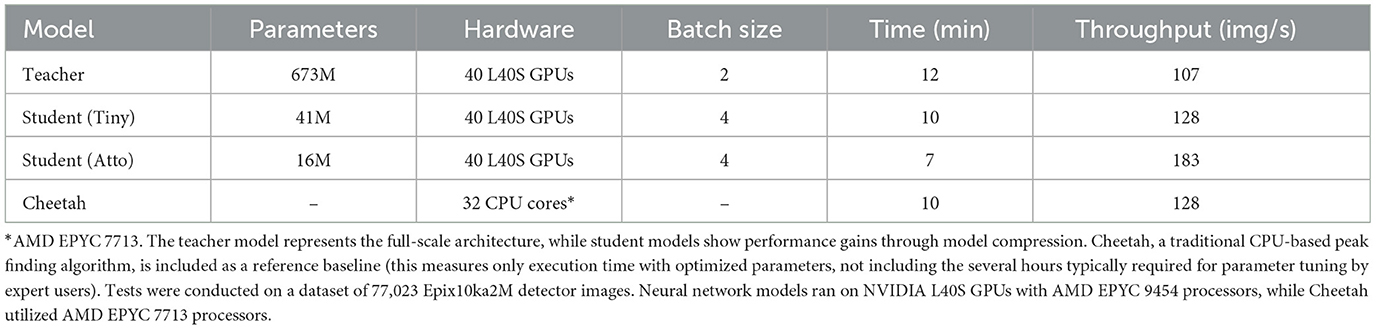
Table 2. Runtime analysis comparing inference performance across different model variants and configurations.

At LCLS, traditional crystallographic software pipelines are tightly integrated with Psana, LCLS's data access framework, using Message Passing Interface (MPI) to optimize runtime performance. This tight coupling between Psana and peak-finding algorithms has historically served the facility well, enabling efficient processing for classical approaches. However, this architecture presents significant limitations for neural network inference at scale, where GPU utilization and batch processing are critical for performance. Our system takes a fundamentally different approach by decoupling Psana data source from model inference through a producer-consumer architecture.

Our distributed inference system implements this decoupling using a two-stage queue design. Detector images are ingested by Psana running on 32 CPU cores, feeding into a primary queue with 3,200-image capacity. This queue acts as a buffer between the data source and processing, allowing the system to smooth out variations in processing time and maintain consistent GPU utilization. Multiple GPU workers process batched images in parallel, with results flowing through a second-stage queue to dedicated CrystFEL-compatible HDF5 file writers running on 10 CPU cores.

This decoupled architecture offers several advantages over traditional MPI-based approaches at LCLS. First, it enables independent scaling of data loading and processing components, and additional GPU workers can be added without modifying the Psana-based data ingestion pipeline. Second, the queuing system facilitates efficient batch processing, critical for maximizing GPU utilization with neural network inference. Finally, the system's modular design simplifies deployment and maintenance, as components can be upgraded or modified independently.

While our current implementation achieves throughput comparable to CPU-based methods, it falls short of the order-of-magnitude speedups typically expected from GPU acceleration. This performance gap stems from several factors, including data transfer overhead, batching constraints, the sequential execution of inference pipeline stages (loading data to GPUs, model inference, and load results to the second queue), and limitations in neural network execution efficiency (e.g., lack of JIT compilation optimizations). However, the GPU-accelerated pipeline with its decoupled producer-consumer architecture and demonstrated model compression capabilities provides a foundation for future optimizations needed to meet the high-throughput requirements of next-generation facilities. These optimizations could include concurrent execution of pipeline stages, such as through Ray's task scheduling system, along with other performance improvements discussed in Section 3.5.

3.5 Future research directions

The architecture developed for Bragg peak detection has potential applications in other scientific domains requiring real-time analysis of high-throughput image data. At synchrotron facilities, High Energy X-ray Diffraction Microscopy (HEDM) and Cryo-crystallography experiments generate complex diffraction patterns that require rapid peak identification for material characterization and molecular structure determination. Similarly, neutron diffraction experiments at spallation sources could benefit from our pipeline's ability to handle varying peak intensities and background conditions. The Data Engine's approach to automated dataset generation could be adapted for these domains, where traditional peak finding algorithms often require extensive tuning specific to facilities, experimental conditions, detector configurations, and sample characteristics.

Looking ahead, our work presents several opportunities for further advancement across multiple aspects of the system. The Data Engine's circular workflow design provides a foundation for continuous improvement of the training dataset and model performance. Future iterations could leverage this capability to systematically enhance peak detection accuracy across diverse experimental conditions through dataset refinement and model retraining, particularly when adapting to new sample types, detector configurations and experimental setups.

A primary focus for future development is accelerating inference speed through architectural innovations. This includes exploring efficiency-optimized architectures like EfficientNet (Tan and Le, 2020, 2021) and MobileNet (Howard et al., 2017; Sandler et al., 2018; Howard et al., 2019; Qin et al., 2024), which incorporate depthwise separable convolutions and compound scaling. Other promising approaches include structured pruning to reduce parameter count while preserving accuracy, mixed-precision quantization for reduced memory bandwidth, and dilated convolutions to maintain receptive field size with fewer parameters.

Model distillation strategies also warrant further investigation. While our current approach relies on teacher-derived “fake” hard labels, future work could explore incorporating true hard labels from ground truth annotations to potentially improve student model performance. This direct supervision from ground truth data could help student models better preserve peak discrimination capabilities during model compression.

Preparing for MHz repetition rates at upcoming XFEL upgrades remains a key priority. This will require both architectural optimization and innovations in distributed computing infrastructure. Potential approaches include hardware-aware neural architecture search to identify optimal model configurations for specific accelerator platforms and developing streaming algorithms for real-time model inference. The producer-consumer model potentially enables cross-site real-time analysis where Advanced Scientific Computing Research (ASCR) facilities can scale the compute infrastructure for inference, particularly valuable for handling peak processing loads during intense experimental campaigns.

4 Conclusion

This work demonstrates the feasibility of scaling deep learning to solve real-time Bragg peak finding through a comprehensive machine learning system. By integrating automated data generation, flexible model architectures, and distributed inference, our pipeline achieves a 37.5% indexing yield that surpasses traditional expert-tuned methods while eliminating manual parameter adjustment. The system's decoupled producer-consumer architecture enables practical deployment at XFEL facilities, achieving 183 images per second throughput with compressed models while maintaining robust peak discrimination. While further optimization is needed for MHz-scale facilities, our systematic approach to the complete machine learning pipeline, from training through deployment, establishes a foundation for integrating deep neural networks into high-throughput scientific applications.

Data availability statement

The datasets presented in this article are not readily available because the datasets generated and analyzed during the current study are proprietary and, therefore, not publicly available. Requests to access the datasets should be directed to Cong Wang, Y3dhbmczMUBzbGFjLnN0YW5mb3JkLmVkdQ==.

Author contributions

CW: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. VM: Conceptualization, Data curation, Methodology, Validation, Writing – original draft, Writing – review & editing. FP: Conceptualization, Data curation, Investigation, Writing – original draft, Writing – review & editing. MA: Formal analysis, Investigation, Methodology, Writing – original draft, Writing – review & editing. JT: Conceptualization, Funding acquisition, Project administration, Resources, Supervision, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This material was based upon work supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Award Number FWP-100643. Use of the Linac Coherent Light Source (LCLS), SLAC National Accelerator Laboratory, is supported by the US DOE, Office of Science, Office of Basic Energy Sciences (contract No. DE-AC02-76SF00515).

Acknowledgments

We gratefully acknowledge Alexandra Tolstikova (Deutsches Elektronen-Synchrotron, DESY) for processing the reference dataset using Cheetah and valuable discussions on training dataset curation strategies. We thank Anton Barty (Deutsches Elektronen-Synchrotron, DESY) for insightful discussions on dataset curation approaches. We are indebted to David Rogers (Oak Ridge National Laboratory) for insights on producer-consumer based data processing architectures. Special thanks to Chun Hong Yoon and Po-Nan Li (formerly at SLAC National Accelerator Laboratory) for their pioneering work on neural network approaches to Bragg peak finding through the original U-Net based PeakNet implementation. Lastly, we acknowledge the assistance of the large language model ChatGPT by OpenAI in refining the language and enhancing the readability of this paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that Gen AI was used in the creation of this manuscript. We used Generative AI (ChatGPT, model GPT-4o, developed by OpenAI) to polish the language and improve the formatting of the manuscript written in LaTeX. The AI-assisted tasks included: (i) Enhancing grammatical accuracy, coherence, and clarity of the text while maintaining the original meaning. (ii) Refining LaTeX code for consistency, structure, and adherence to the desired formatting style. All AI-generated suggestions were manually reviewed to ensure factual accuracy and compliance with ethical standards.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aquila, A., Hunter, M. S., Doak, R. B., Kirian, R. A., Fromme, P., White, T. A., et al. (2012). Time-resolved protein nanocrystallography using an X-ray free-electron laser. Optics Express 20:2706. doi: 10.1364/OE.20.002706

PubMed Abstract | Crossref Full Text | Google Scholar

Barty, A., Kirian, R. A., Maia, F. R. N. C., Hantke, M., Yoon, C. H., White, T. A., et al. (2014). Cheetah: software for high-throughput reduction and analysis of serial femtosecond X-ray diffraction data. J. Appl. Crystallogr. 47, 1118–1131. doi: 10.1107/S1600576714007626

PubMed Abstract | Crossref Full Text | Google Scholar

Bolotovsky, R., White, M. A., Darovsky, A., and Coppens, P. (1995). The ‘seed-skewness' method for integration of peaks on imaging plates. J. Appl. Crystallogr. 28, 86–95. doi: 10.1107/S0021889894009696

Crossref Full Text | Google Scholar

Chapman, H. N., Barty, A., Bogan, M. J., Boutet, S., Frank, M., Hau-Riege, S. P., et al. (2006). Femtosecond diffractive imaging with a soft-X-ray free-electron laser. Nat. Phys. 2, 839–843. doi: 10.1038/nphys461

Crossref Full Text | Google Scholar

Chapman, H. N., Fromme, P., Barty, A., White, T. A., Kirian, R. A., Aquila, A., et al. (2011). Femtosecond X-ray protein nanocrystallography. Nature 470, 73–77. doi: 10.1038/nature09750

PubMed Abstract | Crossref Full Text | Google Scholar

Hadian-Jazi, M., Messerschmidt, M., Darmanin, C., Giewekemeyer, K., Mancuso, A. P., Abbey, B., et al. (2017). A peak-finding algorithm based on robust statistical analysis in serial crystallography. J. Appl. Crystallogr. 50, 1705–1715. doi: 10.1107/S1600576717014340

PubMed Abstract | Crossref Full Text | Google Scholar

Hadian-Jazi, M., Sadri, A., Barty, A., Yefanov, O., Galchenkova, M., Oberthuer, D., et al. (2021). Data reduction for serial crystallography using a robust peak finder. J. Appl. Crystallogr. 54, 1360–1378. doi: 10.1107/S1600576721007317

PubMed Abstract | Crossref Full Text | Google Scholar

Hinton, G., Vinyals, O., and Dean, J. (2015). Distilling the knowledge in a neural network. arXiv [Preprint]. arXiv:1503.02531. doi: 10.48550/arXiv.1503.02531

Crossref Full Text | Google Scholar

Howard, A., Sandler, M., Chen, B., Wang, W., Chen, L.-C., Tan, M., et al. (2019). “Searching for MobileNetV3,” in 2019 IEEE/CVF International Conference on Computer Vision (ICCV) (Seoul: IEEE), 1314–1324. doi: 10.1109/ICCV.2019.00140

Crossref Full Text | Google Scholar

Howard, A. G., Zhu, M., Chen, B., Kalenichenko, D., Wang, W., Weyand, T., et al. (2017). MobileNets: efficient convolutional neural networks for mobile vision applications. arXiv [Preprint]. arXiv:1704.04861. doi: 10.48550/ARXIV.1704.04861

Crossref Full Text | Google Scholar

Ibrahim, M., Fransson, T., Chatterjee, R., Cheah, M. H., Hussein, R., Lassalle, L., et al. (2020). Untangling the sequence of events during the S₂ → S₃ transition in photosystem II and implications for the water oxidation mechanism. Proc. Natl. Acad. Sci. 117, 12624–12635. doi: 10.1073/pnas.2000529117

PubMed Abstract | Crossref Full Text | Google Scholar

Kern, J., Chatterjee, R., Young, I. D., Fuller, F. D., Lassalle, L., Ibrahim, M., et al. (2018). Structures of the intermediates of Kok's photosynthetic water oxidation clock. Nature 563, 421–425. doi: 10.1038/s41586-018-0681-2

PubMed Abstract | Crossref Full Text | Google Scholar

Kupitz, C., Basu, S., Grotjohann, I., Fromme, R., Zatsepin, N. A., Rendek, K. N., et al. (2014). Serial time-resolved crystallography of photosystem II using a femtosecond X-ray laser. Nature 513, 261–265. doi: 10.1038/nature13453

PubMed Abstract | Crossref Full Text | Google Scholar

Liu, Z., Sharma, H., Park, J.-S., Kenesei, P., Miceli, A., Almer, J., et al. (2021). BraggNN: fast X-ray bragg peak analysis using deep learning. arXiv [Preprint]. arXiv:2008.08198. doi: 10.48550/arXiv.2008.08198

PubMed Abstract | Crossref Full Text | Google Scholar

Moritz, P., Nishihara, R., Wang, S., Tumanov, A., Liaw, R., Liang, E., et al. (2018). “Ray: a distributed framework for emerging AI applications,” in OSDI'18: Proceedings of the 13th USENIX conference on Operating Systems Design and Implementation (Berkeley, CA: USENIX Association), 561–577.

Google Scholar

Nango, E., Royant, A., Kubo, M., Nakane, T., Wickstrand, C., Kimura, T., et al. (2016). A three-dimensional movie of structural changes in bacteriorhodopsin. Science 354, 1552–1557. doi: 10.1126/science.aah3497

PubMed Abstract | Crossref Full Text | Google Scholar

Neutze, R., Wouts, R., van der Spoel, D., Weckert, E., and Hajdu, J. (2000). Potential for biomolecular imaging with femtosecond X-ray pulses. Nature 406, 752–757. doi: 10.1038/35021099

PubMed Abstract | Crossref Full Text | Google Scholar

Newville, M., Otten, R., Nelson, A., Stensitzki, T., Ingargiola, A., Allan, D., et al. (2024). Lmfit/lmfit-py: 1.3.2. doi: 10.5281/zenodo.12785036

Crossref Full Text | Google Scholar

Pande, K., Hutchison, C. D. M., Groenhof, G., Aquila, A., Robinson, J. S., Tenboer, J., et al. (2016). Femtosecond structural dynamics drives the trans/cis isomerization in photoactive yellow protein. Science 352, 725–729. doi: 10.1126/science.aad5081

PubMed Abstract | Crossref Full Text | Google Scholar

Qin, D., Leichner, C., Delakis, M., Fornoni, M., Luo, S., Yang, F., et al. (2024). “MobileNetV4-universal models for the mobile ecosystem,” in Computer Vision” ECCV 2024. ECCV 2024. Lecture Notes in Computer Science, Vol. 15098, eds. A. Leonardis, E. Ricci, S. Roth, O. Russakovsky, T. Sattler, and G. Varol (Cham: Springer), 78–96. doi: 10.1007/978-3-031-73661-2_5

Crossref Full Text | Google Scholar

Radosavovic, I., Kosaraju, R. P., Girshick, R., He, K., and Dollar, P. (2020). “Designing network design spaces,” in 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (Seattle, WA: IEEE), 10425–10433. doi: 10.1109/CVPR42600.2020.01044

Crossref Full Text | Google Scholar

Roedig, P., Ginn, H. M., Pakendorf, T., Sutton, G., Harlos, K., Walter, T. S., et al. (2017). High-speed fixed-target serial virus crystallography. Nat. Methods 14, 805–810. doi: 10.1038/nmeth.4335

PubMed Abstract | Crossref Full Text | Google Scholar

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-Net: convolutional networks for biomedical image segmentation. arXiv [Preprint]. arXiv:1505.04597. doi: 10.48550/arXiv.1505.04597

Crossref Full Text | Google Scholar

Sandler, M., Howard, A., Zhu, M., Zhmoginov, A., and Chen, L.-C. (2018). “MobileNetV2: inverted residuals and linear bottlenecks,” in 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (Salt Lake City, UT: IEEE), 4510–4520. doi: 10.1109/CVPR.2018.00474

PubMed Abstract | Crossref Full Text | Google Scholar

Suga, M., Akita, F., Sugahara, M., Kubo, M., Nakajima, Y., Nakane, T., et al. (2017). Light-induced structural changes and the site of O=O bond formation in PSII caught by XFEL. Nature 543, 131–135. doi: 10.1038/nature21400

PubMed Abstract | Crossref Full Text | Google Scholar

Suga, M., Shimada, A., Akita, F., Shen, J.-R., Tosha, T., Sugimoto, H., et al. (2020). Time-resolved studies of metalloproteins using X-ray free electron laser radiation at SACLA. Biochim. Biophys. Acta Gen. Subj. 1864:129466. doi: 10.1016/j.bbagen.2019.129466

PubMed Abstract | Crossref Full Text | Google Scholar

Tan, M., and Le, Q. (2021). “Efficientnetv2: smaller models and faster training,” in Proceedings of the 38th International Conference on Machine Learning, Vol. 139, eds. M. Meila, and T. Zhang (PMLR), 10096–10106.

Google Scholar

Tan, M., and Le, Q. V. (2020). EfficientNet: rethinking model scaling for convolutional neural networks. arXiv [Preprint]. arXiv:1905.11946. doi: 10.48550/arXiv.1905.11946

PubMed Abstract | Crossref Full Text | Google Scholar

Tan, M., Pang, R., and Le, Q. V. (2020). EfficientDet: scalable and efficient object detection. arXiv [Preprint]. arXiv:1911.09070. doi: 10.48550/arXiv.1911.09070

Crossref Full Text | Google Scholar

Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M., Reddy, T., Cournapeau, D., et al. (2020). SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 17, 261–272. doi: 10.1038/s41592-019-0686-2

PubMed Abstract | Crossref Full Text | Google Scholar

White, T. A., Kirian, R. A., Martin, A. V., Aquila, A., Nass, K., Barty, A., et al. (2012). CrystFEL: a software suite for snapshot serial crystallography. J. Appl. Crystallogr. 45, 335–341. doi: 10.1107/S0021889812002312

Crossref Full Text | Google Scholar

Wilkinson, C., Khamis, H. W., Stansfield, R. F. D., and McIntyre, G. J. (1988). Integration of single-crystal reflections using area multidetectors. J. Appl. Crystallogr. 21, 471–478. doi: 10.1107/S0021889888005400

Crossref Full Text | Google Scholar

Winter, G., Waterman, D. G., Parkhurst, J. M., Brewster, A. S., Gildea, R. J., Gerstel, M., et al. (2018). DIALS : implementation and evaluation of a new integration package. Acta Crystallogr. D Struct. Biol. 74, 85–97. doi: 10.1107/S2059798317017235

PubMed Abstract | Crossref Full Text | Google Scholar

Woo, S., Debnath, S., Hu, R., Chen, X., Liu, Z., Kweon, I. S., et al. (2023). “ConvNeXt V2: Co-designing and scaling ConvNets with masked autoencoders,” in 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (Vancouver, BC: IEEE), 16133–16142. doi: 10.1109/CVPR52729.2023.01548

Crossref Full Text | Google Scholar

Yoon, C. H. (2020). “Psocake: GUI for making data analysis a piece of cake,” in in handbook on big data and machine learning in the physical sciences (London: World Scientific Publishing Co Pte Ltd), 169–178. doi: 10.1142/9789811204579_0010

Crossref Full Text | Google Scholar

Young, I. D., Ibrahim, M., Chatterjee, R., Gul, S., Fuller, F. D., Koroidov, S., et al. (2016). Structure of photosystem II and substrate binding at room temperature. Nature 540, 453–457. doi: 10.1038/nature20161

PubMed Abstract | Crossref Full Text | Google Scholar