Optical remote spectral acquisition of elemental stoichiometry

Reeves, Jamie T.; Hasnain, Sarah S.; Nessel, Mark P.; Talbot, Ceara J.; Thomson, Eleanor R.

doi:10.3389/fevo.2024.1505125

REVIEW article

Front. Ecol. Evol., 24 December 2024

Sec. Chemical Ecology

Volume 12 - 2024 | https://doi.org/10.3389/fevo.2024.1505125

This article is part of the Research Topic Advances in Ecological Stoichiometry View all 4 articles

Optical remote spectral acquisition of elemental stoichiometry

Eleanor R. Thomson⁶

¹Department of Integrative Biology, Oklahoma State University, Stillwater, OK, United States
²Department of Biology, Hacettepe University, Ankara, Ankara, Türkiye
³Integrated Sciences and Mathematics, Habib University, Karachi, Sindh, Pakistan
⁴Department of Natural Resource Ecology and Management, Oklahoma State University, Stillwater, OK, United States
⁵Carnegie Science Division of Biosphere Sciences and Engineering, Pasadena, TX, United States
⁶Environmental Change Institute, University of Oxford, Oxford, United Kingdom

Optical remote sensing (RS) enables the study of the elemental composition of Earth’s surface over broad spatial extents by detecting reflected electromagnetic radiation. Covalent bonds of macromolecular structures often reflect electromagnetic radiation at specific wavelengths, and in some cases relate to bonds of specific elemental identity. In other cases, interfering optical properties greatly impact the ability of RS to measure elements directly, but advances in statistical methods and the theoretical understanding of optical properties expand the capacity to quantify diverse elements in many systems. When applied under the framework of ecological stoichiometry, spatially and temporally explicit measurements of elemental composition permit understanding of the drivers of ecological processes and variation over space and through time. However, the multitude of available technologies and techniques present a large barrier of entry into RS. In this paper we summarize the capabilities and limitations of RS to quantify elements in terrestrial and aquatic systems. We provide a practical guide for researchers interested in using RS to quantify elemental ratios and discuss RS as an emerging tool in ecological stoichiometry. Finally, we pose a set of emerging questions which integrating RS and ecological stoichiometry is uniquely poised to address.

Introduction

Ecological stoichiometry seeks to understand the drivers of ecological patterns by studying the flux of chemicals and energy within organisms and ecosystems. Research in this field focuses on how the elemental composition of organisms and their environment influences biological processes and how these processes scale to higher levels of organization. Originally proposed by Sterner and Elser (2002), ecological stoichiometry bridges the gap between individual organismal physiology and broader ecological processes to understand how elemental imbalances drive growth, reproduction, and survival of individual organisms and how in turn, the life-history of these organisms affect the nutrient availability, biogeochemical cycling and productivity across ecosystems. The Redfield ratio, for instance, is a specific, widely observed ratio of carbon, nitrogen, and phosphorus (C:N:P) in marine phytoplankton (106:16:1), and deviations from this ratio indicate nutrient limitation and altered oceanic biogeochemical processes (Redfield, 1958). Ecological stoichiometry has been applied across diverse ecosystem types and levels of biological organization, from terrestrial vegetation-soil interactions (e.g., Zeng et al., 2016) to whole lake food webs (e.g., Elser et al., 2000).

Ecological stoichiometry continues to grow in importance as environmental change, such as eutrophication and shifts in climate, increasingly disrupts the elemental balances that sustain ecosystems. Yet traditional methods of quantifying elemental ratios, mainly chemical analysis from point samples, present significant logistical challenges when applied to large-scale analyses. Optical remote sensing (RS) provides a powerful alternative, enabling the study of ecological stoichiometry across spatially continuous gradients and through time. Using sensors mounted on satellites, rotary or fixed-wing drones, RS captures electromagnetic radiation emitted by the sun and reflected from the Earth's surface (Figure 1). Patterns of absorption and transmission across the visible to short-wave infrared spectrum (400–2500 nm) provide information about the physical and chemical properties of the Earth's surface. Understanding the relationship between the spectral properties of plants, soils and their elemental composition has a relatively long scientific history (Gates et al., 1965; Knipling, 1970). Specific reflection and absorption features in these wavelengths have been directly linked to a leaf’s concentration of cellulose, lignin, chlorophylls, nitrogen, starch, oils, proteins, and water (Curran, 1989). For example, N in leaves, bound in chlorophyll and proteins, is associated with specific wavelengths in the visible to near-infrared (NIR) regions (460–480 nm, 650–670 nm, and 1510–1600 nm; Kokaly, 2001; Smith et al., 2003). Similarly, soil moisture content produces strong absorption features in the short-wave infrared region, particularly at 1400 nm, 1900 nm, and 2200 nm, while high levels of soil organic matter results in lower reflectance at 1700 nm and 2100–2300 nm, linked to the presence of carbon-based compounds (Hunt and Salisbury, 1971; Ben-Dor et al., 1997).

Figure 1

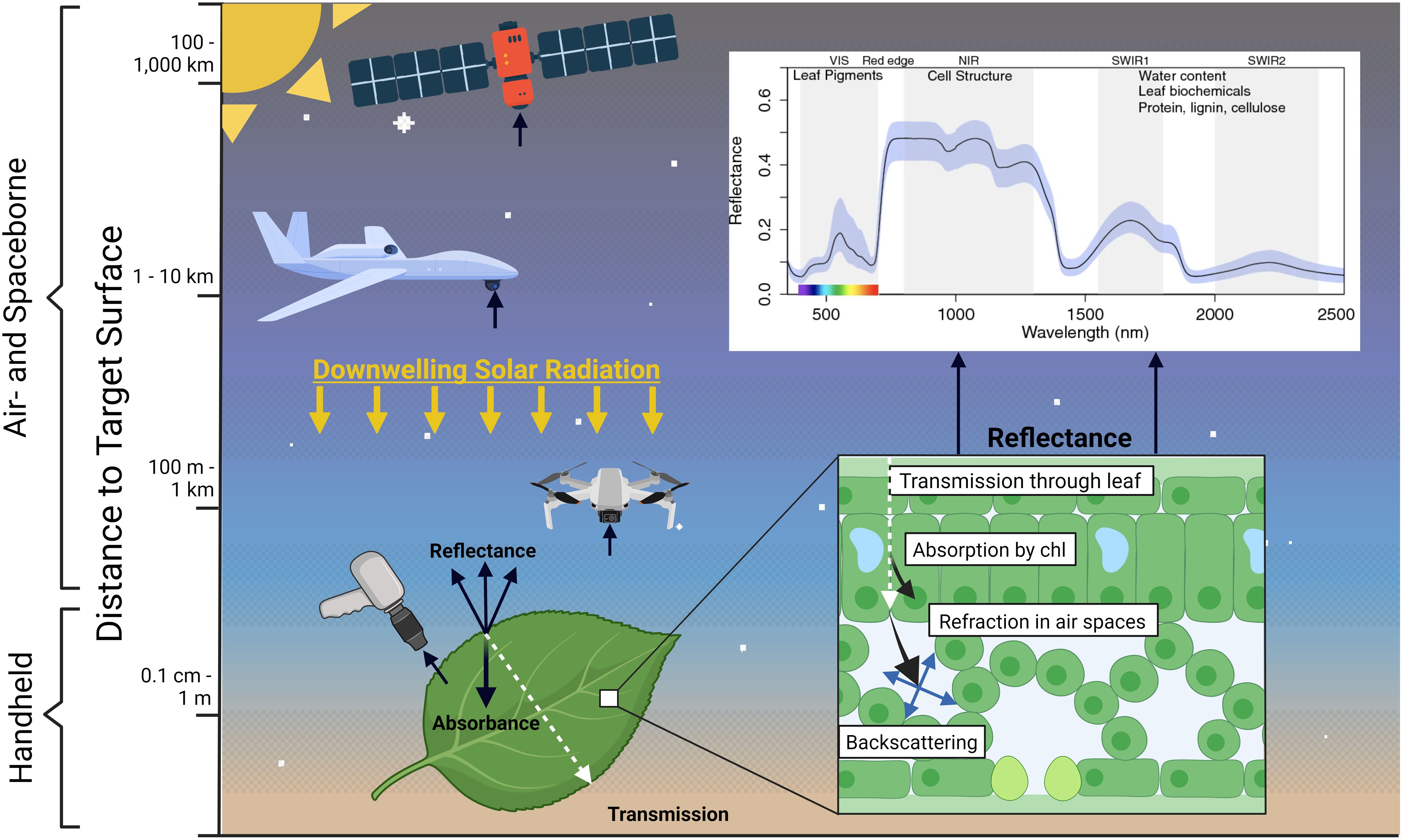
Figure 1. Conceptual diagram depicting light-matter interactions in a leaf and detection by remote sensing platforms. Created in BioRender: BioRender.com/c66i213. Platform image from Adobe Stock. Spectra adapted from Figure 1a in Li et al. (2023), published under Creative Commons license (https://creativecommons.org/licenses/by/4.0/).

By analyzing ecological samples for nutrient content, statistical models can link the spectral reflectance of samples directly to elemental composition. When applied to each pixel across an image, these models can scale up point samples (known as ‘ground truth measurements’) to create spatially continuous maps displaying elemental composition across both space and time. Maps of plant, soil and water elemental composition produced using RS span local to global scales (e.g., Aguirre-Gutiérrez et al., 2021; Asner et al., 2016; Song et al., 2023; Switzer et al., 2003), driving insights across ecosystems. Detailed maps (spatial resolution 0.05 – 5 m) of plant C, N, P, as well as lesser-studied elements such as calcium, potassium, magnesium and sodium reveal patterns of nutrient distribution across temperate and tropical forests (Loozen et al., 2020; Thomson et al., 2018), African savannah (Mutanga and Kumar, 2007), grasslands (Rakotoarivony et al., 2024) and agricultural systems (e.g., Costa et al., 2022; Blekanov et al., 2023). Similarly, soil elemental maps and maps of chlorophyll-a and suspended sediment in water bodies increase understanding of how stoichiometric constraints shape ecosystem function (e.g., Zhang et al., 2019; Tanioka et al., 2022). Monitoring change in elemental composition through time enables insights into seasonal changes (e.g., van Deventer et al., 2015), climate-driven environmental shifts (e.g., Calizza et al., 2022) and pollution events (e.g., Choe et al., 2008; Singh, 2024).

Growing public and commercial availability of imagery and continuing technological advancements supports the development of remote sensing for ecological stoichiometry. Yet, RS remains underutilized in ecological stoichiometry. While the number of RS publications has increased significantly over the past two decades, only a modest number of studies apply RS techniques directly to ecological questions, indicating a significant gap in integration between these fields (Pettorelli et al., 2014). Most RS research tends to be methodological, often published in specialized remote sensing journals rather than in ecology or stoichiometry-focused journals, limiting the exposure of ecologists to these tools. Consequently, many ecologists are unfamiliar with how to effectively apply RS in their research. While there is an increasing amount of open-source technology, and accompanying user guides to help researchers wishing to use optical RS, knowledge of which imagery to acquire, what ground-truth data to collect, and how to combine the two often constitute a high barrier to entry into this field (Schmidtlein et al., 2012). However, leveraging RS to scale up findings from localized studies is essential to test ecological stoichiometry theories across broad spatial and temporal scales. Addressing the integration of RS as a practical tool within the field of ecological stoichiometry is therefore fundamental for furthering stoichiometry research in an era shaped by environmental change (Buchhorn et al., 2020).

The goals of this work are to: 1) Discuss the current capabilities and limits of RS to quantify elements across terrestrial and aquatic systems, 2) Provide a practical guide for applying RS to study ecological stoichiometry at broad extents, and 3) Suggest future research avenues employing RS to advance the field of ecological stoichiometry.

Current capabilities and limitations

Terrestrial ecosystems

The first applications of RS in terrestrial stoichiometry began with handheld spectrometers to measure the spectral reflectance of vegetation and soils in the field. Early spectroradiometric research details how absorption features across the electromagnetic spectrum relate to specific covalent bonding dynamics, like stretching or bending in the C - H bonds in starch, or N - H bonds of protein (e.g., Baumgardner et al., 1986; Curran, 1989; Fourty et al., 1996), and how these spectral features are useful in deriving elemental concentrations (e.g., C or N). The launch of Landsat in 1972, the first satellite-based multispectral sensor, marks the beginning of large-scale environmental mapping, with foundational spectroradiometric research applied to Landsat images to map the ecological stoichiometry of natural ecosystems, soils, and agricultural systems. In 1986, the first imaging spectrometer mounted on a NASA aircraft, with 224 spectral bands, improved both spectral and spatial resolution of optical imagery and facilitated production of high resolution maps of forest elemental composition (e.g., Townsend et al., 2003). However, aircraft-mounted sensors are unavailable to most researchers, whereas the miniaturization of optical sensors and the rise of drones supports the democratization of high-resolution imagery, allowing researchers greater flexibility to study diverse ecosystems and elements.

Leaf N is a key element frequently measured in terrestrial ecosystems due to its influence on photosynthetic pigments, detectable through the red edge and NIR portions of the spectrum (Wessman et al., 1988; Curran, 1989; Fourty et al., 1996; Curran et al., 1997; Martin and Aber, 1997; Kokaly et al., 2009). Leaf C is derivable through its effect on leaf structure components such as cellulose, starch, and lignin (Peterson et al., 1988; Martin and Aber, 1997; Serrano et al., 2002; Wang et al., 2015; Buitrago et al., 2018; Féret et al., 2021). Alternatively, leaf P is present mostly in energetic and genetic molecules (e.g., NADPH and DNA), and low P concentrations typical of leaves do not directly relate to leaf chromophores (Porder et al., 2005; Mutanga and Kumar, 2007; Homolová et al., 2013; Mandelmilch et al., 2021). However, methods which quantify P using indirect spectral chromophores in the NIR-SWIR regions demonstrate relatively high accuracy (R² = 0.54 – 0.96) in spectral P prediction (Mandelmilch et al., 2021). Previous research suggests that water and canopy structure affect P quantification via detection of indirect chromophores, especially in SWIR regions, and that methods accounting for the spectral influence of water and structure perform better than those which do not (Porder et al., 2005; Mutanga and Kumar, 2007; Knox et al., 2011; Homolová et al., 2013; Houborg et al., 2015; Mandelmilch et al., 2021).

Many RS approaches to quantify plant elemental composition originate from agricultural studies, as nutrient management is critical for optimizing yield and sustainability, making accurate nutrient measurement a priority (Haboudane et al., 2004; Huang et al., 2021; Lu et al., 2021). Under laboratory conditions, Pandey et al. (2017) found good-to-high prediction accuracy (R² > 0.60-0.92) between maize and soybean spectra and leaf N, P, potassium (K), magnesium (Mg), calcium (Ca), sulfur (S), iron (Fe), manganese (Mn), copper (Cu), and zinc (Zn) content, but poor prediction accuracy (R² < 0.3) for boron (B) and sodium (Na). In monocultural settings, where plant species are homogeneous, changes in spectral signatures are potentially attributable to differences in elemental content. However, in more natural ecosystems, the diversity of plant species presents challenges for researchers. Across 96 tropical forest species, Asner et al. (2011) found satisfactory-to-good prediction accuracy (R² = 0.4 – 0.77) between leaf spectra and leaf N, P, C, soluble C, K, Ca, Mg, B and Fe but poor prediction accuracy (R² < 0.3) for Zn and Mn. See Table 1 for a comprehensive list of target ecological elements retrieved from RS.

Table 1

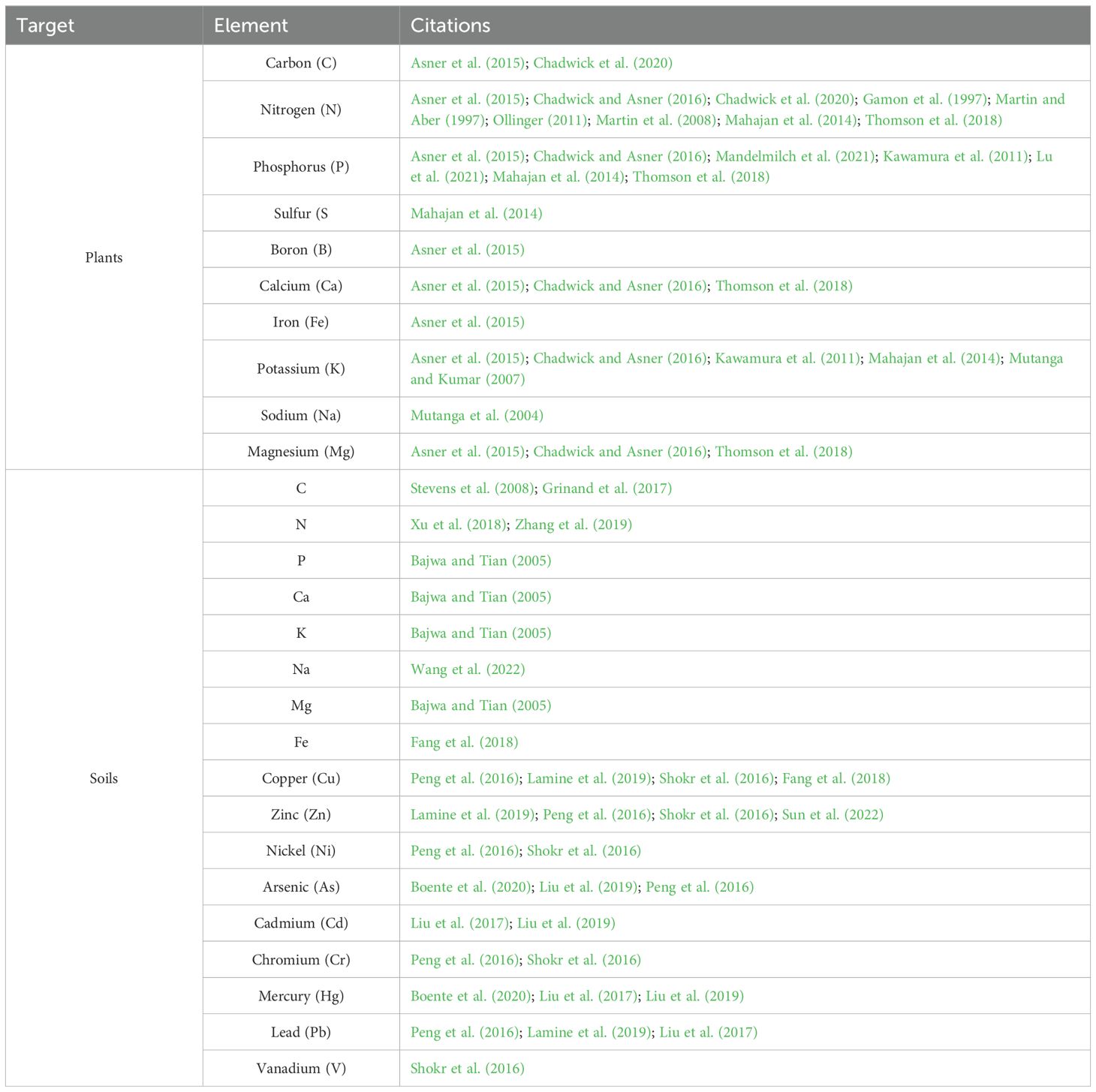
Table 1. Select examples of terrestrial studies demonstrating the capacity to quantify diverse elements.

Most remote sensing studies tend to focus on the retrieval of individual elements rather than element ratios. While ratios are a major focus of ecological stoichiometry, single-element estimates are essential precursors to calculating stoichiometric ratios. Some studies successfully extract plant C:N ratios from RS imagery (e.g., Thomson et al., 2021). However, combining remotely-sensed elements to form ratios requires that models of each element are independent of each other and do not rely on the same correlator (e.g., similar wavelengths) for predictions (Porder et al., 2005). Many aspects of leaf structure and canopy organization similarly relate to patterns of nutrient allocation, and separating the individual influences of elements on spectra (e.g., to measure stoichiometry) thus requires great care (Ollinger, 2011; Mandelmilch et al., 2021).

Scaling up spectra-element models with satellite and airborne imagery, spatially continuous maps of foliar chemistry reflect spatial gradients in temperature (Moreno-Martínez et al., 2018), precipitation (Thomson et al., 2018), soil type (Asner et al., 2016; 2017) and species (Gholizadeh et al., 2022). These maps improve the accuracy of ecosystem models by providing spatially explicit data on key nutrients. RS-derived data inform models of primary productivity and nutrient cycling across landscapes by integrating maps of plant nutrients and associated functioning into large-scale biogeochemical models (Yang et al., 2015; Wieczynski et al., 2022). Despite the large potential for RS to improve biogeochemical modeling estimates, more work in this area is required (Abraham et al., 2023).

Across exposed soils, RS techniques commonly measure properties such as mineral composition, texture, iron content, moisture levels, organic carbon, salinity, and carbonate concentrations (Mulder et al., 2011). Studies of soil chromophores, such as iron oxides, clay, carbonates, water, and soil organic carbon (SOC), demonstrate strong relationships between these components and optical soil reflectance, and relationships between reflectance and many mineral and pollutant elements in soils show promising performance (Ben-Dor et al., 1997, 1999; Gomez et al., 2012; Castaldi et al., 2016; Yu et al., 2020). RS retrieval of soil properties displays better performance at local and regional scales, particularly when soils are exposed, and vegetation cover and moisture levels are minimal (Escribano et al., 2017).

One significant constraint is that RS captures only the surface of ecosystems, such as the canopy layer in forests, while leaving the understory unsampled, where distinct stoichiometric dynamics may occur (e.g., Martin et al., 2020). Similarly, in soils, optical remote sensing detects only surface strata, often missing deeper layers where nutrient cycling, microbial activity, and elemental dynamics may differ (Hagen-Thorn et al., 2004; Mulder et al., 2011; Hengl et al., 2017). Radar-based remote sensing penetrates deeper into forests and soils but is limited in its ability to provide stoichiometric data, as it measures physical structure rather than elemental composition. In densely vegetated areas, inferring below-ground stoichiometry from aboveground optical data remains a challenge (Cavender-Bares et al., 2022; Rakotoarivony et al., 2024) and typically relies on indirect retrievals using soil indicators, such as plant functional groups as proxies (see Escribano et al., 2017 and Mulder et al., 2011 for a review).

Links between the stoichiometry of producer organisms (plants and soils) and consumers (animals) remains an area relatively unexplored using remote sensing. Animals play a key role as vectors of nutrients across landscapes, and mediate biogeochemical processes through their influence on NPP, ecosystem structure and soil physical and chemical properties. Remote sensing may therefore quantify zoogeochemical effects (Schmitz et al., 2018; Abraham et al., 2023). Some work uses active remote sensing, particularly LiDAR, to assess animal impacts on ecosystem structure and carbon stocks (e.g., Petersen et al., 2023; Davies and Asner, 2019; Russo et al., 2023), but fewer studies employ optical remote sensing to study the impact of animals on ecological stoichiometry. Exceptions include Thomson et al., 2021, who investigated the impact of seabird guano on plant nutrient status and Román et al., 2023, who investigated the effect of penguin guano on vegetation chlorophyll production. Thus, there remains a significant gap in understanding how spatial variation in producer stoichiometry cascades through ecosystems and how consumer behavior feeds back to producer stoichiometry, which RS is well-suited to address. Previous efforts to investigate these relationships link the distribution of consumers to resource stoichiometry (see Leroux et al., 2017; Hurley et al., 2014 and Pettorelli et al., 2011 for a review), but more work is needed to directly link remotely-sensed stoichiometric data to animal distributions, performance, and subsequent patterns in ecosystem function (Ellis-Soto et al., 2023; McLeod et al., 2024).

Aquatic ecosystems

The theoretical basis of RS does not differ between terrestrial and aquatic systems, allowing for elemental measures to be derived from several optical targets in water (Table 2). However, differences in the optical properties of fluid and gaseous media, and the ability to isolate image targets from media, greatly influence which elements may be quantified and which methods are successful in each system. In aquatic systems, Radiative Transfer Theory is used to mathematically model how electromagnetic radiation interacts with water and its constituents (e.g., sediments, plankton, dissolved organic matter, etc.) to estimate inherent optical properties (IOPs) and apparent optical properties (AOPs) (Mobley, 1994). These models, known as Radiative Transfer models (RTMs), simulate the absorption and scattering, estimate light propagation, and account for reflection and refraction at the surface-water interface (more details provided in Dickey et al., 2006). RTMs are used to estimate IOPs from AOPs with specific environmental parameters, i.e., direct models, and estimate the spatial and temporal structure of IOPs from normalized spectral water leaving radiance, i.e., inverse models (Dickey et al., 2006). Relationships between IOPs and AOPs can collapse during periods of low sun angle, high concentration of bubbles, and high densities of reflective organisms (e.g., coccolithophores and coccoliths) (Stramska and Frye, 1997; Zhang et al., 1998; Zheng et al., 2002).

Table 2

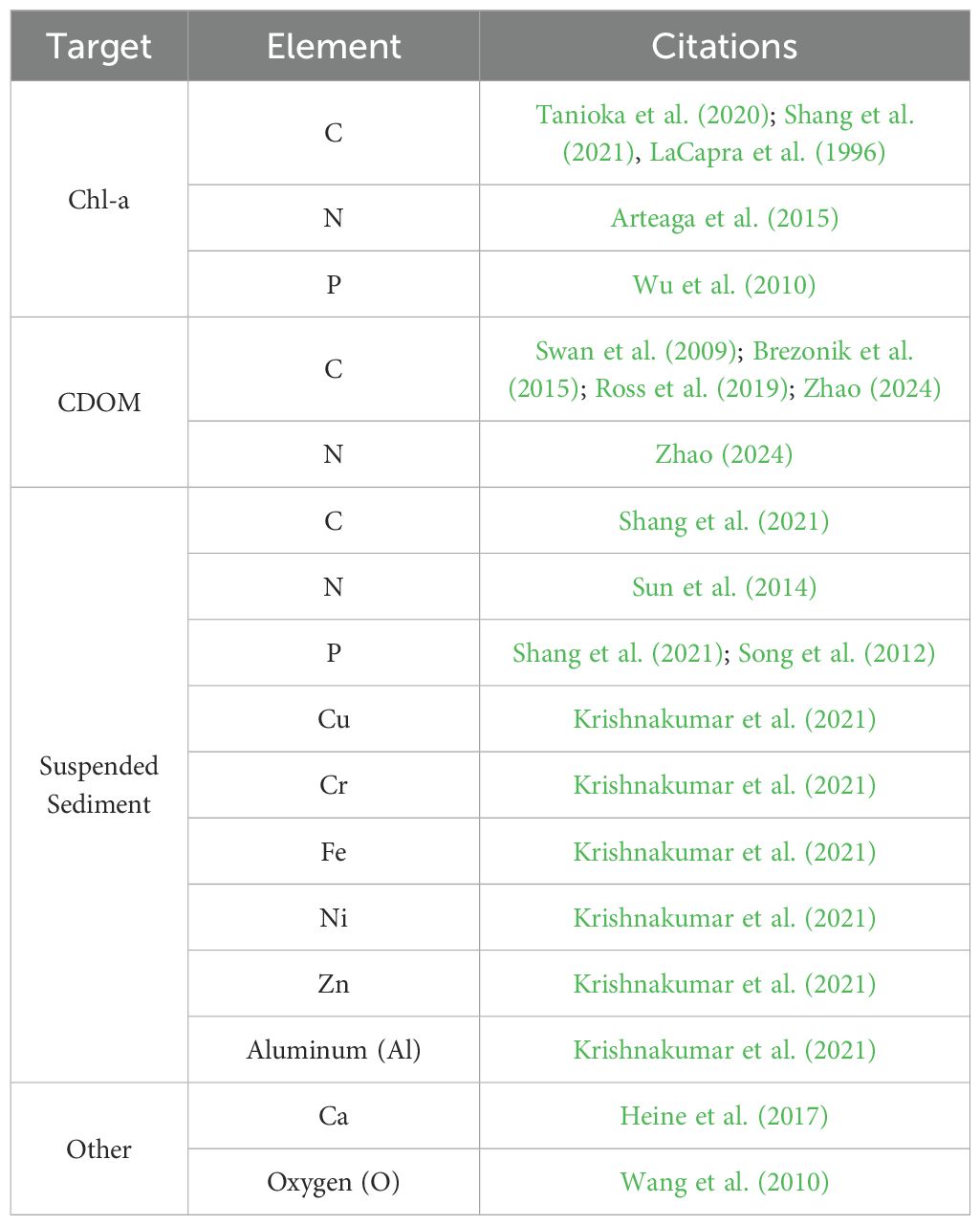
Table 2. Select examples of aquatic studies demonstrating the capacity to quantify diverse elements.

Based on AOPs, aquatic systems are classified into two categories: Case 1 and Case 2. Case 1 primarily consists of the open ocean, while Case 2 waters tend to be shallow coastal and inland waters, where optical properties capture phytoplankton (as Chlorophyll-a), CDOM, and detritus (Wei et al., 2022). In Case 2 waters, suspended particles, minerals, CDOM, and microbubbles impact spectra, and it is more challenging to spectrally detect biological and chemical properties. Many inland freshwater systems are small and spatially complex, requiring moderate to small pixel sizes, although RS of large lakes is feasible with coarser resolution, satellite data (Hestir et al., 2015). It should be noted that Case-1 and Case-2 waters reflect broad categorization of optical properties of diverse water bodies. Recent work has formally classified water bodies globally into 13 distinct optical water body types based on specific combinations of bio-geo-optical characteristics that maximize differences in the spectral shape and magnitude of RS reflectance (Spyrakos et al., 2018; Neil et al., 2019).

Chlorophyll-a (Chl-a) is often used as a proxy for phytoplankton production in aquatic ecosystems and is one of the most optically active variables across systems (Blondeau-Patissier et al., 2014). Primary producers assimilate C from the atmosphere into biomass, supplying energy for consumers and substrate for C burial in sediments (Pacheco et al., 2014). With the advent of satellite-based hyperspectral sensors, algorithms that utilize the entire spectral reflectance range can provide more accurate estimates for Chl-a as compared to multispectral and IOP inversion methods (Zhou et al., 2014; Pahlevan et al., 2021). Further enhancements are expected in the spectral capability to estimate primary production across aquatic ecosystems with the launching of NASA’s Plankton, Aerosol, and Cloud Ecosystem (PACE) this year (NASA 2024). Despite the large amount of work demonstrating that optical properties enable and limitations constraining quantification of Chl-a in aquatic systems, obtaining stoichiometric information from Chl-a is challenging. There are no direct methods for estimating C, N, P or other elements from spectral responses and concentrations of these elements must derive from models (i.e., RTMs) combining Chl-a concentrations with other environmental variables (e.g., sea surface temperature).

Dissolved organic matter (DOM) contains autochthonous and allochthonous detritus, as well as allochthonous refractory material from melting permafrost and pyrogenic (black) carbon, and DOM plays a critical role in the global C cycle (Battin et al., 2008; Dittmar and Paeng, 2009; Dittmar et al., 2012; Coppola et al., 2022; Kong et al., 2024; Ruben et al., 2024). Chromophoric dissolved organic matter (CDOM) is an optically measurable portion of DOM in aquatic ecosystems (Brando and Dekker, 2003), which impacts chemical, physical, and biological processes in the water column. Waters with high CDOM concentrations tend to appear colored and can look green-yellow or brown (Aiken et al., 1985). A summary of the various spectral bands and measurements used for remotely estimating CDOM is provided by Gholizadeh et al. (2016). In contrast to pure water, CDOM absorbs short wavelengths of solar radiation (Brezonik et al., 2015). CDOM is particularly rich in C but contains other elements in abundance as well (e.g., oxygen, hydrogen, N, S, and P; Xenopoulos et al., 2021). Shifts in the optical properties of CDOM have been linked to variation in nutrient concentrations (e.g., N, P; Shang et al., 2021), but relationships between CDOM absorbance and nutrient concentrations are rarely used for predicting nutrient concentrations (Zhao, 2024). However, CDOM composition is optically apparent in a lab setting (Nebbioso and Piccolo, 2013), suggesting that RS could be used to obtain the quantities and ratios of elements in CDOM.

Particulate matter from terrestrial landscapes is exported to aquatic ecosystems and tends to settle in lentic and coastal areas or remain suspended in lentic or riverine systems (i.e., Case 2 waters). Deriving suspended particulate matter concentrations for Case 2 waters requires water body depth to account for impacts from the bottom of water bodies on spectra and local calibration to achieve adequate accuracy (Volpe et al., 2011). Single band and computational ratio algorithms can be used to estimate suspended sediment concentration (Baruah et al., 2002). Turbid, sediment-rich water tends to be rich in C, nutrients, and heavy metals (e.g., Fe, chromium (Cr), Ni, Al, Cu, Zn). Although optical properties of individual elements may be obscured, relationships between sediment and elements (e.g., regression models) based on land use can be used to infer elemental concentrations from spectra detecting suspended sediment.

From optically active constituents, elements can be estimated using modeled relationships. For C, estimates can be derived by models accounting for the various carbon species available in Chl-a, CDOM, and suspended sediments. For CDOM, the largest portion of C is represented by Dissolved Organic Carbon (DOC) (Mohseni et al., 2022). Estimation of DOC is highly dependent on optical water type, for example DOC concentrations in the open ocean are low and consistent (Mohseni et al., 2022) and highly variable in coastal and inland waters (Liu et al., 2014). Correlations between CDOM and DOC are stronger in Case 1 waters (Ferrari, 2000; Del Vecchio and Blough, 2004; Guéguen et al., 2005; Fichot and Benner, 2012) as compared to Case 2 waters. Consequently, satellite-derived CDOM may be used to estimate DOC concentration but is most reliable in the ocean, followed by coastal (Liu et al., 2013; Swan et al., 2009; Matsuoka et al., 2013) and inland waters (De Stefano et al., 2022). Particulate Organic Carbon (POC) can be estimated from Chl-a and suspended sediments using models and algorithms that combine in-situ measurements with multispectral satellite data (Son et al., 2009; Huang et al., 2017; Jiang et al., 2019; Stramski et al., 2022). For Case 1 waters, particulate inorganic C can be estimated from coccolithophore biomass, a halophyte phytoplankton group with strong backscattering properties, using quantitative algorithms (reviewed by Balch and Mitchell, 2023).

While the macromolecular content of phytoplankton protein, carbohydrate, and lipid can be determined from Chl-a (Roy, 2018), only C:P ratios have been estimated using optical RS products. Tanioka et al. (2020) derived phytoplankton growth rates, chlorophyll to C ratios for cyanobacteria, Synechococcus linearis, and nutrient depletion temperatures from a phytoplankton stoichiometry model, which is combined with remotely sensed estimates of Chl-a and POC. This method can be extended to estimate C:N ratios for Case-1 waters globally. There is potential for a similar approach to be used for assessing stoichiometric ratios for other important elements in marine ecosystems such as Ca, Si, Fe, Cd, and Ni.

N and P are macro-elements driving phytoplankton production in freshwater and marine ecosystems. Both of these elements are non-optically active and cannot be directly quantified from spectral reflectance (Wang et al., 2022). However, Total N (TN) and Total P (TP) are highly correlated with optically active constituents such as suspended sediments, Chl-a, CDOM, and Secchi Disk depth (e.g., Song et al., 2012; Arteaga et al., 2015; Shang et al., 2021). The dependence of both N and P on other parameters is a primary limitation on the capacity to study aquatic ecological stoichiometry using RS, as these methods explicitly or parametrically fix stoichiometry. Hyperspectral satellite missions tuned for aquatic systems (e.g., NASA PACE) improve detection of organismal and community traits relevant to nutrient dynamics (e.g., phytoplankton absorption, pigments, community composition, C, etc.) (Cetinić et al., 2020), but the non-optical nature of aquatic N and P remains a primary obstacle to quantifying N:P stoichiometry using remote sensing.

Previous work applies various retrieval models to estimate N and P, ranging from statistical methods to those employing machine learning and deep learning techniques (Li et al., 2022; Siriwardana et al., 2024). Statistical methods retrieve optically active parameters (e.g., Chl-a, CDOM) using spectral reflectance which is corrected for atmospheric interference using high precision algorithms (Li et al., 2022). Only a few studies focus on the retrieval of TN and TP from RS data, primarily from Case 2 inland waters (Song et al., 2012; Liu et al., 2015; Yu et al., 2016; Soomets et al., 2022; Zhong et al., 2024). Due to light reflection from the substrate in shallow waters (e.g., Case 2 coastal regions) estimating N and P can be problematic and validation requires in-situ data (Gholizadeh et al., 2016). In Case 1 waters, recent work in the North-Eastern Baltic Sea and Bohai Sea provides accurate estimates of TN and DIN (Yu et al., 2016; Soomets et al., 2022), and Zhong et al. (2024) provide first estimates of global Sea Surface Nitrate (SSN) using physical variables such as Sea Surface Temperature (SST), Mixing Depth (MD), Photosynthetically Active Radiation (PAR) along with RS sensed Chl-a.

Practical user guide

As ecological RS is highly interdisciplinary, communication of emergent techniques and best practices must be inclusive and ongoing. In this section, we present a practical guide designed to help readers navigate a typical remote sensing workflow. This guide aims to assist in selecting appropriate sensors, understanding the importance of ground-truthing to validate remote sensing findings, as well as highlight essential considerations when scaling up models to create spatially continuous maps. By synthesizing best practices, we aim to equip researchers with the knowledge they need to successfully integrate remote sensing into their ecological research endeavors.

Choosing imagery

When selecting imagery to study ecological stoichiometry, it is important to consider the spectral resolution, spatial resolution, spatial coverage, temporal resolution, temporal record and costs associated with a chosen imagery source (Figure 2; Table 3). Incoming solar radiation interacts with the optical properties of surfaces and is reflected back into the atmosphere (Figure 2.1) (Ustin and Gamon, 2010). The spectral resolution of a sensor defines the number and width of spectral bands captured by the sensor and thus which elements or target features can be captured at what accuracy. The spatial resolution dictates the level of detail in the imagery crucial for observing fine-scale features, while spatial coverage determines the extent of the landscape covered. Temporal resolution (or revisit time) is the frequency at which imagery is captured, which is essential for monitoring changes over time, such as seasonal variations or rapid environmental shifts. The temporal record refers to the duration over which a sensor has been capturing data, which determines how far back in time changes can be detected. The monetary cost may play a critical role in determining which data sources are feasible; although many freely available platforms exist, higher spatial and spectral resolution and more frequent data often come at a higher cost. Balancing these factors with the system and elements in question, and the scale at which target features exist, will help select the most appropriate and cost-effective imagery for your research needs.

Figure 2

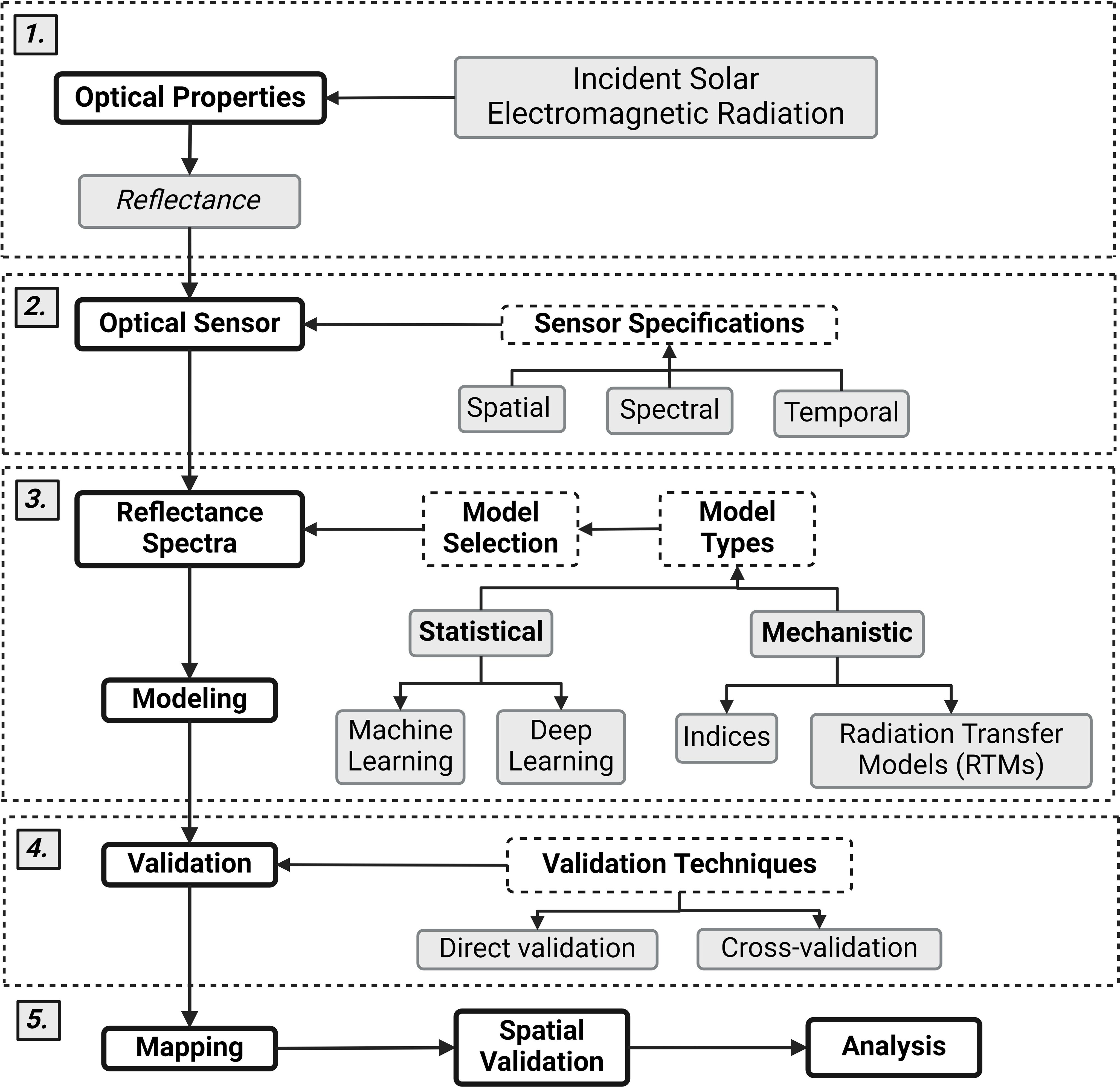
Figure 2. Flow diagram connecting (1) the reflectance of solar electromagnetic radiation to (2) the specifications of optical sensors, (3) modeling frameworks, (4) model validation, and (5) mapping. Created in Biorender. BioRender.com/a76q686.

Table 3

Table 3. Specifications of available imagery platforms (non-exhaustive).

Spectral resolution

Imagery can be single-band, single-band panchromatic (i.e., covers the entire visible spectrum), RGB (three spectral bands: red, green, and blue), multispectral or hyperspectral (Figure 2.2). Generally, multispectral and hyperspectral imagery is well-suited for quantifying elemental composition of targets. Multispectral imagery captures a broad range of wavelengths, typically 4 to 12 bands, including both visible and infra-red (NIR and SWIR) regions. The NIR region (~750 to ~1,300 nm) contains a large amount of ecological information and allows for insights beyond the capabilities of the human eye. For example, reflectance in the NIR region relates strongly to plant N status, and a thorough body of work details several spectral strategies for quantifying plant N (e.g., Kokaly, 2001; Smith et al., 2003; Kanke et al., 2012). Fewer multispectral platforms contain bands in the SWIR region (~1,300 - 2,500 nm), but this region is rich in information related to the water and mineral content of many targets, particularly soil (Hunt and Salisbury, 1971; Ben-Dor et al., 1997). Most freely available and commercial satellites offer multispectral imagery, and there are many options to purchase integrated multispectral drone systems (Table 3). Thus, multispectral imagery is relatively easily accessible for researchers.

Hyperspectral imagery, or imaging spectroscopy, detects radiation continuously in hundreds of narrow spectral bands across the electromagnetic spectrum and allows for the detection of subtle differences in material composition and chemistry. Hyperspectral imagery has been used to retrieve the elemental composition of terrestrial and aquatic systems at high accuracy (Pandey et al., 2017; Asner et al., 2015). However, the decrease in bandwidth resulting from an increase in spectral resolution decreases the signal-to-noise ratio in all bands and may make it more challenging to accurately retrieve spectral properties, especially under low-light conditions or in areas with high atmospheric interference (Castaldi et al., 2016). There are a handful of hyperspectral satellites already in operation, including PRISMA, EnMAP and DESIS, with more planned for launch (e.g., HyspIRI, Tanager, CHIME and SHALOM). Recently, there have also been some hyperspectral drone sensors coming to market (e.g., Headwall Micro-Hyperspec, Cubert UHD and 185-Firefly).

The decision of which spectral resolution is best suited for the research question must be informed by which wavelengths are likely to correspond to the IOPs of a given material or organism. Thus, exploring the spectroscopy literature of the target feature is useful for identifying the specific absorption features and relevant spectral bands for the study’s objectives. While it is tempting to pick imagery at the highest spectral resolution, increasing spectral resolution linearly increases file size and processing requirements. Despite the clear advantage of increased spectral resolution, it has been shown that many of the current limitations to the optical RS of vegetation properties are not related to spectral resolution (Thomson et al., 2021). Instead, improving the collection and georeferencing of ground-truthed data may increase feature retrieval accuracies more than increasing the number of spectral bands.

Spatial resolution and coverage

The spatial resolution of optical imagery determines the level of detail that can be captured and varies widely among providers (Table 3; Figure 2.2). Simply, the ‘spatial resolution’ is the length of one side of a pixel in a given image. Deciding spatial resolution requirements depends on the size of your target feature. For example, delineating individual tree crowns generally requires imagery of < 5 m, while identifying individual alpine plants would require imagery < 10 cm. Satellites often have different spatial resolutions for different bands. Pansharpening is a process that combines a high-resolution panchromatic band with the lower-resolution multispectral bands to enhance the spatial resolution of the multispectral bands. Commercial satellite imagery can often be bought pansharpened. It is important to note that there is a quadratic relationship between spatial resolution and file size, so when the spatial resolution is doubled, the size of the imagery file increases by approximately four times.

The spatial coverage of imagery varies significantly depending on the platform used. Satellite images typically span hundreds or thousands of kilometers, making them ideal for regional or global monitoring. Aircraft imagery, on the other hand, can range from local (e.g., 10s of km, AVIRIS) to country-wide coverage (e.g., Bluesky/Vexcel). Drones offer the most localized spatial extent, making them suitable for small-scale, high-resolution studies. The extent of drone imagery depends on the type of drone. Fixed-wing drones can cover larger areas in a single flight (~100 ha) due to their energy-efficient design, making them ideal for surveying extensive fields or landscapes. Rotary drones (e.g., quadcopters) provide more flexibility in maneuvering and hovering, but they typically cover smaller areas (>10 ha) due to their shorter flight times and lower speeds. In general, there is a trade-off between spatial resolution and coverage, with higher altitude platforms covering more area but at a lower spatial resolution.

Temporal resolution and record

Temporal resolution (or revisit time) is important for change-over-time studies, such as investigating seasonal variations, the impact of climate change or the effect of events such as wildfires or pollution (Figure 2.2). Satellites orbit the earth with a set frequency, and imagery collected at regular intervals supports the study of temporal patterns in ecological stoichiometry at broad extents. Public platforms provide regular imagery for the globe, while most commercial satellites do not image the entire globe but operate on a ‘tasking’ basis - only taking imagery that has been requested on a certain time and date and adding the imagery to the archive catalog after a certain amount of time has elapsed. While images are taken on a set schedule, it is important to remember that for satellite imagery, clouds can substantially decrease the number of usable images. In particularly cloudy parts of the world (e.g., the tropics), or in certain seasons, there may only be one or two cloud-free images available. This is where daily imagery collection comes in handy, as it increases the chances of collecting a time-series of cloud-free images with high temporal resolution. The timescale over which your target feature is likely to change, and the likely cloudiness of your study site is a good place to start when considering the required temporal resolution.

The temporal record of imagery constrains how far back in time your analysis can go. While Landsat started in 1972 and is the longest satellite-based optical sensor in operation, most commercial imagery providers have very short temporal records. When selecting imagery, it is important to ensure that the temporal record of your imagery provider aligns with your spatial, spectral and temporal resolution requirements.

Budget

Lastly, decisions on which imagery to use are always constrained by cost. Landsat, MODIS, and Sentinel satellite imagery are available for free, thanks to initiatives like the USGS's free-and-open data policy established in 2008 for Landsat data. Higher spatial resolution and spectral resolution imagery typically incur costs, which can range from approximately $10 to $500 per square kilometer, depending on the provider. While drones can generate a large volume of high-resolution imagery, they come with high fixed costs, including those for the system and sensor themselves, pilot licensure, vehicle registration, and often hefty subscription costs to imagery processing software (Table 3). Ultimately, the choice of imagery provider involves balancing the need for spatial and temporal resolution against budget constraints and project size.

Integrating ground truth data with imagery

Ground truth data refers to real-world information collected through direct observation or measurement, which is used to train and validate the relationship between raw spectra and the target (i.e., element) of interest. In supervised learning, a model is fed input data (imagery) along with corresponding ground truth data (labels), allowing the model to identify patterns and relationships between the imagery and the labeled outputs. For example, ground truth data might involve collecting leaf samples and analyzing leaf N content. The model uses this labeled ‘ground-truthed’ data to adjust its internal parameters during training, improving its ability to accurately predict leaf N concentration from unseen reflectance spectra. When validating models, ground truth data not used in model training can be used to evaluate a model's accuracy by comparing its predictions to the directly observed, or measured, reality (see Model Evaluation section for more information). When planning ground truth data collection, there are two important points to bear in mind; ensuring that ground truthed data is properly matched to imagery in space and time, and that the scale at which ground truth data is collected is appropriate for the spatial resolution of the imagery.

Ground truth data must be accurately matched to imagery in both space and time. Since models are only as good as the data they learn from, inputting poor-quality or incorrectly aligned training data can lead to inaccurate predictions and suboptimal performance. Ensuring precise alignment between ground truth data and imagery is key to parameterizing the relationship between reflectance and physical measurements. When recording the coordinates of ground truth data, the accuracy of your GPS device should align with the spatial resolution of the feature being studied. For instance, a handheld GPS with an accuracy of 5–10 m may be sufficient for marking the location of large areas of monoculture, where a 10 m spatial offset would still fall within the same species/habitat type. However, it would be inadequate for pinpointing tree crowns, where a 10-meter offset could result in recording the location of a neighboring tree rather than the intended one. In more heterogeneous landscapes, or for precise mapping of small features, a differential GPS with an accuracy of 1–3 cm may be required. To improve the matching of ground truth data to imagery, it can be helpful to mark observation or sampling sites that are visible in the imagery itself. Ground-truthed data must also be matched in time. Natural features may change over time due to seasonal variation, human activity, or natural events, so collecting ground truth data at a different time than the imagery could lead to inaccuracies. In some cases, features may change within a matter of hours (for example nutrient loads in water bodies) so swift imagery collection (or ground truth data collection) is vital.

Scaling up ground truth data to match the pixel size of imagery requires careful consideration of both the spatial resolution of the imagery and the detail of the ground truth data. If your ground truth data exists at a finer scale than the imagery’s resolution (e.g., individual tree measurements vs. a 10 m pixel), you will need to aggregate or generalize the ground truth data. For example, instead of using individual leaves, you may need to average the leaves to generate a single value per tree crown. Or instead of using individual tree data, you may need to average data for all trees within the area represented by a 30 m pixel. The most important question to consider is whether your ground-truth data is representative of the likely pixel value. For example, one soil P measurement within a pixel size of 10 m may not be representative of soil P across the entire pixel.

Model selection

When analyzing imagery, selecting the appropriate model depends on your objectives and target prediction(s). Generally, model analysis falls under two categories: mechanistic models (i.e., RTMs and indices), and statistical models, which include machine learning models, and deep learning techniques (e.g., neural networks: Figure 2.3). Mechanistic models are based on underlying physical principles that describe how light interacts with a surface, such as water, vegetation or soil. These models apply general principles of how radiation is absorbed, reflected, or transmitted to generate insights into the physical characteristics of the surface, for example its extent and biochemical properties. Mechanistic models are grounded in fundamental science, often providing interpretable and generalizable results. In contrast, statistical models rely on data-driven approaches to find patterns and correlations in large datasets without necessarily understanding the underlying mechanisms. These models are highly flexible and accurate in prediction (especially locally) but often function as "black boxes" with less interpretability or insight into the processes driving the observed patterns.

Indices are mathematical combinations of spectral bands designed to highlight specific environmental features. These are commonly used for quick, effective analyses, often over large areas. Examples of indices include Normalized Difference Vegetation Index (NDVI), which is one of the most widely used indices. NDVI captures the absorption of red light by chlorophyll and the high NIR reflectance caused by intercellular backscattering of leaves (Figure 1), and values range from -1 to 1, where values closer to 1 indicate healthier, denser vegetation. This index is often applied to monitor forest cover and drought impacts (e.g., Nanzad et al., 2019; Pompa-García et al., 2021). Other examples of indices include Normalized Difference Water Index (NDWI), Soil-Adjusted Vegetation Index (SAVI), and Enhanced Vegetation Index (EVI) for monitoring water content, reducing soil background effects in sparse vegetation areas, and improving sensitivities in regions with dense vegetation, respectively. While these indices are simple and computationally efficient, they can only model linear relationships and may perform poorly in heterogeneous environments. However, they may be a useful starting point for users new to remote sensing approaches.

Machine learning models are useful to identify more complex relationships from multidimensional datasets. Examples of machine learning models used in RS include Partial Least Squares Regression (PLSR), a powerful regression technique that can model mathematical relationships between several independent variables (spectral bands) and a dependent variable (Haaland and Thomas, 1988). PLSR reduces the dimensionality of the data, making it effective in handling multicollinear data from hyperspectral sensors. Random Forest (RF) is an ensemble classification and regression technique that constructs multiple decision trees to produce robust predictions (Breiman, 2001). It's commonly used for land cover classification (e.g., distinguishing between different types of forests, grasslands, and urban areas) as well as for regression tasks. RF handles large datasets well, manages missing data, and can model complex interactions between variables. Support Vector Machines (SVM) is another common machine learning algorithm used for classification tasks, particularly when separating classes with nonlinear boundaries (Cortes, 1995).

Deep learning techniques, particularly those involving convolutional neural networks (CNNs), enable advanced imagery analysis through automated feature detection and sophisticated pattern recognition. For example, neural networks are excellent for handling large and complex datasets like imagery. These models are particularly useful for identifying features and spatial patterns that might not be immediately apparent through traditional pixel-by-pixel analysis techniques. CNNs excel in tasks like segmenting individual trees, mapping roads and rivers or detecting animals in imagery. Neural networks are capable of both classification (e.g., identifying habitat types; Pérez-Carabaza et al., 2021) and regression (e.g., estimating plant nutrient deficiencies; Watchareeruetai et al., 2018). However, neural networks typically require large, labeled training datasets and significant computational resources.

When choosing a model, it may be helpful to consider the difference between classification and regression. Classification is used when the goal is to categorize data into discrete classes, for example different types of vegetation or land use (e.g., forest, grassland, urban areas). In contrast, regression models are used to predict continuous variables (e.g., leaf N) rather than discrete categories. RF, SVMs and neural networks can be applied to both classification and regression tasks, whereas PLSR can only be used for regression.

There are numerous tools and packages that exist to implement and validate models, and spatially map elements. We do not provide a comprehensive list of these due to the large number available across various programming languages and platforms, and constant development of new approaches. Instead, we encourage the reader to refer to practical RS guides in their field (e.g., Moses et al., 2022) or programming language (e.g., Esmaili, 2021; de Carvalho Alves and Sanches, 2023).

Model evaluation

Evaluating the output of mechanistic and statistical models is crucial to ensure that they have accurately captured a mathematical relationship between the input data (e.g., imagery) and the target feature (e.g., leaf N). For both mechanistic and statistical models, this process typically involves dividing data into training and testing sets, followed by applying various evaluation techniques to assess model performance (Figure 2.4). The training set is a subset of data that is used to train the model, allowing it to learn the relationships between input features (e.g., spectral bands) and output variables (e.g., elements). The testing set is a separate subset of data that is used to evaluate the model's performance on unseen data. Cross-validation techniques frequently split and validate data iteratively with a set percentage of observed data held out (e.g., 10 bootstraps with 70% training and 30% testing). This step is essential to determine how well the model generalizes to new data and avoids overfitting (where the model performs well on the training set but poorly on unseen data).

For RS approaches in particular, spatial autocorrelation should be considered in the modeling process (Figure 2.5). Spatial autocorrelation is related to Tobler’s First Law of Geography, which states that "everything is related to everything else, but near things are more related than distant things." This means that environmental variables, such as leaf N tend to be more similar in locations that are close together than in places that are farther apart. However, predictor variables, such as image reflectance values also tend to be more similar in places that are closer together. This creates a challenge in model validation, as nearby observations can be overly similar due to their proximity, violating the assumption of independence and potentially leading to overoptimistic assessment of model predictive power. For example, Ploton et al. (2020) showed how a RF model appeared to show high predictive power of aboveground biomass in Africa but revealed quasi-null predictive power when spatial autocorrelation effects were accounted for. To account for spatial autocorrelation, Ploton et al. (2020), recommend using a spatial cross-validation approach that ensures an observation point cannot serve as an independent validation of a nearby training data point. This involves spatially ‘buffering’ training points so points that are too close together don’t appear in both the training and validation dataset. Spatial buffering or blocking data are especially important in cases where ground truth data is highly clustered in environmental plots (Roberts et al., 2017; Ploton et al., 2020).

Creating spatially continuous maps

Scaling up quantitative models enables the creation of spatially continuous maps of your variable of interest, allowing for landscape-scale analysis and insights. For indices, the relevant equation can be applied to each imagery pixel to generate a map of that index (e.g., NDVI). For machine learning models (including deep learning models) to scale effectively, maps require all predictor variables used to train the spectral - target model to be present across the entire area where predictions are being made (Roberts et al., 2017). Without an input value for each predictor variable, the model cannot produce a unique output value for each pixel. The same applies for RTMs; input variables for all AOPs and IOPs must occur at every pixel for the model to adequately track the transfer of radiation from the surface to the sensor. Scaling over areas which contain insufficient data leads to inaccurate inference, and these areas should be masked (i.e., removed) from analysis.

When scaling up machine learning and deep learning models, caution must be exercised when scaling to ensure that the target area is well-represented by training data. For example, if a model was trained only on specific habitat types, it won’t be able to predict new habitat classes that it hasn't encountered before. For continuous variables, certain models like Partial Least Squares Regression (PLSR) can extrapolate beyond their training data range, meaning they can make predictions even when input values fall outside what the model has previously seen. In contrast, models like RF cannot extrapolate outside the training range, as they rely on decision trees that are strictly based on values encountered in training data. Therefore, selecting the appropriate model for your scaling task is crucial for producing reliable results. Scaling up should be avoided if your model performs poorly in training or validation, as this indicates that it will likely give inaccurate predictions across larger regions. A poorly calibrated or overfitted model may give misleading results when generalized. In summary, scaling up your machine learning model requires maps of all predictor variables over the target area, a model trained on representative data for the target environment, an understanding of your model’s ability to extrapolate, and caution if the model demonstrates poor performance, as scaling will amplify errors across the landscape.

Discussion

From its inception, ecological stoichiometry has been rooted in linking the elemental composition of organisms and the matrix which they inhabit (i.e., water, soil, and air), with their functional roles across ecological scales, from individual physiology to global element cycling (e.g., C, N, P). Over the last 40 years, ecological stoichiometry research has established two key paradigms: the Growth Rate Hypothesis (GRH) and Elemental Homeostasis (EH). The GRH suggests that C:N ratios in organisms are influenced by the allocation of P to ribosomal RNA during growth (Acharya et al., 2004; Isanta-Navarro et al., 2022). EH refers to the regulatory processes that maintain stable levels of 25 essential elements within organisms compared to their surroundings (Hessen et al., 2013) and is modeled using a variety of techniques (Sterner and Elser, 2002; Meunier et al., 2014). An organism's investment in growth and homeostasis impacts elemental fluxes at broader biological scales, influencing population dynamics, community structure, and ecosystem functioning (Sterner and Elser, 2002; Elser et al., 2010; González et al., 2018). Understanding how elemental fluxes scale across space and time remains a significant challenge, but RS provides a powerful tool for scaling and testing ecological stoichiometry models.

Emerging frameworks, such as ionomics and stoichiometric distribution models, offer promising avenues for integrating RS with ecological stoichiometry to gain deeper insights (Filipiak, 2016; Kaspari and Powers, 2016; Jeyasingh et al., 2017; González et al., 2017; Meunier et al., 2017; Leroux et al., 2017; El-Sabaawi et al., 2023). While optical RS can provide direct estimation of some elements from spectra, alternative approaches include using stoichiometric models to estimate elemental availability indirectly via remotely-sensed proxies, which are then correlated with ground-truth element data. Recent work following this approach include van Beest et al. (2023); Collins et al. (2017); Soranno et al. (2019) and Balluffi-Fry et al. (2020). Such efforts are inherently interdisciplinary, requiring collaboration across fields of ecology, remote sensing, and modeling.

Remote sensing as a tool for assessing ecological stoichiometry across space

Substantial differences exist in the distribution of the 25 essential elements between different habitats, such as terrestrial and aquatic ecosystems, where nutrient availability can vary greatly due to differences in geochemistry and biogeochemical cycling (Williams, 1997; Sterner and Elser, 2002; Kaspari et al., 2008). Optical RS technologies offer the potential to compare the distribution of these essential elements across larger ecological and geographic scales, enabling researchers to assess whether patterns observed at smaller scales, such as within species from a single location, are indicative of broader trends (Asner and Martin, 2016; Ollinger, 2011). Additionally, RS may facilitate integration of spatial patterns in non-metabolic elements (e.g., As, Cd, Pb) and enable inference of the effects of accumulation in biological tissues on function at various levels of organization (Muller et al., 2010; Peace et al., 2021; Rashid et al., 2023). Understanding these complex interactions between organisms and their chemical environment at broad scales requires advanced RS tools, which are increasingly recognized as essential for studying these dynamics in a comprehensive manner (Ustin et al., 2004; Asner et al., 2015).

Identifying limiting elements at different spatial scales using RS data can be useful in developing specific hypotheses for outcomes of selection on the ecological stoichiometry of populations or species of interest at these scales, their expected elemental phenotypes, physiological rates and stoichiometric reaction norms, and response to stressors, which can then be tested using lab and field experiments (Jeyasingh et al., 2014; Leal et al., 2017; El-Sabaawi et al., 2023). Information about the elemental composition and stoichiometry at smaller spatial scales can be juxtaposed with those at larger spatial scales and used in conjunction with field measurements of elemental phenotypes to determine the contributions of selection (i.e., strength of association between elemental phenotype and limiting element availability within a patch) and dispersal (i.e., strength of association between elemental phenotype within a patch and limiting element within a region). Finally, relative availability of elements and elemental constraints provided from optical RS tools can be used to compare the relative strength of selection of ecological stoichiometry to other selective forces such as predation, feeding strategy, and access to mates (Kay et al., 2005).

Remote sensing as an emerging tool for assessing ecological stoichiometry across time

Data from optical RS can be also used to detect temporal patterns in the relative availability of elements across broad spatial scales. These temporal patterns can be linked to the changes in the abundance of elemental phenotypes, populations and species collected from long-term observation studies to identify macroevolutionary trajectories (Kay et al., 2005). For macroelements such as C, N and P, the links between availability and fitness consequences have been established in diverse biota ranging from aquatic snails, green algae, and Drosophila species (Elser et al., 2003; Neiman and Krist, 2016; Bernhardt et al., 2020). Multi-spectral and hyperspectral RS data allows researchers to determine the landscape availability of elements beyond C, N and P. Combined with nutritional geometry experiments, where organisms are reared on resources with different elemental compositions, the relationship between micro elements (e.g., Mn, Fe, Mg) and fitness can be determined (Sperfeld et al., 2016, 2017) and extrapolated using RS.

Changes in nutrient availability can cause cascading effects across multiple ecological scales, from individual organisms to entire ecosystems (Vitousek and Howarth, 1991). Ecosystems respond to nutrient enrichment in diverse ways, with acute responses often differing from chronic ones (Smith et al., 1999; Elser et al., 2007). The scale of measurement also plays a crucial role in understanding these impacts, as localized studies may not capture the broader regional or global patterns driven by widespread human activities (Vitousek et al., 1997). Moreover, organisms within these ecosystems do not respond uniformly to changes in elemental availability; their responses are shaped by their evolutionary and ecological histories, as well as the biochemical characteristics of their habitats (Sterner and Elser, 2002). These interactions can create feedback loops, where changes in nutrient availability further alter ecosystem dynamics and the selective pressures on species (Gruner et al., 2008; Gholizadeh et al., 2024).

At the broadest extent, global climate change affects the ecology of organisms and the flow of matter through ecosystems. Primary producers experience nutrient dilution as a result of rising atmospheric carbon dioxide, whereby plants accumulate C at a faster rate than other non-C nutrients. While the direct consequences for the nutrition of consumers and function of singular ecosystems may be difficult to predict, the global nature of this phenomenon suggests that major reorganization of food webs and shifts in ecosystem function are likely (Kaspari et al., 2022; Kaspari and Welti, 2024; Welti and Kaspari, 2024). The expansive body of literature testing the capabilities of remote sensing to quantify the chemical composition of terrestrial plant tissues may facilitate the study of nutrient dilution and its consequences for function at all levels of biological organization. Although applying RS requires a thorough understanding of the explicit spatial data characteristics and the operational spatial scale of processes in question, gains in understanding of processes related to nutrient dilution (e.g., metabolism of primary producers, mineral nutrient acquisition, herbivory, sediment de-/stabilization, etc.) and their optical properties may permit application of RS to quantify relevant fluxes across broad extents.

Conclusion and outlook

We provided an overview of how researchers can apply RS techniques to obtain data necessary for addressing core ecological stoichiometry research goals. However, incorporating optical RS within an ecological stoichiometry framework can also open new research frontiers. Below, we provide a limited set of questions where data obtained from optical RS can provide new insights and drive progress in our understanding of how elemental availability underpins ecological systems. For example, what is the role of stoichiometry in ecosystem response to global environmental changes, such as permafrost thawing, agricultural intensification, nutrient dilution and ocean acidification? How will stoichiometric observations inform global biogeochemical models used to simulate the distribution of elements in the biosphere? How do stoichiometry and biodiversity feedback through ecological dynamics, such as dispersion, carrying capacity, and species invasion? Finally, are stoichiometric ratios and limits phylogenetically conserved, and how do phenotypic plasticity and genetic variation contribute to the evolutionary outcomes experienced by organisms?

The integration of optical remote sensing (RS) with ecological stoichiometry holds immense potential for advancing our understanding of nutrient dynamics across ecosystems. By enabling the study of elemental ratios over large spatial and temporal scales, RS provides a powerful tool for overcoming the limitations of traditional point-based sampling methods. This paper has outlined the capabilities and limitations of RS in quantifying elements, offered a practical guide for its application in ecological stoichiometry research, and highlighted future research directions which bridge the gap between these fields. As environmental change continues to alter the balance of elements in ecosystems, the adoption of RS in stoichiometric studies is essential for addressing global ecological challenges. Expanding the use of RS will not only enhance the scale and resolution of ecological studies but also pave the way for novel insights into how stoichiometric constraints shape ecosystem function.

Author contributions

JR: Conceptualization, Project administration, Writing – original draft, Writing – review & editing. SH: Writing – original draft, Writing – review & editing. MN: Writing – original draft, Writing – review & editing. CT: Writing – original draft, Writing – review & editing. ET: Writing – original draft, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. We thank Shawn Wilder for providing travel funding for JR. We thank Stephanie Hampton and Carnegie Science for providing travel funding for CT.

Acknowledgments

The authors would like to acknowledge Maarten Boersma and Genevieve Metson for their invaluable insight in communicating these concepts. We acknowledge and thank Cédric Meunier for organizing and facilitating Woodstoich V. Finally, we express our deep gratitude to Dieter Wolf-Gladrow and Cecilia Laspoumaderes for generating thoughtful discussion of unexplored ideas and providing logistical support at Woodstoich V. We thank the Alfred-Wegener-Institut for providing access to the guest research facilities of the Biologische Anstalt Helgoland during the Woodstoich Workshop, grant number AWI_BAH_34.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abraham A. J., Duvall E., Ferraro K., Webster A. B., Doughty C. E., Le Roux E., et al. (2023). Understanding anthropogenic impacts on zoogeochemistry is essential for ecological restoration. Restor. Ecol. 31 (3), e13778. doi: 10.1111/rec.13778