Quantifying the impact of environmental changes on migratory species: a model perturbation framework

Migratory species use different habitats and pathways across their migratory route. Pathway contribution metrics are transient metrics of population growth, derived from population models, and quantify the predicted contribution of an individual, travelling along a specified migratory route, to the total population over a specified length of time. Environmental disturbances or management actions may occur temporally or spatially throughout the process of migration. The impact that a given perturbation may have on pathway contribution metrics is not always obvious owing to the propagation of the perturbation through the migratory cycle. Here, we develop a general modelling framework that incorporates perturbations into a class of matrix migratory population models, and which quantifies the effect that perturbations to the model, in terms of the transition rates of habitats and pathways, have on pathway contribution metrics. We also detail how to calculate the sensitivity of pathway contribution metrics to the perturbations considered. Our framework may be used to provide insights into the impact that environmental disturbances or management actions have on migratory populations. These insights may be used to inform management actions which either buffer against possible deleterious disturbances or increase the population size through targeted interventions. Our theoretical results are illustrated via hypothetical examples and a model inspired by the monarch butterfly; we uncover results that are not clear from the calculation of the pathway contribution metrics alone.

1 Introduction

Migratory species are fundamental to many ecosystems. Migratory populations may be affected by changes in land use and climate across multiple habitats. Conservation or management strategies must account for the fact that these habitats may be subject to different jurisdictions and some may be difficult or impossible to influence. Here, we provide two frameworks that quantify how changes to the vital rates of a migratory population influence the short- and long-term growth of the population.

Climate change poses a risk to many species. Despite migration evolving in response to seasonal changes in climate and habitat (Dingle and Drake, 2007), the unprecedented speed and magnitude of climate change is leading to a decline in many migratory species (Huntley et al., 2006; Robinson et al., 2009; Wilcove and Wikelski, 2008). In fact, migratory species can be more at risk than sedentary species (Runge et al., 2014). This increased risk could be due to migratory species using habitats that are far removed from each other, making it difficult for the species to adapt to the changing environment (Both and Visser, 2001; Shuter et al., 2011); or due to their reliance on high latitude, high altitude and wetland habitats which are more affected by climate change (Hassol, 2004; Robinson et al., 2009).

Migratory species link distant ecosystems and provide them with large inputs of energy and nutrients (Bauer and Hoye, 2014; Wilcove and Wikelski, 2008). Their movements are often predictable, enabling other species to shape their life history strategies around the movements of migratory species to take advantage of the influx of energy and nutrients (Bauer and Hoye, 2014). Changes to the timing and route of migration or the number of individuals migrating may cause wide-ranging environmental, economic or social consequences (Robinson et al., 2009). The conservation of migratory species requires an international and collaborative approach due to their use of different habitats across their migratory cycle (Kirby et al., 2008; Robinson et al., 2009; Runge et al., 2015; Thornton et al., 2018). However this can be challenging and few species are protected across their entire range (Runge et al., 2014, 2015). In fact, IUCN (International Union for Conservation of Nature) targets are met for a smaller proportion of migratory species than for sedentary species (Runge et al., 2015).

Models that assess the importance of different parts of a migratory cycle will arguably be an essential tool in the conservation of migratory species. There are numerous existing metapopulation models, based on the work in Levins (1969), that assess the importance of habitats to the growth of the population. Although these models study similar systems, with movement between discrete habitats, they do not account for the seasonal movement back and forth between habitats, as is required in the study of migratory species (Taylor and Hall, 2012). Thus, models that consider this specific periodic movement are required to fully understand and study the dynamics of migratory species.

Many analytical tools used in the modelling of migratory species consider choices made by an individual (Bowlin et al., 2010). However, contribution metrics that assess the importance of habitats and pathways to the total population are developed across: Runge et al. (2006); Sample et al. (2019); Smith et al. (2022); Wiederholt et al. (2018). These metrics build on existing metapopulation theory, extending it to account for the periodic nature of migratory cycles. The contribution metrics are computed from a population model that is assumed to be fixed, and so their numerical value is constant. Additional insight could be gathered from the contribution metrics by assessing how they change in response to changes in the model parameters. There are a number of scenarios where it is important to gain insight into how changes affect a model, including (Caswell, 2019): when environmental change is expected; when theoretically testing possible management actions; and to identify the parameters that have the biggest effect on the outcome(s) of interest.

To assess the impact that environmental change has on migratory species, recent studies have performed perturbation analyses on migratory networks. Payo-Payo et al. (2022) construct a general annual cycle matrix model and evaluate how the choice of migration route and survival during migration affect the asymptotic growth rate of the population. This framework does not allow for perturbations to the demographic vital rates, only allows for two habitats and does not consider transient dynamics.

Sample et al. (2020) develop a habitat metric that quantifies the effect of perturbing one habitat by a fixed amount in every season of the annual cycle. They also develop a pathway metric that quantifies the effect of perturbing a directed pathway by a fixed amount in every season of the annual cycle. These perturbations are applied to the seasonal population matrices, which contain both the demographic and movement update information. This framework does not allow for perturbations to be applied to specific demographic or migratory rates, or groups of these rates. The impact that the perturbations have on the asymptotic growth of the population is not considered.

Here, we analyse the impact of these perturbations in a general framework that overcomes these limitations. Our methodology allows perturbations to be applied to any of the vital rates of a migratory population modelled using a matrix population model (as in, for example, Caswell (2001)). Applying perturbations directly to specific vital rates ensures that the ecological meaning of the perturbations is clear. Furthermore, perturbations can be applied to any number of vital rates, and so the effects of mixed intervention strategies and trade-offs can be explored.

We provide two frameworks that assess how changes in the vital rates of a migratory population influence the size of the contribution metrics developed in Smith et al. (2022) and the asymptotic growth rate. The first framework is a structured perturbation framework [inspired by Hodgson and Townley (2004)] that uses linear algebra to predict the actual change that a perturbation causes to the contribution metrics and asymptotic growth rate. The second framework uses differential calculus to compute sensitivity formulae [inspired by Caswell (2019)] that predict the rate of change in the contribution metrics and asymptotic growth rate at a given point. These two frameworks can be used together or individually to identify the vital rates that are expected to cause the migratory population to grow, remain stable, or decrease in both the short- and long-term. The results of analyses using these frameworks can be used to inform population management decisions that consider the whole migratory cycle.

The remainder of the paper is organised as follows. In Section 2, we present our two perturbation frameworks. In Section 3, we present examples to illustrate the frameworks’ utility. Section 4 is the discussion. A number of technical details are provided in the Supplementary Material.

2 Materials and methods

Here we present a modelling framework for incorporating perturbations in annual cycle models — a class of discrete-time structured matrix population models for migratory species — and understanding the consequent effects on pathway contribution metrics. To do so, we briefly recap annual cycle models and pathway contribution metrics from Smith et al. (2022). As mentioned there, the underlying annual cycle model is inspired by those appearing in Hunter and Caswell (2005) and Sample et al. (2019); the pathway contribution metrics generalise those developed over Runge et al. (2006); Sample et al. (2019); Wiederholt et al. (2018). The mathematical notation used to define the model is recorded in Table 1.

Table 1

Table 1. Symbols used for parameters and matrices in the annual cycle model.

2.1 The annual cycle model

The annual cycle model uses theory from matrix population models [see, for example, Caswell (2001); Cushing (1998)] to project a population over an annual cycle from a fixed anniversary season. The annual cycle matrix $\mathcal{A}\in {ℝ}_{+}^{cn\times cn}$ stratifies the population by stage structure and spatial location (or habitat) (Sample et al., 2019; Smith et al., 2022); 𝒜 contains both the demographic update information associated with habitats and the migration update information associated with migration pathways. It is assumed that there are c stages and n habitats. The underlying discrete-time annual cycle model is given by

$\begin{array}{ll}x(t+1)=\mathcal{A}x(t)t=0,1,2,\dots ,x(0)=x^0,& (1)\end{array}$

where $x(t)\in {ℝ}_{+}^{cn}$ is the structured population at (annual) time-step t, recorded during the anniversary season. The vector $x^0$ denotes the initial population distribution. The dominant eigenvalue of $\mathcal{A}$, denoted by λ, is known to give the asymptotic growth rate of the population.

Migratory populations experience different vital rates in different seasons. As such, the annual cycle model decomposes each year into s seasons — the word being used roughly to denote some portion of the year — indexed by $k\in \left\{1,\dots ,s\right\}$. For ease of notation, we make the convention that the anniversary season is labelled number one, and subsequent seasons enumerated consecutively.

Then, an order $c\times c$ demographic projection matrix, denoted $D_{j,k}$, is associated with each habitat $j\in \left\{1,\dots ,n\right\}$ and season $k\in \left\{1,\dots ,s\right\}$. Similarly, for each stage $i\in \left\{1,\dots ,c\right\}$, we associate order $n\times n$ movement matrices $P_k^i$ and $S_k^i$, which respectively contain the probabilities that, during season k, an individual of stage i uses a migration pathway and the probabilities that an individual of stage i survives migration. The matrices $D_{j,k}$, $P_k^i$ and $S_k^i$ are the fundamental ingredients of the annual cycle model, and together combine to form seasonal matrices, denoted by $A_k\in {ℝ}_{+}^{cn\times cn}$. The seasonal matrices project the population across all stages and habitats over season k and are given by

$\begin{array}{ll}\begin{array}{c}{A}_k=\left({\displaystyle \sum _{j=1}^n}{E}_{n,jj}\otimes D_{j,k}\right)\left(\left({\displaystyle \sum _{i=1}^c}{P}_k^i\otimes E_{c,ii}\right)\circ \left({\displaystyle \sum _{i=1}^c}{S}_k^i\otimes E_{c,ii}\right)\right)\hfill \\ =:{\mathbb{D}}_k({\mathbb{P}}_k\circ {\mathbb{S}}_k).\hfill \end{array}& (2)\end{array}$

Here: $\otimes$ denotes a Kronecker product; $E_{n,ii}$ is a $n\times n$ matrix of zeros, apart from a one in the $(i,i)$-th entry; $\circ$ denotes Hadamard (entrywise) matrix product. The order of multiplication assumes that, within a season, migration is followed by demography. Then, the annual cycle matrix $\mathcal{A}$ is constructed by taking the product of s seasonal matrices via left multiplication, that is,

$\begin{array}{ll}\mathcal{A}:={\displaystyle \prod _{k=1}^s}{A}_k=A_s\cdots A_2{A}_1.& (3)\end{array}$

Seasonal survival matrices, ${\widehat{A}}_k\in {ℝ}_{+}^{cn\times cn}$, that encode the migratory survival and demographic rates, but, unlike $A_k$, do not include the information regarding the proportion of the population that migrate along pathways, are given by

$\begin{array}{ll}{\widehat{A}}_k:=\left({\displaystyle \sum _{j=1}^n}{E}_{n,jj}\otimes D_{j,k}\right)\left({\displaystyle \sum _{i=1}^c}{S}_k^i\otimes E_{c,ii}\right)=:{\mathbb{D}}_k{\mathbb{S}}_k.& (4)\end{array}$

For further detail about the construction of the annual cycle model, see Smith et al. (2022, Section 2.2).

2.2 Pathway contribution metrics

We describe the pathway contribution metrics introduced in Smith et al. (2022). They define a migratory route to comprise all the pathways that an individual migrates along during an annual cycle; where a pathway is defined to be the migration an individual takes between one habitat and another (or itself) during a season. This is written mathematically by introducing the vector $\mathcal{P}\in {ℝ}_{+}^{s+1}$ to describe the migratory route. The k-th entry of $\mathcal{P}$, written $\mathcal{P}(k)$, denotes the habitat that the subpopulation starts season k in (and ends season $k-1$ in).

When defining the migratory route that a focal subpopulation takes, it is not necessary to specify the pathway taken in every season. If a pathway is not specified in a season, then all valid pathways from the starting habitat are tracked. To help visualise which pathways are specified and unspecified in a migratory route, we use arrows (→) and crossed arrows ($\nrightarrow$), respectively. For example, in an annual cycle model with 3 seasons, if the pathways used during seasons 1 and 3 are unspecified and the pathway used during season 2 is specified, then the focal subpopulation travels along the migratory route

$\begin{array}{ll}\mathcal{P}(1)\nrightarrow \mathcal{P}(2)\to \mathcal{P}(3)\nrightarrow \mathcal{P}(4).& (5)\end{array}$

Once the migratory route has been specified, it is then possible to populate the vector $\mathcal{P}$. To do this, each $\mathcal{P}(k)$ is set to be an integer in $\left\{0,1,\dots ,n\right\}$, where the pathway taken during season $k$ is denoted by $\mathcal{P}(k)$ and $\mathcal{P}(k+1)$. If $\mathcal{P}(k)=0$, then the habitat that the subpopulation starts season k in (and ends season k − 1 in) is unspecified. For example, if the pathway specified in season 2 of Equation 5 is the pathway from habitat 1 to habitat 2, then Equation 5 becomes

$$0\nrightarrow 1\to 2\nrightarrow 0,\text{\hspace{1em}and\hspace{1em}}\mathcal{P}:=[\begin{array}{cccc}0& 1& 2& 0\end{array}].$$

Finally, $\varphi \in \left\{0,1,\dots ,s\right\}$ is set to be the number of seasons for which a pathway is specified, and $\text{Φ}\in {ℝ}^{\varphi }$ stores the labels of these seasons. Once $\mathcal{P}$, $\varphi$ and $\text{Φ}$ have been defined, the pathway contribution metrics can be calculated. The projection matrices for the subpopulation that travels along migratory route $\mathcal{P}$ are extracted from $\mathcal{A}$ using the function

$\begin{array}{ll}{\mathbf{\text{A}}}_k:=\{\begin{array}{ll}{\widehat{A}}_k\circ (E_{n,\mathcal{P}(k+1)\mathcal{P}(k)}\otimes J_c),\hfill & \hfill k\in \Phi ,\\ A_k,\hfill & \hfill \text{otherwise }.\end{array}& (6)\end{array}$

Here, $J_c$ is an c × c matrix of ones.

In Smith et al. (2022), two types of pathway contribution metrics are defined. The first are called the subpopulation pathway contribution metrics, and are defined by

$\begin{array}{ll}\begin{array}{l}C(\mathcal{P}):={\mathbb{𝟙}}_{cn}^{\top }{\displaystyle \prod _{k=1}^s}{\mathbf{\text{A}}}_k={𝟙}_{cn}^{\top }{\mathbf{\text{A}}}_s\cdots {\mathbf{\text{A}}}_2{\mathbf{\text{A}}}_1\\ \begin{array}{ccc}& & =[\begin{array}{ccccccccc}{C}_1^1(\mathcal{P})& \cdots & C_1^c(\mathcal{P})& |& \cdots & |& C_n^1(\mathcal{P})& \cdots & C_n^c(\mathcal{P})\end{array}].\end{array}\end{array}& (7)\end{array}$

Here $C_j^i(\mathcal{P})$ is the per capita contribution of an individual that starts the annual cycle in stage $i$ and habitat $j$ and migrates along $\mathcal{P}$, to the subpopulation that migrates along $\mathcal{P}$.

The second pathway contribution metrics introduced are called the metapopulation pathway contribution metrics, and are defined by

$\begin{array}{ll}\begin{array}{l}\tilde{C}(\mathcal{P}):={𝟙}_{cn}^{\top }{\displaystyle \prod _{k=1}^s}{\mathbf{\text{A}}}_k{\mathbf{P}}_k={𝟙}_{cn}^{\top }{\mathbf{\text{A}}}_s{\mathbf{P}}_s\cdots {\mathbf{\text{A}}}_2{\mathbf{P}}_2{\mathbf{\text{A}}}_1{\mathbf{P}}_1\\ \begin{array}{ccc}& & =[\begin{array}{ccccccccc}{\tilde{C}}_1^1(\mathcal{P})& \cdots & {\tilde{C}}_1^c(\mathcal{P})& |& \cdots & |& {\tilde{C}}_n^1(\mathcal{P})& \cdots & {\tilde{C}}_n^c(\mathcal{P})\end{array}].\end{array}\end{array}& (8)\end{array}$

Here ${\tilde{C}}_j^i(\mathcal{P})$ is the per capita contribution of an individual that starts the annual cycle in stage $i$ and habitat $j$ and travels along the migratory route $\mathcal{P}$, to the total population. The matrices $P_k$ in Equation 8 are given by

$$P_k:=\{\begin{array}{ll}{I}_n\otimes {({\mathbb{P}}_k)}_{\mathcal{P}(k+1),\mathcal{P}(k)},\hfill & \hfill k\in \text{Φ },\\ I_{cn},\hfill & \hfill \text{otherwise }.\end{array}$$

Here: $I_n\otimes {({\mathbb{P}}_k)}_{\mathcal{P}(k+1),(k)}$ is a $cn\times cn$ matrix with the $(\mathcal{P}(k+1),\mathcal{P}(k))$-th block of ${\mathbb{P}}_k$ along the diagonal; ${\mathbb{P}}_k\in {ℝ}_{+}^{cn\times cn}$ contains the proportion of the population travelling along each pathway in season k. Further details on the above two pathway contribution metrics are given in Smith et al. (2022, Section 2.3). We also note that if there are no specified paths, then both pathway contribution metrics recover the so-called habitat contribution metrics developed in Sample et al. (2019). The habitat contribution metrics calculate the expected number of individuals generated from an individual occupying the focal habitat at the start of the annual cycle.

The contribution metrics stored in $\tilde{C}(\mathcal{P})$ can be averaged over stage and habitat to assess the contribution of habitats and stages, respectively; see Smith et al. (2022, Section 2.7) for more detail. A diagram summarising the annual cycle model, its various components and relationships, as well as the pathway contribution metrics, is given in Figure 1.

Figure 1

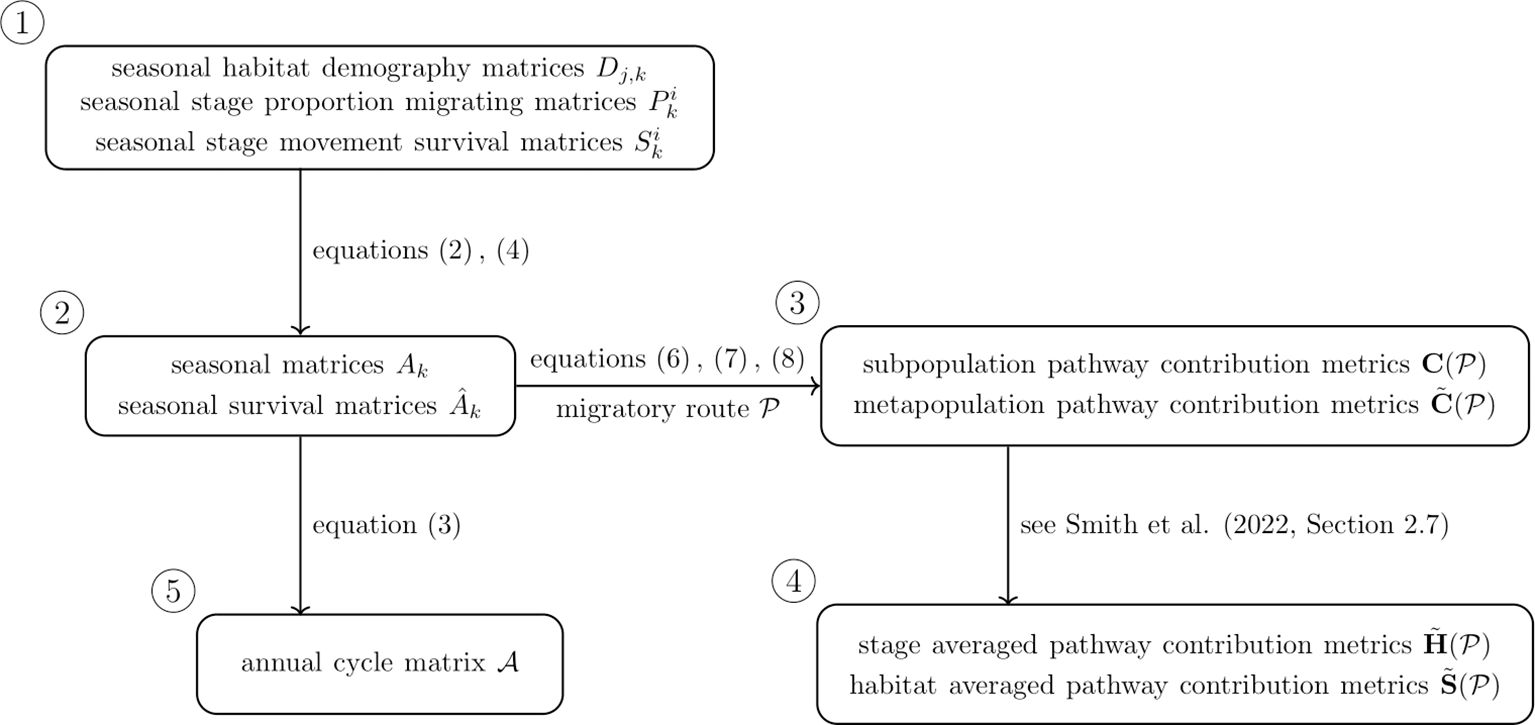
Figure 1. Diagram illustrating components of the annual cycle model (1) and associated pathway contribution metrics.

2.3 Perturbations to annual cycle models and pathway contribution metrics

We describe a modelling framework for incorporating structured perturbations into annual cycle models and, consequently, into pathway contribution metrics. The term structured here essentially means that perturbations are applied to specific model parameters. The framework is general and flexible, and enables each season of the annual cycle and all population states to be perturbed independently of each other. We proceed to outline the method, before giving the mathematical details.

An (additive) structured perturbation to a matrix $M$ means replacing (or updating) $M$ by

$\begin{array}{ll}M+Q\text{Δ}R,& (9)\end{array}$

for matrix terms Q, Δ and R. Here, the matrices Q and R describe the structure of the perturbation, meaning on which entries of M it is assumed to act. For a given structure of perturbation, these matrices are fixed and assumed known. The term Δ describes the magnitude of the perturbation, and is typically assumed to be unknown or at least variable. The case Δ = 0 corresponds to no perturbation of M, sometimes called the nominal or unperturbed model. The simplest case is when $Q=q$ and $R=r^{\top }$ are vectors, and $\text{Δ}=\delta$ is a scalar variable. The matrices Q, R and Δ will in practice have certain constraints, to ensure that the perturbed matrix M +QΔR is still ecologically meaningful. In the context of matrix population projection models (matrix PPMs), structured perturbations of the form Equation 9 have been proposed and studied across, for example: Guiver et al. (2016); Hodgson et al. (2006); Hodgson and Townley (2004); Lubben et al. (2009). They are amenable to analysis by a range of mathematical techniques.

We represent perturbations to the annual cycle model (1) in terms of structured perturbations of the form Equation 9 to the demography matrices, $D_{j,k}$, and the movement matrices, $P_k^i$ and $S_k^i$. These are the fundamental building blocks of the annual cycle model. The entries of the matrices $D_{j,k}$, $P_k^i$ and $S_k^i$ have clear ecological interpretations, and it is natural to assume that proposed management actions, or environmental changes, may affect these. More importantly, ecologically meaningful perturbations to these terms shall, by construction, give rise to an ecologically meaningful perturbed annual cycle model. In general, the effect of a given vital rate in, say, $D_{j,k}$ on the corresponding seasonal matrix $A_k$ or overall annual cycle matrix 𝒜 is complicated, and arguably difficult to capture correctly by perturbing $A_k$ or 𝒜 directly. The upshot is that structured perturbations to $D_{j,k}$, $P_k^i$ and $S_k^i$ will propagate through the annual cycle model and pathway contribution metrics in accordance with Figure 1.

Let 𝒫 denote a given, fixed migratory route. Computing the perturbed pathway contribution metrics in Equations 7, 8, respectively denoted $C(\mathcal{P},\text{Δ})$ and $\tilde{C}(\mathcal{P},\text{Δ})$, we obtain expressions of the form

$\begin{array}{ll}\begin{array}{l}C(\mathcal{P},\text{Δ})=C(\mathcal{P})+E_C(\mathcal{P},\text{Δ})\text{\hspace{1em}and\hspace{1em}}\\ \tilde{C}(\mathcal{P},\text{Δ})=\tilde{C}(\mathcal{P})+E_{\tilde{C}}(\mathcal{P},\text{Δ}),\end{array}& (10)\end{array}$

for some perturbation or error vectors $E(\mathcal{P},\text{Δ})$, where Δ is the collection of all perturbations performed in the annual cycle. Similar formulae are valid for perturbed averaged pathway contribution metrics, presented in Supplementary Material Section 1. Owing to the generality of structured perturbations permitted, the formulae for the $E(\mathcal{P},\text{Δ})$ terms are somewhat complicated, but can be computed exactly and details are given in Supplementary Material Sections 1 and 2. We note that in practice it is likely that the formula will simplify as perturbations need not be applied to all vital rates at once. Computing the formula allows for more insight into the algebra that underpins the perturbation, which can provide analytical insight into how the perturbations are carried through the model. However, if only the values of the perturbed contribution metrics are of interest, then computing the left-hand side of Equation 10 is numerically simpler than computing the right-hand side.

An illustrative example demonstrating the ideas underpinning our perturbation framework and Equation 10 appears in Section 3.1.1. Next, we provide interpretation of the perturbed pathway contribution metrics in Equation 10, with some informative special cases.

2.3.1 First observations and special cases

Consider Equation 10 for perturbation $\text{Δ}$. When the perturbation is non-negative, meaning all the structure matrices $Q_X$, $R_X$ and perturbation magnitudes ${\text{Δ}}_X$ are (componentwise) non-negative, it is clear that $E_C(\mathcal{P},\text{Δ})$ and $E_{\tilde{C}}(\mathcal{P},\text{Δ})$ are also non-negative. So a non-negative perturbation increases the pathway contribution metrics (or leaves them unchanged). This relationship is intuitively clear, as improving vital rates can only increase, or leave unchanged, the contribution of a given individual in the population, regardless of the pathway. Similarly, a non-positive perturbation decreases the pathway contribution metrics.

Thus, the most interesting and subtle case is when $Q_X$, ${\text{Δ}}_X$ or $R_X$ contain mixed signs, often described as trade-offs. In this case, before calculating the metrics, there is no guarantee of any overall sign to $E_C(\mathcal{P},\text{Δ})$ or $E_{\tilde{C}}(\mathcal{P},\text{Δ})$. So, under these perturbations, some pathway contribution metrics may increase whilst others decrease. Given the potential complexity of the annual cycle model and perturbations, teasing out the overall effects of a perturbation on the pathway contribution metrics without resorting to Equation 10 seems intractable. In any case, zero entries of E correspond to stage and habitat combinations which are unchanged by the perturbation.

If a single perturbation of the form $\text{Δ}=\delta I$, for scalar variable $\delta$, is applied in a single season to a single matrix from $D_{j,k}$, $P_k^i$ and $S_k^i$, then the error term E of the perturbed pathway contribution metric depends linearly on the perturbation magnitude δ. To see this, suppose that $D_{j,k}$ is perturbed in this way. Then the corresponding ${\mathbb{D}}_k$ and $A_k$ perturb according to

$${\mathbb{D}}_k(\delta )={\mathbb{D}}_k+(E_{n,jj}\otimes (q\delta r^{\top }))$$

and

$$\begin{array}{l}{A}_k(\delta )={\mathbb{D}}_k(\delta )({\mathbb{P}}_k\circ {\mathbb{S}}_k)=({\mathbb{D}}_k+(E_{n,jj}\otimes (q\delta r^{\top })))({\mathbb{P}}_k\circ {\mathbb{S}}_k)\\ \begin{array}{ccc}& & =A_k+(E_{n,jj}\otimes (q\delta r^{\top }))({\mathbb{P}}_k\circ {\mathbb{S}}_k)=:A_k+{\mathbf{\text{E}}}_{A,k}(\delta ).\end{array}\end{array}$$

Here, $j\in \left\{1,\dots ,n\right\}$ indexes the habitat that is affected by the perturbation. All other model terms ${\mathbb{D}}_l$, ${\mathbb{P}}_l$, ${\mathbb{S}}_l$ for $l\ne k$, and hence $A_l$ as well, remain unchanged. Therefore

$$\begin{array}{l}\mathbf{\text{C}}(\mathcal{P},\delta )={\mathbb{𝟙}}^{\top }{A}_s{A}_{s-1}\cdots A_k(\delta )\cdots A_1\\ ={𝟙}^{\top }{A}_s{A}_{s-1}\cdots A_1+{𝟙}^{\top }{A}_s\cdots {\mathbf{\text{E}}}_{A,k}(\delta )({\mathbb{P}}_k\circ {\mathbb{S}}_k)\cdots A_1\\ \begin{array}{ccc}& & =\mathbf{\text{C}}(\mathcal{P})+\delta {\mathbf{\text{E}}}_0,\end{array}\end{array}$$

for some vector $E_0$ which is independent of δ. This is the case in the example in Section 3.1.1.

If m perturbations of the form $\text{Δ}={\delta }_{l}I$ for $l=1,2,\dots ,m$ are applied across seasons and across the matrices $D_{j,k}$, $P_k^i$ and $S_k^i$, then the above arguments indicate that the pathway contribution metrics perturb according to

$$\mathbf{\text{C}}(\mathcal{P},\delta )=\text{C}(\mathcal{P})+{\text{E}}_m({\delta }_1,{\delta }_2,\dots ,{\delta }_m),$$

where $E_m$ is a vector-valued function which depends linearly on each of the ${\delta }_l$. If each of the ${\delta }_l$ are equal, that is, ${\delta }_l=\delta$ for all l then $E_m$ depends polynomially on $\delta$ (and so, in particular, nonlinearly), with degree at most m.

We conclude this subsection by commenting that one of the reasons for the complexity of Equation 10 is that, roughly speaking, the perturbations we consider to the annual cycle model data $D_{j,k}$, $P_k^i$ and $S_k^i$ are of the form Equation 9, and hence are additive perturbations, yet the annual cycle model inherently combines these ingredients multiplicatively. Since matrix multiplication is not commutative, matrix formulae need not simplify as scalar equations do. Consequently, perturbations of the same magnitude to the same vital rate may have different effects on the resulting pathway contribution metrics if applied in different seasons. In general, seasons occurring earlier in the annual cycle than the perturbed season influence which population states (and hence which ${\mathbf{\text{C}}}_j^i$ and ${\widetilde{\mathbf{\text{C}}}}_j^i$) are perturbed, whilst seasons that occur later in the annual cycle than the perturbed season propagate the perturbation effect through the annual cycle. Ecologically, this makes sense as the population is projected through seasons occurring before the perturbed season; this results in the structure of the population at the time of perturbation differing to the initial population structure, not just due to the matrix R, but also due to the previous seasonal matrices. Following the perturbation, the population is projected through the rest of the annual cycle before being counted. These latter seasons will alter the population structure, but will have no influence on which population states the perturbation acts on as the perturbation has already happened.

2.4 Sensitivities and elasticities of pathway contribution metrics

Sensitivity analysis in ecology broadly refers to a number of calculus-based tools for computing how quantities of interest (outcomes) change with respect to parameters, and dates back to work from the 1960s and 1970s, including: Caswell (1978); Demetrius (1969); Goodman (1971); Hamilton (1966). We note that sensitivity analysis computes the rate of change of outcomes in response to changes to parameters at a given point, whereas the perturbation framework considered in Section 2.3 computes the actual change of outcomes following changes to parameters. The work in this section is inspired by Caswell (2019, Sections 8.2 and 8.3). We provide sensitivity formulae that assess how the pathway contribution metrics respond to changes in the parameters of the annual cycle model. We define p to be a vector of parameters corresponding to vital rates of interest, spread across the relevant matrices ($D_{j,k},P_k^i$ and/or $S_k^i$); it can take multiple forms which are discussed in further detail in Caswell (2019, Section 2.1).

Once $p$ is specified, the sensitivity of the subpopulation pathway contribution metrics is calculated using the derivative

$$\frac{\text{d}C{(\mathcal{P})}^{\top }}{\text{d}{p}^{\top }}={\left(\frac{\text{d}{C}_i(\mathcal{P})}{\text{d}{p}_j}\right)}_{ij}.$$

We use Magnus and Neudecker (1985) notation for matrix differentiation, such that $(\frac{\text{d}{\mathbf{\text{C}}}_i(\mathcal{P})}{\text{d}{\mathbf{\text{p}}}_j})$ is a matrix where the $(i,j)$-th entry is the derivative of $C_i(\mathcal{P})$ with respect to $p_j$. This derivative can then be related to the annual cycle model using the chain rule

$$\frac{\text{d}C{(\mathcal{P})}^{\top }}{\text{d}{p}^{\top }}=\frac{\text{d}C{(\mathcal{P})}^{\top }}{\text{d ve}{\text{c}}^{\top }{\prod }_{k=1}^s{\mathbf{\text{A}}}_k}\frac{\text{d vec }{\prod }_{k=1}^s{\mathbf{\text{A}}}_k}{\text{d}{\mathbf{\text{p}}}^{\top }},$$

where vec vectorises the matrix and${ }^{\top }$computes the transpose. See Caswell (2019, Chapter 2) for more background information about matrix differentiation.

Following cancellation of the subpopulation pathway contribution metrics and the product of the seasonal matrices, we have

$\begin{array}{ll}\begin{array}{c}\frac{\text{d}\mathbf{C}{(\mathcal{P})}^{\top }}{\text{d}{\mathbf{\text{p}}}^{\top }}=(I_{cn}\otimes {𝟙}_{cn}^{\top })\frac{\mathrm{d vec }{\prod }_{k=1}^s{\mathbf{\text{A}}}_k}{\text{d}{\mathbf{\text{p}}}^{\top }}\hfill \\ =(I_{cn}\otimes 1_{cn}^{\top })\sum _{k=1}^s\left({\left({\mathbf{\text{Y}}}_1^{k-1}\right)}^{\top }\otimes {\mathbf{\text{Y}}}_{k+1}^s\right)\frac{\text{d vec }({\mathbf{\text{A}}}_k)}{\text{d}{\mathbf{\text{p}}}^{\top }},\hfill \end{array}& (11)\end{array}$

where $Y_i^j:=A_j\cdots A_i$ with $i\le j$ and $Y_1^0=Y_{s+1}^s=I_{cn}$. For detailed calculations see the Supplementary Material Section 3.

As in the perturbation analysis considered thus far, the sensitivity framework allows for changes to be applied to any parameter of the model. To allow for the suggested changes to be applied in a biologically reasonable way, we break down the sensitivity formula so that it contains the matrices $D_{j,k}$, $P_k^i$ and $S_k^i$. Following some careful calculus which is detailed in Supplementary Material Section 3, we obtain

$\begin{array}{ll}\begin{array}{c}\frac{\text{d vec }({\mathbf{\text{A}}}_k)}{\text{d}{\mathbf{\text{p}}}^{\top }}=(\underset{\text{perturbations of }{D}_{j,k}}{\underbrace{Z_{1,k}\sum _{j=1}^n{X}_1\left(\text{vec }\left(E_{n,jj}\right)\otimes \frac{\text{d vec }{D}_{j,k}}{\text{d}{\mathbf{\text{p}}}^{\top }}\right)}}\hfill \\ \underset{\text{perturbations of }{P}_k^i}{\underbrace{+Z_{2,k}\left(\left(\sum _{i=1}^c{X}_1(\frac{\text{d vec }{P}_k^i}{\text{d}{\mathbf{\text{p}}}^{\top }}\otimes \text{vec }(E_{c,ii})\right)\right)\circ \text{vec }({\mathbb{S}}_k))}}\hfill \\ +\underset{\text{perturbations of }{S}_k^i}{\underbrace{X_{2,k}\left(Z_{3,k}\circ \left(\sum _{i=1}^c{X}_1\left(\frac{\text{d vec }{S}_k^i}{\text{d}{\mathbf{\text{p}}}^{\top }}\otimes \text{vec }(E_{c,ii})\right)\right)\right)}})\circ Z_{4,k},\hfill \end{array}& (12)\end{array}$

which can be substituted into Equation 11 to give a formula for the sensitivity of $\mathbf{\text{C}}(\mathcal{P})$ with respect to the demographic and movement matrices. Here: $X_1:=I_n\otimes K_{c,n}\otimes I_c$, where $K_{c,n}$ is the vec-permutation matrix; $X_{2,k}:=I_{cn}\otimes {\mathbb{D}}_k$; and,

$$\begin{array}{l}{Z}_{1,k}:=\{\begin{array}{lll}{\mathbb{S}}_k^{\top }\otimes I_{cn},\hfill & \hfill & k\in \text{Φ },\hfill \\ {({\mathbb{P}}_k\circ {\mathbb{S}}_k)}^{\top }\otimes I_{cn},\hfill & \hfill & \text{otherwise }.\hfill \end{array}{Z}_{2,k}:=\{\begin{array}{lll}{0}_{c^2{n}^2},\hfill & \hfill & k\in \text{Φ },\hfill \\ I_{cn}\otimes {\mathbb{D}}_k\hfill & \hfill & \text{otherwise }.\hfill \end{array}\\ Z_{3,k}:=\{\begin{array}{lll}\text{vec }(0_{cn}),\hfill & \hfill & k\in \text{Φ },\hfill \\ \text{vec }({\mathbb{P}}_k),\hfill & \hfill & \text{otherwise }.\hfill \end{array}{Z}_{4,k}:=\{\begin{array}{ll}\text{vec }(E_{n,\mathcal{P}(k+1)\mathcal{P}(k)}\otimes J_c),\hfill & \hfill k\in \text{Φ },\\ {\mathbb{𝟙}}_{c^2{n}^2},\hfill & \hfill \text{otherwise }.\end{array}\end{array}$$

Note that $Z_{4,k}$ depends on the exact pathway specified, not just whether a pathway has been specified or not. We recall that the vec-permutation matrix is given by

$${\mathbf{\text{K}}}_{c,n}=\sum _{i=1}^c\sum _{j=1}^n{E}_{ij}\otimes E_{ij}^{\top }\in {ℝ}_{+}^{cn\times cn},$$

where $E_{ij}$ is an c × n zero matrix with a 1 in the $(i,j)$-th entry.

The Equations 11, 12 are for general perturbation structure, and so, due to full generality, are complex. However, though the size of the matrices may be large, many of them are sparse due to the underlying migratory structure they contain, and can be easily computed numerically. Furthermore, in practice it is unlikely that perturbations are applied to all the $D_{j,k}$, $S_k^i$ and $P_k^i$ matrices, so the formula will simplify as the differential of all unperturbed matrices is zero.

A similar formula can be constructed for the sensitivity of the metapopulation pathway contribution metrics, which is given by

$\begin{array}{ll}\begin{array}{l}\frac{\text{d}\widetilde{\mathbf{\text{C}}}{(\mathcal{P})}^{\top }}{\text{d}{\mathbf{\text{p}}}^{\top }}=(I_{cn}\otimes {𝟙}_{cn}^{\top })\frac{\text{d vec }{\prod }_{k=1}^s{\mathbf{\text{A}}}_k{\mathbf{\text{P}}}_k}{\text{d}{\mathbf{\text{p}}}^{\top }}\\ \begin{array}{ccc}& & =(I_{cn}\otimes {𝟙}_{cn}^{\top })\sum _{k=1}^s\left({\left({\text{ϒ}}_1^{k-1}\right)}^{\top }\otimes {\text{ϒ}}_{k+1}^s\right)\left(({\mathbf{\text{P}}}_k^{\top }\otimes I_{cn})\frac{\text{d vec}({\mathbf{\text{A}}}_k)}{\text{d}{\mathbf{\text{p}}}^{\top }}+(I_{cn}\otimes {\mathbf{\text{A}}}_k)\frac{\text{d vec}({\mathbf{\text{P}}}_k)}{\text{d}{\mathbf{\text{p}}}^{\top }}\right)\end{array}.\end{array}& (13)\end{array}$

Here, ${\text{ϒ}}_i^j:=A_j{P}_j\cdots A_i{P}_i$ for $i\le j$ and set ${\text{ϒ}}_1^0={\text{ϒ}}_{s+1}^s=I_{cn}$. As before, the sensitivity of $A_k$ is given by Equation 12. The sensitivity of $P_k$ is given by,

$$\frac{\text{d vec}({\mathbf{\text{P}}}_k)}{\text{d}{\mathbf{\text{p}}}^{\top }}=Z_{5,k}{X}_1(\text{vec }(I_n)\otimes ((T_{2,k}^{\top }\otimes T_{1,k})(\sum _{i=1}^c{X}_1\left(\frac{\text{d vec }(P_k^i)}{\text{d}{\mathbf{\text{p}}}^{\top }}\otimes \text{vec }(E_{c,ii}))\right))).$$

Here, $X_1=I_n\otimes K_{c,n}\otimes I_c$, as before and,

$$\begin{array}{l}{Z}_{5,k}:=\{\begin{array}{lll}{I}_{c^2{n}^2},\hfill & \hfill & k\in \text{Φ },\hfill \\ 0_{c^2{n}^2},\hfill & \hfill & \text{otherwise },\hfill \end{array}\\ T_{1,k}:=e_{n,\mathcal{P}(k+1)}^{\top }\otimes I_c\text{\hspace{1em}and\hspace{1em}}{T}_{2,k}:=e_{n,\mathcal{P}(k)}\otimes I_c,\end{array}$$

where $e_{n,i}$ is a $n\times 1$ vector of zeros with a one in position $i$. We note that the construction of $T_{1,k}$ and $T_{2,k}$ is such that $T_{1,k}$ is a $c\times cn$ zero matrix with the $\mathcal{P}(k+1)$-th block equal to $I_c$ and $T_{2,k}$ is a $cn\times c$ zero matrix with the $\mathcal{P}(k)$-th block equal to $I_c$. Furthermore, $T_{1,k}{\mathbb{P}}_k{T}_{2,k}={({\mathbb{P}}_k)}_{\mathcal{P}(k+1),\mathcal{P}(k)}$. The sensitivity of averaged contribution metrics can be calculated similarly and is presented in Supplementary Material Sections 1, 3.

When parameters are measured on different scales, more appropriate comparisons can be made by calculating the proportional effects of proportional perturbations, otherwise known as elasticities (Caswell, 2019, Section 2.7). The elasticity of the $\mathbf{\text{C}}(\mathcal{P})$ to $\mathbf{\text{p}}$ is defined as

$\begin{array}{ll}\frac{\mathit{Є}\mathbf{\text{C}}{(\mathcal{P})}^{\top }}{\mathit{Є}{\mathbf{\text{p}}}^{\top }}={\left(\frac{{\mathbf{\text{p}}}_j}{{\mathbf{\text{C}}}_i(\mathcal{P})}\frac{\text{d}{\mathbf{\text{C}}}_i(\mathcal{P})}{\text{d}{\mathbf{\text{p}}}_j}\right)}_{ij}.& (14)\end{array}$

Here, we have used the notation used in Caswell (2019) which is adapted from that in Samuelson (1947). To ensure a meaningful definition, we set the elasticity of ${\mathbf{\text{C}}}_i(\mathcal{P})$ to $p_j$ to equal zero when $C_i(\mathcal{P})$ equals zero and is unchanged by perturbation $p_j$. However, we comment that when a non-zero perturbation ${\mathbf{\text{p}}}_j$ causes $C_i(\mathcal{P})$ to equal zero, then the corresponding elasticity is not well-defined. The elasticity formula for the other contribution metrics is calculated similarly from the corresponding sensitivity formula. The derivation of the sensitivities given in this section are provided in Supplementary Material Section 3. An illustrative example demonstrating how Equations 11, 13 are computed, and their connection to the structured perturbation approach in Section 2.3, appears in Section 3.1.2.

2.5 Effects of perturbations on asymptotic behaviour

Here we comment that the pathway contribution metrics are measures of transient (indeed, annual) growth or decline of a population. Consequently, by studying the effects of perturbations on these metrics, we are studying the effects of perturbations on transient behaviour. However, it is of course the case that perturbations to the annual cycle matrix $\mathcal{A}$ in Equation 3 have corresponding effects on the asymptotic behaviour of the solutions of the annual cycle model Equation 1, that is, the predicted long-term behaviour of a migratory population. Recall that the asymptotic behaviour of Equation 1 is determined by its dominant eigenvalue, denoted by λ. Much attention in theoretical ecology has been dedicated to investigating the effects perturbations have on λ, with a number of techniques being prevalent.

On the one hand, classical sensitivity tools can be deployed, such as those in Caswell (2019) to determine the sensitivity of λ with respect to model parameters. The sensitivity of λ when there is no pathway specified, is calculated via Caswell (2019, Equation 3.42), that is

$\begin{array}{ll}\frac{\text{dλ}}{\text{d}{p}^{\top }}=\left(\frac{w^{\top }\otimes v^{\top }}{v^{\top }w}\right)\left(\frac{\text{d vec }\mathcal{A}}{\text{d}{p}^{\top }}\right).& (15)\end{array}$

Here: $v$ and $w$ denote the corresponding left and right eigenvectors of $\mathcal{A}$, respectively; and the sensitivity of $\mathcal{A}$ is given by

$$\frac{\text{d vec }\mathcal{A}}{\text{d}{p}^{\top }}=\sum _{k=1}^s\left({\left(Y_1^{k-1}\right)}^{\top }\otimes Y_{k+1}^s\right)\frac{\text{d vec}(A_k)}{\text{d}{p}^{\top }},$$

where the sensitivity of $A_k$ is given by Equation 12 with no pathways specified.

On the other hand, there are so-called transfer function methods for structured matrix population models, appearing to date back to Hodgson and Townley (2004), and based on concepts from control engineering. These have been explored and further developed across, for example: Hodgson et al. (2006); Lubben et al. (2009). The effect of structured perturbations on so-called population inertia (Koons et al., 2007) is explored in Guiver et al. (2016, Section 4). Since sensitivity analyses compute pointwise rates of change of λ with respect to model parameters, and the underlying relationships are typically nonlinear, it has been argued that sensitivities should be used alongside nonlinear analyses (Carslake et al., 2008). However, we highlight that a recent study has cautioned against the uninformed use of transfer function analysis (McElderry and Gaoue, 2022).

The general idea of transfer function methods can be briefly summarised by noting that the statement¹:

$$p\text{ is an eigenvalue of }\mathcal{A}+\mathcal{Q}\text{Δ}ℛ\text{ or }\mathcal{A}+\mathcal{U}\mathcal{V},$$

(presently the quantities of interest) is mathematically equivalent to

$\begin{array}{ll}1\text{ is an eigenvalue of Δ}ℛ{(pI-\mathcal{A})}^{-1}\mathcal{Q}\text{ or }\mathcal{U}{(pI-\mathcal{A})}^{-1}\mathcal{V}.& (16)\end{array}$

In control engineering functions of the form $ℛ{(sI-\mathcal{A})}^{-1}\mathcal{Q}$, where s is a complex variable, are called transfer functions. Although the above two problems appear a priori similar in nature and complexity — they are both eigenvalue problems — in the case that ℛ and/or 𝒬 are low-rank, then the matrix $\text{Δ }ℛ{(pI-\mathcal{A})}^{-1}𝒬$ may be much smaller than $\mathcal{A}+\mathcal{Q}\text{Δ}ℛ$, perhaps even a scalar quantity. We comment that this is one strong motivation for writing structured perturbations in the form Equation 9. In the case that $\text{Δ}=\delta$ is a scalar parameter and $ℛ{(pI-\mathcal{A})}^{-1}\mathcal{Q}$ is scalar valued, then the first relationship in Equation 16 may be solved in the sense of determining analytically what δ is required to achieve a desired dominant eigenvalue λ of $\mathcal{A}+\mathcal{Q}\text{Δ}ℛ$.

The main purpose of this short section is to emphasise that by using either of the above approaches, it is possible to consider the effects of perturbations on both λ and pathway contribution metrics simultaneously. In other words, the effects of a perturbation on an asymptotic and transient index may be examined concurrently. For instance, one goal could be to maximise $C(\text{Δ},\mathcal{P})$ or $\tilde{C}(\text{Δ},\mathcal{P})$ over all perturbations Δ which maintain λ (of the perturbed annual cycle matrix) above some desired threshold. A similar approach is taken in Guiver et al. (2016, Example 4.3) in the context of maximising population inertia in matrix population projection models for local populations of non-migratory species.

3 Results

We illustrate our results through a selection of examples. First, we consider a simple hypothetical model to illustrate the perturbation framework outlined in Section 2.3 and the sensitivity framework outlined in Section 2.4. Next, we consider a model based on the monarch butterfly (Danaus plexippus) population dynamics to show how the sensitivity framework can be used to identify which vital rates are the most sensitive to perturbations in a given season of the annual cycle. Finally, we use the same monarch butterfly model and apply perturbations, representing threats and conservation actions, in multiple seasons of the annual cycle to illustrate how the perturbation framework can be used to identify how proposed management actions will influence the contribution metrics.

3.1 Simple hypothetical example

3.1.1 The perturbation framework

We begin by illustrating how Equation 10 is derived, using a simple model with two seasons, two habitats and two stages. The model is depicted in Figure 2 and explained further in Smith et al. (2022, Example 2.1) which itself is based on Sample et al. (2019, Section 3.1). The model considers partial migration between a higher quality habitat (habitat 1) and a lower quality habitat (habitat 2). The demography matrices are given in Figure 2 and Sample et al. (2019, p.5). The migration matrices used are the same for all stage and season combinations, see Figure 2 and Smith et al. (2022, Equation 2.14a). The model is specified such that, within a season, movement happens before demography.

Figure 2

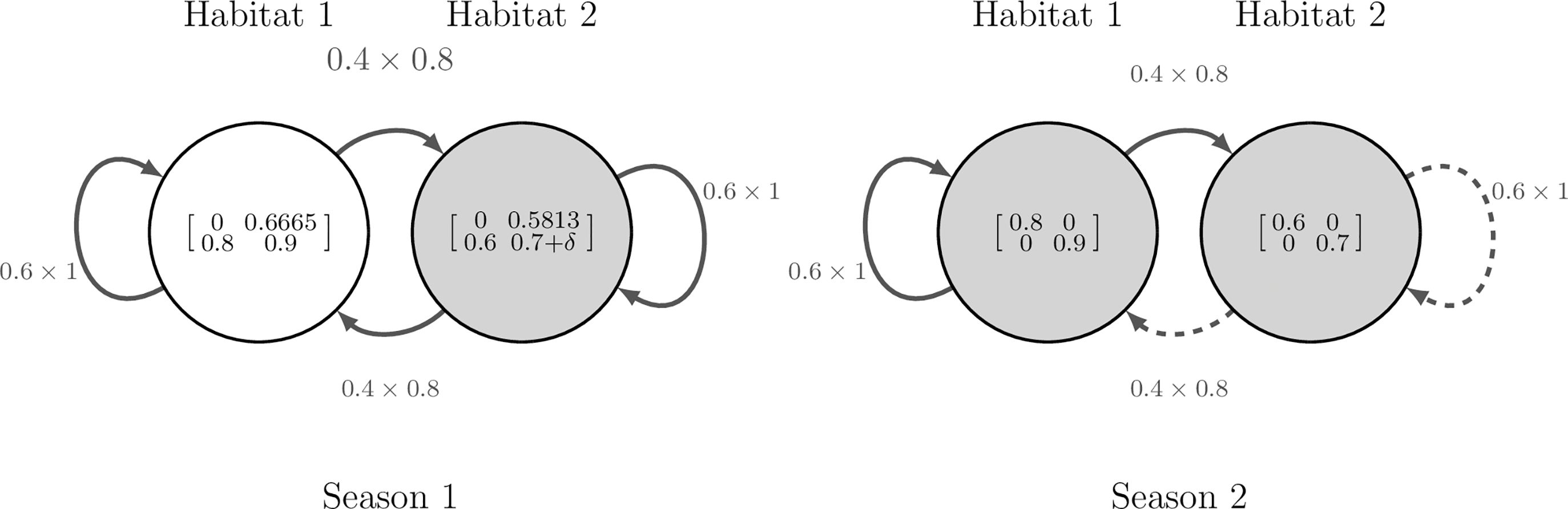
Figure 2. Diagram of the hypothetical model used in Section 3.1.1, with two seasons (s = 2), two habitats (n = 2) and two stages (c = 2). Nodes represent habitats and are labelled with their associated demographic matrices, $D_{j,k}$. Edges represent migratory routes and are labelled with the product of their associated movement rates, $p_k^i\times s_k^i$, which are assumed equal for all stages. The perturbation, δ, is applied to adult survival in habitat 2 during season 1. Shaded nodes and dashed edges represent where variables are influenced by the perturbation.

Suppose that we wish to increase the survival of adults in habitat 2 during the first season of the annual cycle by an additive structured perturbation. Since this corresponds to a scalar perturbation, we write ${\Delta }_{D_{2,1}}=\delta$, and express the perturbation as

$$D_{2,1}(\delta )=D_{2,1}+\left[\begin{array}{cc}0& 0\\ 0& \delta \end{array}\right]=D_{2,1}+\left[\begin{array}{c}0\\ 1\end{array}\right]\delta \left[\begin{array}{cc}0& 1\end{array}\right]=:D_{2,1}+Q\delta R.$$

As $D_{2,1}$ is the only matrix that is perturbed, the matrices $D_{1,1}$, $D_{j,2}$, ${\mathbb{S}}_k$ and ${\mathbb{P}}_k$ (where j, k ∈{1,2}) are unchanged by the perturbation. Thus, substituting $D_{2,1}(\delta )$ into Equations 2, 4 gives

$\begin{array}{ll}{A}_1({\text{Δ}}_1)={\mathbb{D}}_1({\mathbb{P}}_1\circ {\mathbb{S}}_1)+(E_{2,22}\otimes (Q\delta R))({\mathbb{P}}_1\circ {\mathbb{S}}_1)=A_1+(E_{2,22}\otimes (Q\delta R))({\mathbb{P}}_1\circ {\mathbb{S}}_1)& (17)\end{array}$

and

$\begin{array}{ll}{\widehat{A}}_1({\text{Δ}}_1)=({\mathbb{D}}_1+E_{2,22}\otimes (Q\delta R)){\mathbb{S}}_1={\widehat{A}}_1+(E_{2,22}\otimes (Q\delta R)){\mathbb{S}}_1,& (18)\end{array}$

respectively. The seasonal matrices $A_2$, ${\widehat{A}}_2$ and, therefore, $A_2$ are unchanged by the perturbation, whilst substituting Equations 17, 18 into Equation 6 gives

$$\begin{array}{l}{\mathbf{\text{A}}}_1({\text{Δ}}_1):=\{\begin{array}{lll}\hfill & ({\widehat{A}}_1+(E_{2,22}\otimes (Q\delta R)){\mathbb{S}}_1)\circ (E_{2,\mathcal{P}(2)\mathcal{P}(1)}\otimes J_2),\hfill & 1\in \text{Φ },\hfill \\ \hfill & A_1+(E_{2,22}\otimes (Q\delta R))({\mathbb{P}}_1\circ {\mathbb{S}}_1),\hfill & \text{otherwise },\hfill \end{array}\\ \begin{array}{ccc}& & =\{\begin{array}{lll}\hfill & {\mathbf{A}}_1+((E_{2,22}\otimes (Q\delta R)){\mathbb{S}}_1)\circ (E_{2,\mathcal{P}(2)\mathcal{P}(1)}\otimes J_2),\hfill & 1\in \text{Φ },\hfill \\ \hfill & {\mathbf{A}}_1+(E_{2,22}\otimes (Q\delta R))({\mathbb{P}}_1\circ {\mathbb{S}}_1),\hfill & \text{otherwise }.\hfill \end{array}\end{array}\end{array}$$

This is then substituted into Equation 7 to calculate the perturbed subpopulation pathway contribution metrics,

$$\mathbf{C}(\mathcal{P},\text{Δ})={𝟙}_4^{\top }\prod _{k=1}^2{\mathbf{A}}_k({\text{Δ}}_k)={𝟙}_4^{\top }{\mathbf{A}}_2{\mathbf{A}}_1({\text{Δ}}_1),$$

which can be computed numerically. We have provided MATLAB code in an online repository (see Data Availability Statement). Furthermore, the matrices are sparse and noting which blocks of the matrices are zero indicates which contribution metrics will be unchanged by the perturbation. In this example, the perturbation to ${\widehat{A}}_1$ is captured in the matrix

$$\begin{array}{l}(E_{2,22}\otimes (Q\delta R)){\mathbb{S}}_1=\left[\begin{array}{cc}{0}_{2\times 2}& 0_{2\times 2}\\ 0_{2\times 2}& Q\delta R\end{array}\right]\left[\begin{array}{cc}{({\mathbb{S}}_1)}_{1,1}& {({\mathbb{S}}_1)}_{1,2}\\ {({\mathbb{S}}_1)}_{2,1}& {({\mathbb{S}}_1)}_{2,2}\end{array}\right]=\left[\begin{array}{cc}{0}_{2\times 2}& 0_{2\times 2}\\ Q\delta R{({\mathbb{S}}_1)}_{2,1}& Q\delta R{({\mathbb{S}}_1)}_{2,2}\end{array}\right]\\ \begin{array}{cccc}& & & \begin{array}{ccc}& & =\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0.8\delta & 0& \delta \end{array}\right].\end{array}\end{array}\end{array}$$

Here: $0_{2\times 2}\in {ℝ}_{+}^{2\times 2}$ is a matrix of zeros, and ${({\mathbb{S}}_k)}_{i,j}\in {ℝ}_{+}^{2\times 2}$ is the $(i,j)$ -th block of ${\mathbb{S}}_k$. Observing where the non-zero entries are, we see that the perturbation affects adults that migrate from habitat 1 to habitat 2 in season 1, and adults that remain resident in habitat 2 during season 1. Thus, the perturbation only alters the pathway contribution metrics associated with pathways where the population ends the first season in habitat 2.

The distinct migratory routes of the population are,

$$\begin{array}{l}{\mathcal{P}}_1=1\to 1\to 1,{\mathcal{P}}_2=1\to 1\to 2,{\mathcal{P}}_3=1\to 2\to 1,{\mathcal{P}}_4=1\to 2\to 2,\\ {\mathcal{P}}_5=2\to 1\to 1,{\mathcal{P}}_6=2\to 1\to 2,{\mathcal{P}}_7=2\to 2\to 1,{\mathcal{P}}_8=2\to 2\to 2.\end{array}$$

Since ${\mathcal{P}}_1$, ${\mathcal{P}}_2$, ${\mathcal{P}}_5$ and ${\mathcal{P}}_6$ do not end season 1 in habitat 2, the pathway contribution metrics associated with these migratory routes are unchanged, that is,

$$\mathbf{\text{C}}({\mathcal{P}}_i,\text{Δ})=\mathbf{\text{C}}({\mathcal{P}}_i)\text{\hspace{1em}and\hspace{1em}}\tilde{C}({\mathcal{P}}_i,\text{Δ})=\tilde{C}({\mathcal{P}}_i)\mathrm{\forall }i\in \left\{1,2,5,6\right\}.$$

The perturbed subpopulation pathway contribution metrics for individuals using ${\mathcal{P}}_3$ is given by

$$\begin{array}{l}\mathbf{C}({\mathcal{P}}_3,\mathrm{\text{Δ}})={𝟙}_4^{\top }\left[\begin{array}{cc}{({\widehat{A}}_2)}_{1,2}{({\widehat{A}}_1)}_{2,1}+{({\widehat{A}}_2)}_{1,2}Q\delta R{({\mathbb{S}}_1)}_{2,1}& 0_{2\times 2}\\ 0_{2\times 2}& 0_{2\times 2}\end{array}\right]\\ \begin{array}{ccc}& & =𝟙{ }_4^{\top }\left[\begin{array}{cccc}0& 0.2976& 0& 0\\ 0.3456& 0.4032+0.576\delta & 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]\end{array}\\ \begin{array}{ccc}& & =\mathbf{C}({\mathcal{P}}_3)+[\begin{array}{cccc}0& 0.576\delta & 0& 0\end{array}]=[\begin{array}{cccc}0.3456& 0.7008+0.576\delta & 0& 0\end{array}].\end{array}\end{array}$$

The perturbed subpopulation pathway metrics for individuals using paths ${\mathcal{P}}_4$, ${\mathcal{P}}_7$ and ${\mathcal{P}}_8$ are calculated similarly and are given by

$$\begin{array}{l}\mathbf{C}({\mathcal{P}}_4,\text{Δ})=\mathbf{C}({\mathcal{P}}_4)+[\begin{array}{cccc}0& 0.56\delta & 0& 0\end{array}]=[\begin{array}{cccc}0.336& 0.671+0.56\delta & 0& 0\end{array}],\\ \mathbf{C}({\mathcal{P}}_7,\text{Δ})=\mathbf{C}({\mathcal{P}}_7)+[\begin{array}{cccc}0& 0& 0& 0.72\delta \end{array}]=[\begin{array}{cccc}0& 0& 0.432& 0.876+0.72\delta \end{array}],\\ \mathbf{C}({\mathcal{P}}_8,\text{Δ})=\mathbf{C}({\mathcal{P}}_8)+[\begin{array}{cccc}0& 0& 0& 0.7\delta \end{array}]=[\begin{array}{cccc}0& 0& 0.42& 0.8388+0.7\delta \end{array}].\end{array}$$

The perturbation causes subpopulation pathway contribution metrics associated with adults using ${\mathcal{P}}_3$, ${\mathcal{P}}_4$, ${\mathcal{P}}_7$ and ${\mathcal{P}}_8$ to increase linearly by a scalar multiple of δ, which is expected as the perturbation is positive and acts only on one vital rate. The perturbation has the biggest impact on adults that use ${\mathcal{P}}_7$, as this is where the coefficient of δ is the largest. Similarly, the perturbation has the smallest impact on adults that use ${\mathcal{P}}_4$, as this is where the coefficient of δ is the smallest. If the goal of the management action is to increase the survival of adults such that they replace themselves, within the subpopulation using the same migratory route, over an annual cycle, then the required perturbation for: ${\mathcal{P}}_3$ is $\delta \ge 0.5194$; ${\mathcal{P}}_4$ is $\delta \ge 0.5875$; ${\mathcal{P}}_7$ is $\delta \ge 0.1722$; and ${\mathcal{P}}_8$ is $\delta \ge 0.2303$. However, to maintain an ecologically meaningful model requires $\delta \le 0.3$. So, when considering the survival of adults in habitat 2, only the subpopulations using ${\mathcal{P}}_7$ and ${\mathcal{P}}_8$ can be perturbed sufficiently to ensure replacement.

The perturbed metapopulation pathway contribution metrics are calculated via

$$\tilde{\mathbf{C}}(\mathcal{P},\text{Δ})={𝟙}_4^{\top }\prod _{k=1}^2{\mathbf{A}}_k({\text{Δ}}_1){\mathbf{P}}_k({\text{Δ}}_1)={𝟙}_4^{\top }{\mathbf{A}}_2{\mathbf{P}}_2{\mathbf{A}}_1({\text{Δ}}_1){\mathbf{P}}_1,$$

where, as before, only $A_1$ is affected by the perturbation. Therefore, it is only the pathway contribution metrics associated with ${\mathcal{P}}_3$, ${\mathcal{P}}_4$, ${\mathcal{P}}_7$ and ${\mathcal{P}}_8$ that are perturbed. The perturbed metapopulation pathway contribution metrics for individuals using P₃ are given by

$$\begin{array}{l}\widetilde{\mathbf{\text{C}}}({\mathcal{P}}_3,\text{Δ})={𝟙}_4^{\top }\left[\begin{array}{cc}{({\widehat{A}}_2)}_{1,2}{({\mathbb{P}}_2)}_{1,2}{({\widehat{A}}_1)}_{2,1}{({\mathbb{P}}_1)}_{2,1}+{({\widehat{A}}_2)}_{1,2}{({\mathbb{P}}_2)}_{1,2}Q\delta R{({\mathbb{S}}_1)}_{2,1}{({\mathbb{P}}_1)}_{2,1}& 0_{2\times 2}\\ \hfill 0_{2\times 2}\hfill & 0_{2\times 2}\end{array}\right]\\ ={𝟙}_4^{\top }\left[\begin{array}{cccc}0& 0.0476& 0& 0\\ 0.0553& 0.0645+0.0922\delta & 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]\\ =\widetilde{\mathbf{\text{C}}}({\mathcal{P}}_3)+[\begin{array}{cccc}0& 0.0922\delta & 0& 0\end{array}]=[\begin{array}{cccc}0.0553& 0.1121+0.0922\delta & 0& 0\end{array}].\end{array}$$

The perturbed metapopulation pathway contribution metrics for individuals using ${\mathcal{P}}_4$, ${\mathcal{P}}_7$ and ${\mathcal{P}}_8$ are calculated similarly and given by

$$\begin{array}{l}\tilde{\mathbf{C}}({\mathcal{P}}_4,\text{Δ})=\tilde{\mathbf{C}}({\mathcal{P}}_4)+[\begin{array}{cccc}0& 0.1344\delta & 0& 0\end{array}]=[\begin{array}{cccc}0.0806& 0.161+0.1344\delta & 0& 0\end{array}],\\ \tilde{\mathbf{C}}({\mathcal{P}}_7,\text{Δ})=\tilde{\mathbf{C}}({\mathcal{P}}_7)+[\begin{array}{cccc}0& 0& 0& 0.1728\delta \end{array}]=[\begin{array}{cccc}0& 0& 0.1037& 0.2102+0.1728\delta \end{array}],\\ \tilde{\mathbf{C}}({\mathcal{P}}_8,\text{Δ})=\tilde{\mathbf{C}}({\mathcal{P}}_8)+[\begin{array}{cccc}0& 0& 0& 0.252\delta \end{array}]=[\begin{array}{cccc}0& 0& 0.1512& 0.302+0.252\delta \end{array}].\end{array}$$

Note that these metrics and the impact the perturbation has on them is smaller than the corresponding metrics in $C(\mathcal{P})$, due to the calculation of $\tilde{C}(\mathcal{P})$ including the proportion of individuals using a migratory route. As in the case of $C(\mathcal{P})$, the perturbation causes the metapopulation pathway contribution metrics associated with adults using ${\mathcal{P}}_3$, ${\mathcal{P}}_4$, ${\mathcal{P}}_7$ and ${\mathcal{P}}_8$ to increase linearly by a factor of δ. However, this time, the perturbation has the biggest impact on adults that use ${\mathcal{P}}_8$, and the smallest impact on adults that use ${\mathcal{P}}_3$, rather than ${\mathcal{P}}_7$ and ${\mathcal{P}}_4$, respectively. In other words, perturbations of this form that have the biggest impact on the contribution of the focal subpopulation to itself are those applied to ${\mathcal{P}}_7$; whilst perturbations of this form that have the biggest impact on the contribution of the focal subpopulation to the total population are those applied to ${\mathcal{P}}_8$.

The impacts of the perturbation on the habitat contribution metrics can be calculated independently, or by summing the impacts the perturbation has on the metapopulation pathway contribution metrics for all distinct migratory routes. They are given by,

$$\begin{array}{l}\mathbf{C}(\text{Δ})={𝟙}_4^{\top }{A}_2({\text{Δ}}_2)A_1({\text{Δ}}_1)={𝟙}_4^{\top }{A}_2(A_1+(E_{2,22}\otimes (Q\delta R))({\mathbb{P}}_1\circ {\mathbb{S}}_1)\\ \begin{array}{cc}& =\mathbf{C}+[\begin{array}{cccc}0& 0.2266\delta & 0& 0.4248\delta \end{array}]\end{array}\\ \begin{array}{cc}& \end{array}=[\begin{array}{cccc}0.5027& 0.9545+0.2266\delta & 0.4505& 0.8756+0.4248\delta \end{array}].\end{array}$$

The perturbation causes a linear increase in the habitat contribution metrics associated with the adults of the population; and has a greater effect on adults that start the annual cycle in habitat 2. One reasonable management goal could be for the adult populations of both habitats to replace themselves, this would be achieved with 0.2928 ≤ δ ≤ 0.3, to ensure the model remains ecologically meaningful.

3.1.2 The sensitivity framework

We proceed to use the same simple hypothetical model to illustrate the sensitivity framework described in Section 2.4. As before, we are interested in the impact that increasing the survival of adults in habitat 2 during season 1 has on the pathway contribution metrics. In the sensitivity framework, we write this as ${(D_{2,1})}_{2,2}=0.7+\delta$ and $p=\delta$, whilst all other entries remain constant. Hence, we wish to find the sensitivity of the contribution metrics with respect to entry (2,2) in $D_{2,1}$. Thus, we are interested in the matrix function

$$D_{2,1}(\delta )=\left[\begin{array}{cc}0 & 0.5813\\ 0.6 & 0.7+\delta \end{array}\right],$$

as shown in Figure 2. As before, the sensitivity of the contribution metrics corresponding to migratory routes ${\mathcal{P}}_1$, ${\mathcal{P}}_2$, ${\mathcal{P}}_5$ and ${\mathcal{P}}_6$ are zero, as these routes do not end season 1 in habitat 2.

Since only $D_{2,1}$, and hence also only $A_1$, is perturbed, Equation 12 is only non-zero for k = 1. For individuals using ${\mathcal{P}}_3$, Equation 12 condenses to

$$\frac{\text{dvec }(A_1)}{\text{d}{p}^{\top }}=\left(Z_{1,1}{X}_1(\text{vec }(E_{2,22})\otimes \frac{\text{dvec} D_{2,1}}{\text{d}{p}^{\top }}\right))\circ Z_{4,1}.$$

Substituting this into Equation 11, noting that only season 1 is of interest, we get

$$\begin{array}{l}\frac{\text{d}\mathbf{C}{({\mathcal{P}}_3)}^{\top }}{\text{d}{\mathbf{\text{p}}}^{\top }}=(I_4\otimes {𝟙}_4^{\top })\left(\left({({\mathbf{\text{Y}}}_1^0)}^{\top }\otimes {\mathbf{\text{Y}}}_2^2\right)\left(Z_{1,1}{X}_1(\text{vec }(E_{2,22})\otimes \frac{\text{d vec }{D}_{2,1}}{\text{d}{\mathbf{\text{p}}}^{\top }})\right)\circ Z_{4,1}\right)\\ \begin{array}{ccc}\begin{array}{cc}& \end{array}& \hspace{1em}& \begin{array}{l}=(I_4\otimes {𝟙}_4^{\top })(\left(I_4\otimes ({\widehat{A}}_2\circ (E_{2,12}\otimes J_2)\right)(({\mathbb{S}}_1^{\top }\otimes I_4)(I_2\otimes {\mathbf{\text{K}}}_{2,2}\otimes I_2)\left(\text{vec }(E_{2,22})\otimes \frac{\text{d vec }{D}_{2,1}}{\text{d}{\mathbf{\text{p}}}^{\top }}\right))\circ \text{vec }(E_{2,21}\otimes J_2))\\ ={[\begin{array}{cccc}0 & 0.576 & 0 & 0\end{array}]}^{\top }.\end{array}\end{array}\end{array}$$

We note that the constants constants $Z_{4,1}$ and $Y_2^2$ depend on which pathway is used in seasons 1 and 2; they will change between ${\mathcal{P}}_3$, ${\mathcal{P}}_4$, ${\mathcal{P}}_7$ and ${\mathcal{P}}_8$. All other constants will remain the same between calculations of the sensitivities. The sensitivity of the subpopulation pathway contribution metrics for individuals using ${\mathcal{P}}_4$, ${\mathcal{P}}_7$ and ${\mathcal{P}}_8$ are calculated similarly and are given by

$$\frac{\text{d}C{({\mathcal{P}}_4)}^{\top }}{\text{d}{p}^{\top }}=\left[\begin{array}{c}0\\ 0.56\\ 0\\ 0\end{array}\right],\frac{\text{d}C{({\mathcal{P}}_7)}^{\top }}{\text{d}{p}^{\top }}=\left[\begin{array}{c}0\\ 0\\ 0\\ 0.72\end{array}\right],\text{\hspace{1em}and\hspace{1em}}\frac{\text{d}C{({\mathcal{P}}_8)}^{\top }}{\text{d}{p}^{\top }}=\left[\begin{array}{c}0\\ 0\\ 0\\ 0.7\end{array}\right],$$

respectively. As in Section 3.1.1, we see that only the adults using ${\mathcal{P}}_3$, ${\mathcal{P}}_4$, ${\mathcal{P}}_7$ and ${\mathcal{P}}_8$ are affected by the perturbation. Furthermore, since each sensitivity is positive and constant the subpopulation pathway contribution metrics are increasing linearly. In simple examples such as this, where only a single matrix in a single season is perturbed, the sensitivity framework gives the same results as linearising the results of the perturbation framework; that is, the sensitivity of the subpopulation pathway contribution metrics is equal to the coefficient of δ in the perturbation framework.

Similarly, Equation 13 for individuals using ${\mathcal{P}}_3$ condenses to

$$\begin{array}{l}\frac{\text{d}\widetilde{\mathbf{\text{C}}}{({\mathcal{P}}_3)}^{\top }}{\text{d}{\mathbf{\text{p}}}^{\top }}=(I_4\otimes {𝟙}_4^{\top })\left({({\text{ϒ}}_1^0)}^{\top }\otimes {\text{ϒ}}_2^2\right)\left(({\mathbf{\text{P}}}_1^{\top }\otimes I_4)\frac{\text{d vec}({\mathbf{\text{A}}}_1)}{\text{d}{\mathbf{\text{p}}}^{\top }}\right)\\ \begin{array}{ccc}& & \begin{array}{l}=(I_4\otimes {𝟙}_4^{\top })(I_4\otimes \left(({\widehat{A}}_2\circ (E_{2,12}\otimes J_2))(I_2\otimes ({\mathbb{P}}_2{)}_{12}))\right)\left(((I_2\otimes ({\mathbb{P}}_1{)}_{21}{)}^{\top }\otimes I_4)\frac{\text{d vec}({\mathbf{\text{A}}}_1)}{\text{d}{\mathbf{\text{p}}}^{\top }}\right)\\ ={[\begin{array}{cccc}0& 0.0922& 0& 0\end{array}]}^{\top }.\end{array}\end{array}\end{array}$$

Here, ${\text{ϒ}}_2^2$ and ${\mathbf{P}}_1$ depend on which pathway is used in seasons 1 and 2, and so change between ${\mathcal{P}}_3$, ${\mathcal{P}}_4$, ${\mathcal{P}}_7$ and ${\mathcal{P}}_8$. All other constants will remain the same between calculations of the sensitivities. The sensitivity of the metapopulation pathway contribution metrics for individuals using ${\mathcal{P}}_4$, ${\mathcal{P}}_7$ and ${\mathcal{P}}_8$ are calculated similarly and are given by

$$\frac{\text{d}\tilde{C}{({\mathcal{P}}_4)}^{\top }}{\text{d}{p}^{\top }}=\left[\begin{array}{c}0\\ 0.1344\\ 0\\ 0\end{array}\right],\frac{\text{d}\tilde{C}{({\mathcal{P}}_7)}^{\top }}{\text{d}{p}^{\top }}=\left[\begin{array}{c}0\\ 0\\ 0\\ 0.1728\end{array}\right],\text{\hspace{1em}and\hspace{1em}}\frac{\text{d}\tilde{C}{({\mathcal{P}}_8)}^{\top }}{\text{d}{p}^{\top }}=\left[\begin{array}{c}0\\ 0\\ 0\\ 0.252\end{array}\right],$$

respectively. As expected, we see that the sensitivity of the metpopulation pathway contribution metrics is equal to the coefficient of δ in the perturbation framework.

Similarly to the example in Section 3.1.1, the sensitivities of the habitat contribution metrics can be calculated directly from Equation 11 with $k\notin \Phi$ for all k; alternatively, they can be calculated by summing the sensitivities of the metapopulation pathway contribution metrics. They are given by

$$\begin{array}{l}\frac{\text{d}{\mathbf{\text{C}}}^{\top }}{\text{d}{\mathbf{\text{p}}}^{\top }}=(I_4\otimes {𝟙}_4^{\top })\left(({\mathbf{\text{Y}}}_1^0{)}^{\top }\otimes {\mathbf{\text{Y}}}_2^2)\left(\left(Z_{1,1}{X}_1\left(\text{vec }(E_{2,22}\right)\otimes \frac{\text{d vec }{D}_{2,1}}{\text{d}{\mathbf{\text{p}}}^{\top }}\right)\right)\circ Z_{4,1}\right)\\ \begin{array}{cc}& \begin{array}{l}=(I_4\otimes {𝟙}_4^{\top })(I_4\otimes A_2)(((({\mathbb{P}}_1\circ {\mathbb{S}}_1{)}^{\top }\otimes I_4)(I_2\otimes {\mathbf{\text{K}}}_{2,2}\otimes I_2)(\text{vec }(E_{2,22})\otimes \frac{\text{d} \text{vec} D_{2,1}}{\text{d}{\mathbf{\text{p}}}^{\top }}))\circ {𝟙}_{16})\\ ={[\begin{array}{cccc}0& 0.2266& 0& 0.4248\end{array}]}^{\top }.\end{array}\end{array}\end{array}$$

Again, the results of the sensitivity framework and the perturbation framework agree with each other.

3.2 Monarch butterfly

3.2.1 Sensitivity of all the vital rates experienced in a fixed season

Here, we assess the impact of individually altering each vital rate experienced in a fixed season of the annual cycle model. We use the model for the monarch butterfly (Danaus plexippus) in eastern North America described in Smith et al. (2022), based on the previous models in Flockhart et al. (2015) and Sample et al. (2018). The model is for the female population and contains five stages (c = 5), four habitats (n = 4) and twelve seasons (s = 12). The life stages are: immature individuals, including eggs, larval and pupal development until eclosion (1); eclosed butterflies in their first month of life and in reproductive diapause (2); eclosed butterflies in their second month of life or older and in reproductive diapause (3); eclosed butterflies in their first month of life and in breeding condition (4); and, eclosed butterflies in their second month of life or older and in breeding condition (5). The habitats are: Mexico (M or 1), Southern US (S or 2), Central US (C or 3) and Northern US (N or 4). In Smith et al. (2022, Table 3.1), they calculate the pathway contribution metrics for every possible pathway in the migratory cycle. They find that monarchs travelling from habitat 3 to habitat 4 during season 6 contribute the least (smallest value of $C(\mathcal{P})$ and $\tilde{C}(\mathcal{P})$), whereas those travelling from habitat 2 to habitat 3 during this month contribute the most (largest value of $C(\mathcal{P})$ and $\tilde{C}(\mathcal{P})$).

In this example, we calculate the sensitivity of all vital rates in season 6 to establish where perturbations should be applied during season 6 to have the biggest effect on the pathway contribution metrics. In this case, the sensitivity and perturbation formulae give the same results because the proposed perturbations linearly perturb the annual cycle model. The pathways used by monarchs during season 6 are

$$\begin{array}{l}{\mathcal{P}}_1:{\mathcal{P}}_1(6)=2,{\mathcal{P}}_1(7)=3\text{\hspace{1em}and\hspace{1em}}{\mathcal{P}}_1(k)=0\text{\hspace{1em}for }k\notin \left\{6,7\right\},\\ {\mathcal{P}}_2:{\mathcal{P}}_2(6)=2,{\mathcal{P}}_2(7)=4\text{\hspace{1em}and\hspace{1em}}{\mathcal{P}}_2(k)=0\text{\hspace{1em}for }k\notin \left\{6,7\right\},\\ {\mathcal{P}}_3:{\mathcal{P}}_3(6)=3,{\mathcal{P}}_3(7)=3\text{\hspace{1em}and\hspace{1em}}{\mathcal{P}}_3(k)=0\text{\hspace{1em}for }k\notin \left\{6,7\right\},\\ {\mathcal{P}}_4:{\mathcal{P}}_4(6)=3,{\mathcal{P}}_4(7)=4\text{\hspace{1em}and\hspace{1em}}{\mathcal{P}}_4(k)=0\text{\hspace{1em}for }k\notin \left\{6,7\right\}.\end{array}$$

Figures 3, 4 contain the network graphs corresponding to the demography, movement survival and proportion migrating during season 6, respectively.

Figure 3

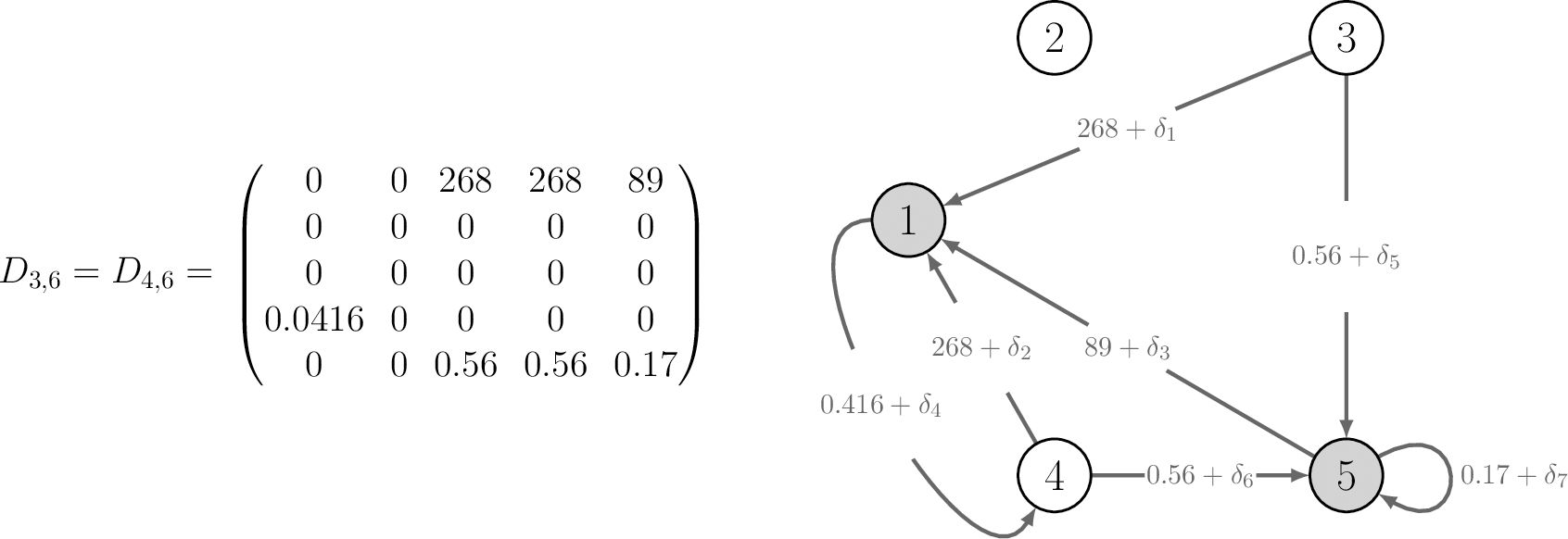
Figure 3. The demographic population projection matrix and corresponding life cycle graph for monarch butterflies in region $j\in \left\{3,4\right\}$ during season 6. Refer to the main text for details of the life stages. Shaded nodes represent stages that are present in habitat 3 at the start of season 6; there are no stages present in habitat 4 at the start of season 6. The perturbations ${\delta }_l$ with $l\in \left\{1,\dots ,7\right\}$ are applied to the vital rates one at a time when calculating the sensitivities of pathway contribution metrics.

Figure 4

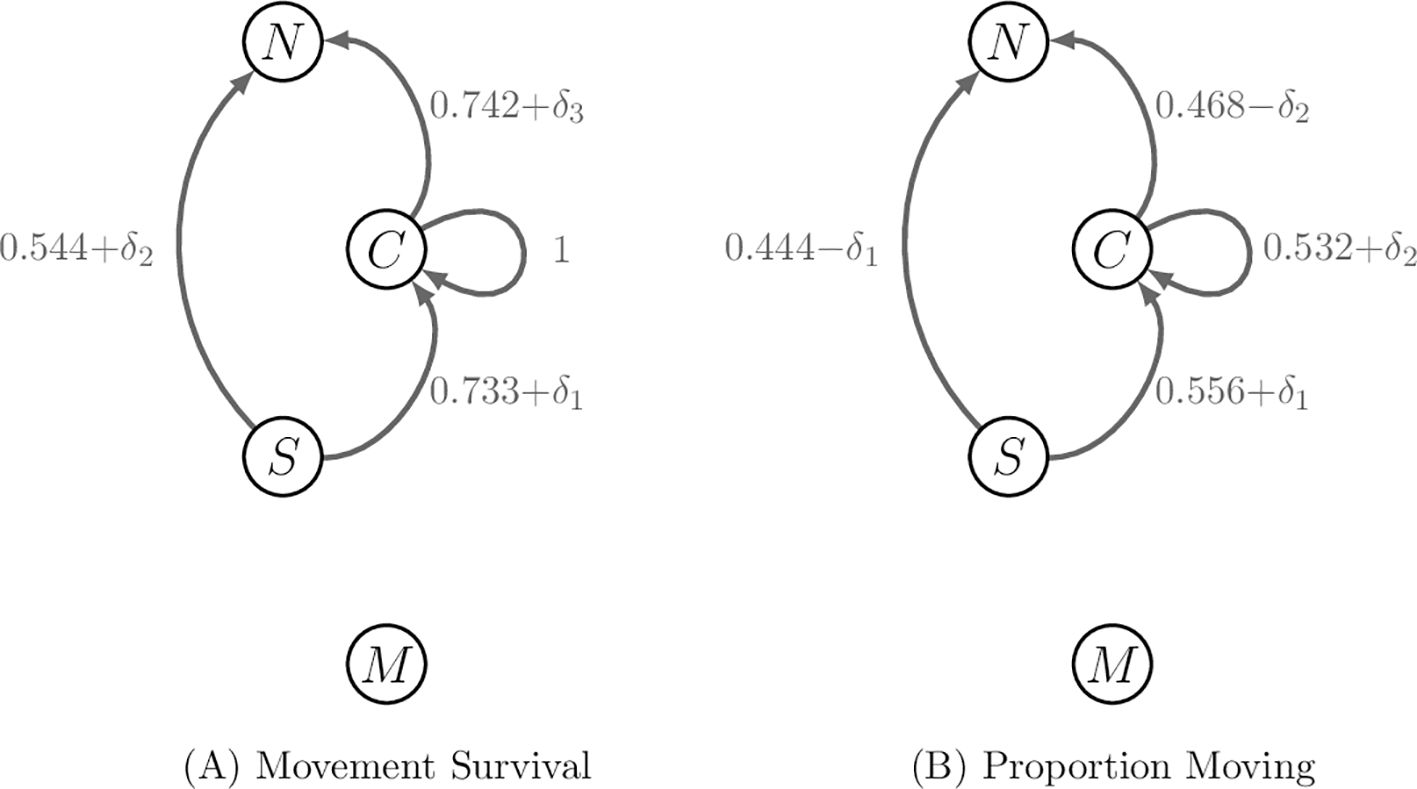
Figure 4. Movement rates of stage 4 and 5 individuals along migratory pathways during season 6. Stages 1–3 do not migrate during season 6. (A) The perturbations to movement survival ${\delta }_l$ with $l\in \left\{1,\dots ,3\right\}$ are applied one at a time when calculating the sensitivities of contribution metrics. The survival rate associated with remaining in habitat 3 is fixed and so cannot be perturbed. (B) The perturbations to the proportion moving ${\delta }_1$ and ${\delta }_2$ are applied separately to each other, but to two pathways at once to ensure the proportions leaving habitat j during season 6 sum to 1.

We begin by perturbing the demographic rates experienced during season 6 of the annual cycle. Since movement happens before demography, the monarch butterflies will undergo demography in habitats 3 and 4. Specifically, individuals using ${\mathcal{P}}_1$ and ${\mathcal{P}}_3$ will undergo demography in habitat 3, whilst individuals using ${\mathcal{P}}_2$ and ${\mathcal{P}}_4$ will undergo demography in habitat 4. There are seven demographic rates, associated with each habitat, which we perturb individually and calculate sensitivities for both $C({\mathcal{P}}_i)$ and $\tilde{C}({\mathcal{P}}_i)$ using Equations 11, 13, respectively.

We outline how to use the equations in Section 2.4, by specifying ${\mathcal{P}}_1$ and perturbing the transition of stage 3 individuals to stage 5 individuals (by ${\delta }_5$, see Figure 3) in habitat 3 during season 6. Thus, j = 3, $\mathcal{P}(6)=2$ and $\mathcal{P}(7)=3$, so that Equation 12 becomes

$\begin{array}{ll}\frac{\text{d vec }(A_6)}{\text{d}{\text{p}}^{\top }}=\left(({\mathbb{S}}_6^{\top }\otimes I_{20})\left(X_1\left(\text{vec }(E_{4,33}\right)\otimes \frac{\text{dvec} D_{3,6}}{\text{d}{p}^{\top }}\right)\right))\circ \text{vec }(E_{4,32}\otimes J_5),& (19)\end{array}$

where $X_1=I_4\otimes K_{5,4}\otimes I_5$. Substituting into Equation 11 gives

$\begin{array}{ll}\begin{array}{l}\frac{\text{d}\mathbf{C}({\mathcal{P}}_1)}{\text{d}{\mathbf{\text{p}}}^{\top }}=(I_{20}\otimes {𝟙}_{20}^{\top })(\left({\mathbf{\text{Y}}}_1^5{)}^{\top }\otimes {\mathbf{\text{Y}}}_7^{12}\right)\frac{\text{d vec }({\mathbf{\text{A}}}_6)}{\text{d}{\mathbf{\text{p}}}^{\top }}\\ \begin{array}{ccc}& & =\left(\begin{array}{cccccccc}0 & 4.47\times {10}^{-2} & 4.47\times {10}^{-2} & 0& 0 & \left|{\mathbf{0}}_5^{\top }\right|& \left|{\mathbf{0}}_5^{\top }\right|& \left|{\mathbf{0}}_5^{\top }\right|\end{array}\right).\end{array}\end{array}& (20)\end{array}$

Note that the sensitivity vector is only populated in the second and third entries of the first sub-block, this is because the only viable states of the population at the start of the annual cycle are individuals that are in stage 2 or stage 3 and in habitat 1.

Similarly, we calculate the sensitivities of $\tilde{C}({\mathcal{P}}_1)$ by inputting Equation 19 into Equation 13, which gives

$$\begin{array}{l}\frac{\text{d}\tilde{C}({\mathcal{P}}_1)}{\text{d}{\mathbf{\text{p}}}^{\top }}=(I_{20}\otimes {𝟙}_{20}^{\top })\left(\right(\left({\text{ϒ}}_1^5{)}^{\top }\otimes {\text{ϒ}}_7^{12}\right)\left(((I_4\otimes ({\mathbb{P}}_6{)}_{3,2})\otimes I_{20})\frac{\text{d vec }({\mathbf{\text{A}}}_6)}{\text{d}{\mathbf{\text{p}}}^{\top }})\right)\\ \begin{array}{ccc}& & =\left(\begin{array}{cccccccc}0& 2.48\times {10}^{-2}& 2.48\times {10}^{-2}& 0& 0& \left|{\mathbf{0}}_5^{\top }\right|& \left|{\mathbf{0}}_5^{\top }\right|& \left|{\mathbf{0}}_5^{\top }\right|\end{array}\right).\end{array}\end{array}$$

Note that $\text{d}{P}_6/\text{d}{p}^{\top }=0$, as only the demography matrices are perturbed. The sensitivities of $\tilde{C}({\mathcal{P}}_1)$ are also only non-zero in the second and third entries, which are equal to each other. In fact, all $C({\mathcal{P}}_i)$ and $\tilde{C}({\mathcal{P}}_i)$ will take this form, and so in our results tables we only record one sensitivity for each vital rate, but note that the sensitivity of all contribution metrics will take the same form as the vector in Equation 20. The sensitivity results for perturbing demographic rates are recorded in Table 2.

Table 2

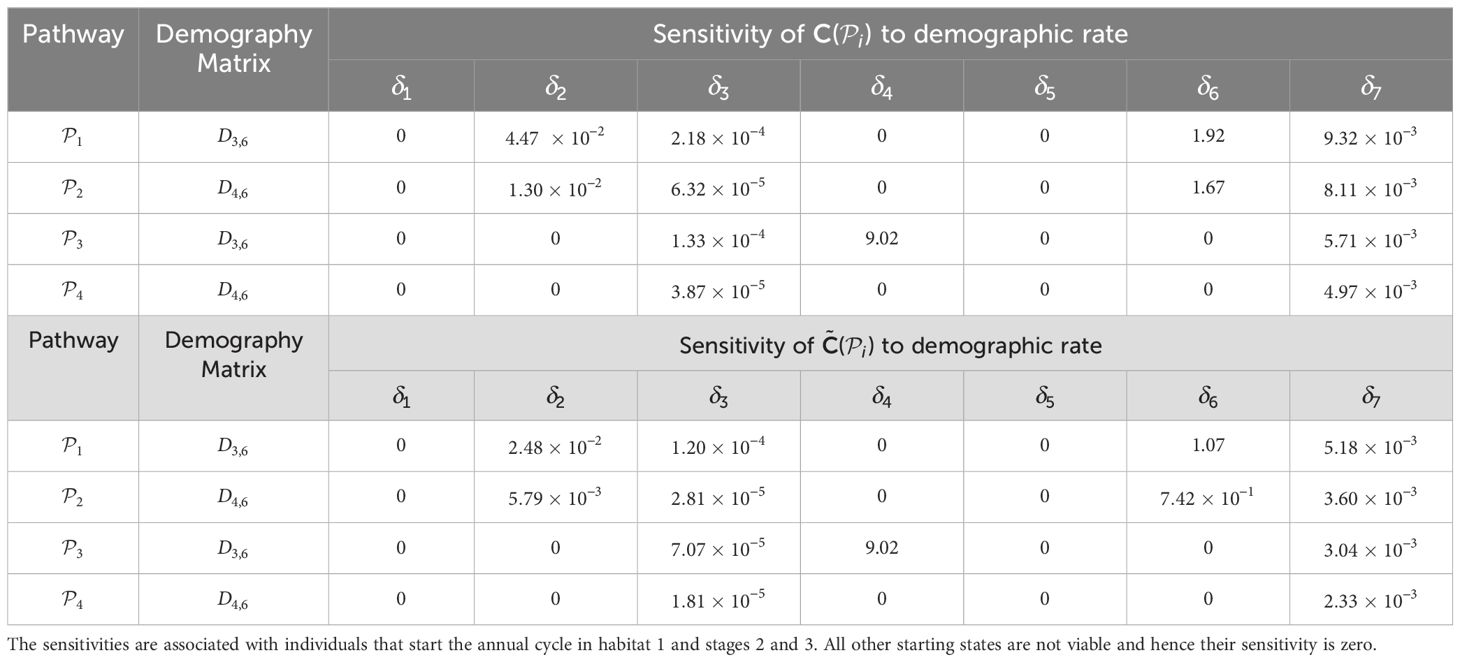
Table 2. Sensitivities of the pathway contribution metrics for the monarch butterfly annual cycle model considered in Section 3.2.1, when demographic rates are perturbed one at a time, as shown in Figure 3.

To allow for easier comparison between the fecundity and survival rates, we also compute the elasticities using Equation 14. In this example, all the perturbed pathway contribution metrics are linearly dependent on δ, resulting in all sensitivities being constant. Thus, Equation 14 becomes

$$\frac{\mathit{Є}C{({\mathcal{P}}_i)}^{\top }}{\mathit{Є}{p}^{\top }}=({\delta }_l\oslash C({\mathcal{P}}_i,{\delta }_l))\left(\frac{\text{d}C({\mathcal{P}}_i,{\delta }_l)}{\text{d}{\delta }_l}\right)=(c_1{\delta }_l)\oslash (c_1{\delta }_l+c_0).$$

Here, $c_0$ is the vector of unperturbed subpopulation pathway contribution metrics and $c_1$ is the sensitivity vector; the division of vectors is computed entrywise. The elasticities of the metapopulation contribution metrics are calculated similarly. We evaluate the elasticities with ${\delta }_l$ equal to 1% of the vital rate that it is perturbing. The elasticity vector takes the same form as the sensitivity vector (see Equation 20) and the results are recorded in Table 3.

Table 3

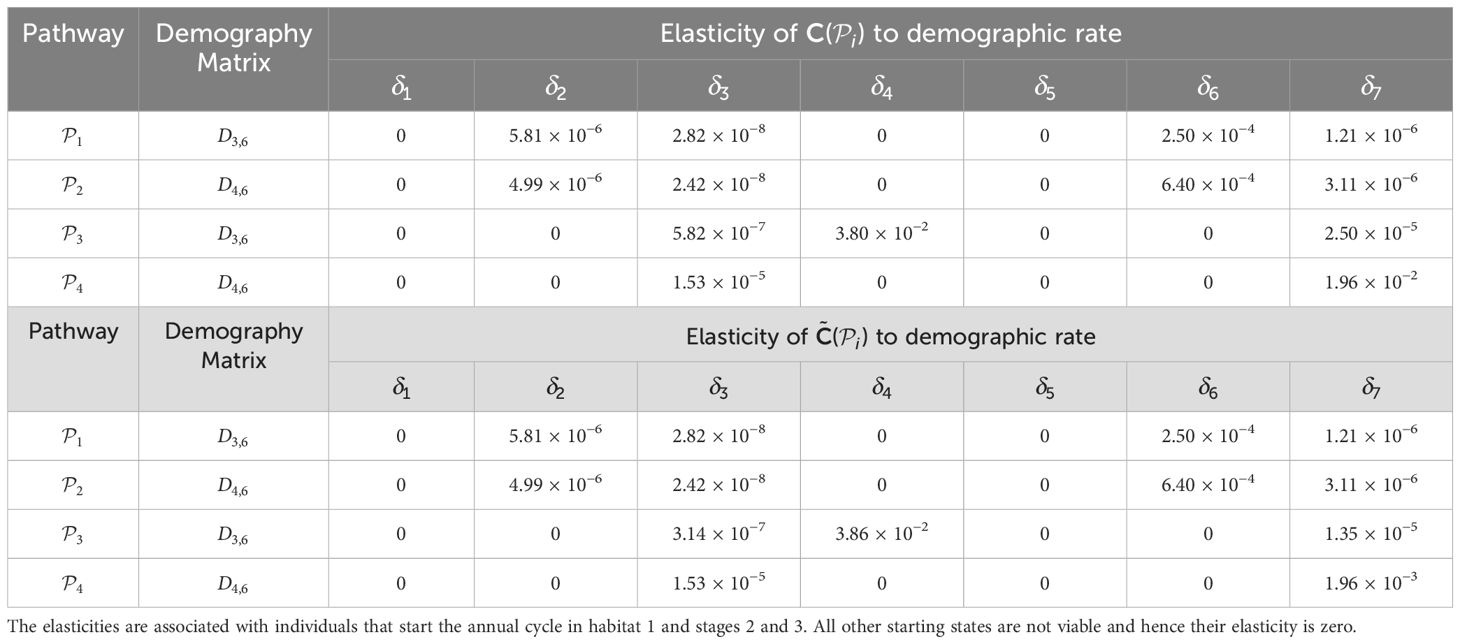
Table 3. Elasticities (evaluated with δ_l equal to 1% of the vital rate that is being perturbed) of the pathway contribution metrics for the monarch butterfly annual cycle model considered in S 3.2.1, when demographic rates are perturbed one at a time, as shown in Figure 3.

Next, we perturb the movement survival during season 6 of the annual cycle, noting that the survival associated with remaining in habitat 3 during season 6 is fixed at 1 and cannot be perturbed. The movement survival associated with the remaining three pathways are perturbed one at a time; only one $\text{dvec }{S}_6^i/\text{d}{p}^{\top }$ is non-zero at a time, as was the case for $\text{d}{D}_{j,6}/\text{d}{p}^{\top }$ when calculating the sensitivities of the demographic rates. The resulting vectors for the sensitivities take the same form as Equation 20 and the value of the non-zero elements are recorded in Table 4; the corresponding elasticities are recorded in Table 5.

Table 4

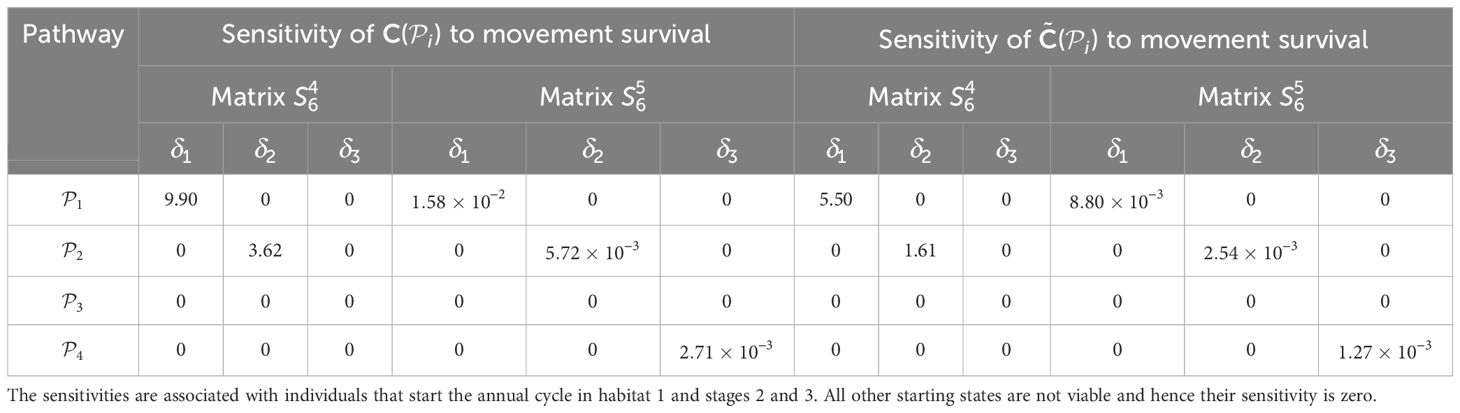
Table 4. Sensitivities of the pathway contribution metrics for the monarch butterfly annual cycle model considered in Section 3.2.1, when perturbing movement survival one at a time, as shown in Figure 4A.

Table 5

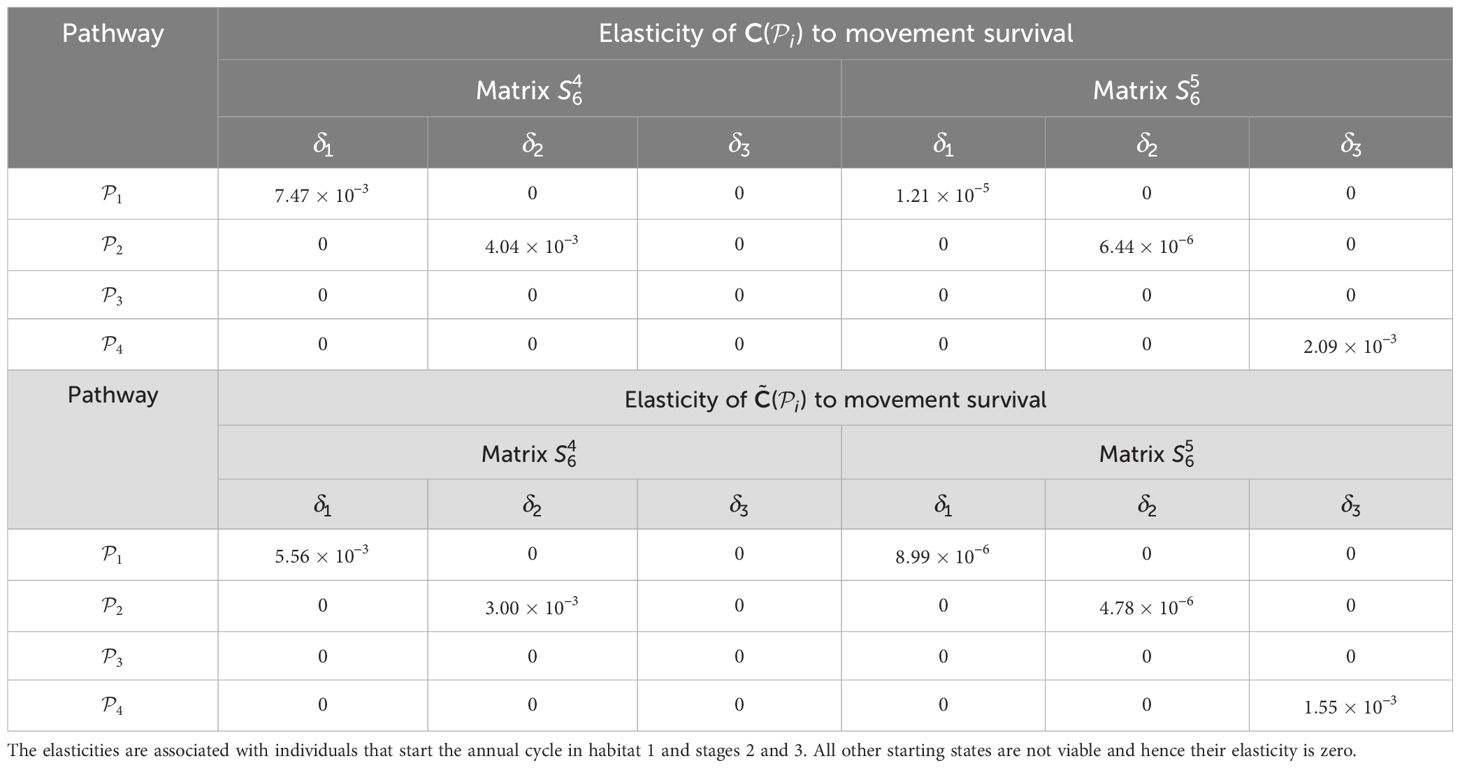
Table 5. Elasticities (evaluated with δ_l equal to 1% of the vital rate that is being perturbed) of the pathway contribution metrics for the monarch butterfly annual cycle model considered in Section 3.2.1, when perturbing movement survival one at a time, as shown in Figure 4A.

Finally, we perturb the proportion of the population that uses a pathway during season 6. We note that all the proportions associated with individuals using pathways from habitat j during season 6 need to sum to 1. Hence, perturbing the proportion of individuals migrating from habitat j to habitat l during season 6 will perturb the proportions associated with all other pathways that start season 6 in habitat j. Since there are only two pathways from each habitat populated at the start of season 6, we achieve this by applying ${\delta }_l$ and − ${\delta }_l$ to the proportions associated with the same starting habitat and compute the sensitivities similarly to before, recording the results in Table 6. When calculating the elasticities, we set ${\delta }_l$ equal to 1% of the vital rate that it is positively perturbing; that is, ${\delta }_1=5.56\times {10}^{-3}$ and ${\delta }_2=5.32\times {10}^{-3}$. The results are recorded in Table 7.

Table 6

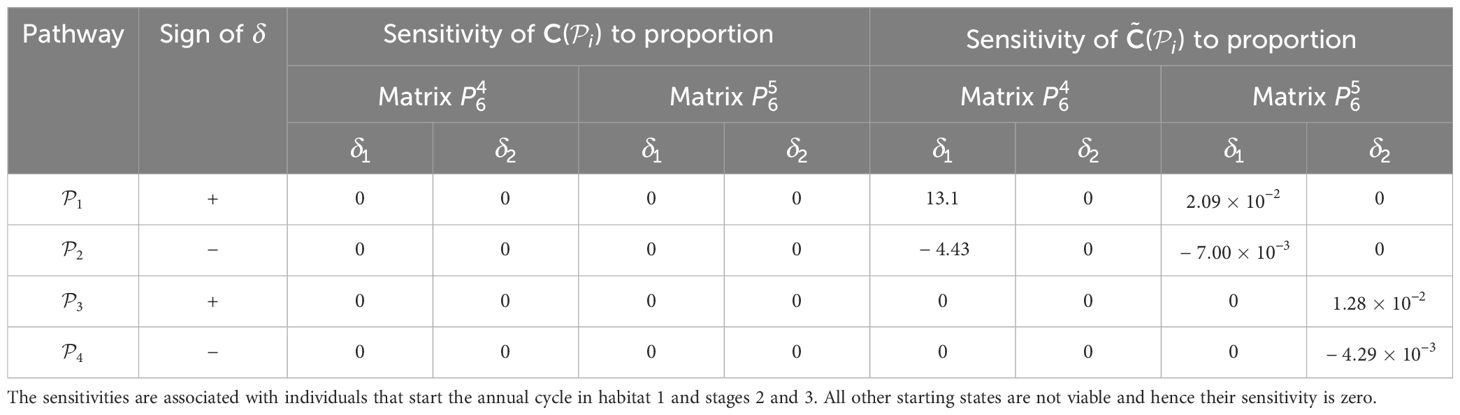
Table 6. Sensitivities of the pathway contribution metrics for the monarch butterfly annual cycle model considered in Section 3.2.1, when proportion of population migrating is perturbed one starting habitat at a time, whilst ensuring that the proportions leaving the starting habitat during season 6 sum to 1, as shown in Figure 4B.

Table 7

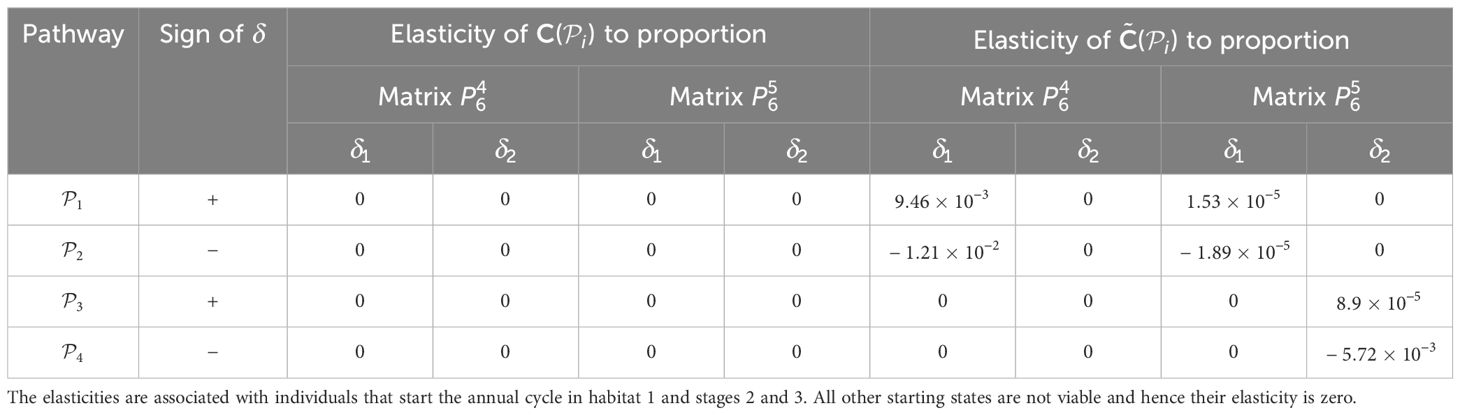
Table 7. Elasticities (evaluated with δ_l equal to 1% of the vital rate that is being positively perturbed) of the pathway contribution metrics for the monarch butterfly annual cycle model considered in Section 3.2.1, when proportion of population migrating is perturbed one starting habitat at a time whilst ensuring that the proportions leaving the starting habitat during season 6 sum to 1, as shown in Figure 4B.

Once the sensitivities have been calculated, population managers can make informed decisions about where to apply management actions to achieve the most desirable results. In Tables 2–5, all non-zero sensitivities are positive; that is, increasing the vital rate results in an increase in the pathway contribution metrics, as we would expect due to the positive nature of the perturbations. The metapopulation pathway contribution metrics ($\tilde{C}({\mathcal{P}}_i)$) are most sensitive to changes to the demographic transition rate from stage 1 to stage 4 (perturbed by ${\delta }_4$) in individuals that use ${\mathcal{P}}_3$. It is predicted that $\tilde{C}({\mathcal{P}}_3)$ will increase by a factor of 9.02. This vital rate is also associated with the largest elasticity, thus requires the smallest percentage change to achieve the same increase to $\tilde{C}({\mathcal{P}}_3)$, compared to the other demographic rates. Across all pathways, perturbing the demographic transition rate from stage 5 to stage 1 (perturbed by ${\delta }_3$) will have the smallest effect on the pathway contribution metrics. Considering the movement survival, the $\tilde{C}({\mathcal{P}}_i)$ are most sensitive to changes to the survival of stage 4 individuals that use ${\mathcal{P}}_1$ (perturbed by ${\delta }_1$). It is predicted that $\tilde{C}({\mathcal{P}}_1)$ will increase by a factor of 5.50; this vital rate is also associated with the largest elasticity. The $\tilde{C}({\mathcal{P}}_i)$ are the least sensitive to changes in the movement survival of stage 5 individuals using ${\mathcal{P}}_4$ (perturbed by ${\delta }_3$), $\tilde{C}({\mathcal{P}}_4)$ is predicted to increase by a factor of 1.27 × 10⁻³. However, stage 5 individuals using ${\mathcal{P}}_2$ (perturbed by ${\delta }_2$) are associated with the smallest elasticity, and so will require the largest proportional change in their movement survival to achieve the same increase in $\tilde{C}({\mathcal{P}}_2)$ as the other $\tilde{C}({\mathcal{P}}_i)$.

When perturbing the proportion of individuals using a pathway, the necessary trade-off between the proportions associated with pathways that start in the same habitat means that some of the sensitivities and elasticities are negative, namely those corresponding to the subpopulations using ${\mathcal{P}}_2$ and ${\mathcal{P}}_4$. However, the sign of the perturbations to these pathways is also negative. Hence, these results mean that decreasing the proportion of individuals that use these pathways decreases the contribution of the subpopulation using these pathways to the total population ($\tilde{C}({\mathcal{P}}_i)$). Therefore, the magnitude of the sensitivities and elasticities informs which vital rates are impacted the most by the proposed perturbations. For example, in Table 6, we see that the $\tilde{C}({\mathcal{P}}_i)$ are most sensitive to increasing the proportion of individuals that use ${\mathcal{P}}_1$ and, consequently, decreasing the proportion of individuals that use ${\mathcal{P}}_2$. However, in Table 7, the elasticities advise that the proportion of individuals that use ${\mathcal{P}}_2$ needs to be increased by a smaller percentage than the proportion of individuals that use ${\mathcal{P}}_1$ to cause the same increase in the $\tilde{C}({\mathcal{P}}_i)$; which is the opposite advice to that given by the sensitivities. This may seem counter-intuitive, but computing the sensitivities and elasticities and associating the perturbations with the opposite signs (i.e. ${\mathcal{P}}_2$ and ${\mathcal{P}}_4$ are associated with positive δ, and ${\mathcal{P}}_1$ and ${\mathcal{P}}_3$ are associated with negative δ) gives exactly the same results for the sensitivities as they are independent of the value of δ, and the elasticites still advise increasing the proportion of the population that use the opposite pathway to the sensitivities (see Supplementary Material Section 4.1).

In practice, multiple management actions could be applied at once. As the perturbations considered in this example are linear and all occur in the same season, they can be summed to find the sensitivities and elasticities of a combination of proposed management actions. For example, it may be reasonable to assume that management actions that improve the quality of a pathway will affect stages 4 and 5 in the same way, as the unperturbed movement survival for stages 4 and 5 are equal to each other. Increasing the movement survival of individuals that use ${\mathcal{P}}_1$ and start season 6 in stages 4 and 5 by the same amount, results in the sensitivity of $\tilde{C}({\mathcal{P}}_1)$ being 5.51. Furthermore, since the movement survival of stages 4 and 5 are being perturbed in exactly the same way, the elasticities of the pathway contribution metrics associated with perturbing stages 4 and 5 separately during season 6, can be summed to obtain the elasticities of the pathway contribution metrics of perturbing stages 4 and 5 simultaneously in season 6.

Alternatively, managers could apply actions across multiple types of vital rates experienced during season 6. Say we simultaneously perturb multiple vital rates experienced by the subpopulation using ${\mathcal{P}}_2$. Specifically: the survival of stage 4 individuals in habitat 4 is increased by ${\delta }_6$; the survival of stage 4 and 5 individuals using ${\mathcal{P}}_2$ is increased by ${\delta }_2$; and the proportion of stage 4 and 5 individuals using ${\mathcal{P}}_2$ is increased by ${\delta }_1$. Due to the linearity of the perturbations applied, the sensitivity of the subpopulation pathway contribution metrics is given by

$$\frac{\text{d}C{({\mathcal{P}}_2)}^{\top }}{\text{d}{p}^{\top }}=\frac{\text{d}{D}_{4,6}}{\text{d}{\delta }_6}+\frac{\text{d}{S}_6^4}{\text{d}{\delta }_2}+\frac{\text{d}{S}_6^5}{\text{d}{\delta }_2}=\underset{{\delta }_6}{\underbrace{1.67}}+\underset{{\delta }_2}{\underbrace{3.62+5.72\times {10}^{-3}}}=5.30,$$

and the sensitivity of the metapopulation pathway contribution metrics is given by

$$\begin{array}{l}\frac{\text{d}\widetilde{\mathbf{\text{C}}}{({\mathcal{P}}_2)}^{\top }}{\text{d}{\mathbf{\text{p}}}^{\top }}=\frac{\text{d}{D}_{4,6}}{\text{d}{\delta }_6}+\frac{\text{d}{S}_6^4}{\text{d}{\delta }_2}+\frac{\text{d}{S}_6^5}{\text{d}{\delta }_2}+\frac{\text{d}{P}_6^4}{\text{d}{\delta }_1}+\frac{\text{d}{P}_6^5}{\text{d}{\delta }_1}\\ \begin{array}{ccc}& & =\underset{{\delta }_6}{\underbrace{7.42\times {10}^{-1}}}+\underset{{\delta }_2}{\underbrace{1.61+2.54\times {10}^{-3}}}+\underset{{\delta }_1}{\underbrace{4.43+7.00\times {10}^{-3}}}=6.79.\end{array}\end{array}$$

Here the underbraces are simply used to attribute the contribution to the total sensitivity from respective perturbations. Another way in which managers could use the information from the sensitivity analysis is to set a target to increase the contribution that a focal population has to the total population. For example, if the aim is to increase $\tilde{C}({\mathcal{P}}_3)$ by 20%, then we can use the perturbation formula where the coefficient of a specified ${\delta }_l$ is the sensitivity of $\tilde{C}({\mathcal{P}}_3)$ to find the minimum value of this ${\delta }_l$ that achieves the target. Stage 4 individuals generated from a stage 1 individual in habitat 3 (perturbing by ${\delta }_4$) during season 6 correspond to the largest sensitivity and elasticity, so would be the optimal place to apply the perturbation; we find that this vital rate would need to increase by 1.9% $({\delta }_4\ge 8.47\times {10}^{-3})$.

All the perturbations considered above will also impact the asymptotic growth of the population, denoted by λ. We calculate the sensitivity of λ when there is no pathway specified for each vital rate experienced during season 6. For example, perturbing the transition of stage 3 individuals to stage 5 individuals in habitat 3 during season 6, perturbs $D_{3,6}$ by ${\delta }_5$ and Equation 15 takes the form

$$\begin{array}{l}\frac{\text{dλ}}{\text{d}{\delta }_5}=\left(\frac{{\mathbf{\text{w}}}^{\top }\otimes {\mathbf{\text{v}}}^{\top }}{{\mathbf{\text{v}}}^{\top }\mathbf{\text{w}}}\right)(({\mathbf{\text{Y}}}_1^5{)}^{\top }\otimes {\mathbf{\text{Y}}}_7^{12})\frac{\text{d vec }{A}_6}{\text{d}{\delta }_5}\\ =\left(\frac{{\mathbf{\text{w}}}^{\top }\otimes {\mathbf{\text{v}}}^{\top }}{{\mathbf{\text{v}}}^{\top }\mathbf{\text{w}}}\right)\left({({\mathbf{\text{Y}}}_1^5)}^{\top }\otimes {\mathbf{\text{Y}}}_7^{12}\right)\left(\left(\left(({\mathbb{S}}_6\circ {\mathbb{P}}_6{)}^{\top }\otimes I_{20})\left(X_1(\text{vec }(E_{4,33})\otimes \frac{\text{d vec }{D}_{3,6}}{\text{d}{\delta }_5}\right)\right)\right)\circ {𝟙}_{400}^{\top }\right)\\ \begin{array}{cc}& =2.48\times {10}^{-2}.\end{array}\end{array}$$

Here: v and w denote the corresponding left and right eigenvectors of $\mathcal{A}$, respectively; and $X_1=I_4\otimes K_{5,4}\otimes I_5$.

The sensitivity of λ to all the other demographic rates is calculated similarly and recorded in Table 8; the corresponding elasticities are recorded in Table 9. We see that λ is most sensitive to the movement survival of stage 4 individuals migrating from habitat 2 to 3 during season 6 (perturbing $S_6^4$ by ${\delta }_1$), which has a sensitivity of 9.90. This is equal to the sensitivity of the contribution that a stage 4 individual using this pathway has to the subpopulation also using this pathway. The movement survival of stage 4 individuals migrating from habitat 2 to 3 during season 6 (using ${\mathcal{P}}_1$) is also the vital rate associated with the biggest elasticity of λ (7.63 × 10⁻³), and so the asymptotic growth rate is predicted to increase the most with the smallest percentage change to this vital rate. We note that the elasticity of λ to this vital rate is bigger than the elasticity of both $C({\mathcal{P}}_1)$ and $\tilde{C}({\mathcal{P}}_1)$ to this vital rate. Therefore, a percentage change in the survival of stage 4 individuals migrating from habitat 2 to 3 during season 6 will have a larger effect on the asymptotic growth rate than the short term growth of both the subpopulation using the ${\mathcal{P}}_1$ and the total population that is attributed to individuals using ${\mathcal{P}}_1$.

Table 8

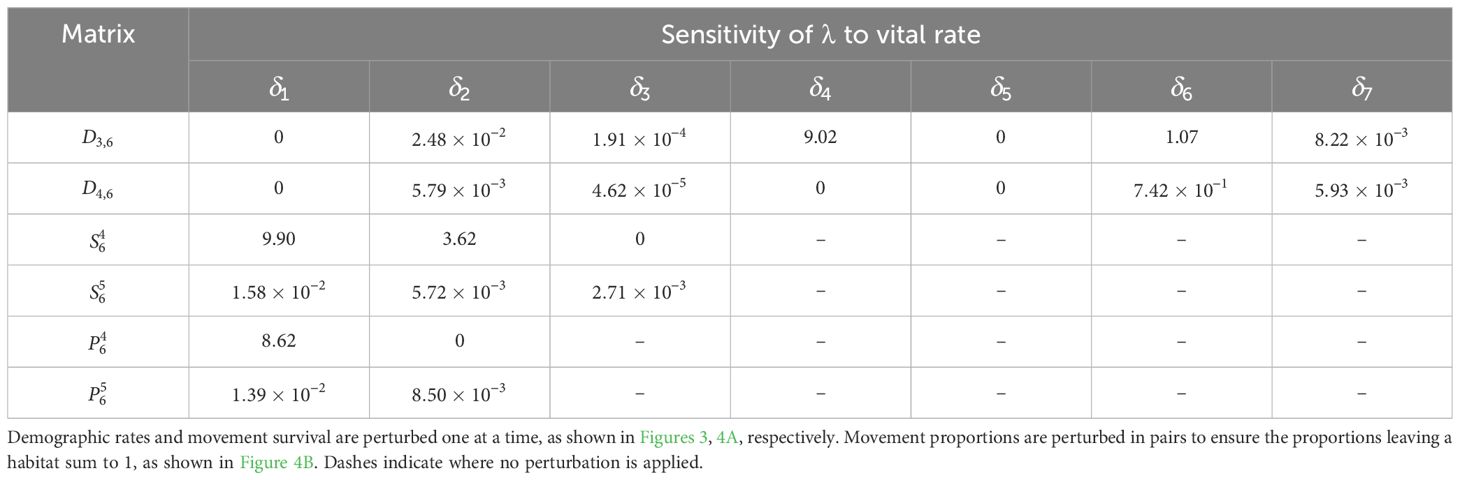
Table 8. Sensitivities of the asymptotic growth rate for the monarch butterfly annual cycle model considered in Section 3.2.1.

Table 9

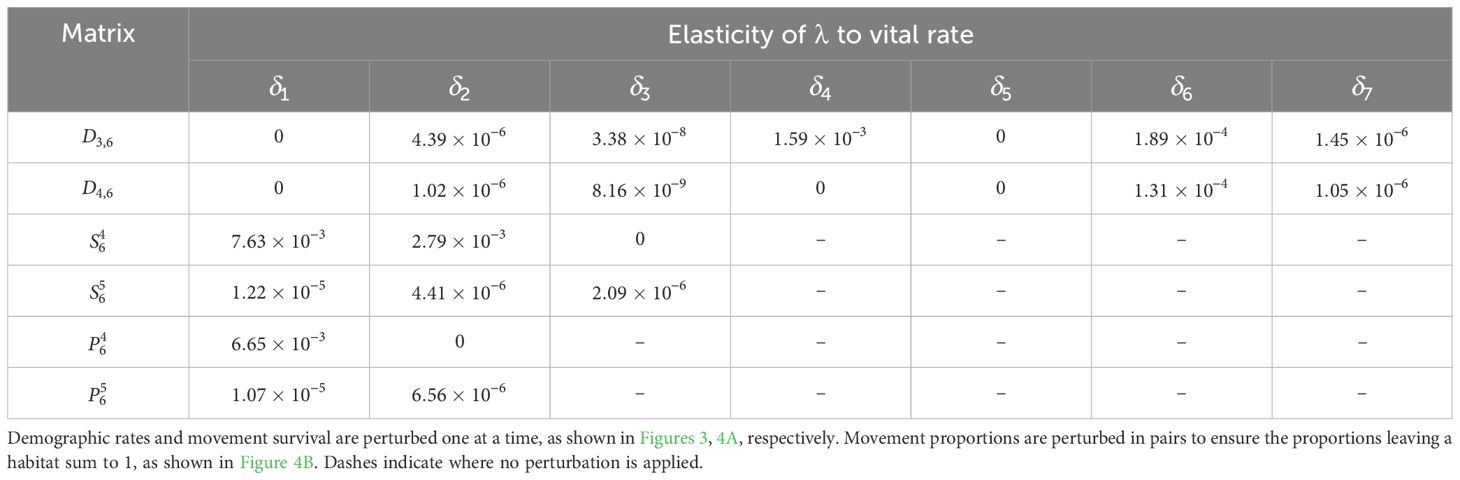
Table 9. Elasticities (evaluated with δ_l equal to 1% of the vital rate that it is being perturbed) of the asymptotic growth rate for the monarch butterfly annual cycle model considered in Section 3.2.1.

3.2.2 Using the perturbation framework to predict the impact of threats and management actions

We proceed by applying perturbations to the monarch butterfly model that correlate to threats and proposed conservation management actions. The perturbations are applied to various vital rates and in multiple seasons of the annual cycle, giving rise to non-linear perturbation structures. As in Smith et al. (2022, Example 3.2), we calculate the pathway contribution metrics for each possible pathway in a season individually. That is, we take $\phi =1$ and set Φ to be each season in turn. The unperturbed pathway contribution metrics are recorded in Smith et al. (2022, Table 3.1); we number the 28 pathways in this table consecutively. We also calculate the habitat contribution metrics (equivalent to summing all the $\tilde{C}({\mathcal{P}}_i)$ for $i\in \left\{1,\dots ,28\right\}$) and denote this as ${\mathcal{P}}_0$.

First, we apply perturbations corresponding to threats. Some of the major threats to the monarch butterfly are climate change and the loss of their overwintering and breeding habitats (Brower et al., 2012; Vidal and Rendón-Salinas, 2014; Wilcox et al., 2019). Climate change causes high heat in the Southern US (habitat 2) during the summer months (k ∈ {6,7,8}) which limits the fecundity of the monarch butterfly (Malcolm et al., 1987; Pocius et al., 2022). Another threat to the monarch population is a large reduction in milkweed availability, largely owing to agricultural practices (Brower et al., 2012; Flockhart et al., 2015; Pleasants and Oberhauser, 2013), which causes the larval survival probability to decrease (Flockhart et al., 2012, Flockhart et al., 2015). The last threat that we consider is the reduction in the size of the overwintering ground in Mexico (habitat 1) caused by illegal logging (Brower et al., 2012; Vidal and Rendón-Salinas, 2014). Using the perturbation framework (see Section 2.3), we simultaneously apply perturbations that represent these threats to the monarch butterfly population model. Specifically, we perturb the model to: reduce the fecundity of stages 3, 4 and 5 in habitat 2 during seasons 6, 7 and 8 by 1%; decrease the survival of larvae (stage 1) in habitats 2, 3 and 4 by 2%; and, decrease the survival of all stages in habitat 1 by 5% in all seasons of the annual cycle. We calculate the change in the pathway contribution metrics (which have the same form as those in Equation 20) and plot the results in Figure 5 using downwards triangles.

Figure 5

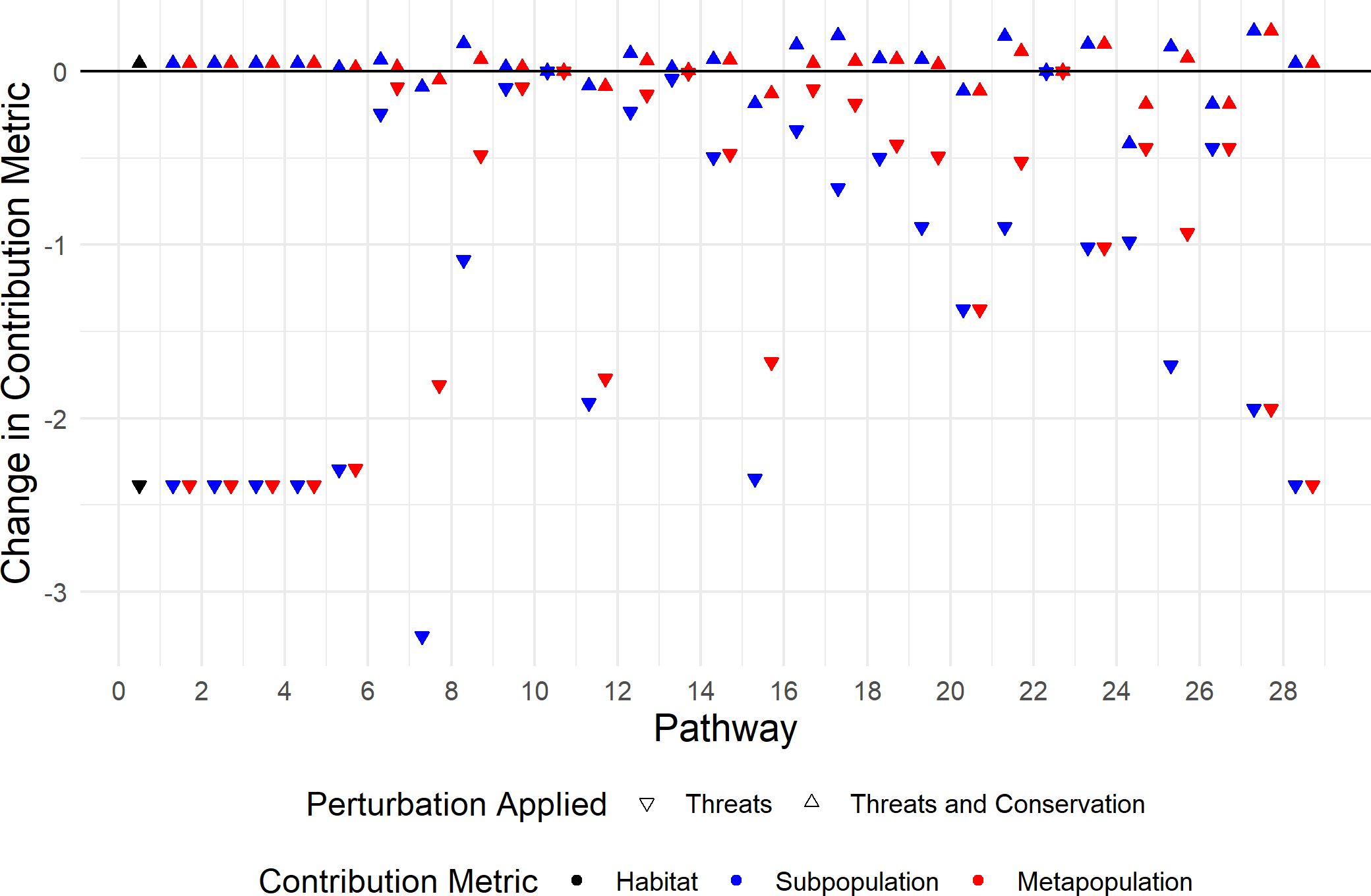
Figure 5. Change in pathway contribution metrics following the perturbations considered in Section 3.2.2. The perturbed habitat contribution metrics $(\text{C}({\mathcal{P}}_0,\Delta ))$, subpopulation pathway contribution metrics (C(P_i,Δ)) and metapopulation pathway contribution metrics $(\tilde{C}({\mathcal{P}}_i,\Delta ))$, where $i\in \left\{1,\dots .28\right\}$, correspond to black, blue and red, respectively. Downwards triangles correspond to only threats being applied and upwards triangles correspond to both threats and conservation actions being applied. The pathway labels correspond to the points to the right hand side of the tick mark.

Perturbations associated with conservation actions can be applied to the monarch butterfly model at the same time as the negative perturbations above that correspond to threats. The WWF recommends a number of climate-adaptive management strategies for monarch butterflies; including, increasing the availability of milkweed and nectar sources throughout their range which will help to restore and increase the stepping stones and movement corridors (Advani, 2015). Other possible conservation actions include reducing the amount of illegal logging in habitat 1, which will increase the survival of individuals in habitat 1. We represent the conservation actions by applying positive perturbations to the model, that: increase the survival of individuals in habitat 1 by 5% during all seasons of the annual cycle; improve the survival of larvae in habitats 2, 3 and 4 by 10% in all seasons of the annual cycle; and, increase the survival of monarchs using the pathways between habitats 2, 3 and 4 by 10% during seasons 5 – 10. We note that the increase to the survival of individuals in habitat 1 does not completely eradicate the effects of the negative illegal logging perturbation, as the threats are applied before the conservation actions. We calculate the change in the pathway contribution metrics when perturbations corresponding to both threats and conservation actions are applied and plot the results in Figure 5 using upwards triangles.

We see that the conservation actions do not completely counter the impact that the threats have for all pathway contribution metrics; there are upwards triangles below the x-axis in Figure 5. However, the conservation actions have resulted in the perturbed habitat contribution metrics $C({\mathcal{P}}_0,\Delta )$ (represented by black triangles) being greater than the unperturbed habitat contribution metrics. Therefore, the overall contribution of an individual over one annual cycle has increased; it is now 4.72 × 10⁻² larger than when no perturbation is applied, which decreased by 2.39 when the threats were applied.

Furthermore, we can compare how the threats and conservation actions impact individual pathways. We see that the $C({\mathcal{P}}_i)$ that is impacted the most by threats is $C({\mathcal{P}}_7)$ which has decreased by 3.26. In other words, the contribution that an individual using ${\mathcal{P}}_7$ (2 → 3 in season 6) has on the subpopulation also using ${\mathcal{P}}_7$ is decreased the most by the threats. Whereas, the $C({\mathcal{P}}_i)$ that is impacted the least by the threats is $C({\mathcal{P}}_{10})$ which has decreased by 1.05 × 10⁻³, and so the contribution that an individual using ${\mathcal{P}}_{10}$ (3 → 4 in season 6) has on the subpopulation also using ${\mathcal{P}}_{10}$ is affected the least by the threats. The highest value of the $C({\mathcal{P}}_i)$ following the application of threats and conservation actions is $C({\mathcal{P}}_{27})$ which has increased by 2.35 × 10⁻¹ compared to the unperturbed contribution metric. In other words, the contribution that an individual using a pathway has on the subpopulation using the same pathway is greatest after threats and conservation have been applied for individuals using ${\mathcal{P}}_{27}$ (2 → 1 in season 11). The smallest value of the $C({\mathcal{P}}_i)$ following the application of threats and conservation actions is $C({\mathcal{P}}_{24})$, which has decreased by 4.17 × 10⁻¹ compared to the unperturbed contribution metric.

To find which pathways are the most improved by the conservation actions, we calculate the difference between the change in subpopulation pathway contribution metrics after threats and the change in them after both threats and conservation. The conservation actions have the least impact on individuals using ${\mathcal{P}}_{10}$; $C({\mathcal{P}}_{10})$ is decreased by 1.05 × 10⁻³ after application of the threats, and is increased by 1.65 × 10⁻³ after the conservation actions. Thus, the total change to $C({\mathcal{P}}_{10})$ after threats and conservation actions is an increase of 6.02 × 10⁻⁴. Conversely, the conservation actions have the most impact on $C({\mathcal{P}}_7)$ which is decreased by 3.26 after application of the threats, and is increased by 3.17 after the conservation actions, resulting in the total change to $C({\mathcal{P}}_7)$ after threats and conservation actions being a decrease of 8.88×10⁻².

The results of the metapopulation pathway contribution metrics can be interpreted similarly. However, the metapopulation pathway contribution metrics may not be altered in the same way as the subpopulation pathway contribution metrics. For instance, the $\tilde{C}({\mathcal{P}}_i)$ that are impacted the most by the threats are $\tilde{C}({\mathcal{P}}_1)$, $\tilde{C}({\mathcal{P}}_2)$, $\tilde{C}({\mathcal{P}}_3)$, $\tilde{C}({\mathcal{P}}_4)$ and $\tilde{C}({\mathcal{P}}_{28})$ which have all decreased by 2.39. That is, the contribution that an individual using ${\mathcal{P}}_1$ (1 → 1 in season 1), ${\mathcal{P}}_2$ (1 → 1 in season 2), ${\mathcal{P}}_3$ (1 → 1 in season 3), ${\mathcal{P}}_4$ (1 → 2 in season 4) or ${\mathcal{P}}_{28}$ (1 → 1 in season 12) has on the total population are decreased the most by threats. However, the $\tilde{C}({\mathcal{P}}_i)$ that is impacted the least by the threats is $\tilde{C}({\mathcal{P}}_{10})$ which has decreased by 4.92×10⁻⁴; the subpopulation pathway contribution metrics associated with ${\mathcal{P}}_{10}$ (3 → 4 in season 6) are also impacted the least by threats. Thus, the contribution that an individual using ${\mathcal{P}}_{10}$ has on the subpopulation also using ${\mathcal{P}}_{10}$ and the contribution that they have on the total population are both affected the least by the threats. The highest value of the $\tilde{C}({\mathcal{P}}_i)$ following the application of threats and conservation actions is $\tilde{C}({\mathcal{P}}_{27})$ which has increased by 2.35 × 10⁻¹; ${\mathcal{P}}_{27}$ (2 → 1 in season 11) is also associated with the highest value of the $\mathit{C}({\mathcal{P}}_i)$ after threats and conservation actions have been applied. The lowest value of the $\tilde{C}({\mathcal{P}}_i)$ following the application of threats and conservation actions is $\tilde{C}({\mathcal{P}}_{24})$ and $\tilde{C}({\mathcal{P}}_{26})$ which have both decreased by 1.88 × 10⁻¹, hence the contribution that an individual using ${\mathcal{P}}_{24}$ (3 → 1 in season 10) or ${\mathcal{P}}_{26}$ (1 → 1 in season 11) has on the total population following the threats and conservation actions are the smallest. Interestingly, individuals using ${\mathcal{P}}_{24}$ (3 → 1 in season 10) contribute the least to both the total population and the subpopulation that uses ${\mathcal{P}}_{24}$. However, individuals using ${\mathcal{P}}_{26}$ contribute the least to the total population, but contribute more to the subpopulation that use ${\mathcal{P}}_{26}$, than individuals that use ${\mathcal{P}}_{24}$ contribute to their subpopulation.

The conservation actions have the least impact on $\tilde{C}({\mathcal{P}}_{10})$ which has decreased by 4.92 × 10⁻⁴ after applications of the threats, and has increased by 7.74×10⁻³ after conservation actions, resulting in the total change to $\tilde{C}({\mathcal{P}}_{10})$ after threats and conservation actions being an increase of 2.82 × 10⁻⁴. Furthermore, the impact that the conservation actions have on an individual’s contribution to the total population and its contribution to the subpopulation that uses the same pathway is smallest for individuals using pathway 10. The conservation actions have the biggest impact on $\tilde{C}({\mathcal{P}}_1)$, $\tilde{C}({\mathcal{P}}_2)$, $\tilde{C}({\mathcal{P}}_3)$, $\tilde{C}({\mathcal{P}}_4)$ and $\tilde{C}({\mathcal{P}}_{28})$ which all decrease by 2.39 following the threats and increase by 2.43 following the conservation actions, resulting in an overall change of 2.82 × 10⁻⁴ from the unperturbed metapopulation pathway contribution metrics.

4 Discussion

We have provided a framework that predicts the effects of perturbations on mathematical models of migratory species, and the associated contribution metrics. The framework allows for perturbations to be applied at any point in the annual cycle, and for multiple perturbations to be applied at once. We have ensured that the perturbations applied to the model are easily linked to their ecological meaning by providing formulae that perturb individual vital rates, rather than individual entries in the seasonal or annual cycle matrices for which the ecological meaning is not always clear (Smith et al., 2022). Thus, complex and nonlinear perturbation structures can be applied to the annual cycle matrix whilst retaining transparent biological interpretation. Our perturbation framework follows two complementary strands. The first is a structured perturbation approach, in the spirit of Hodgson and Townley (2004), and is underpinned by linear algebra tools. The second is a sensitivity approach, in the spirit of Caswell (2019), and is underpinned by differential calculus. The former computes the actual change that the perturbation causes to the annual cycle model and contribution metrics, whilst the latter computes the rate of change to the contribution metrics at a given point. Arguably, both strands have their advantages and disadvantages and, when perturbations are linear, these approaches yield equivalent results. Either framework can be used to quantify the effect that perturbations have on all the contribution metrics defined in Smith et al. (2022). Therefore, the effect perturbations have on different pathways, habitats and stages of the annual cycle model can be computed.

Existing models that quantify how perturbations affect the growth rates of migratory populations have not allowed all vital rates to be perturbed. The two frameworks developed in this paper are general and allow for any vital rate (or combination of vital rates) in the annual cycle model to be perturbed, making it straightforward to evaluate the impact of any combination of management strategies or threats. The combination of these novel elements allows for the trade-offs between threats and conservation actions to be explored analytically, and for conservation strategies that involve multiple actions to be fully defined. This is particularly valuable for migratory species where conservation efforts are challenged by their highly mobile nature which often includes travelling across borders (Kirby et al., 2008; Robinson et al., 2009; Runge et al., 2015; Thornton et al., 2018). Using our framework, population managers could investigate how to buffer against negative impacts that the migratory population is subject to in regions that the managers are unable to influence.

The frameworks developed in this paper can uncover more insight from the annual cycle models than is possible from the pathway contribution metrics alone. When the monarch butterfly model is considered in Smith et al. (2022, Example 3.2), it is suggested that the pathway between habitats 3 and 4 could be improved in season 6 (${\mathcal{P}}_4$ in Section 3.2.1), as the pathway contribution metrics associated with this pathway are the smallest. However, the sensitivity framework deployed in Section 3.2.1 reveals that increasing the movement survival of individuals that use ${\mathcal{P}}_4$ will have a smaller effect than increasing the movement survival along any of the other pathways (that are not associated with remaining resident) used during season 6. Indeed, the pathway contribution metrics developed in Smith et al. (2022) are useful when ranking the importance of pathways for a fixed annual cycle model, but they do not indicate how a change in the annual cycle model will affect the ranking of pathways. Thus, the frameworks developed in this paper are a useful tool for predicting how changes to the annual cycle model affect the value of the pathway contribution metrics.

Furthermore, in Smith et al. (2022, Example 3.2), they also advise increasing the proportion of the population that uses the pathway between habitats 2 and 3 (${\mathcal{P}}_1$) during season 6, as this pathway is associated with the highest pathway contribution metrics. Using the sensitivity framework in Section 3.2.1, we see that individuals that start season 6 in habitat 2 are more sensitive to perturbations in the proportion migrating, than individuals that start season 6 in habitat 3. In particular, increasing the proportion of the population that uses ${\mathcal{P}}_1$ (and hence decreasing the proportion of the population that uses ${\mathcal{P}}_2$) is predicted to have the largest effect on the metapopulation pathway contribution metrics, when considering the sensitivities recorded in Table 6. However, when considering the elasticities recorded in Table 7, it is predicted that increasing the proportion of the population that uses ${\mathcal{P}}_2$ (and hence decreasing the proportion of the population that uses ${\mathcal{P}}_1$) will have the largest effect on the metapopulation pathway contribution metrics. In other words, increasing the proportion of the population that uses ${\mathcal{P}}_2$ by some percentage will have a larger effect on the metapopulation pathway contribution metrics than increasing the proportion of the population that uses ${\mathcal{P}}_1$ by the same percentage. Another insight that we gain from the sensitivity framework is that, among all the vital rates experienced by the population in season 6, the short term population growth is proportionally most sensitive to perturbing the number of stage 4 individuals generated from stage 1 individuals in habitat 3 (see Table 3), whilst the long term population growth is proportionally most sensitive to perturbing the movement survival of stage 4 individuals using ${\mathcal{P}}_1$ (see Table 9). In practice, population managers will need to consider their objectives and the costs associated with changing each vital rate, along with the sensitivities and/or elasticities to decide which actions they take.

In Section 3.2.2, we use the perturbation framework and the monarch butterfly model to assess the expected impact that threats and conservation actions have on the pathway contribution metrics. Threats are applied to demographic rates and movement survival during multiple seasons of the annual cycle. We calculate the impact that these threats have on the pathway contribution metrics associated with each possible pathway. Suggested management actions for conservation are then applied to assess how the proposed conservation actions can buffer against the threats. We find that although some pathways are associated with smaller pathway contribution metrics after the threats and conservation actions have been applied, the contribution that an individual with no specified pathway has on the total population (the value of habitat contribution metrics) has increased compared to the unperturbed annual cycle model. In general, when both positive and negative perturbations are applied to the annual cycle model, whether the overall effect to the contribution metrics is positive or negative is unknown prior to their calculation. In fact, the different pathway contribution metrics calculated from the annual cycle model can be increased or decreased. That is, a subpopulation using one pathway may be overall positively affected by the perturbations, whilst a subpopulation using another pathway may be overall negatively affected by the same perturbations. To see whether the perturbations cause the total population to increase or decrease in the short- or long-term, managers should consider the effect that the perturbations have on the habitat contribution metrics or the asymptotic growth rate, respectively.

We comment that managers must take care when applying perturbations to the population model and ensure that it remains ecologically meaningful. For instance, when defining how perturbations affect the proportion of the population that uses a migratory route, the sum of all the proportions associated with pathways (including loops) that leave a habitat during a set season must sum to one. Hence, necessary trade-offs must be considered when perturbing the proportion of the population that uses a pathway, which requires some vital rates to be negatively perturbed to maintain an ecologically meaningful model. The perturbation and sensitivity frameworks both readily assess the impact that these necessary trade- offs (and other trade-offs that may be occurring between threats and conservation actions) have on the pathway contribution metrics. However, negative elasticities are not well-defined and so care must be taken when calculating the elasticity of a perturbation that includes trade-offs. The elasticities corresponding to the necessary trade-offs considered in Section 3.2.1 are equivalent to the integrated elasticities [see Supplementary Material Section 4.2, Van Tienderen (1995)], but more research would be needed to assess how other trade-off structures influence the elasticities and integrated elasticities.

The perturbation and sensitivity frameworks developed in this paper provide tools that can help to inform the management of a migratory species subject to any number of threats or conservation actions. Questions that we envisage these frameworks being able to answer include: which vital rates in a migratory population are the most responsive to change; during which season/s of the annual cycle should a management action be applied to increase the pathway contribution metrics the most; what is the best vital rate to apply a perturbation to, if the migratory species is experiencing threats in a region where managers are unable to act. We note that, to answer these questions, both frameworks require managers to predict how a proposed action will affect the vital rates of the population. We propose that our framework could be used as part of an adaptive management strategy by integrating field data gathered throughout the full species range to update the migratory model and assess how management actions (perturbations) affect the vital rates experienced by the migratory species, as is encouraged in Mattsson et al. (2022).

Full-annual-cycle models of migratory birds are reviewed in Hostetler et al. (2015). The authors note that although such models can provide more insight than models developed for non-migratory species, it can be challenging to apply full-annual-cycle models to real-world systems owing to the limited availability of empirical data. Indeed, the matrices of the full-annual-cycle models considered presently become large as partitioned according stage class, season and habitat. Consequently, numerous parameters will need to be estimated, and it is likely to be challenging to estimate all of these parameters well. Thus, we envision that the frameworks discussed in this paper could also aid in the development of full-annual-cycle models, by identifying which matrix entries are the most sensitive to change and so which vital rates are the most important to measure accurately.

Future research could seek to use optimal control techniques to optimise conservation targets (which could be defined via the size of the contribution metrics or the asymptotic growth rate) whilst minimising some prescribed cost. To the best of our knowledge, the optimal control of migratory species was first considered by Martin et al. (2007). They seek to find optimal resource allocation strategies that maximise either the number of individuals protected across the wintering range, or the number of individuals protected across the entire species range. More recently, Schuster et al. (2019) used optimal control techniques to develop a multi-species planning tool that optimises conservation targets whilst minimising the total area that is protected. Similar optimal control strategies could be considered alongside our framework with the aim to maximise the habitat contribution metrics and/or the asymptotic growth rate whilst maintaining a minimum size of the pathway contribution metrics for each individual pathway.

Another possible area for future research could investigate how best to manage migratory populations whilst extreme weather patterns, caused by climate change, drive migratory species to adapt their life history strategies. For instance, among-individual and within-individual variation in expression of seasonal migration or residence could be incorporated into the metapopulation model (as is done in Payo-Payo et al. (2022)) to allow for the inclusion of “carry-over effects” such that the vital rates experienced in one season impact those experienced in the following seasons. The perturbation or sensitivity framework could then be used to see how these carry-over effects influence which vital rates will have the biggest effect on increasing the contribution metrics and asymptotic growth rate.

As with our earlier work (Smith et al., 2022), the results presented here assume density-independence (that is, linearity) of the underlying annual cycle model. Thus, the model predictions are unlikely to be realistic over large time periods, as density-dependent factors will have more of an effect once the population reaches carrying capacity. However, since pathway contribution metrics are transient indices, they are not tied to the asymptotic nature of the model. To increase the validity of the model predictions over large time frames, a separate line of enquiry is to develop useful and valid contribution metrics for density-dependent (that is, nonlinear) annual cycle models, or certain interesting classes of density-dependent annual cycle models. Furthermore, the migratory model could be extended to consider how demographic and environmental stochasticity influence the vital rates experienced by the population, and in turn which management actions are advised using the perturbation and sensitivity framework. The frameworks developed in this paper could then be used similarly to assess the impact of perturbations on the model predictions by applying perturbations directly to the vital rates.

In closing, we have provided a framework to assess the impact that perturbations have on both the pathway contribution metrics and the asymptotic growth rate of a migratory population. The framework allows for perturbations to be applied to any vital rate in the annual cycle model, and identifies the critical states that impact the dynamics of the population. Multiple perturbations can be applied at once, which can lead to nonlinear perturbation structures, so that the effects of trade-offs and mixed strategies can be explored. We have provided details of how to assess the impact of these perturbations using either sensitivity analysis or perturbation analysis, so that linear approximations or the full perturbation curves can be evaluated. We believe that our framework provides a novel tool to be used in the management of migratory species.

Data availability statement

Publicly available datasets were analysed in this study. The software code can be found here: https://github.com/psjs22/PerturbingPathwayMetrics.

Author contributions

PS: Conceptualization, Formal analysis, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review & editing. BA: Conceptualization, Supervision, Writing – review & editing. CG: Conceptualization, Methodology, Supervision, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2024.1426018/full#supplementary-material

Footnotes

1. ^ Strictly, assuming that p is not an eigenvalue of A.

References

Advani N. (2015). WWF wildlife and climate change series: monarch butterfly (Washington, DC: World Wildlife Fund).

Google Scholar

Bauer S., Hoye B. J. (2014). Migratory animals couple biodiversity and ecosystem functioning worldwide. Science 344, 1242552. doi: 10.1126/science.1242552

PubMed Abstract | Crossref Full Text | Google Scholar

Both C., Visser M. E. (2001). Adjustment to climate change is constrained by arrival date in a long-distance migrant bird. Nature 411, 296–298. doi: 10.1038/35077063

PubMed Abstract | Crossref Full Text | Google Scholar

Bowlin M. S., Bisson I.-A., Shamoun-Baranes J., Reichard J. D., Sapir N., Marra P. P., et al. (2010). Grand challenges in migration biology. Integr. Comp. Biol. 50, 261–279. doi: 10.1093/icb/icq013

PubMed Abstract | Crossref Full Text | Google Scholar

Brower L. P., Taylor O. R., Williams E. H., Slayback D. A., Zubieta R. R., Ramirez M. I. (2012). Decline of monarch butterflies overwintering in Mexico: is the migratory phenomenon at risk? Insect Conserv. Divers. 5, 95–100. doi: 10.1111/j.1752-4598.2011.00142.x

Crossref Full Text | Google Scholar

Carslake D., Townley S., Hodgson D. J. (2008). Nonlinearity in eigenvalue-perturbation curves of simulated population projection matrices. Theor. Popul. Biol. 73, 498–505. doi: 10.1016/j.tpb.2008.03.004

PubMed Abstract | Crossref Full Text | Google Scholar

Caswell H. (1978). A general formula for the sensitivity of population growth rate to changes in life history parameters. Theor. Popul. Biol. 14, 215–230. doi: 10.1016/0040-5809(78)90025-4

PubMed Abstract | Crossref Full Text | Google Scholar

Caswell H. (2001). Matrix population models: construction, analysis, and interpretation. 2nd edn (Sunderland, MA: Sinauer Associates. Inc.).

Google Scholar

Caswell H. (2019). Sensitivity analysis: matrix methods in demography and ecology (Cham, Switzerland: Springer Nature). doi: 10.1007/978-3-030-10534-1

Crossref Full Text | Google Scholar

Cushing J. M. (1998). An introduction to structured population dynamics (Philadelphia, US: SIAM). doi: 10.1137/1.9781611970005

Crossref Full Text | Google Scholar

Demetrius L. (1969). The sensitivity of population growth rate to pertubations in the life cycle components. Math. Biosci. 4, 129–136. doi: 10.1016/0025-5564(69)90009-1

Crossref Full Text | Google Scholar

Dingle H., Drake V. A. (2007). What is migration? Bioscience 57, 113–121. doi: 10.1641/B570206

Crossref Full Text | Google Scholar

Flockhart D. T. T., Martin T. G., Norris D. R. (2012). Experimental examination of intraspecific density-dependent competition during the breeding period in monarch butterflies (danaus plexippus). PloS One 7, e45080. doi: 10.1371/journal.pone.0045080

PubMed Abstract | Crossref Full Text | Google Scholar

Flockhart D. T. T., Pichancourt J.-B., Norris D. R., Martin T. G. (2015). Unravelling the annual cycle in a migratory animal: breeding-season habitat loss drives population declines of monarch butterflies. J. Anim. Ecol. 84, 155–165. doi: 10.1111/1365-2656.12253

PubMed Abstract | Crossref Full Text | Google Scholar

Goodman L. A. (1971). On the sensitivity of the intrinsic growth rate to changes in the age-specific birth and death rates. Theor. Popul. Biol. 2, 339–354. doi: 10.1016/0040-5809(71)90025-6

Crossref Full Text | Google Scholar

Guiver C., Hodgson D., Townley S. (2016). A note on the eigenvectors of perturbed matrices with applications to linear positive systems. Linear Algebra Appl. 509, 143–167. doi: 10.1016/j.laa.2016.07.010

Crossref Full Text | Google Scholar

Hamilton W. D. (1966). The moulding of senescence by natural selection. J. Theor. Biol. 12, 12–45. doi: 10.1016/0022-5193(66)90184-6

PubMed Abstract | Crossref Full Text | Google Scholar

Hassol S. (2004). Impacts of a warming Arctic-Arctic climate impact assessment (New York, US: Cambridge University Press).

Google Scholar

Hodgson D., Townley S., McCarthy D. (2006). Robustness: predicting the effects of life history perturbations on stage-structured population dynamics. Theor. Popul. Biol. 70, 214–224. doi: 10.1016/j.1018tpb.2006.03.004

PubMed Abstract | Crossref Full Text | Google Scholar

Hodgson D. J., Townley S. (2004). Methodological insight: linking management changes to population dynamic responses: the transfer function of a projection matrix perturbation. J. Appl. Ecol. 41, 1155–1161. doi: 10.1111/j.0021-8901.2004.00959.x

Crossref Full Text | Google Scholar

Hostetler J. A., Sillet T. S., Marra P. P. (2015). Full-annual-cycle population models for migratory birds. Auk 132, 433–449. doi: 10.1642/AUK-14-211.1

Crossref Full Text | Google Scholar

Hunter C. M., Caswell H. (2005). The use of the vec-permutation matrix in spatial matrix population models. Ecol. Mod. 188, 15–21. doi: 10.1016/j.ecolmodel.2005.05.002

Crossref Full Text | Google Scholar

Huntley B., Collingham Y. C., Green R. E., Hilton G. M., Rahbek C., Willis S. G. (2006). Potential impacts of climatic change upon geographical distributions of birds. Ibis 148, 8–28. doi: 10.1111/j.1474-919X.2006.00523.x

Crossref Full Text | Google Scholar

Kirby J. S., Stattersfield A. J., Butchart S. H. M., Evans M. I., Grimmett R. F. A., Jones V. R., et al. (2008). Key conservation issues for migratory land- and waterbird species on the world’s major flyways. Bird Conserv. Int. 18, S49–S73. doi: 10.1017/S0959270908000439

Crossref Full Text | Google Scholar

Koons D. N., Holmes R. R., Grand J. B. (2007). Population inertia and its sensitivity to changes in vital rates and population structure. Ecology 88, 2857–2867. doi: 10.1890/06-1801.1

PubMed Abstract | Crossref Full Text | Google Scholar

Levins R. (1969). Some demographic and genetic consequences of environmental heterogeneity for biological control. Bull. Entomol. Soc Am. 15, 237–240. doi: 10.1093/besa/15.3.237

Crossref Full Text | Google Scholar

Lubben J., Boeckner D., Rebarber R., Townley S., Tenhumberg B. (2009). Parameterizing the growth-decline boundary for uncertain population projection models. Theor. Popul. Biol. 75, 85–97. doi: 10.1016/j.tpb.2008.11.004

PubMed Abstract | Crossref Full Text | Google Scholar

Magnus J. R., Neudecker H. (1985). Matrix differential calculus with applications to simple, hadamard, and kronecker products. J. Math. Psychol. 29, 474–492. doi: 10.1016/0022-2496(85)90006-9

Crossref Full Text | Google Scholar

Malcolm S. B., Cockrell B. J., Brower L. P. (1987). Monarch butterfly voltinism: effects of temperature constraints at different latitudes. Oikos 49, 77–82. doi: 10.2307/3565556

Crossref Full Text | Google Scholar

Martin T. G., Chadès I., Arcese P., Marra P. P., Possingham H. P., Norris D. R. (2007). Optimal conservation of migratory species. PloS One 2, e751. doi: 10.1371/journal.pone.0000751

PubMed Abstract | Crossref Full Text | Google Scholar

Mattsson B. J., Mateo-Tomás P., Aebischer A., Rösner S., Kunz F., Schöll E. M., et al. (2022). Enhancing monitoring and transboundary collaboration for conserving migratory species under global change: the priority case of the red kite. J. Environ. Manage. 317, 115345. doi: 10.1016/j.jenvman.2022.115345

PubMed Abstract | Crossref Full Text | Google Scholar

McElderry R. M., Gaoue O. G. (2022). Pitfalls to avoid in nonlinear perturbation analysis of structured 1047 population models. Popul. Ecol. 64, 365–372. doi: 10.1002/1438-390X.12132

Crossref Full Text | Google Scholar

Payo-Payo A., Acker P., Bocedi G., Travis J. M. J., Burthe S. J., Harris M. P., et al. (2022). Modelling the responses of partially migratory metapopulations to changing seasonal migration rates: from theory to data. J. Anim. Ecol. 91, 1781–1796. doi: 10.1111/1365-2656.13748

PubMed Abstract | Crossref Full Text | Google Scholar

Pleasants J. M., Oberhauser K. S. (2013). Milkweed loss in agricultural fields because of herbicide use: effect on the monarch butterfly population. Insect Conserv. Divers. 6, 135–144. doi: 10.1111/j.1752-4598.2012.00196.x

Crossref Full Text | Google Scholar

Pocius V. M., Majewska A. A., Freedman M. G. (2022). The role of experiments in monarch butterfly conservation: a review of recent studies and approaches. Ann. Entomol. Soc Am. 115, 10–24. doi: 10.1093/aesa/saab036

PubMed Abstract | Crossref Full Text | Google Scholar

Robinson R. A., Crick H. Q. P., Learmonth J. A., Maclean I. M. D., Thomas C. D., Bairlein F., et al. (2009). Travelling through a warming world: climate change and migratory species. Endanger. Species. Res. 7, 87–99. doi: 10.3354/esr00095

Crossref Full Text | Google Scholar

Runge C. A., Martin T. G., Possingham H. P., Willis S. G., Fuller R. A. (2014). Conserving mobile species. Front. Ecol. Environ. 12, , 395–, 402. doi: 10.1890/130237

Crossref Full Text | Google Scholar

Runge J. P., Runge M. C., Nichols J. D. (2006). The role of local populations within a landscape context: defining and classifying sources and sinks. Am. Nat. 167, 925–938. doi: 10.1086/503531

PubMed Abstract | Crossref Full Text | Google Scholar

Runge C. A., Watson J. E. M., Butchart S. H. M., Hanson J. O., Possingham H. P., Fuller R. A. (2015). Protected areas and global conservation of migratory birds. Science 350, 1255–1258. doi: 10.1126/science.aac9180

PubMed Abstract | Crossref Full Text | Google Scholar

Sample C., Bieri J. A., Allen B., Dementieva Y., Carson A., Higgins C., et al. (2019). Quantifying source and sink habitats and pathways in spatially structured populations: a generalized modelling approach. Ecol. Mod. 407, 108715. doi: 10.1016/j.ecolmodel.2019.06.003

Crossref Full Text | Google Scholar

Sample C., Bieri J. A., Allen B., Dementieva Y., Carson A., Higgins C., et al. (2020). Quantifying the contribution of habitats and pathways to a spatially structured population facing environmental change. Am. Nat. 196, 157–168. doi: 10.1086/709009

PubMed Abstract | Crossref Full Text | Google Scholar

Sample C., Fryxell J. M., Bieri J. A., Federico P., Earl J. E., Wiederholt R., et al. (2018). A general modeling framework for describing spatially structured population dynamics. Ecol. Evol. 8, 493–508. doi: 10.1002/ece3.3685

PubMed Abstract | Crossref Full Text | Google Scholar

Samuelson P. A. (1947). Foundations of economic analysis (Cambridge, MA: Harvard University Press).

Google Scholar

Schuster R., Wilson S., Rodewald A. D., Arcese P., Fink D., Auer T., et al. (2019). Optimizing the conservation of migratory species over their full annual cycle. Nat. Commun. 10, 1754. doi: 10.1038/s41467-019-09723-8

PubMed Abstract | Crossref Full Text | Google Scholar

Shuter J. L., Broderick A. C., Agnew D. J., Jonzén N., Godley B. J., Milner-Gulland E. J., et al. (2011). “Conservation and management of migratory species,” in Animal Migration: A Synthesis. Eds. Milner-Gulland E. J., Fryxell J. M., Sinclair A. R. E. (Oxford University Press, Oxford, UK), 172–206.

Google Scholar

Smith P., Guiver C., Adams B. (2022). Quantifying the per-capita contribution of all components of a migratory cycle: a modelling framework. Ecol. Mod. 471, 110056. doi: 10.1016/j.ecolmodel.2022.110056

Crossref Full Text | Google Scholar

Taylor C. M., Hall R. J. (2012). Metapopulation models for seasonally migratory animals. Biol. Lett. 8, 477–480. doi: 10.1098/rsbl.2011.0916

PubMed Abstract | Crossref Full Text | Google Scholar

Thornton D. H., Wirsing A. J., Lopez-Gonzalez C., Squires J. R., Fisher S., Larsen K. W., et al. (2018). Asymmetric cross-border protection of peripheral transboundary species. Conserv. Lett. 11, e12430. doi: 10.1111/conl.12430

Crossref Full Text | Google Scholar

Van Tienderen P. H. (1995). Life cycle trade-offs in matrix population models. Ecology 76, 2482–2489. doi: 10.2307/2265822

Crossref Full Text | Google Scholar

Vidal O., Rendón-Salinas E. (2014). Dynamics and trends of overwintering colonies of the monarch butterfly in Mexico. Biol. Conserv. 180, 165–175. doi: 10.1016/j.biocon.2014.09.041

Crossref Full Text | Google Scholar

Wiederholt R., Mattsson B. J., Thogmartin W. E., Runge M. C., Diffendorfer J. E., Erickson R. A., et al. (2018). Estimating the per-capita contribution of habitats and pathways in a migratory network: a modelling approach. Ecography 41, 815–824. doi: 10.1111/ecog.02718

Crossref Full Text | Google Scholar

Wilcove D. S., Wikelski M. (2008). Going, going, gone: is animal migration disappearing. PloS Biol. 6, e188. doi: 10.1371/journal.pbio.0060188

PubMed Abstract | Crossref Full Text | Google Scholar

Wilcox A. A. E., Flockhart D. T. T., Newman A. E. M., Norris D. R. (2019). An evaluation of studies on the potential threats contributing to the decline of eastern migratory north american monarch butterflies (danaus plexippus). Front. Ecol. Evol. 7, 99. doi: 10.3389/fevo.2019.00099

Crossref Full Text | Google Scholar