Producing non-steady-state gaits (starting, stopping, and turning) in a biologically realistic quadrupedal simulation

Sellers, William Irvin; Cross, Charlotte Francesca; Fukuhara, Akira; Ishiguro, Akio; Hirasaki, Eishi

doi:10.3389/fevo.2022.954838

ORIGINAL RESEARCH article

Front. Ecol. Evol., 08 September 2022

Sec. Behavioral and Evolutionary Ecology

Volume 10 - 2022 | https://doi.org/10.3389/fevo.2022.954838

This article is part of the Research Topic Biologically-Informed Approaches to Design Processes and Applications View all 9 articles

Producing non-steady-state gaits (starting, stopping, and turning) in a biologically realistic quadrupedal simulation

$\r\nWilliam Irvin Sellers*$ William Irvin Sellers^1*

Charlotte Francesca Cross¹

Akira Fukuhara²

Akio Ishiguro²

Eishi Hirasaki³

¹Department of Earth and Environmental Sciences, University of Manchester, Manchester, United Kingdom
²Research Institute of Electrical Communication, Tohoku University, Sendai, Japan
³Primate Research Institute, Kyoto University, Kyoto, Japan

Multibody dynamic analysis (MDA) has become part of the standard toolkit used to reconstruct the biomechanics of extinct animals. However, its use is currently almost exclusively limited to steady state activities such as walking and running at constant velocity. If we want to reconstruct the full range of activities that a given morphology can achieve then we must be able to reconstruct non-steady-state activities such as starting, stopping, and turning. In this paper we demonstrate how we can borrow techniques from the robotics literature to produce gait controllers that allow us to generate non-steady-state gaits in a biologically realistic quadrupedal simulation of a chimpanzee. We use a novel proportional-derivative (PD) reach controller that can accommodate both the non-linear contraction dynamics of Hill-type muscles and the large numbers of both single-joint and two-joint muscles to allow us to define the trajectory of the distal limb segment. With defined autopodial trajectories we can then use tegotae style locomotor controllers that use decentralized reaction force feedback to control the trajectory speed in order to produce quadrupedal gait. This combination of controllers can generate starting, stopping, and turning kinematics, something that we believe has never before been achieved in a simulation that uses both physiologically realistic muscles and a high level of anatomical fidelity. The gait quality is currently relatively low compared to the more commonly used feedforward control methods, but this can almost certainly be improved in future by using more biologically based foot trajectories and increasing the complexity of the underlying model and controllers. Understanding these more complex gaits is essential, particularly in fields such as paleoanthropology where the transition from an ancestral hominoid with a diversified repertoire to a bipedal hominin is of such fundamental importance, and this approach illustrates one possible avenue for further research in this area.

Introduction

Forward dynamic modeling, where muscle forces are used to drive the kinematics of a link-segment model, has a long history in locomotor biomechanics [e.g., (Hatze, 1977; Onyshko and Winter, 1980; Van den Bogart et al., 1989; Yamazaki et al., 1996)]. Its use in paleontology has grown over the last 25 years, particularly in paleoanthropology with the first models attempting to generate movements based on fossil morphology appearing in the late 1990s (Crompton et al., 1998; Kramer, 1999) followed by muscle driven models in the early 2000s (Sellers et al., 2004, 2005; Nagano et al., 2005; Ogihara and Yamazaki, 2006). Other vertebrates have also been simulated, starting with very simple 2D dinosaur models (Sellers and Manning, 2007) which were rapidly extended to 3D (Sellers et al., 2009), with increasing sophistication in terms of anatomical realism and including additional mechanical modalities to reduce the uncertainty of the predictions (Sellers et al., 2017). Whilst there are plenty of non-locomotor studies using MDA [for review see Lautenschlager (2020)], there are far fewer on locomotion. One particularly noteworthy example is a study on the early amniote Orobates that also included validation of the simulation by creating a physical robot (Nyakatura et al., 2019) and there a several examples of purely robotic studies of fossil vertebrates which attempt to understand mechanical and control features of the extinct organism [e.g., (Takita et al., 2000; Fukuoka and Akama, 2014; Zhao et al., 2022)].

Roboticists have been producing legged mobile robots inspired by animals for a much longer time. We can certainly find examples of mechanical legged automata dating back to the 15th century such as Leonardo Da Vinci’s self-propelled mechanical lion (Rosheim, 2006) and the first autonomous, computer-controlled legged robot was probably the “Phony Pony” built by Frank and McGhee (McGhee, 1967; Frank, 1968). Since then, there have been a large number of bipedal and quadrupedal autonomous robots created both physically and as computer simulations. However, very few of these embrace the restrictions imposed by the physiology and anatomy of legged vertebrates. Skeletal muscle contracts in a highly non-linear fashion (Hill, 1938), usually acts in series with relatively compliant passive connective tissue (Hill, 1950), and has a relatively low power availability [maximum 390°Wkg^–1 (Askew et al., 2001)] compared to modern actuators such as brushless DC motors which can easily exceed this by an order of magnitude (Larmine and Lowry, 2012). Similarly, vertebrates are highly redundant in terms of their actuation with a typical high quality quadrupedal musculoskeletal model having over 100 individual muscles (Larmine and Lowry, 2012; Sellers et al., 2013) operating over 12 or 16 joints. The real picture is even more extreme with vertebrate muscular control acting at the motor unit level and each skeletal muscle having 100–200 functional motor units (Gooch et al., 2014), although this level of complexity has yet to find its way into simulations.

This actuator complexity has made generating control patterns for anatomically and physiologically realistic models challenging. The number of actuators and their mixed functions means that the control problem has a high dimensionality and the common solution to this problem has been to rely on various machine learning algorithms to generate activation patterns. One approach is to use genetic algorithms to generate finite state feedforward controllers and this approach can results in spontaneous, high-quality gait (Sellers et al., 2003, 2004), but with the disadvantage that these simulations are computationally very expensive to generate. Alternative feedforward approaches include direct colocation (De Groote et al., 2016) and direct shooting (Anderson and Pandy, 2001) and whilst these are generally much quicker to calculate and excellent techniques when the overall pattern of locomotor kinematics are well-understood, they perform less well when the kinematics are complex or good models for the locomotor patterns do not exist. Instead, fully controlled solutions can be produced where the subsequent activation pattern is dependent entirely on the current state including feedback from sensory inputs. This can include black box solutions based on deep neural net reinforcement learning e.g., (Kidziński et al., 2018; Tsounis et al., 2020) or more transparent control solutions based on modulated central pattern generators e.g., (Aoi et al., 2010; Owaki et al., 2012). The advantage of controlled solutions is that they avoid the instability inherent in feedforward solutions and can potentially generalize to different environments, different gaits, and alterations in the actuators due to injury or fatigue. The disadvantage is that they generally cannot beat the locomotor performance metrics, whether top speed or energy economy, that can be achieved using highly optimized and highly specific feedforward solutions.

The goal of this paper is to extend current high bio-fidelity anatomical and physiological simulations so that they can produce non-steady-state gaits. Accelerating from a standstill to a steady speed, decelerating to stable standing, and being able to turn corners are the minimum competencies required by a legged animal and so these were set as the primary goals. The current work is simulation-based since part of the problem is coping with the challenges of physiologically realistic muscles and these are currently only possible to achieve in simulation although the use of freshly dissected vertebrate muscle as actuators might provide a physical solution in future (Shimizu et al., 2017). We chose our existing chimpanzee simulation framework both for its relevance to human evolution studies as well as representing one of the most detailed and well-tested quadrupedal models currently available (Sellers and Hirasaki, 2018).

Materials and methods

We wanted to provide a simple, transparent approach as an initial proof of concept and so this work is based on the tegotae central pattern generation with the individual oscillators entrained by reaction force feedback (Owaki et al., 2012; Fukuhara et al., 2016, 2018). In a quadrupedal robot this system drives the distal limb contact point in an approximately elliptical trajectory with the angular velocity (omega) modulated by the ground reaction force at the contact. The trajectory shape is controlled by three parameters that specify its horizontal (B) and vertical dimensions (A, Aprime), and there is fifth parameter that specifies the modulation gain from the ground reaction force (sigma), and the initial phase angle of the controller is also specified (phi). This process is illustrated in Figure 1A. This controller was implemented in the freely available open-source code GaitSym2019¹ in TegotaeDriver.cpp and the progression of the trajectory target is specified each time step by the following pseudocode (where N is the ground reaction force, X and Y are the coordinates of the trajectory, and deltaT is the time step of the simulation):

FIGURE 1

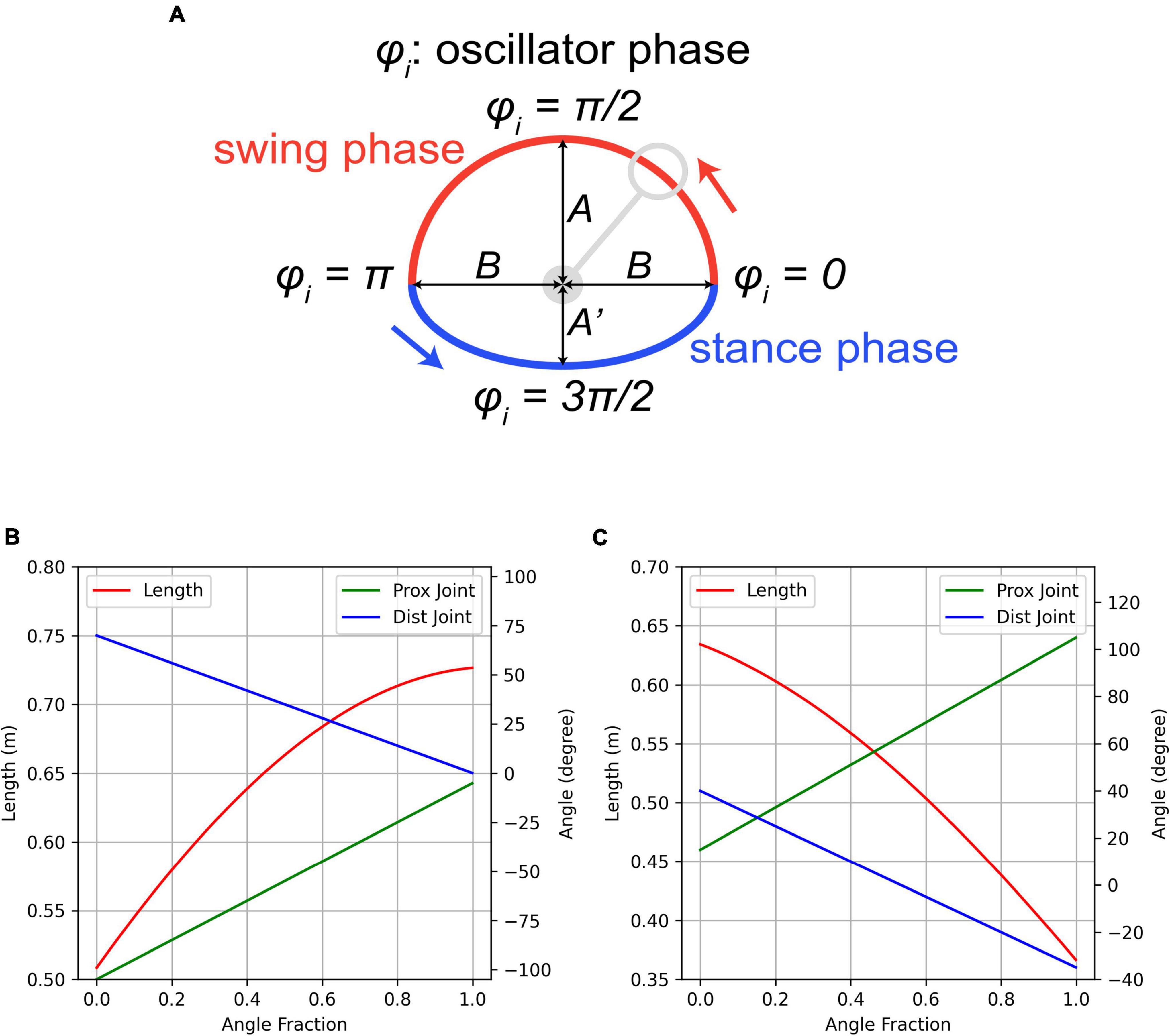
Figure 1. Diagram illustrating the control process. (A) Phase diagram for the tegotae controller illustrating the movement of the target point. (B) Forelimb joint angle controller illustrating how the angle fraction specifies the individual joint angles and the overall length. (C) Hindlimb joint angle controller illustrating how the angle fraction specifies the individual joint angles and the overall length.

phi_dot = omega-sigma * N*cos(phi);

X = B * cos(phi);

if (phi < M_PI) Y = A * sin(phi);

else Y = Aprime * sin(phi);

phi = mod(phi + phi_dot * deltaT, 2 * M_PI);

This is a trajectory-based approach and so we needed to create lower-level controllers for the individual muscles so that the contact point on the autopodia tries to follow the specified path. Reaching to a specified location in space is a completely standard robot arm activity and there are a very large number of algorithms that can achieve this [for review see Gasparetto et al. (2015)]. However, these suffer from exactly the same issues of redundant activators in the bio-realistic vertebrate context and so we developed a novel heuristic approach inspired by our previous work in leaping biomechanics (Sellers, 1996). In this work we needed to generate a specified trajectory for the whole-body center of mass by controlling the individual joint angles in the hindlimb which is an analogous problem to the one presented here. The tegotae controller specifies the desired position of the contact point relative to the proximal joint (the hip or shoulder) so we know the desired total length of the limb. If we allow the two distal joints (knee and ankle, or elbow and wrist) to increase from their minimum to maximum angles, and we have arranged the signs of the joint angles such that minimum angle corresponds to minimum length and maximum angle corresponds to maximum length then we can define a simple function that specifies the joint angles required for a specific limb length. We can also apply weighting factors so that we can prefer to activate a specific joint at different reach lengths. The only requirement is that the controlled change of angles leads to a monotonic change in overall length so that a unique angle fraction can be calculated from a desired length. The interaction between the angle fraction, individual joint angles and the limb length in the chimpanzee fore-and hind-limb are illustrated in Figures 1B,C. Once these angles are known, we can easily calculate the proximal joint angle required to achieve colocation of the distal contact point with the required trajectory. This approach requires certain assumptions about the angular ranges available and will restrict the available positions for the contact point. Fortunately, whilst this might be a problem in the context of reaching for manipulation, it is not a problem for locomotor use since the desired locations are a small subset of all the possible places the autopodia can reach. Once all the desired joint angles are known then we can calculate the desired lengths for all the muscles in the limb including those that cross multiple joints, and we can achieve these desired lengths using simple PD length controllers on the individual muscles. There are issues with co-contraction that can cause problems in edge cases but in the restricted context of a limited reach target domain this approach works adequately and is extremely easy to both implement and calculate. It is implemented in GaitSym2019 as ThreeHingeJointDriver.cpp although the implementation only requires the two distal joints to be hinges, and the proximal joint can be a hinge joint, a universal joint, or a ball joint. The function of this driver can be defined by the following steps:

1. calculate the desired limb length,

2. calculate the angle fraction that generates the desired limb length at the distal two joints,

3. find the rotations about the local X and Y axes at the proximal joint (if this is a hinge joint then the X angle will be zero),

4. create a copy of the limb posed using the calculated angles,

5. read off the muscle lengths from the limb copy,

6. use these lengths as target lengths for the original limb muscles.

Step 5 hides a lot of complexity because the lengths of the various muscles can be quite difficult to calculate, especially if they wrap around objects in their paths. Fortunately, by building the limb copy in the desired pose, all of this calculation is handled by the GaitSym strap functions (TwoPointStrap.cpp, NPointStrap.cpp, CylinderWrapStrap.cpp, and TwoCylinderWrapStrap.cpp) and the required lengths can simply be read from the posed limb copy.

The chimpanzee musculoskeletal model is based on a CT scan of an adult male zoo specimen combined with dissection-based literature values for muscle parameters and has been detailed elsewhere (Sellers et al., 2013; Sellers and Hirasaki, 2018). The full specification of the model (dimensions, mass properties, muscle paths, and joint limits) is available in the human-readable Supplementary Information model data files. The extracted bone and skin meshes are also provided. The previous model used finite state feedforward drivers and these were removed before adding the additional specifications for the new drivers. This includes the PD length controllers for each muscle, the tegotae driver for each limb, and the three-hinge driver for each limb. The gain constants for the PD controllers were set by hand since the simulation proved not to be very sensitive to the specific values chosen (Kp = 200, Kd = 20). The angle limits for the three hinge drivers were set following the likely angular excursions seen in quadrupedal locomotion in chimpanzees (Watson et al., 2009). In the tegotae driver, omega was controlled directly to allow stopping and starting, and the initial value of phi was set to represent an appropriate phase difference between the limbs (Watson et al., 2011). The other values were set using a genetic algorithm optimizer, although since there are only eight independent values (see Table 1) the choice of optimization technique is not important. The optimizer fitness was set in different ways depending on the current goal. For the starting and stopping experiments it was the distance traveled forward. For the turning experiments it was the angle turned as well as the distance traveled in a circle. Omega was set to different values through the experiment to cause the simulation to accelerate from standing at the beginning and decelerate to standing at the end in all cases.

TABLE 1

Table 1. The ranges set for the tegotae controller values before optimization.

The simulation runs in almost real time on a standard desktop computer and each simulated locomotor bout is up to 30 s long. With only eight parameters to find, the optimization process is completed in a few hours since the genetic algorithm optimizer can take advantage of multiple cores on multiple networked computers using the local Condor Cluster at the University of Manchester. Genetic algorithm optimizers do not require any knowledge of gradients and can cope with non-linear and discontinuous fitness functions so functioned well in this case although it is likely that other optimization algorithms could be considerably faster if that was an important consideration.

Results

The initial test was to check whether the reach controller could provide adequate positional control. This was done using a grid of target locations that needed to be lined up with the contact point on the distal limb segment. The target location is moved to the different locations on the grid and the controller then activates the muscles to achieve the required colocation. Figure 2 shows the results of this test for the forelimb controller and shows that the controller can drive a horizontal stride length of at least 0.7 m with a height range that varies depending on the limb position but is likely to be at least 0.2 m at mid stance. The actual range of movement of a chimpanzee hand is very much larger than this, but this range is more than adequate for quadrupedal locomotion. Supplementary Video 1 shows the process of tracking the moving target in action.

FIGURE 2

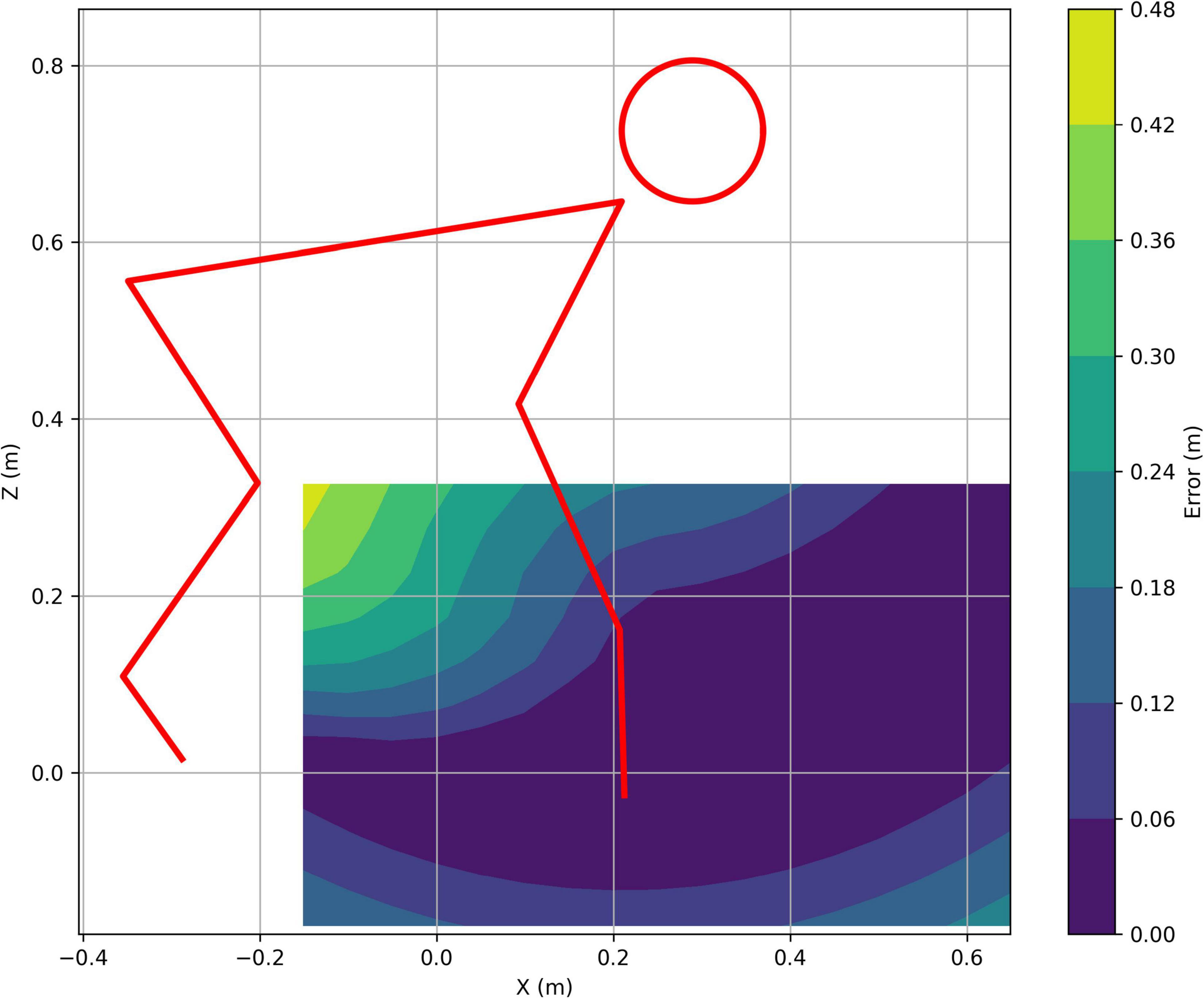
Figure 2. Contour plot of the colocation error magnitude for the forelimb tracking a target. The low error zone in dark blue shows the effective domain of the controller with the specified angular excursions, and the red line shows the initial pose of the model.

The second test was to see whether we could create controllers that could produce bouts of stable starting and stopping. This used a fixed omega of zero for 5 s followed by πrad/s for 5 s, repeated three times for a 30 s start-stop sequence. Figure 3 shows the position and velocity profile of the simulation and Figure 4 shows its appearance at 5 s intervals. An animation of the gait achieved is shown in the Supplementary Video 2. It is clear that the controller is able to achieve the required start-stop locomotion with the simulation coming to rest for 5 s at 5 s intervals. However, the gait during the periods of movement has a very high variability in its forward velocity. There are also periods where the velocity is negative and this represents times when the tegotae driver is at rest and the PD controllers are finding stable muscle lengths.

FIGURE 3

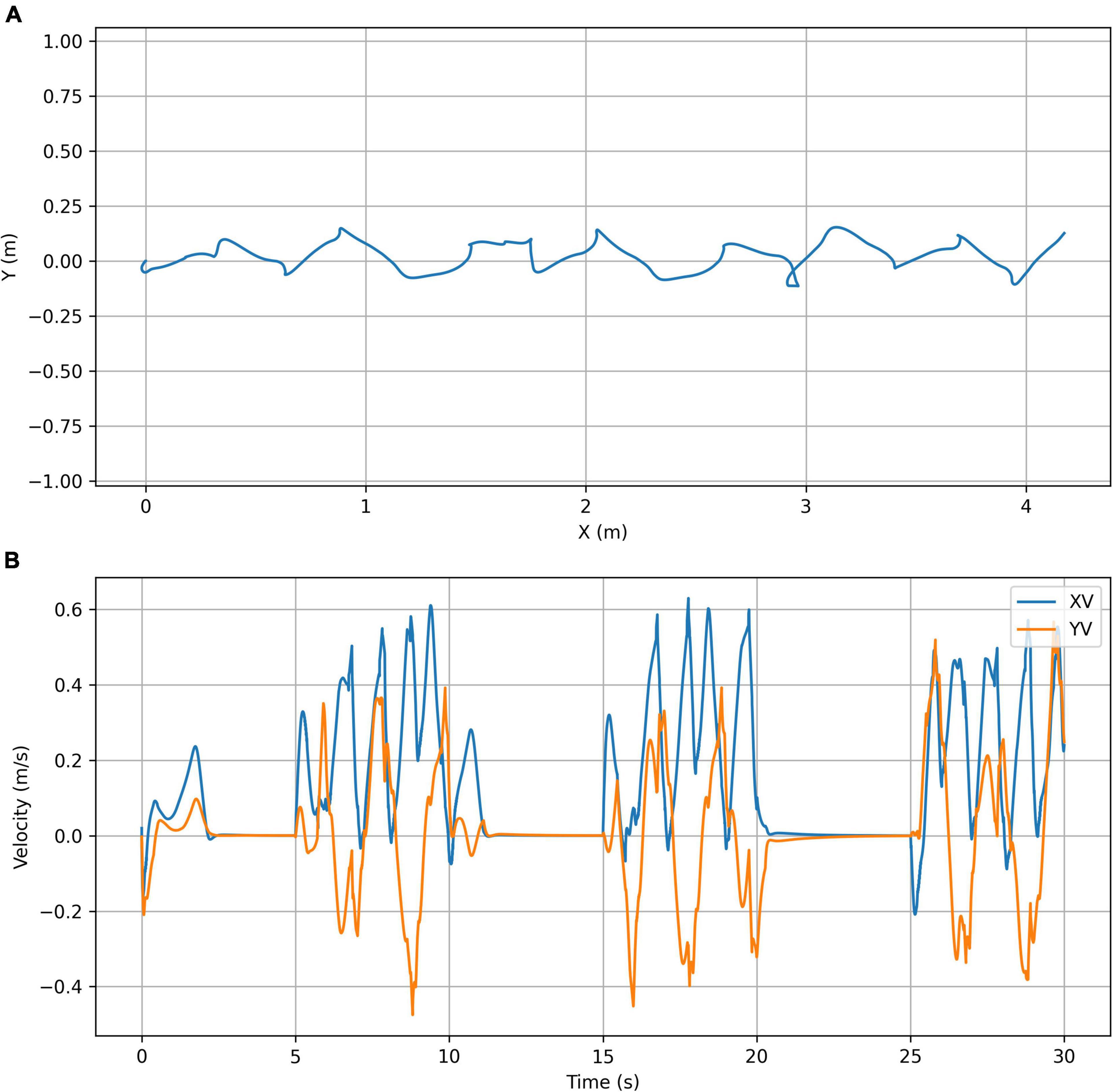
Figure 3. Start-stop simulation plots. (A) Trajectory plot showing the top view of the path taken by the center of mass of the chimpanzee’s torso. (B) Velocity plot showing the X (forward) velocity and Y (lateral) velocity of the center of mass of the chimpanzee’s torso.

FIGURE 4

Figure 4. Still frames from the start-stop animation at 5 s intervals.

The third test was to see whether we could achieve turning locomotion from a standing start. This test used a fixed omega of zero for 5 s, π rad/s for 20 s, and zero for the last 5 s. The values for B (effectively the stride length) on the left side were decreased by 5% whilst the values of B on the right side were increased by 5% so that the simulation would turn to the left. Figures 5A,C,D shows the position and velocity profile of the simulation as well as the vertical impulse under each contact and Figure 6 shows its appearance at 5 s intervals. An animation of the gait achieved is shown in the Supplementary Video 3. In this case, the controller is able to achieve the required turning locomotion relatively easily although falling over was much more common in turning than in traveling in a straight line which would suggest that the gait is less stable than that achieved in the start-stop experiments, and we can see from Figure 5B that the turning velocity is by no means constant.

FIGURE 5

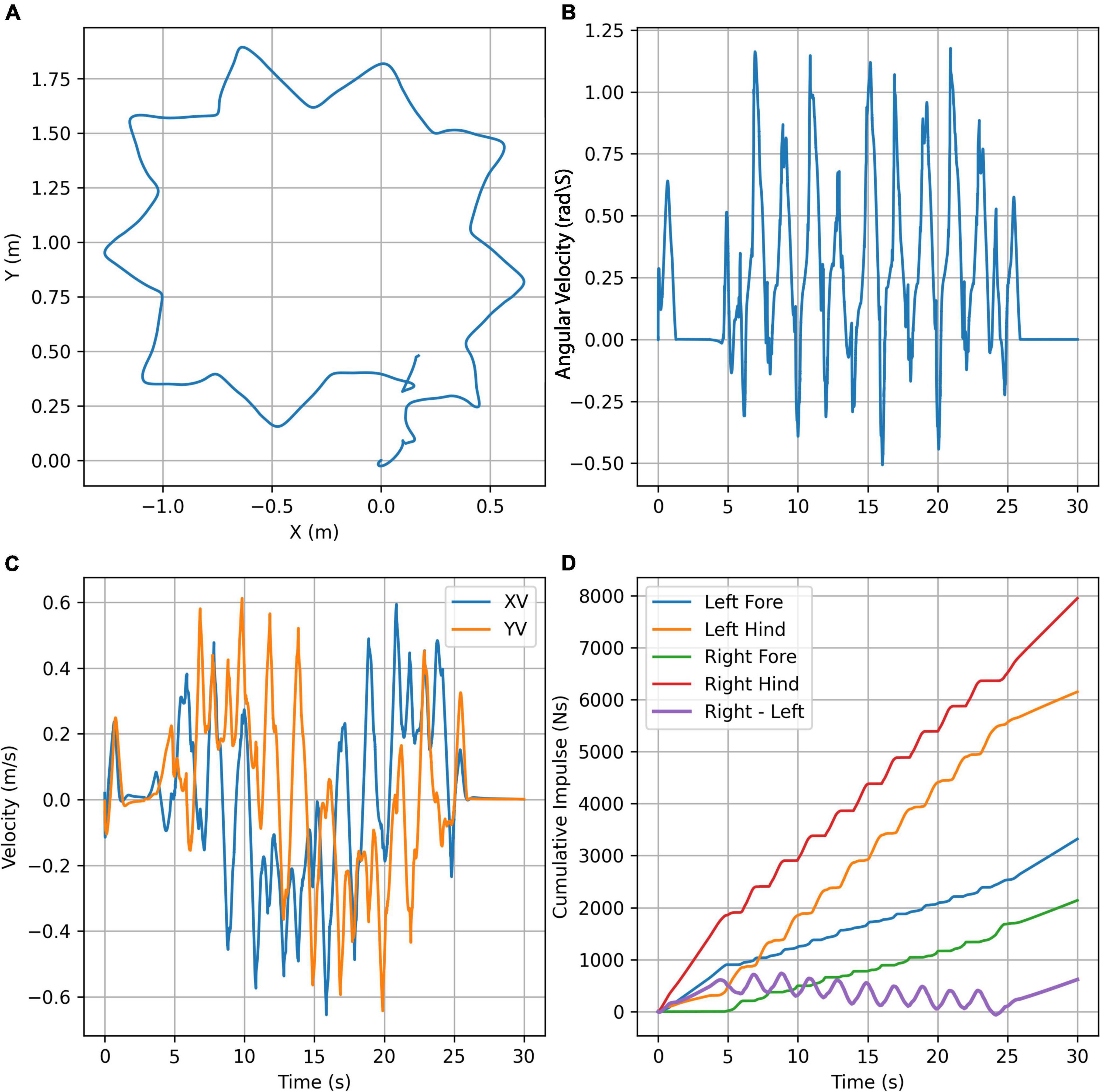
Figure 5. Turning simulation plots. (A) Trajectory plot showing the top view of the path taken by the center of mass of the chimpanzee’s torso. (B) Angular velocity of the torso about the Z (vertical) axis. (C) Velocity plot showing the X (forward) velocity and Y (lateral) velocity of the center of mass of the chimpanzee’s torso. (D) The vertical cumulative impulse at the contact points and the difference between the totals on the right-and left-hand sides.

FIGURE 6

Figure 6. Still frames from the turning animation at 5 s intervals.

It is hard to judge the quality of the achieved gait from the non-steady-state examples since there is very little to compare with. We do not have good performance criteria for non-steady animal gaits either experimentally or in simulation. The most that can be said is that qualitatively the appearance is reasonable but much less fluid than that observed from a living chimpanzee (although that is true for all simulated gaits using rigid torsos). However, it is possible to use the same controllers to generate continuous gaits by including omega as an optimisable parameter and following the gait morphing process where the mid-point of a previous simulation is used as the starting condition for the next simulation (Sellers et al., 2004). We can then use the distance traveled in a specified time as a fitness criterion for maximizing forward velocity, and the distance traveled for a specified metabolic energy cost as a fitness criterion for maximizing the energy efficiency. Table 2 shows the maximum forward velocity and efficiency values achieved by the simulation using the new controllers as well as the values that were obtained with the same model but using feed forward controllers (Sellers and Hirasaki, 2018). Here we can see that whilst the new controllers allow steady-state gait to be produced, their performance is worse than that achieved by highly tuned feedforward controllers, particularly for metabolic energy efficiency. Looking at the trajectory plots (Figures 6, 7) we can see that the continuous gaits still vary in forward velocity but never drop to zero as was found in non-steady-state examples. The montage frames (Figures 8, 9) and their respective animations (Supplementary Videos 4, 5) show much improved gaits compared to non-steady-state examples with much smoother movements. Unlike previous robotics work using the same control system (Owaki and Ishiguro, 2017) we were unable to get spontaneous gait transitions to non-walking gaits. This has been achieved previously in feedforward simulations (Sellers et al., 2009) but was also not achieved with feedforward chimpanzee model (Sellers and Hirasaki, 2018).

TABLE 2

Table 2. Forward velocity and cost of transport values for the current controller optimized for either efficiency or forward velocity compared to values obtained using the same model but with a purely feedforward finite state controller (Sellers and Hirasaki, 2018).

FIGURE 7

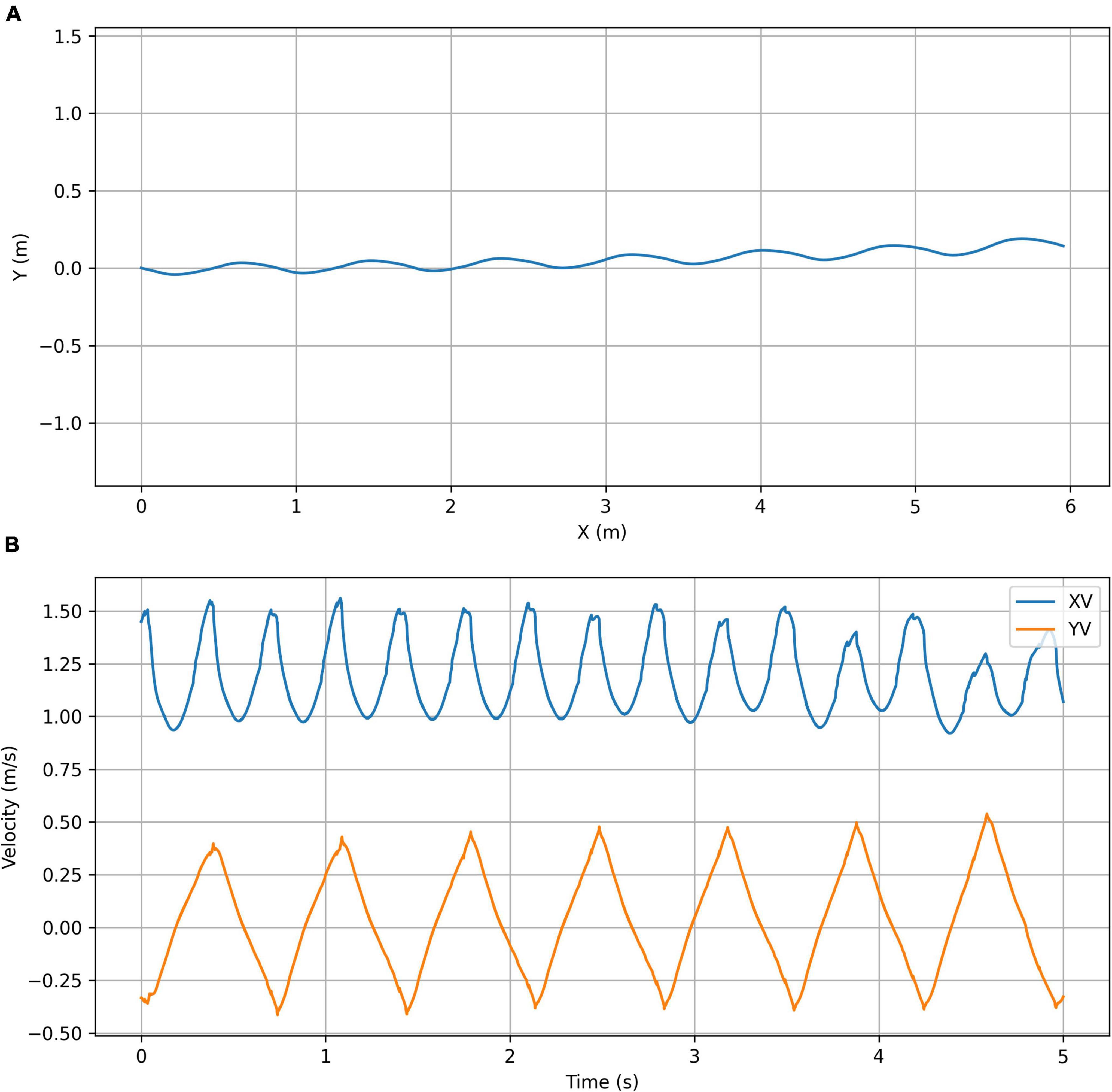
Figure 7. Optimized for forward velocity simulation plots. (A) Trajectory plot showing the top view of the path taken by the center of mass of the chimpanzee’s torso. (B) Velocity plot showing the X (forward) velocity and Y (lateral) velocity of the center of mass of the chimpanzee’s torso.

FIGURE 8

Figure 8. Still frames from the efficiency optimized animation at 0.333 s intervals.

FIGURE 9

Figure 9. Still frames from the forward velocity optimized animation at 0.333 s intervals.

Discussion

Our results demonstrate a novel way of achieving certain steady-state (walking at constant speed) and non-steady-state gaits (starting, stopping, and turning) in an anatomically and physiologically realistic quadrupedal vertebrate. The tegotae controller implementation, originally developed for legged robot control using biologically inspired ideas about central pattern generation (Owaki et al., 2012; Fukuhara et al., 2016), is therefore shown to generalize to a very different actuation and stability environment where the muscles are non-linear, the power availability is relatively low, and the aspect ratio of the body means that the risks of lateral tipping are high. We also demonstrate the utility of our simple heuristic reach controller as a way of coping with the large numbers of muscles that exist in anatomically realistic simulations, which is an essential part of allowing the contacts points in the simulation to follow the trajectories required for the gait controller. The implementation requires minimal computer power because there are relatively few global parameters to be optimized to produce effective locomotion. Starting and stopping are easy to generate (Figures 2, 3) and this matches previous work with this control system (Fukuhara et al., 2016). Turning by changing the step length asymmetrically also works but it is somewhat less successful (Figures 4, 5) probably because it is a considerable over-simplification of the process of turning gaits in quadrupeds [e.g., (Hase and Stein, 1999; Jindrich and Full, 1999; Walter, 2003; Demes et al., 2006)]. The vertical impulse (Figure 5D) illustrates how the turn is driven by increased reaction forces on the outer side with the largest contributions from the rear limbs matching the hind-limb drive model long associated with primate locomotion (Kimura et al., 1979) and highlighted as “hindlimb steering” in primate turning studies (Demes et al., 2006). Ideally the quality of these gaits could be compared to data obtained experimentally. There are excellent chimpanzee treadmill studies [e.g., (Taylor and Rowntree, 1973; Pontzer et al., 2014)] but these focus exclusively on straight line, constant speed locomotion. Kinematic studies on free-ranging chimpanzees [e.g., (Watson et al., 2009; Finestone et al., 2018)] could provide information on starting, stopping, and turning but to date they have also focused exclusively on steady state locomotion. There is an interest in elucidating the role of non-steady state gaits in primate evolution [e.g., (Li et al., 2004)] but, with no formal studies as yet, this should prove a fruitful area for future research. Field researchers have long characterized the frequency of different gaits observed in free ranging chimpanzees [e.g., (Doran, 1992)] illustrating the appreciation that there is a need to understand the full range of locomotor capabilities seen in living and fossil primates. In addition, various forms of locomotion are recognized as a major selective factor in the context of human evolution [e.g., (Taylor and Rowntree, 1973; Pontzer and Wrangham, 2004; Crompton et al., 2010)]. However, getting kinematic information for an extended gait repertoire necessitates working with free-ranging animals and it is only recently that we have had good techniques for obtaining the necessary 3D information relatively easily from unmarked animals (Sellers and Hirasaki, 2014; Nath et al., 2019). We hope that providing a simulation framework that can accommodate some of these gaits will provide the necessary impetus for further work in this important area.

The controller can also produce continuous gaits (Figures 6–8, 10) but these are considerably less accomplished than those produced by feedforward controllers using the same underlying model (Table 2). We would speculate that this is due to the magnitude of the speed changes of the simulation, and that this is probably caused by the variations in the speed of the contact point trajectory not exactly matching the natural pendular speeds of the system. This would mean that the individual limbs need to be driven actively by muscle contraction throughout the gait cycle, whereas in a highly tuned feedforward system, because the various pendular frequencies can be matched, the movement can be driven by a largely passive interchange of kinematic and potential energies within the body (McGeer, 1990).

FIGURE 10

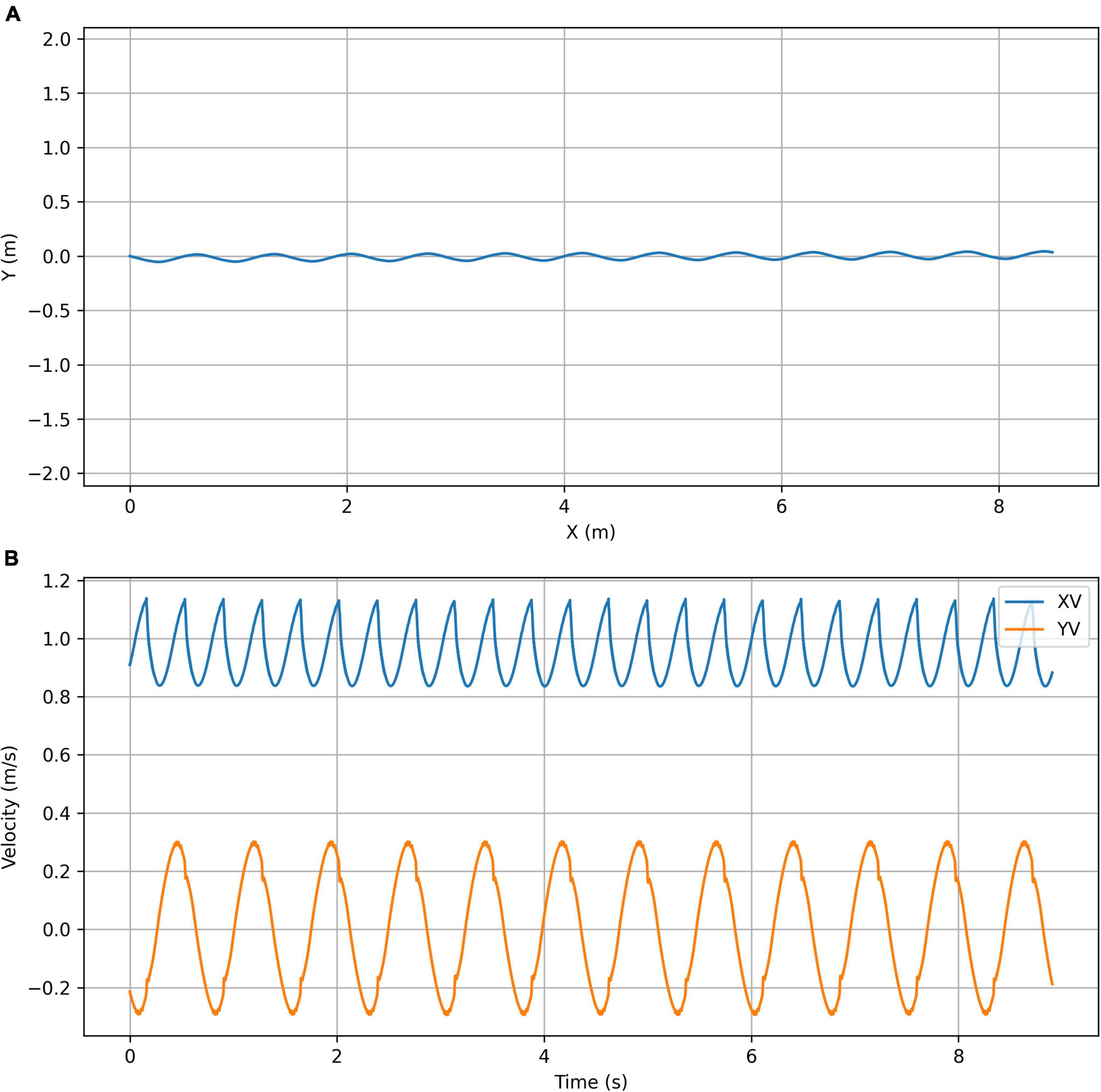
Figure 10. Optimized for efficiency simulation plots. (A) Trajectory plot showing the top view of the path taken by the center of mass of the chimpanzee’s torso. (B) Velocity plot showing the X (forward) velocity and Y (lateral) velocity of the center of mass of the chimpanzee’s torso.

It is very likely that steady-state legged locomotion is a largely feedforward controlled process, if only because the conduction time for neural signals means that direct feedback control is probably not possible and that any necessary error correction occurs at some temporal offset to the error detection (More et al., 2010). However, animals need to cope with non-steady-state activities such as those presented here and these are not currently easy to achieve using current simulation technology when the underlying model attempts to accurately reflect the physiology and anatomy of a cursorial vertebrate. Our current system therefore provides a useful starting point for further work in this area. Our simulation is entirely forward dynamic, and could potentially be driven across a complex environment and have the option of choosing different routes, gaits and velocities as required. This would require a small library of control parameters that could be built up for the different requirements, and since there are only nine required in the current implementation, it should not be hard to transition between the required locomotor outcomes. Whilst this may not currently tell us very much about how animals achieve the precise levels of control they demonstrate, it means that we can expand locomotor reconstructions to consider the complete behavioral repertoire, and we can then analyses the form/function/environment interactions at a completely new level of complexity and brings us one step closer to the “Virtual World of Paleontology” (Cunningham et al., 2014).

To achieve this step change in locomotor simulation we clearly need to improve aspects of our controllers. The heuristic reach control system does not cope well with the problems of co-contraction and so is always likely to increase the energy requirement required for a movement whilst at the same time reducing the maximum power available. Fortunately, there are other more sophisticated reach control algorithms and it would certainly be possible to obtain the required reach behavior using an artificial neural network approach (Vilaplana and Coronado, 2006). Indeed, the current controller could be used to generate training data where the current model state is used as an input, and the muscle activation pattern is used as an output, and the accuracy and speed of the location matching used as a performance indicator. The tegotae controller currently only uses a single reaction force feedback input, and the controlled trajectory is approximately elliptical. However, there are other sensory inputs that could be used to further modify the trajectory, and the trajectory itself can be modeled on generalized foot trajectories obtained from quadrupedal animals using some of the ideas from kinematic motion primitive studies (Spröwitz et al., 2014). Lateral stability could be improved by allowing the lateral location of the desired trajectory to move to compensate for sideways titling of the body and turning performance could be improved by allowing the desired foot trajectory to turn before the body itself. A feature of the physical quadrupeds that previously used this controller is a flexible torso (Fukuhara et al., 2016) and indeed adding extra degrees of freedom in the body and in the limb-girdles may be exactly what is required to improve the fluidity of the movement generated and improve turning performance. All of these changes increase the complexity of the simulations and the numbers of parameters in the controllers but the big advantage of the current approach is that the number of parameters is very small, particularly when compared to the number of controlled elements, so there is plenty of headroom for additional complexity without increasing the simulation or learning times too much.

Conclusion

We demonstrate a completely new approach to controlling high bio-fidelity vertebrate simulations that can cope with large numbers of muscles and non-steady-state locomotor patterns with minimal computational complexity. The current incarnation is a proof of concept and although it functions adequately it does not perform as well as dedicated feedforward controllers in steady-state locomotion. We suggest that the current system is a useful starting point for further work in this area and has the potential to allow us to create freely moving, biologically meaningful simulated legged animals for reconstructing synthetic paleontological worlds.

Data availability statement

The original contributions presented in this study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

WS wrote the software and first draft of the manuscript. CC and WS performed the analysis simulations. EH and WS constructed and modified the chimpanzee model. AF, AI, and WS designed the control system. All authors contributed to conception and design of the study, manuscript revision, read, and approved the submitted version.

Funding

This work was supported by BBSRC grant number: BB/K006029/1 and JSPS Grant-in-Aid for Scientific Research (B) (grant number: 21H01269).

Acknowledgments

We would like to thank staff at the Primate Research Institute (PRI), Kyoto University for access to chimpanzee material, and we would like to acknowledge the assistance given by Research IT and the use of the Condor Cluster at the University of Manchester.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2022.954838/full#supplementary-material

Footnotes

^ https://github.com/wol101/GaitSym2019

References

Anderson, F. C., and Pandy, M. G. (2001). Dynamic optimization of human walking. J. Biomechan. Eng. 123, 381–390. doi: 10.1115/1.1392310