- Department of Geological Sciences, Stanford University, Stanford, CA, United States
Paleobotany is at a crossroads. Long-term trends in the fossil record of plants, encompassing their interactions with herbivores and with the environment, are of the utmost relevance for predicting global change as pCO2 continues to rise. Large data compilations with the potential to elucidate those trends are increasingly easy to assemble and access. However, in contrast to modern ecology and unlike various other paleontological disciplines, paleobotany has a limited history of “big data” meta-analyses. Debates about how much data are needed to address particular questions, and about how to control for potential confounding variables, have not examined paleobotanical data. Here I demonstrate the importance of analytical best practices by applying them to a recent meta-analysis of fossil angiosperms. Two notable analytical methods discussed here are propensity score matching and specification curve analysis. The former has been used in the biomedical and behavioral sciences for decades; the latter is a more recent method of examining relationships between, and inherent biases among, models. Propensity score matching allows one to account for potential confounding variables in observational studies, and more fundamentally, provides a way to quantify whether it is possible to account for them. Specification curve analysis provides the opportunity to examine patterns across a variety of schemes for partitioning data—for example, whether fossil assemblages are binned temporally by stage, epoch, or period. To my knowledge, neither of these methods has been used previously in paleontology, however, their use permits more robust analysis of paleoecological datasets. In the example provided here, propensity score matching is used to separate latitudinal trends from differences in age, climate, and plant community composition. Specification curve analysis is used to examine the robustness of apparent latitudinal trends to the schema used for assigning fossil assemblages to latitudinal bins. These analytical methods have the potential to further unlock the promise of the plant fossil record for elucidating long-term ecological and evolutionary change.
1. Introduction
Many scientific disciplines have been revolutionized by “big data,” or “data-intensive science” (Resnik et al., 2017), which is characterized by “consolidating data from multiple sources” and “repurposing data” (Clarke, 2016). Paleontology has a long history of such large-scale analyses: quantitative paleobiology as a discipline leverages data compilations to search for patterns in the history of life, such as mass extinctions and biotic response to climate change (Sepkoski, 2012).
Groundbreaking early studies noted that the structure of the fossil record—changes in the amount of rock volume through time, geographic patterns in the incompleteness of the fossil record, and so forth—are likely to influence, but not necessarily invalidate, the patterns that emerge when available fossil data are interpreted at face value (Raup, 1972; Sepkoski et al., 1981). For decades, quantitative paleontology has been caught in a cycle in which some authors point out the nonrandomness and incompleteness of paleontological data and the ubiquity of potential confounding factors (Close et al., 2020; Raja et al., 2021) and others point out that methods are available to account for these phenomena (Wang and Bush, 2008; Holland, 2017). All the while, a plurality of workers continue to analyze paleontological data compilations without explicitly controlling for relevant structure and biases in the rock record. Paleontologists' varying levels of concern about structure and biases of the fossil record are but one manifestation of the larger debate surrounding appropriate uses of repurposed, “big” data.
Best practices for analyzing paleontological data are well outlined for studies of marine invertebrates; this is, however, not the case in paleobotany, even though a quantitative approach to paleobotany has become increasingly popular as larger datasets have been compiled and shared (Nowak et al., 2019; Capel et al., 2021; Romero-Lebrón et al., 2022). This trend necessitates an exploration of best analytical practices in the specific context of paleobotany. One key feature of paleobotanical data compilations is that they often reflect interactions—with other organisms, such as herbivores (Labandeira, 2006), or with the environment (Boyce and Zwieniecki, 2012)—rather than simpler taxic trends, such as gamma diversity, that are the focus of many studies of marine invertebrates (Sepkoski et al., 1981; Bush and Bambach, 2015). In other words, for paleobotany, the fundamental unit of analysis is typically an individual fossil specimen, rather than a taxon.
Paleobotanical evidence of trophic and environmental interactions holds tremendous importance for elucidating future global change (Crowley and Berner, 2001; Wappler et al., 2012), and thus, high analytical standards are essential. However, paleobotany has a short history of “big data” studies, and the more straightforward taxic questions typically addressed with marine invertebrate data represent a small fraction of possible questions addressed through quantitative paleobotanical studies (Cleal and Cascales-Miñana, 2014). Standards and guidelines for quantitative paleobotanical research differ from those for invertebrate paleontology. A number of statistical guides have been published for paleobotanical studies focusing on one or a few fossil assemblages (Lamboy and Lesnikowska, 1988; Scott and Titchener, 1999; Cleal et al., 2021; Pardoe et al., 2021), but no such guide exists for analyzing large data compilations.
Best analytical practices for “big data” ensure that data are sufficient to address the questions at hand, and minimize the probability that arbitrary decisions made by researchers compromise the integrity and relevance of any findings. Here I first discuss best practices for paleobotanical “big data” studies, then demonstrate the relevance of these best practices by revisiting a recent study by Currano et al. (2021) using power analysis, propensity score matching, and specification curve analysis (Benedetto et al., 2018; Simonsohn et al., 2020), as well as null models of bipartite network metrics (Dormann et al., 2008) to examine the validity of identified trends in insect herbivory ranging from the Maastrictian to present (72.1-0 Ma). Their analyses focus primarily on presence/absence data for insect damage types (DTs; Labandeira et al., 2007) on each censused leaf. Here I elaborate upon the original analyses (Currano et al., 2021) by implementing the abovementioned analytical best practices.
My discussion of these best practices is based largely on contributions from Shrout and Rodgers (2018) and Makin and Orban de Xivry (2019). Because recent research in psychology has greatly best practices to address the replication crisis (Nosek et al., 2012; Open Science Collaboration, 2015), I draw on these advances to guide my discussion on related issues in paleontology. Comparisons to psychology are particularly apt when discussing paleontology because both disciplines are plagued by small sample sizes. For example, meta-analyses of latitudinal gradients of insect herbivory in modern ecosystems tend to have large sample sizes: 728 localities with an average of 2.6 plant species per locality (Zhang et al., 2016), over 2.5 million leaves from 845 localities (Kozlov et al., 2015), and so forth. A paleontological study of this topic would ideally include more leaves and localities than typically seen in studies of modern ecosystems, because paleontological studies examine change over time and therefore need to identify spatial trends across multiple time bins. A recent data compilation (Currano et al., 2021), however, includes fewer than 80,000 leaves from fewer than 70 fossil assemblages. Considering the amount of time and effort required to excavate and prepare fossil leaves, and then examine them for insect herbivory, tens of thousands of leaves is a tremendous accomplishment. However, because the data compilation ultimately contains less than 1 assemblage per million years, scattered across all continents except Australia, the clear question is: do the authors have enough data to answer the paleoecological questions they are asking?
2. A review of accepted best practices in statistical paleobiology as applied to paleobotany
In this section I discuss the relevance of analytical concepts that are already widely-known in the paleontological literature (Simpson's paradox, cherry-picking, naïve hypotheses, underdetermination) to recent statements about trends in insect folivory on fossil angiosperms. These concepts are outlined before the Results because they do not lead directly to, or necessarily require, specific analyses.
2.1. Simpson's paradox and spurious correlation due to pooling
Currano et al. (2021) did not separate the fossil assemblages in their data compilation by age when analyzing the effects of latitude. However, when data are pooled by a predictor of known importance (in this case, pooled into a single temporal bin for geologic age), spurious correlations can arise—i.e., differences in age may underlie the results of their latitudinal analyses because age distributions vary among the fossil assemblages of different latitudinal bins. The danger of pooling data by predictors that are known to be important (such as age, in this case) is described by “Simpson's paradox.”
2.1.1. General relevance
One often thinks of spurious correlations as occurring due to simple random chance. As Makin and Orban de Xivry (2019) write, “Spurious correlations can also arise from clusters, e.g., if the data from two groups are pooled together when the two groups differ in those two variables.” Simpson's paradox lies at the heart of this problem. In statistical parlance, Simpson's paradox is defined as “a phenomenon whereby the association between a pair of variables (X, Y) reverses sign upon conditioning of a third variable, Z, regardless of the value taken by Z” (Pearl, 2014).
Simpson's paradox was explored by Wang and Bush (2008), who compared the end-Ordovician and end-Permian extinction events (Figure 1). Cephalopods are more prone to extinction than are gastropods. Cephalopod genera outnumbered gastropod genera at the end-Ordovician but not at the end-Permian. Therefore, when the pooled extinction rate for mollusks is calculated for the end-Ordovician and end-Permian events, the rates appear to be similar for both events; this result is due to changes in the prevalence of cephalopods and gastropods throughout the Paleozoic. It is for this reason that the severity of the end-Ordovician and end-Permian events should be calculated separately for each mollusk class: pooling all classes yields a misleading result.
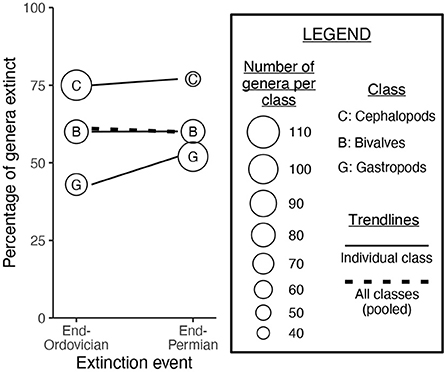
Figure 1. A paleontological example of Simpson's paradox, from Wang and Bush (2008). Cephalopods were slightly more likely to go extinct at the end-Permian as compared to the end-Ordovician, and gastropods were much more likely to go extinct. However, when mollusk classes are pooled together, the end-Permian event appears no more severe than the end-Ordovician. This is because cephalopod genera outnumbered gastropod genera at the end-Ordovician, and gastropod genera outnumbered cephalopod genera at the end-Permian.
2.1.2. Relevance to angiosperm folivory
The benefit of paleontological data is that they provide a glimpse into how biological changes have occurred through time. For example, many studies have examined how latitudinal biodiversity gradients have changed during timescales of tens of millions of years (Jablonski et al., 2006; Powell et al., 2012, 2015; Mondal et al., 2019; Wu et al., 2019; Allen et al., 2020; Dunne et al., 2021). However, the data under re-study are insufficient to separate latitudinal and temporal signals: for example, the compilation contains only one Paleocene assemblage (Wing et al., 2009), one Oligocene assemblage (Currano et al., 2011), and one Miocene assemblage (Currano and Jacobs, 2021) from tropical latitudes (Figure 2). The original study pooled all latitudinal bins when examining temporal differences in herbivory, and pooled all temporal bins when examining latitudinal differences in herbivory.
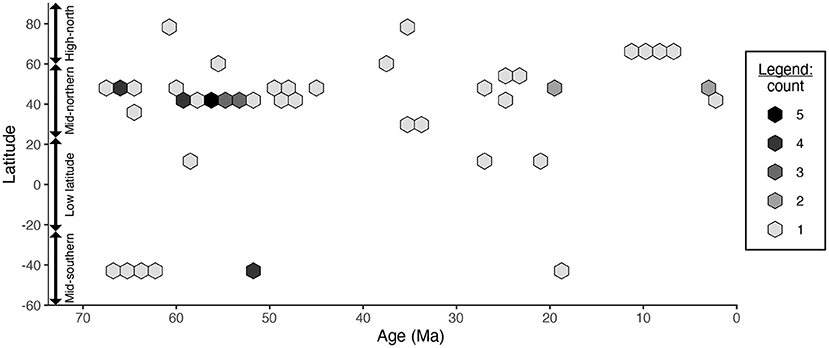
Figure 2. The age and latitude of the fossil assemblages included in Currano et al. (2021)'s latitudinal analyses.
The canonical studies that established the importance of angiosperm–herbivore interactions in the fossil record centered on changes in herbivory across the Cretaceous/Paleogene boundary (Labandeira et al., 2002) and the Paleocene/Eocene Thermal Maximum (Wilf et al., 2001), however, this temporal variability is discarded in the latitudinal analyses of Currano et al. (2021). Whereas it may be impossible for a paleontological analysis to be truly complete, the analyses under re-study are flawed because in each case, at least one widely-recognized major determinant of insect herbivory for which data are available (latitude, age) is ignored.
2.2. Cherry-picking
As more and more analytical techniques are devised, it is not always clear which analysis is most appropriate for any given biological question. “Cherry-picking” is a term used to describe the calculation of multiple metrics to address the same question, and the selective reporting of only a subset of those metrics.
2.2.1. General relevance
According to Shrout and Rodgers (2018), “more complete disclosure of nonsignificant as well as statistically significant findings” is a key step in making research replicable and transparent. Exhortations to publish negative and non-significant results are, of course, not new (Dickersin, 1990). In light of the proliferation of software packages that permit the calculation of dozens of metrics with a single line of code, such as the bipartite network analysis discussed below, complete disclosure of results should be the beginning of a longer process. To avoid cherry-picking, paleontological studies should first evaluate whether the complete suite of results—those that are significant, and those that are not—is best attributed to a true biological signal, or to a low signal-to-noise ratio caused by insufficient data. If the suite of results is best attributed to a true biological signal, the next step is to present a coherent explanation of why some metrics yield significant results and others do not.
2.2.2. Relevance to angiosperm folivory
The original meta-analysis includes an example of cherry-picking that is not suited to specification curve analysis. The authors state that specialized herbivory is more prevalent at mid-southern latitudes (Currano et al., 2021, pg. 8). (The conceptual pitfalls of discerning specialization through damage type data are too discipline-specific to discuss here). The authors also state that specialized herbivory became less prevalent from the Cretaceous into the Paleocene, due to the disproportionate extinction of specialist herbivores at the end-Cretaceous, and that specialized herbivory then became more prevalent during the Eocene as specialist clades of herbivores eventually rebounded.
If this is indeed the case, any increase in the overall richness of damage types from the Cretaceous through Paleocene should be disproportionately attributable to non-specialist damage types, and any decrease in the overall richness of damage types from the Cretaceous through Paleocene should be disproportionately attributable to specialist damage types. Along these lines, the proportion of damage types at each assemblage that are specialized should decrease immediately after the Cretaceous/Paleogene event, and should increase from the Paleocene into the Eocene (Figure 3).
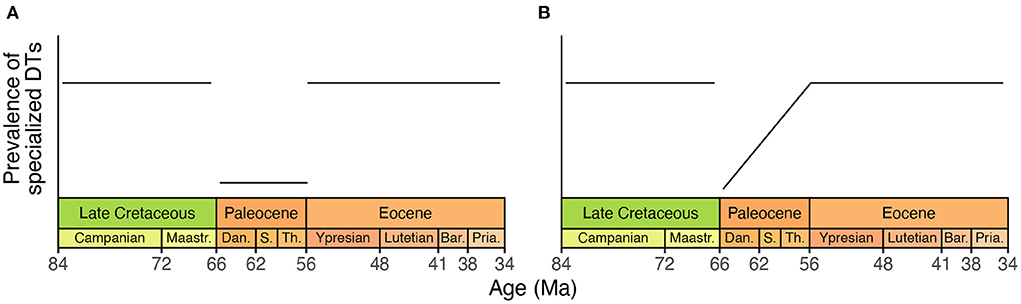
Figure 3. A hypothetical illustration, showing the prevalence of specialist herbivores from the Cretaceous through Eocene according to Currano et al. (2021). (A) A literal interpretation of the scenario that the original study outlined for specialized herbivory during the Cretaceous, Paleocene, and Eocene. (B) An alternative scenario that conforms to the proposed trajectory of specialized herbivory through time while incorporating the potential for the diversity of herbivory to vary within the Paleocene. The timescale used here is from Cohen et al. (2013).
However, the most straightforward reading of this data compilation does not support this scenario (Figure 4). Among all Paleocene assemblages in the compilation, Castle Rock (Wilf et al., 2006) has the lowest prevalence of specialized damage, whether measured as the richness of specialized damage types or the percentage of damage types that are specialized (Figure 4). However, Castle Rock postdates two other fluvial Paleocene assemblages from the western interior of North America—Pyramid Butte and Mexican Hat—that are temporally closer to the Cretaceous/Paleogene event and that have much higher prevalences of specialized damage, however defined. The Paleocene assemblage in the compilation with the second-lowest prevalence of specialized damage is Skeleton Coast (Wilf et al., 2006), which postdates the Cretaceous/Paleogene boundary by over 6.5 Myr. Moreover, the data compilation includes three other assemblages from the same formation that are nearly identical in age—Persites Paradise, Kevin's Jerky, and Haz-Mat—all of which have much more specialized herbivory. In other words, neither of the two assemblages in the compilation that best exemplify low levels of specialized herbivory in the aftermath of the Cretaceous/Paleogene event suggest that their low levels of specialized herbivory were in fact caused by the Cretaceous/Paleogene event.
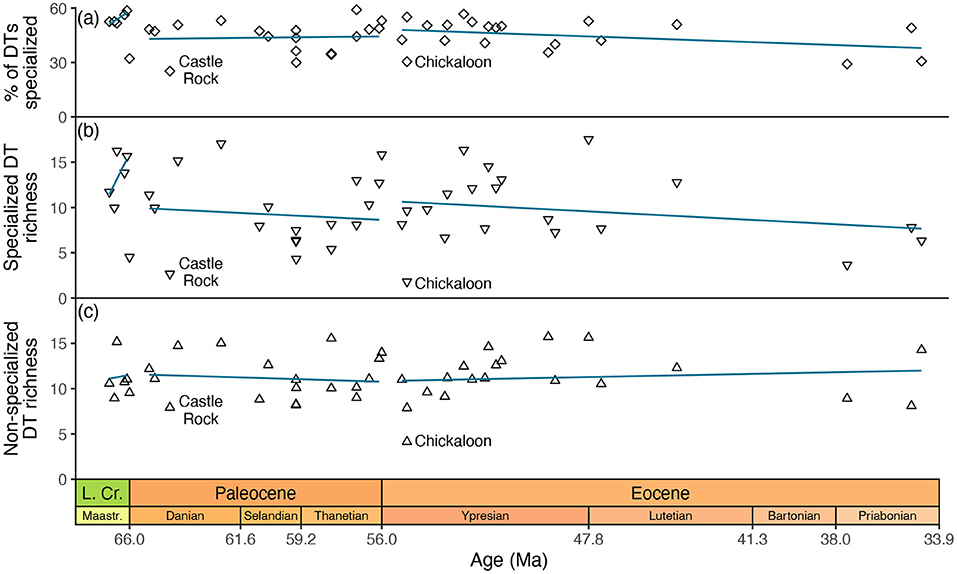
Figure 4. Specialized and non-specialized herbivory at assemblages in Currano et al. (2021)'s compilation that span the Cretaceous through Eocene. The percentages in (a) are based on estimates that were calculated after richness was rarefied to 300 leaves; (b,c) show those estimates. Trendlines for each epoch are in blue.
In lieu of direct evidence, statements about damage type specialization were based on bipartite network metrics, which are complex and can be notoriously difficult to interpret (Blüthgen, 2010). Only three metrics called “connectance,” “niche overlap” for plants, and the “C-score” for plants were used to examine damage type specialization during the Cretaceous through Eocene, with no explanation of the logic in choosing these metrics to examine change through time. Likewise, the authors' discussion of herbivore specialization across latitudinal bins centers exclusively on “interaction evenness” and “H2′” with no explanation of the appropriateness of these metrics for examining changes across space.
The only reported p-value, a Tukey test (p = 0.0020) for the Cretaceous, Paleocene, and Eocene, for bipartite network metrics also suggests cherry-picking. There are five ways to divide the fossil assemblages into three consecutive epochs1, and at least eight bipartite network metrics were calculated, meaning that the reported Tukey test is one of at least 40 that should have been conducted and compared.
In the original study, the network analysis was run with an R package that calculates a total of 77 network- and group-level metrics when run with its default settings (Dormann et al., 2008). Supplementary Table S1 of Currano et al. (2021) lists 22 of these metrics, with no explanation of the criteria for selecting them. Supplementary Table S4 of Currano et al. (2021) lists the results of regression analyses involving eight of these 22 metrics—again, with no explanation of how the authors determined which metrics merited inclusion in regression analyses. Table 1 of Currano et al. (2021) lists six of the eight metrics listed in Supplementary Table S4—again, with no explanation of how the authors determined which metrics merited inclusion.
Recent ecological studies have typically calculated two (Eckerter et al., 2022; Rosa et al., 2022), three (D'Bastiani et al., 2020; Badillo-Montaño et al., 2022; Llaberia-Robledillo et al., 2022; Sonne et al., 2022; Virgo et al., 2022), four (de Matos et al., 2022; González-Castro et al., 2022; Kivlin et al., 2022; Moss and Evans, 2022; Rodríguez-Godínez et al., 2022), or five (Hetherington et al., 2022; Oliveira et al., 2022; Quinto et al., 2022) bipartite network metrics, each of which is associated with a distinct, clearly articulated biological question. A recent study that examined ten bipartite network metrics included a separate biological justification for each (Valido et al., 2019). H2′ is typically the only bipartite network metric used to evaluate specialization (Bucharova et al., 2022; da Silva Goldas et al., 2022; Vinagre-Izquierdo et al., 2022; Virgo et al., 2022). Whereas it is indeed the case that most bipartite network metrics are related to the concept of specialization (Fründ et al., 2016), the decision in the original study to calculate a plethora of metrics for the sake of quantifying the very same phenomenon (specialization) is far from accepted practice in ecology. By calculating so many metrics rather than selecting a few through “a priori choice based on a research hypothesis” (Webber et al., 2020), the original authors have engaged in a questionable research practice termed “metric hacking” (Webber et al., 2020) that is essentially cherry-picking of bipartite network metrics.
2.3. Null models and naïve hypotheses
The original study reported a significant p-value that indicates rejection of the null hypothesis of no relationship between mean annual temperature and the richness of insect herbivory. The utility of this result is questionable: the null hypothesis that was rejected does not warrant testing, as it is biologically unrealistic. Null models and naïve hypotheses permit more sensible analyses, which can yield more meaningful results.
2.3.1. General relevance
Ecologists have long been at the forefront of using null models (Connor and Simberloff, 1986), which are typically called naïve hypotheses in the psychology literature. The reason to use null models and naïve hypotheses is simple: “Researchers should make thoughtful assessments instead of null-hypothesis significance tests” (Schwab et al., 2011). The “thoughtful assessment” in question is a naïve, rather than a null, hypothesis.
Here, I treat null models and naïve hypotheses as distinct concepts, with naïve hypotheses pertaining to the framing of a research question and null hypotheses pertaining to statistical procedures used to determine significance. A naïve hypothesis can be thought of as our baseline expectation of the pattern we would expect to find across an extended period of geologic time: for example, intervals of high pCO2 are relatively warm, and low latitudes are generally warmer than high latitudes. Naïve hypotheses address a major shortcoming of null hypothesis significance testing that isn't discussed particularly often in the paleontological literature: that even in the absence of any particular biological signal under consideration, a null hypothesis of a slope of zero is not a “thoughtful assessment” of what one would expect to see. As a cartoon example to illustrate this point, it would not be productive to test the null hypothesis that mean annual temperature does not change with pCO2. It would be more informative to evaluate relevant empirical data by testing them against the naïve hypothesis that mean annual temperature increases linearly with increased pCO2. In paleontology, naïve hypotheses can be generated with a uniformitarian approach. For any relationship that is well-established in the modern and is under consideration in deep time, the relationship seen in the modern can be used as a naïve hypothesis in paleontological studies.
A null model can be thought of as the relationship we would expect to see when calculating a particular statistic, especially if sampling is incomplete—as is often the case in paleontology. In null hypothesis significance testing, the null hypothesis is typically that there is no relationship between the variables of interest: essentially, that nothing happened. When linear regression is used in null hypothesis significance testing, the null hypothesis is a slope of zero. One of the most infamous shortcomings of null hypothesis significance testing is that, with enough data, nearly any slope can be significantly different from zero due simply to noise in the dataset; the most straightforward way to assess whether signal or noise underlies a significant p-value is to calculate a measure of effect size such as R2 or Cohen's d. Many other metrics, such as the abovementioned bipartite network metrics, can be calculated without any null hypothesis—much less a null model. However, a null model can often be calculated separately: for example, to assess whether sampling is sufficiently complete to satisfy the assumptions under which a bipartite network metric was intended to be calculated.
2.3.2. Relevance to angiosperm folivory
The original study used linear regression to examine the relationship between mean annual temperature (MAT) and damage type richness. This approach involves null hypothesis significance testing, with the null hypothesis being a slope of zero: no change in damage type richness corresponding to a given change in MAT. Any lack of a relationship between MAT and damage type richness in an accurate and complete dataset would be quite shocking in light of the well-established diversity of herbivorous insects in tropical rainforests (Lewinsohn and Roslin, 2008).
In other words, a noisy but discernible positive relationship should have been the naïve hypothesis for the analysis of MAT and insect damage richness at pooled Maastrichtian through Cenozoic assemblages. The most reasonable interpretation of this result is an inability to reject the naïve hypothesis—which is inevitable, given the highly incomplete spatial and temporal coverage of the data that are currently available.
2.4. Underdetermination
Many analyses compare two specific scenarios or hypotheses, neither of which is necessarily correct. A finding that is consistent with multiple hypotheses is the result of an “underdetermined” analysis. Most, if not all, of the potential pitfalls described in this contribution can be attributed to some form of underdetermination. Here I present an instance in which the output of a regression model was misinterpreted (the authors incorrectly extrapolated the direction and strength of an effect from a significant p-value), and I discuss how this misinterpretation fits within the broadening scope of underdetermination.
2.4.1. General relevance
“Underdetermination” describes the phenomenon in which two competing hypotheses or theories have the “same empirical consequences” and are thus “empirically equivalent” (Kukla, 1996). In other words, when evaluating mutually exclusive hypotheses X, Y, and Z, the available facts may be consistent with hypotheses X and Z but not Y. Thus, the difference between hypotheses X and Z is underdetermined. A study that compares hypotheses X and Y may overstate the relevance or explanatory power of hypothesis X by neglecting to consider hypothesis Z.
In paleontology, facies change across a suspected extinction boundary is perhaps the archetypal case of underdetermination. Perturbations to the Earth system can cause both extinction and facies change. When this occurs, the difference between extinction or facies change as the cause of an observed loss of biodiversity, is underdetermined. Many authors have suggested that facies change partially or wholly obscures the true magnitude of extinction events, particularly at local levels and on short timescales (Hallam, 2002; Twitchett, 2006; Chen et al., 2009; Lucas and Tanner, 2015).
A recent contribution (Fletcher, 2021) notes that the concept of underdetermination also encompasses the fidelity with which a sample represents the population from which it was drawn. Consider a study that compares hypotheses J and K, finding support only for hypothesis K. It may be the case that hypothesis K holds no more explanatory power than hypothesis J, and the empirical support for hypothesis K is simply a result of the structure of the fossil record (Holland, 2017) or of biases in the dataset (Raja et al., 2021). Various methodological contributions have shown that it is possible to account for the structure of the fossil record when testing paleontological hypotheses (Wagner and Marcot, 2013; Woolley et al., 2022), but paleontology has not yet reached a point where all studies account for such structure and bias when interpreting analytical results.
2.4.2. Relevance to angiosperm folivory
When discussing which latitudinal bin shows the strongest relationship (lowest p-value) between two variables, the original authors write, “[t]he relationship between MAT [mean annual temperature] and richness of mining DTs [damage types]...peaks in the low latitudes.... Our results may indicate that in deep time, low latitudes were an evolutionary museum and/or cradle of leaf miner biodiversity” (Currano et al., 2021, pg. 13). The terms “cradle” and “museum” (Stebbins, 1974) are used to describe why diversity in the tropics is so high (Jablonski, 1993; Chown and Gaston, 2000)—i.e., for “low latitudes [to be] an evolutionary museum and/or cradle of leaf miner biodiversity,” low-latitude leaf miners (or their damage types) must be very diverse.
A comparison of low-latitude mine richness with other parts of the world, however, contradicts the statement in the original study about low latitudes as a museum or cradle of leaf miner biodiversity (Figure 5). Leaf mining damage type richness is unusually low in the tropics according to the data compilation (Figure 5). Therefore, this use of the terms “cradle” and “museum” contradicts their accepted meaning.
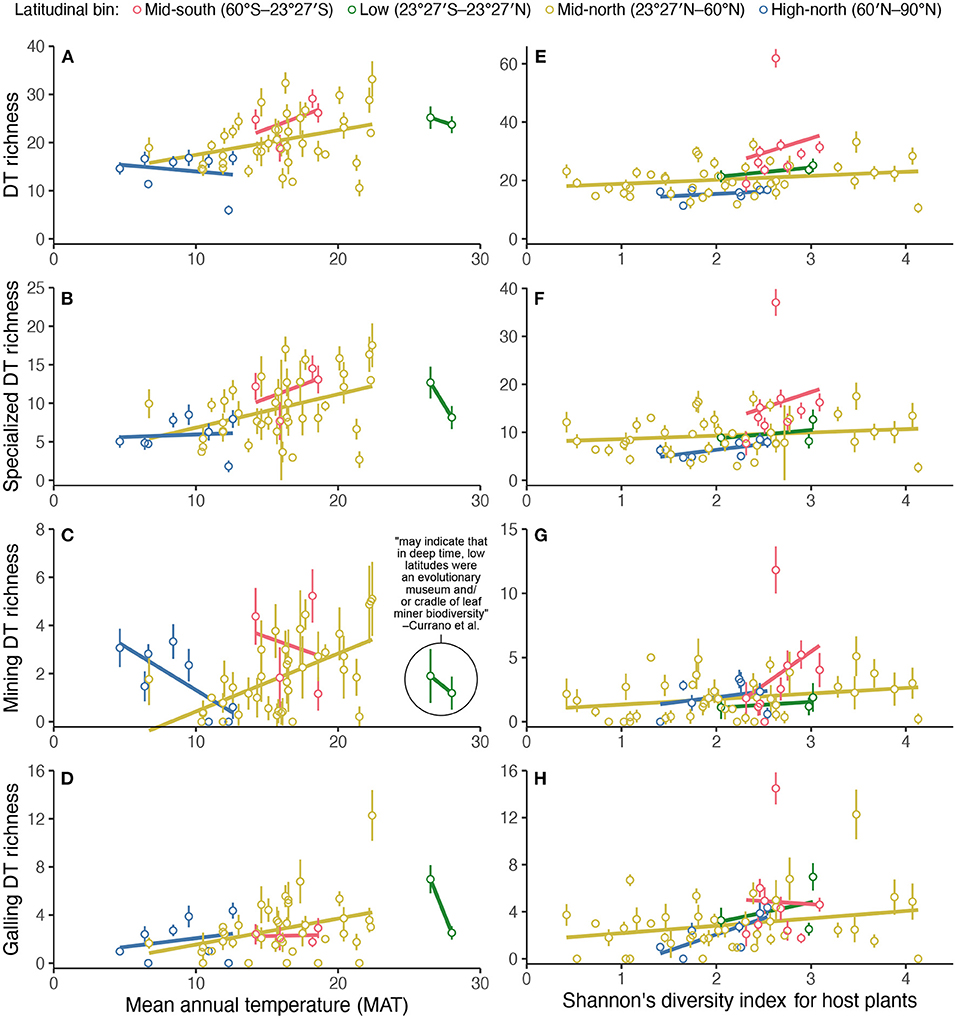
Figure 5. The relationship of damage type (DT) diversity at each assemblage in Currano et al. (2021)'s compilation, rarefied to 300 leaves (y-axis), to mean annual temperature (left) (A–D) and Shannon's diversity index for host plants at each assemblage (right) (E–H). The color scheme is the “bright” qualitative color scheme from Paul Tol's notes (https://personal.sron.nl/p~ault/).
When assessing the two competing hypotheses that leaf mining damage richness is lower at low latitudes, versus higher at low latitudes, a significance test that yields a p-value is underdetermined. A significant p-value denotes that the relationship (slope) between low-latitude leaf mine richness and mean annual temperature differs from the slope for other latitudinal bins. This significant p-value does not necessarily demonstrate that leaf mining damage richness is, on average, any different at low latitudes than in other latitudinal bins. The significant p-value most certainly does not indicate that leaf mining damage richness is greater at low latitudes. Whereas, the significance test itself is underdetermined, simple scatterplots are not (Figure 5).
3. Methods
All analyses were conducted in R (R Development Core Team, 2021).
3.1. Power analysis and propensity score matching
I conducted power analysis and propensity score matching with data from Currano et al. (2021)'s supplemental file “Herbivory metrics by site.csv.” I calculated Cohen's d using the cohen.d function in the effsize package (Torchiano, 2020). I calculated propensity scores with a logit model using the base-R function glm. I then matched mid-southern and mid-northern assemblages according to their propensity score with the MatchIt package (Ho et al., 2011) using the “nearest” method. I conducted this procedure twice. First, I included age, Shannon's diversity index, Pielou's J, rarefied plant richness, mean annual temperature, and mean annual precipitation as covariates. With these covariates I was able to include four mid-southern and 26 mid-northern assemblages. Second, I excluded mean annual temperature and mean annual precipitation so that I was able to include all nine mid-southern assemblages in the analysis, as well as 42 mid-northern assemblages. I calculated standardized mean differences of each covariate between the matched mid-southern and mid-northern assemblages using the smd function in the MBESS package (Kelley, 2007).
3.2. Specification curve analysis
3.2.1. Data and binning
Specification curve analysis can be used to evaluate the finding in the original study of increased damage type richness at mid-southern latitudes. I used the four response variables from their latitudinal analysis: richness of all damage types, of specialized damage types, of mine damage types, and of gall damage types, when rarefied to 300 leaves. I used their two covariates: MAT, and Shannon's diversity index for the plant community at each assemblage. [Shannon's diversity index is a measure of richness and evenness in a community; higher values denote more diverse communities (Shannon, 1948)]. I ran specification curve analysis both with and without the outlier Hindon Maar assemblage (see Appendix for more detail) for all specifications that include Shannon's diversity index as a fixed effect. For the random effect, I used latitudinal bins derived from a variety of methods: Currano et al. (2021)'s binning scheme; bins with boundaries at the astronomically notable latitudes of the Arctic Circle, the Tropic of Cancer, the Tropic of Capricorn, and the Antarctic Circle, which are suggested by Currano et al. (2021)'s method which bounds the low-latitude bin near the Tropics; the ten-degree bins used in various paleontological studies (Jablonski et al., 2006; Powell et al., 2012, 2015; Mondal et al., 2019; Wu et al., 2019; Dunne et al., 2021); the twenty-degree bins used various paleontological studies (Mondal et al., 2019; Wu et al., 2019; Allen et al., 2020); and binning schemes generated with k-means, with three to seven bins.
The k-means procedure was implemented as follows. The base-R function kmeans was used with the default settings. For each number of bins (3–7), the k-means procedure was iterated ten times. Each unique binning arrangement was used in the specification curve analysis. For example, the “5 bins, #2” predictor variable in Figure 10 represents the second unique binning arrangement that was derived from the k-means procedure with five bins, and so forth.
This analysis requires data from Seymour Island and King George Island. I discuss these two assemblages, and the extraction of relevant data, in the Appendix.
3.2.2. Calculating p-values and effect sizes for mixed-effects models
Calculating p-values for mixed effects models is a notoriously perilous endeavor (Luke, 2017). The authors of lme4, perhaps the most popular R package for mixed-effects models, intentionally omitted from this package the option to calculate p-values (Bates et al., 2014). However, they did write, “we have provided a help page to guide users in finding appropriate methods” for calculating p-values (Bates et al., 2014).
R2 values, however, are much more straightforward to calculate for mixed-effects models (Nakagawa and Schielzeth, 2013; Johnson, 2014; Nakagawa et al., 2017). R2 is one of the most common measures of effect size (Ferguson, 2009), taking the form of R2GLMM for mixed-effects models. This measure of effect size also permits a more meaningful assessment of latitudinal patterns. I calculated R2GLMM to generate a value that I term R21. I then lumped the mid-southern assemblages in with the mid-northern assemblages, re-ran the model, and calculated a value that I term R20. This value represents the effect size for the null hypothesis that the mid-southern assemblages have similar richnesses of insect damage to those seen in the mid-northern assemblages. I subtracted R20 from R21 to calculate an effect size corresponding to the contention of higher richness of insect damage at mid-southern latitudes than seen at mid-northern latitudes. An advantage of using the differences in R2 values to evaluate latitudinal trends is that this method can accommodate heightened herbivory at mid-southern latitudes whether this results from a different slope for the relationship between herbivory and MAT/Shannon's diversity index, or a similar slope with a higher intercept. (As Makin and Orban de Xivry, 2019 wrote, “Researchers should compare groups directly when they want to contrast them.” The R2GLMM values calculated here constitute a direct comparison of the mid-southern and mid-northern latitudinal bins).
The mixed-effects models were calculated using the same formulas as the original analysis of this data compilation (Currano et al., 2021), with the lmer function in the lme4 package (Bates et al., 2014). R2GLMM was calculated with the r.squaredGLMM function in the MuMIn package (Barton, 2009).
Of course, adding another parameter to a model without penalizing the R2 value for potential overparameterization will quite often yield a higher R2 value, due to true latitudinal differences or simple noise in the data. For this reason, the significance of an effect size needs to be tested against a null hypothesis. The authors of specification curve analysis suggest iteratively, randomly shuffling all values of the response variable to generate a null distribution of effect sizes; significant effect sizes are those for which the original effect size lies beyond the 2.5th to 97.5th percentile of the effect sizes generated with shuffled values (Simonsohn et al., 2020). I followed this suggested procedure by randomly shuffling the values of the response variable and iterating this procedure 1,000 times for each specification. I then used the 2.5th to 97.5th percentiles of each distribution to generate the 95% confidence interval illustrated in Figure 10.
The procedure for calculating R2GLMM involves comparing the full model to a null model. For this reason, values of R2GLMM can be negative.
3.3. Bipartite networks
I used null models to evaluate the five bipartite network metrics mentioned by the original study regarding temporal and latitudinal trends: connectance, niche overlap (for plants), the C-score (for plants), interaction evenness, and H2′. Data were downloaded from https://github.com/anshuman21111/resampling-fossil-leaves/tree/main/Data_processed_localities.
All analyses were performed with the bipartite package (Dormann et al., 2008). For each assemblage, I repeated the following procedure 1,000 times. I first subsampled data from each assemblage down to 300 leaves, to reproduce the original methods (“empirical subsampled dataset”). I generated 1,000 null datasets using the nullmodel function with the r2d option. I then calculated the above network metrics for the empirical subsampled dataset and the null datasets. I calculated a Z-score following the procedure outlined by Dormann et al. (2008). I converted Z-scores to p-values using the pnorm function in R with the option lower.tail=FALSE. For the Castle Rock assemblage, the dataset was often too sparse for the calculation of bipartite network metrics after it had been subsampled down to 300 leaves. For this reason, Castle Rock is not included in Figure 11.
4. Results and discussion
4.1. Propensity score matching
When a dataset is not complete enough to explicitly include all relevant predictors in a regression analysis, propensity score matching can be used to avoid the pitfalls described by Simpson's paradox. When a dataset is too incomplete for a multiple regression analysis or propensity score matching, further analyses are inadvisable. Propensity score matching can be used to directly quantify whether the data compilation is sufficiently complete for the analyses presented.
4.1.1. General relevance
Simpson's paradox highlights the need to account for all relevant covariates in all analyses. This can be achieved with various forms of multiple regression or mixed-effects models when sufficient data are available. A randomized experiment with a control group and a treatment group can be designed so that values for relevant covariates are as similar as possible among the two groups. When experiments are impossible, as is the case for studies that examine changes in deep time, propensity score matching can be used to generate a balanced distribution of relevant covariates, as would be seen in experimental data.
With propensity score matching, a logit or probit model is used to estimate the relationship between each covariate and the probability that an observation (a patient in the case of medical science, or an assemblage or taxon in the case of paleontology) belongs to the control or treatment group. (In paleontology, analogs for the control and treatment group can be assemblages in lacustrine vs. fluvial settings, genera that did or did not go extinct across a geologic boundary, and so forth). This model can then be used to assign each subject with a probability of belonging to the treatment group: the “propensity score.” Subjects in the control and treatment groups are then matched according to the similarity of their propensity scores. The matching process nearly always involves discarding unmatched subjects (subsampling) or duplicating some data points (resampling) so that all subjects retained in the final dataset are matched.
Two simple methods are typically used to ensure that the matching process is sufficient to eliminate potential bias caused by the covariates. First, the values for each covariate can be plotted against each subject's propensity score for the control and treatment group. The similarity of the lines of best fit for the two groups indicates the efficacy of the procedure. Second is a comparison of the standardized mean difference for the two groups. When the matching process is successful, the standardized mean difference is below 0.1.
4.1.2. Relevance to angiosperm folivory
If the data compilation included assemblages spanning all possible combinations of mean annual temperature, mean annual precipitation, geologic age, host plant richness, and host plant evenness within both the mid-southern and mid-northern latitudinal bins, a regression or mixed-effects model would be sufficient to disentangle the influence of latitude from these covariates. But in actuality, the assemblages in the mid-southern latitudinal bin span only a fraction of the range of mean annual temperature, mean annual precipitation, geologic age, host plant richness, and host plant evenness seen in the mid-northern latitudinal bin (Figures 6A–F).
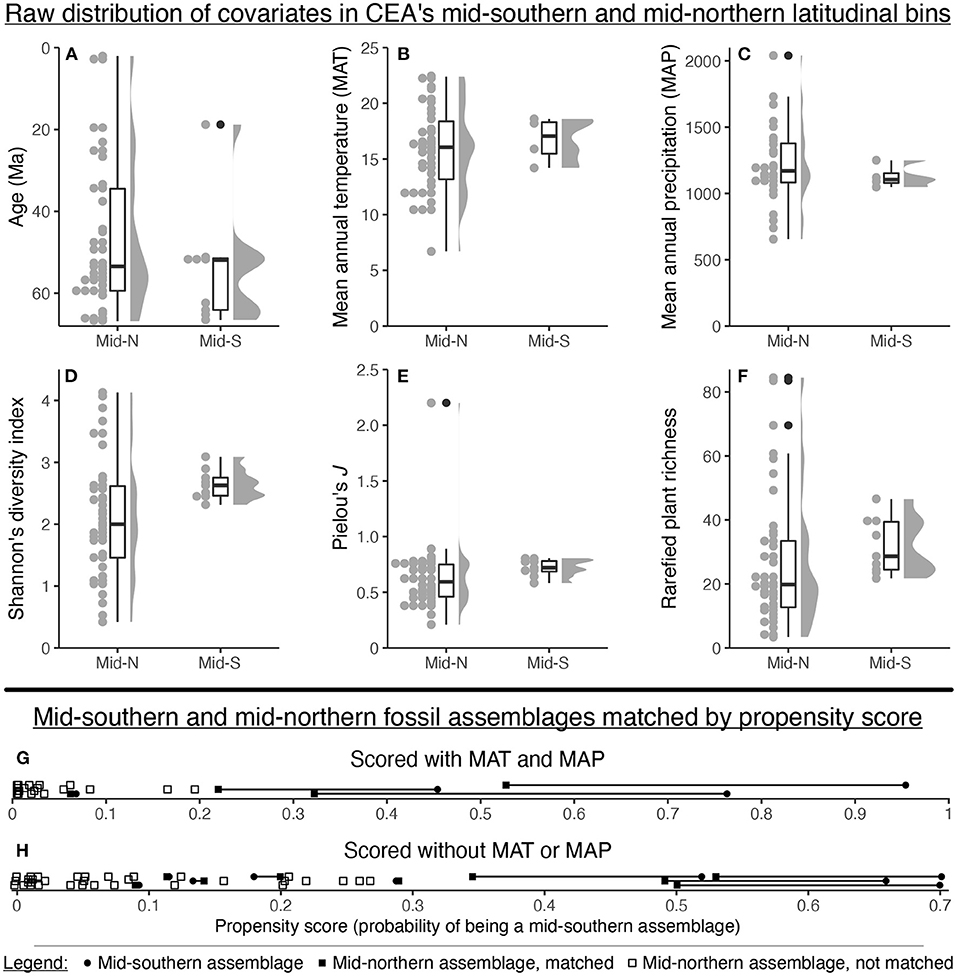
Figure 6. The distribution of various covariates for Currano et al. (2021)'s mid-northern and mid-southern latitudinal bins (A–F), and the results of propensity score matching for these bins (G,H).
Simple visual inspection shows that the matched mid-southern and mid-northern assemblages often have very different propensity scores (Figures 6G,H). When covariate values are plotted against propensity scores, the lines of best fit usually do not overlap (Figure 7). Standardized mean differences confirm these discrepancies, yielding values above the target of 0.1 in eight out of ten cases (Figure 7). The lesson from this exercise is simple: the assemblages in the mid-southern and mid-northern latitudinal bin are so different in terms of age, Shannon's diversity index, Pielou's J, plant richness, temperature, and precipitation, that it is not possible to eliminate potential bias from these covariates when comparing latitudinal trends. Even if we set aside the dubiousness of identifying latitudinal trends for the entire Maastrichtian–Cenozoic with only nine mid-southern assemblages, the potential confounding variables are too discrepant for any findings about latitude to be convincing.
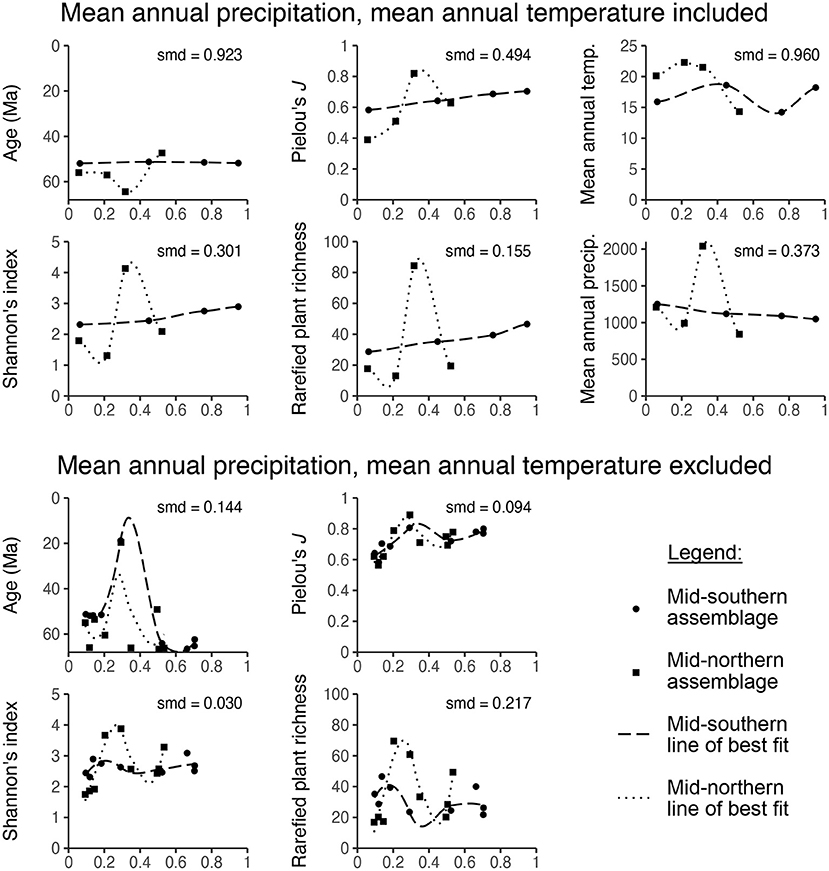
Figure 7. The relationship between propensity score and various covariates for Currano et al. (2021)'s mid-northern and mid-southern latitudinal bins with loess smoothed lines of best fit. The standardized mean difference (smd) among the two latitudinal bins is listed for each comparison.
4.2. Power analysis
Currano et al. (2021) reported heightened richness of insect damage types in their mid-southern latitudinal bin, with a very large effect size. However, at small sample sizes, large effect sizes are a hallmark of spurious, false-positive results. This issue can be addressed with power analysis, which quantifies the probability of correctly rejecting the null hypothesis for a given effect size and sample size.
4.2.1. General relevance
According to Shrout and Rodgers (2018), “One historically important QRP [questionable research practice] is to carry out studies with inadequate statistical power to test interesting effects.” Power analysis is a common practice in many fields. Before collecting any data, researchers can use power analysis to estimate the necessary sample size to correctly reject their null hypothesis. The target sample size will depend on the effect size—a metric for the magnitude of the signal relative to the variance in the data. Effect size is often quantified with Cohen's d (Cohen, 1977). Cohen's d has a minimum value of 0 and is typically no larger than 1, with 0.2 signifying a small effect size, 0.5 signifying an intermediate effect size, and 0.8 signifying a large effect size.
The practice of conducting a power analysis before collecting data is plagued by the difficulty of estimating the relevant effect size in advance (Shrout and Rodgers, 2018). This problem will surely afflict paleontological studies that subsample existing collections. For example, if 50,000 Cretaceous and 50,000 Paleogene bivalves from the same basin are available for a study of changes in the frequency of drilling predation across the Cretaceous/Paleogene boundary, power analysis can be used to estimate the number of bivalves from each period that should be examined. If the difference in drilling predation from the Cretaceous to the Paleogene is large (d = 0.8), a dataset with 170 shells from each period will have a statistical power of 100%. However, if the difference in drilling predation from the Cretaceous to the Paleogene is rather small (d = 0.2), the statistical power of this sampling regime will be only 45%—i.e., an insignificant result due to insufficient sampling is a likely outcome. (All values of d discussed here assume a significance level of α = 0.05. Statistical power is reported as either a proportion ranging from 0 to 1 or a percentage ranging form 0 to 100%. Here, I report power as a percentage to make it easier to distinguish from d).
Small sample sizes are common in behavioral and biomedical sciences, due to the difficulty of recruiting human subjects, and in paleontology, due to the incompleteness of the fossil record among other factors. Power analysis can be conducted after data are collected as a “sanity check” to evaluate whether the data are sufficient to detect a signal with a realistic effect size. Whereas nearly all paleontological datasets are incomplete, power analysis provides an opportunity to ascertain which biological questions can and cannot be responsibly addressed with a given dataset.
Power analysis is also a helpful exercise in cases where biases in a dataset, rather than the biological signal of interest, may underlie any significant results. Methods such as linear regression and mixed-effects models assume by default that data are random and representative. In paleontology, this is rarely the case. Individual fossil assemblages are selected for study, non-randomly, by authors who are interested in specific phenomena such as refugia from the environmental crisis at the end-Cretaceous. When many such studies are brought together into a data compilation, the hope is that the non-random motivations that underlie data collection will offset each other, as was seen with errors in paleobiological databases (Adrain and Westrop, 2000), such that the relevant data are quasirandom and representative in the aggregate. However, the preservation of fossils is not temporally or geographically random (Holland, 2017) and major geographic biases exist in paleontological datasets (Raja et al., 2021). An analysis of nearly 400,000 occurrences of marine animal fossils found that the geographic structure of the fossil record and biases within the scientific community obscure biological phenomena of interest (Close et al., 2020).
Although the geographical nonrandomness in aggregated paleontological data may not constitute “noise” in a strict sense, it most certainly does not constitute the signal of interest in a typical paleontological study. Thus, naïve and unquestioning acceptance of findings generated with a paleontological data compilation risks “over-interpretation of noise” (Munafò et al., 2017).
In summary, power analysis is most relevant to moderate effect sizes in moderately complete datasets, and to large effect sizes in small datasets. To detect a true signal of interest with a small-to-moderate effect size, more data may be needed than are typically collected. Conversely, when a large effect size is observed in a small dataset, this is often an artifact of bias or statistical noise rather than a true reflection of the signal of interest.
4.2.2. Relevance to angiosperm folivory
Currano et al. (2021) state, “the mid-S [mid-southern; 60°S–23°27'S] latitudes stand out as a hotspot for insect damage diversity, particularly when compared with the mid-N [mid-northern; 23°27'N–60°N] and high latitudes.” The data compilation that underlies this statement includes 42 fossil floras from mid-northern latitudes and nine floras from mid-southern latitudes. Power analysis shows that if the effect size (d) of the difference in herbivory among mid-northern and mid-southern latitudes is 0.5—a moderate effect size, according to Cohen—the power to correctly reject the null hypothesis is merely 27%. At the observed sample sizes, d must reach 0.73 for statistical power to reach 50%.
Cohen's d for the difference in the richness of herbivory among assemblages of the mid-southern and mid-northern latitudinal bins in the data compilation is 1.49 (95% CI: 0.70–2.29): a startlingly large effect size. And this is where power analysis, and the calculation of Cohen's d, is perhaps most useful to paleontologists. With the small sample sizes often seen in paleontological studies, an effect size must be rather large to be detectable—perhaps so large that it is better attributed to a sampling artifact than to the biological phenomenon of interest. Because the power to correctly reject a null hypothesis for the data compilation is only 27% with a moderate effect size, there is good reason to suspect that any apparent significant relationship is a sampling artifact.
In the psychology literature, Vul et al. (2009) note that the reliability of a measure limits the detectable strength of a correlation. In other words, any correlation that may exist between high richness of insect herbivory on fossil leaves and location in the mid-southern (vs. mid-northern) latitudes will be obscured, to a certain extent, by other biological differences. These may include latitudinal differences within each latitudinal bin, such as differences in richness at 11°N vs. 19°N within a bin that spans 10°N–20°N; varying diversities of the plant communities in question; differences in temperature, precipitation, and the interaction of these two climatic variables; differences in soil type; the age of each fossil assemblage, and the insect guilds that had and had not yet diversified; differences in the life histories of the plant taxa in each assemblage; and so forth. Some of these factors, such as latitudinal differences within each bin, can be accounted for when modeling differences in the richness of insect herbivory among latitudinal bins. Other factors, such as the maximum annual temperature for each plant community, are uncertain and thus decrease the reliability of observed differences among latitudinal bins. The many unconstrained possible covariates with the potential to obscure differences among latitudinal bins suggest that an effect size of 1.49 may be unachievable for this analysis in the absence of a spurious correlation.
How, then, to reconcile the negligible-to-moderate effect size that one would expect due to the many biological and environmental differences that cannot be accounted for in the data compilation, with the very large effect size that the authors found? The first published study in the mid-southern latitudinal bin focused exclusively on the early Eocene of Patagonia, and suggested that Patagonia may have provided refugia from the environmental stress that swept much of the world during the end-Cretaceous event (Wilf et al., 2005). A subsequent study, from the same lab group, focused on the Paleocene of Patagonia: a time and place where the refugium theory could be more directly evaluated (Donovan et al., 2018). Indeed, the study of Donovan et al. (2018) supports the refugia theory. These two studies (Wilf et al., 2005; Donovan et al., 2018) account for eight of the nine mid-southern-latitude assemblages in the data compilation. The inclusion of assemblages that have been identified as key to resolving outstanding biological questions of major interest, within an analysis that is best conducted with randomly selected assemblages, is one way to produce a large but spurious effect that is independent of the biological phenomenon in question (latitudinal differences in the richness of insect herbivory throughout the entire Maastrichtian–Cenozoic).
In light of the abovementioned findings of geographic biases in paleontological data (Close et al., 2020; Raja et al., 2021), extreme caution is warranted when analyzing small data compilations such as that described here. If the authors were interested in latitudinal patterns only in the wake of the end-Cretaceous event, their analysis serves no purpose because the conclusion about Patagonia as a refugium from the end-Cretaceous bolide impact was already noted by the workers who collected the original data (Wilf et al., 2005; Donovan et al., 2018). However, the authors intended for the conclusions of their latitudinal analyses to hold for the entire Maastrichtian–Cenozoic, as demonstrated by statements given without any caveats such as “the mid southern hemisphere (60°S to 23°27'S) stands out as having frequent and diverse damage” and “the mid-S latitudes stand out as a hotspot for insect damage diversity.” The identification of ostensible latitudinal trends during the past 70 Myr from a compilation that includes only one mid-southern assemblage from the past 50 Myr requires a tremendous leap of faith.
Currano et al. (2021)'s latitudinal analysis illustrates why moderate-to-large effect sizes should be scrutinized for potential geographic, temporal, and other biases before being interpreted at face value—particularly when sample sizes are small, as this can increase the prevalence of false-positive results. As Makin and Orban de Xivry (2019) wrote, “With small sample sizes, the effect size of these false positives is large, giving rise to the significance fallacy: ‘If the effect size is that big with a small sample, it can only be true.”'
4.3. Specification curve analysis
Currano et al. (2021) found a strong effect of latitude after drawing a unique series of boundaries among latitudinal bins. This raises the question of whether a similarly strong effect would be observed with a more conventional binning scheme. This issue can be addressed with specification curve analysis, which quantifies the extent to which researchers' arbitrary decisions underlie analytical results.
4.3.1. General relevance
For many years, researchers were encouraged to conduct only one analysis per research question. Consider, for example, an analysis that examines temporal trends in how average bivalve body size has changed from one time interval to the next. This analysis requires the researcher to choose a temporal binning scheme. In the example illustrated here (Figure 8), bivalve body size has been measured from 50 fossil assemblages over the last 100 Myr. The number of specimens measured varies markedly among assemblages. The assemblages can be binned using a clustering algorithm such as k-means (Figure 8a–i), using 20-Myr bins (Figure 8j–l), using 10-Myr bins (Figure 8m–o), or according to geologic epochs (Figure 8p–r). All fossil assemblages can be included in the analysis (Figure 8a,d,g,j,m,p), or the assemblages with low numbers of specimens measured can be excluded from the analysis (Figure 8b,e,h,k,n,q), or the assemblages with low-to-intermediate numbers of specimens measured can be excluded from the analysis (Figure 8c,f,i,l,o,r). These 18 temporal binning schemes seem more or less equally justifiable.
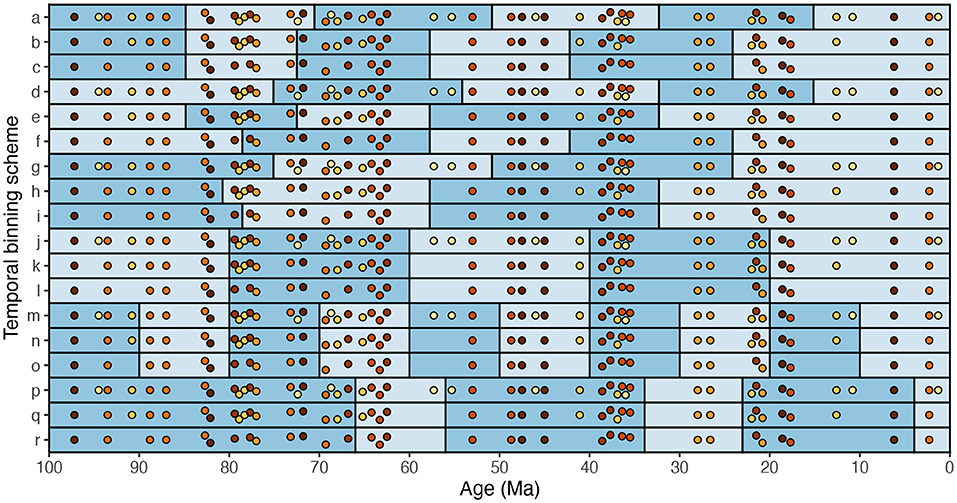
Figure 8. A cartoon example of numerous, equally justifiable schemes for temporal binning of paleontological data. Each dot represents a fossil assemblage and is color-coded by the number of fossils measured therein: darker dots denote more fossils measured (a higher sample size). a–i were binned with k-means: a–c have six bins, d–f have five, and g–i have four. j–l were binned in 20-Myr increments. m–o were binned in 10-Myr increments. p–r were binned by geologic epoch. Binning schemes a,d,g,j,m, and p include all assemblages. Binning schemes b,e,h,k,n, and q exclude the nine assemblages with the lowest sample sizes. Binning schemes c,f,i,l,o, and r exclude the 18 assemblages with the lowest sample sizes.
Until recently, the prevailing wisdom was that only one of these 18 binning schemes should be chosen. If none seem especially appropriate, one should be chosen more or less at random. The reason to perform only one analysis per research question—i.e., to use only one temporal binning scheme—is to avoid “cherry-picking.” The worry is that, if the analysis is run with all 18 binning schemes and seventeen of these do not yield a statistically significant result, the one scheme that did yield a significant result quite possibly did so due to random chance. The researchers who conducted the analyses would have an incentive to cherry-pick the significant result as the only result worth reporting.
When a priori decisions are made to avoid the possibility of cherry-picking, the optimal choices are rarely clear. In the above example, it is not clear which temporal binning scheme should be used. Fortunately, a new statistical tool obviates the need to make these a priori decisions. “Specification curve analysis” addresses the problem of arbitrary statistical choices by re-analyzing data under all justifiable specifications—i.e., all justifiable combinations of predictor variables, response variables, covariates, and criteria for the inclusion of outliers—to determine whether significant results are robust to slight changes in these specifications (Simonsohn et al., 2020).
Specification curve analysis allows researchers to evaluate the robustness of their results to slight changes in specifications; all specifications are considered simultaneously. A pattern in the data is well-supported if, for example, 195 of 200 specifications yield significant results. On the other hand, if only 15 of 200 specifications yield significant results, the finding is not well-supported.
Of note, specification curve analysis addresses a different issue than corrections for multiple comparisons such as the Bonferroni correction. Corrections for multiple comparisons are intended to be used on independent tests, each of which uses different data. Specification curve analysis, in contrast, is to be used on tests that are not independent and that use similar or identical data.
4.3.2. Relevance to angiosperm folivory
A brief glance at a far more complete data compilation than that analyzed here, pertaining to insect herbivory in modern ecosystems, highlights the sensitivity of latitudinal patterns to the binning method used. The compilation of Zhang et al. (2016) contains measurements of the proportion of leaf area removed by insect herbivores at 728 modern sites, with an average of 2.6 plant species per site. When comparing the proportion of herbivorized leaf area per species between a tropical-northern latitudinal bin from 0 to 5°N and a tropical-southern bin from 0 to 5°S, the difference is stark: an average of 6.06% of leaf area is herbivorized in the tropical-northern bin and an average of 12.95% of leaf area is herbivorized in the tropical-southern bin (Figure 9a). Cohen's d for this comparison is quite large: 1.02 (95% CI: 0.68–1.36). However, if we expand the latitudinal bins slightly so that the tropical-northern bin ranges from 0 to 10°N and the tropical-southern bin ranges from 0 to 10°S, the difference between hemispheres all but disappears. An average of 10.08% of leaf area is herbivorized in the tropical-northern bin and an average of 10.10% of leaf area is herbivorized in the tropical-southern bin (Figure 9b). Cohen's d for this comparison is negligible: 0.00 (95% CI: –0.22 to 0.22).
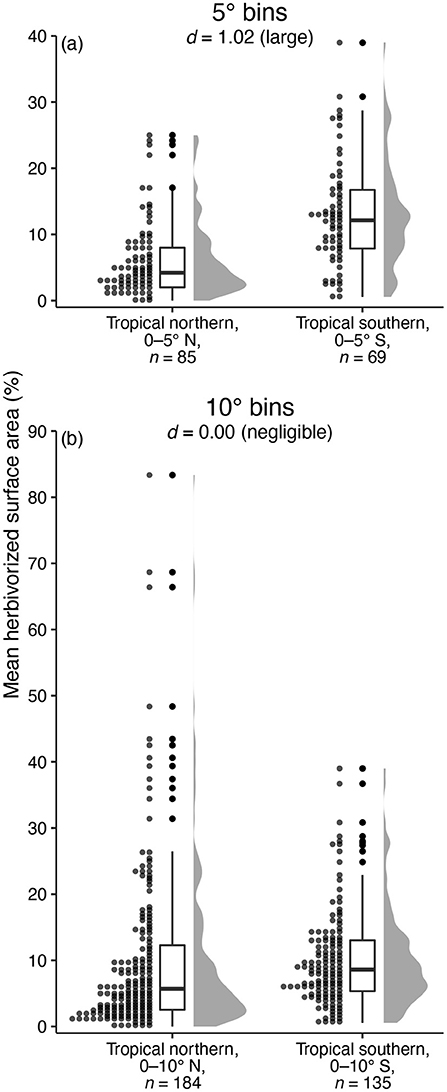
Figure 9. A cautionary tale about binning herbivory data: a comparison of the amount of leaf area lost to insect herbivory at tropical northern and tropical southern latitudes in modern ecosystems, from the compilation of Zhang et al. (2016). The perceived difference in herbivory at tropical northern vs. tropical southern latitudes depends greatly on whether bins extend five (a) or ten (b) degrees from the equator.
The task of binning fossil assemblages by latitude highlights the utility of specification curve analysis. There are many different ways to bin plant assemblages: with ten-degree bins, from 0° to 10°S and so forth; with twenty-degree bins, from 10°N to 10°S and so forth; with a clustering algorithm such as k-means that assigns each assemblage to one of a predetermined number of bins in a way that minimizes within-bin variance and maximizes between-bin variance; or by drawing boundaries between bins at often-discussed latitudes, such as the Tropic of Capricorn (23°26'S) and the Antarctic Circle (66°34'S), that are distinguished by their astronomical—rather than biological—significance. These binning methods may not be equally ecologically and statistically defensible, but they each at least possess a veneer of impartiality. Returning to the analysis under re-study, their mid-southern bin stretches from 60°S to 23°27'S. 60° is a very round number of no astronomical significance, whereas 23°27' holds great astronomical significance but is certainly not a round number. Currano et al. (2021) do not explain why they chose this unique binning method, nor do they provide any citations to support its use.
Specification curve analysis shows that merely 32 of the 204 specifications, or 16%, find a difference in effect sizes that could be consistent with significantly higher richness of insect damage at mid-southern latitudes than at mid-northern latitudes (Figure 10). In contrast, 93 of the specifications, or 46%, yield an effect size below zero. (The possibility of a negative effect size for mixed-effects models is discussed in the Appendix. An effect size below zero indicates that the relationship between insect damage richness and either Shannon's diversity index or MAT is so similar at mid-southern and mid-northern latitudes that treating these two latitudinal bins as separate categories constitutes model overparameterization).
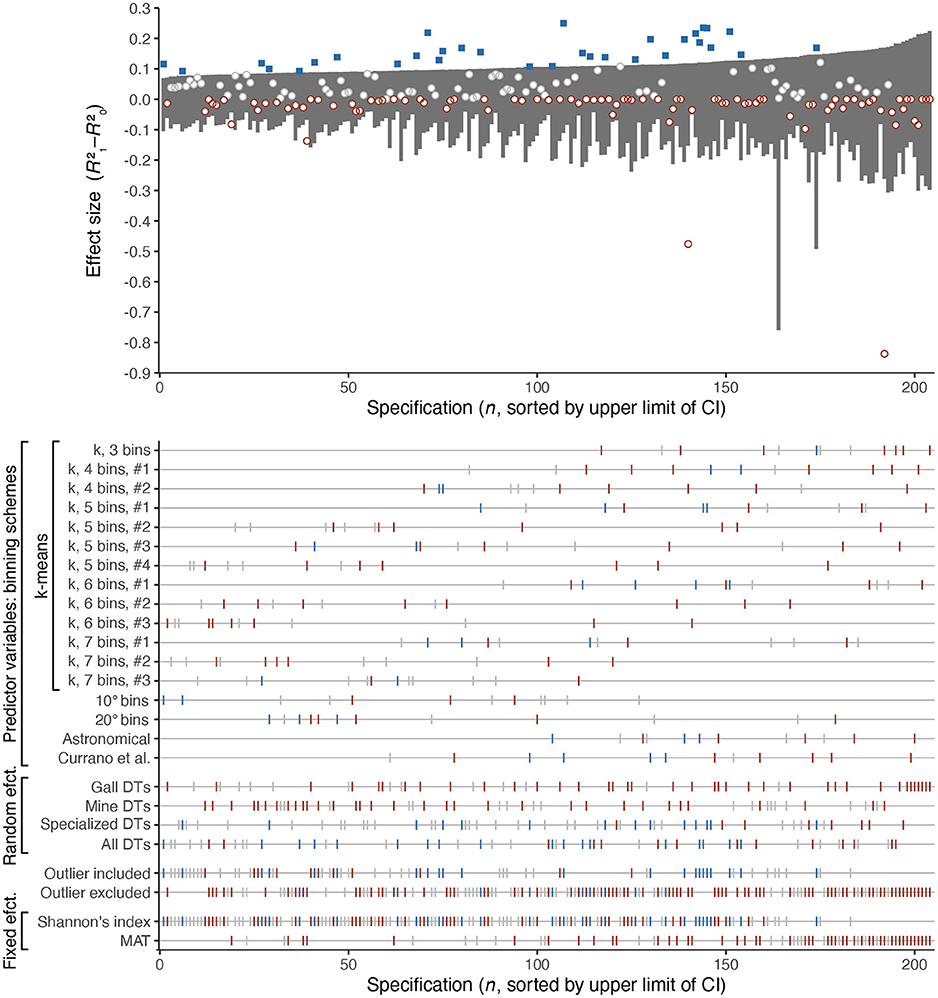
Figure 10. Specification curve analysis of the ostensible heightened richness of insect damage types at mid-southern latitudes. The dark gray rectangles in the upper panel denote the 95% confidence interval for each specification. Blue squares denote specifications for which the effect size is greater than predicted by the 95% confidence interval. Red circles denote specifications for which the effect size is less than zero. Damage type (DT) richness was estimated after rarefying each assemblage to 300 leaves. The method for calculating effect size is explained in the Appendix.
For all binning schemes other than that of Currano et al. (2021), between one and three comparisons (out of twelve) yield an effect size that could be consistent with significantly higher richness of insect damage at mid-southern latitudes (Figure 10). For the binning scheme used by Currano et al. (2021), this number increases to four.
In other words, the previously reported finding of meaningfully higher richness of insect damage at mid-southern latitudes is not supported by the majority of specifications. Evidence against this claim, in the form of an effect size below zero, is approximately three times as prevalent as potential evidence in its favor.
4.4. Null models of bipartite network metrics
As discussed above (in the “Cherry-picking” section), Currano et al. (2021) reported spatial and temporal trends in herbivore specialization based upon the results of bipartite network analysis. However, bipartite network metrics are very sensitive to sampling incompleteness (Blüthgen, 2010). This issue can be addressed with null models, which are recommended by ecologists at the forefront of bipartite network analysis (Dormann et al., 2008).
4.4.1. General relevance
Ecologists have typically used two methods for determining whether sampling is sufficient: subsampling and null models (Blüthgen et al., 2008; Dormann et al., 2009; Fründ et al., 2016). Null models can be used to quantify support for each bipartite network metric; a different null hypothesis corresponds to each bipartite network metric. With null models, the values in an empirical dataset are shuffled in a process that is repeated many times, and bipartite network metrics are calculated for each shuffled dataset. The distribution of these values (their mean and standard deviation) are then compared to the value calculated from the empirical dataset. When the latter is sufficiently different from the former, the null hypothesis is rejected. Failure to reject the null hypothesis can signify that the ecological pattern in question (e.g., specialization) is absent, or that sampling is insufficient to detect it. Null models of bipartite network metrics are extremely common in neontological analyses of trophic interactions among plants and herbivorous insects, and they provide a safeguard against over-interpretation of incomplete datasets.
4.4.2. Relevance to angiosperm folivory
The original authors implored all of their colleagues to only conduct quantitative analyses of fossil assemblages in which at least 1,000 leaves had been censused (Currano et al., 2021, page 4), but themselves conducted analyses of assemblages with as few as 300 leaves. Despite analyzing assemblages with only 30% as many leaves as they state everyone else needs, the authors presented no sensitivity analyses of whether the examined assemblages with barely 300 leaves—or those with over 1,000 leaves, for that matter—were sufficiently well-sampled to meet the assumptions of the various analyses presented.
As a first pass at evaluating whether the threshold of 300 leaves per assemblage is sufficient to reliably estimate bipartite network metrics, I calculated Z-scores using null models. I repeated this process for each of 1,000 subsampling iterations for the five bipartite network metrics that the authors discussed (connectance, niche overlap for plants, C-score for plants, interaction evenness, and H2′), for each assemblage examined in the analysis under re-study. The details of this procedure are outlined in the Appendix.
The conclusion of decreased specialization during the Paleocene, as compared to the Cretaceous and Eocene, is based upon the bipartite network metrics of connectance, niche overlap (for plants), and the C-score (for plants). However, for connectance, an average of only 36% of iterations yield a significant p-value for Cretaceous and Eocene assemblages—which is barely higher than the average of 32% for Paleocene assemblages (Figure 11). For niche overlap for plants, an average of only 29% of iterations yield a significant p-value for Cretaceous and Eocene assemblages: not much higher than the average of 24% for Paleocene assemblages (Figure 11). And for the C-score for plants, an average of only 16% of iterations yield a significant p-value for Cretaceous and Eocene assemblages, not much higher than the average of 12% for Paleocene assemblages (Figure 11).
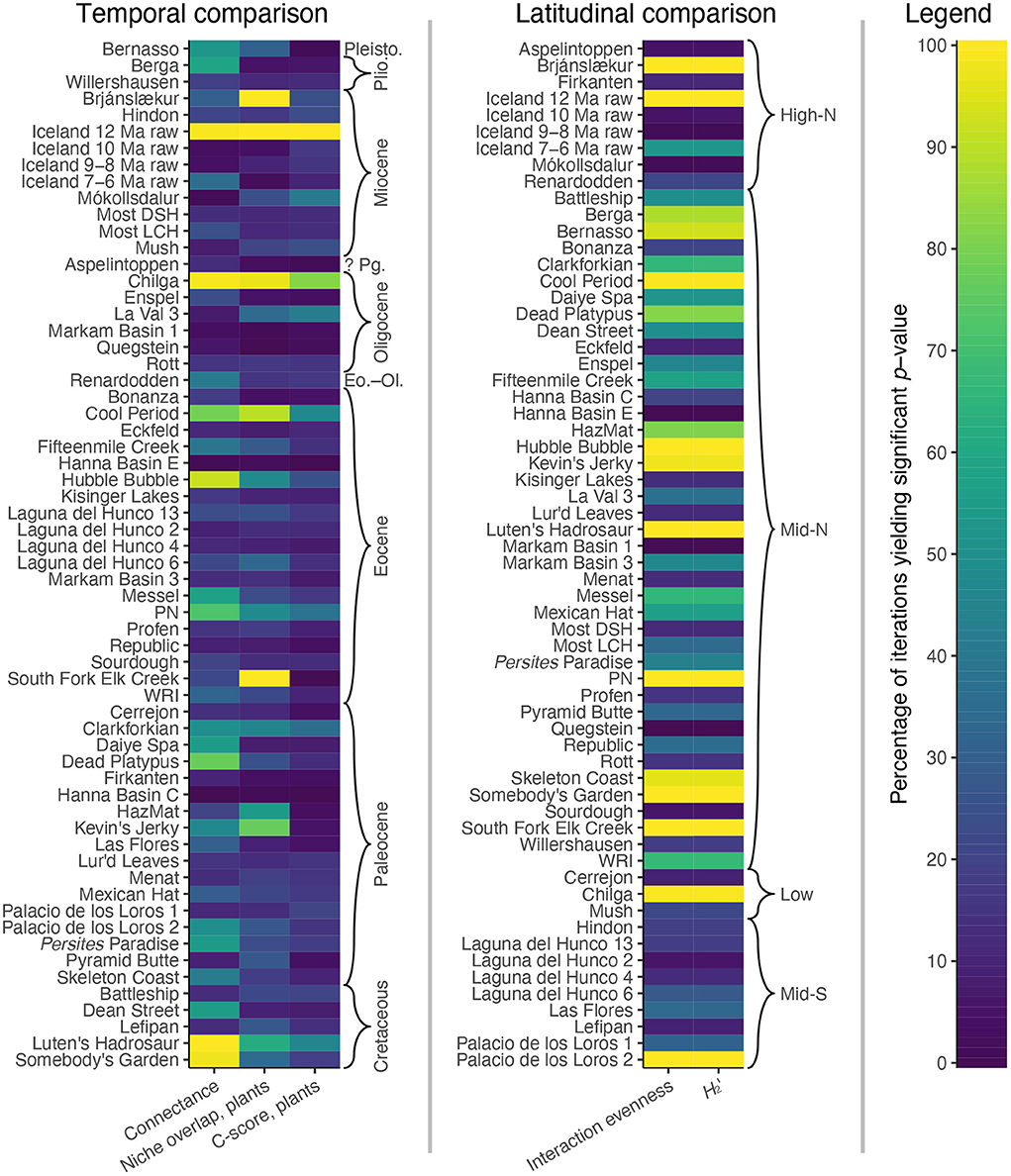
Figure 11. The results of null model comparisons for the bipartite network metrics that underlie (Currano et al., 2021)'s conclusions about trends through time and across latitudes.
Along similar lines, the conclusion about increased specialization at mid-southern latitudes is based upon the bipartite network metrics of interaction evenness and H2′. For interaction evenness, an average of only 30% of iterations yield a significant p-value for mid-southern latitude assemblages (Figure 11). For H2′, an average of only 29% of iterations yield a significant p-value for mid-southern latitude assemblages (Figure 11). For all other latitudinal bins, these average values are much higher, at 47%! The use of null models completely upends the conclusions that the original authors drew from these bipartite network metrics.
In other words, cherry picking—the selective use of bipartite network metrics, rather than direct richness estimates, to quantify changes in specialization—is not the only problem with the reported conclusions about specialized herbivory through time and across latitude. Null models show that the cherry-picked metrics very weakly support the ostensibly heightened specialization of herbivory during the Cretaceous and Eocene, and do not support the ostensibly heightened specialization of herbivory at mid-southern latitudes.
Data availability statement
Publicly available datasets were analyzed in this study. This data can be found at: https://github.com/anshuman21111/resampling-fossil-leaves/tree/main/Data_processed_localities.
Author contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Acknowledgments
Jonathan Payne, C. Kevin Boyce, William DiMichele, and Tyler Kukla provided helpful feedback on an earlier draft of this manuscript. Three reviewers provided additional suggestions that greatly improved the quality of this manuscript.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1. ^Late Cretaceous–Eocene, Paleocene–Oligocene, Eocene–Miocene, Oligocene–Pliocene, Miocene–Pleistocene.
References
Adrain, J. M., and Westrop, S. R. (2000). An empirical assessment of taxic paleobiology. Science 289, 110–112. doi: 10.1126/science.289.5476.110
Allen, B. J., Wignall, P. B., Hill, D. J., Saupe, E. E., and Dunhill, A. M. (2020). The latitudinal diversity gradient of tetrapods across the Permo-Triassic mass extinction and recovery interval. Proc. R. Soc. B Biol. Sci. 287, 20201125. doi: 10.1098/rspb.2020.1125
Badillo-Montaño, R., Amancio, G., Falcón-Brindis, A., León-Cortés, J. L., Von Thaden, J., and Dzul-Cauich, F. (2022). Trophic host-parasitoid interactions of two Neotropical butterfly species in southeastern Mexico. Int. J. Trop Insect. Sci. 42, 1865–1875. doi: 10.1007/s42690-021-00714-1
Bates, D., Mächler, M., Bolker, B., and Walker, S. (2014). Fitting linear mixed-effects models using lme4. arXiv preprint arXiv:1406.5823. doi: 10.18637/jss.v067.i01
Benedetto, U., Head, S. J., Angelini, G. D., and Blackstone, E. H. (2018). Statistical primer: propensity score matching and its alternatives†. Eur. J. Cardio Thoracic Surg. 53, 1112–1117. doi: 10.1093/ejcts/ezy167
Blüthgen, N. (2010). Why network analysis is often disconnected from community ecology: a critique and an ecologist's guide. Basic Appl. Ecol. 11, 185–195. doi: 10.1016/j.baae.2010.01.001
Blüthgen, N., Fründ, J., Vázquez, D. P., and Menzel, F. (2008). What do interaction network metrics tell us about specialization and biological traits. Ecology 89, 3387–3399. doi: 10.1890/07-2121.1
Boyce, C. K., and Zwieniecki, M. A. (2012). Leaf fossil record suggests limited influence of atmospheric CO2 on terrestrial productivity prior to angiosperm evolution. Proc. Natl. Acad. Sci. U.S.A. 109, 10403–10408. doi: 10.1073/pnas.1203769109
Bucharova, A., Lampei, C., Conrady, M., May, E., Matheja, J., Meyer, M., et al. (2022). Plant provenance affects pollinator network: implications for ecological restoration. J. Appl. Ecol. 59, 373–383. doi: 10.1111/1365-2664.13866
Bush, A. M., and Bambach, R. K. (2015). Sustained Mesozoic–Cenozoic diversification of marine Metazoa: a consistent signal from the fossil record. Geology 43, 979–982. doi: 10.1130/G37162.1
Cantrill, D. J., and Poole, I. (2012). “The heat is on: Paleogene floras and the Paleocene-Eocene warm period,” in The Vegetation of Antarctica through Geological Time (Cambridge: Cambridge University Press), 308–389. doi: 10.1017/CBO9781139024990
Capel, E., Cleal, C. J., Gerrienne, P., Servais, T., and Cascales-Miñana, B. (2021). A factor analysis approach to modelling the early diversification of terrestrial vegetation. Palaeogeogr. Palaeoclimatol. Palaeoecol. 566, 110170. doi: 10.1016/j.palaeo.2020.110170
Chen, Z. Q., George, A. D., and Yang, W.-R. (2009). Effects of Middle–Late permian sea-level changes and mass extinction on the formation of the Tieqiao skeletal mound in the Laibin area, South China. Aust. J. Earth Sci. 56, 745–763. doi: 10.1080/08120090903002581
Chown, S. L., and Gaston, K. J. (2000). Areas, cradles and museums: the latitudinal gradient in species richness. Trends Ecol. Evolut. 15, 311–315. doi: 10.1016/S0169-5347(00)01910-8
Cleal, C. J., and Cascales-Miñana, B. (2014). Composition and dynamics of the great Phanerozoic Evolutionary Floras. Lethaia 47, 469–484. doi: 10.1111/let.12070
Cleal, C. J., Pardoe, H. S., Berry, C. M., Cascales-Miñana, B., Davis, B. A., Diez, J. B., et al. (2021). Palaeobotanical experiences of plant diversity in deep time. 1: how well can we identify past plant diversity in the fossil record? Palaeogeogr. Palaeoclimatol. Palaeoecol. 576, 110481. doi: 10.1016/j.palaeo.2021.110481
Close, R. A., Benson, R. B. J., Saupe, E. E., Clapham, M. E., and Butler, R. J. (2020). The spatial structure of Phanerozoic marine animal diversity. Science 368, 420–424. doi: 10.1126/science.aay8309
Cohen, J. (1977). Statistical Power Analysis for the Behavioral Sciences. New York, NY: Academic Press.
Cohen, K. M., Finney, S. C., Gibbard, P. L., and Fan, J.-X. (2013). The ICS international chronostratigraphic chart. Episodes J. Int. Geosci. 36, 199–204. doi: 10.18814/epiiugs/2013/v36i3/002
Connor, E. F., and Simberloff, D. (1986). Competition, scientific method, and null models in ecology. Am. Sci. 74, 155–162.
Crowley, T. J., and Berner, R. A. (2001). CO2 and climate change. Science 292, 870–872. doi: 10.1126/science.1061664
Currano, E. D., Azevedo-Schmidt, L. E., Maccracken, S. A., and Swain, A. (2021). Scars on fossil leaves: an exploration of ecological patterns in plant–insect herbivore associations during the Age of Angiosperms. Palaeogeogr. Palaeoclimatol. Palaeoecol. 582, 110636. doi: 10.1016/j.palaeo.2021.110636
Currano, E. D., and Jacobs, B. F. (2021). Bug-bitten leaves from the early Miocene of Ethiopia elucidate the impacts of plant nutrient concentrations and climate on insect herbivore communities. Glob. Planet Change 207, 103655. doi: 10.1016/j.gloplacha.2021.103655
Currano, E. D., Jacobs, B. F., Pan, A. D., and Tabor, N. J. (2011). Inferring ecological disturbance in the fossil record: a case study from the late Oligocene of Ethiopia. Palaeogeogr. Palaeoclimatol. Palaeoecol. 309, 242–252. doi: 10.1016/j.palaeo.2011.06.007
da Silva Goldas, C., Podgaiski, L. R., Veronese Corrêa da Silva, C., Abreu Ferreira, P. M., Vizentin-Bugoni, J., and de Souza Mendonça, M. (2022). Structural resilience and high interaction dissimilarity of plant–pollinator interaction networks in fire-prone grasslands. Oecologia 198, 179–192. doi: 10.1007/s00442-021-05071-x
D'Bastiani, E., Campião, K. M., Boeger, W. A., and Araújo, S. B. L. (2020). The role of ecological opportunity in shaping host– parasite networks. Parasitology 147, 1452–1460. doi: 10.1017/S003118202000133X
de Matos, L. R. A., Ramalho, W. P., de Arruda, F. V., Ceron, K., Luna, P., Virgílio, L. R., et al. (2022). Environmental drivers and network structure of hylid anurans (Amphibia: Hylidae) in floating meadows from Amazonian oxbow lakes. Wetlands 42, 21. doi: 10.1007/s13157-022-01541-x
Dickersin, K. (1990). The existence of publication bias and risk factors for its occurrence. J. Am. Med. Soc. 263, 1385–1389. doi: 10.1001/jama.263.10.1385
Donovan, M. P., Iglesias, A., Wilf, P., Labandeira, C. C., and Cúneo, N. R. (2018). Diverse plant-insect associations from the latest Cretaceous and early Paleocene of Patagonia, Argentina. Ameghiniana 55, 303–338. doi: 10.5710/AMGH.15.02.2018.3181
Dormann, C. F., Fründ, J., Blüthgen, N., and Gruber, B. (2009). Indices, graphs and null models: analyzing bipartite ecological networks. Open Ecol. J. 2, 7–24. doi: 10.2174/1874213000902010007
Dormann, C. F., Gruber, B., and Fründ, J. (2008). Introducing the bipartite package: analysing ecological networks. Interaction 1.
Dunne, E. M., Farnsworth, A., Greene, S. E., Lunt, D. J., and Butler, R. J. (2021). Climatic drivers of latitudinal variation in Late Triassic tetrapod diversity. Palaeontology 64, 101–117. doi: 10.1111/pala.12514
Eckerter, T., Braunisch, V., Pufal, G., and Klein, A. M. (2022). Small clear-cuts in managed forests support trap-nesting bees, wasps and their parasitoids. For. Ecol. Manag. 509, 120076. doi: 10.1016/j.foreco.2022.120076
Ferguson, C. J. (2009). An effect size primer: a guide for clinicians and researchers. Prof. Psychol. 40, 532–538. doi: 10.1037/a0015808
Fletcher, S. C. (2021). The role of replication in psychological science. Eur. J. Philos. Sci. 11, 23. doi: 10.1007/s13194-020-00329-2
Fründ, J., McCann, K. S., and Williams, N. M. (2016). Sampling bias is a challenge for quantifying specialization and network structure: lessons from a quantitative niche model. Oikos 125, 502–513. doi: 10.1111/oik.02256
González-Castro, A., Morán-López, T., Nogales, M., and Traveset, A. (2022). Changes in the structure of seed dispersal networks when including interaction outcomes from both plant and animal perspectives. Oikos 2022, 08315. doi: 10.1111/oik.08315
Hallam, A. (2002). How catastrophic was the end-Triassic mass extinction? Lethaia 35, 147–157. doi: 10.1080/002411602320184006
Hetherington, E. D., Damian-Serrano, A., Haddock, S. H. D., Dunn, C. W., and Choy, C. A. (2022). Integrating siphonophores into marine food-web ecology. Limnol. Oceanogr. Lett. 7, 81–95. doi: 10.1002/lol2.10235
Ho, D. E., Imai, K., King, G., and Stuart, E. A. (2011). MatchIt: Nonparametric preprocessing for parametric causal inference. J. Stat. Softw. 42, 1–28. doi: 10.18637/jss.v042.i08
Hunt, R. J., and Poole, I. (2003). “Paleogene west antarctic climate and vegetation history in light of new data from king george island,” in Causes and Consequences of Globally Warm Climates in the Early Paleogene Geological Society of America Special Paper, eds S. L. Wing, P. D. Gingerich, B. Schmitz, and E. Thomas (Boulder, CO: Geological Society of America), 395–412.
Jablonski, D. (1993). The tropics as a source of evolutionary novelty through geological time. Nature 364, 142–144. doi: 10.1038/364142a0
Jablonski, D., Roy, K., and Valentine, J. W. (2006). Out of the tropics: evolutionary dynamics of the latitudinal diversity gradient. Science 314, 102–106. doi: 10.1126/science.1130880
Johnson, P. C. (2014). Extension of Nakagawa and Schielzeth's R2GLMM to random slopes models. Methods Ecol. Evolut. 5, 944–946. doi: 10.1111/2041-210X.12225
Kelley, K. (2007). Methods for the behavioral, educational, and social sciences: an R package. Behav. Res. Methods 39, 979–984. doi: 10.3758/BF03192993
Kivlin, S. N., Mann, M. A., Lynn, J. S., Kazenel, M. R., Taylor, D. L., and Rudgers, J. A. (2022). Grass species identity shapes communities of root and leaf fungi more than elevation. ISME Commun. 2, 1–11. doi: 10.1038/s43705-022-00107-6
Kozlov, M. V., Lanta, V., Zverev, V., and Zvereva, E. L. (2015). Global patterns in background losses of woody plant foliage to insects. Global Ecology and Biogeography 24, 1126–1135. doi: 10.1111/geb.12347
Kukla, A. (1996). Does every theory have empirically equivalent rivals? Erkenntnis 44, 137–166. doi: 10.1007/BF00166499
Labandeira, C. C. (2006). “Assessing the fossil record of plant-insect associations: Ichnodata versus body-fossil data,” in Sediment-Organism Interactions: A Multifaceted Ichnology, eds R. G. Bromley, L. A. Buatois, G. Mángano, J. F. Genize, and R. N. Melchor (Tulsa, OK: Society for Sedimentary Geology), 9–26.
Labandeira, C. C., Johnson, K. R., and Wilf, P. (2002). Impact of the terminal Cretaceous event on plant–insect associations. Proc. Natl. Acad. Sci. U.S.A. 99, 2061–2066. doi: 10.1073/pnas.042492999
Labandeira, C. C., Wilf, P., Johnson, K. R., and Marsh, F. (2007). Guide to Insect (and Other) Damage Types on Compressed Plant Fossils (Version 3.0). Washington, DC: Smithsonian Institution.
Lamboy, W., and Lesnikowska, A. (1988). Some statistical methods useful in the analysis of paleoecological data. Paleontol. Soc. Special Publicat. 3, 52–71. doi: 10.1017/S2475262200004883
Lewinsohn, T. M., and Roslin, T. (2008). Four ways towards tropical herbivore megadiversity. Ecol. Lett. 11, 398–416. doi: 10.1111/j.1461-0248.2008.01155.x
Llaberia-Robledillo, M., Balbuena, J. A., Sarabeev, V., and Llopis-Belenguer, C. (2022). Changes in native and introduced host–parasite networks. Biol. Invasions. 24, 543–555. doi: 10.1007/s10530-021-02657-7
Lucas, S. G., and Tanner, L. H. (2015). End-Triassic nonmarine biotic events. J. Palaeogeogr. 4, 331–348. doi: 10.1016/j.jop.2015.08.010
Luke, S. G. (2017). Evaluating significance in linear mixed-effects models in R. Behav. Res. Methods 49, 1494–1502. doi: 10.3758/s13428-016-0809-y
Makin, T. R., and Orban de Xivry, J.-J. (2019). Ten common statistical mistakes to watch out for when writing or reviewing a manuscript. Elife 8, e48175. doi: 10.7554/eLife.48175
McDonald, C. M. (2009). Herbivory in Antarctic fossil forests and comparisons with modem analogues in Chile (Graduate thesis). University of Leeds, Leeds, United Kingdom. p. 295.
McDonald, C. M., Francis, J. E., Compton, S. G. A., Haywood, A., Ashworth, A. C., Hinojosa, L. F., et al. (2007). “Herbivory in antarctic fossil forests: evolutionary and palaeoclimatic significance,” in Antarctica: A Keystone in a Changing World (Washington, DC: The National Academies Press), 1–4.
Mondal, S., Chakraborty, H., and Paul, S. (2019). Latitudinal patterns of gastropod drilling predation intensity through time. Palaios 34, 261–270. doi: 10.2110/palo.2018.075
Moss, E. D., and Evans, D. M. (2022). Experimental climate warming reduces floral resources and alters insect visitation and wildflower seed set in a cereal agro-ecosystem. Front. Plant Sci. 13, 826205. doi: 10.3389/fpls.2022.826205
Munafò, M. R., Nosek, B. A., Bishop, D. V. M., Button, K. S., Chambers, C. D., Percie du Sert, N., et al. (2017). A manifesto for reproducible science. Nat. Hum. Behav. 1, 1–9. doi: 10.1038/s41562-016-0021
Nakagawa, S., Johnson, P. C. D., and Schielzeth, H. (2017). The coefficient of determination R2 and intra-class correlation coefficient from generalized linear mixed-effects models revisited and expanded. J. R. Soc. Interface 14, 20170213. doi: 10.1098/rsif.2017.0213
Nakagawa, S., and Schielzeth, H. (2013). A general and simple method for obtaining R2 from generalized linear mixed-effects models. Methods Ecol. Evolut. 4, 133–142. doi: 10.1111/j.2041-210x.2012.00261.x
Nosek, B. A., Spies, J. R., and Motyl, M. (2012). Scientific utopia: II. Restructuring incentives and practices to promote truth over publishability. Perspect. Psychol. Sci. 7, 615–631. doi: 10.1177/1745691612459058
Nowak, H., Schneebeli-Hermann, E., and Kustatscher, E. (2019). No mass extinction for land plants at the Permian–Triassic transition. Nat. Commun. 10, 384. doi: 10.1038/s41467-018-07945-w
Oliveira, H. F. M., Pinheiro, R. B. P., Varassin, I. G., Rodríguez-Herrera, B., Kuzmina, M., Rossiter, S. J., et al. (2022). The structure of tropical bat–plant interaction networks during an extreme El Niño-Southern Oscillation event. Mol. Ecol. 31, 1892–1906. doi: 10.1111/mec.16363
Open Science Collaboration (2015). Estimating the reproducibility of psychological science. Science 349, aac4716. doi: 10.1126/science.aac4716
Pardoe, H. S., Cleal, C. J., Berry, C. M., Cascales-Mi nana, B., Davis, B. A., Diez, J. B., et al. (2021). Palaeobotanical experiences of plant diversity in deep time. 2: how to measure and analyse past plant biodiversity. Palaeogeogr. Palaeoclimatol. Palaeoecol. 580, 110618. doi: 10.1016/j.palaeo.2021.110618
Pearl, J. (2014). Comment: understanding Simpson's Paradox. Am. Stat. 68, 8–13. doi: 10.1080/00031305.2014.876829
Powell, M. G., Beresford, V. P., and Colaianne, B. A. (2012). The latitudinal position of peak marine diversity in living and fossil biotas. J. Biogeogr. 39, 1687–1694. doi: 10.1111/j.1365-2699.2012.02719.x
Powell, M. G., Moore, B. R., and Smith, T. J. (2015). Origination, extinction, invasion, and extirpation components of the brachiopod latitudinal biodiversity gradient through the Phanerozoic Eon. Paleobiology 41, 330–341. doi: 10.1017/pab.2014.20
Quinto, J., Díaz-Castelazo, C., Rico-Gray, V., Martínez-Falcón, A. P., Abdala-Roberts, L., and Parra-Tabla, V. (2022). Short-term temporal patterns in herbivore beetle assemblages in polyculture neotropical forest plantations. Neotrop Entomol. 51, 199–211. doi: 10.1007/s.13744-021-00933-8
R Development Core Team (2021). R: A Language and Environment for Statistical Computing. Vienna: R Core Team.
Raja, N. B., Dunne, E. M., Matiwane, A., Khan, T. M., Nätscher, P. S., Ghilardi, A. M., et al. (2021). Colonial history and global economics distort our understanding of deep-time biodiversity. Nat. Ecol. Evolut. 6, 145–154. doi: 10.1038/s41559-021-01608-8
Raup, D. (1972). Taxonomic diversity during the Phanerozoic. Science 177, 1065–1071. doi: 10.1126/science.177.4054.1065
Resnik, D. B., Elliott, K. C., Soranno, P. A., and Smith, E. M. (2017). Data-intensive science and research integrity. Account. Res. 24, 344–358. doi: 10.1080/08989621.2017.1327813
Rodríguez-Godínez, R., Sánchez-González, L. A., del Coro Arizmendi, M. d. C., and Almazán-Núñez, R. C. (2022). Bursera fruit traits as drivers of fruit removal by flycatchers. Acta Oecol. 114, 103811. doi: 10.1016/j.actao.2022.103811
Romero-Lebrón, E., Robledo, J. M., Delclòs, X., Petrulevičius, J. F., and Gleiser, R. M. (2022). Endophytic insect oviposition traces in deep time. Palaeogeogr. Palaeoclimatol. Palaeoecol. 590, 110855. doi: 10.1016/j.palaeo.2022.110855
Rosa, R. R., Bellay, S., Baumgartner, M. T., and Bialetzki, A. (2022). Fish larvae-environment networks: co-occurrence patterns, nestedness and robustness of reproductive guilds. Hydrobiologia doi: 10.1007/s10750-022-04853-5
Schwab, A., Abrahamson, E., Starbuck, W. H., and Fidler, F. (2011). Researchers should make thoughtful assessments instead of null-hypothesis significance tests. Organizat. Sci. 22, 1105–1120. doi: 10.1287/orsc.1100.0557
Scott, A. C., and Titchener, F. R. (1999). “Techniques in the study of plant-arthropod interactions,” in Fossil Plants and Spores: Modern Techniques, eds T. P. Jones and N. P. Rowe (London: Geological Society of London), 310–315.
Sepkoski, D. (2012). “Chapter three. the rise of quantitative paleobiology,” in Rereading the Fossil Record (Chicago: University of Chicago Press), 77–112.
Sepkoski, J. J., Bambach, R. K., Raup, D. M., and Valentine, J. W. (1981). Phanerozoic marine diversity and the fossil record. Nature 293, 435–437. doi: 10.1038/293435a0
Shannon, C. E. (1948). A mathematical theory of communication. Bell Syst. Techn. J. 27, 379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x
Shrout, P. E., and Rodgers, J. L. (2018). Psychology, science, and knowledge construction: broadening perspectives from the replication crisis. Annu. Rev. Psychol. 69, 487–510. doi: 10.1146/annurev-psych-122216-011845
Simonsohn, U., Simmons, J. P., and Nelson, L. D. (2020). Specification curve analysis. Nat. Hum. Behav. 4, 1208–1214. doi: 10.1038/s41562-020-0912-z
Sonne, J., Maruyama, P. K., Martín González, A. M., Rahbek, C., Bascompte, J., and Dalsgaard, B. (2022). Extinction, coextinction and colonization dynamics in plant–hummingbird networks under climate change. Nat. Ecol. Evolut. 6, 720–729. doi: 10.1038/s41559-022-01693-3
Stebbins, G. L. (1974). “1. The basic processes of evolution,” in Flowering Plants: Evolution above the Species Level (Cambridge, MA: The Belknap Press of Harvard University Press).
Twitchett, R. J. (2006). The palaeoclimatology, palaeoecology and palaeoenvironmental analysis of mass extinction events. Palaeogeogr. Palaeoclimatol. Palaeoecol. 232, 190–213. doi: 10.1016/j.palaeo.2005.05.019
Valido, A., Rodríguez-Rodríguez, M. C., and Jordano, P. (2019). Honeybees disrupt the structure and functionality of plant-pollinator networks. Sci. Rep. 9, 4711. doi: 10.1038/s41598-019-41271-5
Vinagre-Izquierdo, C., Bodawatta, K. H., Chmel, K., Renelies-Hamilton, J., Paul, L., Munclinger, P., et al. (2022). The drivers of avian-haemosporidian prevalence in tropical lowland forests of New Guinea in three dimensions. Ecol. Evol. 12, e8497. doi: 10.1002/ece3.8497
Virgo, J., Ufermann, L., Lampert, K. P., and Eltz, T. (2022). More than meets the eye: decrypting diversity reveals hidden interaction specificity between frogs and frog-biting midges. Ecol. Entomol. 47, 95–108. doi: 10.1111/een.13095
Vul, E., Harris, C., Winkielman, P., and Pashler, H. (2009). Puzzlingly high correlations in fMRI studies of emotion, personality, and social cognition. Perspect. Psychol. Sci. 4, 274–290. doi: 10.1111/j.1745-6924.2009.01125.x
Wagner, P. J., and Marcot, J. D. (2013). Modelling distributions of fossil sampling rates over time, space and taxa: assessment and implications for macroevolutionary studies. Methods Ecol. Evolut. 4, 703–713. doi: 10.1111/2041-210X.12088
Wang, S. C., and Bush, A. M. (2008). Adjusting global extinction rates to account for taxonomic susceptibility. Paleobiology 34, 434–455. doi: 10.1666/07060.1
Wappler, T., Labandeira, C. C., Rust, J., Frankenhäuser, H., and Wilde, V. (2012). Testing for the effects and consequences of mid Paleogene climate change on insect herbivory. PLoS ONE 7, e40744. doi: 10.1371/journal.pone.0040744
Webber, Q. M., Schneider, D. C., and Vander Wal, E. (2020). Is less more? A commentary on the practice of ‘metric hacking' in animal social network analysis. Anim. Behav. 168, 109–120. doi: 10.1016/j.anbehav.2020.08.011
Wilf, P., Labandeira, C. C., Johnson, K. R., Coley, P. D., and Cutter, A. D. (2001). Insect herbivory, plant defense, and early Cenozoic climate change. Proc. Natl. Acad. Sci. U.S.A. 98, 6221–6226. doi: 10.1073/pnas.111069498
Wilf, P., Labandeira, C. C., Johnson, K. R., and Cuneo, N. R. (2005). Richness of plant–insect associations in Eocene Patagonia: a legacy for South American biodiversity. Proc. Natl. Acad. Sci. U.S.A. 102, 8944–8948. doi: 10.1073/pnas.0500516102
Wilf, P., Labandeira, C. C., Johnson, K. R., and Ellis, B. (2006). Decoupled plant and insect diversity after the end-Cretaceous extinction. Science 313, 1112–1115. doi: 10.1126/science.1129569
Wing, S. L., Herrera, F., Jaramillo, C. A., Gómez-Navarro, C., Wilf, P., and Labandeira, C. C. (2009). Late Paleocene fossils from the Cerrejón Formation, Colombia, are the earliest record of Neotropical rainforest. Proc. Natl. Acad. Sci. U.S.A. 106, 18627–18632. doi: 10.1073/pnas.0905130106
Woolley, C. H., Thompson, J. R., Wu, Y.-H., Bottjer, D. J., and Smith, N. D. (2022). A biased fossil record can preserve reliable phylogenetic signal. Paleobiology 48, 480–495. doi: 10.1017/pab.2021.45
Wu, H., Shi, G. R., and Sun, Y. (2019). The latitudinal gradient of shell ornament–A case study from Changhsingian (Late Permian) brachiopods. Earth Sci. Rev. 197, 102904. doi: 10.1016/j.earscirev.2019.102904
Zhang, S., Zhang, Y., and Ma, K. (2016). Latitudinal variation in herbivory: hemispheric asymmetries and the role of climatic drivers. J. Ecol. 104, 1089–1095. doi: 10.1111/1365-2745.12588
Appendix
The outlier Hindon Maar assemblage
Currano et al. (2021) found the Hindon Maar assemblage to be an outlier for damage type diversity. They excluded Hindon Maar from their boxplots, Tukey tests, and nonmetric multidimensional scaling plot, but included this assemblage in their latitudinal analysis. They provided no explanation of why they included Hindon Maar in some procedures but not others. There is no MAT estimate for Hindon Maar, so this outlier cannot be included in the specifications that use MAT as a fixed effect.
Data from Seymour Island and King George Island
Another irregularity in Currano et al. (2021)'s approach is the exclusion of the two “high-latitude” southern assemblages (McDonald et al., 2007) from the latitudinal analysis. (These two assemblages, Seymour Island and King George Island, occur between 60°S and 66°34'S, and thus are assigned to their “high-south” latitudinal bin but would be assigned to the mid-southern bin if their latitudinal boundaries more consistently followed latitudes of astronomical significance).
The authors justify the exclusion of these two assemblages from their latitudinal analysis by writing, “high S sites were not included due to insufficient sample sizes.” This statement is vague, but neither interpretation withstands scrutiny. This statement cannot be interpreted to mean that the high-south assemblages were excluded due to insufficient sampling of each assemblage, because over 1,000 leaves were examined from each island; the authors included Hanna Basin Level C in their analysis even though it falls two leaves short of their stated 300-leaf threshold for inclusion. However, the other interpretation of their justification does not make much more sense. If they excluded the high-southern latitudinal bin from the latitudinal analysis because it contains merely two assemblages, why did they consider two assemblages to be sufficient to speculate on the importance of the tropics as a museum or cradle of leaf mining diversity as discussed above?
Because the authors did not report damage type richness for Seymour Island and King George Island in their supplemental data, I had to extract these data myself from McDonald (2009). I downloaded all of the electronic supplemental files of McDonald (2009). from the e-thesis online service hosted by the British Library, but these files did not contain any paleontological data. McDonald (2009) did not use the Damage Type system for classifying insect damage, and instead classified damage into “trace morphotypes.” These trace morphotypes appear to correspond roughly to damage types, and were treated here as analogs of damage types).
Damage type data for Seymour Island were extracted from McDonald (2009)'s Table 7.4 on page 190–1. Damage type data for King George Island were extracted from Table 7.1 on page 181, Table 7.2 on page 184, and Table 7.3 on page 188. These data were cross-referenced with Table 3.3 on page 41–2, Table 3.4 on page 46–8, Table 3.5 on page 56–7, and Table 3.6 on page 61. There were only three inconsistencies among Tables 3.3–6 and Tables 7.1–4. Trace morphotype K1.4 is said to occur on two specimens in Table 3.3 and on one specimen in Table 7.1. Trace morphotype K2.17 is said to occur on seven specimens in Table 3.4, and on eight specimens in Table 7.2. Trace morphotype K3.4 is said to occur on five specimens in Table 3.5, but this line is blank in Table 7.3. I treated trace morphotype K3.4 as occurring on five specimens. To split the difference for trace morphotypes K1.4 and K2.17, I treated trace morphotype K1.4 as occurring on two specimens and trace morphotype K2.17 as occurring on seven specimens.
Currano et al. (2021) did not provide a definition of “specialized” damage types, complicating the task of replicating their methods. To estimate which trace morphotypes from King George Island and Seymour Island would be considered “specialized” under their unexplained scoring scheme, I treated all galling and mining trace morphotypes as specialized. I also treated as specialized all other trace morphotypes that were noted on three or more specimens, if all such specimens belong to the same taxonomic family or the same plant morphotype (e.g., “Unknown 6”).
MAT estimates for Seymour Island and King George Island were updated following Cantrill and Poole (2012) and Hunt and Poole (2003), respectively.
To estimate Shannon's diversity index for Seymour Island and King George Island, I used the data from McDonald (2009)'s Figure 3.19 and estimated the abundances of the additional host plants, not included in this figure, by assuming that all additional host plants at King George Island are less abundant than Morphotype 2.18 and that all additional host plants at Seymour Island are less abundant than Morphotype 7. For each island, I simulated Shannon's diversity index for a scenario in which the host plants not illustrated in Figure 3.19 have abundances that decreased linearly by two toward a value of 1. For example: 39, 37, 35...5, 3, 1. Occurrences of the least abundant host plants were subtracted from the vector until the total number of specimens matched the number reported by McDonald (2009).
Keywords: statistics, fossil plants, integrity, sampling, herbivory
Citation: Schachat SR (2022) Examining paleobotanical databases: Revisiting trends in angiosperm folivory and unlocking the paleoecological promise of propensity score matching and specification curve analysis. Front. Ecol. Evol. 10:951547. doi: 10.3389/fevo.2022.951547
Received: 24 June 2022; Accepted: 28 October 2022;
Published: 25 November 2022.
Edited by:
Irene Tunno, Lawrence Livermore National Laboratory (DOE), United StatesReviewed by:
Jen O'Keefe, Morehead State University, United StatesCongyu Yu, Harvard University, United States
Carlos Roberto Candeiro, Universidade Federal de Goiás, Brazil
Copyright © 2022 Schachat. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sandra R. Schachat, sschachat@schmidtsciencefellows.org
 Sandra R. Schachat
Sandra R. Schachat