- Department of Earth Science, University of Oregon, Eugene, OR, United States
Chemotrophic microorganisms face the steep challenge of limited energy resources in natural environments. This observation has important implications for interpreting and modeling the kinetics and thermodynamics of microbial reactions. Current modeling frameworks treat microbes as autocatalysts, and simulate microbial energy conservation and growth with fixed kinetic and thermodynamic parameters. However, microbes are capable of acclimating to the environment and modulating their parameters in order to gain competitive fitness. Here we constructed an optimization model and described microbes as self-adapting catalysts by linking microbial parameters to intracellular metabolic resources. From the optimization results, we related microbial parameters to the substrate concentration and the energy available in the environment, and simplified the relationship between the kinetics and the thermodynamics of microbial reactions. We took as examples Methanosarcina and Methanosaeta – the methanogens that produce methane from acetate – and showed how the acclimation model extrapolated laboratory observations to natural environments and improved the simulation of methanogenesis and the dominance of Methanosaeta over Methanosarcina in lake sediments. These results highlight the importance of physiological acclimation in shaping the kinetics and thermodynamics of microbial reactions and in determining the outcome of microbial interactions.
Introduction
Microorganisms inhabit much of the Earth’s surface environment, account for a large fraction of the living carbon, and play a critical role in the chemistry of the environment (Offre et al., 2013; Flemming and Wuertz, 2019). They serve as catalysts for redox reactions, mineral dissolution and precipitation, and other chemical reactions, driving biogeochemical element cycling and influencing global climate (Douglas and Beveridge, 1998; Rousk and Bengtson, 2014; Soong et al., 2020). In return, natural environments support microbial populations and their growth by providing space, nutrients, energy sources, and other resources (Ponomareva et al., 2018; Soares and Rousk, 2019). In understanding and simulating the interactions between microbes and the environment, a key question is how to evaluate the kinetics and thermodynamics of microbial reactions.
Most models treat microbes as autocatalysts, catalysts that catalyze their own production, and describe microbial metabolism with three processes, catabolism, biomass synthesis, and maintenance (Shapiro et al., 2018; Wu et al., 2021). The thermodynamics of microbial catabolism is characterized with three parameters, the energy ΔGA available in the environment, the energy ΔGC conserved by ATP synthesis, and the thermodynamic drive f of microbial catabolism (Jin and Bethke, 2007). The available energy ΔGA is the negative of the Gibbs free energy change ΔG (J mol–1) of the chemical reaction catalyzed by catabolism, i.e., ΔGA = −ΔG. The conserved energy ΔGC is the product of the ATP yield YP per catabolic reaction and the phosphorylation energy ΔGP (i.e., the Gibbs free energy change of ATP synthesis from ADP and phosphate in the cytoplasm, and the value is ∼45 kJ mol–1) (Jin, 2012). The difference between the available energy ΔGA and the conserved energy ΔGC,
gives the thermodynamic drive f for catabolism.
The rate r at which catabolism catalyzes a chemical reaction can be calculated according to
Here k is the rate constant or the maximum rate per unit biomass (mol g–1 s–1), CX is the biomass concentration in water (g kg–1), and FS and FT are the dimensionless kinetic factor and the thermodynamic potential factor, respectively (Jin and Bethke, 2002, 2003). The kinetic factor FS is
where CS is substrate concentration (molality or M), and KM is the half-saturation constant (M), the concentration at which factor FS reaches 0.5. The thermodynamic potential factor FT is
where χrd is the stoichiometric number of rate-determining step, or the number of times the rate-determining step takes place per catabolic reaction, R is the gas constant (8.3145 J mol–1 K–1), and T is the temperature in Kelvin. The maximum function in Eq. 4 reflects that where thermodynamic drive decreases below zero, the thermodynamic potential factor remains at zero.
Microbes are autocatalysts in that they couple catabolism to biomass synthesis. The ratio of biomass synthesis rate to catabolic rate gives biomass yield YX per catabolic reaction (g mol–1), a parameter whose value depends on the ATP yield YP of catabolism according to
Here YX/P is the biomass yield per ATP and its value is ∼5 g mol–1 for anaerobic metabolisms (Jin, 2012). The rate of microbial growth per unit biomass, or specific growth rate μ (s–1), is the difference between the specific rate of biomass synthesis and decay, and can be calculated according to the revised Verhulst–Pearl equation or the logistic equation (Andrews and Harris, 1986; Mahdinia et al., 2020),
where FX is the biomass capacity factor that accounts for the limitation of microbial growth by environmental resources, such as space and the sources of carbon, nitrogen, and phosphorus, and D is the decay rate per unit biomass or specific decay constant (s–1). The biomass capacity factor FX is
where CX,max is the carrying capacity, or the maximum biomass concentration supported by the environment (g kg–1). Where catabolic rate r is controlled primarily by a substrate and the effects of the biomass capacity factor and biomass decay can be safely neglected, Eqs 2 and 6 can be combined together to give the Monod equation (Monod, 1949).
A point of controversy is applying the autocatalytic model to natural environments. Evaluating Eqs 1–7 requires a series of kinetic and thermodynamic parameters. The kinetic parameters characterize how fast catabolism proceeds and common examples include rate constant k and half-saturation constant KM; the thermodynamic parameters describe the efficiency of microbial metabolism and a typical example is the yield YP of ATPs per catabolic reaction (Jin et al., 2013). Most of these parameters have only been analyzed for laboratory cultures, and their values are widely applied to natural environments. However, due to the differences in growth condition between laboratory bioreactors and natural environments, notable differences are expected between the parameters of laboratory cultures and natural microbes (Pallud and Van Cappellen, 2006; Jin and Roden, 2011). For this reason, direct application of laboratory observations to natural environments has created predictions that deviated from field observations by orders of magnitude (Murphy and Schramke, 1998; Brown et al., 2000; Jin et al., 2013).
A related point of discussion is that microbes are not regular inanimate catalysts, but flexible in that they can acclimate to their ambient environment (Aksnes and Cao, 2011; Flynn et al., 2015). Acclimation refers to reversible changes in phenotypic traits, including microbial kinetic and thermodynamic parameters, induced by changes in environmental conditions. Well-known examples include the variations of microbial kinetic parameters with pH and temperature (Rosso et al., 1995; Jin and Kirk, 2018a). Likewise, microbial kinetic parameters also change with the availability of growth nutrients (Friedrich et al., 2015; Litchman et al., 2015). Such parameter plasticity can arise from active metabolic regulations or occur as an automatic outcome of physicochemical principles, and provide microbes with fitness across wide gradients of environmental conditions (Leroi et al., 1994; Wilson and Franklin, 2002). From this perspective, microbes are also self-adapting catalysts, and their kinetic and thermodynamic parameters may not be constant, but dependent on environmental conditions.
Here we develop an optimization-based model to predict how physiological acclimation changes microbial kinetic and thermodynamic parameters in response to the environmental availability of energy substrates and chemical energies. Our model links microbial parameters to intracellular metabolic resources and assumes that microbes optimize the usage of intracellular resources to gain competitive fitness (Smith et al., 2011; Casey and Follows, 2020). We apply the model by taking acetoclastic methanogenesis as a representative microbial reaction. This pathway dismutates acetate to methane (CH4) and carbon dioxide (CO2),
and accounts for two-thirds of global methane bioproduction (Whitman et al., 2014; Prakash et al., 2019). Two genera, Methanosarcina and Methanosaeta, are capable of the process: Methanosarcina dominates environments with relatively high acetate concentrations, such as anaerobic sludge digesters (Kurade et al., 2019), whereas Methanosaeta prevails in rice fields (Lee et al., 2014), peatlands (Galand et al., 2005), lake sediments (Conrad et al., 2011), marine sediments (Carr et al., 2018), and other environments of low acetate concentrations (Smith and Ingram-Smith, 2007). We illustrate the model application by simulating methanogenesis in lake sediments, and demonstrate that accounting for physiological acclimation improves the simulation of methanogenesis and sheds new light on the niche separation of the two methanogens.
Acclimation Model
The acclimation model builds on the assumption that microbes gain competitive fitness by maximizing the rate of ATP production. This assumption recognizes that ATP is the universal energy currency of life that powers biomass synthesis, maintenance, and other essential functions (Nirody et al., 2020). The rate rP of ATP production depends on both the stoichiometric ATP yield YP and the rate r of microbial catabolism,
To maximize ATP production rate, microbes need to optimize their ATP yields and catabolic rates.
Kinetic Parameters
Microbial catabolism consists of a series of metabolic reactions, from substrate uptake, to the electron transfer between electron donors and acceptors, and to energy conservation. Catalyzing metabolic reactions requires various intracellular resources, such as proteins, ribosomes, and other macromolecules (Figure 1A). Therefore, how these resources are allocated to individual metabolic reactions determines the rate of catabolism. Pahlow (2005) and Smith and Yamanaka (2007) developed an acclimation model that relates cellular resource allocation to the uptake fluxes of growth nutrients. Following their methodology, we link microbial kinetic parameters to cellular resources by assuming that:
• Rate constant k reflects the catabolic rate where substrate concentrations are much larger than the half-saturation constant KM. Under these conditions, catabolic rate is determined by a metabolic reaction, or a rate-limiting step. As a result, the rate constant is determined by the cellular resources allocated to the rate-limiting step.
• The ratio of rate constant k to half-saturation constant KM, i.e., affinity constant α, gives the slope of the increase in catabolic rate at substrate concentrations near zero (Healey, 1980; Button, 1993). Under these conditions, catabolic rate is determined by the flux of substrate uptake from the environment. Accordingly, the affinity constant is determined by the resources allocated to substrate uptake.
• There are limited cellular resources available to the two rate-determining steps at relatively low and relatively high substrate concentrations. The partition of the limited resources between the two rate-determining steps leads to the trade-off between the rate constant and the affinity constant.

Figure 1. Physiological acclimation model. (A) Microbes partition intracellular resources between the rate-determining step at relatively low substrate concentrations, i.e., substrate uptake (T), and the rate-determining step at relatively high substrate concentrations (D), thereby modulating rate constant and affinity constant (Eqs 16, 17). (B) Microbes partition the energy available in the environment between ATP synthesis (P) and thermodynamic drive (F), trading-off the ATP yield against the rate of catabolism (Eq. 20).
These assumptions can be summarized as
and
Here ϕT is the fraction of the available resources allocated to substrate uptake (T), and αmax and kmax are the largest-possible affinity constant and rate constant, respectively. Increases in ϕT raise the affinity constant α, but lower the rate constant k.
The expression of catabolic rate (Eq. 2) can be recast in terms of the rate constant and the affinity constant by assuming that catabolic rate is limited by a single substrate and all the remaining controlling factors can be safely neglected, i.e.,
substituting Eqs 10 and 11 to 12,
This equation suggests that at a given substrate concentration CS, catabolic rate r depends on the partition of the available cellular resources. Assuming that microbes acclimate immediately to ambient substrate concentration, we can take ϕT as a control variable and formulate an optimization problem that maximizes catabolic rate r,
This problem can be solved by setting the derivative of Eq. 13 with respect to ϕT to 0, and the solution gives the optimal fraction ϕT,op for substrate uptake (Smith et al., 2009),
Here CS,a is the substrate concentration to which microbes acclimate. By substituting Eq 15 to 10 and 11 (see Supplementary Material), we can relate the kinetic parameters (i.e., ka, αa, and KM,a) of the microbes acclimating to substrate concentration CS,a to those of laboratory cultures,
and
Here ko and KM,o are the parameters determined for laboratory cultures, and CS,o is the substrate concentration in laboratory growth media.
ATP Yield
Microbial ATP production is subject to the trade-off between the rate and ATP yield of catabolism (Figure 1B; Pfeiffer et al., 2001). This trade-off is captured by Eqs 1, 2, 4, and 9: increases in the ATP yield raise the rate of ATP production (Eq. 9), but lower the thermodynamic drive (Eq. 1) and hence the catabolic rate (Eqs 2, 4), which in turn lowers the rate of ATP production.
From the rate-yield trade-off and by assuming that microbes instantaneously respond to the energy available in the environment, we formulate an optimization problem that maximizes ATP production rate rP by taking ATP yield as a control variable,
Here to ensure that the optimization solution is biochemically feasible, we assume that ATP yield YP does not exceed the yield YP,o of laboratory cultures determined with growth media containing abundant energy resources. We solve the optimization problem by using the brute force method. Briefly, at a given available energy ΔGA, we sweep ATP yield YP from 0 to YP,o. At each step, we compute ATP production rate (Eq. 9) and determine the optimal ATP yield as the value that gives the largest ATP production rate. We then repeat the steps for different levels of the available energy. Where ΔGA ≤ 0, microbial catabolic reaction is not favored by thermodynamics, and no ATP is synthesized (i.e., YP = 0).
We solved the optimization problem at 25°C and by taking the stoichiometric number χrd of rate-determining step per catabolic reaction at 2. The results show that the ATP yield varies nearly linearly with the available energy (Figure 2A) and can be approximated with a power law,
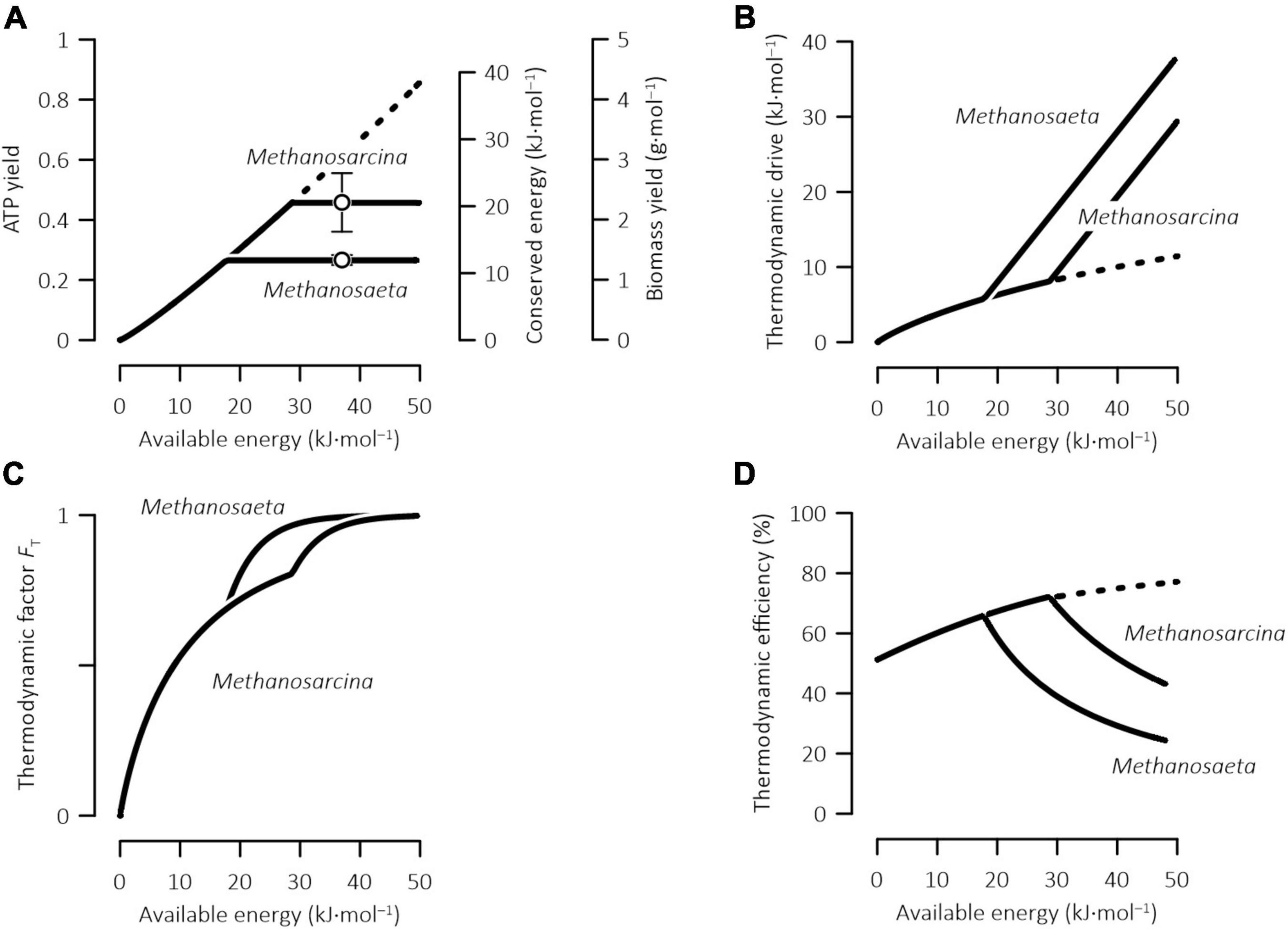
Figure 2. Variations with available energy in the ATP and biomass yields, the energy conserved by ATP synthesis (A), the thermodynamic drive (B), the thermodynamic potential factor (C), and the thermodynamic efficiency (D) of methanogenesis by Methanosarcina and Methanosaeta. Open symbols in panel (A) are the biomass yields determined experimentally for pure cultures and error bars show standard deviations (see Table 1); solid lines are calculated according to Eqs 1, 4, 20, 21; dashed lines indicate that the calculated values exceed those of laboratory cultures and may not be biochemically feasible.
where coefficient a and exponent β are 4.2 × 10–6 and 1.1, respectively.
Application
The acclimation model (Eqs 16–18, 20) builds on the principle of fitness maximization, and predicts the kinetic and thermodynamic parameters of microorganisms acclimating to the substrate concentration and the energy available in the environment. Here we illustrate its application by applying to acetoclastic methanogenesis by Methanosarcina and Methanosaeta.
Laboratory Observations
Applying the acclimation model requires the kinetic and thermodynamic parameters of laboratory cultures. We first compiled the parameter values of the mesophilic laboratory cultures of Methanosarcina and Methanosaeta determined at neutral pH and between 30 and 37°C. The results, summarized in Table 1 (also see Supplementary Table 1), confirm previous observations that Methanosarcina laboratory cultures have larger rate constant, affinity constant, and biomass yield than Methanosaeta cultures (Min and Zinder, 1989; Jetten et al., 1992; Conklin et al., 2006).

Table 1. Mean and standard deviation of kinetic and thermodynamic parameters of mesoneutrophilic Methanosarcina and Methanosaeta laboratory cultures.a
Differences between the two methanogens can be linked to the pathways of acetate activation (Welte and Deppenmeier, 2013). Methanosarcina employs two enzymes, an acetate kinase and a phosphotransacetylase, to convert acetate to acetyl-phosphate and then to acetyl-CoA, a process that consumes one ATP per acetate molecule. Methanosaeta produces acetyl-CoA with a single enzyme, acetyl-CoA synthase, a process that consumes two ATP equivalents per acetate molecule. The different ATP consumptions lead to different ATP yields and different cytoplasmic acetate concentrations, which in turn affect acetate uptake from the environment and hence the kinetic parameters of the two methanogens.
Model Predictions
Figure 3 shows, according to the acclimation model, how physiological acclimation changes the kinetic parameters of Methanosarcina and Methanosaeta at different acetate concentrations. We evaluated Eqs 16–18 with the average rate constants ko and the average half-saturation constants KM,o of laboratory methanogen cultures (see Table 1). In laboratory bioreactors, typical culture media for acetoclastic methanogens contain 50 mM acetate (Whitman et al., 2014, also see Supplementary Table 1). In natural environments, acetate concentrations range across several orders of magnitude, from as low as a few micromolalities in pristine aquifers to a few millimolalities in peatlands (Jakobsen and Postma, 1999; Hansen et al., 2001; Ye et al., 2012).
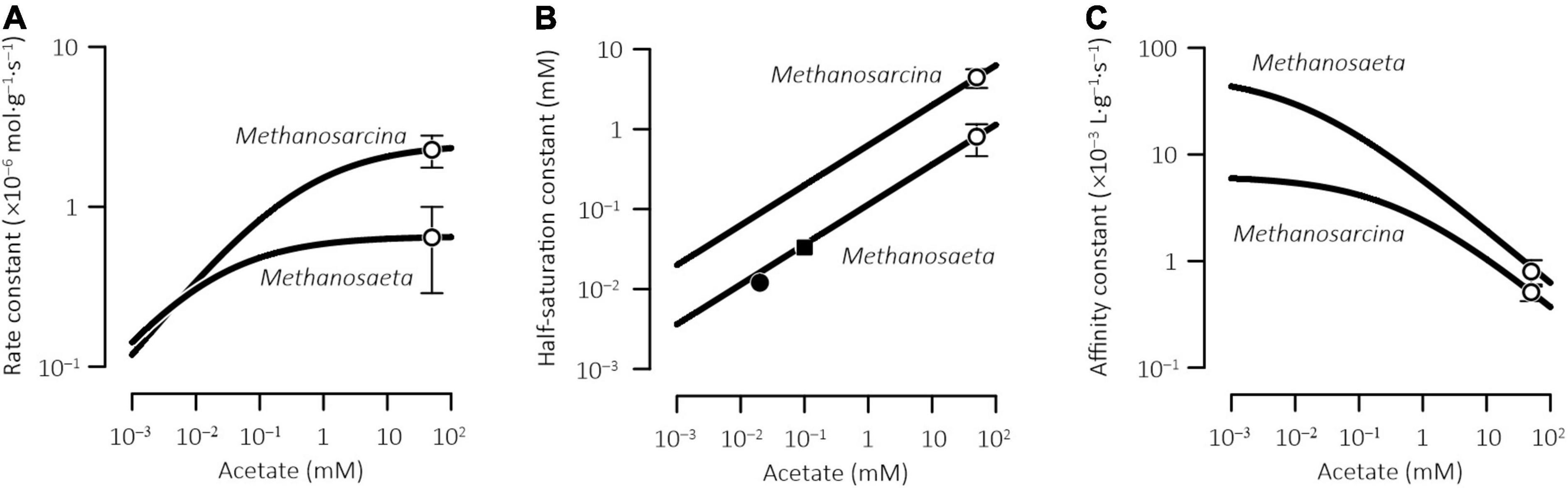
Figure 3. Acclimation model extrapolates the kinetic parameters of methanogenesis determined for laboratory cultures to the environment of different acetate concentrations. Open symbols are the values determined experimentally for pure cultures and error bars show standard deviations (see Table 1); closed symbols are those determined in the sediments from a lake (■, Lovley and Klug, 1983) and a wetland (●, Roden and Wetzel, 2002); solid lines are rate constants (A), half-saturation constants (B), and affinity constants (C) calculated according to Eqs 16–18.
From the model predictions, two patterns emerge. First, by acclimating to different acetate concentrations, methanogens acquire different kinetic parameters. By lowering the acclimation concentration from 50 mM to 1 μM, the rate constants and the half-saturation constants decrease while the affinity constants increase, leading to a positive correlation between the rate constant and the half-saturation constant but a negative correlation between the rate constant and the affinity constant (Figure 3). The variations in the rate constants and the affinity constants are of similar magnitude, about one order, whereas the half-saturation constants vary by more than two orders of magnitude. Second, the two methanogens show different extents of acclimation responses. From the acclimation concentrations of 50 mM to 1 μM, the rate constant decrease is faster in Methanosarcina than in Methanosaeta, whereas the affinity constant increase is faster in Methanosaeta than in Methanosarcina.
By acclimating to the different amounts of energy available in the environment, methanogens also acquire different yields of ATPs (Figure 2A). In laboratory bioreactors, typical growth media have a neutral pH and contain 50 mM acetate and 12 mM dissolved inorganic carbon (Whitman et al., 2014). Assuming an incubation temperature of 37°C and a methane concentration of 1 mM, the energy available from reaction 8 is ∼36 kJ⋅(mol CH4)–1. In natural environments, the available energy can vary notably. In the environment enriched in organic matter, such as the peatland complex near Ottawa, Canada and the bogs of Northern Michigan, United States, the available energy can be relatively large, >30 kJ mol–1 (Beer et al., 2008; Wu et al., 2021). On the other hand, in oligotrophic environments, such as the Rømø aquifer, Denmark, the available energy can be as low as <10 kJ mol–1 (Hansen et al., 2001).
According to the acclimation model (Eq. 20), where the reaction of acetoclastic methanogenesis (Eq. 8) is not favored by thermodynamics (i.e., ΔGA ≤ 0), no ATP is produced. Where the reaction is thermodynamically favorable and ΔGA > 0, the ATP yield increases almost linearly with the available energy, and so do the energy conserved by ATP synthesis and the yield of biomass synthesis (Figure 2A). The slopes of the increases are the same for Methanosaeta and Methanosarcina. Where the available energy reaches 18 kJ mol–1 and above, the ATP yield, the conserved energy, and the biomass yield of Methanosaeta increase to their maximum values, i.e., 0.27 per methane, 12.2 kJ⋅(mol methane)–1, and 1.4 g⋅(mol methane)–1, respectively. At the available energy of 29 kJ mol–1 or more, the ATP yield, the conserved energy, and the biomass yield of Methanosarcina reach their maximum values of 0.48 per methane, 21.6 kJ⋅(mol methane)–1, and 2.4 g⋅(mol methane)–1, respectively.
The difference between the available energy and the conserved energy gives the thermodynamic drive (Eq. 1) and determines the thermodynamic potential factor (Eq. 4). As illustrated in Figures 2B,C, there is no thermodynamic drive and the thermodynamic potential factor is 0, where methanogenesis reaction (Eq. 8) is at thermodynamic equilibrium. Increases in the available energy increases the thermodynamic drive and hence the thermodynamic potential factor, suggesting that the larger the available energy is, the stronger the thermodynamic drive becomes, and the faster the methanogenesis reaction proceeds. Importantly, the slope of the thermodynamic drive increase is less than 1, indicating that more energy is allocated to the ATP synthesis than to the thermodynamic drive.
Where the available energy increases above 18 kJ mol–1, the thermodynamic drive of Methanosaeta increases with the available energy at a 1:1 ratio and, as a result, the thermodynamic potential factor of Methanosaeta increases faster than that of Methanosarcina. These results reflect the prediction that the ATP yield of Methanosaeta reaches its maximum value of 0.27 per methane and, as a result, further increase in the available energy is allocated to the thermodynamic drive. At the available energy above 29 kJ mol–1, the slope of the increase in the thermodynamic drive of Methanosarcina also switches to 1.
Microbial energy conservation can be characterized with thermodynamic efficiency η,
the ratio of the energy conserved by ATP synthesis to the energy available in the environment. Figure 2D shows, according to the model predictions, how the efficiencies of Methanosaeta and Methanosarcina respond to the changes in the available energy. The efficiencies are close to 50% where methanogenesis reaction is close to thermodynamic equilibrium and the available energy is near 0. Increases in the available energy increase the efficiencies. The efficiencies of Methanosaeta and Methanosarcina reach a maximum value of 65 and 71% at the available energy of 18 and 29 kJ mol–1, respectively. With further increases in the available energy, the efficiencies start to decline.
These results highlight that the relationship between the efficiency and the available energy of methanogenesis may not be straightforward. For example, in the Rømø aquifer, Denmark, by assuming that Methanosaeta is the primary driver of acetoclastic methanogenesis and by taking the available energy at 10 kJ⋅(mol methane)–1, the efficiency would be 60%, larger than the efficiency of 50% predicted for methanogenesis close to thermodynamic equilibrium. The relatively large efficiency results from the increase in the efficiency with the available energy. However, in the bogs of Northern Michigan, United States, by taking the available energy at 30 kJ mol–1, the efficiency would be 39%. This value is smaller than the 50% efficiency near thermodynamic equilibrium, and can be accounted for by the prediction that where the available energy is >18 kJ mol–1, the efficiency of Methanosaeta decreases with increasing available energy.
Model Validation
Methanogenesis kinetics has been extensively analyzed in natural environments. However, most efforts focused primarily on bulk fluxes of methane production, and only a few studies analyzed the kinetic parameters of natural methanogens. In particular, two studies reported the half-saturation constants of natural acetoclastic methanogens.
• In the surface sediments of Lawrence Lake, Michigan, United States, acetate of about 50 μM has been reported (Lansdown et al., 1992). The half-saturation constant, determined by incubating sediment samples amended with different acetate concentrations, is 33 μM (Lovley and Klug, 1983).
• In the wetland sediments from Alabama, United States, acetate concentration is about 20 μM. The half-saturation constant determined by laboratory incubation experiments is 12 μM (Roden and Wetzel, 2002).
According to the acclimation model (Figure 3B), at the acclimation concentration of 50 μM, the half-saturation constant is predicted at 26 and 140 μM for Methanosaeta and Methanosarcina, respectively. At the acclimation concentration of 20 μM, the predicted half-saturation constant is 16 and 89 μM for Methanosaeta and Methanosarcina, respectively. Considering that in natural environments, acetoclastic methanogenesis is dominated by Methanosaeta (Smith and Ingram-Smith, 2007), the predicted half-saturation constants stay close to those determined experimentally.
No rate constant, affinity constant, ATP yield, or biomass yield has been analyzed for natural acetoclastic methanogens, which prevents a rigorous test of the model predictions. Nevertheless, the predictions are consistent with the patterns emerging from microbial kinetic parameters determined for other microbes. For example, increasing half-saturation constants with increasing substrate concentrations has been noted for sulfate reducing microbes and for microbes that grow on glucose (Jin et al., 2013; Tarpgaard et al., 2017). Moreover, positive correlations between rate constants and half-saturation constants have been detected for glucose consumption by Escherichia coli (Kovárová-Kovar and Egli, 1998), microbial methane-oxidation (Dunfield and Conrad, 2000), and nitrate consumption by prokaryotes and phytoplanktons (McCarthy et al., 1999; Collos et al., 2005; Litchman et al., 2007; Shaw et al., 2013).
The model predictions are also in agreement with the paradigm that where more energy is available, more energy is conserved by microbes (Jin, 2012). In the acclimation model, the relationship between optimal ATP yield and available energy is constructed from a general relationship between the rates and the thermodynamic drives of microbial reactions (Eqs 2, 4), and the results should be applicable to microbial catabolism in general. Figure 4A compares the optimal ATP yields with those estimated from the biochemical pathways of methanogenesis, sulfate reduction, and ferric iron reduction that utilize dihydrogen and acetate as electron donors. Previous estimations bear relatively large variations and can be attributed to the changes in the efficiency of energy conservation. The general agreement between the predicted and the estimated values supports the yield predictions by the acclimation model.
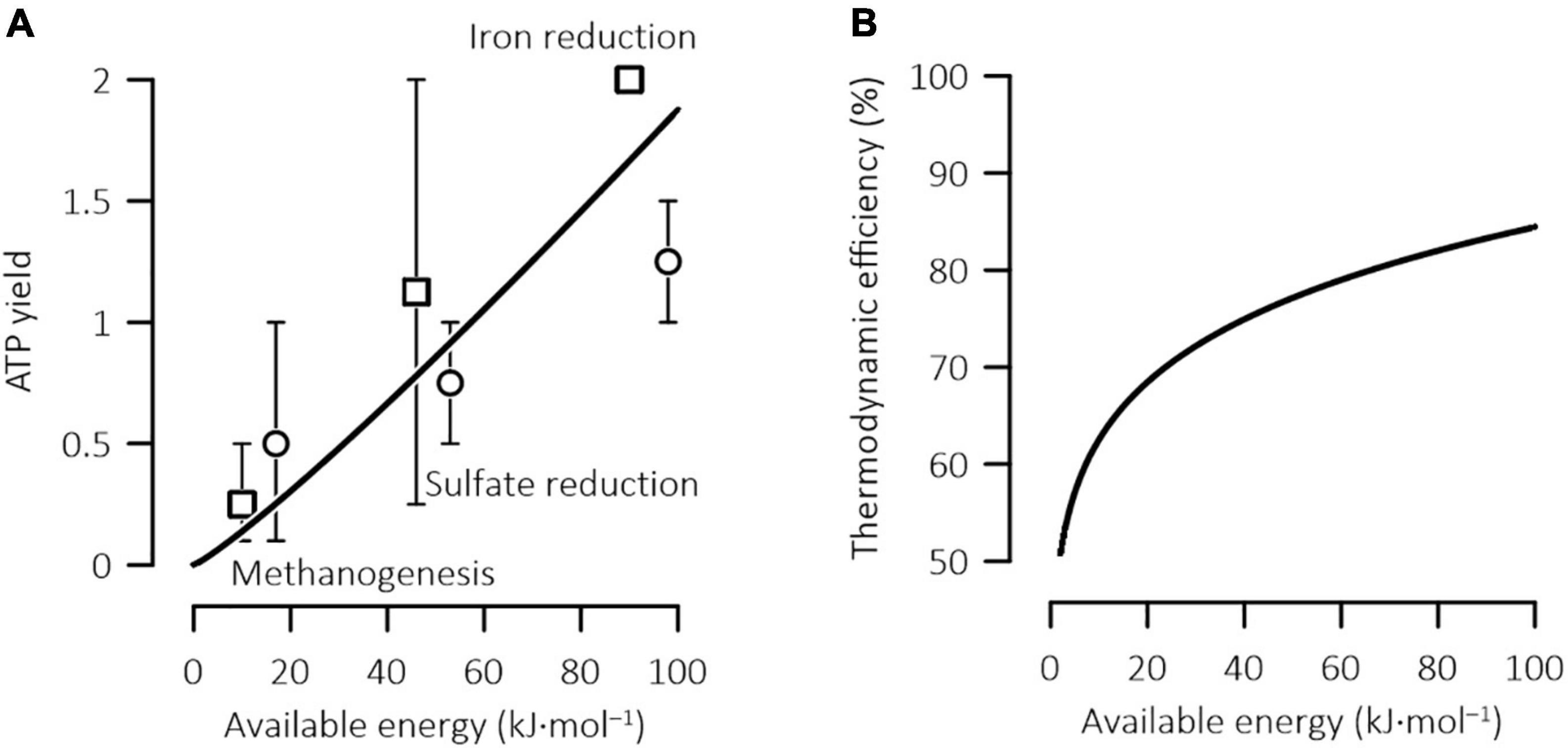
Figure 4. Variations in the ATP yield (A) and thermodynamic efficiency (B) of microbial iron reduction, sulfate reduction, and methanogenesis with the energy available in the environment. The available energy is expressed in terms of one mole of acetate or four moles of H2; solid lines are calculated according to Eqs 20, 21; data points are the ATP yields and available energies estimated previously (□, hydrogenotrophic; ○, acetotrophic), and error bars show the ranges of the estimated values (Jin, 2012).
Lake Sediments
To illustrate how to use the acclimation model to simulate methanogenesis in natural environments, we constructed a reactive transport model of microbial metabolisms in the profundal sediments of Lake Constance, a large mesotrophic prealpine lake in Germany (Schulz and Conrad, 1996; Rothfuss et al., 1997). The sediments host a relatively simple network of microbial reactions (Figure 5). Specifically, fermenting microbes degrade organic carbon and produce acetate that serves as the electron donor for aerobic respiring microbes and methanogens. Aerobic respirers live only in the top few millimeters, but methanogens appear across most of the sediment depths (Frenzel et al., 1990; Rothfuss et al., 1997). Chemical profiles and in situ rate measurements indicate that methanogenesis is dominated by acetoclastic pathway, and acetate consumption by sulfate reducers and other respires are only of secondary importance (Bak and Pfennig, 1991).
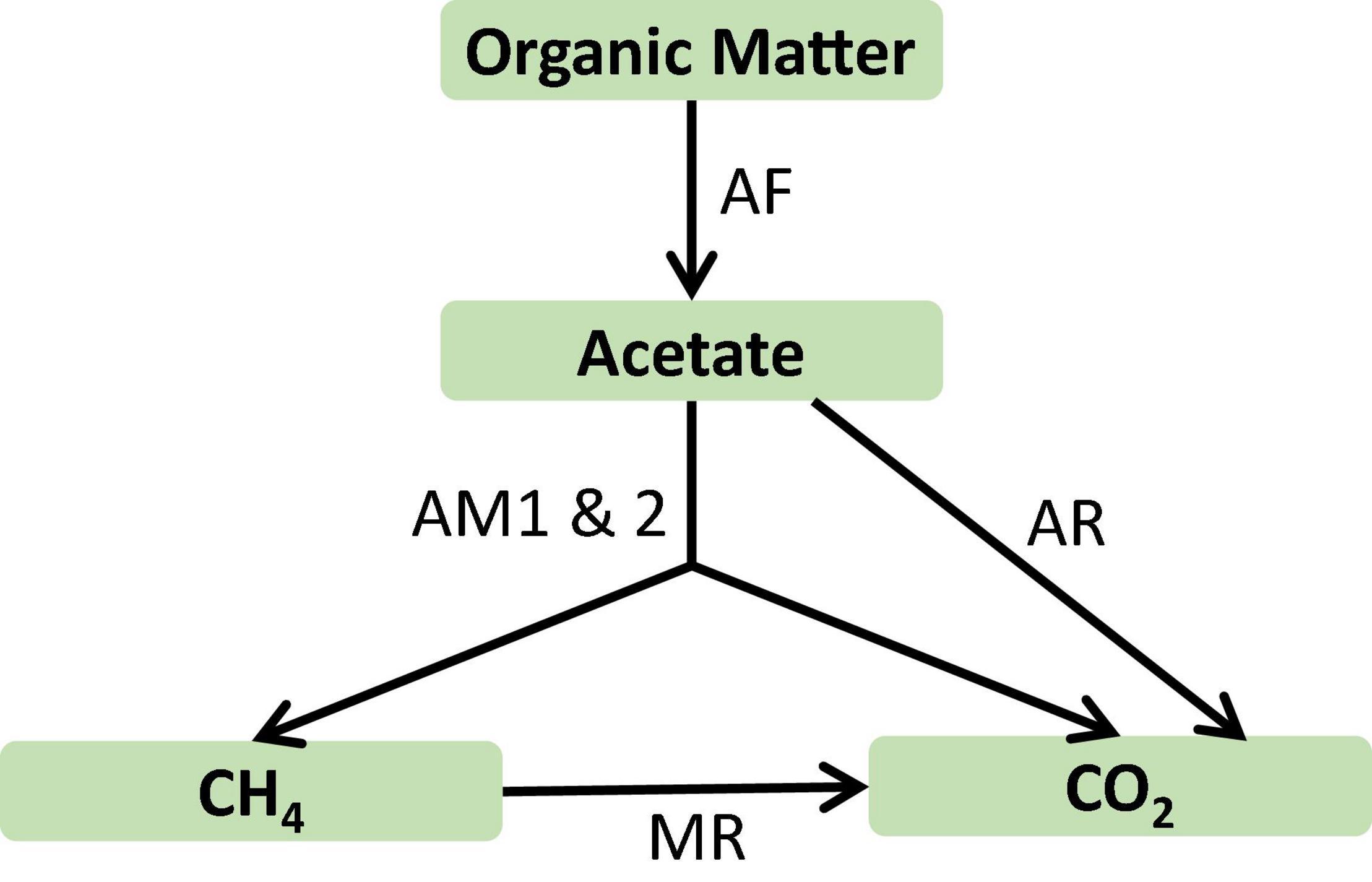
Figure 5. Microbial reaction network in the profundal sediments of Lake Constance, Germany. AF, acetate production from organic carbon by fermenting microbes; AM1 and 2, acetoclastic methanogenesis by Methanosarcina and Methanosaeta, respectively; AR, acetate oxidation by aerobic respiration; MR, methane oxidation by aerobic respiration.
Model Construction
The reactive transport model describes how microbial metabolisms affect the distribution of chemical compounds across different sediment depths. In light of the absence of significant bioturbation and the slow sedimentation rate of ∼0.1 cm a–1 (Rothfuss et al., 1997), we considered diffusion and describe the transport of a reactive compound A, e.g., dissolved dioxygen, acetate, dissolved inorganic carbon (DIC), or methane, according to
Here CA is the molal concentration in the porewater, DA is the diffusion coefficient, rA is the rate (mol cm–3 s–1) at which A is added to (positive) or removed from (negative) the pore fluid by microbial reactions, expressed per unit volume of fluid-saturated sediment, and ϕ is sediment porosity. Rate rA is determined by the metabolisms of four microbial groups, including fermenters, aerobic respirers, and two acetoclastic methanogens – Methanosaeta and Methanosarcina. For example, acetate is added into the pore fluid by organic carbon fermentation, and removed by aerobic respirers and the two methanogens. As another example, methane is produced by the two methanogens and, at the same time, consumed by aerobic respirers.
We assumed that acetate production from organic carbon degradation proceeds at a uniform rate across different sediment depths. This assumption is based on the observations that the sedimentation rate in the lake has remained approximately constant since 1900 (Dominik et al., 1981) and that between 8 and 20 cm sediment depth, total organic carbon content decreases linearly with depth (Kappler et al., 2001). The assumption is also consistent with the observations that in the littoral sediments of the lake, both acetate concentrations and turnover rates remain relatively constant in the upper 20 cm of the sediments (Thebrath et al., 1993). Other models for organic carbon degradation, such as the first-order one-G model, fail in obtaining satisfactory results (see Supplementary Material).
We computed the rates of methanogenesis by combining the autocatalytic model (Eqs 1–7) with the acclimation model (Eqs 16, 18, and 20). Methanogenesis rate in the sediments varies with temperature (Thebrath et al., 1993). The rate reaches its maximum value at 30°C. At the in situ temperature of 4°C, the rate is only ∼7% of the maximum value. Considering that most methanogen kinetic parameters were obtained by using laboratory experiments at temperatures optimal for methanogen growth, between 30 and 37°C (see Supplementary Table 1), we assumed that microbial rates in the sediments are 7% of those calculated with the kinetic parameters of laboratory cultures. Evaluating the biomass capacity factor FX in Eq. 6 requires the maximum biomass concentration supported by the environment. In the sediments, the cell counts of acetoclastic methanogens, determined with the method of most probable number (MPN), is 2.0 × 103 per ml of sediments (Rothfuss et al., 1997). By taking the dry weight per cell as 10–12 g, the biomass concentration of methanogens is 2.0 × 10–9 g cm–3. Assuming that the MPN method underestimates by a factor of 100 (Asakawa et al., 1998), we set the maximum biomass concentration of methanogens at 0.5 μg cm–3.
We computed the rates of aerobic respiration by accounting for the concentrations of both electron donors and dissolved dioxygen (see Supplementary Material). We also set the specific decay rates of the different microbes at 10–8 s–1 (Price and Sowers, 2004). In this way, the model has only one free parameter – the rate of acetate production, which was estimated by fitting the simulation results to the concentration profiles observed for acetate and methane (Figures 6A,B; Frenzel et al., 1990; Schulz and Conrad, 1995).
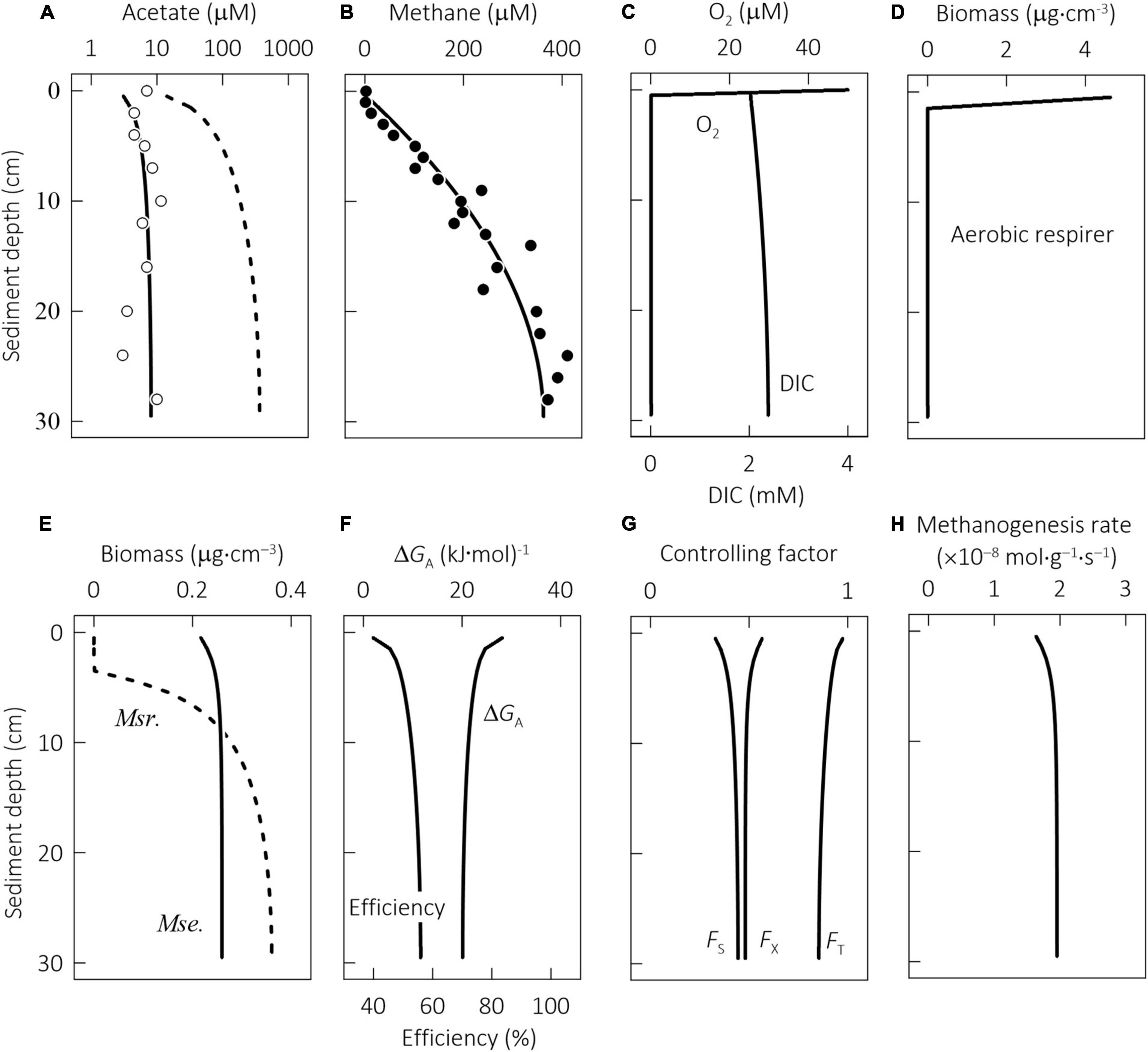
Figure 6. Results at steady state of a reactive transport model constructed for microbial metabolisms in the profundal sediments of Lake Constance, Germany, showing along the sediment depth the concentrations of acetate (A), methane (B), dioxygen (O2), dissolved inorganic carbon (DIC, C), biomass of aerobic respirer (D), Methanosarcina (Msr.) and Methanosaeta (Mse., E), the available energy, the thermodynamic efficiency (F), the kinetic factor of acetate FS, the thermodynamic potential factor FT, the biomass capacity factor FX (G), and methanogenesis rate per unit biomass (H). Data points are the results of previous field investigations with samples recovered from the deepest part of the lake at 143 m depth (Schulz and Conrad, 1995); solid lines are the simulation results that track methanogenesis and growth by combining the autocatalytic model (Eqs 1–7) with the acclimation model (Eqs 16, 18, 20); dashed lines are the simulation results of the autocatalytic model without accounting for physiological acclimation.
We used PHREEQC to integrate numerically the model over time from arbitrary initial conditions and to solve for the apparent steady-state distribution of pore-water chemistry and biomass concentrations in the sediment column. We ran the reactive transport simulation forward for 500 years, more than the period of 100 years required for the simulation results to stabilize. Details of how we constructed the model, the kinetic and thermodynamic parameters of aerobic respirers, and the input file are available in Supplementary Material.
Simulation Results
The steady-state model solutions reproduce well the profiles of methane and acetate in the sediment column (Figures 6A,B). The rate of acetate production was estimated at 5.0 × 10–12 M s–1, close to the rate of 3.3 × 10–12 M s–1 applied previously to the bottom sediments of Lake Washington, Washington, United States (Jin and Bethke, 2009).
In the simulation results (Figure 6), acetate concentration is kept low, i.e., <10 μM, but methane concentration increases from near 0 at the sediment–water interface to ∼400 μM ∼30 cm below the interface. These results can be accounted for by acetoclastic methanogenesis. The acetate consumption and growth of aerobic respirers are limited because dioxygen disappears within the top 1 cm of the sediments. The model considers both Methanosarcina and Methanosaeta, but only Methanosaeta survives (Figure 6E). These results are in agreement with the observations that Methanosaeta dominates acetoclastic methanogenesis in natural environments (Smith and Ingram-Smith, 2007).
Physiological acclimation plays a significant role in the kinetic properties of Methanosaeta. Within the sediment column, acetate concentrations stay small, from 4 μM near the sediment–water interface to 10 μM at 30 cm below the interface. By acclimating to these concentrations, Methanosaeta acquires a rate constant of ∼7.2 × 10–10 mol g–1 s–1 and its half-saturation constant ranges from 6 to 10 μM, much smaller than the respective values of the laboratory cultures (see Table 1). In comparison, the effect of acclimation on the ATP and biomass yields may not be obvious. The available energy from reaction 8 is greatest, ∼30 kJ⋅(mol CH4)–1, at the sediment–water interface and decreases only slightly downward (Figure 6F). At 30 cm depth, the available energy decreases to 20 kJ⋅(mol CH4)–1. Under these conditions, the ATP yield stays at the value of Methanosaeta laboratory cultures, i.e., 0.27 per methane, and so does the biomass yield, which is 1.3 g⋅(mol CH4)–1. As a result, the thermodynamic efficiency increases from ∼40% near the sediment–water interface to close to 56% at 30 cm depth.
The reactive transport model considers the control of methanogenesis rates by the temperature, acetate concentration, and chemical energy of the environment (Figure 6G). The most significant control comes from temperature: the in situ temperature of 4°C lowers the rates by more than one order of magnitude. In comparison, kinetic factor FS accounts for acetate concentrations, and its value increases from 0.3 at the sediment–water interface to 0.4 at 30 cm depth, indicating that acetate concentrations lower methanogenesis rate from the maximum value by more than 50%. The thermodynamic factor FT accounts for the available energy, and its value decreases from near unity at the interface to 0.85 at 30 cm depth, which suggests that due to the thermodynamic limitation, the rate is further lowered by <15%. Taken together, the three factors lower the rate by two orders of magnitude. Furthermore, due to the opposite trends of the kinetic and thermodynamic factors, the methanogenesis rate per unit biomass only increases slightly with depth, from 1.6 × 10–8 mol g–1 s–1 at the interface to 1.9 × 10–8 mol g–1 s–1 at 30 cm depth (Figure 6H).
Microbial growth depends on the availability of environmental resources, which is accounted for by the biomass capacity factor FX. According to the simulation results (Figure 6G), the biomass factor is the largest, 0.57, at the sediment–water interface, and decreases slightly to 0.48 at the depth of 30 cm, which suggests that the environmental resources limit the rate of methanogen growth by ∼50%. Combing the methanogenesis rate per unit biomass with the biomass factor FX and biomass yield YX gives the specific rates of biomass synthesis of 10–8 s–1 across different sediment depths (Eq. 6), the same value assumed for the specific decay rate. These results confirm that methanogen growth in the sediments reaches a steady state. Considering the empirical nature of the biomass factor and the potential importance of the external resources, future research is required to identify the limiting resources and how they affect methanogen growth in the sediments.
Our simulation results highlight the gap between the kinetics of laboratory cultures and natural methanogens, and resonate with the consensus that laboratory observations cannot be directly applied to natural environments (Jin et al., 2013). If we neglected physiological acclimation and applied the parameter values of laboratory cultures directly to the sediments, we would arrive at different results. For example, we could achieve a reasonable fit to the concentration profile of methane by raising the acetate production rate to 1.2 × 10–11 M s–1. However, the simulated acetate concentrations would increase from ∼20 μM at the sediment–water interface to >500 μM at 30 cm depth, nearly two orders of magnitude larger than the field observations (Figure 6A). Moreover, no Methanosaeta would survive in the sediments; instead, methanogenesis would be catalyzed by Methanosarcina (Figure 6E). These results contradict the observations that acetate concentrations remained relatively low in the sediments and that Methanosaeta is the major group of acetoclastic methanogens in the environment of low acetate concentrations.
Competitive Exclusion
The predictions of the acclimation model caution the direct application of laboratory observations to natural environments. For example, the dominance of Methanosaeta over Methanosarcina in the environment of low acetate concentrations has been widely accounted for by the kinetic differences between the laboratory cultures of the two methanogens (Min and Zinder, 1989; Jetten et al., 1992; Conklin et al., 2006). According to the competitive exclusion principle, where Methanosaeta and Methanosarcina compete for the limited supply of acetate, only one can survive. At high acetate concentrations, growth rates of the two methanogens depend on their rate constants and biomass yields. Methanosarcina laboratory cultures have a larger rate constant and a larger biomass yield, and hence can grow faster than Methanosaeta cultures (Table 1). At low acetate concentrations, the smaller half-saturation constant and the larger affinity constant of Methanosaeta cultures confer to competitive fitness, which drives Methanosarcina out of the environment.
The results of our data compilation suggest that laboratory observations alone are not sufficient to account for the dominance of Methanosaeta. Figures 7A,B show, according to the parameters of laboratory cultures (see Table 1), how the rates of methanogenesis and biomass synthesis of Methanosarcina and Methanosaeta vary with acetate concentrations. At acetate concentrations above 0.6 mM, Methanosarcina has larger methanogenesis rates, while Methanosaeta has larger methanogenesis rates at lower concentrations. However, the biomass yield of Methanosarcina laboratory cultures double the yield of Methanosaeta cultures and, as a result, Methanosarcina cultures always grow faster than Methanosaeta. Even at 1 μM acetate, the biomass synthesis of Methanosarcina should be 13% faster than that of Methanosaeta. These predictions are manifested in the above simulation results (Figures 6A,E). By applying the kinetic and thermodynamic parameters of the pure cultures without accounting for physiological acclimation, the model fails to reproduce the concentration profile of acetate and the dominance of Methanosaeta in the sediments.

Figure 7. Variations with acetate concentration in the rates of methanogenesis (A) and biomass synthesis per unit biomass (B) calculated according to the autocatalytic model (Eqs 2, 3, 6) and the parameters of laboratory methanogen cultures (see Table 1), and the rates of methanogenesis (C) calculated by combining the autocatalytic model (Eqs 2, 6) with the acclimation model (Eqs 16, 18). In evaluating the autocatalytic model (Eqs 2, 3, 6), the thermodynamic potential factor FT and the biomass capacity factor FX are set to 1, and the specific decay constant D is set at 0.
Our acclimation model offers an alternative account for the dominance of Methanosaeta in low acetate environments. First, where acetate concentration is low, the energy available in the environment also tends to be limited and, as a result, Methanosarcina loses its competitive advantage given by the relatively large biomass yield of its laboratory cultures. According to the predictions of the acclimation model (Eq. 20), the two methanogens adjust their ATP yields and hence biomass yields in accordance with the energy available in the environment. At available energy <18 kJ mol–1, both organisms are predicted to have the same biomass yields (Figure 3A). Second, by acclimating to low acetate concentrations, Methanosaeta raises its affinity constant and hence biomass synthesis rate quicker than Methanosarcina (Figure 7C). At <0.18 mM acetate, Methanosaeta drives methanogenesis and grows faster than Methanosarcina. These model predictions have been confirmed by the steady-state simulation results (Figure 6): by considering the acclimation of methanogens to both acetate concentration and available energy, Methanosaeta wins the competition against Methanosarcina in the sediments of relatively low acetate concentrations. From these results, we suggest that in applying the competitive exclusion principle to natural environments, we should consider how physiological acclimation affects the kinetic and thermodynamic parameters of microbes.
To further illustrate how physiological acclimation affects the outcome of methanogen competition, we repeated the above simulations by applying different rates of acetate production. Figure 8 shows, according to the simulation results, how acetate concentration in the porewater and the biomass concentrations of the two methanogens vary with the rate of acetate production. Where acetate production rate is <1.1 × 10–11 M s–1, acetate concentration, averaged over the depth, remains at <75 ± 40 μM, no Methanosarcina survives in the sediments, and methanogenesis is dominated by Methanosaeta. At acetate production rate over 5.0 × 10–11 M s–1, acetate concentration increases above 1.1 ± 0.5 mM, and Methanosarcina becomes dominant. At acetate production rate between 1.1 × 10–11 and 5.0 × 10–11 M s–1, Methanosarcina and Methanosaeta co-exist, which contradicts the principle of competitive exclusion. In lake sediments, acetate concentrations vary with trophic states, and appear to be too low to support Methanosarcina as the main driver of acetoclastic methanogenesis. For example, in the bottom sediments of Wintergreen Lake, a hypereutrophic lake in Michigan, United States, acetate concentration is ~100 μM (Lovley and Klug, 1982). In the bottom sediments of Lake Vechten, a mesotrophic in Netherlands, acetate concentration is ∼10 μM (Graaf et al., 1996). Likewise, in aquifers (Jakobsen and Postma, 1999; Hansen et al., 2001), where acetate concentrations are kept below 100 μM, Methanosaeta should also dominate the pathway of acetoclastic methanogenesis.
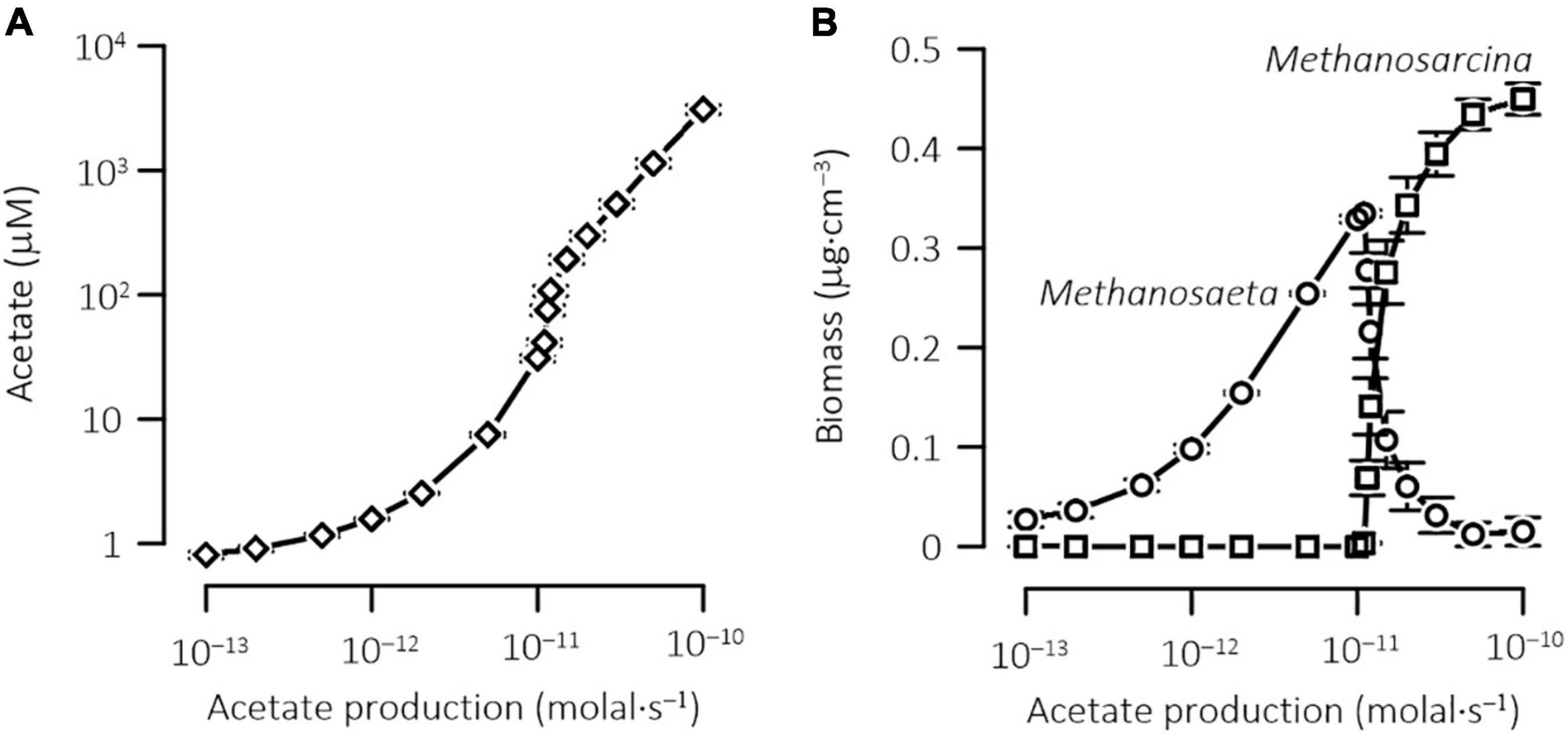
Figure 8. Results at steady state of the reactive transport model, showing the variations in the concentrations of acetate (A) and biomass (B) with the rates of acetate production in the sediments. Data points are the means over the sediment depth; error bars show standard error of the mean.
Discussion
The modeling and analysis presented here suggest that microbes should be described not only as autocatalysts but also as self-adapting catalysts, capable of modifying their kinetic and thermodynamic parameters in accordance with the conditions of ambient environments. Previous efforts have considered the variations of microbial kinetic parameters with the temperature, pH, and nutrient concentrations of the environment (Aksnes and Cao, 2011; Smith et al., 2011, 2014; Fiksen et al., 2013). Our model extends these efforts by considering the substrate concentration and the energy available in the environment. Specifically, we accounted for two mechanisms of physiological acclimation. One is the allocation of intracellular metabolic resources between the two competing metabolic reactions, i.e., the rate-determining steps at relatively low and relatively large substrate concentrations. The other is the partition of the energy available in the environment between the thermodynamic drive and the energy conservation of microbial catabolism. The model builds on the assumption that physiological acclimation is instantaneous, and relates microbial parameters to the substrate concentration and the available energy of the environment, without considering the time duration of physiological acclimation. The model predicts that methanogens acclimate to low available energies by decreasing their ATP yields, and acclimate to low acetate concentrations by lowering their rate constants and half-saturation constants and by raising their affinity constants.
We applied the acclimation model to acetoclastic methanogenesis in lake sediments. The results illustrate that the acclimation model brings about two improvements to the simulation of methanogenesis in natural systems. First, computing microbial rates requires a series of kinetic and thermodynamic parameters. However, directly determining the parameter values of natural microbes is challenging, due to the technical difficulties in differentiating live cells of interest from metabolically inactive ones, in attributing bulk chemical fluxes to microbial groups of interest, and in measuring low chemical fluxes with acceptable accuracy (Shapiro et al., 2018). The acclimation model meets the need by extrapolating the kinetic and thermodynamic parameters of laboratory cultures to natural environments.
Second, the acclimation model simplifies the relationship between the thermodynamics and kinetics of microbial reactions. Thermodynamic control is a key factor of microbial kinetics, especially in anoxic environments, where chemical energies are often limited (Jin and Bethke, 2007, 2009). Evaluating the thermodynamic control requires ATP yield, the value of which is only available to a few well-studied laboratory cultures. Moreover, the efficiency of microbial energy conservation may not be constant, and hence the values of laboratory cultures may not be directly applicable to natural environments. By assuming that microbes optimize the energy partition between thermodynamic drive and energy conservation, we can approximate the ATP yield as a function of the available energy, reducing the number of parameters in the thermodynamic factor. Such simplification is especially useful for microbes whose pathways of energy conservation have yet to be determined.
Our model application focused on acetoclastic methanogens, but the model predictions do shed new light on other microbes. For example, according to the relationship between the optimal ATP yield and the available energy (Eq. 20), different microbes may have very different thermodynamic efficiencies of energy conservation. In natural environments, common microbial reactions include syntrophic oxidation of acetate and other short-chain fatty acids, methanogenesis, sulfate reduction, and iron reduction. While syntrophic reactions often proceed close to thermodynamic equilibrium (Jin and Kirk, 2016, 2018b), the reduction of ferric minerals can release as much as ∼100 kJ of energy by consuming one mole acetate (Jin, 2012). Correspondingly, the efficiency of these anaerobic processes can vary from close to 50% to as high as 85% (Figure 4B).
As a second example, our results highlight the importance of physiological acclimation in predicting the outcome of microbial interactions. Current paradigm accounts for the niche separation between Methanosarcina and Methanosaeta with the kinetic properties of laboratory cultures (Min and Zinder, 1989; Conklin et al., 2006), which does not stand up to scrutiny. Our modeling results attribute the niche separation to the different acclimation responses of the two methanogens, which enable Methanosaeta to dominate in the environment of <∼0.2 mM acetate. Therefore, in exploring the outcome of other microbial interactions, such as redox zonation or the segregation of aerobic respiration, ferric iron reduction, sulfate reduction, and methanogenesis (Bethke et al., 2008), we may need to consider the role of physiological acclimation.
In summary, our results illustrate an important principle of microbial kinetics – microbes should be described not only as autocatalysts but also as self-adapting catalysts. The former is accounted for by standard microbial rate laws (Eqs 2, 6), but the latter feature requires additional models, such as the acclimation model presented here, that relate microbial parameters to the conditions of the ambient environment (e.g., Eqs 16–18, 20). Our acclimation model extrapolates laboratory observations to natural environments by balancing the trade-offs associated with cellular resource allocation and microbial energy conservation, and provides a useful approach to estimate microbial kinetic and thermodynamic parameters in natural environments. We focused on acetoclastic methanogens here, but the approach should be applicable to sulfate reducing microbes and others. By doing so, we hope to bridge the gap between microbial kinetics in laboratory experiments and natural environments, and to improve the understanding and prediction of microbial processes of environmental significance.
Data Availability Statement
The data that support the results of this study are available in the Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
QW carried out the analysis. MG collected the methanogen parameters. QJ designed the project. All authors contributed to the article and approved the submitted version.
Funding
This research was funded by NASA under Grant NNX16AJ59G and by NSF under Award EAR-1636815 and 1753436.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2022.838487/full#supplementary-material
References
Aksnes, D. L., and Cao, F. J. (2011). Inherent and apparent traits in microbial nutrient uptake. Mar. Ecol. Prog. Series 440, 41–51. doi: 10.3354/meps09355
Andrews, J. H., and Harris, R. F. (1986). “r- and K-selection and microbial ecology,” in Advances in Microbial Ecology, ed. K. C. Marshall (Boston, MA: Springer).
Asakawa, S., Akagawa-Matsushita, M., Koga, Y., and Hayano, K. (1998). Communities of methanogenic bacteria in paddy field soils with long-term application of organic matter. Soil Biol. Biochem. 30, 299–303.
Bak, F., and Pfennig, N. (1991). Microbial sulfate reduction in littoral sediment of Lake Constance. FEMS Microbiol. Lett. 85, 31–42. doi: 10.3389/fmicb.2019.00247
Beer, J., Lee, K., Whiticar, M., and Blodau, C. (2008). Geochemical controls on anaerobic organic matter decomposition in a northern peatland. Limnol. Oceanography 53, 1393–1407. doi: 10.4319/lo.2008.53.4.1393
Bethke, C. M., Ding, D., Jin, Q., and Sanford, R. A. (2008). Origin of microbiological zoning in groundwater flows. Geology 36, 739–742. doi: 10.1130/g24859a.1
Brown, C. J., Schoonen, M. A. A., and Candela, J. L. (2000). Geochemical modeling of iron, sulfur, oxygen and carbon in a coastal plain aquifer. J. Hydrol. 237, 147–168. doi: 10.1016/s0022-1694(00)00296-1
Button, D. K. (1993). Nutrient-limited microbial growth kinetics. Antonie von Leeuwenhoek 63, 225–235. doi: 10.1007/BF00871220
Carr, S. A., Schubotz, F., Dunbar, R. B., Mills, C. T., Dias, R., Summons, R. E., et al. (2018). Acetoclastic Methanosaeta are dominant methanogens in organic-rich Antarctic marine sediments. ISME J. 12, 330–342. doi: 10.1038/ismej.2017.150
Casey, J. R., and Follows, M. J. (2020). A steady-state model of microbial acclimation to substrate limitation. PLoS Comp. Biol. 16:e1008140. doi: 10.1371/journal.pcbi.1008140
Collos, Y., Vaquer, A., and Souchu, P. (2005). Acclimation of nitrate uptake by phytoplankton to high substrate levels. J. Phycol. 41, 466–478. doi: 10.3389/fmicb.2016.01310
Conklin, A., Stensel, H. D., and Ferguson, J. (2006). Growth kinetics and competition between Methanosarcina and Methanosaeta in mesophilic anaerobic digestion. Water Environ. Res. 78, 486–496. doi: 10.2175/106143006x95393
Conrad, R., Noll, M., Claus, P., Klose, M., Bastos, W. R., et al. (2011). Stable carbon isotope discrimination and microbiology of methane formation in tropical anoxic lake sediments. Biogeosciences 8, 795–814. doi: 10.5194/bg-8-795-2011
Dominik, J., Mangini, A., and Müller, G. (1981). Determination of recent deposition rates in Lake Constance with radioisotopic methods. Sedimentology 28, 653–677. doi: 10.1111/j.1365-3091.1981.tb01927.x
Douglas, S., and Beveridge, T. J. (1998). Mineral formation by bacteria in natural microbial communities. FEMS Microbiol. Ecol. 26, 79–88. doi: 10.1111/j.1574-6941.1998.tb00494.x
Dunfield, P. F., and Conrad, R. (2000). Starvation alters the apparent half-saturation constant for methane in the type II methanotroph Methylocystis strain LR1. Appl. Environ. Microbiol. 66, 4136–4138. doi: 10.1128/AEM.66.9.4136-4138.2000
Fiksen, Ø, Follows, M. J., and Aksnes, D. L. (2013). Trait-based models of nutrient uptake in microbes extend the Michaelis-Menten framework. Limnol. Oceanography 58, 193–202. doi: 10.4319/lo.2013.58.1.0193
Flemming, H.-C., and Wuertz, S. (2019). Bacteria and archaea on Earth and their abundance in biofilms. Nat. Rev. Microbiol. 17, 247–260. doi: 10.1038/s41579-019-0158-9
Flynn, K. J., St John, M., Raven, J. A., Skibinski, D. O. F., Allen, J. I, Mitra, A., et al. (2015). Acclimation, adaptation, traits and trade-offs in plankton functional type models. J. Plankton Res. 37, 683–691. doi: 10.1093/plankt/fbv036
Frenzel, P., Thebrath, B., and Conrad, R. (1990). Oxidation of methane in the oxic surface layer of a deep lake sediment (Lake Constance). FEMS Microbiol. Ecol. 6, 149–158.
Friedrich, M., Takács, I., and Tränckner, J. (2015). Physiological adaptation of growth kinetics in activated sludge. Water Res. 85, 22–30. doi: 10.1016/j.watres.2015.08.010
Galand, P. E., Fritze, H., Conrad, R., and Yrjälä, K. (2005). Pathways for methanogenesis and diversity of methanogenic archaea in three boreal peatland ecosystems. Appl. Environ. Microbiol. 71, 2195–2198. doi: 10.1128/AEM.71.4.2195-2198.2005
Graaf, W. D., Wellsbury, P., Parkes, R. J., and Cappenberg, T. E. (1996). Comparison of acetate turnover in methanogenic and sulfate-reducing sediments by radiolabeling and stable isotope labeling and by use of specific inhibitors. Appl. Environ. Microbiol. 62, 772–777. doi: 10.1128/aem.62.3.772-777.1996
Hansen, L. K., Jakobsen, R., and Postma, D. (2001). Methanogenesis in a shallow sandy aquifer, Rømø, Denmark. Geochim. Cosmochim. Acta 65, 2925–2935.
Healey, F. P. (1980). Slope of the Monod equation as an indicator of advantage in nutrient competition. Microbial Ecol. 5, 281–286. doi: 10.1007/BF02020335
Huser, B. A., Wuhrmann, K., and Zehnder, A. J. B. (1982). Methanothrix soehngenii gen. nov. sp. nov., a new acetotrophic non-hydrogen-oxidizing methane bacterium. Arch. Microbiol. 132, 1–9.
Jakobsen, R., and Postma, D. (1999). Redox zoning, rates of sulfate reduction and interactions with Fe-reduction and methanogenesis in a shallow sandy aquifer, Romo, Denmark. Geochimica Cosmochimica Acta 63, 137–151.
Jetten, M. S. M., Stams, A. J. M., and Zehnder, A. J. B. (1992). Methanogenesis from acetate. FEMS Microbiol. Rev. 88, 181–198.
Jin, Q., and Bethke, C. M. (2002). Kinetics of electron transfer through the respiratory chain. Biophys. J. 83, 1797–1808.
Jin, Q., and Bethke, C. M. (2003). A new rate law describing microbial respiration. Appl. Environ. Microbiol. 69, 2340–2348. doi: 10.1128/AEM.69.4.2340-2348.2003
Jin, Q., and Bethke, C. M. (2007). The thermodynamics and kinetics of microbial metabolism. Am. J. Sci. 307, 643–677. doi: 10.2475/04.2007.01
Jin, Q., and Bethke, C. M. (2009). Cellular energy conservation and the rate of microbial sulfate reduction. Geology 36, 739–742.
Jin, Q., and Kirk, M. F. (2016). Thermodynamic and kinetic response of microbial reactions to high CO2. Front. Microbiol. 7:1696. doi: 10.3389/fmicb.2016.01696
Jin, Q., and Kirk, M. F. (2018a). pH as a primary control in environmental microbiology. Front. Environ. Sci. 6:21. doi: 10.3389/fenvs.2018.00021
Jin, Q., and Kirk, M. F. (2018b). pH as a primary control in environmental microbiology. Front. Environ. Sci. 6:101. doi: 10.3389/fenvs.2018.00101
Jin, Q., and Roden, E. E. (2011). Microbial physiology-based model of ethanol metabolism in subsurface sediments. J. Contaminant Hydrol. 125, 1–12. doi: 10.1016/j.jconhyd.2011.04.002
Jin, Q., Roden, E. E., and Giska, J. R. (2013). Geomicrobial kinetics. Geomicrobiol. J. 30, 173–185. doi: 10.1080/10934529.2014.937162
Kappler, A., Ji, R., Schink, B., and Brune, A. (2001). Dynamics in composition and size-class distribution of humic substances in profundal sediments of Lake Constance. Organ. Geochem. 32, 3–10. doi: 10.1016/s0146-6380(00)00160-1
Kovárová-Kovar, K., and Egli, T. (1998). Growth kinetics of suspended microbial cells. Microbiol. Mol. Biol. Rev. 62, 646–666. doi: 10.1128/MMBR.62.3.646-666.1998
Kurade, M. B., Saha, S., Salama, E.-S., Patil, S. M., Govindwar, S. P., et al. (2019). Acetoclastic methanogenesis led by Methanosarcina in anaerobic co-digestion of fats, oil and grease for enhanced production of methane. Bioresource Technol. 272, 351–359. doi: 10.1016/j.biortech.2018.10.047
Lansdown, J. M., Quay, P. D., and King, S. L. (1992). CH4 production via CO2 reduction in a temperate bog. Geochim. Cosmochim. Acta 56, 3493–3503. doi: 10.1016/0016-7037(92)90393-w
Lee, H. J., Kim, S. Y., Kim, P. J., Madsen, E. L., and Jeon, C. O. (2014). Methane emission and dynamics of methanotrophic and methanogenic communities in a flooded rice field ecosystem. FEMS Microbiol. Ecol. 88, 195–212. doi: 10.1111/1574-6941.12282
Leroi, A. M., Bennett, A. F., and Lenski, R. E. (1994). Temperature acclimation and competitive fitness. Proc. Natl. Acad. Sci. U S A. 91, 1917–1921. doi: 10.1073/pnas.91.5.1917
Litchman, E., Edwards, K. F., and Klausmeier, C. A. (2015). Microbial resource utilization traits and trade-offs. Front. Microbiol. 6:254. doi: 10.3389/fmicb.2015.00254
Litchman, E., Klausmeier, C. A., Schofield, O. M., and Falkowski, P. G. (2007). The role of functional traits and trade-offs in structuring phytoplankton communities. Ecol. Lett. 10, 1170–1181. doi: 10.1111/j.1461-0248.2007.01117.x
Lovley, D. R., and Klug, M. J. (1982). Intermediary metabolism of organic matter in the sediments of a eutrophic lake. Appl. Environ. Microbiol. 43, 552–560. doi: 10.1128/aem.43.3.552-560.1982
Lovley, D. R., and Klug, M. J. (1983). Sulfate reducers can outcompete methanogens at freshwater sulfate concentrations. Appl. Environ. Microbiol. 45, 187–192. doi: 10.1128/aem.45.1.187-192.1983
Mahdinia, E., Liu, S., Demirci, A., and Puri, V. M. (2020). “Microbial growth models,” in Food Safety Engineering, eds A. Demirci, H. Feng, and K. Krishnamurthy (Cham: Springer International Publishing).
McCarthy, J. J., Garside, C., and Nevins, J. L. (1999). Nitrogen dynamics during the Arabian Sea Northeast Monsoon. Deep Sea Res. Part II 46, 1623–1664.
Min, H., and Zinder, S. H. (1989). Kinetics of acetate utilization by two thermophilic acetotrophic methanogens. Appl. Environ. Microbiol. 55, 488–491. doi: 10.1128/aem.55.2.488-491.1989
Murphy, E. M., and Schramke, J. A. (1998). Estimation of microbial respiration rates in groundwater by geochemical modeling constrained with stable isotopes. Geochimica Cosmochimica Acta 62, 3395–3406.
Nirody, J. A., Budin, I., and Rangamani, P. (2020). ATP synthase. J. General Physiol. 152:e201912475.
Offre, P., Spang, A., and Schleper, C. (2013). Archaea in biogeochemical cycles. Annual Rev. Microbiol. 67, 437–457. doi: 10.1146/annurev-micro-092412-155614
Pahlow, M. (2005). Linking chlorophyll-nutrient dynamics to the Redfield N:C ratio with a model of optimal phytoplankton growth. Mar. Ecol. Progress Series 287, 33–43.
Pallud, C., and Van Cappellen, P. (2006). Kinetics of microbial sulfate reduction in estuarine sediments. Geochim. Cosmochimica Acta 70, 1148–1162. doi: 10.1016/j.watres.2016.01.044
Pfeiffer, T., Schuster, S., and Bonhoeffer, S. (2001). Cooperation and competition in the evolution of ATP-producing pathways. Science 292, 504–507. doi: 10.1126/science.1058079
Ponomareva, A. L., Buzoleva, L. S., and Bogatyrenko, E. A. (2018). Abiotic environmental factors affecting the formation of microbial biofilms. Biol. Bull. 45, 490–496.
Prakash, D., Chauhan, S. S., and Ferry, J. G. (2019). Life on the thermodynamic edge. Sci. Adv. 5:eaaw9059.
Price, P. B., and Sowers, T. (2004). Temperature dependence of metabolic rates for microbial growth, maintenance, and survival. Proc. Natl. Acad. Sci. U S A. 101, 4631–4636. doi: 10.1073/pnas.0400522101
Roden, E. E., and Wetzel, R. G. (2002). Kinetics of microbial Fe(III) oxide reduction in freshwater wetland sediments. Limnol. Oceanography 47, 198–211. doi: 10.4319/lo.2002.47.1.0198
Rosso, L., Lobry, J. R., Bajard, S., and Flandrois, J. P. (1995). Convenient model to describe the combined effects of temperature and pH on microbial growth. Appl. Environ. Microbiol. 61, 610–616.
Rothfuss, F., Bender, M., and Conrad, R. (1997). Survival and activity of bacteria in a deep, aged lake sediment (Lake Constance). Microbial Ecol. 33, 69–77. doi: 10.1007/s002489900009
Rousk, J., and Bengtson, P. (2014). Microbial regulation of global biogeochemical cycles. Front. Microbiol. 5:103. doi: 10.3389/fmicb.2014.00103
Schulz, S., and Conrad, R. (1995). Effect of algal deposition on acetate and methane concentrations in the profundal sediment of a deep lake (Lake Constance). FEMS Microbiol. Ecol. 16, 251–259.
Schulz, S., and Conrad, R. (1996). Influence of temperature on pathways to methane production in the permanently cold profundal sediment of Lake Constance. FEMS Microbiol. Ecol. 20, 1–14. doi: 10.1111/j.1574-6941.1996.tb00299.x
Shapiro, B., Hoehler, T. M., and Jin, Q. (2018). Integrating genome-scale metabolic models into the prediction of microbial kinetics in natural environments. Geochim. Cosmochimica Acta 242, 102–122. doi: 10.1021/es203461u
Shaw, A., Takács, I., Pagilla, K. R., and Murthy, S. (2013). A new approach to assess the dependency of extant half-saturation coefficients on maximum process rates and estimate intrinsic coefficients. Water Res. 47, 5986–5994. doi: 10.1016/j.watres.2013.07.003
Smith, K. S., and Ingram-Smith, C. (2007). Methanosaeta, the forgotten methanogen? Trends Microbiol. 15, 150–155. doi: 10.1016/j.tim.2007.02.002
Smith, S. L., and Yamanaka, Y. (2007). Optimization-based model of multinutrient uptake kinetics. Limnol. Oceanography 52, 1545–1558. doi: 10.4319/lo.2007.52.4.1545
Smith, S. L., Merico, A., Wirtz, K. W., and Pahlow, M. (2014). Leaving misleading legacies behind in plankton ecosystem modelling. J. Plankton Res. 36, 613–620. doi: 10.1093/plankt/fbu011
Smith, S. L., Pahlow, M., Merico, A., and Wirtz, K. W. (2011). Optimality-based modeling of planktonic organisms. Limnol. Oceanography 56, 2080–2094. doi: 10.4319/lo.2011.56.6.2080
Smith, S. L., Yamanaka, Y., Pahlow, M., and Oschlies, A. (2009). Optimal uptake kinetics. Mar. Ecol. Prog. Series 384, 1–12.
Soares, M., and Rousk, J. (2019). Microbial growth and carbon use efficiency in soil. Soil Biol. Biochem. 131, 195–205.
Soong, J. L., Fuchslueger, L., Marañon-Jimenez, S., Torn, M. S., Janssens, I. A., Penuelas, J., et al. (2020). Microbial carbon limitation. Global Change Biol. 26, 1953–1961.
Tarpgaard, I. H., Jørgensen, B. B., Kjeldsen, K. U., and Røy, H. (2017). The marine sulfate reducer Desulfobacterium autotrophicum HRM2 can switch between low and high apparent half-saturation constants for dissimilatory sulfate reduction. FEMS Microbiol. Ecol. 93, 1–11.
Thebrath, B., Rothfuss, F., Whiticar, M. J., and Conrad, R. (1993). Methane production in littoral sediment of Lake Constance. FEMS Microbiol. Ecol. 11, 279–289. doi: 10.1016/S0168-6496(03)00260-5
Welte, C., and Deppenmeier, U. (2013). Bioenergetics and anaerobic respiratory chains of aceticlastic methanogens. Biochim. Biophys. Acta 1837, 1130–1147. doi: 10.1016/j.bbabio.2013.12.002
Whitman, W. B., Bowen, T. L., and Boone, D. R. (2014). “The Methanogenic bacteria,” in The Prokaryotes, eds E. Rosenberg, E. F. DeLong, S. Lory, E. Stackebrandt, and F. Thompson (Berlin: Springer).
Wilson, R. S., and Franklin, C. E. (2002). Testing the beneficial acclimation hypothesis. Trends Ecol. Evol. 17, 66–70.
Wu, Q., Ye, R., Bridgham, S. D., and Jin, Q. (2021). Limitations of the Q10 coefficient for quantifying temperature sensitivity of anaerobic organic matter decomposition. J. Geophys. Res. 126:e2021JG006264.
Keywords: acclimation, Methanosarcina, Methanosaeta, microbial kinetics, Monod equation, trade off, competitive exclusion
Citation: Wu Q, Guthrie MJ and Jin Q (2022) Physiological Acclimation Extrapolates the Kinetics and Thermodynamics of Methanogenesis From Laboratory Experiments to Natural Environments. Front. Ecol. Evol. 10:838487. doi: 10.3389/fevo.2022.838487
Received: 17 December 2021; Accepted: 28 February 2022;
Published: 04 April 2022.
Edited by:
Christof Meile, University of Georgia, United StatesReviewed by:
Christopher Kenneth Algar, Marine Biological Laboratory (MBL), United StatesAdrian Mellage, University of Tübingen, Germany
Copyright © 2022 Wu, Guthrie and Jin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qusheng Jin, cWppbkB1b3JlZ29uLmVkdQ==
 Qiong Wu
Qiong Wu Megan J. Guthrie
Megan J. Guthrie Qusheng Jin
Qusheng Jin