A new development algorithm for permeability prediction: A new milestone

Permeability is one of the most important reservoir rock parameters in petroleum engineering, reservoir, and exploitation. This parameter causes the movement of hydrocarbon reserves in the reservoir rock. Therefore, it is an important parameter from the economic point of view because it greatly impacts the amount of extraction from the reservoir rock. In this study, the combined RBFNN-GA algorithm and 200 data sets collected from a field in the Middle East were used to predict permeability. Water saturation, porosity, and specific surface are the input variables used in this study. GA has advantages such as solving complex optimization problems of continuous functions and multi-objective problems. The advantages of RBF neural networks are that they are easy to design, strongly tolerant to input noise, and have good generalization. The RBFNN-GA model has the advantages of both algorithms. RBFNN-GA algorithm and experimental models have been compared in terms of performance accuracy. The results show that RBFNN-GA with STD = 89.8 and R-square = 0.9011 for the total data set obtained from a field in the Middle East has better accuracy and performance in predicting permeability than experimental models. Compared to other neural network methods, the RBFNN-GA model has a higher performance accuracy and is efficient for predicting other parameters. Oil researchers and engineers can use this method to predict other parameters in their studies and research.

Introduction

Permeability is defined as the ability of the porous rock to move oil and gas (Olatunji et al., 2014). Permeability can be considered one of the most important characteristics of reservoir rock because it indicates the volume of pore fluid and its ability to move (Tabasi et al., 2022). The presence of hydrocarbon resources in reservoirs becomes very important when these resources reach the well for harvesting (Beheshtian et al., 2022; Jafarizadeh et al., 2022; Zhang et al., 2022; Rajabi et al., 2022c); permeability is the factor that enables the movement of hydrocarbon resources in the rock (Rajabi et al., 2022d); therefore, in petroleum engineering, permeability is very important because of production or determines the unproductiveness of the reservoir rock (Rajabi et al., 2022c). Permeability is an important parameter from an economic point of view because it greatly impacts the amount of extraction from the reservoir rock (Rajabi et al., 2022b). Porosity, the geometric shape of the holes, and the connection between them affect the permeability value. The effect of porosity on permeability is done by using macro and microstructures. It is important because it is an important parameter for reservoir modeling based on field development programs (Lideng et al., 2019; Zhong et al., 2019; Liu et al., 2020; Rajabi et al., 2022a). One of the important petrophysical properties is permeability, which is one of the reservoir’s most important properties and plays a significant role in reservoir evaluation, such as reservoir numerical simulation, drilling planning, reservoir quality mapping, and reservoir engineering calculations (Rajabi et al., 2021; Gao et al., 2022). Permeability, as the most important characteristic of hydrocarbon flows, plays an important role in describing hydrocarbon reserves, and its prediction is necessary for exploring these resources (Olatunji et al., 2011; Akande et al., 2015; Rashidi et al., 2020; Hazbeh et al., 2021). The petrophysical characteristics of a reservoir that must be considered for producing hydrocarbons include porosity, permeability, pore, grain distribution, sedimentary environment, facies distribution, and basin description (Adizua and Oruade, 2018; Farsi et al., 2021; Mohamadian et al., 2021). Permeability prediction can manage hydrocarbon reserves using information such as average flow rate and the amount of recoverable oil it provides (Olatunji et al., 2011). To predict permeability, well tests, seismic data, field production data, and well logs are used (Ahmed et al., 1991).

Literature review

Different methods for predicting permeability have been used until now, and most of them are used in homogeneous environments to predict permeability (Newman and Martin, 1977; Pugh and Thomas, 1989). In hydrochloric reservoirs, the porous medium is more heterogeneous, and the homogeneous medium is rarely seen (Dou et al., 2011; Ahmadi and Chen, 2019). Therefore, using these methods to predict permeability, which always considers the porous medium homogeneous, is unsuitable (Newman and Martin, 1977; Rostami et al., 2019b). Permeability depends on porosity, lithology, pore geometry, and fluid (Anifowose et al., 2017). Permeable is estimated from several methods, including direct core measurement, well test analysis, or empirical equations of well report parameters. Some researchers who have used experimental methods to predict permeability include Wyllie and Rose, who in 1950, presented an equation based on porosity and a water-saturated equation (equation 1) (Kamali et al., 2022). After that, Archie in 1952 presented an equation in which permeability is a function of porosity (equation 2) (Kamali et al., 2022). A few years later, in 1990, Chilingrian et al. also presented an equation in which the permeability equation is a logarithmic equation and a function of a specific surface, porosity, and water saturation. The reported equations are as follows (equation 3) (Kamali et al., 2022):

$\begin{array}{ll}K=2.55{\left(10\varphi \right)}^{5.65}& (1)\end{array}$

$\begin{array}{ll}K={\left(79\frac{{\varphi }^3}{S_{wir}}\right)}^2& (2)\end{array}$

$\begin{array}{c}\log K=0.9532-2.7880\times {10}^{-2}{S}_{wir}-5.5597\times {10}^{-4}\mathrm{}{S}_s\\ \mathrm{}+1.3309\times {10}^{-1}\mathrm{}\varphi +1.1707\times {10}^{-5}\mathrm{}{S}_{wir}{S}_s\end{array}\text{ (3)}$

The direct measurement method is a method that takes a lot of time and money, and the empirical equation method cannot explain the heterogeneity of permeability for the reservoir in any condition (Marshall, 1958; Morgan and Gordon, 1970; Ahmadi et al., 2008). Therefore, many intelligent calculation methods can predict permeability with high accuracy. In recent decades, machine learning tools have been used to predict permeability from porosity and well-log data (Unsal et al., 2005; Basbug and Karpyn, 2008; Rostami et al., 2019a).

Moussa et al. (2018) used a self-adaptive differential evolution (SaDE) optimization algorithm to find the optimal control parameters of artificial neural networks (ANNs) to predict permeability, then applied the optimized SaDE-ANN model. The input data of this study are micro-spherical focused resistivity (RSFL), deep resistivity (RT), neutron porosity (NPHI), bulk density (RHOB), and gamma-ray (GR). The results showed that the empirical correlation developed based on the SaDE-ANN model could predict reservoir permeability with high accuracy (mean square error [MSE] 0.0639 and correlation coefficient 0.979). The results of this study can help petroleum engineers to have a better understanding of reservoir performance when laboratory data is not available (Moussa et al., 2018).

Ahmadi and Chen (2019) used different machine learning methods, including conventional ANNs, genetic algorithm (GA), fuzzy decision tree, the imperialist competitive algorithm (ICA), particle swarm optimization (PSO), and a hybrid of those to predict Porosity and paternal influence were compared. The results of this study showed that the combined methods of HGAPSO-LSSVM, a fuzzy decision tree (FDT), and ANN perform better than other methods for prediction (Ahmadi and Chen, 2019).

Adeniran et al. (2019) used a novel competitive ensemble machine learning model to predict permeability in heterogeneous reservoirs. The results of the study showed that the proposed competitive ensemble proposed in this study predicts permeability in heterogeneous reservoirs well (Adeniran et al., 2019).

Mathew Nkurlu et al. (2020) used a group data handling (GMDH) neural network from well-log data of the West arm of the East African Rift Valley to predict permeability. In this study, the comparative analysis of the GMDH permeability model and ANN methods of Backpropagation Neural Network (BPNN) and Radial Basis Function Neural Network (RBFNN) were further investigated. The results obtained from this study show that the proposed GMDH model in this study performed better than BPNN and RBFNN because it reached the R/root mean square error (RMSE) value of 0.0241/0.989 and 0.204/0.868 for prediction, respectively (Mathew Nkurlu et al., 2020).

In this article, 200 data sets collected from the Middle East, including porosity, water-saturated, and specific surface parameters, have been used to predict permeability, one of the most important key parameters in reservoir engineering, exploitation, and production. In order to predict this issue, one of the newest artificial intelligence hybrid algorithms, RBFNN-GA, has been used. Compared to other published articles, the novelty of this article is that no researcher has used this method to predict this key parameter. Therefore, in this research, the effort is that this new method, which can solve complex optimization problems of continuous functions and multi-objective problems, easy design, strong tolerance to input noise, and good generalization, can be applied to the oil and gas industry, as well as to determine other parameters. Reservoir key, operation, and drilling should be used. The results in this article indicate the high accuracy of this algorithm compared to other methods mentioned in the introduction, as well as the original results of experimental methods.

Methodology

GA

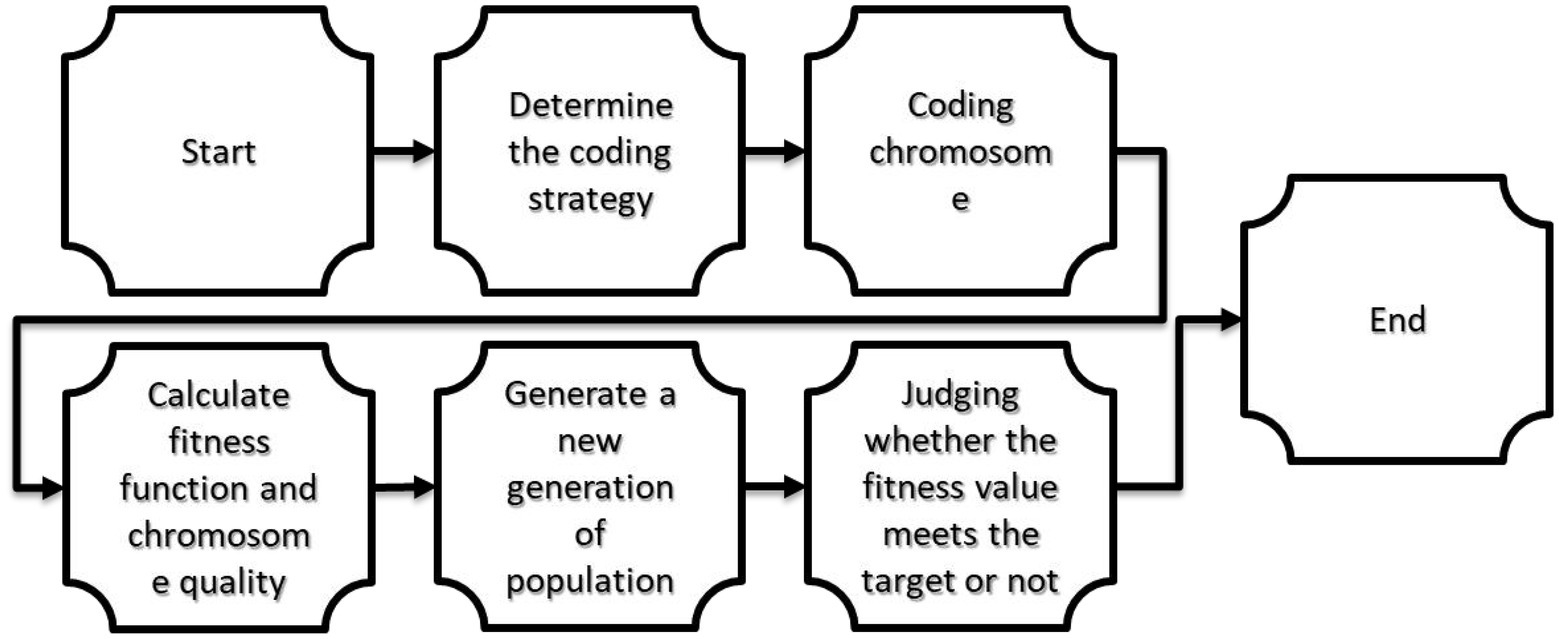
The genetic algorithm is introduced as a function optimization algorithm (Gao et al., 2022). The way of using this algorithm is inspired by way of human evolution. The genetic algorithm is based on the idea of "survival of the fittest.” The genetic algorithm is implemented in such a way that first, the initial population of problem solutions is generated (Farsi et al., 2021). These solutions are considered like chromosomes in biology (Wu and Zhao, 2018). Chromosomes can be good or bad-quality chromosomes in the evolution process. The fitness function evaluates the quality of chromosomes and determines the fitness of each chromosome. The fitness function selects the best population chromosomes for a new population (Hazbeh et al., 2021). The fitness value of each chromosome determines the survival probability of the chromosome. Then the high-quality chromosomes are multiplied by the genetic algorithm, and a new population is created, resulting from the selection, mutation, and mating operators. The children of the new population will be one step closer to producing the optimal global solution. This work continues until the genetic algorithm converges to the optimal global solution. Figure 1 shows the steps of the genetic algorithm.

FIGURE 1

Figure 1. Schematic diagram of genetic algorithm steps.

The first step or determining the coding strategy: genetic parameters are set to determine the fitness function. These parameters are population size, the maximum evolutionary generation, probability of crossover, and probability of mutation (Weerasooriya et al., 1992). The second step or coding chromosome: After the binary coding strategy is selected to be used for coding, the initial population is generated by the system. The third stage: In this stage, the quality of each chromosome is determined by calculating the value of the fitness function. Step 4: In this step, a strategy is chosen to create the next generation of the new population. The fifth stage: In this stage, the conformity of the fitness value with the goal is determined (Weerasooriya et al., 1992).

RBFNN

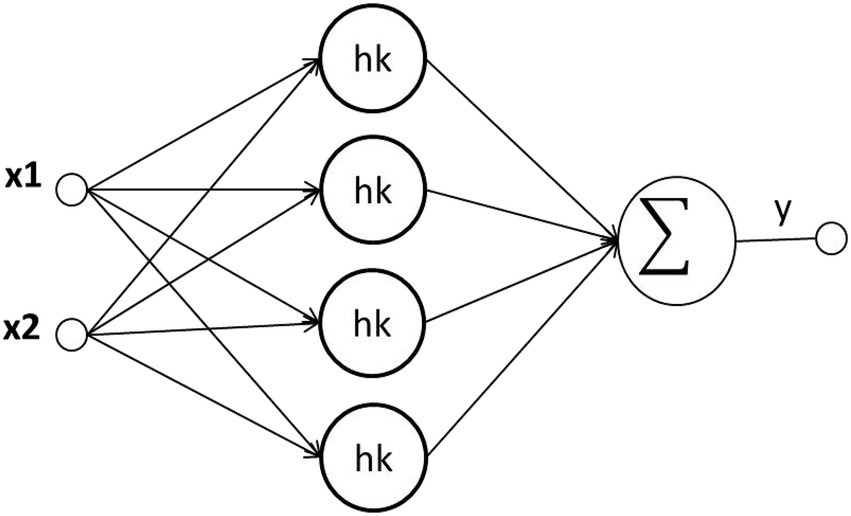
A RBFNN is a network with three layers, one of the layers of this network is hidden, and the other is the output layer (Ghorbani et al., 2020; Luo et al., 2021). Figure 2 shows the RBFNN structure of the l-m-n structure. l represents the number of nodes in the input layer, and m represents the number of nodes in the hidden layer. The number of nodes in the output layer is represented by n. x = [x₁, x₂, …, x_n]^T ∈ R^l is the input vector in the network, W ∈ R^m × n here expresses the output matrix, and the activation function of the j^th hidden node with Φ_j (∗) and y = [y₁, y₂, …, y_n]^T is defined (Luo et al., 2021).

FIGURE 2

Figure 2. Schematic diagram of RBFNN algorithm.

One of the most prominent features of RBFNN is that RBF is used as an activation function. The location of the RBF is near the center of the radially symmetric n space. The distance of the input from the central point and the degree of activation have a direct relationship. When the degree of activation is lower, the distance between the input and the central point is greater (Shen et al., 2020). This feature is called the local feature of the hidden layer node. So, each hidden layer node of RBFNN has a data center (equation 1). The definition of the K output of RBFNN is given in Figure 2.

$\begin{array}{ll}|y_k={\displaystyle \sum }_{j=1}^m{w}_i{\mathrm{\Phi }}_j\left(x-c_j\mathrm{,}{\sigma }_j\right)& (4)\end{array}$

Determining the hidden layer and the output weight: The construction and training of RBFNN have a process of determining the number of neurons of the hidden layer, the center, and the width of each basis function of the hidden layer and the output weight (Shen et al., 2020). Three forms of RBF that can satisfy Micchelli’s theorem are given below (Gaussian, Multiquadric, and Inverse polyquadratic function) (equations 5–7). The special feature of each of these RBFs is that the amount of input samples is equal to the number of hidden nodes (Wang and Li, 2019).

$\begin{array}{ll}\Phi \left(r\right)=\exp \left(\frac{r^2}{2{\sigma }^2}\right)& (5)\end{array}$

$\begin{array}{ll}\Phi \left(r\right)=\frac{1}{1+\exp \left(r^2/{\sigma }^2\right)}& (6)\end{array}$

$\begin{array}{ll}\Phi \mathrm{}\left(r\right)=\frac{1}{{\left(r^2+{\sigma }^2\right)}^{1/2}}& (7)\end{array}$

New hybrid RBFNN-GA

Setting the variance parameters σ, the center of the node transfer function of the hidden layer, and the connection weights between the hidden layer and the output layer are the main parameters in the RBFNN training process (Zhu and Meng, 2021).

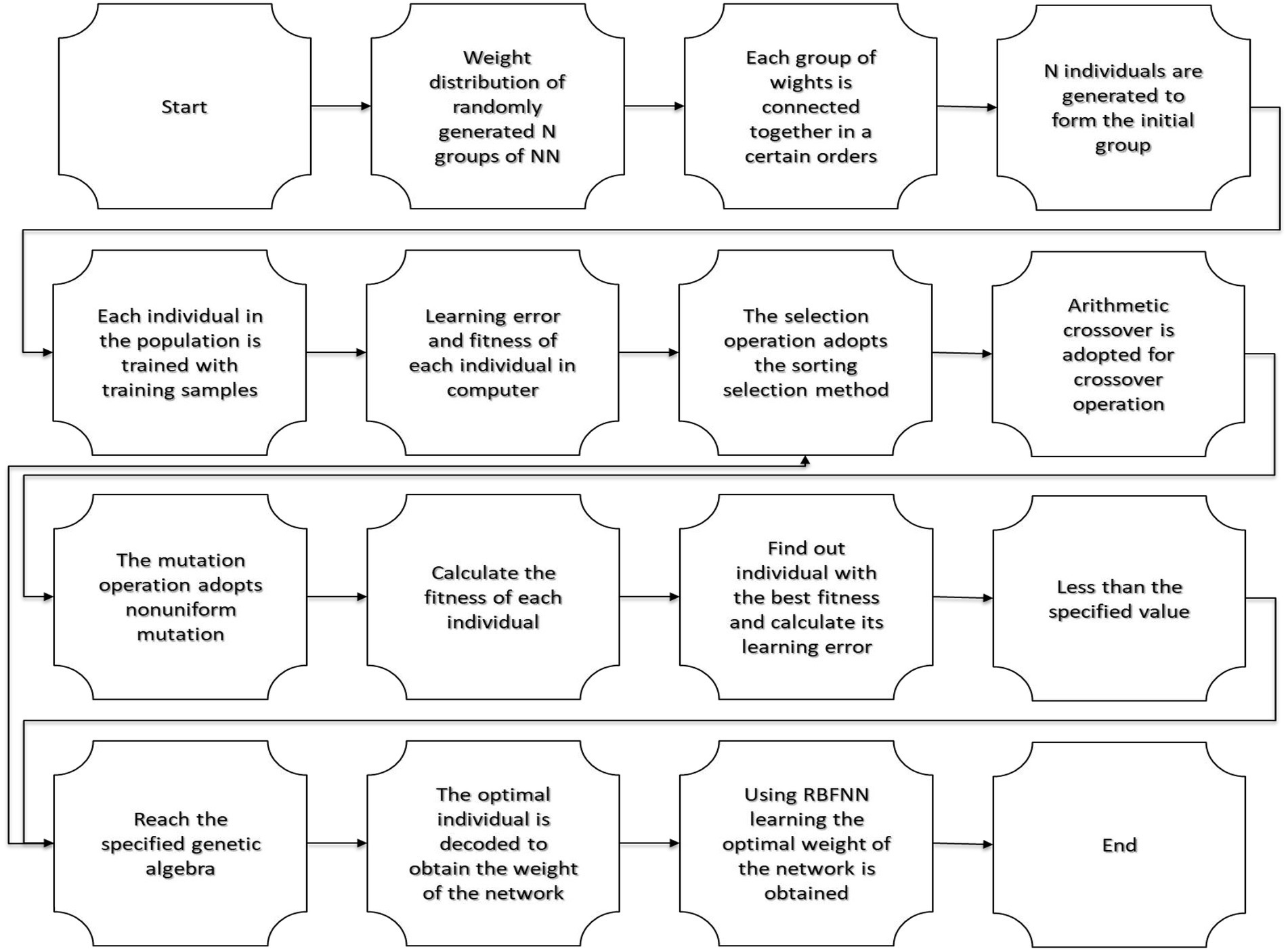
Constant methods, gradient descent, and K-means clustering algorithm are used for neural network training. There are flaws in this algorithm, but its strength is that it is easily implemented. The center c and the connection weight ω between the hidden layer and the output layer and the variance σ of the transfer function are optimized using GA in training the RBFNN prediction model, and the prediction accuracy of RBFNN is increased. Figure 3 shows the flow of the GA algorithm with RBFNN (Bellinger et al., 2017).

FIGURE 3

Figure 3. Schematic diagram of RBFNN-GA algorithm.

The steps mentioned below are the steps of the algorithm: The first step is individual coding, whose components are the network connection weight ω, the hidden layer, and the center c of the transfer function. The second step is an individual evaluation of the algorithm. The fitness measure of an individual in GA determines whether it is possible for an individual to be inherited by the next generation or not. The advantages and disadvantages of the algorithm are measured by the individual fitness measure (Khalick Mohammad et al., 2017). The fitness function of the i^th person in the population is shown below:

$\begin{array}{ll}f=\frac{1}{{{\displaystyle \sum }}_{p=1}^M{{\displaystyle \sum }}_j^N{\left(y_{ij}^0-y_{ij}\right)}^2+1}& (8)\end{array}$

The third step is to determine the RBF center. The center of C_i = (C_i1, C_i2, …, C_il) is the location of parameter m × l. To calculate c_i, the mean clustering method is used, which is explained below and is as follows (Figure 3):

Result and discussion

In this research, we used the petrophysical data of an oil field in the Middle East. The set of data used in this study to predict oil and gas permeability is 200. The cores prepared for drilling hydrocarbon reserves in oil and gas fields were analyzed to prepare these data.

Water saturation, porosity, permeability, and specific surface are introduced as the data used in this study. The mentioned data are obtained from the analysis of cores.

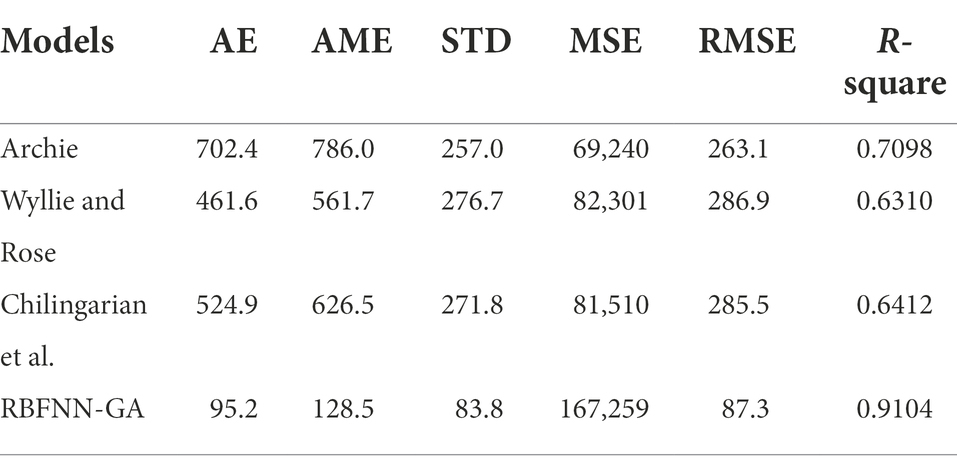
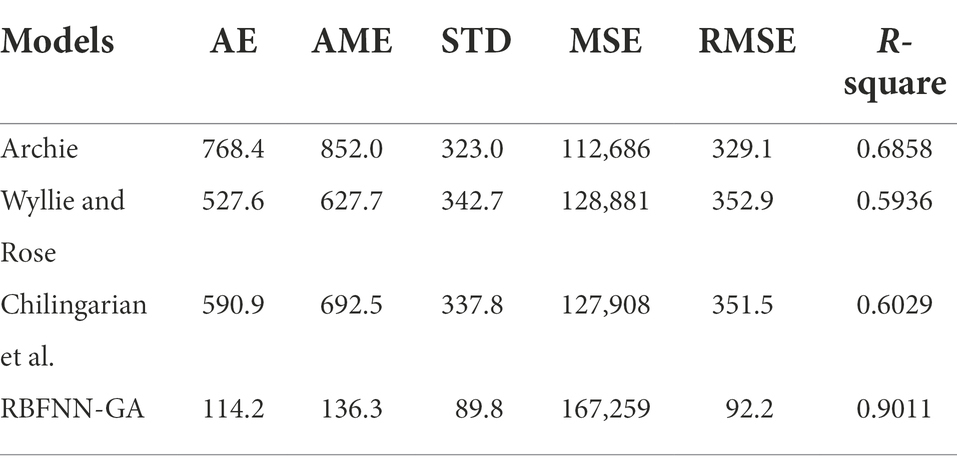
Statistical errors, which are an accurate and widely used method, are superior to artificial intelligence methods and mathematical equations in terms of performance accuracy. For this reason, they have become one of the most widely used methods. In this article, we have investigated statistical errors. In this section, the data is divided into two sections, training data and test data, for which 85% of the data is for training data and 15% is for test data.

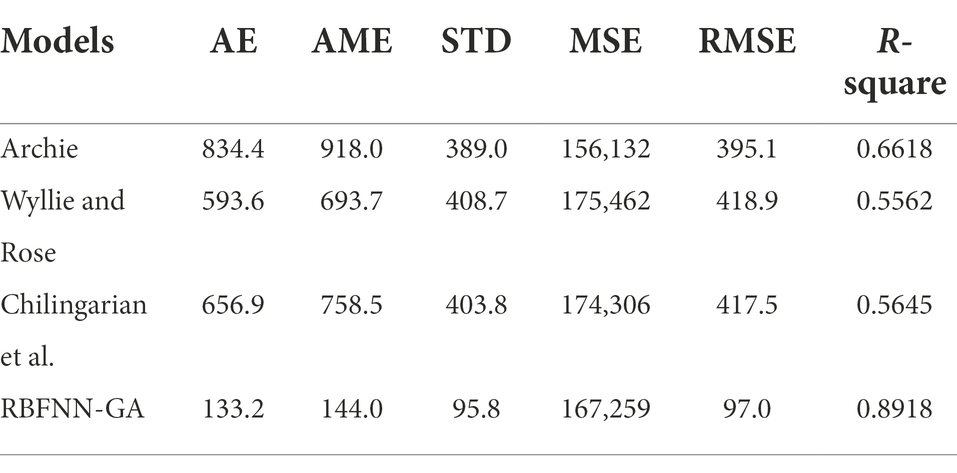
After examining the results given in Tables 1–3, it is clear that RBFNN-GA has a higher performance accuracy. Finally, after checking, it is found that RBFNN-GA has higher accuracy than experimental equations. The results of the new RBFNN-GA hybrid algorithm for train, test, and total data are RMSE_train = 97, RMSE_test = 83.7, and RMSE_total = 92.2.

TABLE 1

Table 1. Determining the static error parameters for predicting k for the training subset.

TABLE 2

Table 2. Determining the static error parameters for predicting k for the testing subset.

TABLE 3

Table 3. Determining the static error parameters for predicting k for the total subset.

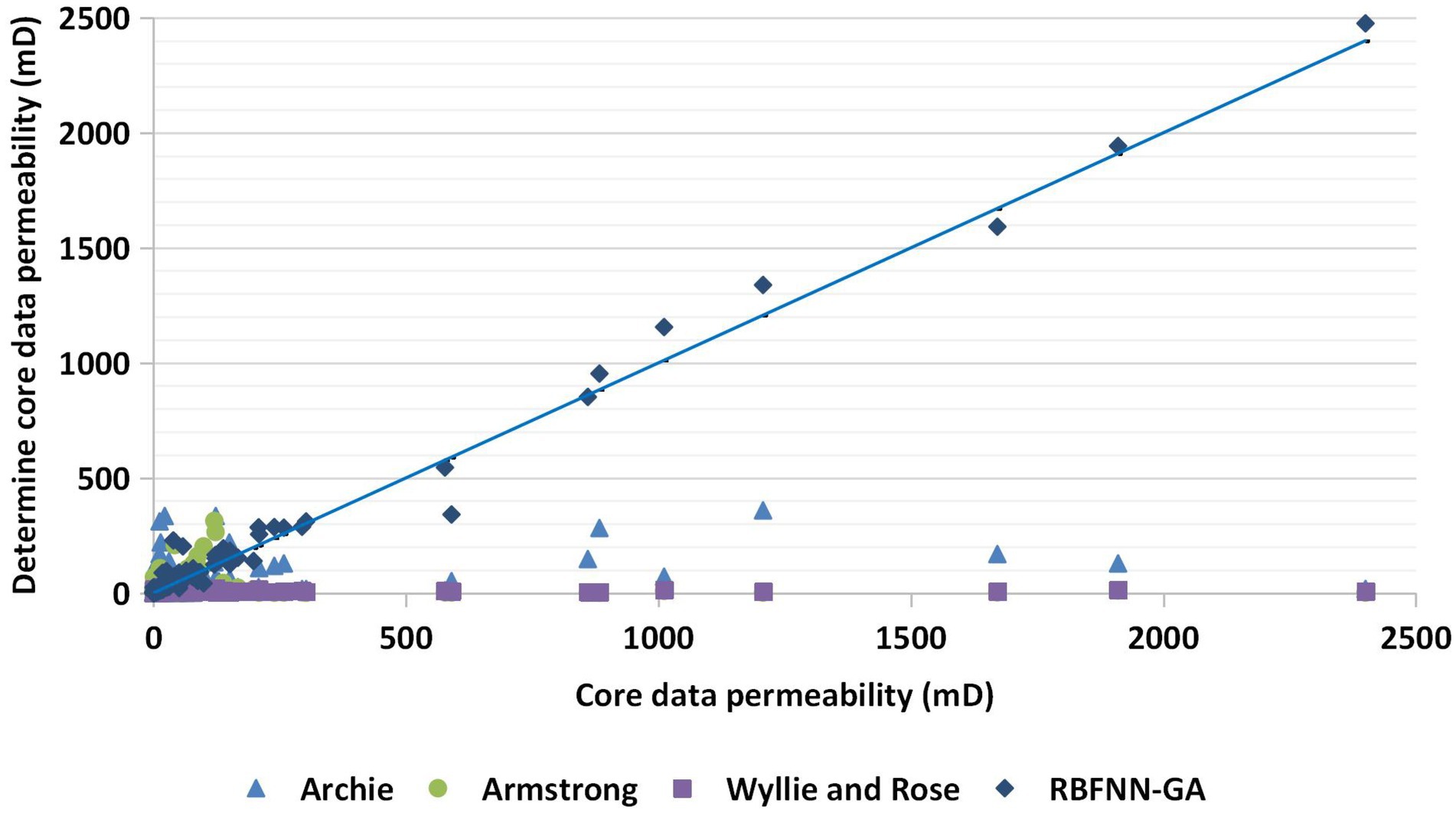
There are many ways to determine the accuracy of the performance. For example, you can determine the average deviation from the average line and draw a cross diagram, and with their help, the accuracy of the performance is determined. Figure 4 shows the cross-plot for predicting permeability for testing, training, and the whole dataset based on the RBFNN-GA algorithm. This algorithm is remarkably high, as shown in this figure.

FIGURE 4

Figure 4. Cross-plot for k prediction based on RBFNN-GA algorithm and empirical equations.

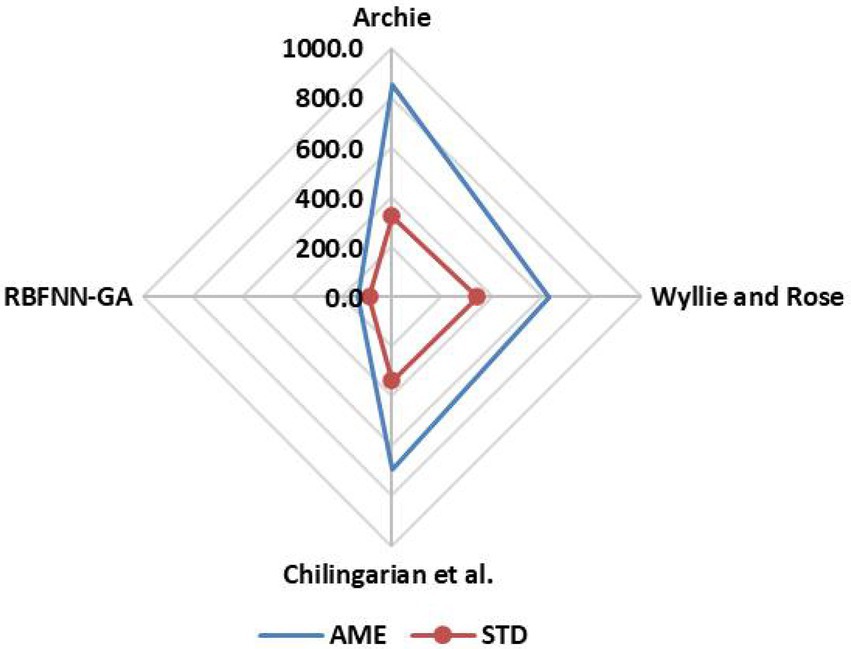
Figure 5 shows the RBFNN-GA algorithm for comparing AME and STD. Table 3 and Figure 4 provide information that shows that the accuracy of the algorithm used in this study is very high. AME and STD have a direct relationship; when RMSE decreases, RMSE also decreases.

FIGURE 5

Figure 5. Comparison of for k prediction based on RBFNN-GA algorithm and empirical equations.

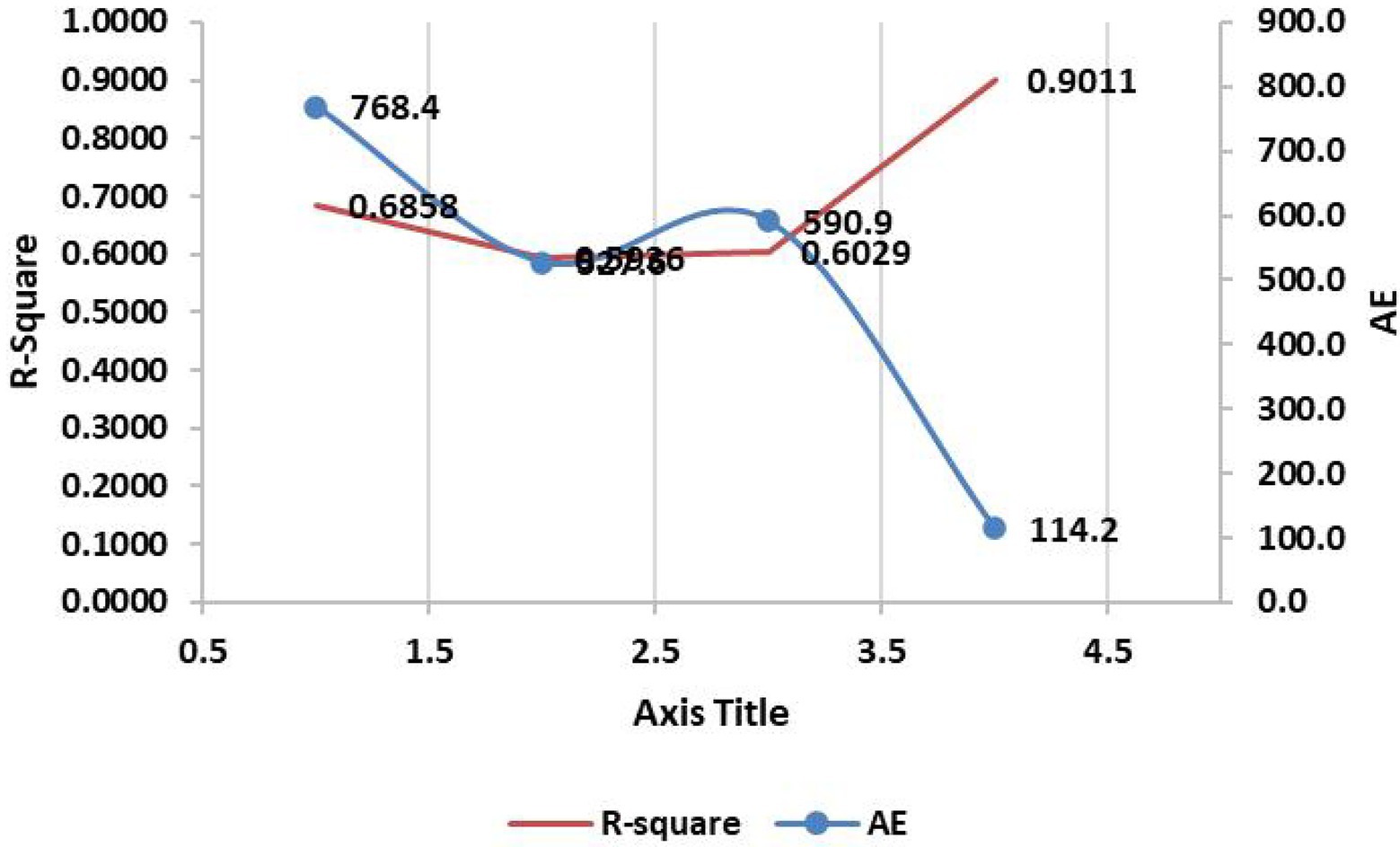
Figure 6 shows the comparison of AE and R-square. Using the information presented in Figure 6 and Table 3, it can be concluded that the RBFNN-GA algorithm used to predict permeability in this study is highly accurate. The relationship between AE and R-square is shown in the graph presented in Figure 6, that is, when AE decreases, R-square increases.

FIGURE 6

Figure 6. Comparison of for k prediction based on RBFNN-GA algorithm and empirical equations.

Conclusion

In this study, k was predicted as one of the most important petrophysical properties of the reservoir, which plays an important role in resevoir numerical modeling, drilling planning, reservoir quality mapping, and reservoir engineering calculations. To predict permeability (k), 200 data from a Middle East field, such as water saturation, porosity, specific surface parameters, and RBFNN-GA algorithm, were used. The RBFNN-GA algorithm was compared with three experimental models. The advantages of GA are solving complex problems and performing better than other artificial intelligence methods despite the noise in the system, optimization of continuous functions, and multi-objective problems. The advantages of RBF neural networks are that they are easy to design, have a strong tolerance to input noise, and have good generalization. The RBFNN-GA model used in this study is superior to the RBF and GA neural network models because it has the advantages of both algorithms, resulting in higher accuracy in permeability prediction. The results show that for the total data, the accuracy of RBFNN-GA is equal to STD = 89.8 and R-square = 0.9011. By examining the obtained results and comparing this algorithm with the experimental equation, it was found that the algorithm proposed in this study has a better performance accuracy and is also a useful method for predicting other parameters. Because this algorithm has been able to show good performance for low data volumes, therefore, this algorithm can be used for articles with small data in which the number of high data is not considered.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

KS collected data, wrote a paper, and made full use of computer programs to carry out experimental simulation. LD was responsible for the guidance and revision of the paper, and provided important theoretical and experimental guidance in the later process of completing the paper. All authors contributed to the article and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adeniran, A. A., Adebayo, A. R., Salami, H. O., Yahaya, M. O., and Abdulraheem, A. (2019). A competitive ensemble model for permeability prediction in heterogeneous oil and gas reservoirs. Appl. Comput. Geosci. 1:100004. doi: 10.1016/j.acags.2019.100004

CrossRef Full Text | Google Scholar

Adizua, O. F., and Oruade, L. (2018). Reservoir characterization of an offshore Niger Delta “X” field using well log data. Int. J. Eng. Appl. Sci. 20, 1–4.

Google Scholar

Ahmadi, M. A., and Chen, Z. (2019). Comparison of machine learning methods for estimating permeability and porosity of oil reservoirs via petro-physical logs. Petroleum 5, 271–284. doi: 10.1016/j.petlm.2018.06.002

CrossRef Full Text | Google Scholar

Ahmadi, M., Saemi, M., and Asghari, K. (2008). Estimation of the reservoir permeability by petrophysical information using intelligent systems. Pet. Sci. Technol. 26, 1656–1667. doi: 10.1080/10916460701675173

CrossRef Full Text | Google Scholar

Ahmed, U., Crary, S. F., and Coates, G. R. (1991). Permeability estimation: the various sources and their interrelationships. J. Pet. Technol. 43, 578–587. doi: 10.2118/19604-PA

CrossRef Full Text | Google Scholar

Akande, K. O., Owolabi, T. O., and Olatunji, S. O. (2015). Investigating the effect of correlation-based feature selection on the performance of support vector machines in reservoir characterization. J. Nat. Gas Sci. Eng. 22, 515–522. doi: 10.1016/j.jngse.2015.01.007

CrossRef Full Text | Google Scholar

Anifowose, F. A., Labadin, J., and Abdulraheem, A. (2017). Hybrid intelligent systems in petroleum reservoir characterization and modeling: the journey so far and the challenges ahead. J. Pet. Explor. Prod. Technol. 7, 251–263. doi: 10.1007/s13202-016-0257-3

CrossRef Full Text | Google Scholar

Basbug, B., and Karpyn, Z. T. (2008). A study of absolute permeability dependence on pore-scale characteristics of carbonate reservoirs using artificial intelligence. Int. J. Oil Gas Coal Technol. 1, 382–398. doi: 10.1504/IJOGCT.2008.020369

CrossRef Full Text | Google Scholar

Beheshtian, S., Rajabi, M., Davoodi, S., Wood, D. A., Ghorbani, H., Mohamadian, N., et al. (2022). Robust computational approach to determine the safe mud weight window using well-log data from a large gas reservoir. Mar. Pet. Geol. 142:105772. doi: 10.1016/j.marpetgeo.2022.105772

CrossRef Full Text | Google Scholar

Bellinger, C., Mohomed Jabbar, M. S., Zaïane, O., and Osornio-Vargas, A. (2017). A systematic review of data mining and machine learning for air pollution epidemiology. BMC Public Health 17, 1–19. doi: 10.1186/s12889-017-4914-3

CrossRef Full Text | Google Scholar

Dou, Q., Sun, Y., and Sullivan, C. (2011). Rock-physics-based carbonate pore type characterization and reservoir permeability heterogeneity evaluation, upper San Andres reservoir, Permian Basin, West Texas. J. Appl. Geophys. 74, 8–18. doi: 10.1016/j.jappgeo.2011.02.010

CrossRef Full Text | Google Scholar

Farsi, M., Mohamadian, N., Ghorbani, H., Wood, D. A., Davoodi, S., Moghadasi, J., et al. (2021). Predicting formation pore-pressure from well-log data with hybrid machine-learning optimization algorithms. Nat. Resour. Res. 30, 3455–3481. doi: 10.1007/s11053-021-09852-2

CrossRef Full Text | Google Scholar

Gao, G., Hazbeh, O., Davoodi, S., Tabasi, S., Rajabi, M., Ghorbani, H., et al. (2022). Prediction of fracture density in a gas reservoir using robust computational approaches. Front. Earth Sci. 1831. doi: 10.3389/feart.2022.1023578

CrossRef Full Text | Google Scholar

Ghorbani, H., Wood, D. A., Choubineh, A., Tatar, A., Abarghoyi, P. G., Madani, M., et al. (2020). Prediction of oil flow rate through an orifice flow meter: artificial intelligence alternatives compared. Petroleum 6, 404–414. doi: 10.1016/j.petlm.2018.09.003

CrossRef Full Text | Google Scholar

Hazbeh, O., Aghdam, S. K.-Y., Ghorbani, H., Mohamadian, N., Alvar, M. A., and Moghadasi, J. (2021). Comparison of accuracy and computational performance between the machine learning algorithms for rate of penetration in directional drilling well. Pet. Res. 6, 271–282. doi: 10.1016/j.ptlrs.2021.02.004

CrossRef Full Text | Google Scholar

Jafarizadeh, F., Rajabi, M., Tabasi, S., Seyedkamali, R., Davoodi, S., Ghorbani, H., et al. (2022). Data driven models to predict pore pressure using drilling and petrophysical data. Energy Rep. 8, 6551–6562. doi: 10.1016/j.egyr.2022.04.073

CrossRef Full Text | Google Scholar

Kamali, M. Z., Davoodi, S., Ghorbani, H., Wood, D. A., Mohamadian, N., Lajmorak, S., et al. (2022). Permeability prediction of heterogeneous carbonate gas condensate reservoirs applying group method of data handling. Mar. Pet. Geol. 139:105597. doi: 10.1016/j.marpetgeo.2022.105597

CrossRef Full Text | Google Scholar

Khalick Mohammad, A. E., Hong, J., and Wang, D. (2017). Polishing of uneven surfaces using industrial robots based on neural network and genetic algorithm. Int. J. Adv. Manuf. Technol. 93, 1463–1471. doi: 10.1007/s00170-017-0524-6

CrossRef Full Text | Google Scholar

Lideng, G. A. N., Yaojun, W., Xianzhe, L. U. O., Zhang, M., Xianbin, L. I., Xiaofeng, D. A. I., et al. (2019). A permeability prediction method based on pore structure and lithofacies. Pet. Explor. Dev. 46, 935–942. doi: 10.1016/S1876-3804(19)602508

CrossRef Full Text | Google Scholar

Liu, J., Song, S., Cao, X., Meng, Q., Pu, H., Wang, Y., et al. (2020). Determination of full-scale pore size distribution of Gaomiaozi bentonite and its permeability prediction. J. Rock Mech. Geotech. Eng. 12, 403–413. doi: 10.1016/j.jrmge.2019.12.005

CrossRef Full Text | Google Scholar

Luo, G., Yang, Z., Zhan, C., and Zhang, Q. (2021). Identification of nonlinear dynamical system based on raised-cosine radial basis function neural networks. Neural. Process. Lett. 53, 355–374. doi: 10.1007/s11063-020-10410-9

CrossRef Full Text | Google Scholar

Marshall, T. J. (1958). A relation between permeability and size distribution of pores. J. Soil Sci. 9, 1–8. doi: 10.1111/j.1365-2389.1958.tb01892.x

CrossRef Full Text | Google Scholar

Mathew Nkurlu, B., Shen, C., Asante-Okyere, S., Mulashani, A. K., Chungu, J., and Wang, L. (2020). Prediction of permeability using group method of data handling (GMDH) neural network from well log data. Energies 13:551. doi: 10.3390/en13030551

CrossRef Full Text | Google Scholar

Mohamadian, N., Ghorbani, H., Wood, D. A., Mehrad, M., Davoodi, S., Rashidi, S., et al. (2021). A geomechanical approach to casing collapse prediction in oil and gas wells aided by machine learning. J. Pet. Sci. Eng. 196:107811. doi: 10.1016/j.petrol.2020.107811

CrossRef Full Text | Google Scholar

Morgan, J. T., and Gordon, D. T. (1970). Influence of pore geometry on water-oil relative permeability. J. Pet. Technol. 22, 1199–1208. doi: 10.2118/2588-PA

CrossRef Full Text | Google Scholar

Moussa, T., Elkatatny, S., Mahmoud, M., and Abdulraheem, A. (2018). Development of new permeability formulation from well log data using artificial intelligence approaches. J. Energy Resour. Technol. 140, 1–8. doi: 10.1115/1.4039270

CrossRef Full Text | Google Scholar

Newman, G. H., and Martin, J. C. (1977). Equipment and experimental methods for obtaining laboratory compression characteristics of reservoir rocks under various stress and pressure conditions. In SPE Annual Fall Technical Conference and Exhibition. OnePetro. ISBN:978-1-55563-732-3.

Google Scholar

Olatunji, S. O., Selamat, A., and Raheem, A. A. A. (2011). Predicting correlations properties of crude oil systems using type-2 fuzzy logic systems. Expert Syst. Appl. 38, 10911–10922. doi: 10.1016/j.eswa.2011.02.132

CrossRef Full Text | Google Scholar

Olatunji, S. O., Selamat, A., and Raheem, A. A. A. (2014). Improved sensitivity based linear learning method for permeability prediction of carbonate reservoir using interval type-2 fuzzy logic system. Appl. Soft Comput. 14, 144–155. doi: 10.1016/j.asoc.2013.02.018

CrossRef Full Text | Google Scholar

Pugh, V. J., and Thomas, D. C. (1989). A statistical analysis of the accuracy and reproducibility of standard Core analysis. Log Anal. 30

Google Scholar

Rajabi, M., Beheshtian, S., Davoodi, S., Ghorbani, H., Mohamadian, N., Radwan, A. E., et al. (2021). Novel hybrid machine learning optimizer algorithms to prediction of fracture density by petrophysical data. J. Pet. Explor. Prod. Technol. 11, 4375–4397. doi: 10.1007/s13202-021-01321-z

CrossRef Full Text | Google Scholar

Rajabi, M., Ghorbani, H., and Aghdam, K.-Y. (2022a). Prediction of shear wave velocity by extreme learning machine technique from well log data. J. Pet. Geomech. 4, 18–35. doi: 10.22107/JPG.2022.298520.1151

CrossRef Full Text | Google Scholar

Rajabi, M., Ghorbani, H., and Aghdam, K.-Y. (2022b). Sensitivity analysis of effective factors for estimating formation pore pressure using a new method: the LSSVM-PSO algorithm. J. Pet. Geomech. 4, 19–39. doi: 10.22107/JPG.2022.298551.1152

CrossRef Full Text | Google Scholar

Rajabi, M., Ghorbani, H., and Lajmorak, S. (2022c). Comparison of artificial intelligence algorithms to predict pore pressure using petrophysical log data. J. Struct. Const. Eng.

Google Scholar

Rajabi, M., Hazbeh, O., Davoodi, S., Wood, D. A., Tehrani, P. S., Ghorbani, H., et al. (2022d). Predicting shear wave velocity from conventional well logs with deep and hybrid machine learning algorithms. J. Pet. Explor. Prod. Technol., 1–24. doi: 10.1007/s13202-022-01531-z

CrossRef Full Text | Google Scholar

Rashidi, S., Mohamadian, N., Ghorbani, H., Wood, D. A., Shahbazi, K., and Alvar, M. A. (2020). Shear modulus prediction of embedded pressurized salt layers and pinpointing zones at risk of casing collapse in oil and gas wells. J. Appl. Geophys. 183:104205. doi: 10.1016/j.jappgeo.2020.104205

CrossRef Full Text | Google Scholar

Rostami, A., Baghban, A., Mohammadi, A. H., Hemmati-Sarapardeh, A., and Habibzadeh, S. (2019a). Rigorous prognostication of permeability of heterogeneous carbonate oil reservoirs: smart modeling and correlation development. Fuel 236, 110–123. doi: 10.1016/j.fuel.2018.08.136

CrossRef Full Text | Google Scholar

Rostami, S., Rashidi, F., and Safari, H. (2019b). Prediction of oil-water relative permeability in sandstone and carbonate reservoir rocks using the CSA-LSSVM algorithm. J. Pet. Sci. Eng. 173, 170–186. doi: 10.1016/j.petrol.2018.09.085

CrossRef Full Text | Google Scholar

Shen, Y., Pan, X., Zheng, Z., and Gerstoft, P. (2020). Matched-field geoacoustic inversion based on radial basis function neural network. J. Acoust. Soc. Am. 148, 3279–3290. doi: 10.1121/10.0002656

PubMed Abstract | CrossRef Full Text | Google Scholar

Tabasi, S., Tehrani, P. S., Rajabi, M., Wood, D. A., Davoodi, S., Ghorbani, H., et al. (2022). Optimized machine learning models for natural fractures prediction using conventional well logs. Fuel 326:124952. doi: 10.1016/j.fuel.2022.124952

CrossRef Full Text | Google Scholar

Unsal, E., Dane, J. H., and Dozier, G. V. (2005). A genetic algorithm for predicting pore geometry based on air permeability measurements. Vadose Zone J. 4, 389–397. doi: 10.2136/vzj2004.0116

CrossRef Full Text | Google Scholar

Wang, S., and Li, S. G. (2019). A novel hybrid carbon Price forecasting model based on radial basis function neural network. Acta Phys. Polon. 135, 368–374. doi: 10.12693/APhysPolA.135.368

CrossRef Full Text | Google Scholar

Weerasooriya, S., El-Sharkawi, M. A., Damborg, M., and Marks, R. J. (1992). Towards Static-Security Assessment of a Large-Scale Power System Using Neural Networks: IET, 64–70.

Google Scholar

Wu, Y., and Zhao, X. (2018). Adaptive backstepping control based on functional link radial basis function neural network for pmlsm. Diangong Jishu Xuebao Trans. China Electrotech. Soc. 33, 4044–4051.

Google Scholar

Zhang, G., Davoodi, S., Shamshirband, S., Ghorbani, H., Mosavi, A., and Moslehpour, M. (2022). A robust approach to pore pressure prediction applying petrophysical log data aided by machine learning techniques. Energy Rep. 8, 2233–2247. doi: 10.1016/j.egyr.2022.01.012

CrossRef Full Text | Google Scholar

Zhong, Z., Carr, T. R., Wu, X., and Wang, G. (2019). Application of a convolutional neural network in permeability prediction: a case study in the Jacksonburg-Stringtown oil field, West Virginia, USA. Geophysics 84, B363–B373. doi: 10.1190/geo2018-0588.1

CrossRef Full Text | Google Scholar

Zhu, M., and Meng, Z. (2021). Macroeconomic image analysis and GDP prediction based on the genetic algorithm radial basis function neural network (RBFNN-GA). Comput. Intell. Neurosci. 2021. doi: 10.1155/2021/2000159

CrossRef Full Text | Google Scholar