Research on the efficiency and spatiotemporal evolution characteristics of agricultural green development in central cities of the Yangtze River Delta

Introduction: Agricultural green development (AGD) prioritizes sustainable growth by integrating economic, ecological, and social dimensions, aiming to harmonize agricultural economic development with environmental protection and social progress.

Methods: This study integrates the three-stage super-efficiency DEA-SBM model with the BP algorithm, creating an advanced DEA-SBM-BP model to overcome the shortcomings of traditional DEA in evaluation and management processes. The study further applies the Dagum Gini coefficient, kernel density estimation (KDE), and Moran’s index to assess and forecast the efficiency and spatiotemporal evolution patterns of green agricultural development in key cities within the Yangtze River Delta.

Results: The analysis shows that AGD in the central city of the Yangtze River Delta is overall balanced; however, substantial variations exist among cities within individual provinces. Factors like macroeconomic conditions, workforce quality, and policy support play a crucial role in promoting the efficiency of AGD. Among these, macroeconomic development level has a negative impact, while labor quality and policy support exhibit bidirectional effects. Infrastructure construction, digitalization of agricultural economy, and rural security have become key factors in the green development of modern agriculture. The green advancement of agriculture in the central Yangtze River Delta region typically exhibits a marked clustering effect; however, the local clustering reveals a trend toward dispersed development.

Discussion: Despite the emergence of new characteristics in agricultural production in China within the context of high-quality development, differences in resource endowments and economic structures among cities continue to be significant factors contributing to regional imbalances and changes in the agglomeration patterns of agricultural development.

1 Introduction

China’s economy has been transformed from a phase of rapid growth to one characterized by high-quality development. The core aspects of high-quality include the vitality, innovation, and competitiveness of the economy, which are closely interconnected with and enhanced by green development. The concept of green development values harmony between humans and nature, takes green, low-carbon cycles as the main principle, and regards the construction of ecological civilization as the basic approach. It not only provides sustainable vitality and innovation for the economy but also serves as one of the sources of economic development. Therefore, developing a comprehensive green, low-carbon, and circular economic system is considered crucial for advancing high-quality development in China. As an important pillar of the Chinese economy, agriculture has historically occupied a crucial position in the national economy, directly affecting the country’s food supply capacity. Ensuring the consistency and growth of agricultural production is essential for maintaining domestic food stability. Simultaneously, agricultural development is closely linked to the economic progress in rural areas of China and the enhancement of farmers’ living standards. Fostering diversified rural economic development through agricultural green development (AGD) is crucial for reducing the urban-rural divide and realizing the aim of establishing a well-off society in all aspects. Currently, China’s agricultural production mode is still dominated by small-scale farming, with small production scale, lagging technological level, and irrational allocation of agricultural resources. This has resulted in increasingly serious challenges, including excessive land exploitation, water resource wastage, and widespread instability in farmers’ incomes, thereby underscoring the significant issues related to agriculture, rural areas, and farmers. The Chinese government pointed out that issues related to agriculture, rural areas, and farmers are fundamental concerns that impact the overall interests of the country and the wellbeing of the people. It is necessary to always prioritize the resolution of agriculture, the countryside, and farmers issues as a top priority of the Party’s work and implement the rural revitalization strategy. Different from the traditional extensive agricultural production, agricultural development under the background of rural revitalization covers various aspects such as improving rural industrial structure, enhancing agricultural productivity, and promoting diversified rural economic development. It emphasizes high-quality AGD and focuses on the coordinated development of agricultural economy, ecological environment, and social progress.

The Yangtze River Delta, located in eastern China, spans four provinces and municipalities including Jiangsu, Anhui, Zhejiang, and Shanghai. It is among the most economically advanced, populous, and culturally influential regions in the country. In recent years, the region has supported the development of precision agriculture through modern agricultural technologies and integrated excellent agricultural resources with tourism, achieving coordinated development of agricultural economy, ecological environment, and social progress. Therefore, a thorough analysis of the characteristics of AGD in the Yangtze River Delta is expected to offer valuable insights for AGD in this region as well as in other regions.

The main contribution of this research: 1) Combining the three-stage super-efficiency DEA-SBM model (3S-DEA-SBM) with the BP algorithm to construct the three-stage super-efficiency DEA-SBM-BP (3S-DEA-SBM-BP) model, thereby addressing the shortcomings of the DEA model in systematic evaluation and proactive management. This model can predict the final efficiency value when determining input planning, facilitating timely adjustment of inputs to ensure that input-output remains in an effective state. 2) From a city perspective, this study utilizes the 3S-DEA-SBM-BP model to minimize the impact of external environmental factors, enabling an objective measurement of AGD efficiency in cities within the Yangtze River Delta. It also predicts development trends for the next 3 years and analyzes the factors influencing AGD. This contributes to managers’ more effective formulation of various policies. 3) Using KDE and the Gini coefficient to simultaneously analyze the differences in AGD efficiency within and between provinces.

2 Literature review

As an agricultural powerhouse, agricultural development occupies a crucial position in China’s economy. However, the traditional agricultural model has long relied on chemical fertilizers, pesticides, and water resources. Although this reliance has significantly increased yield, it has also led to a series of ecological imbalances, including soil pollution, water eutrophication, and excessive groundwater extraction (Craswell, 2021). Therefore, in order to achieve high-quality economic growth, it is imperative to accelerate the green transformation and upgrading of agriculture. Currently, research on AGD, both domestically and internationally, primarily centers on three areas. The first is the exploration of the definition and rich connotations of AGD. AGD is a comprehensive approach that encompasses organic, circular, low-carbon, ecological, and green agricultural principles, aiming to balance economic, ecological, and social benefits. Its core lies in enhancing resource utilization efficiency through technological innovation and alleviating conflicts between agricultural activities and resources, ecology, and the environment (Liu et al., 2020a). AGD does not aim to safeguard the ecological environment at the expense of agricultural growth but seeks a higher level of ecological protection (Yin et al., 2021), emphasizing minimizing resource consumption and environmental impact while enhancing the quality and efficiency of agricultural products to boost agricultural profitability and social prosperity (Zhou and Wen, 2023). Secondly, based on the definition and connotations of AGD, scholars have developed evaluation indicator systems for assessing the level of AGD from various perspectives. Commonly used indicator dimensions in existing research include fundamental agricultural conditions, agricultural sector composition, potential for agricultural development, and intensity of agricultural inputs (Liu et al., 2020b), as well as economic and social transformation, resource consumption, green production, and living standards (Yao et al., 2023). Additionally, indicators such as social macroeconomic conditions, technological advancement, and resource environment are also considered (Chen and Zhang, 2023). In terms of research methods, while qualitative methods such as subjective weighting (Wei et al., 2018), the Delphi method (Flinzberger et al., 2020), and scenario analysis (Mirzabaev et al., 2022) are widely applied, quantitative methods remain predominant. Quantitative methods like entropy weight method (Gao et al., 2023), grey relational analysis (Meili, 2021), DEA models (Liu et al., 2022), and DEA-Malmquist index (Myeki et al., 2023) are extensively used due to their objectivity. With the advancement of research, scholars have increasingly integrated traditional models with machine learning techniques to develop new evaluation models suited for the era of big data (Shen et al., 2022). Finally, in the context of rural revitalization efforts, research on the driving factors of AGD has garnered increasing attention. Digital economy (Min, 2024), industrial integration (Tian et al., 2024), digital finance (Li et al., 2023), and inclusive finance (Gao et al., 2022) have become significant forces driving AGD. These factors inject new momentum into the green transformation of agriculture by enhancing resource allocation efficiency, optimizing industrial chain structure, and reducing production costs. At the same time, mechanization (Zhu et al., 2022), as a key method for improving agricultural production efficiency, remains an important and indispensable indicator in agricultural green production.

In summary, existing research on AGD provides a solid foundation for this study. In the context of high-quality development, we need to recognize that, although there has been a general enhancement in ecological efficiency and AGD levels in China, the overall level remains relatively low (Liu et al., 2023). Moreover, due to differences in resource endowment and economic development levels, there are significant disparities in the implementation of green development concepts across regions. The eastern region benefits from technological and market advantages, resulting in a significantly higher level of AGD compared to the central and western regions (Sun and Sui, 2023). This disparity poses a significant challenge to the comprehensive advancement of agricultural green transformation in our country. Moreover, it is worth noting that although quantitative methods such as the entropy weight method, grey relational analysis, and data envelopment analysis (DEA) models have been widely applied in practice, each of these methods has its limitations. The entropy weight method and grey relational analysis are highly sensitive to data, which may lead to variability and uncertainty in the results. The DEA model demonstrates flexibility in handling various data types and multiple input and output variables, providing significant advantages compared to other evaluation models (Kyrgiakos et al., 2023). However, DEA typically requires that the number of decision-making units (DMUs) be at least two to three times the sum of the input and output indicators, which limits the choice to a few representative indicators and restricts the systematic nature of the evaluation. Additionally, most existing evaluation models are retrospective analyses, lacking predictive capabilities, and are thus inadequate for effectively guiding current production planning. Therefore, there is an urgent need to develop a comprehensive evaluation model that integrates systematic assessment, broad applicability, and predictive ability.

As one of the most economically influential regions in China, the Yangtze River Delta has become a pioneering and demonstrative area for AGD policies, supported by a robust policy framework. In advancing AGD, the region has established various types of demonstration zones, including ecological agriculture demonstration areas, technology-driven agricultural demonstration areas, and agricultural industry integration demonstration zones (Geng et al., 2020; Cheng and Ren, 2024). Although these demonstration zones are all committed to the goal of AGD, they exhibit significant differences in terms of factor allocation and development pathways. AGD encompasses multiple dimensions, including traditional elements and emerging factors such as agricultural digitization, which complicates the rational allocation of resource inputs. Consequently, how to scientifically plan and reasonably allocate various resource inputs has become an important challenge. The three-stage DEA model is capable of fully considering external environmental impacts under diverse input and output conditions, demonstrating significant advantages in the rational allocation of resources. However, its systematic evaluation and predictive capabilities still have limitations. Therefore, this study constructs a 3S-DEA-SBM-BP model based on DEA and BP algorithms to comprehensively analyze the key impacts of various inputs on AGD. Furthermore, this research employs methods such as kernel density estimation (KDE) and Moran’s index to systematically analyze the efficiency and spatiotemporal evolution characteristics of AGD in the Yangtze River Economic Belt at the urban level. The aim is to deeply analyze the AGD characteristics of cities in the Yangtze River Delta and predict their future development trends, providing valuable guidance for AGD planning in this region and beyond.

3 Methodology

3.1 Research region

The Yangtze River Delta is located in the eastern part of China, spanning four provinces and municipalities including Jiangsu, Anhui, Zhejiang, and Shanghai. In the year 2019, the Chinese government released the Outline of the Plan for Integrated Regional Development of the Yangtze River Delta. This strategic framework designates a central zone comprising 27 cities, with the specific distribution of cities shown in Figure 1. This central zone serves as the nucleus for radiating and propelling high-quality development throughout the Yangtze River Delta region. Therefore, this study focuses on these 27 cities, employing a 3S-DEA-SBM-BP model to thoroughly explore the features of AGD and forecast future development trends.

Figure 1

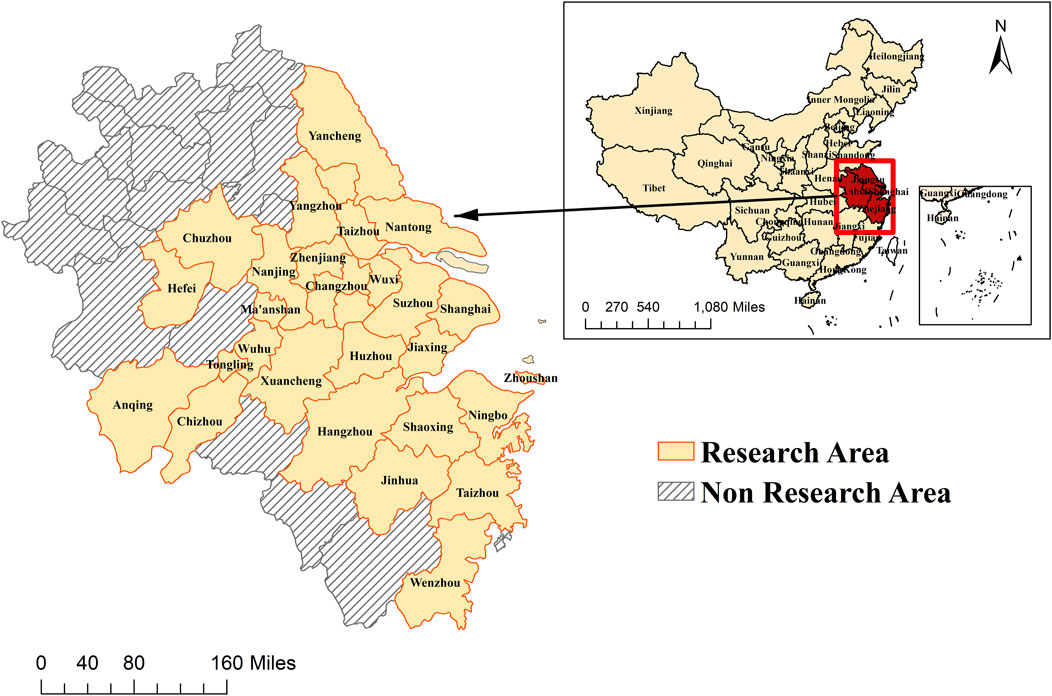
Figure 1. Research Region. Note: County-level cities under the jurisdiction of each municipality are not specially labeled.

In 2017, China explicitly put forward the idea of establishing a sound economic system for green, low-carbon, and circular development. This provided a clear direction for high-quality development in the new era and presented an extremely important theme for the times. Given that the relevant data for 2023 has not been released, this study has chosen the timeframe from 2017 to 2022 and considers 2023 as the future period.

3.2 Research method

3.2.1 DEA-SBM based on non-expected output

Because the CCR and BCC models assume that inputs and outputs change proportionally, Tone (2001) introduced the SBM model, which allows inputs and outputs to vary in different proportions, existing researches have indicated that the SBM solution values are more in line with actual production efficiency values (Gerami et al., 2022). However, the original SBM model can only measure the efficiency of DMUs with expected outputs, while actual production processes often involve non-expected outputs. Tone (2003) proposed the DEA-SBM model based on non-expected outputs, expanding its applicability. The formula can be expressed as (Equation 1).

$\min \rho =\frac{1-\frac{1}{t}{\displaystyle \sum _{i=1}^t}\raisebox{1ex}{$s_i^{-}$}\!\left/ \!\raisebox{-1ex}{$x_{ik}$}\right.}{1+\frac{1}{c_1+c_2}\left({\displaystyle \sum _{r=1}^{c_1}}\raisebox{1ex}{$s_r^{+}$}\!\left/ \!\raisebox{-1ex}{$y_{rk}$}\right.+{\displaystyle \sum _{t=1}^{c_2}}\raisebox{1ex}{$s_t^{b-}$}\!\left/ \!\raisebox{-1ex}{$b_{rk}$}\right.\right)}$

$s.t.\left\{\begin{array}{l}X\lambda +s^{-}=x_k\\ Y\lambda -s^{+}=Y_k\\ B\lambda +s^b=b_k\\ \lambda ,s^{-},s^{+}\ge 0\end{array}\right.(1)$

In which, $x_{ik}$ is the i-th input of the k-th DMU, $y_{rk}$ is the r-th output of the k-th DMU, b stands for non-expected output, $c_1$, $c_2$ represents the number of expected and non-expected outputs respectively. $X$, $Y$, $\lambda$ represent the input matrices and output matrices and coefficient matrices, while $s^{-}$ is input slack variables and $s^{+}$ is output slack variables.

The Super-Efficiency model, with the addition of extra constraints denoted by “ $j\ne k$”, calculates the efficiency values of DMUs by utilizing the production frontier formed by other DMUs. Consequently, the Super-Efficiency SBM model can effectively differentiate the efficiency of DMUs that are in the DEA-efficient state. The formula can be expressed as (Equation 2).

$\min \rho =\frac{1+\frac{1}{t}{\displaystyle \sum _{i=1}^t}\raisebox{1ex}{$s_i^{-}$}\!\left/ \!\raisebox{-1ex}{$x_{ik}$}\right.}{1-\frac{1}{c_1+c_2}\left({\displaystyle \sum _{r=1}^{c_1}}\raisebox{1ex}{$s_r^{+}$}\!\left/ \!\raisebox{-1ex}{$y_{rk}$}\right.+{\displaystyle \sum _{t=1}^{c_2}}\raisebox{1ex}{$s_t^{b-}$}\!\left/ \!\raisebox{-1ex}{$b_{rk}$}\right.\right)}$

$s.t.\left\{\begin{array}{l}{\displaystyle \sum _{j=1,j\ne k}^n}{x}_{ij}{\lambda }_j-s_i^{-}\le x_{ik}\\ {\displaystyle \sum _{j=1,j\ne k}^n}{b}_{tj}{\lambda }_j-s_t^{b-}\le b_{tk}\\ 1-\frac{1}{c_1+c_2}({\displaystyle \sum _{r=1}^{c_1}}\raisebox{1ex}{$s_r^{+}$}\!\left/ \!\raisebox{-1ex}{$y_{rk}$}\right.+{\displaystyle \sum _{t=1}^{c_2}}\raisebox{1ex}{$s_t^{b-}$}\!\left/ \!\raisebox{-1ex}{$b_{rk}$}\right.>0\\ \lambda ,s^{-},s^{+}\ge 0\end{array}\right.(2)$

3.2.2 3S-DEA-SBM based on non-expected outputs

First, the initial efficiency values for each DMU and the slack values for each input indicator are calculated.

Next, the slack variable of the input indicator is used as the dependent variable, and Stochastic Frontier Analysis (SFA) regression is performed with selected external environmental factors as independent variables. The results from this regression are then used to adjust the original inputs. The formula for the SFA regression function is represented in (Equation 3).

$s_{ik}=f\left(Z_K;{\beta }_i\right)+v_{ik}+{\mu }_{ik}(3)$

In which, $s_{ik}$ represents the slack variable for the i-th input of the k-th DMU. $Z_k$ represents the environmental variable. ${\beta }_i$ represents the coefficient to be estimated for the environmental variable. $v_{ik}$ represents the random disturbance. $v_{ik}\sim N\left(0,{\sigma }_v^2\right)$, ${\mu }_{ik}$ represents the inefficient management.

The maximum likelihood estimation method is utilized to estimate location parameters. During the research, the separation formula proposed by Luo is applied to break down the mixed errors into managerial inefficiency and random error (Luo, 2012). The separation formula is shown as (Equation 4).

$\stackrel{\wedge }{E}\left({\mu }_{ik}+v_{ik}\right)=\frac{\sigma \lambda }{1+{\lambda }^2}\left[\frac{\phi \left(\lambda \frac{{\epsilon }_1}{\sigma }\right)}{\mathit{ø}\left(\frac{\lambda {\epsilon }_1}{\sigma }\right)}+\frac{\lambda {\epsilon }_i}{\sigma }\right](4)$

In which, ${\epsilon }_i={\mu }_{ik}+v_{ik}$, $\lambda =\raisebox{1ex}{${\sigma }_{\mu }$}\!\left/ \!\raisebox{-1ex}{${\sigma }_v$}\right.$, $\sigma =\sqrt{{\sigma }_{\mu }^2+{\sigma }_v^2}$;

The final adjusted formula is as follows:

$X_{ik}^A=X_{ik}+\left[\max (f\left(Z_k;{\widehat{\beta }}_K\right)-f\left(Z_k;{\widehat{\beta }}_K\right)\right]+\left(\max \left(v_{ik}\right)-v_{ik}\right)(5)$

In which, $X_{ik}^A$ (Equation 5) is the adjusted input, while $X_{ik}$ is the input before adjustment.

Eventually, the efficiency values, adjusted using SFA, are recalculated with the non-expected Output super-efficiency DEA-SBM model.

3.2.3 BP algorithm

The BP algorithm generally consists of three parts: the input layer, the hidden layer, and the output layer. Existing research indicates that a three-layer BP algorithm can approximate any nonlinear function. Therefore, this paper primarily introduces the training process of the three-layer BP algorithm model. The training process of the BP consists of forward propagation of the signal and backward propagation of the error.

Assume that $x_i$ is the input to the i-th neuron in the input layer. $W_{hi}$ and $W_{oh}$ represent the weights from the hidden layer (h) to the input layer (i) and from the output layer (o) to the hidden layer (h), respectively; ${\theta }_h$ is the threshold of hidden layer neuron h; f and g respectively represent the activation functions for the hidden layer and the output layer; $a_o$ represents the threshold for the neuron o in the output layer, and $y_o$ represents the output of the o-th neuron in the output layer. The training process of the BP algorithm is as follows:

The process of forward signal propagation (Equations 6, 7). The input $ne{t}_h$ and output $z_h$ of the hidden layer node (h):

$ne{t}_h={\displaystyle \sum _{h=1}^M}{W}_{hi}{x}_i+{\theta }_h(6)$

$z_h=f_h\left(ne{t}_h\right)=f\left({\displaystyle \sum _{h=1}^M}{W}_{hi}{x}_i+{\theta }_h\right)(7)$

The input $ne{t}_o$ and output $y_o$ of the output layer node (O):

$ne{t}_o={\displaystyle \sum _{h=1}^q}{W}_{oh}{z}_h+a_o(8)$

$y_o=g\left(ne{t}_o\right)=g\left({\displaystyle \sum _{h=1}^q}{W}_{oh}{z}_h+a_o\right)(9)$

where $M$ and $q$ is the total number of neurons in the input and hidden layer, respectively (Equations 8, 9).

Error backpropagation. The error E for the n-th sample is given by (Equation 10)

$E=\frac{1}{2}{\displaystyle \sum _{o=1}^L}{\left(T_o-y_o\right)}^2(10)$

where $T_o$ is the true value of the o-th neuron, and L denotes the total number of neurons in the output layer.

The total error for N samples is given by:

$E_z={\displaystyle \sum _{n=1}^N}E=\frac{1}{2}{\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{o=1}^L}{\left(T_o-y_o\right)}^2(11)$

As per (Equation 11), it is evident that the total error is a function of the weights and thresholds in each layer. Therefore, by adjusting the weights and thresholds, the error can be reduced. The adjustment of the correction amount $△W_{oh}$ for the output layer weights is carried out using the gradient descent method. Assuming the learning rate is $\eta$, from the partial derivative of (Equation 8), it can be expressed as (Equation 12).

$△W_{oh}=-\eta \frac{\partial E}{\partial W_{oh}}=-\eta \frac{\partial E}{\partial ne{t}_o}\frac{\partial ne{t}_o}{\partial W_{oh}}=-\eta \frac{\partial E}{\partial ne{t}_o}{z}_h(12)$

Similarly, the formulas for the adjustment of the output layer threshold $△a_k$, the hidden layer weight $△W_{ij}$, and the threshold $△{\theta }_i$ can be represented as (Equations 13–15).

$△a_o=-\eta \frac{\partial E}{\partial a_o}=-\eta \frac{\partial E}{\partial ne{t}_o}(13)$

$△W_{hi}=-\eta \frac{\partial E}{\partial W_{hi}}=-\eta \frac{\partial E}{\partial ne{t}_o}{x}_i(14)$

$△{\theta }_h=-\eta \frac{\partial E}{\partial {\theta }_h}=-\eta \frac{\partial E}{\partial ne{t}_h}(15)$

Based on the partial derivatives of (Equations 9, 10), this paper defines the local gradient as (Equation 16).

$\begin{array}{l}{\delta }_o=-\frac{\partial E}{\partial ne{t}_o}=-\frac{\partial E}{\partial o_o}\frac{\partial o_o}{\partial ne{t}_o}\\ =\left(T_o-y_o\right)g^{\prime }\left(ne{t}_o\right)=\left(T_o-y_o\right)y_o\left(1-y_o\right)\end{array}(16)$

The formulas for adjusting the output layer weights and thresholds can be simplified to (Equations 17, 18).

$△W_{oh}=\eta {\delta }_o{y}_h(17)$

$△a_o=-\eta \frac{\partial E}{\partial a_o}=\eta {\delta }_o(18)$

Likewise, define (Equation 19).

$\begin{array}{l}{\delta }_h=-\frac{\partial E}{\partial ne{t}_h}=-\frac{\partial E}{\partial y_h}\frac{\partial y_h}{\partial ne{t}_h}=-\frac{\partial E}{\partial y_h}{f}^{\prime }\left(ne{t}_h\right)\\ =-\frac{\partial E}{\partial ne{t}_o}-\frac{\partial ne{t}_o}{\partial y_h}{f}^{\prime }\left(ne{t}_h\right)=-\frac{\partial E}{\partial ne{t}_o}{W}_{oh}={\delta }_o{W}_{oh}\end{array}(19)$

The formulas for adjusting the hidden layer weights and thresholds can be simplified to (Equations 20, 21):

$△W_{hi}=\eta {\delta }_h{x}_i(20)$

$△{\theta }_h=\eta {\delta }_h(21)$

In the BP algorithm, the weights and thresholds between layers are iteratively adjusted based on the error between the output value and the expected value, until the final sample error is achieved or the specified number of iterations is reached. Therefore, the ultimate performance of the BP algorithm is closely related to factors such as the error threshold, learning rate, and number of iterations.

3.2.4 Dagum Gini coefficient

The Gini coefficient is an important indicator used to measure the inequality of income or wealth distribution. In 1997, Dagum decomposed the Gini coefficient into the contributions of intra-group differences, inter-group net differences, and inter-group super-variable density. This method not only effectively identifies the sources of regional disparities but also explains the issues of cross-terms between subgroups. Therefore, the Dagum Gini coefficient is widely used in analyzing regional disparities, and its specific formula is as follows:

Overall Gini coefficient (Equation 22):

$H=H_w+H_{nb}+H_t(22)$

Intra-regional disparity contribution (Equations 23–26):

$H_w={\displaystyle \sum _{j=1}^m}{H}_{jj}{p}_j{s}_j(23)$

$H_{jj}=\frac{\frac{1}{2{\alpha }_j}{\displaystyle \sum _{i=1}^{o_j}}{\displaystyle \sum _{r=1}^{o_j}}\left|{\rho }_{ji}-{\rho }_{hr}\right|}{n_j^2}(24)$

$p_j=\frac{o_j}{o}(25)$

$s_i=\frac{o_j{\alpha }_j}{no}(26)$

where $\alpha$ represents the overall mean, ${\alpha }_h$ is the average efficiency of AGD in region $h$, $o$ is the number of provinces, $n_j$ represents the number of provinces included in the subgroup $j$, $k$ is the number of regions; $H_{jj}$ is the Gini coefficient within provinces.

Inter-regional net value difference contribution (Equations 27–30):

$H_{nb}={\displaystyle \sum _{j=2}^k}{\displaystyle \sum _{h=1}^{j=1}}{H}_{jh}\left(p_j{s}_h+p_h{s}_j\right)I_{jh}(27)$

$I_{jh}=\frac{s_{jh}-w_{jh}}{s_{jh}+w_{\left.jh\right|}}(28)$

$s_{jh}={\int }_0^{\infty }\mathrm{d}{F}_j\left(\rho \right){\int }_0^{\rho }\left(\rho -x\right)\mathrm{d}{F}_h\left(x\right)(29)$

$w_{jh}={\int }_0^{\infty }\mathrm{d}{F}_h\left(\rho \right){\int }_0^{\rho }\left(\rho -x\right)\mathrm{d}{F}_j\left(x\right)(30)$

where $I_{jh}$ is the relative impact of efficiency between regions $j$ and $h$, $s_{jh}$ represents the difference in efficiency between region $j$ and $h$, and $w_{jh}$ can be understood as the mathematical expectation of ${\rho }_{hr}-{\rho }_{ji}>0$ that satisfy the conditions in regions $j$ and $h$.

Super-variable density difference contribution (Equations 31, 32):

$H_t=H_{jh}\left(p_j{s}_h+p_h{s}_j\right)\left(1-H_{jh}\right)(31)$

$I_{jh}=\frac{s_{jh}-w_{jh}}{s_{jh}+w_{jh}}(32)$

where $I_{jh}$ represents the relative impact between regions $j$ and $h$.

3.2.5 Moran’s index

Moran’s Index is a statistical method used to assess the distribution characteristics and interrelationships of spatial data. Its basic assumption is that spatial data values at neighboring locations may exhibit some form of dependence, which diminishes with increasing distance. Moran’s index can be expressed as (Equations 33, 34).

$I_a=\frac{{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{w}_{ij}\left(x_i-\overline{x}\right)(x_j-\overline{x})}{S^2{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{w}_{ij}}\left(i\ne j\right)(33)$

$I_b=\frac{x_i-\overline{x}}{S^2}{\displaystyle \sum _{j=1}^n}{w}_{ij}\left(x_i-\overline{x}\right)(34)$

Here, $I_a$ and $I_b$ represent the global and local Moran’s Index values, respectively, $n$ represents the total number of provinces under investigation, $i$ and $j$ denote distinct spatial units, $x_i$ and $x_j$ indicate the efficiency values of province $i$ and $j$, $\overline{x}$ and $S^2$ indicate the mean and variance, and $w_{ij}$ serving as the spatial weight matrix. Global spatial autocorrelation analyzes the overall spatial disparities and clustering patterns of AGD. In contrast, the local Moran’s Index focuses on assessing spatial differences among neighboring cities.

3.3 Indicator selection

3.3.1 AGD efficiency input-output indicators

AGD emphasizes following sustainable development principles in the agricultural production process, fully utilizing advanced science and technology and scientific management methods to foster agricultural sustainability and enhance the ecological environment. Agricultural development has its unique characteristics, requiring inputs of land and labor, whether it is traditional or modern agriculture. In the information age, digital economy and green technology innovation have become two key directions leading the transformation of industrial structures, and they naturally influence agricultural development (Yin and Qiu, 2023). Therefore, this paper takes crop sown area, labor force, mechanization level, green technology innovation, and agricultural digital economy as input indicators. In measuring agricultural digital economy indicators, most studies currently consider broadband penetration rate as a substitute indicator for the digital economy. However, with the rise of short video platforms, mobile phones have become important terminals for many farmers to participate in online transactions due to their convenience and low threshold. Therefore, this paper considers the Internet device penetration rate, including broadband penetration rate and mobile terminal penetration rate, as substitute indicators for the digital economy.

AGD emphasizes the pollution-free and sustainability aspects of production. However, inevitably, agricultural production processes will generate unintended outputs such as environmental pollution. Agricultural pollution sources mainly include chemical fertilizers, pesticides, plastic film residues, and agricultural carbon emission. Existing studies often use the quantities or residues of chemical fertilizers, pesticides, and plastic films as surrogate indicators for solid pollution sources, and they use the quantities of various fossil energy sources as surrogate indicators for carbon emission (Liang and Long, 2015), Although this simplifies the calculation steps, it fails to comprehensively reflect agricultural surface pollution sources. Building upon existing research, this article uses the Entropy Weight-TOPSIS method to comprehensively analyze the residues of chemical fertilizers, pesticides, and plastic films residues to obtain an agricultural pollutant emission index. During the calculation process, residues = actual usage * retention rate, with the retention rates for chemical fertilizers, pesticides, and plastic films chosen as the average rates published by the Chinese Ministry of Agriculture, which are 59.8%, 59.4%, and 18.6%, respectively. Regarding agricultural carbon emission, this paper calculates the total carbon emission for each city based on the usage of nine energy sources: coal, coke, crude oil, gasoline, kerosene, diesel, fuel oil, liquefied petroleum gas, and natural gas. The IPCC method is employed for estimation, and the carbon emission from agriculture in each city are estimated based on the proportion of the primary industry.

Furthermore, in the context of rural revitalization, promoting AGD has become a policy tool to narrow the rural-urban disparity and promote common prosperity. AGD emphasizes sustainable development and environmental protection. By adopting eco-friendly production methods, enhancing product added value and quality, it drives the diversified development of industries such as organic agriculture, eco-tourism, and rural e-commerce, continuously enriching the connotation of rural economic development, creating more employment opportunities, reducing the development gap between urban and rural areas, and ultimately achieving the goal of common prosperity. Therefore, this paper utilizes the entropy weight-TOPSIS method to select nine representative indicators in three dimensions: affluence, sharing, and sustainability. These dimensions include per capita GDP, per capita disposable income of rural residents, the proportion of local general budget revenue, urban-rural income ratio, security level, unemployed reemployment, the number of higher education graduates, water resources, and greening rate. These indicators are used to comprehensively analyze and obtain the Rural Shared Prosperity Index to measure the promotion of agricultural development on social equity. As a result, the output indicators in this paper are finally determined as agricultural production value, agricultural pollutant emission index, agricultural carbon emission, and Rural Shared Prosperity Index, balancing economic, environmental, and social benefits. The AGD input-output indicator system is shown in Table 1.

Table 1

Table 1. AGD indicator system.

3.3.2 Environmental variables

Environmental variables are defined as factors that affect production efficiency but cannot be managed by the DMU itself. In order to effectively eliminate the interference of the environment, it is necessary to select environmental factors from multiple dimensions. Yan et al. considered per capita regional GDP, the proportion of primary industry to GDP, the proportion of internal expenditure on scientific activities, along with the total value of trade in goods as the most influential external environmental factors affecting food production (Yan et al., 2022). Chen Y et al. believed that external environmental factors can be decomposed into natural, economic, and policy factors, and further proposed that natural factors such as terrain and precipitation, economic factors including level of economic development and dependence on trade, as well as policy factors like the extent of financial support, are important factors influencing green production in the agricultural sector in China (Chen et al., 2021). Since the differences in resource endowments among regions in the Yangtze River Delta are relatively small, this paper was based on economic and policy factors, combined with the characteristics of agricultural production, to choose three indicators—macroeconomic development level, labor quality, and policy support—as environmental variables. Considering the availability of data, this study uses per capita disposable income of rural residents to measure the macroeconomic development level of each region, the ratio of graduates from higher education institutions to the resident population to measure labor quality, and the funding allocated for agriculture, forestry, and water resources in the overall public budget to measure government policy support.

3.4 Data sources

The data sources include the China Statistical Yearbook, Statistical Yearbooks of Various Cities, China Energy Statistical Yearbook, and the Greenhouse Gas Emissions Inventory for the years 2017–2022. In cases where data was missing for certain years, it was imputed using the historical average growth rates. The Rural Shared Prosperity Index, Agricultural Pollution Emission Index, and Carbon Emission were calculated based on the statistical data using the methods introduced earlier in this paper.

4 Results

The 3S-DEA-SBM-BP model constructed in this study first measures the AGD efficiency of each city using the 3S-DEA-SBM model. Subsequently, the AGD efficiency of each city is used as the output set for training the BP algorithm. The technical roadmap of this study is shown in Figure 2.

Figure 2

Figure 2. The technical roadmap of this study.

4.1 3S-DEA-SBM model

4.1.1 First-stage AGD efficiency

The study first employs the constant returns DEA-SBM model with non-desired outputs to measure the efficiency of AGD, setting the weights of non-desired and desired outputs at a 1:1 ratio. Summarize and organize the calculation results to obtain the average efficiency of AGD in the first stage of each city in Table 3.

From a longitudinal perspective, the average efficiency of AGD in the first stage in the Yangtze River Delta region from 2017 to 2022 ranged from 0.72 to 0.75, showing overall stability. Nonetheless, scale efficiency was marginally greater than pure technical efficiency, suggesting that AGD in the Yangtze River Delta region has reached a relatively mature stage. From a horizontal perspective, there is a significant disparity in the efficiency of AGD among different cities. The lowest efficiency was observed in Tongling City, Anhui Province, with a value of 0.19, while the highest efficiency reached 1, resulting in a gap of 0.81. During the period from 2017 to 2022, there were 13 cities with an efficiency value of 1 under the DEA-SBM model in the first stage. These cities include Anqing, Chuzhou, and Xuancheng in Anhui Province; Changzhou, Nanjing, Nantong, Wuxi, and Yancheng in Jiangsu Province; and Shanghai, as well as Jinhua, Ningbo, Taizhou, and Zhoushan in Zhejiang. This indicates that these 13 cities maintained DEA efficiency over the six-year period. Additionally, there is a considerable difference in AGD efficiency among different provinces. Anhui Province, Jiangsu Province, Shanghai City, and Zhejiang Province had efficiency values of 0.62, 0.87, 1.00, and 0.68, respectively. Shanghai City and Jiangsu Province exhibited higher AGD efficiency, while Anhui Province had relatively lower AGD efficiency.

Due to the large number of DMUs in a DEA-efficient state, this article employs the super-efficiency model to reevaluate the 13 cities that remained DEA-efficient. In the super-efficiency model, Zhoushan City in Zhejiang Province has the highest average efficiency, with a value of 1.99, while Xuancheng in Anhui Province has the lowest, with a value of 1.01. The difference between them is 0.98. This indicates that even among cities in the DEA-effective state, there remains a significant disparity in development efficiency.

The influence of environmental factors and random noise cannot be eliminated by the first-stage DEA model. To achieve a more objective measurement of AGD efficiency, the second stage will utilize a SFA to remove the impact of environmental factors and random noise and obtain more accurate AGD efficiency values.

4.1.2 Second stage SFA analysis

In this stage, the redundant variables of input indicators, measured by the first stage DEA-SBM analysis of AGD efficiency, are taken as the dependent variables. Meanwhile, three environmental variables - macroeconomic development level, labor quality, and policy support - for the years 2017–2022 are selected as independent variables. Logarithmic transformations are applied to the environmental variables, and their impact on the redundant values of various input indicators is calculated using Frontier 4.1 software, as shown in Table 2.

Table 2

Table 2. Results of SFA.

As shown by the coefficients in Table 2, the regression coefficients of the macroeconomic development level on the slack variables of various inputs are positive, and all are statistically significant at the 1% level. This indicates that an improvement in the macroeconomic development level reduces the efficiency of green agricultural development. This may be because in economically developed regions, social capital and high-quality talent are more likely to flow into the more advanced secondary and tertiary industries, thus reducing the efficiency of green agricultural development. The quality of the labor force is significant at the 1% level for the slack variables of all inputs. However, the regression coefficient of labor quality on the slack of agricultural economic digitalization level is negative, indicating that the improvement in labor quality reduces the slack of agricultural economic digitalization but significantly increases the redundancy of other inputs, such as green technology innovation. This could be because high-quality workers possess higher education levels and technical skills, enabling them to utilize modern agricultural technologies and equipment more effectively, thereby reducing the dependence of agricultural production on inputs like land and labor. The regression coefficient of policy support on the slack of mechanization level is positive and significant at the 1% level, while the coefficients on the slack of other input indicators are negative. The slack variables for crop planting area, labor input, and agricultural economic digitalization pass the 1% significance test. This suggests that policy support increases the slack of mechanization level but significantly reduces the redundancy of other inputs. This phenomenon may be due to government support for agricultural production through subsidies for agricultural machinery. As government attention to agricultural production continues to increase, more capital and management talent flow into the agricultural machinery production sector, leading to resource redundancy.

In summary, the selected environmental variables—macroeconomic development level, labor quality, and policy support—all have statistical impacts on AGD. Among them, the macroeconomic development level has a negative impact, while labor quality and policy support exhibit bidirectional effects.

4.1.3 The third stage of AGD efficiency

Recalculate efficiency for the adjusted input data from the second phase using the steps from the first phase. To further distinguish cities that are not in a DEA efficient state, we referenced the research methods of Yi M et al. and categorized the AGD efficiency of each city into four levels (Yi et al., 2019). Specifically, when the AGD technical efficiency is greater than or equal to 1, it indicates that the development efficiency is in a DEA efficient state, with input-output balance and rational resource allocation. When the technical efficiency is between 0.8 and 1, the development efficiency is in a relatively efficient state, indicating that inputs have not been fully converted into outputs, but balance can be achieved through systematic adjustments. When the technical efficiency is between 0.6 and 0.8, it indicates a weakly efficient DEA state, with inputs and outputs weakly efficient, requiring long-term adjustments to achieve balance. When the overall technical efficiency is less than 0.6, it indicates an inefficient DEA state, with obvious problems in resource allocation, necessitating a reconfiguration of inputs. Summarizing and organizing the calculation results, one can obtain the average efficiency of AGD in the third stage for each city in Table 3, along with a spatial distribution comparison of average efficiency between the first and third stages, as illustrated in Figure 3.

Table 3

Table 3. The average efficiency of AGD in each city for the first and third stages.

Figure 3

Figure 3. Comparison of first and third stage super-efficiency values.

From Table 3 and Figure 3, it is evident that the overall AGD efficiency values in the third stage are lower than those in the first stage. This indicates that environmental factors and random disturbances have a significant impact on the measurement of AGD efficiency in the Yangtze River Delta region. Therefore, using SFA to eliminate environmental factors and random disturbances can yield more objective and accurate efficiency values.

From a longitudinal perspective, the average AGD efficiency values in the third stage ranged from 0.63 to 0.71. Compared to the first stage, technical efficiency significantly decreased and exhibited higher fluctuations. The gap between scale efficiency and pure technical efficiency narrowed, indicating that the AGD efficiency in the Yangtze River Delta region is significantly influenced by environmental factors and random disturbances. When viewed across cities, notable disparities in AGD efficiency persist. The lowest value is still found in Tongling City, Anhui Province, with a value of 0.22, while the highest value is 1, resulting in a difference of 0.78. From 2017 to 2022, eight cities achieved an average efficiency value of 1, including Changzhou, Nantong, Wuxi, and Yancheng in Jiangsu Province, as well as Jinhua, Ningbo, Taizhou, and Zhoushan in Zhejiang. The eight cities also had an average efficiency value of 1 in the first stage, indicating their high AGD efficiency, which is attributed to their favorable internal environments. But, Shanghai, Anqing City and Chuzhou City in Anhui Province, Xuanzhou City, and Nanjing City in Jiangsu Province saw their efficiency values drop from 1 in the first stage to 0.34, 0.84, 0.70, 0.88, and 0.74 in the third stage, respectively. This suggests that the previously higher AGD efficiency values of these cities were due to their favorable external environments, such as macroeconomic development and policy support. Among the eight cities in an effective DEA state, Zhoushan City in Zhejiang still had the highest average efficiency value of 1.99, while Taizhou City in Zhejiang had the lowest value at 1.02, resulting in a significant difference in development efficiency. Additionally, there were substantial differences in development efficiency between different provinces in both the first and third stages. The third-stage efficiency values in Anhui, Jiangsu, Shanghai, and Zhejiang were 0.46, 0.86, 0.74, and 0.70, respectively. Compared to the first stage, Zhejiang’s technical efficiency slightly improved, while Anhui, Jiangsu, and Shanghai experienced a decrease in technical efficiency. Among them, Anhui and Shanghai were more affected by external environmental factors.

4.2 BP algorithm

To address the limitations in quantity and the inability to manage in advance between the DEA model DMU and indicators, this paper integrates the BP algorithm to construct a 3S-DEA-SBM-BP model. This model is designed to systematically evaluate the efficiency of AGD.

4.2.1 Construction and training of the BP algorithm

The input set for the BP algorithm in this study, in addition to the input indicators of the DEA model, includes additional input indicators such as agricultural chemicals, energy, resources, environmental protection, security level, export dependence, infrastructure construction, and others. This comprehensive set of inputs aims to measure the economic, environmental, and social aspects of inputs in agricultural production. The input set of BP is shown in Table 4.

Table 4

Table 4. The input indicators for the BP algorithm.

The efficiency values from the third stage of AGD in each city between 2017 and 2022 serve as the output dataset for the BP algorithm. Of this set, 80% is used as the training set, 10% as the validation set, and 10% as the testing set. After min-max normalization, MATLAB 2016a software is employed for computation. The parameter configurations are as follows: a single-layer BP network architecture featuring 6 nodes in the hidden layer; the activation function connecting the input layer to the hidden layer employs the Logsig function, whereas the output layer utilizes the Purelin function as its activation function. The training function is set as Trainlm, with a learning rate of 0.001, a minimum error goal for training of 1E-07, and a maximum number of iterations set at 15,000.

The final 3S-DEA-SBM-BP model in this study achieved fitting coefficients of 0.94, 0.92, and 0.96 for the test set, validation set, and training set, respectively. The overall fitting coefficient was 0.94, indicating a good overall fit, with all fitting coefficients being above 0.9.

It can be observed that the BP algorithm’s test set predictions closely match the actual efficiency changes in DEA (Figure 4). The BP algorithm’s predicted values range from 0.25 to 2.14, while the actual efficiency values range from 0.32 to 2.00. The overall average error is 0.076, with only one instance of a prediction failure, where DEA-effective status was incorrectly predicted as non-DEA effective. The prediction accuracy is 94%. Therefore, the 3S-DEA-SBM-BP model, combining the 3S-DEA-SBM-BP model and BP algorithm, can effectively measure and predict the AGD efficiency.

Figure 4

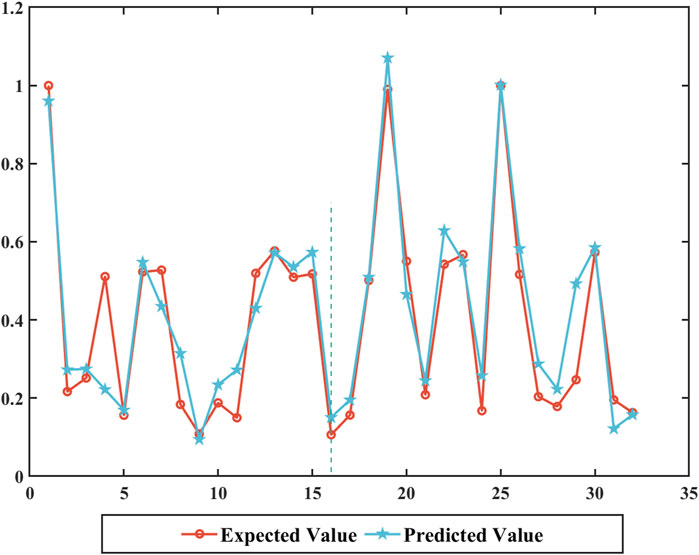
Figure 4. Fitting Results of the DEA-SBM-BP Mode. Note: The left side of the dashed line represents the validation set, and the right side represents the test set.

4.2.2 Weight analysis of indicators

The weights at various layers in the BP algorithm can, to some extent, reflect the influence of the input layer on the output layer. However, the weights obtained by training the BP network only represent the relationships between the neurons in the network, and the weights or their products do not fully reflect the decision weights of the input indicators on the output indicators. Therefore, in this paper, leveraging existing research findings, decision weights are measured by calculating the absolute impact coefficients between input and output indicators (Wu et al., 2006). The formula for calculating the absolute impact coefficients is as follows:

Significant Correlation Coefficients (Equation 35):

$r_{io}={\displaystyle \sum _{h=1}^p}{W}_{hi}\left(1-e^{-W_{oh}}\right)\left(1+e^{-W_{oh}}\right)(35)$

Correlation Index (Equation 36):

$R_{io}=\left|\left(1-e^{-r_{io}}\right)/\left.\left(1+e^{-r_{io}}\right)\right|\right.(36)$

Absolute Impact Coefficient (Equation 37):

$S_{io}=R_{io}/{\displaystyle \sum _{i=1}^m}{R}_{ij}(37)$

where i represents the input layer neuron in the BP algorithm, $i=1,2,\cdots ,m$; j represents the output layer neuron in the BP algorithm, $j=1,2,\cdots ,n$; h represents the hidden layer, $h=1,2,\cdots ,p$; $W_{hi}$ represents the weight between input layer i and hidden layer h; $W_{oh}$ represents the weight between output layer neuron o and hidden layer neuron h; According to the above formula, the weights between each neuron can be calculated to obtain the absolute impact coefficients, i.e., the weights for input indicators on output indicators. Table 5 present the weights and distribution of each input indicator in the 3S-DEA-SBM-BP model constructed in this paper.

Table 5

Table 5. Input indicator weights.

From Table 5, it can be observed that infrastructure development, agricultural digitization, and social security are the most influential factors affecting the efficiency of AGD in the Yangtze River Delta region, with weights all above 12%. This is because agriculture is highly vulnerable to natural factors, and robust agricultural infrastructure helps resist the uncertainties posed by these natural elements, ensuring stable expected returns in agricultural production. In the digital age, the “digital+” approach is driving continuous improvements in agriculture, injecting new energy into rural revitalization. Social security represents social equity, which promotes the rational allocation of resources and ensures that everyone has access to high-quality education and training opportunities, thereby enhancing people’s quality of life. Therefore, improvements in infrastructure development, agricultural digitization, and social security significantly enhance agricultural production efficiency. The next most influential factors affecting the efficiency of AGD in the Yangtze River Delta region are environmental investment, crop planting area, and green technology innovation, each with weights exceeding 10%. As AGD emphasizes the convergence of economic, environmental, and social benefits, the impact of environmental investments on AGD efficiency is gradually increasing. It is noteworthy that among the influencing factors of AGD, traditional agricultural elements such as resources, agricultural labor, energy, agrochemicals, and mechanization, all have weights below 5%. This suggests that traditional extensive agriculture is shifting towards sustainable agriculture.

4.3 Regional disparity analysis

The analysis results from earlier sections indicate that AGD efficiency in the Yangtze River Delta region has gradually improved, yet significant disparities persist among cities within the provinces. Taking Anhui Province as an example, during the study period, Chuzhou City exhibited the highest AGD efficiency, reaching 0.87, while Tongling City showed the lowest efficiency at only 0.22, resulting in a difference of 0.65 between them. In comparison, the differences in AGD efficiency between Anhui Province and Jiangsu Province, Shanghai, and Zhejiang Province were 0.46, 0.28, and 0.36, respectively, highlighting a significant imbalance in development within the province. To objectively assess the degree of AGD imbalance among provinces and cities, this study employs the Dagum Gini coefficient to measure both intra-regional and inter-regional inequality.

The comprehensive Gini coefficient for the Yangtze River Delta region remained around 0.3 during the study period, suggesting that AGD in the region is generally balanced. In terms of the contribution rate of the Gini coefficient, the impact of inter-group differences has decreased, while the contribution rates of intra-group differences and hyper-variable density have increased. This indicates that the imbalance in AGD within provinces is a significant factor affecting the further balanced development of the Yangtze River Delta region. Regarding intra-regional differences, the Gini coefficient of Anhui Province has consistently been higher than the overall level of the Yangtze River Delta, with the coefficient approaching 0.4 in several periods, nearing a warning level. This indicates a severe imbalance in AGD within Anhui Province. The Gini coefficient of Zhejiang Province is similar to the overall level of the Yangtze River Delta, indicating a relatively reasonable range. The Gini coefficient of Jiangsu Province has consistently been lower than the overall level, remaining below 0.1 from 2017 to 2019, indicating an absolutely balanced state of AGD within the province (Figure 5A). However, a certain degree of development disparity can incentivize industrial innovation and technological progress, while an absolutely balanced state might limit further industrial upgrading. In recent years, the Gini coefficient of Jiangsu Province has increased slightly, staying below 0.2, which is still within a reasonable range. Regarding inter-regional differences, the Gini coefficient between Zhejiang Province, Jiangsu Province, and Shanghai is relatively small, indicating that these three have achieved good results in collaborative AGD. The gap between Anhui Province and the other three regions is relatively large, but it shows a decreasing trend (Figure 5B).

Figure 5

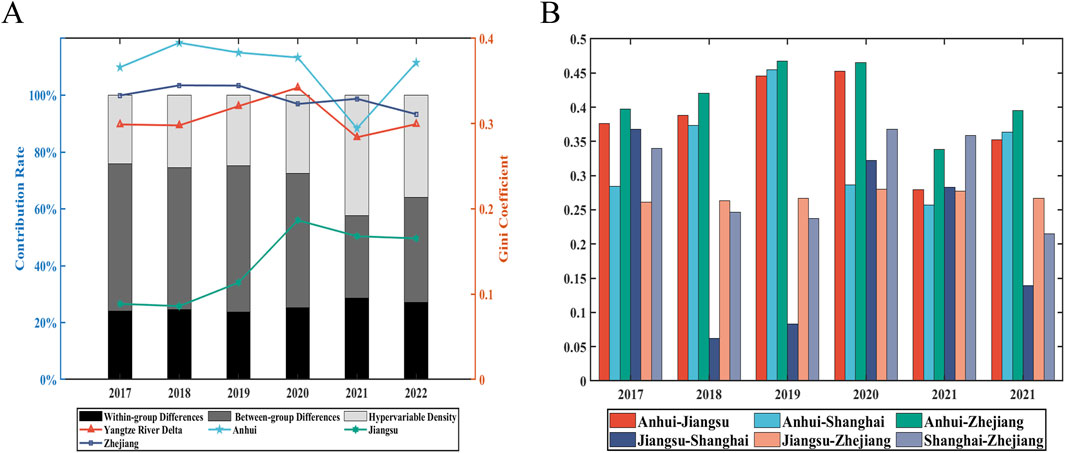
Figure 5. (A) The Gini coefficients within provinces and their decomposition. (B) The Gini coefficients among provinces.

4.4 Analysis of spatiotemporal evolution characteristics

4.4.1 Dynamic distribution and evolution characteristics

Based on the calculation results of AGD efficiency, this paper further analyzes the dynamic distribution characteristics of AGD using the KDE, as shown in Figure 6.

Figure 6

Figure 6. Kernel density curve of AGD efficiency in central cities of the Yangtze river delta.

From 2017 to 2022, the peak height and width of the kernel density curve for AGD efficiency remained relatively stable. Most values were concentrated within a certain range, with relatively few values deviating significantly from the mean, indicating that the absolute differences in AGD across these cities remained generally stable (Figure 6). However, it is noteworthy that the kernel density curve in 2018 exhibited a ‘one main peak and one secondary peak’ bimodal pattern, highlighting a significant polarization trend in AGD in the Yangtze River Delta. Starting from 2019, the secondary peak gradually weakened, indicating a significant reduction in the polarization trend. The reason might be that in 2018, the integration development of the Yangtze River Delta was elevated to a national strategy, but Anhui Province’s economy is relatively lagging, and its industrial structure differs significantly from that of Jiangsu Province, Zhejiang Province, and Shanghai, possibly causing its integration process to be somewhat slower.

4.4.2 Spatial correlation analysis

The preceding analysis reveals notable spatial disparities in AGD across the Yangtze River Delta. Generally, Jiangsu and Zhejiang Provinces demonstrate superior performance, whereas Anhui Province shows comparatively weaker results. To quantitatively examine the spatial distribution differences in AGD within this region, this study utilizes both global and local Moran’s Index for further investigation.

4.4.2.1 Global spatial autocorrelation analysis

Global Moran’s I is a statistical indicator used for spatial data analysis, which measures the overall similarity or correlation of data values in geographic space. The results of the global Moran’s Index analysis are shown in Table 6.

Table 6

Table 6. Analysis results of global Moran’s index.

As shown in Table 6, the Global Moran’s I for AGD efficiency from 2017 to 2022 is greater than 0, and all values pass the 1% significance level test. This suggests a robust positive spatial correlation in the distribution of AGD. Specifically, the Global Moran’s I increased from 0.1522 in 2017 to 0.2047 in 2020, suggesting an increasing spatial agglomeration effect in AGD. After 2020, the Global Moran’s I showed a downward trend, but the Z-values and P-values for 2021–2022 remained significant at the 1% level. This indicates that although the spatial agglomeration characteristics of AGD weakened slightly, they still demonstrate a relatively stable pattern. This change could be attributed to the initiation of the Rural Land Contracting Right Transfer Management Measures in 2021, which kickstarted the reform of land “tri-partite” rights, allowing farmers to transfer land contracting rights through leasing, subcontracting, swapping, and transferring to other farmers or agricultural enterprises. While this policy promotes the scale and intensive use of land, it also leads to fragmented land transfers, altering the original land use pattern. Additionally, for environmental protection, the government has designated important ecological functional zones and ecological environment-sensitive areas in the Yangtze River Delta region, prohibiting or restricting agricultural production and construction activities in these areas, resulting in the transfer of agricultural production to non-protected areas and further changing the original agricultural clustering trend.

4.4.2.2 Local spatial autocorrelation analysis

The global spatial Moran’s I reflects the overall spatial clustering characteristics of AGD at a macro level, but it cannot depict the specific spatial connections between individual cities. Therefore, this paper further employs Local Moran’s I to study the spatial connections between cities, and the LISA cluster map of local spatial autocorrelation is shown in Figure 7.

Figure 7

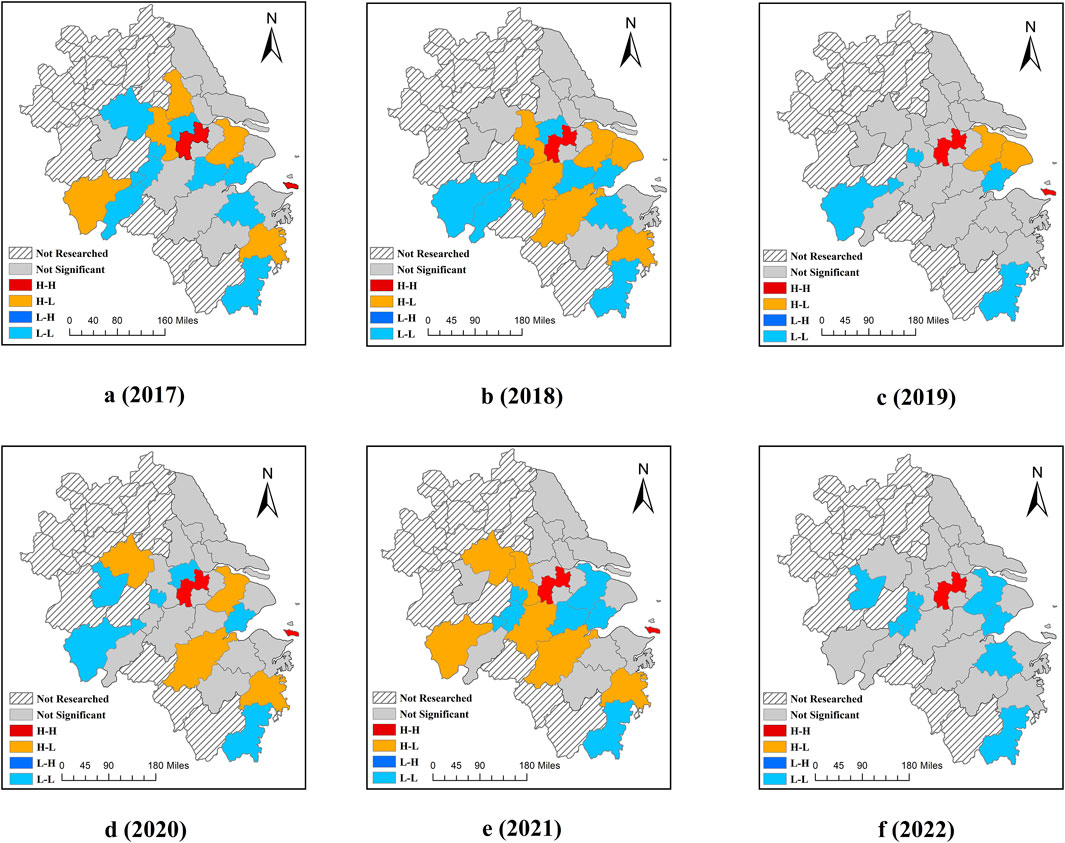
Figure 7. Local spatial autocorrelation LISA clustering for different years. (A) 2017; (B) 2018; (C) 2019; (D) 2020; (E) 2021; (F) 2022.

From 2017 to 2022, an average of 49% of the cities demonstrated LISA spatial agglomeration each year. However, this mainly manifested as low-low and high-low agglomeration types, with only Changzhou and Zhoushan displaying high-high agglomeration characteristics (Figure 7). This indicates that while the AGD in the core cities of the Yangtze River Delta has formed a relatively stable spatial agglomeration effect, there is still significant room for improvement. In 2017, spatial agglomeration characteristics were primarily observed in the northwest part of the core area of the Yangtze River Delta, such as Chuzhou, Nanjing, and Zhenjiang, as well as in the southeastern part, including Taizhou and Wenzhou. Starting from 2018, the agglomeration phenomenon began to shift toward the central region, with a weakening trend in the northwest, gradually forming a central agglomeration area centered around Huzhou and Xuancheng. However, by 2019, the localized agglomeration characteristics in the core area of the Yangtze River Delta had significantly weakened, with only 33% of the cities showing localized agglomeration effects, and the distribution becoming more scattered. This may be due to the initiation of the Yangtze River Delta Regional Integration Development Plan in 2019, which began to promote the marketization of agricultural land, altering the original land use pattern. Between 2020 and 2021, the agglomeration characteristics in the core area of the Yangtze River Delta significantly strengthened and gradually concentrated in the central region, with Huzhou and Xuancheng reemerging as central agglomeration areas. However, by 2022, the clustering characteristics showed a similar situation to that in 2019. This change may be related to further land reforms and the designation of important ecological function zones, among other policy measures.

In General, the central cities in the Yangtze River Delta have experienced a development trend in the local characteristics of AGD characterized by concentration, dispersion, re-concentration, and re-dispersion. Policy factors such as land reform have been significant factors leading to the local dispersion of AGD. However, it is worth noting that the efficiency of AGD in various cities has shown an improving trend over the years, indicating significant differences in the driving factors between the efficiency and spatial distribution of AGD.

4.5 Efficiency forecast

The 3S-DEA-SBM-BP model constructed in this paper, combining the 3S-DEA-SBM model and the BP algorithm, not only allows for a more systematic evaluation of the development efficiency of various sectors but also addresses the inability of existing evaluation models to be managed proactively. When determining the input plans, the 3S-DEA-SBM-BP can predict the final efficiency values, enabling various sectors to adjust inputs promptly to achieve the optimal input-output state. Since the data for input planning beyond 2023 has not been released, this paper first uses the GM (1,1) model to forecast the inputs for the next 3 years (2023, 2024, and 2025). Subsequently, the constructed 3S-DEA-SBM-BP model is applied to predict the AGD efficiency of each city, aiming to analyze in-depth the changing trends in AGD in the future. Due to space limitations, this paper only presents the fitted and forecasted values of input for Anqing City, Anhui Province, as shown in Figure 8.

Figure 8

Figure 8. The forecasted results of input for Anqing City.

The GM (1,1) model demonstrates high accuracy in predicting various inputs, showing consistent trends between predicted and actual values (Figure 8). Additionally, the average relative mean error between the predicted and actual values of each input is only 3.03%. This indicates that the predicted values can effectively reflect the future trends of various agricultural inputs in Anqing City. Based on the projected inputs for agricultural production in each city over the next 3 years, the future AGD efficiency values for each city were forecasted using the three-stage DEA-SBM-BP model constructed in this study. Figure 9 illustrates the projected efficiency values and spatial distribution of AGD in the central cities of the Yangtze River Delta for the years 2023–2025.

Figure 9

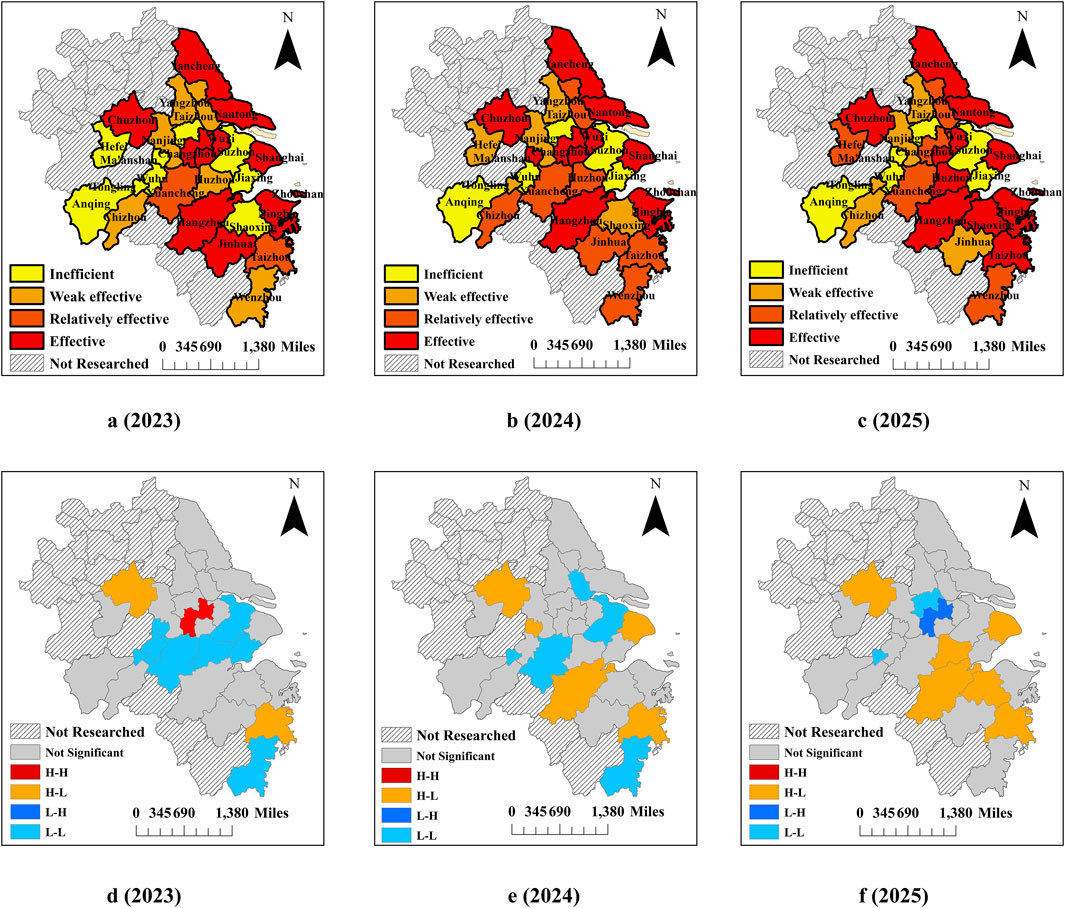
Figure 9. Future trends of AGD and spatial distribution in central cities of the Yangtze River Delta. (A) AGD in 2023; (B) AGD in 2024; (C) AGD in 2025; (D) LISA clustering in 2023; (E) LISA clustering in 2024; (F) LISA clustering in 2025.

Over the next 3 years, the overall efficiency of AGD in the Yangtze River Delta region remains relatively stable. Anhui Province continues to lag behind Jiangsu Province and Zhejiang Province but shows a significant overall improvement trend (Figure 9). Cities such as Hefei and Xuancheng in Anhui Province, as well as Wenzhou and Huzhou in Zhejiang Province, are expected to gradually transition from an inefficient state to a relatively efficient state, with Huzhou projected to reach an efficient state by 2025. Meanwhile, Hangzhou will transition from a relatively efficient state to an efficient state. However, Chizhou City is expected to experience a regression after improving from an inefficient state to a relatively efficient state, indicating the need for further adjustments to various inputs. In the next 3 years, the central cities of the Yangtze River Delta will see a significant enhancement in local agglomeration characteristics, potentially forming new agglomeration centers around Hangzhou and Huzhou.

5 Discussion

The development of agriculture not only directly impacts a nation’s food security and stable economic growth but also serves as a pillar of rural economies, influencing the prosperity and stability of rural societies. This study measures the efficiency of AGD in the central cities of the Yangtze River Delta and analyzes regional differences. The findings indicate that while AGD in the Yangtze River Delta has demonstrated a consistent upward trend in recent years, considerable regional disparities remain. This discovery is consistent with the findings of scholars such as Xu and Lei, although their research primarily focuses on inter-provincial differences and overlooks intra-provincial disparities (Xu and Kong, 2024; Lei and Tu, 2024). Variations in factors such as resource endowments and economic structures among cities contribute to significant regional imbalances in China’s agricultural development, rendering provincial average efficiency values not broadly representative. This study identifies significant imbalances in AGD among cities within Anhui Province, indicating that the overall efficiency value of Anhui Province does not fully represent the development status of cities within the province. This suggests significant shortcomings in previous research, which often substituted provincial efficiency values for regional development levels. Analyzing the development characteristics of individual cities can more comprehensively depict the actual development status of a region. From the viewpoint of the spatiotemporal evolution of AGD, both this study and research by Lu and Xiong confirm significant spatial agglomeration effects in AGD along the Yangtze River Economic Belt (Lu and Xiong, 2023). However, this study finds that there have been drastic changes in the local spatial distribution of AGD between 2019 and 2022. The reasons for this change can be attributed to factors such as the influence of land reform policies. From a methodological perspective, this study and the research by Pan demonstrate the significant impact of external environmental factors on management efficiency (Pan et al., 2022). Efficiency values measured using the 3S-DEA-SBM model are more objective, aiding policymakers in more effectively formulating various policies.

In traditional agricultural production, the area of cultivated crops and labor have always been important factors affecting agricultural productivity. Previous studies have emphasized the feasibility of improving agricultural efficiency by increasing the level of mechanization in agricultural production (Du et al., 2023; Sun et al., 2024). However, this study found that factors such as mechanization level, agricultural chemicals, and energy, which are traditionally relied upon in agriculture, have significantly reduced proportions in agricultural green production. Instead, factors such as infrastructure construction, agricultural economic digitization, and security level have a more significant impact on agricultural production efficiency. This finding aligns with the conclusions of studies by Wang et al., which indicate that in the context of high-quality development, agricultural production exhibits new characteristics (Wang et al., 2024; Wang and Qian, 2024).

While this paper comprehensively evaluates and predicts the efficiency of AGD using the objective 3S-DEA-SBM-BP model and analyzes regional development disparities, it still has two limitations that need to be addressed. Firstly, this study uses the entropy-weighted TOPSIS method to construct the indices of the Rural Shared Prosperity Index and Agricultural Pollution Emission Index. Although the entropy-weighted TOPSIS method has been widely applied in previous research, the indices it generates still have certain limitations. Secondly, this study uses city-level data, which may overlook the efficiency of AGD at the county level. County-level data can more comprehensively reflect the differences within the region.

6 Conclusion

This study combines the 3S-DEA-SBM model with BP neural networks to construct an innovative 3S-DEA-SPM-BP model, thereby providing a systematic and quantitative analytical tool for evaluating and predicting the efficiency of AGD in the Yangtze River Delta region. This model not only addresses the limitations of existing DEA models in predictive capability but also offers a new theoretical perspective for the systematic evaluation of AGD. In the research process, a comprehensive analysis of both traditional and emerging factors reveals the critical impacts of infrastructure construction, agricultural economic digitization, and safety levels on AGD. These findings provide important theoretical support and practical references for the digital transformation of agriculture and infrastructure upgrades. Additionally, this study analyzes the spatiotemporal evolution characteristics of AGD in the central cities of the Yangtze River Delta, revealing significant differences between cities in the region, particularly highlighting the pronounced differentiation within Anhui Province. In recent years, changes in policy factors have further exacerbated this trend. Notably, the predictive results of this study indicate that, in the next 3 years, urban disparities in the Yangtze River Delta are expected to narrow, and the characteristics of agglomeration will significantly strengthen, with the potential formation of new agglomeration centers around Hangzhou and Huzhou. This provides policymakers with forward-looking references for optimizing regional agricultural development layouts. Overall, this study not only provides reliable quantitative analysis tools for evaluating and predicting AGD efficiency but also deepens the understanding of the spatiotemporal dynamics of AGD, further advancing the theory and practice of sustainable agricultural development.

The analysis results presented in this paper provide the following recommendations for AGD in various regions.

6.1 Deepen the planning and regional coordination of intelligent agricultural production to promote sustainable agricultural development

Through rational planning of agricultural production activities, farmers can not only improve efficiency and maximize the utilization of agricultural resources but also contribute to the rational allocation and optimal utilization of agricultural resources. This helps farmers better adapt to market changes and reduce the impact of market fluctuations on farmers’ income. In addition, by coordinating agricultural production plans in different regions, resource sharing and complementary advantages can be achieved, further improving the overall efficiency of agricultural production. Advanced planning also provides the government with fundamental data, aiding in the formulation of agricultural policies and the rational allocation of resources to promote the healthy development of the entire agricultural industry. Therefore, the government should actively promote the establishment of agricultural information systems, providing timely and accurating weather, soil, and market information to assist farmers in making informed decision, such as rational crop selection, planting time, and fertilizer level. Simultaneously, the widespread adoption of technologies such as sensors, drones, and big data analysis in agriculture should be vigorously promoted to achieve precision agricultural management.

6.2 Emphasize the persistent and stable macro-control role of external environmental variables in AGD

Different environmental factors have varying effects on the efficiency of AGD. Macro-control of AGD can be achieved by guiding changes in external environmental variables. While the improvement of macroeconomic development level and labor quality may promote the upgrading of the agricultural structure to some extent, it is more likely to divert idle social funds and high-quality talents towards more developed secondary and tertiary industries, affecting the rapid development of the primary industry. Therefore, policy support is needed to guide idle social funds and high-quality talents toward the primary industry, promoting the high-quality development of agriculture.

6.3 Increase investment in infrastructure and innovative technology

During the transition from traditional extensive agriculture to AGD, factors such as infrastructure construction and agricultural economic digitization have a more significant impact. By optimizing transportation, irrigation, and energy infrastructure, the production and distribution of agricultural products become smoother, effectively reducing the transportation and energy costs of agricultural production. Moreover, robust infrastructure creates favorable conditions for increasing the added value of agricultural products. For example, the construction of agricultural processing plants and cold chain logistics systems helps extend the shelf life of agricultural products, enhance their commercialization, and drive agricultural products towards deep processing and high-end markets, thereby increasing farmers’ income. Additionally, by introducing advanced agricultural technology, farmers can achieve precise agricultural management, thereby improving production efficiency, reducing resource wastage, and advancing agriculture towards digitization and intelligence. Therefore, increasing investment in infrastructure and implementing agricultural economic digitization technologies can accelerate the improvement of current agricultural production efficiency and sustainability.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

GH: Conceptualization, Methodology, Resources, Formal Analysis, Funding acquisition, Supervision, Writing–review and editing. HY: Conceptualization, Data curation, Methodology, Resources, Software, Writing–original draft. HX: Funding acquisition, Supervision, Validation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. Research Project on the Development of Social Sciences in Hebei Province in 2022.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, C., and Zhang, H. (2023). Evaluation of green development level of mianyang agriculture, based on the entropy weight method. Sustainability 15 (9), 7589. doi:10.3390/su15097589

CrossRef Full Text | Google Scholar

Chen, Y., Miao, J., and Zhu, Z. (2021). Measuring green total factor productivity of China's agricultural sector: a three-stage SBM-DEA model with non-point source pollution and CO₂ emissions. J. Clean. Prod. 318, 128543. doi:10.1016/j.jclepro.2021.128543

CrossRef Full Text | Google Scholar

Cheng, N., and Ren, J. (2024). Green technology innovation, tourism industrial structure, and tourism economy: empirical evidence from cities in the Yangtze River Delta. Pol. J. Environ. Stud. 33 (4), 4539–4549. doi:10.15244/pjoes/177166

CrossRef Full Text | Google Scholar

Craswell, E. (2021). Fertilizers and nitrate pollution of surface and ground water: an increasingly pervasive global problem. SN Appl. Sci. 3 (4), 518. doi:10.1007/s42452-021-04521-8

CrossRef Full Text | Google Scholar

Du, M. L., Zhu, H. H., and Yin, X. J. (2023). Study on the impact of agricultural mechanization on agricultural ecological efficiency. Agric. Mod. Res. 44 (06), 1082–1092. doi:10.13872/j.1000-0275.2023.0101

CrossRef Full Text | Google Scholar

Flinzberger, L., Zinngrebe, Y., and Plieninger, T. (2020). Labelling in Mediterranean agroforestry landscapes: a Delphi study on relevant sustainability indicators. Sustain. Sci. 15, 1369–1382. doi:10.1007/s11625-020-00800-2

CrossRef Full Text | Google Scholar

Gao, Q., Cheng, C., Sun, G., and Li, J. (2022). The impact of digital inclusive finance on agricultural green total factor productivity: evidence from China. Front. Ecol. Evol. 10, 905644. doi:10.3389/fevo.2022.905644

CrossRef Full Text | Google Scholar

Gao, Q., Wang, Y. X., and Dou, Y. W. (2023). Spatiotemporal differentiation and driving factors of agricultural green development in the Yangtze River Economic Belt. J. Ecol. Agric. Chin. Engl., 1–14. doi:10.12357/cjea.20240170

CrossRef Full Text | Google Scholar

Geng, X., Zhang, D., Li, C., Li, Y., Huang, J., and Wang, X. (2020). Application and comparison of multiple models on agricultural sustainability assessments: a case study of the Yangtze River delta urban Agglomeration, China. Sustainability 13 (1), 121. doi:10.3390/su13010121

CrossRef Full Text | Google Scholar

Gerami, J., Mozaffari, M. R., Wanke, P. F., and Correa, H. (2022). A novel slacks-based model for efficiency and super-efficiency in DEA-R. Operations Res., 1–38. doi:10.1007/s12351-021-00679-6

CrossRef Full Text | Google Scholar

Kyrgiakos, L. S., Kleftodimos, G., Vlontzos, G., and Pardalos, P. M. (2023). A systematic literature review of data envelopment analysis implementation in agriculture under the prism of sustainability. Operational Res. 23 (1), 7. doi:10.1007/s12351-023-00741-5

CrossRef Full Text | Google Scholar

Lei, X., and Tu, W. L. (2024). Study on regional differences and convergence of agricultural green development in the Yangtze River Economic Belt. Anhui Agric. Sci. 52 (04), 210–213+218. doi:10.3969/j.issn.0517-6611.2024.04.046

CrossRef Full Text | Google Scholar

Li, G., Jia, X., Khan, A. A., Khan, S. U., Ali, M. A. S., and Luo, J. (2023). Does green finance promote agricultural green total factor productivity? Considering green credit, green investment, green securities, and carbon finance in China. Environ. Sci. Pollut. Res. 30 (13), 36663–36679. doi:10.1007/s11356-022-24857-x

CrossRef Full Text | Google Scholar

Liang, J., and Long, S. B. (2015). Growth of green total factor productivity in agriculture and its influencing factors. J. South China Agric. Univ. Soc. Sci. Ed. 14 (03), 1–12. doi:10.7671/j.issn.1672-0202.2015.03.001

CrossRef Full Text | Google Scholar

Liu, H. L., Xiao, H. M., and Liu, H. F. (2023). Measurement of rural revitalization level based on green development and its driving factors. J. Central South Univ. For. Technol. 2023 (08), 202–210. doi:10.14067/j.cnki.1673-923x.2023.08.020

CrossRef Full Text | Google Scholar

Liu, S., Lei, P., Li, X., and Li, Y. (2022). A nonseparable undesirable output modified three-stage data envelopment analysis application for evaluation of agricultural green total factor productivity in China. Sci. Total Environ. 838, 155947. doi:10.1016/j.scitotenv.2022.155947

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Y., Sun, D., Wang, H., Wang, X., Yu, G., and Zhao, X. (2020a). An evaluation of China’s agricultural green production: 1978–2017. J. Clean. Prod. 243, 118483. doi:10.1016/j.jclepro.2019.118483

CrossRef Full Text | Google Scholar

Liu, Y., Zou, L., and Wang, Y. (2020b). Spatial-temporal characteristics and influencing factors of agricultural eco-efficiency in China in recent 40 years. Land Use Policy 97, 104794. doi:10.1016/j.landusepol.2020.104794

CrossRef Full Text | Google Scholar

Lu, S., and Xiong, J. (2023). Research on the spatial-temporal differentiation and influencing factors of agricultural green efficiency in the Yangtze River Economic Belt based on GWR. Sci. Geogr. Sin. 43 (02), 337–348. doi:10.13249/j.cnki.sgs.2023.02.015

CrossRef Full Text | Google Scholar

Luo, D. Y. (2012). Note on inefficiency estimate of three-stage DEA model. Stat. Res. 29 (04), 104–107. doi:10.3969/j.issn.1002-4565.2012.04.017

CrossRef Full Text | Google Scholar

Meili, J. (2021). “Sustainable agriculture and food production in Qinghai: analysis based on grey correlation model,” in IOP Conference Series: Earth and Environmental Science, 831, 012040. doi:10.1088/1755-1315/831/1/012040

CrossRef Full Text | Google Scholar

Min, Z. (2024). Study on the impact of digital economy on the green development of agriculture. Agric. For. Econ. Manag. 7 (2), 9–17. doi:10.23977/agrfem.2024.070202

CrossRef Full Text | Google Scholar

Mirzabaev, A., Sacande, M., Motlagh, F., Shyrokaya, A., and Martucci, A. (2022). Economic efficiency and targeting of the african great green wall. Nat. Sustain. 5 (1), 17–25. doi:10.1038/s41893-021-00801-8

CrossRef Full Text | Google Scholar

Myeki, L. W., Matthews, N., and Bahta, Y. T. (2023). Decomposition of green agriculture productivity for policy in africa: an application of global malmquist–luenberger index. Sustainability 15 (2), 1645. doi:10.3390/su15021645

CrossRef Full Text | Google Scholar

Pan, Z., Tang, D., Kong, H., and He, J. (2022). An analysis of agricultural production efficiency of Yangtze River Economic Belt based on a three-stage DEA malmquist model. Int. J. Environ. Res. Public Health 19 (2), 958. doi:10.3390/ijerph19020958

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, Z., Liu, N., Li, X., and Kang, Z. (2022). A method for evaluating the green economic efficiency of resource-based cities based on neural network improved DEA model. Comput. Intell. Neurosci. 2022, 1–11. doi:10.1155/2022/9521107

CrossRef Full Text | Google Scholar

Sun, Q., and Sui, Y. J. (2023). Agricultural green ecological efficiency evaluation using BP neural network–DEA model. Systems 11 (6), 291. doi:10.3390/systems11060291

CrossRef Full Text | Google Scholar

Sun, Y. H., Yu, X. Y., and Chen, Z. (2024). Analysis of the impact mechanism of agricultural mechanization on the income of mountainous farmers: based on panel data of 26 counties in mountainous areas of Zhejiang Province. Resour. Dev. Mark. 40 (01), 91–98. doi:10.3969/j.issn.1005-8141.2024.01.010

CrossRef Full Text | Google Scholar

Tian, C. H., Li, L., and Liao, B. (2024). Can the integration of primary, secondary, and tertiary industries in rural areas promote agricultural green development? — a case study of 579 counties in the Yangtze River Economic Belt. J. Nat. Resour. 39 (03), 601–619. doi:10.31497/zrzyxb.20240307

CrossRef Full Text | Google Scholar

Wang, H. F., and Qian, Q. (2024). Study on the empowerment of digital economy on the integrated development of the tertiary industry in rural China. Gansu Soc. Sci. 2024 (02), 196–205. doi:10.15891/j.cnki.cn62-1093/c.20240411.002

CrossRef Full Text | Google Scholar

Wang, W., and Lin, L. B.Burenmende (2024). Research on the impact of rural infrastructure on agricultural green total factor productivity: based on the perspective of spatial spillover effects. China Agric. Resour. Regional Plan. 1-10. Available at: https://link.cnki.net/urlid/11.3513.S.20240419.1205.011.

Google Scholar

Wei, Q., Zhang, B., and Jin, S. (2018). Construction and regional comparison of China's agricultural green development index. Issues Agric. Econ. 11, 11–20. doi:10.13246/j.cnki.iae.2018.11.002

CrossRef Full Text | Google Scholar

Wu, Q., Wang, Z. Q., Zhao, Z. M., and Liu, D. H. (2006). Mechanism and vulnerability assessment of groundwater pollution in pressured aquifers in oil and gas field areas. J. Hydraulic Eng. 2006 (07), 851–857. doi:10.3321/j.issn:0559-9350.2006.07.014

CrossRef Full Text | Google Scholar

Xu, D. F., and Kong, L. C. (2024). Measurement and convergence of agricultural green production efficiency in the Yangtze River Economic Belt under carbon emission constraints. Hubei Agric. Sci. 63 (03), 142–149. doi:10.14088/j.cnki.issn0439-8114.2024.03.022

CrossRef Full Text | Google Scholar

Yan, Z., Zhou, W., Wang, Y., and Chen, X. (2022). Comprehensive analysis of grain production based on three-stage super-SBM DEA and machine learning in Hexi Corridor, China. Sustainability 14 (14), 8881. doi:10.3390/su14148881

CrossRef Full Text | Google Scholar

Yao, Q., Zhang, Y. C., Li, X., Liu, M. B., and Hu, Y. G. (2023). Spatiotemporal characteristics of rural green development level in China and its spatial diffusion and convergence effects. Trans. Chin. Soc. Agric. Eng. 39 (07), 256–265. doi:10.11975/j.issn.1002-6819.202209082

CrossRef Full Text | Google Scholar

Yi, M., Zhang, L., Yang, L., and Fu, L. (2019). Spatial-temporal differentiation characteristics and regional equity of China’s science and technology financial efficiency. Sci. Technol. Prog. Policy 36 (10), 34–40. doi:10.6049/kjjbydc.2018090292

CrossRef Full Text | Google Scholar

Yin, C. B., Li, F. D., Wang, S., and Hao, A. B. (2021). The concept, connotation, and principles of agricultural green development in China. Chin. J. Agric. Resour. Regional Plan. (01), 1–6. doi:10.7621/cjarrp.1005-9121.20210101

CrossRef Full Text | Google Scholar

Yin, M. Y., and Qiu, X. X. (2023). Digital economy, green technological innovation, and rural revitalization: an empirical test based on provincial panel data. Bus. Econ. Res. 2023 (12), 100–105. doi:10.3969/j.issn.1002-5863.2023.12.026

CrossRef Full Text | Google Scholar

Zhou, F., and Wen, C. (2023). Research on the level of agricultural green development, regional disparities, and dynamic distribution evolution in China from the perspective of sustainable development. Agriculture 13 (7), 1441. doi:10.3390/agriculture13071441

CrossRef Full Text | Google Scholar

Zhu, Y., Zhang, Y., and Piao, H. (2022). Does agricultural mechanization improve the green total factor productivity of China’s planting industry? Energies 15 (3), 940. doi:10.3390/en15030940

CrossRef Full Text | Google Scholar