Comparative Study of Impacts of Typical Bio-Inspired Optimization Algorithms on Source Inversion Performance

Accurate identification of source information (i.e., source strength and location) is crucial for the air pollution control or effective accidental response. Optimization inversion based on bio-inspired algorithms (BIOs) is an effective method for estimating source information. However, the impacts of different BIOs and the shared parameter of population size in BIOs on source inversion performance have not been revealed. Here the source inversion performance (i.e., accuracy and robustness) of six typical BIOs [i.e., bacterial foraging optimization algorithm (BFO), chicken swarm optimization algorithm (CSO), differential evolution algorithm (DE), genetic algorithm (GA), particle swarm optimization (PSO), and seeker optimization algorithm (SOA)], and their population sizes are evaluated based on the Prairie Grass dataset which covering different atmospheric conditions (i.e., Pasquill stability classes A, B, C, D, E, and F). Results indicated the population size has substantial influence on source inversion. The accuracy of all BIOs in source strength fluctuated greatly when the population size was small, whereas, tended to be stable as the population size increased. Overall, the BFO had the best accuracy with lowest deviations (74.5% for source strength and 29.7 m for location parameter x₀), whereas SOA had the best robustness for all source parameters. Atmospheric conditions indicated an obvious influence on the inversion performance of the BIOs. The BFO and CSO performed the best with the lowest deviations [137.5 and 26.7% for unstable conditions (A, B, and C) and stable condition (E), respectively], all algorithms are comparable (67.4 ± 2.1%) in neutral condition (D), and BFO and CSO had the comparable performances (23.2 and 24.3%) and performed better under extremely stable condition (F). This study enhances the understanding of the factors influencing source inversion and provides a reference for the selection of appropriate bio-inspired algorithms and the reasonable setting of population size parameter for source inversion in practical environmental management.

1 Introduction

Atmospheric pollution caused by daily emissions in industries or abrupt accidents is concerning because it endangers life and property safety, causing substantial economic losses and threatening the ecological environment (Hutchinson et al., 2017; Zhong et al., 2020). Accurate determination of source pollutant emission information or source parameters (e.g., source strength and location) plays a crucial role in the refined control of air pollution or improving emergency response capabilities of abrupt air pollution accidents (Wei et al., 2016; Ma et al., 2020). However, it is generally difficult to directly acknowledge the pollution source information because of the characteristics of concealment of conventional pollution emissions and the harmfulness of accidents. Source inversion based on environmentally observed pollutant concentrations is an effective alternative method for obtaining unknown pollution source parameters (Lamb et al., 2016; Bergamaschi et al., 2018; Ma et al., 2018; Albani et al., 2020).

Source parameters inversion is always an ill-posed inverse problem (Haupt et al., 2007; Ma et al., 2017; Cui et al., 2019). Theories based on probability and optimization are the two main approaches for solving the ill-posed inverse problem (Wang et al., 2017). Probability modeling methods are mainly based on Bayesian inference, and the estimations are obtained using stochastic Monte Carlo (Sohn et al., 2003) or Markov Chain Monte Carlo (Guo et al., 2009; Wang et al., 2017) sampling techniques. However, the effective use of the method depends on a lot of reliable prior information (e.g., measurement errors, parameter bounds and expected inputs) (Zheng and Chen, 2011; Yu M. et al., 2019). This information is hard to be obtained in the real conditions, especially in the case of emergency rescue where rapid decision making is required. Optimization source inversion identifying the source parameters by minimizing the difference between the air dispersion model outputs and the measured concentrations is widely used because of its less dependence on prior information and high estimation accuracy (Zheng and Chen, 2010; Ma et al., 2017). Traditional optimization algorithms such as gradient-based method [e.g., the Nelder Mead simplex method (NM), Shi, 2013; the least-squire, Singh and Rani, 2014] and direct search method [e.g., the Pattern Search (PS), Zheng and Chen, 2010] have been utilized by some scholars to inverse unknown source parameters. However, this category of algorithms is limited in practices when the initial value is not set properly or the objective function is not differentiable. Bio-inspired optimization algorithms (BIOs) have been coming out as one of the best promising optimization techniques, which belongs to the nature-inspired algorithm (based on some principles from physics, biology or ethology) (Boussaïd et al., 2013; Alanis et al., 2018). In recent years, a few BIOs such as genetic algorithm (GA) (Haupt, 2005; Long et al., 2010; Rodriguez et al., 2011; Li and Zhang, 2017; Mao et al., 2020), particle swarm optimization (PSO) (Chen and Chen, 2014), seeker optimization algorithm (SOA) (Hu et al., 2021) and chicken swarm optimization algorithm (CSO) (Chen et al., 2021) are used in related research on source inversion since they does not depend on gradient descent information and has excellent global optimization performance compared with that of traditional algorithms. However, above studies only focused on the performance of the single algorithm in source inversion applications and were carried out based on the virtual cases or the extremely limited field experimental data. Their performance in real-world applications deserves further research. Additionally, some other bio-inspired algorithms have been developed for different applications or research purposes, such as the bacterial foraging optimization algorithm (BFO) (Mishra, 2005; Tripathy et al., 2006) and differential evolution algorithm (DE) (Feoktistov, 2006). Sarkar et al. (2022) made a review on the application of BIOs (e.g., CSO, BFO, DE, etc.) in different food processing and related operations, and had concluded that there is no generic algorithm that will perform well for each optimization problem. However, from our best knowledge, these algorithms with good performance in other research fields have not been applied in source inversion of atmospheric pollutants and their performances in source inversion have not been revealed. In the previous studies, Ma et al. (2013) and Shen et al. (2019) compared the performance of different optimization algorithms in source inversion based on the limited field experiments and found that the different optimization algorithms varied greatly in different source parameters inversion. Therefore, the differences of selecting different BIOs may cause large impact on source parameters inversion. However, up to now, the systematic comparative investigations on the application evaluations of different BIOs in source inversion have not been carried out. Meanwhile, the study of Cui et al. (2019) demonstrated that the atmospheric dispersion conditions had remarkably influence on the performance of the algorithms. Therefore, the performance differences of source inversion caused by selecting different BIOs may also vary for different atmospheric conditions. Additionally, BIOs generally come with some control parameters that have to be set before the algorithm can be used in applications. Thereinto, the population size is one of key control parameters in BIOs (Alanis et al., 2018). A mass of studies have shown that the population size can greatly influence the solving performance of BIOs in real engineering applications (Jansen et al., 2005; Diaz-Gomez and Hougen, 2007; Brest and Maucec, 2008; Mora-Melià et al., 2016; Castelli et al., 2017). Therefore, a prerequisite evaluating objectively estimation performance of algorithms in source inversion is to clarify the influence law of the population size in algorithm on source inversion. However, almost all past studies have ignored the impacts of population size on source parameters inversion. This limits our understanding of the role of population size in BIOs in the applications of source inversion. These deficiencies above of the existing studies limit our understanding of the impacts of BIOs on source inversion. Thus, more researches into the inversion performances are necessary to enhance the understanding of the factors influencing source inversion, and allow for the selection of appropriate bio-inspired algorithms and the reasonable setting of population size parameter for source inversion in practices.

The purpose of this study is to identify the impacts of different BIOs on source inversion performance in real world. Six typical bio-inspired algorithms (BFO, CSO, DE, GA, PSO, and SOA) were evaluated based on the classical Prairie Grass experimental dataset including 68 experiments (Barad, 1958), which comprises atmospheric stability categories (A, B, C, D, E, and F). The estimation performance (i.e., accuracy and robustness) of population sizes from 10 to 100 for different algorithms were firstly evaluated in order to identify the influence laws of population size for each algorithm in source inversion. Then, the inversion performance of different BIOs under different atmospheric dispersion conditions (stability classes A to F) was analyzed and discussed. This study can enhance the understanding of the role of population size in the applications of source inversion for the BIOs and the influence of BIOs on source inversion performance. The conclusions facilitate obtaining source information accurately by selecting the bio-inspired algorithms and setting the population size parameter more reasonably than in the literature for the practical environmental management, especially the considering the varied atmospheric conditions.

2 Methods

2.1 Source Inverse Model

Many forward dispersion models have been proposed to simulate the dispersion of atmospheric pollutants. The Gaussian dispersion model has been widely used in source inversion because of its advantages of high prediction efficiency, simple implementation, and low time cost (Lushi and Stockie, 2010; Stockie, 2011; Ma et al., 2017). In this study, the Gaussian model was also selected to construct the source parameter inverse model. According to the dispersion theory of the Gaussian model (Pasquill and Smith, 1983), the simulated concentration of the Gaussian model at any monitoring point in the downwind direction can be expressed as follows:

$\mathrm{C}\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)=\frac{{\mathrm{Q}}_0}{2·\mathrm{\pi }·\mathrm{u}·{\mathrm{\sigma }}_{{\mathrm{y}}_{\left(\mathrm{x}-{\mathrm{x}}_0\right)}}·{\mathrm{\sigma }}_{{\mathrm{z}}_{\left(\mathrm{x}-{\mathrm{x}}_0\right)}}}\exp \left(-\frac{{\left(\mathrm{y}-{\mathrm{y}}_0\right)}^2}{2·{\mathrm{\sigma }}_{{\mathrm{y}}_{\left(\mathrm{x}-{\mathrm{x}}_0\right)}}^2}\right)\left[\exp \left(-\frac{{\left(\mathrm{z}-{\mathrm{z}}_0\right)}^2}{2·{\mathrm{\sigma }}_{{\mathrm{z}}_{\left(\mathrm{x}-{\mathrm{x}}_0\right)}}^2}\right)+\exp \left(-\frac{{\left(\mathrm{z}+{\mathrm{z}}_0\right)}^2}{2·{\mathrm{\sigma }}_{{\mathrm{z}}_{\left(\mathrm{x}-{\mathrm{x}}_0\right)}}^2}\right)\right],(1)$

where Q₀ is the pollutant emission rate of the source (or source strength), (g/s); C (x, y, z) is the pollutant concentration at monitoring point (x, y, z) in the downwind (g/m³); (x₀, y₀) and z₀ represent the source horizontal location coordinate parameter (m) and the pollutant release height parameter (m), respectively; u is the average wind speed (m/s) near the ground during the sampling period; ${\sigma }_y$ and ${\sigma }_z$ are the dispersion coefficients in the horizontal and vertical directions, respectively (m), which are the functions of downwind distance (x-x₀) and the Pasquill stability (A, B, C, D, E, and F). The dispersion coefficients were computed based on the BRRIGS scheme as Eq. 2 and Eq. 3 (Mao et al., 2020).

${\sigma }_y=a_1·\left(x-x_0\right)·{\left[1+b_1·\left(x-x_0\right)\right]}^{r_1}(2)$

${\sigma }_z=a_2·\left(x-x_0\right)·{\left[1+b_2·\left(x-x_0\right)\right]}^{r_2}(3)$

where a₁, a₂, b₁, b₂, r₁, and r₂ are the parameters for calculating the dispersion coefficients and vary with the Pasquill atmospheric stability classes (Table 1). Note that the Gaussian model is suitable for flat and open terrains and the pollutants dispersion is assumed to be a uniform process. Thus, the forward dispersion model should be selected flexibly according to the specific application scenarios in practice.

TABLE 1

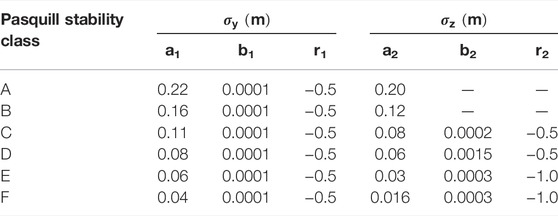
TABLE 1. Constants for calculating dispersion coefficients in BRIGGS scheme (Mao et al., 2020).

Optimization source inversion methods can be treated as to find the optimal fitness between the simulated and observed concentrations. According to the previous studies (Zheng and Chen, 2010; Ma et al., 2013; Cui et al., 2019), the objective function expression of source inversion model in this study is as follows:

$min f={\displaystyle \sum _{n=1}^n{\left[C_{mes}^i-C_{sim}^i\left(Q_0,{\text{x}}_0,y_0,{\text{z}}_0\right)\right]}^2}(4)$

where ${\mathrm{C}}_{\mathrm{m}\mathrm{e}\mathrm{s}}^{\mathrm{i}}$ is the measured concentration at sampling point i, (g/m³); ${\mathrm{C}}_{\mathrm{s}\mathrm{i}\mathrm{m}}^{\mathrm{i}}$ is the simulated concentration of dispersion model [i.e., Eq. (1)] at the sampling point i, (g/m³); and n is the number of sampling points in the downwind. In this study, the pollutant emission source information, namely source strength (Q₀), horizontal coordinate position (x₀, y₀), and release height (z₀), are unknown. The optimal solution obtained by minimizing the objective function (i.e., source inversion model) with the bio-inspired algorithm is the estimated value of unknown source parameters.

2.2 Bio-Inspired Algorithms

2.2.1 Bacterial Foraging Optimization Algorithm

The BFO has been widely accepted as a population-based algorithm of current interest for distributed optimization and control and is inspired by the social foraging behavior of Escherichia coli. A bacterium always tends to migrate toward the highest nutrient source by swim or tumble via rotating whip-like flagella (i.e., chemotaxis movement). The reproductive phase of the bacteria is then initiated followed by the final dispersal or elimination. Thus, the BFO comprises three steps: chemotaxis, reproduction, and elimination—dispersal (Passino, 2002). The BFO has been applied successfully to some engineering problems, such as optimal control, harmonic estimation, and transmission loss reduction (Mishra, 2005; Tripathy et al., 2006).

2.2.2 Chicken Swarm Optimization Algorithm

The CSO algorithm is a bio-inspired algorithm based on a population that mimics the behaviors of a chicken swarm (Meng et al., 2014). The whole swarm can be divided into several groups, each comprising one rooster and many hens and chicks. Different chickens follow different laws of motion. In a particular hierarchy order, the various subgroups compete. The CSO algorithm has the advantages of fast convergence speed and high solving accuracy, but only very limited researches (Chen et al., 2021) have been conducted on leakage source parameter inversion using the CSO.

2.2.3 Differential Evolution Algorithm (DE)

The DE algorithm is a floating point encoding evolutionary algorithm for global optimization over continuous spaces (Feoktistov, 2006), which can also work with discrete variables. DE creates new candidate solutions by combining the parent individual with several other individuals of the same population. A candidate replaces the parent only if the former has a better fitness value than the latter. Many studies on the application of DE in the optimization inversion problem have been conducted (Moll et al., 2004; Gao et al., 2016), but source parameter inversion in atmospheric pollution scenarios requires further research.

2.2.4 Genetic Algorithm

A GA uses principles inspired by the fields of genetics and evolution to optimize the solution to a non-linear problem. A GA works with a population of trial solutions called chromosomes that are manipulated by operations called mating and mutation to create the next generation of offspring. Many studies on source parameter inversion and dispersion model parameter optimization have been conducted using GA and good results have been achieved (Haupt, 2005, 2007; Ma et al., 2013; Mao et al., 2022).

2.2.5 Particle Swarm Optimization (PSO)

PSO is an intelligent optimization algorithm inspired by the social behavior of bird foraging (Chen and Chen, 2014). A flock of birds is regarded as a group of particles. Speed and position which are the inherent attribute characteristics of each particle. In contrast with GAs, all particles of PSO are retained as members of the population through the entire search process (Zahara and Kao, 2009). The optimal solutions of these particles can be recorded and shared, so that all particles can search in the direction of feasible solutions. PSO simulates the movement of these particles and explores various regions in the search space for global optima.

2.2.6 Seeker Optimization Algorithm (SOA)

The SOA is based on the concept of simulating the act of humans’ intelligent search with their memory, experience, and uncertainty reasoning. In this sense, the individual of this population is called a seeker or searcher, from which the new algorithm name is derived. After a given start point, search direction, search radius, and trust degree, every seeker moves to a new position (next solution) based on his social learning, cognitive learning, and uncertainty reasoning based on a simple Fuzzy rule and finally the solving of optimization problem is completed (Dai et al., 2006; Dai et al., 2009; Hu et al., 2021).

Supplementary Figures S1–S6 show the flow charts of optimization steps to six tested BIOs. Note that each algorithm used by this study was a standard implementation. Additionally, except for the parameter of population size that this study focused on, the remaining control parameters that have to be set before the algorithm can be used in applications. The remaining parameters were set based on the empirical values from the previous studies. The specific control parameters of the test algorithms and the corresponding empirical constant values were summarized in Table 2. One thousand independent calculations of source inversion were performed for each field experiment under each algorithm in order to reduce the influence of randomness of algorithm itself on inversion results. The mean values of the inversion results of all experiments were used for the final analysis of this study.

TABLE 2

TABLE 2. Empirical constant values of the remaining control parameters in optimization algorithms.

2.3 Performance Evaluation Method

The absolute value of the relative deviation (ARD) and absolute value of deviation (AD) are calculated to characterize the inversion accuracy of source strength and source location, respectively.

$ARD=\left|({\text{E}}_{\text{Q},\text{I}}-{\text{R}}_{\text{Q},\text{I}})\right|/{\text{R}}_{\text{Q},\text{I}},(5)$

$AD=\left|{\text{E}}_{\text{L},\text{I}}-{\text{R}}_{\text{L},\text{I}}\right|,(6)$

where letters E and R represent the estimation value and real value, respectively; letters Q and L represent the source strength (Q₀) and location parameters (i.e., x₀, y₀, and z₀); letter I represents the serial number of the test experiment. The average of ARDs or ADs of inversion results for 1,000 independent solvings was taken as the result of each field experiment, and the average of ARDs or ADs of all experiments for each atmospheric stability class was taken as the final result of each atmospheric stability class in this study.

The coefficient of variation (CV) is calculated to evaluate the estimation robustness of BIOs in source inversion. The formula is as follows:

$\mathrm{C}\mathrm{V}={\mathrm{\mu }}_{\left(\mathrm{Q},\mathrm{L}\right)}/{\mathrm{m}}_{\left(\mathrm{Q},\mathrm{L}\right)}(7)$

where ${\mathrm{\mu }}_{(\mathrm{Q}, \mathrm{L})}$ represents the standard deviation of ARD for source strength (Q₀) or AD for source location parameters (x₀, y₀, and z₀), and m represents the average value of the inversion deviations (ARDs or ADs) of source strength or location parameter. In this study, the CV of each field experiment was calculated based on the ARDs or ADs of 1,000 independent solvings. Average of CVs of all experiments for each atmospheric stability class was taken as the final result of each atmospheric stability class. The value of CV ranges from 0 to 1. The smaller the CV value is, the better the estimation robustness is. A small CV value less than 0.15 is regarded to have small data discreteness (Luo and Wei, 2011), namely, it represents an excellent estimation robustness.

Both inversion accuracy (ARD or AD) and robustness (CV) are essential indices for inversion performance. However, they were not consistent in dimension. Thus, according to the previous studies (Cui et al., 2019; Mao et al., 2020), the performance of the algorithm in source inversion is comprehensively scored, and the comprehensive score index is further calculated based on all statistical indices of ARD, AD and CV in this study, which is detailed as follows:

2.3.1 Range Standardization

${{\mathrm{X}}^{\prime }}_{\mathrm{J},\mathrm{K}}=\left[{\mathrm{X}}_{\mathrm{J},\mathrm{K}}-\min \left({\mathrm{X}}_{\mathrm{J},\mathrm{K}}\right)\right]/\left[\max \left({\mathrm{X}}_{\mathrm{J},\mathrm{K}}\right)-\min \left({\mathrm{X}}_{\mathrm{J},\mathrm{K}}\right)\right](8)$

where letter K represents the different source parameters (Q₀, x₀, y₀, z₀); letter J represents the evaluation indexes (ARD, AD, CV), and ${\mathrm{X}}_{\mathrm{J}, \mathrm{K}}$ and ${{\mathrm{X}}^{\prime }}_{\mathrm{J},\mathrm{K}}$ are the original values and standardized values.

2.3.2 Comprehensive Scores for Source Strength

${\mathrm{S}}_{{\mathrm{Q}}_0}={\mathrm{\omega }}_1\ast 1/\mathrm{N}\ast {\displaystyle {\sum }_{\mathrm{i}=1}^{\mathrm{N}}{{\mathrm{X}}^{\prime }}_{{\mathrm{Q}}_0,\mathrm{A}\mathrm{R}\mathrm{D}},+{\mathrm{\omega }}_2\ast 1/\mathrm{N}\ast {\displaystyle {\sum }_{\mathrm{i}=1}^{\mathrm{N}}{{\mathrm{X}}^{\prime }}_{{\mathrm{Q}}_0,\mathrm{C}\mathrm{V}}}},(9)$

comprehensive score of source location:

${\mathrm{S}}_{\mathrm{L}}={\mathrm{\omega }}_3\ast \left[{\mathrm{\omega }}_1\ast 1/\mathrm{N}\ast {\displaystyle {\sum }_{\mathrm{i}=1}^{\mathrm{N}}{{\mathrm{X}}^{\prime }}_{{\mathrm{X}}_0,\mathrm{A}\mathrm{D}},+{\mathrm{\omega }}_2\ast 1/\mathrm{N}\ast {\displaystyle {\sum }_{\mathrm{i}=1}^{\mathrm{N}}{{\mathrm{X}}^{\prime }}_{{\mathrm{X}}_0,\mathrm{C}\mathrm{V}}}}\right]+{\mathrm{\omega }}_4\ast \left[{\mathrm{\omega }}_1\ast 1/\mathrm{N}\ast {\displaystyle {\sum }_{\mathrm{i}=1}^{\mathrm{N}}{{\mathrm{X}}^{\prime }}_{{\mathrm{Y}}_0,\mathrm{A}\mathrm{D}},+{\mathrm{\omega }}_2\ast 1/\mathrm{N}\ast {\displaystyle {\sum }_{\mathrm{i}=1}^{\mathrm{N}}{{\mathrm{X}}^{\prime }}_{{\mathrm{Y}}_0,\mathrm{C}\mathrm{V}}}}\right]+{\mathrm{\omega }}_5\ast \left[{\mathrm{\omega }}_1\ast 1/\mathrm{N}\ast {\displaystyle {\sum }_{\mathrm{i}=1}^{\mathrm{N}}{{\mathrm{X}}^{\prime }}_{{\mathrm{Z}}_0,\mathrm{A}\mathrm{D}},+{\mathrm{\omega }}_2\ast 1/\mathrm{N}\ast {\displaystyle {\sum }_{\mathrm{i}=1}^{\mathrm{N}}{{\mathrm{X}}^{\prime }}_{{\mathrm{Z}}_0,\mathrm{C}\mathrm{V}}}}\right](10)$

comprehensive score of all source parameters (strength and location):

$S_{\text{R}}={\text{ω}}_1\ast S_{\text{R}}+{\text{ ω}}_2\ast S_L(11)$

where $X^{\prime }\left({\text{Q}}_0, x_0, y_0, z0\right)$ is the standardized value of different source parameters, N is the number of test experiments, and ω is the weighting coefficients for the standardized indices (ω_1∼2 = 1/2, ω_3∼5 = 1/3).

2.4 Field Experimental Data

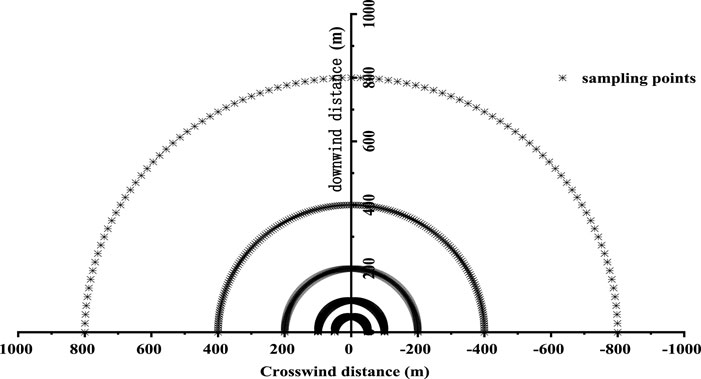
Search algorithms were applied to identify the characteristics of the source based on the Prairie Grass field experiments (Barad, 1958). The experiments were conducted in the relatively open area of northern central Nebraska in the summer of 1956, which comprised of 68 consecutive releases of trace gas SO₂ of 10 min each from a single source, and six atmospheric dispersion conditions (i.e., Pasquill stability classes) (Pasquill and Smith, 1983): extremely unstable (A), unstable (B), slightly unstable (C), neutral (D), stable (E), and extremely stable (F). The number of field experiments for each stability class (A—F) were 5, 5, 10, 31, 5, and 12, respectively (Cervone and Franzese, 2011). The gas release height of experiments No. 1–62 was 0.46 m from the ground, and experiments No. 63–68 were 1.5 m from the ground. The mean concentration of 20 min was measured at sensors positioned along arcs radially located at distances of 50 m, 100 m, 200 m, 400 m, and 800 m from the source. The downwind sample collection adopted a semicircular arrangement of points (Figure 1). The coverage area of each layer was 180°; the first four layers of sampling points were arranged at intervals of 1°; each layer had 180 sampling points; and the fifth layer was arranged at intervals of 2°, with a total of 90 sampling points.

FIGURE 1

FIGURE 1. Sketch of the field experiment monitoring points’ setting pattern.

3 Results

3.1 Impacts of Population Sizes in BIOs on Source Inversion

In this section, the impacts of different population sizes (10–100) in BIOs on source inversion were evaluated. The inversion results of source parameters (i.e., source strength and locations) under different BIOs were calculated for each experiment in the Prairie Grass dataset. Figure 2 shows the mean ARD with a 95% confidence limit and the mean CV of the source strength (i.e., parameter Q₀) inversion results. In terms of accuracy, the population size has a remarkably effect on the accuracy of the source strength for the tested BIOs. All BIOs presented the consistent feature that the estimation deviations showed a certain degree of value fluctuation when the population size was smaller than a certain value and then reached a relatively stable state. This characteristic indicated that the increase of population size has little contribution on the estimation accuracy of these algorithms when the population size was larger than a certain value. Specifically, the fluctuation ranges of ARDs of the BFO, CSO, and DE were relatively greater (66.2–77.8%, 73.1–87.2%, and 83.1–192.2% for BFO, CSO, and DE, respectively) when the population size was less than 50. The ARDs of the GA, PSO, and SOA showed greater fluctuations (44.6–79.5%, 64.0–83.8%, and 85.3–92.7%, respectively) when the population size was less than 30 and reached stable when the population size was greater than 30. Comparing the ARD of each algorithm when it reaches the stable state, BFO performed best in accuracy with lowest ARD (74.5%), DE performed worst with largest ARD (98.6%), and the other algorithms performed similarly with comparable ARDs (82.6 ± 5.8%). In terms of robustness, the population size also shows obviously effects on the performance of source inversion for each algorithm. The CVs of all algorithms except for SOA showed a nonlinearly downward trend as the population size increased and eventually tended to a relatively stable value. However, the SOA performed best with the remarkably lowest value (<0.10) of the CV for each tested population size. Comparing the CV of each algorithm when it reaches the stable state, the statistical analysis of one-way variance (ANOVA) indicated there were significant difference between SOA and most algorithms including BFO (p = 0.003), CSO (p = 0.00001) and GA (p = 0.002). This indicated that SOA had the best inversion robustness.

FIGURE 2

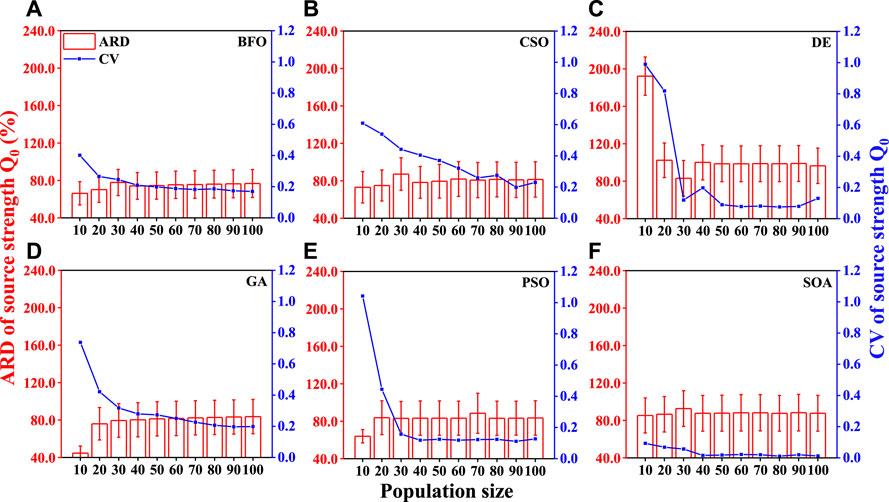
FIGURE 2. Inversion performance (ARDs and CVs) of different BIOs (BFO, CSO, DE, GA, PSO, SOA) for estimations of source strength Q₀ under tested population sizes for different atmospheric conditions (A–F).

Figure 3 shows the inversion results for the source locations (x₀, y₀, z₀). For horizontal location coordinate parameter x₀, the sensitivity of estimation performances of different algorithms to population size varied greatly. For the algorithms of CSO, DE, GA, and PSO, like the source strength parameter, they showed the consistent feature that the estimation deviations showed a certain degree of value fluctuation when the population size was smaller than a certain value and then reached a relatively stable state. Specifically, the ADs of the CSO and DE showed obviously great fluctuations (20.9–31.3 m and 38.2–99.8 m, respectively) when the population sizes were smaller than 50 and 30, respectively; the ADs of the GA, and PSO showed a fluctuation (21.6–35.3 m and 29.6–36.1 m, respectively) when the population size was smaller than 20. However, there is no distinct difference between the BFO and SOA in the inversion results for population sizes from 10 to 100. Of the BIOs, the BFO and CSO performed similarly in accuracy with the comparable ADs (29.7 and 31.3 m) when algorithms reached a relatively stable source inversion, and were slightly better than other algorithms. In robustness, the CVs of all BIOs showed a clearly downward trend as the population size increased, and the robustness of SOA performed distinctly better than that of the others, with the lowest CV (<0.003) for each population size. For horizontal location coordinate parameter y₀ and release height coordinate parameter z₀, from the value of ADs, the variation of population size in BIOs had little influence on the inversion accuracy. Comparing the estimation results of different algorithms, all algorithms showed high estimation accuracy due to the extremely low AD (<8 and 6 m for parameters y₀ and z₀, respectively). Meanwhile, all algorithms performed similarly in accuracy due the comparable ADs. In robustness, the CV of all BIOs showed an obvious downward trend with an increase in population size. Additionally, the CVs of the SOA remained in a steady state with low CVs as the population size increased.

FIGURE 3

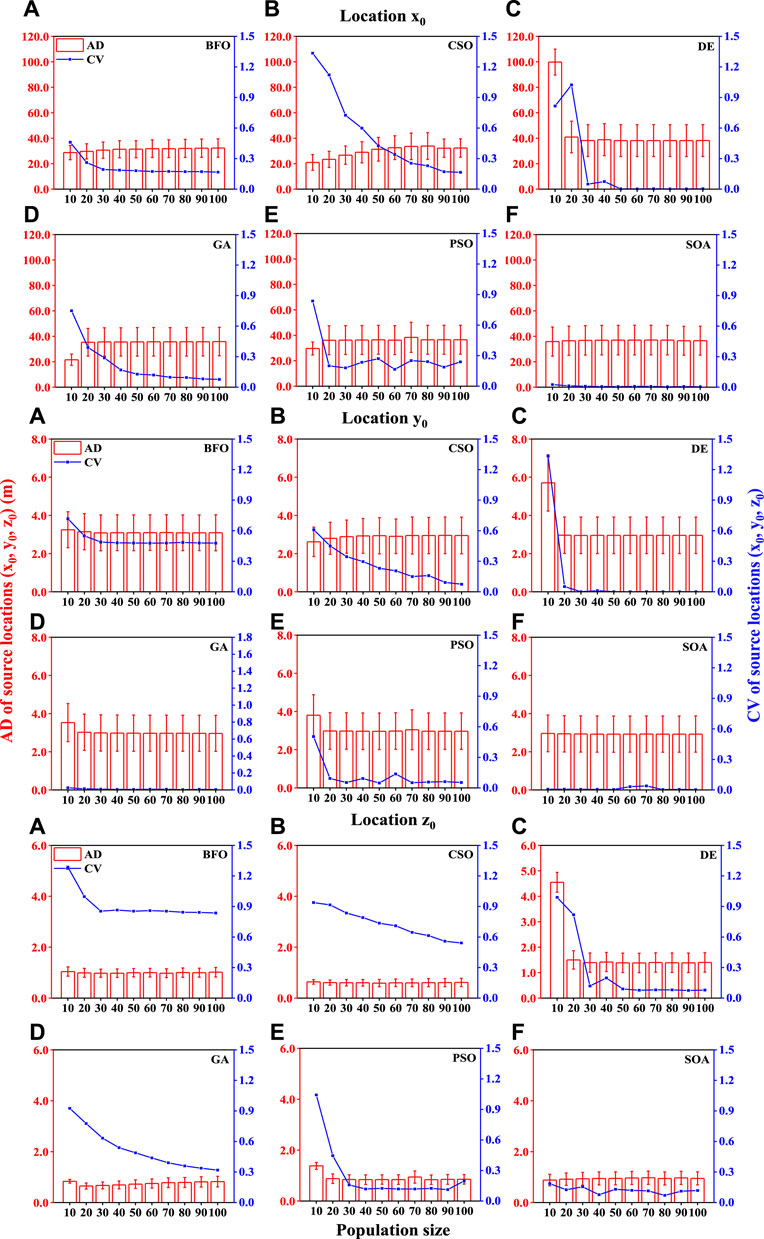
FIGURE 3. Inversion performance (ADs and CVs) of the BIOs (BFO, CSO, DE, GA, PSO, SOA) for estimations of source locations (x₀, y₀, z₀) under all tested population sizes for different atmospheric conditions (A–F).

Above analysis indicated that the population size of the BIOs obviously affected the performance of the algorithm in the application of source parameters inversion. However, the influence laws of population size on the BIOs varied in the different source parameters and performance evaluation indicators. Thus, the comprehensive scores based on all statistical indices of ARD, AD and CV for all BIOs were further calculated to help comprehensively evaluate the impact of population size in BIOs on inversion performance. Figure 4 shows the results of the comprehensive scores for the inversion performance of all the source parameters (Q₀, x₀, y₀, z₀). The comprehensive scores under all BIOs gradually declined as the population size increased and tended to be stable when the population size reached a certain value. This phenomenon indicated that the inversion performance of BIOs was obviously improved and tended to be stable when the population sizes were up to a certain value. Notably, the SOA had the lowest scores (<0.07) under all population size conditions. Furthermore, the deviation of comprehensive scores under the two adjacent population sizes was less than a certain small enough value (e.g., 0.005) as the condition for the source inversion to achieve a stable state in this study. According to the standard, the population sizes required to reach a stable state were 20, 30, 50, 30, 30, and 10 for the BFO, CSO, DE, GA, PSO, and SOA, respectively.

FIGURE 4

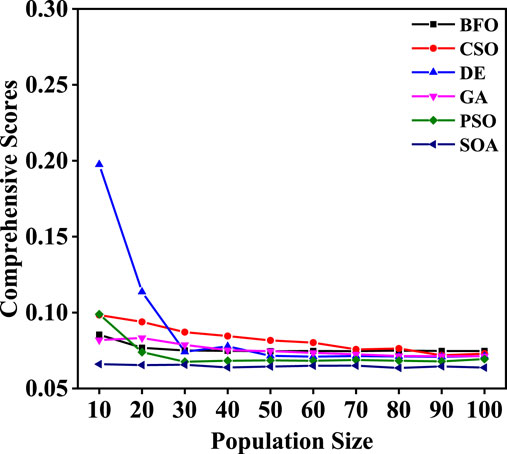
FIGURE 4. Comprehensive scores of different BIOs for all source parameters (Q₀, x₀, y₀, z₀) under different tested population sizes.

3.2 Evaluation of Source Inversion Performance Among Different BIOs

Section 3.1 investigated the impacts of population size in BIOs on source inversion and identified the minimum population size required for stable inversion performance of different BIOs. The past studies (Cui et al., 2019; Shen et al., 2019) have found that atmospheric dispersion conditions have a remarkable influence on estimation performance of optimization algorithms in source parameters inversion. To understand the impacts of atmospheric conditions on the performances of different BIOs in source inversion and improve the technical guidance for real application scenarios, we further analyzed the inversion performance of BIOs under different atmospheric stability classes (A–F). Therefore, combined with the study results of Section 3.1, the inversion results of BIOs under the population size of 50 were used to avoid the interference of population size on the inversion performance of the algorithms. Figure 5 shows the inversion results for the source parameters (Q_0, x₀, y₀, z₀). In terms of source strength Q₀, the inversion accuracy of all BIOs showed obvious fluctuations under all atmospheric conditions. The accuracy was the worst under stability classes A and B. Comparing the inversion results of different BIOs, the BFO had the best accuracy with lower ARDs under stability classes A (136.0%), B (187.7%), and C (88.7%), respectively; whereas, the SOA had the worst accuracy with relatively larger ARDs under stability classes A (177.1%), B (238.2%), and C (116.1%), respectively. The accuracy of all BIOs were comparable with similar ARD (67.4 ± 2.1%) under neutral atmospheric condition (stability class D). CSO performed slightly better than other algorithms due to the relatively lower ARD (26.7%) and PSO performed worst (33.6%) under stable condition (stability class E). Under extremely stable condition (stability class F), BFO and CSO had the comparable ARDs (23.2 and 24.3%) and performed relatively better than other algorithms, and the SOA showed obviously worse accuracy with a larger ARD (48.3). Overall, the accuracy of the BFO was relatively better than that of other BIOs, owing to its better performance under most atmospheric conditions. As for robustness, SOA performed better than the others because the CVs of the SOA were maintained at a low level (CVs <0.15) under all atmospheric conditions. The remaining BIOs showed great fluctuations in CV under different atmospheric conditions. CSO was worst with a highest CV (>0.15) under almost all atmospheric conditions.

FIGURE 5

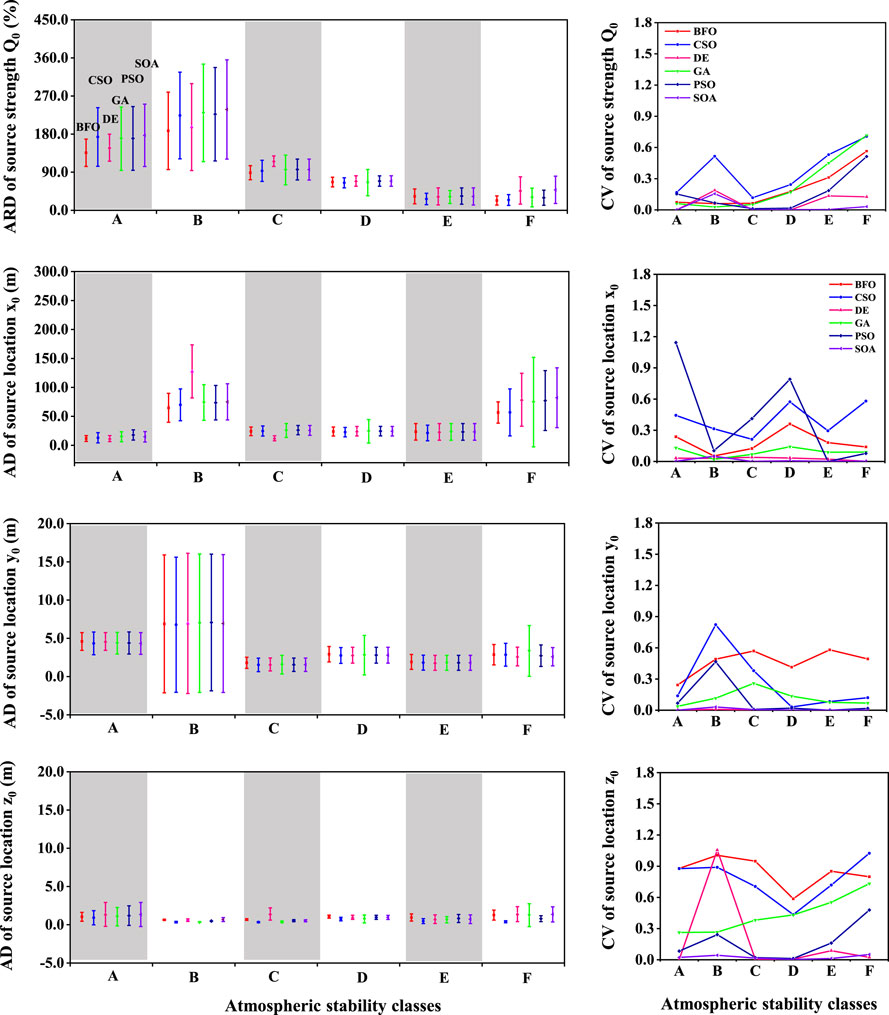
FIGURE 5. Accuracy (mean ARD or AD with 95% confidence limits) and robustness (CV) of different BIOs for the estimation of source parameters (Q₀, x₀, y₀, z₀) under different stability classes (A–F).

In terms of horizontal location parameter x₀, the ADs of the BFO were relatively lower than those of other BIOs under stabilities A (11.7 m), B (64.7 m), and F (56.7 m). DE performed better than other algorithms under stability class C with a lower AD (12.2 m), whereas there was no obviously difference in accuracy among BIOs under stability classes D and E, owing to the comparable ADs. For robustness, the CVs of the SOA and DE were comparable under each stability class and clearly lower (<0.05) than those of other BIOs. CSO performed worst in robustness with the high CVs (the range of CV from 0.21 to 0.58) under all atmospheric conditions. Additionally, from the large fluctuation of CVs under different stability classes, the inversion robustness of CSO and PSO were more sensitive to the variation of atmospheric dispersion condition than other BIOs. In terms of horizontal location parameter y₀, the accuracy of different BIOs showed little difference and the inversion deviations was small (AD <10 m) under different atmospheric conditions. This indicated that all BIOs performed consistently well in estimation accuracy. However, the robustness of different BIOs was distinctly different. The CVs of all BIOs except for SOA fluctuated largely with atmospheric conditions, whereas the CVs of the SOA remained at an extremely low level (<0.04) under each atmospheric condition. In terms of release height parameter z₀, similar to the horizontal location parameter y₀, all BIOs showed extremely small estimation deviations (AD < 5 m) and there was little difference among different algorithms. The CVs of the SOA and DE under stability classes A, C, D, and E were lower. GA and PSO had the better robustness with the relatively lower CVs (0.27 and 0.24) under stability B. However, in stability F, DE and SOA had the better robustness with the lower CVs (0.03 and 0.05). Overall, atmospheric conditions had a remarkably impact on the estimation accuracy of location x₀ and on the robustness of all location parameters. The BFO performed relatively better than other BIOs in the estimation accuracy of source locations, whereas the SOA was obviously better in estimation robustness and was less sensitive to atmospheric conditions.

Comprehensive scores based on all statistical indices of ARD, AD and CV were further calculated to evaluate the overall estimation performance of different BIOs. According to the results of comprehensive scores (Figure 6), the DE and GA performed best with the lowest scores under stability classes A (0.1659) and B (0.1928), respectively. The SOA had the best performance under stability classes C, D, E, F with the scores of 0.1345, 0.0469, 0.0580, and 0.0705, respectively.

FIGURE 6

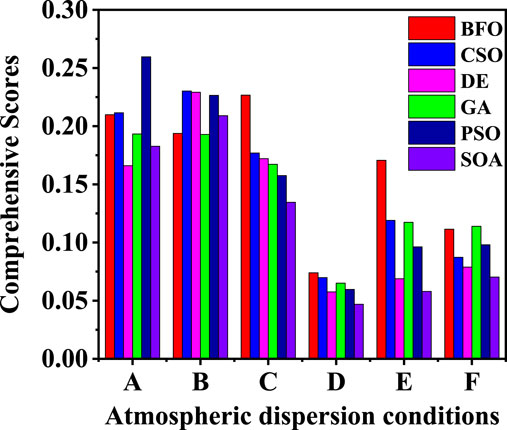
FIGURE 6. Comprehensive scores of the BIOs for all source parameters (Q₀, x₀, y₀, z₀) under different atmospheric dispersion conditions (stability classes (A–F).

4 Discussion

Performance of the various optimization algorithms differ greatly in source parameters inversion (Ma et al., 2013; Shen et al., 2019). Several bio-inspired algorithms (BIOs) have been successfully applied to the source parameters inversion in atmospheric pollutions recently. However, knowledge regarding the impacts of the different BIOs on source inversion performance is lacking. Additionally, the setting of population size (a control parameter shared by BIOs) have been proved a key factor influencing the solution quality of BIOs in the applications of treating real issues, but this parameter has not received enough attention in the researches of source inversion applications. This study analyzed and compared the performance of six BIOs (i.e., BFO, CSO, DE, GA, PSO, SOA) in source inversion applications based on the field experiments which covers different atmospheric conditions (i.e., atmospheric stability classes A to F). In order to objectively evaluate the estimation performance of the tested algorithms, the influence law of the population size of each algorithm on source inversion performance was first investigated.

Section 3.1 showed that population size had a substantial influence on source inversion accuracy and robustness of all tested BIOs. In terms of accuracy, as for source strength Q₀, the accuracy of all BIOs fluctuated greatly when the population size was small, whereas, with the increase of population size, the estimation deviations tended to be stable when the population size was larger than a certain value. The required minimum population size to reach a stable source inversion was different for the bio-inspired algorithms, 50 for BFO, CSO, and DE, and 30 for GA, PSO, and SOA. Comparing the ARD of each algorithm when it reaches the stable inversion state, a big gap of relative deviation (24.1%) between the best algorithm BFO (74.5%) and the worst algorithm DE (98.6%) indicated that the selection of bio-inspired algorithm affected the performance of source strength inversion. As for location parameters, population size had obviously large influences on the horizontal location parameter x₀. The sensitivity of estimation accuracy of different algorithms to population size varied greatly. Thereinto, the accuracy of CSO, DE, GA and PSO in parameter x₀ showed the similar features to that in source strength inversion that the estimation deviations tended to be stable as the increase of population size. However, there is no distinct difference in accuracy under different population sizes for BFO and SOA. Comparing the accuracy of all algorithms, the BFO performed slightly better than others with the lowest AD (29.7 m). In terms of robustness, the CVs of all algorithms except SOA, showed a nonlinearly downward trend as the population size increased. The reason for this characteristic may be that the more population size in these bio-inspired algorithms improves the ability of obtaining global optimization solution in each independent calculation in source inversion. Therefore, the estimation results of all independent calculations are closer for each algorithm in each field experiment. However, SOA showed remarkably less sensitivity to the population size variation than other algorithms because it was always at a prettily low level (CV < 0.3) for each tested population size for all source parameters. This indicated that SOA had more advantages on the robustness of source inversion than the other algorithms. This excellent estimation robustness may be attributed to the difference of optimization mechanism of algorithms, for instance, Dai et al. (2009) has reported the method in SOA determining the search direction and step length based on the Fuzzy rule that can make itself more superior to the PSO, GA and DE in optimization robustness. Comprehensive scores for the inversion performance of all the source parameters (Q0, x0, y0, z0) indicated that the population sizes required to reach a stable state in source inversion for different BIOs differed, with sizes of 20, 30, 50, 30, 30, and 10 for the BFO, CSO, DE, GA, PSO, and SOA, respectively. On the whole, BFO showed the best source inversion accuracy and SOA had the best source inversion robustness.

Section 3.2 revealed that the atmospheric dispersion conditions distinctly affected the estimation performance of BIOs in source inversion. The estimation accuracy of each algorithm in source parameters inversion varied greatly in different atmospheric conditions and the optimal algorithm was not unique. The conclusions are similar to the inversion results of Shen et al. (2019) where the source inversion performances of three hybrid algorithms were compared under unstable, neutral, and stable atmospheric conditions. The reason is that, in addition to the algorithm itself, source inversion performance can also be affected by the atmospheric conditions by influencing the field measured errors and the simulation abilities of forward dispersion models (Cantelli et al., 2017; Cervone and Franzese, 2011; Mao et al., 2020). Additionally, in Figure 5, the inversion accuracy of source strength Q₀ for all algorithms were distinctly worse under stability classes A and B, and source location x₀ for all algorithms under stability class F than the others. The results were basically consistent to that of the previous studies of (Cervone and Franzese, 2011; Cui et al., 2019) where the same dataset was used to test the source inversion performance of the novel proposed algorithms. However, an interesting picture is that, unlike parameter x₀, all algorithms performed well in the estimation accuracy for parameter Q₀ under stability class F. This phenomenon indicated that the solving ability of the optimization algorithms for source location parameter and source strong was different in the practical applications. The difference of solving ability for different source parameters may be attributed to the nonlinear of inversion problems. These results in section 3.2 illustrated that the reasonable selection of BIOs had the important significance on the accurate estimation of source parameters in practices due to the varied atmospheric conditions. Notably, although the SOA may not be the best in inversion accuracy, its robustness of inversion results for source strength or locations always maintained an excellent level under all atmospheric conditions. This remarkable feature means that the SOA algorithm can obtain stable source inversion results with the fewer runs than other algorithms.

The findings above can enhance the understanding of the role of population size in the applications of source inversion for the BIOs and the impacts of BIOs on source inversion. The conclusions can provide a certain reference for the selection of appropriate bio-inspired algorithms and the reasonable setting of population size parameter in algorithm for source inversion in practical environmental management, especially considering the varied atmospheric conditions. However, the study has limitations; for instance, the basic data of Prairie Grass experiments are from flat terrain and a short range (<1 km), and the atmospheric dispersion model is a simple Gaussian plume model; thus, further validation tests for the BIOs may be necessary in complex source inversion scenarios (e.g., complex urban terrains) to improve the support for real world applications. Additionally, the finding that the algorithm selection can cause great estimation difference in source inversion accuracy implies that further improving the source inversion performance by developing a more excellent optimization algorithm is a well potential approach. This study has demonstrated the outstanding robustness and the relatively mediocre accuracy of SOA in source inversion. The previous study (Cui et al., 2019) proved that it was an effective way to improve source inversion accuracy by combining the global algorithm with the local optimization algorithm. Thus, developing a hybrid algorithm by combining the SOA with a local optimization algorithm (e.g., Nelder–Mead simplex search method) may be a feasible approach to solve the problem of accurate source inversion.

5 Conclusion

Bio-inspired optimization algorithms (BIOs) are important methods for inversing source parameters (e.g., source strength and location) in atmospheric pollution events. The control parameter of population size in BIOs may also affect the source inversion performance due the optimization mechanism of BIOs. However, the impacts of different BIOs on source inversion and the role of their shared parameter of population size in BIOs in the applications of source inversion have not been revealed. This study first investigated the impacts of population size in typical BIOs (i.e., BFO, CSO, DE, GA, PSO, and SOA) on source inversion and then compared the differences of six intelligent optimization algorithms in inversion performance based on field datasets under different atmospheric conditions. According to the inversion result of 68 SO₂ leakage experiments, the population size of all tested BIOs has substantial influence on source inversion accuracy and robustness. The accuracy of all BIOs in source strength Q₀ fluctuated greatly when the population size was small, whereas, tended to be stable when the population size was larger than a certain value. The accuracy of CSO, DE, GA and PSO in parameter x₀ showed the similar features to that in source strength inversion, however, the accuracy of BFO and SOA were insensitive to the population size variation. The CVs of all algorithms except SOA, showed a nonlinearly downward trend as the population size increased, whereas SOA showed remarkably less sensitivity to the population size variation. Comprehensive scores for the inversion performance of all the source parameters (Q0, x0, y0, z0) indicated that the population sizes required to reach a stable state in source inversion for different BIOs differed, with sizes of 20, 30, 50, 30, 30, and 10 for the BFO, CSO, DE, GA, PSO, and SOA, respectively. Comparing the results of source inversion of different BIOs indicated that overall, BFO had the best accuracy with the lowest deviations (74.5% for source strength and 29.7 m for location parameter x₀), whereas SOA had the best estimation robustness due a low level of CV (<0.3) for all source parameters. Atmospheric dispersion conditions had an obvious influence on the source inversion performance of the BIOs. The estimation accuracy of each algorithm in source parameters inversion varied greatly in different atmospheric conditions and the optimal algorithm was not unique. The BFO performed the best (137.5%) in unstable conditions (A, B, and C), all algorithms were comparable with similar errors (67.4 ± 2.1%) in neutral condition (D), CSO performed slightly better than other algorithms due to the relatively lower ARD (26.7%) under stable condition (E), and BFO and CSO had the comparable ARDs (23.2 and 24.3%) and performed relatively better than other algorithms under extremely stable condition (F). The results of this study can be used to improve the understanding of the role of population size in the applications of source inversion for the BIOs and the impacts of bio-inspired algorithms on source inversion. The conclusions provide a reference for the selection of appropriate bio-inspired algorithms and the accurate setting of population size parameter in algorithms for source inversion in practical environmental management, especially considering the varied atmospheric condition.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JL contributed to conception and design of the study. SM organized the database and wrote the first draft of the manuscript. FH performed the statistical analysis. TC and SC edited the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This research was financially supported by the National Key R & D Program of China (No. 2017YFC0209905) and Beijing Nova Program (Z201100006820098) from Beijing Municipal Science and Technology Commission.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors are grateful to the reviewers for their insightful comments. In addition, we greatly appreciate the Beijing Municipal Commission of Education and Beijing Municipal Commission of Science and Technology for supporting this work.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2022.894255/full#supplementary-material

References

Alanis, A. Y., Arana-Daniel, N., and López-Franco, C. (2018). “Bio-inspired Algorithms,” in Bio-inspired Algorithms for Engineering (Kidlington, UK: Butterworth-Heinemann (an imprint of Elsevier)), 1–14. doi:10.1016/B978-0-12-813788-8.00001-9

CrossRef Full Text | Google Scholar

Albani, R. A. S., Albani, V. V. L., and Silva Neto, A. J. (2020). Source Characterization of Airborne Pollutant Emissions by Hybrid Metaheuristic/gradient-Based Optimization Techniques. Environ. Pollut. 267, 115618. doi:10.1016/j.envpol.2020.115618

PubMed Abstract | CrossRef Full Text | Google Scholar

Barad, M. L. (1958). Project Prairie Grass, A Field Program in Diffusion. Bedford, USA: Air Force Cambridge Research Center, 300.

Google Scholar

Bergamaschi, P., Karstens, U., Manning, A. J., Saunois, M., Tsuruta, A., Berchet, A., et al. (2018). Inverse Modelling of European CH&lt;sub&gt;4&lt;/sub&gt; Emissions during 2006-2012 Using Different Inverse Models and Reassessed Atmospheric Observations. Atmos. Chem. Phys. 18, 901–920. doi:10.5194/acp-18-901-2018

CrossRef Full Text | Google Scholar

Boussaïd, I., Lepagnot, J., and Siarry, P. (2013). A Survey on Optimization Metaheuristics. Inf. Sci. 237, 82–117. doi:10.1016/j.ins.2013.02.041

CrossRef Full Text | Google Scholar

Brest, J., and Sepesy Maučec, M. (2008). Population Size Reduction for the Differential Evolution Algorithm. Appl. Intell. 29, 228–247. doi:10.1007/s10489-007-0091-x

CrossRef Full Text | Google Scholar

Castelli, M., Manzoni, L., Silva, S., Vanneschi, L., and Popovič, A. (2017). The Influence of Population Size in Geometric Semantic GP. Swarm Evol. Comput. 32, 110–120. doi:10.1016/j.swevo.2016.05.004

CrossRef Full Text | Google Scholar

Cervone, G., and Franzese, P. (2011). Non-Darwinian Evolution for the Source Detection of Atmospheric Releases. Atmos. Environ. 45, 4497–4506. doi:10.1016/j.atmosenv.2011.04.054

CrossRef Full Text | Google Scholar

Chaohua Dai, C., Weirong Chen, W., Yunfang Zhu, Y., and Xuexia Zhang, X. (2009). Seeker Optimization Algorithm for Optimal Reactive Power Dispatch. IEEE Trans. Power Syst. 24 (3), 1218–1231. doi:10.1109/tpwrs.2009.2021226

CrossRef Full Text | Google Scholar

Chen, G., Hu, X., Zhou, L., Men, J., and Chen, Q. (2021). Inversion Method Based on Chicken Swarm Optimization for Hazardous Chemicals Leakage and Diffusion Accident. J. South China Univ. Technol. Nat. Sci. Ed. 49 (9), 56–64. doi:10.12141/j.issn.1000-565X.200695

CrossRef Full Text | Google Scholar

Cui, J., Lang, J., Chen, T., Cheng, S., Shen, Z., and Mao, S. (2019). Investigating the Impacts of Atmospheric Diffusion Conditions on Source Parameter Identification Based on an Optimized Inverse Modelling Method. Atmos. Environ. 205, 19–29. doi:10.1016/j.atmosenv.2019.02.035

CrossRef Full Text | Google Scholar

Dai, C., Chen, W., and Zhu, Y. (2006). “Seeker Optimization Algorithm,” in Proceedings of International Conference on Computational and Information Science, Guangzhou, China, November 3–6, 2006 (Berlin, Heidelberg: Springer), 167–176. doi:10.1109/iccias.2006.294126

CrossRef Full Text | Google Scholar

Diaz-Gomez, P. A., and Hougen, D. F. (2007). “Initial Population for Genetic Algorithms: A Metric Approach,” in Proceedings of International Conference on Genetic & Evolutionary Methods, Las Vegas, Nevada, June 25–28, 2007 (Las Vegas, Nevada, USA: GEM), 43–49.

Google Scholar

Feoktistov, V. (2006). Differential Evolution: In Search of Solutions. New York: Springer. doi:10.1007/978-0-387-36896-2

CrossRef Full Text | Google Scholar

Gao, Q., Han, L., and Chen, L. (2016). Instantaneous Source Inversion Based on Horizontal 2d Flow Model and Inversion Precision Impact Analysis. Sichuan Environ. 35 (03), 67–72. doi:10.14034/j.cnki.schj.2016.03.013

CrossRef Full Text | Google Scholar

Guo, S., Yang, R., Zhang, H., Weng, W., and Fan, W. (2009). Source Identification for Unsteady Atmospheric Dispersion of Hazardous Materials Using Markov Chain Monte Carlo Method. Int. J. Heat Mass Transf. 52, 3955–3962. doi:10.1016/j.ijheatmasstransfer.2009.03.028

CrossRef Full Text | Google Scholar

Guohua, C., and Longkai, C. (2014). Enhancing Situation Awareness of Chemical Release through Source Inversion. Procedia Eng. 84, 742–751. doi:10.1016/j.proeng.2014.10.491

CrossRef Full Text | Google Scholar

Haupt, S. E. (2005). A Demonstration of Coupled Receptor/dispersion Modeling with a Genetic Algorithm. Atmos. Environ. 39, 7181–7189. doi:10.1016/j.atmosenv.2005.08.027

CrossRef Full Text | Google Scholar

Haupt, S. E., Young, G. S., and Allen, C. T. (2007). A Genetic Algorithm Method to Assimilate Sensor Data for a Toxic Contaminant Release. Jcp 2 (6), 85–93. doi:10.4304/jcp.2.6.85-93

CrossRef Full Text | Google Scholar

Hu, F., Lang, J., Mao, S., and Xuan, B. (2021). Comparative Study on Source Parameters Inversion Performance of Typical Cost Functions. China Environ. Sci. 41 (05), 2081–2089. doi:10.19674/j.cnki.issn1000-6923.2021.0220

CrossRef Full Text | Google Scholar

Hutchinson, M., Oh, H., and Chen, W.-H. (2017). A Review of Source Term Estimation Methods for Atmospheric Dispersion Events Using Static or Mobile Sensors. Inf. Fusion 36, 130–148. doi:10.1016/j.inffus.2016.11.010

CrossRef Full Text | Google Scholar

Jansen, T., Jong, K. A. D., and Wegener, I. (2005). On the Choice of the Offspring Population Size in Evolutionary Algorithms. Evol. Comput. 13, 413–440. doi:10.1162/106365605774666921

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, M., Luo, Y. P., and Yang, S. Y. (2007). Stochastic Convergence Analysis and Parameter Selection of the Standard Particle Swarm Optimization Algorithm. Inf. Process. Lett. 102, 8–16. doi:10.1016/j.ipl.2006.10.005

CrossRef Full Text | Google Scholar

Ketabi, A., and Navardi, M. J. (2012). Optimization Shape of Variable-Capacitance Micromotor Using Seeker Optimization Algorithm. J. Electr. Eng. Technol. 7, 212–220. doi:10.5370/JEET.2012.7.2.212

CrossRef Full Text | Google Scholar

Lamb, B. K., Cambaliza, M. O. L., Davis, K. J., Edburg, S. L., Ferrara, T. W., Floerchinger, C., et al. (2016). Direct and Indirect Measurements and Modeling of Methane Emissions in Indianapolis, Indiana. Environ. Sci. Technol. 50, 8910–8917. doi:10.1021/acs.est.6b01198

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, H., and Zhang, J. (2017). Fast Source Term Estimation Using the PGA-NM Hybrid Method. Eng. Appl. Artif. Intell. 62, 68–79. doi:10.1016/j.engappai.2017.03.010

CrossRef Full Text | Google Scholar

Long, K. J., Haupt, S. E., and Young, G. S. (2010). Assessing Sensitivity of Source Term Estimation. Atmos. Environ. 44, 1558–1567. doi:10.1016/j.atmosenv.2010.01.003

CrossRef Full Text | Google Scholar

Luo, L., and Wei, H. (2011). Statistics. Beijing, China: Chinese financial&Economic Publishing House, 49.

Google Scholar

Lushi, E., and Stockie, J. M. (2010). An Inverse Gaussian Plume Approach for Estimating Atmospheric Pollutant Emissions from Multiple Point Sources. Atmos. Environ. 44, 1097–1107. doi:10.1016/j.atmosenv.2009.11.039

CrossRef Full Text | Google Scholar

Ma, D., Deng, J., and Zhang, Z. (2013). Comparison and Improvements of Optimization Methods for Gas Emission Source Identification. Atmos. Environ. 81, 188–198. doi:10.1016/j.atmosenv.2013.09.012

CrossRef Full Text | Google Scholar

Ma, D., Gao, J., Zhang, Z., Zhao, H., and Wang, Q. (2020). Locating the Gas Leakage Source in the Atmosphere Using the Dispersion Wave Method. J. Loss Prev. Process Industries 63, 104031. doi:10.1016/j.jlp.2019.104031

CrossRef Full Text | Google Scholar

Ma, D., Tan, W., Wang, Q., Zhang, Z., Gao, J., Zeng, Q., et al. (2018). Application and Improvement of Swarm Intelligence Optimization Algorithm in Gas Emission Source Identification in Atmosphere. J. Loss Prev. Process Industries 56, 262–271. doi:10.1016/j.jlp.2018.09.008

CrossRef Full Text | Google Scholar

Ma, D., Tan, W., Zhang, Z., and Hu, J. (2017). Parameter Identification for Continuous Point Emission Source Based on Tikhonov Regularization Method Coupled with Particle Swarm Optimization Algorithm. J. Hazard. Mater. 325, 239–250. doi:10.1016/j.jhazmat.2016.11.071

PubMed Abstract | CrossRef Full Text | Google Scholar

Mao, S., Lang, J., Chen, T., Cheng, S., and Hu, F. (2022). Comparative Study of Source Inversion under Multiple Atmospheric Pollutant Emission Scenarios. Front. Environ. Sci. 10, 857701. doi:10.3389/fenvs.2022.857701

CrossRef Full Text | Google Scholar

Mao, S., Lang, J., Chen, T., Cheng, S., Wang, C., Zhang, J., et al. (2020). Impacts of Typical Atmospheric Dispersion Schemes on Source Inversion. Atmos. Environ. 232, 117572. doi:10.1016/j.atmosenv.2020.117572

CrossRef Full Text | Google Scholar

Meng, X., Liu, Y., Gao, X., and Zhang, H. (2014). A New Bio-Inspired Algorithm: Chicken Swarm Optimization. Lect. Notes Comput. Sci. 8794 (1), 86–94. doi:10.1007/978-3-319-11857-4_10

CrossRef Full Text | Google Scholar

Mishra, S. (2005). A Hybrid Least Square-Fuzzy Bacterial Foraging Strategy for Harmonic Estimation. IEEE Trans. Evol. Comput. 9 (1), 61–73. doi:10.1109/TEVC.2004.840144

CrossRef Full Text | Google Scholar

Moll, C. V., Snellen, M., and Simons, D. G. (2004). “Application of Differential Evolution as an Optimisation Method for Geo-Acoustic Inversion,” in Proceedings of the Seventh European Conference on Underwater Acoustics, Delft, Netherlands, July 5–8, 2004 (Delft, Netherlands: ECUA), 721–726.

Google Scholar

Mora-Melià, D., Gutiérrez-Bahamondes, J., Iglesias-Rey, P., and Martínez-Solano, F. (2016). Efficiency Criteria as a Solution to the Uncertainty in the Choice of Population Size in Population-Based Algorithms Applied to Water Network Optimization. Water 8 (12), 583. doi:10.3390/w8120583

CrossRef Full Text | Google Scholar

Niu, B., Wang, J., and Wang, H. (2015). Bacterial-inspired Algorithms for Solving Constrained Optimization Problems. Neurocomputing 148, 54–62. doi:10.1016/j.neucom.2012.07.064

CrossRef Full Text | Google Scholar

Pasquill, F., and Smith, F. B. (1983). Atmospheric Diffusion. Chichester, West Sussex: E. Horwood New York: Halsted Press.

Passino, K. M. (2002). Biomimicry of Bacterial Foraging for Distributed Optimization and Control. IEEE Control Syst. 22 (3), 52–67. doi:10.1109/MCS.2002.1004010

CrossRef Full Text | Google Scholar

Rodriguez, L. M., Ellen Haupt, S., and Young, G. S. (2011). Impact of Sensor Characteristics on Source Characterization for Dispersion Modeling. Measurement 44, 802–814. doi:10.1016/j.measurement.2011.01.014

CrossRef Full Text | Google Scholar

Ronkkonen, J., Kukkonen, S., and Price, K. V. (2005). “Real-parameter Optimization with Differential Evolution, 2005 IEEE Congress on Evolutionary Computation,” in 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2-5 Sept. 2005, 506–513. doi:10.1109/CEC.2005.1554725

CrossRef Full Text | Google Scholar

Sarkar, T., Salauddin, M., Mukherjee, A., Shariati, M. A., Rebezov, M., Tretyak, L., et al. (2022). Application of Bio-Inspired Optimization Algorithms in Food Processing. Curr. Res. Food Sci. 5, 432–450. doi:10.1016/j.crfs.2022.02.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, Z., Lang, J., Cheng, S., Mao, S., and Cui, J. (2019). Comparative and Study on the Application of Typical Hybrid Algorithms in Source Parameter Inversions. China Environ. Sci. 39 (8), 3207–3214. doi:10.19674/j.cnki.issn1000-6923.2019.0379

CrossRef Full Text | Google Scholar

Shi, Y. (2013). Research Onback-Calculation of Source Intensity and Position of Toxic Gas Dispersion from Road Tank Car [D]. Lanzhou: Lanzhou Jiaotong University.

Google Scholar

Singh, S. K., and Rani, R. (2014). A Least-Squares Inversion Technique for Identification of a Point Release: Application to Fusion Field Trials 2007. Atmos. Environ. 92, 104–117. doi:10.1016/j.atmosenv.2014.04.012

CrossRef Full Text | Google Scholar

Sohn, M. D., Sextro, R. G., Gadgil, A. J., and Daisey, J. M. (2003). Responding to Sudden Pollutant Releases in Office Buildings: 1. Framework and Analysis Tools. Indoor Air 13 (3), 267–276. doi:10.1034/j.1600-0668.2003.00183.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Stockie, J. M. (2011). The Mathematics of Atmospheric Dispersion Modeling. SIAM Rev. 53 (2), 349–372. doi:10.1137/10080991x

CrossRef Full Text | Google Scholar

Tripathy, M., Mishra, S., Lai, L. L., and Zhang, Q. P. (2006). Transmission Loss Reduction Based on FACTS and Bacteria Foraging Algorithm. Berlin, Heidelberg: Springer, 222–231. doi:10.1007/11844297_23

CrossRef Full Text | Google Scholar

Wang, J., Zhang, R., Yan, Y., Dong, X., and Li, J. M. (2017). Locating Hazardous Gas Leaks in the Atmosphere via Modified Genetic, MCMC and Particle Swarm Optimization Algorithms. Atmos. Environ. 157, 27–37. doi:10.1016/j.atmosenv.2017.03.009

CrossRef Full Text | Google Scholar

Wei, W., Lv, Z., Yang, G., Cheng, S., Li, Y., and Wang, L. (2016). VOCs Emission Rate Estimate for Complicated Industrial Area Source Using an Inverse-Dispersion Calculation Method: A Case Study on a Petroleum Refinery in Northern China. Environ. Pollut. 218, 681–688. doi:10.1016/j.envpol.2016.07.062

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, M., Cai, X., Song, Y., and Wang, X. (2019a). A Fast Forecasting Method for PM2.5 Concentrations Based on Footprint Modeling and Emission Optimization. Atmos. Environ. 219, 117013. doi:10.1016/j.atmosenv.2019.117013

CrossRef Full Text | Google Scholar

Yu, X., Zhou, L., and Li, X. (2019b). A Novel Hybrid Localization Scheme for Deep Mine Based on Wheel Graph and Chicken Swarm Optimization. Comput. Netw. 154, 73–78. doi:10.1016/j.comnet.2019.02.011

CrossRef Full Text | Google Scholar

Zahara, E., and Kao, Y.-T. (2009). Hybrid Nelder-Mead Simplex Search and Particle Swarm Optimization for Constrained Engineering Design Problems. Expert Syst. Appl. 36, 3880–3886. doi:10.1016/j.eswa.2008.02.039

CrossRef Full Text | Google Scholar

Zheng, X., and Chen, Z. (2010). Back-calculation of the Strength and Location of Hazardous Materials Releases Using the Pattern Search Method. J. Hazard. Mater. 183, 474–481. doi:10.1016/j.jhazmat.2010.07.048

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, X., and Chen, Z. (2011). Inverse Calculation Approaches for Source Determination in Hazardous Chemical Releases. J. Loss Prev. Process Industries 24, 293–301. doi:10.1016/j.jlp.2011.01.002

CrossRef Full Text | Google Scholar

Zhong, Y., Wang, X., and Cheng, S. (2020). Characteristics and Source Apportionment of PM2.5 and O3 during Winter of 2013 and 2018 in Beijing. Atmosphere 11 (12), 1324. doi:10.3390/atmos11121324

CrossRef Full Text | Google Scholar