Bi-objective collaborative optimization of a photovoltaic-energy storage EV charging station with consideration of storage capacity impacts

The rapid growth of renewable energy and electric vehicles (EVs) presents new development opportunities for power systems and energy storage devices. This paper presents a novel integrated Green Building Energy System (GBES) by integrating photovoltaic-energy storage electric vehicle charging station (PV-ES EVCS) and adjacent buildings into a unified system. In this system, the building load is treated as an uncontrollable load and primarily utilized to facilitate the consumption of surplus photovoltaic (PV) power generated by EVCS. First, a strategy for determining the maximum value of the energy storage system (ESS) capacity is presented. Subsequently, to coordinate the charging and discharging plans of ESS, and EVs, a bi-objective optimization model was established focusing on GBES power purchase costs and the load peak-valley difference. The proposed GBES efficiently utilizes the integrated energy system comprising charging stations and adjacent buildings, maximizing the use of photovoltaic energy and external power grids during low-cost periods. In experiments, we compare the proposed optimized charging strategy with the unordered charging case, the simulation results demonstrate that the proposed method for coordinating ESS and EVs charging can respectively reduce the cost of purchased power by 33.2% and the peak-to-valley difference in load by 47.6%.

1 Introduction

There is a general consensus that the large-scale deployment of electric vehicles (EVs) and distributed renewable energy resources can effectively reduce dependence on fossil fuels in the transport sector, thereby reducing carbon emissions (Borén et al., 2017; Khan et al., 2019). The number of EVs is growing by the day, and EVs charging is creating new challenges for the electricity grid, and the global EVs charging demand is expected to grow nearly 11 times in 2030 compared to 2019 (Zou et al., 2023).

The integration of uncoordinated EVs charging into the distribution system presents a number of challenges for the management, operation, and control of the power system. Furthermore, it may also compromise the reliability of the whole power system (Wan et al., 2022; Yin et al., 2023; Mahato et al., 2023). In response to the increasing demand for EVs charging, some cost-effective methods of coordinated EVs charging are being explored. These approaches involved scheduling EVs charging during off-peak hours when grid demand was low, thereby reducing the pressure on the electricity supply during peak hours (Mousa, 2023; Jian et al., 2017). Besides, distribution system operators (DSOs) are considered to have the potential to coordinate EVs and photovoltaic (PV) systems in an aggregated manner, which could help to mitigate adverse effects such as the overloading of network assets (Cortés Borray et al., 2020).

Recently, the researchers have devised a two-phase coordinated charging scheduling solution within an energy market setting, aiming to efficiently schedule EVs charging loads and maximize profitability from the perspective of an EV integrator (Meng et al., 2024; Zheng et al., 2023). Furthermore, multi-objective optimization models are frequently employed to overcome the challenge of electric vehicle charging scheduling. The authors usually propose a multi-objective optimization approach to improve economic efficiency while mitigating adverse effects on the grid (Hou et al., 2020; Li et al., 2022; Mishra et al., 2023). Especially, in Shen et al. (2022), the potential of multi-energy microgrids has been investigated. The authors proposed a microgrid energy storage optimization method that incorporated multi-energy coupled demand response (DR), and established a multi-objective optimization model for multi-energy capacity planning based on demand response. In Ghofrani and Hersi (2024), a multi-objective optimization approach was proposed for integrating EVs and renewable distributed generation (DG) in distribution systems. This method coordinated EVs and DG using vehicle-to-grid (V2G) technologies and system reconfiguration, promoting participation in the renewable arbitrage market while managing increased system loads and power losses from EV charging and energy exchanges. To meet the charging demands of EVs amid limited public charging stations and lower costs, optimizing electric vehicle charging station (EVCS) operations is crucial. This context leads to the proposal of an online multi-objective optimization framework aimed at enhancing EVCS operations, focusing on improving quality of service (QoS) and reducing total charging costs (Li et al., 2024).

The heuristic optimization approach has been proven to be an effective solution for optimizing the aforementioned model, which incorporates EVs charging (Wang et al., 2024). As mentioned in Morais et al. (2020), a novel hybrid approach by combining deterministic techniques with the elitist nondominated sorting genetic algorithm (NSGA-II) was proposed as a solution to the EVs scheduling challenge. A novel microgrid system optimization model was proposed with aiming to optimize the microgrid system by integrating multi-purpose renewable energy (MEM) and EV. The multi-objective grey wolf optimization (MOGWO) algorithm has been used to optimize EVCS and EVs charging costs. Through dynamic pricing based on time, state of charge, and hour-based scheduling, the new proposed optimization strategy can improve system efficiency, encourage off-peak charging, and reduce costs (Sharma and Ali, 2024).

Furthermore, time-of-use (TOU) pricing is also a simple and effective demand response strategy. Previous literature has demonstrated the feasibility of time-sharing tariffs (Qie et al., 2024; Kaur and Singh, 2023). The authors in Enrich et al. (2024) evaluate the effect of a TOU pricing program introduced in Spain on residential electricity consumption. Besides, optimal configuration of energy storage equipment can effectively alleviate the peak and valley pressure on grid load, leading to an improved utilization rate of wind power (Wang et al., 2021). In Ahmad et al. (2024), a parking lot with integrated photovoltaic energy generation and energy storage systems (PV-ES PLs) is proposed to facilitate EVs charging, enhance energy savings, and reduce carbon emissions. The focus is on the energy management strategy (EMS) based on TOU tariffs, which aims to reduce peak-to-valley power demand from the grid and maximize PV utilization. By aligning EVs charging with low-cost periods and utilizing PV generation during the day, the EMS optimizes energy usage and decreases grid dependence. Despite rapid advancements in PV systems and energy storage technologies, the widespread deployment of residential distributed photovoltaic (RDPV) systems encounters complex challenges, including intermittent PV output, fluctuating electricity demand, and increasing adoption of EVs. To address these issues, an integrated RDPV capacity planning model has been proposed in Chen et al. (2024), encompassing EV charging, vehicle-to-home (V2H) systems, and flexible load demand response. Five scenarios were developed to analyze the influence of various factors on the optimal installed capacity of PV systems, electricity costs, self-consumption, and self-sufficiency. Case studies revealed that demand response and V2H technologies can significantly reduce both the optimal installed capacity of PV systems and the total electricity costs.

As previously stated, significant advancements have been made in the field of PV-ES EVCSs, with the utilization of diverse heuristic algorithms. However, a notable limitation persists in the comprehensive optimization of electric loads within the vicinity of the EVCS. Additionally, there is a paucity of research exploring the influence of storage system capacity on the optimization outcome. Inspired by these, in this paper, a novel Green Building Energy System (GBES) will be implemented, which will examine not only the integration of electric vehicle charging stations with photovoltaic generation and energy storage systems, but also the impact of uncontrollable building loads in the vicinity of the charging stations on the shape of the regional power load curve. The system employs a price-based demand response mechanism based on TOU tariffs. The primary objective function is to minimize the system’s electricity purchasing costs, including the portion that needs to be purchased beyond photovoltaic generation. Additionally, in consideration of the augmented peak-to-valley load disparity resulting from the conjunction of electric vehicle loads and uncontrollable building loads, a secondary optimization objective is established with the aim of minimizing the load peak-to-valley difference of the GBES. Moreover, the optimization framework takes into account the influence of fluctuating energy storage system (ESS) capacities on the optimization outcomes.

The main contributions can be summarized as follows:

1. A novel GBES is constructed with considering uncontrollable base loads and EVs charging loads. In order to enhance the utilization of PV and match load peaks, an ESS capacity allocation formula is built, which can be used to obtain an upper limitation of ESS capacity based on the maximum PV redundancy;

2. A bi-objective optimization model with respect to power purchase cost and load peak-to-valley difference for GBES is constructed. The proposed GBES effectively coordinates the ESS and EV charging and discharging schedules, thereby enhancing the utilization of PV generation and optimizing the load management during off-peak periods;

3. Extensive experiments and comparisons demonstrate that the proposed method for coordinating ESS and EVs charging/discharging can reduce the cost of purchased power by 33.2% and the peak-to-valley difference in load by 47.6%.

2 Problem statement and modeling

2.1 Structure of GBES

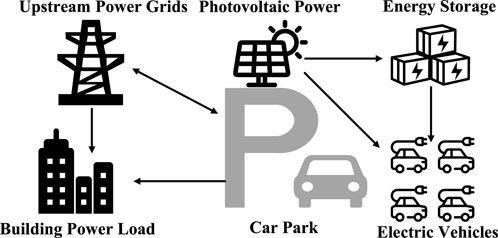
Firstly, we propose a GBES. This energy system can be seen as having three participants, with the external power grid only purchasing and selling electricity. And the other two, adjacent buildings and EVCS, form the proposed GBES. The EVCS contains PV and ESS. The EVCS can supply energy to buildings, primarily from PV, followed by EV discharging and ESS discharging. In addition, EVCS can also sell/purchase electricity from the external power grids end to generate revenue/cost. The adjacent building loads can be supplied through two channels: purchasing from the external power grids and supplying from EVCS, as shown in Figure 1.

Figure 1

Figure 1. The schematic diagram of the proposed GBES.

This system is different from the concept of microgrids and does not consider additional power generation equipment other than PV, such as turbines. Unlike simply considering the charging stations, the inclusion of adjacent buildings is due to the following reasons:

1. Adjacent buildings can share excess PV power, thereby reducing waste and improving overall energy efficiency.

2. Including adjacent buildings allows for better load balancing between EVCS and buildings, enhancing energy demand and supply management.

3. The energy consumption patterns of adjacent buildings and charging stations differ significantly. Considering the significant fluctuations in the load of charging stations, a more elastic and flexible energy system can be formed by combining the two.

4. By optimizing energy use across both buildings and EVCS, we can contribute to reducing carbon emissions and promoting sustainable energy practices.

The scheduling strategy of GBES is as follows, as shown in Figure 2: Firstly, the state of ESS needs to be distinguished. When ESS is considered as an energy supply device: PV is mainly used to meet the energy demand of EVCS, and the remaining part is supplied to adjacent buildings, ESS also supplies energy to adjacent buildings; If there is a shortage of PV, the ESS is replenished for use by EVCS, and the excess ESS energy is used to supply adjacent buildings. At this time, the surplus/shortage electricity of GBES is sold/purchased from the external power grid. When ESS is regarded as an energy consuming device: PV is mainly used to meet the energy demand of the EVCS, and the remaining part charges the ESS before supplying energy to adjacent buildings; if there is a shortage of PV power, the remaining/missing electricity in GBES will be sold/purchased from the external power grid.

Figure 2

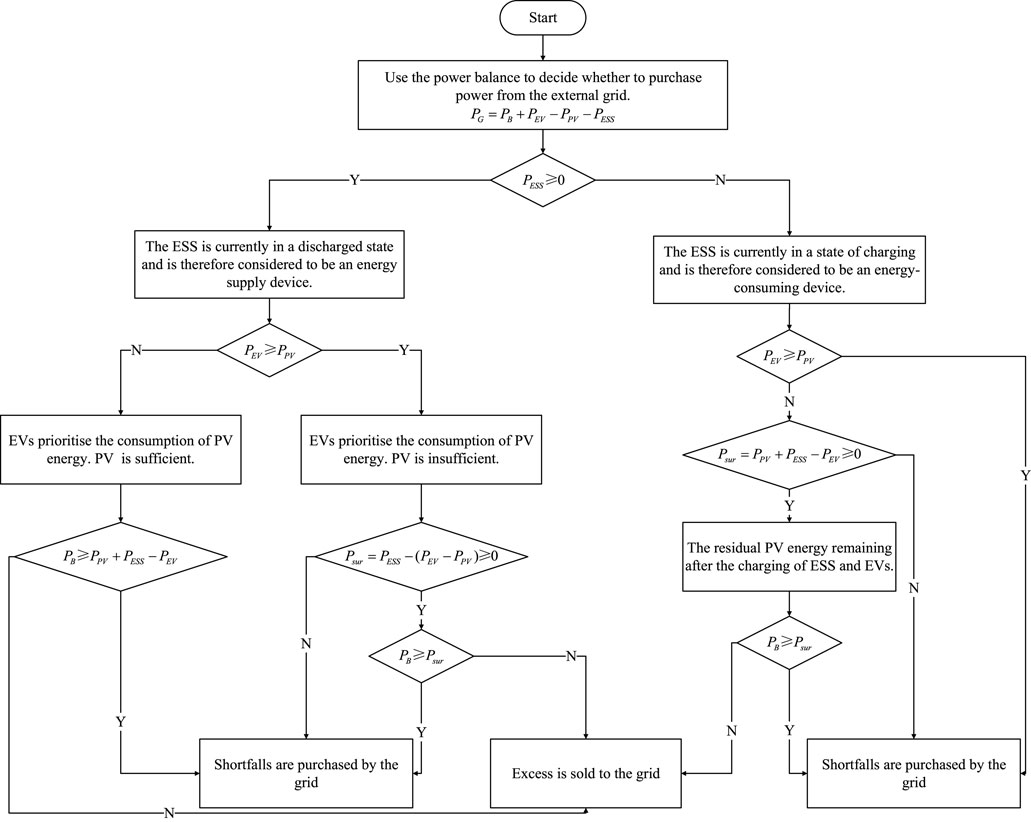
Figure 2. Illustration of GBES strategy: coordinated charging of EVs with concurrent use of ESS and PV.

To minimize costs, we assume that ESS can purchase electricity from the grid only for charging during periods of low electricity prices. In addition, the symbol meanings in Figure 2 are: $P_G$ represents the power exchanged with the grid, $P_B$ is the load of adjacent buildings, $P_{EV}$ is the charging load in the EVCS, $P_{\mathit{ESS}}$ is the exchangeable power of ESS, and $P_{\mathit{sur}}$ is a temporary value used to determine the difference between PV, ESS, and charging demands in the EVCS.

2.2 Models in GBES

This study aims to investigate the impact of coordinated EVs charging on the total costs and power system stability. Consequently, the adjacent building load and PV are not included in the scope of the optimization. The variables to be optimized in this study include the charging and discharging strategies for both EVs and the ESS, as well as the electricity purchased from external power grids. It is important to note that, this paper not only considers the coordinated scheduling of ESS with EVs but also the selection of ESS capacities. This will be detailed in the next section.

2.2.1 Operational model and upper capacity calculation of ESS

To dynamically manage the capacity of the ESS, the State of Charge (SOC) is introduced here. The operating model for an ESS is shown in Equation 1 (Ullah et al., 2023):

$\begin{array}{c}\hfill SO{C}_{\mathit{ESS}}\left(t+1\right)=SO{C}_{\mathit{ESS}}\left(t\right)+\frac{P_{\mathit{ESS,chr}}\left(t\right)*{\eta }_{\mathit{ESS}}*\mathrm{\Delta }t}{Ca{p}_{\mathit{ESS}}}*\frac{P_{\mathit{ESS,dis}}\left(t\right)*\mathrm{\Delta }t}{Ca{p}_{\mathit{ESS}}*{\eta }_{\mathit{ESS}}}\hfill \end{array}(1)$

where, $SO{C}_{\mathit{ESS}}(t)$ indicates the SOC of ESS at time t, and ${\eta }_{\mathit{ESS}}$ represents the charging/discharging efficiency of ESS. $P_{\mathit{ESS,chr}}(t)$ and $P_{\mathit{ESS,dis}}(t)$ respectively denote the charging and discharging power of ESS. $Ca{p}_{\mathit{ESS}}$ corresponds to the capacity of ESS.$\mathrm{\Delta }t$ is the time step of the optimization, which in this paper represents 1 h.

The ESS will discharge discontinuously when the SOC drops below the minimum value and will stop charging when the SOC surpasses the maximum value to extend the battery life. The battery constraint of the ESS is represented by Equation 2:

$SO{C}_{\mathit{ESS}}^{\min }\le SO{C}_{\mathit{ESS}}\left(t\right)\le SO{C}_{\mathit{ESS}}^{\max }(2)$

where $SO{C}_{\mathit{ESS}}^{\min }$ and $SO{C}_{\mathit{ESS}}^{\max }$ respectively represent the minimum and maximum SOC values of the ESS.

The PV is recognized as a green energy source. In order to maximize the storage of PV power that has not been consumed in a timely manner, a method for calculating the maximum capacity of ESS is proposed, as follows:

$C_{\mathit{ESS}}^{\mathit{max}}={\displaystyle \underset{d=1}{\overset{365}{\max }}}\left(\frac{{\max }_{t=1}^{24}|P_{PV}\left(d,t\right)-P_B\left(d,t\right)|*{\eta }_{\mathit{ESS}}}{SO{C}_{\mathit{ESS}}^{\max }-SO{C}_{\mathit{ESS}}^{\min }}\right)(3)$

where $C_{\mathit{ESS}}^{\mathit{max}}$ is the maximum capacity of ESS. The variables $P_{PV}(d,t)$ and $P_B(d,t)$ represent the corresponding values of PV energy and building load at day $d$, moment $t$, respectively. The objective is to ensure that the utilization of PV is maximized. However, due to the requirement of Equation 3 that EVCS provide charging data within a year, predicting a significant amount of EVs charging loads during this period would introduce substantial errors, thereby significantly impacting the upper limit of the ESS capacity. Consequently, Equation 3 does not consider the load associated with EVs.

It should be noted that Equation 3 does not necessarily mean that the maximum ESS capacity will bring the best optimization effect. Therefore, we add Equation 4 and continuously try to find the ESS capacity corresponding to the best optimization result.

$C_{\mathit{ESS}}\left(k+1\right)=C_{\mathit{ESS}}\left(k\right)+c_{\mathit{ESS}},0\le k\le K(4)$

where, $K_{\mathit{ESS}}=\frac{C_{\mathit{ESS}}^{\mathit{max}}}{c_{\mathit{ESS}}}$, and $c_{\mathit{ESS}}$ is the ESS capacity value interval. $C_{\mathit{ESS}}(k+1)$ and $C_{\mathit{ESS}}(k)$represent the values of ESS capacity for the $(k+1)$ and $k$ iterations, respectively.

2.2.2 EVs charging load

The user’s EV charging time is usually after returning to the charging station, and the charging completion time is usually before the next departure time. The power consumption can be expressed as the remaining SOC when the EV arrives at the charging station. Here, MCS is employed to ascertain the charging load profile of EVs.

Note that, the stochastic charging behaviour of EVs is contingent upon the user’s travel rule, specifically whether the EV is charged immediately upon the conclusion of the daily trip. As evidenced in the literature (Li et al., 2023), the return time ($T_r$) of the last trip of the EV is normally distributed. The probability density function (PDF) approximation of the EV departure time (denoted by $T_d$) can also be obtained by the same statistical method. In order for the sequential charging scheduling behaviour of the EV to be completed before the user leaves, it is necessary for the charging process to commence before the user departs.

As mentioned in Li et al. (2021), the remaining SOC$(SO{C}_{\mathit{ini}})$ in the EV upon its arrival at the charging station is assume to follow a normal distribution $N(0.5,0.1^2)$. Then, the charging time of an EV can be calculated as shown in Equation 5:

$T_{\mathit{dur}}=\frac{\left(SO{C}_{\exp }-SO{C}_{\mathit{ini}}\right)Ca{p}_{EV}}{P_{\mathit{EV\; C}}\left(t\right){\eta }_{EV}}(5)$

where $T_{\mathit{dur}}$ is the duration of charging. $P_{\mathit{EV\; C}}(t)$ and ${\eta }_{EV}$ respectively are the charging power and the charging efficiency of the EV. $Ca{p}_{EV}$ is the battery capacity of the EV. $SO{C}_{\mathit{exp}}$ is the expected SOC when leaving the charging station.

The fundamental principle underlying the maximum dispatch time for EVs is to ensure that the departure time of the EVs is not affected. This can be guaranteed by the following equation:

$T_o=\min \left\{\left(T_d-T_r\right),T_{\mathit{dur}}\right\}(6)$

where $T_o$ represents the schedulable time for an individual EV.

3 Optimization model and solution method

This section will analyze and construct the objective function to be optimized, as well as the corresponding constraints that are not mentioned in the previous section.

3.1 Objective function

The goal of optimizing scheduling is to achieve the maximum economic benefits of GBES. The following equation is the cost of purchasing electricity from the power grid.

$\min f_1={\displaystyle \sum _{t=1}^T}\alpha P_{\text{buy}}\left(t\right)-\beta P_{\text{sell}}\left(t\right)(7)$

where, $T$ represents the total number of periods in the scheduling horizon, which is set to 24 h in this study, $\alpha =\{\alpha 1,\alpha 2\}$ represent the current price coefficients of the TOU price, $\alpha 1$ is the purchase price of electricity for building loads that do not participate in regulation and control; $\alpha 2$ is the price for EVs and ESS purchases. $\beta$ is the sale price. $P_{\text{buy}}(t)$ represents the quantity of electricity purchased from the grid at time slot $t$. $P_{\text{sell}}(t)$ denotes the quantity of electricity sold to the grid.

In order to avoid a large number of EVs concentrating on charging during low tariff hours, the difference between load peaks and valleys is considered as a second optimization objective as follows.

$\min f_2=\max P_{\mathit{sum}}\left(t\right)-\min P_{\mathit{sum}}\left(t\right)(8)$

where $f_2$ is the peak-valley difference of the load, $\max P_{\mathit{sum}}(t)$ is the peak value of the electrical load, $\min P_{\mathit{sum}}(t)$ is the valley value of the electrical load, and $P_{\mathit{sum}}(t)=P_B(t)+P_{EV}(t)$.

Considering that $f_1$ and $f_2$ represent completely different goals and have significant numerical differences. In order to establish a consistent framework for subsequent optimization. The objective functions $f_1$ and $f_2$ are calculated based on linear weighting and normalization as

$\min F={\lambda }_1\frac{f_1}{f_{1N}}+{\lambda }_2\frac{f_2}{f_{2N}}(9)$

Equation 9 represents the objective function after weighting $f_{1N}$ is the unscheduled charging cost, $f_{2N}$ is the unscheduled peak-off-peak load fluctuation, ${\lambda }_1$ and ${\lambda }_2$ represent the weighting coefficients with satisfying ${\lambda }_1+{\lambda }_2=1$.

3.2 Constraint conditions

3.2.1 Power balance condition

Here, the power balance condition is shown in Equation 10:

$P_G\left(t\right)+P_{PV}\left(t\right)=P_{\mathit{ESS}}\left(t\right)+P_{EV}\left(t\right)+P_B\left(t\right)(10)$

where $P_G(t)$ is electricity purchased from the grid, and if its value is negative, it represents power will be sold to the grid; $P_{PV}(t)$ represents the solar power output at time t, $P_{\mathit{ESS}}(t)$ represents the power of the ESS. When the value of $P_{\mathit{ESS}}(t)$ is positive, it indicates that the ESS is being charged, and when the value is negative, it indicates that the ESS is being discharged. $P_{EV}(t)$ represents the total charging power of EVs with $P_{EV}(t)={\displaystyle \sum _{i=1}^n}{P}_{\mathit{EV\; C}}(t)$.

3.2.2 Limitations on the charging power

In practice, the charging power of the EVs and ESS and the discharging power of the ESS must comply with their minimum and maximum power limitations. The power constraint is shown in Equation 11:

$0\le P\left(t\right)\le P^{\max }(11)$

where $P(t)=\{P_{\mathit{ESS,chr}}(t),P_{\mathit{ESS,dis}}(t),P_{EV}(t)\}$, $P^{\max }=\{P_{\mathit{ESS,chr}}^{\max },P_{\mathit{ESS,dis}}^{\max },P_{EV}^{\max },\}$, $P_{\mathit{ESS,chr}}^{\max }$ and $P_{\mathit{ESS,dis}}^{\max }$ are the upper limitations of the charging-discharging power of ESS; $P_{EV}^{\max }$ represents the upper limit of charging power for an electric car.

3.3 Optimization algorithm

Next, we will employ a genetic algorithm (GA) and an elitist reserve strategy to address the aforementioned bi-objective optimization problem. The initial step involves the computation of the maximum value for the ESS capacity, which is performed using Equations 3, 4. This is followed by the iterative updating of these formulas. The algorithm’s inputs comprise the following daily forecast data: adjacent building load and PV generation, EVs charging loads predictions (arrival time, departure time and initial SOC), and purchase and selling prices of electricity. The schedulable time windows for EVs are determined by Equation 6, and the optimization process is confined to these specified periods. Since the adjacent building load and PV are not subject to scheduling, the decision variables include hourly schedules for EVs and ESS charging/discharging, as well as power exchange with external power grid. The proposed optimization algorithm is shown in Figure 3.

Figure 3

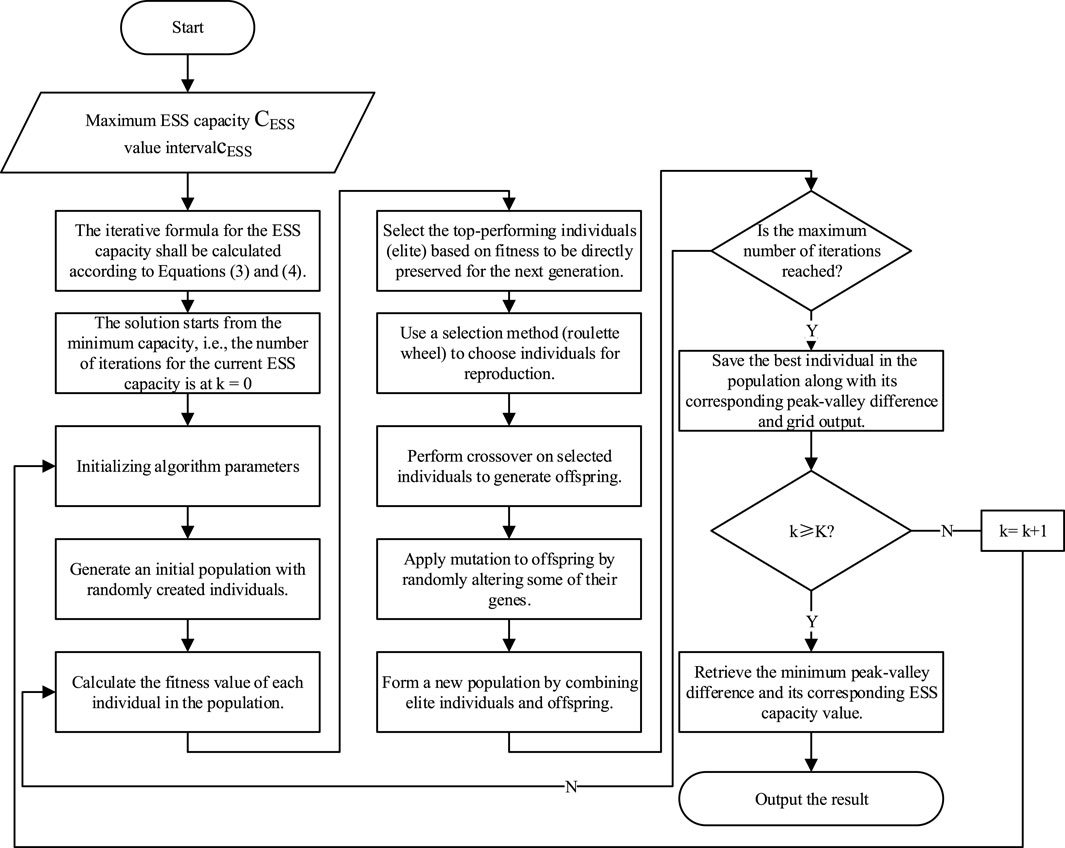
Figure 3. The proposed bi-objective optimization algorithm framework based on an elite genetic algorithm.

4 Experiment results and analysis

4.1 Experiment description

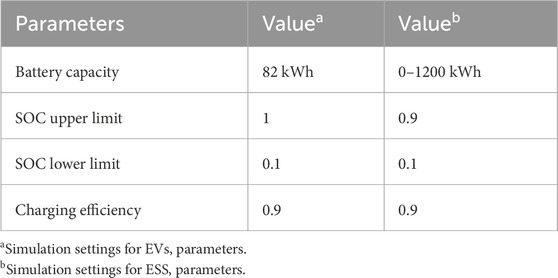
Considering the charging demand of 200 EVs at a single charging station, and with only one adjacent building, the load curve is shown in Figure 4A. The optimization step for the ESS capacity allocation is set to 200 kWh. The maximum value of the ESS capacity allocation is calculated to be 1,200 kWh according to Equation 3. The TOU tariffs are shown in Figure 4A (Liu et al., 2023), and the parameters related to EVs and ESS are shown in Table 1. The forecasts for adjacent building load, PV and EVs load are shown in Figure 4B. The arrival time and departure time of EVs at the charging station follow the distributions $N(\mathrm{19,1}.5^2)$ and $N(7.45,1^2)$ respectively (Xiaodong et al., 2016). The EVs charging power is set to 7.6 kW (Kang et al., 2023). The daily charging load of EVs is obtained by the MCS method.

Figure 4

Figure 4. (A) Time-of-use electricity price. (B) Day-ahead load forecast.

Table 1

Table 1. Corresponding parameter settings.

This article aims to analyze and compare the impact of TOU electricity pricing on the load curve of EVs, as well as the overall performance of GBES systems, mainly comparing the two objective functions in Section 3.1. To this end, three scenarios are proposed:

In Case 1, it is assumed that there is no ESS at the EVCS and that the charging of EVs is conducted in an unordered charging manner. The purpose is to obtain the unordered charging load curve of EVs, which can be used as a benchmark for comparison with the ordered charging load curve in the future.

In Case 2, it is assumed that there is no ESS at the EVCS, but the EVs are charging in an orderly manner, that is, optimizing according to the Bi-objective optimization in Section 3.1. The obtained curve can be compared with Case 1 to verify the advantages after optimization.

In Case 3, the EVCS has an ESS and the EVs are being charged in an orderly manner. The purpose of this case is to compare with Case 2 and demonstrate that the GBES with ESS can achieve better optimization results.

4.2 Optimal ESS capacity

In the proposed GBES, considering the upper limit of ESS capacity calculated by Equation 3, values are taken every 200 kWh from 0 to 1200 kWh to obtain the corresponding bi-objective optimization results, as shown in Figure 5A. The final configuration results, obtained through weighted calculations, indicate that the selected ESS capacity is 1,000 kWh. This configuration is optimal in terms of electricity purchase costs and peak-to-valley load differentials for the GBES. It can be seen that not the maximum ESS capacity can achieve the best optimization results, which also reflects the role of our proposed Equation 4.

Figure 5

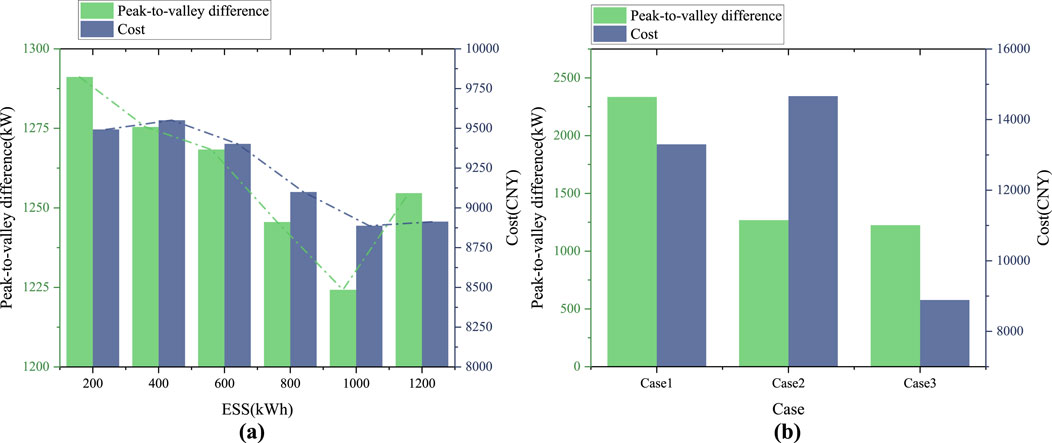
Figure 5. (A) Comparison of optimal ESS capacity configuration results for bi-objectives. (B) Comparison of bi-objective optimization structures across different cases.

As shown in cases 1 to 3, the benefits of orderly charging and the greater improvement after adding an ESS can be compared in sequence. The corresponding bi-objective optimization results for the three cases mentioned in section 4.1 are shown in Figure 5B. It can be observed that both Case 2 and Case 3 show a reduction in the difference between peak and valley loads, indicating an improvement in the load curve, which is beneficial for the power grid system in the region. However, the cost of purchasing electricity in Case 2 is higher than that in Case 1. This is attributed to the inevitable charging that occurs during periods of high electricity prices, which increases costs but helps reduce peak to valley load differences. This is also a benefit of dual objective optimization, which can comprehensively consider the optimization plan from both economic and stability aspects. Case 3 demonstrates the effectiveness of the proposed optimization model in reducing costs and smoothing loads, as it simultaneously has the minimum two objective values, indicating that energy storage systems can further improve optimization effects on the basis of orderly charging for EVs.

4.3 Comparison of case results

From Figure 4B, it can be observed that a new load peak occurs when the unordered charging load of EVs in the charging station is superimposed on the load of adjacent building, posing new challenges to the power system in the region. In comparison to the unordered charging scenario presented in Case 1, the combined adjacent building load and EVs charging load curve in Case 2, where charging is conducted in an orderly manner, is depicted in Figure 6A. The overall load profile is characterised by smaller fluctuations. It can be observed that between 00:00 and 09:00, the Case 2 scenario demonstrates superior utilization of the lower load hours, effectively reducing the power peak between 15:00 and 24:00.

Figure 6

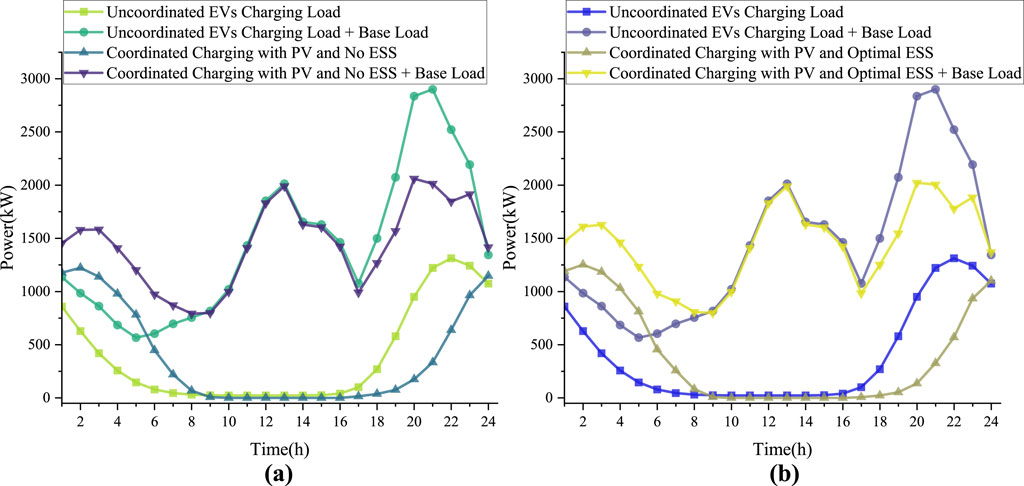
Figure 6. (A) Comparison of daily electric load between Cases 1 and 2. (B) Comparison of daily electric load between Cases 1 and 3.

A comparison between Case 3 and Case 1 yields the same result, as shown in Figure 6B. This indicates that both Case 2 and Case 3, when charged in an orderly manner, bring significant improvements compared to the unordered charging of EVs.

Although Figures 6A, B show similar optimized load curves, based on the previous Figure 5B, we can conclude that there is still a significant difference in the purchase cost between the two cases. The proposed GBES, identified as Case 3, represents the optimal solution.

In addition, the optimization effects of different cases can also be obtained from the trading of electricity with external power grids. Figure 7A shows the amount of electricity purchased by GBES from the external power grid in four cases, including cases 1–3 and the case without PV. It has been observed that in the absence of PV, GBES is required to purchase all power demand through the external power grids, resulting in significant costs. In Case 1, due to the mismatch between EVs charging times and PV generation periods, excess PV energy is fed back to the grid at a low price between 09:00 and 16:00. For charging station operators, this is uneconomical. Case 2 illustrates that the orderly charging of EVs can utilize a greater proportion of PV, resulting in a reduction in the amount of PV sold to the grid between 09:00 and 16:00. Case 3 shows that PV can be utilized by both ESS and EVs, with ESS charging from the external power grids during low price periods and discharging to the external power grid during high price periods. Figure 7B presents a cost/benefit analysis of power exchange between GBES and the external power grid under four different cases. It demonstrates that Case 3 not only exhibits the lowest electricity purchase costs but also generates the highest profit from electricity sales. With regard to the first optimization objective, namely the cost of purchased electricity as expressed in Equation 7, it can be observed that Case 2 is 10.3% higher than Case 1, while Case 3 is 33.2% lower than Case 1. The addition of an ESS to Case 3 not only allows for the storage of excess PV power, but also enables the storage of electricity during periods of low tariff. This results in a notable reduction in the cost of purchased electricity.

Figure 7

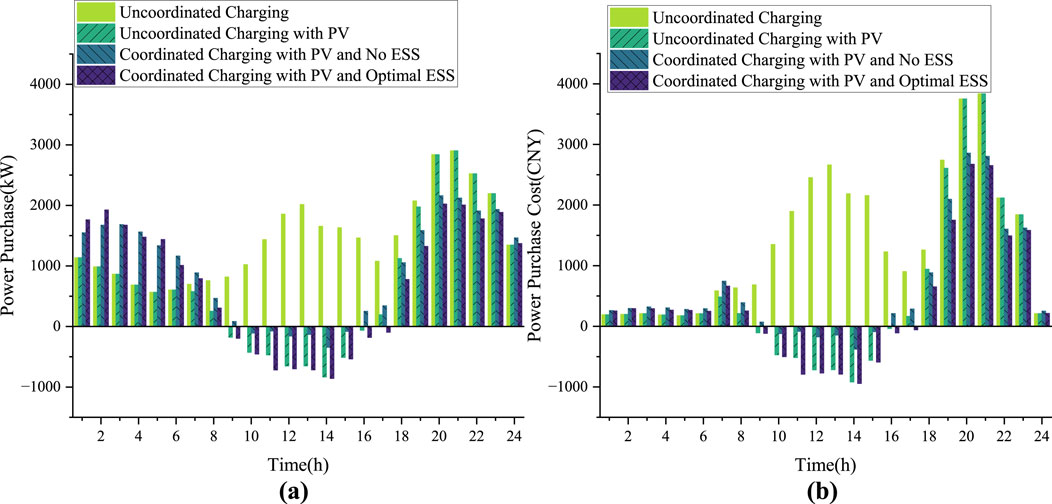
Figure 7. (A) Comparison of GBES power purchases from the grid in four different scenarios. (B) Comparison of GBES cost from the grid in four different scenarios.

With regard to the second optimization objective, namely the load peak and off-peak difference as expressed in Equation 8, Case 2 demonstrates a reduction of 45.7% in comparison to Case 1, while Case 3 exhibits a decrease of 47.6% in relation to Case 1. This evidence suggests that the orderly charging of EVs is an effective strategy for reducing the peak and valley values of loads.

In conclusion, the GBES and its bi-objective optimization model demonstrate advantages in terms of both cost and load profile.

5 Conclusion

In this paper, GBES integrating charging stations and adjacent buildings is developed. The strategy encompasses the energy transaction between GBES and the external power grid, as well as the energy exchange within GBES, with a particular focus on the energy exchange between EVCS and adjacent buildings. On the basis of GBES, a bi-objective model is proposed, with the first objective focused on minimizing the system’s power purchase cost. To prevent excessive concentration of charging load during low price periods, the second objective aims to reduce the peak-to-valley disparity in the system load curve. In this model, the impact of ESS capacity on the optimization outcomes is also taken into account, and a formula for calculating the upper limit of capacity is derived, as illustrated in Equation 3. Finally, the efficacy and superiority of the proposed method were validated through comprehensive comparative experiments. The integration of charging stations and adjacent buildings has the dual benefit of reducing the cost of purchased power and narrowing the gap between peak and valley loads.

The exploration of EVCS in this article is not yet comprehensive. For instance, EVs may offer ancillary services to the external power grid, such as frequency regulation. It is evident that further advancement is required in the field of EVs charging strategies. Moreover, there are uncertainties related to PV generation, EVs charging demands, and electricity prices in the power market. Consequently, it is advisable to examine the impact of these uncertainties to attain more desirable outcomes in the future work.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

WG: Conceptualization, Methodology, Project administration, Writing–review and editing. SS: Conceptualization, Formal Analysis, Writing–review and editing. KN: Conceptualization, Project administration, Writing–review and editing. PT: Conceptualization, Project administration, Writing–review and editing. KW: Formal Analysis, Software, Writing–original draft. ZW: Data curation, Writing–original draft. HW: Formal Analysis, Methodology, Writing–review and editing. MY: Investigation, Writing–review and editing. XB: Data curation, Investigation, Writing–original draft. JD: Methodology, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the State Grid Hebei Electric Power Company Technology Project “Research and Application of Distributed Resource Efficient Aggregation and Optimization Control Technology for Typical Buildings” (SGHEYX00FHJS231011). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

Authors WG, SS, KN, PT, XB, and JD were employed by State Grid Hebei Electric Power Co., Ltd. Authors KW and MY were employed by Wuhan Efficiency Evaluation Co., Ltd. Authors KW and MY were employed by NARI Group Co., Ltd. (State Grid Electric Power Research Institute Co., Ltd.).

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmad, F., Ashraf, I., Iqbal, A., Bilal, M., and Yadav, D. M. (2024). Energy management strategies and cost benefits analysis at electric vehicle parking lots incorporating photovoltaic energy generation and energy storage system. J. Energy Storage 92, 112105. doi:10.1016/j.est.2024.112105

CrossRef Full Text | Google Scholar

Borén, S., Nurhadi, L., Ny, H., Robèrt, K.-H., Broman, G., and Trygg, L. (2017). A strategic approach to sustainable transport system development – part 2: the case of a vision for electric vehicle systems in southeast Sweden. J. Clean. Prod. 140, 62–71. Systematic Leadership towards Sustainability. doi:10.1016/j.jclepro.2016.02.055

CrossRef Full Text | Google Scholar

Chen, J., Qing, J., and Cai, Q. (2024). Impact of bi-directional electric vehicle and demand response on residential distributed pv capacity planning based on tou pricing. J. Environ. Manag. 356, 120689. doi:10.1016/j.jenvman.2024.120689

PubMed Abstract | CrossRef Full Text | Google Scholar

Cortés Borray, A. F., Merino, J., Torres, E., and Mazón, J. (2020). Optimal coordination of pv active power curtailment and evs charging among aggregators. Appl. Sci. 10, 7176. doi:10.3390/app10207176

CrossRef Full Text | Google Scholar

Enrich, J., Li, R., Mizrahi, A., and Reguant, M. (2024). Measuring the impact of time-of-use pricing on electricity consumption: evidence from Spain. J. Environ. Econ. Manag. 123, 102901. doi:10.1016/j.jeem.2023.102901

CrossRef Full Text | Google Scholar

Ghofrani, M., and Hersi, N. (2024). “Multi-objective stochastic optimization for ev and renewable dg integration,” in 2024 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 12-13 February 2024 (IEEE), 1–6. doi:10.1109/TPEC60005.2024.10472239

CrossRef Full Text | Google Scholar

Hou, H., Xue, M., Xu, Y., Xiao, Z., Deng, X., Xu, T., et al. (2020). Multi-objective economic dispatch of a microgrid considering electric vehicle and transferable load. Appl. Energy 262, 114489. doi:10.1016/j.apenergy.2020.114489

CrossRef Full Text | Google Scholar

Jian, L., Zheng, Y., and Shao, Z. (2017). High efficient valley-filling strategy for centralized coordinated charging of large-scale electric vehicles. Appl. Energy 186, 46–55. doi:10.1016/j.apenergy.2016.10.117

CrossRef Full Text | Google Scholar

Kang, Z., Ye, Z., Lam, C.-M., and Hsu, S.-C. (2023). Sustainable electric vehicle charging coordination: balancing co2 emission reduction and peak power demand shaving. Appl. Energy 349, 121637. doi:10.1016/j.apenergy.2023.121637

CrossRef Full Text | Google Scholar

Kaur, A. P., and Singh, M. (2023). Time-of-use tariff rates estimation for optimal demand-side management using electric vehicles. Energy 273, 127243. doi:10.1016/j.energy.2023.127243

CrossRef Full Text | Google Scholar

Khan, W., Ahmad, F., and Alam, M. S. (2019). Fast ev charging station integration with grid ensuring optimal and quality power exchange. Eng. Sci. Technol. Int. J. 22, 143–152. doi:10.1016/j.jestch.2018.08.005

CrossRef Full Text | Google Scholar

Li, J., Shi, Y., Zhang, L., Yang, X., Wang, L., and Chen, X. (2021). Optimization strategy for the energy storage capacity of a charging station with photovoltaic and energy storage considering orderly charging of electric vehicles. Power Syst. Prot. Control 49. doi:10.19783/j.cnki.pspc.201296

CrossRef Full Text | Google Scholar

Li, Y., Cai, Y., Zhao, T., Liu, Y., Wang, J., Wu, L., et al. (2022). Multi-objective optimal operation of centralized battery swap charging system with photovoltaic. J. Mod. Power Syst. Clean Energy 10, 149–162. doi:10.35833/MPCE.2020.000109

CrossRef Full Text | Google Scholar

Li, Y., Duan, J., Pan, L., Ishizaki, T., Gao, L., and Zeng, Z. (2024). Online multi-objective optimization for electric vehicle charging station operation. IEEE Trans. Transp. Electrification, 1. doi:10.1109/TTE.2024.3362707

CrossRef Full Text | Google Scholar

Li, Y., Wang, J., Zhou, Y., Wei, C., Guan, Z., and Chen, H. (2023). Multi-dimension day-ahead scheduling optimization of a community-scale solar-driven cchp system with demand-side management. Renew. Sustain. Energy Rev. 185, 113654. doi:10.1016/j.rser.2023.113654

CrossRef Full Text | Google Scholar

Liu, J., Wang, H., Du, Y., Lu, Y., and Wang, Z. (2023). Multi-objective optimal peak load shaving strategy using coordinated scheduling of evs and bess with adoption of morbhpso. J. Energy Storage 64, 107121. doi:10.1016/j.est.2023.107121

CrossRef Full Text | Google Scholar

Mahato, D., Aharwal, V. K., and Sinha, A. (2023). Multi-objective optimisation model and hybrid optimization algorithm for electric vehicle charge scheduling. J. Exp. and Theor. Artif. Intell. 36, 1645–1667. doi:10.1080/0952813x.2023.2165719

CrossRef Full Text | Google Scholar

Meng, W., Song, D., Huang, L., Chen, X., Yang, J., Dong, M., et al. (2024). A bi-level optimization strategy for electric vehicle retailers based on robust pricing and hybrid demand response. Energy 289, 129913. doi:10.1016/j.energy.2023.129913

CrossRef Full Text | Google Scholar

Mishra, S., Mondal, A., and Mondal, S. (2023). A multi-objective optimization framework for electric vehicle charge scheduling with adaptable charging ports. IEEE Trans. Veh. Technol. 72, 5702–5714. doi:10.1109/TVT.2022.3231901

CrossRef Full Text | Google Scholar

Morais, H., Sousa, T., Castro, R., and Vale, Z. (2020). Multi-objective electric vehicles scheduling using elitist non-dominated sorting genetic algorithm. Appl. Sci. 10, 7978. doi:10.3390/app10227978

CrossRef Full Text | Google Scholar

Mousa, A. (2023). Extended-deep q-network: a functional reinforcement learning-based energy management strategy for plug-in hybrid electric vehicles. Eng. Sci. Technol. Int. J. 43, 101434. doi:10.1016/j.jestch.2023.101434

CrossRef Full Text | Google Scholar

Qie, X., Zhang, R., Xing, Y., Lu, M., Hu, Y., Sun, X., et al. (2024). Bidding strategy and economic evaluation of energy storage systems under the time-of-use pricing mechanism. J. Energy Storage 81, 110539. doi:10.1016/j.est.2024.110539

CrossRef Full Text | Google Scholar

Sharma, S., and Ali, I. (2024). Efficient energy management and cost optimization using multi-objective grey wolf optimization for ev charging/discharging in microgrid. e-Prime - Adv. Electr. Eng. Electron. Energy 10, 100804. doi:10.1016/j.prime.2024.100804

CrossRef Full Text | Google Scholar

Shen, Y., Hu, W., Liu, M., Yang, F., and Kong, X. (2022). Energy storage optimization method for microgrid considering multi-energy coupling demand response. J. Energy Storage 45, 103521. doi:10.1016/j.est.2021.103521

CrossRef Full Text | Google Scholar

Ullah, Z., Wang, S., Wu, G., Hasanien, H. M., Rehman, A. U., Turky, R. A., et al. (2023). Optimal scheduling and techno-economic analysis of electric vehicles by implementing solar-based grid-tied charging station. Energy 267, 126560. doi:10.1016/j.energy.2022.126560

CrossRef Full Text | Google Scholar

Wan, Y., Qin, J., Ma, Q., Fu, W., and Wang, S. (2022). Multi-agent drl-based data-driven approach for pevs charging/discharging scheduling in smart grid. J. Frankl. Inst. 359, 1747–1767. doi:10.1016/j.jfranklin.2022.01.016

CrossRef Full Text | Google Scholar

Wang, K., Zhou, C., Jia, R., Wang, J., and Wang, Z. (2021). “Optimal configuration and economic analysis of energy storage system in regional power grid,” in 2021 3rd Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 26-29 March 2021 (IEEE), 540–545. doi:10.1109/AEEES51875.2021.9403129

CrossRef Full Text | Google Scholar

Wang, Y., Wang, B., and Farjam, H. (2024). RETRACTED: multi-objective scheduling and optimization for smart energy systems with energy hubs and microgrids. Eng. Sci. Technol. Int. J. 51, 101649. doi:10.1016/j.jestch.2024.101649

CrossRef Full Text | Google Scholar

Xiaodong, Y., Youbing, Z., Guoqing, W., Bo, Z., and Xiang, G. (2016). Virtual time-of-use tariffs based optimal scheduling and implementation mechanism of electric vehicles charging and discharging. Trans. China Electrotech. Soc. 31, 52–62. doi:10.19595/j.cnki.1000-6753.tces.2016.17.006

CrossRef Full Text | Google Scholar

Yin, W., Wen, T., and Zhang, C. (2023). Cooperative optimal scheduling strategy of electric vehicles based on dynamic electricity price mechanism. Energy 263, 125627. doi:10.1016/j.energy.2022.125627

CrossRef Full Text | Google Scholar

Zheng, Y., Wang, Y., and Yang, Q. (2023). Two-phase operation for coordinated charging of electric vehicles in a market environment: from electric vehicle aggregators’ perspective. Renew. Sustain. Energy Rev. 171, 113006. doi:10.1016/j.rser.2022.113006

CrossRef Full Text | Google Scholar

Zou, W., Sun, Y., ce Gao, D., Zhang, X., and Liu, J. (2023). A review on integration of surging plug-in electric vehicles charging in energy-flexible buildings: impacts analysis, collaborative management technologies, and future perspective. Appl. Energy 331, 120393. doi:10.1016/j.apenergy.2022.120393

CrossRef Full Text | Google Scholar