Real-time cooperative voltage regulation strategy of distribution network based on approximate dynamic programming

Large-scale distributed renewable energy in the distribution network can result in reliability issues such as exceeding voltage limits and overloading power lines. Additionally, the rapid growth of electric vehicles has caused a surge in power demand in the distribution network. Therefore, how to guarantee the real-time stability of distribution network voltage under uncertain environment using available resources is an urgent problem to be solved. To this end, this paper proposes a cooperative voltage regulation of an on-load voltage regulator and electric vehicles for a distribution network considering multiple uncertainties. Firstly, an optimization model of the electric vehicle clusters considering the charging location and power is established, and the traditional on-load voltage regulator of distribution networks is also considered along with network operational constraints. Subsequently, a real-time cooperative voltage regulation strategy based on approximate dynamic programming is proposed, which employs segmented linear functions to process the value function to reduce the distribution network voltage offset and to ensure optimization accuracy. Numerical simulation results validate the feasibility and the effectiveness of the proposed cooperative voltage regulation technology involving electric vehicles and on-load tap changer in the distribution network.

1 Introduction

As the penetration rate of renewable energy increases, distribution networks shift to active and proactive forms. A high proportion of renewable energy connected to the grid may cause problems such as voltage overruns, line overloads, and increased network losses, thereby reducing the ability of the distribution network to accommodate distributed renewable energy resources (Mesa-Calle et al., 2023). The stochastic nature of renewable energy leads to uncertainty in system currents and voltages (Fu et al., 2019), and the voltage management is crucial for the safe and stable operation of distribution network (Tang et al., 2018). Traditional voltage regulation methods, such as on-load tap changer and shunt capacitors, have problems such as slow regulation speed and low regulator life due to frequent actions (Cheng et al., 2015). Electric vehicles can be used as flexible resources to participate in grid scheduling, and the orderly guidance of their charging and discharging can participate in grid voltage regulation with engineering and economic benefits (Nakamura et al., 2018). The on-load tap changer can realize the overall regulation, whereas the electric vehicle can finely regulate the node voltage, and the two complement each other’s advantages.

Both stochastic optimization and robust optimization are currently important methods for optimal scheduling of distribution networks considering uncertainties. Stochastic optimization uses uncertainty probability as inputs and evaluates their impact on the system output (Abdmouleh et al., 2017), and offers a range of possible solutions with models that are closer to real-world situations, facilitating operators/consumers to assess the risks involved in the uncertainty of renewable energy generation (Zakaria et al., 2020). However, stochastic optimization usually incurs significant computational costs because of the large number of scenarios that need to be considered during the computation (Aien et al., 2014) and suffers from the “curse of dimensionality” when evaluating multivariate and multitemporal problems. In contrast to stochastic optimization, robust optimization does not need a probability distribution function for the uncertainties, but instead uses the uncertainty ensemble to represent the range of its variation and seeks a solution that performs well for all realizations of the uncertainties (Zhang et al., 2019). Robust optimization makes direct decisions based on the worst-case scenario in the uncertainty set; therefore, the optimization results are generally conservative (Ning and You, 2019). The conventional stochastic and robust optimization methods are usually day-ahead and are also difficult to apply to real-time regulation scenarios in real applications.

Approximate dynamic programming (ADP), as a real-time optimization algorithm, has been applied in areas such as rail transit scheduling (Nguyen and Chow, 2023) and electric vehicle frequency regulation (Xizhen et al., 2022). It excels in solving large-scale, sequential decision-making, and high-dimensional problems (Xizhen et al., 2023) and has been shown to be well-suited for real-time scheduling scenarios. Based on the above analysis, this paper investigates a real-time cooperative voltage regulation strategy of distribution network based on approximate dynamic programming, and the contributions of this study can be summarized as follows:

1) A new cooperative voltage regulation model of EV clusters and on-load tap changer for distribution networks is proposed, which facilitates the utilization of the flexibility of EV clusters and the capacity of traditional on-load tap changer.

2) A real-time voltage regulation strategy based on ADP with segmented linear functions to process the value function considering renewable uncertainties is presented. This strategy has also been verified to be more advantageous than other real-time methods.

2 EV cluster dispatch features

The main research focuses on a distribution network system containing distributed renewable energy generation, EV charging stations, and traditional on-load tap changer.

Usually, charging stations are configured at multiple nodes in a distribution system, and how EVs selection of charging stations for charging and power control during charging and discharging is the key to the optimization problem. At present, EVs are widely distributed, and their charging demands are usually uncontrollable due to their traffic attributes and user behaviors, i.e., different EVs access charging stations at different times, in different quantities and with different charging and discharging powers (Trinh et al., 2023; AlNahhal et al., 2022). It is neither economical nor difficult to realize that EVs connected to the distribution network are dispatched individually, and the accessible capacity that individual EVs can provide to participate in the dispatch is limited. Therefore, large-scale EVs participation in the dispatch is required to improve the voltage offset of the grid.

Facing the above problems, this paper considers the group of EVs with similar models and charging demands as an EV cluster for uniform scheduling, and converts the individual variables of a single EV into the group variables of each class of EVs, and the relationship between the EV individual variables and the group variables is shown as follows.

Let $N^{EV}$ EVs be grouped into I classes, the number of vehicles in each class is $N^I$, and $V_{clu}^{EV}$ is a set of EV groups. Each individual variable of an EV can be converted into a group of variables as follows.

$\left\{\begin{array}{l}\sum N^I=N^{EV}\\ P_{c,t}^i=P_{c,t}^I/N^I\\ P_{d,t}^i=P_{d,t}^I/N^I\\ SO{C}_t^i=SO{C}_t^I/N^I\end{array}\right.,\forall i\in I,\forall I\in V_{clu}^{EV}(1)$

where $P_{c,t}^i$ and $P_{c,t}^I$ are the individual and population variables of the EV charging power at time t, respectively; $P_{d,t}^i$ and $P_{d,t}^I$ are the individual and population variables of the EV discharging power at time t, respectively; and $SO{C}_t^i$ and $SO{C}_t^I$ are the individual and population variables of the EV electricity at time t, respectively.

Through the above conversions, the number of EV variables is significantly reduced, which shortens the calculation time and lays the foundation for the subsequent establishment of a concise and efficient real-time voltage optimization model for distribution networks.

3 Distribution network voltage Co-optimization model

In this section, based on the above EV cluster (EVC) scheduling characteristics and considering constraints such as EV-related constraints, on-load tap changer operation constraints, renewable energy output constraints, and tidal current constraints, a voltage cooperative optimization model for distribution networks is constructed with the objective function of minimizing the system voltage offset.

3.1 Regulation constraints

3.1.1 EVC regulation constraints

The selection of the EV charging location is constrained by those of existing charging stations, and it is also assumed that one class of EVs will be charged at only one charging station, and the charging location of each class of EVs will not be changed in the subsequent time periods after the decision is made in the first time period. The charging and discharging power of the EV is limited by the time of accessing the charging station and the maximum charging and discharging power, in addition, the EV cannot be charged and discharged at the $\text{Type\hspace{0.17em}equation\hspace{0.17em}here}.$same time. Therefore, the EVC charging, discharging, and location constraints are expressed in (Equation 2).

$\left\{\begin{array}{l}{U}_{loc}^I\le U_{station}\\ \sum U_{loc}^I=1\\ 0\le P_{c,t}^I\le U_t^I{U}_{loc}^I{U}_{c,t}^I{P}_{c,\max }^I,t_{arr}^I\le t\le t_{dep}^I\\ 0\le P_{d,t}^I\le U_t^I{U}_{d,t}^I{P}_{d,\max }^I,t_{arr}^I\le t\le t_{dep}^I\\ U_{c,t}^I+U_{d,t}^I\le 1\end{array}\right.,\forall I\in V_{clu}^{EV}(2)$

where $U_{loc}^I$ is a 0–1 variable for the charging location of EVs in class I clusters, $U_{station}$ denotes the location of nodes where charging stations are already present in the distribution network, and EVs can be charged and discharged only at nodes where charging stations are present. $U_{c,t}^I$ and $U_{d,t}^I$ are the charging and discharging flag bits of the class I cluster EV in time period t, respectively; $U_t^I$ is the 0–1 variable of the class I cluster EV accessing the charging station in time period t; $P_{c,\max }^I$ and $P_{d,\max }^I$ are the maximum charging and discharging power of the class I cluster EV, respectively; and $t_{arr}^I$ and $t_{dep}^I$ are the times of arrival and departure of the class I cluster EV from the charging station, respectively.

All types of EVCs cannot exceed their upper and lower limits at any time period. When an EV leaves a charging station, the SOC should conform to the user’s expected SOC. However, the rolling decision-making nature of the real-time optimization process makes it difficult to ensure that the above condition is achieved; thus, the upper and lower bounds of the SOC must be reformulated. First, the SOC energy bounds for each cluster EV type are calculated based on the EV operating parameters (i.e., $t_{arr}^I$, $t_{dep}^I$ , $SO{C}_{arr}^i$ , $SO{C}_{dep}^i$ and $P_{c,\max }^I$):

$\left\{\begin{array}{l}SO{C}_{t,\min }^I=\\ \max \{N^{I}SO{C}_{arr}^i,N^I(SO{C}_{dep}^i-\\ \left.\left(t_{dep}^i-t\right)\left(P_{c,\max }^i-\Delta P^i\right)-\Delta P_{flex}^i)\right\}\\ SO{C}_{t,\max }^I=N^{I}SO{C}_{dep}^i\\ t_{arr}^I\le t\le t_{dep}^I\end{array}\right.\forall i\in I,\forall I\in V_{clu}^{EV}(3)$

$\left\{\begin{array}{l}SO{C}_t^I=N^{I}SO{C}_{arr}^i+\eta P_{c,t}^I-P_{d,t}^I/\eta ,t=t_{arr}^I\\ SO{C}_t^I=SO{C}_{t-\Delta t}^I+\eta P_{c,t}^I-P_{d,t}^I/\eta ,t_{arr}^I<t\le t_{dep}^I\end{array}\right.(4)$

where $SO{C}_{dep}^i$ is the desired charge when the ith EVC leaves the charging station, and $SO{C}_{arr}^i$ is the initial charge when the ith EVC arrives at the charging station. $SO{C}_{t-\Delta t}^I$ is the amount of electricity of class I during time period $t-\Delta t$; $\eta$ is the EVC charging and discharging efficiency factor.

3.1.2 On-load tap changer constraints

The on-load tap changer realizes output voltage regulation by changing its junction point to adjust the ratio, which has discrete and step regulation characteristics. In this study, the model is simplified, with the transformer model as a node, without considering the internal branch structure of the transformer, which is an adjustable variable, as follows:

$\left\{\begin{array}{l}{\alpha }_t={\displaystyle \sum _n}{T}_{t,n}^{OLTC}{\alpha }_n\\ {\displaystyle \sum _n}{T}_{t,n}^{OLTC}=1\end{array}\right.(5)$

$\left\{\begin{array}{l}{T}_t^{OLTC,IN}+T_t^{OLTC,DE}\le 1\\ T_t^{OLTC}-T_{t-1}^{OLTC}\le T_t^{OLTC,IN}{K}^{OLTC}-T_t^{OLTC,DE}\\ T_t^{OLTC}-T_{t-1}^{OLTC}\le T_t^{OLTC,IN}-T_t^{OLTC,DE}{K}^{OLTC}\end{array}\right.(6)$

where ${\alpha }_t$ is the regulator ratio at time t, ${\alpha }_n$ is the on-load tap changer gear position, and $T_{t,n}^{OLTC}$ is the 0–1 variable of the on-load tap changer gear position n at time t. $T_t^{OLTC,IN}$ and $T_t^{OLTC,DE}$ are the 0–1 variables of the on-load tap changer gear position rise and fall, respectively, at time t, respectively; $K^{OLTC}$ is the maximum adjustment amount of the gear position at a single time. Equation 5 indicates that the gear position of the on-load tap changer is selected by its 0–1 variable, and that the on-load tap changer is only in one of the gear positions at any moment.

3.1.3 Distribution network operational constraints

There are upper and lower constraints on the output of renewable energy sources, such as wind and solar energy, at all times of the day. The following general constraints exist in the branch flow model:

$\left\{\begin{array}{l}{P}_{new,g\min ,t}\le P_{new,g,t}\le P_{new,g,\max ,t}\\ v_{f,t}=v_{e,t}-2\left(r_{ef}{P}_{ef,t}+x_{ef}{Q}_{ef,t}\right)+\left(r_{ef}^2+x_{ef}^2\right)i_{ef,t}\\ {\displaystyle \sum _{k:f\to k}}{Q}_{fk,t}-{\displaystyle \sum _{e:e\to f}}\left(Q_{ef,t}-x_{ef}{i}_{ef,t}\right)=Q_{f,t},\forall f\\ {\displaystyle \sum _{k:f\to k}}{P}_{fk,t}-{\displaystyle \sum _{e:e\to f}}\left(P_{ef,t}-r_{ef}{i}_{ef,t}\right)=P_{f,t},\forall f\\ v_{e,t}{i}_{ef,t}=P_{ef,t}^2+Q_{ef,t}^2\\ \begin{array}{l}{U}_{e,\min }^2\le v_{e,t}\le U_{e,\max }^2\\ I_{ef,\min }^2\le i_{ef,t}\le I_{ef,\max }^2\end{array}\end{array}\right.(7)$

where: $P_{new,g,\max ,t}$ and $P_{new,g,\min ,t}$ are the upper and lower limits of the output of the renewable energy unit g in tme period t, respectively; $P_{new,g,t}$ is the output of the renewable energy unit g in time period t. e, f, k are the node numbers; $v_{e,t}$ and $v_{f,t}$ are the squares of the voltage amplitudes of node e and node f at time t, respectively; $P_{f,t}$ and $Q_{f,t}$ are the active and reactive power injected into node f at time t, respectively; $x_{ef}$ and $r_{ef}$ are the reactance and resistance values of branch ef, respectively; $P_{ef,t}$ and $Q_{ef,t}$ are the active and reactive power flowing at the first end of branch ef at time t, respectively; $P_{fk,t}$ and $Q_{fk,t}$ are the active and reactive power flowing at the first end of branch fk at time t, respectively; $i_{ef,t}$ is the square of the amplitude of the current flowing in the branch ef at time t. $U_{e,\max }^2$ and $U_{e,\min }^2$ are the upper and lower limits of the squared voltage modulus at node e; $I_{ef,\max }^2$ and $I_{ef,\min }^2$ are the upper and lower limits of the squared current modulus at branch ef, respectively.

Equation 7 contains quadratic terms, which are nonconvex nonlinear constraints, and the exact solution algorithm is ineffective in solving optimization problems with nonconvex nonlinear constraints. Therefore, it is necessary to relax it to a convex linear form using second-order cone relaxation.

${‖\begin{array}{l}2P_{ef}\\ 2Q_{ef}\\ i_{ef}-{\alpha }_e\end{array}‖}_2\le i_{ef}+v_e(8)$

3.2 Optimization objectives

In this study, the system voltage offset is reduced by co-regulating the on-load tap changer and EVC. Here, the sum of the offsets of each node voltage relative to the reference voltage at each time period is used to characterize the system voltage offset (Zhou et al., 2023).

$\min C={\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{e=1}^{N_e}}\left|\frac{{\alpha }_{e,t}-U_n^2}{U_n^2}\right|(9)$

where C is the sum of the voltage offsets for all the optimization periods, $U_n$ is the reference voltage, $N_e$ is the number of system nodes, T is the total optimization period.

4 ADP-based real-time voltage regulation strategy for distribution networks

4.1 Markov decision process reconstruction

The optimization model in the previous section is based on the condition that the exact state information of the full-time period is known, which is difficult to achieve in a real-time optimization process. Therefore, this study adopts the Markov decision process (MDP) to reconstruct the voltage cooperative optimization model of the distribution network, transforms the full-time optimization problem into a single-time optimization problem, and then solves the single-time optimization problem time-by-time using the constraint coupling relationship between time periods.

The MDP process of the distribution network voltage optimization model includes $S_t$, $x_t$, and $W_t$. The state variable $S_t$ is defined as $S_t$ = {$P_{new,g\max ,t}$, $SO{C}_t^I$, $U_t^I$, $P_{f,t}^{load}$, $Q_{f,t}^{load}$, $T_{t,n}^{OLTC}$}. Define the decision variable $x_t$ = {$P_{new,i,t}$, $P_{f,t}^{grid}$, $Q_{f,t}^{grid}$, $U_{loc}^I$, $U_{c,t}^I$, $U_{d,t}^I$, $P_{c,t}^I$, $P_{d,t}^I$, $T_t^{OLTC,IN}$, $T_t^{OLTC,DE}$, ${\alpha }_{e,t}$, ${\beta }_{ef,t}$, $P_{ef,t}$, $Q_{ef,t}$}. There is a prediction error for renewable energy output and conventional load; therefore, the external information for time period t is defined as $W_t$ = {${\widehat{P}}_{new,g,\max ,t}$, ${\widehat{P}}_{e,t}^{load}$}.

The relationship between the state variable $S_t$, decision variable $x_t$, and external information $W_t$, that is, the transfer function, is determined by (Equations 1–8) above. First, at any time period, the state variable $S_t$ of the distribution network in the current time period is obtained, and the decision variable $x_t$ is derived through the current system state. According to the state and decision variables in the current time period, the state variable $S_t^x$ after decision can be obtained, after which the state variable $S_{t+\Delta t}$ in the next time period is updated according to the external information $W_{t+\Delta t}$ in the next time period. The update process is illustrated in Figure 1.

Figure 1

Figure 1. Diagram of Markov decision process.

After modeling the distribution network voltage optimization model as an MDP, the optimal decision sequence for this problem can be obtained by solving the Bellman equation using the dynamic programming (DP) method as follows:

$V_t=\min \left\{C_t\left(S_t,x_t\right)+V_t^x\left(S_t^x\right)\right\}(10)$

where $V_t$ is the state value function at time t, $C_t$ is the system voltage offset at time t as (Equation 9) shows, and $V_t^x$ is the state value function after decision making at time t.

The dynamic programming method transforms the multi-stage optimization problem (Equation 10) into a series of single-stage decision problems, and then utilizes the transfer and constraint relationships between stages to solve the single-stage optimization problems one by one. Based on the real-time state of the system, dynamic decisions are given to achieve the simplification of complex problems. In the application of dynamic programming theory, it is necessary to traverse all the state and decision spaces to obtain the value function at each stage and each state, and in the stochastic environment, the system in a certain state at a certain stage may transfer to an infinite number of different states in the next stage, resulting in the “dimension explosion” problem, which has been explained in more detail in (Powell, 2007).

4.2 Approximation of value functions based on segmented linear functions

Aiming at the problem of “dimension explosion” in solving real-time cooperative voltage regulation models of distribution networks using dynamic programming methods, this study proposes an ADP-based real-time cooperative voltage regulation strategy for distribution networks. The state value function $V_t^x$ in (10) can be approximated in many ways, and the ADP based on the approximation of the segmented linear function (Zhang et al., 2023; Li et al., 2022; Lin et al., 2022) has good results for linear models or mixed-integer linear models with energy storage 0–1 variables (Nascimento and Powell, 2013). Therefore, in this study, the segmented linear function related to EV electricity is used to approximate the state-value function, which in turn solved the Bellman equation and obtained the near-optimal decision sequence. The state value function can be rewritten as the following equation:

$\left\{\begin{array}{l}{V}_t^x\left(S_t^x\right)\approx {\overline{V}}_t^x\left(S_t^x\right)=\sum {\overline{V}}_t^{x,I}\left(SO{C}_t^I\right)\hfill \\ {\overline{V}}_t^{x,I}\left(SO{C}_t^I\right)=U_t^I{\displaystyle \sum _{m=1}^M}{v}_{m,t}^{x,I}SO{C}_{m,t}^I\hfill \\ 0\le SO{C}_{m,t}^I\le \left(SO{C}_{dep}^I-SO{C}_{arr}^I\right)/M\hfill \\ SO{C}_t^I={\displaystyle \sum _{m=1}^M}SO{C}_{m,t}^I\hfill \end{array}\right.,I\in V_{clu}^{EV}(11)$

where ${\overline{V}}_t^x\left(S_t^x\right)$ is the approximation function at time t; M is the number of segments of each class of EVC; $v_{m,t}^{x,I}$ is the slope of the mth segment of class I at time t; and $SO{C}_{m,t}^I$ is the power of the mth segment of class I at time t. As shown above, the power of each class of EVC equals to the sum of the power of its segments, and thus the power of each segment will not exceed the upper and lower limits.

The decision variable for this problem can be solved by the following equation:

$x_t=\mathrm{argmin}\left\{V_t\right\}\approx \mathrm{argmin}\left\{C_t\left(S_t,x_t\right)+{\overline{V}}_t^x\left(S_t^x\right)\right\}(12)$

The slope of the approximate value function (Equation 11) significantly affects the accuracy of the solution result; therefore, it is necessary to update the slope by training to improve the solution accuracy.

Differential way to calculate the slope sampling value, in order to ensure the accuracy of the calculation of the slope sampling value, different cases need to take different slope sampling value calculation method, the specific calculation method is shown below:

${\widehat{v}}_{m,t}^{n,x,I}=\frac{{\left.{\overline{V}}_t^{x,n-1}\right|}_{SO{C}_t^I+\Delta SO{C}^I}-{\left.{\overline{V}}_t^{x,n-1}\right|}_{SO{C}_t^I}}{\Delta SO{C}^I},t=t_{arr}^I(13)$

where $\Delta SO{C}^I$ is the differentiation of the SOC when solving for the slope.

Based on (Equation 13), the slope can be updated using the following method:

$v_{m,t}^{n,x,I}=\left(1-\alpha \right)v_{m,t}^{n-1,x,I}+\alpha {\widehat{v}}_{m,t}^{n,x,I}(14)$

where $v_{m,t}^{n,x,I}$ is the slope of the mth segment of class I at time t of the nth training and α is the slope update step.

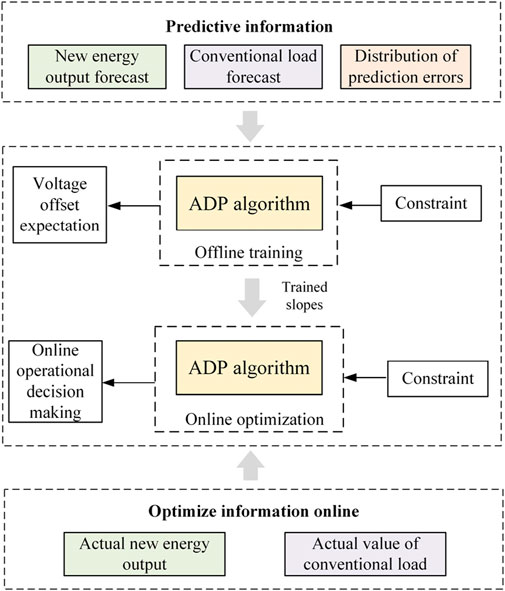
The ADP-based real-time cooperative voltage regulation strategy (Equation 12) for distribution networks is divided into two parts: offline training and online optimization. The specific process is illustrated in Figure 2. Offline training is carried out a few days before, and a series of offline training scenarios are first generated based on the predicted values and prediction error distributions of renewable energy outputs and conventional loads. The slopes are calculated based on the above constraints and the ADP algorithm as (Equation 14) shows. Subsequently, the trained slopes of the segmented linear functions are used for the online optimization of the distribution network dispatch. Online optimization does not need to update various types of forecast information for rolling optimization decisions, which reduces the impact of forecast errors on the optimization results.

Figure 2

Figure 2. Real-time voltage regulation strategy process of distribution network based on ADP.

5 Calculus analysis

5.1 Basic data

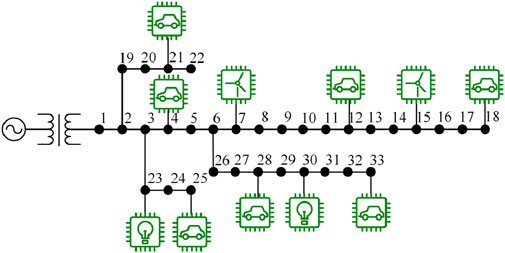
In this section, the effectiveness of the proposed real-time cooperative voltage regulation strategy to improve the voltage excursion in the distribution network is verified through the IEEE-33 node system example. All optimization problems are solved in the MATLAB platform using the Gurobi solver, and the simulation model is shown in Figure 3.

Figure 3

Figure 3. The simulation case based on the IEEE-33 node system.

In the IEEE-33 nodal system, the voltage reference value is 12.66 kV, and the base power of the system is 100 MVA. The root node is equipped with an on-load tap changer, and the regulating stops αn = {0.95 0.96 0.97 0.98 0.99 1.00 1.01 1.02 1.03 1.04 1.05} have a total of 11 stops, and the large regulating amount $K^{OLTC}$ = 2 at a single time, whereas nodes 7 and 15 are connected to 100 kW capacity wind turbines, respectively, and nodes 23 and 30 are connected to 100 kW capacity PV systems. Charging stations exist for EV charging at nodes 4, 12, 18, 21, 25, 28, and 33. Considering the variability of EV user behavior, it is assumed that the time for EVs to access and leave the charging station obeys a Poisson distribution (Bae and Kwasinski, 2012), and the expected time for four classes of EVC to arrive and leave the charging station can be obtained through Poisson process modeling, and the parameters of each class of clustered EVC are shown in Table 1. The optimization time period is 24 h, the initial value of the slope is set to 0, and the update step is α = 0.3. Maximum charging and discharging power of 10 kW for all EV types.

Table 1

Table 1. Parameters of EVCs.

It is assumed that the prediction errors of the wind and light output and conventional loads obey a normal distribution, both of which have a specific distribution of N (0, 0.052). Two hundred training scenarios are generated using the Monte Carlo sampling method, as shown in Figure 4.

Figure 4

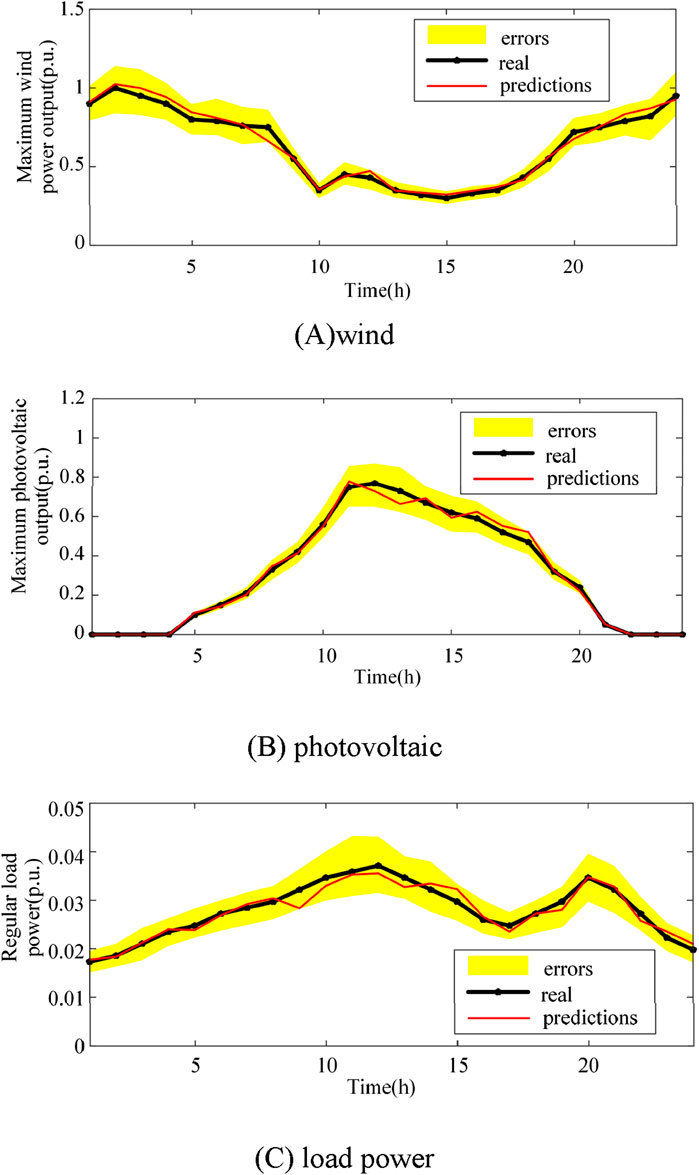
Figure 4. External status information of the distribution system. (A) wind. (B) photovoltaic. (C) load power.

5.2 Basic results of different regulating measures

To verify the effectiveness of the ADP-based real-time cooperative voltage regulation strategy for distribution networks proposed in this study, three optimization scenarios are set up for analysis, in which the number of EVs is 300, and the specific scenarios are set up as follows:

Scenario 1: There are conventional loads and EVC loads in the system, which perform equal power charging, and the charging position of each EVC is fixed at nodes 4, 12, 4, and 12, and the on-load tap changer is used for voltage regulation.

Scenario 2: Conventional loads and EVC loads exist in the system, and the EVC charging positions and charging power are optimized to reduce voltage fluctuations.

Scenario 3: Conventional loads and EVC loads exist in the system, and an on-load tap changer is used for joint voltage regulation with the EVC.

To analyze the superiority of this strategy, one of the above 200 scenarios is selected as the external information for the subsequent comparison algorithms, as shown in Figure 4 with a marked solid line. The optimization results for each scenario are shown in Table 2, where the EVC charging locations in scenarios 2 and 3 are not changed for subsequent periods after the decision.

Table 2

Table 2. Optimized results of scenarios with different regulating measures.

Scenario 1 does not optimize the charging power and charging location of the EVC, and only the on-load tap changer is used for voltage regulation; therefore, the voltage offset is the largest under the full time period, with the lowest voltage of 0.9242, which threatens the stable operation of the distribution network. In Scenario 2, after the optimization of the EVC charging power and charging location, the minimum voltage at end nodes 18 and 33 is significantly increased, while the system voltage offset is significantly reduced by 54.6%. The EVC chooses to charge at the charging stations at nodes 21 and 25 near the root node to avoid a significant voltage drop, whereas the minimum system voltage is increased to 0.9695, effectively avoiding voltage overruns. In Scenario 3, the EVC and on-load tap changer work together to regulate the voltage, and the system voltage offset is further reduced, while the charging locations of all classes of EVC are concentrated in node 25,21 charging station, which is close to the root node to avoid the voltage drop on one hand, and close to the photovoltaic power generation node, to realize renewable energy consumption in site.

Figure 5 shows the charging power changes of each EVC under the three scenarios, with Scenario 1 being constant-power charging. In Scenario 2 and Scenario 3, when EVC participate in voltage regulation, the charging power of EVC is significantly reduced during the regular peak load hours of 12:00–14:00 and 20:00–22:00 to prevent the occurrence of “peak on peak.”

Figure 5

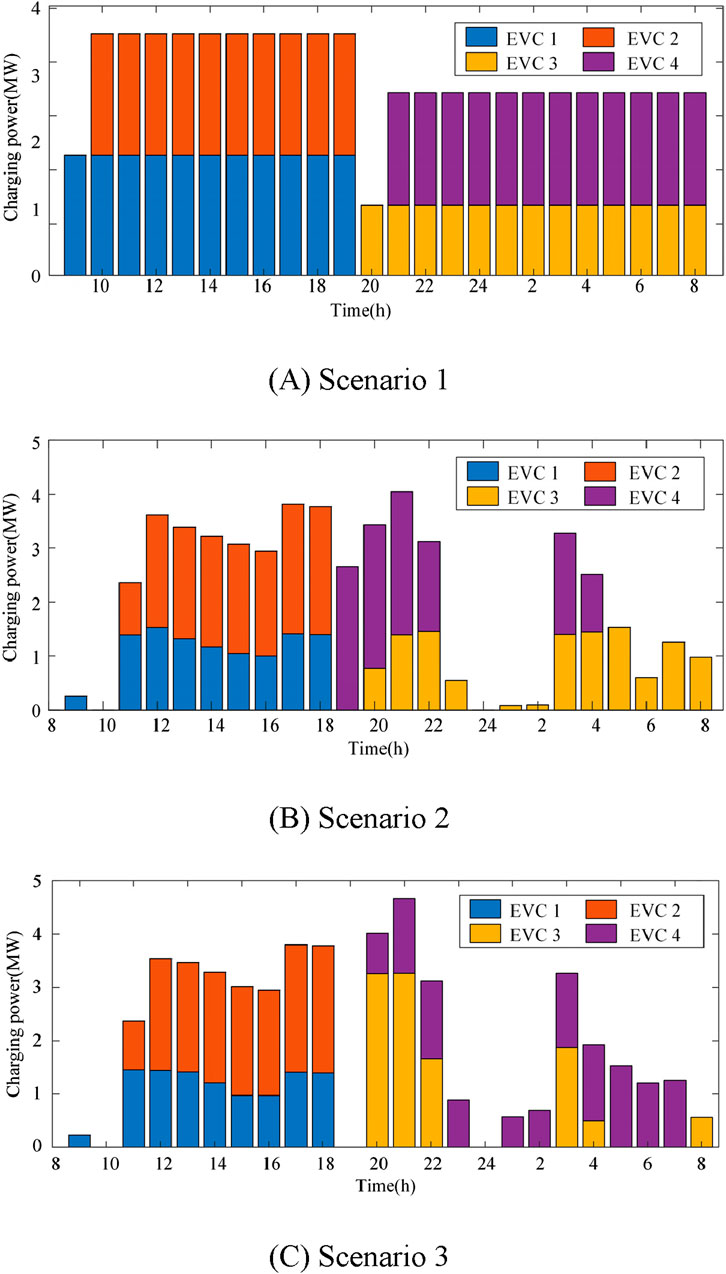
Figure 5. EVC charging power and SOC curves of each cluster in each scenario. (A) Scenario 1. (B) Scenario 2. (C) Scenario 3.

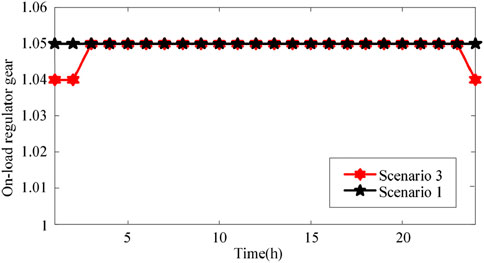
Figure 6 shows the on-load tap changer gear change curves for Scenarios 1 and 3; the on-load tap changer is not optimized in Scenario 2. In Scenario 1, the EVC charging power is unchanged, and the on-load tap changer is always in the highest gear to reduce the occurrence of voltage overruns. In Scenario 3, the EVC charging power is lower in the early morning load trough time from 0:00–6:00, and the on-load tap changer blocking is reduced to reduce voltage fluctuations.

Figure 6

Figure 6. OLTC gear change curve.

5.3 Sensitivity analysis of ADP algorithm parameters

The optimization effect of the ADP algorithm is affected by the nature of the solved problem and the parameters of the algorithm. The problem in this paper is a real-time optimization problem with sequential decision-making and inter-temporal coupling constraints, which is highly compatible with the ADP algorithm. The adjustable parameters affecting the performance of the ADP algorithm are mainly the slope update step α. The step α determines the speed of the slope update; when α is larger, the external error distribution information can be embedded into the slope of the segmented linear function faster, thus accelerating the convergence, but too large α leads to large oscillations in the offline training; when α is smaller, the speed of the external error distribution information embedded into the slope of the segmented linear function is slower, resulting in a slower convergence. Slower convergence, but the magnitude of the oscillations generated in the subsequent offline training process is smaller. Although the value of the step α has an impact on the convergence speed of offline training, as long as it is within a certain range and the number of training times is sufficient, the external error distribution information can be embedded into the slope, so the step α within a reasonable range has little impact on the accuracy of the solution.

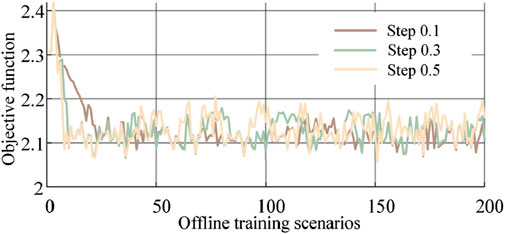
In order to verify the above conclusions, 200 offline scenarios are trained using update steps of 0.1, 0.3, and 0.5, respectively, and the same 200 randomness test scenarios are used for testing, the offline training process is shown in Figure 7, and the statistical results of the test scenarios are shown in Figure 8.

Figure 7

Figure 7. Off-line training results.

Figure 8

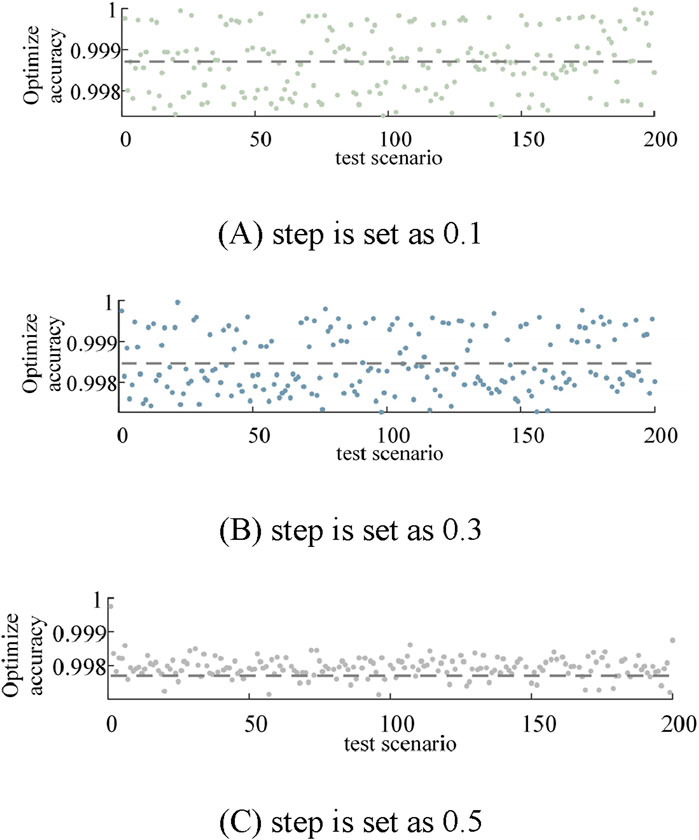
Figure 8. Statistics results of unsynchronized long testing. (A) Step is set as 0.1. (B) Step is set as 0.3. (C) Step is set as 0.5.

Since each iteration uses data from a random scene, the objective function will oscillate to some extent during the iteration process, but the oscillation amplitude is different. From Figure 7, it can be seen that the larger the step size, the faster the convergence speed, and the larger the amplitude of the oscillations generated by the subsequent offline training. From the statistical results of the test scenarios in Figure 8, it can be seen that the optimization accuracies corresponding to step sizes 0.1, 0.3 and 0.5 are 99.87%, 99.84%, and 99.79%, respectively, and the gap between them is negligible, thus verifying the previous conclusion.

5.4 Efficiency analysis of the proposed strategy

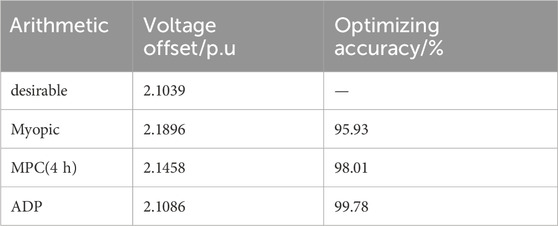
Commonly real-time optimization methods include myopic and model predictive control (MPC), and the optimization results of the proposed strategy are compared with these optimization methods for voltage in distribution network systems. Scenarios with 800 EVs are introduced for the comparison, and the ideal case with an accurate prediction technique is used as the benchmark. The comparison results are shown in Table 3. The Myopic method only makes decisions based on the external information of the current time period, and therefore has the lowest accuracy. The MPC method makes decisions by considering the external information of the future time periods, and therefore has a higher accuracy than the myopic algorithm, which is 98.01%. However, the MPC algorithm relies on the prediction accuracy of external information and lacks consideration of the entire time period, while the ADP algorithm takes into account the impact of the current decision on the future time period and does not rely on the prediction accuracy of external information; thus, the decision obtained by the ADP is almost globally optimal, and the optimization accuracy reaches 99.78%.

Table 3

Table 3. Precision comparison of real-time optimization methods.

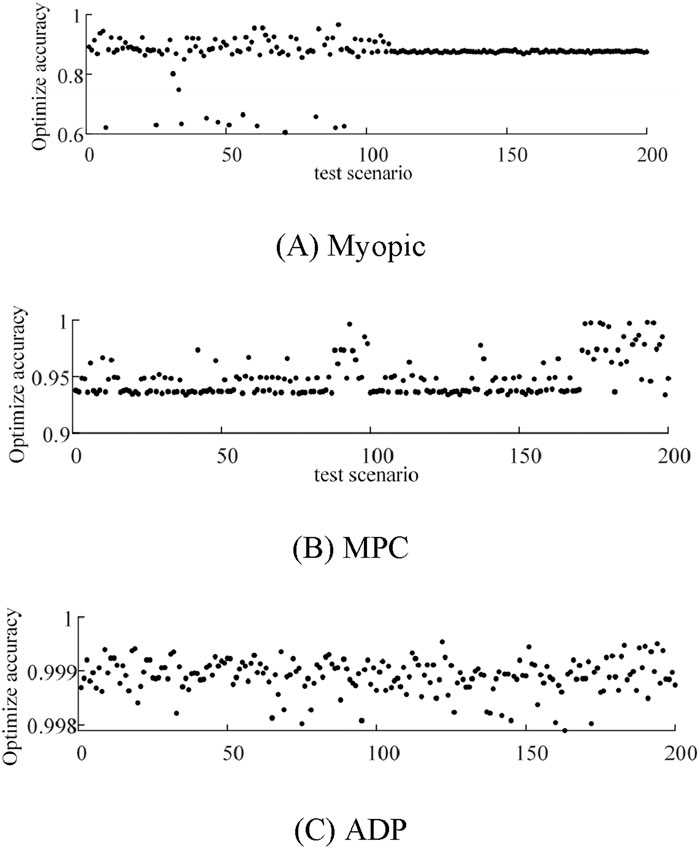
The Monte Carlo method is further used to generate 200 test scenarios to simulate the random changes of actual various uncertainties, and the myopic, MPC, and ADP algorithms are used to optimize the above scenarios; the statistics of the optimization results are shown in Figure 9. In the 200 test scenarios, the average accuracy of the myopic algorithm is 87.83%, which could not meet the requirements of real-time optimization, and the average accuracy of the MPC algorithm is greatly improved to 95.27% compared with that of the myopic algorithm, but it is still difficult to meet the requirements of real-time optimization when the prediction accuracy is insufficient. The average accuracy of the ADP algorithm is further improved to 99.90% compared to that of the MPC algorithm and does not depend on external information such as wind and light output forecasts, which meets the requirements of real-time optimization.

Figure 9

Figure 9. Statistics results of 200 test scenarios. (A) Myopic. (B) MPC. (C) ADP.

Currently, some kind of distribution is generally used to characterize the prediction error of new energy output, such as beta distribution (Bludszuweit et al., 2008) normal distribution (Zhang et al., 2018) and t location-scale distribution (Ding et al., 2013), etc., while the prediction error of load profile usually obeys normal distribution. In order to verify the generalizability of the real-time voltage regulation strategy for distribution networks proposed in this paper, two sets of online test scenario sets are set up: 1) Assuming that the wind power prediction error obeys the beta distribution B (4.5,4.5), and the load profile prediction error obeys the normal distribution N (0,0.05²), and 200 online test scenarios are generated by Monte Carlo sampling method, which is the first set of online test scenario sets; 2) Assuming that the wind and light output prediction error obeys the t location-scale distribution T (0,0.05²,10), and the load curve prediction error obeys the normal distribution N (0,0.05²), 200 online test scenarios are generated by Monte Carlo sampling method, i.e., the second group of online test scenario set. The optimization results are shown in Figure 10, and the average optimization accuracies of the two sets of online test scenarios are 99.88% and 99.86%, respectively. Therefore, the generalizability of the real-time voltage regulation strategy for distribution networks proposed in this paper is verified.

Figure 10

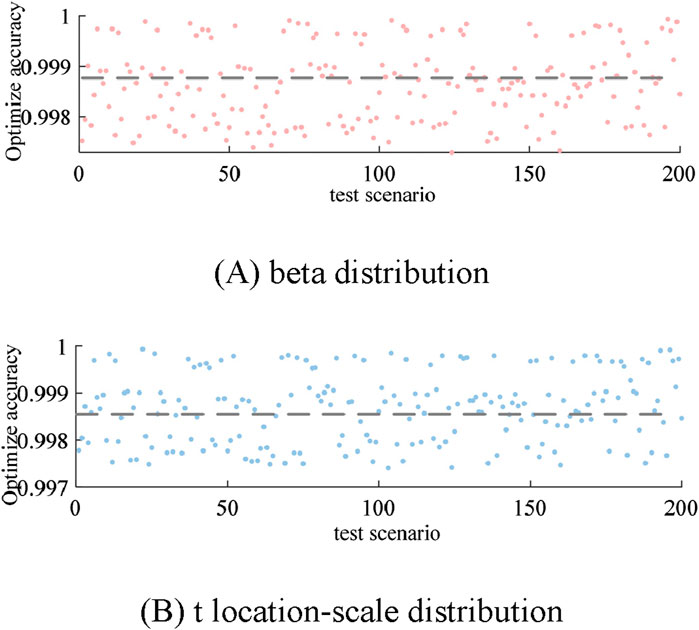
Figure 10. Optimization accuracy under different prediction error distribution. (A) beta distribution. (B) t location-scale distribution.

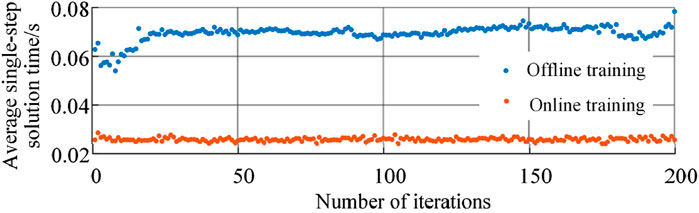
In terms of solution time, the average single-step solution time of each scenario is shown in Figure 11: the average single-step solution time of the 200 offline training scenarios is 0.069 s, and the average single-step solution time of the 200 online test scenarios is 0.026 s. Therefore, the proposed distribution network voltage regulation strategy of this paper also meets the requirements of real-time optimal dispatch in terms of solution time.

Figure 11

Figure 11. Solution time statistics.

6 Conclusion

In this study, a real-time cooperative voltage regulation strategy of electric vehicles and on-load tap changer for distribution networks based on approximate dynamic planning is proposed, and the following conclusions can be drawn from the case studies:

1) Compared with the use of an on-load tap changer and EVC regulation alone, the system voltage offset is reduced by 54.6% and 0.94%, respectively, when using an on-load tap changer and EV cooperative voltage regulation, which effectively improves system security and stability.

2) In terms of coping with renewable energy output and load stochasticity, the real-time optimization method of approximate dynamic programming adopted in this paper can achieve an optimization accuracy of 99.90%, which is better than that of the MPC algorithm of 95.27% and the Myopic algorithm of 87.83%, and it has a good generalization. Thus, the proposed strategy has good accuracy and rapidity and meets real-time voltage regulation requirements.

In this study, we mainly investigated a real-time cooperative regulation strategy for EVs and on-load tap changer in the distribution network considering uncertainties. However, the regulation process incurs regulation costs, including the incentive costs for EVs and the regulation costs for on-load tap changer, which indicates the direction of our future researches about comprehensibly balancing the dispatch costs and economic incentives of EVs, accurate aggregation methods, and the system reliability. Meanwhile, the participation and regulation strategies of other potential flexible resources in distribution network also remains further exploration.

Data availability statement

The data analyzed in this study is subject to the following licenses/restrictions: Just for research. Requests to access these datasets should be directed to Shichang Cui, c2hpY2hhbmdfY3VpQGh1c3QuZWR1LmNu.

Author contributions

JG: Funding acquisition, Resources, Supervision, Validation, Writing–review and editing. MG: Writing–original draft. RL: Writing–original draft. JX: Conceptualization, Writing–review and editing. YY: Data curation, Writing–review and editing. ZH: Data curation, Resources, Writing–review and editing. SC: Investigation, Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by the Jiangxi Power Exchange Center Co., Ltd. Under Grant SGIXJY00JYJS2400010 and the National Natural Science Foundation of China Under Urant 52207108.

Conflict of interest

Authors JG, JX, YY, and ZH were employed by State Grid Jiangxi Electric Power Co., Ltd.

The remaining authors declare that the research is conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from Jiangxi Power Exchange Center Co., Ltd. The funder had the following involvement in the study: original data and main motivation.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdmouleh, Z., Gastli, A., Ben-Brahim, L., Haouari, M., and Al-Emadi, N. A. (2017). Review of optimization techniques applied for the integration of distributed generation from renewable energy sources. Renew. Energy 113, 266–280. doi:10.1016/j.renene.2017.05.087

CrossRef Full Text | Google Scholar

Aien, M., Rashidinejad, M., and Fotuhi-firuzabad, M. (2014). On possibilistic and probabilistic uncertainty assessment of power flow problem: a review and a new approach. Renew. Sustain Energy Rev. 37, 883–895. doi:10.1016/j.rser.2014.05.063

CrossRef Full Text | Google Scholar

AlNahhal, R. H., Naiem, A. F., Shaaban, M. F., and Ismail, M. (2022). Optimal planning of parking lots of PEVs incorporating V2G for reliability improvement of distribution systems. IEEE Access 10, 123521–123533. doi:10.1109/ACCESS.2022.3224753

CrossRef Full Text | Google Scholar

Bae, S., and Kwasinski, A. (2012). Spatial and temporal model of electric vehicle charging demand. IEEE Trans. Smart Grid 3, 394–403. doi:10.1109/TSG.2011.2159278

CrossRef Full Text | Google Scholar

Bludszuweit, H., Domínguez-Navarro, J., and Llombart, A. (2008). Statistical analysis of wind power forecast error. IEEE Trans. Power Syst. 23 (3), 983–991. doi:10.1109/TPWRS.2008.922526

CrossRef Full Text | Google Scholar

Cheng, L., Chang, Y., and Huang, R. (2015). Mitigating voltage problem in distribution system with distributed solar generation using electric vehicles. IEEE Trans. Sustain Energy 6, 1475–1484. doi:10.1109/TSTE.2015.2444390

CrossRef Full Text | Google Scholar

Ding, H., Song, Y., Hu, Z., Wu, J., and Fan, X. (2013). Probability density function of day-ahead wind power forecast errors based on power curves of wind farms. Proc. CSEE 33 (34), 136–144+22. doi:10.13334/j.0258-8013.pcsee.2013.34.019

CrossRef Full Text | Google Scholar

Fu, Y., Liu, H., Su, X., Mi, Y., and Tian, S. (2019). Probabilistic direct load flow algorithm for unbalanced distribution networks considering uncertainties of PV and load. IET Renew. Power Gener. 13, 1968–1980. doi:10.1049/iet-rpg.2018.5802

CrossRef Full Text | Google Scholar

Li, Z., Wu, L., Xu, Y., Moazeni, S., and Tang, Z. (2022). Multi-stage real-time operation of a multi-energy microgrid with electrical and thermal energy storage assets: A data-driven MPC-ADP approach. IEEE Trans Smart Grid. 13, 213–226. doi:10.1109/TSG.2021.3119972

CrossRef Full Text | Google Scholar

Lin, Z., Song, C., Zhao, J., and Yin, H. (2022). Improved approximate dynamic programming for real-time economic dispatch of integrated microgrids. Energy 255. doi:10.1016/j.energy.2022.124513

PubMed Abstract | CrossRef Full Text | Google Scholar

Mesa-Calle, J., Villa-Acevedo, W., and López-Lezama, J. M. (2023). Impact of renewable energy sources on voltage stability and assessment techniques. Rev. UIS Ing., 151–166. doi:10.18273/revuin.v22n3-2023011

CrossRef Full Text | Google Scholar

Nakamura, Y., Hara, R., Kita, H., and Tanaka, E. (2018). Voltage regulation utilizing electric vehicle rapid chargers in a distribution system. Electr. Eng. Jpn. 204, 21–30. doi:10.1002/eej.23095

CrossRef Full Text | Google Scholar

Nascimento, J., and Powell, W. B. (2013). An optimal approximate dynamic programming algorithm for concave, scalar storage problems with vector-valued controls. IEEE Trans. Autom. Control 58, 2995–3010. doi:10.1109/TAC.2013.2272973

CrossRef Full Text | Google Scholar

Nguyen, H. T. M., and Chow, A. H. F. (2023). Adaptive rail transit network operations with a rollout surrogate-approximate dynamic programming approach. Transp. Res. 148, 104021. doi:10.1016/j.trc.2023.104021

CrossRef Full Text | Google Scholar

Ning, C., and You, F. (2019). Optimization under uncertainty in the era of big data and deep learning: when machine learning meets mathematical programming. Comput. Chem. Eng. 125, 434–448. doi:10.1016/j.compchemeng.2019.03.034

CrossRef Full Text | Google Scholar

Powell, W. B. (2007) Approximate dynamic programming: solving the curses of dimensionality, 703. John Wiley and Sons.

Google Scholar

Tang, Z., Hill, D. J., Liu, T., and Ma, H. (2018). Hierarchical voltage control of weak subtransmission networks with high penetration of wind power. IEEE Trans. Power Syst. 33, 187–197. doi:10.1109/TPWRS.2017.2700996

CrossRef Full Text | Google Scholar

Trinh, P. H., Zafar, R., and Chung, I. Y. (2023). Optimal PEV charging and discharging algorithms to reduce operational cost of microgrid using adaptive rolling horizon framework. IEEE Access 11, 133668–133680. doi:10.1109/ACCESS.2023.3337030

CrossRef Full Text | Google Scholar

Xizhen, X., Jiakun, F., Xiaomeng, A., Cui, S., Xu, M., Yao, W., et al. (2022). Real-time joint regulating reserve deployment of electric vehicles and coal-fired generators considering EV battery degradation using scalable approximate dynamic programming. Int. J. Electr. Power Energy Syst. 140, 108017. doi:10.1016/j.ijepes.2022.108017

CrossRef Full Text | Google Scholar

Xizhen, X., Jiakun, F., Xiaomeng, A., Shichang, C., Yazhou, J., and Wei, Y. (2023). A fully distributed ADP algorithm for real-time economic dispatch of microgrid. IEEE Trans. Smart Grid 15, 513–528. doi:10.1109/TSG.2023.3273418

CrossRef Full Text | Google Scholar

Zakaria, A., Ismail, F. B., Lipu, M. S. H., and Hannan, M. A. (2020). Uncertainty models for stochastic optimization in renewable energy applications. Renew. Energy 145, 1543–1571. doi:10.1016/j.renene.2019.07.081

CrossRef Full Text | Google Scholar

Zhang, W., Shao, C., Hu, B., Zhou, J., Cao, M., Xie, K., et al. (2023). Proactive security-constrained unit commitment against typhoon disasters: an approximate dynamic programming approach. IEEE Trans. Ind. Inf. 19, 7076–7087. doi:10.1109/TII.2022.3208574

CrossRef Full Text | Google Scholar

Zhang, Z., Chen, Y., Liu, X., and Wang, W. (2019). Two-stage robust security-constrained unit commitment model considering time autocorrelation of wind/load prediction error and outage contingency probability of units. IEEE Access 7, 25398–25408. doi:10.1109/ACCESS.2019.2900254

CrossRef Full Text | Google Scholar

Zhang, Z., Zhang, Y., Huang, Q., and Lee, W. J. (2018). Market-oriented optimal dispatching strategy for a wind farm with a multiple stage hybrid energy storage system. CSEE J. Power Energy Syst. 4 (4), 417–424. doi:10.17775/CSEEJPES.2018.00130

CrossRef Full Text | Google Scholar

Zhou, Y., Gao, F., Zhang, Z., Zhao, S., Xu, X., Meng, H., et al. (2023). Research on optimal voltage control of distribution network with the participation of EVs and PVs. Appl. Sci. 13, 5987. doi:10.3390/app13105987

CrossRef Full Text | Google Scholar