ResNest-SVM-based method for identifying single-phase ground faults in active distribution networks

Single-phase grounding fault is the most common fault type in the distribution network. An accurate and effective single-phase grounding fault identification method is a prerequisite for maintaining the safe and stable operation of the power grid. Most neutral points of the active distribution network are grounded through arc suppression coils. In the active distribution network, the power supply in the network changes from one to multiple, which may change the direction of the fault current. In this paper, the superposition theorem is used to analyze the difference in the boosting effect of different types of distributed generators (DG) on line mode current in the sequence network diagram when DG is connected upstream or downstream of the fault point. Secondly, the composition of the zero-mode transient current of the fault line is analyzed. A judgment method based on the superposition diagram of transient zero-sequence voltage and current is proposed. Then, this paper improves the ResNest network and modifies the classifier of the last fully connected layer to SVM. Finally, the model in PSCAD is used to simulate single-phase grounding faults to obtain the training set and validation set. These datasets are used to train and test AlexNet, ResNet50, ResNeSt, and ResNeSt-SVM. The results show that under different fault points, transition resistances, DG access upstream and downstream of the fault point, and different fault initial phase angles, the ResNest-SVM model method can accurately identify the fault line and has better anti-noise ability than the other three network structures.

1 Introduction

With the large-scale integration of inverter-interfaced distributed generators (IIDGs) into the distribution network, a new type of active distribution network with wind and solar power (ADNWS) has emerged, distinct from traditional rotational power sources (Meng et al., 2024; Shi et al., 2023; Yan et al., 2024). As the penetration of distributed generation into the distribution network continues to increase, it is important to study its impact on single-phase ground fault detection methods. In ADNWS, a small current grounding method is typically used, and in such systems, the probability of single-phase ground faults reaches up to 80%, similar to conventional distribution networks. Arc extinguishing coils are generally used to extinguish arcs, and to ensure safety, over-compensation is typically employed (Li et al., 2023). This makes the characteristics of faulty and non-faulty lines similar, thereby necessitating the development of new methods for detecting single-phase ground faults in ADNWS.

Currently, the types of distributed generation in active distribution networks are primarily focused on photovoltaic (PV) systems and wind turbines. The commonly used models for wind turbines are mainly divided into two types: one is the distributed generation model with asynchronous motor characteristics, and the other is the model with synchronous generator characteristics (Yan et al., 2023). Since the DC power generated by PV systems needs to be connected to the AC distribution network through inverters, PV power sources are classified as inverter-interfaced distributed generators. The use of inverters introduces higher-order harmonics, so filters are often installed between them and the main grid (Sajadi et al., 2023). The presence of both PV systems and wind turbines in ADNWS complicates the network and presents significant challenges for fault identification.

In traditional distribution networks, fault identification methods are typically classified based on electrical quantity characteristics into steady-state methods and transient methods. Steady-state methods usually rely on the magnitude or polarity of fault electrical quantities and different power flow directions for fault detection and line selection. Transient methods, on the other hand, utilize the magnitude and direction of transient electrical quantities (Pirmani et al., 2024). In (Li et al., 2021), the transient zero-sequence admittance method is employed, using the principle that the transient zero-sequence impedance upstream of the fault point is always greater than the transient zero-sequence impedance downstream of the fault point for the fault location. In (Li et al., 2020), the discrete wavelet transform algorithm is chosen to extract the wavelet energy entropy of zero-sequence currents as a criterion for detecting high-impedance grounding. This algorithm has led to an improvement in the accuracy of high-impedance grounding identification.

In an ADNWS system, researchers have analyzed how the integration of different types of distributed generation alters the line-mode network of a small current grounding system. The fault indicator is determined based on the relative rate of change between the zero-sequence current and the zero-sequence voltage (Zhang et al., 2022). In networks with inverter-based power sources, an active signal injection method is proposed to enhance the fault characteristics, making it easier to identify the faulty line (Xu et al., 2024). From the perspective of high-order harmonics generated by inverter-interfaced power sources, literature (Rustemli et al., 2023) notes that inverters produce the fifth and seventh harmonics, which improves the reliability of harmonic identification. However, the photovoltaic model is overly idealized and does not account for the effects of filters connected after the inverter in real scenarios. With the rise of artificial intelligence, some researchers have also utilized it for fault identification. Literature (Yuan and Jiao, 2023) employs the fundamental and harmonic components, along with wavelet energy from electrical transient quantities, to perform network fault detection. Due to the slow training of deep networks, literature (Wang, 2022) uses the artificial bee colony optimization algorithm to tune parameters of deep neural networks (DNNs) and improves the bee colony algorithm with network weight optimization methods. Literature (Yu et al., 2023) proposes a semi-supervised learning model based on Generative Adversarial Networks (GANs) to reliably identify fault feeders, enhancing fault detection accuracy through the adversarial game between the discriminator and the generator. Using neural networks from the perspective of image feature extraction is less common; literature (Zhang et al., 2023) constructs a fault line selection model with a convolutional neural network incorporating an attention mechanism, which first learns the zero-sequence current at the feeder’s initial segment before fault recognition. Literature (Guo et al., 2017) applies continuous wavelet transform (CWT) to the transient zero-sequence currents of each feeder to obtain the wavelet coefficient grayscale images for each feeder. These images are then fed into a convolutional neural network (CNN) for fault line selection. Literature (Hong et al., 2020) applies discrete wavelet packet transform (DWPT) to the three-phase voltages, zero-sequence voltage, and three-phase currents for time-frequency decomposition, resulting in time-frequency spectrograms. These spectrograms are then used as inputs to a convolutional deep belief network (CDBN) for fault identification. The article constructs the three-phase voltage and current data into two-dimensional matrices, which serve as input data for a CNN for fault identification. Literature (Wu et al., 2023) proposes using transient images as input to a multi-head Long Short-Term Memory Convolutional Neural Network (LSTM-CNN) for fault recognition, a method that can improve issues with white noise. Despite these advancements, there is still room for further improvement in the accuracy of AI-based fault recognition methods.

It can be seen that the identification of single-phase grounding faults in distribution networks is still primarily focused on traditional networks, with limited research on active distribution network scenarios. Meanwhile, the application of artificial intelligence methods in detecting single-phase faults in active distribution networks is still in its early stages. Therefore, this paper proposes a method for identifying single-phase grounding faults in active distribution networks based on an improved neural network architecture. Compared to existing neural network architectures, the proposed new architecture effectively improves the accuracy of the validation set.

This paper first introduces specific models of wind turbines and photovoltaics. Based on this, an active distribution network architecture is constructed, using the superposition theorem to illustrate the impact of distributed generation on line-mode current at the fault location. Subsequently, the characteristics of zero-mode current in fault lines within ADNWS are analyzed. Using the superimposed plots of zero-sequence current and voltage as a dataset for image recognition, an improved convolutional neural network method for identifying single-phase grounding faults in ADNWS is proposed. In the validation section, the improvement in accuracy of the enhanced model compared to previous models is analyzed. Considering the noise impact brought by inverters and other power electronic components in the ADNWS system, the method’s adaptability to noise is further verified.

2 The model of a wind-solar hybrid active distribution network

2.1 Wind turbine model

The wind turbine model used in this study is an asynchronous squirrel-cage motor. The model consists of the wind source, wind turbine, pitch angle control, and the asynchronous squirrel-cage motor. The model of the asynchronous generator is illustrated in Figure 1.

Figure 1

Figure 1. Model of an asynchronous generator.

2.2 Photovoltaic model

The photovoltaic model consists of a solar PV array, Maximum Power Point Tracking (MPPT), DC-DC converter, and DC-AC inverter modules. The MPPT tracking algorithm used is the perturb and observe method. The inverter control strategy employs the PQ control method. After a single-phase ground fault occurs on the line, the phase-locked loop in the control section acquires the initial phase angle during the fault, allowing the control strategy to adapt accordingly (Li, J. et al., 2022). The PQ control method can independently and accurately regulate the active and reactive power output of the inverter. By setting reference values for p and Q separately, the inverter can flexibly respond to changes in load demand and the grid’s reactive power adjustment requirements, thereby helping to maintain voltage stability in the system. The model shown in Figure 2 is used for integrating IIDG into the distribution network.

Figure 2

Figure 2. Photovoltaic model.

2.3 Small current grounding system with wind and solar integration

Active distribution networks often use small current grounding systems to detect ground fault lines by collecting current and voltage data from the lines. A distribution network structure with integrated distributed generation sources is illustrated in Figure 3.

Figure 3

Figure 3. Distribution network structure with DG access.

In Figure 3, F represents the ground fault point, with k feeders connected to a 10 kV bus. T₁ is the main transformer with a transformation ratio of 110/10. The high-voltage side of the main transformer is grounded through an arc suppression coil, indicating that this system is a small current grounding system. T₁ … T_k represents grounding transformers, with a transformation ratio of 10/0.48 when DGn is an inverter-interfaced DG and 10/0.23 when DGn is a rotational DG. Fault points are shown on feeder 1, depicting the situation both upstream and downstream of the DG connection, while other lines are connected to several DGs.

3 Analysis of voltage and current waveform characteristics after DG integration

After integrating distributed generation sources into the existing small current grounding system, it is necessary to analyze the line-mode and zero-sequence currents and voltages. Voltage can be derived from the current multiplied by the impedance through which the current flows; therefore, this study primarily focuses on the analysis of electrical quantities related to current.

3.1 Equivalent impedance analysis of DG and grid-connected transformers

The equivalent impedance of the feeder section with DG integration is generally the combined impedance of the DG and the grid-connected transformer. The combined equivalent positive-sequence impedance of the DG and the transformer is $Z_{DGx}$, as shown in Equation 1.

$Z_{DGx}=\left(Z_T+Z_s\right)//Z_m(1)$

In the formula, $Z_{\mathrm{T}}=R_{\mathrm{T}}+\mathrm{j}\omega L_{\mathrm{T}}$ and $Z_{\mathrm{m}}=R_{\mathrm{m}}+\mathrm{j}\omega L_{\mathrm{m}}$ represent the leakage impedance and excitation impedance of the transformer, respectively, and $Z_{\mathrm{s}}=R_{\mathrm{s}}+\mathrm{j}\omega L_{\mathrm{s}}$ represents the equivalent impedance of the DG.

When a rotating-type DG is connected, its role in the line mode network is similar to that of a small-capacity power source (i.e., the main transformer), with the parallel impedance approximating the transformer’s leakage reactance. In this case, Equation 2 can be expressed as.

$Z_{DGx}\approx Z_T(2)$

When an inverter-based DG is connected, its equivalent impedance $Z_s$ is much larger than the line impedance and the transformer’s magnetizing impedance. In this case, the equivalent impedance $Z_s$ in the analysis of ground faults can be considered nearly infinite. Thus, the impact of the DG’s impedance on the fault current is negligible, as shown in Equation 3:

$Z_{DGx}\approx Z_m(3)$

The role of inverter-based DG in the line mode network is similar to that of a large-capacity load, having little to no impact on the line mode network. This Section 3.2 mainly focuses on rotating DG.

3.2 Analyzing the impact of DG integration on fault line current through sequence network diagrams

By analyzing the sequence network diagram of the line, the impact of multi-source distribution networks on the line mode current at the fault point is evaluated. In the distribution network structure shown in Figure 3, the DG on Feeder one is connected either upstream or downstream of the fault point. The equivalent circuit of a single-phase grounding fault in the line is illustrated in Figure 4A.

Figure 4

Figure 4. Diagram of Current Phase Sequence Composition.

Figure 4A, $u_f$ represents the virtual source at the fault point, while $u_{1f}$, $u_{2f}$ and $u_{0f}$ denote the positive-sequence, negative-sequence, and zero-sequence voltages at the fault point, respectively. $R_f$ is the transition resistance at the fault point. $Z_{1b1}$ and $Z_{1b2}$ are the positive-sequence impedances from the DG (Distributed Generation) access point to the fault point and the end of the line, respectively, when the DG is connected downstream. $Z_{1a1}$ and $Z_{1a2}$ are the positive-sequence impedances from the DG access point to the bus and the fault point, respectively, when the DG is connected upstream. $Z_{1\mathit{Ln}1}$ and $Z_{1\mathit{Ln}2}$ are respectively the positive-sequence impedances from the DG access point to the bus and the end of the line, assuming that DG exists in other lines. $Z_{1L2}$ represents the positive-sequence impedance of the healthy line without DG, and $Z_{1T}$ represents the positive-sequence impedance of the main transformer. $Z_{1d1}$, $Z_{1d2}$ and $Z_{1dn}$ represent the positive-sequence impedances of the faulted line, healthy line $L_2$, and healthy line $L_n$, respectively. $Z_{DG1x}$, $Z_{DG2x}$ represent the combined positive-sequence impedances of the DG and its grid-connected transformer when connected upstream and downstream, respectively. $Z_{0a}$, $Z_{0b}$ represent the zero-sequence impedances of the upstream and downstream segments of the faulted line at the fault point, $C_{0a}$ and $C_{0b}$ represent the zero-sequence distributed capacitances of the fault lines L₂ and L_n. $C_{02}$, $C_{0n}$ represent the zero-sequence distributed capacitances of the fault lines L₂ and L_n.

Figure 4B illustrates the composite network model for low-current grounding faults: From the perspective of the fault point, $Z_{1a}\left(Z_{1b}\right)$, $Z_{2a}\left(Z_{2b}\right)$ and $Z_{0a}\left(Z_{0b}\right)$ represent the first, second, and 0th mode impedances upstream (downstream) of the fault point, respectively; $i_{1a}\left(i_{1b}\right)$, $i_{2a}\left(i_{2b}\right)$ and $i_{0a}\left(i_{0b}\right)$ represent the first, second, and 0th mode currents upstream (downstream) of the fault point, respectively.

When the fault line does not include a distributed generator (DG), the upstream line mode impedance $Z_{1a}$ at the fault point can be expressed as:

$Z_{1\mathrm{a}}=Z_{1\mathrm{a}2}+Z_{1\mathrm{a}1}+Z_{1\mathrm{T}1}//\cdots //\left(Z_{1\mathrm{d}i}+Z_{1{\mathrm{L}}_i}\right)//\cdots //\left[Z_{1{\mathrm{L}}_{n1}}+Z_{1{\text{DG}}_x}//\left(Z_{1{\mathrm{L}}_{n2}}+Z_{1\mathrm{d}n}\right)\right](4)$

$Z_{1{\text{DG}}_x}$ represents the line mode impedance of the DG and its transformer connected in the normal feeder. In the line mode equivalent network of a conventional distribution network without DG, the line mode impedance of the main transformer is very small, so the impedance of the healthy line can be ignored. The equivalent impedance $Z_{1{\text{DG}}_x}$ of a single DG is significantly larger than the line mode impedance of the transformer. Therefore, Equation 4 can be approximated as $Z_{1\mathrm{a}2}+Z_{1\mathrm{a}1}+Z_{1\mathrm{T}1}$.

When the fault line contains DG and the DG is connected downstream of the fault point, the upstream impedance at the fault point can be expressed as:

$Z_{1\mathrm{a}}=Z_{1\mathrm{a}2}+Z_{1\mathrm{a}1}+Z_{1\mathrm{T}1}//\cdots //\left(Z_{1{\mathrm{d}}_i}+Z_{1{\mathrm{L}}_i}\right)//\cdots //\left(Z_{1{\mathrm{L}}_n}+Z_{1\mathrm{d}n}\right)\approx Z_{1\mathrm{a}2}+Z_{1\mathrm{a}1}+Z_{1\mathrm{T}1}(5)$

Based on Equations 4, 5, it can be seen that the impedance upstream of the fault point remains approximately unchanged, regardless of whether the DG is connected. When the fault line does not contain DG, the downstream sequence impedance $Z_{1b}$ at fault point, as shown in Equation 6:

$Z_{1\mathrm{b}}=Z_{1\mathrm{b}1}+Z_{1\mathrm{b}2}+Z_{1\mathrm{d}1}(6)$

When the fault line contains DG and the DG is connected downstream of the fault point, the downstream impedance at the fault point can be expressed as:

$Z_{1\mathrm{b}}=Z_{1\mathrm{b}1}+\left(Z_{1\mathrm{b}2}+Z_{1\mathrm{d}1}\right)//Z_{1\text{DG}2}(7)$

Since the impedance of a rotating DG $Z_{1DG2}$ is much smaller than that of the load and the line mode impedance, the downstream line mode impedance at the fault point can be approximated as the sum of the line mode impedance between the fault point and the DG, and the combined line mode impedance of the DG and its grid-connected transformer. Therefore, Equation 7 can be approximated as $Z_{1\mathrm{b}1}+Z_{1\text{DG}2}$, which is smaller than the downstream impedance in the absence of DG.

When the fault line contains DG and the DG is connected upstream of the fault point, the upstream impedance at the fault point can be expressed as:

$Z_{1\mathrm{a}}=Z_{\text{la}2}+\left(Z_{\text{la}1}+Z_{\text{lT}1}\right)//Z_{1\text{DG}1}(8)$

From Equations 8, 4, it is evident that the upstream impedance decreases when DG is connected upstream of the fault point. In this case, the downstream impedance remains the same as it was without the DG connection.

In summary, the integration of DG alters the line-mode network of low-current grounding faults, reducing both the resistive and inductive components of the line-mode impedance at both upstream and downstream of the fault point. Consequently, when a rotating-type DG is connected upstream of the fault line, the line-mode current at the fault point is slightly larger compared to the situation without DG.

As an example of DG integration upstream of the fault point, the simulation results of the line-mode current in the faulted line are shown in Figure 5.

Figure 5

Figure 5. Simulation diagram of the fault point at the upstream.

From the analysis and simulations, it can be observed that when the fault point is upstream, the rotating DG significantly increases the line-mode current in the faulted line. In contrast, when the inverter-interfaced DG is integrated, the line-mode current in the faulted line remains almost unchanged. This indicates that the integration of distributed generators affects the fault current in the distribution network. When the fault point is downstream, both the rotating DG and inverter-interfaced DG have an impact on the single-phase ground fault line-mode current ${\stackrel{·}{I}}_f$, but the effect is minimal.

To study the characteristics of transient zero-sequence current, it is necessary to analyze the transient fault process. The simplified zero-sequence transient equivalent circuit diagram of a normal line, based on Figure 3, is shown below.

3.3 Transient zero-sequence current characteristics

Since the high-voltage side of the step-up transformer for the DG integrated into the grid is configured in a delta connection, and the low-voltage side in a star connection, the zero-sequence circuit of the DG is not connected to the grid, regardless of whether it is an inverter-interfaced DG or a rotating DG integrated into the ADNWS. Therefore, the steady-state and transient processes of the zero-sequence current experience minimal changes. Consequently, the analysis methods for small current grounding systems can still be applied to ADNWS networks. In this study, the distinction between faulted and normal lines is made using the waveform characteristics of zero-sequence voltage and zero-sequence current.

To study the characteristics of transient zero-sequence current, it is necessary to analyze the transient fault process. The simplified zero-sequence transient equivalent circuit diagram of the normal line is shown in Figure 6A.

Figure 6

Figure 6. The zero-sequence transient equivalent circuit diagram when no fault occurs.

$U_0$ represents the zero-sequence fault voltage, and it is assumed that $U_0=U_m\sin \left(\omega t+\theta \right)$. $C$ represents the line’s capacitance to ground, while L and R represent the line’s inductance and resistance, respectively. The current in a normal line is generally represented by the capacitive current $i_0$.

Based on the equivalent circuit diagram shown above, the following differential equation can be formulated, as shown in Equation 9:

$R_0{i}_c+L_0\frac{d{i}_c}{dt}+\frac{1}{C}\int i_{c}dt=U_m\sin \left(\omega t+\theta \right)(9)$

The solution for the current in the normal line, derived from the differential equation provided earlier, as shown in Equation 10:

$i_0\left(t\right)=i_{\mathrm{C}m}\left[\left(\frac{{\omega }_f}{\omega }\sin \theta \sin \omega t-\cos \theta \cos {\omega }_{f}t\right)e^{-\delta t}+\cos \left(\omega t+\theta \right)\right](10)$

In this equation, $i_{\mathrm{C}m}$ represents the amplitude of the transient capacitive current, and $\delta \left(\delta =\left(R/2L\right)\right)$ is the attenuation factor, $\omega$ stands for the system’s power frequency, while ${\omega }_f$ is the main resonance frequency of the transient. Finally, $\theta$ denotes the initial phase angle at the moment the fault occurs.

Based on Figure 3, the simplified zero-sequence transient equivalent circuit diagram for a faulted line in a system grounded through an arc suppression coil is shown in Figure 6B.

In this diagram, $U_0$ represents the set zero-sequence fault voltage, and it is assumed that $U_0=U_m\sin \left(\omega t+\theta \right)$. $C_{\mathrm{\Sigma }}$ represents the line’s capacitance to ground, while $L_0$ and $R_0$ represent the line’s inductance and resistance. $L_x$ and $R_x$ are the inductance and resistance of the arc suppression coil, respectively. The zero-sequence current in the faulted line can be expressed as the sum of the capacitive current from other lines $i_c$ and the inductive current through the arc suppression coil $i_L$, as shown in Equation 11:

$i_0\left(t\right)=i_c\left(t\right)+i_L\left(t\right)(11)$

The differential equation corresponding to the equivalent circuit diagram shown above is expressed as follows, as shown in Equation 12:

$\left\{\begin{array}{l}{R}_0{i}_c+L_0\frac{d{i}_c}{dt}+\frac{1}{C_0}\int i_{c}dt=U_m\sin \left(\omega t+\theta \right)\\ R_x{i}_L+L_x\frac{d{i}_L}{dt}=U_m\sin \left(\omega t+\theta \right)\end{array}\right.(12)$

The solution for the faulted line current is given by, as shown in Equation 13:

$i_0\left(t\right)=\left(I_{Cm}-I_{Lm}\right)\cos \left(\omega t+\theta \right)+I_{Cm}\times \left(\frac{{\omega }_f}{\omega }\sin \theta \sin \omega t-\cos \theta \cos {\omega }_{f}t\right)e^{-\frac{t}{{\tau }_c}}+I_{Lm}\cos \theta e^{-\frac{t}{{\tau }_L}}(13)$

In this equation, $I_{Cm}$ and $I_{Lm}$ represent the amplitudes of the transient capacitive and inductive currents, respectively. ${\tau }_C$ and ${\tau }_L$ are the decay time constants for the capacitive and inductive circuits, $\omega$ is the system’s power frequency, ${\omega }_f$ is the main resonance frequency of the transient, and $\theta$ denotes the initial phase angle at the moment of the fault. From the above equation, it can be inferred that the transient zero-sequence current in a healthy line is primarily composed of transient capacitive current, whereas the transient zero-sequence current in a faulted line includes both transient capacitive and inductive currents. Therefore, there is a significant difference between the transient zero-sequence currents of healthy and faulted lines.

The simulation results yield the superimposed plots of zero-sequence current and zero-sequence voltage for both types of lines. Analyzing Figure 7, it is observed that as the time approaches the moment of fault occurrence, the zero-sequence current and the derivative of the zero-sequence voltage in the faulted line are in the same direction, whereas in the healthy line, they are in the opposite direction (Gao et al., 2018; Su X et al., 2023). This indicates a significant difference in transient characteristics between faulted and non-faulted conditions, suggesting that neural networks can be employed for fault identification.

Figure 7

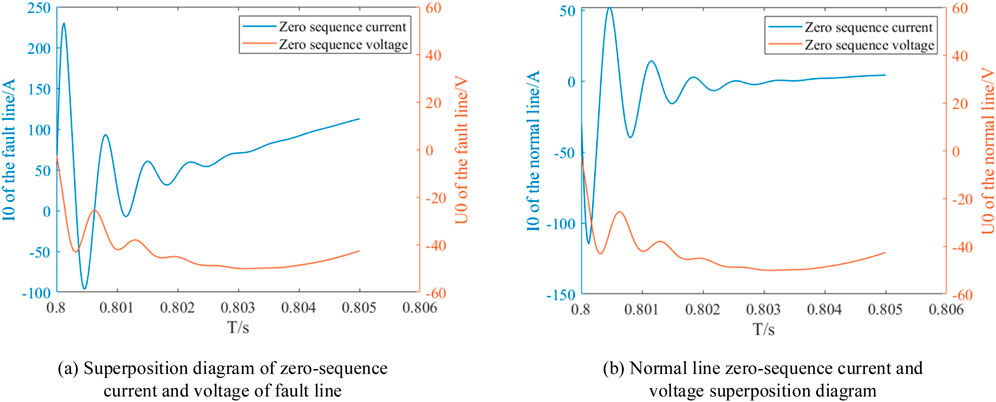
Figure 7. The images of zero-sequence voltage and zero-sequence current superposition when a fault occurs or does not occur on the line.

In summary, the impact of both synchronous DG (Distributed Generation) and inverter-based DG on the line-mode current is minimal when the fault point is either upstream or downstream. However, the transient process during the fault contains a wealth of characteristic information, and these transient components are not affected by the neutral grounding method. Therefore, this study selects a time window after the fault occurrence as the observation period to analyze the transient quantities and extract characteristic components. Compared to using steady-state information, this approach offers higher feasibility for fault identification in low-current grounding systems.

4 Fault identification based on Convolutional Neural Networks

4.1 Convolutional Neural Networks

Convolutional Neural Networks (CNN) are a type of machine learning method used for image recognition. Classic CNN models include LeNet-5 (LeCun et al., 1998), AlexNet (Krizhevsky et al., 2017), and the ResNet neural network introduced by Kaiming He (He et al., 2016; Mirza et al., 2023), among others.

CNNs focus on capturing local features through the convolution of kernels and reduce the number of model training parameters while extracting local features from images using pooling kernels or global pooling kernels (Huang et al., 2023). In current CNN architectures, unsaturated nonlinear functions, such as the ReLU function, are commonly used as activation functions in convolutional layers. The mathematical formula for the ReLU function is as follows, as shown in Equation 14:

$f_{\text{cov}}\left(x\right)=\max \left(0,x\right)(14)$

CNN learns image features through a combination of linear layers and nonlinear activation functions.

4.2 Overview of SVM basic principles

Support Vector Machines (SVM) are binary classification models that operate as linear classifiers with maximum margin in the feature space, distinguishing them from perceptrons (Wang et al., 2023). SVMs also incorporate kernel techniques, which fundamentally transform them into nonlinear classifiers. The learning method of SVM aims to maximize the margin, which can be formulated as a convex quadratic programming problem, equivalent to minimizing a regularized hinge loss function. Essentially, SVM learning methods are optimal algorithms for solving convex quadratic programming problems.

The reference indicates that the Radial Basis Function (RBF) kernel has a broad convergence range, making it adaptable to various sample distributions (Anyanwu et al., 2023). Unless the unique distribution of the samples is well understood and a specific kernel function is chosen accordingly, the RBF kernel is considered an ideal mapping function. Additionally, the RBF kernel is well-suited for addressing binary classification problems.

4.3 ResNest and its improvements

Although ResNet stacks many network layers, its effective depth remains insufficient. The network’s receptive field is not large enough, which may lead to overfitting in certain cases. To address these issues, researchers have proposed the ResNest50 neural network, which introduces a split-attention module and divides the base group into R smaller groups (Wang et al., 2020). This adjustment ensures that the channel dimension input into each residual block is G $=K\times R$ . Finally, each residual block outputs the required dimension for the next block through weighted fusion.

This paper is inspired by the ResNest50 network architecture, the SVM-RBF classifier, and the self-calibrated convolution (SCConv) module in SCNet. In our approach, we replace the convolutions in the group module with self-calibrated convolutions. Additionally, we connect the SVM classifier with an RBF kernel after the final fully connected layer to output the probability of the label, where the highest probability indicates the fault line identified by the machine learning model. The ResNest50-RBF-SVM network structure is illustrated in Figure 8. The network first performs convolution using a 7 × 7 kernel, followed by 16 residual layers. After passing through a fully connected layer and a classifier layer, it outputs the identification results. The residual layers incorporate the self-correcting convolution module from SCNet.

Figure 8

Figure 8. ResNest-SVM network structure diagram.

The processing formula for self-calibrated scale space is as follows, as shown in Equation 15 and Equation 16:

$A_1^{\prime }=Up\left(Down\left(A\right)\times K_2\right)(15)$

$B_1^{\prime }=F_3\left(A_1\right)+\sigma \left(A_1+A_1^{\prime }\right)(16)$

Where $A_1^{\prime }$ represents the input and $B_1^{\prime }$ denotes the output features. “Down” and “Up” refer to the downsampling and upsampling operations, respectively, while K is the scale transformation coefficient.

The self-calibrated branch significantly enhances the perceptual range of the output features, leading to richer feature information. This branch primarily focuses on spatial positional information, which helps avoid overlooking data from areas that do not require management, thereby reducing time consumption. The self-calibrated branch has the capability to encode feature information at various scales, making the feature content more comprehensive. By utilizing the RBF-SVM, the model can better leverage the information from the fully connected layer for binary classification tasks.

4.4 Identification process

Thanks to the high sensitivity of secondary devices, zero-sequence voltage and zero-sequence current on the feeder can be obtained during the initial stages of a fault. The fault identification process illustrated in Figure 9 ultimately provides the line judgment results. The specific identification steps are as follows.

(1) Simulation Data Acquisition: Using the simulation model in PSCAD, zero-sequence voltage and zero-sequence current are calculated from the electrical quantities at the beginning of each feeder. The identification algorithm is triggered if the zero-sequence voltage exceeds a predetermined threshold, typically set to be greater than 0.15U_N (Wang et al., 2019; Fan et al., 2021).

(2) Data Visualization and Preprocessing: After the algorithm is initiated, data from the first quarter cycle of the zero-sequence voltage and zero-sequence current are recorded, with a sampling frequency of 40 kHz. Preprocessing includes denoising, normalization. The denoising method used is the moving average method, and the normalization method is the maximum value normalization. The formula for maximum value normalization is as follows, as shown in Equation 17:

$X^{*}=\frac{X_{T_n}}{X_{T\_\max }}(17)$

$X_{T_n}$ represents the magnitude of the electrical quantity at the current time point, and $X_{T\_\max }$ is the maximum magnitude of the electrical quantity within the period $T$.

Figure 9

Figure 9. Fault identification flow chart based on ResNest-SVM.

And finally resizing the images to 224 × 224 pixels, resulting in images that overlay the zero-sequence voltage and zero-sequence current waveforms.

(3) Model Training and Validation: The training dataset is input into the ResNest network, allowing the network to learn the features of the images and output judgments for each feeder (with a fault line labeled as one and a normal line labeled as 0). The trained model is then saved. A validation set containing high-resistance grounding and noise is constructed, and after passing through the ResNest network, the RBF-SVM classifier is used to make the final judgment output for the feeders.

5 Simulation and validation

5.1 Dataset acquisition

The ADNWS system grounded through an arc suppression coil is built on PSCAD/EMTDC, as shown in Figure 13. In the topology diagram provided in Figure 10, the number of feeders is set to k = 4, and the number of integrated DGs is n = 2, consisting of one wind turbine model and one photovoltaic model. The inductance value of the arc suppression coil is Lg = 0.3 H, and the lengths of the four feeders are 4 km, 5 km, 4 km, and 5 km, respectively. The first feeder is divided into sections of 1.5 km, 1.5 km, and 1 km, while the other feeders are set to half of their lengths, as shown in Figure 10. The segments closer to the bus are overhead lines, while those farther away are cable lines. The line parameters are listed in Table 1. The simulation sampling frequency is set to 40 MHz, and the moment the fault begins is at 0.8 s. The time window for validating the impact of DG on the line mode current is set to two cycles, while the time window for training and validating the neural network is set to one-quarter of a cycle.

Figure 10

Figure 10. Simulation model.

Table 1

Table 1. Line parameters.

Through simulations, multiple sets of zero-sequence voltage and zero-sequence current data are obtained, and the superimposed waveforms of the zero-sequence voltage and zero-sequence current are created. The composition of the training set is shown in Table 2.

Table 2

Table 2. Ground fault parameters of the training dataset.

Based on the above simulations, 1,080 fault scenarios were collected, resulting in 4,320 superimposed waveform images of zero-sequence current and zero-sequence voltage for the feeders. The superimposed waveform images were divided into training, testing, and validation sets in a ratio of 5:3:2, serving as input for the ResNest model. During training, network parameters were updated using the stochastic gradient descent method, and the cross-entropy function was used as the loss function to train the network. The model was able to learn the characteristics of the faults, and the connected layer was integrated with the RBF-SVM for binary classification of the feeders to determine whether they were fault lines, ultimately achieving fault identification with a certain accuracy.

5.2 Model training

Figures 11–14 illustrate the training processes of AlexNet, ResNet50, ResNest, and the improved ResNest-SVM models, respectively. As seen in the figures, the loss values for all four models decrease with the number of iterations and eventually approach zero. In terms of training accuracy, AlexNet’s accuracy surpasses 99% after 14 iterations, ResNet exceeds 99% after nine iterations, ResNest reaches over 99% after seven iterations, and the improved ResNest-SVM achieves over 99% accuracy after just six iterations. Among the models, ResNest-SVM demonstrates the fastest training completion.

Figure 11

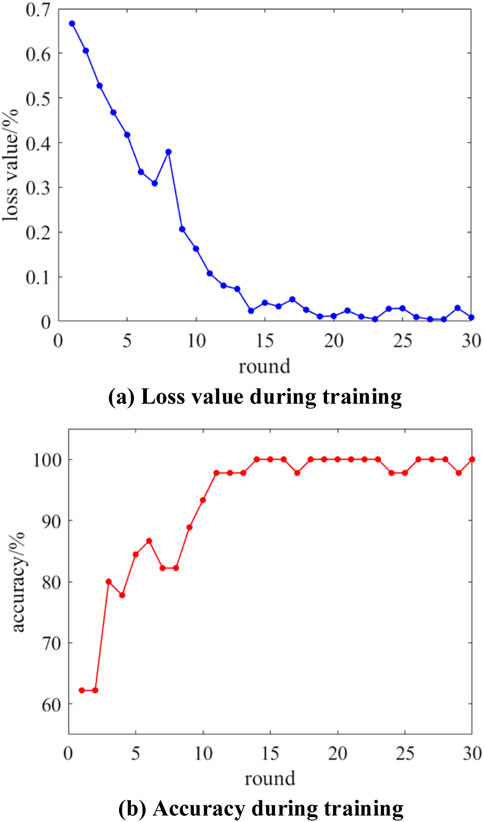
Figure 11. The diagram showing the changes in accuracy and loss values during the training process of the AlexNet neural network.

Figure 12

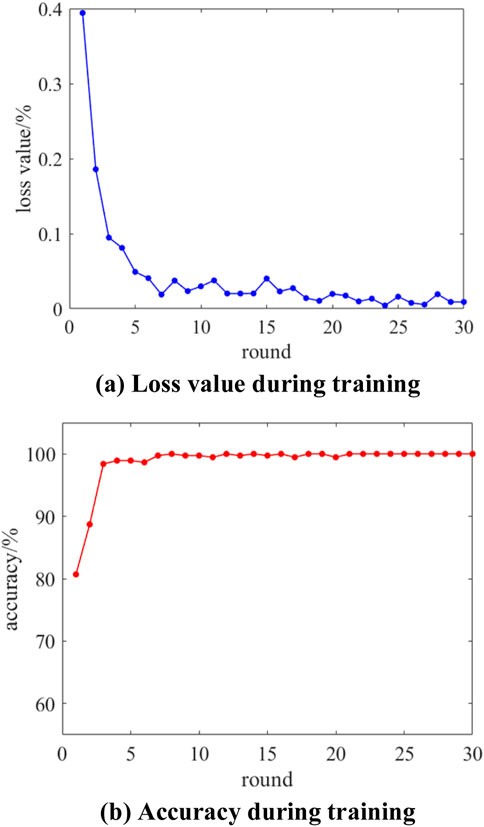
Figure 12. The diagram showing the changes in accuracy and loss values during the training process of the Resnet50 neural network.

Figure 13

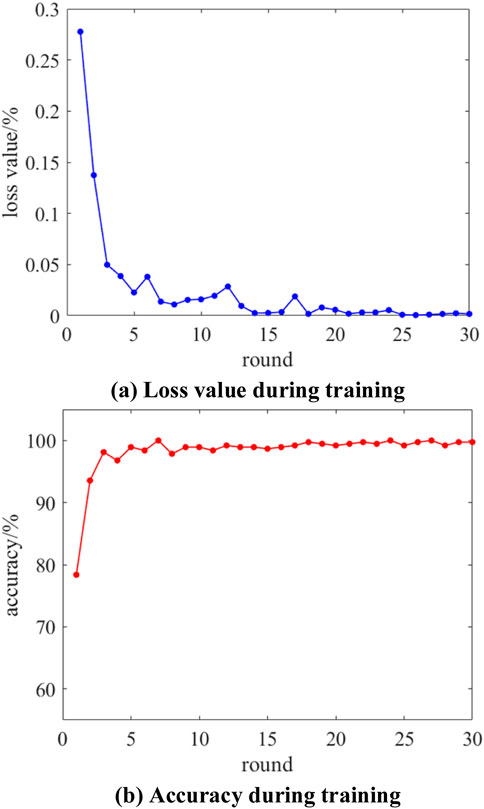
Figure 13. The diagram showing the changes in accuracy and loss values during the training process of the ResNest neural network.

Figure 14

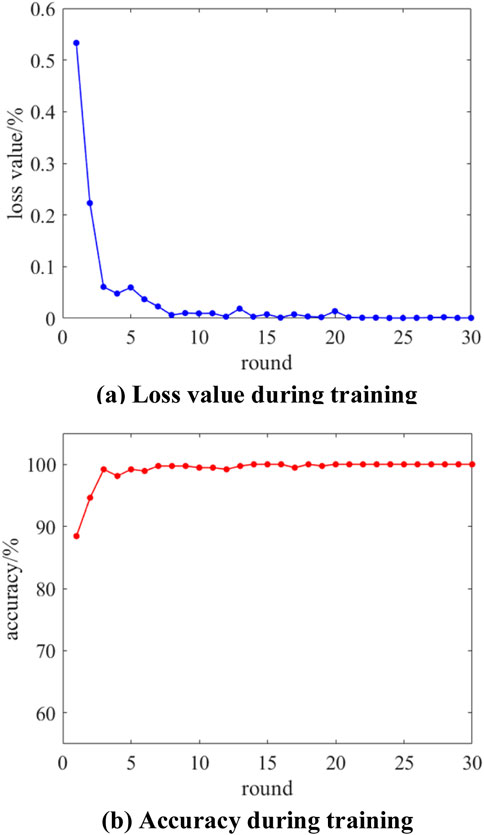
Figure 14. The diagram showing the changes in accuracy and loss values during the training process of the ResNest-SVM neural network.

5.3 High-resistance grounding validation

High-resistance grounding identification has always been a challenge in the detection of low-current single-phase grounding faults. Prolonged high-resistance grounding can lead to arcing overvoltage, which poses a risk to the lines. Therefore, it is essential to validate high-resistance grounding separately. A validation set of 408 images was created by randomly selecting 102 fault scenarios from the parameter settings in Table 3.

Table 3

Table 3. High resistance ground fault parameters.

The accuracy of the validation $\lambda$ is defined as the ratio of the number of correctly identified samples to the total number of samples. The accuracy of the four neural networks on the high-resistance grounding validation set is shown in Table 4. From the table, it can be seen that regardless of whether DG is connected, the fault identification accuracy for high-resistance grounding across all four neural networks is above 90%. Among them, ResNest-SVM demonstrated the highest accuracy in high-resistance grounding identification.

Table 4

Table 4. High resistance ground fault test results.

5.4 Interference resistance analysis

In actual ADNWS systems, power electronic devices such as inverters can generate noise, which impacts the system’s current and voltage and may affect the accuracy of fault identification. Therefore, it is necessary to verify the accuracy of fault identification under noise interference. From the parameter settings in Table 2, 102 fault scenarios were randomly selected, and Gaussian white noise was superimposed on the original signals to create a validation set of 408 images, simulating the effect of power electronic devices. As shown in Figure 12, the waveforms of faulty and normal lines before and after the superposition of 40 dB Gaussian white noise interference are illustrated.

As shown in Figure 15, after adding Gaussian white noise, the initial transient portion of the waveform is not significantly affected, while the latter part, which transitions into the steady state, exhibits noticeable noise. The noise patterns closely resemble waveforms subjected to various noise interferences in the distribution network. After adding white noise ranging from 10 dB to 50 dB, the accuracy of the four neural networks on the noise verification set is shown in Table 5.

Figure 15

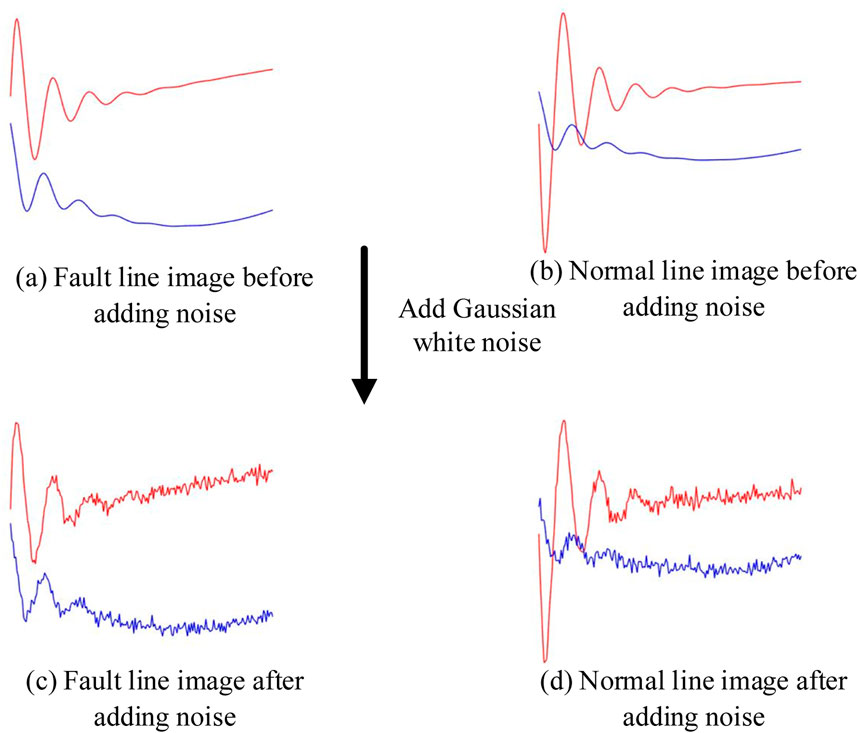
Figure 15. The diagram showing the data after adding white noise to the zero-sequence voltage and zero-sequence current data.

Table 5

Table 5. Noise set test results.

The introduction of noise altered some of the image features, leading to a noticeable drop in accuracy. From the table, it can be seen that regardless of whether DG is connected, the fault identification accuracy for lines with added noise is lower than that for high-resistance grounding verification across all four neural networks. However, the accuracy of the ResNest-SVM network remained above 95%, indicating that the ResNest-SVM network proposed in this paper possesses strong anti-interference capabilities and high adaptability.

6 Conclusion

This paper analyzes the potential impact of DG on the line mode and zero mode structures of distribution networks, focusing on sequence network diagrams for DG connected upstream and downstream of fault points. The analysis results indicate that DG integration can either approximate or increase the line mode current observed by secondary equipment, with varying degrees of augmentation depending on the type of DG. Further analysis of the transient zero mode circuit reveals that the transient zero mode current in normal lines consists solely of capacitive current, while the transient zero mode current in fault lines is composed of both capacitive and inductive currents, highlighting significant differences in the transient zero mode currents between fault and non-fault circuits. Therefore, zero mode voltage and current with transient information are selected to form images used as the basis for identifying single-phase grounding faults. Finally, the paper proposes a fault identification process based on an improved ResNest network. Comparative validation against Alexnet, Resnet50, and ResNest on high-resistance grounding and noise verification datasets demonstrates that the ResNest-SVM network exhibits superior capabilities in identifying high-resistance grounding faults and resisting noise interference.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

QL: Conceptualization, Data curation, Funding acquisition, Methodology, Project administration, Writing–original draft. XL: Formal Analysis, Investigation, Resources, Writing–review and editing. DL: Supervision, Writing–review and editing, Software. CL: Validation, Writing–original draft. BC: Visualization, Writing–review and editing. ZG: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by the Science and Technology Project of State Grid Fujian Electric Power Co., LTD. under Grant 52130423000Y. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

Author QL was employed by State Grid Fujian Electric Power Corporation. Authors XL, DL, CL, and ZG were employed by State Grid Fujian Electric Power Co., LTD. Author BC was employed by Fujian Zhongshi Institute Electric Power Adjustment Test Co., LTD.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anyanwu, G. O., Nwakanma, C. I., Lee, J. M., and Kim, D. S. (2023). RBF-SVM kernel-based model for detecting DDoS attacks in SDN integrated vehicular network. Ad Hoc Netw. 140, 103026. doi:10.1016/j.adhoc.2022.103026

CrossRef Full Text | Google Scholar

Fan, D., Yi, Y., Chen, S., Song, L., and Li, J. (2021). “Transmission line fault type identification based on transfer learning and deep learning,” in 2021 6th international conference on power and renewable energy (ICPRE) (IEEE), 202–207.

CrossRef Full Text | Google Scholar

Gao, J., Cheng, Q., Wang, X., and Chen, M. (2018). Faulty line detection method based on B-spline bistable denoising for distribution network. Int. Trans. Electr. Energy Syst. 28 (7), e2565. doi:10.1002/etep.2565

CrossRef Full Text | Google Scholar

Guo, M. F., Zeng, X. D., Chen, D. Y., and Yang, N. C. (2017). Deep-learning-based earth fault detection using continuous wavelet transform and convolutional neural network in resonant grounding distribution systems. IEEE Sensors J. 18 (3), 1291–1300. doi:10.1109/jsen.2017.2776238

CrossRef Full Text | Google Scholar

He, K., Zhang, X., Ren, S., and Sun, J. (2016). “Deep residual learning for image recognition,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 770–778.

CrossRef Full Text | Google Scholar

Hong, C., Zeng, Z., Fu, Y., and Guo, M. (2020). Deep-belief-Networks based fault classification in power distribution networks. IEEJ Trans. Electr. Electron. Eng. 15 (10), 1428–1435. doi:10.1002/tee.23213

CrossRef Full Text | Google Scholar

Huang, S. Y., An, W. J., Zhang, D. S., and Zhou, N. R. (2023). Image classification and adversarial robustness analysis based on hybrid quantum–classical convolutional neural network. Opt. Commun. 533, 129287. doi:10.1016/j.optcom.2023.129287

CrossRef Full Text | Google Scholar

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2017). ImageNet classification with deep convolutional neural networks. Commun. ACM 60 (6), 84–90. doi:10.1145/3065386

CrossRef Full Text | Google Scholar

LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998). Gradient-based learning applied to document recognition. Proc. IEEE 86 (11), 2278–2324. doi:10.1109/5.726791

CrossRef Full Text | Google Scholar

Li, J., Bi, H., Li, C., Li, J., Zeng, D., and Wang, G. (2022). Analysis and calculation method for multiple faults in low-resistance grounded systems with inverter-interfaced distributed generators based on a PQ control strategy. Int. J. Electr. Power and Energy Syst. 138, 107980. doi:10.1016/j.ijepes.2022.107980

CrossRef Full Text | Google Scholar

Li, J., Feng, J., Bai, H., Wang, H., Li, W., Huang, M., et al. (2023). An adaptive protection scheme for multiple single-phase grounding faults in radial distribution networks with inverter-interfaced distributed generators. Int. J. Electr. Power and Energy Syst. 152, 109221. doi:10.1016/j.ijepes.2023.109221

CrossRef Full Text | Google Scholar

Li, J., Liu, Y., Li, C., Zeng, D., Li, H., and Wang, G. (2021). An FTU-based method for locating single-phase high-impedance faults using transient zero-sequence admittance in resonant grounding systems. IEEE Trans. Power Deliv. 37 (2), 913–922. doi:10.1109/TPWRD.2021.3074217

CrossRef Full Text | Google Scholar

Li, J., Wang, G., Zeng, D., and Li, H. (2020). High-impedance ground faulted line-section location method for a resonant grounding system based on the zero-sequence current’s declining periodic component. Int. J. Electr. Power and Energy Syst. 119, 105910. doi:10.1016/j.ijepes.2020.105910

CrossRef Full Text | Google Scholar

Meng, L., Yang, X., Zhu, J., Wang, X., and Meng, X. (2024). Network partition and distributed voltage coordination control strategy of active distribution network system considering photovoltaic uncertainty. Appl. Energy 362, 122846. doi:10.1016/j.apenergy.2024.122846

CrossRef Full Text | Google Scholar

Mirza, A. F., Mansoor, M., Usman, M., and Ling, Q. (2023). Hybrid Inception-embedded deep neural network ResNet for short and medium-term PV-Wind forecasting. Energy Convers. Manag. 294, 117574. doi:10.1016/j.enconman.2023.117574

CrossRef Full Text | Google Scholar

Pirmani, S. K., Fernando, W. S. P., and Mahmud, M. A. (2024). Single line-to-ground fault current analysis for resonant grounded power distribution networks in bushfire prone areas. Electr. Power Syst. Res. 237, 110883. doi:10.1016/j.epsr.2024.110883

CrossRef Full Text | Google Scholar

Rustemli, S., Satici, M. A., Şahin, G., and van Sark, W. (2023). Investigation of harmonics analysis power system due to non-linear loads on the electrical energy quality results. Energy Rep. 10, 4704–4732. doi:10.1016/j.egyr.2023.11.034

CrossRef Full Text | Google Scholar

Sajadi, A., Rañola, J. A., Kenyon, R. W., Hodge, B. M., and Mather, B. (2023). Dynamics and stability of power systems with high shares of grid-following inverter-based resources: a tutorial. IEEE Access 11, 29591–29613. doi:10.1109/ACCESS.2023.3260778

CrossRef Full Text | Google Scholar

Shi, Q., Yang, P., Tang, B., Lin, J., Yu, G., and Muyeen, S. M. (2023). Active distribution network type identification method of high proportion new energy power system based on source-load matching. Int. J. Electr. Power and Energy Syst. 153, 109411. doi:10.1016/j.ijepes.2023.109411

CrossRef Full Text | Google Scholar

Su, X., Wei, H., Wei, H., Lyu, Z., Zhang, X., and Gao, W. (2023). Fault-line selection method for small-current grounded system based on multi-classifier. J. Electr. Eng. and Technol. 18 (2), 941–952. doi:10.1007/s42835-022-01285-y

CrossRef Full Text | Google Scholar

Wang, H., Hu, L., and Zhang, Y. (2023). SVM based imbalanced correction method for Power Systems Transient stability evaluation. ISA Trans. 136, 245–253. doi:10.1016/j.isatra.2022.10.039

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, N. (2022). Fault line selection of power distribution system via improved bee colony algorithm based deep neural network. Energy Rep. 8, 43–53. doi:10.1016/j.egyr.2022.10.070

CrossRef Full Text | Google Scholar

Wang, S., Liu, Y., Qing, Y., Wang, C., Lan, T., and Yao, R. (2020). Detection of insulator defects with improved ResNeSt and region proposal network. IEEE Access 8, 184841–184850. doi:10.1109/ACCESS.2020.3029857

CrossRef Full Text | Google Scholar

Wang, X., Zhang, H., Shi, F., Wu, Q., Terzija, V., Xie, W., et al. (2019). Location of single phase to ground faults in distribution networks based on synchronous transients energy analysis. IEEE Trans. Smart Grid 11 (1), 774–785. doi:10.1109/tsg.2019.2938667

CrossRef Full Text | Google Scholar

Wu, H., Wang, J., Nan, D., Cui, Q., and Ouyang, J. (2023). Transmission line fault cause identification method based on transient waveform image and MCNN-LSTM. Measurement 220, 113422. doi:10.1016/j.measurement.2023.113422

CrossRef Full Text | Google Scholar

Xu, R., Song, G., Chang, Z., and Yang, J. (2024). A faulty feeder selection method for SLG faults based on active injection approach in non-effectively grounded DC distribution networks. Electr. Power Syst. Res. 234, 110535. doi:10.1016/j.epsr.2024.110535

CrossRef Full Text | Google Scholar

Yan, J., Nuertayi, A., Yan, Y., Liu, S., and Liu, Y. (2023). Hybrid physical and data driven modeling for dynamic operation characteristic simulation of wind turbine. Renew. Energy 215, 118958. doi:10.1016/j.renene.2023.118958

CrossRef Full Text | Google Scholar

Yan, X., Wang, Q., and Bu, J. (2024). High penetration PV active distribution network power flow optimization and loss reduction based on flexible interconnection technology. Electr. Power Syst. Res. 226, 109839. doi:10.1016/j.epsr.2023.109839

CrossRef Full Text | Google Scholar

Yu, X., Gu, J., Zhang, X., and Mao, J. (2023). GAN-based semi-supervised learning method for identification of the faulty feeder in resonant grounding distribution networks. Int. J. Electr. Power and Energy Syst. 144, 108535. doi:10.1016/j.ijepes.2022.108535

CrossRef Full Text | Google Scholar

Yuan, J., and Jiao, Z. (2023). Faulty-feeder detection for single phase-to-ground faults in distribution networks based on waveform encoding and waveform segmentation. IEEE Trans. Smart Grid 14 (5), 4100–4115. doi:10.1109/TSG.2023.3243026

CrossRef Full Text | Google Scholar

Zhang, X., Liu, C., and Sun, Z. (2023). Line Fault detection of DC distribution networks using the artificial neural network. Energy Eng. 120 (7), 1667–1683. doi:10.32604/ee.2023.025186

CrossRef Full Text | Google Scholar

Zhang, Z., Liu, J., Shao, W., and Wang, Y. (2022). Fault line selection using multiple disturbance characteristics of fault phase active grounding in resonant grounded distribution networks. Int. J. Electr. Power and Energy Syst. 138, 107931. doi:10.1016/j.ijepes.2021.107931

CrossRef Full Text | Google Scholar