Power system frequency nadir prediction based on data-driven and power-frequency polynomial fitting

As the proportion of renewable energy and power electronics equipment continues to rise, the level of rotational inertia decreases considerably, resulting in severe frequency stability challenges to the power grid. It is of great significance to accurately predict the frequency nadir following a large disturbance. This paper proposes a novel data-model fusion-driven approach for the prediction of frequency nadir. As the physics-driven part, a Simplified Prediction Model (SPM) based on power-frequency polynomial fitting is developed to quickly produce the frequency nadir. As the data-driven part, Back Propagation Neural Network (BPNN) is deployed to correct the errors of the SPM to achieve more accurate results. This serial integration scheme not only obtains the final prediction result with higher accuracy, but also meets the computational efficiency requirements of online prediction. Compared with existing integration-driven methods, SPM only focuses on the active power-frequency characteristics of the system, which retains the most critical effects and greatly reduces the dependence of BPNN on sample data quality. Case studies on a modified IEEE 39-bus system verify the effectiveness of the proposed approach.

1 Introduction

In order to realize the “dual carbon” development strategy, it is urgent to accelerate the construction of a new power system. With the large-scale integration of clean and low-carbon energy resources such as wind power and photovoltaic generation, the power system with synchronous machines as the main body has gradually evolved to the system with renewable energy as the main body, showing an increasingly decrease trend of rotational inertia level, and the system’s frequency response capability is weakened remarkably. Consequently, the frequency stability of the power system is facing severe challenges under large power disturbances.

Frequency is one of the basic indicators to describe the operating state of the power system. The frequency nadir consists of the maximum frequency deviation and the frequency nadir time. It is not only the key indicator to judge whether the frequency is out of the limit, but also regarded as the decision-making basis for appropriate frequency regulation control. It is very important to quickly and reliably predict the frequency nadir for frequency stability evaluation and control of large power systems (Hatziargyriou et al., 2021).

At present, there are three typical methods to predict the frequency nadir following disturbances: time-domain simulation method, simplified model based method, and data-driven method. The time-domain simulation is the most common used method for analyzing the frequency response of a power grid, which builds a time-domain model of each element of the system (including different generation units with nonlinear control links), and converts it into a series of differential algebraic equations to iteratively calculate the accurate numerical solutions of each state quantity of the power grid (Wen et al., 2023). Common time-domain simulation software includes PSASP, PSD-BPA, DIgSILENT/Power-Factory and PSS/E, etc. However, the time-domain simulation method is often time-consuming when analyzing large-scale power systems, which is more suitable for offline analysis of power grid planning and accident recurrence, but not for real-time online analysis of power grids with strong timeliness requirements. The simplified model method usually solves the dynamic process of the frequency response by retaining the rotor equation of motion and the governor model, such as the average system frequency (ASF) model (Chan et al., 1972) and the system frequency response (SFR) model (Anderson and Mirheydar, 1990; Liu et al., 2020; Egido et al., 2009) decouple power and frequency by breaking the frequency closed loop, and the analytical calculation of the frequency nadir is realized; Shen et al., 2021; Wang et al., 2022b propose multi-machine equivalent SFR models and derive their closed-form solutions to solve the frequency response of power systems with two or three regions. In summary, the simplified model is suitable for online analysis scenarios with high speed requirements, but the prediction accuracy needs to be further improved. With the rapid popularization of wide area measurement system (WAMS) in power grids, Phasor Measurement Unit (PMU) and Supervisory Control And Data Acquisition (SCADA) systems can obtain massive amounts of information about the operation of the power grid in real time, making machine learning based on data analysis more and more widely used in the power system (Kamruzzaman et al., 2021; Yi et al., 2021; Bo et al., 2022). Data-driven method can effectively deal with the nonlinear and complex problems of physical models, and provide new solutions for the establishment of frequency models of complex power systems solutions. However, its prediction accuracy is heavily dependent on the quantity and quality of sample data, the generalization ability is insufficient and the prediction results often lack interpretability.

In order to meet the practical needs of the power system, the simplified model can be combined with data-driven methods, integrating the advantages of both methods, so as to improve the overall performance and be suitable for solving complex physical problems. Feng et al., 2021 discusses the feasibility of integrating model-driven methods and data-driven methods for online frequency stability evaluation. Han et al. (2022) embeds frequency-response related physics in gated recurrent unit neural networks through the basic input eigenquants and the embedded physical knowledge, new input eigenquants are formed and used for model training. However, how to efficiently combine the accurately modeled frequency response model and the data-driven model to achieve complementary advantages remains to be studied.

In this paper, the problem of frequency nadir prediction of a high proportion of renewable energy power systems under large power deficit is studied. Due to the computing speed requirements for real-time applications, a Simplified Prediction Model (SPM) based on system frequency response equivalent is developed. Compared with the traditional frequency response model (Yang et al., 2022), the SPM uses polynomials of different orders to fit the power frequency characteristics of each frequency modulation resource, including synchronous generator, renewable energy, load, and HVDC, so as to analyze and calculate the maximum deviation of the frequency and the frequency nadir time, which has the advantages of low identification difficulty, simple form, and less required information. Therefore, the SPM is selected to be a physical-driven link in this paper to ensure the high computational speed of the fusion model.

The complexity of the data model is positively correlated with the predicted effect, and at the same time, higher requirements are put forward for the quality of data samples. Since this paper only focuses on the active power-frequency characteristics of the power system, in the serial ensemble approach, the role of the data model is to correct the predictions of the physical model, rather than to fit the complex physical mechanisms of the entire power grid. As a shallow neural network, BPNN (Back Propagation Neural Network) has good self-learning, self-adaptive, nonlinear mapping, and generalization capabilities. Therefore, in order to ensure the feasibility and accuracy of the integration-driven method, BPNN is used as the part of the data model.

The serial ensemble method (Wang et al., 2019) is implemented to introduce the SPM to obtain the initial prediction results, which can ensure the prediction efficiency and reduce the dependence of the data model on sample data. The BPNN is deployed to correct the error of the initial prediction results of the physical model. Simulation results on a modified IEEE 39-bus system show that the data-model fusion-driven method can predict the frequency nadir with high accuracy and speed, and provide more reliable indices and basis for the frequency stability analysis and control of the power system.

2 SPM modeling and analytical solution

The frequency response characteristics of the power system with a high proportion of renewable generation are mainly affected by the synchronous generators, load frequency characteristics, auxiliary frequency control strategies of renewable energy units and HVDC links. According to the respective power-frequency response characteristics, the modeling and analysis of each type of frequency modulation resources are explained in this section.

2.1 Power-frequency characteristics of synchronous generators

The mechanical power output curve of a typical synchronous generator governor under power step disturbance can be simply divided into three sections according to its change characteristics, namely, the fast change section, the constant velocity change section, and the steady-state output section. The generator governor changes the output power by changing the prime mover valve, so as to suppress the unbalanced power, and finally restore the frequency to a quasi-steady state. The complete curve change process can be represented by the following higher-order polynomial (Equation 1):

$\Delta P_G\left(f\right)=K_G^0+K_G^1\frac{d\Delta f}{dt}+K_G^2{\left(\frac{d\Delta f}{dt}\right)}^2+K_G^3{\left(\frac{d\Delta f}{dt}\right)}^3+...+K_G^n{\left(\frac{d\Delta f}{dt}\right)}^n(1)$

where ${∆P}_G$ is the mechanical power deviation output by the synchronous generator governor; $K_G^0$, $K_G^1$, and $K_G^2$ are the polynomial coefficients related to the rate of change of each order.

For synchronous generator governors, the higher the order of the above polynomials, the more accurate the power-frequency response characteristic curve of the generator governor in this scenario can be described. However, at the same time, the introduction of higher-order polynomials will bring more cumbersome workload to frequency stability online evaluation, which will seriously slow down the computational speed. For the frequency nadir, the corresponding time coordinates are often located in the uniform velocity change segment, so only the first two curve change links need to be accurately modeled.

Taking the GS-TB type governor in the PSD-BPA software as an example, given a load disturbance of 35 MW, the system frequency deviates. The actual response curve of the governor and its polynomial fitting curves of different orders are compared as shown in Figure 1. It can be seen that the second-order polynomial can accurately fit the power output curve of the governor within the time scale from the moment of fault occurrence to the frequency nadir. Therefore, the second-order polynomial is utilized to describe the active power frequency characteristics of the generator governor before the frequency nadir is reached, and the expression is:

$\Delta P_G\left(f\right)=K_G^0+K_G^1\frac{d\Delta f}{dt}+K_G^2{\left(\frac{d\Delta f}{dt}\right)}^2(2)$

Figure 1

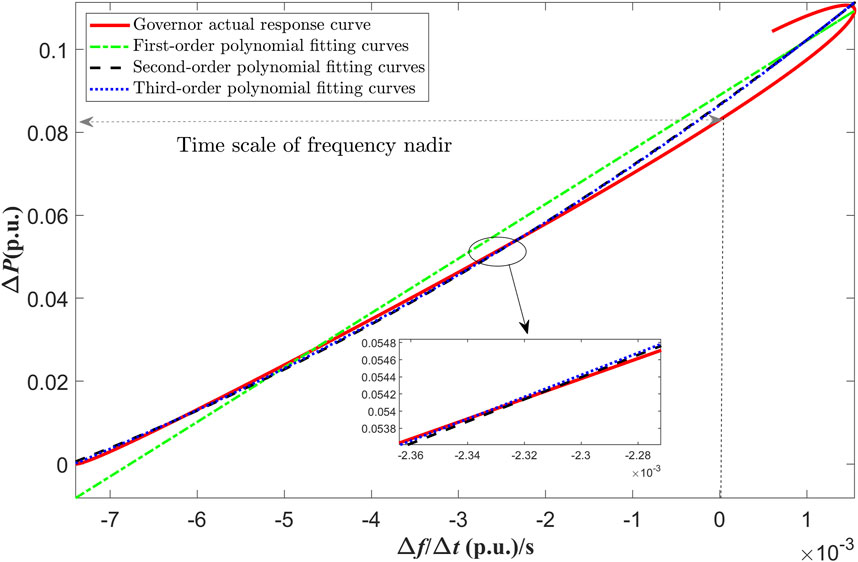
Figure 1. The active power-frequency characteristic curve and its fitting results of the GS-TB type governor.

2.2 Power-frequency characteristics of the active participation of renewable energy units in frequency regulation

Under the conventional control strategy, renewable energy units do not actively participate in the frequency regulation, which leads to a significant reduction in the inertia of the system and a weakening of the frequency control capability. Many studies have been conducted to improve the control strategy to enable them to participate in the support of the power grid frequency. To this end, most of the current renewable energy stations achieve auxiliary frequency response by implementing measures such as virtual synchronous control, virtual inertia control, and droop control. The purpose of these control schemes is to enable the renewable energy stations to simulate the characteristics of the frequency response of synchronous generators through the control of power electronic inverters and algorithms. The active power-frequency characteristics of a renewable energy unit considering virtual inertia and droop control can be expressed as:

$\Delta P_R\left(f\right)=K_d\Delta f+K_v\frac{d\Delta f}{dt}(3)$

where $K_d$ is the equivalent droop coefficient of the renewable energy unit, and $K_v$ is the equivalent virtual inertia coefficient.

2.3 Frequency characteristics of the load

When the frequency changes, the active power absorbed by the load from the grid also changes, which is the frequency characteristic of the load. In the dynamic process prior to the frequency reaches its nadir following the disturbance, the power-frequency dynamic characteristics of the load can be simplified as follows:

$\Delta P_L\left(f\right)=K_p^1\Delta f+K_p^0(4)$

where ${∆P}_L$ is the power deviation of the active load of the system; $K_P^0$ and $K_P^1$ are the frequency-dependent load factors of each order.

2.4 Frequency characteristics of the HVDC frequency limiter

For the high proportion of renewable energy grids, the frequency characteristics can be improved by suppressing the change of electromagnetic power of the generator through the fast and controllable function of HVDC power, reducing the deviation between the generator and the mechanical power. An HVDC frequency limiter can be used to respond to the frequency deviation of the grid and automatically modulate the HVDC power. When the power for HVDC modulation preparation is sufficient, the power-frequency dynamic characteristics can be expressed by the following formula:

$\Delta P_{FLC}\left(f\right)=K_m\Delta f+\int K_I\Delta fdt(5)$

where ${∆P}_{FLC}$ is the power deviation of the HVDC modulator of the system; $K_m$ is the frequency-dependent gain factor, $K_I$ is the integral coefficient. The role of the integration link is mainly reflected in the reduction of the steady-state frequency deviation, and this paper only focuses on the maximum frequency deviation in the frequency response process, and the role of integration control FLC can be ignored. As a result, the power response of FLC control can be further simplified, as shown in Equation 6.

$\Delta P_{FLC}\left(f\right)=K_m\Delta f(6)$

2.5 Polynomial fitting of power–frequency characteristics

For the power system with a high proportion of renewable energy generation, this paper mainly focuses on the stage when the frequency drops to the nadir under the high power shortage, according to the rotor swing equation:

$2H_{sys}\frac{df\left(t\right)}{dt}=\Delta P_{\mathrm{m}}-P_{\mathrm{d}}-D_{sys}\Delta f\left(t\right)(7)$

where H_sys and D_sys are the equivalent inertia and damping constants of the system, Δf is the frequency deviation, P_d is the active disturbances suffered by the system, and ΔP_m is the active output of the resources participating in the primary frequency modulation.

Substituting Equations 2–6 into Equation 7, the following equation can be obtained:

$\Delta f=a{\left(\frac{d\Delta f}{dt}\right)}^2+b\frac{d\Delta f}{dt}+c,\Delta f\in \left[0,\Delta f_{\max }\right](8)$

Where

$a=\frac{K_G^2}{D_{sys}+K_p^1-K_d-K_m},b=\frac{K_G^1+K_v-2H_{sys}}{D_{sys}+K_p^1-K_d-K_m},c=\frac{K_G^0-K_p^0}{D_{sys}+K_p^1-K_d-K_m}(9)$

From the above equations, it can be seen that the rate of change of the system frequency with time and the frequency deviation show a second-order polynomial relationship before the system frequency falls to the nadir, which provides a theoretical basis for the subsequent identification of system parameters and online fitting prediction of the frequency. Although Equation 8 does not explicitly include the relevant variables of renewable energies, it can be seen from Equation 9 that the polynomial parameters identified by the measurement data actually reflect the virtual inertia control and droop control characteristics of renewable energies, and the changes in the operation mode and inertia level of the system are also reflected by the parameters of the second-order polynomial.

2.6 Simplified frequency nadir prediction model

Considering that when the frequency of the system reaches the extreme point, there will be $d\Delta f/dt=0$. According to the correlation properties of the quadratic function, to meet the above conditions, the function image corresponding to Equation 8 must be symmetric with respect to the y-axis, and one obtains (Equation 10):

$b=0(10)$

The frequency nadir can thus be solved by:

$\Delta f_{\max }=c(11)$

Further analysis of the above quadratic function can be rewritten as (Equation 12):

$\sqrt{\frac{a}{\Delta f-c}}d\Delta f=dt(12)$

For the left and right integrals, one obtains (Equation 13):

$t=2\sqrt{-ac}-\sqrt{a\left(\Delta f-c\right)}(13)$

The time of the frequency nadir can be calculated by:

$t_{nadir}=2\sqrt{-ac}(14)$

Equations 11, 14 are the SPM’s expressions proposed in this section. Since it can reflect the characteristics of various frequency modulation resources, the model is suitable for power systems with a high proportion of renewable generation.

3 BPNN modeling and feature selection

3.1 BPNN algorithm

BP neural network, is a multilevel feedforward network structure trained on an error backpropagation algorithm. It adjusts the network weights by passing information forward layer by layer, comparing it to the desired output at the output layer, and then propagating the error backwards to each layer until the preset accuracy requirements are achieved (Wang et al., 2022a). The network topology is shown in Figure 2.

Figure 2

Figure 2. Structure diagram of the BPNN algorithm.

A two-layer feed-forward network with sigmoid hidden neurons and linear output neurons (fitnet), can fit multi-dimensional mapping problems arbitrarily well, given consistent data and enough neurons in its hidden layer. BPNN can obtain the best training results by continuously adjusting the number of neurons in the hidden layer. Considering that the input and output of SPM-BPNN are the maximum frequency deviation and their corresponding time, the number of neurons in the hidden layer is finally determined to be 4 after simulation tests.

3.2 Feature extraction

For the data-driven model, it is necessary to analyze the key factors affecting the frequency nadir in combination with the dynamic process of frequency response to select the eigenvalues, and the frequency response characteristics of the power system are mainly related to the active disturbance amplitude and the physical parameters of the frequency modulation unit.

The essential reason for the dynamic change of system frequency is that there is a power imbalance in the system, which leads to an imbalance between electromagnetic torque and mechanical torque, and ultimately leads to a change in motor speed. Therefore, the active power deficit of the system is a key factor affecting the frequency nadir.

For synchronous generators, the inertia, as a measure of the magnitude of inertia, reflects the rotor energy of the generator set, that is, the difficulty of changing the rotor state. Therefore, the equivalent inertia constant of the system is also a key factor influencing the frequency nadir.

Conventional generator units have the capability of primary frequency modulation, and can also participate in the frequency response when the renewable energy station imposes a specific control strategy. Therefore, the basic parameters of the governor, the virtual inertia coefficient and the equivalent droop coefficient are also the key factor influencing the frequency nadir.

In the process of HVDC FLC participating in frequency modulation, with the increase of frequency deviation, the rapid increase of HVDC power can correspondingly increase the electromagnetic power of the unit, thereby eliminating the unbalanced power, significantly suppressing the high-frequency deviation amplitude, and improving the frequency recovery characteristics. Therefore, the basic parameters of the HVDC frequency modulator are also factors that affect the frequency nadir.

Based on the above analysis, it is necessary to select key variables as input features of BPNN. For the physical data fusion model, BPNN only needs to correct the initial prediction results of the SPM, so its input features can only be the frequency nadir obtained by the SPM.

4 SPM-BPNN fusion modeling

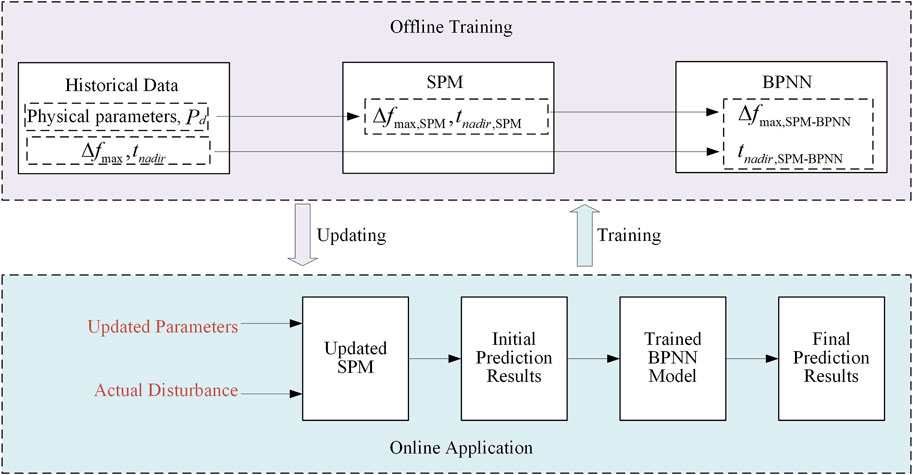
The serial scheme is used to fuse the SPM with the BPNN model to construct the SPM-BPNN model to achieve the purpose of complementing each other’s advantages. Figure 3 shows the schematic diagram of the SPM-BPNN integrated modeling, which includes both offline training and online application.

Figure 3

Figure 3. SPM-BPNN fusion modeling scheme.

4.1 Offline training

During offline training, the physical parameters, power deficit, and actual frequency nadir of the generation units are obtained from the frequency historical data or simulation data. The SPM quickly obtains the initial frequency nadir according to the physical parameters and power deficit of the frequency modulation units, and takes it as the input feature of the BPNN, and the actual frequency nadir as the output feature. The input and output features are normalized and fed into the BPNN for offline training. Finally, the trained BPNN model is used to calculate the frequency nadir online.

4.2 Online application

In the online calculation, the power deficit of the system can be measured by the WAMS and the physical parameters of the generation units can be accessed online. Based on these parameters, the SPM can compute the initial results. Then, the trained BPNN model is used to correct the initial results to obtain the final frequency nadir point. As the operating scenarios of the power system change, the parameters of the physical model also need to be updated accordingly.

5 Case studies

5.1 Case system introduction

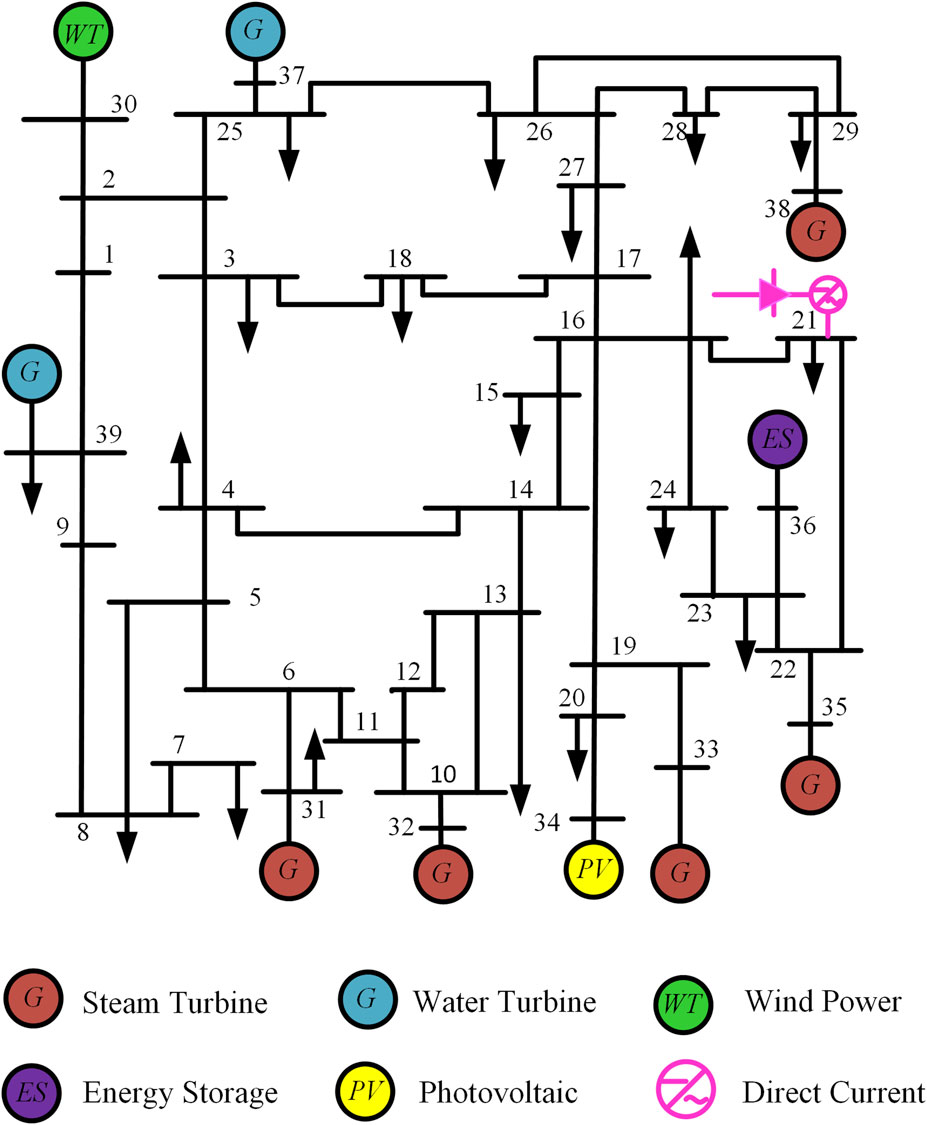
In order to verify the effectiveness and accuracy of the SPM-BPNN fusion model proposed in this paper, a modified IEEE 39 bus system is introduced. The reference frequency is 50 Hz, and its topology is shown in Figure 4, which includes seven synchronous generator units, three renewable energy stations, one feed-in HVDC, and 6,148.6 MW load. All renewable energy stations participate in the frequency response, and the total penetration ratio is 27.9%.

Figure 4

Figure 4. The improved IEEE 39-bus system topology diagram.

The simulation is carried out using the MATLAB/Simulink simulation platform. By randomly sampling the system parameters and invoking Simulink for simulation, a large number of data samples that meet the requirements of the data model can be generated. The actual value of the frequency nadir following perturbation is taken as the output, and the dataset is divided into training samples and test samples according to a certain proportion. The training samples are used to complete the learning of BPNN, and finally the frequency feature prediction model driven by data-model fusion is obtained.

5.2 The selection of the active power-frequency characteristic fitting time window

For various working conditions in the online prediction process, the parameters of SPM need to be identified online based on the measurement data, so the accuracy of the prediction is affected by the long time window of the data. However, due to the differences between the working conditions, the offline determination of the input data time series length is not the optimal choice for some online working conditions (Yan and Xu 2019). If the input data is too short, the prediction method will not obtain enough transient information, and the prediction accuracy will be reduced. If the input data takes too long, the forecasting method will collect “redundant” information, resulting in a decrease in forecasting speed.

In order to solve this problem, taking the data sample obtained in this simulation as an example, the occurrence time of the maximum frequency deviation of COI frequency obtained by the simulation is statistically analyzed. In the low-frequency scenario, the time range is 0.98–4.9s (the system disturbance time is t = 0 s), so the length of the effective data input of the model should not exceed 0.98s. Considering the single run time of the SPM-BPNN (0.01413s on average) and the control reaction time that needs to be reserved for emergency control measures (e.g., low-frequency load shedding), the prediction model proposed in this paper chooses to collect the disturbance moment (500 ms) and the previous data to fit the active power-frequency characteristics of the system, and then achieves a mapping relationship with the real frequency nadir through the correction of BPNN. The selection of a shorter time window can ensure the efficiency of online prediction, and strive for more time for the system’s frequency emergency control and low-frequency load shedding. The introduction of BPNN can ensure high calculation accuracy and make the prediction results more convincing.

5.3 Result analysis

The proposed SPM-BPNN model is compared with the SPM model and the BPNN model in terms of prediction speed and prediction accuracy.

The prediction time of SPM, BPNN and SPM-BPNN models are 1.47 ms, 13.61 ms and 14.13 ms. Compared with a single data or physical model, the SPM-BPNN model proposed in this paper does not have significant advantages in prediction speed, but it can still predict the frequency nadir online at a faster speed.

In the field of machine learning, the performance of regression models is usually evaluated by three metrics: Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), and Root Mean Square Error (RMSE). In this paper, these three indicators are used to evaluate the prediction accuracy of the SPM-BPNN model and the existing SPM and BPNN models.

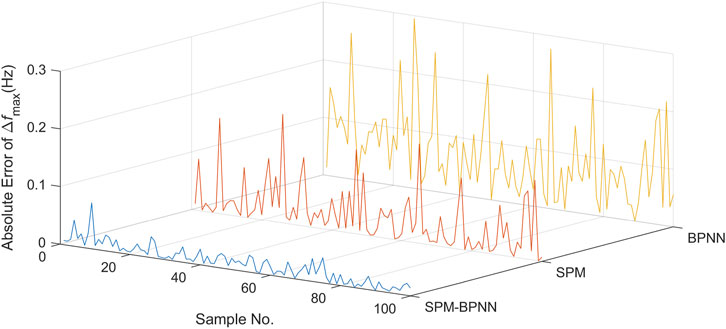
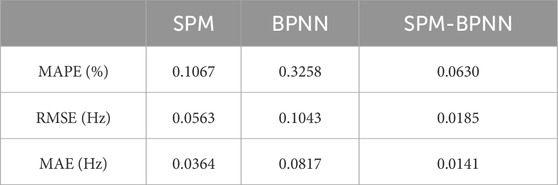
As shown in Figures 5, 6, the prediction accuracy of SPM-BPNN is significantly higher than that of a single SPM or BPNN model. As shown in Tables 1, 2, the performance indicators of the SPM-BPNN model are much smaller than those of other models, which indicates that even under different working conditions and disturbance scenarios, the prediction accuracy can be maintained, and the requirements for sample data are reduced, and the interpretability and generalization ability are stronger than those of the single data model, and has great robustness.

Figure 5

Figure 5. The prediction error comparison of Δf_max.

Figure 6

Figure 6. The prediction error comparison of frequency nadir time.

Table 1

Table 1. The performance indices and comparison of Δf_max.

Table 2

Table 2. The performance indices and comparison of frequency nadir time.

From the accuracy evaluation results in Tables 1, 2, it can be seen that the frequency prediction model driven by data-model fusion proposed in this paper has better performance than the two sub-models in various evaluation indicators. The results of Figures 5, 6 show that the average absolute error of SPM-BPNN is 61.26%, 82.74%, 81.54% and 69.7%, respectively, compared with single SPM and BPNN. The serial method is used to fuse the two sub-models, which effectively improves the accuracy of frequency prediction.

Generally speaking, when the prediction results of the sub-model are more accurate, the SPM-BPNN model can also get better prediction results, but when the prediction accuracy of some samples is poor due to the small number of training samples of BPNN, SPM-BPNN can give full play to the advantages of model and data fusion, effectively modify the prediction results, and greatly reduce the prediction error. However, this does not mean that BPNN is not suitable for the prediction of transient frequencies in power systems. Therefore, choosing the right data model is the key to improve the performance of the fusion model.

6 Conclusion

In this paper, a frequency nadir prediction method based on SPM and BPNN is proposed, which implements the serial integration scheme to combine SPM and BPNN to achieve the purpose of complementing each other’s advantages. Simulation results show that the proposed approach can not only improve the frequency nadir prediction accuracy, but also ensure that the prediction efficiency meets the requirements of online calculation. Constrained by the inherent limitations of analytical methods, this paper only focuses on major influencing factors of the frequency response and ignores minor factors such as reactive power-voltage characteristics, more in-depth study related to this issue can be conducted in future work. We will further investigate the effective combination of different integration methods and different data models to achieve more accurate prediction of the frequency response. It is worth noting that the frequency prediction method proposed in this paper only predicts the extreme value of the center frequency of inertia following the disturbance of the power system. In the next step, the dynamic frequency characteristics of various nodes in the power system can be predicted, so as to study the spatial distribution characteristics of the frequency following a disturbance, and use this as the basis to implement more efficient distributed frequency emergency control measures.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

HL: Conceptualization, Investigation, Supervision, Validation, Writing–review and editing. LW: Conceptualization, Investigation, Writing–original draft, Writing–review and editing. SQ: Investigation, Supervision, Writing–review and editing. ZW: Investigation, Supervision, Writing–review and editing. YW: Investigation, Supervision, Writing–review and editing. SZ: Conceptualization, Investigation, Supervision, Writing–review and editing. WZ: Investigation, Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported by the Science and Technology Project of China Southern Power Grid (090000KK52222151).

Conflict of interest

Authors HL, SQ, and ZW were employed by Shenzhen Power Supply Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anderson, P. M., and Mirheydar, M. (1990). A low-order system frequency response model. IEEE Trans. Power Syst. 5 (3), 720–729. doi:10.1109/59.65898

CrossRef Full Text | Google Scholar

Bo, Y., Yijun, C., Wei, Y., Zhongtuo, S., and Hongchun, S. (2022). Review on stability assessment and decision for power systems based on new-generation artificial intelligence Technology. Automation Electr. Power Syst. 46 (22), 200–223. doi:10.7500/AEPS20220114001

CrossRef Full Text | Google Scholar

Chan, L., Dunlop, R. D., and Schweppe, F. (1972). Dynamic equivalents for average system frequency behavior following major distribances. IEEE Trans. Power Apparatus Syst. PAS- 91 (4), 1637–1642. doi:10.1109/tpas.1972.293340

CrossRef Full Text | Google Scholar

Egido, I., Fernandez-Bernal, F., Centeno, P., and Rouco, L. (2009). Maximum frequency deviation calculation in small isolated power systems. IEEE Trans. Power Syst. 24 (4), 1731–1738. doi:10.1109/tpwrs.2009.2030399

CrossRef Full Text | Google Scholar

Feng, L., Qi, W., jianxiong, H., and Yi, T. (2021). Combined data-driven and knowledge-driven methodology research advances and its applied prospect in power systems. Proc. CSEE 41 (13), 4377–4390.

Google Scholar

Han, Z., Cheng, W., and Tianshu, B. (2022). Online fast frequency calculation after power system disturbance based on fusion of physics and data knowledge. Power Syst. Technol. 46 (11), 4325–4335.

Google Scholar

Hatziargyriou, N., Milanovic, J., Rahmann, C., Ajjarapu, V., Canizares, C., Erlich, I., et al. (2021). Definition and classification of power system stability – revisited and extended. IEEE Trans. Power Syst. 36 (4), 3271–3281. doi:10.1109/tpwrs.2020.3041774

CrossRef Full Text | Google Scholar

Kamruzzaman, M., Duan, J., Shi, D., and Benidris, M. (2021). A deep reinforcement learning-based multi-agent framework to enhance power system resilience using shunt resources. IEEE Trans. Power Syst. 36 (6), 5525–5536. doi:10.1109/tpwrs.2021.3078446

CrossRef Full Text | Google Scholar

Liu, L., Li, W., Ba, Y., Shen, J., Jin, C., and Wen, K. (2020). An analytical model for frequency nadir prediction following a major disturbance. IEEE Trans. Power Syst. 35 (4), 2527–2536. doi:10.1109/tpwrs.2019.2963706

CrossRef Full Text | Google Scholar

Shen, J., Li, W., Liu, L., Jin, C., Wen, K., and Wang, X. (2021). Frequency response model and its closed-form solution of two-machine equivalent power system. IEEE Trans. Power Syst. 36 (3), 2162–2173. doi:10.1109/tpwrs.2020.3037695

CrossRef Full Text | Google Scholar

Wang, Q., Li, F., Tang, Y., and Xu, Y. (2019). Integrating model-driven and data-driven methods for power system frequency stability assessment and control. IEEE Trans. Power Syst. 34 (6), 4557–4568. doi:10.1109/tpwrs.2019.2919522

CrossRef Full Text | Google Scholar

Wang, X., Ding, Q., Li, Z., Zeng, H., Zou, N., Wang, Z., et al. (2022a). “FNP-BPNN integrated model for power system frequency nadir prediction,” in 2022 IEEE sustainable power and energy conference (iSPEC), 1–5.

CrossRef Full Text | Google Scholar

Wang, X., Li, W., Shen, J., Zhao, S., and Zhang, Q. (2022b). A three-machine equivalent system frequency response model and its closed-form solution. Int. J. Electr. Power and Energy Syst. 142, 108344. doi:10.1016/j.ijepes.2022.108344

CrossRef Full Text | Google Scholar

Wen, J., Jiang, L., Zhu, J., Qiu, Z., and Chu, C.-C. (2023). “Design of data distributed service-based distributed Co-simulation platform of power systems,” in 2023 IEEE industry applications society annual meeting (IAS), 1–7.

CrossRef Full Text | Google Scholar

Yan, Z., and Xu, Y. (2019). Data-driven load frequency control for stochastic power systems: a deep reinforcement learning method with continuous action search. IEEE Trans. Power Syst. 34 (2), 1653–1656. doi:10.1109/tpwrs.2018.2881359

CrossRef Full Text | Google Scholar

Yang, S., Meng, Q., Zhang, Y., Hao, Z., and Zhang, B. (2022). Simplified prediction model of frequency nadir for power systems penetrated with renewable energy. IEEE Power and Energy Society General Meeting PESGM, 1–5.

CrossRef Full Text | Google Scholar

Yi, Z., Hengxu, Z., Changgang, L., and Tianjiao, P. (2021). Review on deep learning applications in power system frequency analysis and control. Proc. CSEE 41 (10), 3392–3406.

Google Scholar