Battery swapping scheduling for electric vehicles: a non-cooperative game approach

In recent years, electric vehicle (EV) battery-swapping technology has rapidly evolved and is expected to become widely prevalent shortly. Therefore, it is crucial to develop efficient battery-swapping scheduling algorithms to optimize the operations of battery-swapping systems. This paper proposes a non-cooperative game approach for the battery-swapping scheduling of EVs. To reduce the waiting time for battery swapping and improve the scheduling efficiency of EVs, a swapping process model inspired by the job-shop scheduling problem is proposed, and the cost function of each EV comprehensively considers the travel time, waiting time, and battery swapping price. To capture the competitive relationship among EVs, a non-cooperative game model for battery swapping scheduling is established considering the finite quantities of batteries and swapping grippers. To find the pure strategy Nash equilibrium, an iterative best response algorithm is developed, satisfying constraints including those couple decisions of different EVs. Case studies demonstrate the fairness and scheduling efficiency of the proposed approach.

1 Introduction

In recent years, the rapid growth of electric vehicles (EVs) has been considered an effective method to address environmental and energy crises (Kocer et al., 2022; Yu et al., 2024). Replacing internal combustion engine vehicles with EVs can reduce greenhouse gas emissions (Cui et al., 2023) and significantly improve air quality. As an industry encouraged by the government, EVs have been widely promoted in many cities (Zhao et al., 2024). In the logistics sector, given that the external costs of logistics are primarily associated with air pollution and noise, many logistics companies have already introduced electric trucks for operations (Jie et al., 2019). However, the widespread adoption of EVs is limited by-long charging times (Zhang et al., 2017; Zeng et al., 2023) as well as the increased peak-to-valley difference of the power grid caused by the simultaneous charging of a large number of EVs (Yong et al., 2023). To address these issues, battery swapping stations (BSSs) have been developed as a new method to provide energy to EVs. When EVs arrive at a swapping station, they can replace exhausted batteries with fully charged ones in several minutes (Yang et al., 2023). Moreover, swapping stations can centrally manage batteries that need recharging, thus avoiding adverse impacts on the grid (Ko et al., 2020).

Because of the immense potential of the battery-swapping model, research in this area has been rapidly expanding in recent years. Studies have focused on various aspects such as pricing and charging strategies (Liang and Zhang, 2018), operational models of swapping stations (Sarker et al., 2014), evaluation of the service capacity of a swapping station (Zhang et al., 2018), swapping demand forecasting (Wang et al., 2023), and construction planning for swapping stations (Zhang F. et al., 2024; Zhang Y. et al., 2024). With the widespread proliferation of EVs and swapping stations, allowing EVs to approach swapping stations without coordination may lead to congestion and queues at some stations while others remain underutilized (You et al., 2020). Therefore, the battery swapping scheduling for EVs plays a crucial role in enhancing the operational efficiency of swapping stations. Centralized (You et al., 2017a) and distributed (You et al., 2017b) swapping scheduling methods for electric vehicles were proposed, taking into account constraints related to EVs and power grid operations. An online station allocation algorithm was developed to reduce costs for EVs and alleviate congestion at swapping stations (You et al., 2020). Recently, a swapping station recommendation method based on game theory was presented (Ran et al., 2023).

Existing research on battery swapping scheduling has two main limitations. First, exiting swapping scheduling models ignored the waiting time of EVs caused by a finite number of swapping grippers. A similar issue of waiting time resulting from the occupation of charging equipment was studied in previous works on electric vehicle charging (Guo et al., 2017; Yang et al., 2018), where linear expressions of queue length were used to roughly estimate waiting times affected by variable charging times of vehicles. However, in the context of swapping processes, the swapping time is roughly constant, typically about 5 min (Yang et al., 2014). Furthermore, the approach in (Guo et al., 2017; Yang et al., 2018) overlooked the coupled relationship between waiting time and vehicle arrival time, and might thus lead to inaccurate scheduling results.

Second, few studies consider the complex competitive relationships among EVs in the context of swapping scheduling. EVs may belong to different entities, and battery swapping decisions of an EV not only impact its own swapping efficiency and costs but also potentially influence the decisions of others. Consequently, vehicle owners might not comply with centralized scheduling results. So far, only (Ran et al., 2023) utilized game theory to analyze this issue, where the swapping station with the lowest total cost was recommended for EVs with a pricing function designed to adjust swapping prices. In addition, it is difficult to directly apply game theory-based methods from the related electric vehicle charging scheduling problem (Guo et al., 2017; Yang et al., 2015; Chen and Leung, 2019; Wan et al., 2020) to battery swapping scheduling, since the availability of batteries was not considered. Therefore, it is necessary to develop a new game theory-based method specifically tailored to address the swapping scheduling problem to enhance overall operational efficiency at swapping stations and improve the swapping experience for vehicle owners.

To overcome the above limitations, this paper proposes a non-cooperative game approach for the battery swapping scheduling of EVs. The main contributions are threefold:

1) To reduce the waiting time for battery swapping and improve the scheduling efficiency of EVs, a swapping process model inspired by the job-shop scheduling problem is proposed, and the cost function of each EV comprehensively considers the travel time, waiting time, and battery swapping price.

2) To capture the competitive relationship among EVs, a non-cooperative game model for battery swapping scheduling is established considering the finite quantities of batteries and swapping grippers.

3) To find the pure strategy Nash equilibrium, an iterative best response algorithm is developed satisfying constraints including those couple decisions of different EVs.

The remainder of this paper is organized as follows. Section 2 formulates the problem. Section 3 develops the solution methodology. Section 4 presents the numerical results. Finally, Section 5 concludes the study.

2 Problem formulation

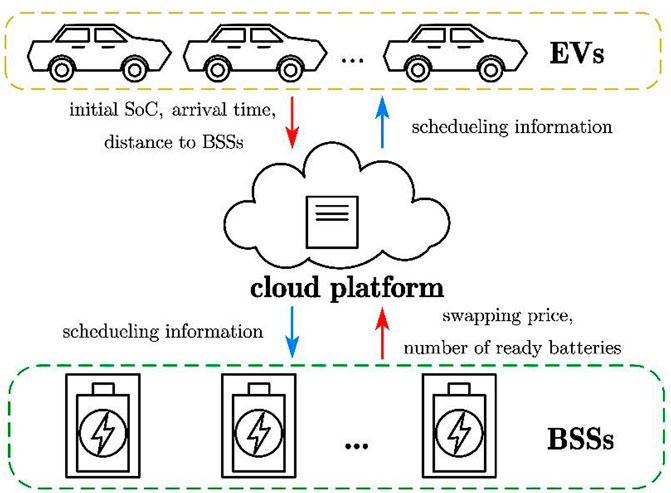
As illustrated in Figure 1, the battery-swapping system consists of EVs, a cloud platform, and BSSs. The cloud platform collects relevant information from BSSs and EVs, runs the scheduling algorithm, and then distributes the results to all EVs and BSSs.

Figure 1

Figure 1. Battery swapping system.

2.1 Operation constraints

This paper focuses on a single scheduling period (Ran et al., 2023; Guo et al., 2017). Let $\mathbb{I}=\left\{1,2,...,I\right\}$ denote the set of EVs requesting battery swapping indexed by i, and $\mathbb{K}=\left\{1,2,...,K\right\}$ represent the set of BSSs indexed by k. Let $\mathbb{T}=\left\{1,2,...,T\right\}$ denote the set of minutes (sufficient) to complete battery swapping actions, indexed by t, determined in this scheduling period. The number of minutes T should be sufficiently large to ensure that all vehicles can complete the battery-swapping process within the time interval from 0 to T. In the worst case, T can be calculated as the latest arrival time among all EVs, plus the product of the average swapping time and the number of EVs. The swapping system administrator can also set the value of T based on his/her experience. It is assumed that the total number of available batteries is greater than or equal to the number of EVs requesting swapping.

1) Decision variables: For each EV i, integer variables b_i and c_i represent the beginning time and completion time of the battery swapping process, respectively. Binary decision variables, u_i,k, represent the assignment relationship between EVs and BSSs: If EV i is assigned to BSS k for battery swapping, then u_i,k = 1; otherwise, u_i,k = 0. The assignment vector of EV i is represented as u_i = (u_i,1, u_i,2, … , u_i,k, … , u_i,K). To further capture the status of EV i at time t, binary decision variables, x_i,k,t, are used: If EV i is engaged in battery swapping at BSS k at time t, then x_i,k,t = 1; otherwise, x_i,k,t = 0. The swapping matrix of EV i is represented as $x_i={\left[x_{i,k,t}\right]}_{k\mathbb{\in }\mathbb{K},t\mathbb{\in }\mathbb{T}}$ In addition, the decision variables of EV i are summarized as ${\mathit{v}}_i=\left(b_i,c_i,{\mathit{u}}_i,{\mathit{x}}_i\right)$.

2) BSS selection constraints: Each EV i chooses one BSS for swapping, i.e.,

${\displaystyle \sum _{k\mathbb{\in }\mathbb{K}}}{u}_{i,k}=1,\hspace{1em}\forall i\mathbb{\in }\mathbb{I},(1)$

3) Travel distance constraints: The assigned BSS should be within the driving distance of the EV given its initial states of charge (SoC), i.e.,

$u_{i,k}{s}_{i,k}\le \gamma q_i,\forall i\mathbb{\in }\mathbb{I},\hspace{1em}\mathbb{\forall }k\mathbb{\in }\mathbb{K},(2)$

where $s_{i,k}$ denotes the distance between EV i and BSS k, $\gamma$ denotes the electric energy consumption per kilometer, and $q_i$ denotes the initial SoC of EV i.

4) Swapping process model: Inspired by the processing time model of the job shop scheduling problem (Yan et al., 2021), the swapping process is modeled as follows. The battery swapping time is roughly constant (typically about 5 min), and the average swapping time is denoted by $\lambda$. The swapping process is non-preemptive, meaning that the end time is equal to the start time plus the required swapping time (minus 1), i.e.,

$c_i=b_i+\lambda -1,\forall i\mathbb{\in }\mathbb{I},\hspace{1em}\mathbb{\forall }t\mathbb{\in }\mathbb{T},(3)$

$0\le b_i,c_i\le T,\hspace{1em}\forall i\mathbb{\in }\mathbb{I}.(4)$

If EV i is assigned to BSS k, the time interval [b_i, c_i] represents the duration when the swapping occurs. According to the definition of binary variables x_i,k,t, the following constraint should be satisfied:

$x_{i,k,t}=\left\{\begin{array}{l}1,\hspace{1em}\text{if\hspace{0.17em}}{b}_i\le t\le c_i\text{\hspace{0.17em}and\hspace{0.17em}}{u}_{i,k}=1,\\ 0,\hspace{1em}\text{otherwise}.\end{array}\right.(5)$

This logical relationship is linearized through the big-M method:

$t\ge b_i-M\left(1-{\displaystyle \sum _{k\mathbb{\in }\mathbb{K}}}{x}_{i,k,t}\right),\hspace{1em}\forall i\mathbb{\in }\mathbb{I},\mathbb{\forall }t\mathbb{\in }\mathbb{T},(6)$

$t\le c_i+M\left(1-{\displaystyle \sum _{k\mathbb{\in }\mathbb{K}}}{x}_{i,k,t}\right),\hspace{1em}\forall i\mathbb{\in }\mathbb{I},\mathbb{\forall }t\mathbb{\in }\mathbb{T},(7)$

${\displaystyle \sum _{t\mathbb{\in }\mathbb{T}}}{x}_{i,k,t}=u_{i,k}\lambda ,\forall i\mathbb{\in }\mathbb{I},\hspace{1em}\mathbb{\forall }k\mathbb{\in }\mathbb{K},(8)$

where M is a big number.

Based on the distance from EV i to BSS k, the corresponding arrival time can be calculated and is denoted by a_i,k. The start time for the battery swap should not be earlier than this arrival time, i.e.,

$b_i\ge {\displaystyle \sum _{k\mathbb{\in }\mathbb{K}}}{u}_{i,k}{a}_{i,k},\hspace{1em}\forall i\mathbb{\in }\mathbb{I}.(9)$

5) Capacity constraints: Each BSS k has a finite number of swapping grippers (typically 1 or 2), denoted by $n_k^G$, constraining the maximum number of swaps that can be conducted simultaneously at that BSS, i.e.,

${\displaystyle \sum _{i\mathbb{\in }\mathbb{I}}}{x}_{i,k,t}\le n_k^G,\hspace{1em}\forall k\mathbb{\in }\mathbb{K},\hspace{1em}\mathbb{\forall }t\mathbb{\in }\mathbb{T}.(10)$

Each BSS k, has a finite number of batteries available for swaps, denoted by $n_k^B$, representing the maximum number of swapping services that BSS can support for the scheduling period, i.e.,

${\displaystyle \sum _{i\mathbb{\in }\mathbb{I}}}{u}_{i,k}\le n_k^B,\hspace{1em}\forall k\mathbb{\in }\mathbb{K}.(11)$

2.2 Game model

It is assumed that each EV acts selfishly, aiming to minimize its own cost. It is evident from Equations 10, 11 that the BSS selection strategies of individual EVs are interdependent. Therefore, the cost for each EV is not only determined by its own decisions but also influenced by the decisions of others. To describe the strategic interactions among EVs, a non-cooperative game model is proposed to ensure fairness in BSS matching. This game Q is defined as follows:

$Q=\left\{\mathbb{I},{\left\{V_i\right\}}_{i\mathbb{\in }\mathbb{I}},{\left\{{\prod }_i\right\}}_{i\mathbb{\in }\mathbb{I}}\right\}(12)$

• Player set $\mathbb{I}$: The EVs that request for battery swapping.

• Strategy set $V_i$: The nonempty, compact, and discrete set of feasible decisions for each EV i.

• Cost function ${\prod }_i$: For each EV i, the cost is a weighted sum of the swapping start time and the battery swapping price.

${\prod }_i\left({\mathit{v}}_i,{\mathit{v}}_{-i}\right)=f_i=\alpha b_i+{\displaystyle \sum _{k\mathbb{\in }\mathbb{K}}}{p}_k{u}_{i,k}(13)$

where v_-i = (v ₁, … , v _i-1, v _i+1, … , v _I) is the strategies of all EVs except for that of i, $\alpha$ is a coefficient to convert time into cost, and p_k denotes the swapping price at BSS k. According to Equation 3, considering the swapping start time b_i in Equation 13 is equivalent to considering the swapping end time c_i. Moreover, the travel time (counted in the arrival time a_i,k) and waiting time for battery swapping are considered in b_i based on the swapping process model Equations 3–9.

Definition 1. Consider the game Q, a vector $\mathit{v}*=\left({\mathit{v}}_i*,{\mathit{v}}_{-i}*\right)\in V$ is called a generalized Nash equilibrium if no player can reduce its cost by unilaterally changing his decisions (Facchinei and Kanzow, 2010), i.e., ${\prod }_i\left({\mathit{v}}_i*,{\mathit{v}}_{-i}*\right)\le {\prod }_i\left({\mathit{v}}_i,{\mathit{v}}_{-i}*\right),\forall \left({\mathit{v}}_i,{\mathit{v}}_{-i}*\right)\in V$ holds for all $\forall i\mathbb{\in }\mathbb{I}$.

The existence of the Nash equilibrium in game Q is discussed in Theorem 1.

Theorem 1. For the battery swapping scheduling game $Q=\left\{\mathbb{I},{\left\{V_i\right\}}_{i\mathbb{\in }\mathbb{I}},{\left\{{\prod }_i\right\}}_{i\mathbb{\in }\mathbb{I}}\right\}$, the pure strategy Nash equilibrium always exists.

Similar to the proof of Theorem 1 in (Ran et al., 2023), Theorem 1 here can be proven based on Theorem 3.1 in (Tian 2015).

3 Solution methodology

To find the pure strategy Nash equilibrium, this section presents a best response algorithm that extends a Jacobi-type algorithm (Sagratella, 2016) to suit for the generalized Nash equilibrium game Q.

The difficulty is to preserve the satisfaction of constraints Equations 1–4 and Equations 6–11 during the iterative solution process, especially constraints Equations 10, 11 that couple different EVs. When updating the decisions of EV i, the original Jacobi-type method that fixes the strategies of all EVs except for EV i cannot be directly applied. To overcome this difficulty, our idea is that decisions of EVs arriving before i should still be kept unchanged, while those of EVs arriving after i should be adjusted properly.

Let ${\mathbb{J}}_i\mathbb{\subseteq }\mathbb{I}$ represent the set of EVs that arrived before it, when EV i is updating its decisions. Constraints Equation 10 become Equation 14,

${\displaystyle \sum _{j\in {\mathbb{J}}_i}}{x}_{j,k,t}+x_{i,k,t}\le n_k^G,\forall k\mathbb{\in }\mathbb{K},\mathbb{\forall }t\mathbb{\in }\mathbb{T},(14)$

where ${\displaystyle \sum _{j\in {\mathbb{J}}_i}}{x}_{j,k,t}$ is fixed as input data, while $x_{i,k,t}$ are decision variables.

Similarly, Equation 11 becomes Equation 15,

${\displaystyle \sum _{j\in {\mathbb{J}}_i}}{u}_{j,k}+u_{i,k}\le n_k^B,\hspace{1em}\forall k\mathbb{\in }\mathbb{K},(15)$

where ${\displaystyle \sum _{j\in {\mathbb{J}}_i}}{u}_{j,k}$ is fixed as input data, while $u_{i,k}$ are decision variables.

For EV i, its response at an iteration is obtained by solving problem P_i as follows:

$\left\{\begin{array}{l}\underset{u_{i,k},x_{i,k,t},b_i,c_i}{\min }{f}_i=\alpha b_i+{\displaystyle \sum _{k\mathbb{\in }\mathbb{K}}}{p}_k{u}_{i,k},\\ \begin{array}{l}s.t.\left(1\right)-\left(4\right),\left(6\right)-\left(9\right)\text{\hspace{0.17em}for\hspace{0.17em}}i,\\ \left(14\right),\left(15\right).\end{array}\end{array}\right.(16)$

EV i selects its target BSS by solving problem P_i (Equation 16) in order to minimize its cost iteratively in Algorithm 1. EVs that were originally scheduled to arrive after EV i may need to adjust their schedules to reflect shifts in their timings in line 7. If EV i was scheduled to BSS k₁ (in the previous iteration) and is updated to BSS k₂, EVs that would arrive at k₁ will be moved forward in time, while those that would arrive at k₂ will be moved backward. As illustrated in Figure 2, if EV 3 was originally scheduled to BSS k₁ in iteration m-1 and is then updated to BSS k₂ (in line 5) in iteration m, the schedules of EVs 4, 6 and 7 will be adjusted. EV 4 will be moved forward in the queue at BSS k₁, while EVs 6 and 7, will be moved backward in the queue at BSS k₂. The algorithm iterates until no EV deviates from its decisions, i.e., a Nash equilibrium has been found.

Figure 2

Figure 2. Illustration of EV schedule update in an iteration.

Algorithm 1.Extended Jacobi-type method.

Input: Initial SoC, distance to BSS, arrival time at the BSS, swapping price;

Output: Scheduling results v

1: choose a starting point ${\mathit{v}}^0\in V$ and set m: = 1, i: = 1;

2: while ${\mathit{v}}^m$ is not a solution of the Nash equilibrium do

3:  for $j\mathbb{\in }\mathbb{I}$ do

4:   set ${\mathit{v}}_j^m:={\mathit{v}}_j^{m-1}$;

5:  compute a best response ${\mathit{v}}_i^m\in V_i\left({\mathit{v}}_{-i}^m\right)$ by solving P_i (Equation 16);

6:  for $j\mathbb{\in }\mathbb{I}-\mathbb{J}-\left\{i\right\}$ do

7:   adjust ${\mathit{v}}_j^m$;

8:  end

9:  set $m:=m+1$, $i:=i+1$;

10:  if $i=I+1$

11:   $i:=1$

12:  end if

13: end

4 Case studies

The proposed battery-swapping scheduling approach is tested in two cases. In Case 1, a smaller size example is tested to demonstrate the fairness and reduced waiting time of our approach. In Case 2, a larger size example is tested to demonstrate the advantages of our approach on the swapping success rate and average cost compared with the shortest arrival time approach. Both cases demonstrate the computational efficiency of the proposed algorithm.

Testing is conducted on a system with an Intel Core i5-13500H CPU, 32 GB of RAM, using Python 3.11 in PyCharm and Gurobi 10.0.1.

4.1 Case 1

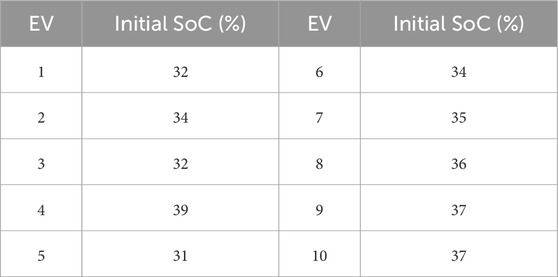
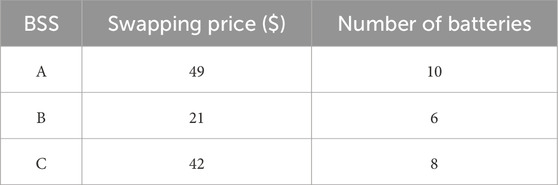
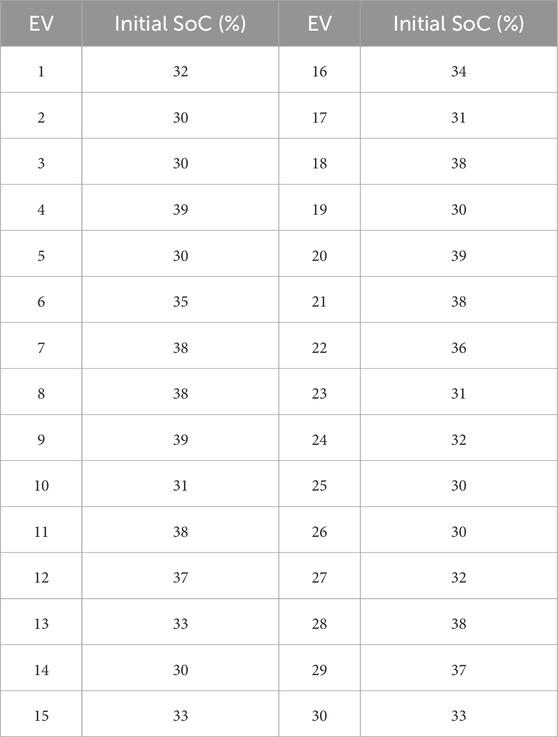
In this example, we consider an area with 3 BSSs and 10 EVs requesting battery swapping. Each EV’s location and initial SoC are generated randomly, with an average driving speed of 24 km/h. All batteries are of the same specification, allowing a battery-swapped EV to travel up to 230 km. The swapping prices and the number of batteries at each BSS are also generated randomly. Input data of EVs and BSSs are presented in Tables 1, 2, respectively. The number of minutes T is set to 70.

Table 1

Table 1. Initial SOCs of EVs in case 1.

Table 2

Table 2. Input data of BSSs in Case 1.

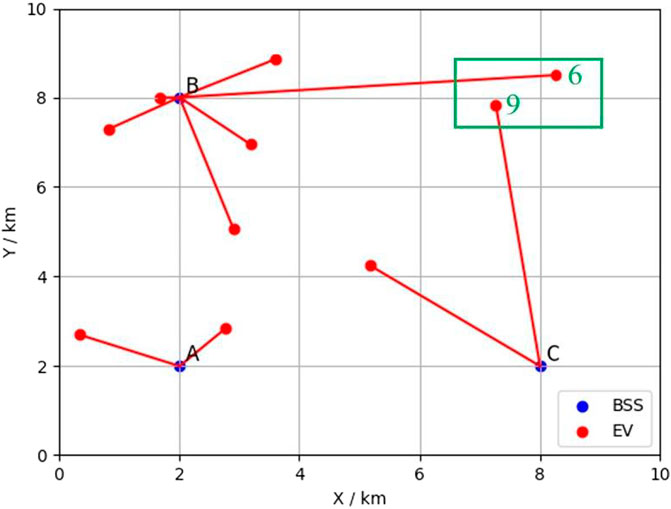
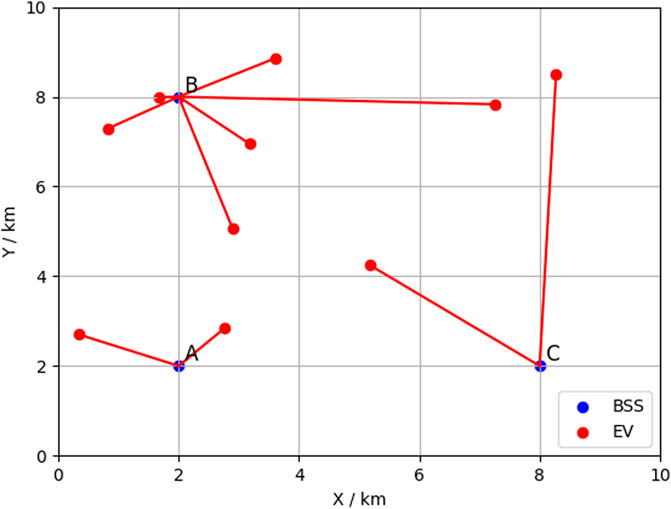
Figure 3 illustrates the results using a centralized optimization approach that minimizes the total cost of all EVs. In the scheduling results, two EVs highlighted in the green box have tendencies to change their target BSSs. EV 6 prefers to switch its target from BSS B to BSS C, reducing its cost from $54.4 to $49.8, and EV 9 prefers to switch from BSS C to BSS B, lowering its cost from $63.4 to $48.6. This indicates that the centralized optimization method lacks fairness.

Figure 3

Figure 3. Scheduling results of centralized optimization.

Figure 4 displays the results using the proposed non-cooperative game approach. The results compose a schedule where no EV can reduce its cost by unilaterally changing its decisions, i.e., a Nash equilibrium.

Figure 4

Figure 4. Scheduling results of our approach in Case 1.

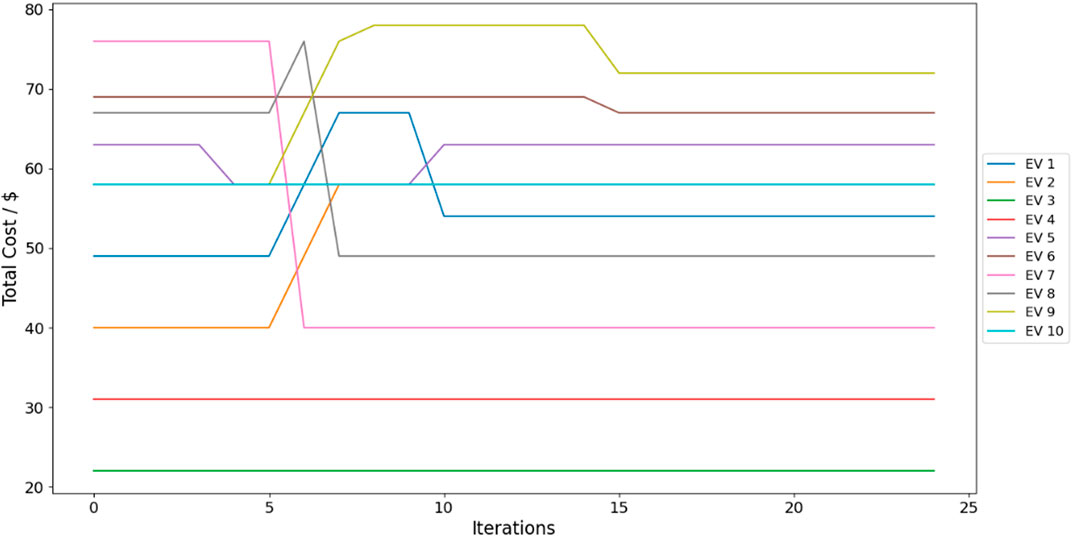
To demonstrate Algorithm 1’s performance, iteration results are illustrated in Figure 5. After 15 iterations, each EV’s cost becomes a stable value (and then examined in the last 9 iterations), confirming that the algorithm successfully converges to a pure strategy Nash equilibrium. The solution time of 24 iterations is 1.01 s.

Figure 5

Figure 5. Total costs of EVs over iterations in Case 1.

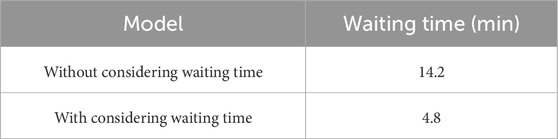
To demonstrate the benefits of our swapping process model, the following battery swapping waiting time is calculated from the scheduling results, according to Equation 17

$w_i=b_i-{\displaystyle \sum _{k\mathbb{\in }\mathbb{K}}}{a}_{i,k}{u}_{i,k}.(17)$

For comparison purposes, our non-cooperative game approach is also tested without considering the waiting time, i.e., the swapping process model is omitted and the swapping start time in Equation 13 is substituted by the arrival time. The average waiting times of all EVs with and without considering the waiting time are compared in Table 3. The results demonstrate that modeling the waiting time in the scheduling formulation can significantly reduce the average waiting time.

Table 3

Table 3. Comparison of average waiting times between two models.

4.2 Case 2

In Case 2, we increase the number of BSSs to 5 and the number of EVs to 30. Input data of EVs and BSSs are presented in Tables 4, 5, respectively. The number of minutes T is set to 100.

Table 4

Table 4. Initial SOCs of EVs in case 2.

Table 5

Table 5. Input data of BSSs in Case 2.

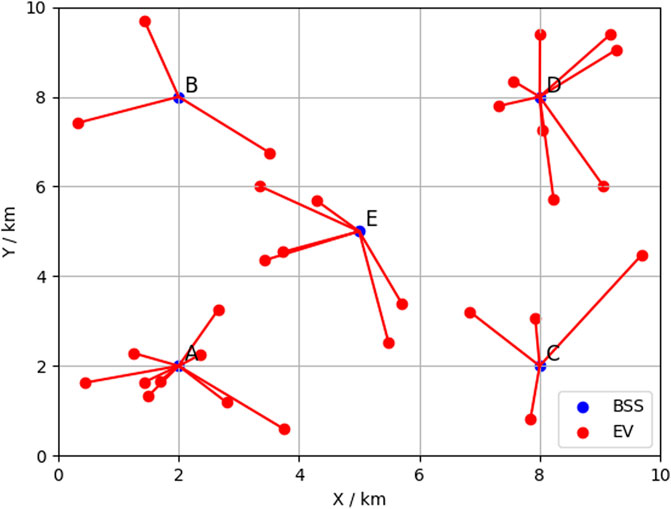
Figure 6 presents the scheduling results using the shortest arrival time approach. BSS A is assigned 9 EVs despite having only 7 batteries, and BSS D is assigned 8 EVs despite having only 6 batteries. Although each EV reaches the nearest BSS, 4 EVs failed to swap their batteries.

Figure 6

Figure 6. Scheduling results of shortest arrival time.

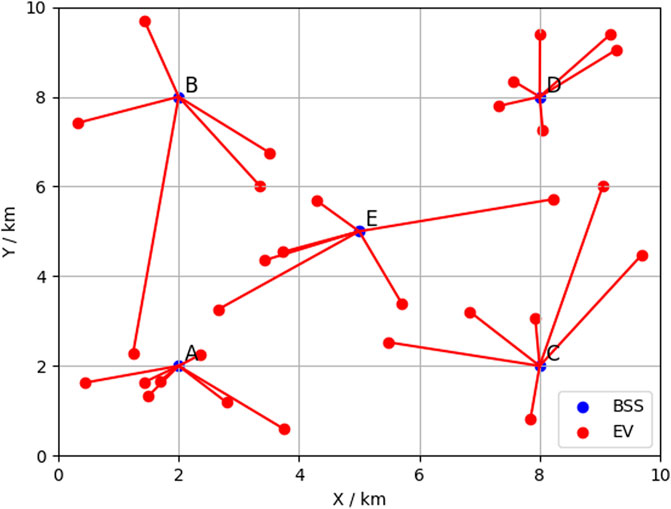
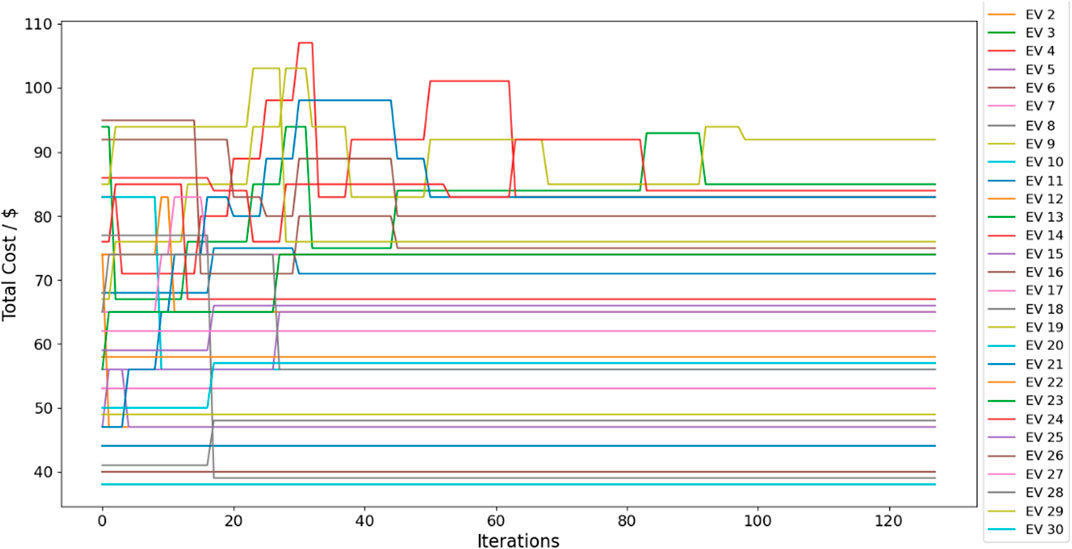
Figure 7 illustrates the scheduling results using our method. The iterative process of the algorithm is shown in Figure 8, where Algorithm 1 converges after 128 (= 99 + 29) iterations. The solution time is 8.24 s, demonstrating the computational efficiency of our method.

Figure 7

Figure 7. Scheduling results of our approach in Case 2.

Figure 8

Figure 8. Total costs of EVs over iterations in Case 2.

For better comparison, Table 6 summarizes the swapping success rates and average total costs using these two approaches. It appears that the swapping success rate of the shortest arrival approach is only 86.7%, while that of our approach is 100%. Furthermore, the average cost of all EVs is reduced from $81.7 using the shortest arrival time approach to $62.8 using our approach, by 23.1%. Note that for a convenient comparison of the average cost, the number of batteries in BSS A is increased to 9, and that in BSS D is increased to 8 to avoid EVs from unsuccessful battery swapping. These results demonstrate that the non-cooperative game approach increases the swapping success rate while reducing the average cost of EVs.

Table 6

Table 6. Comparison of results.

5 Conclusion

This paper proposes a non-cooperative game approach for the battery-swapping scheduling of EVs. A swapping process model inspired by the job-shop scheduling problem is proposed, and the cost function of each EV comprehensively considers the travel time, waiting time, and battery swapping price. A non-cooperative game model for battery swapping scheduling is established considering the finite quantities of batteries and swapping grippers. An iterative best response algorithm is developed satisfying constraints including those couple decisions of different EVs. Two cases are tested. In Case 1, a smaller size example is tested to demonstrate the fairness and reduced waiting time of our approach. In Case 2, a larger size example is tested to demonstrate the advantages of our approach on the swapping success rate and average cost compared with the shortest arrival time approach. Both cases demonstrate the computational efficiency of the proposed algorithm.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YZ: Writing–original draft. TH: Writing–original draft. WH: Writing–review and editing. JX: Writing–review and editing. LC: Writing–review and editing. ZM: Writing–review and editing. SL: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the research project of China Yangtze Power Co., Ltd., under Grant Z412302053.

Conflict of interest

Authors YZ, TH, and WH were employed by Three Gorges Electric Power Co., Ltd. Authors JX, LC, and ZM were employed by China Yangtze Power Co., Ltd.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from China Yangtze Power Co., Ltd. The funder had the following involvement in the study: study design, analysis of data, the writing of this article, and the decision to submit it for publication.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, X., and Leung, K. C. (2019). Non-cooperative and cooperative optimization of scheduling with vehicle-to-grid regulation services. IEEE Trans. Veh. Technol. 69 (1), 114–130. doi:10.1109/tvt.2019.2952712

CrossRef Full Text | Google Scholar

Cui, D., Wang, Z., Liu, P., Wang, S., Dorrell, D. G., Li, X., et al. (2023). Operation optimization approaches of electric vehicle battery swapping and charging station: a literature review. Energy 263, 126095. doi:10.1016/j.energy.2022.126095

CrossRef Full Text | Google Scholar

Facchinei, F., and Kanzow, C. (2010). Generalized Nash equilibrium problems. Ann. Operations Res. 175 (1), 177–211. doi:10.1007/s10479-009-0653-x

CrossRef Full Text | Google Scholar

Guo, T., You, P., and Yang, Z. (2017). Recommendation of geographic distributed charging stations for electric vehicles: a game theoretical approach. IEEE Power and Energy Soc. General Meet., 1–5. doi:10.1109/PESGM.2017.8274435

CrossRef Full Text | Google Scholar

Jie, W., Yang, J., Zhang, M., and Huang, Y. (2019). The two-echelon capacitated electric vehicle routing problem with battery swapping stations: formulation and efficient methodology. Eur. J. Operational Res. 272 (3), 879–904. doi:10.1016/j.ejor.2018.07.002

CrossRef Full Text | Google Scholar

Ko, H., Pack, S., and Leung, V. C. (2020). An optimal battery charging algorithm in electric vehicle-assisted battery swapping environments. IEEE Trans. Intelligent Transp. Syst. 23 (5), 3985–3994. doi:10.1109/tits.2020.3038274

CrossRef Full Text | Google Scholar

Kocer, M. C., Onen, A., Ustun, T. S., and Albayrak, S. (2022). Optimization of multiple battery swapping stations with mobile support for ancillary services. Front. Energy Res. 10, 945453. doi:10.3389/fenrg.2022.945453

CrossRef Full Text | Google Scholar

Liang, Y., and Zhang, X. (2018). Battery swap pricing and charging strategy for electric taxis in China. Energy 147, 561–577. doi:10.1016/j.energy.2018.01.082

CrossRef Full Text | Google Scholar

Ran, L., Wan, Y., Qin, J., Fu, W., Zhang, D., and Kang, Y. (2023). A game-based battery swapping station recommendation approach for electric vehicles. IEEE Trans. Intelligent Transp. Syst. 24 (9), 9849–9860. doi:10.1109/tits.2023.3269570

CrossRef Full Text | Google Scholar

Sagratella, S. (2016). Computing all solutions of Nash equilibrium problems with discrete strategy sets. SIAM J. Optim. 26 (4), 2190–2218. doi:10.1137/15m1052445

CrossRef Full Text | Google Scholar

Sarker, M. R., Pandžić, H., and Ortega-Vazquez, M. A. (2014). Optimal operation and services scheduling for an electric vehicle battery swapping station. IEEE Trans. power Syst. 30 (2), 901–910. doi:10.1109/tpwrs.2014.2331560

CrossRef Full Text | Google Scholar

Tian, G. (2015). On the existence of equilibria in games with arbitrary strategy spaces and preferences. J. Math. Econ. 60, 9–16. doi:10.1016/j.jmateco.2015.06.001

CrossRef Full Text | Google Scholar

Wan, Y., Qin, J., Li, F., Yu, X., and Kang, Y. (2020). Game theoretic-based distributed charging strategy for PEVs in a smart charging station. IEEE Trans. Smart Grid 12 (1), 538–547. doi:10.1109/tsg.2020.3020466

CrossRef Full Text | Google Scholar

Wang, S., Chen, A., Wang, P., and Zhuge, C. (2023). Short-term electric vehicle battery swapping demand prediction: deep learning methods. Transp. Res. Part D Transp. Environ. 119, 103746. doi:10.1016/j.trd.2023.103746

CrossRef Full Text | Google Scholar

Yan, B., Bragin, M. A., and Luh, P. B. (2021). An innovative formulation tightening approach for job-shop scheduling. IEEE Trans. Automation Sci. Eng. 19 (3), 2526–2539. doi:10.1109/tase.2021.3088047

CrossRef Full Text | Google Scholar

Yang, H., Xie, X., and Vasilakos, A. V. (2015). Noncooperative and cooperative optimization of electric vehicle charging under demand uncertainty: a robust Stackelberg game. IEEE Trans. Veh. Technol. 65 (3), 1043–1058. doi:10.1109/tvt.2015.2490280

CrossRef Full Text | Google Scholar

Yang, J., Liu, W., Ma, K., Yue, Z., Zhu, A., and Guo, S. (2023). An optimal battery allocation model for battery swapping station of electric vehicles. Energy 272, 127109. doi:10.1016/j.energy.2023.127109

CrossRef Full Text | Google Scholar

Yang, S., Yao, J., Kang, T., and Zhu, X. (2014). Dynamic operation model of the battery swapping station for EV (electric vehicle) in electricity market. Energy 65, 544–549. doi:10.1016/j.energy.2013.11.010

CrossRef Full Text | Google Scholar

Yang, Z., Guo, T., You, P., Hou, Y., and Qin, S. J. (2018). Distributed approach for temporal–spatial charging coordination of plug-in electric taxi fleet. IEEE Trans. Industrial Inf. 15 (6), 3185–3195. doi:10.1109/tii.2018.2879515

CrossRef Full Text | Google Scholar

Yong, J. Y., Tan, W. S., Khorasany, M., and Razzaghi, R. (2023). Electric vehicles destination charging: an overview of charging tariffs, business models and coordination strategies. Renew. Sustain. Energy Rev. 184, 113534. doi:10.1016/j.rser.2023.113534

CrossRef Full Text | Google Scholar

You, P., Low, S. H., Tushar, W., Geng, G., Yuen, C., Yang, Z., et al. (2017a). Scheduling of EV battery swapping—Part I: centralized solution. IEEE Trans. Control Netw. Syst. 5 (4), 1887–1897. doi:10.1109/tcns.2017.2773025

CrossRef Full Text | Google Scholar

You, P., Low, S. H., Zhang, L., Deng, R., Giannakis, G. B., Sun, Y., et al. (2017b). Scheduling of EV battery swapping–Part II: distributed solutions. IEEE Trans. Control Netw. Syst. 5 (4), 1920–1930. doi:10.1109/tcns.2017.2774012

CrossRef Full Text | Google Scholar

You, P., Pang, J. Z., and Low, S. H. (2020). Online station assignment for electric vehicle battery swapping. IEEE Trans. Intelligent Transp. Syst. 23 (4), 3256–3267. doi:10.1109/tits.2020.3033731

CrossRef Full Text | Google Scholar

Yu, Y., Chen, Y., Jiang, J., and Li, Y. (2024). Low-carbon scheduling of integrated hydrogen transport and energy system. Int. J. Hydrogen Energy 52, 655–666. doi:10.1016/j.ijhydene.2023.04.064

CrossRef Full Text | Google Scholar

Zeng, L., Chen, S. Z., Zhong, C., Xiong, T., and Tian, L. (2023). Hierarchical transactive power exchange method on expressways for EV energy supplement. Front. Energy Res. 11, 1213883. doi:10.3389/fenrg.2023.1213883

CrossRef Full Text | Google Scholar

Zhang, F., Lv, H., Xing, Q., and Ji, Y. (2024a). Deployment of battery-swapping stations: integrating travel chain simulation and multi-objective optimization for delivery electric micromobility vehicles. Energy 290, 130252. doi:10.1016/j.energy.2024.130252

CrossRef Full Text | Google Scholar

Zhang, G., Tan, S. T., and Wang, G. G. (2017). Real-time smart charging of electric vehicles for demand charge reduction at non-residential sites. IEEE Trans. Smart Grid 9 (5), 4027–4037. doi:10.1109/tsg.2016.2647620

CrossRef Full Text | Google Scholar

Zhang, T., Chen, X., Yu, Z., Zhu, X., and Shi, D. (2018). A Monte Carlo simulation approach to evaluate service capacities of EV charging and battery swapping stations. IEEE Trans. Industrial Inf. 14 (9), 3914–3923. doi:10.1109/tii.2018.2796498

CrossRef Full Text | Google Scholar

Zhang, Y., He, P., Ren, W., Jiao, J., Long, Z., and Jian, Y. (2024b). A customer satisfaction-based optimization model for the charging and discharging path and battery swapping stations’ site selection of electric vehicles. Front. Energy Res. 12, 1353268. doi:10.3389/fenrg.2024.1353268

CrossRef Full Text | Google Scholar

Zhao, Z., Lee, C. K., and Ren, J. (2024). A two-level charging scheduling method for public electric vehicle charging stations considering heterogeneous demand and nonlinear charging profile. Appl. Energy 355, 122278. doi:10.1016/j.apenergy.2023.122278

CrossRef Full Text | Google Scholar