
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 25 September 2024
Sec. Sustainable Energy Systems
Volume 12 - 2024 | https://doi.org/10.3389/fenrg.2024.1485135
This article is part of the Research Topic Advanced Data-Driven Uncertainty Optimization for Planning, Operation, and Analysis of Renewable Power Systems View all 16 articles
With the rapid development of 5G base station construction, significant energy storage is installed to ensure stable communication. However, these storage resources often remain idle, leading to inefficiency. To enhance the utilization of base station energy storage (BSES), this paper proposes a co-regulation method for distribution network (DN) voltage control, enabling BSES participation in grid interactions. In this paper, firstly, an energy consumption prediction model based on long and short-term memory neural network (LSTM) is established to accurately predict the daily load changes of base stations. Secondly, a BSES aggregation model is constructed by using the power feasible domain maximal inner approximation method and Minkowski summation to evaluate the charging and discharging potential and adjustable capacity of BSES clusters. Subsequently, a BSES demand assessment and optimal scheduling model for low voltage regulation in DN is developed. This model optimizes the charging and discharging strategies of BSES to alleviate low voltage problems in DN. Finally, the simulation results effectively verify the feasibility of the proposed optimal scheduling method of BSES for voltage regulation in DN.
In recent years, advancements in new energy technologies have progressed rapidly, and the proportion of new energy sources such as wind energy and solar energy has been increasing. The landscape of large-scale new energy consumption remains unclear, necessitating urgent adjustments in flexible resource allocation. As the best flexible resource, energy storage can control the input and output of power and energy at different time scales, thereby improving the stability and operation characteristics of high-proportion new energy power systems, promoting flexible dispatching of power grids, and solving the adverse effects of large-scale grid-connected clean energy. However, its widespread adoption is impeded by high costs. Meanwhile, China has clearly proposed to speed up the development of new infrastructure. Operators of 5G base stations have invested in constructing numerous communication facilities and configured extensive energy storage batteries to ensure the stability and reliability of communication. However, the growing strength and stability of the distribution system have significantly enhanced the energy supply reliability of 5G base stations, making the redundant 5G BSES devices idle for a long time. Therefore, considering the unique backup power supply requirements of energy storage resources at communication base stations, it is urgent to investigate the influence of the communication load characteristics on the backup power demand and deeply explore the schedulable potential of the backup energy storage. This will enable the efficient utilization of idle resources at 5G base stations in the collaborative interaction of the power system, fostering mutual benefit and win-win between the power grid and the communication operators.
The research on 5G base station load forecasting technology can provide base station operators with a reasonable arrangement of energy supply guidance, and realize the energy saving and emission reduction of 5G base stations. Currently, the research primarily focuses on statistical learning methods and machine learning techniques (Shang et al., 2022). In (Morosi et al., 2013), the exponential smoothing technique is used to predict the traffic in all coverage areas of the base station. In (Pan et al., 2015), a Block Regression (BR) model for base station traffic prediction considering the time correlation of base station load is proposed. Although the proposed model boasts low complexity and the mathematical formula is clear and easy to understand, it suffers from poor scalability as it constructs only a single model for all base stations. Moreover, the prediction results using these statistical learning models are not satisfactory when dealing with long-term problems, especially when predicting violently fluctuating base station network traffic data (Cheng et al., 2023). For the machine learning load forecasting model, a neural network load forecasting training method based on the maximum correntropy criterion (NTPMCC) is proposed in (Qu et al., 2013). This method takes into account the nonlinear characteristics of network load, but the overall improvement in prediction accuracy is moderate. Reference (Qu et al., 2019) introduces a base station load forecasting model that leverages spatio-temporal characteristics. To achieve this, a clustering algorithm based on artificial neural networks is employed to establish specific models for various types of base stations. Additionally, in reference (Stolojescu-Crisan, 2012), the Stationary Wavelet Transform (SWT) method is introduced during the data preprocessing stage. This method is combined with the Auto-Regressive Integrated Moving Average (ARIMA) model and Artificial Neural Networks (ANNs) to accomplish the load forecasting tasks. While the above-mentioned base station load forecasting method cannot shield the interference caused by the drastic fluctuation of 5G base station load data, which leads to a large static error in the prediction results, so there is an urgent need to study a more efficient and applicable base station load prediction method to effectively improve the base station load prediction accuracy.
Addressing the efficient utilization of flexible resources in 5G base stations, literature (Ye, 2021; Yin et al., 2022) proposes installing photovoltaic systems to enhance energy storage capabilities. However, for the existing 5G base stations that have been completed, the measure of reinstalling photovoltaic devices is difficult to implement. Several scholars have proposed a dynamic clustering method of energy storage utilizing virtual power plant technology to address the challenge that the energy storage of communication base stations with a large number and wide distribution is difficult to schedule (Suo et al., 2022; Yang et al., 2020). Nevertheless, the energy storage model is too simplified, and the spatial and temporal differences between BSES are ignored in order to improve the solution efficiency. Other studies have deeply explored the adjustable capacity of energy storage, and proposed energy storage resource aggregation optimization methods (Yang et al., 2023; Yu et al., 2023). Reference (Sajjad et al., 2016) pointed out that the idea of describing the feasible region of energy storage resource cluster operation can be divided into two kinds: top-down and bottom-up. Among them, top-down refers to the direct construction of the feasible region of cluster operation through data analysis and probabilistic modeling. From bottom to top, it refers to describing the feasible domain of a single resource first, and then aggregating multiple independent operating domains into a unified whole. Following a top-down approach, reference (Sajjad et al., 2016) estimates the flexibility level according to the probability of changing the collective behavior of aggregated users. Reference (Ma et al., 2013) developed a flexibility standard based on reinforcement learning methods to distinguish different load types, thereby assessing the total adjustment potential of resources. The current mainstream research tends to be bottom-up, considering the shortcomings of complexity, uncertainty, high computational cost and poor interpretability in constructing feasible regions directly through data analysis and probabilistic modeling. Following a bottom-up approach, reference (Müller et al., 2019) pointed out that the flexibility of each resource is mathematically regarded as a feasible region bounded by polytope, and the essence of the flexibility aggregation problem is the Minkowski sum of polytope provided by all flexible resources. However, the above method is not feasible in practical solution. As the dimension of the polyhedron increases, both the number of vertices and the permutations and combinations grow exponentially. This results in a phenomenon known as dimension explosion (Barot and Taylor, 2017; Althoff et al., 2010), significantly escalating the computational complexity of Minkowski summation. In (Müller et al., 2019), the zonotope set was proposed to aggregate distributed resource flexibility. The internal approximation method of the power feasible region ensures the feasibility of the model solution, but it also entails varying degrees of flexibility loss. The above research focuses on aggregating multiple flexible resources in the power system, but does not systematically investigate aggregation methods as backup resources for BSES. Therefore, it is necessary to thoroughly consider the characteristics of the standby power supply of the BSES resources, conduct in-depth research on its dynamic aggregation method, and quantitatively evaluate the power adjustment ability of the BSES cluster.
Research on 5G BSES in the power system focuses on integrating with the operation and dispatching of the DN (Li et al., 2022). The primary objective is to support the DN in integrating new energy consumption (Liang et al., 2023), peak shaving, valley filling (Yang et al., 2023), and optimizing economic dispatching (Chai et al., 2014). In (Jia et al., 2023), research focuses on mobile energy storage technology aimed at enhancing the consumption of distributed energy within station areas, which improves the consumption rate of new energy and ensures the stable and reliable operation of the DN in the station area. Reference (Zhang et al., 2023) proposed a model to optimize the energy storage configuration of 5G base stations. The objective is to alleviate the pressure of peak load on the power grid by minimizing the total investment over the battery system’s entire lifecycle. Reference (Han et al., 2021) proposed a Stackelberg game collaborative optimization method for DN and 5G mobile network based on demand response. The DN operator (DNO) acts as the leader, selecting an optimal interactive electricity price to reduce peak-valley differences in net load. The mobile network operator (MNO), as a follower, adjusts its energy costs by responding to the electricity price set by the DNO. In (Zhou and Xu, 2021), the mobile BSES system is used to provide local reactive power support. A day-ahead reactive power scheduling model is proposed, considering the system and the conventional reactive power compensation device, aimed at minimizing the node voltage deviation in the active DN. The above research works have established methods for BSES to participate in DN optimization and dispatch from different perspectives, but there is a lack of research related to making full use of BSES resources to participate in voltage regulation of DNs.
In summary, the existing research on 5G BSES lacks a BSES co-regulation method based on aggregation technology for voltage regulation of DNs. Therefore, in order to fill the above research gaps, this paper firstly proposes a BSES aggregation model taking into account the base station energy consumption prediction, and then proposes a BSES co-regulation method for the voltage regulation of base stations in distribution grids, which makes full use of the large amount of idle energy storage resources in 5G base stations and realizes the mutual benefits of telecommunication operators and power grids. The main contributions of this paper are as follows.
• The specific composition of 5G base station energy consumption is analysed, and a 5G base station energy consumption prediction model based on long short-term memory (LSTM) is constructed.
• Considering the power supply characteristics of BSES backup supply, we constructed a BSES aggregation model taking into account the energy consumption prediction of 5G base stations, and quantitatively evaluated the maximum adjustable capacity and charging/discharging potential of BSES.
• A BSES co-regulation method based on BSES aggregation technology for voltage regulation of DNs is proposed to quantitatively assess the minimum energy storage regulation capacity required for voltage regulation of DNs and optimize the charging and discharging strategy of each BSES based on the balanced charge state scheduling method of energy storage.
The rest of this paper is organized as follows: In Section 2, it proposes a method for predicting 5G base station energy consumption using LSTM and constructs a BSES aggregation model considering this prediction. In Section 3, it proposes a coordinated control method of BSES for low voltage governance of DN based on BSES aggregation technology. In Section 4, simulations are performed on a real distribution network test system. The conclusion is put forward in Section 5.
To meet the communication requirements of large capacity and low delay, the commissioning of new equipment has significantly improved the performance of 5G base stations compared with the previous generation base stations. At the same time, the new equipment has altered the power load characteristics of base stations. In the 5G technology framework, the 5G base station comprises macro and micro variants. The micro base station serves indoor blind spots with minimal power consumption. The macro base station exhibits greater potential for demand response. This section primarily analyzes the current mainstream commercial 5G macro base stations.
The load of a 5G base station primarily consists of communication equipment and auxiliary components. The communication equipment mainly includes Active Antenna Unit (AAU) and Base Band Unit (BBU). AAU is a combination of radio frequency unit and antenna array of 5G base station. Its main functions include converting baseband digital signal into analog signal, modulating it into high frequency radio frequency signal, and then amplifying it to enough power to be transmitted through the antenna. AAU is the most energy-consuming equipment in 5G base stations, accounting for up to 90% of their total energy consumption. Auxiliary equipment includes power supply equipment, monitoring and lighting equipment. The power supply equipment manages the distribution and conversion of electrical energy among equipment within the 5G base station. During main power failures, the energy storage device provides emergency power for the communication equipment.
A set of 5G base station main communication equipment is generally composed of a baseband BBU unit and multiple RF AAU units. Equation 1 serves as the base station load model:
where
The load change of base station mainly depends on the communication behavior of users, exhibiting significant time correlation and random fluctuations. As a special deep recurrent neural network, the LSTM network can basically smooth the interference caused by fluctuation to the training model, making it suitable for base station energy consumption prediction with large fluctuations in time series data.
The LSTM model is an advanced extension of the Recurrent Neural Network (RNN) model, specifically designed to handle sequence data. It addresses the long-term dependency problem, enabling it to better capture long-term dependencies in sequence data. This allows the model to effectively learn patterns and features in temporal data.
According to the energy consumption characteristics of the base station, a 5G base station energy consumption prediction model based on the LSTM network is constructed to provide data support for the subsequent BSES aggregation and collaborative scheduling. The prediction flow chart is shown in Figure 1, and the specific prediction process is as follows.
Step (1) The data is collected and preprocessed. After deleting the abnormal data, the data is normalized according to Equation 2. Then, the processed data set is divided into training set and test set according to a certain proportion.
where
Step (2) The LSTM model is created and the training set sample data is imported into the LSTM load forecasting model for training. The specific LSTM model principle can be referenced in (Fu, 2020).
Step (3) The test set sample data is imported into the trained model for 5G base station load forecasting, and compared with the actual 5G base station load to calculate the evaluation index of the model. The root mean square error
where
The feasible domain of a single BSES power can be described as:
where
To facilitate the derivation of the subsequent equations, Equation 7 can be written in the following compact form, as illustrated in Equation 8.
where
where
where
To reduce decision-making complexity at the distribution network operator level, BSES aggregators need to aggregate the operational feasible regions of all BSES units to form the operational feasible region of the BSES cluster. The aggregated operational feasible region represents the adjustable range of the flexible resources when all BSES units are simultaneously controlled. The mathematical essence of the feasible region aggregation problem is the Minkowski sum (M-Sum). The aggregation calculation process is as follows.
The expression for the aggregated power when the number of BSES units is N is presented in Equation 14.
The aggregated feasible domain
where
However, when the number of energy storage units in the base station is high, the number of sets and dimensions involved in the operation increases, and the planes describing the boundary of the feasible domain increase exponentially, which leads to the difficulty of the Minkowski summation and makes the solution of its aggregated power feasible domain non-computable. Therefore, in order to reduce the computational complexity, this paper adopts an aggregated power feasible domain maximal inner approximation method (Zhao et al., 2017), whose principle schematic is shown in Figure 2.
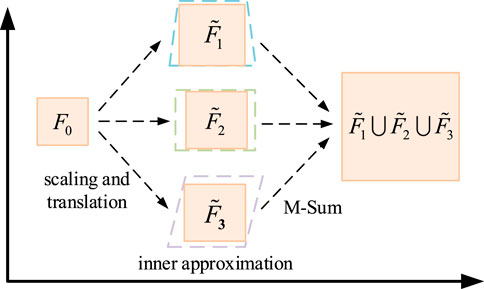
Figure 2. The principle of the maximum inner approximation method in the feasible domain of aggregation power.
The feasible region aggregation problem is characterized by large computational scale and strong temporal coupling. The exact feasible region of the aggregate is often difficult to compute and typically requires approximation of the feasible region for individual objects first. Initially, a basic power feasible region
where
The expression of
where
Equation 17 can be written in a compact form, as show in Equation 18:
where
where
where
Scaling and translation of
Let
By solving the above optimization problem, the parameters
where each boundary parameter is expressed as Equations 25-28:
where
This chapter aims to study 5G BSES participation in DN coordinated scheduling methods for optimal operation in low-voltage scenarios. It first establishes a DN model and introduces a quantitative assessment method for low-voltage regulation demand, which guides base station operators in coordinating with the DN. The chapter then proposes a cooperative scheduling method for BSES, optimizing its charging and discharging strategies to regulate DN voltage and improve grid safety and stability.
Since the DN is a radial structure, the DN topology containing N nodes is defined as
where if
For a radial DN, the following tidal equations are used to represent the branch-circuit tidal models (Li et al., 2019).
Equations 30, 31 represent the active and reactive power balance at node i, respectively, and Equation 32 represents the voltage link between two neighboring nodes, Where
Since the original branch-current models (30)–(32) are non-convex, the convex optimization solution method cannot be directly applied. To ensure the efficient solution of the problem, after approximating, and neglecting the higher terms of the equations, the linear branch-current model can be obtained as shown in Equations 33–35.
When the distribution network system experiences excessive load, certain nodes may encounter low voltage issues. These issues can be addressed by aggregators scheduling the charging and discharging actions of 5G BSES, effectively adjusting the flexible active load of the 5G base stations. From the perspective of the power grid, the aim is to resolve low voltage problems with minimal energy storage adjustment requirements. Therefore, the objective function is to minimize the energy storage adjustment demand F at each node of the base station over a day, as shown in Equation 36.
where T is 24 time periods in a day;
Equations 37-39 represent the linear power flow constraints of the line where
Equation 40 ensures the load active power balance of node i; Equation 41 ensures the load reactive power balance of node I, where
Equation 42 ensures that the node voltage of the DN does not exceed the limit. Where
where
Equations 45-47 indicates the operational constraints of AES where
Building on the BSES demand assessment model for low voltage regulation in distribution networks, the power adjustment demand for aggregated BSES at each network node has been calculated. However, the individual BSES output at each node remains unknown. To address this, an optimized scheduling model is proposed, which balances the state of charge and optimizes BSES charging and discharging strategies to mitigate low voltage issues in the distribution network.
Charging and discharging is carried out with the goal that the SOC of each base station’s energy storage state of charge is close to 0.5 after scheduling, to realize the fair distribution of power among each base station’s energy storage resources, as shown in Equation 48.
where N denotes the number of BSES inside the node; T denotes the BSES scheduling time period;
The sum of the node’s internal BSES energy should be balanced with the node’s AES energy value, as described in Equation 49.
Equation 50 illustrates the relationship between the energy stored in BSES j and its input power, Equation 51 shows the upper and lower bounds of energy stored in BSES j where
Equation 52 ensures the power balance of AES, Equation 53 enforces the lower and upper bounds to the power input of BSES j where
To validate the effectiveness of the proposed method, a simulation analysis was conducted using a 22-node distribution network in a specific region. The network topology is shown in Figure 3, and the line parameters are listed in Table 1. The nodes are uniformly distributed, with the maximum and minimum node voltages set at 1.05 p. u and 0.95 p. u, respectively. The typical daily load curve is depicted in Figure 4. In this region, the communication base stations are equipped with energy storage systems with a rated capacity of 48 kWh and a maximum charge/discharge power of 15.84 kW. The self-discharge efficiency is set at 0.99, and the state of charge (SOC) is allowed to range between a maximum of 0.9 and a minimum of 0.1.
The training and test datasets were imported into the LSTM-based load forecasting model for 5G base stations. The error convergence for the training and test datasets is shown in Figure 5, while the load forecasting for the test dataset samples is illustrated in Figure 6. The root mean square error (RMSE) for the test dataset samples was calculated to be 0.22 kW, with an average relative error of 0.06. As seen in Figure 5, the loss function value converges to a minimum after 24 training epochs. Figure 6 indicates that the model accurately reflects the load data trends over time, demonstrating good tracking performance. In summary, these results validate that the LSTM load forecasting model performs well in predicting the load data of 5G base stations.
The simulation results for the aggregated power feasible region of 10 BSES units are shown below. Figures 7, 8 illustrate the charging and discharging potential and the energy state boundaries of the aggregated 10 base stations over 24 time periods in a day. The adjustable capacity of the aggregated energy storage is influenced by factors such as individual BSES parameters and the load size of the base stations, resulting in temporal fluctuations. The charging and discharging potential is related to the charge/discharge power parameters of each storage unit. The minimum energy state of the aggregated storage is associated with the base station load size, while the maximum energy state is linked to the rated capacity parameters of each storage unit. Therefore, the proposed BSES aggregation model can quantitatively assess the charging and discharging potential and the adjustable capacity of the controllable BSES group, providing data support for the subsequent participation of BSES in coordinated scheduling with the distribution network.

Figure 7. Charging and discharging potential of aggregated energy storage for 10 base stations over 24 time periods.
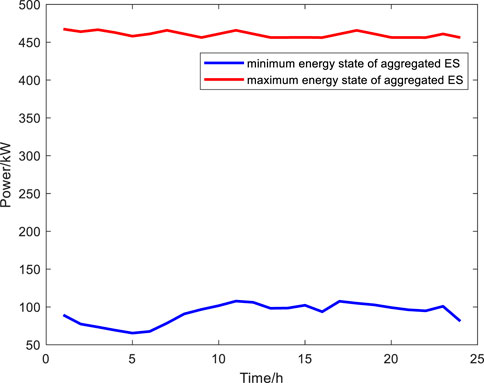
Figure 8. Energy state boundaries of aggregated energy storage for 10 base stations over 24 time periods.
Based on the distribution network branch power flow model presented in this paper and utilizing existing data, the voltage magnitudes at each node of the distribution network were calculated before the participation of BSES in the scheduling across multiple time scales. Figure 9 illustrates the voltage magnitudes at each node of the distribution network over 24 time periods before BSES participated in the scheduling. As shown in the figure, low voltage phenomena (voltage magnitude per unit value less than 0.95, indicated by the green sections) occur at certain times at the end nodes of the distribution network.
Using the BSES demand assessment model proposed in this paper, and combining it with existing data, the voltage magnitudes at each node of the distribution network and the energy storage adjustment requirements for low voltage mitigation were calculated after the participation of BSES in the scheduling across multiple time scales. Figure 10 shows the voltage magnitudes at each node of the distribution network over 24 time periods after the BSES participated in the scheduling. As depicted in the figure, the coordinated scheduling of BSES effectively improves the voltage magnitudes at the end nodes, achieving low voltage mitigation. The multi-time scale adjustment requirements of the aggregated BSES power for low voltage mitigation in the distribution network nodes are shown in Figure 11.
Based on the BSES optimization scheduling model proposed in this paper and utilizing existing data, the coordinated scheduling of BSES at each node was calculated. Taking node 22 as an example for the analysis of internal BSES coordination, Figure 12 illustrates the charging and discharging conditions of BSES at node 22 over 24 time periods. The figure shows that the model can achieve coordinated scheduling of BSES, optimizing the charging and discharging strategies of the energy storage units and effectively managing low voltage issues.
In this paper, a BSES aggregation method that takes into account both the base station energy consumption and the backup power characteristics of BSES is proposed. Furthermore, with the goal of fully utilizing the energy storage resources of 5G base stations, a BSES co-regulation method for voltage regulation in DNs is proposed. The feasibility of the proposed method is verified by case analysis, and the following conclusions can be drawn.
• The 5G base station energy consumption prediction model based on LSTM proposed in this paper takes into account the energy consumption characteristics of 5G base stations. The prediction results have high accuracy and provide data support for the subsequent research on BSES aggregation and optimal scheduling.
• The BSES aggregation model proposed in this paper, which considers the prediction of base station energy consumption, accurately and quantitatively evaluates the power adjustability and adjustable capacity of BSES clusters, and enables the centralized management and scheduling of massive BSES.
• The BSES optimization scheduling model constructed in this paper for voltage regulation of DNs further exploits the dispatchable potential of BSES to participate in DN synergy and interaction. It addresses the low-voltage problem of the DN and improves the security and stability of the grid while ensuring a sufficient and stable backup supply for 5G base stations.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
PS: Conceptualization, Data curation, Formal Analysis, Methodology, Validation, Writing–original draft. MZ: Supervision, Validation, Writing–review and editing. HL: Investigation, Methodology, Writing–original draft. YD: Investigation, Methodology, Writing–original draft. QR: Investigation, Methodology, Writing–original draft.
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Althoff, M., Stursberg, O., and Buss, M. (2010). Computing reachable sets of hybrid systems using a combination of zonotopes and polytopes. Nonlinear Anal. Hybrid. Syst. 4 (2), 233–249. doi:10.1016/j.nahs.2009.03.009
Barot, S., and Taylor, J. A. (2017). A concise, approximate representation of a collection of loads described by polytopes. Int. J. Electr. Power & Energy Syst. 84, 55–63. doi:10.1016/j.ijepes.2016.05.001
Chai, B., Chen, J., Yang, Z., and Zhang, Y. (2014). Demand response management with multiple utility companies: a two-level game approach. IEEE Trans. Smart Grid 5 (2), 722–731. doi:10.1109/tsg.2013.2295024
Cheng, J., Zhang, H., and Xu, J. (2023) “Traffic prediction model for telecommunication base stations based on improved WOA optimized LSTM and EMD,” in 2023 IEEE 5th international conference on power, intelligent computing and systems (ICPICS), 1075–1084.
Fu, L. (2020) “Time series-oriented load prediction using deep peephole LSTM,” in 2020 12th international conference on advanced computational intelligence (ICACI), 86–91.
Han, J., Liu, N., Huang, Y., and Zhou, Z. (2021). Collaborative optimization of distribution network and 5G mobile network with renewable energy sources in smart grid. Int. J. Electr. Power & Energy Syst. 130, 107027. doi:10.1016/j.ijepes.2021.107027
Jia, Z., Gao, H., Yang, Y., Liu, L., Li, Z., Liu, S., et al. (2023) “Research on mobile energy storage technology based on improving distributed energy consumption in substation area,” in 2023 IEEE 7th information technology and mechatronics engineering conference (ITOEC), 156–159.
Li, C., Wang, Y., Wang, R., Liu, H., Tao, X., Zhong, H., et al. (2022) “Load recovery strategy based on mobile energy storage flexibility and DN reconfiguration,” in 2022 IEEE 5th international electrical and energy conference (CIEEC), 2905–2910.
Li, J., Xu, Z., Zhao, J., and Zhang, C. (2019). Distributed online voltage control in active distribution networks considering PV curtailment. IEEE Trans. Industrial Inf. 15 (10), 5519–5530. doi:10.1109/tii.2019.2903888
Liang, H., Li, J., Deng, Y., Song, F., and Yu, X. (2023) “Optimization method for energy storage system planning based on dispatchable potential of 5G base station and cluster partition of DN,” in 2023 IEEE 6th international electrical and energy conference (CIEEC), 4334–4340.
Ma, J., Silva, V., Belhomme, R., Kirschen, D. S., and Ochoa, L. F. (2013). Evaluating and planning flexibility in sustainable power systems. IEEE Trans. Sustain. Energy 4 (1), 200–209. doi:10.1109/tste.2012.2212471
Morosi, S., Piunti, P., and Del Re, E. (2013) “A forecasting driven technique enabling power saving in LTE cellular networks,” in 2013 IEEE 9th international conference on wireless and mobile computing, networking and communications (WiMob), 217–222.
Müller, F. L., Szabó, J., Sundström, O., and Lygeros, J. (2019). Aggregation and disaggregation of energetic flexibility from distributed energy resources. IEEE Trans. Smart Grid 10 (2), 1205–1214. doi:10.1109/tsg.2017.2761439
Pan, H., Liu, J., Zhou, S., and Niu, Z. (2015). A block regression model for short-term mobile traffic forecasting. IEEE/CIC Int. Conf. Commun. China (ICCC), 1–5. doi:10.1109/iccchina.2015.7448619
Qu, H., Ma, W., Zhao, J., and Wang, T. (2013). Prediction method for network traffic based on Maximum Correntropy Criterion. China Commun. 10 (1), 134–145. doi:10.1109/cc.2013.6457536
Qu, H., Zhang, Y., and Zhao, J. (2019) “A spatio-temporal traffic forecasting model for base station in cellular network,” in 2019 IEEE 19th international conference on communication technology (ICCT), 567–571.
Sajjad, I. A., Chicco, G., and Napoli, R. (2016). Definitions of demand flexibility for aggregate residential loads. IEEE Trans. Smart Grid 7 (6), 2633–2643. doi:10.1109/tsg.2016.2522961
Shang, Y., Liu, J., Ma, J., Qiu, Y., Zhang, Z., and Liu, C. (2022) “A prediction method of 5G base station cell traffic based on improved transformer model,” in 2022 IEEE 4th international conference on civil aviation safety and information technology (ICCASIT), 40–45.
Stolojescu-Crisan, C. (2012) “Data mining based wireless network traffic forecasting,” in 2012 10th international symposium on electronics and telecommunications, 115–118.
Suo, S., Kuang, X., Cheng, R., Chen, L., Huang, K., and Zhao, W. (2022) “Research of real-time monitoring and control technology for distributed energy storage based on 5G,” in 2022 IEEE/IAS industrial and commercial power system asia (I&CPS asia), 1496–1500.
Yang, J., Lin, G., Lv, R., Gao, C., and Chen, T. (2020) “Research on construction and dispatching of virtual power plant based on reserve energy storage of communication base station,” in 2020 IEEE 4th conference on energy internet and energy system integration (EI2), 398–403.
Yang, L., Zhang, L., Yu, K., and Ma, X. (2023) “Research on interaction between power grid and 5G communication base station storage energy,” in 2023 8th asia conference on power and electrical engineering. IEEE: ACPEE, 592–596.
Ye, G. (2021) “Research on reducing energy consumption cost of 5G Base Station based on photovoltaic energy storage system,” in 2021 IEEE international conference on computer science, electronic information engineering and intelligent control technology (CEI), 480–484.
Yin, X., Lv, G., Wang, Z., Lu, Z., Liu, Y., and Yu, K. (2022) “Research on 5G BSES configuration taking photovoltaics into account,” in 2022 7th asia conference on power and electrical engineering (ACPEE), 591–595.
Yu, K., Yang, L., Zhang, L., and Ma, X. (2023) “Summary of research on key technologies of 5G base station flexible resources,” in 2023 8th asia conference on power and electrical engineering. IEEE: ACPEE, 2129–2133.
Zhang, L., Yu, K., Yang, L., and Ma, X. (2023) “A study on energy storage configuration of 5G communication base station participating in grid interaction,” in 2023 8th asia conference on power and electrical engineering. IEEE: ACPEE, 608–612.
Zhao, L., Zhang, W., Hao, H., and Kalsi, K. (2017). A geometric approach to aggregate flexibility modeling of thermostatically controlled loads. IEEE Trans. Power Syst. 32 (6), 4721–4731. doi:10.1109/tpwrs.2017.2674699
Keywords: 5G base station energy storage, aggregation, distribution network, voltage regulation, optimal scheduling
Citation: Sun P, Zhang M, Liu H, Dai Y and Rao Q (2024) Coordinated scheduling of 5G base station energy storage for voltage regulation in distribution networks. Front. Energy Res. 12:1485135. doi: 10.3389/fenrg.2024.1485135
Received: 23 August 2024; Accepted: 13 September 2024;
Published: 25 September 2024.
Edited by:
Minghao Wang, University of Macau, ChinaReviewed by:
Xu Xu, Xi’an Jiaotong-Liverpool University, ChinaCopyright © 2024 Sun, Zhang, Liu, Dai and Rao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mengwei Zhang, 2464152664@hnu.edu.cn
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.